Круг (фигура) — это… Что такое Круг (фигура)?

ФИГУРА — (лат. figura, от fingere лепить, ваять). 1) наружный вид предмета, внешнее очертание. 2) в геометрии: очерк плоскости, чертеж. 3) в картах: туз, король, дама, валет. 4) в риторике: украшение речи, оборот, употребляемый для красоты слога. 5) в… …   Словарь иностранных слов русского языка

КРУГ — один из наиболее распространённых элементов мифопоэтической символики гетерогенного происхождения и значения, но чаще всего выражающий идею единства, бесконечности и законченности, высшего совершенства. К. как фигура, образуемая правильной кривой …   Энциклопедия мифологии

Фигура (в геометрии) — Фигура  термин, формально применимый к произвольному множеству точек; тем не менее обычно фигурой называют множества на плоскости, которые ограничены конечным числом линий. Например: квадрат, круг, угол …   Википедия

КРУГ — КРУГ, плоская геометрическая фигура, являющаяся местом точек, расположенных на одинаковом расстоянии от некоторой точки (центра). Это расстояние называется радиусом круга (r). Площадь круга вычисляется по формуле pr2, а длина окружности равна 2pr …   Научно-технический энциклопедический словарь

Круг (значения) — В Викисловаре есть статья «круг» …   Википедия

КРУГ — первичный символ единства и бесконечности, знак абсолюта и совершенства. Как бесконечная линия, круг символизирует время в вечности, а как макро космический знак образует круг Зодиака. Он является древнейшим мистическим символом, традиционно… …   Символы, знаки, эмблемы. Энциклопедия

Фигура постоянной ширины — Треугольник Рело. Кривая постоянной ширины a плоская выпуклая кривая, длинa ортогональной проекции которой на любую прямую равна a. Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя… …   Википедия

круг — ▲ плоская фигура ↑ внутри, окружность круг область (плоская фигура), ограниченная окружностью. в радиусе каком …   Идеографический словарь русского языка

Фигура (геометрия) — У этого термина существуют и другие значения, см. Фигура. Фигура термин, формально применимый к произвольному множеству точек; тем не менее, обычно фигурой называют множества на плоскости, которые ограничены конечным числом линий. Примеры Квадрат …   Википедия

Фигура —         (от лат. figura внешние очертания, образ, изображение, способ, характер, свойство).         1) Характерная группа звуков (мелодич. Ф.) или ритмич. долей, длительностей (ритмич. Ф.), обычно неоднократно повторяющаяся.         2) Элемент… …   Музыкальная энциклопедия

dic.academic.ru

Круг — это… Круг — геометрическая фигура

Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас – атомы и молекулы – имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды – основы всего живого – тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо – птицы вьют его также в этой форме.

Данная фигура в древних помыслах культур

Круг – это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.

Издавна круг – это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в этой фигуре эквивалентны, линия круга не имеет ни начала, ни конца.

А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг – конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.

Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?

Что такое окружность

Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.

По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.

Что необходимо знать и чем уметь пользоваться, чтобы построить окружность

Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.

Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей. С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.

Какими величинами характеризуется окружность

Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим радиус окружности. Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.

Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.

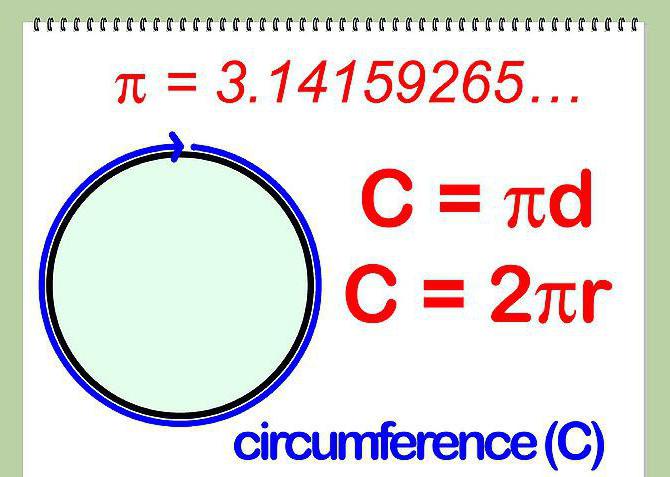
В этой формуле С – длина окружности, r – радиус окружности, d – диаметр, а число Пи – константа со значением 3,14.

Кстати, константа Пи была вычислена как раз из окружности.

Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.

В чем же главное отличие круга от окружности

По сути, окружность – это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее – это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.

Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг – это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.

Перейдем непосредственно к понятию круга

Круг – геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.

Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).

В данной формуле S – площадь, r – радиус круга. Число Пи – снова та же константа, равная 3,14.

Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.

Одна четвертая появляется из того, что радиус – это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:

r*r = 1/2*d*1/2*d;

r*r = 1/4*d*d.

Круг – это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.

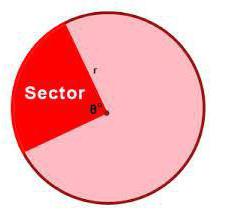
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.

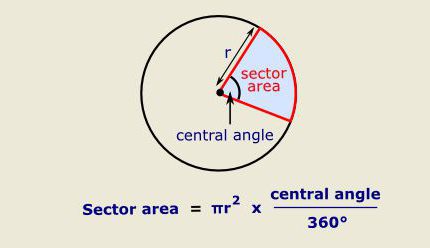
Использование фигуры в задачах с многоугольниками

Также круг – геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.

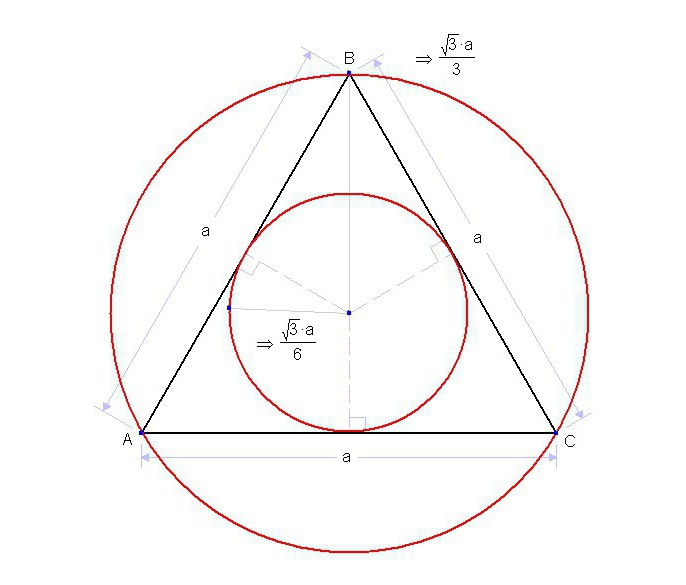
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.

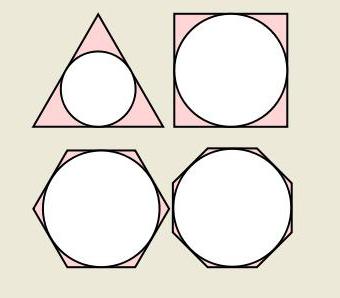
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.

Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).

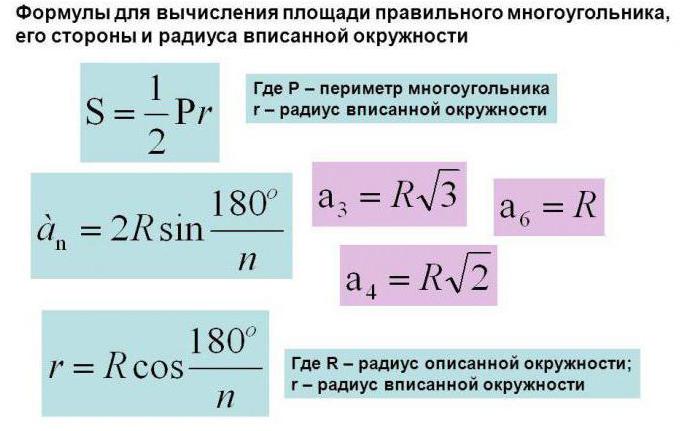
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью

Перед нами канализационный люк. Если он открыт, то железная каемка люка – это окружность. Если он закрыт, то крышка выступает в роли круга.

Окружностью также можно назвать любое кольцо – золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, – тоже окружность.

А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, –это круг.

Горлышко бутылки или банки при виде сверху – это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.

Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.

fb.ru

Окружность и круг — геометрия и искусство

В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.

В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет.

На рис. 2 изображены две окружности и цепочка окружностей, каждая из которых касается этих двух окружностей и двух соседей по цепочке.  Швейцарский геометр Якоб Штейнер около 150 лет назад доказал следующее утверждение: если при некотором выборе третьей окружности цепочка замкнется, то она замкнется и при любом другом выборе третьей окружности. Отсюда следует, что если однажды цепочка не замкнулась, то она не замкнется при любом выборе третьей окружности. Художнику, рисовавшему изображенную цепочку, пришлось бы немало потрудиться, чтобы она получилась, или обратиться к математику для расчета расположения двух первых окружностей, при котором цепочка замыкается.

Вначале мы упомянули о колесе, но еще до колеса люди использовали круглые бревна — катки для перевозки тяжестей.

А можно ли использовать катки не круглой, а какой-нибудь другой формы? Немецкий инженер Франц Рело обнаружил, что таким же свойством обладают катки, форма которых изображена на рис. 3. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.

Энц. «Я познаю мир. Математика», 2006

geometry-and-art.ru

Круг (геометрия) — Циклопедия

Круг Окружность и круг // Мрия Урок [12:19]

Круг — плоская геометрическая фигура, ограниченная окружностью. Иными словами, круг — это множество, состоящее из всех точек плоскости, расстояние от которых до данной точки (центр круга) не превышает заданного расстояния (радиуса). Окружность является границей круга.

Круг называется замкнутым или открытым в зависимости от того содержит ли он окружность, его ограничивающую. В декартовых координатах, открытый круг с центром [math](a, b)[/math] и радиусом R задаётся формулой:

[math]D=\{(x, y)\in {\mathbb R^2}: (x-a)^2+(y-b)^2 \lt R^2\}[/math]

Закрытый круг задается нестрогим неравенством

[math]\overline{ D }=\{(x, y)\in {\mathbb R^2}: (x-a)^2+(y-b)^2 \leqslant R^2\}.[/math]

Окружность является обобщением понятия круга на метрическом пространстве.

Иногда вместо термина круг используют термин диск.

Центр, радиус, хорда и диаметр круга являются центром, радиусом, хордой и диаметром соответствующего круга.

Площадью круга называется площадь плоской фигуры, ограниченной окружностью. Площадь круга вычисляется по формуле:

[math]S=\pi r^2 \ [/math], де [math] \pi \approx 3{,}141592654[/math] — число пи (математическая константа).

Периметром круга называют длину окружности, его ограничивающей:

[math]L=2\pi r .[/math]

cyclowiki.org

Круг. Круг — геометрическая фигура

Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас – атомы и молекулы – имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды – основы всего живого – тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо – птицы вьют его также в этой форме.

Данная фигура в древних помыслах культур

Круг – это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.

Издавна круг – это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в этой фигуре эквивалентны, линия круга не имеет ни начала, ни конца.

А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг – конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.

Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?

Что такое окружность

Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.

По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.

Что необходимо знать и чем уметь пользоваться, чтобы построить окружность

Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.

Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей. С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.

Какими величинами характеризуется окружность

Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим радиус окружности. Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.

Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.

В этой формуле С – длина окружности, r – радиус окружности, d – диаметр, а число Пи – константа со значением 3,14.

Кстати, константа Пи была вычислена как раз из окружности.

Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.

В чем же главное отличие круга от окружности

По сути, окружность – это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее – это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.

Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг – это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.

Перейдем непосредственно к понятию круга

Круг – геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.

Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).

В данной формуле S – площадь, r – радиус круга. Число Пи – снова та же константа, равная 3,14.

Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.

Одна четвертая появляется из того, что радиус – это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:

r*r = 1/2*d*1/2*d;

r*r = 1/ d*d.

Круг – это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.

Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.

Использование фигуры в задачах с многоугольниками

Также круг – геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.

Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.

Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.

Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).

Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью

Перед нами канализационный люк. Если он открыт, то железная каемка люка – это окружность. Если он закрыт, то крышка выступает в роли круга.

Окружностью также можно назвать любое кольцо – золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, – тоже окружность.

А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, –это круг.

Горлышко бутылки или банки при виде сверху – это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.

Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.

autogear.ru

Конспект проекта по математике :»Окружность и круг

МБОУ Большекрупецкая СОШ

Окружность и круг – это одна и та же

фигура или нет?

Проект выполнен Матвеевым Владиславом, учеником 5 класса

Учитель:Сергачева К.В.

Д. Большой Крупец

План

1. Введение

2. Основная часть

1).Из истории

2).Понятия круга и окружности и их элементов

3).Круг и окружность в природе, повседневной жизни и стихах

3. Заключение

4. Литература

Введение

Многие предметы вокруг нас имеют форму, похожую на геометрические фигуры. Чтобы разобраться, что такое окружность и чем она отличается от круга, необходимо иметь чёткое представление об этих фигурах.

Данная работа посвящена геометрическим фигурам — кругу и окружности. Выбор темы не случаен. Люди встречаются с кругом и окружностью в жизни практически на каждом шагу. Однако не все могут отличить окружность от круга. Проведённый мною опрос учащихся школы и некоторых взрослых показал: что различают эти фигуры только 50% опрошенных.

Задача данного проекта: систематизировать сведения о круге и окружности.

Презентация по теме будет в помощь и ученикам и учителям.

Из истории

Еще в древности людям были известны многие геометрические фигуры, в том числе окружность и круг. Об этом свидетельствуют археологические раскопки. Еще тогда приходилось решать задачи на вычисление длины окружности.

  Легенда гласит, что когда древнегреческий город Сиракузы, где жил в своё время Архимед, захватили римляне, учёный, занимаясь научными исследованиями, чертил окружности на песке. Солдату, который пришёл убить его, он воскликнул: “Убей меня, но не тронь моих кругов”.

В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении.

Но еще до колеса люди использовали круглые бревна — катки для перевозки тяжестей. Рисунки на стенах египетских пирамид рассказывают нам, что именно так доставлялись огромные камни на строительство этих пирамид.

Понятия круга и окружности и их элементов

Если поставить круглый стакан на лист бумаги и обвести его карандашом, получится линия, изображающая окружность. Если рассмотреть эту линию под микроскопом, то мы увидим толстую неровную черту. Геометрическая окружность не имеет ширины. Все её точки одинаково удалены от центра. Кольцо, обруч напоминают своей формой окружность. Окружность –самая простая кривая линия

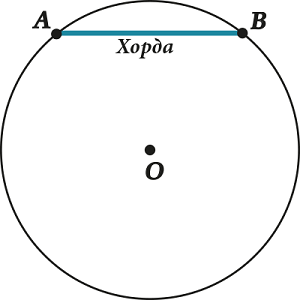
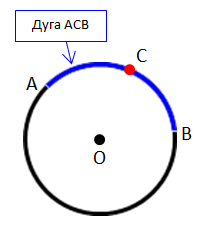
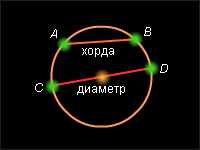
Рис 1. Рис.2 Рис.3

Окружностью называется фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки. Эта точка называется центром окружности и обычно обозначается О. (рис 1.,2.)

Что же такое круг? Круг мы можем вырезать из бумаги. Арена цирка, дно стакана или тарелка имеют форму круга. Если окружность это «черта» (мы можем ниточкой выложить окружность), то круг это все, что находится внутри окружности.

Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние – радиусом круга . Границей круга является окружность с теми же центром и радиусом.

Окружность и круг состоят из разнообразных частей.

Расстояние от точек окружности до её центра называется радиусом окружности и обычно обозначается R . Радиусом также называется любой отрезок, соединяющий точку окружности с её центром. Радиус – происходит от латинского слова «радиус» — «спица колеса».

Отрезок, соединяющий две точки окружности, называется хордой окружности, и хордой круга, ограниченного этой окружностью. ( Рис.1.,3) Хорда – греческое слово и переводится – «струна».

Хорда, проходящая через центр окружности или круга, называется диаметром окружности или круга. Диаметр делит круг на два полукруга, а окружность – на две полуокружности. (Рис 3.) Диаметр – «диаметрос» — тоже греческое слово, переводится – «поперечник».

Диаметр делится центром окружности пополам, и поэтому он равен двум радиусам. Два радиуса разбивают круг на секторы. Хорда разбивает круг на сегменты.

Круг и окружность в природе, повседневной жизни, в стихах

1.В природе

Одно из самых таинственных мест в Германии – Гозейский круг, памятник, сделанный из земли, гравия, и деревянных палисадов, который считается самым ранним примером примитивной “солнечной обсерватории.” Круг состоит из ряда круглых канав, окруженных стенами палисада (которые были с тех пор восстановлены). Считается, что памятник был построен приблизительно в 4900 году до н.э. Неолитическими народами.

Точная и качественная постройка памятника принудила много ученых полагать, что Круг был построен, чтобы служить некоторым примитивным солнечным или лунным календарем, но его точное использование — все еще источник дебатов. Согласно свидетельствам, так называемый “солнечный культ” был широко распространен в древней Европе. Это привело к предположению, что Круг использовался в некотором ритуале, возможно даже в приношении человеческой жертвы. Эта гипотеза должна все же быть доказана, но археологи извлекли несколько человеческих костей, включая безголовый скелет.

Световые явления в природе. Фотография ночного неба

В 1980-х годах в Англии было обнаружено около 500 колец

2. В повседневной жизни

Гончарный круг Спасательный круг Зодиакальный круг

Тротуарная плитка Вязание по кругу

Горный велосипед Часы

3.В стихах

Окружность

У круга есть одна подруга,

Знакома всем ее наружность!

Она идет по краю круга

И называется – окружность!

Круг    Э. Лиссауэр
   Я кругу говорил: Ты в странствии живешь
   И в поступи твоей есть сдержанная мощь;
   Твой путь весь состоит из путеобращений,
   Начало и конец в любом твоем движенье.

   А круг ответил мне: «Верь, жизни я не рад
   Мой путь — не путь вперед, а лишь всегда возврат.
   Есть в мире уголок один, где все мне мило,
   Его я обхожу: ступить туда — не в силах.»

Циркуль Н. Глазков
            Танцевальное вращение
            Совершеннейшей ноги,
            И круги, круги, круги,
            Вызывали восхищенье.
            Балерина создавала
            Точный круг в один момент,
            Подивился ей немало
            Достославный геометр.
            О прекрасной балерине
            Вспоминал частенько он —
            Не по этой ли причине
            Циркуль был изобретен?

*

Чтоб окружность начертить, 
Надо с циркулем дружить.
Закружит одной ногой
Циркуль твой – циркач лихой.

Часто видишь на дороге
Знак запрета очень строгий
Круг, заметив с «кирпичом” —
Помни, въезд здесь запрещён!

На дежурстве в центре вод
Лодка с надписью «ОСВОД”.
Знай, придёт на помощь круг, 
Он в беде надёжный друг.

Дождь пришёл на небе ярко
Засияло диво – арка.
Появился полукруг
Разноцветных радуг – дуг.

Лихо мчится птица-тройка.
Чудо дуги плещут бойко.
Кони быстрые летят,
Колокольчики звенят. (Э. Звоницкий.)

Загадка 1.

Эта форма у клубка,
У планеты, колобка,
Но сожми ее, дружок,
И получится … (кружок)

Загадка 2

Нет углов у меня,

И похож на блюдце я,

На тарелку и на крышку,

На кольцо, на колесо.

Кто же я такой, друзья? (Круг)

Загадка 3.

Если взял бы я окружность,
С двух сторон немного сжал,
Отвечайте дети дружно —
Получился бы …(овал)

Загадка 4.

Ноги очень интересны
У таинственного друга:
Если первая на месте,
То другая ходит кругом!
(циркуль)

Заключение

В 5 классе мы только начали изучать элементы геометрии. В средние века на мусульманском Востоке было распространено мнение, что геометрия очищает и совершенствует человеческий ум. Не может совершить ошибку человек, постоянно занимающийся геометрией. Эта мысль прививалась с самого раннего детства.

Данный проект завершен. Поле деятельности для дальнейшего изучения вопроса широко: задача о длине окружности, площади круга, возникновении числа 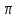(пи) , о непосредственном использовании этого на практике и многое другое. Думаю, что теперь большее количество из мною опрошенных смогут различить круг от окружности.

Литература

1.Математика 5 ,Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд, «Мнемозина», Москва 2012

2. © www.tutoronline.ru

3. gigart.ru

4. http://www.VeloMotoMagazin.ru/Velotovary/Velosipedy/Gornye/Dvuh

5. http://forum.meta.ua/topic/t/49934/asc/59595.html

6. Математика. 10-11 классы: рефераты. Сост. Видеман и др. – Волгоград: Учитель,2009

infourok.ru

Исследовательская работа «Круг в нашей жизни»

Введение.

Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор.

Вокруг нас много круглых предметов. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезло все круглое! Казалось бы – пусть все будет квадратным. Разве нельзя прожить без круглых труб, а к квадратным колесам нельзя привыкнуть? Можно ли вообще представить жизнь человека без использования круга? Почему так много тел имеют круглую форму? Чтобы найти ответы на все эти вопросы, в первую очередь, необходимо рассмотреть историю возникновения этих понятий и дальнейшее их развитие.

История возникновения и развития геометрических понятий “круг” и “окружность”.

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.

Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо. К сожалению, неизвестен непосредственный изобретатель колеса.

Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму. Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания.

Математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой. В Древней Греции все разрозненные знания привели в систему, геометрия стала бурно развиваться как наука. Только в Древней Греции “окружность” и “круг” получили свои названия, почти все названия геометрических фигур греческого происхождения, как и само слово геометрия (“гео” – земля, а “метрио” – мерить). Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.

В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”. В течение многих веков “Начала” были единственной учебной книгой, по которой молодежь изучала геометрию. И даже сейчас, в наше время, учебники написаны под большим влиянием “Начал” Евклида.

Окружность и круг – это плоские фигуры. Мы живем в мире трех измерений. А в какое геометрическое тело превратятся окружность и круг, если попадут в пространство? Это сфера и шар. “Сфера” – произошло от греческого слова “сфайра”, в переводе – “мяч”. Кроме этого геометрия пространства рассматривает и другие круглые тела – это “цилиндр” (от греческого слова “кюлиндрос”, что означает “валик”, “каток”) и “конус” (от греческого слова “конос”, означающего “сосновая шишка”). Самым важным среди круглых тел был шар.

Итак, в Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса (Приложение 5). (Приложение 2).

Круг – “циркулус” – латинское слово, от него же и “циркуль”, без которого бы мы не построили круг. Циркуль и линейка – самые старые чертежные инструменты на Земле. (Приложение 3.)

Элементы окружности и круга (Приложение 2):

Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой (по-латыни – спица колеса).

Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”).

Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого– “струна”).

Дуга окружности – это часть окружности, ограниченная двумя точками.

Часто в практических задачах нужно узнать длину окружности. А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок? Есть несколько способов измерения длины окружности (Приложение 1).

Однако эти способы непосредственного измерения длины окружности малоудобны и дают приближенные результаты. Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость: С:d ≈ 3,1.

Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, его стали обозначать греческой буквой π-οервая буква греческого слова “периферия” – круг.

С:d = π, где С – длина окружности, d – длина диаметра, отсюда и формула длины окружности C = πd или C = 2πr.

Изучив исследования ученых математиков, мы провели следующие измерения и вычисления:

1. Вычисление числа пи : а) с помощью тонкой нити измерили длину окружности С некоторых предметов быта; б) чтобы точнее найти длину диметра d, приложили этот предмет к листу бумаги и обвели карандашом, вырезали, свернули пополам, линия сгиба – это диаметр, измерили его с помощью линейки; в) нашли отношение С:d, данные занесли в таблицу:

Таблица 1.

Предметы	Длина окружности С	Диаметр d	Отношение С:d
Стакан	22 см	7 см	3.1428
Ведро	82 см	26 см	3.1538
Тарелка	62 см	19,5 см	3,1794
Кастрюля	69 см	22 см	3.1363
Бидон	52 см	16,5 см	3,1515

2. Границы значения числа пи: а) с помощью циркуля вписали круг в квадрат: если диаметр равен 1,то длина окружности равна π. Периметр квадрата со стороной 1 равен 4. Значит π меньше 4. (Приложение 6. Рис.1). б) в этот же круг вписали правильный шестиугольник: диаметр круга снова 1, длина окружности равна π. Сторона правильного шестиугольника равна радиусу, т.е.0,5,а периметр равен 6·0,5=3,значит π больше 3 (Приложение 6. Рис.2).

В результате мы убедились, что отношение длины окружности к ее диаметру (число π) есть число постоянное и 3 ‹ π ‹ 4 ,т.е. мы подтвердили исследования ученых – математиков.

Одна из загадок числа π состоит в том, что оно не может быть выражено какой – либо точной дробью. История числа π достойна восхищения, многие математики затратили на его вычисления не один десяток лет. Уточнялись нижняя и верхняя оценки числа и предпринимались неудачные попытки представить π в виде дроби и, таким образом, окончательно найти его значение (Приложение 4). Пока рекорд принадлежит японскому математику, в 2004 году – Ясума Канада из Токио рассчитал число π на компьютере до 1,24 триллиона знаков.

π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ….

Зачем нужно π, да еще с такой точностью? Число π чрезвычайно важно для ученых и инженеров. Все, что круглое и все, что движется по кругу (как колеса или планеты), содержит π. Без π люди не могли создать автомобили, понять движение планет или сосчитать сколько гороха поместится в консервную банку. Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, и, по-прежнему, волнует ученых. В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Все это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.

Изучив литературу и проделав собственные измерительные исследования с окружностью и кругом, мы пришли к следующим выводам: окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра. Это свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль, и почему колеса делают круглыми, а не квадратными или треугольными.

Круг в окружающей жизни.

Исследуя вопрос о роли круга в окружающей жизни, мы провели анкетирование обучающихся 5-9 классов и педагогов МО ШИСП (всего 90 человек):

1. Какие круглые тела вы встречаете в окружающей жизни?
2. Какое значение имеет круг в других науках?
3. Какие практические задачи повседневной жизни решаются, используя знания о круге и окружности?
4. Как вы считаете, почему встречается так много круглых тел в природе?

Ответы на первый вопрос представлены в презентации.

Из ответов учителей – предметников на второй вопрос анкеты мы поняли, что круг имеет большое значение не только в математике, но и в других науках:

Предмет	Использование
Физика и астрономия	Движение небесных тел происходит по круговым орбитам. Зодиакальный круг, астрономический круг. Круг с точкой в центре символизирует солнце.
География	Меридианы и параллели, определяющие положение тела на земном шаре, экватор. Круговые процессы-циклы: круговорот воды и веществ в природе. Смена времен года, смена дня и ночи.
Химия	Строение атома: ядро круглое, электроны вращаются вокруг ядра по круговым орбитам.
Биология	У всех клеток есть круглое ядро. Круглую форму имеют клетки крови, цилиндрическую – клетки многих желез. Стебли растений и стволы деревьев, кости человека – круглые. Кровообращение идет по кругу. Овощи и фрукты имеют шарообразную или конусовидную форму. Цикличность развития живых существ.
Русский язык	В русском языке слово “круглый” означает высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”. От слова круг образовано множество различных слов: круглый, кругленький, округлить, округлиться, округлый, кругом, вокруг, окружать, кружить и многое другое. Округлые формы, круглое лицо, кругленькие щеки, круглый год, голова идет кругом, ходить по кругу – часто употребляемые выражения.
История и обществознание	“Круглый стол” – конференции, кругооборот капитала, круг семьи , колесо истории, “большой и малый круг истории” – исторические циклы.

Проанализировав ответы на третий вопрос анкеты, мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сделать круглую крышу, окно или крышку, сшить головной убор, связать салфетку, сделать елочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.п.

Таким образом, круг в жизни человека имеет очень важную роль, и в жизни без круглых предметов обойтись невозможно.

Не все, кого мы анкетировали, смогли дать ответ на четвертый вопрос.

Здесь мы помещаем самые интересные и распространенные ответы:

• Только круглые предметы могут катиться, и поэтому их легче перемещать.
• Потому что, куда бы мы не пошли, мы возвращаемся, т.е. идем по кругу.
• У круга нет углов, и поэтому он удобен в применении, например, круглые монеты не могут порвать карман, о них не уколешься, не порежешься.
• Мячик не может быть квадратным, он не будет отпрыгивать.
• Посуду делали из глины, и округлую форму было легче придать, чем квадратную. Круглую посуду легче мыть, не надо выскребать из углов, в ней удобней размешивать.
• Легче изготовить круглое, чем угловатое. Многие технические процессы легче для тел вращения.
• На круглую форму идет меньше материала, чем на квадратную.
• Круглая крышка люка никогда не провалится, в отличие от квадратной.
• Все банки и крышки круглой формы, т.к. каждая точка окружности является точкой концентрации напряжения, и ее легко открыть, у прямоугольной формы такими точками являются только углы.
• Потому ,что солнце круглое, а без солнца мы не могли бы существовать.
• Круглая форма универсальна в природе.

Почему же на самом деле встречается так много круглых тел? Мы обратились к научным источникам. На этот вопрос можно ответить, рассмотрев мыльный пузырь, т.к. он идеально круглой формы. Силы поверхностного натяжения не дают лопнуть мыльному пузырю и стремятся придать мыльному пузырю максимально компактную форму. Самая компактная форма в природе – это шар. При шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.

В небе много круглых объектов: Солнце, Луна, планеты, звезды. Почему не быть хотя бы одной некруглой планете? Ну, пусть одна, будет кубическая или пирамидальная. Но это невозможно? Есть сила, которая во всей Вселенной превращает миры в гладкие шары. Эта сила – сила тяготения. Каждый предмет имеет свою гравитацию, притягивает к себе другие тела, а также и свои части. Чем больше тело, тем сила тяжести увеличивается. Земля наша огромная, поэтому она имеет свою большую силу тяжести, которая заставляет притягиваться все к ее центру, а тело преобразовываться в шар. Если бы в силу каких-то причин удалось изменить наш

urok.1sept.ru