Плоские геометрические фигуры

Плоские геометрические фигуры

Пономарев П.В. 1

---

1МБОУ «Школа № 91 с углубленным изучением отдельных предметов»

Калина О.В. 1

---

1ФГБОУ ВО «Нижегородский государственный архитектурно-строительный университет»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Геометрия – одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.

В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий – понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии – теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).

На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества [1]. Таким образом,

целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.

Объект исследования: Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.

Задачи исследования: Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.

Теоретическая и практическая значимость исследования состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.

Объем и структура исследования:

Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.

Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1.1. Основные геометрические фигуры в архитектуре зданий и сооружений

В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.

В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии – планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.

Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.

Самой простой геометрической фигурой является точка. Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.

Прямая— одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.

Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):

Прямые

Таблица 1

Параллельные прямые	Свойства параллельных прямых	Примеры в архитектуре зданий и сооружений
	Если прямые параллельны, то их одноименные проекции параллельны:	Ессентуки, здание грязелечебницы (фото автора)
Пересекающиеся прямые	Свойства пересекающихся прямых	Примеры в архитектуре зданий и сооружений
	Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи:	Здания «горы» на Тайване https://www.sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
Скрещивающиеся прямые	Свойства скрещивающихся прямых	Примеры в архитектуре зданий и сооружений
	Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. , ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях.	Робер, Гюбер – Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287

1.2. Плоские геометрические фигуры. Свойства и определения

Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.

Четырехугольники:

Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Признаки параллелограмма:

Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Параллелограмм, у которого все углы прямые, называется прямоугольником.

Параллелограмм, у которого все стороны равны, называется ромбом.

Трапеция— это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Треугольник — это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами

треугольника, а отрезки — сторонами треугольника. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.

Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:

	«Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения, лежат, на одной окружности». Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности.
Рис. 1.Окружность девяти точек

Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.

	Тем удивительнее было открытие, сделанное американским математиком Франком Морли. Он доказал, что если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника (1899).
Рис. 2.Открытие Франка Морли

Многоуго́льник — это геометрическая фигура, обычно определяемая как замкнутая ломаная.

Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.

Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.

Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.

Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР

2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.

Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».

Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» ( греч. — «буква»).

Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5, квадрат 6 и параллелограмм 7. Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.

Рис.3. Элементы игры «Танграм» и геометрические фигуры

Рис.4. Задания «Танграм»

Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.

Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.

Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).

Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.

Рис. 5. Приёмы разрезаний

На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.

Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части[1].

Рис.6.Примеры задач на разрезание:

—— — воссозданный квадрат; — разрез ножницами;

— основная фигура

2.2.Равновеликие и равносоставленные фигуры

Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.

	На рисунке 6 показано как разбить многоугольники на одинаковое число соответственно равных частей (равные части отмечены одинаковыми цифрами). Эти два многоугольника являются равносоставленными[2].
Рис.6. Равносоставленные многоугольники

Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.

Отсюда вытекает следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.

На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).

А Б

Рис.7. Преобразование «греческого креста»

В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).

На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет[1].

Рис.8. Паркет, собранный из греческого креста

Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).

	Зная формулу площади прямоугольника, находим, что площадь параллелограмма равна произведению длин его стороны и соответствующей высоты.
Рис.9. Равносоставленные параллелограмм и прямоугольник

Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.

	Еще одну интересную задачу на равносотавленный треугольник и параллелограмм, можно использовапть для вычисления площадей многоугольников, способ этот был известен еще Евклиду, который жил более 2000 лет назад.
Рис.10. Равносоставленные треугольник и параллелограмм

Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.

Отметим, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены.

Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.

Заключение

В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.

Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.

В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».

Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.

Библиографический список

1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. – Нижний Новгород: Изд-во НГТУ, 2002. – 73 с.

2. Энциклопедический словарь юного математика /Сост. А.П. Савин. – М.: Педагогика, 1985. – 352 с.

3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane

4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053

Приложение 1

Анкета-опросник для одноклассников

1. Знаете ли вы, что такое головоломка «Танграм»?

2. Что такое «греческий крест»?

3. Было бы вам интересно узнать, что такое «Танграм»?

4. Было бы вам интересно узнать, что такое «греческий крест»?

Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.

Приложение 2

Элементы игры «Танграм» и геометрические фигуры

Преобразование «греческого креста»

Просмотров работы: 3100

school-science.ru

Геометрические фигуры плоские и объёмные

Цели урока:

• Познавательная: создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
• Коммуникативная: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного  отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
• Регулятивная: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых  операций, корректировать свою деятельность.
• Личностная: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.

Планируемые результаты:

личностные:

• формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
  самостоятельность в приобретении новых знаний и практических умений;
• формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.

метапредметные:

• овладение навыками самостоятельного приобретения новых знаний;
• организация учебной деятельности, планирования;
• развитие теоретического мышления на основе формирования умений устанавливать факты.

предметные:

• усвоить  понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.

УУД общенаучные:

• поиск и выделение необходимой информации;
• применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.

УУД личностные:

• оценивать свои и чужие поступки;
• проявление доверия, внимательности, доброжелательности;
• умение  работать в паре;
• выражать  положительное отношение к процессу познания.

Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи,  Толковый  словарь.

Тип урока: изучение нового материала.

Методы:  словесные, исследовательские, наглядные, практические.

Формы работы:  фронтальная, групповая, парная, индивидуальная.

1. Организация начала урока.

Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!

2. Актуализация знаний.

Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!

Чтобы дойти до цели, надо прежде всего идти.

Перед вами высказывание, прочитайте. Что означает это высказывание?

(Чтобы чего-то добиться, нужно что-то делать)

— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.

— Начнем наш путь к достижению цели сегодняшнего урока.

3.  Подготовительная работа.

— Посмотрите на экран. Что вы видите? (Геометрические фигуры)

Назовите эти фигуры.

— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)

— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.

— По какому признаку вы разделили эти фигуры?

• Плоские и объемные фигуры
• По основаниям объемных фигур

— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?

—  Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)

—  Чему мы должны научиться на уроке?

4. «Открытие» нового знания в практической  исследовательской работе.

(Учитель показывает куб и квадрат.)

—  Чем они похожи?

—  Можно ли сказать, что это одно и тоже?

—  Чем же отличается куб от квадрата?

—  Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)

—  Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?

! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)

—  Можно ли куб полностью (весь) прижать к парте? Проверим.

—  Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?

! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)

ВЫВОДЫ:  Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)

ПЛОСКИЕ

• Можно целиком расположить на одной плоской поверхности.
  

ОБЪЁМНЫЕ

• занимают определённое пространство,
• возвышаются над плоской поверхностью.
  

Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.

4. Открытие новых знаний.

1. Назовите фигуры, изображенные на рисунке.

— Какую форму имеют основания этих фигур?

— Какие еще формы можно увидеть на поверхности куба и призмы?

2. Фигуры и линии на поверхности объемных фигур имеют свои названия.

 

 

— Предложите свои названия.

— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.

— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.

Работа с тетрадями: чтение нового материала

Соотнесение реальных объектов и объёмных тел.

— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.

+ Коробка – параллелепипед.

• Яблоко – шар.
• Пирамидка – пирамида.
• Банка – цилиндр.
• Горшок из-под цветка — конус.
• Колпачок – конус.
• Ваза – цилиндр.
• Мяч – шар.

5. Физминутка.

1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.

(Ученики «обхватывают» руками и гладят воображаемый шар.)

А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.

Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками  по боковой  поверхности.

Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!

6. Групповая работа:

(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1.  (Для изучения параллелепипеда)

Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .

Группа 2.  (Для изучения пирамиды)

Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .

Группа 3.  (Для изучения куба)

Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .

Далее каждая группа выступает, представляя свою объемную фигуру другим.

7. Решение кроссворда

8. Итог урока. Рефлексия деятельности.

Решение кроссворда в презентации

— Что нового вы для себя сегодня открыли?

+ Все геометрические фигуры можно разделить на объёмные и плоские.

+ А я узнал названия объёмных фигур

urok.1sept.ru

Проект по математике на тему » В мире плоских и объемных фигур»

IV Всероссийская (с международным участием)

научная конференция учащихся им. Н.И. Лобачевского

Секция «Математика»

Исследовательская работа

В МИРЕ ПЛОСКИХ И ОБЪЕМНЫХ ФИГУР

Люлин Никита, 4 класс

Направляющая организация:

МБОУ « Большеполянская оош » Алексеевского муниципального района Республики Татарстан

Научные руководители: учитель математики Люлина М.А

Казань 2019

Каждый человек на Земле замечал как много разных геометрических фигур. Люди давно заинтересовались их разнообразием, строением и свойствами. Мне тоже стало интересно происхождение геометрических фигур: почему фигуры получили такие названия, где и когда они впервые появились. А самое интересное то, что окружающие нас предметы, похожи на геометрические фигуры.

В связи с этим целью данной работы стало изучение объемных и плоских геометрических фигур. Для достижения данной цели были поставлены следующие задачи:

• • • Познакомиться с одним из разделов математики — геометрией.

    • Выделить основные геометрические фигуры.

    • Выяснить происхождение геометрических фигур.

    • Изучить сведения о плоских фигурах и объемных.

    • Провести наблюдение окружающих нас природных объектов и сопоставить их с геометрическими формами.

Геометрия – это один из разделов математики. Как систематическая наука она появилась в Древней Греции, ее аксиоматические начала построения описаны в «Началах» Евклида. В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и так далее. Если взять во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.

Все фигуры подразделяются на плоские и объёмные. Плоскостные — это фигуры, которые изображают на плоскости. Плоскость это например: лист бумаги, доска, стена, парта и.т.д. Примерами плоских фигур являются: точка, круг, ромб и т.д. Объёмные фигуры – это фигуры, внутри которых есть объём (пространство). У них есть грани. Гранями объёмных фигур могут быть плоскостные фигуры. В объёмную фигуру можно поместить какой-то предмет (голову, ручку).

Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.

Появление и развитие знаний связано с повседневной деятельностью людей. Геометрических фигур очень много. В древности у фигур никаких имён не было. Люди нашли гениальный выход: они стали называть фигуры словами, обозначавшими предметы похожей формы. К примеру, название конуса произошло от греческого «conos», что значит сосновая шишка. Действительно, конус похож на шишку, рисунок 1.

Рисунок 1 – Конус и шишка

Рассмотрим такую фигуру, как треугольник. Треугольник представляет собой важнейшую фигуру в геометрии. Это многоугольник, который имеет три стороны и три вершины. Крыша дома имеет треугольную форму, но этот треугольник повторяется со всех четырёх сторон. А это уже объёмная геометрическая фигура, которая называется пирамидой. Она имеет такую форму, чтобы дождь и снег не задерживались на ней.

Теперь рассмотрим геометрическую фигуру под названием «круг». Круг — это геометрическая фигура, ограниченная окружностью. Окружность – это граница круга. Для чего же в нашей жизни были внедрены предметы округлой формы? Круглые тела еще в древности заинтересовали человека. В Древнем Египете для постройки пирамид. Огромные каменные глыбы требовали постоянной переноски, так египтяне заметили, что ставя тележку на тонкие круглые пластинки, которые они вырезали из стволов деревьев, перетаскивать грузы стало намного проще.

Квадрат — это прямоугольник, у которого все стороны ровны. Казалось бы, квадрат — одна из самых простых геометрических фигур. Но на самом деле она имеет множество до сих пор не разгаданных тайн. В древнем мире квадрат символизировал четыре стороны света. Египтяне в свою очередь обожествляли квадрат.

Все предметы в нашем доме напоминают различные геометрические фигуры. Рассмотрим и опишем некоторые из них.

Заглянем на кухню. Холодильник, микроволновая печь, газовая плита, кухонный шкаф, стиральная машина имеют форму прямоугольного параллелепипеда. У параллелепипеда все противолежащие грани — прямоугольники. Таких прямоугольников всего 6, кроме того 12 ребер, 8 вершин, есть три измерения – длина, ширина, высота. Еще можно эти предметы назвать прямыми призмами, у них все углы между гранями прямые.

А чайник похож на усеченный конус. Дно чайника круг, а крышку откроем, увидим еще одну окружность только меньшего размера.

Кастрюли цилиндрической формы. И действительно, у них имеется два круга, лежащие в параллельных плоскостях и стенка, которую можно представить как множество отрезков, соединяющих соответствующие точки на этих кругах.

Тарелки напоминают круг, край тарелки — окружность. Крышка стола прямоугольник, я попробовал измерить углы они прямые.

Давайте заглянем вовнутрь холодильника и что же мы видим, и здесь без геометрии не обошлось. На полках стоят «цилиндры» — банка сгущенки, банка молока, консервы.

Прогуляемся по спальне. Шкаф, кровать, трельяж, стол – прямоугольные параллелепипеды. Ковер на полу прямоугольной формы. Горшки с цветами на подоконниках цилиндрической формы.

Толстая книга похожа на параллелепипед. Двери имеют форму прямоугольников. Стены, потолок, окна так же напоминают прямоугольники.

Если мы выйдем на улицу, то видим постройки, дома различной геометрической формы. Например дом, баня имеют форму параллелепипеда. Крыши дома – углы. Столб, бочка для воды имеют форму цилиндра. Фонарные столбы вдоль дороги напоминают отрезки прямой. А провода можно представить, как параллельные прямые.

В огороде можно тоже встретить геометрию. Грядки как напоказ вычерчены прямоугольники. Морковка уродилась цилиндрической формы. Капуста, тыква, арбуз – шар.

Геометрия в космосе.

Поиск геометрических фигур в предметах, которые нас окружают, был бы не полным, если бы мы не обратились к космическим объектам и не определили, форму каких фигур они имеют. Планеты имеют шарообразную форму. Доказано, что все планеты солнечной системы своей формой напоминают шар. Звёзды, так же являясь космическими объектами, как и планеты, имеют форму шара.

В своей работе я исследовал, какие геометрические фигуры и тела окружают нас, и убедился, насколько много разных геометрических форм и поверхностей использует человек в своей жизни при строительстве различных сооружений и просто в повседневной жизни.

Понял, что проявляют люди свой интерес к геометрическим фигурам не просто из-за любви к их форме, а потому что свойства этих фигур позволяют с наибольшей простотой решать сложные задачи.

Хочу сделать акцент на то, что самым интересным для меня в работе было осознать насколько раньше я не задумывался о геометрии окружающего нас мира. Теперь я не просто смотрю на предметы, а пытаюсь логически объяснить выбор формы.

Таким образом, можно сделать вывод, что геометрические фигуры играют очень важную роль в жизни человека, а знания их свойств может существенно её облегчить.

1. Депман И. /За страницами учебника математики/ И.Я. Депман, Н.Я. Виленкин /Просвещене – 1989 г.

2. Дорохов А. /Что такое? Кто такой?/ А.А. Дорохов, М.М. Михайлов, Г.М. Куценко, А.А. Назаров / Дрофа – 2005 г.

3. Звонкина А. /Малыши и математика/ А.К. Звонкина/ Москва – 2007

4. Лонг Л. /Отличная геометрия/ Линетт Лонг/ Попурри — 2014

5. Перельман Я. /Занимательная геометрия/ Я.И. Перельман/ Москва – 1950

6. Википедия [Электронный ресурс]. – URL: https://ru.wikipedia.org

infourok.ru

Пространственные и плоскостные фигуры. Действия с многозначными числами

Цель: формирование представлений о пространственных и плоскостных фигурах и совершенствование вычислительных навыков через практическую исследовательскую деятельность.

Планируемые результаты образования.

Предметные:

• умеют различать пространственные и плоскостные фигуры, приводить примеры каждого вида;
• выполняют устные и письменные вычисления с многозначными числами;
• владеют компьютерным письмом, создают текстовые сообщения, оформляют и сохраняют их.

Метапредметные:

Регулятивные:

• планирование – определение промежуточных целей для достижения планируемого результата;
• саморегуляция как способность к мобилизации сил и энергии.

Коммуникативные:

• участвуют в диалоге, слушают и понимают других, высказывают свою точку зрения на события и поступки;
• отстаивают свою точку зрения, соблюдая правила речевого этикета, аргументируют свою точку зрения с помощью фактов;
• сотрудничать в совместном решении проблемы.

Познавательные:

• ориентируются в учебнике: определяют умения, которые будут сформированы на основе изучения данной темы;
• самостоятельно предполагают, какая дополнительная информация будет нужна для изучения незнакомого материала, отбирают необходимые источники информации среди предложенных;
• анализируют, сравнивают, группируют;
• делают выводы, перерабатывают информацию, преобразовывают её.

Личностные:

• ценят и принимают такие базовые ценности как “родина” и “природа”;
• умеют осознавать свои трудности и стремятся к их преодолению;
• осознают себя как индивидуальность и одновременно, как члена общества.

Оборудование : ноутбуки по 1 на парту, мультимедийная система, объёмные и плоскостные геометрические фигуры (по 1 фигуре на парте) и карточки с названиями фигур (по 1 на парте), атлас “Республика Хакасия” по 1 на парту, “Журнал исследователя” на каждого ученика, программа-тренажёр “Устный счёт” авт. Иваненко А. С.

Ход урока

1. Актуализация знаний.

– Ребята, сегодня на уроке нашему научному клубу (Презентация. Слайд 1) предстоит выполнить небольшое исследование с помощью математических знаний. А чтобы оно было точным, вам нужно стараться безошибочно выполнять действия с многозначными числами, преобразовывать единицы длины и правильно решать задачи.

– Фотографии края, который мы будем исследовать обозначены многозначными числами (Слайд 2).

– Среди предложенных чисел назовите многозначные.

– Что заметили общего в этих числах? (Одинаковая цифра в разряде десятков тысяч.)

– Запишите их в порядке возрастания.

– Проверим. (Ученик зачитывает 97831,98000, 99999) (Слайд 3)

– Какой край будем исследовать? (Республику Хакасия.)

– Настоящие исследователи должны быть упорными и сообразительными, чтобы узнать много интересного. Сейчас мы будем тренировать эти качества.

– 5 человек выполняют задания на индивидуальных карточках (сложение и вычитание многозначных чисел), а остальные в парах работают на ноутбуках. (Тренажёры.)

2. Изучение нового материала.

– Без новых знаний жизнь неинтересна,
об этом знает каждый ученик.

Откройте учебники на с.3. Тема нашего урока спрятана в № 244. [1, с.3].

– По каким признакам разделите фигуры на группы?

– Дайте название каждой группе. (Пространственные и плоскостные.)

– Определите тему урока? (Слайд 4)

– Чему будете учиться? (Распознавать пространственные и плоскостные фигуры.)

– Как отличить пространственную фигуру от плоскостной?

3. Осознание и осмысление учебного материала.

– На рабочем столе ваших ноутбуков откройте папку “Задания для 4 класса”. Я подготовила для вас задание, откройте документ “Фигуры”. (Слайд 5)

Вы видите названия геометрических фигур и сами фигуры. Распределите их в две группы – пространственные и плоскостные фигуры.

– Назовите пространственные фигуры; плоскостные. (Слайд 6)

– В какую группу вы отнесли гексаэдр?

– Где можно найти значение этого слова? (В “Большой Российской энциклопедии”.)

– Да, совершенно верно, куб по-другому называется “гексаэдр”. (Слайд 7)

Физкультминутка.

4. Применение знаний и умений.

– Теперь мы готовы приступить к исследованию. У каждого из вас есть журнал исследователя со специальными заданиями (см. Приложение2), которые помогут вам получить интересную информацию о Хакасии. После того, как вы его заполните, он станет вашим помощником не только на уроках, но и в обычной жизни.

– Познакомьтесь с первым заданием.

(Задание 1. Почти 2/3 территории республики Хакасии занято горами, всё остальное – степи. Узнайте, какую территорию занимают степи.)

– Что скажете? (Не хватает данных.)

– Где можно взять недостающую информацию? (В атласе.)

– Какой из атласов подойдёт? (Предлагается атлас “Материков и океанов”, атлас “Республика Хакасия”.)

– Правильно, вам понадобится атлас “Республика Хакасия”. Посмотрите внимательно на с.5 этого атласа и найдите нужные данные. [4, с. 5] (Слайд 8)

– Выполните задание. Решение записывайте в тетради, а результаты в журнал исследователя.

– Зачитайте решение задачи. (61875-61875:3х2= 20625 км² )

– Кто решил по-другому?

1) 3/3 – 2/3=1/3 (часть) занята степями.
2) 61875:3х1= 20625 (км²) занимают степи.

– Какой способ решения наиболее удобный? Докажите.

– Назовите пространственные и плоскостные объекты из этого задания. (Степь – плоскостной объект, гора – пространственный.)

– Какие знания вам потребуются для выполнения второго задания? (Масштаб 1см : 17500 м и расстояние между объектами в см.)

– Как найти по карте расстояние между объектами?

(1. Измерить расстояние между объектами при помощи линейки.
2. Умножить масштаб на полученное число.
3. Выразить полученное число в километрах.)

Задание 2. Узнайте расстояние:

• от Абакана до Черногорска (17500х1 = 17500м
  17500м = 17км 500м)
• от Абакана до Сорска (1 7500х5 = 87500м
  87500м = 87км 500м)

– Ребята, только что по электронной почте пришёл запрос от МЧС респ. Хакасия. Им нужна информация о расстоянии от Абакана до СШГЭС.

– В парах обсудите полученные данные, на рабочем столе откройте “блокнот”, создайте текстовое сообщение с вашими данными и отправьте его по сетевому окружению на головной компьютер. (17500х6 = 105000м
105000м = 105км)

– Пока я проверяю ваши данные на своём компьютере, выполните в группах 3 и 4 задания.

(Задание 3. В каких архитектурных ансамблях и памятниках в нашем родном городе Абакане использованы такие пространственные фигуры, как шар, цилиндр и параллелепипед.

Задание 4. Хакасия богата полезными ископаемыми. В республике располагаются крупные запасы высококачественных углей. Важной отраслью является добыча железных руд. А также Хакасия – один из старейших золотоносных районов. Вспомни плоскостные фигуры, которые обозначают эти ископаемые на карте: золото – ___, уголь –_____, железная руда – _____ )

– Проверим, что у вас получилось в заданиях по группам. (Задание 3. Пространственные фигуры шар, цилиндр и параллелепипед можно увидеть в строении памятника Петру и Февронии, Спасо-Преображенского собора, стелы Лора, стелы “Добрый ангел мира”.)

(Слайд 9)

– Дома выполните последнее задание, а правильность полученного данного проверьте, используя разные источники информации.

(Задание 5. Из Абакана и из Москвы навстречу друг другу вышли два поезда. Скорость одного 50 км/ч, а другого 60 км/ч. Через 28 часов, до встречи поездов осталось 1138 км.

Узнайте расстояние от Абакана до Москвы.)

5. Рефлексия.

– Что на уроке было интересным?
– Когда было трудно?
– Дорисуйте смайлик, отражающий ваше настроение.

Приложение 2.

Список использованных источников

1. Аргинская И. И., Ивановская Е. И., Кормишина С.Н. Математика: Учебник для 4 класса: В 2 частях. – Самара: Издательство “Учебная литература”: Издательский дом “Фёдоров”, 2010. Часть II. – 144 с. – ISBN 978-5-9507-1086-5.
2. Лободина Н.В. Математика. 4 класс: поурочные планы по учебнику И. И. Аргинской. II полугодие. – Волгоград: Учитель, 2007. – 383 с. – ISBN 978-5-7057-1189-5.
3. Узорова О.В. Устный счёт и математические диктанты. 4 класс: / Пособие для начальной школы. – М.: Аквариум, 1998. – 240 с. – ISBN 5-85684-258-8.
4. Атлас республики Хакасия / составлен и подг. к изданию Восточно-Сибирским аэрогеодезическим предприятием в 1998 г.: отв. ред. Овчинникова Н.С. – 32 с.
5. Большая Российская энциклопедия: в 30 т./ Председатель Науч.– ред. совета Ю. С. Осипов. Отв. ред. С.Л. Кравец. Т.6.Восьмеричный путь. – Германцы. М.: Большая Российская энциклопедия. 2006. – 767 с.: ил.: карт. – ISBN 5-85270-33.

urok.1sept.ru

Плоские и объемные фигуры. 2-й класс

Этапы урока	Деятельность учителя	Деятельность учащихся
I. Самоопределение к деятельности	1) – Как называется место, в котором мы живём? – Сегодня на уроке математики мы отправляемся с вами в путешествие по городу. На доске иллюстрация города.   – Чтобы в городе был порядок, у каждого дома есть свой номер, но чтобы узнать номера домов нужно выполнить задание: Слайд № 2 2) Учитель предлагает детям записать полученные числа в тетрадь и задаёт вопросы: – Что можно сказать про эти числа, дайте характеристику? – Как вы думаете, а какие номера должны быть у следующих трёх домов? – А можно ли продолжить этот ряд чисел?	Дети отвечают, что мы живём в городе и объясняют свой ответ. Дети выполняют задание, определив закономерность получают следующие результаты: Слайд № 2 Дети записывают: 11, 13, 15, Дети отвечают, что это числа двузначные, нечётные. Ребята называют: 17, 19, 21… Ребята отвечают, что можно и объясняют, почему ставим многоточие (т.к. ряд можно продолжить до бесконечности)
II. Актуализация знаний.	1)– Ребята, а вы заметили, что наш город необычный? Что в нём такого необычного, интересного? – Какие геометрические фигуры вы видите?	Ребята отвечают, что город математический, состоит из геометрических фигур.
	– Сколько четырёхугольников? (10) – Сколько треугольников? (6) – Сколько кругов?(3) – Сколько всего фигур? (19)	Ребята отвечают, что они видят круги, квадраты, прямоугольники, треугольники, пятиугольник.
III. Работа с геометрическими фигурами. (Создание проблемной ситуации)	1. – Посмотрите на фигуры на ваших партах. Все ли фигуры, возможно, разместить на нашем рисунке? – Все ли фигуры удобно поместить на нашем рисунке? – Какие фигуры трудно будет поместить на нашем рисунке? Почему? 2. Исходя из этого задания, на какие две группы можно разложить все фигуры? – Почему в первую группу вы объединили именно эти фигуры, а во вторую группу эти фигуры? На экране: Слайд № 3.	Ребята выбирают различные фигуры, кто-то плоские, а кто-то объёмные, но путем примеров, приходят к выводу, что в данной ситуации лучше подойдут фигуры плоские. Дети раскладывают фигуры на две группы, советуясь с соседом по парте.
IV. Открытие нового знания.	– Возьмите любую фигуру из первой группы. Положите на тетрадь и прижмите ладонью. – Что произошло? Изменилась ли фигура? Почему так получилось? – Положите на парту фигуру из другой группы. – Можно ли прижать ладонью эту фигуру, не сломав её? – Почему? – У фигур из первой группы, есть какие измерения? – А у фигур из второй группы есть длина, ширина и…высота. Т. е. Такие фигуры называют трёхмерными или объёмными. – Так как назовём фигуры первой группы, второй группы? Слайд № 3.	Ребята кладут плоскую фигуру на тетрадь и прижимают ладонью. Делают вывод о том, что фигура не изменилась. Дети пробуют проделать этот же опыт и с объёмной фигурой, но понимают, что это невозможно. Дети делают вывод о том, что у фигуриз первой группы есть 2 меры: ширина и длина, а у фигур из второй группы есть не только длина, ширина, но ещё и высота. Ребята дают названия группам: объёмные фигуры и плоские фигуры.
V. Постановка цели урока	– Что же на уроке для нас сегодня будет важным? Чему будет посвящён урок?	Дети ставят сами цель урока, что урок будет посвящён фигурам плоским и объёмным и их отличию.
VI. Знакомство с названиями объёмных фигур.	Работаем по учебнику: стр. 47 № 3.	Дети приводят примеры объёмных тел в жизни. Ребята рассматривают иллюстрации и читают названия каждой объёмной фигуры: куб, параллелепипед, конус, цилиндр, шар и т.д.
VII. Первичное закрепление.	– Нам трудно было разместить на нашем рисунке объёмные фигуры, но в жизни они нам часто встречаются? На слайде изображены предметы, которые встречаются в быту. – Назовите предмет на рисунке. Этот предмет в виде какой объёмной фигуры? Слайд № 4 Слайд № 5 – Что для вас сегодня было новым? С чем вы уже давно знакомы? – Так чем же отличаются объёмные фигуры от плоских?	Ребята называют предмет и фигуру: Коробка – параллелепипед Ёлочный шарик – шар Банка – цилиндр Пирамидка детская – конус Египетские пирамиды – пирамида. Слайд № 4 Слайд № 5 Дети поясняют, что плоские фигуры имеют 2 измерения (длина и ширина), а объёмные – 3 измерения (длина, ширина, высота)
VIII. Физминутка.
IX. Составление и решение задачи.	– Посмотрите на доску. Составьте задачу по этой схеме. – Всего 19 фигур. – Каких фигур? (плоских) – Чем отличаются плоские фигуры от объёмных?	Ребята составляют задачу и выполняют решение с объяснением у доски: I способ: 1) 3 + 10 =13 (ф) – столько четырёхугольников и кругов вместе. 2) 19 – 13 = 6 (ф.) – столько треугольников. 19 – (3 + 10) = 6 (ф) II способ: 19 – 3 = 16 (ф) – столько четырёхугольников и треугольников. 16 – 10 = 6 (ф) – столько треугольников. 19 – 3 – 10 = 6 (ф) Можно, если позволяет время ещё 1 способ.
X. Задания в группах и парах.	Набираю две небольшие группы. Даю задания: Первая группа ищет в классе предметы, демонстрирующие плоские фигуры, вторая группа ищет в классе предметы объёмные по своей форме. Оставшаяся половина класса за партами в парах выполняют задания на листках: Из всех фигур раскрась только объёмные. Слайд № 6	Ребята первых двух групп ходят по классу и ищут предметы плоских и объёмных форм, затем рассказывают с какие плоскиеи объёмные тела встречаются в кабинете . Ребята второй группы, совещаясь друг с другом раскрашивают только объёмные фигуры. Ребята проверяют свою работу и называют фигуры: параллелепипед, куб, цилиндр, конус. Слайд № 6
XI. Закрепление.	– Вот такое у нас получилось путешествие по геометрическому городу. Вам понравилось путешествие? А сейчас мы попадём в город настоящий. Как называется город в котором мы живём? А на улицах нашего города встречаем ли мы объёмные тела? (детям предлагаются слайды с зарисовками нашего города) Слайд № 7. И т.д. Наш город красивый! Вы любите свой город? Что бы вы сделали для города?	Ребята рассматривают фотографии города и называют предметы объёмных форм, также называют какую объёмную фигуру представляет этот предмет. Например: Здания – куб, параллелепипед; Крыши – пирамиды, Колонны – цилиндр и т.д.
XII. Создание города.	“Возвращение к началу”: – Посмотрите, ребята, на наш геометрический город, чем он отличается от настоящего? – А можем ли мы с вами создать свой такой же объёмный город? ( у детей на партах с начала урока лежат наборы объёмных фигур из цветной бумаги (кубы, пирамиды, цилиндры) – Мы получили объёмный город благодаря чему? – С какими фигурами удобнее работать, а с какими интереснее?	Ребята отвечают, что настоящий город объёмный… Ребята берут свои фигуры (на всех фигурах на одной из граней наклеен двусторонний скотч и детям только остаётся отклеить верхний слой и наклеить свою фигуру) и приклеивают их на плоскость (заготовленную заранее) Благодаря объёмным фигурам мы можем выполнять многие работы. Дети объясняют, что с плоскими фигурами удобнее работать, потому что легко сложить, переносить и т.д. Но с объёмными интереснее…
XIII. Рефлексия.	– А теперь, ребята, оцените себя. У вас на парте лежат 4 кружка. Всё ли вы запомнили, всё ли вам понятно? Покажите с помощью кружка, как вы оцениваете свои знания? Слайд № 8.	Ребята показывают при помощи одного или даже двух кружков оценку своим знаниям.

urok.1sept.ru

Тема 19. Геометрические фигуры на плоскости и их свойства

Содержание

1. Понятие геометрической фигуры.

2. Углы.

3. Параллельные и перпендикулярные прямые.

4. Треугольники.

5. Четырехугольники.

6. Многоугольники.

7. Окружность и круг.

8. Построение геометрических фигур на плоскости.

9. Преобразования геометрических фигур. Понятие преобразования

Основная литература 4, 5, 13, 14, 15, 28, 29, 34;

Дополнительная литература 13, 49, 51, 65, 68, 75, 76, 78, 85

1. Понятие геометрической фигуры

Геометрическую фигуру определяют как любое множество точек.

Отрезок, прямая, круг, шар — геометрические фигуры.

Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской.

Например, отрезок, прямоугольник — это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.

Так как понятие геометрической фигуры определено через понятие множества, то можно говорить о том, что одна фигура включена в другую (или содержится в другой), можно рассматривать объединение, пересечение и разность фигур.

Например, объединением двух лучей АВ и МК (рис. 1) является прямая КВ, а их пересечение есть отрезок АМ.

К А М В

Рис. 1

Различают выпуклые и невыпуклые фигуры.

Фигура называется выпуклой, если она вместе с любыми двумя своими точками содержит также соединяющий их отрезок.

Фигура F₁, изображенная на рисунке 2, выпуклая, а фигура F₂ — невыпуклая.

F₂

X

Y

В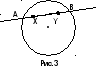ыпуклыми фигурами являются плоскость, прямая, луч, отрезок, точка. Нетрудно убедиться в том, что выпуклой фигурой является круг (рис. 3). Если продолжить отрезокXY до пересечения с окружностью, то получим хорду АВ. Так как хорда содержится в круге, то отрезок XY тоже содержится в круге и, значит, круг — выпуклая фигура.

Для многоугольников известно другое определение: многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону.

Так как равносильность этого определения и данного выше для многоугольника доказана, то можно пользоваться и тем, и другим.

Основываясь на этих понятиях, рассмотрим другие геометрические фигуры, изучаемые в школьном курсе планиметрии. Рассмотрим их определения и основные свойства, принимая их без доказательства. Знание этого материала и умение применять к решению несложных геометрических задач является той основой, на которой можно строить методику обучения младших школьников элементам геометрии.

2. Углы

Напомним, что угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи называются сторонами угла, а их общее начало — его вершиной.

Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и две точки на сторонах угла: А, (k,l), АВС.

Угол называется развернутым, если его стороны лежат на одной прямой.

Угол, составляющий половину развернутого угла, называется прямым. Угол, меньший прямого, называется острым. Угол, больший прямого, но меньший развернутого, называется тупым.

Кроме понятия угла, данного выше, в геометрии рассматривают понятие плоского угла.

Плоский угол — это часть плоскости, ограни­ченная двумя различными лучами, исходящими из одной точки.

Углы, которые рассматривают в планиметрии, не превосходят развернутого.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.

Сумма смежных углов равна 180°. Справедливость этого свойства вытекает из определения смежных углов.

Д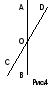ва угла называютсявертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Углы АОВ и СОВ, а также углы АОС и D0В — вертикальные (рис. 4).

Вертикальные углы равны.

Справедливость этого свойства вытекает из определения верти­кальных углов и свойства смежных углов.

studfile.net

Изучаем геометрические фигуры: игры для детей дошкольного возраста

Одним из важных аспектов развития математических представлений у дошкольников является изучение основ геометрии. В ходе знакомства с геометрическими фигурами, ребенок приобретает новые знания о свойствах предметов (форме) и развивает логическое мышление. В этой статье мы поговорим о том, как помочь дошкольнику запомнить геометрические фигуры, как правильно организовать игры для обучения геометрии, а также о том, какие материалы и пособия можно использовать для развития математических способностей малыша.

В каком возрасте можно начинать изучать геометрические фигуры?

Многих родителей посещает вопрос, нужно ли маленьким детям знакомиться с геометрическими фигурами. Специалисты считают, что занятия в игровой непринужденной форме оптимально начинать с 1,5 лет. До этого возраста уместно проговаривать ребенку названия форм предметов, с которыми малыш встречается в реальной жизни (например, «тарелка круглая», «стол квадратный»).

Знакомя ребенка с геометрическими фигурами, ориентируйтесь на его реакцию. Если малыш начал проявлять к ним интерес в раннем возрасте (играя с сортером или рассматривая картинки), поощряйте его любопытство.

В 2 года малыш должен уметь различать:

• Круг;
• Квадрат;
• Треугольник.

К 3 года к ним можно добавить:

• Овал;
• Ромб;
• Прямоугольник.

В более старшем возрасте ребенок может запомнить такие фигуры, как трапеция, пятиугольник, шестиугольник, звезда, полукруг. Также дети, посещающие Монтессори-центр «Созвездие», с интересом знакомятся с геометрическими телами.

Как помочь ребенку запомнить геометрические фигуры?

Обучение ребенка геометрическим формам должно происходить поэтапно. Приступать к новым фигурам нужно только после того, как малыш запомнит предыдущие. Самой простой фигурой считается круг. Покажите ребенку круглые предметы, пощупайте их, пусть малыш проведет по ним пальчиком. Также можно сделать аппликацию из кругов, слепить круг из пластилина. Чем больше ощущений, связанных с изучаемым понятием, получит ребенок, тем лучше малыш его запомнит.

Для знакомства с формами можно использовать объемные фигуры. Это могут быть делали конструктора, сортера, шнуровки, рамок-вкладышей. Так как в раннем возрасте наиболее развит наглядно-действенный тип мышления, то различные действия с фигурами помогут лучше их запомнить.

Как дети разного возраста воспринимают геометрические фигуры

Операции, которые ребенок может производить с геометрическими фигурами, и то, как он воспринимает формы, зависят от возраста малыша. В соответствии с возрастными особенностями, можно выделить следующие этапы обучения:

1. На втором году жизни малыш способен зрительно распознавать знакомые ему фигуры и сортировать предметы по форме.
2. В 2 года ребенок может найти нужную фигуру среди ряда других геометрических фигур.
3. К 3 годам малыши могут называть фигуры.
4. В 4 года ребенок способен соотносить объемную фигуры с плоским изображением.
5. В старшем дошкольном возрасте (а иногда и раньше) можно начинать изучение геометрических тел (шар, куб, пирамида). Также в этом возрасте ребенок может анализировать сложные картинки, состоящие из множества фигур.

В независимости от возраста малыша старайтесь обращать его внимание на формы окружающих предметов и сопоставлять их с известными геометрическими фигурами. Это можно делать дома и на прогулке.

Игры для изучения геометрических фигур

Чтобы ребенку было интересно, обучение геометрическим фигурам должно происходить в игровой форме. Следует также подбирать яркие и красочные материалы для занятий (их можно приобрести в магазине или сделать своими руками). Вот некоторые примеры игр и пособий для изучения геометрических фигур:

1. Сортировка. Игры с сортером можно начинать уже с 1 года. Предложите малышу найти для фигуры ее окошко. Так ребенок будет не только запоминать геометрические фигуры, то и развивать мелкую моторику, мышление и пространственные представления, ведь чтобы деталь попала в отверстие, нужно повернуть ее под правильным углом. Сортировать можно и любые другие предметы, например, элементы конструктора, блоки Дьенеша или счетный материал.
2. Рамки вкладыши. По сути, это пособие аналогично сортеру. Для каждой геометрической фигуры необходимо найти ее место.
3. Геометрическое лото. Для игры понадобится поле с изображением геометрических фигур и раздаточные карточки с каждой фигурой в отдельности. Маленькие карточки ребенок может доставать из сундучка или мешочка, а затем искать их место на игровом поле. Эта игра также отлично тренирует внимание малыша.
4. Геометрическая аппликация. Вырежьте из бумаги различные геометрические фигуры и вместе с ребенком составьте из них картинку (например, из треугольников можно сделать елочку, из квадрата и треугольника – домик).

5. Рисование (в том числе, при помощи трафаретов).
6. Лепка.
7. Выкладывание фигур из счетных палочек.
8. Геометрическая мозаика.
9. Шнуровки с геометрическими фигурами.
10. Игры с карточками.
11. «Угадай на ощупь».
12. Активные игры. На асфальте мелом нарисуйте геометрические фигуры. Попросите малыша представить, что фигуры – это домики, в которые надо забежать по сигналу. Далее Вы называете геометрическую фигуру, а ребенок бежит к ней.

Кроме того, для изучения геометрических фигур можно использовать развивающие мультфильмы. Вот один из них:

Выводы

Обучение основам геометрии в дошкольном возрасте является важной частью формирования у ребенка математических и сенсорных представлений. Знакомство с фигурами должно происходить постепенно (сначала простые фигуры – круг, квадрат, треугольник). Чтобы малышу было интересно, занимайтесь изучением геометрических фигур в игровой форме. Вашими помощниками в этом могут стать такие развивающие пособия, как рамки-вкладыши, мозаики, лото, сортеры, наборы геометрических фигур и тел, трафареты. Изучать геометрические фигуры можно и на улице: просто проговаривайте с ребенком, что вы видите вокруг и на какие фигуры похожи эти предметы. Тогда малыш обязательно научится различать геометрические фигуры и запомнит их названия.

Заключение

Для всестороннего и гармоничного развития каждого малыша в детском центре «Созвездие» специально создана Монтессори-среда. В процессе свободной работы в ней дети не только знакомятся с основами геометрии, но и развивают свои познавательные процессы, мелкую моторику, учатся писать, читать, считать. Кроме этого Монтессори-среда дает ребенку возможность в полной мере проявить самостоятельность и ответственность. Будем рады видеть Вас и Вашего малыша у нас в центре!

www.center-sozvezdie.ru