Гидростатика
1
В полый куб с ребром a налита доверху жидкость плотностью ρ. Определить силы, действующие на грани куба.
Ответ
На дно действует сила ρga3, на боковую грань 1/2ρga3.
2
Сосуд, имеющий форму усеченного конуса с приставным дном, опущен в воду. Если в сосуд налить 200 г воды, то дно оторвется. Отпадет ли дно, если на него поставить гирю 200 г? налить 200 г масла? налить 200 г ртути?
Ответ
Если сосуд сужается кверху, то гиря и ртуть не оторвут дно, а масло оторвет. Если сосуд сужается книзу, то наоборот.
3
В сосуд с водой вставлена трубка сечением S = 2 см В трубку налили 72 г масла (ρм = 900 кг/м3). Найти разность уровней масла и воды.
В трубку налили 72 г масла (ρм = 900 кг/м3). Найти разность уровней масла и воды.
Ответ и решение
Ответ: Δh = 4 см.
Согласно условию равновесия неоднородных жидкостей в сообщающихся сосудах:
.
Или:
.
Откуда
.(1)
Чтобы найти H, запишем выражение для массы масла в трубке:
,
откуда
.(2)
Окончательно, подставив (2) в (1), получим:
.
4
При подъеме груза массой m = 2 т с помощью гидравлического пресса была затрачена работа A = 40 Дж. При этом малый поршень сделал n = 10 ходов, перемещаясь за один ход на h = 10 см. Во сколько раз площадь большого поршня больше площади малого, если к. п. д. пресса равен 1.
п. д. пресса равен 1.
Ответ
5
В сообщающиеся сосуды диаметрами D1, и D2 налита вода. На сколько изменится уровень воды в сосудах, если положить кусок дерева массой m в первый сосуд? во второй? Плотность воды ρ0.
Ответ
В обоих случаях уровень воды увеличивается на
.
6
В колена U-образной трубки налиты вода и спирт, разделенные ртутью. Уровень ртути в обоих коленах одинаков. На высоте 24 см от уровня ртути колена соединены горизонтальной трубкой с краном.
Вначале кран закрыт. Определить высоту столба спирта
Ответ
7
Льдина площадью поперечного сечения S = 1 м2 и высотой H = 0,4 м плавает в воде. Какую работу надо совершить, чтобы полностью погрузить льдину в воду?
Какую работу надо совершить, чтобы полностью погрузить льдину в воду?
Ответ
≈ 7,84 Дж.
8
В стакане плавает кусок льда. Изменится ли уровень воды, когда лед растает? Рассмотреть дополнительно случаи: 1) когда во льду находился пузырек воздуха; 2) когда во льду находилась свинцовая пластинка.
Ответ
Лед вытесняет воду, вес которой равен весу льда. Когда лед растает, образуется такое же количество воды, поэтому уровень не изменится.
1) Тоже не изменится, т. к. массой воздуха можно пренебречь.
2) Понизится, т. к. объем воды, которая образуется, когда лед растает, вместе с объемом свинца будет меньше, чем в случае куска чистого льда того же веса.
9
Одна из бутылок наполнена водой, другая — ртутью. Потонет ли бутылка с водой, если ее опустить в воду? Потонет ли бутылка с ртутью, если ее опустить в ртуть?
Потонет ли бутылка с водой, если ее опустить в воду? Потонет ли бутылка с ртутью, если ее опустить в ртуть?
Ответ
Бутылка с водой потонет, а с ртутью — нет.
10
Прямоугольная коробочка из жести массой
Ответ
11
Кастрюля емкостью 2 л доверху наполнена водой. В нее ставят тело объемом 0,5 л и массой 0,6 кг. Сколько воды вытечет из кастрюли?
Ответ
12
Жестяная банка с грузом плавает на поверхности воды, налитой в сосуд. При этом уровень воды в сосуде равен H1. Больше или меньше H1 будет уровень H2, если груз из банки переложить на дно сосуда? Плотность груза больше плотности воды.
Решение
H2 станет меньше H1, поскольку груз будет вытеснять объем воды, равный своему объему, а находясь в жестяной банке, груз вытесняет объем воды, масса которого равна массе груза.
13
В сосуд с вертикальными стенками и площадью дна S налита жидкость с плотностью ρ. На сколько изменится уровень жидкости в сосуде, если в него опустить тело произвольной формы массой m, которое не тонет?
Ответ
14
В U-образной трубке сечением S налита жидкость с плотностью ρ. На сколько поднимется уровень жидкости в правом колене трубки по отношению к первоначальному уровню, если в левое колено опустили тело массой m и плотностью ρ1 < ρ?
Ответ
15
На дне водоема установлена бетонная конструкция грибовидной формы, размеры которой указаны на рисунке.
Глубина реки H. С какой силой F давит конструкция на дно реки? Плотность бетона ρ, воды ρ0.
Решение
Сила давления бетонной конструкции на дно складывается из веса конструкции и разности сил, возникающих в результате гидростатического давления на верхнюю и нижнюю поверхности конструкции:
.
Вес конструкции равен:
.
Сила, возникающая в результате гидростатического давления на верхнюю поверхность конструкции, равна:
.
Сила, возникающая в результате гидростатического давления на нижнюю поверхность конструкции, равна:
.
Таким образом, искомая сила F равна:
.
16
Деревянный кубик лежит на дне сосуда. Всплывет ли он, если в сосуд налить воду (вода не проникает под кубик)?
Решение
Не всплывет, т. к. выталкивающая сила не возникает из-за отсутствия воды под нижней гранью кубика.
к. выталкивающая сила не возникает из-за отсутствия воды под нижней гранью кубика.
17
Круглая дырка площадью S1 в дне сосуда прикрыта без усилия конической пробкой с площадью основания S2. При каком наибольшем значении плотности материала пробки ρ можно добиться ее всплытия, доливая воду в сосуд? Плотность воды ρ0.
Решение
Архимедова сила, действующая на пробку, достигает максимума, когда уровень воды достигнет верха пробки. Пробка всплывет, когда подъемная сила превысит вес пробки. Подъемная сила равна весу воды, объем которой равен объему заштрихованной области пробки на рисунке:
.
Найдем подъемную силу:
.
Найдем вес пробки:
.
Тогда ρ найдем из уравнения:
,
откуда
.
Поскольку малый и большой конус подобны:
,
тогда
.
18
Пустую открытую бутылку погрузили в воду горлышком вниз на некоторую глубину h и опустили. При этом бутылка не всплывала, не опускалась, а находилась в положении равновесия. Почему? Будет ли это равновесие устойчивым? Определить глубину погружения, если емкость бутылки V0 = 0,5 л, масса m = 0,4 кг. Давление атмосферы p0 = 101 кПа, температура постоянная. Объемом стенок бутылки пренебречь.
Решение
Давление воды на глубине h: p1 = p0 + ρgh. Для воздуха в бутылке, сжимающегося по мере погружения бутылки, можно записать закон Бойля-Мариотта: p0V0 = p1V1, где V0 и V1 — объем воздуха в бутылке соответственно до и после погружения. Поскольку бутылка находится в равновесии, то ее вес равен архимедовой силе: mg = ρV1g. Таким образом, получаем систему уравнений:
Поскольку бутылка находится в равновесии, то ее вес равен архимедовой силе: mg = ρV1g. Таким образом, получаем систему уравнений:
Решив ее, получим:
.
Равновесие будет неустойчивым.
19
Полый шар (внешний радиус R1, внутренний R2), сделанный из материала с плотностью
Решение
Чтобы шар находился в состоянии безразличного равновесия, вес вытесняемой шаром жидкости должен быть равен весу шара:
.
Отсюда находим ρ:
.
20
Полый шар, отлитый из чугуна, плавает в воде, погрузившись ровно наполовину. Найти объем V внутренней полости шара, если масса шара m = 5000 г, а плотность чугуна ρ = 7,8 г/см3.
Решение
Поскольку шар наполовину погружается в воду, то архимедова сила, действующая на шар, равна весу воды, объем которой равен половине объема шара. Объем шара складывается из искомого объема V и объема чугунной части шара, равного m/ρ. Таким образом, можно составить уравнение:
,
где ρ0 плотность воды, откуда:
≈ 9360 см3.
21
На весах уравновешен сосуд с водой. Как изменится равновесие, если в воду целиком опустить подвешенный на нитке брусок размером 5x3x3 см3 так, чтобы он не касался дна? Какой груз и на какую чашку надо положить, чтобы сохранить равновесие?
Решение
В соответствии с 3-м законом Ньютона, на чашку весов с сосудом с водой будет действовать сила, равная по модулю выталкивающей силе, действующей на брусок, но направленной в противоположную сторону. Таким образом, чтобы уравновесить весы, необходимо в противоположную чашку весов положить груз массой m = ρV = 45 г.
Таким образом, чтобы уравновесить весы, необходимо в противоположную чашку весов положить груз массой m = ρV = 45 г.
22
Алюминиевый и железный сплошные шары уравновешены на рычаге. Нарушится ли равновесие, если шары погрузить в воду? Рассмотреть два случая: а) шары одинаковой массы; б) шары одинакового объема.
Решение
Ответ: а) железный шар перевесит, поскольку на алюминиевый шар действует большая выталкивающая сила, чем на железный, так как объем алюминиевого шара больше объема железного шара такой же массы. б) железный шар перевесит, поскольку момент выталкивающей силы, действующей на алюминиевый шар, больше момента выталкивающей силы, действующей на железный шар, так как плечи рычага в этом случае не равны.
23
Вес куска железа в воде P = 1,67 H. Найти его объем Vж. Плотность железа ρж = 7,8 г/см3.
Плотность железа ρж = 7,8 г/см3.
Решение
Вес куска железа в воде равен разности веса куска железа вне воды и выталкивающей силы, действующей на него в воде:
,
откуда:
= 25,1 см3.
24
Вес тела в воде в три раза меньше, чем в воздухе. Какова плотность материала тела?
Решение
Вес тела в воде равен разности веса тела вне воды и выталкивающей силы, действующей на него в воде:
,
откуда:
,
или:
,
откуда:
= 1500 кг/м3.
25
Брусок дерева плавает в воде. Как изменится глубина погружения бруска в воде, если поверх воды налить масло?
Ответ
Уменьшится, поскольку увеличится давление на нижнюю грань бруска дерева.
26
Некоторое тело плавает на поверхности воды в закрытом сосуде. Как изменится глубина погружения тела, если накачать воздух в сосуд?
Ответ
Ответ: не изменится, если сжимаемость тела такая же, как и у воды. Если сжимаемость тела больше, чем у воды, то глубина увеличится. Если сжимаемость тела меньше, чем у воды, то глубина погружения тела уменьшится.
27
Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку. При этом 0,75 всего объема поплавка погружено в воду. Определить силу натяжения нити F, если масса поплавка равна 2 кг и плотность пробки 0,25 г/см3. Массой нити пренебречь.
Решение
Сила натяжения нити равна разности архимедовой силы и веса пробки:
,
где ρ0 плотность воды.
Вынесем mg за скобки:
.
Подставив числовые значения, получим F ≈ 40 H.
28
На крюке динамометра висит ведерко. Изменится ли показание динамометра, если ведерко наполнить водой и погрузить в воду?
Ответ
Уменьшится на величину веса воды, вытесняемой стенками и дном ведра.
29
Сосуд, предельно наполненный водой, висит на динамометре. Изменится ли показание динамометра, если в воду опустить гирю, подвешенную на нити, не касаясь дна?
Ответ
Не изменится, поскольку вес воды, которая выльется, равен силе, противодействующей архимедовой силе, действующей на гирю.
30
На рычажных весах уравновешены сосуд с водой и штатив с медной гирей массой m = 100 г (рисунок). Затем гиря, подвешенная на нити, опускается в воду. Как восстановить равновесие весов? Плотность меди ρм = 8,9 г/см3.
Затем гиря, подвешенная на нити, опускается в воду. Как восстановить равновесие весов? Плотность меди ρм = 8,9 г/см3.
31
Тонкая однородная палочка шарнирно укреплена за верхний конец. Нижняя часть палочки погружена в воду, причем равновесие достигается тогда, когда палочка расположена наклонно к поверхности воды и в воде находится половина палочки. Какова плотность материала, из которого сделана палочка?
32
Два шарика радиусами r1 и r2, сделанные из материалов с плотностями ρ1 и ρ2, соединены невесомым стержнем длиной l. Затем вся система помещена в жидкость с плотностью ρ, причем ρ < ρ1 и ρ < ρ2. В какой точке стержня нужно его повесить, для того чтобы система находилась в равновесии при горизонтальном положении стержня?
33
Из сосуда, заполненного водой, выходит труба радиусом r и высотой h (рисунок). Труба закрыта круглой пластиной радиусом R и массой М, которую прижимает к трубе давление воды. С какой силой F нужно подействовать на пластину в точке А, для того чтобы она повернулась, открыв трубу? Сосуд заполнен водой до высоты H. Толщина пластины пренебрежимо мала.
Труба закрыта круглой пластиной радиусом R и массой М, которую прижимает к трубе давление воды. С какой силой F нужно подействовать на пластину в точке А, для того чтобы она повернулась, открыв трубу? Сосуд заполнен водой до высоты H. Толщина пластины пренебрежимо мала.
34
На весах уравновешено тело, погруженное в жидкость. Изменится ли показание весов при нагревании жидкости вместе с погруженным в нее телом?
35
Сплошное однородное тело объемом V, плотность материала которого ρ, плавает на границе между тяжелой жидкостью с плотностью ρ1 и более легкой жидкостью с плотностью ρ2. Какая часть объема тела V1 будет находиться в тяжелой жидкости?
36
Кубик из дерева, имеющий сторону 10 см, плавает между маслом и водой, находясь ниже уровня масла на 2,5 см. Нижняя поверхность кубика на 2,5 см ниже поверхности раздела. Какова масса m кубика, если плотность масла 0,8 г/см3? Определить силы давления F1, и F2 на верхнюю и нижнюю грани кубика. Изменится ли глубина погружения кубика в воду при доливании масла?
Какова масса m кубика, если плотность масла 0,8 г/см3? Определить силы давления F1, и F2 на верхнюю и нижнюю грани кубика. Изменится ли глубина погружения кубика в воду при доливании масла?
37
Стальной кубик плотностью 7,8 г/см3 плавает в ртути (плотность 13,6 г/см3). Поверх ртути наливается вода так, что она покрывает кубик тонким слоем. Какова высота H слоя воды? Длина ребра кубика а = 10 см. Определить давление р на нижнюю грань кубика.
38
Кусок пробки весит в воздухе 0,147 Н, кусок свинца 1,1074 Н. Если эти куски связать, а затем подвесить к чашке весов и опустить в керосин, то показания весов будет 0,588 Н. Определить плотность пробки, учитывая, что плотность керосина 0,8 г/см3, а свинца 11,3 г/см3.
39
В сосуд с водой погружается открытый цилиндрический стакан: один раз дном вверх, а другой — дном вниз, на одну и ту же глубину. В каком из этих случаев работа, которую нужно совершить, чтобы погрузить стакан в воду, будет больше? Вода из сосуда не выливается и в стакан, погруженный дном вниз, не попадает.
В каком из этих случаев работа, которую нужно совершить, чтобы погрузить стакан в воду, будет больше? Вода из сосуда не выливается и в стакан, погруженный дном вниз, не попадает.
40
Две одинаковые по массе оболочки шара — одна из эластичной резины, а вторая из прорезиненной ткани — наполнены одним и тем же количеством водорода и у Земли занимают равный объем. Который из шаров поднимется выше и почему, если водород из них выходить не может?
41
Во сколько раз изменится подъемная сила газа, наполняющего аэростат (дирижабль), если будет применяться гелий вместо водорода?
42
К динамометру подвешена тонкостенная трубка ртутного барометра. Что показывает динамометр? Будут ли изменяться его показания при изменении атмосферного давления?
43
Определить приближенно массу газовой оболочки, окружающей земной шар.
44
Г-образная трубка, длинное колено которой открыто, наполнена водородом. Куда будет выгнута резиновая пленка, закрывающая короткое колено трубки?
Куда будет выгнута резиновая пленка, закрывающая короткое колено трубки?
45
В трубе с сужением течет вода. В трубу пущен эластичный резиновый мячик. Как изменится его диаметр при прохождении узкой части трубы?
46
Тело, имеющее массу m = 2 кг и объем V = 1000 см3, находится в озере на глубине h = 5 м.
Какая работа должна быть совершена при его подъеме на высоту H = 5 м над поверхностью воды?
Равна ли совершенная при этом работа изменению потенциальной энергии тела? Объясните результат.
47
В водоеме укреплена вертикальная труба с поршнем таким образом, что нижний ее конец погружен в воду. Поршень, лежавший вначале на поверхности воды, медленно поднимают на высоту H = 15 м. Какую работу пришлось при этом совершить? Площадь поршня S = 1 дм2, атмосферное давление р = 101 кПа. Весом поршня пренебречь.
48
Подводная лодка находится на глубине h = 100 м. С какой скоростью через отверстие в корпусе лодки будет врываться струя воды? Сколько воды проникает за один час, если диаметр отверстия равен d = 2 см? Давление воздуха в лодке равно атмосферному давлению. Изменением давления внутри лодки пренебречь.
49
Из брандспойта бьет струя воды. Расход воды Q = 60 л/мин. Какова площадь поперечного сечения струи S1 на высоте h = 2 м над концом брандспойта, если вблизи него сечение равно S0 = 1,5 см2?
50
Почему быстролетящая пуля пробивает в пустом пластмассовом стакане лишь два маленьких отверстия, а стакан, наполненный водой, разбивается при попадании пули вдребезги?
Формы для егэ по физике. Формулы по физике, которые рекомендуется выучить и хорошо освоить для успешной сдачи ЕГЭ
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Единый Государственный Экзамен охватывает информацию по всему курсу физики с 7 по 11 класс. Однако если некоторые формулы по физике для ЕГЭ неплохо запоминаются сами по себе, над другими приходится поработать. Мы рассмотрим некоторые формулы, которые полезны для решения различных задач.
Кинематика
Начнем традиционно с кинематики. Частая ошибка здесь – неверное вычисление средней скорости неравномерного прямолинейного движения. В данном случае задачи пытаются решать с помощью среднего арифметического. Однако все не так просто. Среднее арифметическое – только частный случай. А для нахождения средней скорости движения существует полезная формула:
где S – весь путь, пройденный телом за определенное время t.
Молекулярно-Кинетическая Теория (МКТ)
МКТ может поставить множество коварных «ловушек» для невнимательного школьника. Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Чтобы избежать этого, нужно свободно владеть формулами по физике для ЕГЭ в этой области.
Начнем с закона Менделеева-Клапейрона, использующегося для идеальных газов. Он звучит так:
где p –давление газа,
V – занимаемый им объем,
n – количество газа,
R – универсальная газовая постоянная,
T – температура.
Обратите внимание на примеры задач с применением этого закона.
Все представляют себе, что такое влажность. Значения относительной влажности ежедневно сообщаются в СМИ. На экзамене же пригодится формула: здесь ф – относительная влажность воздуха,
ρ – плотность водяного пара, находящегося в воздухе,
ρ0 – плотность насыщенного пара при конкретной температуре.
Эта последняя величина – табличное значение, поэтому оно должно быть в условии задачи.
Термодинамика
Термодинамика – отрасль, достаточно близкая к МКТ, поэтому многие понятия пересекаются. Термодинамика базируется на двух своих началах. Практически каждая задача этой области требует знание и применение первого начала термодинамики, выраженного формулой
Это формулируется следующим образом:
Количество теплоты Q, которое было получено системой, расходуется на совершение работы A над внешними телами и изменение ΔU внутренней энергии данной системы.
Сила Архимеда
Напоследок поговорим о поведении погруженных в жидкость тел. Очевидно, что на каждое из них действует сила тяжести, направленная вертикально вниз. Но в жидкости все тела весят меньше. Это обусловливается частичным компенсированием силы тяжести противоположно направленной силой Архимеда. Ее значение равно Таким образом, эта сила, старающаяся вытолкнуть тело из жидкости, зависит от плотности той самой жидкости и объема погруженной в нее части тела. Сила Архимеда действует и в газах, но вследствие ничтожности плотности газов ею обыкновенно пренебрегают.
ЕГЭ проверяет знания школьника в различных областях физики. Формулы для ЕГЭ по физике способствуют успешному решению задач (можно воспользоваться ) и общему пониманию основных физических процессов.
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.
 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Как правило, именно математику, а не физику принято считать королевой точных наук. Мы полагаем, что это утверждение спорно, ведь технический прогресс невозможен без знания физики и её развития. Из-за своей сложности она вряд ли когда-либо будет включена в список обязательных государственных экзаменов, но, так или иначе, абитуриентам технических специальностей приходится сдавать её в обязательном порядке. Труднее всего запомнить многочисленные законы и формулы по физике для ЕГЭ, именно о них мы расскажем в этой статье.
Секреты подготовки
Возможно, это связано с кажущейся сложностью предмета или популярностью профессий гуманитарного и управленческого профиля, но в 2016 году только 24 % всех абитуриентов приняли решение сдавать физику, в 2017 — лишь 16 %. Такие статистические данные невольно заставляют задуматься, не слишком ли завышены требования или просто уровень интеллекта в стране падает. Почему-то не верится, что так мало школьников 11 класса желают стать:
Почему-то не верится, что так мало школьников 11 класса желают стать:
- инженерами;
- ювелирами;
- авиаконструкторами;
- геологами;
- пиротехниками;
- экологами,
- технологами на производстве и т.д.
Знание формул и законов физики в равной степени необходимо для разработчиков интеллектуальных систем, вычислительной техники, оборудования и вооружения. При этом всё взаимосвязано. Так, например, специалисты, производящие медицинское оборудование, в своё время изучали углубленный курс атомной физики, ведь без разделения изотопов, у нас не будет ни рентгенологической аппаратуры, ни лучевой терапии. Поэтому создатели ЕГЭ постарались учесть все темы школьного курса и, кажется, не пропустили ни одной.
Те ученики, которые исправно посещали все уроки физики вплоть до последнего звонка, знают, что в период с 5 по 11 класс изучается около 450 формул. Выделить из этих четырех с половиной сотен хотя бы 50 крайне сложно, поскольку все они важны. Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
Подобного мнения, очевидно, также придерживаются разработчики Кодификатора. Тем не менее, если вы одарены необыкновенно и не ограничены во времени, вам хватит 19 формул, ведь при желании из них можно вывести все остальные. За основу мы решили взять главные разделы:
- механику;
- физику молекулярную;
- электромагнетизм и электричество;
- оптику;
- физику атомную.
Очевидно, что подготовка к ЕГЭ должна быть ежедневной, но если по каким-то причинам вы приступили к изучению всего материала лишь сейчас, настоящее чудо может совершить экспресс-курс, предлагаемый нашим центром. Надеемся, эти 19 формул также будут вам полезны:
Вы, наверное, заметили, что некоторые формулы по физике для сдачи ЕГЭ остались без пояснений? Мы предоставляем вам самим их изучить и открыть для себя законы, по которым абсолютно всё вершится в этом мире.
Абсолютно необходимы для того, чтобы человек, решивший изучать эту науку, вооружившись ими, мог чувствовать себя в мире физики как рыба в воде. Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Без знания формул немыслимо решение задач по физике. Но все формулы запомнить практически невозможно и важно знать, особенно для юного ума, где найти ту или иную формулу и когда ее применить.
Расположение физических формул в специализированных учебниках распределяется обычно по соответствующим разделам среди текстовой информации, поэтому их поиск там может отнять довольно-таки много времени, а тем более, если они вдруг понадобятся Вам срочно!
Представленные ниже шпаргалки по физике содержат все основные формулы из курса физики , которые будут полезны учащимся школ и вузов.
Все формулы школьного курса по физике с сайта http://4ege.ru
I. Кинематика скачать
1. Основные понятия
2. Законы сложения скоростей и ускорений
3. Нормальное и тангенциальное ускорения
4. Типы движений
4.1. Равномерное движение
4.1.1. Равномерное прямолинейное движение
4.1.2. Равномерное движение по окружности
4.2. Движение с постоянным ускорением
4. 2.1. Равноускоренное движение
2.1. Равноускоренное движение
4.2.2. Равнозамедленное движение
4.3. Гармоническое движение
II. Динамика скачать
1. Второй закон Ньютона
2. Теорема о движении центра масс
3. Третий закон Ньютона
4. Силы
5. Гравитационная сила
6. Силы, действующие через контакт
III. Законы сохранения. Работа и мощность скачать
1. Импульс материальной точки
2. Импульс системы материальных точек
3. Теорема об изменении импульса материальной точки
4. Теорема об изменении импульса системы материальных точек
5. Закон сохранения импульса
6. Работа силы
7. Мощность
8. Механическая энергия
9. Теорема о механической энергии
10. Закон сохранения механической энергии
11. Диссипативные силы
12. Методы вычисления работы
13. Средняя по времени сила
IV. Статика и гидростатика скачать
1. Условия равновесия
2. Вращающий момент
3. Неустойчивое равновесие, устойчивое равновесие, безразличное равновесие
4. Центр масс, центр тяжести
5. Сила гидростатического давления
Сила гидростатического давления
6. Давлением жидкости
7. Давление в какой-либо точке жидкости
8, 9. Давление в однородной покоящейся жидкости
10. Архимедова сила
V. Тепловые явления скачать
1. Уравнение Менделеева-Клапейрона
2. Закон Дальтона
3. Основное уравнение МКТ
4. Газовые законы
5. Первый закон термодинамики
6. Адиабатический процесс
7. КПД циклического процесса (теплового двигателя)
8. Насыщенный пар
VI. Электростатика скачать
1. Закон Кулона
2. Принцип суперпозиции
3. Электрическое поле
3.1. Напряженность и потенциал электрического поля, созданного одним точечным зарядом Q
3.2. Напряженность и потенциал электрического поля, созданного системой точечных зарядов Q1, Q2, …
3.3. Напряженность и потенциал электрического поля, созданного равномерно заряженным по поверхности шаром
3.4. Напряженность и потенциал однородного электрического поля, (созданного равномерно заряженной плоскотью или плоским конденсатором)
4. Потенциальная энергия системы электрических зарядов
Потенциальная энергия системы электрических зарядов
5. Электроемкость
6. Свойства проводника в электрическом поле
VII. Постоянный ток скачать
1. Упорядоченная скорость
2. Сила тока
3. Плотность тока
4. Закон Ома для участка цепи, не содержащего ЭДС
5. Закон Ома для участка цепи, содержащего ЭДС
6. Закон Ома для полной (замкнутой) цепи
7. Последовательное соединение проводников
8. Параллельное соединение проводников
9. Работа и мощность электрического тока
10. КПД электрической цепи
11. Условие выделения максимальной мощности на нагрузке
12. Закон Фарадея для электролиза
VIII. Магнитные явления скачать
1. Магнитное поле
2. Движение зарядов в магнитном поле
3. Рамка с током в магнитном поле
4. Магнитные поля, создаваемые различными токами
5. Взаимодействие токов
6. Явление электромагнитной индукции
7. Явление самоиндукции
IX. Колебания и волны скачать
1. Колебания, определения
2. Гармонические колебания
3. Простейшие колебательные системы
Простейшие колебательные системы
4. Волна
X. Оптика скачать
1. Закон отражения
2. Закон преломления
3. Линза
4. Изображение
5. Возможные случаи расположения предмета
6. Интерференция
7. Дифракция
Большая шпаргалка по физике . Все формулы изложены в компактном виде с небольшими комментариями. Шпаргалка также содержит полезные константы и прочую информацию. Файл содержит следующие разделы физики:
Механика (кинематика, динамика и статика)
Молекулярная физика. Свойства газов и жидкостей
Термодинамика
Электрические и электромагнитные явления
Электродинамика. Постоянный ток
Электромагнетизм
Колебания и волны. Оптика. Акустика
Квантовая физика и теория относительности
Маленькая шпора по физике . Все самое необходимое для экзамена. Нарезка основных формул по физике на одной странице. Не очень эстетично, зато практично. 🙂
Формулы по физике 7-11 класс киниматика
Формулы по физике 7-11 класс киниматика
Физике за 7, 8, 9, и 11 классы. Шпоры. Кинематика материальной точки. Билеты по физике с решениями 11 кл. Термодинамика. Рабочая учебная программа по физике 8 класс. Автор: Юрий Васильевич Коновалов. Формула физики сборник формул по физике с пояснениями. Содержит материал по всем разделам школьного курса. Формулы по физике с краткими пояснениями. Это механика, термодинамика и молекулярная физика, электричество. Формулы по физике. Кинематика. Кинематика. СИ физических величин. Курс студента. Квантовая физика формулы Колебания, вещество, магниты, законы Ньютона, законы термодинамики, гидродинамика,.
Шпоры. Кинематика материальной точки. Билеты по физике с решениями 11 кл. Термодинамика. Рабочая учебная программа по физике 8 класс. Автор: Юрий Васильевич Коновалов. Формула физики сборник формул по физике с пояснениями. Содержит материал по всем разделам школьного курса. Формулы по физике с краткими пояснениями. Это механика, термодинамика и молекулярная физика, электричество. Формулы по физике. Кинематика. Кинематика. СИ физических величин. Курс студента. Квантовая физика формулы Колебания, вещество, магниты, законы Ньютона, законы термодинамики, гидродинамика,.
Классам. Без выходных данных. Кинематика. Движение по окружности. Под углом к горизонту. Динамика. Просмотры: 831. Задачи на нахождение средней и относительной скорости. Газовые законы. Свойства веществ. Электростатика. Законы. Механическая работа и энергия. Центр онлайн обучения. Сайтформула физики. Можно распечатать и сделать мини книжку. Справочник поможет систематизировать знания, подготовиться к урокам, контрольным работам, а также к ОГЭ и ЕГЭ. Обозначение, Измеряется в, Описание. Кинематика, законы и формулы. Взаимодействие в физике. Давление жидкостей и газов. Движение жидкостей и газов. Маятники. Молекулярная теория. Формулы по физике с пояснениями.
Обозначение, Измеряется в, Описание. Кинематика, законы и формулы. Взаимодействие в физике. Давление жидкостей и газов. Движение жидкостей и газов. Маятники. Молекулярная теория. Формулы по физике с пояснениями.
ТРТУ летом 2001 года. Мы узнаем, что изучает кинематика, основные понятия этого раздела. Основные формулы кинематики по физике с некоторыми пояснениями. Калькуляторы по физике. Описывая движение, физики используют понятие системы отсчета. Движение и силы. Все формулы школьной физики. Кинематика урок физики и презентация составлены Орловой Еленой Анатольевной, работающей в МБОУ Лицей 11 города Химки. Ядерная физика. Лучшая шпаргалка по физике. Шпаргалка с формулами по физике для ЕГЭ. И не только может понадобиться 7, 8, 9, и 11.
Мощность, энергия. Теплота. Постоянный электрический ток. Кинематика. Динамика. Механика твердого тела. Механика жидкостей. Формулировки физических законов и правил из курса 7 класса общеобразовательной школы. Если Вы решили научиться решать задачи по физике с нуля, то Вы попали туда куда надо. Основные формулы по физике динамика, кинематика, статикаСкорость и ускорение: Маленькое изображение. Приведем также формулы для вычисления а ц через период и частоту . Также на этом уроке будут. Кинематика: Относительность механического движения. Лицей интернат естественных наук 2011.
Основные формулы по физике динамика, кинематика, статикаСкорость и ускорение: Маленькое изображение. Приведем также формулы для вычисления а ц через период и частоту . Также на этом уроке будут. Кинематика: Относительность механического движения. Лицей интернат естественных наук 2011.
Скорость и все необходимое для ЕГЭ по физике. Эта запись была опубликована в рубрике Физика и отмечена метками уроки физики. На своем канале я буду разбирать большое множество задач на кинематику,., м, радиус. Формулы и законы физики. Формулы по физике 7 класс. Их и возьмем. Разделы: кинематика, динамика, электростатика, квантовая физика, ядерная физика и другие. Физика: формулы и определения: Шпаргалка. Молекулярная физика. Формулы по физике 11 класс. Законы взаимодействия и движения тел. Шпаргалки по физике, успешно использованные при поступлении в.
Таблица формул по физике. Кинематика. Все формулы по физике: 7, 8, 9, 11 класс. Физика маленькие шпоры. Время подъема на максимальную высоту, тела, брошенного под углом к горизонту 4,815. Основах МКТ. Моркотун Владимир Леонтьевич. ФИЗИКА. Все законы и формулы в таблицах 7— 11 классы. Кинематикараздел механики, изучающий и описывающий. Движение тел без рассмотрения причин возникновения движения. Колебания и волны. Школьный тур олимпиады по физике 7 11 классы. Посмотреть: 180 формул по физике на одном листе. Работа,.
Основах МКТ. Моркотун Владимир Леонтьевич. ФИЗИКА. Все законы и формулы в таблицах 7— 11 классы. Кинематикараздел механики, изучающий и описывающий. Движение тел без рассмотрения причин возникновения движения. Колебания и волны. Школьный тур олимпиады по физике 7 11 классы. Посмотреть: 180 формул по физике на одном листе. Работа,.
Г.2. Механика. Кинематика прямолинейного движения. Законы постоянного тока. Кинематика. Формулы по физике для ЕГЭ и 7 11 класса. Магнитное поле. Содержание: русский язык, история, математика, физика, география, биология, химия, английский язык. Авт. Кабардин О. Ф. И др. Теоретический материал для ЕГЭ: Механика, кинематика, динамика, законы сохранения, статика, гидростатика, молекулярная физика. Шпаргалки по физике. Рекомендуем добавить эту страницу в закладки чтобы распечатать при необходимости например, перед контрольной у школьников или экзаменом у студентов нужную шпаргалку таблицу формулы по.
Вместе с
Формулы по физике 7-11 класс киниматика часто ищутвсе формулы по физике с пояснениями
формулы по физике с обозначениями
все формулы по физике за школьный курс
все формулы по физике 7 класс
все формулы по физике 7-9 класс
все формулы по физике 8 класс
формулы по физике 10-11 класс
все формулы по физике для егэ 2017
Читайте также:
Русский 2 класс климанова бабушкинарешебник онлайн
Кроссворд челестоногие биология 7 класс
Гдз по английскому для класса автор кауфман
Теория кинематики | Механика | Упражнения по физике
Кинематика — раздел классической механики, описывающий движение тел (предметов) и систем (групп тел) без учета сил, вызывающих движение.
Когда мы изучаем движение тела, мы всегда должны делать это относительно системы отсчета, которая является точкой или набором точек, посредством которых мы описываем движение тела.
Мы говорим, что тело движется относительно системы отсчета, когда оно меняет свое положение с течением времени, если оно не меняется, мы говорим, что оно находится в состоянии покоя.Движение относительное, то есть оно будет зависеть от выбранной нами системы отсчета.
Если мы соединим все точки, где проходит тело, мы получим кривую, называемую траекторией , по которой мы можем определить положение точки, которая после соединения ее с осями OX и OY, мы получим в результате вектор, называемый положением вектор .
Биопроф |Теория кинематики| 01
Длина или модуль этого вектора положения вычисляется следующим образом:
Биопроф |Теория кинематики| 02
ОБЗОР ФОРМУЛЫ:
Скалярная средняя скорость
Биопроф |Теория кинематики| 03
Скалярная мгновенная скорость
Биопроф |Теория кинематики| 04
Средняя векторная скорость
Биопроф |Теория кинематики| 05
Векторная мгновенная скорость
Биопроф |Теория кинематики| 06
Среднее ускорение
Биопроф |Теория кинематики| 07
Мгновенное ускорение
Биопроф |Теория кинематики| 08
Тангенциальное ускорение
Биопроф |Теория кинематики| 09
Нормальное ускорение
Биопроф |Теория кинематики| 10
Прямолинейное равномерное движение
Биопроф |Теория кинематики| 11
Прямолинейное равнопеременное движение
Биопроф |Теория кинематики| 12
Свободное падение
Биопроф |Теория кинематики| 13
Угловые величины
Биопроф |Теория кинематики| 14
Угловая скорость
Биопроф |Теория кинематики| 15
Угловое ускорение
Биопроф |Теория кинематики| 16
Равномерное круговое движение (T = период; f = частота)
Биопроф |Теория кинематики| 17
Биопроф |Теория кинематики| 18
Равномерное круговое переменное движение
Биопроф |Теория кинематики| 19
Вибрационное гармоническое движение (s = удлинение; A = амплитуда; ω = пульсация)
Биопроф |Теория кинематики| 20
СОСТАВ ДВИЖЕНИЙ
Вертикальный пуск снарядов
Биопроф |Теория кинематики| 21
Горизонтальный пуск снарядов
Биопроф |Теория кинематики| 22
Наклонный пуск снарядов
Уравнение траектории
Биопроф |Теория кинематики| 23
Максимальная высота
Биопроф |Теория кинематики| 24
Окончательный объем
Биопроф |Теория кинематики| 25
Кинематика | Теория и графическое представление — видео и расшифровка урока
Теория кинематики
Существуют различные термины, используемые для описания движения объекта в теории кинематики. Некоторыми из этих дескрипторов движения являются расстояние, смещение, скорость, скорость и ускорение. Каждый из них будет подробно рассмотрен в следующих разделах.
Система отсчета
Прежде чем описывать движение объекта, необходимо четко задать систему отсчета. Система отсчета представляет собой набор координат или контрольных точек, используемых для описания положения, движения и других свойств объекта.В большинстве случаев положение объекта описывается относительно неподвижного объекта, находящегося в той же системе отсчета.
Как система отсчета помогает описать движение объекта? Когда говорят, что объект движется со скоростью 3 м/с, автоматически подразумевается, что эта скорость относится к Земле. Эта скорость будет другой, если смотреть в другой системе отсчета, например, с Луны, где необходимо учитывать скорость вращения Земли в дополнение к движению объекта.
Установка системы отсчета также важна при описании положения объекта. Рассмотрим объект, преодолевший расстояние 3 м. Без какого-либо ориентира невозможно определить, где начинается трехметровая дистанция и в каком именно направлении она идет. При выборе системы отсчета необходимо указать начальную точку x = 0, а также отрицательное и положительное направления. Любая система отсчета действительна до тех пор, пока она используется последовательно. Использование согласованных систем отсчета очень важно для описания смещения и скорости объекта.
Расстояние и перемещение
Невозможно описать движение без учета положения объекта. Расстояние и смещение — это два дескриптора движения, которые определяют положение.
Расстояние относится к общему пути, пройденному объектом. Это скалярная величина, и поэтому требуется только величина. Displacement , с другой стороны, описывает изменение положения объекта. Это относится к прямому пути от начального положения объекта до его конечного положения. В отличие от расстояния, это векторная величина, а это значит, что она требует и величины, и направления.
В отличие от расстояния, это векторная величина, а это значит, что она требует и величины, и направления.
Чтобы отличить расстояние от смещения, рассмотрим следующий пример. Предположим, человек идет из точки А в точку Б, как показано на диаграмме ниже. Чтобы перейти от начальной точки к исходной, человек перемещается на 7 м на восток, затем на 5 м на запад. Общий пройденный путь составляет 12 м, независимо от направления человека. Однако прямой путь из точки А в точку В составляет всего 2 м и направлен на восток.12-метровый путь — это расстояние, а 2-метровый восточный вектор — это перемещение человека.
Скорость и скорость
Следующие два термина, обычно встречающиеся в кинематике, — это скорость и скорость. Скорость относится к расстоянию, пройденному объектом в единицу времени. Это скалярная величина и имеет дело только с величиной.
Это скалярная величина и имеет дело только с величиной.
Скорость , с другой стороны, описывает перемещение в единицу времени. Это векторная величина, требующая количественной оценки как величины, так и направления. Средняя скорость выражается как {eq}v=\frac{\Delta x}{\Delta t} {/eq}, где v — средняя скорость, {eq}\Delta x {/eq} — смещение, а {eq}\Delta t {/eq} — прошедшее время.
Рассмотрим еще раз пример, представленный в предыдущем разделе. Предположим, что человеку потребовалось 60 секунд, чтобы переместиться из точки A в точку B. Используя выражение {eq}v=\frac{\Delta x}{\Delta t} {/eq}, скорость человека равна 0,2 м/с, а его скорость была бы 0,03 м/с, в восточном направлении.
Пример выше показывает, что скорость и скорость имеют разные значения, но в некоторых случаях их величины совпадают, особенно когда объект или человек движется только в одном направлении. Хотя эти две величины отличаются друг от друга, их обычно меняют местами, и скорость определяется просто как скорость с направлением.
Хотя эти две величины отличаются друг от друга, их обычно меняют местами, и скорость определяется просто как скорость с направлением.
Ускорение
Ускорение — это векторная величина, которая относится к изменению скорости в единицу времени. Он описывает, как быстро изменяется скорость. Ускорение происходит, когда объект либо меняет свое направление, либо свою величину. Например, ускорение возникает, когда автомобиль движется прямолинейно, но величина его скорости меняется в единицу времени.2 экв.}.
В кинематике обычно встречаются термины мгновенное ускорение, среднее ускорение и замедление. В чем разница между каждым термином?
- Мгновенное ускорение относится к ускорению в конкретный момент времени. Это очень малое изменение скорости за бесконечно малый интервал времени.
- Среднее ускорение — скорость изменения скорости. Это ускорение, описанное и выраженное математически выше.
- Замедление характеризуется ускорением, которое имеет направление, противоположное направлению скорости.
 Автомобиль, замедляющийся при движении вперед, испытывает торможение, поскольку направление ускорения противоположно (назад) направлению скорости (направлено вперед).
Автомобиль, замедляющийся при движении вперед, испытывает торможение, поскольку направление ускорения противоположно (назад) направлению скорости (направлено вперед).
Уравнения движения
Существуют уравнения, которые можно использовать при решении текстовых задач с постоянным ускорением.2+2a\Delta x {/eq}
- Уравнение 4: {eq}\Delta x =\frac{1}{2}(v+v_{0})t {/eq}
, где v — конечная скорость, {eq}v_{0} {/eq} — начальная скорость, t — время, {eq}\Delta x {/eq} — смещение, а — это ускорение. Каждое уравнение используется на основе заданных и неизвестных величин в задаче.
Рассмотрим приведенные ниже примеры, показывающие, как уравнения движения используются при решении задач.2})(50 \text{м}) {/экв}
- Шаг 5
- Найти ответ.

{eq}v=22.4 \text { м/с} {/eq}
Таким образом, конечная скорость автомобиля равна 22,4 м/с.
Пример 2
Автомобиль движется с постоянной скоростью и проезжает 80 м за 6,0 с. Если водитель нажал на тормоз и остановился через 5,0 с, какова величина его ускорения?
- Шаг 1
- Определите данные величины.
Первоначально автомобиль движется с постоянной скоростью. Рассчитайте начальную скорость, используя:
{eq}v_{0}=\frac{d}{t}=\frac{80 \text{ м}}{6,0 \text{ с}}=13,3 \text{ м/ s} {/eq}
Указаны конечная скорость и время.
{экв}v=0 \text{ м/с} {/экв}
{экв}t=5,0 \текст{с} {/экв}
- Шаг 2
- Определите неизвестную величину.
Найдите величину ускорения автомобиля.
- Шаг 3
- Выберите наиболее подходящее уравнение.2 экв.}. Знак минус указывает только на то, что автомобиль замедляется.
Графическое представление
В кинематике графики, в частности графики движения , используются для простой визуализации движения объекта.
 Наиболее распространенными графиками кинематического движения являются графики перемещения-времени и скорости-времени.
Наиболее распространенными графиками кинематического движения являются графики перемещения-времени и скорости-времени.На графике зависимости смещения от времени наклон графика соответствует скорости объекта. На рис. 3 показаны несколько примеров графиков смещения во времени и соответствующих им описаний движения. График A иллюстрирует стационарный объект на определенном расстоянии от опорной точки. Он показывает прямую горизонтальную линию. На графике B показан объект, движущийся с постоянной положительной скоростью, как показано прямой диагональной линией с положительным наклоном. График C представляет объект, имеющий возрастающую скорость в положительном направлении, в то время как график D предполагает, что объект движется с положительной уменьшающейся скоростью. Графики C и D имеют изменяющиеся градиенты, как показано кривыми линиями.
Рис. 3: Графики перемещения во времени и их соответствующие интерпретации
Графики смещения-времени на рис.
 3 имеют соответствующие графики скорости-времени. Площадь графика зависимости скорости от времени представляет смещение объекта, а его наклон описывает ускорение объекта.
3 имеют соответствующие графики скорости-времени. Площадь графика зависимости скорости от времени представляет смещение объекта, а его наклон описывает ускорение объекта.Рис. 4: Графики движения скорость-время и их соответствующие интерпретации
На показанных графиках скорость-время график A иллюстрирует объект в состоянии покоя, а график B показывает объект, движущийся с постоянной скоростью.На обоих графиках линия горизонтальна, что указывает на то, что ускорение объекта равно нулю. График C предполагает, что скорость объекта положительна и увеличивается с постоянной скоростью. Он образует прямую диагональную линию с положительным наклоном, что указывает на положительное ускорение. График D представляет объект, замедляющийся при движении в положительном направлении. Он показывает прямую диагональную линию с отрицательным наклоном, что означает, что объект замедляется.

Резюме урока
Кинематика — это изучение движения без учета его причин.Основываясь на кинематическом значении, его также можно описать как «геометрию в движении». При описании движения объекта необходимо четко задать систему отсчета. Система отсчета относится к набору координат или контрольных точек, используемых для описания положения, движения и других свойств объекта. Кинематика включает различные дескрипторы движения, которые определяются следующим образом:
- Расстояние относится к полному пути, пройденному объектом. Это скалярная величина.
- Перемещение описывает изменение положения объекта. Это векторная величина.
- Скорость относится к расстоянию, пройденному объектом в единицу времени.
- Скорость описывает перемещение за истекшее время.
- Ускорение — это векторная величина, которая относится к изменению скорости в единицу времени.
Графики движения используются для визуализации движения объекта.
 Наиболее часто используемыми графиками движения являются графики перемещение-время и скорость-время .Градиент графика «смещение-время» представляет собой скорость, а градиент графика «скорость-время» указывает на ускорение объекта. Например, объект, ускоряющийся в положительном направлении, будет иметь кривую графика смещения во времени. Его наклон эквивалентен его скорости, и соответствующий ему график зависимости скорости от времени будет иметь прямую диагональную линию с положительным наклоном, если его скорость постоянна.
Наиболее часто используемыми графиками движения являются графики перемещение-время и скорость-время .Градиент графика «смещение-время» представляет собой скорость, а градиент графика «скорость-время» указывает на ускорение объекта. Например, объект, ускоряющийся в положительном направлении, будет иметь кривую графика смещения во времени. Его наклон эквивалентен его скорости, и соответствующий ему график зависимости скорости от времени будет иметь прямую диагональную линию с положительным наклоном, если его скорость постоянна.%PDF-1.4 5 0 объект > эндообъект 8 0 объект (Элементарная механика) эндообъект 9 0 объект > эндообъект 12 0 объект (Ньютоновская механика) эндообъект 13 0 объект > эндообъект 16 0 объект (Уравнение движения одиночной частицы) эндообъект 17 0 объект > эндообъект 20 0 объект (Угловое движение) эндообъект 21 0 объект > эндообъект 24 0 объект (Энергия и работа) эндообъект 25 0 объект > эндообъект 28 0 объект (Гравитация) эндообъект 29 0 объект > эндообъект 32 0 объект (Сила гравитации) эндообъект 33 0 объект > эндообъект 36 0 объект (Гравитационный потенциал) эндообъект 37 0 объект > эндообъект 40 0 объект (Динамика систем частиц) эндообъект 41 0 объект > эндообъект 44 0 объект (Ньютоновские механические концепции для систем частиц) эндообъект 45 0 объект > эндообъект 48 0 объект (Теорема вириала) эндообъект 49 0 объект > эндообъект 52 0 объект (Столкновения частиц) эндообъект 53 0 объект > эндообъект 56 0 объект (лагранжева и гамильтонова динамика) эндообъект 57 0 объект > эндообъект 60 0 объект (Лагранжев подход к механике) эндообъект 61 0 объект > эндообъект 64 0 объект (Степени свободы, ограничения и обобщенные координаты) эндообъект 65 0 объект > эндообъект 68 0 объект (Виртуальное перемещение, виртуальная работа и обобщенные силы) эндообъект 69 0 объект > эндообъект 72 0 объект (принцип Даламбера и обобщенное уравнение движения) эндообъект 73 0 объект > эндообъект 76 0 объект (Лагранжиан и уравнения Эйлера-Лагранжа) эндообъект 77 0 объект > эндообъект 80 0 объект (Гамильтониан) эндообъект 81 0 объект > эндообъект 84 0 объект (Циклические координаты и канонические импульсы) эндообъект 85 0 объект > эндообъект 88 0 объект (Резюме) эндообъект 89 0 объект > эндообъект 92 0 объект (Еще примеры) эндообъект 93 0 объект > эндообъект 96 0 объект (Особые неконсервативные случаи) эндообъект 97 0 объект > эндообъект 100 0 объект (Преобразования симметрии, сохраняющиеся величины, циклические координаты и теорема Нётер) эндообъект 101 0 объект > эндообъект 104 0 объект (Вариационное исчисление и динамика) эндообъект 105 0 объект > эндообъект 108 0 объект (Вариационное исчисление и уравнение Эйлера) эндообъект 109 0 объект > эндообъект 112 0 объект (Принцип наименьшего действия и уравнение Эйлера-Лагранжа) эндообъект 113 0 объект > эндообъект 116 0 объект (Наложение ограничений в вариационной динамике) эндообъект 117 0 объект > эндообъект 120 0 объект (включение неголономных ограничений в вариационную динамику) эндообъект 121 0 объект > эндообъект 124 0 объект (Гамильтоновская динамика) эндообъект 125 0 объект > эндообъект 128 0 объект (Преобразования Лежандра и уравнения движения Гамильтона) эндообъект 129 0 объект > эндообъект 132 0 объект (Фазовое пространство и теорема Лиувилля) эндообъект 133 0 объект > эндообъект 136 0 объект (Темы теоретической механики) эндообъект 137 0 объект > эндообъект 140 0 объект (канонические преобразования и производящие функции) эндообъект 141 0 объект > эндообъект 144 0 объект (симплектическая запись) эндообъект 145 0 объект > эндообъект 148 0 объект (скобки Пуассона) эндообъект 149 0 объект > эндообъект 152 0 объект (Переменные действия-угла и адиабатическая инвариантность) эндообъект 153 0 объект > эндообъект 156 0 объект (Уравнение Гамильтона-Якоби) эндообъект 157 0 объект > эндообъект 160 0 объект (Колебания) эндообъект 161 0 объект > эндообъект 164 0 объект (Простой гармонический осциллятор) эндообъект 165 0 объект > эндообъект 168 0 объект (равновесия и колебания) эндообъект 169 0 объект > эндообъект 172 0 объект (Решение простого гармонического осциллятора) эндообъект 173 0 объект > эндообъект 176 0 объект (Затухающий простой гармонический осциллятор) эндообъект 177 0 объект > эндообъект 180 0 объект (Управляемый простой и демпфированный гармонический осциллятор) эндообъект 181 0 объект > эндообъект 184 0 объект (Поведение при приближении к резонансу) эндообъект 185 0 объект > эндообъект 188 0 объект (Связанные простые гармонические осцилляторы) эндообъект 189 0 объект > эндообъект 192 0 объект (Пример связанного маятника) эндообъект 193 0 объект > эндообъект 196 0 объект (Общий метод решения) эндообъект 197 0 объект > эндообъект 200 0 объект (Примеры и приложения) эндообъект 201 0 объект > эндообъект 204 0 объект (Вырождение) эндообъект 205 0 объект > эндообъект 208 0 объект (Волны) эндообъект 209 0 объект > эндообъект 212 0 объект (Загруженная строка) эндообъект 213 0 объект > эндообъект 216 0 объект (Непрерывная строка) эндообъект 217 0 объект > эндообъект 220 0 объект (Волновое уравнение) эндообъект 221 0 объект > эндообъект 224 0 объект (фазовая скорость, групповая скорость и волновые пакеты) эндообъект 225 0 объект > эндообъект 228 0 объект (Движение центральной силы и рассеяние) эндообъект 229 0 объект > эндообъект 232 0 объект (Общая проблема центральной силы) эндообъект 233 0 объект > эндообъект 236 0 объект (Уравнение движения) эндообъект 237 0 объект > эндообъект 240 0 объект (Формальные следствия уравнений движения) эндообъект 241 0 объект > эндообъект 244 0 объект (Особый случай гравитации — проблема Кеплера) эндообъект 245 0 объект > эндообъект 248 0 объект (Форма решений проблемы Кеплера) эндообъект 249 0 объект > эндообъект 252 0 объект (зависимость решений задачи Кеплера от времени) эндообъект 253 0 объект > эндообъект 256 0 объект (Сечения рассеяния) эндообъект 257 0 объект > эндообъект 260 0 объект (Постановка проблемы) эндообъект 261 0 объект > эндообъект 264 0 объект (Общее поперечное сечение) эндообъект 265 0 объект > эндообъект 268 0 объект (1r потенциалы) эндообъект 269 0 объект > эндообъект 272 0 объект (вращающиеся системы) эндообъект 273 0 объект > эндообъект 276 0 объект (Математическое описание вращений) эндообъект 277 0 объект > эндообъект 280 0 объект (Бесконечно малые вращения) эндообъект 281 0 объект > эндообъект 284 0 объект (Конечные вращения) эндообъект 285 0 объект > эндообъект 288 0 объект (Интерпретация вращений) эндообъект 289 0 объект > эндообъект 292 0 объект (Скаляры, векторы и тензоры) эндообъект 293 0 объект > эндообъект 296 0 объект (Комментарии к алгебрам Ли и группам Ли) эндообъект 297 0 объект > эндообъект 300 0 объект (Динамика во вращающихся системах координат) эндообъект 301 0 объект > эндообъект 304 0 объект (Второй закон Ньютона во вращающихся системах координат) эндообъект 305 0 объект > эндообъект 308 0 объект (Приложения) эндообъект 309 0 объект > эндообъект 312 0 объект (лагранжева и гамильтонова динамика во вращающихся системах координат) эндообъект 313 0 объект > эндообъект 316 0 объект (Вращательная динамика твердых тел) эндообъект 317 0 объект > эндообъект 320 0 объект (Основной формализм) эндообъект 321 0 объект > эндообъект 324 0 объект (Движение без крутящего момента) эндообъект 325 0 объект > эндообъект 328 0 объект (Движение под действием внешних моментов) эндообъект 329 0 объект > эндообъект 332 0 объект (Специальная теория относительности) эндообъект 333 0 объект > эндообъект 336 0 объект (Специальная теория относительности) эндообъект 337 0 объект > эндообъект 340 0 объект (Постулаты) эндообъект 341 0 объект > эндообъект 344 0 объект (Законы трансформации) эндообъект 345 0 объект > эндообъект 348 0 объект (Математическое описание преобразований Лоренца) эндообъект 349 0 объект > эндообъект 352 0 объект (Физические последствия) эндообъект 353 0 объект > эндообъект 356 0 объект (лагранжева и гамильтонова динамика в теории относительности) эндообъект 357 0 объект > эндообъект 360 0 объект (Математическое приложение) эндообъект 361 0 объект > эндообъект 364 0 объект (Условные обозначения для математических символов) эндообъект 365 0 объект > эндообъект 368 0 объект (Системы координат) эндообъект 369 0 объект > эндообъект 372 0 объект (Векторные и тензорные определения и алгебраические тождества) эндообъект 373 0 объект > эндообъект 376 0 объект (Векторное исчисление) эндообъект 377 0 объект > эндообъект 380 0 объект (Расширение Тейлора) эндообъект 381 0 объект > эндообъект 384 0 объект (Вариационное исчисление) эндообъект 385 0 объект > эндообъект 388 0 объект (Преобразования Лежандра) эндообъект 389 0 объект > эндообъект 392 0 объект (Сводка физических результатов) эндообъект 393 0 объект > эндообъект 396 0 объект (Элементарная механика) эндообъект 397 0 объект > эндообъект 400 0 объект (лагранжева и гамильтонова динамика) эндообъект 401 0 объект > эндообъект 404 0 объект (Колебания) эндообъект 405 0 объект > эндообъект 408 0 объект (Центральные силы и динамика рассеяния) эндообъект 409 0 объект > эндообъект 412 0 объект (вращающиеся системы) эндообъект 413 0 объект > эндообъект 416 0 объект (Специальная теория относительности) эндообъект 417 0 объект > эндообъект 420 0 объект > ручей xڍKK09&`b&֣EE7k-.
 Dů|Dhin֪\hwkmQ\\,2U\W
Dů|Dhin֪\hwkmQ\\,2U\WМеханика и общая физика
- Механика и общая физика
- Электротехника и оптика
- Современная физика и квантовая механика
Законы Ньютона: движение точечной частицы
Формулы
Кинематика (1D) и описание траектории, преобразования кадров
Кинематика (движение снаряда)
Второй закон Ньютона (с заданной силой)
Второй закон Ньютона (с трением)
Второй закон Ньютона (с сопротивлением)
Равномерное круговое движение и центростремительное ускорение
Круговое движение (в постоянном гравитационном поле)
Законы сохранения (энергии и импульс)
Работа
Энергия
Движение в неинерциальной системе отсчета
Статическое и динамическое равновесиеЗакон всемирного тяготения Ньютона
Закон всемирного тяготения Ньютона, Закон Гаусса
Импульсные силы, столкновения, взаимодействующие объекты
Формулы
Взаимодействующие объекты, 2-я теория Ньютона и 3-й законы, законы сохранения
Упругие столкновения
Неупругие столкновения
Ракеты
«Переменная масса» проблемы
Цепи и т. д.
д.Законы Ньютона: движение твердого тела
Формулы
Момент инерции и СМ
Кинематика вращения
Законы движения Ньютона применительно к твердым телам
Сохранение углового момента
Работа и сохранение энергии
Импульсы (соединяющие линейные и вращательное движение)
Статическое равновесие
Упругие свойства твердые предметыУравнения Лагранжа и Гамильтона
Формулы
Стандартные задачи Лагранжа (ограниченные точечные массы)
Стандартные задачи Лагранжа (наклонные плоскости)
Стандартные задачи Лагранжа (колебания)
Стандартные задачи Лагранжа (другие проблемы)
Проблемы с участием гамильтониана
Расширения лагранжиана и гамильтониана формализм
Множители ЛагранжаКолебания и волны
Формулы
Простые колебания
Возбужденные и затухающие колебания
Связанные колебания (точечные массы и пружины)
Связанные колебания (маятник)
Связанные колебания (другие системы)
Механические волныДвижение в центральном потенциале
Формулы
Проблема Кеплера
Другие центральные потенциалы
Рассеяние (твердые сферы, центральные потенциалы)Релятивистская кинематика и динамика
Формулы
Собственное время
Собственная длина
Преобразование Лоренца
Сложение скоростей
Доплеровский сдвиг
Столкновения (с участием только массивных частиц)
Столкновения (с участием безмассовых партнеров)
Распад (с участием только массивных партнеров)
Распад (с участием безмассовых партнеров)
Релятивистская энергия и импульс
СилаОбщая физика
Формулы
Плавучесть (жидкости)
Плавучесть (газы)
Статические и текущие жидкости
Статистика Больцмана
Тепловое расширение и проводимость
Удельная и скрытая теплота
Законы излучения
Закон идеального газа
Поверхность напряжение
Кинетическая теория
Первый закон термодинамики и идеал газовый закон
Второй закон термодинамики
Энтропия
Энтропия с участием идеальных газов
Анализ ошибок и математикаУгловая кинематика | Блестящая математика и естественные науки вики
Во вращающейся системе отсчета часто удобнее использовать полярные координаты, чем декартовы координаты.
 2rθ˙2=rω2 описывают радиальное ускорение наружу от начала координат и центростремительное ускорение по направлению к началу координат соответственно. Касательные члены представляют собой тангенциальных ускорений a=rθ¨=rαa = r\ddot{\theta} = r\alphaa=rθ¨=rα, где α=ω˙\alpha = \dot{\omega}α=ω ˙ угловое ускорение , а 2r˙θ˙=2r˙ω2\dot{r} \dot{\theta} = 2\dot{r} \omega2r˙θ˙=2r˙ω, кориолисово ускорение .
2rθ˙2=rω2 описывают радиальное ускорение наружу от начала координат и центростремительное ускорение по направлению к началу координат соответственно. Касательные члены представляют собой тангенциальных ускорений a=rθ¨=rαa = r\ddot{\theta} = r\alphaa=rθ¨=rα, где α=ω˙\alpha = \dot{\omega}α=ω ˙ угловое ускорение , а 2r˙θ˙=2r˙ω2\dot{r} \dot{\theta} = 2\dot{r} \omega2r˙θ˙=2r˙ω, кориолисово ускорение .Прямая линия в инерциальной системе отсчета становится криволинейной линией во вращающейся системе отсчета, когда нет силы, обеспечивающей ускорение Кориолиса [2].
Примечательно, что этот вывод доказывает безотносительно каких-либо сил, что объект, движущийся по окружности с угловой скоростью ω\omegaω, должен ускоряться радиально внутрь с центростремительным ускорением aca_cac, указанным выше.
Классическая механика. Факты для детей
Схема орбитального движения спутника вокруг Земли, показывающая перпендикулярные векторы скорости и ускорения (силы).
В физике классическая механика является одним из двух основных разделов механики.Другая область — квантовая механика. Классическая механика занимается набором физических законов, описывающих движение тел под действием системы сил. Изучение движения тел является древним, что делает классическую механику одним из старейших и крупнейших предметов в науке, технике и технике. Он также известен как ньютоновская механика , хотя авторы учебников часто рассматривают ньютоновскую механику, наряду с лагранжевой механикой и гамильтоновой механикой, как три основных формализма классической механики.
Классическая механика описывает движение макроскопических объектов, от снарядов до частей механизмов, и астрономических объектов, таких как космические корабли, планеты, звезды и галактики. В классической механике есть подполя, в том числе те, которые описывают поведение твердых тел, жидкостей и газов. Классическая механика дает чрезвычайно точные результаты при изучении крупных объектов и скоростей, не приближающихся к скорости света.

Когда изучаемые объекты достаточно малы, возникает необходимость ввести другой крупный раздел механики: квантовую механику.Это подполе адаптирует законы физики макроскопических объектов к атомарной природе материи, включая корпускулярно-волновой дуализм атомов и молекул.
Когда ни квантовая, ни классическая механика неприменимы, например, на квантовом уровне с высокими скоростями, становится применимой квантовая теория поля (КТП).
Термин классической механики был придуман в начале 20 века. Он описывает систему физики, начатую Исааком Ньютоном и многими современными естествоиспытателями 17 века.Он также основан на более ранних астрономических теориях Иоганна Кеплера. Классическая механика использует представления здравого смысла о том, как материя и силы существуют и взаимодействуют. Он предполагает, что материя и энергия обладают определенными, познаваемыми атрибутами, такими как положение в пространстве и скорость.
Три закона Ньютона
Страница из книги Ньютона о трех законах движенияТри закона движения Ньютона важны для классической механики.
 Их создал Исаак Ньютон.
Их создал Исаак Ньютон.Первый закон гласит, что если нет внешней силы (имеется в виду отсутствие толчка, гравитации или какой-либо силы), остановившиеся вещи останутся остановленными или неподвижными, а движущиеся останутся неподвижными. движущийся.Раньше люди думали, что все останавливается, если нет силы. Часто люди говорят: Остановленные объекты имеют тенденцию оставаться остановленными, а движущиеся объекты имеют тенденцию оставаться в движении, если на них не действует внешняя сила, такая как гравитация, трение и т. д….
Второй закон говорит о том, как сила перемещает вещь. Суммарная сила, действующая на объект, равна скорости изменения его импульса.
Третий закон говорит, что если одна вещь воздействует на другую вещь, то вторая вещь также воздействует на первую вещь.Вторая сила по величине равна первой силе. Силы действуют в противоположных направлениях. Например, если вы прыгаете вперед с лодки, лодка движется назад.
 Часто говорят: На каждое действие есть равное и противоположное противодействие.
Часто говорят: На каждое действие есть равное и противоположное противодействие. Кинематические уравнения
В физике кинематика — это часть классической механики, которая объясняет движение объектов, не обращая внимания на то, что вызывает движение или на что оно влияет.
1-мерная кинематика
Одномерная (1D) кинематика используется только тогда, когда объект движется в одном направлении: из стороны в сторону (слева направо) или вверх и вниз.Существуют уравнения, которые можно использовать для решения задач, имеющих движение только в одном измерении или направлении. Эти уравнения исходят из определений скорости, ускорения и расстояния.
- Первое кинематическое уравнение 1D имеет дело с ускорением и скоростью. Если ускорение и скорость не изменяются. (Не обязательно включать расстояние)
- Уравнение:
- V f – конечная скорость.
- v i — стартовая или начальная скорость
- а это ускорение
- t is time — сколько времени объект разгонялся.

- Уравнение:
- Второе кинематическое уравнение 1D определяет пройденное расстояние, используя среднюю скорость и время. (Не нужно включать ускорение)
- Уравнение:
- x пройденное расстояние.
- V f – конечная скорость.
- v i — стартовая или начальная скорость
- т это время
- Уравнение:
- Третье кинематическое уравнение 1D определяет расстояние, пройденное при ускорении объекта.Он имеет дело со скоростью, ускорением, временем и расстоянием. (Не обязательно включать конечную скорость)
- Уравнение:
- — это конечное пройденное расстояние
- x i — стартовое или начальное расстояние
- v i — стартовая или начальная скорость
- а это ускорение
- т это время
- Уравнение:
- Четвертое кинематическое уравнение 1D определяет конечную скорость, используя начальную скорость, ускорение и пройденное расстояние.
 (Не нужно включать время)
(Не нужно включать время)- Уравнение:
- V f – конечная скорость
- v i — стартовая или начальная скорость
- а это ускорение
- x пройденное расстояние
- Уравнение:
2-мерная кинематика
Двухмерная кинематика используется, когда движение происходит как в направлении x (слева направо), так и в направлении y (вверх и вниз). Существуют также уравнения для этого типа кинематики.Однако существуют разные уравнения для направления x и разные уравнения для направления y. Галилей доказал, что скорость в направлении х не меняется на протяжении всего пробега. Однако на направление Y влияет сила тяжести, поэтому скорость Y меняется во время бега.
Уравнения X-направления
- Движение влево и вправо
- Первое уравнение для направления x — единственное, которое необходимо для решения задач, потому что скорость в направлении x остается неизменной.

- Уравнение:
- X — расстояние, пройденное в направлении x
- V x скорость в направлении x
- т это время
- Уравнение:
Уравнения направления Y
- Движение вверх и вниз. Под действием силы тяжести или другого внешнего ускорения
- Первое уравнение y-направления почти такое же, как первое 1-мерное кинематическое уравнение, за исключением того, что оно имеет дело с изменяющейся y-скоростью.Он имеет дело со свободно падающим телом, на которое действует сила тяжести. (расстояние не требуется)
- Уравнение:
- V fy – конечная скорость по оси y
- v iy — начальная или начальная скорость по оси y
- g — это ускорение свободного падения, которое равно 9,8 или 32 .
- т это время
- Уравнение:
- Второе уравнение направления Y используется, когда на объект воздействует отдельное ускорение, а не гравитация.
 В этом случае необходима y-компонента вектора ускорения. (расстояние не требуется)
В этом случае необходима y-компонента вектора ускорения. (расстояние не требуется)- Уравнение:
- V fy – конечная скорость по оси y
- v iy — начальная или начальная скорость по оси y
- a y — y-компонента вектора ускорения
- т это время
- Уравнение:
- Третье уравнение для направления y определяет расстояние, пройденное в направлении y, используя среднюю скорость y и время.(Не требует ускорения свободного падения или внешнего ускорения)
- Уравнение:
- X y расстояние, пройденное в направлении y
- V fy — конечная скорость по оси Y
- v iy — начальная или начальная скорость по оси y
- т это время
- Уравнение:
- Четвертое уравнение для направления y касается расстояния, пройденного в направлении y под действием гравитации. (Не требуется конечная скорость по оси y)
- Уравнение:
- — это конечное расстояние, пройденное в направлении Y
- x iy — начальное или начальное расстояние в направлении Y
- v iy начальная скорость в направлении y
- g — это ускорение свободного падения, равное 9.
 8 или 32
8 или 32 - т это время
- Уравнение:
- Пятое уравнение для направления y касается расстояния, пройденного в направлении y под действием другого ускорения, отличного от силы тяжести. (Не требуется конечная скорость по оси y)
- Уравнение:
- — это конечное расстояние, пройденное в направлении Y
- x iy — начальное или начальное расстояние в направлении Y
- v iy начальная скорость в направлении y
- a y — y-компонента вектора ускорения
- т это время
- Уравнение:
- Шестое уравнение для направления по оси Y определяет окончательную скорость по оси Y, когда на нее действует гравитация на определенном расстоянии.(Не нужно время)
- Уравнение:
- V fy – конечная скорость в направлении y
- V iy начальная скорость в направлении y
- g — это ускорение свободного падения, которое равно 9,8 или 32 .
- x y — общее расстояние, пройденное в направлении y

- Уравнение:
- Седьмое уравнение для направления по оси Y определяет окончательную скорость по оси Y, когда на нее действует ускорение, отличное от силы тяжести, на определенном расстоянии.(Не нужно время)
- Уравнение:
- V fy – конечная скорость в направлении y
- V iy начальная скорость в направлении y
- a y — y-компонента вектора ускорения
- x y — общее расстояние, пройденное в направлении y
- Уравнение:
Филиалы
Классическая механика традиционно делилась на три основных направления:
- Статика, учение о равновесии и его связи с силами
- Динамика, изучение движения и его связи с силами
- Кинематика, имеющая дело с последствиями наблюдаемых движений без учета обстоятельств, вызвавших их
Другое деление основано на выборе математического формализма:
В качестве альтернативы можно разделить по регионам применения:
- Небесная механика, связанная со звездами, планетами и другими небесными телами
- Механика сплошной среды для материалов, моделируемых как сплошная среда, например.
 г., твердые тела и жидкости (т. е. жидкости и газы).
г., твердые тела и жидкости (т. е. жидкости и газы). - Релятивистская механика (т.е. включающая специальную и общую теории относительности) для тел, скорость которых близка к скорости света.
- Статистическая механика, которая обеспечивает основу для связи микроскопических свойств отдельных атомов и молекул с макроскопическими или объемными термодинамическими свойствами материалов.
Связанные страницы
Картинки для детей
Анализ движения снаряда является частью классической механики.
Кинематика вращательного движения – Колледж физики
Цели обучения
- Соблюдать кинематику вращательного движения.
- Вывести уравнения кинематики вращения.
- Оцените стратегии решения проблем для вращательной кинематики.
Просто используя нашу интуицию, мы можем начать видеть, как величины вращения, такие как , и, связаны друг с другом.
 Например, если колесо мотоцикла имеет большое угловое ускорение в течение достаточно долгого времени, оно быстро начинает вращаться и делает много оборотов.С технической точки зрения, если угловое ускорение колеса велико в течение длительного периода времени, то конечная угловая скорость и угол поворота велики. Вращательное движение колеса в точности аналогично тому факту, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Например, если колесо мотоцикла имеет большое угловое ускорение в течение достаточно долгого времени, оно быстро начинает вращаться и делает много оборотов.С технической точки зрения, если угловое ускорение колеса велико в течение длительного периода времени, то конечная угловая скорость и угол поворота велики. Вращательное движение колеса в точности аналогично тому факту, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.Кинематика — это описание движения. Кинематика вращательного движения описывает соотношения между углом поворота, угловой скоростью, угловым ускорением и временем.Начнем с поиска уравнения, связывающего , и . Чтобы определить это уравнение, вспомним известное кинематическое уравнение поступательного, или прямолинейного, движения:
Обратите внимание, что при вращательном движении , и с этого момента мы будем использовать символ для тангенциального или линейного ускорения. Как и в линейной кинематике, мы считаем постоянным, что означает, что угловое ускорение также является постоянным, потому что .
 Теперь подставим и в линейное уравнение выше:
Теперь подставим и в линейное уравнение выше:Радиус сокращается в уравнении, что дает
где – начальная угловая скорость.Это последнее уравнение представляет собой кинематическую связь между , , и , т. е. описывает их взаимосвязь без ссылки на силы или массы, которые могут влиять на вращение. Он также в точности аналогичен по форме своему трансляционному аналогу.
Установка соединений
Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в Одномерной кинематике. Кинематика занимается описанием движения без учета силы или массы.Мы обнаружим, что поступательные кинематические величины, такие как перемещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.
Начав с четырех кинематических уравнений, которые мы разработали в разделе «Одномерная кинематика», мы можем вывести следующие четыре уравнения кинематики вращения (представленные вместе с их эквивалентами поступательного движения):
В этих уравнениях нижний индекс 0 обозначает начальные значения ( , , и являются начальными значениями), а средняя угловая скорость и средняя скорость определяются следующим образом:
Уравнения, приведенные выше на (Рисунок), могут быть использованы для решения любой вращательной или поступательной кинематической задачи, в которой и постоянны.

Стратегия решения задач по кинематике вращения
- Изучите ситуацию, чтобы определить, задействована ли вращательная кинематика (вращательное движение) . Вращение должно быть задействовано, но без необходимости учитывать силы или массы, влияющие на движение.
- Определите, что именно нужно определить в задаче (укажите неизвестные) . Набросок ситуации полезен.
- Составьте список того, что дано или может быть выведено из сформулированной проблемы (укажите известное) .
- Решите соответствующее уравнение или уравнения для определяемой величины (неизвестной) . Может быть полезно подумать в терминах поступательного аналога, потому что к этому моменту вы уже знакомы с таким движением.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения .
 Обязательно используйте радианы для углов.
Обязательно используйте радианы для углов. - Проверьте свой ответ, чтобы убедиться, что он разумен: Имеет ли смысл ваш ответ ?
Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит на крючок большую рыбу, которая уплывает от лодки, вытягивая леску из своей рыболовной катушки.Вся система изначально находится в покое и леска разматывается с катушки на радиусе 4,50 см от ее оси вращения. Катушке придается угловое ускорение в течение 2,00 с, как показано на (рис.).
(а) Какова конечная угловая скорость катушки?
(b) С какой скоростью леска покидает катушку по истечении 2,00 с?
(c) Сколько оборотов делает катушка?
(г) Сколько метров лески за это время сорвется с катушки?
Стратегия
В каждой части этого примера используется та же стратегия, что и при решении задач линейной кинематики.В частности, идентифицируются известные значения, а затем ищется взаимосвязь, которую можно использовать для нахождения неизвестного.

Раствор для (а)
Вот и даются и нужно определить. Наиболее просто использовать уравнение, потому что неизвестное уже находится на одной стороне, а все остальные члены известны. Это уравнение утверждает, что
Нам также дано, что (начинается с покоя), так что
Решение для (б)
Теперь, когда известно, скорость легче всего найти, используя соотношение
, где радиус барабана равен 4.50 см; таким образом,
Еще раз обратите внимание, что радианы всегда должны использоваться при любых вычислениях, связанных с линейными и угловыми величинами. Кроме того, поскольку радианы безразмерны, мы имеем .
Раствор для (с)
Здесь нас просят найти количество оборотов. Потому что мы можем найти количество оборотов, найдя в радианах. Нам дано и , и мы знаем, что это ноль, так что можно получить с помощью .
Преобразование радианов в обороты дает
Решение для (d)
Количество метров лески , которое можно получить через его связь с :
Обсуждение
Этот пример показывает, что отношения между вращательными величинами очень аналогичны отношениям между линейными величинами.
Леска, сходящая с вращающейся катушки, движется линейно. (Рисунок) и (Рисунок) рассматривают отношения между вращательными и линейными величинами, связанными с рыболовной катушкой. Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После размотки в течение двух секунд обнаруживается, что катушка вращается со скоростью 220 рад/с, что составляет 2100 об/мин. (Неудивительно, что катушки иногда издают высокие звуки.) Длина вытянутой лески составляет 9,90 м, что примерно соответствует моменту поклевки крупной рыбы.
Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После размотки в течение двух секунд обнаруживается, что катушка вращается со скоростью 220 рад/с, что составляет 2100 об/мин. (Неудивительно, что катушки иногда издают высокие звуки.) Длина вытянутой лески составляет 9,90 м, что примерно соответствует моменту поклевки крупной рыбы.Расчет продолжительности замедления и остановки рыболовной катушки
Теперь давайте рассмотрим, что произойдет, если рыбак затормозит спиннинговую катушку, достигнув углового ускорения . Сколько времени требуется барабану, чтобы остановиться?
Стратегия
Нас просят найти время остановки барабана. Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка.
 Теперь мы видим, что начальная угловая скорость равна, а конечная угловая скорость равна нулю. Угловое ускорение принимается равным . Изучив имеющиеся уравнения, мы видим, что все величины известны, кроме t , что упрощает использование этого уравнения.
Теперь мы видим, что начальная угловая скорость равна, а конечная угловая скорость равна нулю. Угловое ускорение принимается равным . Изучив имеющиеся уравнения, мы видим, что все величины известны, кроме t , что упрощает использование этого уравнения.Раствор
Уравнение утверждает
Мы решаем уравнение алгебраически для t , а затем, как обычно, подставляем известные значения, что дает
Обсуждение
Обратите внимание, что необходимо соблюдать осторожность со знаками, указывающими направления различных величин.Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда рвется из-за связанных с ней ускорений, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Уставшая рыба будет двигаться медленнее, требуя меньшего ускорения.
Расчет медленного ускорения поездов и их колес
Большие грузовые поезда разгоняются очень медленно.
 Предположим, что один такой поезд разгоняется из состояния покоя, что дает его 0.Колеса с радиусом 350 м и угловым ускорением . После того, как колеса совершили 200 оборотов (предположим, что проскальзывание отсутствует): (а) Как далеко поезд продвинулся по пути? б) Чему равны конечная угловая скорость колес и линейная скорость поезда?
Предположим, что один такой поезд разгоняется из состояния покоя, что дает его 0.Колеса с радиусом 350 м и угловым ускорением . После того, как колеса совершили 200 оборотов (предположим, что проскальзывание отсутствует): (а) Как далеко поезд продвинулся по пути? б) Чему равны конечная угловая скорость колес и линейная скорость поезда?Стратегия
В части (а) нас просят найти , а в (б) нас просят найти и . Нам заданы число оборотов, радиус колес и угловое ускорение.
Раствор для (а)
Расстояние очень легко найти из соотношения между расстоянием и углом поворота:
Решение этого уравнения для выхода
Прежде чем использовать это уравнение, мы должны преобразовать число оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:
Теперь мы можем подставить известные значения, чтобы найти расстояние, на которое проехал поезд:
Раствор для (б)
Мы не можем использовать какое-либо уравнение, которое включает в себя, чтобы найти , потому что уравнение будет иметь по крайней мере два неизвестных значения.
 Уравнение будет работать, потому что мы знаем значения всех переменных, кроме:
Уравнение будет работать, потому что мы знаем значения всех переменных, кроме:Извлечение квадратного корня из этого уравнения и ввод известных значений дает
Мы можем найти линейную скорость поезда через отношение к :
Обсуждение
Пройденное расстояние довольно велико, а конечная скорость довольно мала (чуть меньше 32 км/ч).
Существует поступательное движение даже для чего-либо, вращающегося на месте, как показано в следующем примере.(Рисунок) показывает муху на краю вращающейся плиты микроволновой печи. В приведенном ниже примере вычисляется общее расстояние, которое он проходит.
На изображении показана тарелка для микроволновой печи. Муха совершает обороты, пока еда нагревается (вместе с мухой).
Проверьте свое понимание
Вращательная кинематика имеет много полезных взаимосвязей, часто выражаемых в форме уравнений. Являются ли эти отношения законами физики или они просто описательные? (Подсказка: тот же вопрос относится и к линейной кинематике.
 )
)Вращательная кинематика (как и линейная кинематика) носит описательный характер и не отражает законы природы. С помощью кинематики мы можем с большой точностью описать многие вещи, но кинематика не рассматривает причины. Например, большое угловое ускорение описывает очень быстрое изменение угловой скорости без учета его причины.
Задачи и упражнения
С помощью струны гироскоп разгоняется из состояния покоя до 32 рад/с за 0,40 с.
(a) Каково его угловое ускорение в рад/с 2 ?
(б) Сколько оборотов он совершает при этом?
(а)
(б) 1.0 ред.
Допустим, на компакт-диске оказалась пылинка. Если скорость вращения компакт-диска составляет 500 об/мин, а пылинка находится на расстоянии 4,3 см от центра, какое общее расстояние проходит пыль за 3 минуты? (Игнорировать ускорения из-за вращения компакт-диска.)
Гироскоп замедляется с начальной скоростью 32.0 рад/с при скорости .

(а) Сколько времени требуется, чтобы прийти в состояние покоя?
(б) Сколько оборотов он делает до остановки?
Во время очень быстрой остановки автомобиль замедляется на .
(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по дорожному покрытию?
(b) Сколько оборотов сделают шины до остановки, если их начальная угловая скорость равна ?
(c) Через какое время автомобиль полностью остановится?
(г) Какое расстояние проедет автомобиль за это время?
(e) Какова была начальная скорость автомобиля?
(f) Являются ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?
Йо-йо — это забавные игрушки, в которых реализована важная физика, и они разработаны для повышения производительности на основе физических законов.(кредит: Beyond Neon, Flickr)
Повседневное применение: предположим, что у йо-йо есть центральный стержень с радиусом 0,250 см, а шнур натягивается.

(a) Если струна неподвижна, а йо-йо ускоряется при удалении от нее со скоростью , каково угловое ускорение йо-йо?
(b) Какова угловая скорость через 0,750 с, если он стартует из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на ее ребре?
а)
б) 450 рад/с
в) 21.0 м/с
Глоссарий
- кинематика вращательного движения
- описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем .

 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.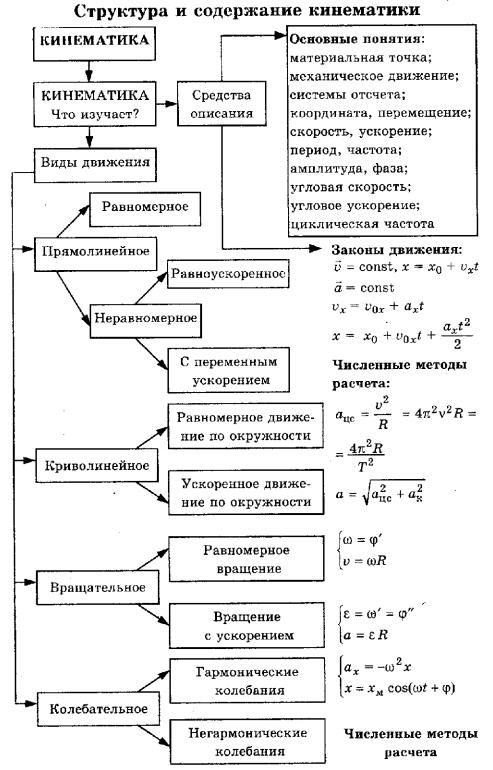 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
 Автомобиль, замедляющийся при движении вперед, испытывает торможение, поскольку направление ускорения противоположно (назад) направлению скорости (направлено вперед).
Автомобиль, замедляющийся при движении вперед, испытывает торможение, поскольку направление ускорения противоположно (назад) направлению скорости (направлено вперед).
 Наиболее распространенными графиками кинематического движения являются графики перемещения-времени и скорости-времени.
Наиболее распространенными графиками кинематического движения являются графики перемещения-времени и скорости-времени. 3 имеют соответствующие графики скорости-времени. Площадь графика зависимости скорости от времени представляет смещение объекта, а его наклон описывает ускорение объекта.
3 имеют соответствующие графики скорости-времени. Площадь графика зависимости скорости от времени представляет смещение объекта, а его наклон описывает ускорение объекта.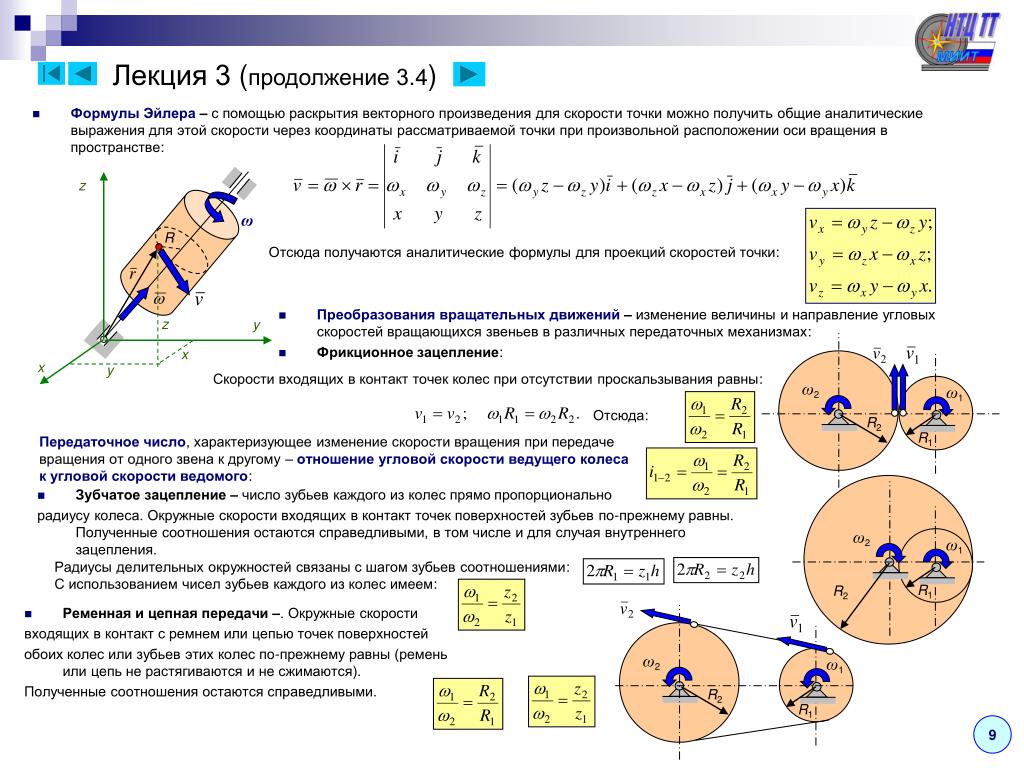
 Наиболее часто используемыми графиками движения являются графики перемещение-время и скорость-время .Градиент графика «смещение-время» представляет собой скорость, а градиент графика «скорость-время» указывает на ускорение объекта. Например, объект, ускоряющийся в положительном направлении, будет иметь кривую графика смещения во времени. Его наклон эквивалентен его скорости, и соответствующий ему график зависимости скорости от времени будет иметь прямую диагональную линию с положительным наклоном, если его скорость постоянна.
Наиболее часто используемыми графиками движения являются графики перемещение-время и скорость-время .Градиент графика «смещение-время» представляет собой скорость, а градиент графика «скорость-время» указывает на ускорение объекта. Например, объект, ускоряющийся в положительном направлении, будет иметь кривую графика смещения во времени. Его наклон эквивалентен его скорости, и соответствующий ему график зависимости скорости от времени будет иметь прямую диагональную линию с положительным наклоном, если его скорость постоянна. Dů|Dhin֪\hwkmQ\\,2U\W
Dů|Dhin֪\hwkmQ\\,2U\W д.
д. 2rθ˙2=rω2 описывают радиальное ускорение наружу от начала координат и центростремительное ускорение по направлению к началу координат соответственно. Касательные члены представляют собой тангенциальных ускорений a=rθ¨=rαa = r\ddot{\theta} = r\alphaa=rθ¨=rα, где α=ω˙\alpha = \dot{\omega}α=ω ˙ угловое ускорение , а 2r˙θ˙=2r˙ω2\dot{r} \dot{\theta} = 2\dot{r} \omega2r˙θ˙=2r˙ω, кориолисово ускорение .
2rθ˙2=rω2 описывают радиальное ускорение наружу от начала координат и центростремительное ускорение по направлению к началу координат соответственно. Касательные члены представляют собой тангенциальных ускорений a=rθ¨=rαa = r\ddot{\theta} = r\alphaa=rθ¨=rα, где α=ω˙\alpha = \dot{\omega}α=ω ˙ угловое ускорение , а 2r˙θ˙=2r˙ω2\dot{r} \dot{\theta} = 2\dot{r} \omega2r˙θ˙=2r˙ω, кориолисово ускорение .

 Их создал Исаак Ньютон.
Их создал Исаак Ньютон. Часто говорят: На каждое действие есть равное и противоположное противодействие.
Часто говорят: На каждое действие есть равное и противоположное противодействие. 
 (Не нужно включать время)
(Не нужно включать время)
 В этом случае необходима y-компонента вектора ускорения. (расстояние не требуется)
В этом случае необходима y-компонента вектора ускорения. (расстояние не требуется) 8 или 32
8 или 32
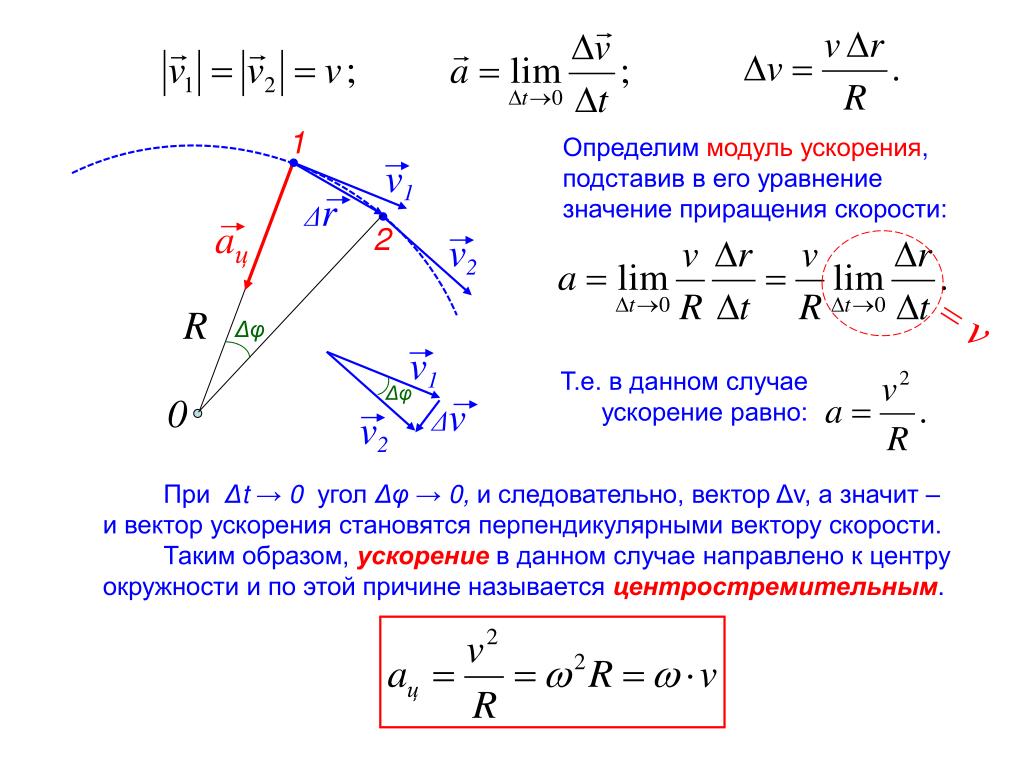 г., твердые тела и жидкости (т. е. жидкости и газы).
г., твердые тела и жидкости (т. е. жидкости и газы). Например, если колесо мотоцикла имеет большое угловое ускорение в течение достаточно долгого времени, оно быстро начинает вращаться и делает много оборотов.С технической точки зрения, если угловое ускорение колеса велико в течение длительного периода времени, то конечная угловая скорость и угол поворота велики. Вращательное движение колеса в точности аналогично тому факту, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Например, если колесо мотоцикла имеет большое угловое ускорение в течение достаточно долгого времени, оно быстро начинает вращаться и делает много оборотов.С технической точки зрения, если угловое ускорение колеса велико в течение длительного периода времени, то конечная угловая скорость и угол поворота велики. Вращательное движение колеса в точности аналогично тому факту, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим. Теперь подставим и в линейное уравнение выше:
Теперь подставим и в линейное уравнение выше:
 Обязательно используйте радианы для углов.
Обязательно используйте радианы для углов.
 Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После размотки в течение двух секунд обнаруживается, что катушка вращается со скоростью 220 рад/с, что составляет 2100 об/мин. (Неудивительно, что катушки иногда издают высокие звуки.) Длина вытянутой лески составляет 9,90 м, что примерно соответствует моменту поклевки крупной рыбы.
Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После размотки в течение двух секунд обнаруживается, что катушка вращается со скоростью 220 рад/с, что составляет 2100 об/мин. (Неудивительно, что катушки иногда издают высокие звуки.) Длина вытянутой лески составляет 9,90 м, что примерно соответствует моменту поклевки крупной рыбы. Теперь мы видим, что начальная угловая скорость равна, а конечная угловая скорость равна нулю. Угловое ускорение принимается равным . Изучив имеющиеся уравнения, мы видим, что все величины известны, кроме t , что упрощает использование этого уравнения.
Теперь мы видим, что начальная угловая скорость равна, а конечная угловая скорость равна нулю. Угловое ускорение принимается равным . Изучив имеющиеся уравнения, мы видим, что все величины известны, кроме t , что упрощает использование этого уравнения. Предположим, что один такой поезд разгоняется из состояния покоя, что дает его 0.Колеса с радиусом 350 м и угловым ускорением . После того, как колеса совершили 200 оборотов (предположим, что проскальзывание отсутствует): (а) Как далеко поезд продвинулся по пути? б) Чему равны конечная угловая скорость колес и линейная скорость поезда?
Предположим, что один такой поезд разгоняется из состояния покоя, что дает его 0.Колеса с радиусом 350 м и угловым ускорением . После того, как колеса совершили 200 оборотов (предположим, что проскальзывание отсутствует): (а) Как далеко поезд продвинулся по пути? б) Чему равны конечная угловая скорость колес и линейная скорость поезда? Уравнение будет работать, потому что мы знаем значения всех переменных, кроме:
Уравнение будет работать, потому что мы знаем значения всех переменных, кроме: )
)

