Формула архимеда – Равновесие, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук | ЕГЭ по физике — Детская игровая комната «Волшебный лес»

Posted on 30.03.202031.12.2019 by alexxlab

Содержание

Архимедова сила. Видеоурок. Физика 7 Класс

Древнегреческий ученый Архимед (рис. 1) прославился многочисленными открытиями.

Рис. 1. Архимед (287–212 гг. до н. э.)

Именно он первым обнаружил, объяснил и сумел рассчитать выталкивающую силу. На прошлом уроке мы выяснили, что эта сила действует на любое тело, погруженное в жидкость или газ (рис. 2).

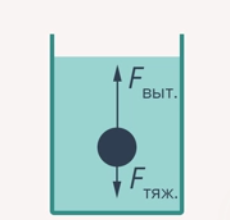
Рис. 2. Сила Архимеда

В честь Архимеда эта сила называется также архимедовой силой. Расчетным путем мы получили формулу для вычисления этой силы. На данном уроке мы воспользуемся экспериментальным методом, чтобы выяснить, от каких факторов зависит выталкивающая сила, а от каких факторов она не зависит.

Для проведения эксперимента мы будем использовать тела различного объема, сосуд с жидкостью и динамометр.

Прикрепим груз меньшего объема к динамометру и измерим вес этого груза сначала в воздухе: 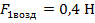, а затем опустив груз в жидкость: 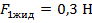. При этом можно заметить, что величина деформации пружины после опускания груза в жидкость практически не изменилась. Это говорит о том, что выталкивающая сила, действующая на груз, невелика.

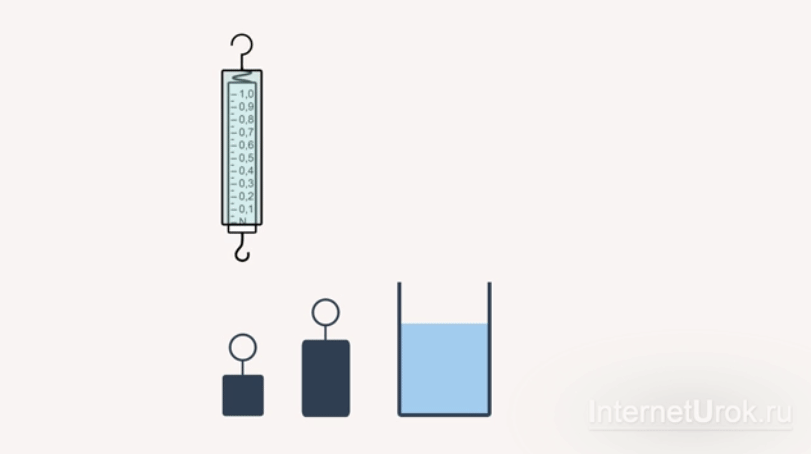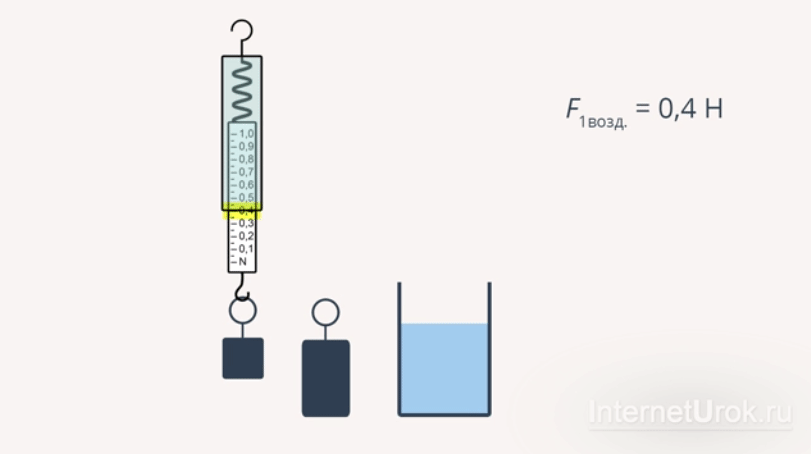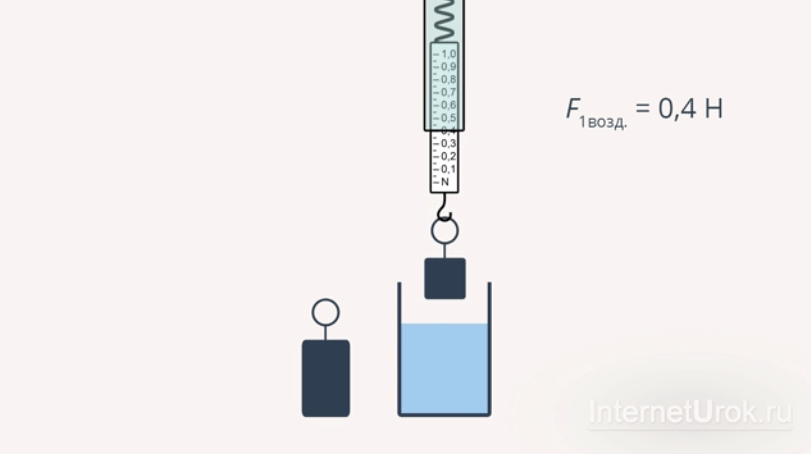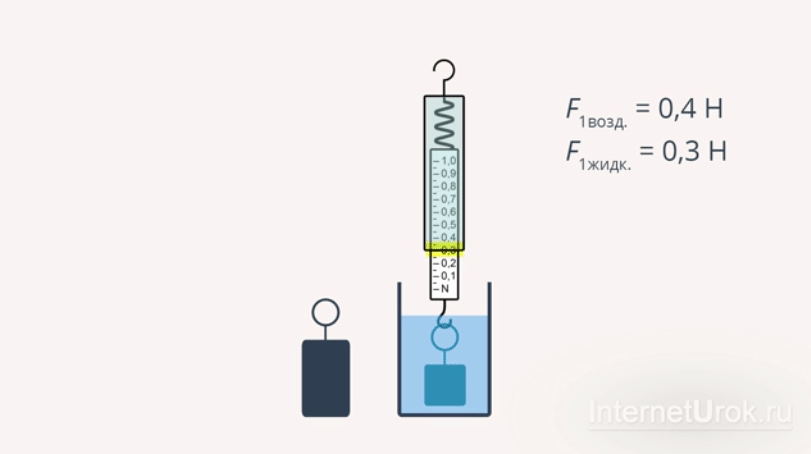
Рис 3. Эксперимент с грузом малого объема

Теперь прикрепим к пружине динамометра груз большего объема и погрузим его в жидкость. Мы увидим, что деформация пружины уменьшилась значительнее.

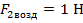
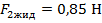
Это произошло благодаря тому, что величина выталкивающей силы стала больше.

Рис 4. Эксперимент с грузом большего объема

По результату данного эксперимента можно сделать промежуточный вывод.

Чем больше объем погруженной в жидкость части тела, тем больше выталкивающая сила, действующая на тело.

Возьмем два тела одинакового объема, но изготовленные из разных материалов. Это значит, что у них различная плотность. Подвесим к динамометру сначала один груз и опустим его в жидкость. По изменению показаний динамометра найдем выталкивающую силу.

Рис. 5 Эксперимент с первым грузиком

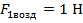
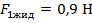
Затем такую же операцию проведем со вторым грузом.

Рис. 6 Эксперимент со вторым грузиком

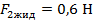
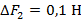
Хотя вес первого и второго груза разные, но при погружении в жидкость показания динамометра уменьшатся на одну и ту же величину.

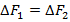
Это означает, что в обоих случаях значение выталкивающей силы одно и то же, хотя грузы выполнены из разного материала.

Таким образом, можно сделать еще один промежуточный вывод.

Величина выталкивающей силы не зависит от плотности тел, погруженных в жидкость.

Прикрепим груз к пружине динамометра и опустим его в воду таким образом, чтобы он был полностью погружен в жидкость. Отметим показания динамометра 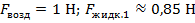. Теперь будем медленно подливать жидкость в сосуд. Мы заметим, что показания динамометра практически не изменяются 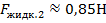. А значит, не меняется и выталкивающая сила.

Рис. 7 Эксперимент № 3

Третий промежуточный вывод.

Величина выталкивающей силы не зависит от высоты столба жидкости над погруженным в жидкость телом.

Прикрепим груз к пружине динамометра. Заметив показания динамометра, когда тело находится в воздухе: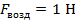

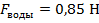, погрузим тело сначала в воду:

, а затем в масло:

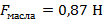. По изменению показаний динамометра можно судить, что выталкивающая сила, действующая на тело в воде, больше, чем выталкивающая сила, действующая на то же самое тело в масле.

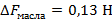
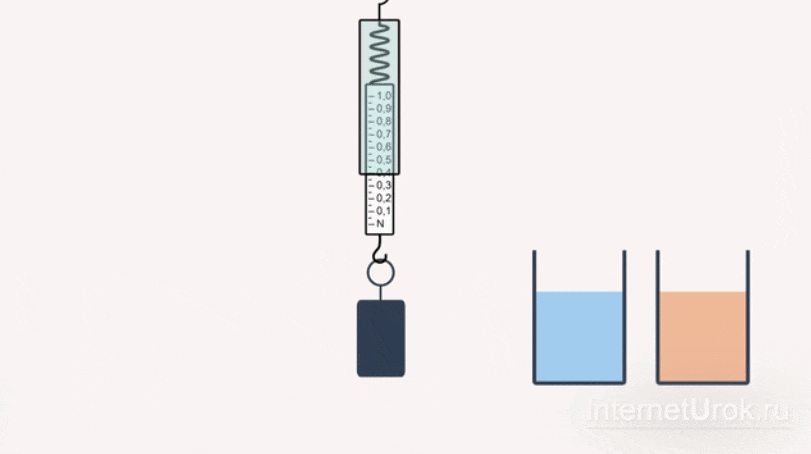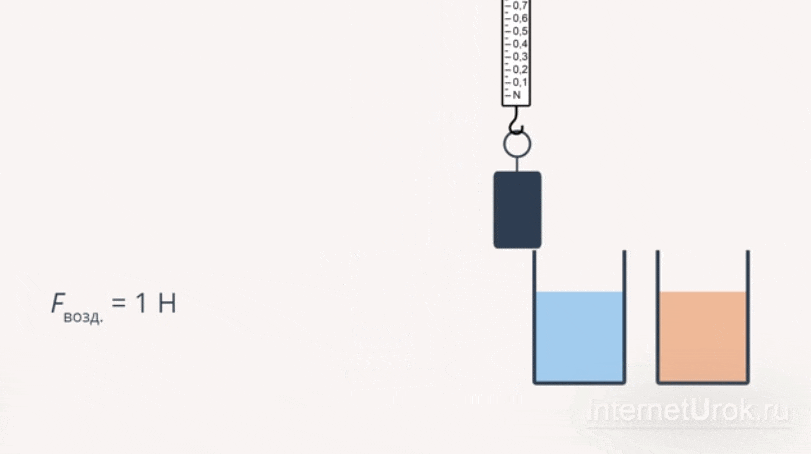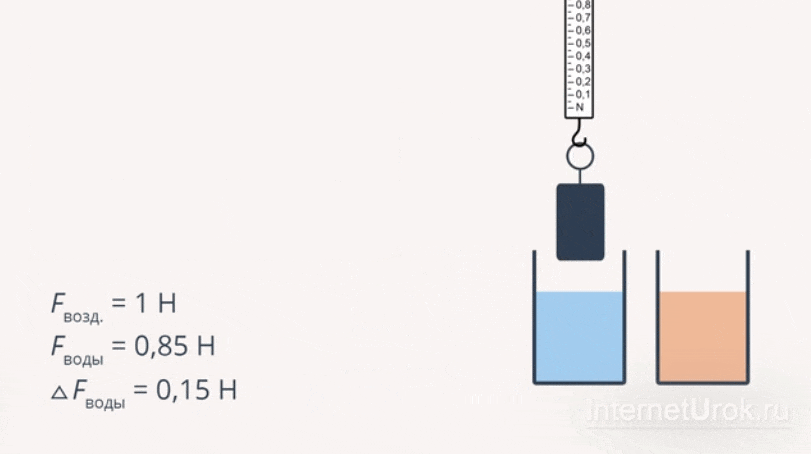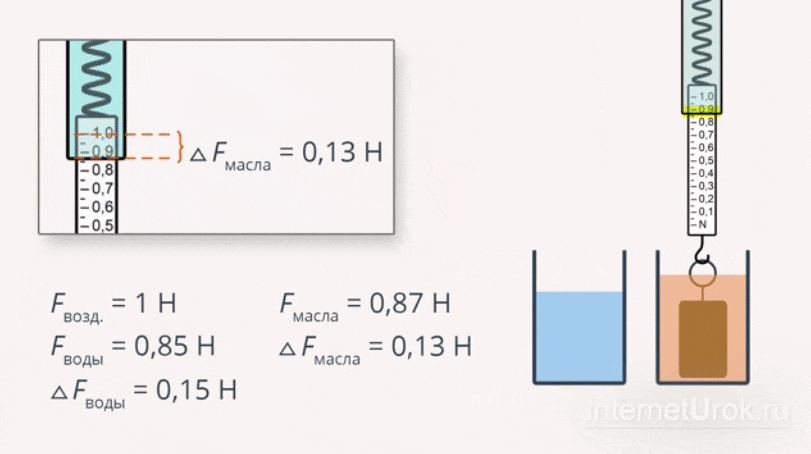
Рис. 8 Эксперимент № 4

Отметим, что плотность воды равна 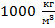, а плотность масла меньше и составляет только 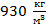. Это приводит к следующему выводу.

Чем больше плотность жидкости, в которую погружено тело, тем больше выталкивающая сила, действующая на тело со стороны данной жидкости.

Итак, обобщив результаты проделанных экспериментов, можно заключить, что величина выталкивающей силы

зависит:

1) от плотности жидкости ;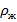

2) от объема погруженной части тела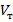

;

не зависит:

1) от плотности тела;

2) от формы тела;

3) от высоты столба жидкости над телом;

Полученные результаты находятся в полном соответствии с формулой для величины выталкивающей силы, полученной на предыдущем уроке:

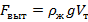
В эту формулу, кроме ускорения свободного падения, входят только две величины, описывающие условия проведенных экспериментов: плотность жидкости и объем погруженной части тела.

Список литературы

Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
А.В. Перышкин Физика 7 кл.: учеб. для общеобразоват. учреждений. – 2-е изд., стереотип. – М.: Дрофа, 2013. – 221 с.
Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал «eduspb.com» (Источник)
Интернет-портал «class-fizika.narod.ru» (Источник)
Интернет-портал «krugosvet.ru» (Источник)

Домашнее задание

Что такое выталкивающая сила? Запишите формулу для нее.
Куб определенного объема поместили в воду. Как изменится выталкивающая сила, которая действует на куб, если его объем уменьшить в 2 раза?
Одинаковые тела поместили в разные жидкости: одно поместили в масло, а второе – в воду. В каком случае выталкивающая сила, действующая на тела, будет больше?

interneturok.ru

Закон Архимеда | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Закон (Сила) Архимеда — На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.

В интегральной форме

Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.

Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами

В формуле мы использовали :

— Сила Архимеда

— Плотность жидкости

— Объем погруженного тела

— Ускорение свободного падения

— Давление в произвольной точке

xn--b1agsdjmeuf9e.xn--p1ai

Сила Архимеда

В этой статье представляю задачи, связанные с плаванием тел и силой Архимеда. Как обычно, сначала пытаемся решить задачи простые, а затем перейдем к более сложным, которые вы найдете в следующей статье.

Задача 1. В воду погружен стеклянный кубик с ребром 10 см. Нижняя его грань находится на глубине 30 см. Рассчитайте силу давления, действующую: а) на верхнюю грань кубика; б) на нижнюю грань кубика; в) на правую грань; г) на левую грань; д) на переднюю и заднюю грани. Найдите равнодействующую всех этих сил.

Давление на грани кубика

Давление столба жидкости может быть вычислено по формуле $P=\rho g h$ , а сила давления может быть найдена из формулы $P=\frac {F}{S}$ , из которой находим: $F=S\cdotP$ .

Не забываем, что очень важно помнить про перевод всех данных задачи в систему СИ, поэтому все расстояния и глубины из сантиметров переводим в метры.

Тогда сила давления на грань: $F=\rho g h S=\rho g h l^2$ , где – длина ребра кубика в метрах, – глубина, причем для боковых граней возьмем среднее значение ( $\frac{h}{2}$ ) так как давление у верхнего края боковых граней и у нижнего – разное.

Сила давления на верхнюю грань, Н:

$F_v=\rho g h l^2=10^3\cdot10\cdot{0,2}\cdot{{0,1}^2}=20$

Сила давления на нижнюю грань, Н:

$F_n=\rho g h l^2=10^3\cdot10\cdot{0,3}\cdot{{0,1}^2}=30$

Сила давления на боковые грани, заднюю и переднюю, Н:

$F_{bok}=\rho g h l^2=10^3\cdot10\cdot{0,25}\cdot{{0,1}^2}=25$

Понятно, что все силы, действующие на боковые, заднюю и переднюю грани друг друга компенсируют, а равнодействующая всех сил будет в итоге суммой сил давления на нижнюю и верхнюю грани:

$F_{ravn}= F_n - F_v=30-20=10$

Так как сила давления на нижнюю грань больше, чем на верхнюю, то равнодействующая направлена вверх.

Задача 2. Определите объем куска алюминия, на который в керосине действует архимедова сила величиной 120 Н.

Сила Архимеда может быть вычислена как $F_A=\rho g V$ , где $\rho$ – плотность жидкости, а – объем самого тела. То есть сила Архимеда не зависит от того, из чего сделано тело, а только от его объема. Вы спросите: почему тогда одинаковые по объему тела, например, шарики равных радиусов, сделанные из дерева и какого-либо металла, по-разному себя ведут в воде: один плавает, второй – тонет? Да просто есть ведь и сила тяжести, которая зависит как раз от массы тела, и в случае деревянного шарика сила Архимеда достаточна, чтобы компенсировать силу тяжести, а в случае с металлическим шариком – нет.

Рассчитаем объем: $V=\frac{F_A}{\rho\cdotg}=\frac{120}{800\cdot10}=0.015$ м

Задача 3. Плавающий деревянный брусок вытесняет 0,5 л воды. Сколько весит брусок?

Так как брусок плавает, то сила Архимеда равна силе тяжести. Нас спрашивают в задаче про вес бруска. Так как система в покое и ускорения нет, то вес бруска равен силе тяжести:

$P=mg=F_A=\rho g V$

$P=10^3\cdot10\cdot{0,5}\cdot10^{-3}=5$

Можно эту задачу решить иначе: вес тела равен весу воды, вытесняемой им. Брусок вытеснил 0,5 литра воды. Воспользовавшись формулой плотности вещества, определяем, что масса такого количества воды равна 0,5 кг, а вес, значит, 5Н.

Задача 4. Тела изготовлены из дерева, пробки и стали. Они имеют объем 100 см каждое. Найдите архимедову силу, действующую на каждое тело, если его погрузить в воду.

Как было показано в одной из предыдущих задач, неважно, из чего изготовлено тело, а важен его объем, поэтому, раз тела обладают одним и тем же объемом, то и сила Архимеда на них действует одинаковая:

$F_A=\rho g V=10^3\cdot10\cdot10^2\cdot10^{-6}=1$

Ответ: 1 Н

Задача 5.Тело при погружении в воду становится легче в 5 раз, чем в воздухе. Определите плотность этого тела.

Мы с вами помним, конечно, что на всякое тело, погруженное как в жидкость, так и в газ, действует сила Архимеда. Поэтому в воздухе она также будет действовать на тело. Однако плотность воздуха так мала по сравнению с плотностью воды, что, я думаю, мы этой силой пренебрежем, и примем вес тела в воздухе равным силе тяжести.

Тогда вес тела P=mg – на воздухе, а вес тела в воде $P_v=\frac{mg}{5}$ . А уменьшился вес этого тела в воде благодаря силе Архимеда: $P_v=mg-F_A=mg-\rho_{v} g V$ , откуда получаем, что

$mg-\rho_{v} g V=mg-\frac{4mg}{5}$

$\rho_{v} g V=\frac{4mg}{5}$

$\rho_{v}V =\frac{4m}{5}$

Масса тела равна произведению его плотности на объем: $m=\rho_{t}V$

Подставим:

$\rho_{v}V =\frac{4\rho_{t}V}{5}$

$\rho_{v} =\frac{4\rho_{t}}{5}$

Откуда и найдем плотность тела:

$\rho_{t} =\rho_{v}\cdot\frac{5}{4}=10^3\cdot{1.25}=1250$

Ответ: плотность тела 1250 кг/м

Задача 6. На предмет, целиком погруженный в керосин, действует выталкивающая сила величиной 2 кН. Какой будет архимедова сила, действующая на него в воде? А в спирте?

Чтобы узнать, какой будет Архимедова сила, нужно знать объем предмета. Определим его, зная Архимедову силу в керосине: $F_{A1}=\rho_{k} g V$ , откуда получаем, что $V=\frac{F_{A1}}{\rho_{k} g}$ .

Зная объем, определяем Архимедову силу в воде, Н:

$F_{A2}=\rho_{v} g \frac{F_{A1}}{\rho_{k} g}=10^4 \frac{2\cdot10^3}{800\cdot10}=2500$

Так как плотность спирта равна плотности керосина, то и Архимедовы силы в этих жидкостях будут одинаковы.

Задача 7.Цинковый шар имеет массу 360 г. При погружении в воду его вес становится равным 2,8 Н. Сплошной этот шар или полый?

Определим объем шара в предположении, что полости в нем нет, по формуле плотности (то есть найдем объем куска цинка массой 360 г):

$V=\frac{m}{\rho}$

Плотность цинка равна $\rho=7100$ кг/м, объем получается $V=\frac{0,36}{7100}=5,1\cdot10^{-5}$ м

Теперь определим реальный объем шара, то есть тот, который он вытесняет, по известному весу в жидкости. Вес шара $P=mg=0,36\cdot 10=3,6$ Н, вес в жидкости равен $P_v=P-F_A=mg-\rho gV$ , откуда объем вытесняемой жидкости (и объем шара)

$V=\frac{mg-P_v}{\rho g}=\frac{3,6-2,8}{10^4}=8\cdot10^{-5}$

мы получили больший объем, чем в первом случае, то есть шар имеет полость внутри, которая и влияет на его внешний объем.

Задача 8. Камень имеет объем 7,5 дм и массу 18,7 кг. Какую силу придется приложить, чтобы удерживать его в воздухе и в воде?

Чтобы удержать такой камень в воздухе, нужно преодолеть силу тяжести, то есть Н.

Теперь определим, какую силу достаточно будет приложить в воде, ведь там нам поможет сила Архимеда!

$F_A=\rho g V=10^3\cdot10\cdot{7,5}\cdot10^{-3}=75$

Тогда сила, которую нужно приложить в воде для удержания камня (или, проще, вес этого камня в воде) равна Н

Задача 9. Сплошное однородное тело, будучи погруженным в воду, весит 170 мН, а в глицерин – 144 мН. Каким будет вес этого тела, если его погрузить в четыреххлористый углерод?

Запишем систему уравнений по тем условиям, что описаны в задаче. Вес тела в воде равен весу тела на воздухе, уменьшенному на силу Архимеда:

$P_v=P-F_{A1}=P-\rho_v g V_t$

Вес тела в глицерине равен весу тела на воздухе, уменьшенному на силу Архимеда – только в глицерине сила Архимеда отличается от той, что действовала на тело в воде:

$P_{gl}=P-F_{A2}=P-\rho_{gl} g V_t$

Из этих двух уравнений, объединив их в систему, можно найти объем тела. Вычтем второе уравнение из первого:

$P_v- P_{gl}= F_{A2}- F_{A1}=\rho_{gl} g V_t-\rho_v g V_t$

$P_v- P_{gl}= V_t ( \rho_{gl} g -\rho_v g)$

$V_t =\frac{P_v- P_{gl}}{\rho_{gl} g -\rho_v g }$

Подставляем числа:

$V_t =\frac{(170- 144)\cdot10^{-3}}{12600 -10000}=\frac{26\cdot10^{-3}}{2600}=10^{-5}$

Теперь, когда мы знаем объем тела и плотность четыреххлористого углерода, можно найти силу Архимеда в нем:

$F_{A3}=\rho g V_t=1630\cdot10\cdot10^{-5}=110\cdot10^{-3}$

Ответ: 110 мН

Задача 10. Кусок парафина толщиной 5 см плавает в воде. Он имеет форму прямоугольного параллелепипеда. Какая часть куска выступает над водой?

Если кусок парафина плавает, а не тонет, значит, сила Архимеда достаточна для того, чтобы компенсировать силу тяжести. Тогда можно записать:

$mg=\rho_v gV_{pogr}$

Представим массу куска через его объем и плотность:

$\rho_p g V=\rho_v gV_{pogr}$

Здесь – объем всего куска, а $V_{pogr}$ – объем погруженной части.

Тогда:

$\rho_p V=\rho_v V_{pogr}$

$\frac{ V_{pogr}}{V} =\frac{\ rho_p }{\rho_v}$

Так как объем – это произведение площади основания на высоту, то можно сократить площадь:

$\frac{ h_{pogr}}{h} =\frac{\ rho_p }{\rho_v}$

$\frac{h_{pogr}}{5} =\frac{900}{1000}$

Откуда делаем вывод, что $h_{pogr}=4,5$ , то есть из пяти см выступает 0,5 см.

Задача 11. Прямоугольная баржа после приема груза осела на 0,5 м. Принимая длину баржи 5 м, а ширину – 3 м, рассчитать вес принятого ею груза.

Рассчитаем объем воды, который был вытеснен баржей после осадки:

$V=a\cdot{b}\cdot{h}=5\cdot{3}\cdot{0,5}=7,5$ м

Такой объем воды весит 7,5 тонн – это легко понять, помня величину плотности воды.

То есть вес груза, принятого баржей, равен $P=mg=7500\cdot10=75\cdot10^3$ , или 75 кН.

Задача 12. Плот состоит из 12 бревен, каждое из которых имеет объем 0,8 м. Бревна сосновые. Можно ли на этом плоту переправить на другой берег автомобиль массой 1,5 тонны?

Рассчитаем вес плота: $P=mg=\rho_{sosn} g V=400\cdot10\cdot(12\cdot0,8)=38400$ Н

К этому весу будет еще добавлен вес автомобиля: Н

Определим силу Архимеда. Если она окажется больше, чем суммарный вес плота и автомобиля, то плот выдержит (не будет затоплен при переправе), а если меньше, то переправлять автомобиль нельзя. Предположим, весь объем плота оказывается в воде при погрузке автомобиля. Тогда сила Архимеда: $F_A= \rho_v g V=1000\cdot 10\cdot(12\cdot0,8)=96000$ Н.

Так как , то делаем вывод, что плот может переправить автомобиль и даже не погрузится при переправе целиком в воду, то есть колеса не намокнут.

Задача 13. Теплоход, вес которого вместе с оборудованием составляет 20 МН, имеет объем подводной части при погружении до ватерлинии 6000 м. Как велика грузоподъемность теплохода?

Сразу вычислим силу Архимеда, так как знаем водоизмещение судна:

$F_A= \rho_v g V=1000\cdot 10\cdot 6000=6\cdot10^7$

Н.

Часть этой силы пойдет на компенсацию веса самого судна с оборудованием:

$F_A-P=6\cdot10^7-20\cdot10^6=4\cdot10^7=40\cdot10^6$ , или 40 МН – такого веса груз можно нагрузить на теплоход.

Задача 14. В сообщающиеся сосуды диаметром каждый налита жидкость плотностью $\rho$ . В один сосуд опустили тело массой , которое стало плавать в жидкости. Как и на сколько изменится уровень жидкости в сосудах?

Тело в одном из двух сосудов

Так как тело плавает, то заключаем, что сила Архимеда достаточна, чтобы скомпенсировать вес тела. Тогда запишем это формулой:

$F_A=P$

$\rho g V=mg$

$V=\frac{m}{\rho}$

Так как сосудов два, и по закону уровень воды в них одинаков, то, если общий объем воды увеличивается на благодаря телу, то в каждом сосуде он поднимется на $\frac{V}{2}$ .

Высота подъема воды равна $h=\frac{0,5V}{S}=\frac{0,5V}{\frac{\pi d^2}{4}}=\frac{2V}{\pi d^2}$

Или $h=\frac{2m}{\rho \pi d^2}$

easy-physic.ru

Вычисление силы Архимеда

В предыдущем параграфе мы назвали две формулы, при помощи которых силу Архимеда можно измерить. Теперь выведем формулу, при помощи которой силу Архимеда можно вычислить.

Закон Архимеда для жидкости выражается формулой (см. § 3-е):

Fарх = Wж

Примем, что вес вытесненной жидкости равен действующей силе тяжести:

Wж = Fтяж = mжg

Масса вытесненной жидкости может быть найдена из формулы плотности:

r = m/V Ю mж = rжVж

Подставляя формулы друг в друга, получим равенство:

Fарх = Wж = Fтяж = mж g = rжVж g

Выпишем начало и конец этого равенства:

Fарх = rж gVж

Вспомним, что закон Архимеда справедлив для жидкостей и газов. Поэтому вместо обозначения «rж» более правильно использовать «rж/г». Также заметим, что объём жидкости, вытесненной телом, в точности равен объёму погруженной части тела: Vж = Vпчт. С учётом этих уточнений получим:

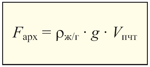Форм. 3.22. Частный случай закона Архимеда – формула для вычисления архимедовой силы.

Fарх – архимедова сила, Н
rж/г – плотность жидкости, кг/м3
g – коэффициент силы тяжести, Н/кг
Vпчт – объём погруженной части тела, м3

Итак, мы вывели частный случай закона Архимеда – формулу, выражающую способ вычисления силы Архимеда. Вы спросите: почему же эта формула – «частный случай», то есть менее общая?

Поясним примером. Вообразим, что мы проводим опыты в космическом корабле. Согласно формуле Fарх = Wж, архимедова сила равна нулю (так как вес жидкости равен нулю), согласно же формуле Fарх = rж/г gVпчт архимедова сила нулю не равна, так как ни одна из величин (r, g, V) в невесомости в ноль не обращается. Перейдя от воображаемых опытов к настоящим, мы убедимся, что справедлива именно общая формула.

Продолжим наши рассуждения и выведем ещё один частный случай закона Архимеда. Посмотрите на рисунок. Поскольку бревно находится в покое, следовательно, на него действуют уравновешенные силы – сила тяжести и сила Архимеда. Выразим это равенством:

Fарх = Fтяж

Или, подробнее:

rж gVпчт = mт g

Разделим левую и правую части равенства на коэффициент «g»:

rж Vпчт = mт

Вспомнив, что m = rV, получим равенство:

rж Vпчт = rт Vт

Преобразуем это равенство в пропорцию:

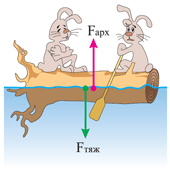Рис. 3.24. При плавании тела действующие на него сила тяжести и архимедова сила взаимно уравновешивают друг друга. Это значит, что числовые значения сил равны, а направления их векторов противоположны.

В левой части этой пропорции стоит дробь, показывающая долю, которую составляет объём погруженной части тела от объёма всего тела. Поэтому всю дробь называют погруженной долей тела:

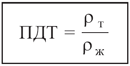Форм. 3.25. Погруженная доля тела равна отношению плотности этого тела к плотности окружающей жидкости.

Используя эту формулу, предскажем, чему должна быть равна погруженная доля бревна при его плавании в воде:

ПДТ (полена) » 500 кг/м³ : 1000 кг/м³ = 0,5

Число 0,5 означает, что плавающее в воде бревно погружено наполовину. Так предсказывает теория, и это совпадает с практикой.

Итак, обе формулы в рамках являются менее общими, чем исходная, то есть имеют более узкие границы применимости. Почему же так произошло? Причина – применение нами формулы W = F_тяж. Вспомним, что она не верна, если тело или его опора (подвес) движутся непрямолинейно (см. § 3-г). Упоминавшийся нами космический корабль именно так и движется – по круговой орбите вокруг Земли.

questions-physics.ru

Формула силы Архимеда в физике

Определение и формула силы Архимеда

Эмпирически еще в древней Греции было получено, что тело, погруженное в жидкость, весит меньше, чем находящееся в воздухе. На тело в жидкости со всех сторон она оказывает давление. Силы давления направлены перпендикулярно поверхности тела в каждой его точке. В том случае, если все силы, действующие на тело, были бы равны по модулю, то это тело испытывало только всестороннее сжатие. Мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.

Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.

Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.

Величина силы Архимеда

Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.

Рассмотрим тело в виде прямоугольного параллелепипеда полностью находящееся в жидкости рис.1. Предположим, что верхнее и нижнее основания располагаются параллельно горизонту.

Силы давления, действующие на боковые грани параллелепипеда, попарно уравновешены (например, ${\overline{F}}_{12}$=$-{\overline{F}}_{21}$). Они только сжимают параллелепипед. Силы, которые действуют на верхнюю и нижнюю грани параллелепипеда не равны между собой. Сила ($F_1$), действия столба жидкости на верхнюю грань, будет равна:

\[F_1=p_1S=(\rho gh_1+p_0)S\ \left(1\right),\]

где $\rho $ — плотность жидкости; $S$ — площадь основания; $h_1$ — высота столба жидкости над верхним основанием параллелепипеда.$\ p_0-$ давление атмосферы на поверхность жидкости.

Сила давления жидкости на нижнее основание параллелепипеда:

\[F_2=p_2S=(\rho gh_2+p_0)S\ \left(2\right),\]

где $h_2$ — высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль результирующей силы, действующей на тело со стороны жидкости:

\[F_A=F_2-F_1=\rho g{S(h}_2-h_1)\ (3).\ \]

Если обозначить высоту параллелепипеда как $h=h_2-h_1$, получим:

\[F_A=\rho gSh=\rho gV\ \left(4\right),\]

где $V$ — объем параллелепипеда. При нахождении тела в жидкости (газе) частично, то под V понимают объем погруженный в вещество (жидкость, газ). Правую часть выражения (4) еще называют весом жидкости, которую вытесняет тело, погруженное в нее.

На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещ