Формула для геометрической прогрессии: Геометрическая прогрессия — урок. Алгебра, 9 класс. — Детская игровая комната «Волшебный лес»

Posted on 15.02.197020.06.2021 by alexxlab

Содержание

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Определение 1. Числовую последовательность

b₁, b₂, … b_k , …

все члены которой отличны от нуля, называют геометрической прогрессией, если справедливы равенства

Определение 2. Если последовательность чисел

b₁, b₂, … b_k , …

является геометрической прогрессией, то число q , определенное формулой

называют знаменателем этой геометрической прогрессии.

Из определений 1 и 2 следует, что для того, чтобы задать геометрическую прогрессию, нужно знать два числа, например, первый член геометрической прогрессии b₁ и знаменатель геометрической прогрессии q . Если числа b₁ и q известны, то все остальные члены прогрессии можно найти по формулам:

b₂ = b₁q ,

b₃ = b₂q ,

…

b_k = b_{k – 1}q

…

(1)

По этой причине многие задачи на геометрическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел b₁ и q.

Из формул (1) вытекает общая формула

b_k = b₁q^{k – 1},
k = 1, 2, 3, …

(2)

позволяющая по любому номеру k вычислить член b_k геометрической прогрессии, зная первый член и знаменатель прогрессии. Эта формула носит название формулы общего члена геометрической прогрессии.

Из формулы (2) вытекает утверждение, называемое характеристическим свойством геометрической прогрессии. Это свойство формулируется так: — «Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению своих соседних членов». Таким образом, характеристическое свойство геометрической прогрессии утверждает, что при справедливо равенство

(3)

В случае, когда

b₁ > 0 и q > 0

все члены геометрической прогрессии будут положительными, и формулу (3) можно переписать в другом виде:

(4)

Равенство (4) означает, что каждый член такой геометрической прогрессии, начиная со второго, равен среднему геометрическому своих соседних членов.

Если для суммы первых k членов геометрической прогрессии ввести обозначение

S_k = b₁ + b₂ + … + b_k ,
k = 1, 2, 3, …

то, воспользовавшись равенствами (1), получаем

q S_k =
= b₁q + b₂q + … + b_kq =
= b₂ + b₃ + … + b_{k +1} .

Следовательно,

S_k – q S_k = b₁ – b_{k +1} .

Таким образом , при будет справедливо равенство

которое называется формулой для суммы первых k членов геометрической прогрессии.

В случае, когда q = 1, все члены геометрической прогрессии равны, что не представляет особого интереса.

Бесконечно убывающая геометрическая прогрессия

Определение 3. Геометрическую прогрессию называют бесконечно убывающей, если её знаменатель удовлетворяет неравенству

| q | < 1 .

В этом случае выполнено равенство

а величину S называют суммой бесконечно убывающей геометрической прогрессии.

Более подробно с понятием предела числовой последовательности можно ознакомиться в в разделе «Пределы числовых последовательностей» нашего справочника.

С примерами решений различных задач по теме «Геометрическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Геометрическая прогрессия (ЕГЭ — 2021)

Многие знают, что шахматная игра была придумана в Индии. Когда индусский царь познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.

Узнав, что она изобретена одним из его подданных, царь решил лично наградить его. Он вызвал изобретателя к себе и приказал просить у него все, что он пожелает, пообещав исполнить даже самое искусное желание.

Сета попросил время на размышления, а когда на другой день Сета явился к царю, он удивил царя беспримерной скромностью своей просьбы. Он попросил выдать за первую клетку шахматной доски $ \displaystyle 1$ пшеничное зерно, за вторую $ \displaystyle 2$ пшеничных зерна, за третью $ \displaystyle -4$, за четвертую $ \displaystyle -8$ и т.д.

Царь разгневался, и прогнал Сета, сказав, что просьба слуги недостойна царской щедрости, но пообещал, что слуга получит свои зерна за все $ \displaystyle 64$ клетки доски.

А теперь вопрос: используя формулу суммы членов геометрической прогрессии, посчитай, сколько зерен должен получить Сета?

Начнем рассуждать. {64}}=1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 1024\cdot 64\)

Конечно, если ты хочешь, то можешь взять калькулятор и посчитать, что за число в итоге у тебя получится, а если нет, придется поверить мне на слово: итоговым значением выражения будет $ \displaystyle 18~\ 446~\ 744~\ 073~\ 709~\ 551~\ 615$.

То есть:

$ \displaystyle 18$ квинтильонов $ \displaystyle 446$ квадрильонов $ \displaystyle 744$ триллиона $ \displaystyle 73$ миллиарда $ \displaystyle 709$ миллионов $ \displaystyle 551$ тысяч $ \displaystyle 615$.

Фух) Если желаете представить себе огромность этого числа, то прикиньте, какой величины амбар потребовался бы для вмещения всего количества зерна.

При высоте амбара $ \displaystyle 4$ м и ширине $ \displaystyle 10$ м длина его должна была бы простираться на $ \displaystyle 300\text{ }000\text{ }000$ км, — т.е. вдвое дальше, чем от Земли до Солнца.

Если бы царь был бы силен в математике, то он мог бы предложить самому ученому отсчитывать зерна, ведь чтобы отсчитать миллион зерен, ему бы понадобилось не менее $ \displaystyle 10$ суток неустанного счета, а учитывая, что необходимо отсчитать $ \displaystyle 18$ квинтильонов, зерна пришлось бы отсчитывать всю жизнь.

А теперь решим простую задачку на сумму членов геометрической прогрессии.

Геометрическая прогрессия | umath.ru

Определение геометрической прогрессии

Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.

То есть геометрическая прогрессия определяется рекуррентным соотношением

Итак, для n-го члена геометрической прогрессии справедлива формула

Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:

Доказательство. Из определения геометрической прогрессии

Следовательно,

откуда

Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.

Сумма первых n членов геометрической прогрессии

Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :

(1)

Умножим это равенство на :

или

(2)

Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как имеем

или

(3)

Так как то формулу (3) можно переписать в виде

(4)

Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.

Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?

Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии

По формуле (3) получаем

Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.

Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.

Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.

Сумма бесконечно убывающей геометрической прогрессии

Рассмотрим геометрическую прогрессию Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.

Сумма бесконечно убывающей геометрической прогресcии выражается формулой

(5)

Члены геометрической прогрессии | Онлайн калькулятор

Члены геометрической прогрессии представляют собой числа, выстроенные строго по порядковым номерам, где непосредственно порядковый номер определяет значение члена последовательности. Первый член геометрической прогрессии может быть любым числом, кроме нуля (b≠0). Для того чтобы найти n член геометрической прогрессии необходимо первый член умножить на знаменатель прогрессии нужное количество раз.

Знаменателем прогрессии является заданное число, которое неизменно на протяжении всего числового ряда. Для того чтобы увидеть суть последовательности, рассмотрим числовой ряд, где выписаны b_n— это первые несколько членов прогрессии с порядковым номером n, а q — это знаменатель прогрессии.
b₁
b₂=b₁ q
b₃=b₂ q=b₁ qq=b₁ q^{2
b₄=b₃ q=b₁ q² q=b₁ q³
…}

Отсюда наглядно видно, что знаменатель геометрической прогрессии собирается в степень, показателем которой является число на одну единицу меньше порядкового номера члена прогрессии, который нужно найти, и все члены зависят от первого. Общая формула членов геометрической прогрессии будет выглядеть так: b_n=b₁ q^(n-1)

Исходя из этого, зная первый член геометрической прогрессии, можно найти первые три, четыре члена прогрессии, умножая на знаменатель в нужной степени. Подобный онлайн калькулятор рассчитывает и в обратную сторону, то есть, зная любой из членов последовательности, можно найти первый. Чтобы проделать подобную операцию, калькулятор переворачивает формулу, в которой первый член геометрической прогрессии будет равен отношению заданного по условиям задачи члена к знаменателю, возведенному в степень n-1

, где n — это порядковый номер известного члена.

Другой способ найти первый член геометрической прогрессии заложен в определении суммы первых нескольких членов прогрессии. Сама сумма равна произведению первого члена прогрессии на разность знаменателя в степени порядкового номера последнего участвующего члена и единицы, затем полученный результат необходимо разделить на еще одну разность знаменателя, в этот раз без степени, и единицы:

Порядок уменьшаемого и вычитаемого в скобках может меняться, это не будет влиять на результат до тех пор, пока это происходит синхронно:

Тогда при перераспределении параметров в формуле выходит, что первый член прогрессии равен произведению суммы с разностью единицы и знаменателя, деленной на разность единицы и знаменателя в степени н:

Формула суммы n первых членов геометрической прогрессии + примеры

Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число.

Геометрическая прогрессия обозначается b1,b2,b3, …, bn, … .

Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.

Монотонная и постоянная последовательность

Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … .

Если q>0 (q не равно 1), то прогрессия является монотонной последовательностью. Например, последовательность, 2, 4,8,16,32, … является монотонно возрастающей последовательностью (b1=2, q=2).

Если в геометрической погрешности знаменатель q=1, то все члены геометрической прогрессии будут равны между собой. 8 -1))/(3-1) = 19 680.

Нужна помощь в учебе?

Предыдущая тема: Определение геометрической прогрессии: формула n-го члена прогрессии
Следующая тема:&nbsp&nbsp&nbspСумма бесконечной геометрической прогрессии при |q|

Геометрическая прогрессия на примерах

Геометрическая прогрессия не менее важная в математике по сравнению с арифметической. Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают

Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя прогрессия является монотонной последовательностью, причем если это последовательность чисел является монотонно убывающей и при монотонно возрастающей. Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса

Общий член геометрической прогрессии вычисляют по формуле

Сумма n первых членов геометрической прогрессии определяют по формуле

Рассмотрим решения классических задач на геометрическую прогрессию. Начнем для понимания с простейших.

Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.

Решение: Запишем условие задачи в виде

Для вычислений используем формулу n-го члена геометрической прогрессии

На ее основе находим неизвестные члены прогрессии

Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом

Пример 2. Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.

Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения

Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле

На этом задача решена.

Пример 3. Геометрическая прогрессия задана двумя ее членами . Найти десятый член прогрессии.

Решение:

Запишем заданные значения через формулы

По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем

Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим

Если полученное значение умножить на шестой член, получим десятый

Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.

Пример 4. Геометрическая прогрессия задано рекуррентными формулами

Найти знаменатель геометрической прогрессии и сумму первых шести членов.

Решение:

Запишем заданные данные в виде системы уравнений

Выразим знаменатель разделив второе уравнение на первое

Найдем первый член прогрессии из первого уравнения

Вычислим следующие пять членов для нахождения суммы геометрической прогрессии

Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель

В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам. Наконец найденные значения добавить.

Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.

Похожие материалы:

формула n-го члена прогрессии 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 12.

Геометрическая прогрессия.

Давай рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:

2; 2²; 2³; 2⁴; 2⁵; …

Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером

геометрической последовательности.

Давай дадим определение: Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Другими словами, последовательность (b_n)– геометрическая прогрессия, если для любого натурального n выполняются условия:

b_n ≠ 0 и b_n+1 = b_n⋅ q,где q – некоторое число. Значит, в последовательности натуральных степеней числа 2, для любого натурального n верно равенство b_n₊₁ = b_n⋅ 2, то есть q=2.

Из определения геометрической прогрессии следует, что отношение ее любого члена, начиная со второго, к предыдущему равно q, то есть bn+1bn=q

Это равенство верно при любом натуральном n.
Число q – называют знаменателем геометрической прогрессии, который всегда отличен от 0.
Чтобы задать геометрическую прогрессию достаточно указать ее первый член и знаменатель.
Например:
Если b₁= 2 и q = 3, то мы получим геометрическую прогрессию:
2, 6, 18, 54, …
Если и b₁= 3 и q = -2, то мы получим геометрическую прогрессию:
3, -6, 12, -24,…
Если b₁= 5 и q = 1, то получим геометрическую прогрессию:
5, 5, 5,…
Зная первый член и знаменатель геометрической прогрессии, можно последовательно найти второй, третий и вообще любой член прогрессии:
b2=b1∙q
b3=b2∙q=b1∙q∙q=b1q2
b4=b3∙q=b1∙q2∙q=b1q3

Значит, чтобы найти n-ый член надо первый член умножить на знаменатель в степени на единицу меньше, то есть
bn=b1qn-1
Это и есть формула n-го члена геометрической прогрессии.
Рассмотрим пару примеров:
Найти девятый член геометрической прогрессии:
-2; 4; -8;…
В данном случае: b1=-2,q=4-2=-2
b9=b1q8=-2∙-28=-2∙256=-512
Ответ: -512
Найдите первый член геометрической прогрессии, если шестой член равен 9, а знаменатель равен 3.
b6=b1∙q5
9=b1∙35
b1=935=127
Ответ: 127
Геометрическая прогрессия обладает следующим свойством:
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению последующего и предыдущего ее членов (произведению своих соседей)

То есть bn2=bn+1∙bn-1
Например, надо найти третий член геометрической прогрессии, если известно, что ее второй член равен 6, а четвертый – равен 24.
Давай воспользуемся этим свойством геометрической прогрессии, тогда
b32=b2∙b4
b32=6∙24=144
b3=±12
Ответ: 12 или –12.
Сумма первых n членов геометрической последовательности
Если последовательность геометрическая, существуют способы найти сумму первых n элементов. термины, обозначенные Sn, без фактического добавления всех терминов.
Чтобы найти сумму первых Sn члены геометрической последовательности используют формулу
Sn = a1 (1 − rn) 1 − r, r ≠ 1,
, где n — количество слагаемых, a1 — первый член, а r это обычное отношение.
Сумма первых n термины геометрической последовательности называется геометрической серией.
Пример 1:
Найдите сумму первых 8 членов геометрического ряда, если a1 = 1 и r = 2.
S8 = 1 (1-28) 1-2 = 255
Пример 2:
Найдите S10 геометрической последовательности 24,12,6, ⋯.
Сначала найдите r.
r = r2r1 = 1224 = 12
Теперь найдите сумму:
S10 = 24 (1− (12) 10) 1−12 = 306964
Пример 3:
Вычислить.
∑n = 1103 (−2) n − 1
(Вы находите S10 для ряда 3−6 + 12−24 + ⋯, значащий коэффициент которого равен −2.)
Sn = a1 (1 − rn) 1 − rS10 = 3 [1 — (- 2) 10] 1 — (- 2) = 3 (1−1024) 3 = −1023
Для того, чтобы бесконечный геометрический ряд имел сумму, знаменатель r должно быть между -1 и 1. Тогда при n увеличивается, рН становится все ближе и ближе к 0. Чтобы найти сумму бесконечного геометрического ряда, имеющего отношения с абсолютным значением меньше единицы, используйте формулу S = a11 − r, где a1 — первый член, а r это обычное отношение.

Пример 4:
Найдите сумму бесконечной геометрической последовательности
27,18,12,8, ⋯.
Сначала найдите r:
r = a2a1 = 1827 = 23
Затем найдите сумму:
S = a11 − r
S = 271−23 = 81
Пример 5:
Найдите сумму бесконечной геометрической последовательности
8,12,18,27, ⋯ если он существует.
Сначала найдите r:
r = a2a1 = 128 = 32
Так как r = 32 не меньше единицы. Серия не имеет суммы.
Существует формула для вычисления n ^th члена геометрического ряда, то есть суммы первых n члены геометрической последовательности.
См. Также: сигма-обозначение ряда и сумма первых n члены арифметической последовательности

Геометрическая серия
А геометрическая серия это ряд чьи родственные последовательность геометрический. Это результат добавления термины из геометрическая последовательность .
Пример 1:
Конечная геометрическая последовательность: 1 2 , 1 4 , 1 8 , 1 16 , … , 1 32768
Связанные конечные геометрические ряды: 1 2 + 1 4 + 1 8 + 1 16 + . .. + 1 32768
Написано в сигма-нотации: ∑ k знак равно 1 15 1 2 k
Пример 2:
Бесконечная геометрическая последовательность: 2 , 6 , 18 , 54 , …
Связанные бесконечные геометрические серии: 2 + 6 + 18 + 54 + …
Написано в сигма-нотации: ∑ п знак равно 1 ∞ ( 2 ⋅ 3 п — 1 )
Конечный геометрический ряд
Чтобы найти сумму конечного геометрического ряда, используйте формулу
S п знак равно а 1 ( 1 — р п ) 1 — р , р ≠ 1 ,
где п это количество терминов, а 1 это первый член и р это обычное отношение .
Пример 3:
Найдите сумму первых 8 члены геометрического ряда, если а 1 знак равно 1 а также р знак равно 2 .
S 8 знак равно 1 ( 1 — 2 8 ) 1 — 2 знак равно 255
Пример 4:
Находить S 10 , десятая частичная сумма бесконечного геометрического ряда 24 + 12 + 6 + … .
Сначала найдите р .
р знак равно а 2 а 1 знак равно 12 24 знак равно 1 2
Теперь найдите сумму:
S 10 знак равно 24 ( 1 — ( 1 2 ) 10 ) 1 — 1 2 знак равно 3069 64
Пример 5:
Оценивать.
∑ п знак равно 1 10 3 ⋅ ( — 2 ) п — 1
(Вы находите S 10 для сериала 3 — 6 + 12 — 24 + … , обыкновенное отношение которого — 2 .)
S п знак равно а 1 ( 1 — р п ) 1 — р S 10 знак равно 3 [ 1 — ( — 2 ) 10 ] 1 — ( — 2 ) знак равно 3 ( 1 — 1024 ) 3 знак равно — 1023
Бесконечная геометрическая серия
Чтобы найти сумму бесконечного геометрического ряда, имеющего отношения с абсолютная величина меньше единицы, используйте формулу S знак равно а 1 1 — р ,
где а 1 это первый член и р это обычное отношение.
Пример 6:
Найдите сумму бесконечного геометрического ряда
27 + 18 + 12 + 8 + … .
Первая находка р :
р знак равно а 2 а 1 знак равно 18 27 знак равно 2 3
Затем найдите сумму:
S знак равно а 1 1 — р S знак равно 27 1 — 2 3 знак равно 81 год
Пример 7:
Найдите сумму бесконечного геометрического ряда
8 + 12 + 18 + 27 + . .. если он существует.
Первая находка р :
р знак равно а 2 а 1 знак равно 12 8 знак равно 3 2
С р знак равно 3 2 не меньше единицы, ряды не сходятся.То есть в нем нет суммы.
Формулы геометрической прогрессии, геометрические ряды, бесконечные геометрические ряды
В математике геометрическая прогрессия (последовательность) (также неточно известная как геометрическая последовательность ) представляет собой последовательность чисел, так что частное любых двух последовательных членов последовательности является константой, называемой обычное отношение последовательности.
Геометрическую прогрессию можно записать как:
ar ⁰ = a, ar ¹ = ar, ar ², ar ³,…
где r ≠ 0, r — обычное отношение, а a — коэффициент масштабирования (также первый член).
Примеры
Геометрическая прогрессия с общим соотношением 2 и масштабным коэффициентом 1 равна
1, 2, 4, 8, 16, 32 …
Геометрическая последовательность с общим соотношением 3 и масштабным коэффициентом 4 равна
4, 12, 36, 108, 324 …
Геометрическая прогрессия с общим соотношением -1 и масштабным коэффициентом 5 равна
5, -5, 5, -5, 5, -5, …
Формулы
Формулу для n-го члена можно определить как:
a _n = a _n-1 r
a _n = a ₁ ⋅r ^n-1
Формула обыкновенного отношения:
Если общее соотношение:
Отрицательный, результаты будут чередоваться между положительными и отрицательными .
Пример:
1, -2, 4, -8, 16, -32 … — обычное отношение равно -2, а первый член равен 1.
Больше чем 1, будет экспоненциальный рост к бесконечности (положительный) .
Пример :
1, 5, 25, 125, 625 … — обычное отношение равно 5.
Менее -1, будет экспоненциальный рост к бесконечности (положительный и отрицательный) .
Пример :
1, -5, 25, -125, 625, -3125, 15625, -78125, 3
, -1953125… — знаменатель -5.
Между 1 и -1, будет экспоненциальный спад к нулю .
Пример :
4, 2, 1, 0,5, 0,25, 0,125, 0,0625 … — обычное отношение $ \ frac {1} {2} $
4, -2, 1, -0,5, 0,25, -0,125, 0,0625 … — обычное отношение $ — \ frac {1} {2} $.
Ноль, результаты останутся на нуле .
Пример :
4, 0, 0, 0, 0 … — обычное отношение равно 0, а первый член равен 4.
Свойства геометрической прогрессии
a ² _k = a _k-1 ⋅a _{k + 1}
a ₁ ⋅a _n = a ₂ ⋅a _n-1 =.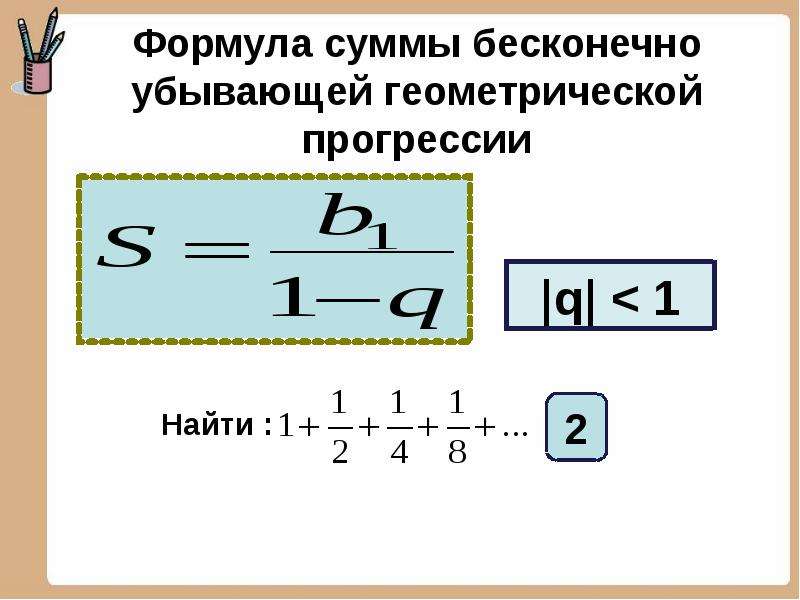 .. = a _k ⋅a _{n-k + 1}
Формула суммы первых n чисел геометрического ряда
S _n = a ₁ — a _n r 1 — г = ₁. 1 — р ^н 1 — г
Бесконечный геометрический ряд, где | r |
<1
Если | r | <1, тогда a _n -> 0, когда n -> ∞.
Сумма S такого бесконечного геометрического ряда определяется формулой:
что справедливо только при | r | <1.
₁ — первый член.
Калькулятор геометрической прогрессии
Задачи геометрической прогрессии
Задача 1.
Последовательность 2, 4, 6, 8 … геометрическая прогрессия?
Решение: Нет, это не так. (2, 4, 8 — геометрическая прогрессия)
Задача 2
Если 2, 4, 8 … образуют геометрическую прогрессию. Какой 10-й срок?
Решение: Мы можем использовать формулу a _n = a ₁ ⋅ r ^n-1
a ₁₀ = 2 ⋅ 2 ^10-1 = 2 ⋅ 512 = 1024
Задача 3
Найдите масштабный коэффициент и командное отношение геометрической прогрессии, если
a ₅ — a ₁ = 15
a ₄ — a ₂ = 6
Решение: есть две геометрические прогрессии. У первого есть масштабный коэффициент 1 и общее отношение = 2
, второе решение -16, 1/2
Дополнительные задачи:
Геометрическая прогрессия — задачи
Задачи с прогрессиями
Геометрические прогрессии на математическом форуме
Присоединяйтесь к нашему математическому форуму (регистрация не требуется!)
Форумы с прогрессиями
Калькулятор геометрической прогрессии — Расчет высокой точности
[1] 2021/03/28 16:30 Мужчина / 30 лет / Инженер / Очень /
Цель использования
Использование для нахождения дисконтированных денежных потоков для моей жизни страховой полис
[2] 2020/07/11 02:59 Мужчина / До 20 лет / Высшая школа / Университет / аспирант / Очень /
Цель использования
Здравствуйте, может кто подскажет геометрическую погрешность между -4 и -9 с пояснениями пожалуйста.Большое спасибо!
[3] 2020/06/04 10:42 Мужской / До 20 лет / Старшая школа / Университет / аспирант / Очень /
Цель использования
Расчет внутриигровых ресурсов
Комментарий / Запрос
Очень точный, может отображать большие числа цифра за цифрой
[4] 2020/04/16 21:47 Мужчина / 20-летний уровень / Инженер / Полезно /
Цель использования
Расчет моей пенсионной суммы : P
Комментарий / запрос
Точно и кратко
[5] 03. 03.2020 18:35 Женский / 30-летний уровень / Средняя школа / Университет / аспирант / Очень /
Цель использования
За результат
[6] 2019/09/05 04:55 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень /
Цель использования
Learning The Math.
Комментарий / запрос
Изучение математики
[7] 15.04.2019 19:26 Мужчина / 20-летний уровень / Средняя школа / Университет / аспирант / Очень /
Цель использования
Чтобы рассчитать возможные возвраты для ставки на сборщик.
[8] 2019/02/15 08:04 Мужской / До 20 лет / Начальная школа / Младший школьник / Полезно /
Цель использования
математическая задача
Комментарий / Запрос
круто
[9] 2018/03/17 07:43 Женский / Моложе 20 лет / Старшая школа / Университет / аспирант / Не совсем /
Цель использования
Я искал калькулятор, чтобы найти общее отношение последовательности, когда даны первые 3 числа этой последовательности. Кажется, я не могу найти один из таких …
[10] 23.03.2013 03:56 Мужчина / 50 лет / Другое / Немного /
Цель использования
Фон Нейман оценка зондирования. 400 миллиардов звезд в галактике, сколько итераций перед воспроизводящим зондом дает число, эквивалентное одному зонду на звезду. Предположим, что исходный зонд производит 1 раз в месяц, пока не будет достигнуто T. Каждый зонд после этого делает то же самое по прибытии. Среднее время путешествия между звездами предполагает 50 лет.
Геометрические последовательности и серии | Безграничная алгебра
Геометрические последовательности
Геометрическая последовательность — это упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на константу, называемую [латекс] r [/ латекс], обычное отношение.
Цели обучения
Вычислить [латекс] n [/ латекс] -й член геометрической последовательности с учетом начального значения [латекс] a [/ латекс] и общего отношения [латекс] r [/ латекс]
Основные выводы
Ключевые точки
Общая форма геометрической последовательности: [латекс] a, ar, ar ^ 2, ar ^ 3, ar ^ 4, \ cdots [/ latex]
[латекс] n [/ латекс] -й член геометрической последовательности с начальным значением [латекс] n [/ латекс] и общим соотношением [латекс] r [/ латекс] задается следующим образом: [латекс] {a} _ { n} = a {r} ^ {n-1} [/ латекс].
Ключевые термины
геометрическая последовательность : упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением. Также известна как геометрическая прогрессия.
Определение геометрических последовательностей
Геометрическая прогрессия, также известная как геометрическая последовательность, представляет собой упорядоченный список чисел, в котором каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое обычным соотношением [латекс] r [/ латекс ].{n-1} [/ latex]
Такая геометрическая последовательность также следует рекурсивному соотношению:
[латекс] a_n = ra_ {n-1} [/ латекс]
для каждого целого числа [латекс] n \ ge 1. [/ Latex]
Поведение геометрических последовательностей
Обычно, чтобы проверить, является ли данная последовательность геометрической, просто проверяют, все ли последовательные записи в последовательности имеют одинаковое соотношение. Обычное отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Поведение геометрической последовательности зависит от значения общего отношения. Если общее отношение:
Положительно, все термины будут того же знака, что и исходные
Отрицательное, условия будут чередоваться между положительным и отрицательным
Больше, чем [latex] 1 [/ latex], будет экспоненциальный рост в сторону положительной бесконечности ([latex] + \ infty [/ latex])
[latex] 1 [/ latex], прогрессия будет постоянной
Между [латексом] -1 [/ латексом] и [латексом] 1 [/ латексом], но не между [латексом] 0 [/ латексом] будет экспоненциальный спад в сторону [латекса] 0 [/ латекса]
[latex] -1 [/ latex], прогрессия — чередующаяся последовательность (см. Чередующиеся серии)
Меньше, чем [latex] -1 [/ latex], для абсолютных значений наблюдается экспоненциальный рост в сторону положительной и отрицательной бесконечности (из-за чередования знаков)
Геометрические последовательности (с общим соотношением, не равным [латекс] -1 [/ латекс], [латекс] 1 [/ латекс] или [латекс] 0 [/ латекс]) показывают экспоненциальный рост или экспоненциальное затухание, в отличие от линейный рост (или снижение) арифметической прогрессии, такой как [латекс] 4, 15, 26, 37, 48, \ cdots [/ латекс] (с общим отличием [латекс] 11 [/ латекс]).Этот результат был получен T.R. Мальтуса в качестве математической основы его принципа народонаселения. Обратите внимание, что два вида прогрессии связаны: возведение в степень каждого члена арифметической прогрессии дает геометрическую прогрессию, а логарифм каждого члена в геометрической прогрессии с положительным общим отношением дает арифметическую прогрессию.
Интересным результатом определения геометрической прогрессии является то, что для любого значения общего отношения любые три последовательных термина [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс] удовлетворяет следующему уравнению:
[латекс] {b} ^ {2} = ac [/ latex]
Суммирование первых n членов геометрической последовательности
Используя обычное отношение и первый член геометрической последовательности, мы можем суммировать его члены. {n}} {1-r}} [/ латекс].
Ключевые термины
геометрическая серия : Бесконечная последовательность добавляемых чисел, члены которой находятся путем умножения предыдущего члена на фиксированное ненулевое число, называемое обычным отношением.
геометрическая прогрессия : серия чисел, в которой каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое общим отношением.
Геометрические ряды — это примеры бесконечных рядов с конечными суммами, хотя не все из них обладают этим свойством.Исторически геометрические ряды играли важную роль в раннем развитии исчисления, и они по-прежнему занимают центральное место в изучении сходимости рядов. Геометрические ряды используются в математике и имеют важные приложения в физике, инженерии, биологии, экономике, информатике, теории очередей и финансах.
Члены геометрического ряда образуют геометрическую прогрессию, что означает, что соотношение следующих друг за другом членов в ряду постоянно. {n}}}} [/ латекс]
является геометрическим, потому что каждый последующий член может быть получен умножением предыдущего члена на [latex] \ displaystyle {\ frac {1} {2}} [/ latex].{n}}} [/ латекс]
Эту концепцию можно визуализировать с помощью диаграммы:
Бесконечная геометрическая серия: Каждый из фиолетовых квадратов получается путем умножения площади следующего большего квадрата на [latex] \ displaystyle {\ frac {1} {4}} [/ latex]. Площадь первого квадрата составляет [латекс] \ displaystyle {\ frac {1} {2} \ cdot \ frac {1} {2} = \ frac {1} {4}} [/ latex], а площадь второй квадрат — [латекс] \ displaystyle {\ frac {1} {4} \ cdot \ frac {1} {4} = \ frac {1} {16}} [/ latex].
Ниже приведены несколько геометрических рядов с разными общими отношениями.Поведение терминов зависит от общего соотношения [латекс] г [/ латекс]:
[латекс] 4 + 40 + 400 + 4000 + \ точки [/ латекс] имеет общее соотношение [латекс] 10 [/ латекс]
[латекс] \ displaystyle {9 + 3 + 1 + \ frac {1} {3} + \ frac {1} {9} + \ dots} [/ latex] имеет общее соотношение [латекс] {\ frac {1 } {3}} [/ латекс]
[латекс] 3 + 3 + 3 + 3 + \ точки [/ латекс] имеет общее соотношение [латекс] 1 [/ латекс]
[латекс] \ displaystyle {1- \ frac {1} {2} + \ frac {1} {4} — \ frac {1} {8} + \ dots} [/ latex] имеет общее соотношение [латекс] — \ frac {1} {2} [/ latex]
[латекс] 3-3 + 3-3 + \ точки [/ латекс] имеет общее соотношение [латекс] -1 [/ латекс]
Значение [latex] r [/ latex] предоставляет информацию о характере серии:
Если [латекс] r [/ латекс] находится между [латекс] -1 [/ латекс] и [латекс] +1 [/ латекс], члены ряда становятся все меньше и меньше, приближаясь к нулю в пределе, и ряд сходится к сумме. Рассмотрим последовательность, в которой [latex] r [/ latex] составляет половину [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которых равна единице.
Если [latex] r [/ latex] больше [latex] 1 [/ latex] или меньше [latex] -1 [/ latex], члены ряда становятся все больше и больше по величине. Сумма членов также становится все больше и больше, и в серии нет суммы. Сериал расходится.
Если [latex] r [/ latex] равно [latex] 1 [/ latex], все члены серии совпадают.Сериал расходится.
Если [latex] r [/ latex] равно [latex] -1 [/ latex], термины принимают поочередно два значения [latex] \ left (\ text {eg}, 2, -2,2, -2,2 , -2, \ cdots \ right) [/ латекс]. Сумма членов колеблется между двумя значениями [latex] \ left (\ text {eg.}, 2,0,2,0,2,0, \ cdots \ right) [/ latex]. Это другой тип дивергенции, и снова у ряда нет суммы.
Мы можем использовать формулу, чтобы найти сумму конечного числа членов в последовательности. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
Бесконечная геометрическая серия
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Вычислить сумму бесконечного геометрического ряда и определить, когда геометрический ряд будет сходиться
Основные выводы
Ключевые точки
Сумма геометрического ряда конечна, пока члены приближаются к нулю; поскольку числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
Для бесконечного геометрического ряда, который сходится, его сумму можно вычислить по формуле [latex] \ displaystyle {s = \ frac {a} {1-r}} [/ latex].
Ключевые термины
сходиться : приблизиться к конечной сумме.
геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно меняются с общим соотношением.
Геометрический ряд — это бесконечный ряд, члены которого находятся в геометрической прогрессии или чьи последовательные члены имеют общее отношение. Если члены геометрического ряда стремятся к нулю, сумма его членов будет конечной. Когда числа близки к нулю, они становятся незначительно малыми, что позволяет вычислить сумму, несмотря на бесконечность ряда.
Говорят, что геометрический ряд с конечной суммой сходится. Ряд сходится тогда и только тогда, когда абсолютное значение общего отношения меньше единицы:
.
[латекс] \ левый | г \ право | <1 [/ латекс]
Что следует на примере бесконечного ряда с конечной суммой. Подсчитаем сумму [latex] s [/ latex] следующей серии:
[латекс] \ displaystyle {s = 1+ \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ cdots} [/ latex]
Эта серия имеет общее соотношение [латекс] \ displaystyle {\ frac {2} {3}} [/ latex].Если мы умножим на это обычное соотношение, то начальный член [латекс] 1 [/ latex] станет [latex] \ displaystyle {\ frac {2} {3}} [/ latex], [latex] \ displaystyle {\ frac {2} {3}} [/ latex] становится [latex] \ displaystyle {\ frac {4} {9}} [/ latex] и так далее:
[латекс] \ displaystyle {\ frac {2} {3} s = \ frac {2} {3} + \ frac {4} {9} + \ frac {8} {27} + \ frac {16} { 81} + \ cdots} [/ латекс]
Эта новая серия такая же, как и исходная, за исключением того, что отсутствует первый член. Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
[латекс] \ displaystyle {\ begin {align} s- \ frac {2} {3} s & = 1 \\ \ поэтому s & = 3 \ end {align}} [/ latex]
Подобный метод можно использовать для вычисления любого самоподобного выражения.n \ rightarrow 0 \\ & = \ frac {a} {1-r} \ end {align}} [/ latex]
Следовательно, для [latex] | r | <1 [/ latex] мы можем записать бесконечную сумму как:
[латекс] \ Displaystyle {s = \ frac {a} {1-r}} [/ латекс]
Пример
Найдите сумму бесконечного геометрического ряда [латекс] 64+ 32 + 16 + 8 + \ cdots [/ latex]
Сначала найдите [latex] r [/ latex], или постоянное соотношение между каждым членом и тем, что ему предшествует:
[латекс] \ displaystyle {\ begin {align} r & = \ frac {32} {64} \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Подставьте [латекс] a = 64 [/ latex] и [latex] \ displaystyle r = \ frac {1} {2} [/ latex] в формулу суммы бесконечного геометрического ряда:
[латекс] \ displaystyle {\ begin {align} s & = \ frac {64} {1- \ frac {1} {2}} \\ & = \ frac {64} {\ frac {1} {2} } \\ & = 128 \ end {align}} [/ latex]
Применения геометрической серии
Геометрические ряды применяются в математике и естественных науках и являются одним из простейших примеров бесконечных рядов с конечными суммами.
Цели обучения
Применение геометрических последовательностей и рядов к различным физическим и математическим темам
Основные выводы
Ключевые точки
Повторяющееся десятичное число можно рассматривать как геометрическую последовательность, общее отношение которой равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].
Архимед использовал сумму геометрического ряда для вычисления площади, заключенной между параболой и прямой линией.
Внутренняя часть снежинки Коха представляет собой объединение бесконечного множества треугольников.При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры.
Знание бесконечных рядов позволяет нам решать древние проблемы, такие как парадоксы Зенона.
Ключевые термины
геометрическая серия : бесконечная последовательность суммированных чисел, члены которой постепенно изменяются с общим соотношением.
фрактал : природное явление или математический набор, который демонстрирует повторяющийся узор, который можно увидеть в любом масштабе.
Геометрические ряды сыграли важную роль в раннем развитии исчисления и продолжают оставаться центральной частью изучения сходимости рядов. Геометрические ряды используются во всей математике. У них есть важные приложения в физике, инженерии, биологии, экономике, информатике, теории массового обслуживания и финансах.
Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами, хотя не все из них обладают этим свойством.
Повторяющаяся десятичная дробь
Повторяющееся десятичное число можно рассматривать как геометрический ряд, общее отношение которого равно степени [латекс] \ displaystyle {\ frac {1} {10}} [/ latex].Например:
[латекс] \ displaystyle {0,7777 \ cdots = \ frac {7} {10} + \ frac {7} {100} + \ frac {7} {1000} + \ frac {7} {10000} + \ cdots} [/ латекс]
Формула суммы геометрического ряда может использоваться для преобразования десятичной дроби в дробь:
[латекс] \ displaystyle {\ begin {align} 0,7777 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {7} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {7} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {7} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {7} {9} \ end {align}} [/ latex]
Формула работает для любого повторяющегося термина. Еще несколько примеров:
[латекс] \ displaystyle {\ begin {align} 0.123412341234 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1234} {10000}} {1- \ frac {1 } {10000}} \\ & = \ frac {\ left (\ frac {1234} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left ( \ frac {1234} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1234} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,0
0909 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {100}} {1- \ frac {1 } {100}} \\ & = \ frac {\ left (\ frac {9} {100} \ right)} {\ left (\ frac {99} {100} \ right)} \\ & = \ left ( \ frac {9} {100} \ right) \ left (\ frac {100} {99} \ right) \\ & = \ frac {9} {99} \\ & = \ frac {1} {11} \ конец {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0.143814381438 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {1438} {10000}} {1- \ frac {1} {10000}} \\ & = \ frac { \ left (\ frac {1438} {10000} \ right)} {\ left (\ frac {9999} {10000} \ right)} \\ & = \ left (\ frac {1438} {10000} \ right) \ left (\ frac {10000} {9999} \ right) \\ & = \ frac {1438} {9999} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} 0,9999 \ cdots & = \ frac {a} {1-r} \\ & = \ frac {\ frac {9} {10}} {1- \ frac {1 } {10}} \\ & = \ frac {\ left (\ frac {9} {10} \ right)} {\ left (\ frac {9} {10} \ right)} \\ & = \ left ( \ frac {9} {10} \ right) \ left (\ frac {10} {9} \ right) \\ & = \ frac {9} {9} \\ & = 1 \ end {align}} [/ латекс]
То есть повторяющаяся десятичная дробь с повторяющейся частью длины [латекс] n [/ latex] равна частному повторяющейся части (как целое число) и [латекс] 10 ^ n — 1 [/ latex].
Квадратура Параболы Архимеда
Архимед использовал сумму геометрического ряда для вычисления площади, заключенной между параболой и прямой линией. Его метод заключался в том, чтобы разрезать область на бесконечное количество треугольников.
Теорема Архимеда: Разбиение Архимеда параболического сегмента на бесконечное количество треугольников.
Теорема Архимеда утверждает, что общая площадь под параболой равна [latex] \ displaystyle {\ frac {4} {3}} [/ latex] площади синего треугольника.{3} + \ cdots} [/ latex]
Первый член представляет площадь синего треугольника, второй член — площади двух зеленых треугольников, третий член — площади четырех желтых треугольников и так далее. Упрощение дробей дает:
[латекс] \ displaystyle {1+ \ frac {1} {4} + \ frac {1} {16} + \ frac {1} {64} + \ cdots} [/ latex]
Это геометрическая серия с общим соотношением [латекс] \ displaystyle {\ frac {1} {4}} [/ latex], а дробная часть равна [latex] \ displaystyle {\ frac {1} {3} }[/латекс].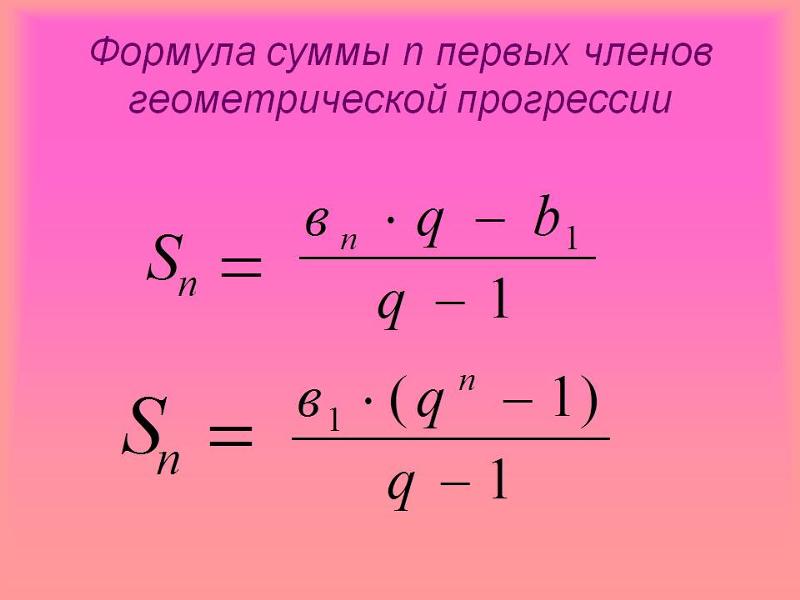
Фрактальная геометрия
Снежинка Коха: Внутренняя часть снежинки Коха состоит из бесконечного количества треугольников.
Снежинка Коха — это фрактальная форма, внутренность которой состоит из бесконечного количества треугольников. При изучении фракталов геометрические ряды часто возникают как периметр, площадь или объем самоподобной фигуры. В случае снежинки Коха ее площадь можно описать геометрическим рядом.
Построение снежинки Коха: первые четыре итерации: каждая итерация добавляет набор треугольников снаружи формы.
Область внутри снежинки Коха можно описать как объединение бесконечного числа равносторонних треугольников. На диаграмме выше треугольники, добавленные во второй итерации, имеют размер [latex] \ displaystyle {\ frac {1} {3}} [/ latex], равный размеру стороны наибольшего треугольника, поэтому они имеют ровно [latex ] \ displaystyle {\ frac {1} {9}} [/ latex] область. Точно так же каждый треугольник, добавленный во второй итерации, имеет [latex] \ displaystyle {\ frac {1} {9}} [/ latex] площадь треугольников, добавленных в предыдущей итерации, и так далее. {3} + \ cdots} [/ latex]
Первый член этого ряда представляет площадь первого треугольника, второй член — общую площадь трех треугольников, добавленных во второй итерации, третий член — общую площадь двенадцати треугольников, добавленных в третьей итерации, и т. Д. . Исключая начальный термин [латекс] 1 [/ латекс], этот ряд является геометрическим с постоянным соотношением [латекс] \ displaystyle {r = \ frac {4} {9}} [/ latex]. Первый член геометрического ряда — [латекс] \ displaystyle {a = 3 \ frac {1} {9} = \ frac {1} {3}} [/ latex], поэтому сумма составляет:
[латекс] \ displaystyle {\ begin {align} 1+ \ frac {a} {1-r} & = 1 + \ frac {\ frac {1} {3}} {1- \ frac {4} {9 }} \\ & = \ frac {8} {5} \ end {align}} [/ latex]
Таким образом, снежинка Коха имеет [латекс] \ displaystyle {\ frac {8} {5}} [/ latex] площади основного треугольника.
Парадоксы Зенона
Парадоксы Зенона — это набор философских проблем, изобретенных древнегреческим философом для поддержки учения о том, что истина противоречит нашим чувствам.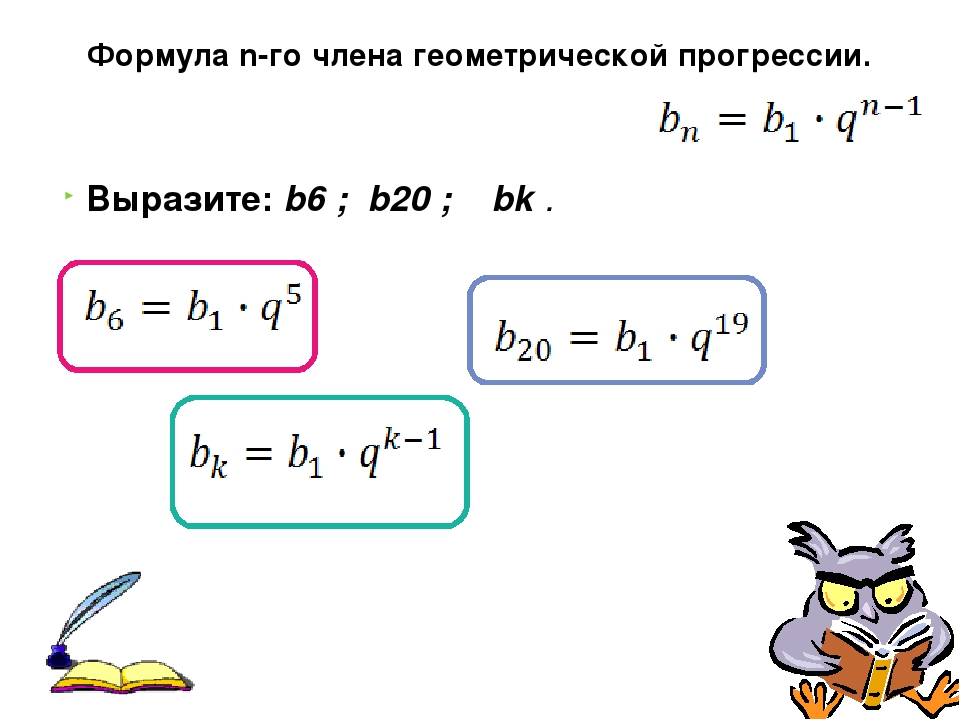 Проще говоря, один из парадоксов Зенона гласит: существует точка A, которая хочет переместиться в другую точку B. Если A перемещается только на половину расстояния между ней и точкой B за один раз, она никогда не доберется туда, потому что вы можете продолжать делить оставшееся пространство пополам навсегда. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной.Теперь мы знаем, что его парадокс не соответствует действительности, о чем свидетельствует сходимость геометрического ряда с [латексом] \ displaystyle {r = \ frac {1} {2}} [/ latex]. Эта проблема была решена современной математикой, которая может применить концепцию бесконечного ряда, чтобы найти сумму пройденных расстояний.
Использование формулы для геометрического ряда
Так же, как сумма членов арифметической последовательности называется арифметическим рядом, сумма членов геометрической последовательности называется геометрическим рядом . {k} [/ латекс]
Решение
Пример 5: Решение прикладной задачи с помощью геометрической серии
На новой работе стартовая зарплата сотрудника составляет 26 750 долларов. Он получает повышение на 1,6% годовых. Найдите его общий заработок по истечении 5 лет.
Решение
Задачу можно представить в виде геометрического ряда с [латексом] {a} _ {1} = 26,750 [/ latex]; [латекс] n = 5 [/ латекс]; и [латекс] r = 1,016 [/ латекс]. Подставьте значения для [latex] {a} _ {1} [/ latex], [latex] r [/ latex] и [latex] n [/ latex] в формулу и упростите, чтобы найти общую сумму заработка в конце. от 5 лет.{5} \ right)} {1 — 1.016} \ приблизительно 138 \ text {,} 099.03 \ hfill \ end {array} [/ latex]
К концу 5 лет он заработает в общей сложности 138 099,03 долларов.
Попробуй 8
На новой работе стартовая зарплата сотрудника составляет 32 100 долларов. Ежегодно она получает 2% -ное повышение. Сколько она заработает к концу 8 лет?
Решение
Использование формулы суммы бесконечного геометрического ряда
До сих пор мы рассматривали только конечные серии. Иногда, однако, нас интересует сумма членов бесконечной последовательности, а не сумма только первых [latex] n [/ latex] членов.{\ infty} 2k [/ latex], где верхний предел суммирования равен бесконечности. Поскольку члены не стремятся к нулю, сумма ряда неограниченно увеличивается по мере того, как мы добавляем новые члены. Следовательно, сумма этого бесконечного ряда не определена. Когда сумма не является действительным числом, мы говорим, что ряд расходится на .
Определение, определена ли сумма бесконечного геометрического ряда
Если члены бесконечного геометрического ряда приближаются к нулю, можно определить сумму бесконечного геометрического ряда.{n} [/ latex] становятся очень маленькими и приближаются к нулю. Каждый последующий член влияет на сумму меньше, чем предыдущий член. По мере того, как каждый последующий член приближается к 0, сумма членов приближается к конечному значению. Члены любого бесконечного геометрического ряда с [latex] -1
Общее примечание: определение того, определена ли сумма бесконечного геометрического ряда
Сумма бесконечного ряда определяется, если ряд геометрический и [латекс] -1
Как сделать: учитывая первые несколько членов бесконечного ряда, определите, существует ли сумма ряда.
Найдите отношение второго члена к первому.
Найдите отношение третьего члена ко второму.
Продолжайте этот процесс, чтобы обеспечить постоянство отношения одного члена к предыдущему. Если да, то серия геометрическая.
Если общее соотношение, [латекс] r [/ латекс], было найдено на шаге 3, проверьте, [латекс] -1
Решение
Отношение второго члена к первому составляет [латекс] \ frac {\ text {2}} {\ text {3}} [/ latex],
, что не совпадает с отношением третьего члена к второй, [латекс] \ frac {1} {2} [/ latex]. Серия не геометрическая.
Отношение второго члена к первому такое же, как отношение третьего члена ко второму. Ряд геометрический с общим соотношением [латекс] \ frac {2} {3} \ text {.} [/ Latex] Сумма бесконечного ряда определена.
Данная формула является экспоненциальной с основанием [латекс] \ frac {1} {3} [/ latex]; серия геометрическая с общим соотношением [латекс] \ frac {1} {3} \ text {.} [/ latex] Сумма бесконечного ряда определена.
Данная формула не является экспоненциальной; ряд не является геометрическим, потому что члены возрастают, и поэтому не может дать конечной суммы.
Определите, определена ли сумма бесконечного ряда.
Попробуйте 9
[латекс] \ frac {1} {3} + \ frac {1} {2} + \ frac {3} {4} + \ frac {9} {8} +.{k} [/ латекс]
Решение
геометрических прогрессий | Блестящая вики по математике и науке
Важная терминология
Начальный член: В геометрической прогрессии первое число называется «начальным членом».
Общий коэффициент: отношение между термином в последовательности и термином перед ним называется «обычным отношением».
Рекурсивная формула
Мы можем описать геометрическую последовательность с помощью рекурсивной формулы, которая определяет, как каждый член соотносится с предыдущим.Поскольку в геометрической прогрессии каждый член определяется произведением предыдущего члена и общего отношения, мы можем записать рекурсивное описание следующим образом:
Срок = Предыдущий срок × Общий коэффициент. \ text {Term} = \ text {Предыдущий термин} \ times \ text {Обычное соотношение}. Срок = Предыдущий срок × Общий коэффициент.
Если говорить кратко, то при обыкновенном соотношении rrr имеем
an = an − 1 × r.a_n = a_ {n-1} \ times r.an = an − 1 × r.
Явная формула
Хотя приведенная выше рекурсивная формула позволяет нам описать взаимосвязь между членами последовательности, часто бывает полезно иметь возможность написать явное описание терминов в последовательности, которое позволило бы нам найти любой термин.
Если мы знаем начальный член, следующие члены связаны с ним путем многократного умножения обыкновенного отношения. Таким образом, явная формула
Срок = Начальный член × Общий коэффициент × ⋯ × Общий коэффициент Количество шагов от начального срока. \ text {Term} = \ text {Начальный термин} \ times \ underbrace {\ text {Общий коэффициент} \ times \ dots \ times \ text {Общий коэффициент}} _ {\ text {Количество шагов от начального члена}} . Срок = Начальный член × Количество шагов от начального члена Общее соотношение × ⋯ × Общее соотношение.{n-k} .an = ak × rn-k.
Теперь давайте разработаем несколько основных примеров, которые могут познакомить вас с приведенными выше определениями.
Какова явная формула для геометрической последовательности 4,12,36,108,…? 4, 12, 36, 108, \ точек? 4,12,36,108,…?
Показать ответ
Начальный член равен 444. Поскольку каждый последующий член является произведением предыдущего члена и 333, общее отношение равно 333. Таким образом, формула, описывающая эту последовательность, имеет вид
an = 4 × 3n − 1.{n} 5⋅5н
Что из следующего является явной формулой геометрической прогрессии?
5,10,20,40,…? 5, 10, 20, 40, \ точки? 5,10,20,40,…?
.