формулы на все случаи жизни :: SYL.ru
На простой вопрос «Как найти высоту трапеции?» существует несколько ответов, и все потому, что могут быть даны разные исходные величины. Поэтому и формулы будут различаться.
Эти формулы можно запомнить, но они несложно выводятся. Нужно только применять ранее изученные теоремы.
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с2 — (((а — в)2 + с2 — d2)/(2(а — в)))2). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с2 — (а — в)2/4). Номер 2.
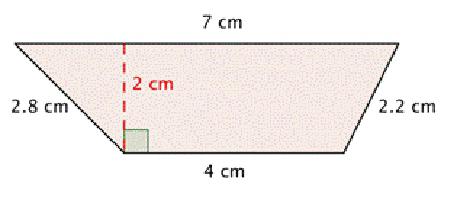
В задаче даны: боковые стороны и углы при нижнем основании
Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:
н = с * sin α= d * sin β. Номер 3.
Если фигура равнобедренная, то можно воспользоваться таким вариантом:
н = с * sin α= ((а — в) / 2) * tg α. Номер 4.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
н = (d1* d2 * sin γ) / (а + в) или н = (d1* d2 * sin δ) / (а + в). Номер 5.
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d12 * sin γ) / (а + в) или н = (d12 * sin δ) / (а + в). Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d1* d2 * sin γ) / 2m или н = (d1* d2 * sin δ) / 2m. Номер 5а.
н = (d12 * sin γ) / 2m или н = (d12 * sin δ) / 2m. Номер 6а.
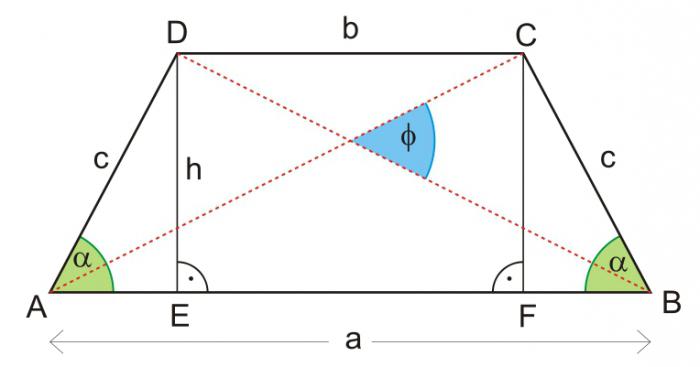
Среди известных величин: площадь с основаниями или средней линией
Это, пожалуй, самые короткие и простые формулы того, как найти высоту трапеции. Для произвольной фигуры она будет такой:
н = 2S / (а + в). Номер 7.
Она же, но с известной средней линией:
н = S / m. Номер 7а.
Как ни странно, но для равнобедренной трапеции формулы будут выглядеть так же.

Задачи
№1. На определение углов при нижнем основании трапеции.
Условие. Дана равнобедренная трапеция, боковая сторона которой 5 см. Ее основания равны 6 и 12 см. Требуется найти синус острого угла.
Решение. Для удобства следует ввести обозначение. Пусть левая нижняя вершина будет А, все остальные по часовой стрелке: В, С, Д. Таким образом, нижнее основание будет обозначено АД, верхнее — ВС.
Нужно провести высоты из вершин В и С. Точки, которые укажут концы высот будут обозначены Н1 и Н2, соответственно. Поскольку в фигуре ВСН1Н2 все углы прямые, то она является прямоугольником. Это означает, что отрезок Н1Н2 равен 6 см.
Теперь нужно рассмотреть два треугольника. Они равны, так как являются прямоугольными с одинаковыми гипотенузами и вертикальными катетами. Отсюда следует, что и меньшие катеты у них равны. Поэтому их можно определить как частное от разности. Последняя получится от вычитания из нижнего основания верхнего. Делиться оно будет на 2. То есть 12 — 6 нужно поделить на 2. АН1 = Н2Д = 3 (см).
Теперь из теоремы Пифагора нужно найти высоту трапеции. Она необходима для нахождения синуса угла. ВН1 = √(52 — 32) = 4 (см).
Воспользовавшись знанием о том, как находится синус острого угла в треугольнике с прямым углом, можно записать такое выражение: sin α= ВН1 / АВ = 0,8.
Ответ. Искомый синус равен 0,8.
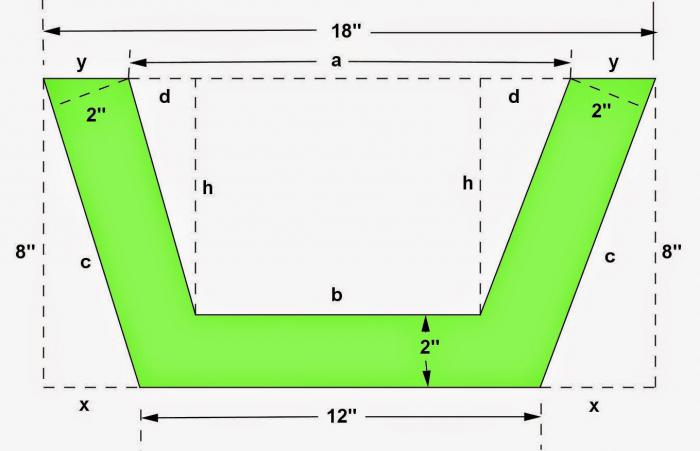
№2. На нахождение высоты трапеции по известному тангенсу.
Условие. У равнобедренной трапеции нужно вычислить высоту. Известно, что ее основания равны 15 и 28 см. Дан тангенс острого угла: 11/13.
Решение. Обозначение вершин такое же, как в предыдущей задаче. Снова нужно провести две высоты из верхних углов. По аналогии с решением первой задачи нужно найти АН1 = Н2Д, которые определятся как разность 28 и 15, деленная на два. После подсчетов получается: 6,5 см.
Поскольку тангенс — это отношение двух катетов, то можно записать такое равенство: tg α= АН1 / ВН1. Причем это отношение равно 11/13 (по условию). Так как АН1 известен, то можно вычислить высоту: ВН1= (11 * 6,5) / 13. Простые расчеты дают результат в 5,5 см.
Ответ. Искомая высота равна 5,5 см.
№3. На вычисление высоты по известным диагоналям.
Условие. О трапеции известно, что ее диагонали равны 13 и 3 см. Нужно узнать ее высоту, если сумма оснований составляет 14 см.
Решение. Пусть обозначение фигуры будет таким же, как раньше. Предположим, что АС — меньшая диагональ. Из вершины С нужно провести искомую высоту и обозначить ее СН.
Теперь потребуется выполнить дополнительное построение. Из угла С нужно провести прямую, параллельную большей диагонали и найти точку ее пересечения с продолжением стороны АД. Это будет Д1. Получилась новая трапеция, внутри которой начерчен треугольник АСД1. Он-то и нужен для дальнейшего решения задачи.
Искомая высота окажется еще и ей же в треугольнике. Поэтому можно воспользоваться формулами, изученными в другой теме. Высота треугольника определяется как произведение числа 2 и площади, деленное на сторону, к которой она проведена. А сторона оказывается равна сумме оснований исходной трапеции. Это исходит из правила, по которому выполнено дополнительное построение.
В рассматриваемом треугольнике все стороны известны. Для удобства введем обозначения х = 3 см, у = 13 см, z = 14 см.
Теперь можно сосчитать площадь, воспользовавшись теоремой Герона. Полупериметр будет равен р = (х + у + z)/ 2 = (3 + 13 + 14) / 2 = 15 (см). Тогда формула для площади после подстановки значений будет выглядеть так: S = √(15 * (15 — 3) * (15 — 13) * (15 — 14)) = 6 √10 (см2).
Теперь нужно сосчитать высоту: н = (2 * 6 √10) / 14 = 6√10 / 7 (см).
Ответ. Высота равна 6√10 / 7 см.
№4. Для поиска высоты по сторонам.
Условие. Дана трапеция, три стороны которой равны 10 см, а четвертая 24 см. Нужно узнать ее высоту.
Решение. Поскольку фигура равнобедренная, то потребуется формула под номером 2. В нее нужно просто подставить все значения и сосчитать. Это будет выглядеть так:
н = √(102 — (10 — 24)2/4) = √51 (см).
Ответ. н = √51 см.
Как найти высоту трапеции формула
Как найти высоту трапеции, формула
Формул для вычисления длины высоты трапеции много. Одни формулы можно получить из других. Нашей задачей будет рассмотреть основные из этих формул при разном наборе исходных данных (например, при известных боковых сторонах, углах при основании, диагоналях, площади и т.д.).
Для удобства чтения формул примем следующие обозначения:
Обозначим боковые стороны трапеции через st1 и st2, нижнее и верхнее основание через osn1 и osn2 соответственно, углы при первой и второй боковой стороне — ugol1 и ugol2.
- Высота трапеции через боковые стороны и углы при основании
- Высота трапеции через диагонали и углы между ними
Обозначим диагонали трапеции через diag1 и diag2, углы между диагоналями — через ugol1 ugol2, а среднюю линию — через :
- Высота трапеции через площадь
Этот небольшой набор формул поможет Вам решать задачи разного уровня сложности.
Как найти высоту трапеции?
В нашей жизни очень часто приходится сталкиваться с применением геометрии на практике, например, в строительстве. Среди наиболее часто встречающихся геометрических фигур есть и трапеция. И для того, чтобы проект был успешным и красивым, необходим правильный и точный расчет элементов для такой фигуры.
Что собой представляет трапеция? Это выпуклый четырехугольник, который имеет пару параллельных сторон, именуемых основаниями трапеции. Но есть еще две другие стороны, соединяющие эти основания. Их называют боковыми. Один из вопросов, касающийся данной фигуры, это: «Как найти высоту трапеции?» Сразу необходимо обратить внимание, что высота — это отрезок, определяющий расстояние от одного основания до другого. Существует несколько способов для определения этого расстояния, в зависимости от известных величин.
1. Известны величины обоих оснований, обозначим их b и k, а так же площадь данной трапеции. Используя известные величины, найти высоту трапеции в этом случае очень легко. Как известно из геометрии, площадь трапеции вычисляется, как произведение половины суммы оснований и высоты. Из этой формулы можно легко вывести искомую величину. Для этого необходимо площадь разделить на половину суммы оснований. В виде формул это будет выглядеть так:
S=((b+k)/2)*h, отсюда h=S/((b+k)/2)=2*S/(b+k)
2. Известна длина средней линии, обозначим ее d, и площадь. Для тех, кто не знает, средней линией называю расстояние между серединами боковых сторон. Как найти высоту трапеции в этом случае? Согласно свойству трапеции, средняя линия соответствует половине суммы оснований, то есть d=(b+k)/2. Опять же прибегаем к формуле площади. Заменив половину суммы оснований на величину средней линии, получим следующее:
S=d*h
Как видим из полученной формулы очень легко вывести высоту. Разделив площадь на величину средней линии, мы найдем искомую величину. Запишем это формулой:
h=S/d
3. Известна длина одной боковой стороны (b) и угол, образующийся между этой стороной и наибольшим основанием. Ответ на вопрос, как найти высоту трапеции, есть и в этом случае. Рассмотрим трапецию ABCD, где AB и CD являются боковыми сторонами, причем AB=b. Наибольшим основанием является AD. Угол, образованный AB и AD обозначим α. Из точки B опустим высоту h на основание AD. Теперь рассмотрим полученный треугольник ABF, который является прямоугольным. Сторона AB является гипотенузой, а BF-катетом. Из свойства прямоугольного треугольника отношение значения катета и значению гипотенузы соответствует синусу угла, противолежащего катету (BF). Поэтому, исходя из вышеизложенного, для вычисления высоты трапеции перемножаем значение известной стороны и синус угла α. В виде формулы это выглядит следующим образом:
h = b *sin(α)
4. Аналогично рассматривается случай, если известны размер боковой стороны и угол, обозначим его β, образующийся между этой стороной и меньшим основанием. При решении такой задачи величина угла между известной боковой стороной и проведенной высотой будет 90°- β. Из свойства треугольников — отношение длины катета и гипотенузы соответствует косинусу угла, расположенного между ними. Из этой формулы легко вывести величину высоты:
h = b *cos(β-90°)
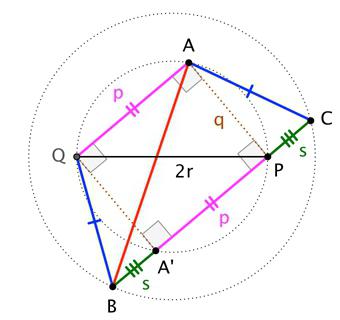
5. Как найти высоту трапеции, если известен лишь радиус вписанной окружности? Из определения окружности, она касается одной точкой каждого основания. Кроме того, эти точки находятся на одной линии с центром окружности. Из этого следует, что расстояние между ними является диаметром и, в то же время, высотой трапеции. Выглядит так:
h=2*r
6. Часто встречаются задачи, в которых необходимо найти высоту равнобедренной трапеции. Напомним, что трапеция, имеющая равные боковые стороны, называется равнобедренной. Как найти высоту равнобедренной трапеции? При перпендикулярных диагоналях высота равна половине суммы оснований.
Но, что делать, если диагонали не перпендикулярны? Рассмотрим равнобедренную трапецию ABCD. Согласно ее свойствам, основания параллельны. Из этого следует, что углы при основаниях также будут равны. Проведем две высоты BF и CM. Исходя из вышесказанного, можно утверждать, что треугольники ABF и DCM равны, то есть AF= DM = (AD – BC)/2 = (b-k)/ 2. Теперь, исходя из условия задачи, определимся с известными величинами, а уж потом находим высоту, учитывая все свойства равнобедренной трапеции.
Как найти высоту трапеции
Как найти высоту трапеции
Четырехугольник с двумя параллельными противоположными сторонами называют трапецией. Эти параллельные стороны называют основаниями трапеции (верхним и нижним), а остальные две непараллельные стороны этой фигуры называют ее боковыми сторонами. Высотой трапеции является расстояние между обоими основаниями.
Рассмотрим несколько вариантов вычисления длины высоты трапеции.
1-й вариант. Известны основания и площадь.
В таком случае необходимо сначала вспомним формулу площади трапеции, которая равна произведению половины суммы оснований на высоту. Поэтому для того, чтобы найти эту высоту необходимо площадь трапеции разделить на эту полусумму:
2-й вариант. Известна средняя линия и площадь.
В этом случае формула для определения высоты вытекает из предыдущего варианта, так как средняя линия является ничем иным, как полусуммой обоих оснований трапеции. Поэтому:
3-й вариант. Известна одна боковая сторона и острый угол между ней и основанием.
В этом случае используется определение синуса прямоугольного треугольника, который образуется высотой и известной боковой стороной. Тогда высоту можно найти следующим образом:
4-й вариант. Известна одна боковая сторона и тупой угол между ней и основанием.
В этом случае используется определение синуса прямоугольного треугольника, который образуется высотой и известной боковой стороной. Тогда высоту можно найти следующим образом: