Кинетическая энергия — урок. Физика, 8 класс.
Энергию, которой обладают только движущиеся тела, называют кинетической энергией.
Если тело находится в состоянии покоя, его кинетическая энергия равна нулю.Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).
Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.
Определяют кинетическую энергию по формуле:
Eкин=m⋅v22.
Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:
m=2⋅Eкинv2 и v=2⋅Eкинm.
С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.
Если масса увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается также в \(2\) раза.
Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной \(2 м/с\).
Рис. \(1\). График, зависимость кинетической энергии от массы
\(1\). График, зависимость кинетической энергии от массы
С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости.
Если скорость увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается в \(4\) раза.
Зависимость кинетической энергии от скорости движения можно отобразить на данном графике, если принять массу тела постоянной и равной \(2 кг\).
Рис. \(2\). График, зависимость кинетической энергии от скорости движения
Пример:
Автомобиль, масса которого \(1400 кг\), из состояния покоя развивает скорость до значения \(5 м/с\).
Какова кинетическая энергия автомобиля на конечном этапе движения?
Eкин=m⋅v22=1400⋅522=17500Дж.
Источники:
Рис. 1. График, зависимость кинетической энергии от массы. © ЯКласс.
Рис. 2. График, зависимость кинетической энергии от скорости движения. © ЯКласс.
Формула кинетической энергии в физике
Содержание:
Определение и формула кинетической энергии
Определение
Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю. {2}}{2 J}=\frac{L \omega}{2}(4)$$
{2}}{2 J}=\frac{L \omega}{2}(4)$$
где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
$$E_{k}=\frac{\bar{L} \bar{\omega}}{2}(5)$$ $\bar{L}$ – момент импульса рассматриваемого тела относительно точки О.Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
[Ek]=Дж (джоуль),
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 107 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета. {2}}+1}$
{2}}+1}$
Читать дальше: Формула массы тела.
Глава 26. Элементы квантовой физики и специальной теории относительности. Атомная и ядерная физика
В программу ЕГЭ по физике входит достаточно большой круг вопросов по атомной и ядерной физике, фотоэлектрическому эффекту, основам специальной теории относительности. Тем не менее, эти вопросы касаются, в основном, только фактического материала, не требуют его глубокого осмысления и поэтому их достаточно легко выучить. Кратко рассмотрим этот материал.
Фотоэлектрическим эффектом (или просто фотоэффектом) называют явление испускания электронов поверхностью металла под действием света. Экспериментально было установлено, что максимальная кинетическая энергия фотоэлектронов пропорциональна частоте и не зависит от интенсивности излучения. При частоте света, меньшей некоторого значения (которое называется красной границей фотоэффекта и является характеристикой каждого металла), фотоэффект прекращается. От интенсивности излучения зависит число электронов, испускаемых поверхностью металла в единицу времени, но не их энергия.
От интенсивности излучения зависит число электронов, испускаемых поверхностью металла в единицу времени, но не их энергия.
Впервые фотоэффект изучали с помощью вакуумного фотоэлемента или вакуумного фотодиода, который представляет собой стеклянный баллон с откачанным из него воздухом и впаянными электродами. Фотодиод включается в электрическую цепь, как показано на рисунке. Естественно, в цепи нет электрического тока, поскольку в баллоне нет свободных носителей электрического заряда. Однако когда электрод, соединенный с отрицательным полюсом источника (катод) освещается светом, в цепи возникает электрический ток, что свидетельствует о появлении между катодом и анодом свободных зарядов. По величине тока в цепи (фототока) можно сделать вывод о количестве вырванных с поверхности катода зарядов. Если же поменять полярность источника, то приложенное напряжение будет тормозить фотоэлектроны. Напряжение, при котором фототок в цепи прекращается, называется задерживающим (или запирающим).
(26.1) |
где — масса электрона, — элементарный заряд, — задерживающее напряжение. Таким образом, измеряя задерживающее напряжение, можно измерить максимальную кинетическую энергию электронов.
Для объяснения фотоэффекта А. Эйнштейн предположил, что свет представляет собой поток частиц — фотонов, движущихся со скоростью света. Каждый из них обладает энергией, зависящей от частоты (или длины волны) света
(26.2) |
и импульсом
(26.3) |
Фотон, как и любая частица, может поглощаться или излучаться только как единое целое. В формулах (26.2)-(26.3) Дж • с — постоянная, которая называется постоянной Планка, — скорость света в вакууме, — частота света, — длина волны. Поглощая один фотон, свободный электрон в металле увеличивает свою энергию на величину (26.2) и может вылететь с поверхности металла, если его новая энергия достаточна для этого, т.е. превосходит работу , которую необходимо совершить, чтобы покинуть металл. Эта работа называется работой выхода электрона из металла и является характеристикой каждого металла. В результате закон сохранения энергии дает для кинетической энергии вылетевшего электрона
В формулах (26.2)-(26.3) Дж • с — постоянная, которая называется постоянной Планка, — скорость света в вакууме, — частота света, — длина волны. Поглощая один фотон, свободный электрон в металле увеличивает свою энергию на величину (26.2) и может вылететь с поверхности металла, если его новая энергия достаточна для этого, т.е. превосходит работу , которую необходимо совершить, чтобы покинуть металл. Эта работа называется работой выхода электрона из металла и является характеристикой каждого металла. В результате закон сохранения энергии дает для кинетической энергии вылетевшего электрона
(26.4) |
В формуле (26.4) пренебрегается начальной энергией электрона. Кроме того, возможны дополнительные потери энергии, связанные со столкновениями с другими электронами, поэтому формула (26.4) определяет максимальную кинетическую энергию электронов. Формула (26.4) называется уравнением Эйнштейна для фотоэффекта.
(26.5) |
(или при длине волны , где ) фотоэффект не имеет место. Поскольку для большинства металлов эта частота лежит в области красного света, ее назвали красной границей фотоэффекта.
Рассмотрим теперь вопросы, связанные со строением атома. Атомы состоят из частиц трех типов: протонов, нейтронов и электронов. Протоны и нейтроны имеют близкие массы, и входят в состав атомного ядра — очень маленького образования, расположенного внутриатома Поэтому и атомное ядро заряжено положительным электрическим зарядом. Электроны — отрицательно заряженные элементарные частицы — движутся по определенным орбитам вокруг атомного ядра. Количество электронов в атоме равно количеству протонов, а поскольку заряды этих частиц равны по величине, то атомы в целом не заряжены. Поскольку масса протона и нейтрона примерно в 2000 раз больше массы электрона, то практически вся масса атома сосредоточена в атомном ядре.
Поэтому и атомное ядро заряжено положительным электрическим зарядом. Электроны — отрицательно заряженные элементарные частицы — движутся по определенным орбитам вокруг атомного ядра. Количество электронов в атоме равно количеству протонов, а поскольку заряды этих частиц равны по величине, то атомы в целом не заряжены. Поскольку масса протона и нейтрона примерно в 2000 раз больше массы электрона, то практически вся масса атома сосредоточена в атомном ядре.
Атомы обозначаются следующим образом. Во-первых, указывается химический символ элемента, например, (водород), (гелий), (кислород), (железо), (свинец) и т.д. Во-вторых, перед символом элемента в виде нижнего индекса указывают количество электронов (или протонов) в данном атоме. Например, , , , , и т.д. Поскольку количество электронов в атоме (или количество протонов) полностью определяет его химические свойства, атомы, имеющие разное количество электронов (и протонов) — это атомы разных химических элементов. Поэтому нижний индекс и символ химического элемента однозначно связаны друг с другом.
обозначает атом урана, содержащий 92 электрона и 238 протонов и нейтронов в ядре, из которых 92 протона и 146 = 238 – 92 нейтронов. Существуют атомы, которые имеют одинаковое количество протонов и электронов, но разное количество нейтронов. Такие атомы имеют близкие химические свойства и потому относятся к одному и тому же химическому элементу. Они называются изотопами. Например, изотопами являются атомы свинца , , , , в состав которых входят соответственно 124, 125, 126 и 127 нейтронов.
Электроны в атоме могут совершать переходы с одних орбит на другие с излучением или поглощением фотона. Такое излучение имеет место, в частности, при нагревании парóв любого химического элемента до высокой температуры. При переходе электрона из состояния с энергией в состояние с меньшей энергией , электрон излучает фотон с частотой , которая определяется соотношением
(26. |
где — постоянная Планка. Для перехода на орбиту с большей энергией электрон должен поглотить фотон с энергией, равной разности энергий конечной и начальной орбит. А поскольку в каждом атоме существует только небольшое количество электронных орбит с определенными энергиями, атом каждого вещества излучает свет с небольшим числом разных частот, что означает, что спектр излучения атомов является линейчатым 1. На индивидуальности спектров каждого элемента основан метод определения химического состава вещества, который называется спектральный анализ
Некоторые атомы могут самопроизвольно испускать определенные частицы (в результате чего атомы одних элементов превращаются в атомы других). Такое явление называется радиоактивностью. Существует несколько видов радиоактивности, которые получили название -, — и -радиоактивности. Альфа-излучение представляет собой поток ядер атомов гелия, состоящих их двух протонов и двух нейтронов. Альфа-частицы формируются внутри ядра распадающегося атома из его «собственных» протонов и нейтронов, а затем вылетают из ядра. После этого атом теряет два внешних электрона и становится электрически нейтральным атомом элемента, у которого меньше на два нейтрона и два протона. Этот процесс можно схематически записать в виде уравнения, которое называется уравнением ядерной реакции:
После этого атом теряет два внешних электрона и становится электрически нейтральным атомом элемента, у которого меньше на два нейтрона и два протона. Этот процесс можно схематически записать в виде уравнения, которое называется уравнением ядерной реакции:
(26.7) |
Здесь и — химические символы распадающегося и образовавшегося элементов (например, при -распаде уран превращается в торий ), и — число нейтронов и протонов в распадающемся атоме, — символ -частицы.
При -распаде атом излучает электрон, причем электрон вылетает из атомного ядра. А поскольку «собственных» электронов в ядре нет, то в процессе -распада происходит превращение одного из нейтронов ядра в протон и электрон, протон остается в ядре, а электрон улетает. Этот процесс можно записать в виде уравнения
(26.8) |
Обратим внимание читателя на то, что в процессе -распада суммарное число нейтронов и протонов не изменяется. На самом деле в процессе -распада образуется еще одна частица — антинейтрино, которая имеет очень маленькую или вообще нулевую (это пока неизвестно) массу. Эта частица очень слабо взаимодействует с веществом и потому долгое время ее не могли обнаружить экспериментально.
На самом деле в процессе -распада образуется еще одна частица — антинейтрино, которая имеет очень маленькую или вообще нулевую (это пока неизвестно) массу. Эта частица очень слабо взаимодействует с веществом и потому долгое время ее не могли обнаружить экспериментально.
При -распаде атомное ядро излучает кванты электромагнитного излучения (-частицы или -кванты), т.е. частицы той же физической природы, что и фотоны. Однако -частицы имеют очень большую частоту (и малую длину волны) по сравнению с фотонами видимого света и даже рентгеновским излучением (частота -лучей порядка 1020 Гц). Из-за очень малой длины волны -излучение практически не проявляет волновых свойств, а ведет себя как поток частиц. Поскольку при -распаде из атома не вылетают электроны, протоны или нейтроны, атом остается структурно тем же самым, но с меньшей энергией, поскольку часть энергии уносит -квант.
При радиоактивных распадах зависимость количества распадающихся атомов от времени подчиняется следующему закону: количество атомов данного радиоактивного вещества уменьшается в два раза за некоторое фиксированное время независимо от их первоначального количества. Это время называется периодом (или временем) полураспада данного вещества. Например, если в некоторый момент времени имеется 1000 атомов радиоактивного вещества с периодом полураспада 1 год, то через год останется 500 атомов. А если бы в начальный момент имелось 10000 атомов этого вещества, то через год их осталось бы 5000. Такая зависимость количества распавшихся атомов от времени свидетельствует о том, что, во-первых, распад каждого атома происходит независимо от других, а во-вторых, имеет вероятностный характер. Поэтому приведенный выше закон распада выполняется приближенно, причем тем точнее, чем большее количество атомов вещества распадется.
Это время называется периодом (или временем) полураспада данного вещества. Например, если в некоторый момент времени имеется 1000 атомов радиоактивного вещества с периодом полураспада 1 год, то через год останется 500 атомов. А если бы в начальный момент имелось 10000 атомов этого вещества, то через год их осталось бы 5000. Такая зависимость количества распавшихся атомов от времени свидетельствует о том, что, во-первых, распад каждого атома происходит независимо от других, а во-вторых, имеет вероятностный характер. Поэтому приведенный выше закон распада выполняется приближенно, причем тем точнее, чем большее количество атомов вещества распадется.
Последней темой, которая рассматривается в школьном курсе физики, является специальная теория относительности. Надо сказать, что это рассмотрение является весьма поверхностным, и потому в программу ЕГЭ по физике входит очень небольшое количество вопросов по данной теме. Мы нашли в опубликованных вариантах раздела «А» ЕГЭ прошлых лет всего три вопроса, которые с минимальными вариациями повторяются из года в год. Можно утверждать со значительной вероятностью, что именно эти вопросы будут повторяться и в будущем. Итак, дадим краткий обзор необходимого минимума сведений по теории относительности, входящих в школьный курс физики.
Можно утверждать со значительной вероятностью, что именно эти вопросы будут повторяться и в будущем. Итак, дадим краткий обзор необходимого минимума сведений по теории относительности, входящих в школьный курс физики.
Специальная теорияотносительности1 рассматривает вопросы, связанные с механикой и электродинамикой тел, движущихся со скоростями, близкими к скорости света в вакууме. Оказалось, что физические законы, управляющие поведением таких тел, значительно отличаются от законов физики Ньютона, которую в этом контексте принято называть классической. Экспериментальной основой теории относительности является опыт Майкельсона, который с помощью прямых измерений доказал, что скорость света в вакууме не зависит от скорости наблюдателя или источника. Этот факт Эйнштейн взял в качестве одного изпостулатов2 своей теории. Второй постулат называется принципом относительности и говорит о том, что все уравнения и законы физики имеют один и тот же вид во всех инерциальных системах отсчета, и, следовательно, все физические явления протекают во всех инерциальных системах отсчета одинаково (аналогичное утверждение, касающееся только механических явлений, называется принципом относительности Галилея). Опираясь только на эти два постулата, Эйнштейн доказал целый ряд удивительных утверждений. Оказалось, в частности, что интервалы времени и длины отрезков зависят от системы отсчета, т.е. являются, как говорят, относительными величинами. Кроме того, для тел, движущихся с большими скоростями, изменяются ряд физических законов (в частности, законы Ньютона), выражения для некоторых физических величин (энергии, импульса и др.). Эйнштейн получил и новый закон сложения скоростей, который при малых скоростях переходит в «обычный» закон сложения скоростей Галилея, а при больших скоростях тел приводит к постоянству скорости света во всех инерциальных системах отсчета.
Опираясь только на эти два постулата, Эйнштейн доказал целый ряд удивительных утверждений. Оказалось, в частности, что интервалы времени и длины отрезков зависят от системы отсчета, т.е. являются, как говорят, относительными величинами. Кроме того, для тел, движущихся с большими скоростями, изменяются ряд физических законов (в частности, законы Ньютона), выражения для некоторых физических величин (энергии, импульса и др.). Эйнштейн получил и новый закон сложения скоростей, который при малых скоростях переходит в «обычный» закон сложения скоростей Галилея, а при больших скоростях тел приводит к постоянству скорости света во всех инерциальных системах отсчета.
Рассмотрим теперь приведенные в первой части книги задачи.
Как это описывалось во введении к настоящей главе, максимальная кинетическая энергия фотоэлектронов зависит только от частоты падающего света, но не зависит от интенсивности излучения (задача 26.1.1 — ответ 1).
От интенсивности излучения зависит количество фотоэлектронов. Поэтому если уменьшить интенсивность света без изменения его частоты (задача 26.1.2), то уменьшится количество фотоэлектронов, но никак не изменится их максимальная скорость.
Поэтому если уменьшить интенсивность света без изменения его частоты (задача 26.1.2), то уменьшится количество фотоэлектронов, но никак не изменится их максимальная скорость.
Электрон, поглощая фотон с энергий 1,5 эВ (задача 26.1.3), приобретает именно такую энергию и не сможет покинуть металл, если работа выхода электрона из металла составляет 2 эВ. Поэтому при данных условиях фотоэффект идти не будет (ответ 3).
Согласно формуле (26.5) работа выхода электрона из данного металла равна энергии фотона, отвечающего красной границе фотоэффекта для данного металла. Поэтому правильный ответ в задаче 26.1.4 — 3.
Максимальную энергию фотоэлектронов , которую они приобретают при освещении цезия фотонами с энергией 2,1 эВ (задача 26.1.5) найдем по уравнению Эйнштейна для фотоэффекта (26.4): эВ. Отсюда следует, что для увеличения энергии фотоэлектронов вдвое (до величины 0,4 эВ) нужно увеличить энергию фотонов до 2,3 эВ, т. е. на 0,2 эВ (ответ 2).
е. на 0,2 эВ (ответ 2).
Из уравнения Эйнштейна следует, что максимальная кинетическая энергия электронов в задаче 26.1.6 равна 1 эВ. Величину задерживающего напряжения можно найти по формуле (26.1). Вычислительно это процедура является очень простой, если для измерения энергии электрона используется внесистемная единица «электрон-вольт» (эВ). По определению 1 электрон-вольт — это кинетическая энергия, которую приобретает электрон, пройдя ускоряющее напряжение 1 Вольт (В). И наоборот, электроны с кинетической энергией 1 эВ будут остановлены задерживающим напряжением 1 В и фотоэффект полностью прекратится. Таким образом, правильный ответ в этой задаче — 3.
Согласно правилам обозначения атомов нижний индекс указывает число протонов в ядре и электронов на орбитах. Поэтому число электронов в атоме (задача 26.1.7) равно 26 (ответ 2).
Импульс фотона связан с его энергией формулой (26.3) (задача 26.1.8 — ответ 1).
Электрон в атоме излучает фотон, совершая переход и состояния с большей энергией в состояние с меньшей энергией. При этом по закону сохранения энергии разность начальной и конечной энергий электрона уносится фотоном. Используя формулу, связывающую энергию и частоту фотона (26.2), находим (задача 26.1.9):
(26.8) |
(ответ 1).
Как указывалось во введении к настоящей главе, спектры излучения парóв химических элементов являются линейчатыми, причем характер расположения линий излучения в спектре уникален для каждого элемента. Поэтому если в образце имеется какой-то элемент, в спектре излучения парóв этого образца будут обязательно представлены спектральные линии, характерные для этого элемента. Спектр излучения неизвестного образца в задаче 26.1.10 содержит все линии спектра стронция, не содержит ни одной линии спектра кальция и содержит ряд дополнительных линий. Это значит, что неизвестный образец содержит стронций и не содержит кальция (ответ 4). Кроме того, этот образец содержит еще какой-то элемент, который и дает лишние (по сравнению с линиями стронция) линии в спектре.
Это значит, что неизвестный образец содержит стронций и не содержит кальция (ответ 4). Кроме того, этот образец содержит еще какой-то элемент, который и дает лишние (по сравнению с линиями стронция) линии в спектре.
Атомное ядро состоит из протонов и нейтронов (задача 26.2.1 — ответ 2).
Согласно правилам обозначения атомов нижний индекс у символа химического элемента представляет число протонов, верхний — сумму числа протонов и нейтронов. Поэтому в ядре (задача 26.2.2) содержится 30 = 56 − 26 нейтронов (ответ 2).
Из уравнения (26.7) для -распада находим, что при -распаде ядра радона (задача 26.2.3) образуется ядро полония (ответ 4).
Из уравнения (26.8) для -распада находим, что при -распаде ядра тория (задача 26.2.4) образуется ядро протактиния (ответ 3).
При поглощении нейтрона (задача 26.2.5) число нейтронов в ядре увеличивается на единицу, число протонов не изменяется. Поэтому получится ядро свинца (ответ 1).
Поэтому получится ядро свинца (ответ 1).
При двух -распадах тория (задача 26.2.6) два нейтрона в ядре превращаются в два протона. Поэтому получается ядро урана . При его -распаде число нейтронов и число протонов уменьшаются на две единицы каждое. В результате образуется ядро тория, но с другим по сравнению с начальным ядром количеством нейтронов (ответ 2).
За время, равное одному периоду полураспада (задача 26.2.7), количество атомов распадающегося вещества уменьшится вдвое и станет равным . Еще за один период полураспада вдвое уменьшится и это количество атомов, поэтому останется атомов вещества. А за еще один период полураспада (т.е. за время после начала наблюдения) вдвое уменьшится и это количество. Поэтому через время после начала наблюдения останется атомов вещества (ответ 3).
Постулатами теории относительности являются (см. введение к настоящей главе): утверждение о постоянстве скорости света во всех инерциальных системах отсчета и равноправность всех инерциальных систем для описания любых физических явлений (принцип относительности). Поэтому правильный ответ в задаче 26.2.8 — 2.
Поэтому правильный ответ в задаче 26.2.8 — 2.
Скорость света во всех инерциальных системах одинакова. Поэтому скорость фотонов, излученных фарами первого автомобиля в системе отсчета, связанной со вторым автомобилем (задача 26.2.9), равна = 3 • 108 м/с (ответ 3).
Как отмечалось во введении к настоящей главе, интервалы времени между событиями и длины отрезков меняются при переходе от одной инерциальной системы отсчета к другой. Как и в классической физике при переходе к другим системам отсчета меняются импульсы тел. Поэтому из перечисленных в задаче 26.2.10 величин не меняется только скорость света (ответ 4).
Энергия реакции, порог реакции
Энергия реакции, порог реакцииНапишем закон сохранения энергии для ядерной реакции в следующем виде:
, (2.1)
где mi, mf — массы, а Ti, Tf -кинетические энергии в начальном и конечном состояниях.
Энергией реакции называется разность масс начального и конечного состояний системы.
. (2.2)
Реакция может идти с образованием в конечном состоянии возбужденных ядер.
Таким образом массы их m больше, чем в основном состоянии, m = m + Евозб/c2,
где Евозб — энергия возбуждения ядра, что необходимо учитывать при
расчетах по формуле (2.2).
Если Q > 0, реакция называется экзотермической и сопровождается увеличением суммарной кинетической энергии.
Если Q < 0, то реакция называется эндотермической и сопровождается уменьшением суммарной кинетической энергии. Для реализации
эндотермической реакции необходимо, чтобы энергия сталкивающихся частиц была
больше некоторой величины, которая в системе центра инерции (с.ц.и.)
тождественно равняется Q. Суммарная кинетическая энергия частиц в конечном
состоянии при этом равна нулю. В лабораторной системе (л. с.) энергия,
необходимая для реализации эндотермической реакции должна быть больше Q, так как
часть энергии расходуется на движение центра инерции.
с.) энергия,
необходимая для реализации эндотермической реакции должна быть больше Q, так как
часть энергии расходуется на движение центра инерции.
Минимальная кинетическая энергия налетающей частицы в
лабораторной системе координат, при которой реакция становится возможной,
называется порогом реакции.
Получим формулу для расчета порога реакции. Рассмотрим
реакцию A(a,b)B. Законы сохранения энергии и импульса в лабораторной системе:
Ea + mAc2 = Eb + EB = ε, (2.3)
a = b + B =
.
(2.4)
В системе центра инерции
E‘a + E‘A = E‘b + E‘B = ε‘, (2.5)
‘a + ‘A = ‘b + ‘B = ‘. (2.6)
(2.6)
В выражениях (2.3, 2.5) E — полная энергия. Кинетическая энергия налетающей частицы в л.с. равна пороговой, когда в с.ц.и. кинетические энергии продуктов реакции равны 0, т.е.
E‘b = mbc2; E‘B = mBc2; ‘b = ‘B = 0;
(2.7)
ε‘ = (mb + mB)c2;
‘ = 0.
(2.8)
Выпишем релятивистский инвариант в с.ц.и.
(ε‘)2 − c2(‘)2 = (mb + mB)2c4. (2.9)
В лабораторной системе, учитывая, что Ea = mac2 +Tпор,
ε2 − c22 = (mac2 + mAc2 + Tпор)2 −с2pa2.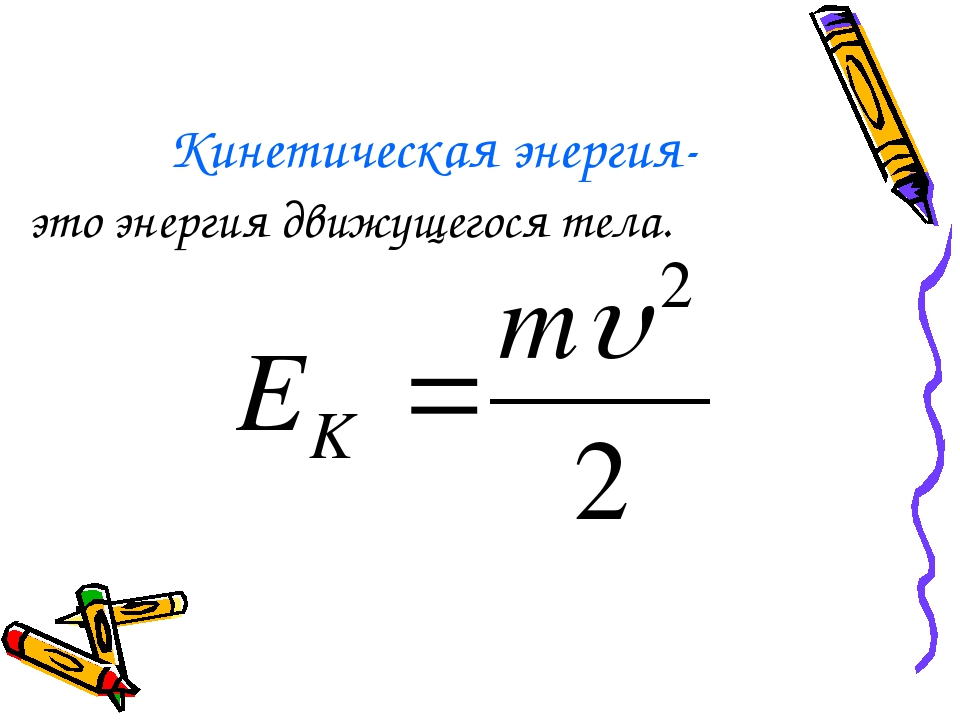 (2.10)
(2.10)
Подставив в (2.10) вместо импульса его выражение через кинетическую энергию
, (2.11)
получим
ε2 − c22 = (ma + mA)2c4 + TпорmAc2. (2.12)
Учитывая, что
ε2 − c22 = (ε‘)2 − c2(‘)2 = inv., (2.13)
получим
или
(2.14)
где Q -энергия реакции, ma — масса налетающей частицы, mA — масса ядра мишени.
В нерелятивистском приближении (Q<< 2mAc2)
(2.14a)
Отметим, что выражения (2.14) и (2.14а) справедливы и для реакций с любым
количеством частиц в конечном состоянии.
Кинетическая энергия
Энергия – это физическая величина, показывающая, какую работу может совершить тело.
Единица измерения энергии — Джоуль [1Дж]
Кинетическая энергия — скалярная физическая величина, равная половине произведения массы тела на квадрат его скорости.
Это энергия, которой тело обладает вследствие своего движения, т.е. любое тело, которое движется (едет, летит, падает, плывет и т.д.) обладает кинетической энергией.
Пусть тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.
Как мы знаем, работа постоянной силы вычисляют по формуле A=FScosa. Так как в рассматриваемом нами случае направление силы F и перемещения S совпадают, то cosa=1, и тогда у нас получается, что работа силы равна А=FS. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения перемещение тела можно найти по формуле:
По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения перемещение тела можно найти по формуле:
Подставляя найденные значения F и S в формулу работы, и получаем:
Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины . А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина представляет собой энергию, обусловленную движением тела. Эту энергию и называют кинетической. Она обозначается Wк или Ек.
Если взять выведенную нами формулу работы, то у нас получится:
Данная формула выражает теорему о кинетической энергии:работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела
Обозначения:
Wк,Eк — Кинетическая энергия
m — Масса тела
v — Скорость движения тела
v1 — Начальная скорость тела
v2 — Конечная скорость тела
A — Работа тела
a — Ускорение тела
F — Сила, действующая на тело
S — Перемещение тела
Энергия тела кинетическая — Энциклопедия по машиностроению XXL
Кинетическая энергия тела. Кинетическая энергия Т определяется формулой
[c.146]
Кинетическая энергия Т определяется формулой
[c.146]Кинетическая энергия тела. Кинетическая энергия тела определяется выражением [c.491]
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения. [c.302]
Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс. [c.303]
Таким образом, кинетическая энергия тела в общем случае движения (в частности, и при плоскопараллельном движении) равна кинетической энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг оси, проходящей через центр масс. [c.304]
Задача 137. Q детали Л, движущейся поступательно со скоростью И, имеются направляющие, по которым со скоростью v перемещается тело В массой т. Зная угол а (рис. 305), определить кинетическую энергию тела В.
[c.304]
Зная угол а (рис. 305), определить кинетическую энергию тела В.
[c.304]
Кинетическая энергия тела, движущегося вокруг неподвижной точки. Так как любое элементарное перемещение твердого тела, имеющего неподвижную точку О, представляет собой элементарный поворот с угловой скоростью (О вокруг мгновенной оси вращения 01, проходящей через эту точку (см. 60), то кинетическую энергию тела можно определить по формуле [c.341]
Поступательное движение твердого тела. При поступательном движении твердого тела скорости всех его точек в каждый момент времени геометрически равны между собой (рис. 152). Кинетическая энергия тела определится (67.1) [c.179]
Таки.м образом, кинетическая энергия тела, движущегося поступательно, вычисляется как кинетическая энергия материальной точки, имеющей массу этого тела. [c.180]
Кинетическая энергия тела [c.180]
Здесь 1/2-шос —кинетическая энергия тела в поступательном движении вместе с центром масс, а 1/2 — кинетическая энергия во вращении тела вокруг подвижной оси С , определенная на основании формулы
[c. 181]
181]
Сферическое движение твердого тела. Скорости точек твердого тела при сферическом движении в каждый момент можно рассматривать как вращательные вокруг мгновенной оси вращения (рис. 155). Поэтому кинетическая энергия тела, совершающего сферическое движение в данный момент, онреде-ляется по формуле [c.181]
Таким образом, кинетическая энергия твердого тела в общем случае его движения равна сумме кинетической энергии тела в его переносном поступательном движении вместе с центром масс и его кинетической энергии в сферическом движении относительно центра масс. [c.181]
Потеря кинетической энергии тел за время удара То — Г = 1/2 mi (v — и ) + 1/2 (и.] — = [c.267]
Обозначим кинетическую энергию тел, соответствующую их потерянным скоростям Т. Ее величина [c.268]
Формула (101.5) выражает теорему Карно кинетическая энергия, потерянная телами при неупругом ударе, равна кинетической энергии тел, соответствующей их потерянным скоростям. [c.268]
[c.268]
Вычислим кинетическую энергию системы в ко 1еч ом положении как сумму кинетических энергий тел 1, 2, 3, 4, 5 [c.199]
Кинетическая энергия тела, соответствующая потерянным скоростям его точек, [c.233]
Найдем кинетическую энергию системы, равную сумме кинетических энергий тел 1, 2, 6 4 [c.313]
Момент инерции тела 1 относительно центральной оси Момент инерции тела 4 относительно оси вращения J4 = tnJ /3. Кинетическая энергия тел 1, 2, 3 и 4 имеет вид [c.335]
Первая сумма представляет собой кинетическую энергию тела в его переносном движении вместе с точкой О. Она равна [c.170]
Для того чтобы определить кинетическую энергию То-, обратим внимание на то, что в относительном движении точка О неподвижна (она находится в начале координат системы х, у, г ), и поэтому Го- подсчитывается как кинетическая энергия тела, имеющего неподвижную точку. При наличии неподвижной точки всегда существует мгновенная ось вращения, проходящая через эту точку. В рассматриваемое мгновение скорости распределяются так, как если бы тело вращалось с угловой скоростью о вокруг этой оси, поэтому
[c.171]
При наличии неподвижной точки всегда существует мгновенная ось вращения, проходящая через эту точку. В рассматриваемое мгновение скорости распределяются так, как если бы тело вращалось с угловой скоростью о вокруг этой оси, поэтому
[c.171]
Кинетическая энергия и кинетический момент твердого тела, имеющего неподвижную точку [c.184]
Кинетическая энергия. Если известен момент инерции тела относительно мгновенной оси (о, то кинетическая энергия тела, разумеется, равна [c.185]
Следовательно, кинетическая энергия тела с неподвижной точкой в общем случае не равна сумме кинетических энергий трех вращений, происходящих относительно трех связанных с телом осей с угловыми скоростями, равными проекциям угловой скорости тела на эти оси. Такое простое соотношение получается лишь в том исключительном случае, когда оси, связанные с телом, совпадают с главными осями инерции для неподвижной точки. При любом ином выборе связанных осей необходимо учитывать еще дополнительные члены, обусловленные центробежными моментами инерции и выписанные в формуле (42). [c.186]
[c.186]
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТЕЛА. [c.148]
Кинетическая энергия твердого тела складывается из кинетических энергий его отдельных точек. При поступательном движении тела скорости всех его точек равны между собой и равны Ъс — скорости центра масс тела (рис. 1.178). Поэтому легко понять, что кинетическая энергия тела при [c.148]
Понятие о работе и мощности. Внутренняя и внегиняя энергия тел кинетическая и потенциальная энергия тел. Закон сохранения и пренрандения энергии (М. В. Ломоносов — 1748 г., Р. Майер — 1842 г.). Современные промышленные источники эиергии. [c.604]
Это есть момент инерции вращающегося в.месте со звеном А В тела, кинетическая энергия которого в каждом рассматриваемом полоо сении механизма равна сумме кинетических энергий есех его звеньев. [c.338]
Под кинетической энергией тела с переменной массой, вычисленной отиосительно неподвижного начала координат О (рнс. 18.2), понимают выран[c.367]
18.2), понимают выран[c.367]
Повышение температуры тела свидетельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению попенциаль-ной энергии частиц. В результате внутренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него давление, то при расширении оно производит механическую работу 6L против сил внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии [c.14]
Известно, что при нагревании тела кинетическая энергия его молекул возрастает. Частицы более нагретой части тела, сталкиваясь при своем беспорядочном дви>кении с соседни.ми частица.ми тела, сообщают им часть своей кинетической энергии. Этот процесс постепенно распространяется по всему телу. Например, если нагревать один конец металлического стержня, то через некоторое время температура другого его конца также повысится. Перенос теплоты теплопроводностью зависит от физических свойств тела, от его геометрических размеров, а также от разности температур между различными частями тела. При определении переноса теплоты теплопроводностью в реальных телах встречаются известные трудности, которые на практике до сих пор удовлетворително не решены. Эти тоудности состоят в том, что тепловые процессы развиваются в Н2
[c.345]
При определении переноса теплоты теплопроводностью в реальных телах встречаются известные трудности, которые на практике до сих пор удовлетворително не решены. Эти тоудности состоят в том, что тепловые процессы развиваются в Н2
[c.345]
Следовательно, кинетическая энергия тела при вращательном движении вокруг ненодвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела. [c.176]
Общий случай движения твердого тела. Движение свободного твердого тела в общем случае mojkfio разложить на два составляющих движения на переносное поступательное движение вместе с центром масс и относительное сферическое движение относительно центра масс (рис. 156). Тогда кинетическая энергия тела определится по формуле Кенига [c.181]
Тогда выражение (101.2), определяющее потерю кинетической энергии тел при ударе, прпмет вид
[c.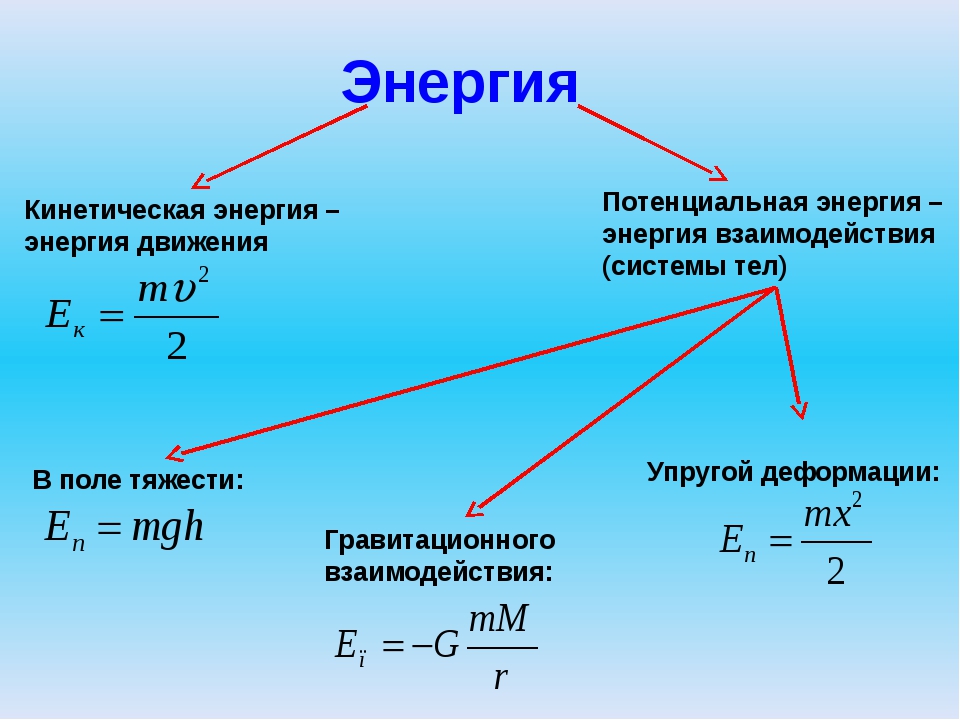 268]
268]
Решен не. Как известно, коэффициент полезного действия машины равен отношению полезной работы к работе, затрачиваемой на приведение маши1гы в движение. В данном слу 1ае полезной является работа, израсходованная па деформацто металла,, 9та работа равна потере кинетической энергии тел при ударе Т —Т. [c.276]
Работа, атрачнвасмая на подъем молота, равна увелнченпю его потенциальной энергии, т, е. Gih. При падении молота его потенциальная энергия переходит в кинетическую. Таким образом, затрачиваемая работа равна кинетической энергии тел до удара Т . Коэффициент полезного действия молота [c.276]
Найтп кинетическую энергию системы как сумму кинетических энергий тел I, 2, 3 п 4 [c.334]
Кинетическая энергия твердого тела равна кинетической энергии, которую имела бы материальная точка, расположенная в центре инерции тела, если бы в ней была сосредоточена вся масса тела, плюс кинетическая энергия тела в его движении относительно системы отсчета, связанной с центром инерции и движущейся вместе с ним поступательно (теорема Кёнига i)). [c.170]
[c.170]
Это замечание касается вращения тела относительно неподвижной оси /. Для подсчета кинетической энергии тела в этом случае нет нуж ы использовать теорему Кёнига даже в том случае, когда центр инерции тела не лежит на оси и имеет скорость, отличную от нуля. Действительно, можно выбрать начало координат на неподвижной оси и рассуждать точно так же, как это делалось в конце замечания 5° при подсчете То-, поскольку формула (8) определяет в этом случае не относительную, а абсолютную скорость, если считать, что рг — расстояние от i-й точки до оси вращения. Поэтому в случае движения тела относительно неподвижной оси [c.172]
Начиная с этого параграфа, мы всегда будем считать, что оси I, т), направлены по главным осям тела для точки О. При таком выборе осей кинетическая энергия тела, как это было выяснено в 3, может быть предстгвлена формулой (43). Положим 1 = г1з, 2 = Ф. = 0 и, собираясь составить уравнения Лагранжа для тела с неподвижной точксй, прежде всего найдем, чему равны обобщенные силы, соответствующие эйлеровым углам. [c.191]
[c.191]
Кинетическая энергия тела при сложном его движении (при плоскопараллельном, в частности) складывается из кинетической энергии поступательного движения со скоростью центра масс а кинетической энергии враицательного движения с угловой скоростью вокруг оси, проходящей через центр масс, т. е. [c.149]
Кинетическая энергия пружины — формула и определение
На данном уроке мы поговорим о том, что такое сила упругости, научимся вычислять ее работу, введя в рассмотрение новую разновидность потенциальной энергии, а также поговорим о потенциальной энергии и об упругом столкновении тел.
Блок: 1/5 | Кол-во символов: 228
Источник: https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/rabota-sily-uprugosti-potentsialnaya-energiya-uprugo-deformirovannogo-tela?konspekt
Введение
На прошлом уроке мы с вами показали, что для применения теоремы об изменении кинетической энергии мы должны уметь вычислять работу основных сил в природе. И мы уже научились это делать на примере работы силы тяжести. Было показано, что эту величину очень просто рассчитать, если ввести в рассмотрение новый вид энергии – потенциальную энергию тела, притягивающуюся к земле. Сегодня сделаем то же самое для силы упругости.
И мы уже научились это делать на примере работы силы тяжести. Было показано, что эту величину очень просто рассчитать, если ввести в рассмотрение новый вид энергии – потенциальную энергию тела, притягивающуюся к земле. Сегодня сделаем то же самое для силы упругости.
Рассмотрим простую систему: массивный груз, прикрепленный к пружине (см. рис. 1).
Рис. 1. Груз, прикрепленный к пружине
Пусть изначально система находится в состоянии равновесия, то есть пружина не деформированная, и груз покоится. Выведем эту систему из равновесия и сделаем так, чтобы пружина стала в сжатом состоянии (см. рис. 2).
Рис. 2. Система выведена из равновесия
Если направить ось ОХ так, как показано на рис. 2, и расположить начало координат там, где до начала сжатия был расположен центр груза, то проекцию возникающей силы упругости на нашу ось ОХ можно записать в виде:
,
где k – жесткость пружины, величина деформации пружины. Если предоставить пружину самой себе, то груз будет смещаться влево, при этом сила упругости будет совершать работу. Предположим, что левый конец пружины вместе с грузом переместился из положения А в положение В (см. рис. 3).
Предположим, что левый конец пружины вместе с грузом переместился из положения А в положение В (см. рис. 3).
Рис. 3. Перемещение груза
В этом положении деформация пружины равна уже не , а . А перемещение конца пружины и одновременно перемещение центра груза равно разности координат . Попытаемся вычислить работу силы упругости, совершенную при таком движении груза.
Блок: 2/5 | Кол-во символов: 1573
Источник: https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/rabota-sily-uprugosti-potentsialnaya-energiya-uprugo-deformirovannogo-tela?konspekt
Понятие энергии
Для работы двигателей, которые придают движение автомобилям, тракторам, тепловозам, самолетам, нужно топливо, которое является источником энергии. Электродвигатели придают движение станкам при помощи электроэнергии. За счет энергии воды, падающей с высоты, оборачиваются гидротурбины, соединенные с электрическими машинами, производящими электрический ток. Человеку для того, чтобы существовать и работать, также нужна энергия. Говорят, что для того, дабы выполнять какую-нибудь работу, необходима энергия. Что же такое энергия?
Говорят, что для того, дабы выполнять какую-нибудь работу, необходима энергия. Что же такое энергия?
- Наблюдение 1. Поднимем над землей мяч. Пока он пребывает в состоянии спокойствия, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на землю с определенной высоты. Во время падения мяча выполняется механическая работа.
- Наблюдение 2. Сомкнем пружину, зафиксируем ее нитью и поставим на пружину гирьку. Подожжем нить, пружина распрямится и поднимет гирьку на некую высоту. Пружина выполнила механическую работу.
- Наблюдение 3. На тележку закрепим стержень с блоком в конце. Через блок перекинем нить, один конец которой намотан на ось тележки, а на другом висит грузик. Отпустим грузик. Под действием силы тяжести он будет опускаться книзу и придаст тележке движение. Грузик выполнил механическую работу.
После анализа всех вышеперечисленных наблюдений можно сделать вывод, что если тело или несколько тел во время взаимодействия выполняют механическую работу, то говорят, что они имеют механическую энергию, либо энергию.
Блок: 2/14 | Кол-во символов: 1498
Источник: https://autogear.ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/
Вычисление работы силы упругости
Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.
О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.
Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.
Рис. 4. Зависимость силы упругости от координаты движения
Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).
Рис. 5. Площадь фигуры
Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.
6.
Рис. 6. Площадь большой фигуры
Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:
К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:
,
где среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:
Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.
Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.
Блок: 3/5 | Кол-во символов: 3872
Источник: https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/rabota-sily-uprugosti-potentsialnaya-energiya-uprugo-deformirovannogo-tela?konspekt
Потенциальная энергия упруго деформированного тела
Здесь поступим аналогичным образом. Величину, равную половине произведения жесткости пружины на квадрат ее удлинения, назовем потенциальной энергией деформированной пружины. Мы имеем право это сделать, поскольку изменение данной величины, взятой с обратным знаком, равно работе силы упругости. Теперь формулу для вычисления работы силы упругости можно озвучить по-другому: работа силы упругости равна изменению потенциальной энергии упруго деформированного тела (пружины), взятому с обратным знаком:
Величину, равную половине произведения жесткости пружины на квадрат ее удлинения, назовем потенциальной энергией деформированной пружины. Мы имеем право это сделать, поскольку изменение данной величины, взятой с обратным знаком, равно работе силы упругости. Теперь формулу для вычисления работы силы упругости можно озвучить по-другому: работа силы упругости равна изменению потенциальной энергии упруго деформированного тела (пружины), взятому с обратным знаком:
Работа силы упругости, как и работа силы тяжести, зависит только от начального и конечного положения центра груза – это означает, что работа силы упругости не зависит от формы траектории груза, а в том случае, когда траектория является замкнутой, работа силы упругости равна 0.
Если за начало отсчета принять положение груза при недеформированной пружине, а после принять, что удлинение пружины равно (см. рис. 7), то формула для работы силы упругости приобретает вид:
Рис. 7. Вычисление работы силы упругости
Но – это потенциальная энергия пружины при ее удлинении на величину , следовательно, потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе тела (пружины) в состояние, в котором его деформация равна 0.
Когда мы описывали потенциальную энергию тела, поднятого над землей, мы говорили, что потенциальная энергия – это энергия взаимодействия тел и в том случае это была энергия взаимодействия двух тел – груза и земли. Что касается силы упругости, то о ней можно сказать почти то же самое – это тоже энергия взаимодействия, однако теперь это энергия взаимодействия не различных тел, а частей одного и того же тела – в нашем случае это энергия взаимодействия частей пружины.
Теперь рассмотрим задачу.
Блок: 4/5 | Кол-во символов: 1808
Источник: https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/rabota-sily-uprugosti-potentsialnaya-energiya-uprugo-deformirovannogo-tela?konspekt
Энергия кинетическая: формула и определение
Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, — это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии. Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения.
Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения.
Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:
Где К — кинетическая энергия, m — масса тела, v — скорость.
Блок: 6/14 | Кол-во символов: 1313
Источник: https://autogear.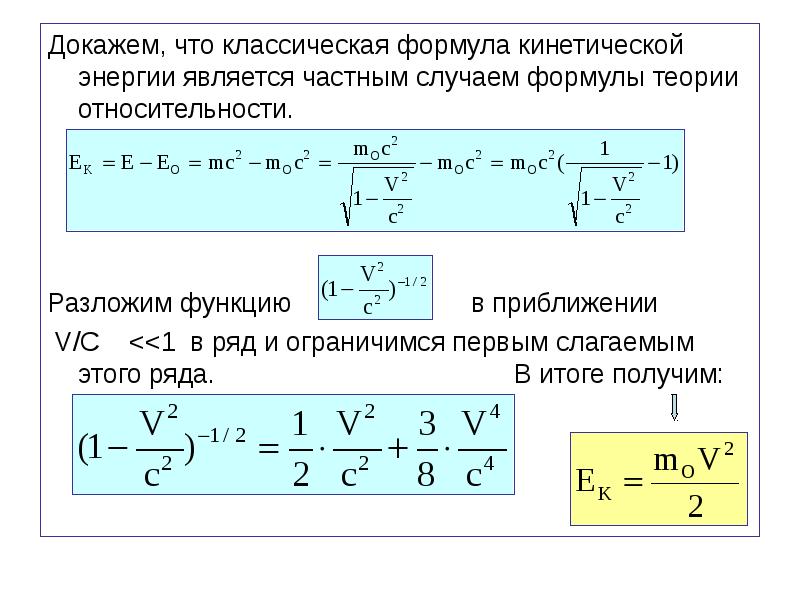 ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/
ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/
Закон сохранения энергии
Для замкнутой системы тел справедлив закон сохранения энергии:
- полная механическая энергия замкнутой системы тел есть величина постоянная:
В случае, когда на тело (или систему тел) действуют внешние силы, например, сила трения, закон сохранения механической энергии не выполняется. В этом случае изменение полной механической энергии тела (системы тел) равно работе внешних сил:
Закон сохранения энергии позволяет установить количественную связь между различными формами движения материи. Так же, как и закон сохранения импульса, он справедлив не только для механических движений, но и для всех явлений природы. Закон сохранения энергии говорит о том, что в энергию в природе нельзя уничтожить так же, как и создать из ничего.
В наиболее общем виде закон сохранения энергии можно сформулировать так:
- энергия в природе не исчезает и не создается вновь, а только превращается из одного вида в другой.

Блок: 4/5 | Кол-во символов: 947
Источник: http://ru.solverbook.com/spravochnik/mexanika/dinamika/zakon-soxraneniya-energii/
Задача
Динамометр, рассчитанный на 40 Н, имеет пружину жесткостью 500 . Какую работу нужно совершить, чтобы растянуть пружину от середины шкалы до последнего деления?
Решение задачи
В условии нам не дано значений удлинения пружины динамометра, поэтому введем его сами. Пусть удлинение пружины на середине шкалы равно (см. рис. 8).
Рис. 8. Удлинение шкалы
Следовательно, когда пружина растянута с максимальной силой, то удлинение равно . Воспользуемся для последнего случая законом Гука, поскольку мы знаем значение максимальной силы и жесткости пружины.
Откуда:
Следовательно, нам необходимо рассчитать работу при удлинении от 4 см до 8 см. Воспользуемся формулой, полученной на уроке:
Работа равна разности между значениями потенциальной энергии пружины, растянутой до полного удлинения и до полвины.
Ответ:.
Теперь мы с вами можем рассчитывать потенциальную энергию тела, поднятого над землей, и потенциальную энергию тела, которое испытывает упругую деформацию.
Список литературы
1. Соколович Ю.А., Богданова Г.С Физика: справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Перышкин А.В. Физика: учебник 10 класс. – Издательство: Дрофа.: 2010. – 192 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт fizika.in (Источник)
2. Интернет-сайт Единой коллекции цифровых образовательных ресурсов (Источник)
Домашнее задание
1. Что такое сила упругости?
2. Напишите формулу, по которой можно найти работу силы упругости.
3. Что такое потенциальная энергия тела?
Блок: 5/5 | Кол-во символов: 1591
Источник: https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/rabota-sily-uprugosti-potentsialnaya-energiya-uprugo-deformirovannogo-tela?konspekt
Средняя кинетическая энергия молекул газа
Многочисленными опытами было установлено, что средняя кинетическая энергия молекул газа в поступательном движении при заданной температуре одна и та же, и не зависит от рода газа. Кроме того, было установлено также, что при нагревании газа на 1 оС СКЭ увеличивается на одно и то же самое значение. Сказать точнее, это значение равно: ΔЕк = 2,07 х 10-23Дж/оС. Для того чтобы вычислить, чему равна средняя кинетическая энергия молекул газа в поступательном движении, необходимо, помимо этой относительной величины, знать еще хотя бы одно абсолютное значение энергии поступательного движения. В физике достаточно точно определены эти значения для широкого спектра температур. К примеру, при температуре t = 500 оС кинетическая энергия поступательного движения молекулы Ек = 1600 х 10-23Дж. Зная 2 величины (ΔЕк и Ек), мы можем как вычислить энергию поступательного движения молекул при заданной температуре, так и решить обратную задачу — определить температуру по заданным значениям энергии.
Кроме того, было установлено также, что при нагревании газа на 1 оС СКЭ увеличивается на одно и то же самое значение. Сказать точнее, это значение равно: ΔЕк = 2,07 х 10-23Дж/оС. Для того чтобы вычислить, чему равна средняя кинетическая энергия молекул газа в поступательном движении, необходимо, помимо этой относительной величины, знать еще хотя бы одно абсолютное значение энергии поступательного движения. В физике достаточно точно определены эти значения для широкого спектра температур. К примеру, при температуре t = 500 оС кинетическая энергия поступательного движения молекулы Ек = 1600 х 10-23Дж. Зная 2 величины (ΔЕк и Ек), мы можем как вычислить энергию поступательного движения молекул при заданной температуре, так и решить обратную задачу — определить температуру по заданным значениям энергии.
Напоследок можно сделать вывод, что средняя кинетическая энергия молекул, формулакоторой приведена выше, зависит только от абсолютной температуры (причем для любого агрегатного состояния веществ).
Блок: 9/14 | Кол-во символов: 1226
Источник: https://autogear.ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/
Релятивизм
Когда скорость тела близка к скорости света, кинетическую энергию находят по следующей формуле:
Кинетическая энергия тела, формула которой была написана выше, может также рассчитываться по такому принципу:
Блок: 12/14 | Кол-во символов: 214
Источник: https://autogear.ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/
В заключение
Энергия — это важнейшая составляющая во всех аспектах жизни, ведь без нее никакие тела не смогли бы выполнять работу, в том числе и человек. Думаем, статья вам внятно дала понять, что собой представляет энергия, а развернутое изложение всех аспектов одной из ее составляющих — кинетической энергии — поможет вам осознать многие процессы, происходящих на нашей планете. А уж о том, как найти кинетическую энергию, вы можете узнать из приведенных выше формул и примеров решения задач.
А уж о том, как найти кинетическую энергию, вы можете узнать из приведенных выше формул и примеров решения задач.
Блок: 14/14 | Кол-во символов: 494
Источник: https://autogear.ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/
Количество использованных доноров: 3
Информация по каждому донору:
- https://autogear.ru/article/136/655/energiya-kineticheskaya-formula-opredelenie-kak-nayti-kineticheskuyu-energiyu-molekulyi-postupatelnogo-dvijeniya-prujinyi-tela-molekulyi-gaza/: использовано 5 блоков из 14, кол-во символов 4745 (32%)
- https://interneturok.ru/lesson/physics/10-klass/bzakony-sohraneniya-v-mehanikeb/rabota-sily-uprugosti-potentsialnaya-energiya-uprugo-deformirovannogo-tela?konspekt: использовано 5 блоков из 5, кол-во символов 9072 (61%)
- http://ru.solverbook.com/spravochnik/mexanika/dinamika/zakon-soxraneniya-energii/: использовано 1 блоков из 5, кол-во символов 947 (6%)
Кинетическое уравнение — обзор
8.
 2 Функция распределения (ФР) заряженных частиц в газе «Лоренц» физика газового разряда, долгая история которой восходит к попытке Пиддака в 1913 г. рассчитать скорость дрейфа ионов в газах [166]. Следует также упомянуть работы Комптона, посвященные вычислению ФР заряженных частиц и их моментов [167, 168].Позднее Друйвестейн [169, 170] и Давыдов [171] получили аналитические выражения для ФР и транспортных коэффициентов для частного случая упругих столкновений. Более поздние работы (отметим, в частности, монографию [172]) были направлены главным образом на исследование влияния неупругих столкновений на ФР и процессы переноса в рамках БКТ. Важно отметить, что расчет DF сильно зависит от принятой модели взаимодействия частиц и, следовательно, в конечном счете от задействованных сечений столкновений.Например, распределение Давыдова-Друйвестейна, полученное в предположении постоянной длины свободного пробега l для упруго сталкивающихся заряженных частиц газа, значительно занижает число «горячих» частиц в хвосте ФР и приводит в конечном итоге к неприемлемым результатам.
2 Функция распределения (ФР) заряженных частиц в газе «Лоренц» физика газового разряда, долгая история которой восходит к попытке Пиддака в 1913 г. рассчитать скорость дрейфа ионов в газах [166]. Следует также упомянуть работы Комптона, посвященные вычислению ФР заряженных частиц и их моментов [167, 168].Позднее Друйвестейн [169, 170] и Давыдов [171] получили аналитические выражения для ФР и транспортных коэффициентов для частного случая упругих столкновений. Более поздние работы (отметим, в частности, монографию [172]) были направлены главным образом на исследование влияния неупругих столкновений на ФР и процессы переноса в рамках БКТ. Важно отметить, что расчет DF сильно зависит от принятой модели взаимодействия частиц и, следовательно, в конечном счете от задействованных сечений столкновений.Например, распределение Давыдова-Друйвестейна, полученное в предположении постоянной длины свободного пробега l для упруго сталкивающихся заряженных частиц газа, значительно занижает число «горячих» частиц в хвосте ФР и приводит в конечном итоге к неприемлемым результатам. при распространении теории на расчет кинетики неупругих процессов [172].
при распространении теории на расчет кинетики неупругих процессов [172].Мы применяем GBE
(8.2.1)Fe⋅∂fe∂ve−τ∂2fe∂ve∂ve:FeFe=Jea,
для рассмотрения стационарных заряженных частиц в газе Лоренца, подверженном стационарное внешнее электрическое поле, где
Fe=eE/me
Кинетическое уравнение Больцмана обычно решается путем разложения ФР в степенной ряд твердотельных сферических гармоник нулевого порядка, т.е.е. полиномов Лежандра. Соответствующая система связанных уравнений была получена в [173, 174]. Решение ОУБ (8.2.1) удобно искать в виде разложения по твердым сферическим гармоникам:
(8.2.2)fve=f0ve+Fe⋅vef1ve+FeFe:ve0vef2ve+⋯
0 v e — тензор нулевого следа. Для наших дальнейших расчетов в этом разделе мы предполагаем, что сила F e направлена в положительном направлении некоторой выбранной координатной оси.Теперь подставим разложение (8.2.2) в уравнение. (8.2.1) и преобразовать соответствующие члены; имеем, например, следующие соотношения:
(8.2.1) и преобразовать соответствующие члены; имеем, например, следующие соотношения:
(8.2.3)Fe⋅∂∂vef2FeFe:ve0ve=Fe⋅ve3ve∂f2∂ve−13Fe2ve(Fe⋅ve)∂f2∂ve+43Fe2f2ve⋅Fe,
(8.2.4)∂2∂ve∂ve:f2FeFe:ve0veFeFe=5Fe2Fe⋅ve2ve∂f2∂ve+2f2Fe4+Fe⋅ve4ve2∂2f2∂ve2−Fe⋅ve4ve3∂f2∂ve−13∑i=13Fei2Fe2∂2∂ vei2f2ve2
Левая часть Y GBE принимает форму
(8.2.5)Y=Fe⋅ve1ve∂f0∂ve+Fe2f1+Fe⋅ve2ve∂f1∂ve+Fe⋅ve3ve∂f2 ∂ve−13Fe2veFe⋅ve∂f2∂ve+43Fe2f2Fe⋅ve−τFe⋅ve2ve∂∂ve1ve∂f0∂ve+Fe2ve∂f0∂ve+3Fe2Fe⋅veve∂f1∂ve−Fe⋅ve3ve3∂f1∂ve+Fe⋅ ve3ve2∂2f1∂ve2+4Fe2Fe⋅ve2ve∂f2∂ve+43f2Fe2+Fe⋅ve4ve2∂2f2∂ve2−13Fe2Fe⋅ve2∂2f2∂ve2−Fe⋅ve4ve3∂f2∂ve−13Fe4ve∂f2∂ve.
, обозначающий угол между векторами F E и V E на θ (0 ≤ θ ≤ π ), умножение GBE на D COS θ , а также интегрируя по всему диапазону углов, получаем 1Fe2Jеа.
Умножение GBE на cos ϑ d cos ϑ аналогичная процедура приводит к результату
(8. 2.7)∂f0∂ve+415Fe2ve2∂f2∂ve+43Fe2vef2−35τFe24∂f1∂ve+ve∂2f1∂ve2=−321FeJ1.
2.7)∂f0∂ve+415Fe2ve2∂f2∂ve+43Fe2vef2−35τFe24∂f1∂ve+ve∂2f1∂ve2=−321FeJ1.
Как уже было указано, термины коллизии J ea и J 1 в ГБКТ могут быть взяты в том виде, в котором они обычно записываются в ВЕ. В рассматриваемом ниже случае, если предположить, что изменение энергии электрона за счет упругого столкновения [примерно равное много меньше энергии электрона до столкновения, в приближении Фоккера-Планка имеем
(8.2.8)Jea=memaTˆave2∂∂veve3υf0Tˆ+1meve∂f0∂ve,
(8.2.9)J1=23Feve2ℓf1,
где Tˆa – энергетическая температура нейтрального газа Tˆa=kBTa, υ , которая обычно зависит от скорости, а ℓ — длина свободного пробега для столкновений нейтральных и заряженных частиц. Именно соотношения (8.2.6)–(8.2.9) дают необходимую основу для определения ФР и ее моментов. Традиционно два предельных ситуация рассматриваются в деталях:
- (1)
постоянная частота частоты, υ = const, υ = τ — 1 = V E ℓ − 1 и
- (2)
постоянная длина свободного пробега между столкновениями заряженных и нейтральных частиц, ℓ = const.

Сначала рассмотрим первое дело. Умножение уравнения (8.2.6) через 3 v e 2 и используя уравнение. (4.2.8) после некоторой алгебры находим, что
(8.2.10)Fe2ddveve3f1−τve2df0dve=3Tˆameτmaddveve3f0Tˆa+1mevedf0dve
или при интегрировании по +3TˆaFe2maτdf0dve+3Fe2memaveτf0,
, поскольку постоянная интегрирования равна нулю из-за того, что как левая, так и правая части уравнения(8.2.11) обращается в нуль при v e = 0. Уравнение (8.2.11) получено при условии (которое также будет использовано в дальнейшем анализе), что малые члены, пропорциональные f 2 , могут быть сброшенным. Подставляя уравнение (8.2.11) в уравнение. (8.2.9) и используя полученный результат для исключения f 1 из уравнения. (8.2.7), приходим к следующему уравнению в F 0 :
(8.2.12) ve2τ + 3TaFe2maτd3f0dve3 + ve2τ + 3meFe2maτve2 + 6TaFe2maτd2f0dve2 + -2τ-103τFe2ve2-5Taτ3Fe4mave2 + 12meFe2maτve2-6TaFe2maτdf0dve-5meFe4τ3mave3f0 = 0 .
Чтобы решить уравнение. (8.2.12) необходимы три граничных условия. На самом деле они совершенно очевидны. Действительно, для v e = 0 можно указать некоторое значение f 0 , определяемое только нормировкой функции. Из уравнения (8.2.12) также видно, что f 0 ′ = 0 for v e = 0. f 0 → 0 для v e → ∞.
Таким образом, уравнение. (8.2.12) легко решается, например, методом прогонки. Для этого удобно сначала привести уравнение к безразмерному виду, введя следующие безразмерные величины, помеченные дугами над символами:
(8.2.13)v∨e=veFeτ,ɛ∨=meFe2τ2Tˆa,f0∨= f0f0ve=0.
Процедура реализована для получения
(8.2.14)ve2∨1+3memaɛ∨d3f0∨dve3∨+ve∨2+6memaɛ∨+3memave2∨d2f0∨dve2∨−2+6memaɛ∨+ve2∨103+5memaɛ∨+ve2∨103+5memaɛ∨+ve2∨103+5memaɛ∨ ∨−12memadf0∨dve∨−5memave3∨f0∨=0.
Определим энергетическую температуру заряженных частиц следующим образом:
(8. 2.15)Tˆe=13ne∫femeve2dve≅13ne∫f0meve2dve.
2.15)Tˆe=13ne∫femeve2dve≅13ne∫f0meve2dve.
Это означает, например, что в терминах определений (4.2.13) максвелловская функция fΜ∨ имеет вид
(8.2.16)fM∨=exp−Tˆaɛ∨2Tˆeve2∨.
Рассмотрим асимптотику функции f 0 при больших скоростях v e . Из уравнения (8.2.14) следует, что для v e → ∞ выполняется уравнение:
(8.2.17)d2f0dve2−53Fe2τ2f0=0,
, имеющее решение
(8.2.18)f0~exp−53veFeτ.
Отметим, что в рассматриваемом нами предельном случае классическое решение УБ [175] приводит к максвелловской функции распределения (МФР) с температурой Tˆe, отличной от температуры нейтрального газа Tˆa. Таким образом, решение ОУБ приводит к большому количеству «горячих» заряженных частиц на хвосте ДФ. Конечно, моменты ФР — температура Tˆe и скорость дрейфа v¯ex — могут быть найдены путем правильного интегрирования ФР после решения уравнения (1).(8.2.14) найдено. Однако в этом нет необходимости. Действительно, умножая уравнение (8.2.14) через v e и интегрируя почленно, получаем
Действительно, умножая уравнение (8.2.14) через v e и интегрируя почленно, получаем
(8.2.19)3Tˆamaτ2Fe2+2∫0∞f0ve2dve=memaτ2Fe2∫0∞f0ve4dve.
Предполагая, что
(8.2.20)∫fdve≅∫f0dve=4π∫0∞f0ve2dve=ne,
, как это было сделано в уравнении (8.2.15) получается, что
(8.2.21)Tˆe=Tˆa+23maτ2Fe2.
Аналогичным образом, без явного решения уравнений. (8.2.11) и (8.2.12), мы можем определить скорость дрейфа.Для этого умножим уравнение (8.2.11) почленно на v e 3 и интегрируем полученное выражение, чтобы получить ∫0∞f0ve4dve,
приводит к
(8.2.23)v¯ex=3Tˆe−TˆamaτFe−τFe,
, так как по определению выполняются следующие соотношения:
(8.2.24)v¯ex= 1ne∫fvexdve=4πFe3ne∫0∞f1ve4dve.
Используя выражения (8.2.21) и (8.2.23), получаем искомый результат:
(8.2.25)v¯ex=τFe.
Сравнение соотношений (8.2.21) и (8.2.25) с известными классическими результатами (см. [175], с. 108) показывает, что в предельном случае υ = const скорость дрейфа остается неизменной, а Tˆe увеличивается [классический аналог уравнения. (8.2.21) содержит числовой коэффициент 1/2 вместо 2/3]. Заканчивая обсуждение этого предельного случая, приведем соответствующую форму уравнения. (8.2.14) м e ≪ м a для ɛ∨>~1
[175], с. 108) показывает, что в предельном случае υ = const скорость дрейфа остается неизменной, а Tˆe увеличивается [классический аналог уравнения. (8.2.21) содержит числовой коэффициент 1/2 вместо 2/3]. Заканчивая обсуждение этого предельного случая, приведем соответствующую форму уравнения. (8.2.14) м e ≪ м a для ɛ∨>~1
(8.2.26)ve2∨d3f0∨dve3∨+2+3memave2∨ve∨d2f0∨dve2∨−2+103ve2∨df0∨dve∨−5memave3∨f0∨=0.
Для проверки правильности приведенных выше результатов обратите внимание, что если F e ≡ 0, то уравнение (8.2.11) приводит, как и должно быть, к МДФ f 0M
(8.2.27)df0dve=−meveTˆf0,
(8.2.28)f0=Cexp−meve22Tˆ.
Перейдем теперь ко второму предельному случаю, ℓ = const. В этом случае аналог уравнения. (8.2.11) выглядит следующим образом:
(8.2.29)f1ve=τ+3TˆveFe2maℓdf0dve+3Fe2memave2ℓf0.
по той же процедуре, используемой в предельном случае υ = const, мы приходим на следующее уравнение в F 0 :
(8. 2.30) VE2τ + 3TaveFe2maℓd3f0dve3 + 2τ + 12Tamaℓfe2ve + 3meve3maℓfe2ve2f0dve2 + 18memaℓfe2v0-2τ- 5ve23τFe2−53Fe2ℓve3−5TˆaτFe4maℓ2ve4df0dve+ve212meFe2maℓ−5meτFe4maℓ2ve3f0=0.
2.30) VE2τ + 3TaveFe2maℓd3f0dve3 + 2τ + 12Tamaℓfe2ve + 3meve3maℓfe2ve2f0dve2 + 18memaℓfe2v0-2τ- 5ve23τFe2−53Fe2ℓve3−5TˆaτFe4maℓ2ve4df0dve+ve212meFe2maℓ−5meτFe4maℓ2ve3f0=0.
Опять же, это легко увидеть, умножив уравнение. (8.2.30) почленно на F e 4 что обращение в нуль внешней силы F e приводит к уравнению.(8.2.27), а затем, после интегрирования, в МДФ (8.2.28). Граничные условия для уравнения. (8.2.30) имеют следующий вид: f 0 указано для v e = 0 в соответствии с выбранной нормировкой; для v e = 0 по формуле (8.2.30) предполагает f 0 ′ = 0 и, наконец, f 0 → 0, когда v e → ∞.
Последний результат становится очевидным, если сначала разделить уравнение.(8.2.30) через v e 5 . Чтобы численно интегрировать уравнение (8.2.30) это уравнение удобно привести к безразмерному виду, используя безразмерные величины
(8.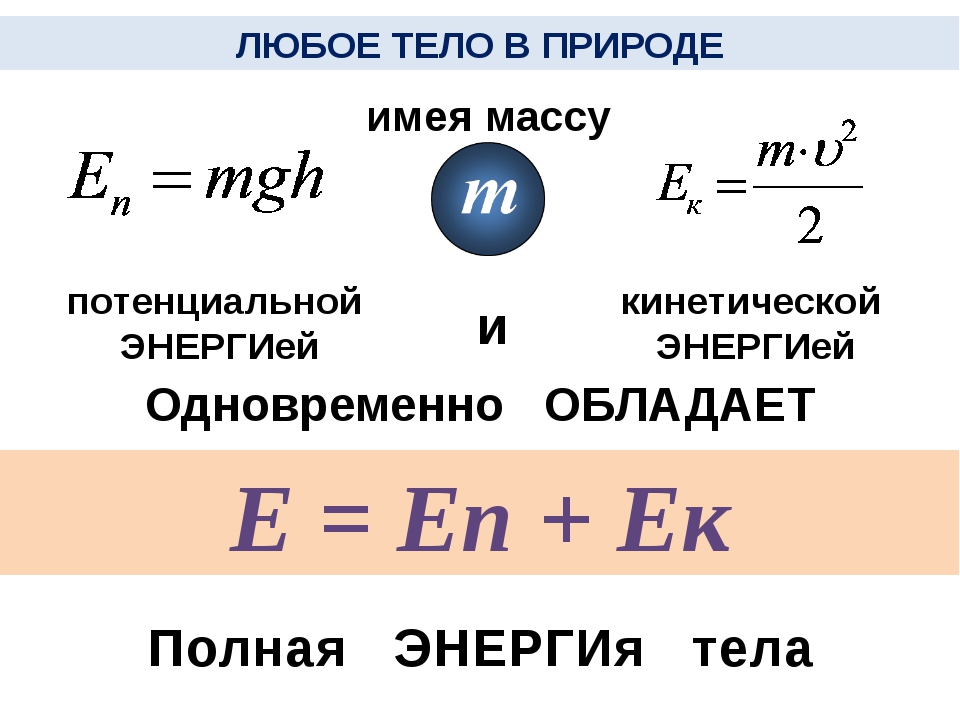 2.31)ve∨=veℓ/τ,ɛ∨=meFe2τ2Tˆa,A∨=Fe2τ4ℓ2,
2.31)ve∨=veℓ/τ,ɛ∨=meFe2τ2Tˆa,A∨=Fe2τ4ℓ2,
, чтобы получить обыкновенное дифференциальное уравнение −53−18memave3∨−5memave4∨ɛ∨df0∨dve∨+ve2∨mema12−5ve3∨A∨f0∨=0,
с граничными условиями
(8.2.33)f0∨0=1,f0′∨0=0,f0∨∞=0.
Здесь почленное интегрирование больше не приводит к элегантным результатам, подобным уравнениям. (8.2.21) и (8.2.25). Однако мы можем дать полезную формулу для вычисления скорости дрейфа v¯ex, которая получается из уравнения (8.2.32) умножая его на v e 3 и затем интегрируя, получаем ,
с C = f 0 ( v e = 0).
Хотя уравнение. (8.2.34), конечно, можно использовать только после численного интегрирования уравнения. (8.2.33), интересно отметить, что, в отличие от уравнения. (8.2.25), в этом предельном случае скорость дрейфа является нелинейной функцией F e . Рассмотрим здесь некоторые численные результаты для ФР заряженных частиц во внешнем электрическом поле, получаемые при использовании ОУБ. Численное интегрирование соответствующих дифференциальных уравнений осуществлялось трехдиагональным методом исключения Гаусса для обыкновенных дифференциальных уравнений (см. Приложение 5).
Численное интегрирование соответствующих дифференциальных уравнений осуществлялось трехдиагональным методом исключения Гаусса для обыкновенных дифференциальных уравнений (см. Приложение 5).
На рис. 8.1 безразмерная ФР f0∨ представлена в зависимости от безразмерной скорости ve∨ для ɛ∨=10−3 и τ = const. Линия 1 соответствует ФР, а кривая 2 — ФР, полученной с помощью ОГЭ. По мере уменьшения ɛ∨ два распределения приближаются друг к другу. Заметим, что функция f0∨GBE лежит выше функции Максвелла.
Рисунок 8.1. Зависимость f0∨ от ve∨ для τ = const. 1, МДФ; 2, f0∨GBE.
На рисунках 8.2 и 8.3 представлены f0∨, рассчитанные для л = const при условиях ɛ∨=10–2,A∨=1 и ɛ∨=10–2,A∨=10–1 соответственно .Кривые 1, 2 и 3 на рис. 8.2 и 8.3 соответствуют MDF, GBE и Druyvesteyn DF соответственно. Интересно отметить, что ФР f0∨GBE может лежать как между функциями Максвелла и Друйвестейна, так и над ними двумя. В практических расчетах, подчеркнем еще раз, ФР можно нормировать на числовую плотность вовлеченных заряженных частиц.
Рисунок 8.2. Зависимость f0∨ от ve∨ для ℓ = const, ɛ∨=10−2, A∨=1. 1, МДФ; 2, f0∨GBE; 3, Друйвестейн Д.Ф.
Рисунок 8.3. Зависимость f0∨ от ve∨ для ℓ = const, ɛ∨=10–2, A∨=10–1. 1, МДФ; 2, f0∨GBE; 3, Друйвестейн Д.Ф.
Предыдущие рассуждения могут быть применены в теории процессов переноса в невырожденных полупроводниках. Рассмотрим стационарный одномерный дрейф электронов в изотропном полупроводнике. В этом случае для выбранного направления x мы имеем из уравнения. (8.2.1)
(8.2.35)−eEme∂fe∂vex−τeEme2∂2fe∂vex2=JeB,
e — абсолютный заряд электрона.Очевидно, соответствующее УБ имеет вид
(8.2.36)−eEme∂fe∂vex=JeB,
. .38) IE, en = -∫meve22feτɛɛdve,
где ɛ = м = м v v E 2 /2, τ p , и τ ɛ – время релаксации импульса и время релаксации энергии соответственно. Рассеяние электронов на акустических фононах для непьезоэлектрических кристаллов можно взять из [176] .41)1τa=2G2mekBT3/2πρs2ℏ4,
Рассеяние электронов на акустических фононах для непьезоэлектрических кристаллов можно взять из [176] .41)1τa=2G2mekBT3/2πρs2ℏ4,
T и ρ – температура и плотность решетки, с – продольная скорость звука, G – константа взаимодействия, имеющая энергию измерение. Применение отношений (8.2.37)–(8.2.41) нуждается в явном выражении для ФР. Введем типичное приближенное выражение ФР (по сравнению с уравнением (8.2.2))
(8.2.42)fe=f0ɛ+Ef1ɛvex+E2f2ɛve2cos2θ−13+⋯
, где θ — угол между скоростью v e направление и ось x . Используя модель Бхатнагара-Гросса-Крука (BGK) и отношения (8.2.35), уравнение. (8.2.42) приводит в первом приближении
(8.2.43)f1ɛ=τpɛemevex∂f0∂vex,
Тогда для скорости дрейфа
(8.2.44)v¯ex=1ne∫fevevexdve
как для BE так и GBE в первом приближении
(8.2.45)v¯ex=eEmene∫τpɛ∂f0∂vexvexdve
аппроксимируется МДФ с эффективной электронной температурой T e
(8. 2.46)f0=neme2πkBTe3/2exp−ɛkBTe
2.46)f0=neme2πkBTe3/2exp−ɛkBTe
и, как следствие, к одинаковым дрейфовым скоростям для BE и GBE
(8.2. 47)v¯ex=vex0TTe1/2
, где
(8.2.48)vex0=−4eEτa3πme.
Оцените теперь температуру электронов в результате эволюции электронов в электрическом поле напряженностью E . Из уравнения гидродинамической энергии (BE-модель)
(8.2.49)v¯exeneE=Ie,en
и для GBE
(8.2.50)v¯exeneE−τe2E2mene=Ie,en.
Для интеграла релаксации находим
(8.2.51)Ie,en=−∫meve22feτɛɛdve=−8πmes2τaTeT3/2−TeT1/2.
Перепишите уравнения энергии (8.2.49) и (8.2.50) (для модели Больцмана)
(8.2.52)eE23meτaTTe1/2=2mes2τaTeT3/2−TeT1/2,
(для нелокальной модели)
(8.2.53)eE2meτ+4eE23πmeτaTTe1/2=8mes2τaπTeT3/2−TeT1/2.
Зависимость T e от T для модели Больцмана следует из (8.2.51)
Уравнение преобразования (8.2.53) с использованием замены y = ( T e / T ) 1/2 .
(8.2.55)y4−y2−π8eEme2ττas2y−16eEme2τa2s2=0.
Мы находим «локальные» и «нелокальные» комбинации в уравнении. где
Решения уравнения четвертой степени (8.2.55) могут быть получены в аналитическом (но довольно сложном) виде. Гораздо проще асимптотические решения уравнения. (8.2.55). Для горячих электронов ( T e ≫ T ) находим (для модели Больцмана)
(8.2.59)Te=T16eEmeτas,
(для нелокальной теории)
(8.2.60)Te=Tπ1/34eEme4/3ττas22/3
или
(8.2.61)Te=Tπ1/4πEmeℓBT/22ρeEme4BT/22ρeEme4BT 32/3.
В отличие от кинетики Больцмана, нелокальная кинетическая теория приводит к нелинейной зависимости эффективной температуры электрона от напряженности электрического поля, T e ~ E 4/3 .
Для так называемых теплых носителей заряда ( T e − T ≪ T ) из соотношений (8.2.52) и (8.2.53)(BE-модель)
(8. 2.62)Te=T1+τa26s2eEme2,
2.62)Te=T1+τa26s2eEme2,
(нелокальная теория)
(8.2.63)Te=T1+τa26s2eEme21+3π4ττa.
Как видим температура теплых носителей T e GBE выше чем T e BE . Сравните теперь теоретические и экспериментальные результаты. Для этого получим соотношение между интенсивностью E и подвижностью носителей заряда μ . Из уравнения(8.2.47)
(8.2.64)µ=µ0TTe1/2,
где
(8.2.65)µ0=v¯ex0/E,
и из соотношений (8.2.52) и (8.2. 53) соответственно (BE)
(8.2.66)E2=6s2τa2mee2μ0μ2μ0μ2−1,
(GBE)
(8.2.67)E2=6s2τa2mee2μ0μ2μ0/μ2−11+3π/4τ/τaμ0/μ.
Можно ввести нелокальную поправку, определяемую коэффициентом
(8.2.68)α=3π4ττa,
, а именно
(8.2.69)E2=6s2τa2mee2µ0µ2µ0/µ2−11+αµ0/µ.
Рассеяние электронов на продольных акустических фононах является основным механизмом рассеяния при достаточно высоких температурах, когда не нужно учитывать рассеяние на ионизированной легирующей примеси.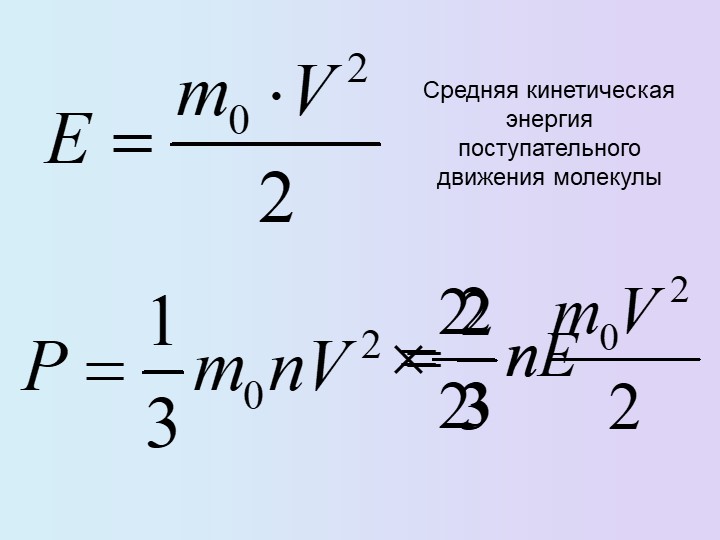 В то же время температура должна быть достаточно низкой для исключения рассеяния на оптических фононах [177]. Такая ситуация соответствует, например, случаю рассеяния электронов в ковалентных кристаллах Ge и Si при температурах 20 < T < 100 K [177–179]. μ / μ 0 — зависимость E в логарифмических координатах показана на рис. Рисунки 8.5 и 8.6 приведены аналогичные зависимости для n -Si, полученные по измерению скорости дрейфа при 20 и 77 К [181]. На всех приведенных рисунках приведены данные, полученные для α = 0, α = 1, α = 2. Случай α = 0 отвечает локальной модели Больцмана. Постоянная энергии G является практически неизвестной величиной для локальных моделей и сравнение с экспериментальными данными достигается после параллельного сдвига теоретической кривой по оси E .
В то же время температура должна быть достаточно низкой для исключения рассеяния на оптических фононах [177]. Такая ситуация соответствует, например, случаю рассеяния электронов в ковалентных кристаллах Ge и Si при температурах 20 < T < 100 K [177–179]. μ / μ 0 — зависимость E в логарифмических координатах показана на рис. Рисунки 8.5 и 8.6 приведены аналогичные зависимости для n -Si, полученные по измерению скорости дрейфа при 20 и 77 К [181]. На всех приведенных рисунках приведены данные, полученные для α = 0, α = 1, α = 2. Случай α = 0 отвечает локальной модели Больцмана. Постоянная энергии G является практически неизвестной величиной для локальных моделей и сравнение с экспериментальными данными достигается после параллельного сдвига теоретической кривой по оси E .
Рисунок 8.4. LG ( μ / μ 0 ) -dependence на LG E для N -Ge ( T = 77 K, Dim E = V / см)
Рисунок 8. 5. µ / µ 0 — зависимость E в логарифмических координатах для n -Si ( T = 20 K), (слева).
5. µ / µ 0 — зависимость E в логарифмических координатах для n -Si ( T = 20 K), (слева).
Рисунок 8.6. µ / µ 0 — зависимость E в логарифмических координатах для n -Si ( T = 77 K), (справа), (dim E = 9000 В) .
Из рис. 8.4–8.6 следует, что расхождение между локальными моделями ( α = 0) весьма существенно, но «нелокальные» кривые (рассчитанные для α = 1 и α = 2) гораздо лучше реагируют на эксперимент .Рисунки 8.7 и 8.8 демонстрируют сходимость μ / μ 0 – зависимость E . Давайте подробно исследуем этот эффект с математической точки зрения, используя следующую форму уравнения. (8.2.69) (см. также уравнения8.2.41 и 8.2.68)
Рисунок 8.7. Зависимость lnE~ от мк / мк 0 .
Рисунок 8.8. Зависимость lnE~ от мк / мк 0 .
(8.2.70)E~=1y4−1y211+α/y,
, где y=μ/μ0,E~=E6sτamee−1,0
Рисунок 8.8 также построен с использованием обозначений Maple для случая
y=Ai=lnqrt1x4−1×2·1sqrt1+i−1×0,3,1≤i≤31,0,001≤x≤1.
В этом случае α -параметр изменяется в зависимости (8.2.70) в пределах 0 ≤ α ≤ 9. Как и ранее, верхняя кривая на рис. 8.8 ( α = 0) соответствует локальной теории
Черные области на рис. 8.7 и 8.8 отражают сходимость «семейства» кривых по увеличению α -параметра.
Кинетическая энергия – Гиперучебник по физике
Обсуждение
Кинетическая энергия — это простое понятие с простым уравнением, которое легко вывести. Давайте сделаем это дважды.
Давайте сделаем это дважды.
Вывод с использованием только алгебры (и в предположении, что ускорение постоянно). Начните с теоремы о работе и энергии, затем добавьте второй закон движения Ньютона.
∆ K = W = F ∆ с = мА ∆ с
Возьмите соответствующее уравнение из кинематики и немного переформулируйте его.
v 2 = v 0 2 + 2 a ∆ s 6| | |
| а ∆ с = | v 2 — v 0 2 |
| 2 |
Объедините два выражения.
| ∆ К = м | ⎛ ⎜ ⎝ | v 2 — v 0 2 | ⎞ ⎟ ⎠ |
| 2 |
А теперь кое-что немного необычное. Расширять.
Расширять.
| ∆ К = | 1 | мв 2 — | 1 | мв 0 2 |
| 2 | 2 |
Если кинетическая энергия есть энергия движения, то, естественно, кинетическая энергия покоящегося объекта должна быть равна нулю. Следовательно, второй член нам не нужен, а кинетическая энергия объекта равна просто…
.К = ½ мв 2
Вывод с использованием исчисления (но теперь нам не нужно ничего предполагать об ускорении).Опять же, начните с теоремы о работе и энергии и добавьте второй закон движения Ньютона (версия с исчислением).
| |||||
| |||||
|
Переставьте дифференциальные члены, чтобы получить интеграл и функцию в виде
соглашение.
| |||||
| |||||
|
Интеграл которого достаточно просто вычислить в пределах от начальной скорости ( v ) до конечной скорости ( v 0 ).
| ∆ К = | 1 | мв 2 — | 1 | мв 0 2 |
| 2 | 2 |
Естественно, кинетическая энергия покоящегося объекта должна быть равна нулю.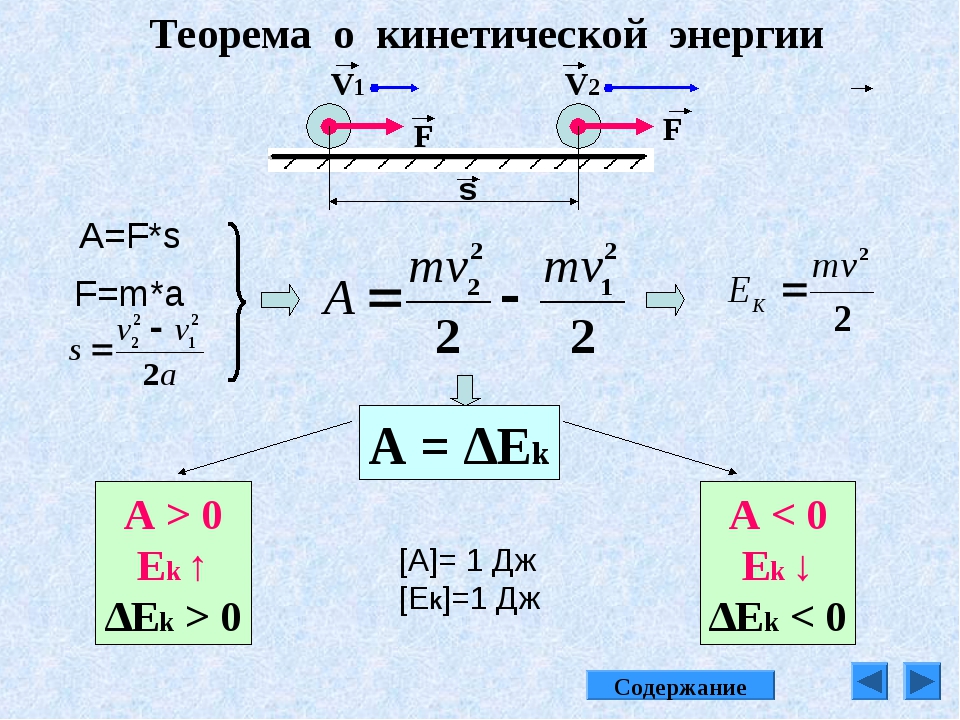 Таким образом, кинетическая энергия объекта определяется математически следующим уравнением…
Таким образом, кинетическая энергия объекта определяется математически следующим уравнением…
К = ½ мв 2
Томас Янг (1773–1829) вывел аналогичную формулу в 1807 году, хотя он забыл добавить ½ впереди и не использовал слова «масса» и «вес» с той точностью, которую мы используем в наши дни.Он также был первым, кто использовал слово «энергия» в его нынешнем значении в лекции о столкновениях, прочитанной перед Королевским институтом.
Термин энергия может быть с большим правом применен к произведению массы или веса тела на квадрат числа, выражающего его скорость. Таким образом, если вес в одну унцию движется со скоростью фута в секунду, мы можем назвать его энергию равной 1; если второе тело в две унции имеет скорость три фута в секунду, его энергия будет вдвое больше квадрата трех, или 18.
Томас Янг, 1807
Янг только что назвал это энергией. Уильям Томсон, лорд Кельвин (1824–1907) добавил прилагательное «кинетический», чтобы отделить его от «потенциальной энергии», которую назвал Уильям Рэнкин (1820–1872) в 1853 году.
Кинетическая энергия иногда обозначается буквой T . Вероятно, это происходит от французского travail mécanique (механическая работа) или quantité de travail (количество работы).
Работа, энергия и мощность
Кинетическая энергия – это энергия движения.Объект, который движется — будь то вертикальное или горизонтальное движение — обладает кинетической энергией. Существует много форм кинетической энергии: колебательная (энергия колебательного движения), вращательная (энергия вращательного движения) и поступательная (энергия движения из одного места в другое). Для простоты сосредоточимся на поступательной кинетической энергии. Количество поступательной кинетической энергии (далее фраза «кинетическая энергия» будет относиться к поступательной кинетической энергии), которой обладает объект, зависит от двух переменных: массы (m) объекта и скорости (v) объекта.Следующее уравнение используется для представления кинетической энергии (KE) объекта.
KE = 0,5 • m • v 2
где м = масса объекта
v = скорость объекта
Это уравнение показывает, что кинетическая энергия объекта прямо пропорциональна квадрату его скорости. Это означает, что при двукратном увеличении скорости кинетическая энергия увеличится в четыре раза.При трехкратном увеличении скорости кинетическая энергия увеличится в девять раз. А при четырехкратном увеличении скорости кинетическая энергия увеличится в шестнадцать раз. Кинетическая энергия зависит от квадрата скорости. Как часто говорят, уравнение — это не только рецепт решения алгебраических задач, но и руководство к размышлению о связи между величинами.
Кинетическая энергия является скалярной величиной; у него нет направления. В отличие от скорости, ускорения, силы и импульса кинетическая энергия объекта полностью описывается только величиной.2.
1 Джоуль = 1 кг • м 2 /с 2
Мы хотели бы предложить.
 .. Как скорость автомобиля (и, следовательно, его кинетическая энергия) влияет на расстояние, которое потребуется ему, чтобы затормозить до полной остановки? Взаимодействуйте, исследуйте и узнавайте ответ на этот вопрос с помощью нашего интерактива Stopping Distance. Вы можете найти его в разделе Physics Interactives на нашем сайте.Интерактивное приложение Stopping Distance позволяет учащимся изучить влияние скорости на тормозной путь игрушечной машинки.
.. Как скорость автомобиля (и, следовательно, его кинетическая энергия) влияет на расстояние, которое потребуется ему, чтобы затормозить до полной остановки? Взаимодействуйте, исследуйте и узнавайте ответ на этот вопрос с помощью нашего интерактива Stopping Distance. Вы можете найти его в разделе Physics Interactives на нашем сайте.Интерактивное приложение Stopping Distance позволяет учащимся изучить влияние скорости на тормозной путь игрушечной машинки.
Проверьте свое понимание
Используйте свое понимание кинетической энергии, чтобы ответить на следующие вопросы. Затем нажмите кнопку, чтобы просмотреть ответы.
1. Определить кинетическую энергию автомобиля американских горок массой 625 кг, движущегося со скоростью 18.3 м/с.
2. Если бы автомобиль американских горок в приведенной выше задаче двигался с удвоенной скоростью, то какова была бы его новая кинетическая энергия?
3. Мисси Диуотер, бывшая ныряльщица цирка братьев Ринглинг, имела кинетическую энергию 12 000 Дж непосредственно перед тем, как столкнуться с ведром с водой. Если масса Мисси 40 кг, то какова ее скорость?
Мисси Диуотер, бывшая ныряльщица цирка братьев Ринглинг, имела кинетическую энергию 12 000 Дж непосредственно перед тем, как столкнуться с ведром с водой. Если масса Мисси 40 кг, то какова ее скорость?
4.Компактный автомобиль массой 900 кг, движущийся со скоростью 60 миль в час, имеет кинетическую энергию примерно 320 000 Дж. Оцените его новую кинетическую энергию, если он движется со скоростью 30 миль/ч. (СОВЕТ: используйте уравнение кинетической энергии как «руководство к размышлению».)
для начинающих Путеводитель по движению Воздух
Температура и кинетическая энергия Прежде чем начать:
Для этой деятельности вам нужно будет выполнить аналогичные расчеты, а затем использовать ваши ответы в формуле кинетической энергии. ОТВЕТЬТЕ НА СЛЕДУЮЩИЕ ВОПРОСЫ:
|
Кинетическая энергия — Видео по физике от Brightstorm
Энергия движущегося объекта называется кинетической энергией .2.
Кинетическая энергия — это энергия движения, поэтому любые движущиеся объекты обладают кинетической энергией, так что кинетическая энергия по формуле, которую мы используем для кинетической энергии, равна половине массы объекта, умноженной на квадрат скорости объекта. Итак, если вы можете вспомнить одну половину mv в квадрате, это кинетическая энергия объекта в любое время. Если объект не движется, 0 кинетической энергии, если объект имеет массу 0, 0 кинетической энергии, хорошо, поэтому давайте рассмотрим пару задач, которые вас могут попросить решить с использованием кинетической энергии.Хорошо, во-первых, какова кинетическая энергия 5-килограммового шара для боулинга, движущегося со скоростью 2 метра в секунду? Итак, опять же, формула для кинетической энергии — это половина массы, умноженная на скорость в квадрате. Хорошо, и в этом случае мы находим кинетическую энергию, поэтому мы просто говорим, что половина умножается на 5 килограммов, умноженная на 2 метра в секунду в квадрате. Итак, чтобы решить, что 2 в квадрате — это 4 метра в квадрате на секунду в квадрате, умноженные на 5 килограммов, равно 20, а половина этого равна 10, и помните, что единицы энергии всегда в джоулях.Итак, 10 джоулей энергии в этом шаре для боулинга, хорошо?
Если объект не движется, 0 кинетической энергии, если объект имеет массу 0, 0 кинетической энергии, хорошо, поэтому давайте рассмотрим пару задач, которые вас могут попросить решить с использованием кинетической энергии.Хорошо, во-первых, какова кинетическая энергия 5-килограммового шара для боулинга, движущегося со скоростью 2 метра в секунду? Итак, опять же, формула для кинетической энергии — это половина массы, умноженная на скорость в квадрате. Хорошо, и в этом случае мы находим кинетическую энергию, поэтому мы просто говорим, что половина умножается на 5 килограммов, умноженная на 2 метра в секунду в квадрате. Итак, чтобы решить, что 2 в квадрате — это 4 метра в квадрате на секунду в квадрате, умноженные на 5 килограммов, равно 20, а половина этого равна 10, и помните, что единицы энергии всегда в джоулях.Итак, 10 джоулей энергии в этом шаре для боулинга, хорошо?
Давайте рассмотрим другую задачу. Допустим, у нас есть шар для боулинга весом 4 кг и его кинетическая энергия составляет 20 джоулей. Какова его скорость? Итак, это выглядит похоже, но мы немного изменили массу, и мы все еще можем решить это с помощью той же формулы, хорошо, так что скажем, кинетическая энергия равна половине, а mv в квадрате, хорошо, на этот раз что у нас есть? У нас есть кинетическая энергия 20 джоулей, и она будет равна половине нашей массы 4 килограмма, но мы не знаем квадрат нашей скорости, это то, что мы решаем в этой задаче, хорошо? Итак, как только мы настроим это снова, довольно простая задача, которую нужно решить, поэтому у меня есть 20 джоулей, равных 2 пополам, умноженным на 4, это 2 килограмма скорости в квадрате, хорошо.А теперь я хочу разделить на 2, и я получу 10 джоулей, равных моей скорости в квадрате, так что это будет чуть больше 3, 3,1, так что моя скорость равна 3,1 метра в секунду, хорошо. Итак, снова 2 разных способа использовать эту идею кинетической энергии, номер 1, учитывая количество энергии, какова скорость, мы также можем решить для массы или мы можем просто взять массу и скорость и вычислить количество кинетической энергии в объект.
Какова его скорость? Итак, это выглядит похоже, но мы немного изменили массу, и мы все еще можем решить это с помощью той же формулы, хорошо, так что скажем, кинетическая энергия равна половине, а mv в квадрате, хорошо, на этот раз что у нас есть? У нас есть кинетическая энергия 20 джоулей, и она будет равна половине нашей массы 4 килограмма, но мы не знаем квадрат нашей скорости, это то, что мы решаем в этой задаче, хорошо? Итак, как только мы настроим это снова, довольно простая задача, которую нужно решить, поэтому у меня есть 20 джоулей, равных 2 пополам, умноженным на 4, это 2 килограмма скорости в квадрате, хорошо.А теперь я хочу разделить на 2, и я получу 10 джоулей, равных моей скорости в квадрате, так что это будет чуть больше 3, 3,1, так что моя скорость равна 3,1 метра в секунду, хорошо. Итак, снова 2 разных способа использовать эту идею кинетической энергии, номер 1, учитывая количество энергии, какова скорость, мы также можем решить для массы или мы можем просто взять массу и скорость и вычислить количество кинетической энергии в объект. Пока этот объект движется, он обладает кинетической энергией.
Пока этот объект движется, он обладает кинетической энергией.
Кинетическая температура, тепловая энергия
Статистические методы становятся более точным способом изучения природы, когда количество частиц велико.Итак, мы ожидаем, что описание скоростей молекул в газе будет на самом деле наиболее вероятным распределением, поскольку мы имеем дело с числами частиц в диапазоне числа Авогадро. Но это наиболее вероятное распределение (распределение Максвелла-Больцмана) подчиняется ограничениям, а именно тому, что число частиц постоянно и полная энергия постоянна (сохранение энергии). Максимизация распределения вероятностей с учетом этих ограничений в целом является сложной математической задачей (см., Например). Один из способов приблизиться к решению более интуитивным образом — обратиться к известному нам физическому примеру, а именно к физике атмосферы под действием гравитации, отраженной в барометрической формуле. Следующее лечение следует за разработкой Рольфа.
В этом подходе мы используем тот факт, что средняя кинетическая энергия молекул может быть выражена через кинетическую температуру. Кроме того, мы знаем, что сохранение энергии в этом случае включает в себя просто уравновешивание кинетической энергии и гравитационной потенциальной энергии, пока мы рассматриваем атмосферу как идеальный газ.
Из выражения для кинетической температуры
у нас есть экспериментально проверенное выражение для молекулярной кинетической энергии. В барометрической формуле:
у нас есть описание идеальной газовой системы, которое можно использовать, чтобы помочь разработать аргумент правдоподобия для распределения скоростей Максвелла. Этапы этого процесса следующие:
Для одного направления в пространстве этот процесс дает выражение:
, а когда включены все направления скорости, получается отношение распределения скорости Максвелла:
Следует отметить, что, хотя мы использовали физическую ситуацию, зависящую от гравитации, для получения распределения скоростей, гравитация не появляется в конечном результате. То есть полученный результат является общим, не содержащим g. Барометрическая формула использовалась просто как конструкция, связывающая распределение скоростей с ограничениями по энергии и числу частиц.
То есть полученный результат является общим, не содержащим g. Барометрическая формула использовалась просто как конструкция, связывающая распределение скоростей с ограничениями по энергии и числу частиц.
Вычисление кинетической энергии — Физика средней школы
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
.

 6)
6)


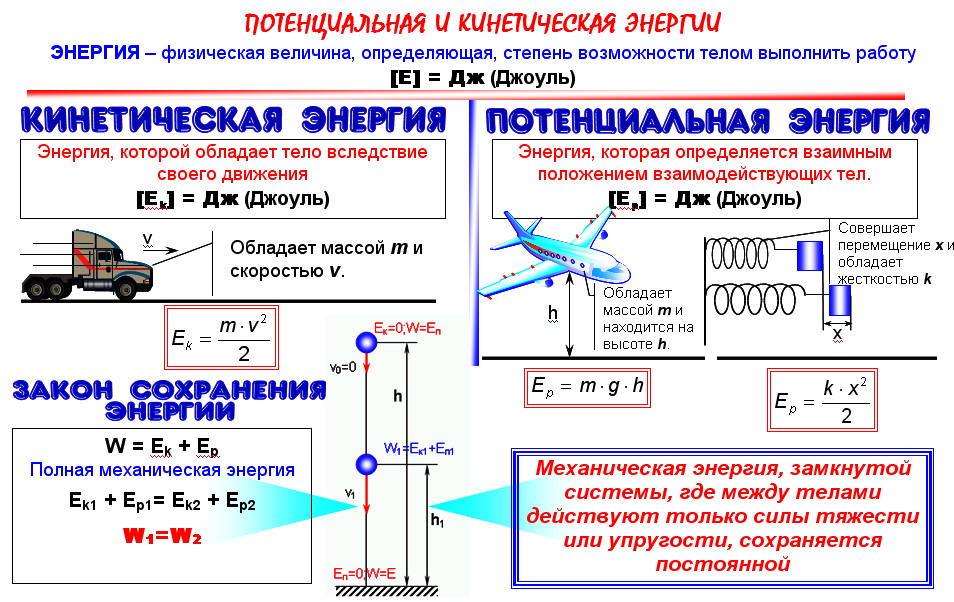 html). ]
html). ] 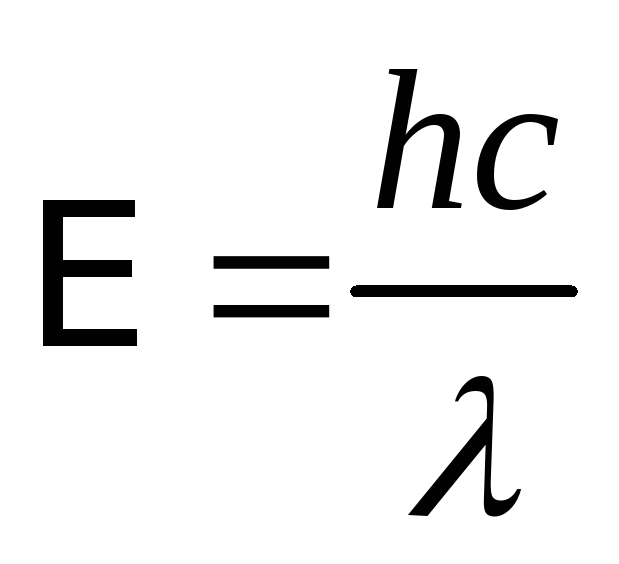
 Что
формула для определения кинетической энергии?
Что
формула для определения кинетической энергии?  Используя формулу кинетической энергии вместе с вашим ответом на вопрос
8, рассчитайте кинетическую энергию водорода.
Используя формулу кинетической энергии вместе с вашим ответом на вопрос
8, рассчитайте кинетическую энергию водорода.