Формула площадь герона – Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса. — Детская игровая комната «Волшебный лес»

Posted on 27.03.202019.01.2020 by alexxlab

Содержание

Формула Герона — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 июля 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 июля 2019; проверки требуют 2 правки.

Фо́рмула Герона позволяет вычислить площадь треугольника S{\displaystyle S} по его сторонам a,b,c{\displaystyle a,b,c}:

S=p(p−a)(p−b)(p−c),{\displaystyle S={\sqrt {p(p-a)(p-b)(p-c)}},}

где p{\displaystyle p} — полупериметр треугольника: p=a+b+c2{\displaystyle p={\frac {a+b+c}{2}}}.

Доказательство 1 (тригонометрическое):

S=12ab⋅sin⁡γ{\displaystyle S={1 \over 2}ab\cdot \sin {\gamma }},

где γ{\displaystyle \ \gamma } — угол треугольника, противолежащий стороне c{\displaystyle c}. По теореме косинусов:

c2=a2+b2−2ab⋅cos⁡γ,{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma ,}

Отсюда:

cos⁡γ=a2+b2−c22ab,{\displaystyle \cos \gamma ={a^{2}+b^{2}-c^{2} \over 2ab},}

Значит,

sin2⁡γ=1−cos2⁡γ=(1−cos⁡γ)(1+cos⁡γ)={\displaystyle \ \sin ^{2}\gamma =1-\cos ^{2}\gamma =(1-\cos \gamma )(1+\cos \gamma )=}

=2ab−a2−b2+c22ab⋅2ab+a2+b2−c22ab={\displaystyle ={{2ab-a^{2}-b^{2}+c^{2}} \over 2ab}\cdot {{2ab+a^{2}+b^{2}-c^{2}} \over 2ab}=}

=c2−(a−b)22ab⋅(a+b)2−c22ab=14a2b2(c−a+b)(c+a−b)(a+b−c)(a+b+c){\displaystyle ={{c^{2}-(a-b)^{2}} \over 2ab}\cdot {{(a+b)^{2}-c^{2}} \over 2ab}={1 \over 4a^{2}b^{2}}(c-a+b)(c+a-b)(a+b-c)(a+b+c)}.

Замечая, что a+b+c=2p{\displaystyle a+b+c=2p}, a+b−c=2p−2c{\displaystyle a+b-c=2p-2c}, a+c−b=2p−2b{\displaystyle a+c-b=2p-2b}, c−a+b=2p−2a{\displaystyle c-a+b=2p-2a}, получаем:

sin⁡γ=2abp(p−a)(p−b)(p−c).{\displaystyle \sin \gamma ={2 \over ab}{\sqrt {p(p-a)(p-b)(p-c)}}.}

Таким образом,

S=12absin⁡γ=p(p−a)(p−b)(p−c),{\displaystyle S={1 \over 2}ab\sin \gamma ={\sqrt {p(p-a)(p-b)(p-c)}},}

ч.т.д.

Доказательство 2 (на основе теоремы Пифагора):

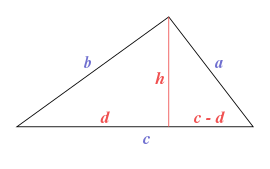$S={1 \over 2}ab\sin \gamma ={\sqrt {p(p-a)(p-b)(p-c)}},$

Треугольник со сторонами a, b, c и высотой h, разделяющей основание c на d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a² = h² + (c − d)² и b² = h² + d² — см. рисунок справа. Вычитая из первого равенства второе, получаем a² − b² = c² − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

d=−a2+b2+c22c{\displaystyle d={\frac {-a^{2}+b^{2}+c^{2}}{2c}}}

Для высоты h у нас было равенство h² = b² − d², в которое можно подставить полученное выражение для d и применить формулы для квадратов:

h3=b2−(−a2+b2+c22c)2=(2bc−a2+b2+c2)(2bc+a2−b2−c2)4c2=((b+c)2−a2)(a2−(b−c)2)4c2=(b+c−a)(b+c+a)(a+b−c)(a−b+c)4c2{\displaystyle {\begin{aligned}h^{2}&=b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}={\frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\\&={\frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={\frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\\\end{aligned}}}

Замечая, что b+c−a=2p−2a{\displaystyle b+c-a=2p-2a}, a+b+c=2p{\displaystyle a+b+c=2p}, a+b−c=2p−2c{\displaystyle a+b-c=2p-2c}, a−b+c=2p−2b{\displaystyle a-b+c=2p-2b}, получаем:

h3=2(p−a)⋅2p⋅2(p−c)⋅2(p−b)4c2=4p(p−a)(p−b)(p−c)c2{\displaystyle {\begin{aligned}h^{2}&={\frac {2(p-a)\cdot 2p\cdot 2(p-c)\cdot 2(p-b)}{4c^{2}}}={\frac {4p(p-a)(p-b)(p-c)}{c^{2}}}\end{aligned}}}

Используя основное равенство для площади треугольника S=ch3{\displaystyle S={\frac {ch}{2}}} и подставляя в него полученное выражение для h, в итоге имеем:

S=c24⋅4p(p−a)(p−b)(p−c)c2=p(p−a)(p−b)(p−c){\displaystyle {\begin{aligned}S={\sqrt {{\frac {c^{2}}{4}}\cdot {\frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={\sqrt {p(p-a)(p-b)(p-c)}}\end{aligned}}}

ч.т.д.

Эта формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник.

Выразив полупериметр через полусумму всех сторон данного треугольника, можно получить три эквивалентные формулы Герона:

S=14(a2+b2+c2)2−2(a4+b4+c4){\displaystyle S={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}}

S=142(a2b2+a2c2+b2c2)−(a4+b4+c4){\displaystyle S={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}}

S=14(a+b−c)(a−b+c)(−a+b+c)(a+b+c).{\displaystyle S={\frac {1}{4}}{\sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}.}

S=144a2b2−(a2+b2−c2)2.{\displaystyle S={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}.}

Формулу Герона можно записать с помощью определителя в виде^[1]:
−16S2=|0a2b21a20c21b2c2011110|=|abc0ba0cc0ab0cba|{\displaystyle -16S^{2}={\begin{vmatrix}0&a^{2}&b^{2}&1\\a^{2}&0&c^{2}&1\\b^{2}&c^{2}&0&1\\1&1&1&0\end{vmatrix}}={\begin{vmatrix}a&b&c&0\\b&a&0&c\\c&0&a&b\\0&c&b&a\end{vmatrix}}}
Первый определитель последней формулы является частным случаем определителя Кэли — Менгера (англ.)русск. для вычисления гиперобъёма симплекса.

Аналоги формулы Герона[править | править код]

Имеются три формулы, по структуре аналогичные формуле Герона, но выражаемые в терминах других различных параметров треугольника.

Первая формула выражает площадь через медианы, опущенные на стороны a, b и c, обозначенные соответственно через m_a, m_b и m_c, если их полусумма есть σ = (m_a + m_b + m_c)/2. Тогда мы имеем ^[2]
S=43σ(σ−ma)(σ−mb)(σ−mc).{\displaystyle S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}}.}
Обозначим высоты, проведенные к сторонам a, b и c треугольника соответственно через h_a, h_b и h_c, а полусумму их обратных величин обозначим через H=(ha−1+hb−1+hc−1)/2{\displaystyle H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2}. Тогда имеем ^[3]

S−1=4H(H−ha−1)(H−hb−1)(H−hc−1){\displaystyle S^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}}

или в развернутом виде

S=1(1ha+1hb+1hc)(1hc+1hb−1ha)(1ha+1hc−1hb)(1ha+1hb−1hc){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}})({\frac {1}{h_{c}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{a}}})({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}})({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}})}}}}

Наконец, обозначим полусумму синусов углов треугольника через s = [(sin α) + (sin β) + (sin γ)]/2, тогда имеем ^[4]

S=D2s(s−sin⁡α)(s−sin⁡β)(s−sin⁡γ).{\displaystyle S=D^{2}{\sqrt {s(s-\sin \alpha )(s-\sin \beta )(s-\sin \gamma )}}.}

Здесь через D обозначен диаметр описанной окружности треугольника: D=asin⁡α=bsin⁡β=csin⁡γ.{\displaystyle D={\tfrac {a}{\sin \alpha }}={\tfrac {b}{\sin \beta }}={\tfrac {c}{\sin \gamma }}.}

где p=a+b+c+d2{\displaystyle p={\frac {a+b+c+d}{2}}} — полупериметр четырёхугольника. (Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Например, при d=0)

Та же Формула Брахмагупты через определитель^[5]:
S=14−|abc−dba−dcc−dab−dcba|{\displaystyle S={\frac {1}{4}}{\sqrt {-{\begin{vmatrix}a&b&c&-d\\b&a&-d&c\\c&-d&a&b\\-d&c&b&a\end{vmatrix}}}}}
Для тетраэдров верна формула Герона — Тарталья, которая обобщена также на случай других многогранников (см. изгибаемые многогранники): если у тетраэдра длины рёбер равны l1,l2,l3,l4,l5,l6{\displaystyle l_{1},l_{2},l_{3},l_{4},l_{5},l_{6}}, то для его объёма V{\displaystyle V} верно выражение
144V2=l12l52(l22+l32+l42+l62−l12−l52){\displaystyle 144V^{2}=l_{1}^{2}l_{5}^{2}(l_{2}^{2}+l_{3}^{2}+l_{4}^{2}+l_{6}^{2}-l_{1}^{2}-l_{5}^{2})}+l22l62(l12+l32+l42+l52−l22−l62){\displaystyle +l_{2}^{2}l_{6}^{2}(l_{1}^{2}+l_{3}^{2}+l_{4}^{2}+l_{5}^{2}-l_{2}^{2}-l_{6}^{2})}+l32l42(l12+l22+l52+l62−l32−l42){\displaystyle +l_{3}^{2}l_{4}^{2}(l_{1}^{2}+l_{2}^{2}+l_{5}^{2}+l_{6}^{2}-l_{3}^{2}-l_{4}^{2})}−l12l22l42−l22l32l52−l12l32l62−l42l52l62{\displaystyle -l_{1}^{2}l_{2}^{2}l_{4}^{2}-l_{2}^{2}l_{3}^{2}l_{5}^{2}-l_{1}^{2}l_{3}^{2}l_{6}^{2}-l_{4}^{2}l_{5}^{2}l_{6}^{2}}.
Предыдущая формула может быть выписана для тетраэдра в явном виде: Если U, V, W, u, v, w являются длинами ребер тетраэдра (первые три из них образуют треугольник; и , например, ребро u противоположно ребру U и т.д.), тогда справедливы формулы ^[6]
V=(−a+b+c+d)(a−b+c+d)(a+b−c+d)(a+b+c−d)192uvw{\displaystyle {\text{V}}={\frac {\sqrt {\,(-a+b+c+d)\,(a-b+c+d)\,(a+b-c+d)\,(a+b+c-d)}}{192\,u\,v\,w}}}

где

a=xYZb=yZXc=zXYd=xyzX=(w−U+v)(U+v+w)x=(U−v+w)(v−w+U)Y=(u−V+w)(V+w+u)y=(V−w+u)(w−u+V)Z=(v−W+u)(W+u+v)z=(W−u+v)(u−v+W).{\displaystyle {\begin{aligned}a&={\sqrt {xYZ}}\\b&={\sqrt {yZX}}\\c&={\sqrt {zXY}}\\d&={\sqrt {xyz}}\\X&=(w-U+v)\,(U+v+w)\\x&=(U-v+w)\,(v-w+U)\\Y&=(u-V+w)\,(V+w+u)\\y&=(V-w+u)\,(w-u+V)\\Z&=(v-W+u)\,(W+u+v)\\z&=(W-u+v)\,(u-v+W).\end{aligned}}}

Теорема Люилье. Площадь сферического треугольника выражается через его стороны θa=aR,θb=bR,θc=cR{\displaystyle \theta _{a}={\frac {a}{R}},\theta _{b}={\frac {b}{R}},\theta _{c}={\frac {c}{R}}} как:
S=4R2arctg⁡tg⁡(θs2)tg⁡(θs−θa2)tg⁡(θs−θb2)tg⁡(θs−θc2){\displaystyle S=4R^{2}\,\operatorname {arctg} {\sqrt {\operatorname {tg} \left({\frac {\theta _{s}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}}}, где θs=θa+θb+θc2{\displaystyle \theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}} — полупериметр.

↑ Weisstein, Eric W. Heron’s Formula. From MathWorld—A Wolfram Web Resource.
↑ Benyi, Arpad, «A Heron-type formula for the triangle,» Mathematical Gazette» 87, July 2003, 324–326.
↑ Mitchell, Douglas W., «A Heron-type formula for the reciprocal area of a triangle,» Mathematical Gazette 89, November 2005, 494.
↑ Mitchell, Douglas W., «A Heron-type area formula in terms of sines,» Mathematical Gazette 93, March 2009, 108–109.
↑ Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1], pp. 16-17.

§258 в А. П. Киселёв, «Геометрия по Киселёву», arΧiv:1806.06942v3 [math.HO]

Николаев Н. О площади треугольника (рус.) // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора

Формула Герона для нахождения площади треугольника. Видеоурок. Геометрия 8 Класс

Цель урока – вывести формулу для вычисления площади треугольника по трем его сторонам, т. е. решить следующую задачу:

Дано: ,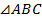

;

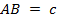
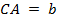(см. Рис. 1).

Доказать: 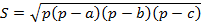, где .

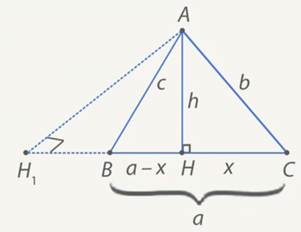
Рис. 1. Иллюстрация к доказательству формулы Герона

Доказательство

Есть треугольник

. Мы знаем формулу для вычисления площади треугоольника:

, где

– основание,

– высота.

Что взять за основание, что за высоту?

В любом треугольнике как минимум два угла острые. Если бы это было не так, то сумма углов треугольника была бы больше .

Домустим, что углы и

острые, если бы это было не так, то

, а есть еще угол

, то есть это невозможно.

Углы и 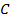– острые, тогда прямую 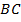расположим горизонтально. В этом случае высота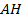

находится внутри треугольника

Почему?

В противном случае треугольник не имел бы права на существование, т. к. угол – прямой угол, угол при вершине – тупой угол, а значит, их сумма превышает , а это невозможно.

Итак, высота находится внутри треугольника, чертеж обоснован.

Осознаем задачу. Треугольник задан тремя сторонами, его площадь равняется половине основания , умноженной на высоту . Задача сводится к нахождению – высоты – по трем сторонам, и решается она известным приемом.

Пусть , тогда . У нас есть две неизвестные:

. Теорема Пифагора для обоих прямоугольных треугольников

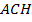даст систему уравнений относительно этих неизвестных.

Решим систему:

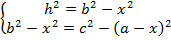
Решаем второе уравнение относительно

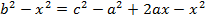
Одно неизвестное нашли, осталось найти второе неизвестное.

Из нашей системы найдем .

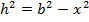
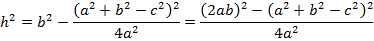
По существу, задача решена. Нам известно , , 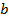, мы получили выражение для площади через , , 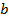и

. Но более двух тысяч лет тому назад Герон упростил это выражение и получил изящную формулу. Потрудимся и мы, и получим эту формулу. Надо преобразовать подкоренное выражение.

Во-первых, извлечем корень из знаменателя – это возможно:

Подкоренное выражение разложим на множители:

Теперь рассмотрим по очереди оставшиеся скобки:

Пусть – полупериметр:

Все четыре скобки преобразовали и выразили через полупериметр.

Теперь мы в состоянии записать подкоренное выражение:

Подставим преобразованное подкоренное выражение в формулу для площади:

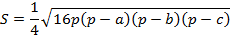
Формула Герона доказана.

Не забудьте важный прием, который позволил найти высоту по сторонам треугольника.

Далее решим конкретную задачу на применение формулы Герона.

В треугольнике известны стороны: ; ; .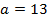

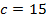Найти: .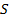

Решение:

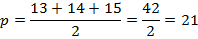
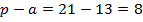
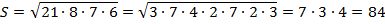
Ответ: 84.

Итак, на этом уроке мы доказали формулу Герона для нахождения площади треугольника по трем его сторонам. Закрепили эту формулу решением конкретной задачи.

Список литературы

1. Геометрия, 7-9 классы, Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. 15-е изд., М.: Просвещение, 2005.

2. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.

3. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.

4. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «Презентации для школьников» (Источник)

2. Интернет портал «Формулы, интерактивный справочник» (Источник)

3. Интернет портал «Математика, которая мне нравится» (Источник)

Домашнее задание

1. Найдите площадь треугольника по трем сторонам:

а) 17; 65; 80; б) 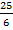; ; 6; в) 15; 37; 47; г) 2; 3; 1,83.

2. Стороны треугольника равны , , 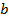. Найдите высоту треугольника, опущенную на сторону .

3. Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную

Итерационная формула Герона — Википедия

В этой статье не хватает ссылок на источники информации.Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 13 мая 2011 года.

Итерацио́нная фо́рмула Геро́на имеет вид

xn+1=12 (xn+axn) {\displaystyle x_{n+1}={\frac {1}{2}}~\left(x_{n}+{\frac {a}{x_{n}}}\right)\ },

где a — фиксированное положительное число, а x1{\displaystyle x_{1}} — любое положительное число.

Итерационная формула задаёт убывающую (начиная со 2-го элемента) последовательность, которая при любом выборе x1{\displaystyle x_{1}} быстро сходится к величине a{\displaystyle {\sqrt {a}}} (квадратный корень из числа), то есть

limn→∞xn=a{\displaystyle \lim _{n\rightarrow \infty }x_{n}={\sqrt {a}}}

Эту формулу можно получить, применяя метод Ньютона к решению уравнения a−x2=0{\displaystyle a-x^{2}=0}.

Попробуем вычислить квадратный корень для 25, используя округления при вычислениях. Пусть нашим первым предположением для значения 25{\displaystyle {\sqrt {25}}} будет значение 3.

n	xn{\displaystyle x_{n}}	xn+1=12 (xn+axn) {\displaystyle x_{n+1}={\frac {1}{2}}~\left(x_{n}+{\frac {a}{x_{n}}}\right)\ }	Приблизительное значение xn+1{\displaystyle x_{n+1}}
1	3	12 (3+253) {\displaystyle {\frac {1}{2}}~\left(3+{\frac {25}{3}}\right)\ }	12 (3+8.33)=12⋅11.33≈5.67{\displaystyle {\frac {1}{2}}~(3+8.33)={\frac {1}{2}}\cdot 11.33\approx 5.67}
2	5.67	12 (5.67+255.67) {\displaystyle {\frac {1}{2}}~\left(5.67+{\frac {25}{5.67}}\right)\ }	12 (5.67+4.41)=12⋅10.08=5.04{\displaystyle {\frac {1}{2}}~(5.67+4.41)={\frac {1}{2}}\cdot 10.08=5.04}
3	5.04	12 (5.04+255.04) {\displaystyle {\frac {1}{2}}~\left(5.04+{\frac {25}{5.04}}\right)\ }	12 (5.04+4.96)=12⋅10=5{\displaystyle {\frac {1}{2}}~(5.04+4.96)={\frac {1}{2}}\cdot 10=5}
4	5	12 (5+255) {\displaystyle {\frac {1}{2}}~\left(5+{\frac {25}{5}}\right)\ }	12 (5+5)=12⋅10=5{\displaystyle {\frac {1}{2}}~(5+5)={\frac {1}{2}}\cdot 10=5}

Эта формула имеет простую геометрическую интерпретацию. Рассмотрим прямоугольник с площадью а и стороной x₁. Будем производить его итерационное квадрирование. А именно — одну сторону нового прямоугольника сделаем равной среднему арифметическому обеих сторон предыдущего шага. А вторую сторону возьмём такой, чтобы площадь нового прямоугольника снова была равна а. На следующих шагах будем повторять этот же процесс.

Ancient Square Roots
Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures

Для улучшения этой статьи желательно:

Проставив сноски, внести более точные указания на источники.

Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.

Теорема Герона для вычисления площади треугольника

Эту теорему также называют формулой Герона.

Доказательство теоремы Герона

Будем считать известной и доказанной формулу для нахождения площади треугольника:

где – угол треугольник лежащий против стороны (Рис. 1). По теореме косинусов:

Выразим из последнего равенства , получим

По основному тригонометрическому тождеству , тогда

Правая часть последнего равенства является разностью квадратов, поэтому по формулам сокращенного умножения может быть представлена в виде

Подставим в последнее равенство выражения для косинуса

Приведем к общему знаменателю дроби в скобках и преобразуем их, группируя и используя формулы сокращенного умножения

Далее учитывая, что

получим

Извлечем корень из левой и правой части последнего равенства

Таким образом, подставляя найденное значение синуса в формулу площади, окончательно получим

Теорема доказана.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Формула Герона / Площадь / Справочник по геометрии 7-9 класс

Теорема

Доказательство

Дано: 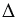АВС, АВ = , ВС = , АС = 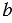, — площадь АВС.

Доказать: , где .

Доказательство:

В любом треугольнике по крайней мере два угла острые (свойство треугольника). Пусть в АВС углы А и В — острые. Тогда основание Н высоты СН лежит на стороне АВ. Пусть СН =, АН =, НВ =.