Масса полой детали | Математика для ювелиров
1.06.2013 // Владимир ТруновНикогда не устану повторять, что масса тела — это его объем  , умноженный на плотность его материала
, умноженный на плотность его материала  (см. таблицы плотностей):
(см. таблицы плотностей):
Однако, в случае полой или пустотелой детали мы будем иметь дело не с объемом ее тела, а с объемом ее стенок. Объем стенок полой детали проще всего представить как разность объемов двух сплошных тел: с внешними размерами и с внутренними (из полного объема тела вычитается объем внутренней пустоты).
Формулы для объема сплошных тел можно найти в статье «Масса сплошной детали».
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой  обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
1. Масса трубки (полого цилиндра)
 Объем стенок трубки:
Объем стенок трубки:  , где
, где  — внешний диаметр трубки,
— внешний диаметр трубки,  — длина трубки,
— длина трубки,  — толщина стенки.
— толщина стенки.
После упрощения получаем формулу для объема: 
Тогда масса трубки:

2. Масса полого (пустотелого) шара
 Объем стенок шара:
Объем стенок шара:  , где
, где  — внешний диаметр шара,
— внешний диаметр шара,  — толщина стенки.
— толщина стенки.
Тогда масса:

3. Масса полого сегмента шара
 Объем стенок сегмента шара:
Объем стенок сегмента шара:  , где
, где  — внешний диаметр основания сегмента,
— внешний диаметр основания сегмента,  — высота сегмента,
— высота сегмента,  — толщина стенки*.
— толщина стенки*.
После упрощения получаем формулу для объема: 
Тогда масса:

4. Масса полого усеченного конуса
 Объем стенок круглого усеченного конуса:
Объем стенок круглого усеченного конуса:  , где
, где  — внешний диаметр большего основания,
— внешний диаметр большего основания,  — внешний диаметр меньшего основания,
— внешний диаметр меньшего основания,  — высота конуса,
— высота конуса,  — толщина стенки*.
— толщина стенки*.
После упрощения получаем формулу для объема: 
Тогда масса:

5. Масса полой усеченной пирамиды
 Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок:
Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок:  , где
, где  — внешний размер большего основания,
— внешний размер большего основания,  — внешний размер меньшего основания,
— внешний размер меньшего основания,  — высота пирамиды,
— высота пирамиды,  — толщина стенки*.
— толщина стенки*.
После упрощения получаем формулу для объема: 
Тогда масса:

* в данном случае  — это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та
— это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та  , что стоит в формулах за скобкой, это точно толщина стенки, а та
, что стоит в формулах за скобкой, это точно толщина стенки, а та  , которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.
, которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.
tvlad.ru
Объем цилиндра ℹ️ определение, формулы расчета через диаметр и площадь основания, примеры нахождения объема полого цилиндра, онлайн-калькулятор
Как найти объем цилиндра? Любой грамотный человек обязан отличить радиус от диаметра, знать, что такое высота, помнить основные формулы геометрии и уметь рассчитать объем шара или куба.
Практическое использование геометрических формул в повседневной жизни очень высоко. Рассчитать объем в кубических метрах перевозимого груза транспортной компанией, пропускную способность трубы под домом и многое другое — во всех этих и подобных им случаях поможет геометрия.
Как найти объем цилиндра
При упоминании о цилиндре на ум приходит классический головной убор. Кроме него в окружении можно встретить много разновидностей этой фигуры.
В теории — это тело, которое ограничено цилиндрической поверхностью и пересекающими её параллельными плоскостями.

Рассчитать его объем возможно следующим образом:
V = πr2h
где
-
r – радиус;
-
h – высота.
Как видите, формула проста и прозрачна, и если обывателю нужно, как вариант, определить объем цистерны воды, можно смело ее использовать. Хотя, если возникают сомнения в правильности расчетов, для этой цели можно использовать калькулятор и определить объем онлайн.
Формула объема цилиндра через диаметр
К сожалению, случается, что при расчете объема фигуры известны не все размеры. Так, например, может не быть данных о радиусе.

В данном случае, если знать диаметр или иметь возможность его измерить, можно воспользоваться следующей формулой:
V = 4πd2h
где
-
d– диаметр;
-
h – высота.
Объем полого цилиндра
Расчет полого цилиндра нужен, когда необходимо, например, рассчитать вес полой трубы. Ее масса равна произведению плотности материала и объема.

Формула для вычисления:
V = π (r12 — r22)h
где
Примеры задач с решениями
Задача №1
Высота бочки с водой равна 3 метрам, радиус составляет 0,75 метра. Рассчитать в литрах, сколько нужно жидкости, чтобы заполнить емкость наполовину?
Решение:

Ответ: 2,65 литров.
Задача №2
В цехе подготовили заготовку цилиндра. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.
Вычисляем:

Ответ: 100480 см3.
Задача №3
На производстве нужно изготовить две трубы с двумя равными поверхностями. Внешний радиус первой трубы равен 5см, а внутренний 4 см, высота 200 см. Внутренний радиус второй равен 3 см.
Сколько понадобится материала для изготовления труб?
Решение:

Ответ: 15700 см3.
nauka.club
Измерение объема полого цилиндра

Произвести по три измерения каждой из величин d,D,h с помощью штангенциркуля, определив предварительно его инструментальную погрешность.
Задав надежность Р=0.95, произвести обработку результатов n=3 прямых измерений каждой из величин d,D,h.
Вычислить объем полого цилиндра по формуле
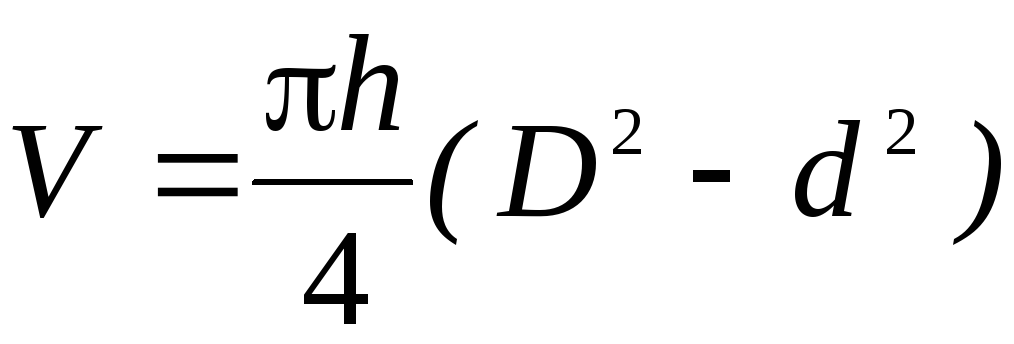
Вывести формулы для абсолютной и относительной погрешностей измерения V и рассчитать их величины, используя результаты соответствующих прямых измерений.
Записать результат в стандартном виде
 и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.
и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.
Контрольные вопросы.
Дать определение прямых и косвенных измерений.
Что такое погрешности измерения и как они классифицируются?
Что такое плотность вероятности распределения результатов измерений?
Как вычисляются абсолютная и относительная погрешности косвенных измерений по результатам прямых измерений?
Литература
Х.Н. Сотская Введение к физическому практикуму. Конспект лекций. – Мн.: МРТИ, 1973.
О.Н. Касандрова, В.В.Лебедев. Обработка результатов измерений. М.: Наука, 1970.
Л.З. Румшинский. Математическая обработка результатов эксперимента. – М.: Наука, 1971.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А 1.2
Измерение скорости пули с помощью баллистического маятника
Цель работы:
1.Изучить законы изменения и сохранения момента импульса и пол -ной механической энергии системы.
2.Измерить скорость пули с помощью баллистического маятника.
Теоретическое обоснование работы
Баллистический маятник, являющийся разновидностью физического маятника, состоит из заполненного пластилином полого цилиндра, закрепленного на конце металлического стержня. На противоположном концетержня имеются треугольные опорные призмы, уменьшающие силу трения в опоре. В маятник стреляют в горизонтальном направлении из пружинного пистолета пулей массой .
После неупругого соударения маятник
с пулей начинает колебаться под
действием силы тяжести. Установка
содержит масштабную линейку Л,
предназначенную для определения
пройденного свободным концом маятника
пути, и секундомерCдля
определения периода колебаний маятника.
.
После неупругого соударения маятник
с пулей начинает колебаться под
действием силы тяжести. Установка
содержит масштабную линейку Л,
предназначенную для определения
пройденного свободным концом маятника
пути, и секундомерCдля
определения периода колебаний маятника.
Рис.1.2.1
Законы изменения и сохранения момента импульса и
полной механической энергии системы
Для получения формулы для скорости пули, выраженной через величины, определяемые в прямых измерениях, воспользуемся законами сохранения момента импульса и полной механической энергии системы.
Моментом импульса системы n-материальных точек относительно точки 0 называют величину
 ,
(1)
,
(1)
где 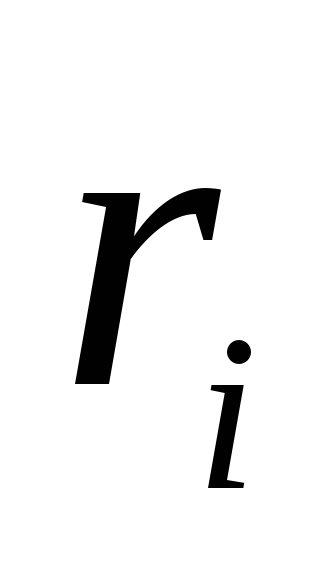 и
и — соответственно радиус-векторi-
й материальной точки, проведенный из
точки 0, и ее импульс в момент времениt. Квадратные скобки
обозначают векторное произведение.
— соответственно радиус-векторi-
й материальной точки, проведенный из
точки 0, и ее импульс в момент времениt. Квадратные скобки
обозначают векторное произведение.
Если
на систему действуют внешние силы 
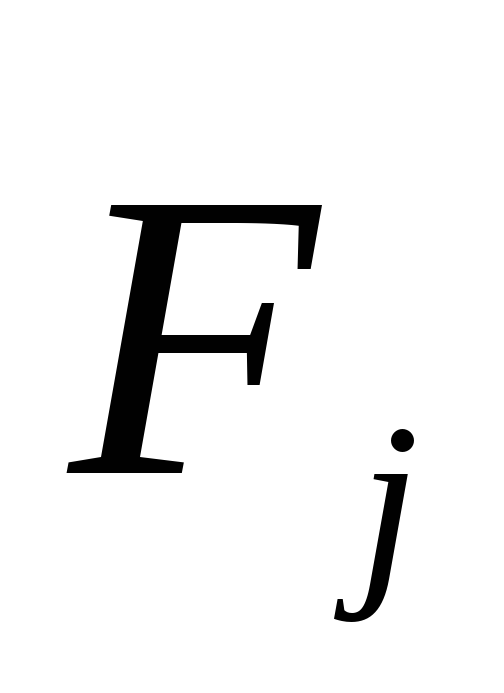 ,
,  тоизменяется
по закону
тоизменяется
по закону
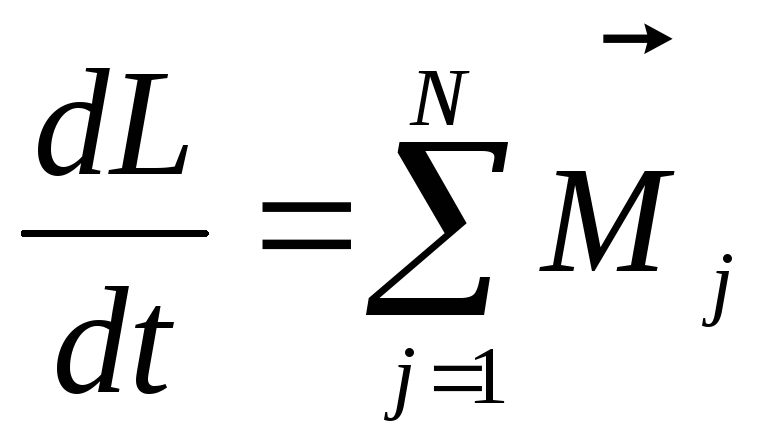 ,
(2)
,
(2)
где 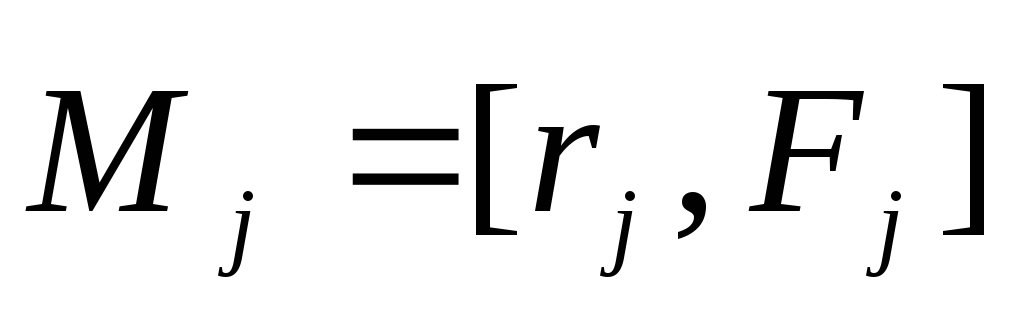 — моментj-й
внешней силы относительно точки 0.
— моментj-й
внешней силы относительно точки 0.
Из
(2) следует, что если сумма моментов
внешних сил, действующих на систему,
равна нулю, то ее момент импульса
сохраняется, т.е.  = const.
= const.
В случае твердого тела, вращающегося вокруг неподвижной оси OZ, проекция его момента импульса на эту ось дается формулой (cм. лаб. работу №1.3)
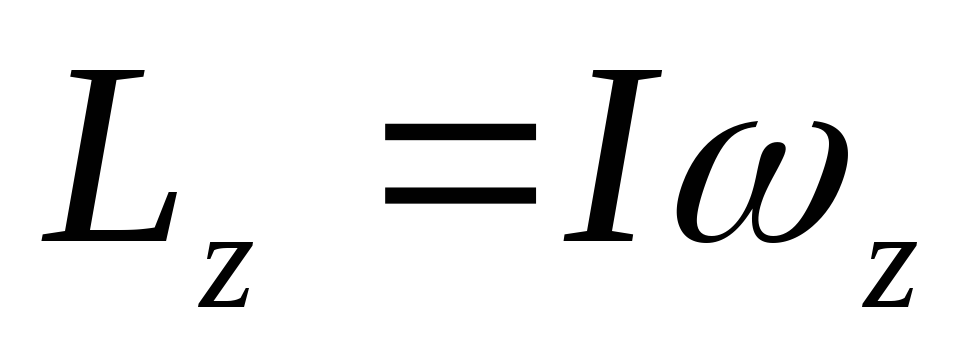 ,
(3)
,
(3)
где
I
— момент инерции твердого тела относительно
оси OZ, 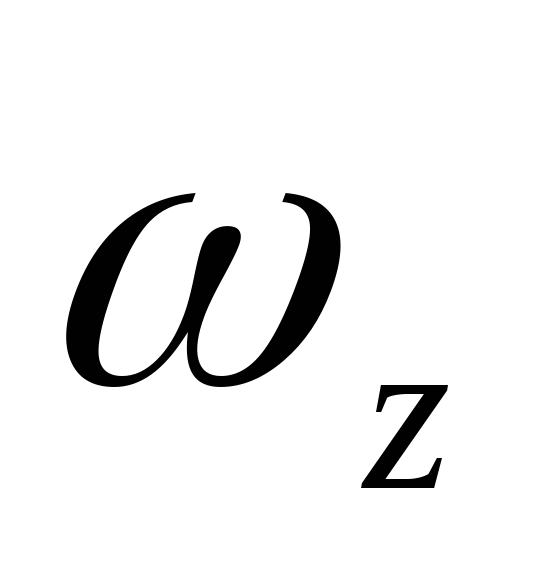 — проекция вектора угловой скорости на
эту ось.
— проекция вектора угловой скорости на
эту ось.
Кинетической энергией системы n-материальных точек называется величина
 ,
(4)
,
(4)
где  — масса i-й
материальной точки,
— масса i-й
материальной точки,  — величина ее скорости в момент времениt
.
— величина ее скорости в момент времениt
.
Кинетическая
энергия твердого тела, вращающегося
вокруг фиксированной оси с угловой
скоростью  ,
задается формулой
,
задается формулой
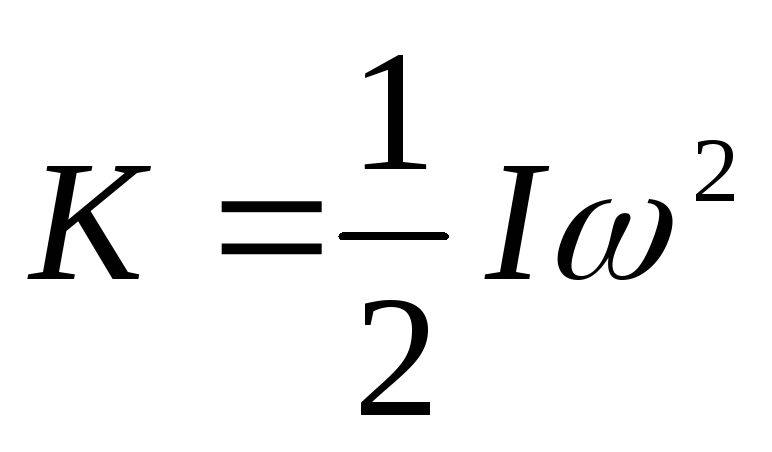 ,
(5)
,
(5)
где I — момент инерции твердого тела относительно этой оси.
Полной механической энергией системы n-материальных точек во внешнем поле называют величину
 ,
(6)
,
(6)
где  — потенциальная энергия взаимодействия
частиц системы,
— потенциальная энергия взаимодействия
частиц системы, -потенциальная
энергия частиц системы во внешнем поле.
-потенциальная
энергия частиц системы во внешнем поле.
Закон изменения Е при переходе системы из одного механического состояния в другое можно записать в виде
 ,
(7)
,
(7)
где  — суммарная работа всех внешних н е к о
н с е р в а т и в н ы х с и л,
— суммарная работа всех внешних н е к о
н с е р в а т и в н ы х с и л,
действующих
на систему,  суммарная работа всех внутренних
неконсервативных сил взаимодействия.
суммарная работа всех внутренних
неконсервативных сил взаимодействия.
Из (7) вытекает, что если на систему не действуют внешние неконсервативные силы и отсутствуют внутренние неконсервативные, то полная механическая энергия системы сохраняется, т.е. E = const.
Вывод формулы для скорости пули
Обратимся
теперь к выводу формулы для скорости
пули. Рассмотрим систему маятник + пуля.
На нее действуют внешние силы тяжести,
сопротивления воздуха, реакции опоры
и трения в опорных призмах маятника.
Кроме того, в течение времени соударения
пули с маятником  (т.е. времени, в течение которого скорость
пули относительно маятника станет
равной нулю) между ними действуют силы
внутреннего трения, не являющиеся
консервативными. В дальнейшем будем
считать, что сила сопротивления воздуха
и силы трения в опорных призмах
пренебрежимо малы.
(т.е. времени, в течение которого скорость
пули относительно маятника станет
равной нулю) между ними действуют силы
внутреннего трения, не являющиеся
консервативными. В дальнейшем будем
считать, что сила сопротивления воздуха
и силы трения в опорных призмах
пренебрежимо малы.
Пусть
Т период колебаний маятника с пулей,
возникающих после соударения. Если
предположить, что  <<T
, то за время
<<T
, то за время  отклонение маятника с пулей от положения
равновесия незначительно, и момент силы
тяжести относительно точки 0 (рис.1.2.1) в
течение этого времени можно считать
равным нулю. Поскольку момент силы
реакции опоры относительно точки 0
всегда равен нулю, а другими внешними
силами мы пренебрегаем, то согласно (2)
в течение времени соударения
отклонение маятника с пулей от положения
равновесия незначительно, и момент силы
тяжести относительно точки 0 (рис.1.2.1) в
течение этого времени можно считать
равным нулю. Поскольку момент силы
реакции опоры относительно точки 0
всегда равен нулю, а другими внешними
силами мы пренебрегаем, то согласно (2)
в течение времени соударения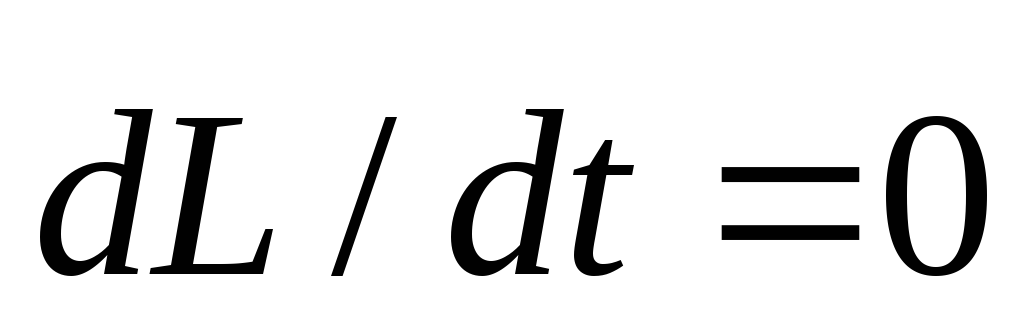 ,
т.е. момент импульса системы маятник+пулясохраняется
для всех
,
т.е. момент импульса системы маятник+пулясохраняется
для всех 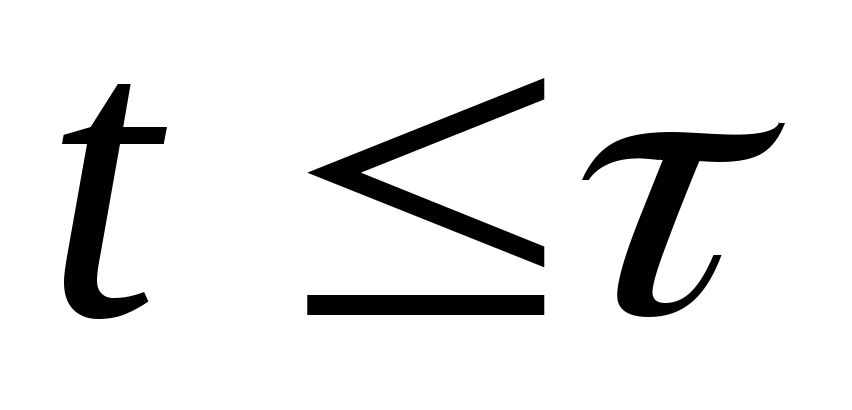
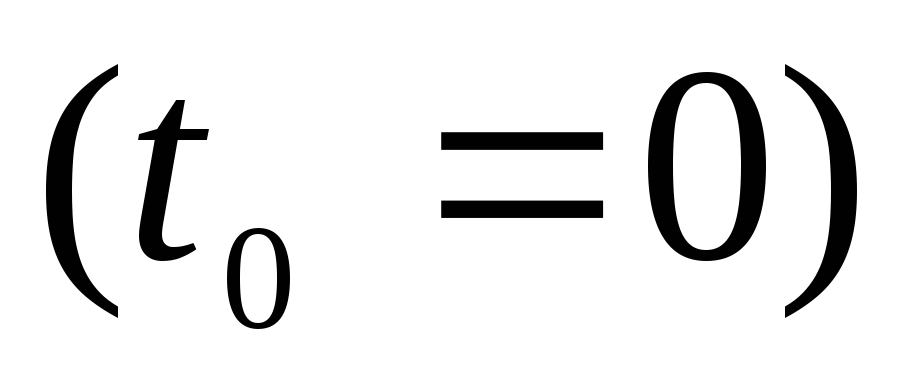 .
.
Поскольку
в соответствии с (1) и (3) 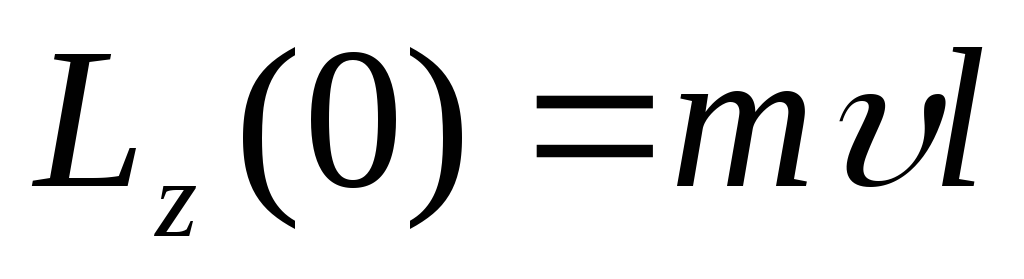 ,
а
,
а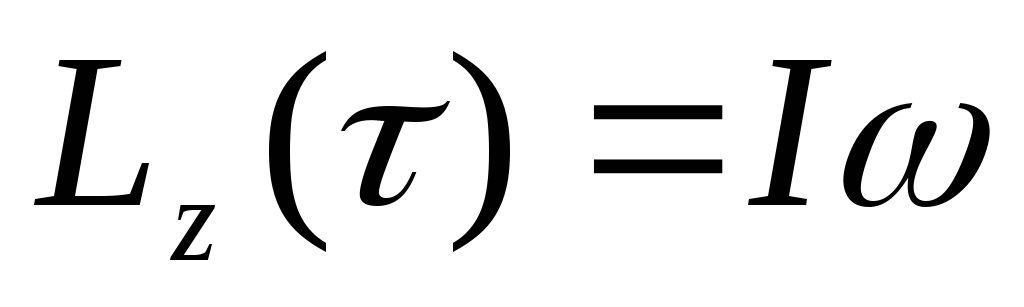 ,
где
,
где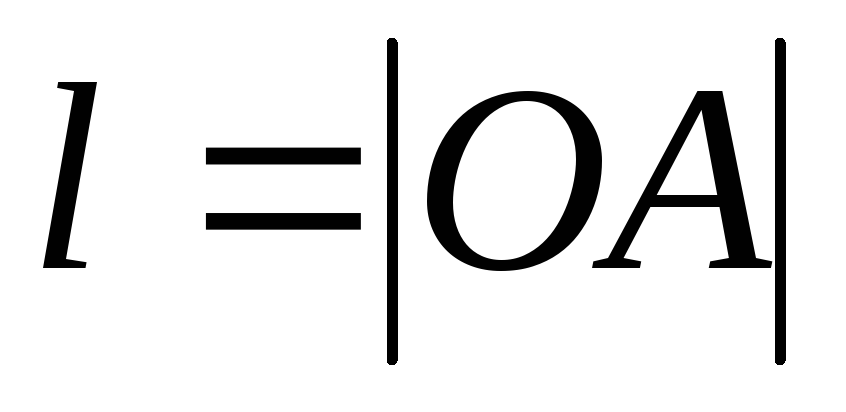 (рис.1.2.1),
(рис.1.2.1),  —
скорость пули, I
— момент инерции маятника с пулей
относительно оси OZ,
—
скорость пули, I
— момент инерции маятника с пулей
относительно оси OZ,  — угловая скорость вращения маятника
в момент
— угловая скорость вращения маятника
в момент , то
, то
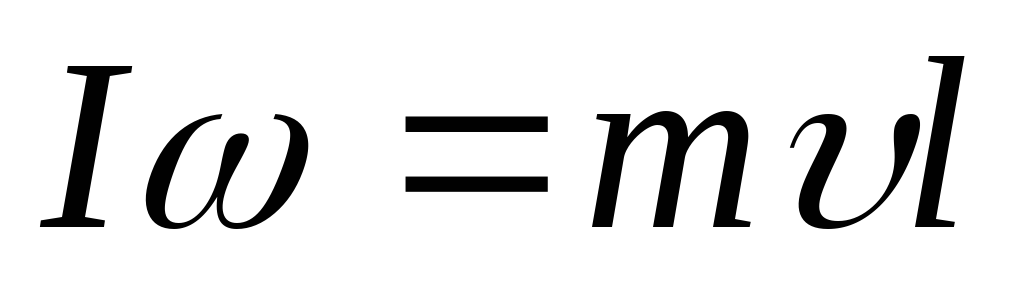 .
(8)
.
(8)
Так
как после соударения действие сил
внутреннего трения прекращается, а силы
сопротивления воздуха и трения в опорных
призмах пренебрежимо малы, то для всех 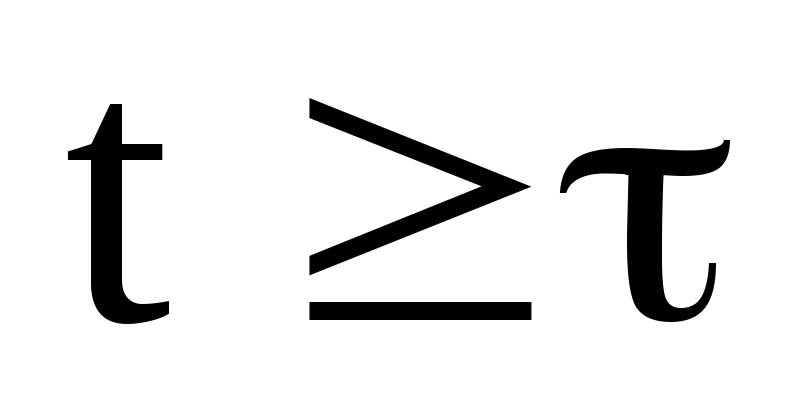
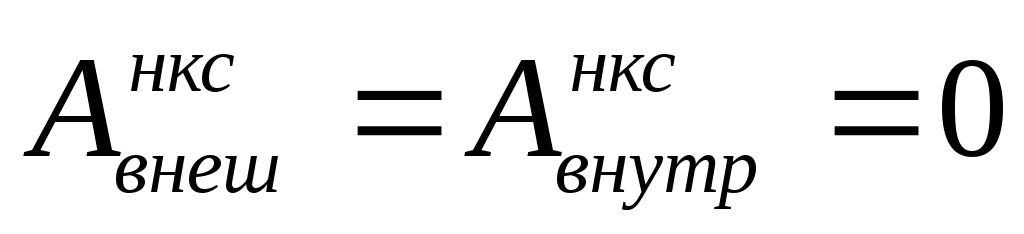 , и, согласно (7)
, и, согласно (7)
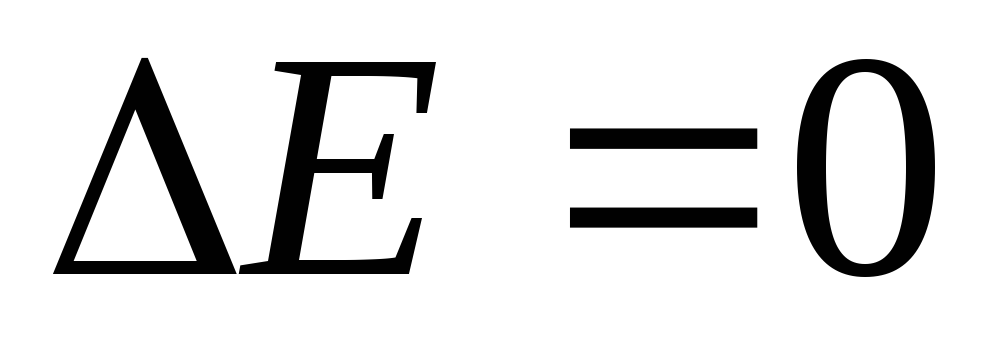 ,
(9)
,
(9)
т.е. полная механическая энергия системы маятник+пуля после соударения сохраняется.
studfile.net
Рассчитать объем цилиндра
Рассчитать объем цилиндра.
Рассчитать объем цилиндра вы можете по высоте и радиусу основания, высоте и площади основания, высоте и диаметру основания.
Калькулятор расчета объема цилиндра
Формулы расчета объема цилиндра
Цилиндр, виды цилиндров
Калькулятор расчета объема цилиндра:
Выберите, по каким параметрам вы хотите рассчитать объем цилиндра. Результат расчета получается в литрах, кубическим сантиметрах и кубических метрах.
Формулы расчета объема цилиндра:
Формула расчета объема цилиндра по высоте и радиусу основания:
V = π · r² · h,
где
V – объем цилиндра,
π – число пи, π ≈ 3,1415926535,
r – радиус основания,
h – высота цилиндра.
Формула расчета объема цилиндра по высоте и площади основания:
V = S · h,
где
V – объем цилиндра,
S – площадь основания цилиндра,
h – высота цилиндра.
Формула расчета объема цилиндра по высоте и диаметру основания:
V = π · d2/4h,
где
V – объем цилиндра,
π – число пи, π ≈ 3,1415926535,
d – диаметр цилиндра,
h – высота цилиндра.
Цилиндр:
Цилиндр (др.-греч. κύλινδρος – «валик, каток») – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
В свою очередь цилиндрическая поверхность – это поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.
Основания цилиндра – это плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.
Боковая поверхность цилиндра – это цилиндрическая поверхность между плоскостями оснований.
Виды цилиндров:
Прямой цилиндр – это цилиндр, у которого образующие перпендикулярны основанию.
Наклонный цилиндр – это цилиндр, у которого образующие не перпендикулярны основанию.
Круговой цилиндр – это цилиндр, основанием которого является окружность (круг).
Прямой круговой цилиндр – это цилиндр, который одновременно является и прямым, и круговым. Прямой круговой цилиндр – это тело вращения, которое получается при вращении прямоугольника на 360° вокруг его стороны, являющейся одновременно осью симметрии цилиндра.
У прямого кругового цилиндра образующая (l) равна его высоте (h).
Радиус цилиндра (r) – это радиус основания цилиндра.
Диаметр цилиндра (d) – это диаметр основания цилиндра.
Высота цилиндра (h) – это расстояние между основаниями цилиндра.
Ось симметрии прямого кругового цилиндра – это прямая, соединяющая центры окружности оснований цилиндра.
Осевое сечение прямого кругового цилиндра – это сечение прямого кругового цилиндра плоскостью, которая проходит через его ось. Данное сечение является прямоугольником.
Примечание: © Фото https://www.pexels.com, https://pixabay.com




карта сайта
Коэффициент востребованности 23
xn--80aaafltebbc3auk2aepkhr3ewjpa.xn--p1ai
Измерение объема полого цилиндра

Произвести по три измерения каждой из величин d,D,h с помощью штангенциркуля, определив предварительно его инструментальную погрешность.
Задав надежность Р=0.95, произвести обработку результатов n=3 прямых измерений каждой из величин d,D,h.
Вычислить объем полого цилиндра по формуле

Вывести формулы для абсолютной и относительной погрешностей измерения V и рассчитать их величины, используя результаты соответствующих прямых измерений.
Записать результат в стандартном виде
 и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.
и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.
Контрольные вопросы.
Дать определение прямых и косвенных измерений.
Что такое погрешности измерения и как они классифицируются?
Что такое плотность вероятности распределения результатов измерений?
Что такое доверительный интервал прямых измерений и как он вычисляется?
Как вычисляются абсолютная и относительная погрешности косвенных измерений по результатам прямых измерений?
Литература
Х.Н. Сотская Введение к физическому практикуму. Конспект лекций. – Мн.: МРТИ, 1973.
О.Н. Касандрова, В.В.Лебедев. Обработка результатов измерений. М.: Наука, 1970.
Л.З. Румшинский. Математическая обработка результатов эксперимента. – М.: Наука, 1971.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А 1.2
Измерение скорости пули с помощью баллистического маятника
Цель работы:
1.Изучить законы изменения и сохранения момента импульса и пол -ной механической энергии системы.
2.Измерить скорость пули с помощью баллистического маятника.
Теоретическое обоснование работы
Баллистический
маятник, являющийся разновидностью
физического маятника, состоит из
заполненного пластилином полого
цилиндра, закрепленного на конце
металлического стержня. На противоположном
концетержня имеются треугольные опорные
призмы, уменьшающие силу трения в опоре.
В маятник стреляют в горизонтальном
направлении из пружинного пистолета
пулей массой 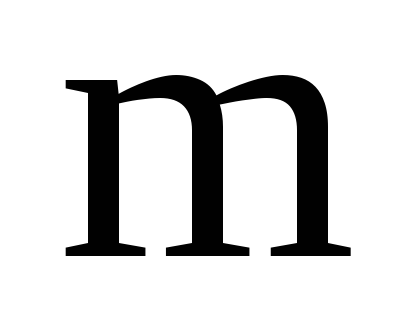 .
После неупругого соударения маятник
с пулей начинает колебаться под
действием силы тяжести. Установка
содержит масштабную линейку Л,
предназначенную для определения
пройденного свободным концом маятника
пути, и секундомерCдля
определения периода колебаний маятника.
.
После неупругого соударения маятник
с пулей начинает колебаться под
действием силы тяжести. Установка
содержит масштабную линейку Л,
предназначенную для определения
пройденного свободным концом маятника
пути, и секундомерCдля
определения периода колебаний маятника.

Рис.1.2.1
Законы изменения и сохранения момента импульса и
полной механической энергии системы
Для получения формулы для скорости пули, выраженной через величины, определяемые в прямых измерениях, воспользуемся законами сохранения момента импульса и полной механической энергии системы.
Моментом импульса системы n-материальных точек относительно точки 0 называют величину
 ,
(1)
,
(1)
где  и
и — соответственно радиус-векторi-
й материальной точки, проведенный из
точки 0, и ее импульс в момент времениt. Квадратные скобки
обозначают векторное произведение.
— соответственно радиус-векторi-
й материальной точки, проведенный из
точки 0, и ее импульс в момент времениt. Квадратные скобки
обозначают векторное произведение.
Если
на систему действуют внешние силы 
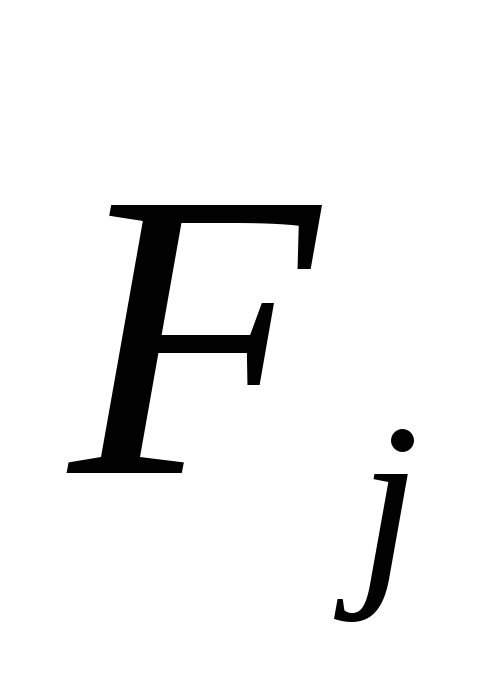 ,
,  то
то изменяется
по закону
изменяется
по закону
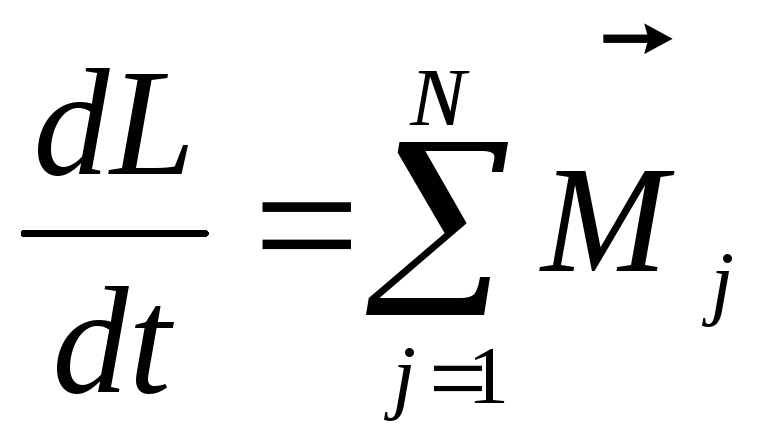 ,
(2)
,
(2)
где  — моментj-й
внешней силы относительно точки 0.
— моментj-й
внешней силы относительно точки 0.
Из
(2) следует, что если сумма моментов
внешних сил, действующих на систему,
равна нулю, то ее момент импульса
сохраняется, т.е.  = const.
= const.
В случае твердого тела, вращающегося вокруг неподвижной оси OZ, проекция его момента импульса на эту ось дается формулой (cм. лаб. работу №1.3)
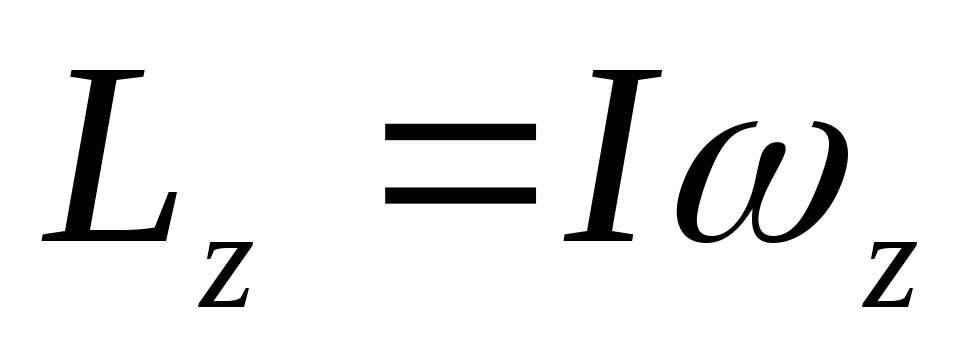 ,
(3)
,
(3)
где
I
— момент инерции твердого тела относительно
оси OZ,  — проекция вектора угловой скорости на
эту ось.
— проекция вектора угловой скорости на
эту ось.
Кинетической энергией системы n-материальных точек называется величина
 ,
(4)
,
(4)
где  — масса i-й
материальной точки,
— масса i-й
материальной точки,  — величина ее скорости в момент времениt
.
— величина ее скорости в момент времениt
.
Кинетическая
энергия твердого тела, вращающегося
вокруг фиксированной оси с угловой
скоростью  ,
задается формулой
,
задается формулой
 ,
(5)
,
(5)
где I — момент инерции твердого тела относительно этой оси.
Полной механической энергией системы n-материальных точек во внешнем поле называют величину
 ,
(6)
,
(6)
где  — потенциальная энергия взаимодействия
частиц системы,
— потенциальная энергия взаимодействия
частиц системы, -потенциальная
энергия частиц системы во внешнем поле.
-потенциальная
энергия частиц системы во внешнем поле.
Закон изменения Е при переходе системы из одного механического состояния в другое можно записать в виде
 ,
(7)
,
(7)
где  — суммарная работа всех внешних н е к о
н с е р в а т и в н ы х с и л,
— суммарная работа всех внешних н е к о
н с е р в а т и в н ы х с и л,
действующих
на систему,  суммарная работа всех внутренних
неконсервативных сил взаимодействия.
суммарная работа всех внутренних
неконсервативных сил взаимодействия.
Из (7) вытекает, что если на систему не действуют внешние неконсервативные силы и отсутствуют внутренние неконсервативные, то полная механическая энергия системы сохраняется, т.е. E = const.
Вывод формулы для скорости пули
Обратимся
теперь к выводу формулы для скорости
пули. Рассмотрим систему маятник + пуля.
На нее действуют внешние силы тяжести,
сопротивления воздуха, реакции опоры
и трения в опорных призмах маятника.
Кроме того, в течение времени соударения
пули с маятником  (т.е. времени, в течение которого скорость
пули относительно маятника станет
равной нулю) между ними действуют силы
внутреннего трения, не являющиеся
консервативными. В дальнейшем будем
считать, что сила сопротивления воздуха
и силы трения в опорных призмах
пренебрежимо малы.
(т.е. времени, в течение которого скорость
пули относительно маятника станет
равной нулю) между ними действуют силы
внутреннего трения, не являющиеся
консервативными. В дальнейшем будем
считать, что сила сопротивления воздуха
и силы трения в опорных призмах
пренебрежимо малы.
Пусть
Т период колебаний маятника с пулей,
возникающих после соударения. Если
предположить, что  <<T
, то за время
<<T
, то за время  отклонение маятника с пулей от положения
равновесия незначительно, и момент силы
тяжести относительно точки 0 (рис.1.2.1) в
течение этого времени можно считать
равным нулю. Поскольку момент силы
реакции опоры относительно точки 0
всегда равен нулю, а другими внешними
силами мы пренебрегаем, то согласно (2)
в течение времени соударения
отклонение маятника с пулей от положения
равновесия незначительно, и момент силы
тяжести относительно точки 0 (рис.1.2.1) в
течение этого времени можно считать
равным нулю. Поскольку момент силы
реакции опоры относительно точки 0
всегда равен нулю, а другими внешними
силами мы пренебрегаем, то согласно (2)
в течение времени соударения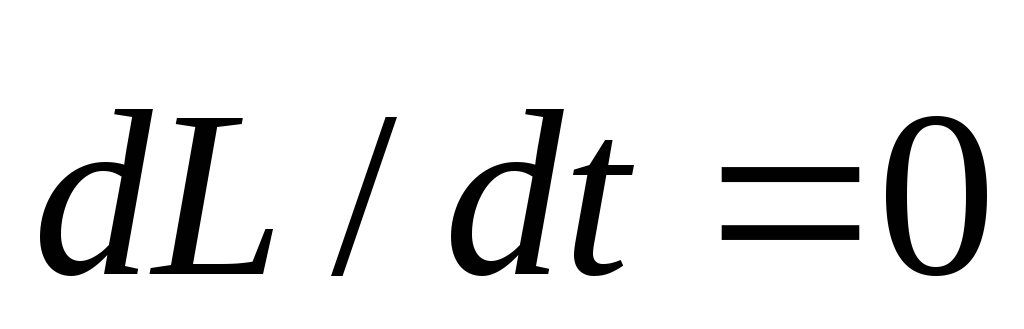 ,
т.е. момент импульса системы маятник+пулясохраняется
для всех
,
т.е. момент импульса системы маятник+пулясохраняется
для всех 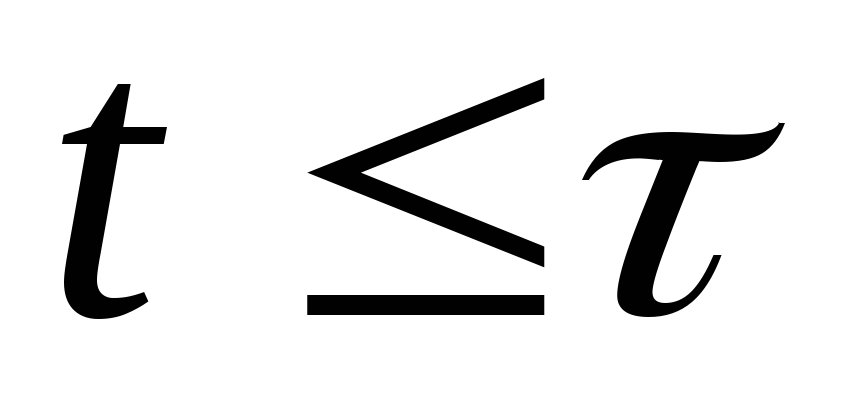
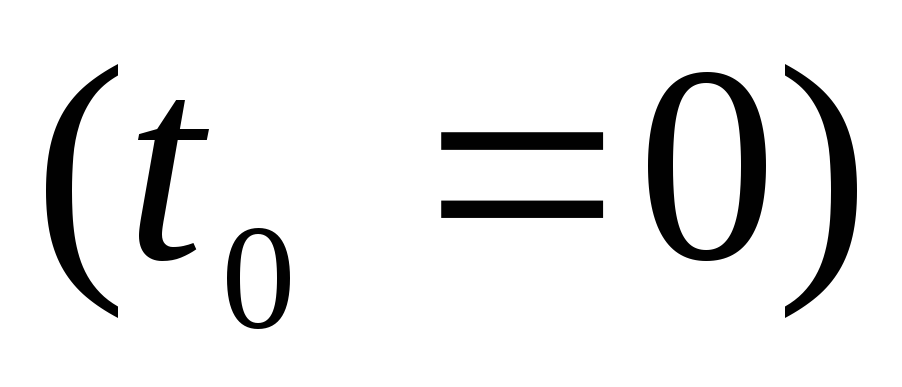 .
.
Поскольку
в соответствии с (1) и (3) 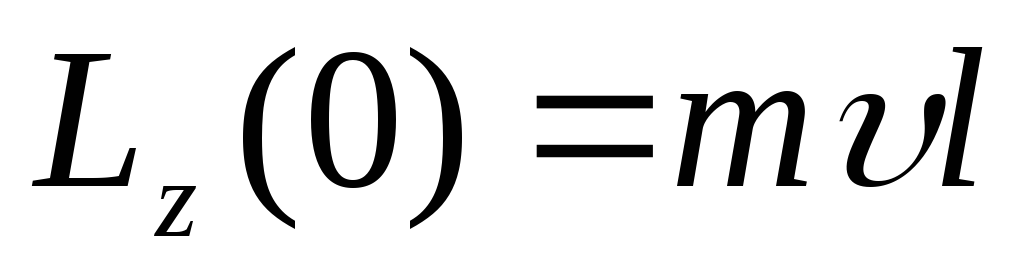 ,
а
,
а ,
где
,
где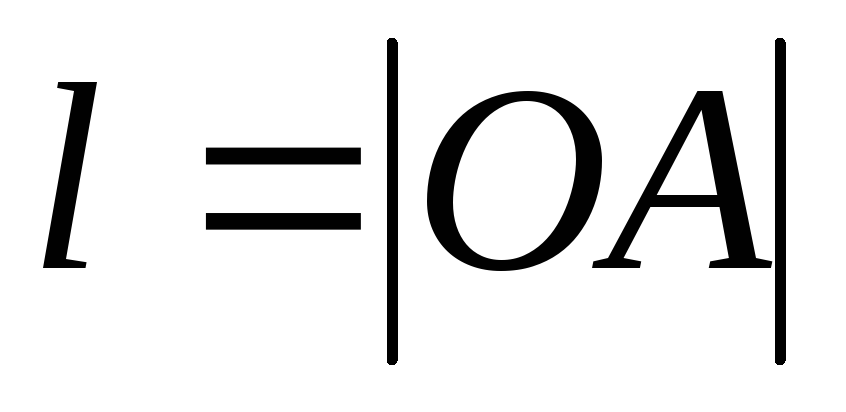 (рис.1.2.1),
(рис.1.2.1),  —
скорость пули, I
— момент инерции маятника с пулей
относительно оси OZ,
—
скорость пули, I
— момент инерции маятника с пулей
относительно оси OZ,  — угловая скорость вращения маятника
в момент
— угловая скорость вращения маятника
в момент , то
, то
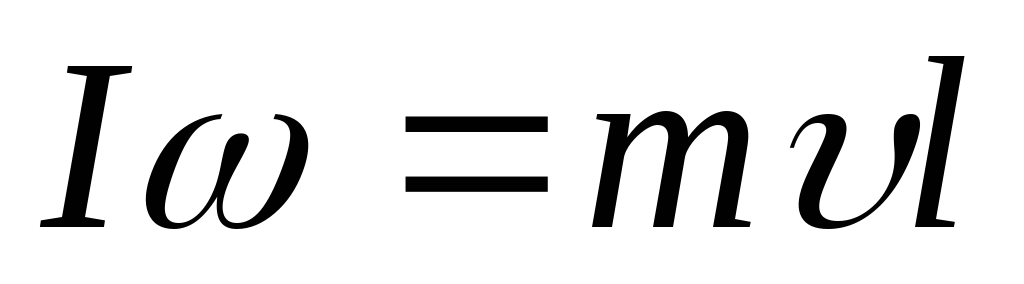 .
(8)
.
(8)
Так
как после соударения действие сил
внутреннего трения прекращается, а силы
сопротивления воздуха и трения в опорных
призмах пренебрежимо малы, то для всех 
 , и, согласно (7)
, и, согласно (7)
 ,
(9)
,
(9)
т.е. полная механическая энергия системы маятник+пуля после соударения сохраняется.
studfile.net
Онлайн калькулятор: Объем геометрических фигур
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
 Размеры куба
Размеры куба
Формула:

Объем куба
Длина ребра куба (H)
Точность вычисленияЗнаков после запятой: 5
save Сохранить share Поделиться extension Виджет
Объем прямоугольной призмы
 Размеры прямоугольной призмы
Размеры прямоугольной призмы
Формула:

Объем прямоугольной призмы
Точность вычисленияЗнаков после запятой: 5
save Сохранить share Поделиться extension Виджет
Объем пирамиды
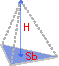 Размеры пирамиды
Размеры пирамиды
Формула:

Объем пирамиды
Площадь основания
Точность вычисленияЗнаков после запятой: 5
save Сохранить share Поделиться extension Виджет
Объем усеченной пирамиды
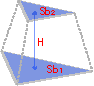 Размеры усеченной пирамиды
Размеры усеченной пирамиды
Формула:

Объем усеченной пирамиды
Точность вычисленияЗнаков после запятой: 5
planetcalc.ru
Формула объема цилиндра
Прежде чем говорить о формуле объема цилиндра разберемся с основополагающими моментами.
Цилиндр сам по себе является геометрической фигурой, которую ограничивают две находящиеся друг против друга области и пересекают цилиндрическую область. Данную цилиндрическую область можно получить путем направленных вперед движений образующих прямые линии так, чтобы образующая точка двигалась продольно направляющей кривой. Боковая область — та область фигуры которая ограничивается цилиндрической поверхностью. На основание приходиться другая часть, тем самым формы границы и направляющей совпадают.
Чаще всего это тело представляют в виде кругового прямого цилиндра, в котором окружность , прямая дающая направление и две основные области относительно образующей будут перпендикулярны. В данном теле будет ось симметрии.
Есть много типов цилиндров, которые различаются по форме основания, разрезу или наклону образующей. Бывают косые и наклонные, эллиптические, параболические и гиперболические.
Для того чтобы узнать объем цилиндра, необходимо знать высоту данного цилиндра или другими словами расстояние от одного основания до другого.

Объем цилиндра конечно же находиться при помощи формул, о которых и пойдет речь дальше. Для этого существуют две формулы: Формула объема цилиндра №1.
V = Sо*h
в которой V — это объем, Sо — площадь основания, h — это высота тела.
Формула объема цилиндра №2.
V = ? * R2 * h
в которой V — это объем, R — это радиус, h- это высота.
С помощью данной формулы, объем находится при помощи радиуса, числа ? и высоты. Данная формула применима только для кругового прямого цилиндра.
При использовании данных формул можно вычислить объем любой емкости, единственная поправка — это то что значения будут в метрах. А результат в кубических метрах.
Рассчитаем для наглядности
Дан цилиндр размер которого 0,5м. высота и диаметр 0,3м
Воспользуемся в расчетах формулой №2, в результате чего получаем:
V = 3,14 * 0,15 * 0,15 * 0,5 = 0,035325 кб/м
0,035325 кб/м = 35,325 литров.
Как видите в этом нет ничего сложного. Интересных вам вычислений!
Если вы ищите Полиуретан, пенополиуретан, оборудование для ППУ (http://puinfo.ru/), перейдите по ссылке на информационный сайт, в котором Вы найдете много нужной и интересной информации.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
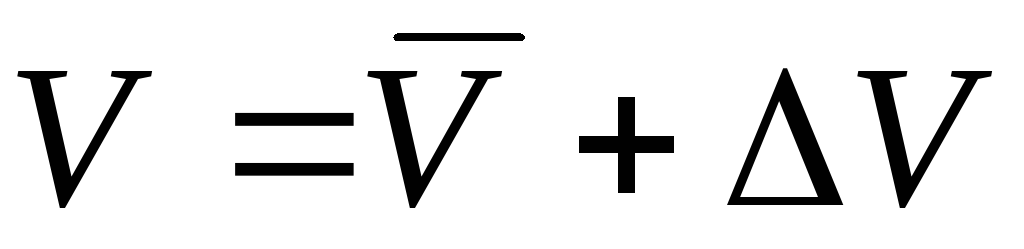 и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.
и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты. и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.
и
сделать вывод о проделанной работе,
отразив используемый метод измерений
и полученные результаты.