Формулы арифметической прогрессии. Формула n числа арифметической прогрессии. Формула для вычисления суммы арифметической прогрессии.
Прогрессия-это последовательность объектов, которые следуют определенному порядку. Арифметическая прогрессия — это последовательность чисел, в которой разница между двумя последовательными числами одинакова.
Арифметическая прогрессия представляет собой последовательность чисел, где разница между любыми двумя последовательными числами постоянна.

Другими словами, в арифметической прогрессии, результат одинаков, когда число вычитается из его следующего числа, по всей ее последовательности. Результат, когда число вычитается из его следующего числа, называется шагом или разностью арифметической прогрессии.
Пример арифметической прогресии: \(1,3,5,7,9,11\), к каждому последующему числу мы прибавляем \(2\).
Для того чтобы решать задачи по арифметической прогрессии, важно понимать формулировку символов.
Обозначения в формулах арифметической прогрессии:
- Первый член в арифметической прогрессии \(a_1\):
\(1,3,5,7,9\) \(1 -a_1\)
- Какой-либо член в арифметической прогрессии \(a_n\) :
\(1,3,5,7,9\) например \(a_n-3\), также это может быть любое число из прогрессии.
- Следующий член \(a_{n+1}\):
\(1,3,5,7,9\) \(3-n,\; \; \; 5-a_{n+1}\).
- Предыдущий член арифметической прогрессии \(a_{n-1}\)
\(1,3,5,7,9\) \(5-n,\; \; \; 3-a_{n-1}\).
- Сумма членов арифметической прогрессии \(S_n\):
\(1,3,5,7,9\) \(S_n=1+3+5+7+9=25\).
- Шаг арифметической прогрессии \(d\):
\(1,3,5,7,9\) \(3-1=5-3=7-5=9-7=2(d)\)
- Номер члена арифметической прогрессии \(n\):
\(1,3,5,7,9\) \(1\)–первый член \((n=1)\); \(3-\)второй член \((n=2)\); третий член\(-5\) \((n=3)\).
Формулы
Формула для нахождения \(a_n\) , если нам известно \(a_1\)и \(d\):
\(a_n=a_1+d(n-1)\)
Формула для нахождения \(a_{n+1}\) , если нам известно \(a_{n}\) и \(d\), также мы можем выразить любое слагаемое:
\(a_{n+1}=a_n+d\)
Предыдущий член арифметической прогрессии, если мы знаем \(a_n\) и \(d\):
\(a_{n-1}=a_n-d\)
Формула если нам известно \(a_{n+1}\) , \(a_{n-1}\), \(n\):
\(a_{n}=\frac{a_{n-1}+a_{n+1}}{2}\), где \(n>1\)
Формула нахождения суммы арифметической прогрессии, если мы знаем \(a_1\), \(a_n,n\):
\( S_n=\frac{(a_1+a_n)*n}{2}\)
Формула нахождения суммы арифметической прогрессии, если мы знаем \(a_1,d,n\):
\(S_n=\frac{2a_1+d(n-1)n}{2}\)
Также не забываем, что мы можем выразить неизвестную нам искомую величину, в любой вышеперечисленной формуле.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Арифметическая прогрессия | umath.ru
Определение арифметической прогрессии
Определение. Числовая последовательность, каждый член которой получается из предыдущего прибавлением одного и того же числа называется арифметической прогрессией . Число
называется арифметической прогрессией . Число 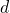 называется разностью арифметической прогрессии.
называется разностью арифметической прогрессии.То есть арифметическая прогрессия определяется рекуррентным соотношением
![\[a_{n+1} = a_n + d.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-5734397107e54233a2710dd171ec6c7a_l3.png)
Например, последовательность нечётных натуральных чисел
![\[1, 3, 5, 7, 9, \ldots\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-b1075776d86233f031e888dd989f825f_l3.png)
является арифметической прогрессией, так как любой её член отличается от предыдущего на 2.
Общий член арифметической прогрессии  задаётся формулой
задаётся формулой
![\[a_n = d(n - 1) + a_1.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-2127c08d521e5bc9ef9709e0efe460ef_l3.png)
Например, последовательность  образует арифметическую прогрессию с разностью
образует арифметическую прогрессию с разностью 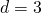 и первым членом
и первым членом  Поэтому её общий член может быть задан соотношением
Поэтому её общий член может быть задан соотношением
![\[a_n = 2 + 3(n-1) = 3n - 1.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-817d7d57faa917b81aa440142bf3260d_l3.png)
Пример 1. Найти одиннадцатый член арифметической прогрессии, если её первый член 
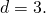
Решение. По формуле для общего члена арифметической прогрессии имеем
![\[a_{11} = 5 + 3(11 - 1) = 35.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-e0e5c13698b02ff00970647cc2ca03b6_l3.png)
Теорема. Последовательность 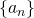 тогда и только тогда является арифметической прогрессией, когда каждый её член, начиная со второго, равен полусумме предыдущего и последующего членов:
тогда и только тогда является арифметической прогрессией, когда каждый её член, начиная со второго, равен полусумме предыдущего и последующего членов:
![\[a_n = \frac{a_{n - 1} + a_{n+1}}{2}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-e22566c22277bd1bd7cf176e1a3aeb44_l3.png)
Доказательство. По определению арифметической прогрессии для всех 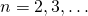
![\[d = a_n - a_{n-1} = a_{n+1} - a_n.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-dfdd3997b4b26a3453e4f2c13034914f_l3.png)
Отсюда
![\[2a_n = a_{n-1} + a_{n+1},\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-3af0a7609daafb49db541ed95c665502_l3.png)
то есть
![\[a_n = \frac{a_{n-1} + a_{n+1}}{2}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-d69430c186d9c375f08cdf8d4c92f2f4_l3.png)
Сумма первых n членов арифметической прогрессии
В качестве примера найдём сумму всех натуральных чисел от 1 до 100, то есть вычислим сумму
![\[S = 1 + 2 + 3 + \ldots + 99 + 100.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-9f7303fa1e9c8b4b190d1b54ee7b0751_l3.png)
Решение. Можно сидеть и долго складывать все числа по порядку. Но есть более простой способ. Запишем сумму этих чисел, а под ней — ту же сумму, но в обратной последовательности:
![\[\begin{array}{cccccccccc} S = & 1& + & 2& + & 3& + \ldots + &99& + &100, \\ S = &100& + &99& + &98& + \ldots + & 2& + & 1. \end{array}\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-aecfe8459224c43bd3dfeed1422f9e75_l3.png)
Теперь почленно сложим эти суммы:
![\[2S = (1 + 100) + (2 + 99) + (3 + 98) + \ldots + (100 + 1)=\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-a98ecdbfbfc46c678bfa3e46400d735e_l3.png)
![\[= \underbrace{101 + 101 + \ldots + 101}_{100} = 100 \cdot 101 = 10100.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-386faa10a670b19b43722513f8e5c186_l3.png)
Отсюда 
По легенде, школьный учитель математики, надеясь надолго занять детей, предложил им сосчитать эту сумму. Среди тех детей был будущий великий математик Карл Гаусс. Юный Гаусс быстро заметил, что попарные суммы членов с противоположных концов равны: 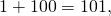
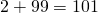 и т.д, и уже через несколько минут подошёл к учителю с ответом:
и т.д, и уже через несколько минут подошёл к учителю с ответом: 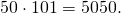
Этим же приёмом удобно воспользоваться и при вычислении суммы первых 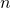
![\[a_k + a_{n+1-k} = a_1 + a_n.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-cee1494a271bc69e0c27ad7e6bf12d6c_l3.png)
Действительно,
![\[a_k + a_{n+1-k} = a_1 + d(k - 1) + a_1 + d(n-k) = \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-6cc0e805fc9a18d62b2025e576702244_l3.png)
![\[a_1 + (a_1 + d(n-1)) = a_1 + a_n.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-ac9bffab76e0d4b86c8a1f98883a2e8b_l3.png)
Сумма первых n членов арифметической прогресиии
![\[S_n = a_1 + a_2 + \ldots + a_n\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-bdc9a56644e1c4566222a62871c3195f_l3.png)
равна полусумме первого и n-ного её членов, умноженной на число членов, то есть
![\[S_n = \frac{a_1 + a_n}{2}\cdot n.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-2ec76d77a969f078b960ecccd02d4cf3_l3.png)
Доказательство. Запишем сумму  сначала в прямом порядке, а затем — в обратном:
сначала в прямом порядке, а затем — в обратном:
![\[S_n = a_1 + a_2 + \ldots + a_{n-1} + a_n,\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-7bc385557c9284e6445eb1c38871e06c_l3.png)
![\[S_n = a_n + a_{n-1} + \ldots + a_2 + a_1.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-fdb057b3a0671f4d5abb7ebb61167c98_l3.png)
Сложим почленно эти два равенства и воспользуемся тем, что 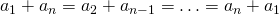 :
:
![\[2S_n = (a_1 + a_n) + (a_2 + a_{n-1}) + \ldots + (a_n + a_1) = \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-e9edabf9c6d31afe092f1476d77ec391_l3.png)
![\[=(a_1 + a_n)n.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-af5a74cb0fc1b98327f0b0e3ccba8503_l3.png)
Отсюда находим
![\[S_n = \frac{a_1 + a_n}{2}\cdot n.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-2ec76d77a969f078b960ecccd02d4cf3_l3.png)
umath.ru
Последовательности. Арифметическая и геометрическая прогрессии
Математика создает инструменты, которые помогают описывать и структурировать различные вещи, которые нас окружают. Одним из таких инструментов является числовая последовательность.
Само слово «последовательность» мы часто используем в обычной жизни. Чем последовательность отличается от произвольного набора? Тем, что в последовательности важен порядок ее элементов. Например, мы говорим про алгоритм, т. е. про последовательность действий, когда нам важно, что нужно сделать первым, что вторым и т. д. Так, мы сначала надеваем рубашку, потом – пиджак. А вот разницы, какой носок сначала надеть – левый или правый – для нас обычно нет. График дежурств по школе определяет последовательность, в которой классы должны убирать и следить за порядком в школе (см. рис. 1).

Рис. 1. График дежурств по школе определяет последовательность
А вот алфавит – это набор букв. Да, мы договорились об определенном порядке:  – первая буква алфавита,
– первая буква алфавита,  – вторая и т. д., так нам удобно его запоминать и работать с ним. Но, по сути, никакого значения этот порядок не имеет. С таким же успехом можно было считать первой буквой алфавита букву
– вторая и т. д., так нам удобно его запоминать и работать с ним. Но, по сути, никакого значения этот порядок не имеет. С таким же успехом можно было считать первой буквой алфавита букву  или
или 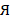 .
.
Что же такое последовательность как математический инструмент? Обратите внимание, что поскольку для последовательности важен порядок элементов, то для их нумерации можно использовать числа –  и т. д. Например,
и т. д. Например, 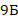 класс дежурит каждую пятую неделю: в первую, шестую и т. д. (см. рис. 2).
класс дежурит каждую пятую неделю: в первую, шестую и т. д. (см. рис. 2).

Рис. 2. Расписание дежурств
Алгоритм можно расписать по пунктам:
- надеть рубашку;
- надеть пиджак;
- …
Мы будем изучать числовые последовательности, т. е. последовательности, элементами которых являются числа.
Номер телефона можно считать числовой последовательностью:  . Пин-код кредитной карты или телефона тоже примеры числовых последовательностей:
. Пин-код кредитной карты или телефона тоже примеры числовых последовательностей: 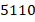 .
.
Это действительно последовательности, а не наборы чисел – если поменять местами цифры в номере телефона, то получится совершенно другой номер. А введя нужные цифры пин-кода, но в неправильном порядке, вы не разблокируете смартфон.
Приведенные выше примеры числовых последовательностей – это конечные последовательности, ведь они содержат конечное количество элементов. Могут быть и бесконечные последовательности. Ряд натуральных чисел – это простейший пример бесконечной числовой последовательности:

Поскольку одна из функций натуральных чисел – это задание порядка, то логично, что именно натуральные числа мы будем использовать для нумерации других последовательностей.
Например, последовательность простых чисел:

Первое простое число – 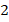 , второе простое число –
, второе простое число –  , третье –
, третье – 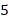 и т. д. Для удобства записи принято обозначать элементы последовательности латинскими буквами, а их номер указывать индексом. Например, в последовательности простых чисел
и т. д. Для удобства записи принято обозначать элементы последовательности латинскими буквами, а их номер указывать индексом. Например, в последовательности простых чисел 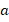 :
:

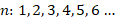
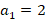

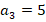
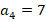


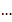
При этом элементы числовой последовательности принято называть членами последовательности.
А как можно задать числовую последовательность? Если последовательность конечная, то можно просто перечислить все ее члены. Можно описать свойства элементов последовательности. Например, «простые числа в порядке возрастания» или «последовательность домов нечетной стороны проспекта Гагарина». Есть ли еще какие-то способы задания последовательности?
Мы сказали, что члены последовательности можно нумеровать натуральными числами. Посмотрим на это с другой стороны: мы ставим в соответствие натуральному числу некоторое число:

Знакомо? Да это же определение функции! Только аргументом ее могут быть не любые действительные числа, а только натуральные. Т. е. последовательность можно задать как функцию натурального аргумента. Сравните записи:
1. 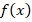 – значение функции
– значение функции 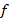 при аргументе
при аргументе  :
:

2.  – член последовательности
– член последовательности 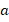 с номером
с номером  :
:

На самом деле, мы можем записать даже так:

Тогда мы увидим полное сходство с обозначением функции. Но принято номер записывать не в скобках, а нижним индексом. Поэтому дальше будем придерживаться общепринятого обозначения:

Рассмотрим последовательность, которая задана следующим образом:

Такой способ задания последовательности, с помощью формулы, называют аналитическим. Подставляя вместо  натуральные числа, мы получим члены этой последовательности:
натуральные числа, мы получим члены этой последовательности:

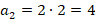

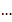
Получим последовательность четных чисел. Обратите внимание: последовательность натуральных чисел содержит последовательность четных чисел:

Т. е. кажется, что натуральных чисел больше. Но мы же только что показали, что каждому натуральному числу  мы можем поставить в соответствие четное число
мы можем поставить в соответствие четное число  . Значит, их должно быть одинаковое количество! В чем же подвох?
. Значит, их должно быть одинаковое количество! В чем же подвох?
Дело в том, что привычный нам инструмент «количество» имеет свои ограничения. Он помогает сравнивать множества с конечным набором элементов. А для бесконечных множеств уже не подходит.
Что же делать с бесконечными множествами? Вспомним, что количество мы использовали для сравнения, сопоставления элементов конечных множеств. Во множестве  больше элементов, чем во множестве
больше элементов, чем во множестве  , если мы не можем найти пару для элемента
, если мы не можем найти пару для элемента  из
из  (см. рис. 3).
(см. рис. 3).

Рис. 3. Во множестве  больше элементов, чем во множестве
больше элементов, чем во множестве 
Этот инструмент можно расширить и на бесконечные множества – если между элементами множеств можно установить взаимно однозначное соответствие, то они в каком-то смысле эквивалентны по количеству элементов. Но, т. к. термин «количество» мы оставили для конечных множеств, то для бесконечных множеств этот инструмент расширили и назвали мощность. Подробнее об этом ниже.
Мощность множества
Итак, у двух конечных множеств одинаковое количество элементов, если между их элементами можно установить взаимно однозначное соответствие. Например, 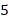 пальцев и
пальцев и 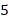 машин (см. рис. 4) (в детстве мы именно так и учились считать – загибали палец для каждого следующего элемента множества).
машин (см. рис. 4) (в детстве мы именно так и учились считать – загибали палец для каждого следующего элемента множества).

Рис. 4. У двух конечных множеств одинаковое количество элементов, если между их элементами можно установить взаимно однозначное соответствие:  пальцев –
пальцев –  машин
машин
А как сравнить количество капель в озере и количество деревьев в лесу? Понятно, что в нашем понимании оба множества можно считать бесконечными. Интуитивно мы понимаем, что количество капель в озере больше (потому что само понятие капли, в отличие от дерева, гораздо более «размытое»). Но когда мы говорим о математическом инструменте, необходимо дать строгое определение.
Обобщим идею сопоставления элементов для бесконечных множеств. Говорят, что если между элементами двух множеств можно установить взаимно однозначное соответствие, то их мощности равны (см. рис. 5).

Рис. 5. Множества с равной мощностью
Для конечных множеств мощность – это просто количество элементов ( – мощность множества):
– мощность множества):


Для бесконечных множеств за эталон берется натуральный числовой ряд:
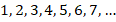
Все множества, элементы которых можно занумеровать натуральными числами, называются счетными. Если же между элементами бесконечного множества и натуральными числами нельзя установить взаимно однозначное соответствие, то такие множества называются несчетными (см. рис. 6).

Рис. 6. Множество действительных чисел – пример несчетного множества
Мы показали, что между всеми натуральными и всеми четными числами можно установить такое соответствие, значит, мощности этих множеств равны. Даже несмотря на то, что натуральных чисел «кажется, больше». Т. е. множество четных чисел тоже счетное.
Интересно, что можно установить взаимно однозначное соответствие между натуральными числами и целыми, т. е. можно пронумеровать все целые числа! Опять же, может показаться, что целых должно быть почти в 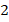 раза больше, ведь это все натуральные, столько же обратных, да еще и ноль. Но так сравнивать бесконечные множества не получится. Можно сравнивать их «мощности», и они будут равны.
раза больше, ведь это все натуральные, столько же обратных, да еще и ноль. Но так сравнивать бесконечные множества не получится. Можно сравнивать их «мощности», и они будут равны.
Покажем это: числу 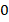 поставим в соответствие
поставим в соответствие  . Далее нумеруем поочередно: положительное, отрицательное, положительное, отрицательное.
. Далее нумеруем поочередно: положительное, отрицательное, положительное, отрицательное.



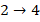

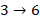

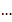
Таким образом, мы установим взаимооднозначное соответствие между целыми и натуральными числами, значит, мощности этих множеств равны. И множество целых чисел тоже счетное.
Еще более интересно то, что все рациональные числа также можно пронумеровать! Можете самостоятельно попробовать придумать, как это сделать. Т. е. множества натуральных 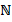 , целых
, целых 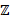 , рациональных чисел
, рациональных чисел 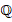 – счетные. А вот множество действительных чисел
– счетные. А вот множество действительных чисел 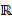 – несчетное. Можно сказать, что действительных чисел в каком-то смысле больше, чем рациональных. Для мощности множества действительных чисел даже ввели специальное название – континуум (от лат. continuum – непрерывное, сплошное).
– несчетное. Можно сказать, что действительных чисел в каком-то смысле больше, чем рациональных. Для мощности множества действительных чисел даже ввели специальное название – континуум (от лат. continuum – непрерывное, сплошное).
Как мы уже сказали, последовательность можно задать как функцию натурального аргумента. Соответственно, для работы с последовательностями нам пригодятся все те навыки, которые мы приобрели при работе с функциями. Кроме того, характеристики функций можно использовать и для описания последовательностей.
Например, возрастающая последовательность – это последовательность, у которой каждый член больше предыдущего:

И наоборот, убывающая последовательность – это последовательность, у которой каждый член меньше предыдущего:

Задание 1. Найти первый отрицательный член последовательности:

Решение.
Член последовательности должен быть отрицательным:

Решаем неравенство:


Переменная  – это номер члена последовательности, т. е. натуральное число. Нужно найти первый отрицательный член последовательности, т. е. его номер должен быть наименьшим натуральным числом, которое больше
– это номер члена последовательности, т. е. натуральное число. Нужно найти первый отрицательный член последовательности, т. е. его номер должен быть наименьшим натуральным числом, которое больше  . Это число
. Это число  , тогда:
, тогда:
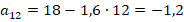
Ответ:  .
.
Задание 2. Найти номер наименьшего члена последовательности:

Решение.
Чтобы найти наименьшее значение выражения, выделим полный квадрат:

Перепишем последовательность:
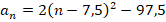
Т. к.  , то:
, то:

Т. е. минимально возможное значение  равно
равно 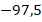 . Но достигается оно при
. Но достигается оно при  , а
, а  должно быть натуральным числом. Таким образом, член последовательности будет наименьшим при ближайших натуральных значениях
должно быть натуральным числом. Таким образом, член последовательности будет наименьшим при ближайших натуральных значениях  :
:


Проверим:
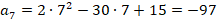
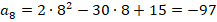
Получили одинаковые значения, именно они и будут наименьшими.
Ответ:
interneturok.ru
Арифметическая прогрессия — это… Что такое Арифметическая прогрессия?
У этого термина существуют и другие значения, см. Прогрессия.Арифмети́ческая прогре́ссия — числовая последовательность вида
- ,
то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага или разности прогрессии):
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
Арифметическая прогрессия является монотонной последовательностью. При она является возрастающей, а при — убывающей. Если , то последовательность будет стационарной. Эти утверждения следуют из соотношения для членов арифметической прогрессии.
Свойства
Общий член арифметической прогрессии
Член арифметической прогрессии с номером может быть найден по формуле
- , где — первый член прогрессии, — ее разность.
Доказательство
Характеристическое свойство арифметической прогрессии
Последовательность есть арифметическая прогрессия для ее элементов выполняется условие .
Доказательство
Необходимость:
Поскольку — арифметическая прогрессия, то для выполняются соотношения:
.
Сложив эти равенства и разделив обе части на 2, получим .
Достаточность:
Имеем, что для каждого элемента последовательности, начиная со второго, выполняется . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду . Поскольку соотношения верны при всех , с помощью математической индукции покажем, что .
База индукции :
— утверждение истинно.
Переход индукции:
Пусть наше утверждение верно при , то есть . Докажем истинность утверждения при :
Но по предположению индукции следует, что . Получаем, что .
Итак, утверждение верно и при . Это значит, что .
Обозначим эти разности через . Итак, , а отсюда имеем для . Поскольку для членов последовательности выполняется соотношение , то это есть арифметическая прогрессия.
Сумма первых членов арифметической прогрессии
Сумма первых членов арифметической прогрессии может быть найдена по формулам
- , где — первый член прогрессии, — член с номером , — количество суммируемых членов.
- , где — первый член прогрессии, — разность прогрессии, — количество суммируемых членов.
Доказательство
Сходимость арифметической прогрессии
Арифметическая прогрессия расходится при и сходится при . Причем
Доказательство
Записав выражение для общего члена и исследуя предел , получаем искомый результат.
Связь между арифметической и геометрической прогрессиями
Пусть — арифметическая прогрессия с разностью и число . Тогда последовательность вида есть геометрическая прогрессия со знаменателем .
Доказательство
Проверим характеристическое свойство для образованной геометрической прогрессии:
Воспользуемся выражением для общего члена арифметической прогрессии:
Итак, поскольку характеристическое свойство выполняется, то — геометрическая прогрессия. Ее знаменатель можно найти, например, из соотношения .
Арифметические прогрессии высших порядков
Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:
- 0, 1, 4, 9, 16, 25, 36…,
разности которых образуют простую арифметическую прогрессию с разностью 2:
- 1, 3, 5, 7, 9, 11…
Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.
Примеры
- .
См. также
Ссылки
med.academic.ru
Арифметическая прогрессия Википедия
У этого термина существуют и другие значения, см. Прогрессия.Арифмети́ческая прогре́ссия — числовая последовательность вида
- a1, a1+d, a1+2d, …, a1+(n−1)d, …{\displaystyle a_{1},\ a_{1}+d,\ a_{1}+2d,\ \ldots ,\ a_{1}+(n-1)d,\ \ldots },
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d{\displaystyle d} (шага, или разности прогрессии):
- an=an−1+d{\displaystyle a_{n}=a_{n-1}+d\quad }
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
- an=a1+(n−1)d{\displaystyle a_{n}=a_{1}+(n-1)d}
Арифметическая прогрессия является монотонной последовательностью. При d>0{\displaystyle d>0} она является возрастающей, а при d<0{\displaystyle d<0} — убывающей. Если d=0{\displaystyle d=0}, то последовательность будет стационарной. Эти утверждения следуют из соотношения an+1−an=d{\displaystyle a_{n+1}-a_{n}=d} для членов арифметической прогрессии.
ruwikiorg.ru
Арифметическая прогрессия | Онлайн калькулятор
Арифметическая прогрессия — это некая последовательность чисел, каждый следующий член которой отличается от предыдущего на одно и то же число d, называемое шаг прогрессии или разность прогрессии. Калькулятор арифметической прогрессии, используя следующие формулы, может найти первый член арифметической прогрессии , n-ный член прогрессии, найти сумму первых членов или разность.
Арифметическая прогрессия как последовательность, составленная из действительных чисел, связывает их между собой заданной закономерностью ряда. Как правило, числовой ряд начинается с того, что дан первый член арифметической прогрессии, как отправная точка. Далее каждый следующий член прогрессии получается путем прибавления к предыдущему одного и того же параметра, называемого разность арифметической прогрессии или шаг арифметической прогрессии. Если разность является положительным числом, то вся последовательность будет стремиться к плюс бесконечности, так как значения членов будут увеличиваться по мере возрастания их порядковых номеров.
Если разность арифметической прогрессии представлена отрицательным числом, каждый следующий член будет меньше предыдущего и вся последовательность будет стремиться к минус бесконечности. В некоторых случаях предел арифметической прогрессии будет конкретным числом. Это происходит, если шаг прогрессии (разность) равен нулю, тогда первый член арифметической прогрессии совпадает со всеми остальными.
Формулы арифметической прогрессии включают в себя следующие равенства:
• формула первого члена арифметической прогрессии;
• формула n-ного члена прогрессии;
• формула разности арифметической прогрессии;
• формула суммы первых членов арифметической прогрессии или суммы определенной выборки членов.
По всем формулам онлайн калькулятор рассчитывает необходимые значения, используя условия, по которым дана арифметическая прогрессия. Числа, выстроенные в симметричной последовательности, дают возможность вычислить любой член или сумму прогрессии, опираясь всего на два или три параметра в зависимости от уровня сложности задания.
allcalc.ru
Арифметическая прогрессия. Часть 1
 Прежде чем мы начнем решать задачи на арифметическую прогрессию, рассмотрим, что такое числовая последовательность, поскольку арифметическая прогрессия — это частный случай числовой последовательности.
Прежде чем мы начнем решать задачи на арифметическую прогрессию, рассмотрим, что такое числовая последовательность, поскольку арифметическая прогрессия — это частный случай числовой последовательности.
Числовая последовательность — это числовое множество, каждый элемент которого имеет свой порядковый номер. Элементы этого множества называются членами последовательности. Порядковый номер элемента последовательности обозначается индексом:
 — первый элемент последовательности;
— первый элемент последовательности;
 — пятый элемент последовательности;
— пятый элемент последовательности;
 — «энный» элемент последовательности, т.е. элемент, «стоящий в очереди» под номером n.
— «энный» элемент последовательности, т.е. элемент, «стоящий в очереди» под номером n.
Между значением элемента последовательности и его порядковым номером существует зависимость. Следовательно, мы можем рассматривать последовательность как функцию, аргументом которой является порядковый номер элемента последовательности. Другими словами можно сказать, что последовательность — это функция от натурального аргумента:

Последовательность можно задать тремя способами:
1. Последовательность можно задать с помощью таблицы. В этом случае мы просто задаем значение каждого члена последовательности.
Например, Некто решил заняться личным тайм-менеджментом, и для начала посчитать в течение недели, сколько времени он проводит ВКонтакте. Записывая время в таблицу, он получит последовательность, состоящую из семи элементов:

В первой строке таблицы указан номер дня недели, во второй — время в минутах. Мы видим, что  , то есть в понедельник Некто провел ВКонтакте 125 минут,
, то есть в понедельник Некто провел ВКонтакте 125 минут,  , то есть в четверг — 248 минут, а
, то есть в четверг — 248 минут, а  , то есть в пятницу всего 15.
, то есть в пятницу всего 15.
2. Последовательность можно задать с помощью формулы n-го члена.
В этом случае зависимость значения элемента последовательности от его номера выражается напрямую в виде формулы.
Например, если  , то
, то



Чтобы найти значение элемента последовательности с заданным номером, мы номер элемента подставляем в формулу n-го члена.
То же самое мы делаем, если нужно найти значение функции, если известно значение аргумента. Мы значение аргумента подставляем вместо  в уравнение функции:
в уравнение функции:
Если, например,  , то
, то 
Ещё раз замечу, что в последовательности, в отличие от произвольной числовой функции, аргументом может быть только натуральное число.
3. Последовательность можно задать с помощью формулы, выражающей зависимость значения члена последовательности с номером n от значения предыдущих членов. В этом случае нам недостаточно знать только номер члена последовательности, чтобы найти его значение. Нам нужно задать первый член или несколько первых членов последовательности.
Например, рассмотрим последовательность  ,
, 
Мы можем находить значения членов последовательности один за другим, начиная с третьего:



То есть каждый раз, чтобы найти значение n-го члена последовательности, мы возвращаемся к двум предыдущим. Такой способ задания последовательности называется рекуррентным, от латинского слова recurro — возвращаться.
Теперь мы можем дать определение арифметической прогрессии. Арифметическая прогрессия — это простой частный случай числовой последовательности.
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

Число  называется разностью арифметической прогрессии. Разность арифметической прогрессии может быть положительной, отрицательной, или равной нулю.
называется разностью арифметической прогрессии. Разность арифметической прогрессии может быть положительной, отрицательной, или равной нулю.
Если 
 , то каждый член арифметической прогрессии больше предыдущего, и прогрессия является возрастающей.
, то каждый член арифметической прогрессии больше предыдущего, и прогрессия является возрастающей.
Например, 2; 5; 8; 11;… 
Если 
 , то каждый член арифметической прогрессии меньше предыдущего, и прогрессия является убывающей.
, то каждый член арифметической прогрессии меньше предыдущего, и прогрессия является убывающей.
Например, 2; -1; -4; -7;… 
Если  , то все члены прогрессии равны одному и тому же числу, и прогрессия является стационарной.
, то все члены прогрессии равны одному и тому же числу, и прогрессия является стационарной.
Например, 2;2;2;2;…
Основное свойство арифметической прогрессии:
Посмотрим на рисунок.
Мы видим, что
 , и в то же время
, и в то же время

Сложив эти два равенства, получим:
 .
.
Разделим обе части равенства на 2:

Итак, каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:

Больше того, так как
 , и в то же время
, и в то же время
 , то
, то
 , и, следовательно,
, и, следовательно,
 Каждый член арифметической прогрессии, начиная с
Каждый член арифметической прогрессии, начиная с 
 , равен среднему арифметическому двух равноотстоящих.
, равен среднему арифметическому двух равноотстоящих.
Формула  го члена.
го члена.
Мы видим, что для членов арифметической прогрессии выполняются соотношения:



…
и, наконец, 
Мы получили формулу n-го члена.

ВАЖНО! Любой член арифметической прогрессии можно выразить через  и
и  . Зная первый член и разность арифметической прогрессии можно найти любой её член.
. Зная первый член и разность арифметической прогрессии можно найти любой её член.
Сумма n членов арифметической прогрессии.
В произвольной арифметический прогрессии суммы членов, равноотстоящих от крайних равны между собой:



Рассмотрим арифметическую прогрессию, в которой n членов. Пусть сумма n членов этой прогрессии равна  .
.
Расположим члены прогрессии сначала в порядке возрастания номеров, а затем в порядке убывания:

Сложим попарно:
Сумма в каждой скобке равна  , число пар равно n.
, число пар равно n.
Получаем:


Итак, сумму n членов арифметической прогрессии можно найти по формулам:
Рассмотрим решение задач на арифметическую прогрессию.
1. Последовательность задана формулой n-го члена:  . Докажите, что эта последовательность является арифметической прогрессией.
. Докажите, что эта последовательность является арифметической прогрессией.
Докажем, что разность между двумя соседними членами последовательности равна одному и тому же числу.


Мы получили, что разность двух соседних членов последовательности не зависит от их номера и является константой. Следовательно, по определению, эта последовательность является арифметической прогрессией.
2. Дана арифметическая прогрессия -31; -27;…
а) Найдите 31 член прогрессии.
б) Определите, входит ли в данную прогрессию число 41.
а) Мы видим, что  ;
; 
Запишем формулу n-го члена для нашей прогрессии.
В общем случае 
В нашем случае  , поэтому
, поэтому 
Получаем:

б) Предположим, что число 41 является членом последовательности. Найдем его номер. Для этого решим уравнение:




Мы получили натуральное значение n, следовательно, да, число 41 является членом прогрессии. Если бы найденное значение n не было бы натуральным числом, то мы бы ответили, что число 41 НЕ является членом прогрессии.
3. а) Между числами 2 и 8 вставьте 4 числа так, чтобы они вместе с данными числами составляли арифметическую прогрессию.
б) Найдите сумму членов полученной прогрессии.
а) Вставим между числами 2 и 8 четыре числа:

Мы получили арифметическую прогрессию, в которой 6 членов. 
Найдем разность этой прогрессии. Для этого воспользуемся формулой n-го члена:


Теперь легко найти значения чисел:
3,2; 4,4; 5,6; 6,8
б) 
Ответ: а) да; б) 30
4. Грузовик перевозит партию щебня массой 240 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено на двенадцатый день, если вся работа была выполнена за 15 дней.
По условию задачи количество щебня, которое перевозит грузовик, каждый день увеличивается на одно и то же число. Следовательно, мы имеем дело с арифметической прогрессией.
Сформулируем эту задачу в терминах арифметической прогрессии.
За первый день было перевезено 2 тонны щебня: [pmath size=14]a_1=2[/pmath].
Вся работа была выполнена за 15 дней:  .
.
Грузовик перевозит партию щебня массой 240 тонн: 
Нам нужно найти  .
.
Сначала найдем разность прогрессии. Воспользуемся формулой суммы n членов прогрессии.

В нашем случае:




Найдем  по формуле n-го члена:
по формуле n-го члена:

Ответ: 24.
Продолжение статьи — решение основных типов задач на арифметическую прогрессию — читайте здесь.
И.В. Фельдман, репетитор по математике.

ege-ok.ru