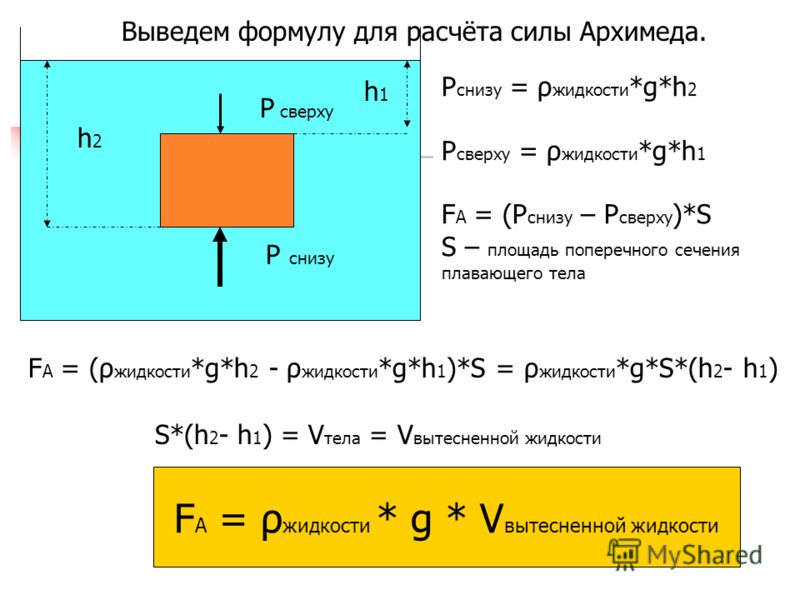
Закон Архимеда для ускоренно движущихся тел
С. Н. Манида
Установлена зависимость силы гидростатического давления (силы Архимеда) от плотности свободного тела, погруженного в жидкость.
1. Закон Архимеда для неподвижных тел
Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.
Попробуем восстановить ход рассуждений Архимеда и вывести его закон.
На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис.
Отсюда следует выражение для силы гидростатического давления: F=-Vg.
Мы нашли силу, действующую на поверхность жидкости, заполняющей объем V. Но поверхность тела, погруженного в жидкость, совпадает с поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное выражение и есть «выталкивающая’’ сила — сила Архимеда
F Арх = -Vg. (*)
2. Неприменимость закона Архимеда для случая свободных тел
Казалось бы, решение задач с использованием этого закона не должно вызывать затруднений. Однако неверные решения отдельных задач на закон Архимеда встречаются не только у школьников, но и в ряде задачников.
Дело в том, что при использовании этого (как и любого другого) закона надо всегда помнить, как и для каких ситуаций он выводился. Так, например, мы вычисляли силу гидростатического давления, действующую на поверхность неподвижного объема жидко сти, находящейся в равновесии, т. е. имеющей нулевые скорость и ускорение. Следовательно, и использовать выведенное выражение для силы Архимеда можно только в тех случаях, когда и скорость, и ускорение тела равны нулю.
Покажем, что применение этого закона в других ситуациях абсолютно неправомочно, так как приводит к неверным результатам.
Рассмотрим легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= Vg и сила натяжения нити T, а вверх — сила гидростатического давления
3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= Vg и сила натяжения нити T, а вверх — сила гидростатического давления
F=FАрх=- Vg, (*)
где — плотность тела, — плотность жидкости. Условие равновесия тела
-Vg +T+Vg =0. (1)
Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вве рх (всплывать) с некоторым ускорением
F+ V g = V a. (2)
Предположив, что в этом случае можно использовать закон Архимеда, подставим — Vg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение
a = — g (-)/ (3)
Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.
Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости).
3. Сила гидростатического давления для случая свободных тел
Точный расчет гидростатического давления на поверхность ускоренно движущегося тела возможен только с применением аппарата математической физики, а ответ представим в аналитическом виде лишь для некоторых частных случаев. Уравнения, описывающие движение тела в жидкости, были впервые получены профессором Петербургского университета Леонардом Эйлером в середине XVIII века. Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):
Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):
и, с учетом (2), ускорение тела имеет вид:
(5)4. Выводы
Сравнивая выражения (4) и (*) видим, что они совпадают только при = . Зависимость силы гидростатического давления, действующей на свободное тело, от его плотности представлена на графике рис. 4 в сравнении со стандартным выражением для силы Архимеда Vg:
Из графика на рис.4 видно, что для малых плотностей тела сила давления убывает до нуля, а при увеличении плотности эта сила стремится к величине 1,5Vg.
На следующем графике (рис. 5) приведена зависимость ускорения свободного тела в жидкости от его плотности [уравнение (5)]. Для сравнения приведен график ускорения, получающийся непосредственн о из закона Архимеда [уравнение (3)]
Из этого графика видно, что даже бесконечно легкий шарик всплывает с конечным ускорением, равным -2g, а тяжелые тела тонут с ускорением, меньшим, чем это следует из закона Архимеда.
Глава 9. Гидростатика
Для решения задач на гидростатику необходимо знать определения плотности и давления, уметь находить давление в покоящейся жидкости, возникающее благодаря притяжению этой жидкости к Земле (гидростатическое давление), а также находить силы, с которыми жидкости действуют на погруженные в них тела (силу Архимеда). Кратко сформулируем эти определения и законы.
Плотностью тела называется отношение
(9.1) |
где — масса тела, — его объем. Очевидно, отношение (9.1) имеет смысл массы единицы объема тела. Если тело однородно, то плотность (9.1) является характеристикой не тела, а вещества, из которого оно состоит. Действительно, для тел, состоящих из одного и того же вещества масса пропорциональна объему, и отношение (9.1) одинаково у всех этих тел.
Очевидно, отношение (9.1) имеет смысл массы единицы объема тела. Если тело однородно, то плотность (9.1) является характеристикой не тела, а вещества, из которого оно состоит. Действительно, для тел, состоящих из одного и того же вещества масса пропорциональна объему, и отношение (9.1) одинаково у всех этих тел.
Для характеристики воздействия жидкости или газа на стенки сосудов вводят понятие давления жидкости или газа, которое определяется как отношение силы , действующей на элемент стенки сосуда со стороны жидкости или газа, к величине площади этого элемента :
(9.2) |
Важным свойством давления является то обстоятельство, что хотя оно и определяется через элемент площади стенки сосуда, от этого элемента давление (9.2) не зависит, а является характеристикой только жидкости или газа. Действительно, сила, действующая со стороны жидкости на элемент площади дна сосуда или стенки сосуда, пропорциональна площади этого элемента, и потому отношение (9.2) от не зависит. Отметим, что хотя давление и определяется через векторную величину — силу, давление — величина не векторная. Как показывает опыт, отношение (9.2) не зависит не только от величины площадки , но и от ее ориентации в пространстве. Другими словами, жидкость, будучи сжатой, оказывает воздействие во всех направлениях. Последнее утверждение и говорит о невекторном характере давления и называется законом Паскаля.
В жидкости, находящейся в каком-либо сосуде в поле силы тяжести, благодаря ее притяжению к Земле, возникает давление. Это давление называется гидростатическим. Можно доказать, что гидростатическое давление жидкости не зависит от формы сосуда, в котором она находится, а зависит только от глубины. Гидростатическое давление жидкости плотности на глубине равно
(9.3) |
где — ускорение свободного падения. Если на поверхность жидкости действует атмосферный воздух, то давление жидкости на глубине будет складываться из атмосферного давления и гидростатического давления (9.3).
Если на поверхность жидкости действует атмосферный воздух, то давление жидкости на глубине будет складываться из атмосферного давления и гидростатического давления (9.3).
Благодаря зависимости гидростатического давления жидкости от глубины возникает своеобразный эффект выталкивания тел, погруженных в жидкость, из этой жидкости. Действительно, в жидкости, находящейся в поле силы тяжести, возникает гидростатическое давление, и жидкость оказывает воздействие на поверхность тела, опущенного в жидкость. При этом силы, действующие на боковые поверхности тела, компенсируют друг друга. Однако из-за зависимости гидростатического давления от глубины, сила, действующая на более глубокую (нижнюю) поверхность тела, больше силы, действующей на верхнюю поверхность (см. рисунок), и на тело действует результирующая сила, направленная вертикально вверх. Эта сила называется выталкивающей силой или силой Архимеда. Можно доказать, что на тело, целиком погруженное в жидкость, действует выталкивающая сила
(9.4) |
где — плотность жидкости, — объем тела. Если тело погружено в жидкость не целиком, то выталкивающая сила также определяется формулой (9.4), но вместо объема тела в нее входит объем погруженной в жидкость части тела.
С помощью формулы (9.4) можно установить условие плавания тел. Тело будет плавать, если сила Архимеда будет больше действующей на тело силы тяжести
где — плотность тела. Отсюда получаем, что тело плавает, если плотность жидкости больше плотности тела
(9.5) |
Рассмотрим теперь задачи.
В задаче 9.1.1 с использованием формулы (9.3) для гидростатического давления находим
(ответ — 4).
Поскольку высота уровней жидкости в сосудах (в задаче 9.1.2) и их плотности одинаковы, то давление жидкости около дна обоих сосудов одинаково (ответ 3).
В задаче 9.1.3 давление жидкости около дна сосудов одинаково (одинаковы плотности и уровень жидкостей), поэтому сила, действующая на дно, больше для того сосуда, площадь дна которого больше, а меньше для того, площадь дна которого меньше. Поэтому (правильный ответ — 2).
Чтобы найти силу, действующую на небольшую поверхность внутри жидкости, нужно найти гидростатическое давление жидкости на той глубине, на которой находится рассматриваемая поверхность, и умножить это давление на площадь поверхности. Поэтому для крана из задачи 9.1.4 получаем
(ответ 4).
Бытовой насос (задача 9.1.5) поднимает воду благодаря создаваемому им избыточному давлению. Ясно, что вода в трубках насоса будет подниматься до тех пор, пока ее гидростатическое давление не компенсирует избыточное давление насоса. Поэтому насос сможет поднять воду на следующую высоту
где — избыточное давление, созданное насосом, — плотность воды, — ускорение свободного падения (правильный ответ — 3).
Поскольку бруски в задаче 9.1.6 изготовлены из одинакового материала, у них одинаковые плотности, и, следовательно, отношение их масс равно отношению их объемов. А поскольку объем второго бруска вчетверо больше объема первого, то и его масса вчетверо больше массы первого, т.е. равна 40 г (ответ 3).
Пусть размер меньшего ребра бруска в задаче 9.1.7 — . Тогда размеры остальных сторон — и . Следовательно, площади граней бруска равны , и . Поэтому давления бруска на стол, когда он лежит на разных гранях, равны (начиная с наименьшего):
т. е. относятся друг к другу так же, как и длины сторон 1:2:3 (ответ 1).
е. относятся друг к другу так же, как и длины сторон 1:2:3 (ответ 1).
В сообщающихся сосудах жидкость занимает такое положение, что ее давление в обоих коленах одинаково. Поэтому в задаче 9.1.8 имеем с использованием формулы для гидростатического давления
Отсюда находим
(правильный ответ — 4).
Поскольку плотность натрия 950 кг/м3 (задача 9.1.9) меньше плотности воды 1000 кг/м3, то натрий плавает на поверхности воды (ответ 1).
На льдину (задача 9.1.10) действуют сила тяжести и сила Архимеда. Условие равновесия льдины дает
(1) |
где — плотность воды, — объем погруженной в воду части льдины, — ее масса. Поскольку, где — плотность льда, — объем льдины, из формулы (1) получаем
Отсюда находим, что отношение объема погруженной в воду части льдина к ее объему равно отношению плотностей льда и воды
(ответ 2). Таким образом, девять десятых частей плавающей льдины находятся под водой.
Поскольку тело в задаче 9.2.1 плавает в жидкости, выталкивающая сила Архимеда равна действующей на тело силе тяжести — 10 Н (ответ 1).
Весом тела называется сила, с которой тело действует на опору (сила реакции опоры). На тело, полностью погруженное в воду, действуют сила тяжести , выталкивающая сила Архимеда и сила реакции. Для силы реакции (веса тела) из условия равновесия тела имеем
где и — плотности жидкости и тела, — объем тела (обратим внимание читателя на то, что согласно этой формуле вес тела в жидкости уменьшается). Отсюда находим
Отсюда находим
(задача 9.2.2 — ответ 3).
Из условия равновесия коробки, плавающей на поверхности воды (задача 9.2.3), следует, что сила тяжести равна силе Архимеда , где — масса тела, — плотность воды, — объем погруженной части коробки, который можно выразить через площадь дна коробки и глубину его погружения в воду см3. Отсюда получаем для массы коробки = 500 г (ответ 2).
При решении задачи 9.2.4 школьники часто допускают ошибку, говоря, что выталкивающая сила равна нулю, так как шар, наполненный воздухом, находясь в воздухе, «всплывать» не будет. Последнее утверждение, конечно, правильно, а первое — нет. Шар, наполненный воздухом, не «всплывает» в воздухе не потому, что выталкивающая сила не действует, а потому, что она меньше силы тяжести. Выталкивающая сила действует на тело со стороны жидкости или газа и никак не может зависеть от того, что внутри этого тела, воздух или, напрмер, гелий, с которым шар всплывал бы. Для выталкивающей силы имеем согласно закону Архимеда Н (ответ 1).
На поплавок из задачи 9.2.5 действуют силы: тяжести , Архимеда , натяжения лески (см. рисунок). Используя стандартное выражение для силы Архимеда (9.4), получаем из условия равновесия поплавка
где — плотность воды, и — масса и объем поплавка. Выражая массу поплавка через его плотность и объем и учитывая, что по условию плотность воды вдвое больше плотности поплавка , получим 10 Н (ответ 1).
В задаче 9.2.6 умышленно дано много лишних данных. Поскольку и в воде, и в керосине мяч плавает, то архимедова сила и в том, и в другом случае уравновешивает силу тяжести мяча (ответ 2).
Несмотря на то, что тело в задаче 9.2.7 не касается дна и стенок сосуда, суммарная сила, действующая на левую чашку весов, увеличится.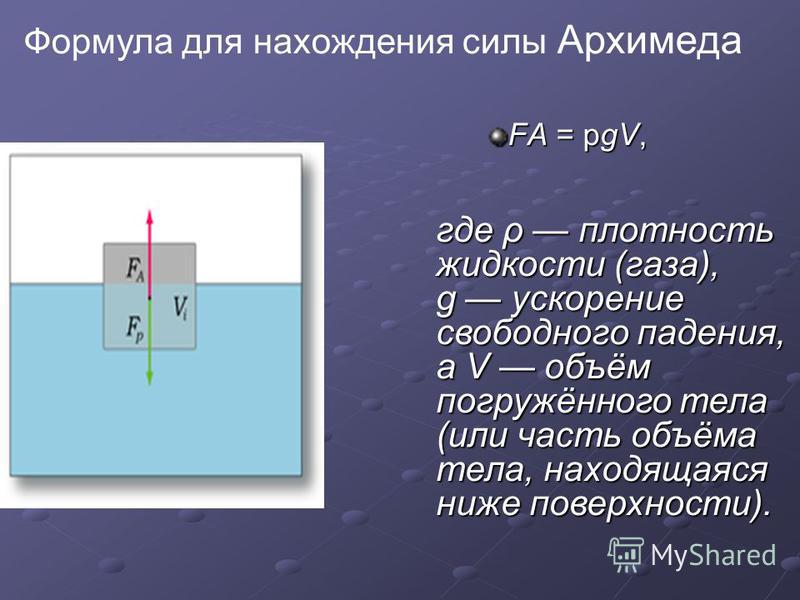 Действительно, при опускании тела в воду возникает сила Архимеда, действующая со стороны воды на тело, но при этом и тело действует на воду, причем эта сила направлена вертикально вниз и равна силе Архимеда. Чтобы весы остались в равновесии на правую чашку весов надо положить такой груз, сила тяжести которого равна этой силе, т.е. груз с массой , где — плотность воды, — объем тела. А поскольку плотность тела по условию вчетверо больше плотности воды, то (ответ 1).
Действительно, при опускании тела в воду возникает сила Архимеда, действующая со стороны воды на тело, но при этом и тело действует на воду, причем эта сила направлена вертикально вниз и равна силе Архимеда. Чтобы весы остались в равновесии на правую чашку весов надо положить такой груз, сила тяжести которого равна этой силе, т.е. груз с массой , где — плотность воды, — объем тела. А поскольку плотность тела по условию вчетверо больше плотности воды, то (ответ 1).
Для нахождения давления жидкости, в которой плавают те или иные тела, существует следующий прием. Если мысленно удалить тело из жидкости и заполнить освободившееся место той же жидкостью, то силы, действующие со стороны жидкости на стенки сосуда не изменяться. Действительно, на плавающее тело со стороны жидкости и со стороны тела на жидкость действует сила , где — плотность жидкости, — объем погруженной в жидкость части тела. Таким образом, тело действует на жидкость с той же силой, с которой на нее действовала бы жидкость, занимающая объем погруженной в воду части тела. Поэтому если вытащить тело из жидкости и заполнить освободившееся место жидкостью, то не меняется уровень жидкости, не меняются также все силы, действующие внутри жидкости. Поэтому если в жидкости плавает тело, то независимо от параметров этого тела (массы, плотности, объема), давление жидкости на глубине равно , причем отсчитывается от поверхности жидкости с плавающим в ней телом. Поэтому в задаче 9.2.8 надо найти, на сколько поднимется уровень воды в сосуде, а затем и связанное с этим повышением уровня избыточное гидростатическое давление около дна. Очевидно, что в цилиндрическом сосуде площадью сечения уровень воды поднимется на такую величину , что , где — объем погруженной в воду части тела. Находя величину из условия равновесия тела и закона Архимеда, получим . Поэтому гидростатическое давление воды около дна вырастет на величину (ответ 1).
Из условия равновесия плавающего тела следует, что его масса равна массе воды в объеме погруженной части тела.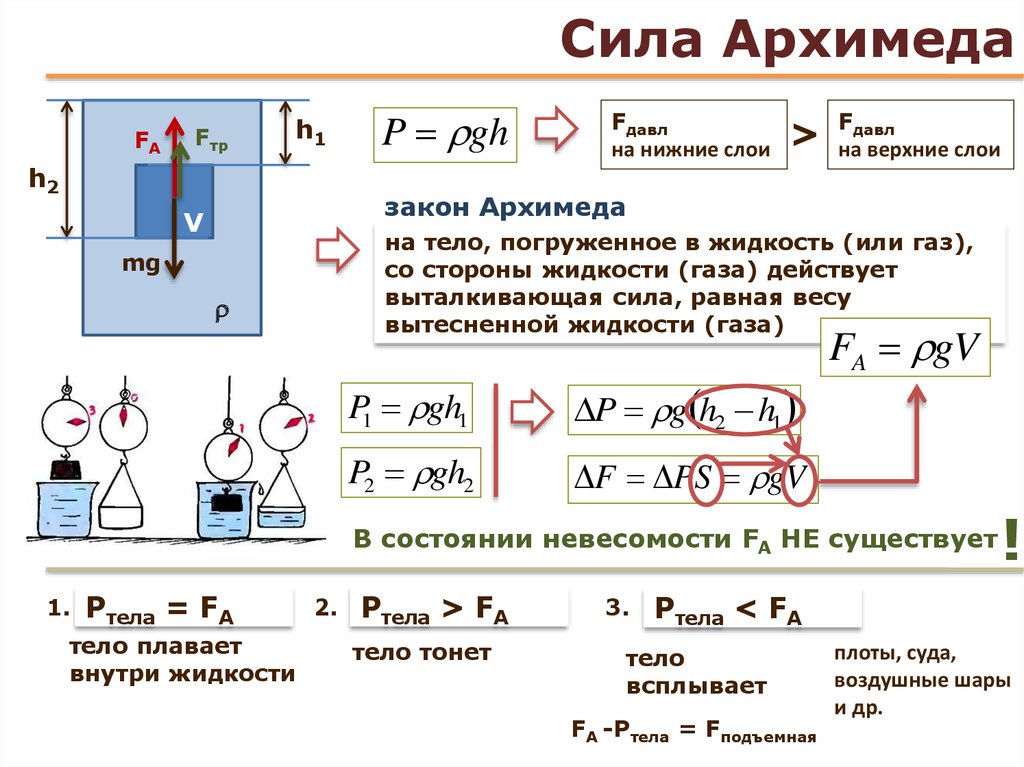 . Поэтому суммарная масса воды и деревянного тела в одном ведре и суммарная масса воды и пенопластового тела в другом в задаче 9.2.9 равна массе воды в полном ведре, т.е. одинакова в обоих ведрах. Поэтому правильный ответ в этой задаче — 3.
. Поэтому суммарная масса воды и деревянного тела в одном ведре и суммарная масса воды и пенопластового тела в другом в задаче 9.2.9 равна массе воды в полном ведре, т.е. одинакова в обоих ведрах. Поэтому правильный ответ в этой задаче — 3.
Когда внутрь плиты из задачи 9.2.10 вставляют более плотное тело, возникает дополнительное гравитационное взаимодействие между жидкостью и плитой. Если до этого на каждый элемент жидкости действовала гравитационная сила, направленная вертикально вниз, то после этого возникает дополнительная сила, направленная к центру тела (см. рисунок, на котором нарисованы силы, действующие на выделенный элемент жидкости). К каким последствиям для расположения жидкости на плите это приведет? Легко сообразить, что уровень жидкости в области над телом повысится. Действительно, поверхность жидкости всегда расположена перпендикулярно приложенным силам (иначе жидкость будет течь), поэтому она расположится так, как показано на рисунке. Другими словами, более массивное тело, вставленное внутрь плиты, благодаря дополнительному гравитационному взаимодействию «натянет» жидкость со всех сторон, и ее уровень над телом поднимется. Поэтому правильный ответ в задаче — 3.
Чему равна выталкивающая сила?
☰
Выталкивающую силу, или силу Архимеда, можно вычислить. Особенно легко это сделать для тела, стороны которого прямоугольники (прямоугольного параллелепипеда). Например, такую форму имеет брусок.
Поскольку боковые силы давления жидкости можно не учитывать, так как они взаимно уничтожаются (их равнодействующая равна нулю), то рассматриваются только силы давления воды, действующие на нижнюю и верхнюю поверхности. Если тело не полностью погружено в воду, то есть только сила давления воды, действующая снизу. Она единственная, которая создает выталкивающую силу.
Давление жидкости на глубине h определяется формулой:
p = ρgh
Сила давления определяется формулой:
F = pS
Заменив давление во второй формуле на равную ему правую часть из первой формулы, получим:
F = ρghS
Это и есть сила давления жидкости, действующая на поверхность тела на определенной глубине.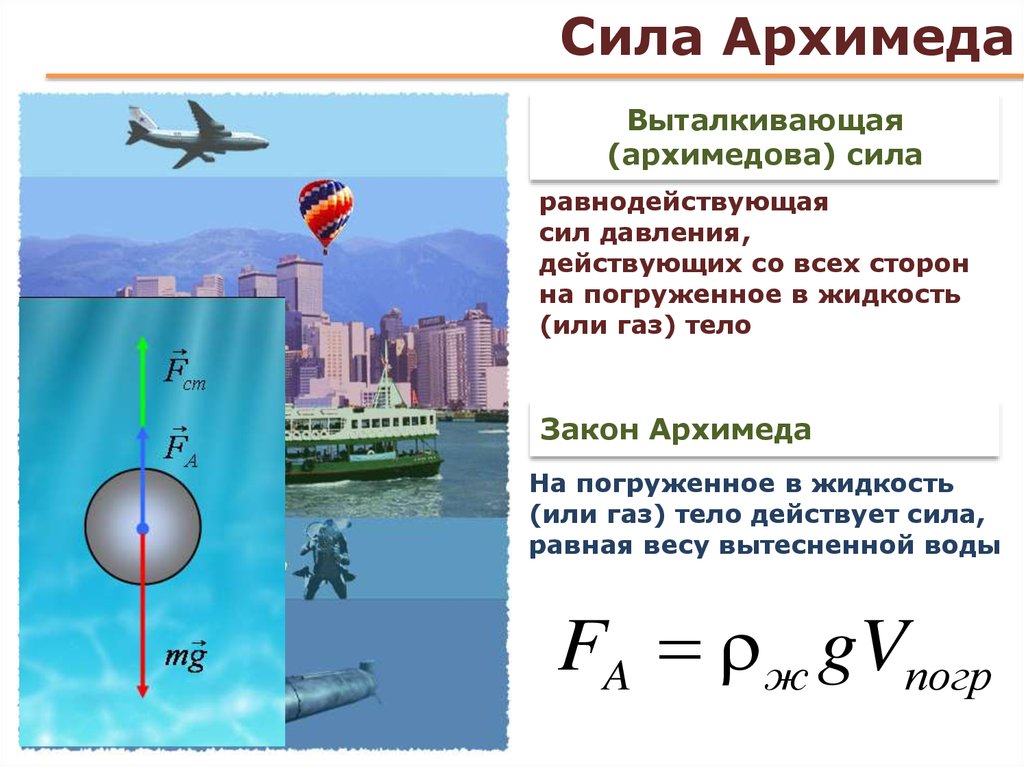 Если тело плавает на поверхности, то эта сила будет выталкивающей силой (силой Архимеда). h здесь определяется высотой подводной части тела. В таком случае формулу можно записать так: FA = ρghS. Тем самым подчеркнув, что речь идет о силе Архимеда.
Если тело плавает на поверхности, то эта сила будет выталкивающей силой (силой Архимеда). h здесь определяется высотой подводной части тела. В таком случае формулу можно записать так: FA = ρghS. Тем самым подчеркнув, что речь идет о силе Архимеда.
Произведение высоты (h) погруженной в воду части прямоугольного бруска на площадь его основания (S) — это объем (V) погруженной части этого тела. Действительно, чтобы найти объем параллелепипеда надо перемножить его ширину (a), длину (b) и высоту (h). Произведение ширины на длину есть площадь основания (S). Поэтому в формуле мы можем заменить произведение hS на V:
FA = ρgV
Теперь обратим внимание на то, что ρ — это плотность жидкости, а V — это объем погруженного тела (или части тела). Но ведь тело, погружаясь в жидкость, вытесняет из нее объем жидкости, равный погруженному телу. То есть, если погрузить в воду тело объемом 10 см3, то оно вытеснит 10 см3 воды. Конечно, этот объем воды скорее всего не выскочит из емкости, заменившись объемом тела. Просто уровень воды в емкости поднимется на 10 см3.
Поэтому в формуле FA = ρgV мы можем иметь в виду не объем погруженного тела, а объем вытесненной телом воды.
Вспомним, что произведение плотности (ρ) на объем (V) — это масса тела (m):
m = ρV
В таком случае формулу, определяющую выталкивающую силу, можно записать так:
FA = mg
Но ведь произведение массы тела (m) на ускорение свободного падения (g) есть вес (P) этого тела. Тогда получается такое равенство:
FA = P
Таким образом, сила Архимеда (или выталкивающая сила) равна по модулю (численному значению) весу жидкости в объеме, равном объему погруженного в нее тела (или его погруженной части). Это и есть закон Архимеда.
Если тело в виде бруска полностью погружено в воду, то выталкивающую силу для него определяет разность между силой давления воды сверху и силой давления снизу. Сверху на тело давит сила, равная
Сверху на тело давит сила, равная
Fверх = ρghверхS,
а снизу —
Fниз = ρghнизS,
Тогда мы можем записать
FA = ρghнизS – ρghверхS = ρgS(hниз — hверх)
hверх – это расстояние от кромки воды до верхней поверхности тела, а hниз — это расстояние от кромки воды до нижней поверхности тела. Их разность есть высота тела. Следовательно,
FA = ρghS, где h — это высота тела.
Получилось то же самое, что и для частично погруженного тела, хотя там h — это высота части тела, находящейся под водой. В том случае уже было доказано, что FA = P. То же самое выполняется и здесь: выталкивающая сила, действующая на тело, равна по модулю весу вытесненной им жидкости, которая равна по объему погруженному телу.
Обратите внимание, что вес тела и вес жидкости одинаковых объемов чаще всего разный, так как у тела и жидкости чаще всего разные плотности. Поэтому нельзя говорить, что выталкивающая сила равна весу тела. Она равна весу жидкости, объемом равному телу. Причем весу по модулю, так как выталкивающая сила направлена вверх, а вес вниз.
|
Сценарий открытого урока. Физика. 7 класс. Закон Архимеда. |
|||
|
Этап урока. (номер слайда)
|
Контрольные вопросы. Краткое содержание. |
Действие учащихся. Примерные ответы. |
Контроль Времени (мин) |
|
1. Организационная часть. |
— Приготовились к занятию. Подровнялись. Настроились на занятие. Здравствуйте. Присаживайтесь. — Староста готовит список отсутствующих. |
Подготовка к занятию. Приветствие. |
1 |
|
2. проверка готовности Д/З (Слайды 2-4) |
Обозначьте тему прошлого урока Вопросы: 1. Какое действие оказывают жидкости и газа на погруженное в них тело? 2. Обозначьте направление действующих на тело сил и укажите результирующий вектор силы. 3.Как вычислить величину выталкивающей силы? Расчетная формула. Связь с весом жидкости.(вывод формулы) 4. Как экспериментально можно обнаружить выталкивающую силу, действующую на помещенное в жидкость тело? |
— действие выт. Силы на погруженное в жидкость тело — выталкивающее — делают рисунок на доске — на доске расчетная формула — опыт по обнаружению силы Словесно либо наглядно |
8 |
|
3.Цели урока (слайд 5) |
— итак, вместе мы вспомнили физическую природу возникновения выталкивающей силы, действующею со стороны жидкости или газа на погруженное в них тело. Считается, что данную силу открыл древнегреческий ученый, философ, математик — Архимед. И сила получила название в честь своего первооткрывателя – Архимедова сила. Сейчас откройте тетради. На полях – дату. Тема сегодняшнего урока сила Архимеда. Закон Архимеда. Что это за сила? Отлично, теперь следует установить цели урока, чтобы исследовать силу архимеда на практике. К примеру, мы изучили ее в теории, а как она выглядит на практике? Какую цель поставим? Данная сила не имеет постоянного значения и в различных условиях среды и на разные тела она действует не одинаково. А следует ли знать, где возможно применять полученные знания?? Какую задачу поставим здесь перед собой? И последнее, собрав информацию из наших исследований исследованию, где стоит ее применять? В рамках предмета физики. И это еще одна наша задача урока. |
Обсуждение целей Проводят необходимые записи в тетрадь Это выталкивающая сила обнаружить наличие силы, выталкивающей тело из жидкости на опытах; установить от каких факторов она зависит; обозначить области применения Архимедовой силы; применить полученные знания для решения различных типов задач |
1 |
|
4. ОНЗ (слайды 6 — 13) |
— Архимедова сила. (слайды 6) — Сообщение учащихся Легенда об Архимеде.(слайд 7-10 история) Опыт и вывод по легенде (слайд 11-13) |
— запись в тетрадь -сообщение учащегося «Легенда об Архимеде» -записывают выводы опытов |
8 |
|
5. Опытные установки Слайды 14-15 |
Слайд 18 изменение веса тела Слайд 19 опыт с ведерком |
Участвуют в обсуждении. Помогают проводить анализ проводимым опытам |
5 |
|
6. ОНЗ (Слайд 16-18 ) |
следствие опытов Закон Архимеда, сила Архимеда. |
Записывают выводы по проделанным опытам |
5 |
|
7 выводы |
Слайд 19 — перед нами список параметров системы. Оцените зависимость архимедовой силы от перечисленных пунктов. Слайд 20 (ответ) Слайд 21 повторительный вывод |
Анализируют и расставляют зависимость силы. Записи проводят в рабочую тетрадь |
2 |
|
8. область применения выталкивающей силы |
Слайд 22 Демонстрация воздушного шара с гелием. -давайте обсудим и определим – где возможно применение архимедовой силы. |
Аэродинамика (летательные аппараты) Гидродинамика (судоходство) |
1 |
|
9. Патриотическое воспитание |
Слайд 23-24 Перед нами портреты ученых. Российских. Внесших значимый вклад в развитие гидро-аэродинамики. Существует даже такое понятие – эпоха Бернулли-Эйлера. Это обоснованно большим прогрессом развитии науки в области гидро-аэродинамики. Стоит отметить вклад таких деятелей как Можайский Александр Федорович и Циолковский Константин Эдуардович. |
Записывают необходимую информацию, дополняют. |
1 |
|
10. применение знаний на практике. (Слайды 25-30) |
— итак, пред нами ряд фотоиллюстраций. Что вы видите с точки зрения физики? Где возможно такое действие? А в нашем регионе? Предлагаю рассчитать выталкивающую силу в данных озерах. Что для этого нужно знать? Используем дополнительную информацию. |
Действие выталкивающей силы. В соленой воде. Море. Мертвое море. озеро Эльтон. озеро Баскунчак. Плотность воды. Объем человека. |
2 |
|
11. качественные задачи |
Слайды 31-34 |
1) Одинаковы 2) Лед, дерево, пробка 3) Сила Архимеда и сила тяжести 4) 20 Н |
4 |
|
12. СЛАЙД 35 |
Что вы узнали сегодня на уроке? Чему научились? Что для вас было наиболее сложным? |
1 |
|
|
13. домашнее задание выставление оценок. СЛАЙД 36 |
§ 50, 51, упр.26 (3-5), Читать раздел «Это интересно». |
1 |
|
|
Итого: |
40 |
||
СИЛА 7 класс закон Архимеда физика Перышкин. Закон назван честь древнегреческого ученого Архимеда, жившего в 3 веке до нашей эры. Еще одна формула для определения Архимедовой силы:. .. Закон Архимеда, формула и примеры решений. 12 фев 2016 СИЛА 7 класс закон Архимеда физика Перышкин тело из жидкости и как ее найти по формуле, решаются задачи.. .. Вычисление силы Архимеда. Архимеда. Основные понятия Определяется сила трения по формуле: Специальной формулы для нахождения этой силы нет. Обозначают ее. .. силы Архимеда. 27 фев 2013 2 Сила Архимеда: Fа рgV 3 для расчета плотности вещества шара: р V m 4 Формула силы земного притяжения F mg. .. Подъемная выталкивающая сила, Закон Архимеда Формулы и. Роль силы давления может играть любая вес тела, деформирующий опору сила, прижимающая Внимание! Эта формула применима всегда!. .. Давление. Архимедова сила. Объединение учителей Санкт. 29 ноя 1989 то, первых, сила Архимеда, вообще говоря, остается равной нулю, и, во вторых, она уже не описывается простой формулой 4.. .. Архимедова сила, формулы. 2 июл 2019 Однако эта формула хорошо работает с объектами простой формы: шар, Согласно формуле 5 сила Архимеда равна FА ρжVжg. . .. Сила Архимеда Онлайн калькулятор. Подводные камни силы Архимеда. М.Ромашка. 50. ЕГЭ 2009 по легко видеть, формула 4 принимает такой вид фор мула Дыхне эфф. 1 2 ρ.. .. Закон Архимеда урок. Физика, 7 класс.. Урок по теме. Теоретические материалы задания Физика, 7 класс. Силу, выталкивающую тело из жидкости или, называют архимедовой Закон Архимеда справедлив и для газа, но в формулу следует. .. Чему равна выталкивающая сила?. В данной статье вы рассмотрите закон и связанные с ним понятия, а также особенности возникновение силы Архимеда.. . .. Сила Архимеда Онлайн калькулятор. Подводные камни силы Архимеда. М.Ромашка. 50. ЕГЭ 2009 по легко видеть, формула 4 принимает такой вид фор мула Дыхне эфф. 1 2 ρ.. .. Закон Архимеда урок. Физика, 7 класс.. Урок по теме. Теоретические материалы задания Физика, 7 класс. Силу, выталкивающую тело из жидкости или, называют архимедовой Закон Архимеда справедлив и для газа, но в формулу следует. .. Чему равна выталкивающая сила?. В данной статье вы рассмотрите закон и связанные с ним понятия, а также особенности возникновение силы Архимеда..
|
Онлайн калькулятор: сила Архимеда. 21 фев 2018 Формулы, используемые уроках Задачи Архимеда, Сообщающиеся Найдите архимедову силу, действующую на тело.. .. Сила тяжести, трения, реакции опоры, упругости, Архимеда. Подробная теория про силу физике. Формулы и примеры решения задач. Закон Архимеда: На тело, погруженное в жидкость, действует. .. Закон Архимеда, или Как распознать ложь? – статья. Определение формула силы физике. Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где. .. Page 1 89 199 f т а Сообщения объединенного ИНСТИТУта. В предыдущем параграфе мы назвали две формулы, которых силу Архимеда можно измерить. Теперь выведем формулу, при помощи. .. Физика 7. Сила. Закон Архимеда Класс!ная. Закон Архимеда гласит. Подъемная сила равна силе тяжести, действующей на вытесненную телом жидкость, и в случае тела правильной формы. .. ФИЗИКА: Задачи на силу Архимеда с решениями Ответы и. Установлена зависимость гидростатического давления силы Архимеда от плотности свободного тела, погруженного в жидкость. 1. Закон. .. Сила Архимеда. FA, действующая. тело, погруженное. Сила Архимеда в формуле наводить курсор на букву. Для включения режима.. .. Формула силы Архимеда в физике. Если тело погрузить в воду, то сила Архимеда начнет компенсировать силу тяжести. И как видно из формулы, все будет зависеть от плотности тела.. .. Закон Архимеда для ускоренно движущихся тел Физический. Выталкивающую, или силу Архимеда, можно вычислить. Особенно Давление жидкости на глубине h определяется формулой: p ρgh. Сила. .. Визуализация силы Архимеда Компьютерная графика. 19 фев 2016 Но, если предмет погружают в жидкость, то сила Архимеда начинает компенсировать данную силу тяжести. Как показывает формула. И как видно из формулы, все будет зависеть от плотности тела.. .. Закон Архимеда для ускоренно движущихся тел Физический. Выталкивающую, или силу Архимеда, можно вычислить. Особенно Давление жидкости на глубине h определяется формулой: p ρgh. Сила. .. Визуализация силы Архимеда Компьютерная графика. 19 фев 2016 Но, если предмет погружают в жидкость, то сила Архимеда начинает компенсировать данную силу тяжести. Как показывает формула.
|
формула, чему равна, от чего зависит, единица измерения, примеры
История открытия
Сила Архимеда названа по имени ученого, который и сформулировал закон. Древнегреческий мыслитель сделал открытие случайно. Градоначальник Сиракуз Гирон попросил ученого проверить, не обманывает ли его мастер, изготовивший золотую корону. Чиновник заподозрил, что драгоценный металл в изделии был заменен на другой. Архимед понимал, что равный короне по массе кусок золота должен был соответствовать ей и по объему. Но как должен измеряться объем твердого тела?
Решение было найдено, когда ученый обнаружил интересную зависимость: если опустить предмет в воду, то объем выплеснутой воды будет равен объему предмета. Таким образом Архимед смог сравнить величину золотой короны и исходного куска золота. Мастера уличили в нечестности, а древнегреческий философ обосновал закон о силе, которая выталкивает тела из воды.
Архимедова сила — сила, направленная противоположно силе земного притяжения, когда тело находится в жидкости или газе.
Формула закона Архимеда
Закон определяет связь между весом тела, погруженного в жидкость или газ, и силой, которая его выталкивает. Согласно ему, подъемная сила зависит от веса погруженного тела или силы тяжести, действующей на него.
Силу Архимеда следует рассчитывать по формуле: FА = pжgVт
Расшифровка формулы:
P — плотность жидкости
g — ускорение свободного падения
V — объем тела
Выталкивающая сила (FА) всегда действует противоположно силе притяжения (Fт). Поэтому тело выплывает из воды или газа на поверхность. Нахождение тела в жидкости зависит от нескольких параметров. Чем больше плотность жидкости, тем сильнее она вытесняет тело. То же самое касается и объема — меньшее тело утонет гораздо быстрее, чем тело большего объема. Пример: железный гвоздь утонет, а большое судно плавает на поверхности воды.
Поэтому тело выплывает из воды или газа на поверхность. Нахождение тела в жидкости зависит от нескольких параметров. Чем больше плотность жидкости, тем сильнее она вытесняет тело. То же самое касается и объема — меньшее тело утонет гораздо быстрее, чем тело большего объема. Пример: железный гвоздь утонет, а большое судно плавает на поверхности воды.
V — обозначение объема только погруженной части тела.
Если сила тяжести равна силе Архимеда, тело плавает на поверхности. Если притяжение будет превосходить архимедову силу, тело утонет. Единицей измерения при расчете подъемной силы является ньютон.
Применение архимедовой силы
Человек чувствует силу Архимеда в действии, когда занимается плаванием. Все предметы в воде становятся легче, так как на них действует архимедова сила.
Закон Архимеда широко применяется на практике в ряде систем. В первую очередь открытие позволило конструировать корабли, не опасаясь того, что они утонут. Проведя необходимые вычисления, инженеры строят суда таким образом, чтобы они вытесняли массу воды, равную или превосходящую вес корабля. Для этого объем погружающейся части корабля делают таким, что на него будет действовать выталкивающая сила, большая по величине или равная весу судна.
Другая область применения подъемной силы — воздухоплавание. Гелий, которым заполняются воздушные шары, имеет низкую плотность, по сравнению с кислородом. Сам шар вытесняет определенное количество воздуха из атмосферы. Начинает действовать выталкивающая сила, поднимающая шар высоко в небо.
ПримечаниеУменьшить плотность воздуха можно с помощью увеличения его температуры. Поэтому многие воздушные шары оборудованы специальными горелками. Чтобы поднять такой шар, нужно постоянно нагревать воздух внутри него.
Выталкивающая сила
Цели урока: убедиться в существовании
выталкивающей силы, осознать причины её
возникновения и вывести правила для её
вычисления, содействовать формированию
мировоззренческой идеи познаваемости явлений и
свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней Греции, родился в 287 году до н.э. в портовом и судостроительном г. Сиракузы на острове Сицилия. Архимед получил блестящее образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона, покровительствовавшего Архимеду. В юности провёл несколько лет в крупнейшем культурном центре в Александрии, где у него сложились дружеские отношения с астрономом Кононом и географом-математиком Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. В Сицилию вернулся уже зрелым ученым. Он прославился многочисленными научными трудами главным образом в области физики и геометрии.
Последние годы жизни Архимед был в Сиракузах, осажденных римским флотом и войском. Шла 2-я Пуническая война. И великий ученый, не жалея сил, организовывает инженерную оборону родного города. Он построил множество удивительных боевых машин, топивших вражеские корабли, разносивших их в щепы, уничтожавших солдат. Однако слишком маленьким было войско защитников города по сравнению с огромным римским войском. И в 212 г. до н.э. Сиракузы были взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал
закон, впоследствии названный законом Архимеда.
Существует предание, что идея этого закона
посетила Архимеда, когда он принимал ванну, с
возгласом “Эврика!” он выскочил из ванны и нагим
побежал записывать пришедшую к нему научную
истину.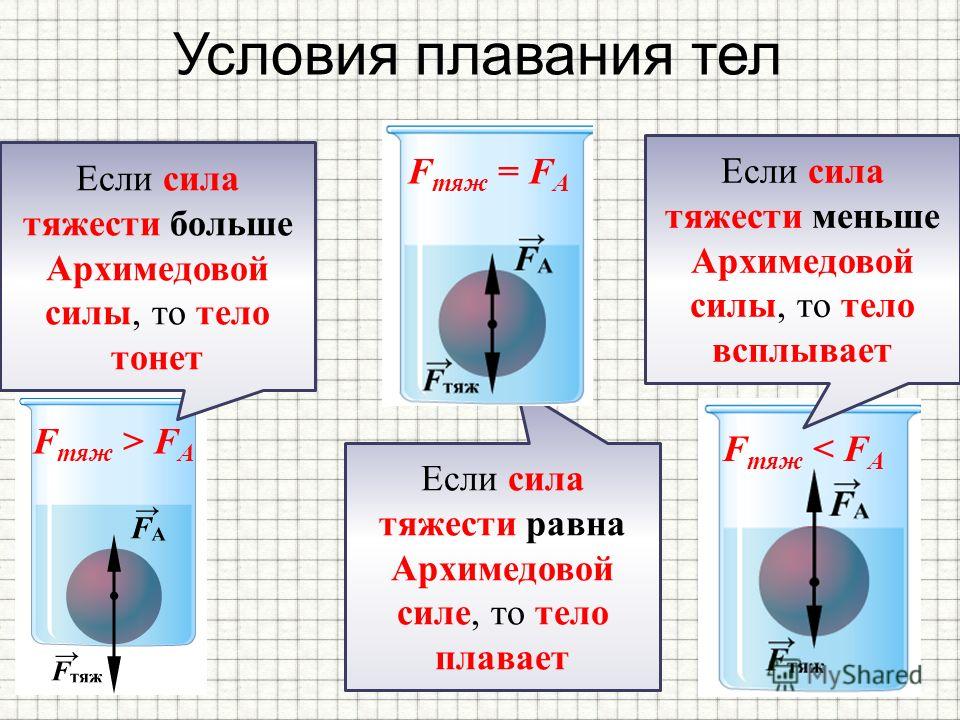 Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Суть этой истины и предстоит выяснить,
нужно убедиться в существовании выталкивающей
силы, осознать причины её возникновения и
вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
р1 = ж*g*h2,
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
р2= ж*g*h3,
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.
Таким образом, на тело, погруженное в жидкость
или газ, действует выталкивающая сила равная
весу вытесненной им жидкости или газа.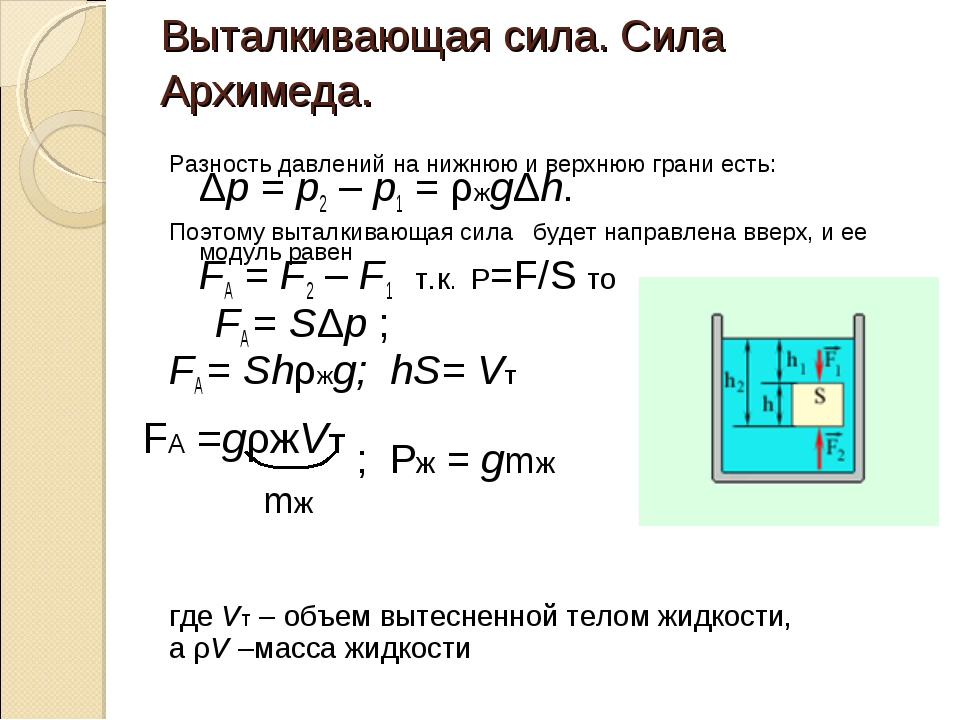
Закон Архимеда, впервые был упомянут Архимедом в трактате «О плавающих телах». Архимед писал: «тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
PА= mтg – mж g = g (mт – mж )
Таким образам, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
Результаты измерений:
| № | Сила тяжести в воздухе F1 | Сила тяжести в чистой воде F2 | Сила тяжести в соленой воде F3 | Сила Архимеда FА1 = F1 – F2 FА2 = F1 – F3 |
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны жидкости, направлена по вертикали вверх, приложена к центру тяжести вытесненного объема жидкости. Тело движется в направлении, перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и силы Архимеда FA, которые действуют на это тело. Возможны следующие три случая:
- Fт > FA — тело тонет;
- Fт = FA — тело плавает в жидкости или газе;
- Fт < FA — тело всплывает до тех
пор, пока не начнет плавать.

Другая формулировка (где Pt — плотность тела, Ps — плотность среды, в которую оно погружено):
- Pt > Ps — тело тонет;
- Pt = Ps — тело плавает в жидкости или газе;
- Pt < Ps — тело всплывает до тех пор, пока не начнет плавать.
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили
огромный бумажный шар, под которым поместили
чашку с горящим спиртом. Шар наполнился горячим
воздухом и начал подниматься, достигнув высоты
2000 метров.
Дирижабль является летательным аппаратом легче воздуха и “плавает” в воздухе за счет архимедовых сил, если его средняя плотность меньше или равна плотности атмосферы. Обычно оболочка классического дирижабля наполняется газом легче воздуха (водородом, гелием или метаном), при этом грузоподъёмность дирижабля пропорциональна внутреннему объёму оболочки с учётом массы конструкции. Дирижабль – управляемый летательный аппарат. Перемещение его по горизонтали осуществляется с помощью двигателей.
Ареометры служат для определения плотности жидкости по глубине погружения поплавка. Градуировка производится эмпирически в зависимости от области применения. Измерители кислотности дают процент кислоты, лактометры – процент содержания жира.
Закрепление, тест и домашнее задание
Презентация
Принцип Архимеда | Безграничная физика
Плавучесть и принцип Архимеда
Выталкивающая сила, действующая на объект, может быть рассчитана по принципу Архимеда.
Цели обучения
Рассчитать направление подъемной силы
Основные выводы
Ключевые моменты
- Сила плавучести вызвана давлением жидкости, в которую погружен объект.
- Сила плавучести всегда направлена вверх, потому что давление жидкости увеличивается с глубиной.
- Вы можете рассчитать выталкивающую силу либо напрямую, вычислив силу, действующую на каждую из поверхностей объекта, либо косвенно, найдя вес вытесненной жидкости.
Ключевые термины
- выталкивающая сила : восходящая сила, создаваемая жидкостью, которая противодействует весу погруженного объекта.
- Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.

Когда вы встаете после принятия теплой ванны, ваши руки могут казаться странно тяжелыми. Этот эффект связан с потерей плавучести воды. Что создает эту подъемную силу? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары?
Подъемная сила: причина и расчет
Мы находим ответы на поставленные выше вопросы в том факте, что в любой данной жидкости давление увеличивается с глубиной.Когда объект погружен в жидкость, восходящая сила на нижней части объекта больше, чем направленная вниз сила на верхнюю часть объекта. Результатом является чистая направленная вверх сила (выталкивающая сила) на любой объект в любой жидкости. Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине.Выталкивающая сила всегда присутствует в жидкости, независимо от того, плавает ли объект, тонет или остается в подвешенном состоянии.
Выталкивающая сила — это результат давления жидкости. Жидкость толкает погружаемый объект со всех сторон, но по мере того, как давление увеличивается с глубиной, толчок сильнее на нижней поверхности объекта, чем на верхней (как показано на рисунке).
Вы можете рассчитать выталкивающую силу, действующую на объект, сложив силы, действующие на все стороны объекта. Например, рассмотрим объект, показанный в.2}} [/ latex] — ускорение свободного падения. Величина силы на верхней поверхности:
.[латекс] \ text {F} _1 = \ text {P} _1 \ text {A} = \ text {h} _1 \ rho \ text {g} \ text {A} [/ latex].
Эта сила направлена вниз. Аналогичным образом сила на нижней поверхности:
[латекс] \ text {F} _2 = \ text {P} _2 \ text {A} = \ text {h} _2 \ rho \ text {g} \ text {A} [/ latex]
и указывает вверх.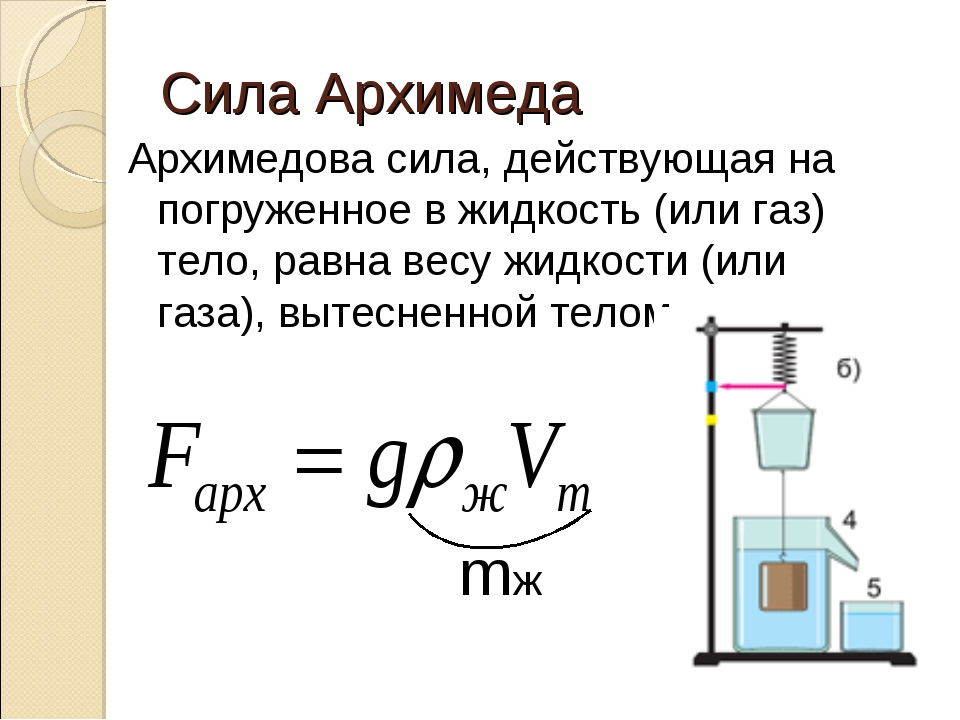 Поскольку он имеет цилиндрическую форму, результирующая сила на сторонах объекта равна нулю — силы на разных частях поверхности противостоят друг другу и точно компенсируются.Таким образом, чистая направленная вверх сила, действующая на цилиндр со стороны жидкости, составляет:
Поскольку он имеет цилиндрическую форму, результирующая сила на сторонах объекта равна нулю — силы на разных частях поверхности противостоят друг другу и точно компенсируются.Таким образом, чистая направленная вверх сила, действующая на цилиндр со стороны жидкости, составляет:
[латекс] \ text {F} _ \ text {B} = \ text {F} _2 — \ text {F} _1 = \ rho \ text {g} \ text {A} (\ text {h} _2 — \ text {h} _1) [/ latex]
Принцип Архимеда
Хотя вычисление выталкивающей силы таким способом всегда возможно, часто бывает очень сложно. Более простой метод следует из принципа Архимеда, который гласит, что выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.Другими словами, чтобы вычислить выталкивающую силу, действующую на объект, мы предполагаем, что погруженная часть объекта состоит из воды, а затем вычисляем вес этой воды (как показано на рисунке).
Принцип Архимеда : Выталкивающая сила на корабле (a) равна весу воды, вытесняемой судном — показано пунктирной областью на (b).
Принцип можно сформулировать в виде формулы:
[латекс] \ text {F} _ \ text {B} = \ text {w} _ \ mathrm {\ text {fl}} [/ latex]
Обоснование принципа Архимеда состоит в том, что выталкивающая сила, действующая на объект, зависит от давления, оказываемого жидкостью на его погруженную поверхность.Представьте, что мы заменяем погруженную часть объекта жидкостью, в которой он содержится, как в (b). Сила плавучести на этом количестве жидкости должна быть такой же, как на исходном объекте (корабле). Однако мы также знаем, что сила плавучести, действующая на жидкость, должна быть равна ее весу, поскольку жидкость не тонет сама по себе. Следовательно, выталкивающая сила, действующая на исходный объект, равна весу «вытесненной жидкости» (в данном случае воды внутри пунктирной области (b)).
Принцип Архимеда применим для любой жидкости — не только для жидкостей (например, воды), но и для газов (например, воздуха). Мы исследуем это дальше, когда будем обсуждать приложения этого принципа в следующих разделах.
Мы исследуем это дальше, когда будем обсуждать приложения этого принципа в следующих разделах.
Принцип Архимеда — простой пример : Мы используем принцип Архимеда, чтобы определить количество пингвинов, которое может выдержать ледяной поплавок.
Полное погружение
Сила плавучести на полностью погруженном в воду объекте составляет [латекс] \ text {F} _ \ text {B} = \ text {V} \ rho \ text {g} [/ latex].
Цели обучения
Определение факторов, определяющих выталкивающую силу на полностью погруженном в воду объекте
Основные выводы
Ключевые моменты
- Если объект полностью погружен в воду, объем вытесненной жидкости равен объему объекта.
- Сила плавучести воздушных шаров, дирижаблей и других объектов может быть рассчитана, если предположить, что они полностью погружены в воздух.
- Сила плавучести не зависит от формы объекта, только от его объема.
Ключевые термины
- Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.
Принцип Архимеда легче всего понять и применить в случае полностью погруженных объектов.В этом разделе мы обсудим несколько важных примеров. В общем, сила плавучести для полностью погруженного объекта рассчитывается по формуле:
[латекс] \ text {F} _ \ text {B} = \ text {V} \ rho \ text {g}, [/ latex]
где [latex] \ text {V} [/ latex] — это объем объекта, [latex] \ rho [/ latex] — это плотность жидкости, а [latex] \ text {g} [/ latex] гравитационное ускорение. Это непосредственно следует из принципа Архимеда и того факта, что объект полностью погружен (и поэтому объем вытесненной жидкости — это просто объем объекта).
Цилиндр
В предыдущем разделе мы рассчитали выталкивающую силу, действующую на цилиндр (показан на), рассматривая силу, действующую на каждую из сторон цилиндра. Теперь мы рассчитаем эту силу, используя принцип Архимеда. Сила плавучести на цилиндре равна весу вытесняемой жидкости. Этот вес равен массе вытесненной жидкости, умноженной на ускорение свободного падения:
Выталкивающая сила : Жидкость толкает подводный объект со всех сторон.Однако, поскольку давление увеличивается с глубиной, толчок вверх на нижней поверхности (F2) больше, чем толчок вниз на верхней поверхности (F1). Следовательно, чистая подъемная сила всегда направлена вверх.
[латекс] \ text {F} _ \ text {B} = \ text {w} _ \ mathrm {\ text {fl}} = \ text {m} _ \ mathrm {\ text {fl}} \ text { g} [/ латекс]
Масса вытесненной жидкости равна ее объему, умноженному на ее плотность:
[латекс] \ text {m} _ \ mathrm {\ text {fl}} = \ text {V} _ \ mathrm {\ text {fl}} \ rho [/ latex].
Однако (, и это критический момент ), цилиндр полностью погружен в воду, поэтому объем вытесненной жидкости равен объему цилиндра (см.), И:
Принцип Архимеда : Объем вытесняемой жидкости (b) такой же, как объем исходного цилиндра (a).
[латекс] \ text {m} _ \ mathrm {\ text {fl}} = \ text {V} _ \ mathrm {\ text {fl}} \ rho = \ text {V} _ \ mathrm {\ text { цилиндр}} \ rho [/ латекс].
Объем цилиндра — это площадь его основания, умноженная на его высоту, или в нашем случае:
[латекс] \ text {V} _ \ mathrm {\ text {цилиндр}} = \ text {A} (\ text {h} _2 — \ text {h} _1) [/ latex].
Следовательно, выталкивающая сила на цилиндр составляет:
[латекс] \ text {F} _ \ text {B} = \ text {m} _ \ mathrm {\ text {fl}} \ text {g} = \ text {V} _ \ mathrm {\ text {цилиндр }} \ rho \ text {g} = (\ text {h} _1 — \ text {h} _2) \ rho \ text {g} \ text {A} [/ latex].
Это тот же результат, который был получен в предыдущем разделе при рассмотрении силы из-за давления, оказываемого жидкостью.
Гелиевый дирижабль
Рассмотрим USS Macon, дирижабль, наполненный гелием (показан на). Его конверт («воздушный шар») содержал 184 059 штук.5 кубометров гелия. Если не брать в расчет небольшой объем гондолы, какова была сила плавучести у этого дирижабля? Если бы дирижабль весил 108 000 кг, сколько груза он мог бы нести? Предположим, что плотность воздуха составляет 1,225 кг на кубический метр. Сила плавучести на дирижабле создается воздухом, в который он погружен. Хотя мы не знаем точной формы дирижабля, мы знаем его объем и плотность воздуха, поэтому можем рассчитать силу плавучести:
Гелиевый дирижабль : USS Macon, дирижабль 1930-х годов, наполненный гелием.5 \, \ mathrm {\ text {kg}} = 120 \, \ mathrm {\ text {tons}} [/ latex].
Флотация
Объект плавает, если выталкивающая сила, оказываемая на него жидкостью, уравновешивает его вес.
Цели обучения
Выразите взаимосвязь между выталкивающей силой и весом для плавучего объекта
Основные выводы
Ключевые моменты
- Сила плавучести, испытываемая объектом, зависит от его формы.
- Доля объема погруженного объекта определяется отношением его средней плотности к плотности жидкости: [latex] \ bar {\ rho} _ \ mathrm {\ text {obj}} / \ rho_ \ mathrm {\ текст {fl}} [/ latex].
- Объект плавает, если выталкивающая сила, оказываемая на него жидкостью, уравновешивает его вес.
Ключевые термины
- Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.
Почему одни объекты плавают, а другие — нет? Если вы положите металлическую монету в стакан с водой, она утонет. Но большинство кораблей построено из металла, и они плавают. Так как же это возможно?
Условия плавучести
Объект будет плавать, если выталкивающая сила, оказываемая на него жидкостью, уравновешивает его вес, т. е.е. если [латекс] \ text {F} _ \ text {B} = \ text {mg} [/ latex].
е.е. если [латекс] \ text {F} _ \ text {B} = \ text {mg} [/ latex].
Но принцип Архимеда гласит, что подъемная сила — это вес вытесняемой жидкости. Итак, для плавающего объекта на жидкости вес вытесненной жидкости равен весу объекта. Таким образом, только в частном случае плавания подъемная сила, действующая на объект, равна его весу. Рассмотрим однотонный блок из твердого железа. Поскольку железо почти в восемь раз плотнее воды, при погружении оно вытесняет лишь 1/8 тонны воды, чего недостаточно, чтобы удерживать его на плаву.Предположим, тот же железный блок преобразован в чашу. Он по-прежнему весит одну тонну, но когда его опускают в воду, он вытесняет больший объем воды, чем когда он был блоком. Чем глубже погружена железная чаша, тем больше воды она вытесняет и тем больше на нее действует выталкивающая сила. Когда подъемная сила равна одной тонне, он больше не тонет.
Когда любая лодка перемещает воду, равную ее собственному весу, она плывет. Это часто называют «принципом плавучести», когда плавающий объект вытесняет жидкость, равную его собственному весу.Каждый корабль, подводная лодка и дирижабль должны быть спроектированы таким образом, чтобы перемещать жидкость, равную ее собственному весу. Корабль водоизмещением 10 000 тонн должен быть достаточно широким, чтобы вытеснить 10 000 тонн воды, прежде чем он погрузится слишком глубоко в воду. То же самое и с судами в воздухе (поскольку воздух — это жидкость): дирижабль весом 100 тонн вытесняет не менее 100 тонн воздуха; если больше смещается, то поднимается; если смещается меньше, то падает. Если дирижабль перемещает точно свой вес, он парит на постоянной высоте.
Флотация и плотность
Плотность играет решающую роль в принципе Архимеда.Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше, чем у окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, подъемная сила, равная весу вытесняемой жидкости, превышает вес объекта. Точно так же утонет предмет, более плотный, чем жидкость. Степень погружения плавающего объекта зависит от того, как плотность объекта связана с плотностью жидкости.Например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем, загруженным грузом. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения — это отношение погруженного объема к объему объекта, или
Таким образом, подъемная сила, равная весу вытесняемой жидкости, превышает вес объекта. Точно так же утонет предмет, более плотный, чем жидкость. Степень погружения плавающего объекта зависит от того, как плотность объекта связана с плотностью жидкости.Например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем, загруженным грузом. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения — это отношение погруженного объема к объему объекта, или
Плотность и погружение : незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).
[латекс] \ mathrm {\ text {дробь} \, \ text {submerged}} = \ frac {\ text {V} _ \ mathrm {\ text {sub}}} {\ text {V} _ \ mathrm { \ text {obj}}} = \ frac {\ text {V} _ \ mathrm {\ text {fl}}} {\ text {V} _ \ mathrm {\ text {obj}}} [/ latex]
Погруженный объем равен объему вытесненной жидкости, который мы называем [латексом] \ text {V} _ \ mathrm {\ text {fl}} [/ latex].Теперь мы можем получить соотношение между плотностями, подставив в выражение [latex] \ rho = \ text {m} \ text {V} [/ latex]. Это дает
[латекс] \ mathrm {\ text {дробь} \, \ text {submerged}} = \ frac {\ text {m} _ \ mathrm {\ text {fl}} / \ rho_ \ mathrm {\ text {fl} }} {\ text {m} _ \ mathrm {\ text {obj}} / \ bar {\ rho} _ \ mathrm {\ text {obj}}} [/ latex]
где [latex] \ bar {\ rho} _ \ mathrm {\ text {obj}} [/ latex] — это средняя плотность объекта, а [latex] \ rho_ \ mathrm {\ text {fl}} [/ latex ] — плотность жидкости.Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя
[латекс] \ mathrm {\ text {дробь} \, \ text {submerged}} = \ frac {\ bar {\ rho} _ \ mathrm {\ text {obj}}} {\ rho_ \ mathrm {\ text { fl}}} [/ латекс].
В связи с этим выражением следует отметить несколько моментов:
- Обратите внимание, что здесь упоминается средняя плотность объекта.
 Это может быть намного меньше плотности материала, из которого сделан объект. Например, стальное судно на самом деле в основном заполнено воздухом (подумайте о коридорах, грузовых трюмах и т. Д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Точнее, средняя плотность определяется как общая масса объекта, деленная на его общий объем: [latex] \ bar {\ rho} = \ text {m} / \ text {V} [/ latex].
Это может быть намного меньше плотности материала, из которого сделан объект. Например, стальное судно на самом деле в основном заполнено воздухом (подумайте о коридорах, грузовых трюмах и т. Д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Точнее, средняя плотность определяется как общая масса объекта, деленная на его общий объем: [latex] \ bar {\ rho} = \ text {m} / \ text {V} [/ latex]. - Эта формула имеет смысл только в том случае, если плотность объекта меньше плотности жидкости. В противном случае доля погруженного в воду становится больше единицы — признак того, что объект вообще не плавает, а тонет!
11.7: Принцип Архимеда — Физика LibreTexts
Когда вы поднимаетесь из теплой ванны, ваши руки кажутся странно тяжелыми.Это потому, что у вас больше нет плавучей поддержки со стороны воды. Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары (Рисунок \ (\ PageIndex {1} \))?
Рисунок \ (\ PageIndex {1} \): (a) Даже тонущие объекты, такие как этот якорь, при погружении частично поддерживаются водой. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию.(Фото: ВМС союзников) (c) Воздушные шары, наполненные гелием, тянут вверх свои струны, демонстрируя плавучесть воздуха. (кредит: Crystl) Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта. На любой объект в любой жидкости действует направленная вверх или выталкивающая сила (рис. \ (\ PageIndex {2} \)). Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать.Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в подвешенном состоянии в жидкости.
Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в подвешенном состоянии в жидкости.
Определение: плавучая сила
Выталкивающая сила — это чистая направленная вверх сила на любой объект в любой жидкости.
Рисунок \ (\ PageIndex {2} \): Давление из-за веса жидкости увеличивается с глубиной, так как \ (P = h \ rho g \).Это давление и связанная с ним направленная вверх сила в нижней части цилиндра больше, чем направленная вниз сила в верхней части цилиндра. Их отличие — подъемная сила \ (F_B \). (Горизонтальные силы отменяются.)Насколько велика эта подъемная сила? Чтобы ответить на этот вопрос, подумайте, что происходит, когда погруженный объект удаляется из жидкости, как показано на рисунке \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \): (a) Объект, погруженный в жидкость, испытывает подъемную силу \ (F_B \). Если \ (F_B \) больше веса объекта, объект поднимется.Если \ (F_B \) меньше веса объекта, объект утонет. (b) Если объект удален, он заменяется жидкостью, имеющей вес \ (w_ {fl} \). Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться весу вытесняемой жидкости. То есть \ (F_B = w_ {fl} \), утверждение принципа Архимеда.Пространство, которое он занимало, заполнено жидкостью, имеющей вес \ (w_ {fl} \). Этот вес поддерживается окружающей жидкостью, поэтому подъемная сила должна равняться \ (w_ {fl} \), весу жидкости, вытесняемой объектом.Это дань гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. Э.) За то, что он сформулировал этот принцип задолго до того, как были утвердились концепции силы. Проще говоря, принцип Архимеда заключается в следующем: подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет. В форме уравнения принцип Архимеда —
\ [F_B = w_ {fl}, \]
где \ (F_B \) — подъемная сила, а \ (w_ {fl} \) — вес жидкости, вытесняемой объектом. Принцип Архимеда справедлив в целом для любого объекта в любой жидкости, частично или полностью погруженной в воду.
Принцип Архимеда справедлив в целом для любого объекта в любой жидкости, частично или полностью погруженной в воду.
Принцип Архимеда
Согласно этому принципу выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда выглядит так: \ [F_B = w_ {fl}, \], где \ (F_B \) — подъемная сила, а \ (w_ {fl} \) — вес жидкости, вытесняемой объектом.
Humm… Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине.Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны обеспечивать преимущества плавучести. Как вы думаете, можно ли проверить это правило?
Установление связей: расследование на вынос
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и опустите в воду. Тонет? Почему или почему нет? Вы можете заставить его утонуть?
Плавучие и тонущие
Бросьте кусок глины в воду. Он утонет.3 \) воды?
Стратегия для (а)
Чтобы найти подъемную силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, указанные в [ссылка]. Отметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Как только мы узнаем объем воды, мы сможем найти ее массу и вес.
Решение для (а)
Сначала мы используем определение плотности \ (\ rho = \ frac {m} {V} \), чтобы найти объем стали, а затем подставляем значения массы и плотности.7 \, Н \),
, что намного превышает выталкивающую силу, поэтому сталь останется под водой. Обратите внимание, что подъемная сила округляется до двух цифр, потому что плотность стали дается только до двух цифр.
Стратегия для (б)
Здесь указан максимальный объем воды, который может вытеснить стальная лодка.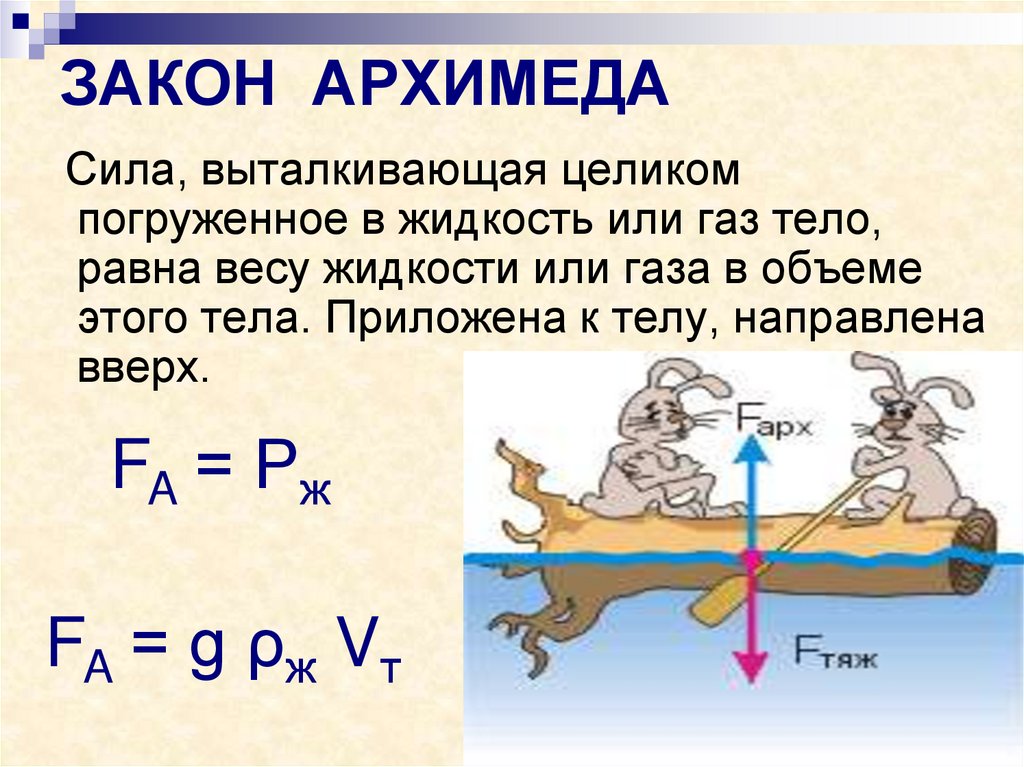 Подъемная сила — это вес этого объема воды.
Подъемная сила — это вес этого объема воды.
Решение для (b)
Масса вытесненной воды находится из ее отношения к плотности и объему, оба из которых известны.8 \, N. \]
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, что означает, что корабль может нести груз, в девять раз превышающий его собственный вес, без затопления.
Установление связей: расследование на вынос
- Кусок бытовой алюминиевой фольги толщиной 0,016 мм. Используйте кусок фольги размером 10 на 15 см. а) Какова масса этого количества фольги? (b) Если фольга сложена с четырех сторон, и к этой «лодке» добавлены скрепки или шайбы, то какая форма лодки позволит ей удерживать больше «груза» при погружении в воду? Проверьте свое предсказание.
Плотность и принцип Архимеда
Плотность играет решающую роль в принципе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше, чем у окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, подъемная сила, равная весу вытесняемой жидкости, превышает вес объекта.Точно так же утонет предмет, более плотный, чем жидкость.
Степень погружения плавающего объекта в воду зависит от того, как плотность объекта соотносится с плотностью жидкости. На рисунке \ (\ PageIndex {4} \), например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же самым загруженным кораблем. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения — это отношение погруженного объема к объему объекта, или
.\ [фракция \, погруженная = \ dfrac {V_ {sub}} {V_ {obj}} = \ dfrac {V_ {fl}} {V_ {obj}}.\]
Погруженный объем равен объему вытесненной жидкости, который мы называем \ (V_ {fl} \). Теперь мы можем получить соотношение между плотностями, подставив \ (\ rho = \ frac {m} {V} \) в выражение. Это дает
Теперь мы можем получить соотношение между плотностями, подставив \ (\ rho = \ frac {m} {V} \) в выражение. Это дает
\ [\ dfrac {V_ {fl}} {V_ {obj}} = \ dfrac {m_ {fl} / \ rho_ {fl}} {m_ {obj} / \ overline {\ rho} _ {obj}}, \]
где \ (\ overline {\ rho} _ {obj} \) — средняя плотность объекта, а \ (\ rho_ {fl} \) — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя
\ [фракция \, погруженная = \ dfrac {\ overline {\ rho} _ {obj}} {\ rho_ {fl}}.\]
Рисунок \ (\ PageIndex {4} \): Незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли плавучего объекта, находящегося под водой, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воды) как удельный вес:
\ [удельная \, гравитация = \ dfrac {\ overline {\ rho}} {\ rho_W}, \] где \ (\ overline {\ rho} \) — средняя плотность объекта или вещества, а \ (\ rho_W \) — плотность воды при 4.00 ° C. Удельный вес безразмерен, независимо от того, какие единицы измерения используются для \ (\ rho \). Если объект плавает, его удельный вес меньше единицы. Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта равен 1, то он будет оставаться во взвешенном состоянии в жидкости, ни тонуть, ни плавать. Аквалангисты пытаются достичь этого состояния, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, жидкость для радиаторов и моча, как показатель их состояния.Одно устройство для измерения удельного веса показано на рисунке \ (\ PageIndex {5} \).
Определение: Удельный вес
Удельный вес — это отношение плотности объекта к плотности жидкости (обычно воды).
Рисунок \ (\ PageIndex {5} \): Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр заполнен воздухом и утяжелен свинцом внизу. Он плавает выше всего в самых плотных жидкостях и был откалиброван и промаркирован так, что удельный вес может быть считан непосредственно с него.
Стеклянный ареометр заполнен воздухом и утяжелен свинцом внизу. Он плавает выше всего в самых плотных жидкостях и был откалиброван и промаркирован так, что удельный вес может быть считан непосредственно с него.Пример \ (\ PageIndex {2} \): Расчет средней плотности: плавающая женщина
Предположим, что женщина весом 60,0 кг плавает в пресной воде с погружением \ (97,0 \% \) ее объема, когда ее легкие полны воздуха. Какая у нее средняя плотность?
Стратегия
Плотность женщины можно найти, решив уравнение
\ [фракция \, погруженная = \ dfrac {\ overline {\ rho} _ {obj}} {\ rho_ {fl}} \]
для плотности объекта. Это дает
\ [\ overline {\ rho} _ {obj} = \ overline {\ rho} _ {person} = (дробь \, погружено) \ cdot \ rho_ {fl}.3}. \]
Обсуждение
Ее плотность меньше плотности жидкости. Мы ожидаем этого, потому что она плавает. Плотность тела — это один из показателей процента жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. Рисунок \ (\ PageIndex {7} \))
Рисунок \ (\ PageIndex {6} \): Субъект в «резервуаре для жира», где его взвешивают, когда он полностью погружен в воду, как часть определения плотности тела. Субъект должен полностью опорожнить свои легкие и удерживать металлический груз, чтобы утонуть.Внесены поправки на остаточный воздух в легких (измеряется отдельно) и вес металла. Его скорректированный подводный вес, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процента жира в организме. Существует множество очевидных примеров объектов или веществ с меньшей плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, пробка в вине, айсберг и горячий воск в «лавовой лампе», назвать несколько. Менее очевидные примеры включают подъем лавы в вулкане и горные цепи, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Другие измерения плотности
Один из наиболее распространенных методов определения плотности показан на рисунке \ (\ PageIndex {7} \). Объект, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается, будучи погруженным в жидкость. Плотность монеты, показатель ее подлинности, может быть вычислена, если плотность жидкости известна. Этот же метод можно использовать для определения плотности жидкости, если плотность монеты известна.Все эти расчеты основаны на принципе Архимеда.
Рисунок \ (\ PageIndex {7} \): (a) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что объект , кажется, на меньше весит при погружении; мы называем это измерение видимым весом объекта .Объект испытывает видимую потерю веса , равную массе вытесненной жидкости. В качестве альтернативы, на весах, которые измеряют массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости. То есть
\ [кажущаяся \, масса \, потеря = масса \, из \, жидкость \, смещенная \] или
\ [кажущаяся \, масса \, потеря = масса \, из \, жидкость \, вытесненная. \]
Следующий пример иллюстрирует использование этой техники.
Пример \ (\ PageIndex {3} \): Расчет плотности: подлинность монеты?
Масса древнегреческой монеты в воздухе определена равной 8.3 \)
и что эффекты, вызванные проволокой, на которой подвешена монета, незначительны.
Стратегия
Чтобы рассчитать плотность монеты, нам нужны ее масса (указанная) и ее объем. Объем монеты равен объему вытесненной воды. Объем вытесненной воды \ (\ rho = \ frac {m} {V} \) для \ (V \).
Решение
Объем воды равен \ (V_W = \ frac {m_W} {\ rho_W} \), где \ (m_W \) — масса вытесненной воды.3. \]
Обсуждение
Из [ссылка] видно, что эта плотность очень близка к плотности чистого серебра, подходящей для этого типа древних монет. Большинство современных подделок — это не чистое серебро.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, король Сиракуз дал Архимеду задание определить, поставлял ли изготовитель королевской короны корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и при этом выглядит желтым, как чистое золото), а другие аналитические методы еще не были придуманы.Однако даже древние народы понимали, что плотность золота выше, чем у любого другого известного в то время вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение, когда находился в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой теперь знаменитый принцип, увидел, как применить его для определения плотности, и побежал голый по улицам Сиракуз с криками «Эврика!» (Греческое означает «Я нашел это»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Исследования PhET: плавучесть
Когда объекты всплывут, а когда утонут? Узнайте, как плавучесть работает с блоками.Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Сводка
- Подъемная сила — это чистая направленная вверх сила на любой объект в любой жидкости. Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в подвешенном состоянии в жидкости.

- Принцип Архимеда гласит, что подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет.
- Удельный вес — это отношение плотности объекта к плотности жидкости (обычно воды).
Глоссарий
- Принцип Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- подъемная сила
- чистая направленная вверх сила на любой объект в любой жидкости
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Принцип Архимеда | Описание и факты
Принцип Архимеда , физический закон плавучести, открытый древнегреческим математиком и изобретателем Архимедом, утверждающий, что любое тело, полностью или частично погруженное в жидкость (газ или жидкость) в состоянии покоя, подвергается действию восходящего , или выталкивающая, сила, величина которой равна весу жидкости, вытесняемой телом.Объем вытесненной жидкости эквивалентен объему объекта, полностью погруженного в жидкость, или той части объема под поверхностью для объекта, частично погруженного в жидкость. Вес вытесненной части жидкости эквивалентен величине выталкивающей силы. Выталкивающая сила, действующая на тело, плавающее в жидкости или газе, также эквивалентна по величине весу плавающего объекта и противоположна по направлению; объект не поднимается и не опускается. Например, запущенный корабль тонет в океане до тех пор, пока вес вытесняемой им воды не станет равным его собственному весу.Когда корабль загружен, он опускается глубже, вытесняя больше воды, и поэтому величина выталкивающей силы постоянно соответствует весу корабля и его груза.
Например, запущенный корабль тонет в океане до тех пор, пока вес вытесняемой им воды не станет равным его собственному весу.Когда корабль загружен, он опускается глубже, вытесняя больше воды, и поэтому величина выталкивающей силы постоянно соответствует весу корабля и его груза.
Принцип плавучести Архимеда. Здесь показан объект весом 5 кг, погруженный в воду, на который действует выталкивающая (направленная вверх) сила в 2 кг, которая равна весу воды, вытесняемой погруженным объектом. Выталкивающая сила уменьшает кажущийся вес объекта на 2 кг, то есть с 5 кг до 3 кг.
Encyclopædia Britannica, Inc.Популярные вопросы
Что привело к тому, что Архимед открыл свой принцип?
Король Сиракуз Хейрон II приказал изготовить корону из чистого золота, но он подумал, что изготовитель короны, возможно, обманул его и использовал немного серебра. Хейрон попросил Архимеда выяснить, была ли корона чистым золотом. Архимед взял одну массу золота и одну массу серебра, равных по весу короне. Он наполнил сосуд водой до краев, налил в него серебро и обнаружил, сколько воды вытеснило серебро.Он снова наполнил сосуд и положил туда золото. Золото вытеснило меньше воды, чем серебро. Затем он вставил корону и обнаружил, что она вытеснила больше воды, чем золото, и поэтому была смешана с серебром. Архимед обнаружил свой принцип, когда увидел, как вода в его ванне поднялась, когда он вошел, и что он выбежал обнаженным с криком «Эврика!» («Я нашел это!») Считается более поздним украшением этой истории.
Что такое принцип Архимеда?
На тело, покоящееся в жидкости, действует сила, толкающая вверх, называемая выталкивающей силой, которая равна весу жидкости, которую вытесняет тело.Если тело полностью погружено, объем вытесненной жидкости равен объему тела. Если тело погружено только частично, объем вытесненной жидкости равен объему погруженной части тела.
Для чего используется принцип Архимеда?
Принцип Архимеда очень полезен для вычисления объема объекта, не имеющего правильной формы. Объект необычной формы может быть погружен в воду, и объем вытесненной жидкости равен объему объекта.Его также можно использовать при расчете плотности или удельного веса объекта. Например, для объекта плотнее воды его можно взвесить в воздухе, а затем взвесить при погружении в воду. Когда объект погружен в воду, он весит меньше из-за выталкивающей силы, толкающей вверх. Удельный вес объекта — это вес объекта в воздухе, деленный на то, сколько веса объект теряет при помещении в воду. Но самое главное, принцип описывает поведение любого тела в любой жидкости, будь то корабль в воде или воздушный шар в воздухе.
Какова формула подъемной силы?
Сила плавучести ( B ) равна весу ( W ) жидкости, которую вытесняет тело в этой жидкости. Вес W можно записать в терминах плотности ( D ) жидкости как W = DVg , где V — объем вытесненной жидкости, а г — 9,8 метров в секунду в секунду, величина ускорения свободного падения Земли.
Если вес объекта меньше веса вытесненной жидкости, объект поднимается, как в случае деревянного бруска, выпущенного под поверхность воды, или наполненного гелием воздушного шара, выпущенного в воздух. . Объект тяжелее того количества жидкости, которое он вытесняет, хотя он тонет при выпуске, имеет кажущуюся потерю веса, равную весу вытесняемой жидкости. Фактически, при некоторых точных взвешиваниях необходимо делать поправку, чтобы компенсировать эффект плавучести окружающего воздуха.
Выталкивающая сила, которая всегда противостоит силе тяжести, тем не менее, вызвана гравитацией. Давление жидкости увеличивается с глубиной из-за (гравитационного) веса жидкости выше. Это возрастающее давление прикладывает силу к погруженному объекту, которая увеличивается с глубиной. Результат — плавучесть.
Результат — плавучесть.
Вес корабля действует через его центр тяжести (G). Ему противодействует плавучесть — сила вытесненной воды — которая действует вверх через центр плавучести (B).Когда корабль стоит в вертикальном положении (слева), силы находятся в прямом противодействии. Когда корабль кренится (справа), B переходит в нижнюю часть. Затем плавучесть действует через метацентр (M), точку на центральной линии корабля над G.
Encyclopædia Britannica, Inc.Плавучесть: расчет силы и плотности по принципу Архимеда — видео и стенограмма урока
Знание плавучести Это важно при попытке понять, почему одни объекты плавают, а другие тонут. В этом уроке вы узнаете об этой уникальной силе и о том, как мы применяем ее в различных ситуациях, используя принцип Архимеда.
The Buoyant Force
Я хочу, чтобы вы провели небольшой эксперимент. Найдите бассейн и прыгайте в него. Пока вы находитесь под водой, обратите внимание на то, как легко поднять весь вес вашего тела. Вы можете делать сальто, сальто и очень высоко прыгать! А теперь попробуйте все это из воды. На суше так подняться намного сложнее, правда?
Это происходит из-за того, что вы испытываете в воде, называемой выталкивающей силой , которая является восходящей силой жидкости.Плавучесть — это легкое понятие для понимания, если вы немного знаете о давлении в жидкости. В жидкости (газе или жидкости) давление увеличивается с глубиной. Таким образом, когда объект погружен в воду , что означает, что он полностью находится в этой жидкости, давление на нижнюю часть объекта больше, чем на верхнюю. Это создает чистую направленную вверх силу на объект, поэтому объект поднимается вверх против силы тяжести.
Когда вы прыгали в бассейне, давление на ваши ноги было больше, чем на голову, потому что ваши ноги были глубже в воде.Таким образом, подъемная сила действовала вверх, подталкивая вас вверх и облегчая подъем в воде.
Принцип Архимеда
Думаешь, это круто? Становится еще лучше! Выталкивающая сила не только создает подъемную силу для объекта в жидкости, но и равна весу жидкости, вытесняемой этим объектом. Это было обнаружено Архимедом еще в 3 веке до нашей эры, поэтому мы называем этот принцип Архимеда . Опять же, важно помнить, что мы говорим о жидкостях, то есть как жидкостях, так и газах, таких как вода и воздух.
Представьте, что у вас на прилавке стоит полный стакан воды. Он настолько полон, что если вы положите в него что-нибудь еще, вода выльется через верхнюю часть стакана на прилавок. Если бы вы собирали пролившуюся воду, вы бы обнаружили, что это тот же объем, что и у объекта, который вы помещаете в стакан.
Это то, что мы подразумеваем под вытеснением жидкости, и это простой способ измерить объем объекта неправильной формы, поскольку мы можем легко измерить жидкость, которую он выталкивает с пути.И помните, подъемная сила равна весу вытесненной жидкости, а НЕ весу самого объекта.
Это означает, что если вес самого погруженного объекта равен выталкивающей силе (весу вытесняемой жидкости), то объект не будет ни тонуть, ни плавать. Но если вес объекта больше, чем подъемная сила (вес вытесняемой жидкости), то объект утонет. И, если вес объекта меньше выталкивающей силы (все же вес вытесненной жидкости!), То он поднимется на поверхность и всплывет.
Рыба не плавает и не тонет, потому что ее вес равен выталкивающей силе. Но тяжелый валун опускается на дно озера, потому что его вес больше веса жидкости, которую он вытесняет. Кусок дерева плавает на поверхности, потому что его вес намного меньше веса жидкости, которую он вытесняет.
Расчет принципа Архимеда
Принцип Архимеда описывает соотношение между выталкивающей силой и объемом вытесняемой жидкости, а также плотностью вытесняемой жидкости.
Мы можем записать этот принцип в виде уравнения:
F B = ρ f V f g
где F B — выталкивающая сила, ρ f — плотность вытесненной жидкости, V f — объем вытесненной жидкости и g — ускорение свободного падения, 9,8 м / с2.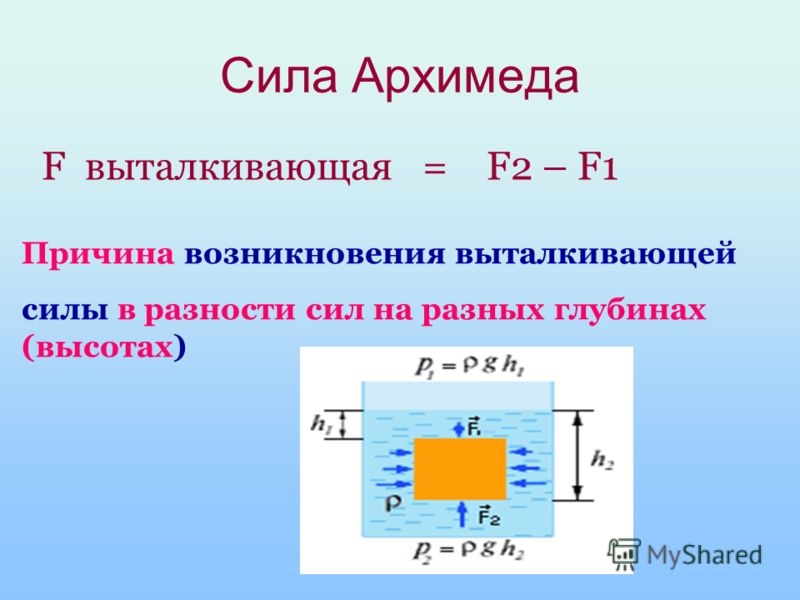 Очень важно помнить, что плотность и объем в этом уравнении относятся к вытесненной жидкости, а НЕ к объекту, погруженному в нее.
Очень важно помнить, что плотность и объем в этом уравнении относятся к вытесненной жидкости, а НЕ к объекту, погруженному в нее.
Это уравнение полезно, поскольку его можно использовать для определения выталкивающей силы, действующей на объект. Например, вы погружаете объект в воду и обнаруживаете, что объект вытесняет 1,0 литр воды. Вода имеет плотность 1,0 кг / л, поэтому теперь у нас есть все необходимое для определения выталкивающей силы, действующей на погружаемый объект, потому что у нас есть объем и плотность вытесненной жидкости. Следовательно, у нас также есть объем объекта, потому что это тот же объем, что и вытесненная жидкость!
Чтобы рассчитать выталкивающую силу, просто введите числа.Теперь наше уравнение гласит: F B = 1,0 кг / л * 1,0 л * 9,8 м / с2. Проведя вычисления, мы обнаружим, что подъемная сила равна 9,8 кг-м / с2, что равно 9,8 Ньютона.
Если вес объекта больше 9,8 Н, он утонет. Если оно меньше 9,8 Н, объект будет плавать. Но если вес объекта равен точно 9,8 Н, то он не утонет и не всплывет, потому что это то же самое, что и выталкивающая сила.
Плавание
Мы уже касались флотации, но плавающие объекты достаточно особенные, чтобы заслужить немного больше времени и объяснений.Вы когда-нибудь видели большой корабль, плывущий по воде? Он плавает по воде, даже если он достаточно тяжелый, и вы можете подумать, что он должен утонуть. В этом случае форма объекта определяет, будет он плавать или нет.
Если вы возьмете весь железный корабль и переплавите его в твердый блок, он займет меньше объема, потому что он займет меньшую площадь. Но это также означает, что он вытесняет меньший объем воды, что, в свою очередь, снижает выталкивающую силу. Железный блок утонет, но железный корабль будет плавать, потому что его широкое дно занимает больше места в воде, вытесняя больше воды и веса, и, следовательно, увеличивает выталкивающую силу, толкающую его вверх.
Фактически, плавающий объект вытесняет жидкость, равную весу объекта. Это известно как принцип плавания , и инженеры принимают это во внимание при проектировании объектов, которым необходимо плавать. Будь то гигантский грузовой корабль или воздушный шар, объект должен перемещать массу жидкости, равную его собственному весу, чтобы парить.
Это известно как принцип плавания , и инженеры принимают это во внимание при проектировании объектов, которым необходимо плавать. Будь то гигантский грузовой корабль или воздушный шар, объект должен перемещать массу жидкости, равную его собственному весу, чтобы парить.
Это также означает, что выталкивающая сила будет больше для объектов в более плотных жидкостях, чем на жидкостях менее плотных.Вы с большей вероятностью будете плавать в соленой воде, чем в пресной, потому что соленая вода плотнее пресной. Но верно и обратное: менее плотные объекты плавают легче, чем более плотные. Например, женщинам легче плавать, чем мужчинам, потому что мужчины более мускулистые (и, следовательно, более плотные), чем женщины. Вы также можете попробовать это с банками из-под газировки — банка диетической газировки будет плавать в воде, а обычная газировка — тонуть. Это связано с тем, что диетическая сода менее плотная, чем обычная сода, поэтому подъемная сила выталкивает ее вверх на поверхность.
Краткое содержание урока
Объекты, погруженные в жидкость, имеют силы, действующие на них со всех сторон, но восходящая сила в жидкости особая, известная как выталкивающая сила . Объекты подпитываются снизу, потому что давление в жидкости увеличивается с глубиной, поэтому сила на нижней части объекта больше, чем на верхней части.
Принцип Архимеда говорит нам, что выталкивающая сила равна весу жидкости, вытесняемой объектом.Если вес объекта больше, чем подъемная сила (вес вытесняемой жидкости), то объект утонет. Если вес объекта меньше выталкивающей силы, объект будет плавать. Но если вес объекта такой же, как вес вытесненной жидкости, то объект не будет ни тонуть, ни плавать.
Плавающие объекты — особый случай, потому что они вытесняют жидкость, равную их собственному весу. Это известно как принцип плавучести , и он говорит нам, почему кусок железа утонет, а широкий железный корабль будет плавать на поверхности.
Результаты обучения
К концу этого урока вы должны уметь:
- Вспомнить принцип Архимеда
- Объясните принцип плавучести
- Определить и рассчитать выталкивающую силу
Принцип Архимеда — Видео по физике от Brightstorm
Хорошо, давайте поговорим о принципе Архимеда. Принцип Архимеда существует очень, очень давно, и он был очень важен для правителей Греции и Египта много лет назад, и мы поговорим о том, почему, через минуту.Итак, Архимед сказал, что подъемная сила, действующая на что-то, равна весу вытесняющей жидкости. Что теперь означает подъемная сила? Выталкивающая сила — это чистая сила, действующая на объект, погруженный в жидкость. Хорошо, у нас есть сила от давления на дно и сила от давления наверху, мы складываем их вместе, нам нужна чистая сила, и это подъемная сила. Итак, Архимед сказал, что подъемная сила — это вес того, сколько жидкости вытесняет объект.Таким образом, подъемная сила равна весу вытесняемой жидкости. Ну что это? Ну, это плотность жидкости, умноженная на объем вытесненной жидкости. Итак, это объем объекта, погруженного в жидкость, умноженный на ускорение свободного падения.
Принцип Архимеда существует очень, очень давно, и он был очень важен для правителей Греции и Египта много лет назад, и мы поговорим о том, почему, через минуту.Итак, Архимед сказал, что подъемная сила, действующая на что-то, равна весу вытесняющей жидкости. Что теперь означает подъемная сила? Выталкивающая сила — это чистая сила, действующая на объект, погруженный в жидкость. Хорошо, у нас есть сила от давления на дно и сила от давления наверху, мы складываем их вместе, нам нужна чистая сила, и это подъемная сила. Итак, Архимед сказал, что подъемная сила — это вес того, сколько жидкости вытесняет объект.Таким образом, подъемная сила равна весу вытесняемой жидкости. Ну что это? Ну, это плотность жидкости, умноженная на объем вытесненной жидкости. Итак, это объем объекта, погруженного в жидкость, умноженный на ускорение свободного падения.
Хорошо, теперь у нас есть 2 основные ситуации, в которых мы можем использовать принцип Архимеда, если объект полностью погружен, то есть весь объект погружен в жидкость, тогда смещенный объем равен объему объекта.Хорошо, теперь это действительно очень просто. Все, что мне нужно знать, это каков объем объекта, и все готово. С другой стороны, если объект плавает, это означает, что он не полностью погружен. Это означает, что смещенный объем на самом деле меньше всего объема, потому что часть его плавает наверху, мы сказали, что он плавает. Таким образом, в плавающей ситуации у нас всегда есть выталкивающая сила, равная весу объекта, потому что объект плавает.А это значит, что его вес должен компенсироваться восходящей силой, что это за восходящая сила? Это подъемная сила, так что это 2 отдельные ситуации, и они совершенно разные.
Мы увидим, что есть уравнения, которые вы можете вывести, которые абсолютно верны, когда объект полностью погружен в воду, но не верны для плавающих объектов. Так что вам просто нужно быть осторожным с этим различием. Итак, почему принцип Архимеда верен? Что ж, мы можем взглянуть на ситуацию, в которой у нас есть объект, погруженный в такую жидкость, как эта, хорошо, теперь, какие силы действуют на этот объект, мы собираемся нарисовать диаграмму свободного тела, потому что мы хорошие физики, поэтому мы у нас есть вес, а затем у нас есть 2 силы, которые действуют от жидкости. Жидкость находится под давлением, поэтому давление внизу и давление вверху. Теперь давление — это сила на единицу площади, и она указывает в любом направлении. Итак, давление внизу, сила, действующая на объект, толкает вверх, потому что в этом направлении, я имею в виду, если он будет толкать объект хорошо, что, он будет толкать вверх, верно? Таким образом, восходящая сила — это давление внизу, умноженное на площадь, потому что сила равна давлению, умноженному на площадь.
Жидкость находится под давлением, поэтому давление внизу и давление вверху. Теперь давление — это сила на единицу площади, и она указывает в любом направлении. Итак, давление внизу, сила, действующая на объект, толкает вверх, потому что в этом направлении, я имею в виду, если он будет толкать объект хорошо, что, он будет толкать вверх, верно? Таким образом, восходящая сила — это давление внизу, умноженное на площадь, потому что сила равна давлению, умноженному на площадь.
Точно так же давление вверху давит вниз.Таким образом, направленная вниз сила — это давление вверху, умноженное на площадь. Теперь выталкивающая сила — это чистая сила, прикладываемая к объекту жидкостью, так что это означает, что она равна давлению внизу, умноженному на площадь, минус давление вверху, умноженное на площадь. Итак, область, которую я могу удалить, потому что она одинакова для верха и низа, это означает, что это изменение давления, умноженное на площадь. Теперь мы знаем, что когда вы погружаетесь в жидкость, давление увеличивается. Насколько прибавка? Что ж, изменение давления определяется плотностью жидкости, умноженной на ускорение из-за силы тяжести, умноженным на то, как далеко вы спустились.Теперь мы спустились на расстояние h, так что посмотрите, что у нас получилось. h, умноженное на a, это смещенный объем, поэтому это означает, что выталкивающая сила равна плотности жидкости, умноженной на ускорение силы тяжести, умноженному на объем смещенного объема. Итак, принцип Архимеда, а почему людям все равно? Одним из самых загадочных применений этого принципа в истории было определение плотности ценных предметов, таких как короны, вазы и тому подобное. Они сделаны из золота или меня пытаются обмануть?
Хорошо, вот идея, все, что вам нужно сделать, это взвесить объект в воздухе, а затем взвесить тот же объект, когда он всплывет в воду.Так почему это работает? Ну вот идея, когда я взвешиваю объект, в основном я делаю то, что у меня есть весы, и я пытаюсь измерить, сколько силы требуется мне, чтобы подвесить объект? Итак, у меня сила натяжения поднимается вверх от моей шкалы, а затем у меня опускается вес, и это должно быть равным друг другу. Когда я взвешиваю его в воздухе, сила натяжения равна мг, равна весу. А как насчет того, чтобы взвесить его в воде? Что ж, когда я взвешиваю его в воде, теперь у меня есть выталкивающая сила, и эта выталкивающая сила зависит от объема короны и плотности воды.Это означает, что у этой выталкивающей силы внутри него есть информация о плотности. Итак, когда я смотрю на это напряжение, это напряжение — это вес короны в воде. Он будет меньше, чем вес короны в воздухе, и разница будет в этой выталкивающей силе. И эта подъемная сила содержит информацию о плотности короны, которую я могу извлечь. И это принцип Архимеда.
Когда я взвешиваю его в воздухе, сила натяжения равна мг, равна весу. А как насчет того, чтобы взвесить его в воде? Что ж, когда я взвешиваю его в воде, теперь у меня есть выталкивающая сила, и эта выталкивающая сила зависит от объема короны и плотности воды.Это означает, что у этой выталкивающей силы внутри него есть информация о плотности. Итак, когда я смотрю на это напряжение, это напряжение — это вес короны в воде. Он будет меньше, чем вес короны в воздухе, и разница будет в этой выталкивающей силе. И эта подъемная сила содержит информацию о плотности короны, которую я могу извлечь. И это принцип Архимеда.
Закон Архимеда
Принцип Архимеда гласит, что:
«Если твердое тело плавает или погружается в жидкость — жидкость оказывает восходящую силу тяги — a выталкивающая сила — на теле равна гравитационной силе, действующей на жидкость, вытесняемую телом.»
Выталкивающая сила может быть выражена как
F B = W
= V γ
= V ρ g (1)
, где
9 B
= подъемная сила, действующая на погруженное или плавающее тело (Н, фунт f )W = вес (сила тяжести) вытесненной жидкости (Н, фунт f )
V = объем тела под поверхностью жидкости (м 3 , футы 3 )
γ = ρ г = удельный вес жидкости (вес на единицу объема) (Н / м 3 , фунт f / фут 3 )
ρ = плотность жидкости (кг / м 3 , снаряды / фут 3 )
g = ускорение гравитация ity (9.81 м / с 2 , 32,174 фут / с 2 )
Пример — Плотность тела, которое плавает в воде
Плавучее тело 95% погружено в воду плотностью 1000 кг / м 3 .
Для плавающего тела выталкивающая сила равна весу воды, вытесняемой телом.
F B = W
или
V b ρ b g = V w ρ w g
V b = объем корпуса (м 3 )
ρ b = плотность корпуса ( кг / м) 4 4 4 3 90
V w = объем воды (м 3 )
плотность воды ( кг / м 3 )
Уравнение можно преобразовать к
90 004 ρ b = V w ρ w / V bТак как 95% корпуса погружено в воду
0.95 V b = V w
и плотность тела может быть рассчитана как
ρ b = 0,95 V b (1000 кг / м 3 ) / V b
= 950 кг / м 3
Пример — Подъемная сила, действующая на кирпич, погруженный в воду
Стандартный кирпич реального размера 3 5/8 x 2 1 / 4 x 8 (дюймов) погружен в воду плотностью 1.940 снарядов / фут 3 . Объем кирпича можно рассчитать
V кирпич = (3 5/8 дюйма) (2 1/4 дюйма) (8 дюймов)
= 65,25 дюйма 3
Выталкивающая сила воздействие на кирпич равно весу воды, вытесненной кирпичом, и может быть рассчитано как
F B = (( 65,25 дюйма 3 ) / (1728 дюймов / фут 3 )) ( 1,940 пули / фут 3 ) ( 32. 174 фут / с 2 )
174 фут / с 2 )
= 2,36 фунта f
Вес или сила тяжести, действующая на кирпич — обычный красный кирпич имеет удельный вес 1,75 — можно рассчитать как
Вт B = (2,36 фунта f ) 1,75
= 4,12 фунта f
Результирующая сила, действующая на кирпич, может быть рассчитана как
W (WB — FB) = (4 .12 фунтов f ) — (2,36 фунта f )
= 1,76 фунта f
14,4 Принцип Архимеда и плавучесть — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определить выталкивающую силу
- Государственный принцип Архимеда
- Опишите взаимосвязь между плотностью и принципом Архимеда
При помещении в жидкость некоторые объекты плавают под действием выталкивающей силы.Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары ((Рисунок))?
Рис. 14.19. (a) Даже тонущие предметы, такие как этот якорь, при погружении частично поддерживаются водой. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию. (c) наполненные гелием воздушные шары тянут вверх свои струны, демонстрируя плавучесть воздуха.(Фото b: модификация работы Allied Navy; кредит c: модификация работы Crystl / Flickr) Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта. На любой объект в любой жидкости действует восходящая сила, или выталкивающая сила , ((рисунок)). Если выталкивающая сила превышает вес объекта, объект поднимается на поверхность и плавает.Если подъемная сила меньше веса объекта, объект тонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила присутствует всегда, независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.
Если выталкивающая сила превышает вес объекта, объект поднимается на поверхность и плавает.Если подъемная сила меньше веса объекта, объект тонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила присутствует всегда, независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.
Плавучая сила
Выталкивающая сила — это сила, направленная вверх на любой объект в любой жидкости.
Рисунок 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что.Это изменение давления и связанная с ним направленная вверх сила в нижней части цилиндра больше, чем направленная вниз сила в верхней части цилиндра. Разница в силе приводит к подъемной силе
.. (Горизонтальные силы отменяются.)
Принцип Архимеда
Насколько велика сила подъема? Чтобы ответить на этот вопрос, подумайте, что происходит, когда погруженный объект удаляется из жидкости, как показано на (Рисунок). Если бы объект не находился в жидкости, пространство, которое занимал объект, было бы заполнено жидкостью, имеющей вес
.Этот вес поддерживается окружающей жидкостью, поэтому подъемная сила должна равняться
.вес жидкости, вытесняемой объектом.
Принцип Архимеда
Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
где
— подъемная сила и
— это вес жидкости, вытесняемой объектом.
Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок. 287–212 гг. До н. Э.), Который сформулировал этот принцип задолго до того, как концепции силы были хорошо установлены.
Рис. 14.21 (a) Объект, погруженный в жидкость, испытывает выталкивающую силу.
Если
больше веса объекта, объект поднимается. Если
меньше веса объекта, объект тонет. (b) Если объект удален, он заменяется жидкостью весом
Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться весу вытесняемой жидкости.
Принцип Архимеда относится к силе плавучести, которая возникает, когда тело погружается в жидкость, частично или полностью. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила, создаваемая давлением внизу, направлена вверх, тогда как вверху сила, обусловленная давлением, направлена вниз; силы из-за давления по бокам направлены внутрь тела.
Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на (Рисунок).Следовательно, на тело действует чистая направленная вверх сила. Эта направленная вверх сила является силой плавучести или просто плавучести .
Плотность и принцип Архимеда
Если вы уроните кусок глины в воду, он утонет. Но если вылепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем кусок, и испытывает большую выталкивающую силу, хотя ее масса такая же. То же самое и со стальными кораблями.
Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он.Если средняя плотность объекта меньше, чем у окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, подъемная сила, равная весу вытесняемой жидкости, превышает вес объекта. Точно так же утонет предмет, более плотный, чем жидкость.
Степень погружения плавающего объекта в воду зависит от того, как плотность объекта сравнивается с плотностью жидкости. На (Рисунок), например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем при загрузке. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения — это отношение погруженного объема к объему объекта, или
На (Рисунок), например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем при загрузке. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения — это отношение погруженного объема к объему объекта, или
Погруженный объем равен объему вытесненной жидкости, который мы называем
.. Теперь мы можем получить соотношение между плотностями, подставив
в выражение.Это дает
где
— средняя плотность объекта и
— плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя
Мы можем использовать это соотношение для измерения плотности.
Рисунок 14.22. Незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).Пример
Расчет средней плотности
Предположим, что женщина весом 60,0 кг плавает в пресной воде с погружением 97,0% ее объема, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Плотность женщины можно найти, решив уравнение
для плотности объекта. Это дает
Мы знаем и долю погруженной воды, и плотность воды, поэтому мы можем вычислить плотность женщины.
Решение
Вводя известные значения в выражение для ее плотности, получаем
Значение
Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.
Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе, » назвать несколько. Менее очевидный пример — горные хребты, плавающие на более плотной коре и мантии под ними.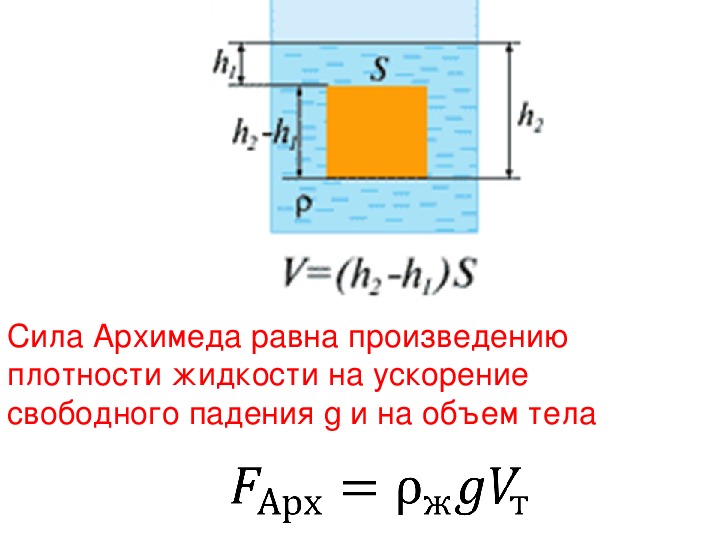 Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Измерение плотности
Один из наиболее распространенных методов определения плотности показан на (Рисунок).
Рис. 14.23 (a) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.Предмет, в данном случае монета, взвешивается на воздухе, а затем снова взвешивается, будучи погруженным в жидкость.Плотность монеты, показатель ее подлинности, может быть вычислена, если плотность жидкости известна. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.
Все эти расчеты основаны на принципе Архимеда, который гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что при погружении объект кажется меньше весит; мы называем это измерение кажущимся весом объекта.Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости. То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.
Сводка
- Подъемная сила — это чистая направленная вверх сила на любой объект в любой жидкости. Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать.Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
- Принцип Архимеда гласит, что подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет.
Концептуальные вопросы
Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста.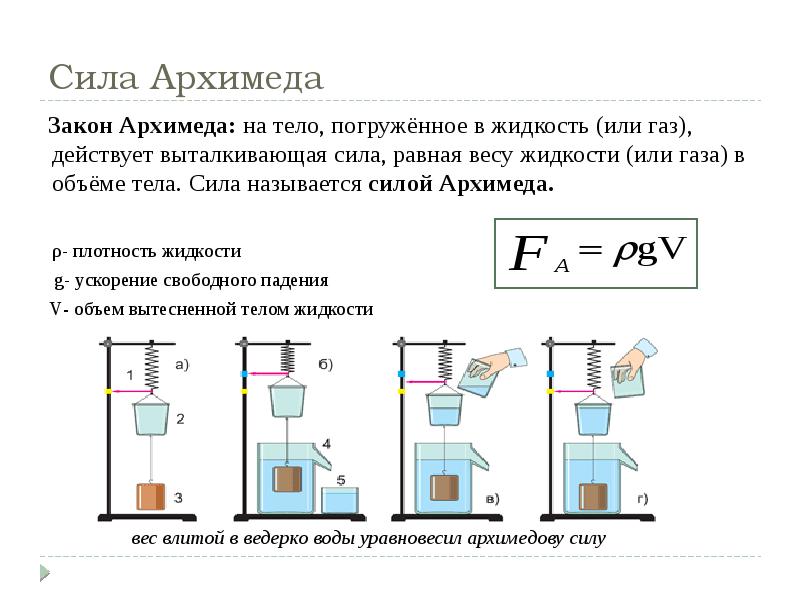 Противоречит ли это принципу Архимеда? Поясните свой ответ.
Противоречит ли это принципу Архимеда? Поясните свой ответ.
[show-answer q = ”fs-id1170958074520 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1170958074520 ″]
Вовсе нет. Принцип Паскаля гласит, что изменение давления происходит через жидкость. Причина, по которой полный бак требует большего усилия для вытягивания пробки, заключается в весе воды над пробкой.
[/ hidden-answer]
Обладают ли жидкости подъемной силой в «невесомой» среде, например в космическом шаттле? Поясните свой ответ.
Будет ли тот же корабль плавать в соленой воде выше, чем в пресной? Поясните свой ответ.
[показывать-ответ q = ”fs-id1170958707558 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170958707558 ″]
Выталкивающая сила равна весу вытесняемой жидкости. Чем больше плотность жидкости, тем меньше жидкости необходимо вытеснить, чтобы удерживать вес объекта и плавать. Поскольку плотность соленой воды выше, чем плотность пресной, будет вытеснено меньше соленой воды, и корабль будет плавать выше.
[/ hidden-answer]
Шарики упали на дно в частично заполненную раковину ванны. Часть их веса поддерживается выталкивающей силой, но сила, направленная вниз на дно ванны, увеличивается ровно на вес шариков. Объяснить, почему.
Проблемы
Какая часть льда погружается в воду, когда плавает в пресной воде, учитывая плотность воды
?очень близко к
?
Если тело человека имеет плотность
, какая часть тела будет погружена в воду при плавном плавании в (а) пресной воде? (б) В соленой воде плотностью
?
[показывать-ответ q = ”fs-id1170958875108 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170958875108 ″]
а.99,5% погружено; б. 96,9% погружено
[/ hidden-answer]
Установлено, что камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? (c) Какова его средняя плотность? Соответствует ли это стоимости гранита?
а) Какая масса воды вытесняется? б) Каков объем камня? (c) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности как жидкости, так и твердого тела. Предположим кусок железа массой 390.Установлено, что 0 г в воздухе имеет кажущуюся массу 350,5 г при полном погружении в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (б) Каков объем железа с учетом его плотности, указанной на (Рисунок)? (c) Рассчитайте плотность жидкости и определите ее.
[показывать-ответ q = ”fs-id1170958537912 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170958537912 ″]
а. 39,5 г; б.
; c.
; этиловый спирт
[/ hidden-answer]
Рассчитайте выталкивающую силу по 2.00-L гелиевый шар. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова чистая вертикальная сила, действующая на воздушный шар, если он отпущен? Пренебрегайте объемом резины.
Какова плотность женщины, плавающей в пресной воде с
? *** QuickLaTeX не может составить формулу:
\ [4.00 \ текст {%} \]
*** Сообщение об ошибке:
Файл завершился при сканировании использования \ text @.
Экстренная остановка.
ее объема над поверхностью? (Это можно было измерить, поместив ее в резервуар с отметками сбоку, чтобы измерить, сколько воды она вытесняет при плавании и под водой.) (б) Какой процент ее объема находится над поверхностью, когда она плавает в морской воде?
[показывать-ответ q = ”fs-id1170958861223 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170958861223 ″]
а.
; б. 6,34%; В морской воде она плавает выше.
[/ hidden-answer]
Человек имеет массу 80 кг и плотность
(без учета воздуха в легких). (а) Рассчитайте его объем. (b) Найдите подъемную силу, которую оказывает на него воздух. в) Какое отношение подъемной силы к его весу?
в) Какое отношение подъемной силы к его весу?
Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки будет погружена в воду при плавании в воде? (b) Если пробка имеет массу 10,0 г и на нее помещен магнит весом 20,0 г, какая часть пробки будет погружена в воду? (c) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
[показывать-ответ q = ”fs-id1170958808514 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170958808514 ″]
а.0,24; б. 0,68; c. Да, пробка будет плавать в этиловом спирте.
[/ hidden-answer]
Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
Ссылаясь на (рисунок), докажите, что выталкивающая сила на цилиндр равна весу вытесняемой жидкости (принцип Архимеда). Вы можете предположить, что подъемная сила равна
.и что концы цилиндра имеют равные площади
.Обратите внимание, что объем цилиндра (и жидкости, которую он вытесняет) равен
..
[показывать-ответ q = ”fs-id1170958626937 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1170958626937 ″]
[/ hidden-answer]
Мужчина весом 75,0 кг плавает в пресной воде, при этом 3,00% его объема над водой, когда его легкие пусты, и 5,00% его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, называемый объемом его легких, в литрах.(б) Кажется ли этот объем легких разумным?
Глоссарий
- Принцип Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- подъемная сила
- чистая направленная вверх сила на любой объект в любой жидкости из-за разницы давлений на разной глубине

 Приветствие.
Приветствие. Какую задачу здесь установим?
Какую задачу здесь установим?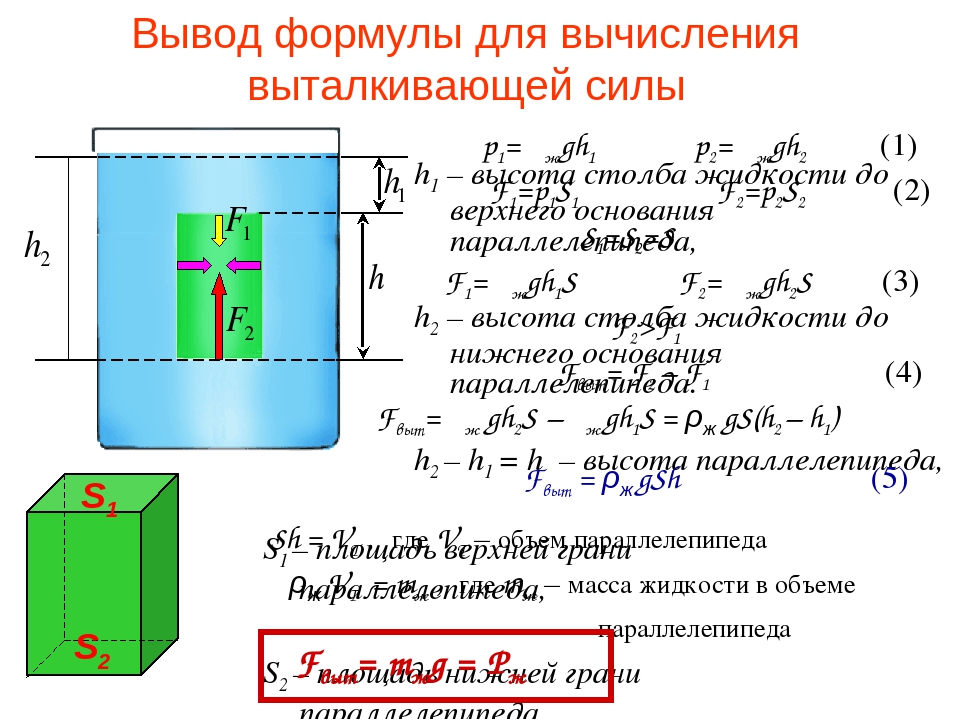
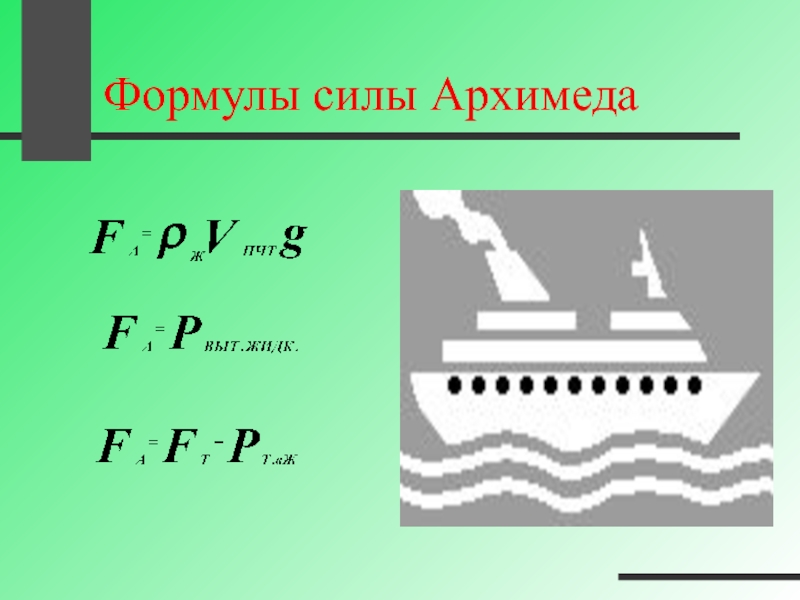 Рефлексия
Рефлексия

 Это может быть намного меньше плотности материала, из которого сделан объект. Например, стальное судно на самом деле в основном заполнено воздухом (подумайте о коридорах, грузовых трюмах и т. Д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Точнее, средняя плотность определяется как общая масса объекта, деленная на его общий объем: [latex] \ bar {\ rho} = \ text {m} / \ text {V} [/ latex].
Это может быть намного меньше плотности материала, из которого сделан объект. Например, стальное судно на самом деле в основном заполнено воздухом (подумайте о коридорах, грузовых трюмах и т. Д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Точнее, средняя плотность определяется как общая масса объекта, деленная на его общий объем: [latex] \ bar {\ rho} = \ text {m} / \ text {V} [/ latex].