Обсуждение:Закон Архимеда — Википедия
 | 18-21 декабря 2006 года сведения из статьи «Закон Архимеда» появлялись на заглавной странице в колонке «Знаете ли вы». В колонке был представлен текст: «По легенде царь Герон II попросил Архимеда определить, является ли его корона подлинной. Вопреки устоявшемуся мнению, Архимеду вовсе не требовался закон Архимеда, чтобы вычислить плотность легендарной короны. Он просто нашёл хороший способ определения объёмов тел неправильной формы». С полным выпуском колонки можно ознакомиться в архиве рубрики «Знаете ли вы». |  |
- Я изменил пример (было: Так, например, закон Архимеда нельзя применить к бочечной пробке, половина которой находится в бочке с жидкостью, а вторая половина находится наружи
- Дейстивительно нельзя применить. ну представьте пробку, вставленну. в дно бочки. Как ни странно, но сила выталкивания направлена вниз, а не вверх. vinograd 15:08, 10 ноября 2006 (UTC)
- Понял. Такой пример как-то перекликается с моим, который в статье. Но описание первым предложением, похоже, некорректное. Как бы его исправить? infovarius 15:20, 10 ноября 2006 (UTC)
- Смешно. Дело в том, что правильной будет формула интеграла по поверхности, но её лучше не писать. Поэтому я склоняюсь к тому, чтобы вообще не упоминать про проблемы применения. Отговорите меня пожалуйста. vinograd 15:42, 10 ноября 2006 (UTC)
- Не хочу отговаривать. Энциклопедия не только для школьников — пусть будет и высшая математика 🙂 Статья пока и так не очень большая — мне кажется, что замечательно будет, если она по тексту будет всё глубже раскрывать основное понятие — это будет действительно полезно. infovarius 14:57, 12 ноября 2006 (UTC)
- Понял. Такой пример как-то перекликается с моим, который в статье. Но описание первым предложением, похоже, некорректное. Как бы его исправить? infovarius 15:20, 10 ноября 2006 (UTC)
- Дейстивительно нельзя применить. ну представьте пробку, вставленну. в дно бочки. Как ни странно, но сила выталкивания направлена вниз, а не вверх. vinograd 15:08, 10 ноября 2006 (UTC)
- Написал про любое однородное поле сил и задумался — а применим ли закон для центрального поля — например, поля тяжести планеты (не у поверхности), или той самой поля центробежной силы? infovarius 14:57, 12 ноября 2006 (UTC)
- Конечно справедлив. vinograd 16:02, 12 ноября 2006 (UTC)
- Да, насчет бочки в дне актуальный пример. На самом деле будет туда направленна, куда интеграл. А как это узнать? Буду думать. Добавил немного высшей математики. Denis Kulagin 19:07, 29 декабря 2006 (UTC)
- Если так рассуждать, то от физики ничего не останется. Во-первых, если бы выталкивающая сила зависела от формы тела, глубины погружения и формы контакта с дном, то закона этого никогда бы не было. Поэтому на пробку, которая хоть в какой-то части погружена в жидкость, будет действовать выталкивающая сила. В случае пробки часть эта ограничена поверхностью раздела пробка-жидкость и поверхностью сечения пробки дном. Кроме этой, на пробку действует сила тяжести (пропорциональна массе) и давление жидкости (которое тоже сила), пропорциональное площади сечения пробки горизонтальной плоскостью и высоте столба жидкости над ним. Нужно сказать, что есть ещё и сила трения между пробкой и стенками отверстия. Придумывать выталкивающую силу, действующую вниз — это в раздел юмора.—Egor 18:04, 7 января 2007 (UTC)
- Не согласен с Егором. Если пробка имеет форму параллелипипеда и вбита в дно, то боковые давления скомпенсированы, а давление на верхнюю поверхность, очевидно, создает силу, направленную вниз. Denis Kulagin 15:33, 2 февраля 2007 (UTC)
- Если пробка вбита в дно, то на неё уже действует сила Паскаля F=ρgh, направленная вниз по оси
у, ну а сила трения между стенками отверстия и пробкой вверх и мешает силе Паскаля. Ярик 15:02, 20 февраля 2007 (UTC)
- Даже в случае герметичного касания телом дна сила Архимеда продолжает действовать на поверхность касания. Просто давление жидкости на дно передаётся дном телу. Все истории про прилипание подлодок к грунту основаны на другом эффекте. —Лёва 12:56, 1 февраля 2013 (UTC)
О выводе формулы для закона Архимеда
Интегралы, конечно, штука хорошая, но сомневаюсь, что Архимед выводил эту формулу именно так. А как насчёт более элементарного доказательства закона? Ярик 10:03, 21 февраля 2007 (UTC)
- Не уверен, что Архимед рисовал какие-то крючки. Думаю он просто знал закон на качественном уровне. Denis Kulagin 07:10, 25 февряля 2007 (UTC)
- Кстати, при выводе используется не формула Остроградского-Гаусса, а интегральная теорема для градиента (см. статью «Градиент»)Clothclub (обс.) 17:51, 11 января 2019 (UTC)
Однотипное обозначение векторов[править код]
Примите, пожалуйста, участие в обсуждении по последним правкам в этой и другим статьям ВП:ВУ#Однотипное обозначение векторов —cаша (krassotkin) 14:00, 7 октября 2009 (UTC)
Закон в невесомости не работает?[править код]
Очень смешно! В отсутствиЕ веса — вес равен 0! Ну, и сила тоже. Она, вместе с законом, может, и не работает (привычным для нас образом, но и невесомость мягко говоря непривычна), но в другом смысле этого слова. Обычно под «не работает» имеется в виду не выполняется. Кстати, по поводу математического «доказательства» (кавычки потому, что неясно, из ЧЕГО закон выводится): очевидное и короткое доказательство в духе «мысленного эксперимента» Галилея, без «вышки», есть в статье «Гидростатика». А еще очень странной кажется история открытия, с «Эврикой». Там Архимед вроде бы и открыл только, как измерять объем тел объемом вытесненной (реально, а не воображаемо) жидкости. (??)
188.134.33.205 09:31, 11 сентября 2011 (UTC)
У космонавтов на орбите космической станции невесомость, но гравитационное поле там присутствует.195.208.248.34 09:07, 18 сентября 2019 (UTC)
В статье следовало бы уточнить информацию о точке приложения силы Архимеда. Такой точкой является центр водоизмещения, который совпадает не с центром тяжести погруженной части тела, а с центром тяжести объема погруженной части тела. Также следует исправить рисунок, где эта точка оказалась совмещена с центром тяжести. ОТ исправленного рисунка уместно сделать ссылку на статью «Плавучесть». PeteSBS 03:53, 22 апреля 2012 (UTC) Сила Архимеда — это результатирующая сила подъёма тела, поэтому у неё недолжно быть одной точки. Вес тела тоже не имеет одной точки. Что подразумевается под «центром тяжести тела»?
судя по ссылке «↑ Легенда приведена у Витрувия, «Об архитектуре», книга IX, глава 3.» легенда должна быть там:
«Витрувий. Десять книг об архитектуре. Содержание.
КНИГА ДЕВЯТАЯ.
ГЛАВА III.
Путь солнца по двенадцати знакам.
1. Когда солнце вступает в знак Овна и проходит восьмую часть его, оно делает весеннее равноденствие. При приближении к хвосту Тельца и к созвездию Плеяд, откуда выступает передняя половина Тельца, оно пробегает в большую половину мирового пространства, продвигаясь к северу. Вступая из Тельца в Близнецов, при восхождении Плеяд, оно еще больше поднимается над землею и увеличивает долготу дня. Затем, вступая из Близнецов в Рака, занимающего наименьшее пространство неба, и достигая восьмой его части, оно делает летнее солнцестояние и, продолжая путь, доходит до головы и груди Льва, относящихся к знаку Рака. 2. По выходе же солнца из груди Льва и пределов Рака и поминовании остальных частей Льва, оно уменьшает величину дня и размеры своей дуги и снова равняет свой пробег с тем, какой был у него в Близнецах. Тут, переходя от Льва к Деве, оно у пазухи ее одежды еще более стягивает свою дугу и уравнивает размеры своего пробега с тем, какой бывает в Тельце. Проходя же от Девы по пазухе, находящейся уже в начале Весов, оно в восьмой части Весов делает осеннее равноденствие. Здесь его пробег бывает равен его дуге в знаке Овна. 3. Когда же солнце вступает в Скорпиона, при захождении Плеяд, оно уменьшает длину дней, приближаясь к южным областям. Когда оно, выходя из Скорпиона, вступает в Стрельца у его бедер, то пролетает по еще более сокращенному дневному пути. Когда же, начиная от бедер Стрельца, относящихся уже к Козерогу, оно доходит до восьмой части этого знака, оно пробегает кратчайшее пространство по небу. Вследствие этого, по краткости дня, пора эта называется кратчайшей (bruma) и кратчайшими днями (dies brumales). Переходя же из Козерога в Водолея, солнце увеличивает долготу дня, уравнивая ее с длиною дней в Стрельце. Из Водолея вступает оно в Рыб, что бывает, когда начинает дуть Фавоний, и здесь его пробег совпадает по длине с пробегом в Скорпионе. Таким образом, солнце, обегая кругом знаки, в определенные времена года увеличивает или уменьшает долготу дней и часов. Теперь я скажу о прочих созвездиях, образованных сочетаниями звезд справа и слева от зодиакального пояса в южной и в северной части мира.»
Ну и где, блин, здесь эта легенда?! =_= 188.19.198.34 14:12, 31 января 2013 (UTC) look-dono
Влияние формы на подъёмну силу.[править код]
Интересуют уточнения по теме силы Архимеда, описывающие влияние формы, если учесть неоднородность силы тяжести и неоднородность плотности (по высоте) среды, вызванной в том числе и неоднородностью силы тяжести по высоте. Тем более, что форма объекта, как известно, влияет и на общий вес самого данного объекта из-за неоднородности силы тяжести по высоте в пределах объёма данного. Например, какая форма сделает «воздухоплавание» или «подводоплавание» более эффективными?
Выталкивающая сила
Цели урока: убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления, содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира.
Задачи урока: Работать над формированием умений анализировать свойства и явления на основе знаний, выделять главную причину, влияющую на результат. Развивать коммуникативные умения. На этапе выдвижения гипотез развивать устную речь. Проверить уровень самостоятельности мышления школьника по применению учащимися знаний в различных ситуациях.
Архимед – выдающийся ученый Древней Греции, родился в 287 году до н.э. в портовом и судостроительном г. Сиракузы на острове Сицилия. Архимед получил блестящее образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона, покровительствовавшего Архимеду. В юности провёл несколько лет в крупнейшем культурном центре в Александрии, где у него сложились дружеские отношения с астрономом Кононом и географом-математиком Эратосфеном. Это послужило толчком к развитию его выдающихся способностей. В Сицилию вернулся уже зрелым ученым. Он прославился многочисленными научными трудами главным образом в области физики и геометрии.
Последние годы жизни Архимед был в Сиракузах, осажденных римским флотом и войском. Шла 2-я Пуническая война. И великий ученый, не жалея сил, организовывает инженерную оборону родного города. Он построил множество удивительных боевых машин, топивших вражеские корабли, разносивших их в щепы, уничтожавших солдат. Однако слишком маленьким было войско защитников города по сравнению с огромным римским войском. И в 212 г. до н.э. Сиракузы были взяты.
Гений Архимеда вызывал восхищение у римлян и римский полководец Марцелл приказал сохранить ему жизнь. Но солдат, не знавший в лицо Архимеда, убил его.
Одним из важнейших его открытий стал закон, впоследствии названный законом Архимеда. Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну, с возгласом “Эврика!” он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину. Суть этой истины и предстоит выяснить, нужно убедиться в существовании выталкивающей силы, осознать причины её возникновения и вывести правила для её вычисления.
Давление в жидкости или газе зависит от глубины погружения тела и приводит к появлению выталкивающей силы, действующей на тело и направленной вертикально вверх.
Если тело опустить в жидкость или газ, то под действием выталкивающей силы оно будет всплывать из более глубоких слоев в менее глубокие. Выведем формулу для определения силы Архимеда для прямоугольного параллелепипеда.
Давление жидкости на верхнюю грань равно
р1 = ж*g*h2,
где: h2 – высота столба жидкости над верхней гранью.
Сила давления на верхнюю грань равна
F1= р1*S = ж*g*h2*S,
Где: S – площадь верхней грани.
Давление жидкости на нижнюю грань равно
р2= ж*g*h3,
где: h3 – высота столба жидкости над нижней гранью.
Сила давления на нижнюю грань равна
F2= p2*S = ж*g*h3*S,
Где: S – площадь нижней грани куба.
Поскольку h3 > h2, то р2 > р1 и F2 > F1.
Разность между силами F2 и F1 равна:
F2 – F1 = ж*g*h3*S – ж*g*h2*S = ж*g*S* (h3 – h2).
Так как h3 – h2 = V – объему тела или части тела, погруженной в жидкость или газ, то F2 – F1 = ж*g*S*H = g* ж*V
Произведение плотности на объем есть масса жидкости или газа. Следовательно, разность сил равна весу вытесненной телом жидкости:
F2 – F1= mж*g = Pж = Fвыт.
Выталкивающая сила есть сила Архимеда, определяющая закон Архимеда
Равнодействующая сил, действующих на боковые грани равна нулю, поэтому в расчетах не участвует.
Таким образом, на тело, погруженное в жидкость или газ, действует выталкивающая сила равная весу вытесненной им жидкости или газа.
Закон Архимеда, впервые был упомянут Архимедом в трактате «О плавающих телах». Архимед писал: «тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела».
Рассмотрим, как зависит сила Архимеда и зависит ли от веса тела, объема тела, плотности тела и плотности жидкости.
Исходя из формулы силы Архимеда, она зависит от
плотности жидкости, в которую погружено тело, и
от объёма этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в
жидкость, так как эта величина не входит в
полученную формулу.
Определим теперь вес тела, погружённого в
жидкость (или газ). Так как две силы, действующие
на тело в этом случае, направлены в
противоположные стороны (сила тяжести вниз, а
архимедова сила вверх), то вес тела в жидкости
будет меньше веса тела в вакууме на архимедову
силу:
PА= mтg – mж g = g (mт – mж )
Таким образам, если тело погружено в жидкость (или газ), то оно теряет в своём весе столько, сколько весит вытесненная им жидкость (или газ).
Следовательно:
Сила Архимеда зависит от плотности жидкости и объема тела или его погруженной части и не зависит от плотности тела, его веса и объема жидкости.
Определение силы Архимеда лабораторным методом.
Оборудование: стакан с чистой водой, стакан с соленой водой, цилиндр, динамометр.
Ход работы:
- определяем вес тела в воздухе;
- определяем вес тела в жидкости;
- находим разницу между весом тела в воздухе и весом тела в жидкости.
4. Результаты измерений:
| № | Сила тяжести в воздухе F1 | Сила тяжести в чистой воде F2 | Сила тяжести в соленой воде F3 | Сила Архимеда FА1 = F1 – F2 FА2 = F1 – F3 |
Сделать вывод как зависит сила Архимеда от плотности жидкости.
Выталкивающая сила действует на тела любых геометрических форм. В технике наиболее распространены тела цилиндрической и сферической форм, тела с развитой поверхностью, полые тела в форме шара, прямоугольного параллелепипеда, цилиндра.
Гравитационная сила приложена к центру масс погруженного в жидкость тела и направлена перпендикулярно к поверхности жидкости.
Подъемная сила действует на тело со стороны жидкости, направлена по вертикали вверх, приложена к центру тяжести вытесненного объема жидкости. Тело движется в направлении, перпендикулярном к поверхности жидкости.
Выясним условия плавания тел, которые основываются на законе Архимеда.
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и силы Архимеда FA, которые действуют на это тело. Возможны следующие три случая:
- Fт > FA — тело тонет;
- Fт = FA — тело плавает в жидкости или газе;
- Fт < FA — тело всплывает до тех пор, пока не начнет плавать.
Другая формулировка (где Pt — плотность тела, Ps — плотность среды, в которую оно погружено):
- Pt > Ps — тело тонет;
- Pt = Ps — тело плавает в жидкости или газе;
- Pt < Ps — тело всплывает до тех пор, пока не начнет плавать.
Плотность организмов живущих в воде почти не отличается от плотности воды, поэтому прочные скелеты им не нужны! Рыбы регулируют глубину погружения, меняя среднюю плотность своего тела. Для этого им необходимо лишь изменить объем плавательного пузыря, сокращая или расслабляя мышцы.
Если тело лежит на дне в жидкости или газе, то сила Архимеда равна нулю.
Закон Архимеда используется в судостроении и воздухоплавании.
Схема плавающего тела:
Линия действия силы тяжести тела G проходит через центр тяжести K (центр водоизмещения) вытесненного объема жидкости. В нормальном положении плавающего тела центр тяжести тела Т и центр водоизмещения K размещены по одной вертикали, называемой осью плаванья.
При качке центр водоизмещения К перемещается в точку К1, и сила тяжести тела и Архимедова сила FА образуют пару сил, которая стремится либо вернуть тело в исходное положение, либо увеличить крен.
В первом случае плавающее тело обладает статической устойчивостью, во втором случае устойчивость отсутствует. Устойчивость тела зависит от взаимного расположения центра тяжести тела Т и метацентра М (точки пересечения линии действия архимедовой силы при крене с осью плавания).
В 1783 году братья МОНГОЛЬФЬЕ изготовили огромный бумажный шар, под которым поместили чашку с горящим спиртом. Шар наполнился горячим воздухом и начал подниматься, достигнув высоты 2000 метров.
Дирижабль является летательным аппаратом легче воздуха и “плавает” в воздухе за счет архимедовых сил, если его средняя плотность меньше или равна плотности атмосферы. Обычно оболочка классического дирижабля наполняется газом легче воздуха (водородом, гелием или метаном), при этом грузоподъёмность дирижабля пропорциональна внутреннему объёму оболочки с учётом массы конструкции. Дирижабль – управляемый летательный аппарат. Перемещение его по горизонтали осуществляется с помощью двигателей.
Ареометры служат для определения плотности жидкости по глубине погружения поплавка. Градуировка производится эмпирически в зависимости от области применения. Измерители кислотности дают процент кислоты, лактометры – процент содержания жира.
Закрепление, тест и домашнее задание
Презентация
03-ж. Вычисление силы Архимеда
§ 03-ж. Вычисление силы Архимеда
В предыдущем параграфе мы назвали две формулы, при помощи которых силу Архимеда можно измерить. Теперь выведем формулу, при помощи которой силу Архимеда можно вычислить.
Закон Архимеда для жидкости выражается формулой (см. § 3-е):
Fарх = Wж
Примем, что вес вытесненной жидкости равен действующей силе тяжести:
Wж = Fтяж = mжg
Масса вытесненной жидкости может быть найдена из формулы плотности:
r = m/V Ю mж = rжVж
Подставляя формулы друг в друга, получим равенство:
Fарх = Wж = Fтяж = mж g = rжVж g
Выпишем начало и конец этого равенства:
Fарх = rж gVж
Вспомним, что закон Архимеда справедлив для жидкостей и газов. Поэтому вместо обозначения «rж» более правильно использовать «rж/г». Также заметим, что объём жидкости, вытесненной телом, в точности равен объёму погруженной части тела: Vж = Vпчт. С учётом этих уточнений получим:
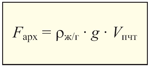
Итак, мы вывели частный случай закона Архимеда – формулу, выражающую способ вычисления силы Архимеда. Вы спросите: почему же эта формула – «частный случай», то есть менее общая?

Поясним примером. Вообразим, что мы проводим опыты в космическом корабле. Согласно формуле Fарх = Wж, архимедова сила равна нулю (так как вес жидкости равен нулю), согласно же формуле Fарх = rж/г gVпчт архимедова сила нулю не равна, так как ни одна из величин (r, g, V) в невесомости в ноль не обращается. Перейдя от воображаемых опытов к настоящим, мы убедимся, что справедлива именно общая формула.
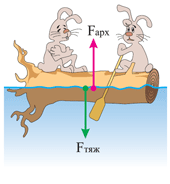
Продолжим наши рассуждения и выведем ещё один частный случай закона Архимеда. Посмотрите на рисунок. Поскольку бревно находится в покое, следовательно, на него действуют уравновешенные силы – сила тяжести и сила Архимеда. Выразим это равенством:
Fарх = Fтяж
Или, подробнее:
rж gVпчт = mт g
Разделим левую и правую части равенства на коэффициент «g»:
rж Vпчт = mт
Вспомнив, что m = rV, получим равенство:
rж Vпчт = rт Vт
Преобразуем это равенство в пропорцию:
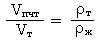
В левой части этой пропорции стоит дробь, показывающая долю, которую составляет объём погруженной части тела от объёма всего тела. Поэтому всю дробь называют погруженной долей тела:
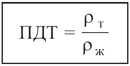
Используя эту формулу, предскажем, чему должна быть равна погруженная доля бревна при его плавании в воде:
ПДТ (полена) » 500 кг/м3 : 1000 кг/м3 = 0,5
Число 0,5 означает, что плавающее в воде бревно погружено наполовину. Так предсказывает теория, и это совпадает с практикой.

Итак, обе формулы в рамках являются менее общими, чем исходная, то есть имеют более узкие границы применимости. Почему же так произошло? Причина – применение нами формулы W = Fтяж. Вспомним, что она не верна, если тело или его опора (подвес) движутся непрямолинейно (см. § 3-г). Упоминавшийся нами космический корабль именно так и движется – по круговой орбите вокруг Земли.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Источник информации
×Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Формула силы выталкивания
ОПРЕДЕЛЕНИЕВыталкивающая сила, она же сила Архимеда, действующая на тело, погружённое в жидкость, равна весу жидкости, вытесненной этим телом.
Здесь – сила Архимеда, – плотность жидкости, – ускорение свободного падения ( м/с), – объём вытесненной жидкости.
Единица измерения силы – Н (ньютон).
Это векторная величина. Причина существования выталкивающей силы – разница в давлении на верхнюю и нижнюю часть тела.
Указанное на рисунке давление из-за большей глубины.Для возникновения силы Архимеда достаточно того, чтобы тело было погружено в жидкость хотя бы частично. Так, если тело плывёт по поверхности жидкости, значит выталкивающая сила, действующая на погружённую в жидкость часть этого тела равна силе тяжести всего тела. Если плотность тела больше плотности жидкости, то тело тонет, если меньше – то всплывает.
Формула верна не только для жидкостей но и для газов.
Примеры решения задач по теме «Сила выталкивания»
| Понравился сайт? Расскажи друзьям! | |||