Закон сохранения массы — Википедия. Что такое Закон сохранения массы
Закон сохранения массы — закон физики, согласно которому масса физической системы сохраняется при всех природных и искусственных процессах.
В метафизической форме, согласно которой вещество несотворимо и неуничтожимо, этот закон известен с древнейших времён. Позднее появилась количественная формулировка, согласно которой мерой количества вещества является вес (с конца XVII века — масса).
С точки зрения классической механики и химии, сохраняются общая масса закрытой физической системы, равная сумме масс компонентов этой системы (то есть масса считается аддитивной). Этот закон с большой точностью верен в области применимости ньютоновской механики и химии, так как релятивистские поправки в этих случаях пренебрежимо малы.
В современной физике концепция и свойства массы существенно пересмотрены. Масса более не является мерой количества вещества, а закон сохранения массы тесно связан с законом сохранения внутренней энергии системы. В отличие от классической модели, сохраняется масса только изолированной физической системы, то есть при отсутствии энергообмена с внешней средой. Не сохраняется сумма масс компонентов системы (масса неаддитивна). Например, при радиоактивном распаде в изолированной системе, состоящей из вещества и радиации, совокупная масса вещества уменьшается, но масса системы сохраняется, несмотря на то что масса радиации может быть нулевая.
Исторический очерк
Закон сохранения массы исторически понимался как одна из формулировок закона сохранения материи. Одним из первых его сформулировал древнегреческий философ Эмпедокл (V век до н. э.)[1]:
Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.
Ранее Эмпедокла «принцип сохранения» применялся представителями Милетской школы для формулировки теоретических представлений о первовеществе, основе всего сущего[2]. Позже аналогичный тезис высказывали Демокрит, Аристотель и Эпикур (в пересказе Лукреция Кара).
Средневековые учёные также не высказывали никаких сомнений в истинности этого закона. Фрэнсис Бэкон в 1620 году провозгласил: «Сумма материи остается всегда постоянной и не может быть увеличена или уменьшена… ни одна мельчайшая её часть не может быть ни одолена всей массой мира, ни разрушена совокупной силой всех агентов, ни вообще как-нибудь уничтожена»[3].
В ходе развития алхимии, а затем и научной химии, было замечено, что при любых химических превращениях суммарный вес реагентов не меняется. В 1630 году Жан Рэ, химик из Перигора, писал Мерсенну[4][5][6]:
Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.
С появлением в трудах Ньютона понятия массы как меры количества вещества, формулировка закона сохранения материи была уточнена: масса есть инвариант, то есть при всех процессах общая масса не уменьшается и не увеличивается (вес, как указал Ньютон, инвариантом не является, поскольку форма Земли далека от идеальной сферы).
В 1673 году опыты Роберта Бойля поставили закон сохранения массы под сомнение — у него при химической реакции с нагреванием вес вещества увеличился. Бойль из этого сделал вывод, что носитель теплоты («флогистон», по тогдашней терминологии) имеет вес; эта гипотеза восстанавливала доверие к сохранению массы. Однако сразу после публикации Бойля французский химик Шерубен д’Орлеан (Chérubin d’Orleans, 1679 год) указал на ошибку Бойля: увеличение веса происходило за счёт воздуха, а в запаянном сосуде вес сохранялся неизменным[7]. Позднее, в 1755 году об этом писал и М. В. Ломоносов в письме Л. Эйлеру (см. текст в Викитеке):
Все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования и т. д.
В СССР на основании этой фразы М. В. Ломоносова объявили автором закона сохранения массы, хотя он никогда не претендовал на такой приоритет и в своём «Обзоре важнейших открытий» данный закон не упоминает. Современные историки подобные претензии считают безосновательными[8][9][10]. Ошибочно мнение, что закон сохранения массы был Ломоносовым доказан опытным путём[11];
Всеобщий закон сформулирован Ломоносовым на основе общефилософских материалистических соображений, никогда не подвергался им сомнению или проверке, а напротив, служил ему твёрдой исходной позицией во всех исследованиях на всём протяжении его жизни.
В дальнейшем, вплоть до создания физики микромира, закон сохранения массы считался истинным и очевидным. Иммануил Кант объявил этот закон постулатом естествознания[12] (1786). Лавуазье в «Начальном учебнике химии» (1789) привёл точную количественную формулировку закона сохранения массы вещества, однако не объявил его каким-то новым и важным законом, а просто упомянул мимоходом как давно известный и достоверно установленный факт. Для химических реакций Лавуазье сформулировал закон в следующих выражениях[13]:
Ничто не творится ни в искусственных процессах, ни в природных, и можно выставить положение, что во всякой операции [химической реакции] имеется одинаковое количество материи до и после, что качество и количество начал остались теми же самыми, произошли лишь перемещения, перегруппировки. На этом положении основано всё искусство делать опыты в химии.
Другими словами, сохраняется масса закрытой физической системы, в которой происходит химическая реакция, а сумма масс всех веществ, вступивших в эту реакцию, равна сумме масс всех продуктов реакции (то есть тоже сохраняется). Масса, таким образом, считается аддитивной.
Современное состояние
В XX веке обнаружились два новых свойства массы.
(M1) Масса физического объекта зависит от его внутренней энергии (см. Эквивалентность массы и энергии). При поглощении внешней энергии масса растёт, при потере — уменьшается. Отсюда следует, что масса сохраняется только в изолированной системе, то есть при отсутствии обмена энергией с внешней средой. Особенно ощутимо изменение массы при ядерных реакциях. Но даже при химических реакциях, которые сопровождаются выделением (или поглощением) тепла, масса не сохраняется, хотя в этом случае дефект массы ничтожен. Академик Л. Б. Окунь пишет[14]:
Чтобы подчеркнуть, что масса тела меняется всегда, когда меняется его внутренняя энергия, рассмотрим два обыденных примера:
- 1) при нагревании железного утюга на 200° его масса возрастает на величину Δm/m≈10−12{\displaystyle \Delta m/m\approx 10^{-12}};
- 2) при полном превращении некоторого количества льда в воду Δm/m≈3.7⋅10−12{\displaystyle \Delta m/m\approx 3.7\cdot 10^{-12}}.
(M2) Масса не является аддитивной величиной: масса системы не равна сумме масс её составляющих. Примеры неаддитивности:
- Электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.
- Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
- При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
- Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).
Таким образом, при физических процессах, которые сопровождаются распадом или синтезом физических структур, не сохраняется сумма масс составляющих (компонентов) системы, но сохраняется общая масса этой (изолированной) системы:
- Масса системы получившихся при аннигиляции фотонов равна массе системы, состоящей из аннигилирующих электрона и позитрона.
- Масса системы, состоящей из дейтрона (с учётом энергии связи), равна массе системы, состоящей из одного протона и одного нейтрона отдельно.
- Масса системы, состоящей из получившегося при термоядерных реакциях гелия, с учётом выделенной энергии, равна массе водорода.
Сказанное означает, что в современной физике закон сохранения массы тесно связан с законом сохранения энергии и выполняется с таким же ограничением — надо учитывать обмен системы энергией с внешней средой.
Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один[15].
Более детально
Чтобы более детально пояснить, почему масса в современной физике оказывается неаддитивной[16] (масса системы не равна — вообще говоря — сумме масс компонент), следует вначале заметить, что под термином масса в современной физике понимается лоренц-инвариантная величина:
- m=E2/c4−p2/c2,{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}},}
где E{\displaystyle E} — энергия, p→{\displaystyle {\vec {p}}} — импульс,c{\displaystyle c} — скорость света. И сразу заметим, что это выражение одинаково легко применимо к точечной бесструктурной («элементарной») частице, так и к любой физической системе, причём в последнем случае энергия и импульс системы вычисляются просто суммированием энергий и импульсов компонент системы (энергия и импульс — аддитивны).
- Можно попутно заметить также, что вектор импульса-энергии системы — это 4-вектор, то есть его компоненты преобразуются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца, поскольку так преобразуются его слагаемые — 4-векторы энергии-импульса составляющих систему частиц. А поскольку масса, определённая выше, есть длина этого вектора в Лоренцевой метрике, то она оказывается инвариантной (лоренц-инвариантной), то есть не зависит от системы отсчёта, в которой её измеряют или рассчитывают.
Кроме того, заметим, что c{\displaystyle c} — универсальная константа, то есть просто число, которое не меняется никогда, поэтому в принципе можно выбрать такую систему единиц измерения, чтобы выполнялось c=1{\displaystyle c=1}, и тогда упомянутая формула будет менее загромождена:
- m=E2−p2,{\displaystyle m={\sqrt {E^{2}-p^{2}}},}
как и остальные связанные с нею формулы (и мы ниже будем для краткости использовать именно такую систему единиц).
Рассмотрев уже самый парадоксальный на вид случай нарушения аддитивности массы — случай, когда система нескольких (для простоты ограничимся двумя) безмассовых частиц (например фотонов) может иметь ненулевую массу, легко увидеть механизм, порождающий неаддитивность массы.
Пусть есть два фотона 1 и 2 с противоположными импульсами: p→1=−p→2{\displaystyle {\vec {p}}_{1}=-{\vec {p}}_{2}}. Масса каждого фотона равна нулю, следовательно можно записать:
- 0=E12−p12,{\displaystyle 0={\sqrt {E_{1}^{2}-p_{1}^{2}}},}
- 0=E22−p22,{\displaystyle 0={\sqrt {E_{2}^{2}-p_{2}^{2}}},}
то есть энергия каждого фотона равна модулю его импульса. Заметим попутно, что масса равна нулю за счет вычитания под знаком корня ненулевых величин друг из друга.
Рассмотрим теперь систему этих двух фотонов как целое, посчитав её импульс и энергию. Как видим, импульс этой системы равен нулю (импульсы фотонов, сложившись, уничтожились, так как эти фотоны летят в противоположных направлениях)[17]:
- p→=p→1+p→2=0→.{\displaystyle {\vec {p}}={\vec {p}}_{1}+{\vec {p}}_{2}={\vec {0}}.}.
Энергия же нашей физической системы будет просто суммой энергий первого и второго фотона:
- E=E1+E2.{\displaystyle E=E_{1}+E_{2}.}
Ну и отсюда масса системы:
- m=E2−p2=E2−0=E≠0,{\displaystyle m={\sqrt {E^{2}-p^{2}}}={\sqrt {E^{2}-0}}=E\neq 0,}
(импульсы уничтожились, а энергии сложились — они не могут быть разного знака).
В общем случае всё происходит аналогично этому, наиболее отчётливому и простому примеру. Вообще говоря, частицы, образующие систему, не обязательно должны иметь нулевые массы, достаточно, чтобы массы были малы или хотя бы сравнимы с энергиями или импульсами[18], и эффект будет большим или заметным. Также видно, что точной аддитивности массы нет практически никогда, за исключением лишь достаточно специальных случаев.
Масса и инертность
Отсутствие аддитивности массы, казалось бы, вносит затруднения. Однако они искупаются не только тем, что определённая так (а не иначе, например, не как энергия деленная на квадрат скорости света) масса оказывается лоренц-инвариантной, удобной и формально красивой величиной, но и имеет физический смысл, точно соответствующий обычному классическому пониманию массы как меры инертности.
А именно для системы отсчёта покоя физической системы (то есть той системы отсчета, в которой импульс физической системы ноль) или систем отсчёта, в которых система покоя медленно (по сравнению со скоростью света) движется, упомянутое выше определение массы
- m=E2/c4−p2/c2{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}}}
— полностью соответствует классической ньютоновской массе (входит во второй закон Ньютона).
Это можно конкретно проиллюстрировать, рассмотрев систему, снаружи (для внешних взаимодействий) являющейся обычным твердым телом, а внутри содержащую быстро движущиеся частицы. Например, рассмотрев зеркальный ящик с идеально отражающими стенками, внутри которого — фотоны (электромагнитные волны).
Пусть для простоты и большей четкости эффекта сам ящик (почти) невесом. Тогда, если, как в рассмотренном в параграфе выше примере, суммарный импульс фотонов внутри ящика ноль, то ящик будет в целом неподвижен. При этом он должен под действием внешних сил (например если мы станем его толкать), вести себя как тело с массой, равной суммарной энергии фотонов внутри, деленной на c2{\displaystyle c^{2}}.
Рассмотрим это качественно. Пусть мы толкаем ящик, и он приобрел из-за этого некоторую скорость вправо. Будем для простоты сейчас говорить только об электромагнитных волнах, бегущих строго вправо и влево. Электромагнитная волна, отражающаяся от левой стенки, повысит свою частоту (вследствие эффекта Доплера) и энергию. Волна, отражающаяся от правой стенки, напротив, уменьшит при отражении свои частоту и энергию, однако суммарная энергия увеличится, так как полной компенсации не будет. В итоге тело приобретет кинетическую энергию, равную mv2/2{\displaystyle mv^{2}/2} (если v<<c{\displaystyle v<<c}), что означает, что ящик ведет себя как классическое тело массы m{\displaystyle m}. Тот же результат можно (и даже легче) получить для отражения (отскока) от стенок быстрых релятивистских дискретных частиц (для нерелятивистских тоже, но в этом случае масса просто окажется[19] суммой масс частиц, находящихся в ящике).
Примечания
- ↑ Пер. Э. Радлова (см., напр. здесь).
- ↑ Энциклопедия Кругосвет
- ↑ Ф. Бэкон, Сочинения, Том 2, Мысль, 1978, стр. 341—342,
- ↑ Jean Rey, Essais sur la recherche de la cause pour laquelle l’étain et le plomb augmentent de poids quand on les calcine, nouvelle édition revue sur l’exemplaire original et augmentée sur les manuscrits de la Bibliothèque du Roi et des Minimes de Paris, avec des notes, par M. Gobet, Paris, Ruault, 1777, p. 21.
- ↑ Van Praagh, Gordon. Physical Chemistry, Experimental and Theoretical: An Introductory Text-book. — Cambridge University Press, 1950. — P. 63. — 295 p.
- ↑ Письмо Жана Рэ
- ↑ Всемирная история физики, 2007, с. 321—322..
- ↑ Шубинский В. И. Ломоносов: Всероссийский человек. — М.: Молодая гвардия, 2010. — С. 346-351.. — 471 с. — (Жизнь замечательных людей). — ISBN 978-5-235-03323-8.
- ↑ Сонин А. С. Несколько эпизодов борьбы с «космополитизмом» в физике. Вестник АН СССР, № 8 (1990), стр. 122—133.
- ↑ Дмитриев И. С. «Одарован самым счастливым остроумием» (Химические работы М. В. Ломоносова в контексте европейской науки века Просвещения). Проверено 19 апреля 2018.
- ↑ Дорфман Я. Г. Закон сохранения массы при химических реакциях и физические воззрения Ломоносова // Ломоносов М.В. Сборник статей и материалов. — М.-Л.: Издательство АН СССР, 1961. — Т. 5. — С. 182-193.
- ↑ И. Кант. Метафизические начала естествознания. Соч., том VI, стр. 148.
- ↑ Лавуазье.
- ↑ Понятие массы, 1989, с. 519.
- ↑ 1917 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 553.
- ↑ Приближенно аддитивной она, конечно же, может быть — в приближении нерелятивистской механики, однако как только в системе имеются движения со скоростями, сравнимыми со скоростью света, аддитивность массы как правило нарушается вполне заметно или даже сильно.
- ↑ Выбрав (по условию) именно противоположные (и равные по величине) импульсы, мы получили сразу же и удобное для нас обстоятельство: первоначально выбранная система отсчёта тогда сразу оказывается системой, в котором система покоится (это и значит формально, что её импульс равен нулю; да это и интуитивно так). Поэтому энергия нашей физической системы, которую мы посчитаем, как раз и будет сразу её энергией покоя.
- ↑ В нашей системе единиц c=1{\displaystyle c=1}, для того, чтобы выразить это условие в других (любых) системах единиц надо не забыть умножать или делить на нужные степени c{\displaystyle c}.
- ↑ В принципе — конечно, лишь приближенно.
Литература
wiki.sc
Закон сохранения массы — WiKi
Закон сохранения массы исторически понимался как одна из формулировок закона сохранения материи. Одним из первых его сформулировал древнегреческий философ Эмпедокл (V век до н. э.)[1]:
Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.
Ранее Эмпедокла «принцип сохранения» применялся представителями Милетской школы для формулировки теоретических представлений о первовеществе, основе всего сущего[2]. Позже аналогичный тезис высказывали Демокрит, Аристотель и Эпикур (в пересказе Лукреция Кара).
Средневековые учёные также не высказывали никаких сомнений в истинности этого закона. Фрэнсис Бэкон в 1620 году провозгласил: «Сумма материи остается всегда постоянной и не может быть увеличена или уменьшена… ни одна мельчайшая её часть не может быть ни одолена всей массой мира, ни разрушена совокупной силой всех агентов, ни вообще как-нибудь уничтожена»[3].
В ходе развития алхимии, а затем и научной химии, было замечено, что при любых химических превращениях суммарный вес реагентов не меняется. В 1630 году Жан Рэ, химик из Перигора, писал Мерсенну[4][5][6]:
Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.
С появлением в трудах Ньютона понятия массы как меры количества вещества, формулировка закона сохранения материи была уточнена: масса есть инвариант, то есть при всех процессах общая масса не уменьшается и не увеличивается (вес, как указал Ньютон, инвариантом не является, поскольку форма Земли далека от идеальной сферы).
В 1673 году опыты Роберта Бойля поставили закон сохранения массы под сомнение — у него при химической реакции с нагреванием вес вещества увеличился. Бойль из этого сделал вывод, что носитель теплоты («флогистон», по тогдашней терминологии) имеет вес; эта гипотеза восстанавливала доверие к сохранению массы. Однако сразу после публикации Бойля французский химик Шерубен д’Орлеан (Chérubin d’Orleans, 1679 год) указал на ошибку Бойля: увеличение веса происходило за счёт воздуха, а в запаянном сосуде вес сохранялся неизменным[7]. Позднее, в 1755 году об этом писал и М. В. Ломоносов в письме Л. Эйлеру (см. текст в Викитеке):
Все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования и т. д.
В СССР на основании этой фразы М. В. Ломоносова объявили автором закона сохранения массы, хотя он никогда не претендовал на такой приоритет и в своём «Обзоре важнейших открытий» данный закон не упоминает. Современные историки подобные претензии считают безосновательными[8][9][10]. Ошибочно мнение, что закон сохранения массы был Ломоносовым доказан опытным путём[11];
Всеобщий закон сформулирован Ломоносовым на основе общефилософских материалистических соображений, никогда не подвергался им сомнению или проверке, а напротив, служил ему твёрдой исходной позицией во всех исследованиях на всём протяжении его жизни.
В дальнейшем, вплоть до создания физики микромира, закон сохранения массы считался истинным и очевидным. Иммануил Кант объявил этот закон постулатом естествознания[12] (1786). Лавуазье в «Начальном учебнике химии» (1789) привёл точную количественную формулировку закона сохранения массы вещества, однако не объявил его каким-то новым и важным законом, а просто упомянул мимоходом как давно известный и достоверно установленный факт. Для химических реакций Лавуазье сформулировал закон в следующих выражениях[13]:
Ничто не творится ни в искусственных процессах, ни в природных, и можно выставить положение, что во всякой операции [химической реакции] имеется одинаковое количество материи до и после, что качество и количество начал остались теми же самыми, произошли лишь перемещения, перегруппировки. На этом положении основано всё искусство делать опыты в химии.
Другими словами, сохраняется масса закрытой физической системы, в которой происходит химическая реакция, а сумма масс всех веществ, вступивших в эту реакцию, равна сумме масс всех продуктов реакции (то есть тоже сохраняется). Масса, таким образом, считается аддитивной.
В XX веке обнаружились два новых свойства массы.
(M1) Масса физического объекта зависит от его внутренней энергии (см. Эквивалентность массы и энергии). При поглощении внешней энергии масса растёт, при потере — уменьшается. Отсюда следует, что масса сохраняется только в изолированной системе, то есть при отсутствии обмена энергией с внешней средой. Особенно ощутимо изменение массы при ядерных реакциях. Но даже при химических реакциях, которые сопровождаются выделением (или поглощением) тепла, масса не сохраняется, хотя в этом случае дефект массы ничтожен. Академик Л. Б. Окунь пишет[14]:
Чтобы подчеркнуть, что масса тела меняется всегда, когда меняется его внутренняя энергия, рассмотрим два обыденных примера:
- 1) при нагревании железного утюга на 200° его масса возрастает на величину Δm/m≈10−12{\displaystyle \Delta m/m\approx 10^{-12}} ;
- 2) при полном превращении некоторого количества льда в воду Δm/m≈3.7⋅10−12{\displaystyle \Delta m/m\approx 3.7\cdot 10^{-12}} .
(M2) Масса не является аддитивной величиной: масса системы не равна сумме масс её составляющих. Примеры неаддитивности:
- Электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.
- Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
- При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
- Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).
Таким образом, при физических процессах, которые сопровождаются распадом или синтезом физических структур, не сохраняется сумма масс составляющих (компонентов) системы, но сохраняется общая масса этой (изолированной) системы:
- Масса системы получившихся при аннигиляции фотонов равна массе системы, состоящей из аннигилирующих электрона и позитрона.
- Масса системы, состоящей из дейтрона (с учётом энергии связи), равна массе системы, состоящей из одного протона и одного нейтрона отдельно.
- Масса системы, состоящей из получившегося при термоядерных реакциях гелия, с учётом выделенной энергии, равна массе водорода.
Сказанное означает, что в современной физике закон сохранения массы тесно связан с законом сохранения энергии и выполняется с таким же ограничением — надо учитывать обмен системы энергией с внешней средой.
Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один[15].
Более детально
Чтобы более детально пояснить, почему масса в современной физике оказывается неаддитивной[16] (масса системы не равна — вообще говоря — сумме масс компонент), следует вначале заметить, что под термином масса в современной физике понимается лоренц-инвариантная величина:
- m=E2/c4−p2/c2,{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}},}
где E{\displaystyle E} — энергия, p→{\displaystyle {\vec {p}}} — импульс,c{\displaystyle c} — скорость света. И сразу заметим, что это выражение одинаково легко применимо к точечной бесструктурной («элементарной») частице, так и к любой физической системе, причём в последнем случае энергия и импульс системы вычисляются просто суммированием энергий и импульсов компонент системы (энергия и импульс — аддитивны).
- Можно попутно заметить также, что вектор импульса-энергии системы — это 4-вектор, то есть его компоненты преобразуются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца, поскольку так преобразуются его слагаемые — 4-векторы энергии-импульса составляющих систему частиц. А поскольку масса, определённая выше, есть длина этого вектора в Лоренцевой метрике, то она оказывается инвариантной (лоренц-инвариантной), то есть не зависит от системы отсчёта, в которой её измеряют или рассчитывают.
Кроме того, заметим, что c{\displaystyle c} — универсальная константа, то есть просто число, которое не меняется никогда, поэтому в принципе можно выбрать такую систему единиц измерения, чтобы выполнялось c=1{\displaystyle c=1} , и тогда упомянутая формула будет менее загромождена:
- m=E2−p2,{\displaystyle m={\sqrt {E^{2}-p^{2}}},}
как и остальные связанные с нею формулы (и мы ниже будем для краткости использовать именно такую систему единиц).
Рассмотрев уже самый парадоксальный на вид случай нарушения аддитивности массы — случай, когда система нескольких (для простоты ограничимся двумя) безмассовых частиц (например фотонов) может иметь ненулевую массу, легко увидеть механизм, порождающий неаддитивность массы.
Пусть есть два фотона 1 и 2 с противоположными импульсами: p→1=−p→2{\displaystyle {\vec {p}}_{1}=-{\vec {p}}_{2}} . Масса каждого фотона равна нулю, следовательно можно записать:
- 0=E12−p12,{\displaystyle 0={\sqrt {E_{1}^{2}-p_{1}^{2}}},}
- 0=E22−p22,{\displaystyle 0={\sqrt {E_{2}^{2}-p_{2}^{2}}},}
то есть энергия каждого фотона равна модулю его импульса. Заметим попутно, что масса равна нулю за счет вычитания под знаком корня ненулевых величин друг из друга.
Рассмотрим теперь систему этих двух фотонов как целое, посчитав её импульс и энергию. Как видим, импульс этой системы равен нулю (импульсы фотонов, сложившись, уничтожились, так как эти фотоны летят в противоположных направлениях)[17]:
- p→=p→1+p→2=0→.{\displaystyle {\vec {p}}={\vec {p}}_{1}+{\vec {p}}_{2}={\vec {0}}.} .
Энергия же нашей физической системы будет просто суммой энергий первого и второго фотона:
- E=E1+E2.{\displaystyle E=E_{1}+E_{2}.}
Ну и отсюда масса системы:
- m=E2−p2=E2−0=E≠0,{\displaystyle m={\sqrt {E^{2}-p^{2}}}={\sqrt {E^{2}-0}}=E\neq 0,}
(импульсы уничтожились, а энергии сложились — они не могут быть разного знака).
В общем случае всё происходит аналогично этому, наиболее отчётливому и простому примеру. Вообще говоря, частицы, образующие систему, не обязательно должны иметь нулевые массы, достаточно, чтобы массы были малы или хотя бы сравнимы с энергиями или импульсами[18], и эффект будет большим или заметным. Также видно, что точной аддитивности массы нет практически никогда, за исключением лишь достаточно специальных случаев.
Масса и инертность
Отсутствие аддитивности массы, казалось бы, вносит затруднения. Однако они искупаются не только тем, что определённая так (а не иначе, например, не как энергия деленная на квадрат скорости света) масса оказывается лоренц-инвариантной, удобной и формально красивой величиной, но и имеет физический смысл, точно соответствующий обычному классическому пониманию массы как меры инертности.
А именно для системы отсчёта покоя физической системы (то есть той системы отсчета, в которой импульс физической системы ноль) или систем отсчёта, в которых система покоя медленно (по сравнению со скоростью света) движется, упомянутое выше определение массы
- m=E2/c4−p2/c2{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}}}
— полностью соответствует классической ньютоновской массе (входит во второй закон Ньютона).
Это можно конкретно проиллюстрировать, рассмотрев систему, снаружи (для внешних взаимодействий) являющейся обычным твердым телом, а внутри содержащую быстро движущиеся частицы. Например, рассмотрев зеркальный ящик с идеально отражающими стенками, внутри которого — фотоны (электромагнитные волны).
Пусть для простоты и большей четкости эффекта сам ящик (почти) невесом. Тогда, если, как в рассмотренном в параграфе выше примере, суммарный импульс фотонов внутри ящика ноль, то ящик будет в целом неподвижен. При этом он должен под действием внешних сил (например если мы станем его толкать), вести себя как тело с массой, равной суммарной энергии фотонов внутри, деленной на c2{\displaystyle c^{2}} .
Рассмотрим это качественно. Пусть мы толкаем ящик, и он приобрел из-за этого некоторую скорость вправо. Будем для простоты сейчас говорить только об электромагнитных волнах, бегущих строго вправо и влево. Электромагнитная волна, отражающаяся от левой стенки, повысит свою частоту (вследствие эффекта Доплера) и энергию. Волна, отражающаяся от правой стенки, напротив, уменьшит при отражении свои частоту и энергию, однако суммарная энергия увеличится, так как полной компенсации не будет. В итоге тело приобретет кинетическую энергию, равную mv2/2{\displaystyle mv^{2}/2} (если v<<c{\displaystyle v<<c} ), что означает, что ящик ведет себя как классическое тело массы m{\displaystyle m} . Тот же результат можно (и даже легче) получить для отражения (отскока) от стенок быстрых релятивистских дискретных частиц (для нерелятивистских тоже, но в этом случае масса просто окажется[19] суммой масс частиц, находящихся в ящике).
ru-wiki.org
Закон сохранения массы веществ — параграф 19 ГДЗ химия 8 Рудзитис
1. Сформулируйте закон сохранения массы веществ и объясните его с точки зрения атомно-молекулярного учения. Проиллюстрируйте его примерами.
Масса веществ, вступивших в химическую реакцию, равна массе продуктов реакции. Это связано с тем, что в результате химической реакции происходит только перегруппировка атомов.
Примеры: масса сульфида железа будет равна массе массе серы и железа, вступивших в реакцию. Если прокаливать некоторое вещество (железо, магний, фосфор) в закрытой колбе, заполненной воздухом, то масса колбы не измениться. Хотя из вещества образуется оксид.
Я особо выделили слово химическая реакция. Т.к. есть еще ядерные реакции, в которых изменение массы веществ возможно.
2. В реторту насыпали порошок цинка, закрыли газоотводную трубку зажимом, реторту взвесили и содержимое прокалили. Когда реторта остыла, ее вновь взвесили. Изменилась ли ее масса и почему? Затем открыли зажим. Остались ли чашки весов в равновесии и почему?
Реторта была закрыта, поэтому ее масса после прокаливания не изменилась.
После открытия реторты чашки весов вышли из равновесия. В результате прокаливания цинка произошла химическая реакция:
2Zn +O2 = 2 ZnO
в результате которой кислород воздуха перешел в оксид и давление внутри реторты упало (стало ниже атмосферного давления воздуха). Поэтому, при открытии реторты, внутрь устремился воздух.
3. Почему при горении спиртовки масса спирта постоянно уменьшается? Не нарушается ли при этом закон сохранения массы веществ?
При горении спирта образуются газообразные продукты горения, которые улетучиваются. Поэтому никакого нарушения закона сохранения массы веществ нет. Если проводить горение спиртовки в замкнутом сосуде, то мы увидим, что масса сосуда со спиртовкой остается постоянной.
C2H6O + 3O2 = 2CO2↑ + 3H2O↑
4. Какое теоретическое и практическое значение имеет закон сохранения массы веществ? Приведите примеры.
Теоретическое значение: закон способствовал дальнейшему развитию химии как науки.
Практическое значение: позволяет рассчитывать массу продуктов реакции, зная массу исходных веществ. И наоборот, зная массу продукта для получения, можно рассчитать массу исходных веществ. Кроме того, зная соотношения масс исходных веществ и продуктов реакции, можно составлять уравнения химических реакций.
Тестовые задания
Медь соединяется с серой в массовом отношении 2 : 1. Для приготовления 21 г сульфида меди (II) потребуется:
1) Cu — 14 г, S — 7 г; 3) Cu — 7 г, S — 14 г;
2) Cu — 12 г, S — 9 г; 4) Cu — 16 г, S — 5 г;
Из условий задачи нам известно, что масса продукта (сульфида меди) равна 21 г. Согласно закону сохранения массы веществ, масса меди и серы также будет равна 21 г.
m (CuS) = m (Cu) + m (S)
Также нам известно, что меди для реакции требуется в 2 раза больше, чем серы, поэтому:
m (CuS) = 2*m (Cu) + m (S)
Или:
2*m (Cu) + m (S) = 21
Откуда: m (Cu) = 14 г, m (S) = 7 г.
Ответ: 1.
2. При разложении 4,34 г оксида ртути (II) образовалось 4,02 г ртути. Масса выделившегося при этом кислорода равна
1) 0,16 г; 2) 0,32 г; 3) 3,2 г; 4) 1,6 г
Согласно закону сохранения массы веществ, масса оксида ртути равна массе ртути и кислорода:
m (HgO) = m (Hg) + m (O)
Значит:
m (O) = m (HgO) — m (Hg) = 4,34 — 4,02 = 0,32 г
Ответ: 2.
himgdz.ru
Закон сохранения массы в химии. Открытие закона :: SYL.ru
Закон сохранения массы является основой для расчета физических процессов во всех сферах человеческой деятельности. Его справедливость не оспаривается ни физиками, ни химиками, ни представителями других наук. Этот закон, как строгий бухгалтер, следит за соблюдением точной массы вещества до и после его взаимодействия с другими веществами. Честь открытия этого закона принадлежит русскому ученому М. В. Ломоносову.
Первоначальные представления о составе веществ
Строение вещества на протяжении многих веков оставалось тайной для любого человека. Различные гипотезы будоражили ученые умы и подвигали мудрецов на длительные и бессмысленные споры. Один утверждал, что все состоит из огня, другой отстаивал совершенно иную точку зрения. В массе теорий промелькнула и была незаслуженно забыта теория древнегреческого мудреца Демокрита о том, что все вещества состоят из крошечных, невидимых глазу мельчайших частиц вещества. Демокрит назвал их «атомами», что значит «неделимые». К сожалению, в течение целых 23 веков его предположение было забыто.
Алхимия
В основном научные данные средних веков базировались на предрассудках и различных домыслах. Возникает и широко распространяется алхимия, которая представляла собой свод скромных практических познаний, тесно сдобренных самыми фантастическими теориями. Например, известные умы того времени старались превратить свинец в золото и найти неведомый философский камень, исцеляющий от всех болезней. В процессе поисков постепенно накапливался научный опыт, состоящий из многих необъясненных реакций химических элементов. Например, было выяснено, что многие вещества, названные впоследствии простыми, не распадаются. Таким образом возродилась древняя теория о неделимых частичках материи. Понадобился великий ум, чтобы превратить этот склад информации в стройную и логичную теорию.

Теория Ломоносова
Точным количественным методом исследования химия обязана русскому ученому М. В. Ломоносову. За блестящие способности и упорный труд он получил звание профессора химии и стал членом Российской академии наук. При нем была организованна первая в стране современная химическая лаборатория, в которой и был открыт знаменитый закон сохранения массы веществ.

В процессе изучения течения химических реакций Ломоносов взвешивал исходные химические вещества и продукты, появившиеся после проведения реакции. При этом он открыл и сформулировал закон сохранения массы вещества. В 17 веке понятие массы часто путали с термином «вес». Поэтому массы веществ часто называли «весами». Ломоносов определил, что строение вещества находится в прямой зависимости от частичек, из которых оно построено. Если содержит частички одного сорта, то такое вещество ученый называл простым. При разнородном составе корпускул получается сложное вещество. Эти теоретические данные позволили Ломоносову сформулировать закон сохранения массы.
Определение закона
После многочисленных экспериментов М. В. Ломоносов установил закон, суть которого сводилась к следующему: вес веществ, которые вступили в реакцию, равен весу веществ, которые получились в итоге реакции.

В русской науке данный постулат носит название «Закон сохранения массы веществ Ломоносова».
Это закон был сформулирован в 1748 году, а самые точные эксперименты с реакцией обжига металлов в запаянных сосудах были проведены в 1756 году.
Опыты Лавуазье
Европейская наука открыла закон сохранения массы после публикации описания работ великого французского химика Антуана Лавуазье.
 Этот ученый смело применял в своих экспериментах теоретические представления и физические методы того времени, что позволило ему разработать химическую номенклатуру и создать реестр всех известных на то время химических веществ.
Этот ученый смело применял в своих экспериментах теоретические представления и физические методы того времени, что позволило ему разработать химическую номенклатуру и создать реестр всех известных на то время химических веществ.Своими экспериментами Лавуазье доказал, что в процессе любой химической реакции соблюдается закон сохранения массы веществ, вступающих в соединение. Кроме этого, он расширил распространение закона сохранения на массу каждого из элементов, которые принимали участие в реакции в составе сложных веществ.
Таким образом, на вопрос, кто открыл закон сохранения массы веществ, можно ответить двояко. М. В. Ломоносов первым провел эксперименты, наглядно демонстрирующие закон сохранения, и подвел его под теоретическую базу. А. Лавуазье в 1789 году независимо от русского ученого самостоятельно открывает закон сохранения масс и распространяет его принцип на все элементы, участвующие в химической реакции.
Масса и энергия
В 1905 году великий А. Эйнштейн показал связь между массой вещества и его энергией. Она выражалась формулой:
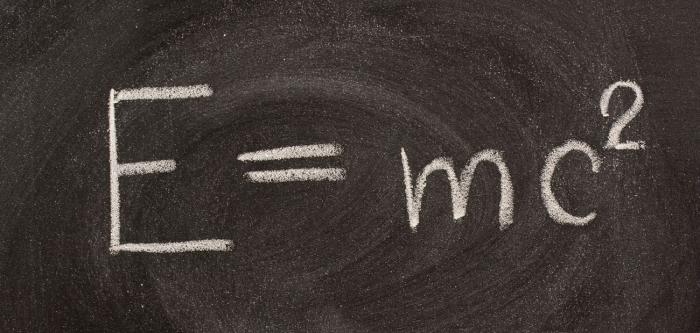
Уравнение Эйнштейна подтверждает закон сохранения массы и энергии. Данная теория утверждает, что всякая энергия имеет массу и изменение этой энергии несет изменение массы тела. Потенциальная энергия любого тела очень велика, и высвободиться она может лишь в особых условиях.
Закон сохранения массы справедлив для любых тел микро- и макромира. Любая химическая реакция принимает участие в преобразовании внутренней энергии вещества. Поэтому при расчете массы веществ, участвующих в химических реакциях, нужно было бы учитывать прирост или убыль массы, вызванных выделением или поглощением энергии в данной реакции. На самом деле в макромире этот эффект настолько незначителен, что такие изменения можно не принимать во внимание.
www.syl.ru
Закон сохранения массы — Википедия
Закон сохранения массы — закон физики, согласно которому масса физической системы сохраняется при всех природных и искусственных процессах.
В метафизической форме, согласно которой вещество несотворимо и неуничтожимо, этот закон известен с древнейших времён. Позднее появилась количественная формулировка, согласно которой мерой количества вещества является вес (с конца XVII века — масса).
С точки зрения классической механики и химии, сохраняются общая масса закрытой физической системы, равная сумме масс компонентов этой системы (то есть масса считается аддитивной). Этот закон с большой точностью верен в области применимости ньютоновской механики и химии, так как релятивистские поправки в этих случаях пренебрежимо малы.
В современной физике концепция и свойства массы существенно пересмотрены. Масса более не является мерой количества вещества, а закон сохранения массы тесно связан с законом сохранения внутренней энергии системы. В отличие от классической модели, сохраняется масса только изолированной физической системы, то есть при отсутствии энергообмена с внешней средой. Не сохраняется сумма масс компонентов системы (масса неаддитивна). Например, при радиоактивном распаде в изолированной системе, состоящей из вещества и радиации, совокупная масса вещества уменьшается, но масса системы сохраняется, несмотря на то что масса радиации может быть нулевая.
Исторический очерк
Закон сохранения массы исторически понимался как одна из формулировок закона сохранения материи. Одним из первых его сформулировал древнегреческий философ Эмпедокл (V век до н. э.)[1]:
Ничто не может произойти из ничего, и никак не может то, что есть, уничтожиться.
Ранее Эмпедокла «принцип сохранения» применялся представителями Милетской школы для формулировки теоретических представлений о первовеществе, основе всего сущего[2]. Позже аналогичный тезис высказывали Демокрит, Аристотель и Эпикур (в пересказе Лукреция Кара).
Средневековые учёные также не высказывали никаких сомнений в истинности этого закона. Фрэнсис Бэкон в 1620 году провозгласил: «Сумма материи остается всегда постоянной и не может быть увеличена или уменьшена… ни одна мельчайшая её часть не может быть ни одолена всей массой мира, ни разрушена совокупной силой всех агентов, ни вообще как-нибудь уничтожена»[3].
В ходе развития алхимии, а затем и научной химии, было замечено, что при любых химических превращениях суммарный вес реагентов не меняется. В 1630 году Жан Рэ, химик из Перигора, писал Мерсенну[4][5][6]:
Вес настолько тесно привязан к веществу элементов, что, превращаясь из одного в другой, они всегда сохраняют тот же самый вес.
Оригинальный текст (фр.)
La pesanteur est si étroitement jointe à la première matière des éléments que, se changeant de l’un en l’autre, ils gardent toujours le même poids.
С появлением в трудах Ньютона понятия массы как меры количества вещества, формулировка закона сохранения материи была уточнена: масса есть инвариант, то есть при всех процессах общая масса не уменьшается и не увеличивается (вес, как указал Ньютон, инвариантом не является, поскольку форма Земли далека от идеальной сферы).
В 1673 году опыты Роберта Бойля поставили закон сохранения массы под сомнение — у него при химической реакции с нагреванием вес вещества увеличился. Бойль из этого сделал вывод, что носитель теплоты («флогистон», по тогдашней терминологии) имеет вес; эта гипотеза восстанавливала доверие к сохранению массы. Однако сразу после публикации Бойля французский химик Шерубен д’Орлеан (Chérubin d’Orleans, 1679 год) указал на ошибку Бойля: увеличение веса происходило за счёт воздуха, а в запаянном сосуде вес сохранялся неизменным[7]. Позднее, в 1755 году об этом писал и М. В. Ломоносов в письме Л. Эйлеру (см. текст в Викитеке):
Все встречающиеся в природе изменения происходят так, что если к чему-либо нечто прибавилось, то это отнимается у чего-то другого. Так, сколько материи прибавляется к какому-либо телу, столько же теряется у другого, сколько часов я затрачиваю на сон, столько же отнимаю от бодрствования и т. д.
В СССР на основании этой фразы М. В. Ломоносова объявили автором закона сохранения массы, хотя он никогда не претендовал на такой приоритет и в своём «Обзоре важнейших открытий» данный закон не упоминает. Современные историки подобные претензии считают безосновательными[8][9][10]. Ошибочно мнение, что закон сохранения массы был Ломоносовым доказан опытным путём[11];
Всеобщий закон сформулирован Ломоносовым на основе общефилософских материалистических соображений, никогда не подвергался им сомнению или проверке, а напротив, служил ему твёрдой исходной позицией во всех исследованиях на всём протяжении его жизни.
В дальнейшем, вплоть до создания физики микромира, закон сохранения массы считался истинным и очевидным. Иммануил Кант объявил этот закон постулатом естествознания[12] (1786). Лавуазье в «Начальном учебнике химии» (1789) привёл точную количественную формулировку закона сохранения массы вещества, однако не объявил его каким-то новым и важным законом, а просто упомянул мимоходом как давно известный и достоверно установленный факт. Для химических реакций Лавуазье сформулировал закон в следующих выражениях[13]:
Ничто не творится ни в искусственных процессах, ни в природных, и можно выставить положение, что во всякой операции [химической реакции] имеется одинаковое количество материи до и после, что качество и количество начал остались теми же самыми, произошли лишь перемещения, перегруппировки. На этом положении основано всё искусство делать опыты в химии.
Другими словами, сохраняется масса закрытой физической системы, в которой происходит химическая реакция, а сумма масс всех веществ, вступивших в эту реакцию, равна сумме масс всех продуктов реакции (то есть тоже сохраняется). Масса, таким образом, считается аддитивной.
Современное состояние
В XX веке обнаружились два новых свойства массы.
(M1) Масса физического объекта зависит от его внутренней энергии (см. Эквивалентность массы и энергии). При поглощении внешней энергии масса растёт, при потере — уменьшается. Отсюда следует, что масса сохраняется только в изолированной системе, то есть при отсутствии обмена энергией с внешней средой. Особенно ощутимо изменение массы при ядерных реакциях. Но даже при химических реакциях, которые сопровождаются выделением (или поглощением) тепла, масса не сохраняется, хотя в этом случае дефект массы ничтожен. Академик Л. Б. Окунь пишет
Чтобы подчеркнуть, что масса тела меняется всегда, когда меняется его внутренняя энергия, рассмотрим два обыденных примера:
- 1) при нагревании железного утюга на 200° его масса возрастает на величину Δm/m≈10−12{\displaystyle \Delta m/m\approx 10^{-12}};
- 2) при полном превращении некоторого количества льда в воду Δm/m≈3.7⋅10−12{\displaystyle \Delta m/m\approx 3.7\cdot 10^{-12}}.
(M2) Масса не является аддитивной величиной: масса системы не равна сумме масс её составляющих. Примеры неаддитивности:
- Электрон и позитрон, каждый из которых обладает массой, могут аннигилировать в фотоны, не имеющие массы поодиночке, а обладающие ею только как система.
- Масса дейтрона, состоящего из одного протона и одного нейтрона, не равна сумме масс своих составляющих, поскольку следует учесть энергию взаимодействия частиц.
- При термоядерных реакциях, происходящих внутри Солнца, масса водорода не равна массе получившегося из него гелия.
- Особенно яркий пример: масса протона (≈938 МэВ) в несколько десятков раз больше массы составляющих его кварков (около 11 МэВ).
Таким образом, при физических процессах, которые сопровождаются распадом или синтезом физических структур, не сохраняется сумма масс составляющих (компонентов) системы, но сохраняется общая масса этой (изолированной) системы:
- Масса системы получившихся при аннигиляции фотонов равна массе системы, состоящей из аннигилирующих электрона и позитрона.
- Масса системы, состоящей из дейтрона (с учётом энергии связи), равна массе системы, состоящей из одного протона и одного нейтрона отдельно.
- Масса системы, состоящей из получившегося при термоядерных реакциях гелия, с учётом выделенной энергии, равна массе водорода.
Сказанное означает, что в современной физике закон сохранения массы тесно связан с законом сохранения энергии и выполняется с таким же ограничением — надо учитывать обмен системы энергией с внешней средой.
Дорелятивистская физика знала два фундаментальных закона сохранения, а именно:закон сохранения энергии и закон сохранения массы; оба эти фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности слила их в один[15].
Более детально
Чтобы более детально пояснить, почему масса в современной физике оказывается неаддитивной[16] (масса системы не равна — вообще говоря — сумме масс компонент), следует вначале заметить, что под термином масса в современной физике понимается лоренц-инвариантная величина:
- m=E2/c4−p2/c2,{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}},}
где E{\displaystyle E} — энергия, p→{\displaystyle {\vec {p}}} — импульс,c{\displaystyle c} — скорость света. И сразу заметим, что это выражение одинаково легко применимо к точечной бесструктурной («элементарной») частице, так и к любой физической системе, причём в последнем случае энергия и импульс системы вычисляются просто суммированием энергий и импульсов компонент системы (энергия и импульс — аддитивны).
- Можно попутно заметить также, что вектор импульса-энергии системы — это 4-вектор, то есть его компоненты преобразуются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца, поскольку так преобразуются его слагаемые — 4-векторы энергии-импульса составляющих систему частиц. А поскольку масса, определённая выше, есть длина этого вектора в Лоренцевой метрике, то она оказывается инвариантной (лоренц-инвариантной), то есть не зависит от системы отсчёта, в которой её измеряют или рассчитывают.
Кроме того, заметим, что c{\displaystyle c} — универсальная константа, то есть просто число, которое не меняется никогда, поэтому в принципе можно выбрать такую систему единиц измерения, чтобы выполнялось c=1{\displaystyle c=1}, и тогда упомянутая формула будет менее загромождена:
- m=E2−p2,{\displaystyle m={\sqrt {E^{2}-p^{2}}},}
как и остальные связанные с нею формулы (и мы ниже будем для краткости использовать именно такую систему единиц).
Рассмотрев уже самый парадоксальный на вид случай нарушения аддитивности массы — случай, когда система нескольких (для простоты ограничимся двумя) безмассовых частиц (например фотонов) может иметь ненулевую массу, легко увидеть механизм, порождающий неаддитивность массы.
Пусть есть два фотона 1 и 2 с противоположными импульсами: p→1=−p→2{\displaystyle {\vec {p}}_{1}=-{\vec {p}}_{2}}. Масса каждого фотона равна нулю, следовательно можно записать:
- 0=E12−p12,{\displaystyle 0={\sqrt {E_{1}^{2}-p_{1}^{2}}},}
- 0=E22−p22,{\displaystyle 0={\sqrt {E_{2}^{2}-p_{2}^{2}}},}
то есть энергия каждого фотона равна модулю его импульса. Заметим попутно, что масса равна нулю за счет вычитания под знаком корня ненулевых величин друг из друга.
Рассмотрим теперь систему этих двух фотонов как целое, посчитав её импульс и энергию. Как видим, импульс этой системы равен нулю (импульсы фотонов, сложившись, уничтожились, так как эти фотоны летят в противоположных направлениях)[17]:
- p→=p→1+p→2=0→.{\displaystyle {\vec {p}}={\vec {p}}_{1}+{\vec {p}}_{2}={\vec {0}}.}.
Энергия же нашей физической системы будет просто суммой энергий первого и второго фотона:
- E=E1+E2.{\displaystyle E=E_{1}+E_{2}.}
Ну и отсюда масса системы:
- m=E2−p2=E2−0=E≠0,{\displaystyle m={\sqrt {E^{2}-p^{2}}}={\sqrt {E^{2}-0}}=E\neq 0,}
(импульсы уничтожились, а энергии сложились — они не могут быть разного знака).
В общем случае всё происходит аналогично этому, наиболее отчётливому и простому примеру. Вообще говоря, частицы, образующие систему, не обязательно должны иметь нулевые массы, достаточно, чтобы массы были малы или хотя бы сравнимы с энергиями или импульсами[18], и эффект будет большим или заметным. Также видно, что точной аддитивности массы нет практически никогда, за исключением лишь достаточно специальных случаев.
Масса и инертность
Отсутствие аддитивности массы, казалось бы, вносит затруднения. Однако они искупаются не только тем, что определённая так (а не иначе, например, не как энергия деленная на квадрат скорости света) масса оказывается лоренц-инвариантной, удобной и формально красивой величиной, но и имеет физический смысл, точно соответствующий обычному классическому пониманию массы как меры инертности.
А именно для системы отсчёта покоя физической системы (то есть той системы отсчета, в которой импульс физической системы ноль) или систем отсчёта, в которых система покоя медленно (по сравнению со скоростью света) движется, упомянутое выше определение массы
- m=E2/c4−p2/c2{\displaystyle m={\sqrt {E^{2}/c^{4}-p^{2}/c^{2}}}}
— полностью соответствует классической ньютоновской массе (входит во второй закон Ньютона).
Это можно конкретно проиллюстрировать, рассмотрев систему, снаружи (для внешних взаимодействий) являющейся обычным твердым телом, а внутри содержащую быстро движущиеся частицы. Например, рассмотрев зеркальный ящик с идеально отражающими стенками, внутри которого — фотоны (электромагнитные волны).
Пусть для простоты и большей четкости эффекта сам ящик (почти) невесом. Тогда, если, как в рассмотренном в параграфе выше примере, суммарный импульс фотонов внутри ящика ноль, то ящик будет в целом неподвижен. При этом он должен под действием внешних сил (например если мы станем его толкать), вести себя как тело с массой, равной суммарной энергии фотонов внутри, деленной на c2{\displaystyle c^{2}}.
Рассмотрим это качественно. Пусть мы толкаем ящик, и он приобрел из-за этого некоторую скорость вправо. Будем для простоты сейчас говорить только об электромагнитных волнах, бегущих строго вправо и влево. Электромагнитная волна, отражающаяся от левой стенки, повысит свою частоту (вследствие эффекта Доплера) и энергию. Волна, отражающаяся от правой стенки, напротив, уменьшит при отражении свои частоту и энергию, однако суммарная энергия увеличится, так как полной компенсации не будет. В итоге тело приобретет кинетическую энергию, равную mv2/2{\displaystyle mv^{2}/2} (если v<<c{\displaystyle v<<c}), что означает, что ящик ведет себя как классическое тело массы m{\displaystyle m}. Тот же результат можно (и даже легче) получить для отражения (отскока) от стенок быстрых релятивистских дискретных частиц (для нерелятивистских тоже, но в этом случае масса просто окажется[19] суммой масс частиц, находящихся в ящике).
Примечания
- ↑ Пер. Э. Радлова (см., напр. здесь).
- ↑ Энциклопедия Кругосвет
- ↑ Ф. Бэкон, Сочинения, Том 2, Мысль, 1978, стр. 341—342,
- ↑ Jean Rey, Essais sur la recherche de la cause pour laquelle l’étain et le plomb augmentent de poids quand on les calcine, nouvelle édition revue sur l’exemplaire original et augmentée sur les manuscrits de la Bibliothèque du Roi et des Minimes de Paris, avec des notes, par M. Gobet, Paris, Ruault, 1777, p. 21.
- ↑ Van Praagh, Gordon. Physical Chemistry, Experimental and Theoretical: An Introductory Text-book. — Cambridge University Press, 1950. — P. 63. — 295 p.
- ↑ Письмо Жана Рэ
- ↑ Всемирная история физики, 2007, с. 321—322..
- ↑ Шубинский В. И. Ломоносов: Всероссийский человек. — М.: Молодая гвардия, 2010. — С. 346-351.. — 471 с. — (Жизнь замечательных людей). — ISBN 978-5-235-03323-8.
- ↑ Сонин А. С. Несколько эпизодов борьбы с «космополитизмом» в физике. Вестник АН СССР, № 8 (1990), стр. 122—133.
- ↑ Дмитриев И. С. «Одарован самым счастливым остроумием» (Химические работы М. В. Ломоносова в контексте европейской науки века Просвещения). Проверено 19 апреля 2018.
- ↑ Дорфман Я. Г. Закон сохранения массы при химических реакциях и физические воззрения Ломоносова // Ломоносов М.В. Сборник статей и материалов. — М.-Л.: Издательство АН СССР, 1961. — Т. 5. — С. 182-193.
- ↑ И. Кант. Метафизические начала естествознания. Соч., том VI, стр. 148.
- ↑ Лавуазье.
- ↑ Понятие массы, 1989, с. 519.
- ↑ 1917 г. Эйнштейн А. Собрание научных трудов. Том 1. стр. 553.
- ↑ Приближенно аддитивной она, конечно же, может быть — в приближении нерелятивистской механики, однако как только в системе имеются движения со скоростями, сравнимыми со скоростью света, аддитивность массы как правило нарушается вполне заметно или даже сильно.
- ↑ Выбрав (по условию) именно противоположные (и равные по величине) импульсы, мы получили сразу же и удобное для нас обстоятельство: первоначально выбранная система отсчёта тогда сразу оказывается системой, в котором система покоится (это и значит формально, что её импульс равен нулю; да это и интуитивно так). Поэтому энергия нашей физической системы, которую мы посчитаем, как раз и будет сразу её энергией покоя.
- ↑ В нашей системе единиц c=1{\displaystyle c=1}, для того, чтобы выразить это условие в других (любых) системах единиц надо не забыть умножать или делить на нужные степени c{\displaystyle c}.
- ↑ В принципе — конечно, лишь приближенно.
Литература
wikipedia.green
Сохранения массы закон — это… Что такое Сохранения массы закон?
- Сохранения массы закон
- исторически сложившееся в химии (См. Химия) название закона, по котором у общая масса (вес) веществ, вступающих в реакцию, равна общей массе (весу) продуктов реакции. С. м. з. был открыт М. В. Ломоносовым в 1748 и им же экспериментально подтвержден в 1756 на примере обжигания металлов в запаянных сосудах. Широкое распространение в химии закон получил благодаря трудам А. Лавуазье, который сформулировал его в 1789. С. м. з. лежит в основе количественных расчётов реакций химических (См. Реакции химические). Строго говоря, с точки зрения современных представлений о связи между массой и энергией, закон не точен (см. Сохранения законы).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Сохранения законы
- Сохранная расписка
Смотреть что такое «Сохранения массы закон» в других словарях:
СОХРАНЕНИЯ МАССЫ ЗАКОН — общая масса веществ, вступающих в химическую реакцию, равна общей массе продуктов реакции. Открытый М. В. Ломоносовым (1748), в общем виде сформулирован А. Лавуазье (1789). Современная формулировка закона сохранения массы: сумма массы вещества… … Большой Энциклопедический словарь
сохранения массы закон — общая масса веществ, вступающих в химическую реакцию, равна общей массе продуктов реакции. Открытый М. В. Ломоносовым (1748), в общем виде сформулирован А. Лавуазье (1789). Современная формулировка закона сохранения массы: сумма массы вещества… … Энциклопедический словарь
СОХРАНЕНИЯ МАССЫ ЗАКОН — общая масса в в, вступивших в хим. р цию, равна общей массе продуктов р ции. При этом под массой понимали величину, характеризующую кол во материи. В нач. 20 в. формулировка С. м. з. подверглась пересмотру в связи с появлением теории… … Химическая энциклопедия
СОХРАНЕНИЯ МАССЫ ЗАКОН — общая масса в в, вступающих в хим. реакцию, равна общей массе продуктов реакции. Открытый М. В. Ломоносовым (1748), в общем виде сформулирован А. Лавуазье (1789). Совр. формулировка С. м. з.: сумма массы в ва системы и массы, эквивалентной… … Естествознание. Энциклопедический словарь
Сохранения массы закон — … Википедия
СОХРАНЕНИЯ ЭНЕРГИИ ЗАКОН — в изолир. системе энергия системы остается постоянной, возможны лишь переходы одного вида энергии в другой. В термодинамике С. э. з. соответствует первое начало термодинамики, к рое выражается ур нием Q = DU + W, где Q кол во сообщенной системе… … Химическая энциклопедия
СОХРАНЕНИЯ ЭНЕРГИИ ЗАКОН — фундамент, закон природы, согласно к рому энергия сохраняется в изолир. системе; она может только переходить из одной формы в другую, но её кол во остаётся постоянным. С. э. з. является строгим законом природы, справедливым для всех известных… … Естествознание. Энциклопедический словарь
Закон сохранения массы — Механика сплошных сред … Википедия
ЗАКОН СОХРАНЕНИЯ МАССЫ — фундаментальный закон нерелятивистской ньютоновской механики, согласно которому масса вещества, поступающего в замкнутую систему, либо накапливается в ней, либо покидает ее, т. е. масса поступающего в систему вещества минус масса выходящего из… … Экологический словарь
ЗАКОН СОХРАНЕНИЯ МАССЫ — важнейший закон химии, установленный в 1748 г. М. В. Ломоносовым, а позже и А. Л. Лавуазье. В соответствии с этим законом общая масса всех веществ, участвующих в хим. реакции, в ее начале равна их массе в конце, какие бы реакции ни происходили.… … Большая политехническая энциклопедия
dic.academic.ru
Закон сохранения массы веществ.
Тема урока: Закон сохранения массы веществ.
Цель урока: Познакомить учащихся с законом сохранения массы,
его сущностью и значением.
На основании закона сохранения массы веществ
научить учащихся записывать уравнения реакций и
подбирать в них коэффициенты.
Оборудование: портрет М.В Ломоносова, Лавуазье, весы со стаканами, компьютер, мультимедийная доска.
Тип урока: урок формирования знаний ,навыков и умений.
Ход урока.
Организация деятельности учащихся.
Актуализация опорных знаний.
Что изучает химия?
Что такое атом, молекула?
Согласно какому принципу составляются формулы ?
Перечислите элементы с постоянной и переменной
Валентностью?
*Перечислите физические и химические явления .
*Перечислить известные реакции, проходящие в природе.
Изучение нового материала.
Подумайте и дайте свой вариант ответа. Спали в топке 1 кг угля
Собрали выделяющийся газ и то, что осталось после горения и сложили. Совпадет исходная масса до и после реакции или нет.
Варианты ответов: а) останется неизменным, б) изменится.
Просмотр видео-нагревание железа реторте.
Закон сохранения массы в химических реакциях был сформулирован на основе работ по прокаливанию металлов.
В XVIIвеке английский ученый Р.Бойль проводил опыты по прокаливанию свинца. (Обсуждение просмотренного фрагмента)
Русский ученый М.В.Ломоносов повторил опыты Р.Бойля(обсуждение просмотренного фрагмента)
В 1748 г. М.В Ломоносов сделал вывод» Все перемены в натуре случающиеся, суть такого состояния, что сколько чего у одного тела отнимется, столько у другого присовокупится»
В 1789 году французский химик А.Лавуазье объяснил причину разных результатов взвешивания. Он доказал, что образование окалины происходит за счет присоединения к металлу кислорода, содержащегося в воздухе.
На основании работ М.В.Ломоносова и А Лавуазье был сформулирован закон сохранения массы.
« Масса веществ вступивших в реакцию, равна массе
образовавшихся веществ»
С точки зрения атомно-молекулярного учения этот закон объясняется тем, что при химических реакциях общее количество атомов не изменяется, а происходит лишь их перегруппировка.
Закон сохранения массы веществ является основополагающим законом химии-все расчеты по химическим реакциях проводятся на его основе. Именно с открытием этого закона связывают возникновение современной химии как точной науки.
Закон сохранения массы веществ применяется при составлении уравнений реакции.
Химические уравнения-это условная запись химической реакции при помощи химических формул и коэффициентов.
Подобрать коэффициенты -это « уравновесить число атомов до и после реакции»
Правила составления и записи химических реакций.
Вещества, вступающие в реакцию, называются исходными веществами или реагентами.
*Вещества, образующиеся в результате реакции, называются продуктами реакции.
Подберем коэффициенты в реакции
Al + S→Al2S3
В левой части ( до реакции) 1 атом алюминия, а после-2.Значит, перед атомом алюминия ставим коэффициент 2
2Al + S →Al2S3 Теперь проверяем серу- до реакции 1 атом, а после-3 атома. Значит, согласно закона сохранения массы ,число атомов должно быть одинаковым Перед атомом серы в левой части ставим коэффициент3.
2 Al + 3 S → Al2S3 коэффициенты подобраны.
P + O 2 →P2O5
В таких реакциях желательно подбирать коэффициенты с того элемента, где больше атомов- -это кислород. В правой частиих-2, в правой-5. Находим наименьшее общее кратное(НОК) Это число 10 и делим его на количество атомов. Это и будут коэффициенты -перед кислородом-5, а перед всей формулой после реакции-2
Р + 5 О2 →2 Р2О5 Но мы увеличили число атомов фосфора- их после реакции-1, а после- 4. Значит, пере атомом фосфора ставим коэффициент4. Уравнение принимает окончательный вид
4 Р + 5 О2→2 Р2О5.
Fe(OH)3→ Fe2O3 + H2O
Начинаем подбор коэффициентов с железа.
2 Fe(OH)3 → Fe2O3 + H2O Остаются два элемента-кислород и водород. В сложных реакциях. В отличие от двух первых реакций лучше и проще заканчивать подбор-кислородом.
До реакции водорода-6 атомов, а после-2. Перед формулой воды ставим коэффициент3.
2 Fe(OH)3→ Fe2O3 + 3 H2O.
*Пример более трудной реакции.
Na + h3O →NaOH + h3 В подобных реакциях надо посмотреть на число атомов водорода- До реакци-их 2 и они в одном соединении Н2О. После реакции он в разных соединениях. В соединении NaOH -он 1(нечетное число), а в воде-2( четное число) Чтобы подобрать коэффициенты, надо перед веществом, там, где нечетное число атомов ,поставить коэффициент-2( удвоить)
Na + 2 h3O →2 NaOH + h3 Поставив коэффициенты 2 были уравновешены атомы и водорода и кислорода. Поставив коэффициент 2 перед NaOH , было увеличено число атомов натрия. Значит, перед атомом натрия до реакции надо тоже поставить коэффициент 2
2 Na+2 NaOH →2 NaOH + h3
*Еще один пример» трудной» реакции
HNO3→NO +H2O + O2 В данной реакции легко и быстро будут
Подобраны коэффициенты, если удвоить атомы кислорода.
HNO3→2 NO +2 H2O + O2 Удвоив число атомов водорода, надо перед молекулой исходного вещества поставить коэффициент 4
4 HNO3 → 2 NO + 2 h3O + O2В этой реакции надо будет изменить число атомов азота в веществе NO c 2 на 4-
и уравнение принимает вид.
4HNO3→4 NO +2 Н2О + О2. И последним проверяем кислород. До реакции его-12, после-7. Значит, перед молекулой кислорода надо поставить коэффициент3
4 HNO3→4NO +2 H2O + 3 O2
Получив определенные навыки подбора коэффициентов,
Предлагается новый вид задания- записав уравнение реакции, надо « доказать» действие закона сохранения массы вешеств , Na + Cu(NO3)2 →NaNO3 + Cu
Первое действие-подобрать коэффициенты
2Na + Cu(NO3)2 →2NaNO3 + Cu
2.Определить и подписать под формулами значения атом
ных и молекулярных масс
2Na + Cu(NO3)2 →2 NaNO3 + Cu
46 + 188 170 + 64
234 = 234
И еще одно задание, где предлагается составить уравнения реакций между простыми вещества , составить формулы продуктов реакции согласно валентности и подобрать в этих реакциях коэффициенты.
Составить уравнения реакций между натрием, кальцием, и алюминием с кислородом, составить формулу продуктов реакции и подобрать коэффициенты.
Надо напомнить ученикам, что некоторые элементы могут быть одновременно и атомами и молекулами. Если атом-то нет индекса 2. Если молекула-обязательно у элемента индекс 2
Атом O H CI Br I F N
Молекула O2 h3 CI2 Br2 I2 F2 N2
Na + O2→Na2O Ca + O2 →CaO AI + O2→Al2О3
С коэффициентами уравнения принимает правильный вид
4 Na + O2 →2 Na2O 2 Ca + O2 →2 CaO 4 Al+ 3O2→2Al2O3
Закрепление изученного материала.
Что называется химической реакцией?
Сформулировать закон сохранения массы.
Почему этот закон еще называют « Законом сохранения материи»
Как называются еще иначе исходные вещества?
Какое правило составления уравнения реакции?
Подобрать коэффициенты в следующих реакциях:
Na + H3PO4 →Na3PO4 + h3
KNO3→KNO2 + O2
H2O2→H2O + O2
Задание на дом: 1. Выучить параграф №
Тщательно прочитать конспект урока.
Выполнить письменно № .
infourok.ru