Антимагия. Квадратное уравнение с чётным вторым коэффициентом. | Партизанская математика
В прошлой статье из серии Антимагия мы показали, как решаются квадратные уравнения в общем виде. Там мы рассмотрели, что такое дискриминант, откуда он появляется и зачем он нужен.
Однако помимо общей формулы для решения квадратных уравнений есть и частные случаи, для которых есть свои более удобные способы решения. В первую очередь это касается случая, когда второй коэффициент в квадратном уравнении чётный.
*********
Например, решим такое уравнение:
Используем уже знакомый нам алгоритм и постараемся выделить слева полный квадрат:
Обратите внимание, как легко удалось это сделать. За счёт того, что второй коэффициент был чётным, мы сразу выделили множитель 2, который отвечает за удвоение в формуле квадрата двучлена. То есть одночлен с x стал равен 2⋅3⋅x, откуда становится очевидным, что второе слагаемое в двучлене это 3.
Теперь проведём наши рассуждения для более общего случая. Пусть у нас второй коэффициент в квадратном уравнении — чётный. Тогда удобно записать наше уравнение в виде:
Решим это уравнение также через выделение полного квадрата:
Однако, пока мы рассмотрели лишь приведённое квадратное уравнение (то есть такое, в котором коэффициент при равен 1). Для неприведённого уравнения алгоритм такой же, только сначала нам нужно будет разделить его на первый коэффициент. После этого повторим алгоритм поиска корней для полученного уравнения.
Квадратный корень удобно упростить:
В итоге получаем следующие корни:
И окончательный результат для корней:
Есть и другой способ получить ту же самую формулу.
Для уравнения ax²+bx+c=0 мы уже знаем формулы корней
Возьмём теперь уравнение ax²+2kx+c=0 и используем для его решения общую формулу корней.
Далее, на примере первого корня, упростим получившиеся дроби:
Для второго корня результат аналогичен:
Выражение k²—ac называется сокращённым дискриминантом или коротко «дэ на четыре» (т.к. оно в 4 раза меньше обычного дискриминанта).
*********
Сокращённый дискриминант старшеклассники используют не часто. Обычно запоминают формулу для простого дискриминанта и не видят необходимости в поиске корней через сокращённый дискриминант. Или же используют более продвинутые способы решения.
Однако, во многих случаях он может быть полезен.
Например, решим такое уравнение через обычный дискриминант:
Сразу намечаются некоторые вычислительные сложности.
Нужно посчитать 38² (это обычно делается столбиком), потом 4⋅9⋅8 (можно в уме, но на практике чаще тоже считают столбиком), потом вычесть результаты (1444—288, тоже столбиком).
Получается дискриминант равен 1156. Но ведь из него ещё нужно правильно извлечь корень! Мало кто помнит квадрат какого числа равен 1156. Приходится дополнительно находить этот корень подбором по соответствующему алгоритму. Получим, что дискриминант равен 34².
Далее находим сами корни:
С сокращённым же дискриминантом вычисления будут гораздо проще:
38 = 2k, т.е. k = 19
19² легко посчитать, т.к. квадраты чисел до 20 часто знают наизусть. Вычитание можно выполнить в уме. А что 289 = 17² мы получаем снова благодаря знанию таблицы квадратов.
И сами корни легко ищутся по формулам:
Ещё отметим, что при расчёте через дискриминант с чётным вторым коэффициентом вам всегда нужно будет сокращать дроби на 2. Это лишнее действие, которое при сокращённом дискриминанте отсутствует.
Конечно, чтобы овладеть этим инструментом нужна практика. Обычно ученики ленятся запоминать эту формулу и просто пытаются всё посчитать через обычный дискриминант. Также поначалу они забывают, что в знаменателе уже нет умножения на 2 или что первое слагаемое в числителе не число b, а k (то есть его половина, b/2). В таком случае важно несмотря на ошибки всё равно пробовать решать через сокращённый дискриминант, даже если не удаётся запомнить формулу с первого раза.
Обычно ученики ленятся запоминать эту формулу и просто пытаются всё посчитать через обычный дискриминант. Также поначалу они забывают, что в знаменателе уже нет умножения на 2 или что первое слагаемое в числителе не число b, а k (то есть его половина, b/2). В таком случае важно несмотря на ошибки всё равно пробовать решать через сокращённый дискриминант, даже если не удаётся запомнить формулу с первого раза.
Рекомендации учащимся 8-го класса по изучению темы «Решение квадратных уравнений»
Что нужно знать и уметь, чтобы решать квадратные уравнения.
- Определение квадратного уравнения;
- Формула дискриминанта квадратного уравнения;
- Формула корней квадратного уравнения;
- Формулы дискриминанта и корней квадратного уравнения, если второй коэффициент четное число;
- Теорема Виета.
Выучи и запомни!
Квадратным уравнением называется уравнение
вида abx
+ c = 0, где x – переменная, a 0, b,c —некоторые числа.
Числа a, b и c – коэффициенты квадратного уравнения. Число a называют первым коэффициентом, b – вторым коэффициентом и c – свободным членом.
Дискриминантом квадратного уравнения abx + c = 0 (“дискриминант” по-латыни – различитель)
- Если D>0, то квадратное уравнение имеет два действительных корня;
- Если D=0, то квадратное уравнение имеет один действительный корень;
- Если D<0, то квадратное уравнение действительных корней не имеет.
Формула корней квадратного уравнения имеет вид:
При решении квадратного уравнения по формуле целесообразно поступать следующим образом:
- Вычислить дискриминант и сравнить его с нулем;
- Если дискриминант положителен или равен нулю,
то воспользоваться формулой корней, если
дискриминант отрицателен, то записать, что
действительных корней нет.

Для квадратных уравнений, у которых второй коэффициент является четным числом, формулу корней удобно записывать в другом виде:
, где k = .
Полезно запомнить, что если сумма коэффициентов квадратного уравнения равна нулю, то один из корней равен единице.
Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Справедливо утверждение, обратное теореме Виета.
Теорема. Если числа m и n таковы, что их сумма равна –p, а произведение равно q, то эти числа являются корнями уравнения х + px + q =0.
Теперь попробуй выполнить следующие задания.
1. Для каждого уравнения вида abx + c = 0 укажи значения
a, b, c.
а) 3х + 6x -9 = 0;
б) х — 4x +4 = 0;
в) х — 2x -15 = 0;
г) -3х + 8x -18 = 0;
2.
а) 5х — 7х + 2 = 0, D = (-7)? -
4*5*2 = 49 – 40 = …;
б) х — х – 2 = 0, D = (-1)? -
4*1*(-2) = …;
в) х — 2x -15 = 0, D = (-2) — 4 …;
г) -3х + 8x -18 = 0, D = …;
3. Внимательно рассмотри решение квадратных уравнений. 3х — 5х – 2 = 0:
Вычислим дискриминант по формуле D = b — 4 ac. D =(-5) — 4*3*(-2) = 25 + 24 =49, D>0, значит уравнение имеет два действительных корня. Найдем их значения по формуле . = = 2, = = — =- . Ответ: 2; ;
9х — 6х + 1 = 0: D=0, значит, уравнение имеет один действительный корень=; 9х — 6х + 10 = 0: D= 36 – 360 = — 324, D< 0, значит, уравнение действительных корней не имеет.
4. Реши уравнение:
а) 3х — 13х + 4 = 0;
б) 2х — 9х -5 = 0;
в) 5х — 13х + 6 = 0;
г) 9х — 12х + 4 = 0;
д) 4х — х + 1 = 0;
е) 49х — 28х + 3 = 0.
Проверь себя!
Дискриминант равен а) 121; б) 121; в) 49; г) 0; д) -15; е) 196.
Ответ: а); 4; б) ; 5; в) ; 2; г) ; д) корней нет; е) и .
Оцени себя!
- Если все уравнения решены правильно, то молодец! Работа выполнена на 5 баллов.
- Если допустил одну ошибку, то ничего страшного. Будь внимательней! Работа выполнена на 4 балла.
- Если ошибок намного больше, не огорчайся. Помни! Не ошибается тот, кто ничего не делает. Попробуй еще раз.
Советую изучить следующую литературу:
- Энциклопедический словарь юного математика. А.П.Савин-М:Педагогика,1985-352с.
- Математика. Школьная энциклопедия. С.М.Никольский -М: Большая Российская энциклопедия. Дрофа 1997-527с.
- За страницами учебника алгебры. Л.Ф.Пичурин.
Москва, Просвещение, 2008г.

- Алгебра, учебник для 8 класса. В.Г. Дорофеев. Москва, Просвещение, 2010г.
- Алгебра, учебник для 8 класса. А.Г.Мордкович. Москва, Просвещение, 2008г.
- Алгебра, учебник для 8 класса Ю. Н. Макарычев, Н. Г. Миндюк, К.И.Нешков, С. Б. Суворова. Москва, Просвещение, 2010г.
Как решается через дискриминант. Решение квадратных уравнений
Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.
О каких уравнениях пойдет речь?
На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.
Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.
Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.
Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.
Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.
Решения уравнения в математике называют его корнями.
Способы решения уравнений второго порядка
Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:
- с помощью факторизации;
- используя формулу для полного квадрата;
- применяя график соответствующей квадратичной функции;
- используя уравнение дискриминанта.
Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.
Формула для получения корней уравнения
Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).
Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).
Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.
В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).
В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.
Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.
Она имеет вид, который представлен на фото ниже.
Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.
Понятие о дискриминанте
В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.
Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:
- D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
- D=0: у уравнения всего один корень, и он является действительным числом.
Задача на определение дискриминанта
Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.
Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.
Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.
Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.
Пример неравенства через дискриминант
Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.
В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Решение полученного неравенства приводит к результату: c>-3.
Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.
Пример решения уравнения
Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.
В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.
Геометрическая задача
Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.
У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.
Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.
Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.
Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.
», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Важно!
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
- 5x 2 − 14x + 17 = 0
- −x 2 + x + = 0
- x 2 + 0,25x = 0
- x 2 − 8 = 0
Важно! Общий вид квадратного уравнения выглядит так:
A x 2 + b x + c = 0
«a », «b » и «c » — заданные числа.- «a » — первый или старший коэффициент;
- «b » — второй коэффициент;
- «c » — свободный член.
Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».
Давайте потренируемся определять
коэффициенты «a
», «b
»
и «c
» в квадратных уравнениях.
| Уравнение | Коэффициенты |
|---|---|
| |
| x 2 − 8 = 0 |
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .
Запомните!
Чтобы решить квадратное уравнение нужно:
- привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
- использовать формулу для корней:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
X 2 − 3x − 4 = 0
Уравнение «
x 2 − 3x − 4 = 0
» уже приведено к общему виду «ax 2 + bx + c = 0
» и не требует дополнительных упрощений.
Определим коэффициенты «a », «b » и «c » для этого уравнения.
x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
С её помощью решается любое квадратное уравнение.
В формуле «x 1;2 =
» часто заменяют подкоренное выражение
«b 2 − 4ac
» на букву «D
» и называют
дискриминантом
. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант ».
Рассмотрим другой пример квадратного уравнения.
x 2 + 9 + x = 7x
В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».
X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0
Теперь можно использовать формулу для корней.
X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.
Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b 2 – 4ас.
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .
Например. Решить уравнение х 2 – 4х + 4= 0.
D = 4 2 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х 2 + х + 3 = 0.
D = 1 2 – 4 · 2 · 3 = – 23
Ответ: корней нет .
Решить уравнение 2х 2 + 5х – 7 = 0 .
D = 5 2 – 4 · 2 · (–7) = 81
х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1 .
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х 2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3
х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 · 3) = 3√3
х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.
D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 · 3) = 2√3
х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).
При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).
Формула (уравнение) дискриминанта квадратного уравнения
Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.
Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю
Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.
Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.
Решение квадратного уравнения через дискриминант
Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.
В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.
Может ли дискриминант быть меньше нуля
При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут. При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».
Поясняющее видео:
Презентация по алгебре (8 класс) на тему «Вторая формула корней квадратного уравнения»
Формула корней квадратного уравнения.
Решите уравнение: 8х2 – 22х – 6 = 0
Рассмотрим способ решения, где вычисления можно упростить.
b = – 22 = 2 ∙ (– 11)
D = b2 – 4ac = (2 ∙ (– 11))2 – 4 ∙ 8 ∙ (– 6) =
=4 ∙ (– 11)2 – 4 ∙ (– 48) = 4 ∙ (121 – (– 48)) = 4 ∙ 169
= = = = = = = ;
= = = = = = = 3.
Рассмотрим уравнение ах2 + bх + c = 0,
Пусть второй коэффициент четное число b = 2k
Тогда дискриминант
D = b2 – 4ac = (2k)2 – 4 ас = 4 ∙ k2 – 4 ас =
= 4 ∙ (k2 – ас)
D1 = k2 – ас, тогда D = 4 ∙ (k2 – ас) = 4D1
= = = =
= =
= = = =
= =
Если b = 2k, то k = . Заменим в новых формулах k на .
Заменим в новых формулах k на .
D1 = k2 – ас = – ас, то есть D1 = – ас
= = ; = =
Очевидно, что если D1 < 0 то квадратное уравнение не имеет корней.
Выполнить № 449 (в,г), 450 (в,г), 453* (б)
Ответьте на вопросы.
1. Как вычислить дискриминант квадратного уравнения с четным коэффициентом b?
2. По каким числам вычисляются корни квадратного уравнения с четным коэффициентом b?
Домашнее задание:
п. 3.3, № 449 (а,б), 450 (а,б), 453* (а).
3.3, № 449 (а,б), 450 (а,б), 453* (а).
примеры решения уравнений. Как решить квадратное уравнение через дискриминант и четверть дискриминанта Чему равен дискриминант 1 формула
Прежде чем мы узнаем, как найти дискриминант квадратного уравнения вида ax2+bx+c=0 и как найти корни данного уравнения, нам необходимо вспомнить определение квадратного уравнения. Уравнение, которое имеет вид ax 2 + bx + c = 0 (где a,b и c — любые числа, также надо помнить, что a ≠ 0) является квадратным. Все квадратные уравнения мы разделим на три разряда:
- те, у которых нет корней;
- имеется один корень в уравнении;
- есть два корня.
Для того чтобы определить количество корней в уравнении нам необходим дискриминант.
Как найти дискриминант. Формула
Нам дано: ax 2 + bx + c = 0.
Формула дискриминанта: D = b 2 — 4ac .
Как найти корни дискриминанта
По знаку дискриминанта определяется количество корней:
- D = 0, у уравнения один корень;
- D > 0, у уравнения два корня.

Корни у квадратного уравнения находятся по следующей формуле:
X1= -b + √D/2а; X2= -b + √D/2a.
Если D = 0, то Вы можете смело использовать любую из представленных формул. У Вас получится одинаковый ответ в любом случае. А если получается так, что D > 0, то тогда Вам не придется ничего считать, так как корней уравнение не имеет.
Надо сказать, что находить дискриминант — это не так уж сложно, если знать формулы и внимательно осуществлять подсчеты. Иногда возникают ошибки при подстановке отрицательных чисел в формулу (нужно помнить, что минус на минус дает плюс). Будьте внимательны, и все получится!
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Виды квадратных уравнений
Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.
Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.
Говоря математическим языком, квадратное уравнение — это уравнение вида:
Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:
Здесь а =1; b = 3; c = -4
Здесь а =2; b = -0,5; c = 2,2
Здесь а =-3; b = 6; c = -18
Ну, вы поняли…
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.
Такие квадратные уравнения называются полными.
А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается. ) Получается, например:
) Получается, например:
5х 2 -25 = 0,
2х 2 -6х=0,
-х 2 +4х=0
И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:
2х 2 =0,
-0,3х 2 =0
Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.
Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…
Вот и все главные виды квадратных уравнений. Полные и неполные.
Решение квадратных уравнений.
Решение полных квадратных уравнений.
Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно. ) Главное — правильно определить все коэффициенты, а , b и c .
) Главное — правильно определить все коэффициенты, а , b и c .
Формула для нахождения корней квадратного уравнения выглядит так:
Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:
а =1; b = 3; c = -4. Вот и записываем:
Пример практически решён:
Это ответ.
Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Если есть проблемы с вычислениями, так и делайте !
Предположим, надо вот такой примерчик решить:
Здесь a = -6; b = -5; c = -1
Допустим, вы знаете, что ответы у вас редко с первого раза получаются.
Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:
Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!
Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:
Узнали?) Да! Это неполные квадратные уравнения .
Решение неполных квадратных уравнений.
Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .
Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !
Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.
И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .
Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.
Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:
Остаётся корень извлечь из 9, и всё. Получится:
Тоже два корня. х 1 = -3 , х 2 = 3 .
Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…
Дискриминант. Формула дискриминанта.
Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:
D = b 2 — 4ac
И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.
Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.
1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.
2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.
Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)
Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?
Вы поняли, что ключевое слово здесь – внимательно?
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1.
Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.
Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.
Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:
Вот и всё! Решать – одно удовольствие!
Итак, подытожим тему.
Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.
3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.
4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!
Делайте это!
Теперь можно и порешать.)
Решить уравнения:
8х 2 — 6x + 1 = 0
х 2 + 3x + 8 = 0
х 2 — 4x + 4 = 0
(х+1) 2 + x + 1 = (x+1)(x+2)
Ответы (в беспорядке):
х 1 = 0
х 2 = 5
х 1,2 = 2
х 1 = 2
х 2 = -0,5
х — любое число
х 1 = -3
х 2 = 3
решений нет
х 1 = 0,25
х 2 = 0,5
Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.
Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!
Очень помогает!
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b 2 – 4ас.
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
Когда дискриминант положительное число (D > 0),
тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .
Например. Решить уравнение х 2 – 4х + 4= 0.
D = 4 2 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х 2 + х + 3 = 0.
D = 1 2 – 4 · 2 · 3 = – 23
Ответ: корней нет .
Решить уравнение 2х 2 + 5х – 7 = 0 .
D = 5 2 – 4 · 2 · (–7) = 81
х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1 .
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
Тогда
D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х 2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3
х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 · 3) = 3√3
х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.
D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 · 3) = 2√3
х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Квадратное уравнение — презентация онлайн
.Составил: учитель математики МКОУ «Синелипяговская СОШ»
Нижнедевицкий муниципальный район
Воронежская область
Дедова Татьяна Викторовна
2012 год
Проект разработан с использованием ИКТ и элементами модульной педагогической
технологии.
 Он может быть проведен с учащимися 8-9 классов. Проект охватывает
Он может быть проведен с учащимися 8-9 классов. Проект охватываетизучение тем: «Квадратное уравнение и его корни», « Формула корней квадратного
уравнения» .
Основная цель — создать такую систему, которая бы обеспечивала бы
образовательные потребности каждого ученика в соответствии с его склонностями,
интересами и возможностями.
Данный проект формирует понятия квадратного уравнения, умение решать
неполные квадратные уравнения, умение применять формулу корней квадратного
уравнения. Знакомит учащихся с методом выделения полного квадрата, с формулой
корней приведенного квадратного уравнения, формула корней квадратного
уравнения со вторым четным коэффициентом., а также рассмотрены некоторые
нестандартные приемы решения квадратных уравнений.
При проведении проекта с опорой на формирующее оценивание учитель помогает
ученикам в развитии их навыков решению квадратных уравнений разными
способами, организует самостоятельные исследования по учебной теме.

План оценивания в ходе проекта направлен на реализацию деятельного подхода в
обучении, в центре внимания учебные потребности ребенка, развитие навыков
самоуправления обучением, самооценивание, взаимное оценивание.
1.Аннотация проекта.
2. Цели.
3. Ожидаемые результаты.
4. Вопросы, направляющие проект.
4.1 Основополагающий вопрос;
4.2 Проблемные вопросы;
4.3 Учебные вопросы.
5. Теоретический материал.
6. Дидактический материал.
7. Критерии оценивания.
8. Литература.
Изучив этот проект, учащиеся должны:
Знать, что такое квадратное уравнение, неполное
квадратное уравнение, приведенное квадратное уравнение;
формулы дискриминанта и корней квадратного уравнения,
терему Виета и обратную ей.
Уметь решать квадратные уравнения выделением квадрата
двучлена, решать квадратные уравнения по формуле, решать
неполные квадратные уравнения, решать квадратные
уравнения с помощью теоремы, обратной теореме Виета,
использовать теорему Виета для нахождения коэффициентов
и свободного члена квадратного уравнения.

Ожидаемые результаты обучения:
После завершения проекта учащиеся смогут:
Решать квадратные уравнения различными способами
Основополагающий вопрос:
Решение квадратных уравнений.
Проблемные вопросы: Какими способами можно решать
квадратные уравнения?
Учебные вопросы:
1.Что такое квадратное уравнение?
2.Какие существуют виды квадратных уравнений?
3.Что называется дискриминантом квадратного
уравнения?
4.От чего зависит количество корней квадратного
уравнения?
5. Каковы формулы для нахождения корней квадратного
уравнения?
6.Как формулируется теорема Виета?
Определение квадратного уравнения, его виды.
Квадратным уравнением называется уравнение вида
ax2 + bx + c = 0,
где х- переменная, а,b и с-некоторые числа,
причем, а ≠ 0.
Если в квадратном уравнении ах2 + bx + c = 0 хотя бы один
из коэффициентов b или с равен нулю, то такое уравнение
называют неполным квадратным уравнением.
 Неполные
Неполныеквадратные уравнения бывают трёх видов: 1) ах2 + с = 0, где с ≠ 0;
2) ах2 + bх = 0, где b ≠ 0;
3) ах2 = 0.
Приведённым называют квадратное уравнение, в котором
старший коэффициент равен единице. Такое уравнение
может быть получено делением всего выражения на
старший коэффициент a :
х2 +px + q = 0
Различные способы решения квадратных уравнений.
1) Разложение левой части уравнения на множители.
Решим уравнение х2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Так как произведение равно нулю, то по крайне мере один из его
множителей равен нулю. Поэтому левая часть уравнения
обращается в нуль при х = 2, а также при х = — 12. это означает, что
числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 = 0.
2) Метод выделения полного квадрата
Решим уравнение х2 + 6х – 7 = 0
Выделим в левой части полный квадрат.
 Для этого запишем выражение
Для этого запишем выражениех2 + 6х в следующем виде:
х2 + 6х = х2 + 2· х ·3.
В полученном выражении первое слагаемое – квадрат числа х, а второе
– удвоенное произведение х на 3. поэтому чтобы получить полный
квадрат, нужно прибавить 32, так как
х2 + 2· х ·3 + 32 = (х + 3)2 .
Преобразуем теперь левую часть уравнения
х2 + 6х – 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х – 7 = х2 + 2· х ·3 + 32 – 32 – 7 = (х + 3)2 – 9 – 7 = (х + 3)2 – 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 –16 = 0, т.е. (х + 3)2 = 16.
Следовательно, х = 3 = 4, х1 = 1, или х +3 = — 4 , х2 = – 7.
Решение неполных квадратных уравнений.
1. Если ах2 = 0. Уравнения такого вида решаются по алгоритму:
1) найти х2;
2) найти х.
Например, 5х2 = 0 . Разделив обе части уравнения на 5 получается:
х2 = 0, откуда х = 0.
2. Если ах2 + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:
1) перенести слагаемые в правую часть;
2) найти все числа, квадраты которых равны числу с.

Например, х2 — 5 = 0, х2 = 5. Следовательно, надо найти все числа, квадраты которых равны
5
ичислу 5. Таких чисел только два
5
Таким образом, уравнение х2 — 5 = 0 имеет два корня: x1 =
5
,
x2 = —
5
и других корней не имеет.
3. Если ах2 + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:
1) вынести общий множитель за скобки;
2) найти x1, x2.
Например, х2 — 3х = 0. Перепишем уравнение х2 – 3х = 0 в виде
х ( х – 3 ) = 0. Это уравнение имеет, очевидно, корни x1 = 0, x2 = 3. Других корней оно не имеет,
ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х
( х – 3 ) = 0 получится число, не равное нулю.
Вывод:
1) если уравнение имеет вид ах2 = 0, то оно имеет один корень х = 0;
2) если уравнение имеет вид ах2 + bх = 0, то используется метод
разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b
= 0. В итоге получается два корня: x1 = 0; x2 = — ;
3) если уравнение имеет вид ах2 + с = 0, то его преобразуют к виду
c
2
2
ах = — с и далее х = — a В случае, когда — ac
не имеет корней (значит, не имеет корней и исходное уравнение
ах2 +с=0).

В случае, когда — c > 0, т.е.
a
—
c
a
=m,
где m>0, уравнение х2 = m имеет два корня
x1
=
m
2
=-
m
Таким образом, неполное квадратное уравнение
может иметь два корня, один корень, ни одного корня.
Решение полных квадратных уравнений
ах2 + bx + c = 0, где a,b,c – заданные числа, а ≠ 0, х – неизвестное.
Рассмотриваются следующие случаи решения полных квадратных уравнений: D 0.
1. Если D
Например, 2х2 + 4х + 7 = 0.
Решение: здесь а = 2, b = 4, с = 7.
D = b2 – 4ас = 42 – 4*2*7 = 16 – 56 = — 40.
Так как D
2. Если D = 0, то квадратное уравнение ах2 + bx + c = 0 имеет один корень, который
b
находится по формуле
2a
Например, 4х – 20х + 25 = 0. Решение: а = 4, b = — 20, с = 25.
D = b2 – 4ас = (-20) 2 – 4*4*25 = 400 – 400 = 0.
Так как D = 0, то данное уравнение имеет один корень. Этот корень находится по формуле b
2a
20
2,5.
2*4
3.
 Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня, которые находятся по
Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня, которые находятся поформулам:
b D
b D
1
; 2
(1)
2a
2a
Например, 3х2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b2 – 4ас = 82 – 4*3*(-11) = 64 + 132 = 196.
Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:
1
b D 8 196
b D 8 196
11
1; 2
2a
2*3
2a
2*3
3
Вывод:
Если D
Если D = 0, то квадратное уравнение имеет один корень,
b
который находится по формуле
.
2a
Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два
корня
b D
b D
1
2a
;
2
2a
.
Решение приведенных квадратных уравнений
Теорема Виета. Сумма корней приведенного квадратного уравнения
равна второму коэффициенту, взятому с противоположным знаком, а
произведение корней равно свободному члену.

Иначе говоря, если x1 и x2 — корни уравнения х2 +px + q = 0, то
x1 + x2 = — p,
x1 x2 = q.
Теорема, обратная теореме Виета. Если для чисел x1, x2, p, q
справедливы формулы то x1 и x2 — корни уравнения х2 +px + q = 0 .
а) Если свободный член q
приведенного квадратного уравнения положителен (q >0), то уравнение имеет два одинаковых
по знаку корня и это зависит от второго коэффициента p.
Если p>0, то оба корня отрицательные, если p
б) Если свободный член q
приведенного квадратного уравнения отрицателен (q
знаку корня, причем больший по модулю корень будет положителен, если p
если p>0.
Метод переброски.
Рассмотрим полное квадратное уравнение ax2 + bx + c = 0; (1)
Для его решения мы вначале используем формулу
дискриминанта:D = b2 – 4ac и если D > 0, то с помощью формул
корней полного квадратного уравнения находим x1 и x2:
1.2
b b2 4ac
2a
Теперь рассмотрим другое полное приведенное квадратное
уравнение
y2 + by + ac = 0.
 (2)
(2)Первый коэффициент у этого уравнения равен 1, а второй
коэффициент равен b и совпадает со вторым коэффициентом
уравнения (1). Свободный член уравнения (2) равен ac и
получен как произведение первого коэффициента и свободного
члена уравнения (1) (то есть можно сказать, что a
«перебросилось» к c).
Найдем дискриминант и корни квадратного уравнения (2): D =
b2 – 4ac, т.о. он полностью совпадает с дискриминантом
уравнения (1). Корни уравнения (2): y1,2 = (-b ± √D) / 2.
Если теперь корни x1,2 сравнить с корнями y1,2, то легко видеть, что
корни уравнения (1) можно получить из корней уравнения (2)
делением на a.
Теперь рассмотрим примеры, в которых очень удобно пользоваться
приведенным выше методом «переброски».
Пример 1.
Решить уравнение 6×2 – 7x – 3 = 0.
Решение.
Выполним «переброску» и решим новое уравнение с помощью
теоремы Виета:
y2 – 7y – 3 · 6 = 0;
y2 – 7y – 18 = 0.
По теореме Виета y1 = 9; y2 = -2.

Теперь вернемся к переменной x. Для этого разделим полученные
результаты y1,2 на первый коэффициент исходного уравнения, т.е. на
6. Получим:
x1 = 9/6; x2 = -2/6.
После сокращения будем иметь x1 = 1,5; x2 = -1/3.
Ответ: -1/3; 1,5.
Свойства коэффициентов квадратного уравнения.
ах2 + bх + с = 0, а ≠ 0.
А. Пусть дано квадратное уравнение
1.Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю),
то х1 = 1, х2 = ас
2. Если а — b + с = 0, или b = а + с, то х1 = – 1, х2 = –
с
а
Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то х1 = 1, х2 =
Ответ: 1; –
208
345
Решим уравнение 132х2 + 247х + 115 = 0
Решение. Т. к. а-b+с = 0 (132 – 247 +115=0), то
115
х1= — 1, х2= -132
Ответ: — 1; — 115
132
208
345
Б. Если второй коэффициент b = 2k – четное число, то D = k2 – ac и
формулу корней
х1,2 =
b b2 4ac
2a
можно записать в виде х1,2
k k 2 ac
=
a
Решим уравнение 3х2 – 14х + 16 = 0.

Решение. Имеем: а = 3, b = – 14, c = 16, k = – 7;
D = k2 – ac = (– 7)2 – 3 · 16 = 49 – 48 = 1, D>0, два различных корня;
х = k D 7 1 7 1
8
a
3
; х1 2, х2 .
3
3
8
Ответ: 2; 3
Графическое решение квадратного уравнения
Если в уравнении
x2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
x2 = – px – q .
Построим графики зависимостей у = х2 и у = – px – q .
График первой зависимости – парабола, проходящая через начало
координат.
График второй зависимости – прямая.
Возможны следующие случаи: прямая и парабола могут пересекаться в
двух точках, абсциссы точек пересечения являются корнями
квадратного уравнения;
— прямая и парабола могут касаться (только одна общая точка),т.е.
уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение
не имеет корней.
Решим графически уравнение х2 – 3х – 4 = 0.
Решение.
 Запишем уравнение в виде
Запишем уравнение в видех2 = 3х + 4
Построим параболу у = х2 и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N
(3;13).
Прямая и парабола пересекаются в двух точках А и B с
абсциссами х1 = – 1 и х2 = 4.
В
А
Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на
с.83 (см. Брадис В.М. Четырехзначные математические таблицы. – М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не
решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам:
а
ОВ = 1 z
z2
.
, АВ =
1 z
Полагая ОС = р, ЕD = q, ОЕ = а ( все в см), из подобия треугольников САН и СDF получим пропорцию
p q
a
p AB OB
откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.

1. Для уравнения
z2 – 9z + 8 = 0.
Номограмма дает корни
z1 = 8, 0 и z2 = 1, 0 (рис. 12).
2. Решим с помощью
номограммы уравнение
2z2 – 9 z + 2 = 0.
Разделим коэффициенты этого
уравнения на 2,получим уравнение
z2 – 4, 5 + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения
решали не алгебраически, а геометрически. Приведем ставший знаменитым пример из
«Алгебры» ал-Хорезми.
Примеры
Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники
так, что другая сторона каждого из них равна 2 1 , следовательно, площадь каждого равна 2 1 х
2
2
Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в
углах четыре равных квадрата, сторона каждого из них 2 1 , а площадь 6 1 .

2
D
x
1
.
4
2 1х
2
1
.
64
21 х
6
A
C
2
1
.
4
6
1
2
2 х
x2
1
2 х
2
х
1
6 .
4
B
4
Площадь S квадрата ABCD можно представить как сумму
площадей: первоначального квадрата х2, четырех
прямоугольников
(4 ∙ 2 1
= 10х )
2
х
и четырех пристроенных квадратов
(6 1 4 25 ), т.е.
4
S = х2 + 10х = 25. Заменяя х2 + 10х числом 39,
получим что S = 39+ 25 = 64, откуда следует, что
сторона квадрата АВСD, т.е. отрезок АВ = 8. Для
искомой стороны х первоначального квадрата
получим
х=8
— 2 12
–21 =3
2
. А вот, например, как древние греки решали уравнение
у2 + 6у – 16 = 0.
Решение представлено на рис., где
у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение .Выражения у2 + 6у – 16 +9 – 9 = 0 – одно и то же
уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2,
у2 = – 8.

2
у
у
у2
3у
3
3
3у
9
1.
Решите квадратное уравнение, разлагая его
левую часть на множители:
2
а) х – х = 0;
е) х2 – 4х + 4 = 0;
б) х2 + 2х = 0;
ж) х2 + 6х + 9 = 0;
в) 3 х2 – 3х = 0;
з) х2 + 4х +3 = 0;
г) х2 – 81 = 0;
и) х2 + 2х – 3 = 0.
1
= 0;
д) 4 х2 –
4. Решите уравнения, используя метод «переброски»:
1)2х2 – 9х +9 = 0
5) 3х2 + х – 4 = 0
2) 10х2 – 11х + 3 = 0
6) 5х2 – 11х + 6 = 0
3) 3х2 +11х +6 = 0
7) 2х2 + х – 10 = 0
4) 4х2 +12х + 5 = 0
8) 6х2 +5х – 6 = 0
144
2. Решите уравнения по формуле:
а) 2х2 – 5х + 2= 0
г) 4х2 – 12х +9 =
0
б) 6х2 + 5х + 1=0
д) 10х2 – 6х + 0,9
=0
в) 3х2 – 7х – 1 = 0
е) 2х2 – 3х + 2 =
0
3. Не решая квадратного уравнения, определите
знаки его корня:
2
1) х – 2х – 15 = 0
7) х2 – 2х + 1 = 0
2) х2 + 2х – 8 = 0
8) х2 + 4х + 4 = 0
3) х2 + 10х + 9 = 0
9) х2 – 6х + 9 = 0
4) х2 – 12х + 35 = 0
10) 4х2 + 7х – 2 = 0
5)3 х2 +1 4х + 16 = 0
11) 5х2 – 9х – 2 = 0
6) х2 – 5х + 6 = 0
12) х2 – 11х + 15 = 0
5.
 Решите уравнения, используя свойства коэффициентов:
Решите уравнения, используя свойства коэффициентов:1) 5х2 – 7х + 2 = 0
5) 839х2 – 448х – 391 = 0
2) 3х2 + 5х – 8 = 0
6) 939х2 + 978х +39 = 0
3) 11х2 + 25х – 36 = 0
7) 313х2 + 326х + 13 = 0
4) 11х2 + 27х +16 = 0
8) 2006х2 – 2007х + 1 = 0
6. Решите уравнения по формуле четного
коэффициента:
1) 4х2 – 36х + 77 = 0
3) 4х2 + 20х + 25 = 0
2) 15х2 – 22х – 37 = 0
4) 9х2 – 12х + 4 = 0
7. Решите приведенные квадратные уравнения по
формуле:
1) х2 – 8х – 9 = 0
3) х2 + 18х + 81 = 0
2) х2 + 6х – 40 = 0
4) х2 — 56х + 64 = 0
8. Решите графически уравнения:
1) х2 – х – 6 = 0;
4) х2 – 2х – 3 = 0;
2) х2 – 4х + 4 = 0;
5) х2 + 2х – 3 = 0;
3) х2 + 4х +6 = 0;
6) 4х2 – 4х – 1 = 0.
9. Решите с помощью номограммы уравнения:
1) z2 – 7z + 6 = 0;
4) z2 – z – 6 = 0 ;
2) z2 + 5z + 4 = 0;
5) z2 – 11z + 18 = 0;
3) z2 – 4z + 4 = 0;
6) z2 – 2z + 3 = 0.
Критерии оценивания
Формы оценивания:
промежуточное (формирующее) оценивание:
— самооценка, взаимооценка участников проекта своей
деятельности для выявления потребности в необходимой или
дополнительной информации; процесса в понимании
теоретического материала.

Способы оценивания :
тесты, проверочные работы, самостоятельные работы,
подготовленные учителем и соответствующие учебной
программе и стандарту (Раздаточный материал, дидактический
материал).
Итоговое оценивание:
— оценка содержания итогового материала, его соответствие
стандарту и учебной программе;
— оценка навыков совместной деятельности (групповой) и
индивидуальной;
— оценка навыков мышления (достигнута цель).
1.Ю.Н Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов. Под ред. С.А.
Теляковского. Алгебра: Учебник для 8 класса- изд.- М:Просвещение,2010.
2.Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. Дидиктические материалы
по алгебре для 8 класса.- 15изд.- М.: Просвещение, 2010.
3. Энциклопедический словарь юного математика.А.П.СавинМ:Педагогика,19854. Брадис В. М. Четырехзначные математические таблицы для среденй
школы. – М., Просвещение, 1990
5 http://www.uchportal.ru/load/27-1-0-29503
http://ru.
 wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%ED%EE%E5_%F3%F0
wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%ED%EE%E5_%F3%F0%E0%E2%ED%E5%ED%E8%E5
http://www.egesdam.ru/page221.html
6.Математика. Алгебра. Функции. Анализ данных. 8 класс: Учебник для
общеобразовательных учреждений / Г. В. Дорофеев и др. – М.: Дрофа, 2004
7. Гусев В. А., Мордкович А. Г. Математика: Справочные материалы:
Книга для учащихся. – М.: Просвещение, 1988
8. Глейзер Г. И. История математики в школе. – М.: Просвещение, 1982
Номогра́мма (греч. νομοσ — закон) — графическое
представление функции от нескольких переменных,
позволяющее с помощью простых геометрических
операций (например, прикладывания линейки)
исследовать функциональные зависимости без
вычислений. Например, решать квадратное уравнение
без применения формул
Х в квадратном уравнении. Квадратные уравнения. Исчерпывающий гид (2019)
Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает «корень» на латыни).
Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y 2 = x.
Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x
Приведем два простых примера:
√9 = 3, поскольку 3 2 = 9; √(-9) = 3i, поскольку i 2 = -1.
Итерационная формула Герона для нахождения значений корней квадратных
Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).
Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
a n+1 = 1/2(a n +x/a n), где lim n->∞ (a n) => x.
Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a 0 (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a 0) 2 было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a 1 , которое уже будет ближе к искомому значению. После этого необходимо уже a 1 подставить в выражение и получить a 2 . Эту процедуру следует повторять до получения необходимой точности.
Пример применения итерационной формулы Герона
Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a 0).
Приведем простой пример: необходимо вычислить √11. Выберем a 0 = 3, так как 3 2 = 9, что ближе к 11, чем 4 2 = 16. Подставляя в формулу, получим:
a 1 = 1/2(3 + 11/3) = 3,333333;
a 2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a 3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Дальше нет смысла продолжать вычисления, поскольку мы получили, что a 2 и a 3 начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.
В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.
Уравнения второго порядка
Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.
Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.
Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x 2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Поскольку рассматриваемое уравнение имеет 2-й порядок (x 2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Нахождения корней квадратного уравнения (формула)
Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:
Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x 1 отличается от расчета x 2 только знаком перед корнем квадратным. Подкоренное выражение, которое равно b 2 — 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x 1 и x 2 .
Теорема Виета или некоторые свойства корней уравнений второго порядка
В конце XVI века один из основоположников современной алгебры француз изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:
x 1 + x 2 = -b / a и x 1 * x 2 = c / a.
Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.
Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.
Задача на закрепление полученных знаний
Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.
Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.
Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:
x 1 + x 2 = -b / a = 4;
x 1 * x 2 = c / a = -13.
Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x 2 — 4x — 13 = 0.
Воспользуемся формулой с дискриминантом, получим следующие корни:
x 1,2 = (4 ± √D)/2, D = 16 — 4 * 1 * (-13) = 68.
То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a 0 = 4, тогда:
a 1 = 1/2(4 + 17/4) = 4,125;
a 2 = 1/2(4,125 + 17/4,125) = 4,1231.
В вычислении a 3 нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x 1,2 , получим:
Подставляя его в формулу для x 1,2 , получим:
x 1 = (4 + 8,246)/2 = 6,123 и x 2 = (4 — 8,246)/2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.
Просто. По формулам и чётким несложным правилам. На первом этапе
надо заданное уравнение привести к стандартному виду, т.е. к виду:
Если уравнение вам дано уже в таком виде — первый этап делать не нужно. Самое главное — правильно
определить все коэффициенты, а , b и c .
Формула для нахождения корней квадратного уравнения.
Выражение под знаком корня называется дискриминант . Как видим, для нахождения икса, мы
используем только a, b и с . Т.е. коэффициенты из квадратного уравнения . Просто аккуратно подставляем
значения a, b и с в эту формулу и считаем. Подставляем со своими знаками!
Например , в уравнении:
а =1; b = 3; c = -4.
Подставляем значения и записываем:
Пример практически решён:
Это ответ.
Самые распространённые ошибки — путаница со знаками значений a, b и с . Вернее, с подстановкой
отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы
с конкретными числами. Если есть проблемы с вычислениями, так и делайте!
Предположим, надо вот такой пример решить:
Здесь a = -6; b = -5; c = -1
Расписываем все подробно, внимательно, ничего не упуская со всеми знаками и скобками:
Часто квадратные уравнения выглядят слегка иначе. Например, вот так:
А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок.
Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду.
Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:
Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с.
Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:
Избавьтесь от минуса. Как? Надо умножить всё уравнение на -1. Получим:
А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример.
Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.
Приём второй. Проверяйте корни! По теореме Виета .
Для решения приведённых квадратных уравнений, т.е. если коэффициент
x 2 +bx+c=0,
тогда x 1 x 2 =c
x 1 +x 2 =− b
Для полного квадратного уравнения, в котором a≠1 :
x 2 + b x+ c =0,
делим все уравнение на а:
→ →
где x 1 и x 2 — корни уравнения.
Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте
уравнение на общий знаменатель.
Вывод. Практические советы:
1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .
2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего
уравнения на -1.
3. Если коэффициенты дробные — ликвидируем дроби умножением всего уравнения на соответствующий
множитель.
4. Если икс в квадрате — чистый, коэффициент при нём равен единице, решение можно легко проверить по
Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:
Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:
Квадратное уравнение – это уравнение вида:
где коэффициенты a, b и с произвольные числа, при чём a≠0.
В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:
1. Имеют два корня.
2. *Имеют только один корень.
3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней
Как вычисляются корни? Просто!
Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:
Под этим «страшным» словом лежит вполне простая формула:
Формулы корней имеют следующий вид:
*Эти формулы нужно знать наизусть.
Можно сразу записывать и решать:
Пример:
1. Если D > 0, то уравнение имеет два корня.
2. Если D = 0, то уравнение имеет один корень.
3. Если D
Давайте рассмотрим уравнение:
По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…
Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:
х 1 = 3 х 2 = 3
Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.
Теперь следующий пример:
Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.
Вот и весь процесс решения.
Квадратичная функция.
Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).
Это функция вида:
где х и у — переменные
a, b, с – заданные числа, при чём a ≠ 0
Графиком является парабола:
То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.
Рассмотрим примеры:
Пример 1: Решить 2x 2 +8 x –192=0
а=2 b=8 c= –192
D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600
Ответ: х 1 = 8 х 2 = –12
*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.
Вычисления будут проще.
Пример 2: Решить x 2 –22 x+121 = 0
а=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0
Получили, что х 1 = 11 и х 2 = 11
В ответе допустимо записать х = 11.
Ответ: х = 11
Пример 3: Решить x 2 –8x+72 = 0
а=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
Дискриминант отрицательный, решения в действительных числах нет.
Ответ: решения нет
Дискриминант отрицательный. Решение есть!
Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.
Понятие комплексного числа.
Немного теории.
Комплексным числом z называется число вида
z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.
Мнимая единица равна корню из минус единицы:
Теперь рассмотрим уравнение:
Получили два сопряжённых корня.
Неполное квадратное уравнение.
Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.
Случай 1. Коэффициент b = 0.
Уравнение приобретает вид:
Преобразуем:
Пример:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Случай 2. Коэффициент с = 0.
Уравнение приобретает вид:
Преобразуем, раскладываем на множители:
*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Пример:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0
x 1 = 0 x 2 = 5
Случай 3. Коэффициенты b = 0 и c = 0.
Здесь понятно, что решением уравнения всегда будет х = 0.
Полезные свойства и закономерности коэффициентов.
Есть свойства, которые позволяют решить уравнения с большими коэффициентами.
а x 2 + bx + c =0 выполняется равенство
a + b + с = 0, то
— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство
a + с = b , то
Данные свойства помогают решить определённого вида уравнения.
Пример 1: 5001 x 2 –4995 x – 6=0
Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит
Пример 2: 2501 x 2 +2507 x +6=0
Выполняется равенство a + с = b , значит
Закономерности коэффициентов.
1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.
Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.
х 1 = –6 х 2 = –1/6.
2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.
Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.
х 1 = 15 х 2 = 1/15.
3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны
аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.
Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.
х 1 = – 17 х 2 = 1/17.
4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.
Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.
х 1 = 10 х 2 = – 1/10
Теорема Виета.
Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.
Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.
СПОСОБ ПЕРЕБРОСКИ
При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Если а ± b+c ≠ 0, то используется прием переброски, например:
2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)
По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1
Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим
х 1
= 5 х 2
=
0,5.
Каково обоснование? Посмотрите что происходит.
Дискриминанты уравнений (1) и (2) равны:
Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:
У второго (изменённого) корни получаются в 2 раза больше.
Потому результат и делим на 2.
*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.
Ответ: х 1 = 5 х 2 = 0,5
Кв. ур-ие и ЕГЭ.
О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).
Что стоит отметить!
1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:
15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.
Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).
2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.
Эта тема поначалу может показаться сложной из-за множества не самых простых формул. Мало того что сами квадратные уравнения имеют длинные записи, еще и корни находятся через дискриминант. Всего получается три новые формулы. Не очень просто запомнить. Это удается только после частого решения таких уравнений. Тогда все формулы будут вспоминаться сами собой.
Общий вид квадратного уравнения
Здесь предложена их явная запись, когда самая большая степень записана первой, и дальше — по убыванию. Часто бывают ситуации, когда слагаемые стоят вразнобой. Тогда лучше переписать уравнение в порядке убывания степени у переменной.
Введем обозначения. Они представлены в таблице ниже.
Если принять эти обозначения, все квадратные уравнения сводятся к следующей записи.
Причем коэффициент а ≠ 0. Пусть эта формула будет обозначена номером один.
Когда уравнение задано, то непонятно, сколько корней будет в ответе. Потому что всегда возможен один из трех вариантов:
- в решении будет два корня;
- ответом будет одно число;
- корней у уравнения не будет совсем.
И пока решение не доведено до конца, сложно понять, какой из вариантов выпадет в конкретном случае.
Виды записей квадратных уравнений
В задачах могут встречаться их разные записи. Не всегда они будут выглядеть как общая формула квадратного уравнения. Иногда в ней будет не хватать некоторых слагаемых. То что было записано выше — это полное уравнение. Если в нем убрать второе или третье слагаемое, то получится нечто другое. Эти записи тоже называются квадратными уравнениями, только неполными.
Причем исчезнуть могут только слагаемые у которых коэффициенты «в» и «с». Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими:
Итак, видов всего два, кроме полных, есть еще и неполные квадратные уравнения. Пусть первая формула будет иметь номер два, а вторая — три.
Пусть первая формула будет иметь номер два, а вторая — три.
Дискриминант и зависимость количества корней от его значения
Это число нужно знать для того, чтобы вычислить корни уравнения. Оно может быть посчитано всегда, какой бы ни была формула квадратного уравнения. Для того чтобы вычислить дискриминант, нужно воспользоваться равенством, записанным ниже, которое будет иметь номер четыре.
После подстановки в эту формулу значений коэффициентов, можно получить числа с разными знаками. Если ответ положительный, то ответом уравнения будут два различных корня. При отрицательном числе корни квадратного уравнения будут отсутствовать. В случае его равенства нулю ответ будет один.
Как решается квадратное уравнение полного вида?
По сути, рассмотрение этого вопроса уже началось. Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.
Поскольку в ней стоит знак «±», то значений будет два. Выражение под знаком квадратного корня — это дискриминант. Поэтому формулу можно переписать по-другому.
Формула номер пять. Из этой же записи видно, что если дискриминант равен нулю, то оба корня примут одинаковые значения.
Если решение квадратных уравнений еще не отработано, то лучше до того, как применять формулы дискриминанта и переменной, записать значения всех коэффициентов. Позже этот момент не будет вызывать трудностей. Но в самом начале бывает путаница.
Как решается квадратное уравнение неполного вида?
Здесь все гораздо проще. Даже нет необходимости в дополнительных формулах. И не понадобятся те, что уже были записаны для дискриминанта и неизвестной.
Сначала рассмотрим неполное уравнение под номером два. В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.
Второй получится при решении линейного уравнения.
Неполное уравнение под номером три решается переносом числа из левой части равенства в правую. Потом нужно разделить на коэффициент, стоящий перед неизвестной. Останется только извлечь квадратный корень и не забыть записать его два раза с противоположными знаками.
Далее записаны некоторые действия, помогащие научиться решать всевозможные виды равенств, которые превращаются в квадратные уравнения. Они будут способствовать тому, что ученик сможет избежать ошибок по невнимательности. Эти недочеты бывают причиной плохих оценок при изучении обширной темы «Квадратные уравнения (8 класс)». Впоследствии эти действия не нужно будет постоянно выполнять. Потому что появится устойчивый навык.
- Сначала нужно записать уравнение в стандартном виде. То есть сначала слагаемое с самой большой степенью переменной, а потом — без степени и последним — просто число.
- Если перед коэффициентом «а» появляется минус, то он может усложнить работу для начинающего изучать квадратные уравнения.
 От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.
От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.
- Таким же образом рекомендуется избавляться от дробей. Просто умножить уравнение на соответствующий множитель, чтобы знаменатели сократились.
Примеры
Требуется решить следующие квадратные уравнения:
х 2 − 7х = 0;
15 − 2х − х 2 = 0;
х 2 + 8 + 3х = 0;
12х + х 2 + 36 = 0;
(х+1) 2 + х + 1 = (х+1)(х+2).
Первое уравнение: х 2 − 7х = 0. Оно неполное, поэтому решается так, как было описано для формулы под номером два.
После вынесения за скобки получается: х (х — 7) = 0.
Первый корень принимает значение: х 1 = 0. Второй будет найден из линейного уравнения: х — 7 = 0. Легко заметить, что х 2 = 7.
Второе уравнение: 5х 2 + 30 = 0. Снова неполное. Только решается оно так, как описано для третьей формулы.
После перенесения 30 в правую часть равенства: 5х 2 = 30. Теперь нужно выполнить деление на 5. Получается: х 2 = 6. Ответами будут числа: х 1 = √6, х 2 = — √6.
Теперь нужно выполнить деление на 5. Получается: х 2 = 6. Ответами будут числа: х 1 = √6, х 2 = — √6.
Третье уравнение: 15 − 2х − х 2 = 0. Здесь и далее решение квадратных уравнений будет начинаться с их переписывания в стандартный вид: − х 2 − 2х + 15 = 0. Теперь пришло время воспользоваться вторым полезным советом и умножить все на минус единицу. Получается х 2 + 2х — 15 = 0. По четвертой формуле нужно вычислить дискриминант: Д = 2 2 — 4 * (- 15) = 4 + 60 = 64. Он представляет собой положительное число. Из того, что сказано выше, получается, что уравнение имеет два корня. Их нужно вычислить по пятой формуле. По ней получается, что х = (-2 ± √64) / 2 = (-2 ± 8) / 2. Тогда х 1 = 3, х 2 = — 5.
Четвертое уравнение х 2 + 8 + 3х = 0 преобразуется в такое: х 2 + 3х + 8 = 0. Его дискриминант равен такому значению: -23. Поскольку это число отрицательное, то ответом к этому заданию будет следующая запись: «Корней нет».
Пятое уравнение 12х + х 2 + 36 = 0 следует переписать так: х 2 + 12х + 36 = 0. После применения формулы для дискриминанта получается число ноль. Это означает, что у него будет один корень, а именно: х = -12/ (2 * 1) = -6.
После применения формулы для дискриминанта получается число ноль. Это означает, что у него будет один корень, а именно: х = -12/ (2 * 1) = -6.
Шестое уравнение (х+1) 2 + х + 1 = (х+1)(х+2) требует провести преобразования, которые заключаются в том, что нужно привести подобные слагаемые, до того раскрыв скобки. На месте первой окажется такое выражение: х 2 + 2х + 1. После равенства появится эта запись: х 2 + 3х + 2. После того как подобные слагаемые будут сосчитаны, уравнение примет вид: х 2 — х = 0. Оно превратилось в неполное. Подобное ему уже рассматривалось чуть выше. Корнями этого будут числа 0 и 1.
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b 2 – 4ас.
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .
Например. Решить уравнение х 2 – 4х + 4= 0.
D = 4 2 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х 2 + х + 3 = 0.
D = 1 2 – 4 · 2 · 3 = – 23
Ответ: корней нет .
Решить уравнение 2х 2 + 5х – 7 = 0 .
D = 5 2 – 4 · 2 · (–7) = 81
х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5
х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1 .
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида
ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .
На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.
Пример. Решить уравнение
3х 2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3
х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27
√(D 1) = √27 = √(9 · 3) = 3√3
х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3
х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.
D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12
√(D 2) = √12 = √(4 · 3) = 2√3
х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3
х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Объяснение урока: Квадратные уравнения с комплексными коэффициентами
В этом объяснении мы узнаем, как решать квадратные уравнения с комплексными коэффициентами, используя квадратную формулу.
Из фундаментальной теоремы алгебры мы знаем, что любое квадратное число будет иметь два корня. Для квадратных уравнений с действительными коэффициентами теорема о сопряженных корнях говорит нам, что если у него есть какой-либо невещественный корень, его корни будут комплексно-сопряженная пара, тогда как если она имеет действительных корней, он может иметь либо два различных действительных корня, либо один повторяющийся корень.Чтобы различать эти три разных случаях используем дискриминант.
Дискриминант
Дискриминант квадратного уравнения 𝑎𝑥+𝑏𝑥+𝑐=0 определяется как
𝑏−4𝑎𝑐. Часто Δ используется для обозначения дискриминанта.
Используя дискриминант, мы идентифицируем три различных случая квадратных уравнений следующим образом.
- 40012
- Положительный дискриминант : 𝑏-4𝑎𝑐> 0, два реальных корня
- Ноль-дискриминант : 𝑏-4𝑎𝑐 = 0, один повторный реальный корня
- Отрицательный дискриминант : 𝑏-4𝑎𝑐0, комплексное сопряжение корни
На графиках ниже показан каждый случай.
В этом объяснении мы ослабим условие того, что квадратное уравнение имеет действительные коэффициенты и исследовать то, что мы можем заключить о корнях квадратных уравнений с комплексными коэффициентами.
Рассмотрим, как решить общее квадратное уравнение 0=𝑎𝑧+𝑏𝑧+𝑐, где 𝑎≠0. Начнем с деления уравнения на 𝑎, что дает 0=𝑧+𝑏𝑎𝑧+𝑐𝑎.
Теперь мы можем завершить квадрат 0=𝑧+𝑏2𝑎−𝑏4𝑎+𝑐𝑎=𝑧+𝑏2𝑎−𝑏−4𝑎𝑐4𝑎.
Переставляя, получаем
| 𝑧+𝑏2𝑎=𝑏−4𝑎𝑐4𝑎. | (1) |
Все шаги, которые мы предприняли до этого момента, одинаково действительны, будь то 𝑎,
𝑏 и 𝑐 являются реальными или мнимыми. Следующий шаг, где мы берем квадрат
root, это то, с чем нам, возможно, следует быть осторожным, так как получение корней комплексного числа возвращает несколько
ценности. Однако рассмотрим случай общего комплексного числа 𝑤=𝑟𝑒. Используя теорему де Муавра, два возможных квадратных корня этого числа равны
𝛼=√𝑟𝑒 и
𝛽=√𝑟𝑒().С учетом второго корня 𝛽 имеем
𝛽=√𝑟𝑒=√𝑟𝑒.()
Следующий шаг, где мы берем квадрат
root, это то, с чем нам, возможно, следует быть осторожным, так как получение корней комплексного числа возвращает несколько
ценности. Однако рассмотрим случай общего комплексного числа 𝑤=𝑟𝑒. Используя теорему де Муавра, два возможных квадратных корня этого числа равны
𝛼=√𝑟𝑒 и
𝛽=√𝑟𝑒().С учетом второго корня 𝛽 имеем
𝛽=√𝑟𝑒=√𝑟𝑒.()
Используя свойства показательных функций, мы можем выразить это как 𝛽=√𝑟𝑒𝑒.
Однако, благодаря тождеству Эйлера, мы знаем 𝑒=−1; следовательно, 𝛽=−√𝑟𝑒=−𝛼.
Следовательно, так же, как мы берем как положительные, так и отрицательные корни действительных чисел,
мы можем найти корень комплексного числа, используя теорему де Муарва, а затем второй корень
будет его отрицательным.Следовательно, возвращаясь к уравнению (1), мы можем взять квадрат
корни и рассмотрим как положительные, так и отрицательные значения, что дает
𝑧+𝑏2𝑎=±√𝑏−4𝑎𝑐2𝑎.
Следовательно, 𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎.
Следовательно, даже для квадратичных уравнений с комплексными коэффициентами мы можем использовать квадратичную формулу хотя нам, возможно, придется обратиться к теореме де Муарва, чтобы вычислить значение квадратный корень из дискриминанта недействительных чисел.
В первых двух примерах мы рассмотрим частный случай, когда, несмотря на тот факт, что у нас есть некоторые невещественные коэффициенты, дискриминант все еще является действительным числом.
Пример 1. Невещественные квадратные уравнения с действительными отрицательными дискриминантами
Решите 3𝑧+5𝑖𝑧−2=0.
Ответ
Используя квадратичную формулу 𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎, у нас есть 𝑧=−5𝑖±(5𝑖)−4×3(−2)2×3=−5𝑖±√−25+246=−5𝑖±𝑖6.
Следовательно, 𝑧=−23𝑖 и 𝑧=−𝑖 решения уравнения.
Обратите внимание, что в предыдущем примере, несмотря на то, что у нас был отрицательный дискриминант,
два решения не являются комплексно-сопряженной парой. Следовательно, правило относительно отрицательного дискриминанта
не просто обобщается на уравнения с комплексными коэффициентами.
Следовательно, правило относительно отрицательного дискриминанта
не просто обобщается на уравнения с комплексными коэффициентами.
Пример 2. Невещественные квадратные уравнения с вещественными положительными дискриминантами
Решите 𝑧+(2+𝑖)𝑧+𝑖=0.
Ответ
Используя квадратичную формулу 𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎, у нас есть 𝑧=−(2+𝑖)±(2+𝑖)−4𝑖2=−2−𝑖±√3+4𝑖−4𝑖2=−2−𝑖±√32.
Следовательно, 𝑧=−2+√32 −𝑖2 и 𝑧=−2−√32−𝑖2 — решения уравнения.
В предыдущем примере у нас был положительный дискриминант; однако эти два решения не являются реальными.Следовательно, правило о положительном дискриминанте не просто обобщается на уравнения с комплексными коэффициентами.
Пример 3. Невещественные квадратные уравнения с вещественными дискриминантами
Решить (2+3𝑖)𝑧+4𝑧−6𝑖+4=0.
Ответ
Применение квадратичной формулы
𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎,
у нас есть
𝑧=−4±√4−4(2+3𝑖)(4−6𝑖)2(2+3𝑖)=−4±√4(4−(2+3𝑖)(4−6𝑖))2(2+3𝑖 ).
Вынимая 4 из квадратного корня, мы имеем 𝑧=−4±2√4−(2+3𝑖)(4−6𝑖)2(2+3𝑖).
Сокращая множитель 2 в числителе и знаменателе, мы имеем 𝑧=−2±√4−(2+3𝑖)(4−6𝑖)2+3𝑖.
Обратите внимание, что 4−6𝑖=2(2−3𝑖). Следовательно, (2+3𝑖)(4−6𝑖) в два раза больше комплексного числа в 2+3𝑖 раза больше сопряженного. Следовательно, (2+3𝑖)(4−6𝑖)=22+3=26, и, таким образом, 𝑧=−2±√4−262+3𝑖=−2±𝑖√222+3𝑖.
Умножение числителя и знаменателя на комплексное сопряжение знаменателя дает 𝑧=−2±𝑖√22(2−3𝑖)(2+3𝑖)(2−3𝑖)=−4+6𝑖±3√22+2𝑖√2213.
Следовательно, 𝑧=−4+3√2213+6+2√2213𝑖 и 𝑧=−4−3√2213+6−2√2213𝑖 являются решениями уравнения.
Обратите внимание, что, в отличие от первых двух примеров, два корня в предыдущих примерах не лежат на
вертикальная или горизонтальная линия в комплексной плоскости. На следующих рисунках представлен график модуля
каждого уравнения, нанесенного над комплексной плоскостью. Две точки, где график встречается с комплексом
плоскости являются корнями уравнений.
Две точки, где график встречается с комплексом
плоскости являются корнями уравнений.
Пример 4. Невещественные квадратные уравнения с нулевыми дискриминантами
Решите 𝑧−(4+4𝑖)𝑧+8𝑖=0.
Ответ
Используя квадратичную формулу 𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎, у нас есть 𝑧=4+4𝑖±(−(4+4𝑖))−4(8𝑖)2=4+4𝑖±√32𝑖−32𝑖2=2+2𝑖.
Следовательно, уравнение имеет единственный повторяющийся корень из 𝑧= 2+2𝑖.
Предыдущий пример демонстрирует возможность существования повторяющихся невещественных корней. Более того, мы видим, что когда это произошло, дискриминант был равен нулю. Просто рассматривая квадратичную формулу, мы можем видеть, что правило относительно определителя нуля обобщается на случай, когда у нас есть невещественное коэффициенты.На самом деле это одно из ключевых свойств дискриминанта: он равен нулю, если и только если уравнение имеет повторяющийся корень.
В следующих примерах мы рассмотрим случай, когда дискриминант является общим
комплексное число. Мы начнем с простого примера, где коэффициент 𝑧
равно нулю, что, конечно, эквивалентно простому нахождению квадратных корней комплексного числа.
Мы начнем с простого примера, где коэффициент 𝑧
равно нулю, что, конечно, эквивалентно простому нахождению квадратных корней комплексного числа.
Пример 5. Решение квадратных уравнений путем извлечения квадратного корня из комплексных чисел
Решите (1+2𝑖)𝑧−3+𝑖=0.Округлите ответы до трех значащих цифр.
Ответ
Добавление 3−𝑖 к обеим частям уравнения дает (1+2𝑖)𝑧=3−𝑖.
Теперь разделим на (1+2𝑖), чтобы выделить 𝑧 в левой части уравнения: 𝑧=3−𝑖1+2𝑖.
Умножая числитель и знаменатель на комплексное сопряжение знаменателя, мы можем упростить сложную дробь следующим образом: 𝑧=(3−𝑖)(1−2𝑖)(1+2𝑖)(1−2𝑖)=3−6𝑖−𝑖−25=15−75𝑖.
Чтобы найти квадратные корни этого комплексного числа, нам нужно рассчитать его модуль и
аргумент.Модуль определяется выражением
15+−75=√2. Поскольку он лежит в четвертом квадранте, его аргумент определяется выражением
𝜃=−=(−7). arctanarctan
arctanarctan
Применяя теорему Муавра, два квадратных корня задаются формулой ±√212𝜃+𝑖12𝜃.cossin
Подставляя значение 𝜃 и округляя наши ответы до трех значащих цифр, имеем 𝑧=0,898−0,779𝑖(3с.ф.) и 𝑧=-0,898+0,779𝑖(3с.ф.).
Пример 6. Квадратные уравнения с комплексными дискриминантами
Решить 𝑧+(2−2𝑖)𝑧−(7+26𝑖)=0.
Ответ
Используя квадратичную формулу 𝑧=−𝑏±√𝑏−4𝑎𝑐2𝑎, у нас есть
| ±√28+96𝑖2. | (2) |
Чтобы вычислить квадратный корень из 28+96𝑖, нам сначала нужно вычислить модуль и аргумент. Модуль определяется как √28+96=100. Поскольку комплекс число лежит в первом квадранте, его аргумент определяется выражением 𝜃=9628=247арктанарктан.Применяя теорему де Муавра, два квадратных корня задаются выражением ±√10012𝜃+𝑖12𝜃=±1012𝜃+𝑖12𝜃.cossincossin
Подставляя значение 𝜃, находим cos12𝜃=0,8
и sin12𝜃=0,6.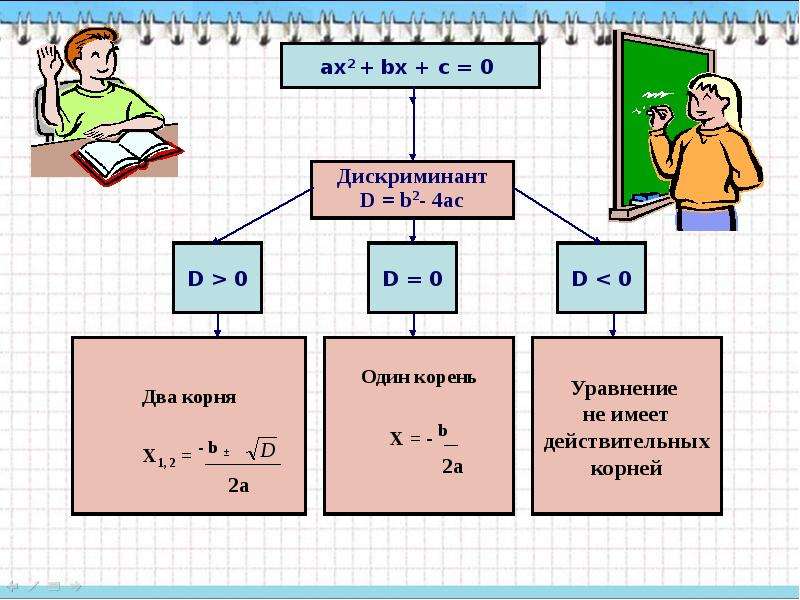 Следовательно, два квадратных корня равны
8+6𝑖 и −8−6𝑖. Подставляя эти значения обратно в
(2), имеем
𝑧=−(2−2𝑖)±(8+6𝑖)2=−1+𝑖±(4+3𝑖).
Следовательно, два квадратных корня равны
8+6𝑖 и −8−6𝑖. Подставляя эти значения обратно в
(2), имеем
𝑧=−(2−2𝑖)±(8+6𝑖)2=−1+𝑖±(4+3𝑖).
Следовательно, два корня уравнения равны 𝑧=3+4𝑖 и 𝑧=−5−2𝑖.
Закончим рассмотрением последнего примера.
Пример 7. Многочлены с невещественными коэффициентами
Решите 𝑧+6+6𝑖√(3)𝑧+32−32𝑖√(3).
Ответ
Сначала заметим, что у нас есть квадратное число в 𝑧. Поэтому мы начинаем путем замены 𝑤=𝑧, что дает 𝑤+6+6𝑖√(3)𝑤+32−32𝑖√(3).
Мы можем решить это с помощью квадратичной формулы 𝑤=−𝑏±√𝑏−4𝑎𝑐2𝑎 следующее: 𝑤=−6+6𝑖√3±6+6𝑖√3−432−32𝑖√32=−6−6𝑖√3±−72+72𝑖√3−128+128𝑖√32 =−6−6𝑖√3±−200+200𝑖√32.
Сокращая 2 из числителя и знаменателя, мы имеем
| 𝑤=−3−3𝑖√3±−50+50𝑖√3. | (3) |
Чтобы вычислить квадратный корень из −50+50𝑖√3, нам нужно сначала вычислить его модуль и
аргумент. Модуль определяется выражением (−50)+50√3=100. Поскольку это комплексное число лежит во втором квадранте, его аргумент 𝜃 определяется выражением
𝜃=−50√350+𝜋=−√3+𝜋=−𝜋3+𝜋=2𝜋3.arctanarctan
Модуль определяется выражением (−50)+50√3=100. Поскольку это комплексное число лежит во втором квадранте, его аргумент 𝜃 определяется выражением
𝜃=−50√350+𝜋=−√3+𝜋=−𝜋3+𝜋=2𝜋3.arctanarctan
Используя теорему де Муавра, его квадратные корни определяются выражением ±√10012𝜃+𝑖12𝜃=±10𝜋3+𝑖𝜋3.cossincossin
Преобразуя это обратно в алгебраическую форму, мы получаем, что два корня 5+5𝑖√3 и −5−5𝑖√3. Замена их в (3), мы получаем 𝑤=−3−3𝑖√3±5+5𝑖√3.
Следовательно, два корня равны 2+2𝑖√3 и −8−8𝑖√3. Ну наконец то,
чтобы найти возможные значения 𝑧, нам нужно взять квадратные корни каждого из
эти комплексные числа, начиная с 2+2𝑖√3. Мы можем выразить это в
экспоненциальная форма как 4𝑒. Применяя теорему де Муавра,
два квадратных корня равны ±2𝑒, которые мы можем выразить в
алгебраическая форма как √3+𝑖 и −√3−𝑖.Аналогично для
−8−8𝑖√3, мы можем выразить это в экспоненциальной форме как
16𝑒. Применяя теорему де Муавра, два квадратных корня
задаются как ±4𝑒, что мы можем выразить в алгебраической форме как
2−2𝑖√3 и −2+2𝑖√3.
Применяя теорему де Муавра, два квадратных корня
задаются как ±4𝑒, что мы можем выразить в алгебраической форме как
2−2𝑖√3 и −2+2𝑖√3.
Следовательно, четыре корня уравнения равны 𝑧=√3+𝑖, 𝑧=−√3−𝑖, 𝑧=2−2𝑖√3 и 𝑧=−2+2𝑖√3.
Ключевые моменты
- Мы можем решать квадратные уравнения с комплексными коэффициентами, используя квадратную формулу.
- Если дискриминант равен нулю, уравнение имеет один повторяющийся корень. Если все коэффициенты реальны, корень будет реален.
- Общая квадратичная функция с комплексными коэффициентами может иметь любую комбинацию действительных и невещественные корни.
- Если квадратное уравнение имеет действительные коэффициенты, дискриминанта достаточно, чтобы полностью классифицировать типы решений.
Как определить опережающие коэффициенты в квадратных уравнениях
Старшие коэффициенты
Итак, мы понимаем коэффициенты, но что такое старший коэффициент? Подумайте о термине.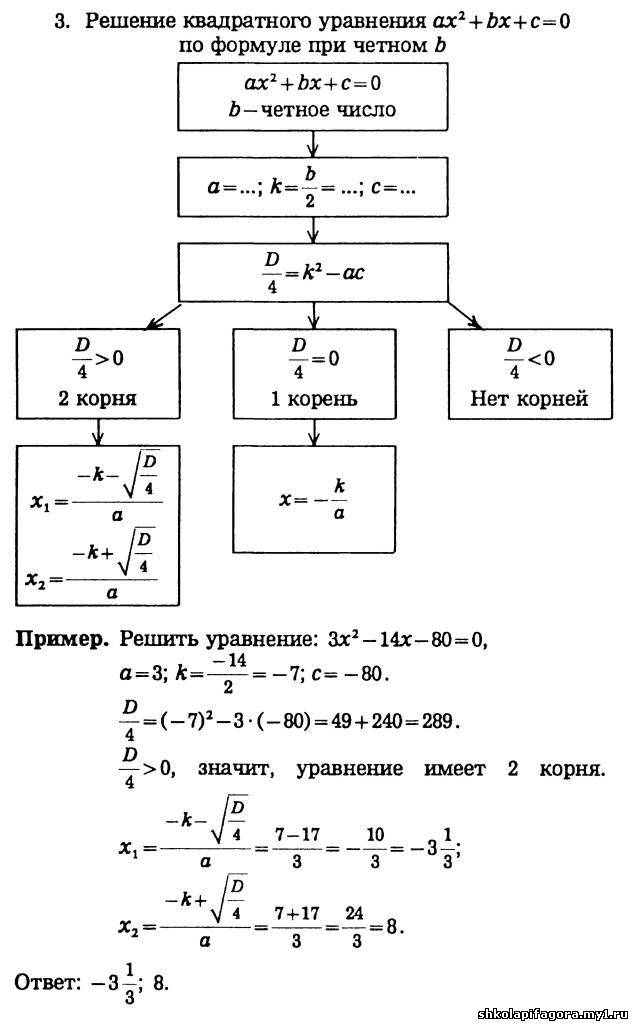 .. лидерство обычно означает, что вы впереди или первым! Когда выражение или уравнение записаны в правильной форме, то есть в порядке убывания показателей степени, старший коэффициент будет стоять первым. Это означает, что старший коэффициент является коэффициентом, присоединенным к переменной с наивысшим показателем степени.
.. лидерство обычно означает, что вы впереди или первым! Когда выражение или уравнение записаны в правильной форме, то есть в порядке убывания показателей степени, старший коэффициент будет стоять первым. Это означает, что старший коэффициент является коэффициентом, присоединенным к переменной с наивысшим показателем степени.
Таким образом, когда ваше выражение записывается со старшими членами экспоненты сначала, старший экспонент будет, но только это… впереди и впереди! Но иногда ваши выражения или уравнения не будут записаны в порядке убывания, так что будьте осторожны!
Давайте рассмотрим пример.Допустим, у нас есть выражение 7 y 9 + 3 y 5 + 2 y 2. Оно записано в правильном порядке: первым идет член с наивысшим показателем степени 9, за которым следует член с наивысшим показателем степени 5. идет следующим, а наименьший показатель степени 2 идет последним. Поскольку он находится в правильном порядке, старший коэффициент — это просто тот коэффициент, который стоит первым. В данном случае это будет 7! Другой способ взглянуть на это состоит в том, что наивысший показатель степени переменной в этом выражении равен 9.Чему равен коэффициент этого члена? Это 7!
В данном случае это будет 7! Другой способ взглянуть на это состоит в том, что наивысший показатель степени переменной в этом выражении равен 9.Чему равен коэффициент этого члена? Это 7!
В другом выражении -3 x 2 + 4 x 5 члены расположены неправильно. Чтобы найти старший коэффициент здесь, мы можем либо правильно расположить его как 4 x 5 — 3 x 2 и таким образом найти старший коэффициент. Или мы можем просто найти член с наивысшим показателем и найти его коэффициент.В этом случае наивысший показатель степени равен 5, поэтому старший коэффициент будет равен -3.
Квадратные уравнения
Теперь, когда у нас все это за плечами, давайте поговорим о квадратных уравнениях. Квадратные уравнения — это уравнения, в которых старший показатель степени переменной равен двойке. Обычно они имеют вид y = x 2 + bx + c , где a не может равняться нулю. Пример квадратного уравнения: y = 4x 2 + 2 x + 1, где a = 4, b = 2 и c = 1.
Пример квадратного уравнения: y = 4x 2 + 2 x + 1, где a = 4, b = 2 и c = 1.
По определению, мы знаем, что квадратные уравнения будут иметь член с показателем степени, равным двум, и это будет наибольший показатель степени. Это говорит вам о том, что старший коэффициент всегда будет присоединен к переменной с показателем степени, равным двум! Глядя на общую форму, y = x 2 + bx + c , старший коэффициент всегда будет значением a .
Возвращаясь к нашему примеру y = 4 x 2 + 2 x + 1 и зная, что 4 равно a , должно быть ясно, что 4 является нашим старшим коэффициентом.Это верно, потому что это квадратное уравнение, а наивысший показатель степени переменной равен 2, поэтому этот член всегда будет содержать старший коэффициент!
Примеры
Пример 1
y = -6 x 2 + 2 x — 3
В примере 1 старший коэффициент равен -6. Это верно, потому что это квадратное уравнение, а наибольшая переменная в показателе степени равна 2. не похоже на квадратное уравнение, но при ближайшем рассмотрении вы увидите, что оно просто не в порядке.Это должно быть записано как х = -9 х 2 + 2 х + 8. Теперь должно быть ясно, что старший коэффициент равен -9.
Это верно, потому что это квадратное уравнение, а наибольшая переменная в показателе степени равна 2. не похоже на квадратное уравнение, но при ближайшем рассмотрении вы увидите, что оно просто не в порядке.Это должно быть записано как х = -9 х 2 + 2 х + 8. Теперь должно быть ясно, что старший коэффициент равен -9.
Пример 3
y = 12 x 2
Пример 3 поначалу может сбить вас с толку, потому что в нем нет трех членов, как в общей форме y = ax 902 2 b 4 x 24 + 90 с . Но, если подумать об определении, квадратным уравнениям не нужны эти другие термины, только переменная с наивысшим показателем, равным двум.Вы также можете думать об этом как a = 12, b = 0 и c = 0. Помните, что a всегда будет старшим коэффициентом в квадратных уравнениях, поэтому 12 является старшим коэффициентом в примере 3.
Резюме урока
Коэффициенты — это числа, которые умножаются на такие переменные, как x . Старшие коэффициенты — это коэффициенты, которые идут первыми, когда выражение или уравнение записываются в порядке убывания показателей степени.При поиске ведущих коэффициентов с квадратными уравнениями вы всегда будете искать значение a . Это связано с тем, что квадратные уравнения не могут иметь переменных с показателями степени выше двух.
Старшие коэффициенты — это коэффициенты, которые идут первыми, когда выражение или уравнение записываются в порядке убывания показателей степени.При поиске ведущих коэффициентов с квадратными уравнениями вы всегда будете искать значение a . Это связано с тем, что квадратные уравнения не могут иметь переменных с показателями степени выше двух.
Что такое формула дискриминанта 1. Как решить квадратное уравнение с помощью дискриминанта и четверти дискриминанта
Надеюсь, изучив эту статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения; для решения неполных квадратных уравнений используются другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие квадратные уравнения называются полными? Это уравнений вида ax 2 + b x + c = 0 , где коэффициенты a, b и c не равны нулю. Итак, чтобы решить полное квадратное уравнение, нужно вычислить дискриминант D.
Д = б 2 — 4ас.
В зависимости от того, какое значение имеет дискриминант, запишем ответ.
Если дискриминант отрицательный (D
Если дискриминант равен нулю, то x = (-b) / 2a. Когда дискриминант является положительным числом (D > 0),
, то x 1 = (-b — √D) / 2a и x 2 = (-b + √D) / 2a.
Например. Решите уравнение x 2 — 4x + 4 = 0.
Д = 4 2 — 4 4 = 0
х = (- (-4)) / 2 = 2
Ответ: 2.
Решение уравнения 2 x 2 + х + 3 = 0.
Д = 1 2 — 4 2 3 = — 23
Ответ: нет корней .
Решение уравнения 2 x 2 + 5x — 7 = 0 .
D = 5 2 — 4 · 2 · (–7) = 81
х 1 = (-5 — √81) / (2 2) = (-5 — 9) / 4 = — 3,5
х 2 = (-5 + √81) / (2 · 2) = (-5 + 9) / 4 = 1
Ответ: — 3,5; один .
Итак, представим решение полных квадратных уравнений по схеме на рисунке 1.
Эти формулы можно использовать для решения любого полного квадратного уравнения. Просто нужно следить за тем, чтобы уравнение было записано в виде стандартного многочлена
Просто нужно следить за тем, чтобы уравнение было записано в виде стандартного многочлена
а x 2 +bx+c, иначе можно ошибиться. Например, записывая уравнение x + 3 + 2x 2 = 0, вы можете ошибочно решить, что
a = 1, b = 3 и c = 2. Тогда
D = 3 2 — 4 · 1 · 2 = 1 и тогда уравнение имеет два корня.И это неправда. (См. решение примера 2 выше).
Следовательно, если уравнение не записано в виде полинома стандартного вида, сначала полное квадратное уравнение должно быть записано в виде полинома стандартного вида (на первом месте должен быть моном с наибольшим показателем, то есть а x 2 , то с меньшим – бх а потом свободный член С.
При решении редуцированного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором члене можно использовать другие формулы.Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении для второго члена коэффициент четный (b = 2k), то уравнение можно решить по формулам, приведенным на схеме на рисунке 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равно единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение можно дать для решения, либо оно получается делением всех коэффициентов уравнения на коэффициент стоит на x 2 .
На рис. 3 показана схема решения сокращенного квадратного уравнения
. Рассмотрим пример применения формул, рассмотренных в этой статье.
Пример. Решить уравнение
3 x 2 + 6х — 6 = 0.
Решим это уравнение по формулам, показанным на схеме на рисунке 1.
D = 6 2 — 4 3 (- 6) = 36 + 72 = 108
√D = √108 = √ (363) = 6√3
x 1 = (-6 — 6√3) / (2 3) = (6 (-1- √ (3))) / 6 = –1 — √3
x 2 = (-6 + 6√3) / (2 · 3) = (6 (-1+ √ (3))) / 6 = –1 + √3
Ответ: -1 — √3; –1 + √3
Вы можете заметить, что коэффициент при x в этом уравнении является четным числом, то есть b = 6 или b = 2k, откуда k = 3. Затем попробуем решить уравнение по формулам, приведенным в схеме на рисунке D 1 = 3 2 — 3 · (- 6 ) = 9 + 18 = 27
Затем попробуем решить уравнение по формулам, приведенным в схеме на рисунке D 1 = 3 2 — 3 · (- 6 ) = 9 + 18 = 27
√ (D 1) = √ 27 = √ (9 3) = 3 √ 3
x 1 = (-3 — 3√3) / 3 = (3 (-1 — √ (3))) / 3 = — 1 — √3
х 2 = (-3 + 3√3) / 3 = (3 (-1 + √ (3))) / 3 = — 1 + √3
Ответ: -1 — √3; –1 + √3 … Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и произведя деление, получим редуцированное квадратное уравнение x 2 + 2x — 2 = 0. Решим это уравнение по формулам редуцированного квадратного уравнения
Уравнения Рисунок 3.
D 2 = 2 2 — 4 (- 2) = 4 + 8 = 12
√ (Д 2) = √ 12 = √ (4 3) = 2 √ 3
x 1 = (-2 — 2√3) / 2 = (2 (-1 — √ (3))) / 2 = — 1 — √3
x 2 = (-2 + 2√3) / 2 = (2 (-1+ √ (3))) / 2 = — 1 + √3
Ответ: -1 — √3; –1 + √3.
Как видите, при решении этого уравнения по разным формулам мы получили одинаковый ответ. Поэтому, хорошо усвоив формулы, изображенные на схеме рисунка 1, вы всегда сможете решить любое полное квадратное уравнение.
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Прежде чем мы узнаем, как найти дискриминант квадратного уравнения формы ax2 + bx + c = 0 и как найти корни данного уравнения, нам нужно вспомнить определение квадратного уравнения. Уравнение, имеющее вид ax 2 + bx + c = 0 (где a, b и c — любые числа, нужно также помнить, что a ≠ 0) является квадратным. Разделим все квадратные уравнения на три категории:
- не имеющие корней;
- в уравнении один корень;
- есть два корня.
Для того, чтобы определить количество корней в уравнении, нам нужен дискриминант.
Как найти дискриминант. Формула
Нам дано: ax 2 + bx + c = 0.
Дискриминантная формула: D = b 2 — 4ac.
Как найти корни дискриминанта
Количество корней определяется знаком дискриминанта:
- D = 0, уравнение имеет один корень;
- D>0, уравнение имеет два корня.
Корни квадратного уравнения находятся по следующей формуле:
X1 = -b + √D/2а; Х2 = -b + √D/2а.
Если D = 0, то можно смело использовать любую из представленных формул. В любом случае вы получите один и тот же ответ. А если окажется, что D > 0, то и считать ничего не придется, так как уравнение не имеет корней.
Надо сказать, что найти дискриминант не так уж и сложно, если знать формулы и аккуратно проводить расчеты. Иногда возникают ошибки при подстановке в формулу отрицательных чисел (нужно помнить, что минус на минус дает плюс). Будьте осторожны и все получится!
Квадратные уравнения изучаются в 8 классе, так что ничего сложного здесь нет.Умение решать их абсолютно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, а a ≠ 0.
Перед изучением конкретных методов решения отметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Иметь ровно один корень;
- У них два разных корня.

Это важное различие между квадратными и линейными уравнениями, где корень всегда существует и уникален.Как определить, сколько корней имеет уравнение? Для этого есть замечательная штука — дискриминант .
Дискриминант
Пусть задано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминантом будет просто число D = b 2 — 4ac.
Эту формулу нужно знать наизусть. Откуда оно родом — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение.А именно:
- Если D
- Если D = 0, то корень ровно один;
- Если D>0, корней будет два.
Обратите внимание: дискриминант указывает количество корней, а вовсе не их признаки, как почему-то многие считают. Посмотрите примеры — и сами все поймете:
Задание. Сколько корней имеют квадратные уравнения:
- х 2 — 8 х + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- х 2 — 6 х + 9 = 0.
Запишем коэффициенты первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 — 4 1 12 = 64 — 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два разных корня. Аналогично анализируем второе уравнение:
а = 5; б = 3; с = 7;
Д = 3 2 — 4 5 7 = 9 — 140 = -131.
Дискриминант отрицательный, корней нет. Остается последнее уравнение:
а = 1; б = -6; с = 9;
D = (−6) 2 — 4 1 9 = 36 — 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что коэффициенты были записаны для каждого уравнения. Да, долго, да, скучно — зато коэффициенты не перепутаешь и глупых ошибок не наделаешь. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не нужно будет выписывать все коэффициенты. Вы будете выполнять такие операции в своей голове. Большинство людей начинают это делать где-то после того, как решено 50-70 уравнений — в общем, не так уж и много.
Квадратичные корни
Теперь перейдем к решению. Если дискриминант D > 0, то корни можно найти по формулам:
Основная формула для корней квадратного уравнения
При D = 0 можно использовать любую из этих формул — получится то же число, которое будет будь ответом. Наконец, если Д
- х 2 — 2 х — 3 = 0;
- 15 — 2х — х 2 = 0;
- х 2 + 12 х + 36 = 0,
Первое уравнение:
х 2 — 2 х — 3 = 0 ⇒ а = 1; б = -2; с = -3;
Д = (-2) 2 — 4 1 (-3) = 16.
D> 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 — 2x — x 2 = 0 ⇒ a = −1; б = -2; с = 15;
D = (-2) 2 — 4 (-1) 15 = 64.
D> 0 ⇒ уравнение снова имеет два корня. Найдите их
\[\begin(align)&((x)_(1))=\frac(2+\sqrt(64))(2\cdot\left(-1\right))=- 5; \&((x)_(2))=\frac(2-\sqrt(64))(2\cdot\left(-1\right))=3. \\end(align)\]
Наконец, третье уравнение:
х 2 + 12 х + 36 = 0 ⇒ а = 1; б = 12; с = 36;
Д = 12 2 — 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первый:
Как видно из примеров, все очень просто. Если вы знаете формулы и умеете считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет описанная выше методика: смотрите на формулу буквально, описывайте каждый шаг – и очень скоро вы избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении.Например:
- х 2 + 9 х = 0;
- х 2 — 16 = 0,
Легко видеть, что в этих уравнениях отсутствует один из членов. Такие квадратные уравнения решаются еще проще, чем стандартные: для них даже не нужно вычислять дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободном элементе равен нулю.
Конечно, возможен очень сложный случай, когда оба эти коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, что такое уравнение имеет единственный корень: х = 0,
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл только при (−c / a) ≥ 0.Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполняется неравенство (−c / a) ≥ 0, то корней будет два. Формула приведена выше;
- Если (-с / а)
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже не обязательно помнить о неравенстве (−c/a) ≥ 0. Достаточно выразить значение x 2 и посмотреть, что стоит по ту сторону знака равенства.Если число положительное, то корней будет два. Если отрицательный, корней не будет вообще.
Если отрицательный, корней не будет вообще.
Теперь займемся уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Здесь все просто: корней всегда будет два. Достаточно вынести многочлен:
Вынося в скобки общий множительПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда и корни. В заключение разберем несколько таких уравнений:
Задание.Решите квадратные уравнения:
- х 2 — 7 х = 0;
- 5x 2 + 30 = 0;
- 4x 2 — 9 = 0.
х 2 — 7 х = 0 ⇒ х (х — 7) = 0 ⇒ х 1 = 0; х 2 = — (- 7) / 1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = -30 ⇒ x 2 = -6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 — 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; х 2 = -1,5.
[PDF] Дискриминант и определитель гиперповерхности четной размерности
ПОКАЗЫВАЕТСЯ 1-10 ИЗ 35 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные статьиНедавность
Дискриминант кубической поверхности
27 строк на a На ${{\mathbb Q}}$$ действует конечное частное от $${{\rm Gal}(\overline{\mathbb Q}/{\mathbb Q})}$$ . Мы создаем явные примеры, такие что… Expand
Мы создаем явные примеры, такие что… Expand
- View 1 выдержка, ссылки background
Дополнения к Mordell
Цель этой главы состоит в том, чтобы дать некоторые дополнительные результаты, в основном об обобщениях конечно порожденных расширений Q. Аналогичные результаты были получены другими людьми, и на… Развернуть
Вещественная алгебраическая геометрия
1. Упорядоченные поля, вещественные замкнутые поля.- 2. Полуалгебраические множества.- 3. Вещественные алгебраические многообразия.- 4. Вещественная алгебра.- 5. Принцип Тарского-Зейденберга как средство переноса.- 6. 17-я проблема Гильберта.… Expand
Гипотеза Мамфорда-Тейта для модулей Дринфельда
Рассмотрим представление Галуа на модуле Тейта модуль Дринфельда над конечно порожденным полем в общей характеристике. Основная цель этой статьи — определить образ Галуа… Expand
Элементы алгебры геометрии
© Publications mathématiques de l’I.H.E.S., 1965, tous droits reservés. L’accès aux archives de la revue « Математические публикации I.H.E.S. » (http://… Expand
L’accès aux archives de la revue « Математические публикации I.H.E.S. » (http://… Expand
Algebraic Geometry
Introduction to Algebraic Geometry. By Serge Lang. Pp. xi + 260. (Addison-Wesley: Reading, Massachusetts, 1972.)
Темы классической алгебраической геометрии
Устройство для непрерывного придания нагретому листу из термопластичной синтетической смолы желаемой конфигурации с последующей любой необходимой обработкой, при этом лист из синтетической смолы выдавливается из… Expand
Квадратные формы и удлинения в характеристиках 2
© Annales de l’institut Fourier, 1985 , tous droits reservés.L’accès aux archives de la revue «Annales de l’institut Fourier» (http://annalif.ujf-grenoble.fr/) implique l’accord avec les Conditions… Expand
Многочлены с действительными коэффициентами | СпрингерЛинк
Действия
‘) var buybox = document. querySelector(«[data-id=id_»+ метка времени +»]»).parentNode ;[].кусочек.call(buybox.querySelectorAll(«.buying-option»)).forEach(initCollapsibles) функция initCollapsibles(подписка, индекс) {
var toggle = подписка.querySelector(«.цена-варианта-покупки»)
подписка.classList.remove(«расширенный»)
var form = подписка.querySelector(«.форма-варианта-покупки») если (форма) {
вар formAction = form.getAttribute(«действие»)
форма.setAttribute(«действие», formAction.replace(«/checkout», «/cart»))
document.querySelector(«#ecommerce-scripts»).addEventListener(«load», bindModal(form, formAction, timestamp, index), false)
} var priceInfo = подписка.querySelector(«.Информация о цене»)
var PurchaseOption = toggle.
querySelector(«[data-id=id_»+ метка времени +»]»).parentNode ;[].кусочек.call(buybox.querySelectorAll(«.buying-option»)).forEach(initCollapsibles) функция initCollapsibles(подписка, индекс) {
var toggle = подписка.querySelector(«.цена-варианта-покупки»)
подписка.classList.remove(«расширенный»)
var form = подписка.querySelector(«.форма-варианта-покупки») если (форма) {
вар formAction = form.getAttribute(«действие»)
форма.setAttribute(«действие», formAction.replace(«/checkout», «/cart»))
document.querySelector(«#ecommerce-scripts»).addEventListener(«load», bindModal(form, formAction, timestamp, index), false)
} var priceInfo = подписка.querySelector(«.Информация о цене»)
var PurchaseOption = toggle. parentElement если (переключить && форма && priceInfo) {
переключать.setAttribute(«роль», «кнопка»)
toggle.setAttribute(«tabindex», «0») toggle.addEventListener («щелчок», функция (событие) {
var expand = toggle.getAttribute(«aria-expanded») === «true» || ложный
toggle.setAttribute(«aria-expanded», !expanded)
form.hidden = расширенный
если (! расширено) {
покупкаВариант.classList.add («расширенный»)
} еще {
покупкаOption.classList.remove(«расширенный»)
}
priceInfo.hidden = расширенный
}, ложный)
}
} функция bindModal (форма, formAction, метка времени, индекс) {
var weHasBrowserSupport = window.
parentElement если (переключить && форма && priceInfo) {
переключать.setAttribute(«роль», «кнопка»)
toggle.setAttribute(«tabindex», «0») toggle.addEventListener («щелчок», функция (событие) {
var expand = toggle.getAttribute(«aria-expanded») === «true» || ложный
toggle.setAttribute(«aria-expanded», !expanded)
form.hidden = расширенный
если (! расширено) {
покупкаВариант.classList.add («расширенный»)
} еще {
покупкаOption.classList.remove(«расширенный»)
}
priceInfo.hidden = расширенный
}, ложный)
}
} функция bindModal (форма, formAction, метка времени, индекс) {
var weHasBrowserSupport = window. fetch && Array.from функция возврата () {
var Buybox = EcommScripts ? EcommScripts.Ящик для покупок: ноль
var Modal = EcommScripts ? EcommScripts.Modal : ноль if (weHasBrowserSupport && Buybox && Modal) {
var modalID = «ecomm-modal_» + метка времени + «_» + индекс var modal = новый модальный (modalID)
modal.domEl.addEventListener («закрыть», закрыть)
функция закрыть () {
форма.querySelector(«кнопка[тип=отправить]»).фокус()
} форма.setAttribute(
«действие»,
formAction.replace(«/checkout», «/cart?messageOnly=1»)
) form.
fetch && Array.from функция возврата () {
var Buybox = EcommScripts ? EcommScripts.Ящик для покупок: ноль
var Modal = EcommScripts ? EcommScripts.Modal : ноль if (weHasBrowserSupport && Buybox && Modal) {
var modalID = «ecomm-modal_» + метка времени + «_» + индекс var modal = новый модальный (modalID)
modal.domEl.addEventListener («закрыть», закрыть)
функция закрыть () {
форма.querySelector(«кнопка[тип=отправить]»).фокус()
} форма.setAttribute(
«действие»,
formAction.replace(«/checkout», «/cart?messageOnly=1»)
) form. addEventListener(
«Отправить»,
Buybox.interceptFormSubmit(
Буйбокс.fetchFormAction(окно.fetch),
Buybox.triggerModalAfterAddToCartSuccess(модальный),
консоль.лог,
),
ложный
) document.body.appendChild(modal.domEl)
}
}
} функция initKeyControls() {
документ.addEventListener(«keydown», функция (событие) {
if (document.activeElement.classList.contains(«цена-варианта-покупки») && (event.code === «Пробел» || event.code === «Enter»)) {
если (document.activeElement) {
событие.
addEventListener(
«Отправить»,
Buybox.interceptFormSubmit(
Буйбокс.fetchFormAction(окно.fetch),
Buybox.triggerModalAfterAddToCartSuccess(модальный),
консоль.лог,
),
ложный
) document.body.appendChild(modal.domEl)
}
}
} функция initKeyControls() {
документ.addEventListener(«keydown», функция (событие) {
if (document.activeElement.classList.contains(«цена-варианта-покупки») && (event.code === «Пробел» || event.code === «Enter»)) {
если (document.activeElement) {
событие. preventDefault()
документ.activeElement.click()
}
}
}, ложный)
} функция InitialStateOpen() {
var buyboxWidth = buybox.смещениеШирина
;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) {
var toggle = option.querySelector(«.цена-варианта-покупки»)
var form = option.querySelector(«.форма-варианта-покупки»)
var priceInfo = option.querySelector(«.Информация о цене»)
если (buyboxWidth > 480) {
переключить.щелчок()
} еще {
если (индекс === 0) {
переключать.щелчок()
} еще {
toggle.
preventDefault()
документ.activeElement.click()
}
}
}, ложный)
} функция InitialStateOpen() {
var buyboxWidth = buybox.смещениеШирина
;[].slice.call(buybox.querySelectorAll(«.опция покупки»)).forEach(функция (опция, индекс) {
var toggle = option.querySelector(«.цена-варианта-покупки»)
var form = option.querySelector(«.форма-варианта-покупки»)
var priceInfo = option.querySelector(«.Информация о цене»)
если (buyboxWidth > 480) {
переключить.щелчок()
} еще {
если (индекс === 0) {
переключать.щелчок()
} еще {
toggle. {2}}+dx+e=0ax4 +bx3+cx2+dx+e=0
{2}}+dx+e=0ax4 +bx3+cx2+dx+e=0Здесь x — переменная, где a, b, c, d и e — действительные числа, а коэффициент a≠0.4}D=64a3e−16a2c2+16ab2c−16a2bd−3b4
Теперь, глядя на дискриминант данного уравнения четвертой степени, мы можем найти некоторые случаи природы корней. Эти случаи таковы:
Когда Δ<0,\Delta <0,Δ<0, тогда два корня, образованные уравнением, являются действительными корнями, а остальные два являются комплексно-сопряженными, недействительными корнями.
Когда Δ>0 \Delta >0\, Δ>0, то все корни данного уравнения четвертой степени действительны и различны.
Когда P<0P<0 P<0 и D<0, D<0, D<0, то все четыре корня уравнения действительны и различны.
Когда P>0P>0P>0 и D>0,D>0, D>0, то из четырех корней уравнения есть две пары невещественных комплексно-сопряженных корней.
Уравнение может иметь несколько корней. В случае, если Δ=0, \Delta = 0, Δ=0, возникают следующие условия:
Когда D>0D>0 D>0 или P>0P>0 P>0 и D≠0D \ne {\rm{ }}0 D=0 или R≠0,R \ne {\rm { }}0, R=0, то корни действительные двойные корни и два комплексно-сопряженных корня.

Когда Δ0=0{\Delta _0} = {\rm{ }}0 Δ0=0 и D≠0,D \ne {\rm{ }}0, D=0, то действительные тройные корни и действительный одиночный корень.
Когда P<0P<0 P<0 и D<0D<0D<0 и Δ0≠0,{\Delta _0} \ne 0, Δ0=0, тогда корни действительные два действительных одиночных корня.
Когда D=0, D=0,D=0, условия следующие:
Когда P<0,P<0,P<0, то корни уравнения являются действительными двойными корнями.
Когда P>0P>0P>0 и R=0,R=0,R=0, то корни уравнения являются комплексно-сопряженными двойными корнями.
Когда Δ0=0,{\Delta _0} = {\rm{ }}0,Δ0=0, то все корни уравнения равны −b4a.\frac{-b}{4a }.4а-б.
Теперь давайте посмотрим на некоторые приложения, которые помогают нам в реальной жизни.
Решение квадратных уравнений с использованием квадратичной формулы и дискриминанта
Название: Разрешение квадратичных уравнений с использованием квадратичной формулы и дискриминантногоРазработчик задач: Джинс Gresset Charles
Ученая площадь и содержание: Оценки 10-12 / ALGEBRA II
Целевая дата преподавания: 1 февраля 2007 г.

ШКОЛА: Средняя школа имени Джона Кеннеди
СТАНДАРТЫ:
ШАБЛОНЫ И АЛГЕБРА – 9-12 КЛАСС
СТАНДАРТ 4.3 ОБРАЗЦЫ И АЛГЕБРА: Все учащиеся будут представлять и анализировать отношения между переменными величинами и решать задачи, связанные с моделями, функциями и алгебраическими понятиями и процессами.
Strand D. Процедуры: Основываясь на знаниях и навыках, полученных в предыдущих классах, к концу 12-го класса учащиеся будут:
2. Выбирать и использовать соответствующие методы для решения уравнений и неравенств.
- Линейные уравнения — алгебраически
- Квадратные уравнения — разложение на множители (когда коэффициент X 2 равен 1) и использование квадратной формулы
- Все типы уравнений с использованием методов построения графиков, компьютера и графического калькулятора
МОДЕЛИ И АЛГЕБРА — 9-12 КЛАСС
СТАНДАРТ 4.3 ОБРАЗЦЫ И АЛГЕБРА: Все учащиеся будут представлять и анализировать отношения между переменными величинами и решать задачи, связанные с моделями, функциями и алгебраическими понятиями и процессами.
Strand D. Процедуры: Основываясь на знаниях и навыках, полученных в предыдущих классах, к концу 12-го класса учащиеся будут:
2. Выбирать и использовать соответствующие методы для решения уравнений и неравенств.
- Линейные уравнения — алгебраически
- Квадратные уравнения — разложение на множители (когда коэффициент X 2 равен 1) и использование квадратной формулы
- Все типы уравнений с использованием методов построения графиков, компьютера и графического калькулятора
Наверх
НАСТРОЙКА:
Реальная установка: Образование
Учащиеся смогут решать квадратные уравнения вида: ax2 +bx +c = 0.Учащиеся смогут устанавливать связи между этими уравнениями и параболическими уравнениями/функциями. В качестве примеров практического применения таких уравнений можно использовать различные типы приемников параболических антенн.
Основная цель — помочь учащимся освоить различные методы решения квадратных уравнений и найти их применение в реальном мире. учащиеся будут использовать различные примеры для моделирования и решения квадратных уравнений.
учащиеся будут использовать различные примеры для моделирования и решения квадратных уравнений.
Наверх
НАВЫКИ SMARTSKILLS:
Уровень I: Сбор данных — Данные, которые учащиеся получат при выполнении этого стандартного задания:
Словарь: x = (-b ± √(b≤ -4ac))/2a.Выражение (b≤ -4ac) под знаком радикала называется дискриминантом. Решения могут быть реальными или мнимыми. Если дискриминант отрицательный, решения мнимые или комплексные. В противном случае решения реальны. эти слова будут определены с использованием математических примеров в классе.
Уровень III: Применение знаний — Визуализированная информация, которая представляет собой прикладные знания в этой стандартной задаче:
Решение задач: Для решения прикладных задач будет использован метод дискриминанта.Студенты смогут идентифицировать решения как действительные или мнимые на основе знака дискриминанта.
Наверх
ПРЕДПОЧТЕНИЯ:
Вовлеченность учащихся — Учащиеся выполнят задание:
Каждый учащийся попытается решить заданные задачи индивидуально, используя квадратичную формулу. Затем, как совместные группы, они будут совместно работать над решением различных проблем, поставленных перед каждой группой. В конце выбранный ученик из каждой группы представит совместную работу классу, показав процесс и решения.
Затем, как совместные группы, они будут совместно работать над решением различных проблем, поставленных перед каждой группой. В конце выбранный ученик из каждой группы представит совместную работу классу, показав процесс и решения.
Инструкция — Занятия будут организованы и проведены путем дифференцирования сложности квадратных уравнений и их решений. Если класс является инклюзивным, учащимся с особыми потребностями будет уделено особое внимание и внимание. Возможна индивидуальная сессия.
Калькулятор — Учащиеся будут использовать калькуляторы или другие технические средства, которые могут быть доступны.
Заказчик студенческих работ — Учащийся представляет свою работу в качестве доказательства выполнения задания своим сверстникам в виде презентации класса и учителю в виде печатной копии от каждой группы.Их работа будет оцениваться баллами.
Отчет о результатах — Результаты оценивания будут представлены в виде баллов по процентильной рубрике, которая эквивалентна рубрике Нью-Джерси, но с другой шкалой. Рубрика оценки соответствует критериям оценки государственных школ Патерсона.
Рубрика оценки соответствует критериям оценки государственных школ Патерсона.
Временная шкала — Приблизительное время, необходимое для планирования и проведения этого урока, составляет один-два урока. Во время второго урока учащиеся будут оцениваться.
Наверх
ДЕЯТЕЛЬНОСТЬ:
Математика средней школы
Согласование: Учебные мероприятия будут разработаны в соответствии со стандартами основной учебной программы штата Нью-Джерси в соответствии с учебной программой по математике школьного округа Патерсон. Студенты смогут решать различные типы задач, связанных с квадратными уравнениями. Однако учащиеся будут ограничены использованием строго квадратичной формулы для решения этих задач.
Основной вопрос: Я задам ученикам следующие вопросы. Как определить квадратное уравнение? Что означают коэффициенты и постоянный член?
Выступления: К концу этого урока учащиеся смогут решать квадратные уравнения, используя квадратную формулу. Они поймут, как идентифицировать действительные корни и мнимые корни (также называемые комплексными числами). Я возлагаю большие надежды на успеваемость учащихся.Я буду измерять их успеваемость с помощью оценочного теста/викторины и их участия в классе.
Они поймут, как идентифицировать действительные корни и мнимые корни (также называемые комплексными числами). Я возлагаю большие надежды на успеваемость учащихся.Я буду измерять их успеваемость с помощью оценочного теста/викторины и их участия в классе.
1. Что учащиеся скажут или сделают, чтобы показать, что они понимают (как во время, так и в конце урока)?
Ожидается, что учащиеся смогут идентифицировать квадратные уравнения из набора различных уравнений. Они должны уметь дифференцировать коэффициенты a, b переменной x и постоянный член c. Они должны показать, что могут использовать квадратную формулу для решения квадратных уравнений.
2. Какие вопросы я могу задать, чтобы раскрыть мышление учащихся?
Я дам им набор уравнений, включая показательные уравнения, линейные уравнения, квадратные уравнения и т. д., и попрошу определить квадратные уравнения. Я также дам им несколько квадратных уравнений и их решения и попрошу их определить знак дискриминанта в каждом случае.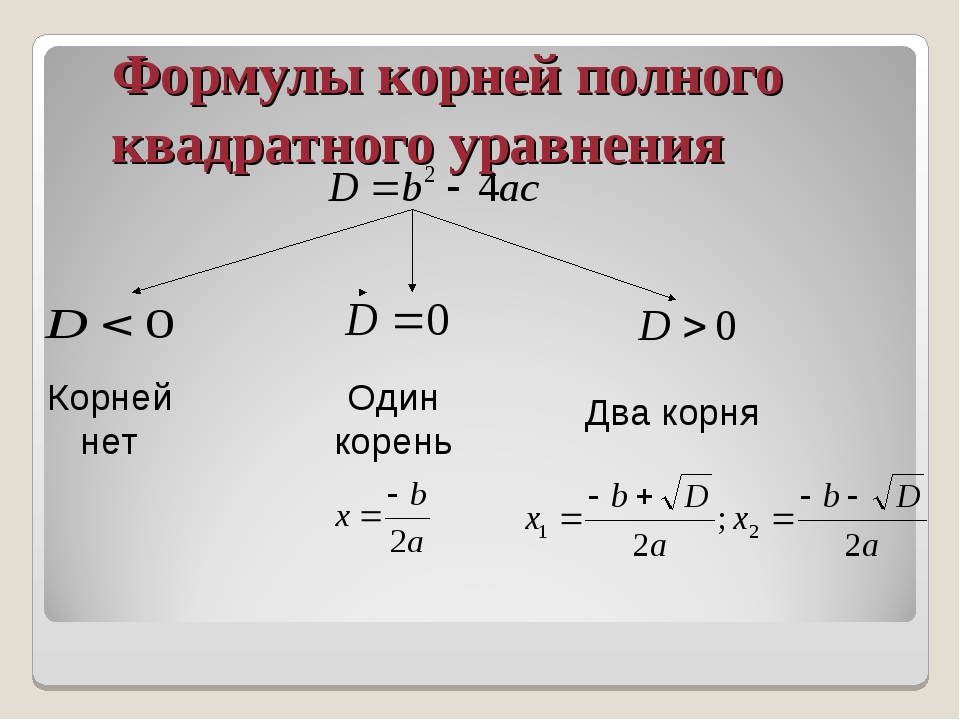 Я также попрошу их установить связь между квадратными уравнениями и некоторыми объектами, которые они могут использовать.
Я также попрошу их установить связь между квадратными уравнениями и некоторыми объектами, которые они могут использовать.
Что такое «крючок», который первоначально заинтересует учащихся на уроке?
Я спрошу, использовал ли кто-нибудь квадратную формулу для решения уравнений в своих предыдущих классах. Если да, то насколько сложной или легкой может быть для них эта формула. Прежде чем начать преподавать, я вовлеку их в короткое обсуждение в классе.
Где учащиеся могут застрять и как их выпутать:
- Застрял: некоторые учащиеся могут ошибаться в знаках, в то время как другим может быть трудно определить значения a, b и c, используя квадратичную формулу.
- Unstuck: Я помогу этим ученикам правильно использовать знак и правильно выполнять операции.
Вопросы, которые я могу задать, чтобы подтолкнуть учащихся к размышлению (без непосредственного управления их мышлением):
- Можете ли вы найти реальное приложение для моделирования квадратного уравнения?
- Как решить реальную задачу, используя метод решения квадратных уравнений?
- Можете ли вы применить квадратичную формулу для решения задач в области финансов, инженерии и любых других областях?
В начале урока. ..
..
Опишите, чем вы и учащиеся будете заниматься:
- Я попрошу учащихся прочитать определения.
- Я заставлю их понять квадратичную формулу
- Я буду использовать примеры
Опишите, почему они выполнят указанные выше шаги:
Эти шаги помогут учащимся решить задачу решения квадратных уравнений с использованием квадратной формулы.Их навыки решения проблем могут быть увеличены.
В середине урока…
Опишите, чем вы и учащиеся будете заниматься:
- Учащиеся будут выполнять упражнения из своей книги.
- Они будут участвовать в групповом обсуждении
- Они будут задавать вопросы и отвечать на них.
Опишите, почему они выполнят указанные выше шаги:
В математике практика остается одним из самых важных инструментов для успеха учащихся. Я часто говорил своим ученикам, что день без занятий математикой подобен дню без солнечного света.
Я часто говорил своим ученикам, что день без занятий математикой подобен дню без солнечного света.
В конце урока:
Опишите, чем вы и учащиеся будете заниматься:
- Я буду давать домашнее задание своим ученикам.
- Я объясню домашнее задание.
- Я установлю требования к этому домашнему заданию и крайний срок его возврата.
Опишите, почему они выполнят указанные выше шаги:
Я смогу измерить способность учащихся использовать квадратную формулу, прежде чем дать им оценочный тест/викторину.
Источник: Адаптировано из модели математики средней школы BCPSS
Наверх
БЕНЧМАРКИНГ:
Успеваемость учащихся 1:
Пример сравнительного анализа: фактический контрольный показатель успеваемости учащихся для моего первого урока, основанного на данных, установлен на уровне 75/100. Учащиеся, получившие оценку ниже этой, нуждаются в дополнительной практике, чтобы улучшить свои результаты для следующей оценки.
Учащиеся, получившие оценку ниже этой, нуждаются в дополнительной практике, чтобы улучшить свои результаты для следующей оценки.
Наверх
БАЛЛЫ:
Квалификационный тест средней школы Нью-Джерси (HSPT)
Целостное руководство по подсчету очков для открытых заданий по математике (общая рубрика) | |
3-точечный отклик | Ответ показывает полное понимание основных математических понятий задачи.Учащийся полностью выполняет процедуры и дает соответствующие ответы на все части задания. Ответ содержит несколько незначительных ошибок, если таковые имеются. Ответ содержит четкое и эффективное объяснение, подробно описывающее, как проблема была решена, чтобы читателю не нужно было делать выводы, как и почему были приняты решения. |
| 2-точечный датчик (70-84) | Ответ показывает почти полное понимание основных математических концепций задачи. |
| Одноточечный ответ (60-69) | Ответ показывает ограниченное понимание основных математических концепций задачи.Ответ и процедуры могут быть неполными и/или содержать серьезные ошибки. Неполное объяснение того, как была решена проблема, может вызвать вопросы о том, как и почему были приняты решения. |
| 0-балльная реакция (до 60 лет) | Ответ показывает недостаточное понимание основных математических понятий задачи. У них может не быть объяснения решения, или читатель может быть не в состоянии понять объяснение.Читатель может быть не в состоянии понять, как и почему были приняты решения. |
| Источник : Департамент образования штата Нью-Джерси | |
Наверх
РЕЗУЛЬТАТЫ:
Анализ: Я записал оценки учеников для оценки моего первого урока, основанного на данных, и я изучу данные, чтобы найти тенденции, способствующие факторы в серии оценок одного и того же стандарта обучения.
- Тенденции: Во время теста на 3-й. Делая период, я включил 2 задачи с квадратными уравнениями и попросил их использовать любой метод для решения одной из них и использовать квадратную формулу для другой. Большинство студентов решили обе задачи, используя квадратичную формулу. Эта тенденция свидетельствует о том, что большинству из них удобно пользоваться квадратичной формулой. Студенты показали хорошие результаты. У некоторых учащихся результаты тестов увеличились на 5–10 %, и 82.1 % учащихся сдали этот тест. Это на 8,62% больше, чем в предыдущем тесте.

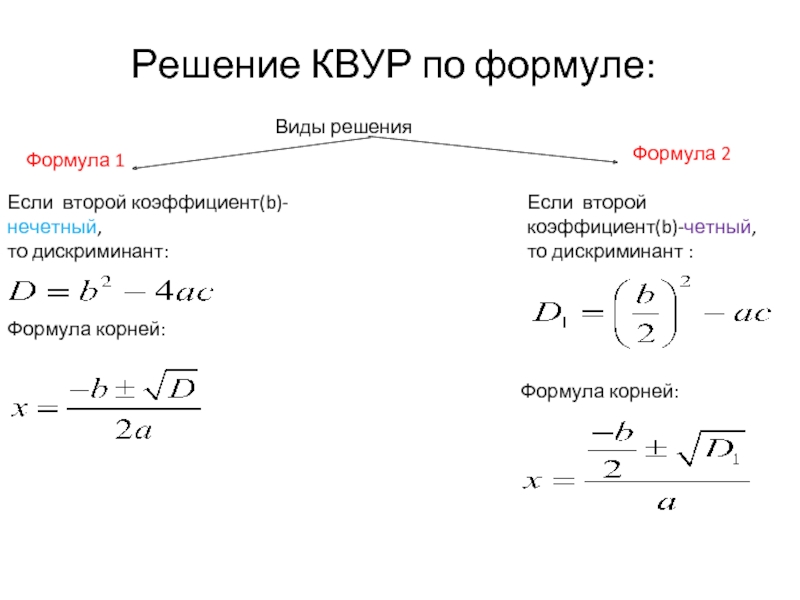

 От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.
От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.



 Студент выполняет почти все процедуры и дает соответствующие ответы на большинство частей задания. Ответ может содержать незначительные ошибки. Объяснение, подробно описывающее, как была решена проблема, может быть неясным, что заставит читателя сделать некоторые выводы.
Студент выполняет почти все процедуры и дает соответствующие ответы на большинство частей задания. Ответ может содержать незначительные ошибки. Объяснение, подробно описывающее, как была решена проблема, может быть неясным, что заставит читателя сделать некоторые выводы.