Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)

Название функции	Формула функции	График функции	Название графика	Комментарий
Линейная, прямая пропорциональность	y = kx		Прямая	Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Линейная, прямая пропорциональность со сдвигом	y = kx + b		Прямая	Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1.
Квадратичная функция	y = x2		Парабола	Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат.
Квадратичная функция	y = ax2 + bx + c		Парабола	Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа
Степенная функция	y = x3		Кубическая парабола	Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — корень квадратный	y = x1/2		График функции y = √x	Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — обратная пропорциональность	y = k/x		Гипербола	Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1.
Показательная функция	y = ex		Экспонента	Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590…
Показательная функция	y = ax		График показательной функции а>1	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1).
Показательная функция	y = ax		График показательной функции 0<a<1	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1).
Логарифмическая функция	y = ln(x)		График логарифмической функции — натуральный логарифм	График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой.
Логарифмическая функция	y = log ax		График логарифмической функции — логарифм по основанию а>1	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1).
Логарифмическая функция	y = logax		График логарифмической функции 0<a<1	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1).
Синус	y = sinx		Синусоида	Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Косинус	y = cosx		Косинусоида	Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Тангенс	y = tgx		Тангенсоида	Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Котангенс	y = сtgx		Котангенсоида	Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».

tehtab.ru

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

 

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

 

Линейная функция – функция вида y=ax+b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:

 

Если a>0, прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y.

 

Если a<0, прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y.

 

Если a=0, функция принимает вид y=b.

 

Отдельно выделим график уравнения x=a.

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

 

Графиком функции y=ax2+bx+c является парабола.

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:

1. Коэффициент a указывает на то, куда направлены ветки параболы.

• Если a>0 , ветки параболы направлены вверх.
• Если a<0 , ветки параболы направлены вниз.

1. Коэффициент c указывает, в какой точке парабола пересекает ось y.
2. Коэффициент b помогает найти xв – координату вершины параболы.

xв=−b2a

1. Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

• Если D>0 – две точки пересечения.
• Если D=0 – одна точка пересечения.
• Если D<0 – нет точек пересечения.

 

Графиком функции y=kx является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.

Если k  <  0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.

 

 

Функция y  =  x имеет следующий график:

 

Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.

 

 

Скачать домашнее задание к уроку 5.

 

epmat.ru

Функции и графики — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Координаты и базовые понятия о функциях

К оглавлению…

Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:

Функция – это соответствие вида y 

= f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.

Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.

Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).

Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.

Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.

Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.

Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.

Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.

Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень

х приходится отрицательный корень –х.

Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.

 

График линейной функции

К оглавлению…

Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):

 

График квадратичной функции (Парабола)

К оглавлению…

График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x₁; 0) и (x₂; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x₀; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):

При этом:

• если коэффициент a > 0, в функции y = ax² + bx + c, то ветви параболы направлены вверх;
• если же a < 0, то ветви параболы направлены вниз.

Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

 

Графики других функций

К оглавлению…

Степенной функцией называют функцию, заданную формулой:

Приведем несколько примеров графиков степенных функций:

Обратно пропорциональной зависимостью называют функцию, заданную формулой:

В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.

Показательной функцией с основанием а называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:

График функции y = |x| выглядит следующим образом:

 

Графики периодических (тригонометрических) функций

К оглавлению…

Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:

где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T₁, который определяется формулой:

Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

educon.by

Графики функций 〽️ и их формулы, потсроение и свойства гиперболических, показательных, степенных, квадратичных, линейных функций, решения

Решение различных видов функций

Фактически данное задание может быть решено двумя различными способами:

• Первый способ состоит в банальном решении каждой из функций путем подстановки различных переменных, и на основе этого составлении таблицы координат;
• Вторым методом является запоминание уравнений по строению и их примерных изображений.

Важно! Решение данного задания вторым способом на деле не только более надежно, но и сэкономит большое количество времени, которое в дальнейшем можно спокойно потратить на решение более сложных заданий.

Всю подробную информацию о графиках классических функций и их внешнем виде можно найти в данной статье ниже по тексту.

Линейные

Линейные — являются первыми функциями, которые проходятся в школьном курсе математики. Получается, что они представляют собой обычные прямые линии.

Пример: y=4x, y=3x-7, y=5-6x

Для того чтобы построить график линейной функции по правилам математики, достаточно всего двух точек. В первую очередь для примера возьмем уравнение y=-2x+1. Нужно взять 2 не сильно отдаленных друг от друг числа, в нашем случае это будут 2 и -2. Далее нужно построить таблицу: в графу “x” вставить числа, которые мы придумали, а в графу “y” вставить результаты получившихся уравнений (табл.1).

Таблица 1. Координаты точек y=-2x+1

В конечном итоге после построения точек необходимо соединить их прямой линией (рис.1). Рис. 1. Изображение формулы y=-2x+1

Квадратичные

В функциях такого типа обязательным параметром является возведение x во вторую степень. В общем виде формула выражается уравнением:

\[ y\;=\;ax^2+b \]

Одной из особенностей такого выражения является невозможность появления в третьей и четвертой четверти без дополнительных коэффициентов . В зависимости от наличия дополнительных действий сложения и вычитания, график может быть повернут как вверх, так и вниз. Однако в любом случае он будет представлять собой дугу, которая в математике называется параболой. Также стоит обратить внимание, что самой нижней точке параболы является так называемая вершина. Находится же она с помощью специальной формулы:

\[ x=\frac{-b}{2a} \]

Подставив x в формулу параболы, находим значение координаты y. Для того чтобы построить такой график, необходимо знать как минимум 5 точек — координаты вершины параболы и по 2 точки на каждой из двух дуг. В частном случае, когда а=1, а b=0, имеем формулу y=x². В этом случае вершину находить нет необходимости, так как она будет находиться в точке отсчета (0; 0) (рис.2).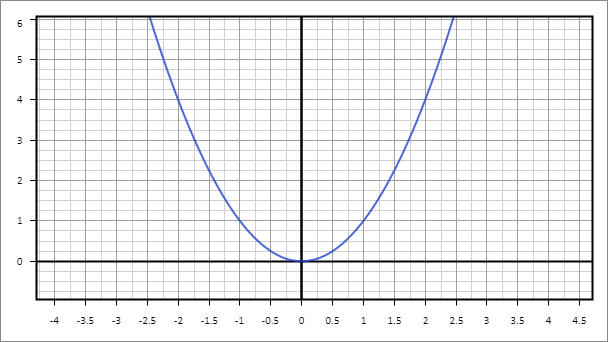 Рис. 2. Изображение формулы y=x²

Кубические и гиперболы

Кубическими называют уравнения, в которых имеется переменная в третьей степени, чаще всего x³.

\[ \;y=ax^3+b \]

При том, что по внешнему виду формула похожа на квадратичную функцию, на деле они имеют совершенно разное строение. В случае квадратичной любое число, даже отрицательное, при возведении во вторую степень становится положительным. Благодаря этому график и имеет симметричную форму, а также всегда только плюсовые значения. В третьей же степени отрицательные числа, соответственно, могут после всех действий становиться меньше нуля, из-за чего кубический график выглядит следующим образом (рис.3). Рис. 3. Изображение кубической формулыФормулы гипербол имеют выражения, в которых любое число делится на x. В общем виде формула выглядит следующим образом: ​\( y=\frac аx+b \)​​. Изображение ее так же, как большинства схожих заданий, строится с помощью 4 точек (риc.4). 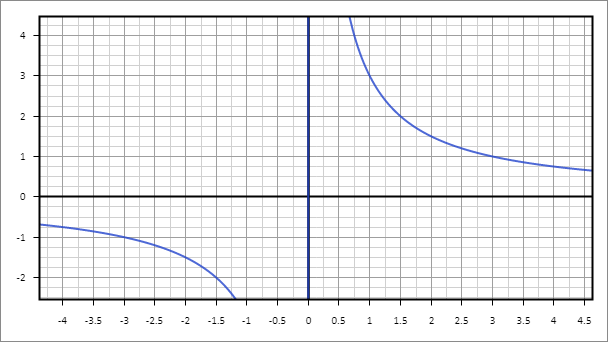Рис. 4. Гиперболические значения ​​\( y=\frac аx+b \)​

Подкоренные выражения

В общем виде данные уравнения выражаются как ​\( y=a\sqrt x+b \)​. Особенность графиков данного вида заключается в полном отсутствии каких-либо значений в третьей и четвертой четвертях координатной плоскости.

Важно! Такой феномен можно наблюдать благодаря тому, что под корнем не может быть отрицательное число (рис.5).

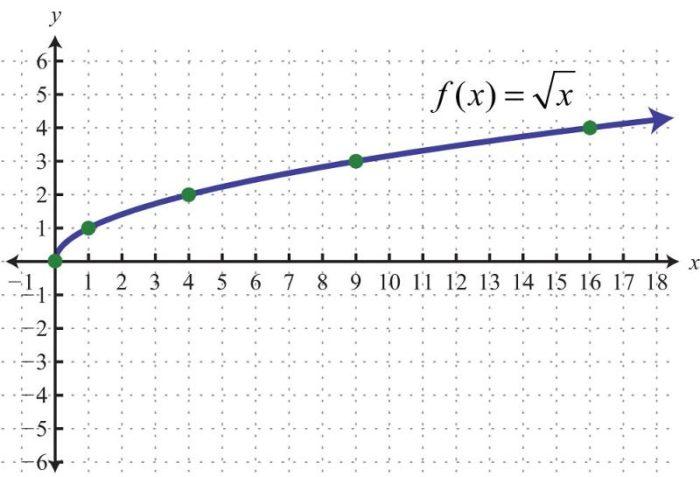Рис. 5. Изображение подкоренного выражения

Тригонометрические функции и их особенности

Отдельной темой представлены тригонометрические графики. Так, фактически уравнения синуса и косинуса являются четными, непрерывными волнами. На рис.6 функция y = sin x изображена синим цветом, а y = cos x — красным.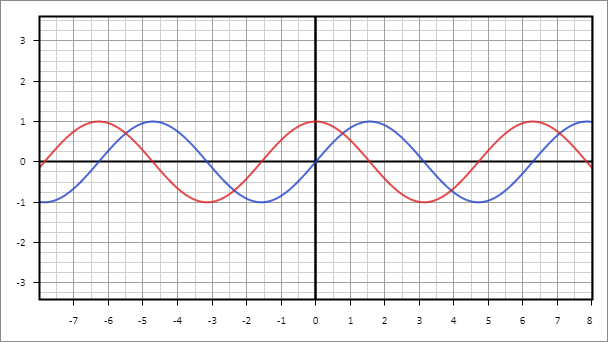 Рис. 6. График функций y = sin x и y = cos xПериод такой функции, то есть момент, за который функция проходит полный круг и возвращается в исходную точку, равен ​\( 2\mathrm\pi \)​. Тангенс и котангенс также имеют свои графики и по сути являются линиями пересечения выражений синуса и косинуса. На рисунке 7, что представлен ниже, график y = tg x синего цвета, а функции y = ctg x, соответственно, красного. 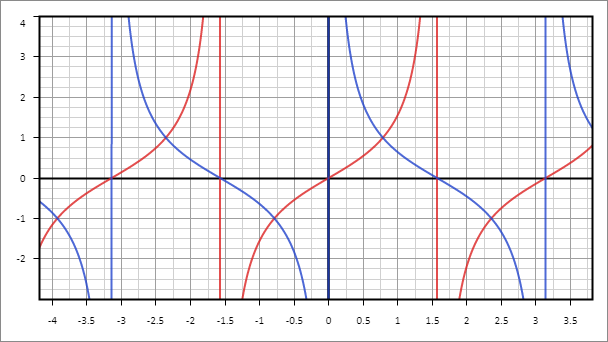Рис. 7. Графики функций y = tg x и y = ctg xВыучив все виды функций, можно легко увеличить средний балл за абсолютно любой тест порой на целых 3-4 единицы. Это может повлиять не просто на итоговую оценку, а даже на поступление в университет.

nauka.club

Виды функций и их графики

Понятие функции

Зависимость одной переменной у от другой х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функцией.

Общий вид функции: у = f(х),

где х – независимая переменная (аргумент), у – зависимая переменная (функция).

Область определения функции D(f)— множество, на котором задаётся функция. Другими словами: множество значений, которые может принимать аргумент.

Область значений функции E(f)— множество, состоящее из всех значений, которые принимает функция.

График функции – множество точек на координатной плоскости, координатами которых являются пары чисел (х; у), где х – значение аргумента, у – соответствующее ему значение функции.

Нули функции – значения аргумента, при которых функция равна 0.

Виды функций и их графики

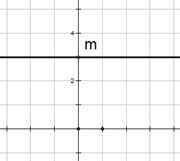
ü Линейная функция y = kx + m

График функции – прямая.

Коэффициент k отвечает за угол наклона (k>0 – угол острый, k<0 – угол тупой, k=0 – горизонтальная прямая), m – за сдвиг графика вверх-вниз (m>0 – вверх, m<0 – вниз).

у = kx – частный случай линейной функции при m=0.

В этом случае график функции обязательно проходит через начало координат.

Свойства функции y = kx + m

1) D(f) = (-∞; +∞)

2) Возрастает, если k > 0; убывает, если k < 0

3) Не ограничена ни снизу, ни сверху

4) Нет ни наибольшего, ни наименьшего значений

5) E(f) = (-∞; +∞)

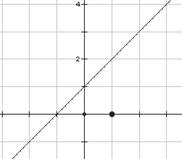
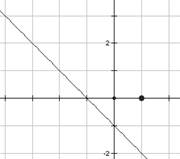
ü Функция y = kx² (k ≠ 0)График функции – парабола.

Свойства функции y = kx² 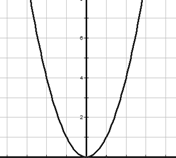Если k > 0

1) D(f) = (-∞; +∞)

2) Убывает на луче (-∞; 0], возрастает на луче [0; +∞)

3) Ограничена снизу, не ограничена сверху

4)

y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

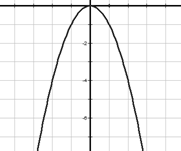
Если k < 0

1)

D(f) = (-∞; +∞)

2) Возрастает на луче (-∞; 0], убывает на луче [0; +∞)

3) Не ограничена снизу, ограничена сверху

4) y наим не существует, у наиб = 0

5) Непрерывна

6) E(f) = (-∞; 0]

ü Квадратичная функция y = ax² + bx + c

График функции – парабола, у которой:

® вершинарасполагается в точке (x0; y0), где x0 = 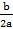, y0 = f(x0)

® ветви, направлены вверх, если а > 0, и вниз, если а < 0

® прямая х = х0 является осью симметрии параболы.

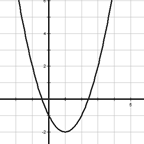Число с – ордината точки пересечения параболы с осью Оу.

Свойства функции y = ax² + bx + c

Если а > 0

1) D(f) = (-∞; +∞)

2)

Убывает на луче (-∞; —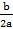 ], возрастает на луче [- ; +∞)

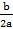3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [y0; +∞)

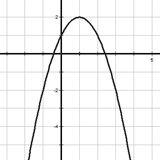Если а > 0

1)

D(f) = (-∞; +∞)

2) Возрастает на луче (-∞; — 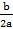], убывает на луче [- ; +∞)

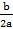3) Не ограничена снизу, ограничена сверху

4) y_наим не существует, у_наиб = 0

5) Непрерывна

6) E(f) = (-∞; y₀]

ü

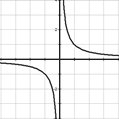Функция обратной пропорциональности y =

График функции – гипербола.

Свойства функции y =

1) D(f) = (-∞; 0) (0; +∞)

2) Если k > 0, то функция убывает на промежутке (-∞; 0) (0; +∞)

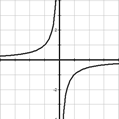Если k < 0, то функция возрастает на промежутке (-∞; 0) (0; +∞)

3) Не ограничена ни снизу, ни сверху

4) Нет ни наименьшего, ни наибольшего значений

5) Функция непрерывна на открытом луче (-∞; 0) и на открытом луче (0; +∞)

6) E(f) = (-∞; 0) (0; +∞)

ü Функция y =

График функции – ветвь параболы, перевернутая «набок».

Свойства функции y =

1) D(f) = [0; +∞)

2) 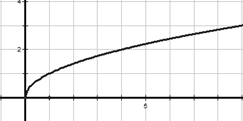Возрастает

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

ü Функция y =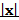

График функции – объединение двух лучей: y = x, x ≥ 0 и y = -x, x ≤ 0

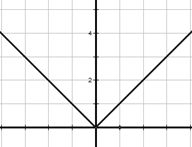Свойства функции y =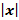

1) D(f) = (-∞; +∞)

2) Убывает на луче (-∞; 0], возрастает на луче [0; +∞)

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

 

y = xⁿ (n = 3, 5, 7, 9…)

График функции – кубическая парабола (при n=3)

Свойства функции

1)

D(f) = (-∞; +∞)

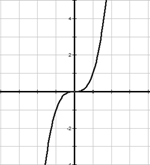
2) Возрастает

3) Не ограничена ни снизу, ни сверху

4) Нет ни наименьшего, ни наибольшего значений

5) Непрерывна

6) E(f) = (-∞; +∞)

Преобразования графика функции y = f(x)

1) y = f(x) + a

Сдвиг вверх на а единиц, если a > 0

Cдвиг вниз, если a < 0

2) y = f(x + a)

Сдвиг влево на а единиц, если a > 0

Сдвиг вправо, если a < 0

3) — y = f(x)

Зеркальное отражение относительно Ох

4) y = f(-x)

Зеркальное отражение относительно Оу

5) y = a·f(x)

Растяжение вдоль Оу, если a > 1

Растяжение вдоль Ох, если 0 < a < 1

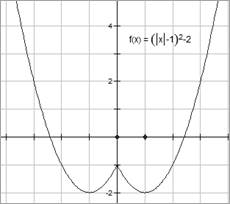
6) y = f(|x|)

Для x ≥ 0, y = f(x)

Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую.

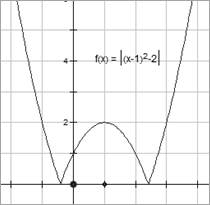
7) y = |f(x)|

Для f(x) ≥ 0, |f(x)| = f(x)

Для f(x) < 0, |f(x)| = -f(x)

Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox.

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

poisk-ru.ru

Гиперболические функции свойства графики формулы

Справочные данные по гиперболическим функциям. Определения, графики и свойства гиперболического синуса, косинуса, тангенса и котангенса. Формулы сумм, разностей и произведений. Производные, интегралы, разложения в ряды. Выражения через тригонометрические функции.

Определения гиперболических функций, их области определений и значений

sh x – гиперболический синус

,     –∞ < x < +∞;   –∞ < y < +∞.

ch x – гиперболический косинус

,     –∞ < x < +∞;   1 ≤ y < +∞.

th x – гиперболический тангенс

,     –∞ < x < +∞;   – 1 < y < +1.

cth x – гиперболический котангенс

,     x ≠ 0;   y < –1   или   y > +1.

Графики гиперболических функций

График гиперболического синуса   y = sh x

График гиперболического косинуса   y = ch x

График гиперболического тангенса   y = th x

График гиперболического котангенса   y = cth x

Формулы с гиперболическими функциями

Связь с тригонометрическими функциями

sin iz = i sh z ;     cos iz = ch z
sh iz = i sin z ;     ch iz = cos z
tg iz = i th z ;     ctg iz = – i cth z
th iz = i tg z ;     cth iz = – i ctg z
Здесь   i – мнимая единица,   i² = –1.

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Четность

sh(–x) = – sh x;   ch(–x) = ch x.
th(–x) = – th x;   cth(–x) = – cth x.

Функция   ch(x)   – четная. Функции   sh(x),   th(x),   cth(x) – нечетные.

Разность квадратов

ch² x – sh² x = 1.

Формулы суммы и разности аргументов

sh(x &pm; y) = sh x ch y &pm; ch x sh y,
ch(x &pm; y) = ch x ch y &pm; sh x sh y,
,
,

sh 2x = 2 sh x ch x ,
ch 2x = ch² x + sh² x = 2 ch² x – 1 = 1 + 2 sh² x,
.

Формулы произведений гиперболического синуса и косинуса

,
,
,

,
,
.

Формулы суммы и разности гиперболических функций

,
,
,
,
.

Связь гиперболического синуса и косинуса с тангенсом и котангенсом

,     ,
,     .

Производные

,

Интегралы от sh x, ch x, th x, cth x

,
,
.

Разложения в ряды

.

,

,

.

Обратные функции

Ареасинус

При   – ∞ < x < ∞   и   – ∞ < y < ∞   имеют место формулы:
,
.

Ареакосинус

При   1 ≤ x < ∞   и   0 ≤ y < ∞   имеют место формулы:
,
.

Вторая ветвь ареакосинуса расположена при   1 ≤ x < ∞   и   – ∞ < y ≤ 0  :
.

Ареатангенс

При   – 1 < x < 1   и   – ∞ < y < ∞   имеют место формулы:
,
.

Ареакотангенс

При   – ∞ < x < – 1   или   1 < x < ∞   и   y ≠ 0   имеют место формулы:
,
.

Автор: Олег Одинцов.     Опубликовано: 27-07-2014

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

1cov-edu.ru

Изображение функций — формула, таблица, график | Формулы и расчеты онлайн

Формула — изображение функций

Многие функциональные зависимости могут быть представлены простыми формулами. Например, зависимость между площадью круга S и радиусом r представляется формулой:

\[ S = \pi r^2\]

Зависимость между высотой s брошенного тела и временем t, протекшим от момента броска выражается формулой:

\[ s = u_0 t — \frac{1}{2} gt^2\]

Последняя формула — приближенная, так как она не учитывает многих факторов, таких как, сопротивление воздуха, ослабления силы земного притяжения с увеличением высоты.

Часто функциональную зависимость не удается представить в виде формулы, или если удается, то формула неудобна для вычислений. В таких случаях используют иные способы, табличный и графический.

Таблица — изображение функций

Функциональная зависимость между давлением пара p и температурой воды T не удается представить одной формулой которая с нужной точностью охватывала бы все важные случаи. Такая зависимость представляется таблицей.

Для удобства вычислений значения одной переменной большей частью берутся через равные промежутки. Эта переменная называется аргументом таблицы.

Всех значений аргумента никакая таблица не может содержать, но практически пригодная таблица должна содержать столько значений аргумента, чтобы для остальных значение функции можно было получить с нужной точностью при помощи интерполяции.

График — изображение функций

Чтобы графически изобразить заданную функциональную зависимость, на координатной плоскости, на оси абсцисс отмечаем ряд значений x₁, x₂, x₃ … одной из переменных x и строим ординаты y₁, y₂, y₃ … представляющие соответствующие значения переменной y. Получается ряд точек M(x₁,y₁), M(x₂,y₂), M(x₃,y₃) … Соединяя их на глаз плавной кривой линией, получается график данной функциональной зависимости.

Преимуществом графического изображения в сравнении с табличным является его наглядность и легкая обозримость.

Недостатком — малая степень точности. Большое практическое значение имеет удачный выбор масштабов.

В помощь студенту

Изображение функций — формула, таблица, график	стр. 105

www.fxyz.ru