Решение простейших тригонометрических уравнений с помощью аркфункций
Задача 1
Решите уравнение \[\sin x=-a, \quad 0<a<1\]
Решение
\(\arcsin(-a)\) – это такой угол из отрезка \(\left[-\dfrac{\pi}2;
\dfrac{\pi}2\right]\), синус которого равен \(-a\): 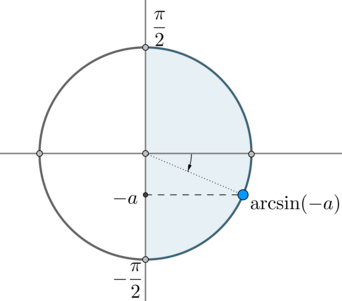
Следовательно, одна серия решений данного уравнения – это \(x=\arcsin(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, синус в которой равен \(-a\) – угол \(\alpha\): 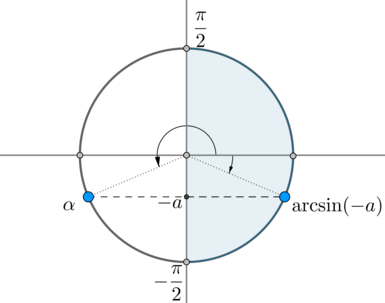
Заметим, что \(\alpha=\pi+(-\arcsin(-a))\). Так как \(\arcsin(-a)=-\arcsin a\), то \(\alpha=\pi+\arcsin a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=-\arcsin a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=\pi+\arcsin a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\]
Задача 2
Решите уравнение \[\cos x=-a, \quad 0<a<1\]
Решение
\(\arccos(-a)\) – это такой угол из отрезка \(\left[0; \pi\right]\), косинус которого равен \(-a\): 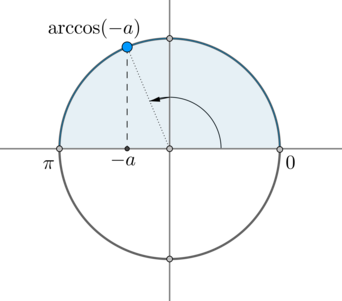
Следовательно, одна серия решений данного уравнения – это \(x=\arccos(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, косинус в которой равен \(-a\) – угол \(\alpha\): 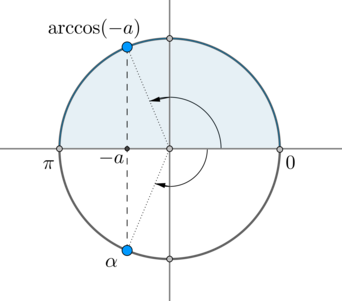
Заметим, что \(\alpha=-\arccos(-a)\). Так как \(\arccos(-a)=\pi-\arccos
a\), то \(\alpha=-\pi+\arccos a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=\pi-\arccos
a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=-\pi+\arccos a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\]
Задача 3
Решите уравнение \[\mathrm{tg}\, x=-a, a>0\]
Решение
\(\mathrm{arctg}\,(-a)\) – это такой угол из промежутка \(\left(-\dfrac{\pi}2;\dfrac{\pi}2\right)\), тангенс которого равен \(-a\): 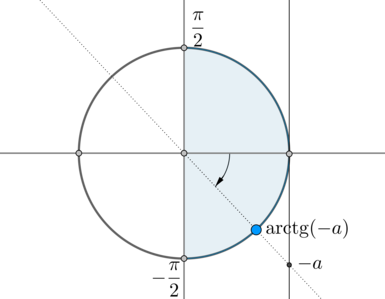
Следовательно, одна серия решений данного уравнения – это \(x=\mathrm{arctg}\,(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, тангенс в которой равен \(-a\) – угол \(\alpha\): 
Заметим, что \(\alpha=\mathrm{arctg}\,(-a)+\pi\). Так как \(\mathrm{arctg}\,(-a)=-\mathrm{arctg}\, a\), то \(\alpha=\pi-\mathrm{arctg}\, a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=-\mathrm{arctg}\, a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=\pi-\mathrm{arctg}\, a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\] Заметим, что так как углы \(-\mathrm{arctg}\, a\) и \(\pi-\mathrm{arctg}\, a\) отличаются друг от друга на \(\pi\), то ответ можно записать в виде одной серии корней с периодом \(\pi\): \[x=-\mathrm{arctg}\, a+\pi m, m\in\mathbb{Z}\]
Задача 4
Решите уравнение \[\mathrm{ctg}\, x=-a, a>0\]
Решение
\(\mathrm{arcctg}\,(-a)\) – это такой угол из промежутка \(\left(0;\pi\right)\), котангенс которого равен \(-a\): 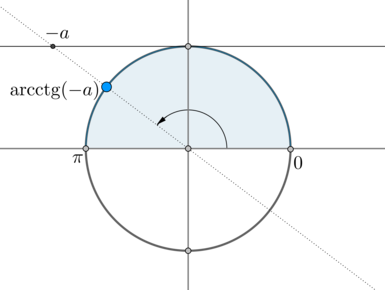
Следовательно, одна серия решений данного уравнения – это \(x=\mathrm{arcctg}\,(-a)+2\pi n, n\in\mathbb{Z}\).
Но на окружности есть еще одна точка, котангенс в которой равен \(-a\) – угол \(\alpha\): 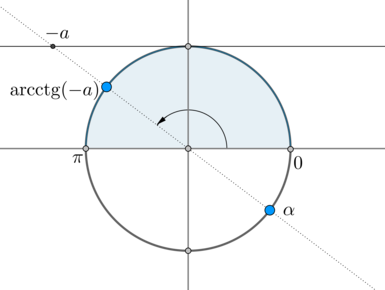
Заметим, что \(\alpha=\mathrm{arcctg}\,(-a)+\pi\). Так как \(\mathrm{arcctg}\,(-a)=\pi-\mathrm{arcctg}\, a\), то \(\alpha=2\pi-\mathrm{arcctg}\, a\). Следовательно, ответ в нашем уравнении: \[\left[\begin{gathered}\begin{aligned}
&x=\pi-\mathrm{arcctg}\, a+2\pi n, n\in\mathbb{Z}\\[2ex]
&x=2\pi-\mathrm{arcctg}\, a+2\pi k,
k\in\mathbb{Z}\end{aligned}\end{gathered}\right.\] Заметим, что так как углы \(2\pi-\mathrm{arcctg}\, a\) и \(\pi-\mathrm{arcctg}\, a\) отличаются друг от друга на \(\pi\), то ответ можно записать в виде одной серии корней с периодом \(\pi\): \[x=\pi-\mathrm{arcctg}\, a+\pi m, m\in\mathbb{Z}\]
shkolkovo.net
«Решение простейших тригонометрических уравнений». 10-й класс
Тип занятия: изучение нового материала.
Цели урока:
- Дидактическая: ввести понятия простейших тригонометрических уравнений, формул их корней; закрепить умение находить значения обратных тригонометрических функций
- Развивающая: формировать умение анализировать, искать аналоги и различные варианты решения.
- Воспитательная: воспитывать внимательность, уверенность; активность, наблюдательность; стремление в взаимовыручке, умение работать в группе и самостоятельно.
Форма проведения: работа в группах, индивидуальная, самостоятельная.
Формы контроля: текущий.
Оборудование: презентация «Простейшие тригонометрические уравнения», проектор, экран; доска, цветной мел; листы отчета работы в группах; карточки-тесты, индивидуальные задания на карточках; листы.
В результате изучения новой темы студенты должны:
- знать: понятия простейших тригонометрических уравнений и формулы их корней; частные случаи простейших тригонометрических уравнений;
- уметь: применять формулы корней уравнений при решении упражнений; находить значения обратных тригонометрических функций на единичной окружности.
План проведения занятия:
- Организационный момент
- Проверка знаний, воспроизведение и коррекция
опорных знаний.
- Тест с выбором ответа (по 2 вариантам)
- Мотивационный момент
- Изучение нового материала
- Первичное применение приобретенных знаний
- Работа под руководством преподавателя
- Работа в группах
- Рефлексия
- Самостоятельная работа студентов
- Итог занятия
- Задание на дом
Структура занятия
1. Организационный момент
Приветствие, перекличка.
2. Проверка знаний, воспроизведение и коррекция опорных знаний.
Тест с выбором ответа по 2 вариантам на карточках. (Приложение)
3. Мотивационный момент
– обоснование необходимости изучения данной
темы, сообщение темы
– вовлечение студентов в процесс постановки
целей и задач занятия (Приложение
\ Презентация, слайды
№ 1-2)
4. Изучение нового материала
Определение Простейшие тригонометрические уравнения – уравнения вида Sinx = a, Cosx = a, tgx = a, ctgx = a.
Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента, при котором данная тригонометрическая функция принимает значение а.
Рассмотрим решения данных уравнений
Уравнение Cos x = a
Т.к. функция у = Cosxимеет смысл при , то рассмотрим основные случаи решения данного уравнения.
(Приложение \ Презентация, слайды № 3, 4)
Рассмотрим ещё несколько случаев решения данного уравнения, при решении которых используется единичная окружность.
Частные случаи
(Приложение \ Презентация, слайды № 5-6)
Рассмотрим пример
(разбираем решение на доске).
Уравнение Sinx = a
Т.к. функция у = Sinxтакже имеет смысл при , то аналогично рассмотрим основные случаи решения данного уравнения.
(Приложение \ Презентация, слайды № 7, 8)
Замечание:
при .
Рассмотрим также несколько случаев решения данного уравнения, при решении которых используется единичная окружность.
Частные случаи
(Приложение \ Презентация, слайды № 9-10)
Рассмотрим примеры
1) (разбираем решение на доске).
2) (разбираем решение по презентации)
(Приложение \ Презентация, слайд № 11)
Уравнение tgx = a (вспомнить линиюtgxна окружности!)
.
Т.о.
(Приложение \ Презентация, слайд № 12)
Уравнение ctgx = a
Аналогично рассматривается
(Приложение \ Презентация, слайд № 13)
Рассмотрим пример
(разбираем решение на доске).
5. Первичное применение приобретенных знаний
Работа под руководством преподавателя
№ 1. Решить уравнения:
а)
б)
Работа в группах
Разделяю студентов на группы, выдаю листы
отчета работы в группах
№ 2. Решить уравнения (Приложение
\ Презентация – слайд
№ 14)
Далее проводим проверку и разбор решения по
ответам на экране (Приложение
\ Презентация, слайд №
15)
6. Рефлексия
Самостоятельная работа студентов
Проводится в трех вариантах + Работа по
индивидуальным заданиям – карточкам
Задания по вариантам – Приложение
\ Презентация, слайд №
16)
Задания по карточкам – Приложение
Проверка и оценивание самостоятельной работы и
оценок по карточкам проводится во время записи
домашнего задания студентами
7. Итог урока
Во фронтальной беседе повторить основные моменты нового материала. Подведение итогов, выставление оценок.
8. Задание на дом:
а) теория – учебник Н.В. Богомолова «Математика» (п. 39), конспект
б) № 3. Решить уравнения.
urok.1sept.ru
Простейшие тригонометрические уравнения
Цель : изучить формулы корней простейших тригонометрических уравнений.
Задачи Образовательные: повторить определение арксинуса действительного числа; повторить определение синуса действительного числа; изучить формулу корней уравнения ; сформировать умение решать уравнения этого вида; провести проверку усвоения знаний.
Ожидаемые результаты
Предметные: решает простейшие тригонометрические уравнения вида
Метопредметные: умеет планировать свою деятельность и самостоятельно решать
Личностные: формирование у учащихся интеллектуальной честности и объективности
Тип урока: изучения и первичного закрепления новых знаний
Формы работы учащихся: фронтальная, работа в парах и индивидуальная.
Необходимое техническое оборудование: компьютерный класс на 10 рабочих мест, мультимедийный комплекс.
Литература: Базовый учебник: Алгебра и начала анализа 10. Ю.М Колягин, М.В. Ткачева и др. под редакцией А.Б.Жижченко.
Структура и ход урока
| № | Этап урока | Название используемых ЭОР (с указанием порядкового номера из Таблицы 2) |
Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) |
Деятельность ученика | Время (в мин.) |
| 1 | Организация начала урока | Объявляется тема урока, цели урока и задачи | Слушают и записывают тему урока в тетрадь | ||
| 2 | Подготовка к активной УПД каждого ученика на основном этапе урока. | №1 |
Решают устно упражнения | ||
| 3 | Усвоение новых знаний | №1 | 1) Предлагает решить уравнение 2) Демонстрирует вывод формул корней уравнения . 3) Демонстрирует вывод формул частных случаев 4) Демонстрирует образец решения уравнений |
1) Решают уравнение с помощью
тригонометрического круга 2) Заполняют таблицу 3) Решают задания и проводится самопроверка |
|
| 5 | Закрепление знаний. | №2 | 1) Раздает задание для работы с
тренажером 2) Консультирует |
Работают на компьютере (работа парами) | |
| 6 | Первичная проверка | 1) Проводит первичную проверку знаний и умений. | Выполняют проверочную работу | ||
| 7 | Подведение итогов урока (рефлексия достижения цели). | №1 | Предлагает решить уравнение сводящееся к простейшему | Решают и обсуждают решение упражнение | |
| 8 | Информация о домашнем задании. Инструктаж по его выполнению | Знакомит с содержанием домашнего
задания (выучить формулы), №18, 19, 20 (четные) |
Приложение 1
Простейшие тригонометрические уравнения
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
urok.1sept.ru