Функция и его график
Обозначим символами A и B два числовых множества.
Такими множествами могут быть к примеру сегмент [a; b], интервал (a; b).
Определение.
Если для каждого числа x из множества A по определенному закону или правилу сопоставляется только одно число y из множества B, тогда говорим что на множестве A задана функция y=f(x).
Пример:
a). Функция y=x+1 сопоставляет каждому числу x число y=x+1, здесь f(x) равно x+1.
b). Функция y=sinx сопоставляет каждому числу x число y=sinx, здесь f(x) равно sinx.
График функций
Совокупность всех точек (x=x, y=f(x)) на координатной плоскости XOY называется графиком функций. Обычно совокупность таких точек, то есть график является определенным геометрическим объектом.
К примеру графиком функций y=x+1 будет прямая на плоскости:
Упражнение.
Построите график для функций y=x2.
Области определения и значений функций
Совокупность всех точек x для которых определена функция y=f(x) называется областью определения функций y=f(x), а совокупность всех чисел вида y=f(x) называется областью значении функций y=f(x). Обозначают эти множества соответственно через E и D.
К примеру функция y=x+1 определена на всей вещественной оси, а областью значений также является вся вещественная ось. Поэтому E = (–∞ ; +∞ ), D = (–∞ ; +∞).
Упражнение.
Для функций определите области определения и области значении.
Общие свойства функций и построение графиков
График функции и его построение
Определение 1
Графиком функции $f(x)$ будет называться множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.
Схема для построения графиков функций:
- Найти $D(f)$ и $E(f)$.
- Исследовать на свойство четности и нечетности, а также на свойство периодичности.
- Найти пересечение с координатными осями и промежутки, на которых $f\left(x\right) >0$ и $f\left(x\right)
- Найти промежутки где функция возрастает и убывает, найти экстремумы.
- Найти интервалы выпуклости $и$ вогнутости функции.
- Вычислить пределы на границах $D(f)$.
- Найти дополнительные точках при необходимости.
- Изобразить график.
Четность и нечетность функции
Определение 2
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]График этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Рисунок 1.
Определение 3
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
\[f\left(-x\right)=-f(x)\]График этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

Рисунок 2.
Для исследования функции в её аналитической записи заменяют переменную $x$ на переменную $-x$, производят, при необходимости элементарные преобразования, и проверяют условия определений 2 и 3.
Возрастание и убывание функции
Определение 4
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть возрастающей, если подставив любые две точки получим, что$»$ будет верно $f(x’)
Определение 5
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть убывающей, если подставив любые две точки получим, что будет верно $f\left(x’\right) >f(x»)$.
Чаще всего функции исследуют на возрастание и убывание с помощью средств математического анализа, а именно производной.
Приведем схему для такого исследования.
- Найти $D(f)$;
- Найти $f'(x)$;
- точки, когда $f’\left(x\right)=0$;
- точки, когда $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные выше точки;
- знак $f'(x)$ на всех получившихся промежутках;
- Сделать вывод: там, где $f’\left(x\right)0$ функция будет возрастать.
Выпуклость и вогнутость функции
Определение 6
Функция $y=f(x)$, которая имеет своей областью определения множество $X$ будет называться выпуклой, если подставив любые две точки получим, что неравенство
\[f\left(\frac{x’+x»}{2}\right)\le \frac{f(x’)+f(x»)}{2}\]верно.
Функция $y=f(x)$, которая имеет своей областью определения множество $X$ будет называться вогнутой, если подставив любые две точки получим, что неравенство
\[f\left(\frac{x’+x»}{2}\right)\ge \frac{f(x’)+f(x»)}{2}\]верно.
Схема исследования:
Найти
- $D(f)$;
- $f»(x)$;
- точки, когда $f»\left(x\right)=0$;
- точки, когда $f»(x)$ не будет существовать;
- знак $f»(x)$ на каждом из найденных промежутков;
- если $f»\left(x\right)0$ то вогнутой.
Пример исследования и построения функции
Пример 1
Исследовать данную функцию и построить график:
\[f\left(x\right)=sinx-cosx\]$D\left(f\right)=R$
\[\ E\left(f\right)=\left(-\infty ,0\right)\cup (0,+\infty ).\]- \[f\left(-x\right)=-cosx-sinx\]
Следовательно, данная функция — общего вида.
- \[sinx-cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
Пересечение с осью $Ox$: $\left(\frac{\pi }{4}+\pi n,0\right)$
Пересечение с осью $Oy$: $\left(0,-1\right)$
На интервале $x\in \left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция будет принимать положительные значения, на интервале $x\in \left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция будет принимать отрицательные значения.
- \[y’=sinx+cosx\] \[sinx+cosx=0\] \[x=-\frac{\pi }{4}+\pi n,n\in Z\]
Функция возрастает на $\left(-\frac{\pi }{4}+2\pi n,\frac{3\pi }{4}+2\pi n\right)$ и убывает на$\left(\frac{3\pi }{4}+2\pi n,\frac{7\pi }{4}+2\pi n\right)$.
- \[y^{»}=cosx-sinx\] \[-sinx+cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
На интервале $\left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция вогнута, на интервале $\left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция выпукла.

Рисунок 3.
Функции и их графики
В этом определении множество $D$ называется областью определения функции, а множество $E$ — областью значения функции.
$x$ — независимая переменная.
$y$ — зависимая переменная (значение функции).
Способы задания функции
Существуют три основных способа задания функции: аналитический, табличный и графический. Рассмотрим подробнее каждый из этих способов.
Аналитический способ
Здесь для начала введем понятие аналитического выражения.
В основу аналитического способа здания функции лежит задание функции с помощью аналитического выражения.
Примеры: $y=x^2+5x+3$, $y=\frac{x+1}{x+2}$, $y=cos2x$.
Преимущества:
- Формулы определяют значение функции для любого значения независимой переменной;
- Возможность при изучении функции пользоваться аппаратом математического анализа.
Недостатки:
- Недостаточная наглядность.
- Необходимость производить подчас очень громоздкие вычисления.
Табличный способ
При табличном задании функции просто выписывается ряд значений независимой переменной и соответствующие им значения функции.
Пример:

Преимущество:
Для каждого значения независимой переменной, входящей в таблицу, сразу можно найти соответствующее значение функции.
Недостатки:
- При нем, чаще всего, невозможно задать функцию полностью;
- Недостаточная наглядность.
Графический способ
Введем определение графика функции:
Задание графика функции называется графическим способом задания функции $f(x)$.
Пример: рис. 1.

Рис. 1. График функции $y=f(x)$.
Схема для построения графика функции
- Область определения $D(f)$ и область значения $E(f)$.
- Четность ($f\left(x\right)=f\left(-x\right))$, нечетность ($f\left(x\right)=-f\left(x\right))$, периодичность ($f\left(x\right)=f\left(x+T\right))$.
- Точки пересечения с осями координат и промежутки, где $f\left(x\right)>0$ и $f\left(x\right)
- Исследовать на возрастание ${(f}’\left(x\right)>0)$, убывание ${(f}’\left(x\right)
- Исследовать на точки перегиба и интервалы выпуклости $(f^{»}\left(x\right) > 0)$, вогнутости ($f^{»}\left(x\right)
- Вычислить пределы на границах области определения.
- Значения в дополнительных точках.
- График.
Правила построения графиков
- $y=f(x-a)$ получается из графика $f(x)$ сдвигом вдоль оси $Ox$ на $|a|$ вправо, если $a > 0$ и влево, если $a
- $y=f\left(x\right)+b$ получается из графика $f(x)$ сдвигом вдоль оси $Oy$ на $|b|$ вверх, если $b>0$ и вниз, если $\ b
- $y=f(kx)$ получается из графика $f(x)$ сжатием к оси $Oy$, если $k>1$ и растяжением, если $0
- $y=kf(x)$ получается из графика $f(x)$ растяжением от оси $Ox$ в $k$ раз, если $k > 1$ и сжатием к оси $Ox$ в $\frac{1}{k}$ раз, если $0
- $y=f(-x)$ получается из графика $f(x)$ симметричным отображением относительно оси $Oy$.
- $y=-f(x)$ получается из графика $f(x)$ симметричным отображением относительно оси $Ox$.
- $y=|f\left(x\right)|$ получается из графика $f(x)$ следующим образом: часть графика $f(x)$,лежащая над осью $Ox$ остается неизменна, а лежащая под $Ox$ отображается симметрично относительно оси $Oy$.
- $y=f\left(|x|\right)$ получается из графика $f(x)$ следующим образом: часть графика $f(x)$,лежащая справа от оси $Oy$ остается неизменна, а затем эта часть отображается симметрично относительно оси $Oy$, заменяя часть, лежащую слева от $Oy$.
Пример исследования и построения функции
7 Порядок оформления и построения графиков функций
Отчет по лабораторной работе оформляется по требованиям, изложенным в настоящих методических указаниях (см. ниже). В некоторых случаях при обработке результатов измерений удобно пользоваться графическим методом. Этот метод позволяет проследить зависимость одной физической величины от другой (например, зависимость периода колебаний физического маятника от расстояния между его центром масс и осью вращения). Иногда построение графиков необходимо для определения усредненных значений тех или иных параметров. ( Можно, к примеру, найти ускорение тела по графику зависимости пути от квадрата времени).
На основе проведенных расчетов в конспекте лабораторной работы должны быть построены экспериментальные графики зависимостей физических величин, предусмотренные методическими указаниями. Назначение графиков — наглядное представление результатов, поэтому основное требование к ним – аккуратное и четкое исполнение. Графики должны легко читаться, для этого необходимо соблюдать некоторые общие правила, изложенные ниже.
Если в работе предусмотрено графическое представление результатов, то графики в отчёте выполняются только либо на миллиметровой бумаге и вклеиваются на листы А4, либо компьютерным способом. (бумага в клетку для такой цели не совсем подходит). В протоколе (конспекте) лабораторной работы также строятся графики, но с меньшей точностью, при этом это возможно на бумаге в клетку.
Считается, что Вас в школе научили правилам построения графиков по экспериментальным точкам, т.е. по таким точкам, для которых указаны погрешности, с которыми они определены.
При построении графиков обычно используется прямоугольная система координат с равномерным масштабом. В первую очередь нужно решить, какая из двух переменных величин будет отложена по горизонтали (по оси абсцисс или по оси X), а какая — по вертикали (по оси ординат или по оси Y). Полученные экспериментальные данные наносятся в виде графика Y = Y(Х), где точки имеют координаты Хn , Yn., Y = Y(Х) — функциональная зависимость, Х — независимая переменная (аргумент функции). Значения аргумента (причину) следует откладывать по оси X , а значение функции (следствие) — по оси Y. Масштаб может быть произвольным, но при его выборе рекомендуем руководствоваться следующими указаниями.
Г р а ф и к (требования):
на миллиметровке или компьютерным способом, размер не менее 1/2 тетрадного листа,
на графике: оси декартовой системы, на концах осей — стрелки, индексы величин, единицы измерения, множители,
Рисунок 1 Внешний вид координатной плоскости с осями со стрелками
на каждой оси — РАВНОМЕРНЫЙ МАСШТАБ (риски через равные промежутки, числа через равное количество рисок, в каждой клетке 1,2,5·10±N физических единиц),
под графиком — полное название графика Словами,
на графике — экспериментальные и теоретические точки ярко, каждую точку можно обвести в кружок или треугольник (если известны погрешности тех величин, для которых строится график, то их необходимо отложить в виде прямолинейных отрезков от каждой экспериментальной точки в обе стороны),
форма графика соответствует теоретической зависимости (не ломаная).
Толщину линий принято отсчитывать от толщины координатной оси – S (0,5 — 1,5 мм), при этом толщина координатной сетки и штрихов выбирается S/2 ÷ S/3, а самой изображаемой функциональной зависимости – 2S (числа приблизительные, для обеспечения требуемой точности отсчета допускается выполнять линии большей или меньшей толщины). Когда на одной диаграмме изображаются две или более функциональные зависимости, целесообразно изображать их линиями разных типов сплошными, штриховыми, разным цветом и т.д..
Если график строится без помощи компьютера, то нужно выбрать величину расстояния между соседними метками в миллиметрах миллиметровки или в клетках, если бумага в клетку (для протоколов лабораторных работ). Проводимая кривая должна занимать весь лист используемой миллиметровой бумаги. При этом следует иметь в виду, что пересечение координатных осей совсем необязательно должно совпадать с нулевыми значениями аргумента и функции. Важную роль играет также удобство построения и использования графиком. При выборе нужно следить за тем, чтобы график получился достаточно квадратным и чтобы расстояние между соседними метками выражалось круглым числом сантиметров (или клеток) или удвоенным или упятеренным круглым числом.
Т.е. надо поэтому выбирать такой масштаб, чтобы координаты любой точки графика могли быть быстро и легко определены. Это условие всегда выполняется, если в единице масштаба (например, в 1 см) заключается 10n , 2·10n или 5·10n единиц измерения физических величин, откладываемых по осям координат (n — любое целое число).
Рассмотрим требования, предъявляемые к оформлению графиков на примере зависимости тока от напряжения в некоторой гипотетической схеме. Пусть результаты измерений представлены в виде таблицы.
Таблица 2 Результаты измерений в некоторой гипотетической схеме
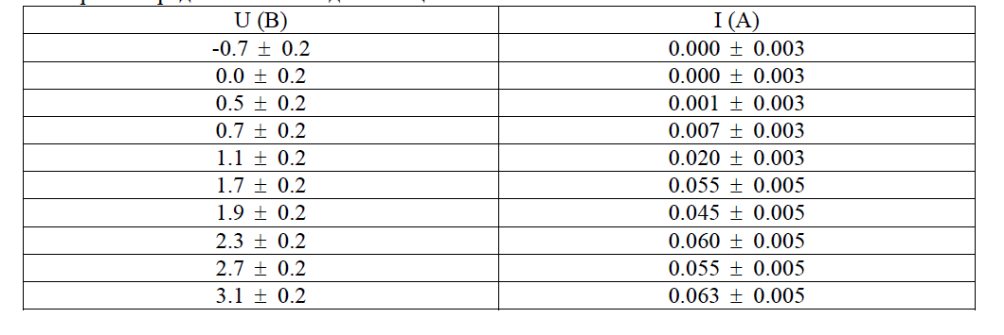
В первую очередь нужно решить, какая из двух переменных величин будет отложена по горизонтали (по оси абсцисс или по оси X), а какая — по вертикали (по оси ординат или по оси Y). Нужно стараться причину откладывать по оси абсцисс, а следствие — по оси ординат. В нашем примере логично предположить, что приложенное к схеме напряжение является причиной тока. Напряжение отложим по оси X, а силу тока — по оси Y.
Во вторую очередь нужно определить диапазон изменения каждой из двух переменных величин. В рассматриваемом примере напряжение U меняется от -0.7 Вольт до 3.1 Вольта, сила тока I изменяется в пределах от 0 Ампер до 0.063 Ампера.
Далее нужно выбрать величину шага меток, которые будут по осям графика. Метки могут быть двух типов: с подписями в виде чисел и без них. Мы будем обсуждать только метки с подписями. Метки без подписей можно поставить между метками с подписями в два или пять раз чаще. Метки нужно ставить через круглые значения или через удвоенные круглые значения или через упятеренные круглые значения. Никогда не ставьте метки кратные трем (тем более семи) единицам. Начинают построение диаграмм с выбора осей и нанесения масштаба. Обычно на осях делают 5 ÷ 10 делений, рядом с делениями наносят их числовые значения, обычно с противоположной стороны оси. Измеренные значения на шкалы не наносят! Ось – это рабочая линейка.
Масштаб выбирают удобным для считывания, он сохраняется на всей оси (или до точек разрыва оси, если они есть). Обычно выбирают числа не более чем из двух цифр, заканчивающиеся на 1, 2, 5. Чтобы не писать нулей, повторяющихся во всех цифрах и засоряющих график, масштабный множитель 10n выносят 1) в множитель к символу измеряемой величины – рисунок 2 в) или 2) в единицу ее измерения – рисунок 2
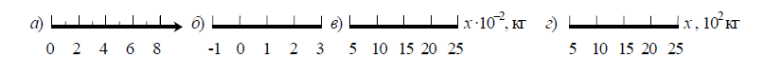
Рисунок 2 Примеры правильного нанесения масштаба на оси графика

Рисунок 3 Примеры распространенных ошибок при выборе масштабов
Вернёмся к нашему примеру: по каждой оси нужно поставить от трех до девяти меток. Диапазон изменения меток должен быть таким же или чуть шире, чем диапазон изменения соответствующей переменной величины.
Разберемся с метками по оси напряжений. Если взять метки с шагом 0.5 Вольта, то метки надо ставить в диапазоне от -1.0 Вольта до 3.5 Вольта. Всего десять меток. Это чуть больше, чем хотелось бы, но вполне допустимо. Если взять метки с шагом 1 Вольт, то диапазон изменения меток можно взять от -1 Вольта до 3 Вольт. Всего пять меток.
Формально нужно было бы поставить еще метку 4 Вольта, но можно ее и не ставить, так как метка 3 Вольта очень близка к наибольшему значению напряжения 3.1 Вольта. Если брать метки с шагом 2 Вольта, то диапазон меток от -2 Вольт до 4 Вольт. Всего четыре метки. Что тоже допустимо, но лучше остановиться на шаге в 1 Вольт.
Метки по оси ординат удобно выбрать с шагом 0.01 Ампера (от 0 Ампер до 0.07 Ампера) или с шагом 0.02 Ампера (от 0 Ампер до 0.06 Ампер или до 0.08 Ампер). Все три варианта одинаково приемлемы. Выберем второй вариант.
В
нашем примере выберем расстояние между
соседними метками 2 см по каждой оси.
После того, как масштаб выбран, следует
начертить координатные оси, отметив на
них деления масштаба и указать буквенные
обозначения и размерность откладываемых
величин. Если эти величины очень малы
(или очень велики) при нанесении масштаба
удобно использовать рационализированную
форму записи, указывая порядок величины
рядом с ее буквенным обозначением. При
этом допускается два вида записи. Пусть,
например, индукция магнитного поля
катушки с током меняется в пределах
(2÷8) 10
Возьмем бумагу в клетку, нарисуем оси координат, расставим метки по осям, поставим точки на плоскости, соответствующие экспериментальным значениям тока и напряжения. Каждую экспериментальную точку на графике нужно обозначить крестиком, размер которого по горизонтали и вертикали соответствует погрешностям измерения данной точки. Возьмем бумагу в клетку, нарисуем оси координат, расставим метки по осям, поставим точки на плоскости, соответствующие экспериментальным значениям тока и напряжения. Каждую экспериментальную точку на графике нужно обозначить крестиком, размер которого по горизонтали и вертикали соответствует погрешностям измерения данной точки.
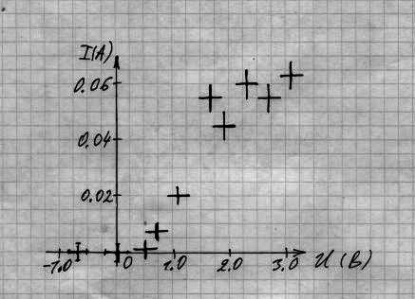
Рисунок 4 Пример построения экспериментальных точек
Теперь через экспериментальные точки нужно провести линию графика. Линия не должна быть ломаной, она не должна соединять центры всех точек. Линия должна быть плавной. Если Вы считаете, что точки должны лежать на прямой линии, то можно приложить линейку и, подобрав на глаз наклон и смещение, провести прямую. Если точки не обязаны лежать на прямой линии, то проведите плавную линию с тем количеством изгибов, которые, по Вашему мнению, не случайны, а соответствуют природе явления. Кривая на графике проводится таким образом, чтобы были видны отдельные точки, полученные в результате эксперимента. Вначале кривая проводится карандашом, чтобы можно было вносить необходимые поправки при анализе окончательных результатов.
Оси могут начинаться не с нуля, а с любого удобного значения, чтобы график занимал наибольшее пространство на координатной плоскости и не оставалось пустых мест, но при этом все точки графика должны быть внутри и не попадать на ограничительные оси / линии сетки:
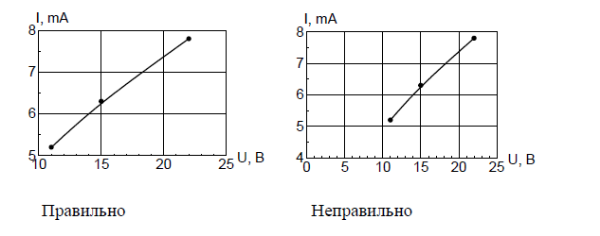
Рисунок 5 Примеры построения графиков
Если и горизонтальная и вертикальная оси начинаются с нуля, «0» наносят только один раз (см. рисунок 5).
При изображении графика, располагающегося более чем в одном квадранте координатной плоскости, штрихи, по возможности, направляются в сторону графика, а цифры масштаба располагаются с противоположной стороны оси
Переменную величину можно обозначать:
1. Наименованием или наименованием и символом — то есть непосредственно написать словами, что отложено по осям. Располагается такая надпись вдоль оси, по ее центру.
2. Символом (R, C, U )
3.
Символьным математическим выражением  , sin(ωt)
, sin(ωt)
Символы должны быть общепринятыми или разъяснены в подписи к графику и/или в тексте.
Обозначения в виде символов и математических выражений следует располагать горизонтально вне зависимости от ориентации самой оси.
Обозначения символом или математическим выражением обычно располагаются в конце соответствующей оси, при этом их единицы измерения, как и для варианта 1, располагаются сразу после обозначения изображаемой переменной через запятую или в скобках. Единицы измерения нужно указывать только в унифицированном сокращенном виде по Российскому (кириллицей) или международному (латиницей) стандарту. Обозначения изображаемых переменных величин и их единиц измерения.
Каждый график должен иметь краткую подпись (обязательно внизу), поясняющую его содержание и обозначение показанных величин. На поле самого графика допускается размещение краткой текстовой или иной существенной информации, облегчающей понимание результатов. (см рисунок 5)

Рисунок 5 Пример построения функции по экспериментальным точкам
Если график строится с помощью компьютера, то возможно Вы не знаете, как поставить крестики нужного размера, и как провести плавную кривую. Пусть тогда компьютер не рисует ни того, ни другого. Экспериментальные точки пусть только наметит маленькими точками, а крестики нужного размера и плавную кривую (или прямую) нарисуйте авторучкой.
Если все значения какой-то переменной смещены далеко от нуля, то изображение ортогональной оси можно провести не через нулевую точку данной переменной, а через удобную смещенную точку, но только совпадающую с одной из меток оси.
Ни в коем случае не отмечайте на осях графика значения экспериментальных точек, отмечайте только круглые значения меток. Некоторые студенты умудряются откладывать по осям не экспериментальные значения, а номера точек. А значения приписывают по осям вместо меток. В результате независимо от природы измеряемых величин получается прямая линия под 45 градусов. Надеюсь, Вы так делать не будете.
