Показательная функция — Википедия

Материал из Википедии — свободной энциклопедии

Показательная функция — математическая функция f(x)=ax{\displaystyle f(x)=a^{x}}, где a{\displaystyle a} называется основанием степени, а x{\displaystyle x} — показателем степени.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

Определение показательной функции[править | править код]

Пусть a{\displaystyle a} — неотрицательное вещественное число, x{\displaystyle x} — рациональное число: x=mn{\displaystyle x={\frac {m}{n}}}. Тогда ax{\displaystyle a^{x}} определяется по следующим правилам.

Для произвольного вещественного показателя x{\displaystyle x} значение ax{\displaystyle a^{x}} можно определить как предел последовательности arn{\displaystyle a^{r_{n}}}, где rn{\displaystyle r_{n}} — рациональные числа, сходящиеся к x{\displaystyle x}. Для экспоненты есть и другие определения через предел, например:

ex=limn→∞(1+xn)n.{\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.}

Свойства[править | править код]

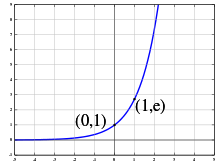График экспоненты

Используя функцию натурального логарифма lnx{\displaystyle \ln \,x}, можно выразить показательную функцию с произвольным положительным основанием через экспоненту:

ax=ex⋅ln⁡a{\displaystyle a^{x}=e^{x\cdot \ln a}}

Эта связь позволяет ограничиться изучением свойств экспоненты.

Аналитические свойства:

ddxax=(ln⁡a)ax.{\displaystyle {d \over dx}a^{x}=(\ln a)a^{x}.}

В частности:

ddxex=ex{\displaystyle {d \over dx}e^{x}=e^{x}}

Доказательство

Разложение в ряд:

ex=∑n=0∞xnn!=1+x+x22!+x33!+x44!+⋯{\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }.

Асимптотика[править | править код]

Показательная функция растёт на бесконечности быстрее любой полиномиальной:

limx→∞xnax=0{\displaystyle \lim \limits _{x\to \infty }{\frac {x^{n}}{a^{x}}}=0}

Большая скорость роста может быть проиллюстрирована, например, задачей о складывании бумаги.

Для расширения экспоненты на комплексную плоскость определим её с помощью того же ряда, заменив вещественный аргумент на комплексный:

ez=∑n=0∞znn!=1+z+z22!+z33!+z44!+⋯{\displaystyle e^{z}=\sum _{n=0}^{\infty }{z^{n} \over n!}=1+z+{z^{2} \over 2!}+{z^{3} \over 3!}+{z^{4} \over 4!}+\cdots }

Эта функция имеет те же основные алгебраические и аналитические свойства, что и вещественная. Отделив в ряде для eix{\displaystyle e^{ix}} вещественную часть от мнимой, мы получаем знаменитую формулу Эйлера:

eix=cos⁡x+isin⁡x{\displaystyle e^{ix}=\cos x+i\sin x}

Отсюда вытекает, что комплексная экспонента периодична вдоль мнимой оси:

ez+2πi=ez{\displaystyle e^{z+2\pi i}=e^{z}}

Показательная функция с произвольным комплексным основанием и показателем степени легко вычисляется с помощью комплексной экспоненты и комплексного логарифма.

Пример: ii=ei ln⁡(i){\displaystyle i^{i}=e^{i~\ln(i)}}; поскольку ln⁡(i)=iπ2{\displaystyle \ln(i)=i{\frac {\pi }{2}}} (главное значение логарифма), окончательно получаем: ii=eiiπ2=e−π2{\displaystyle i^{i}=e^{i{\frac {i\pi }{2}}}=e^{-{\frac {\pi }{2}}}}.

График функции y=a(x-m)^2

Найдём связь между графиками функций  и .

Для этого изобразим в одной координатной плоскости графики функций , , .

Составим таблицы значений для функций:

Видно, что график функции  можно получить из графика  в квадрате параллельным переносом относительно оси х вправо на 6 единиц, m=6. А график функции  параллельным переносом влево на 6 единиц, m=-6.

Определение:

График функции  является

параболой, которую можно получить из графика функции  с помощью параллельного переноса вдоль оси х на m единиц вправо, если m>0, и на —m единиц влево, если m<0.

Пример.

Изобразить графики функций вида , пользуясь уже известными определениями.

Используя шаблон , изобразим графики функции .

Сначала рассмотрим шаблон. Не трудно составить таблицу значений этой функции:

Получаем параболу.

Взглянем на формулу, которой задана функция . Это функция вида , в данном случае m=-4. Получить график этой функции можно с помощью параллельного переноса параболы  относительно оси х на 4 единицы влево.

Получили график функции

. Вершина данной параболы имеет координаты (-4,0).

Заметим, что вершина параболы  будет иметь координаты (m,0).

Определение:

Функция вида  – это парабола, которую можно получить из графика функции  в квадрате с помощью двух параллельных переносов:

1.     вдоль оси y на n единиц вверх, если n>0, и на —n единиц вниз, если n<0;

2.     вдоль оси

x на m единиц вправо, если m>0, и на —m единиц влево, если m<0.

Параллельные переносы можно производить в любом порядке.

Вершина этой параболы будет иметь координаты (m,n).

Пример.

С помощью шаблона параболы  изобразить график функции .

На рисунке видно, что m=-4, сдвигаем точки шаблона на 4 единицы влево и n=-3, сдвигаем полученный график на 3 единицы вниз. Получили график функции

. Вершина имеет координаты (-4,-3).

Функция (математика) — Википедия

У этого термина существуют и другие значения, см. функция.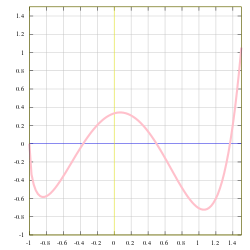 График функции
f(x)=(4×3−6×2+1)x+13−x{\displaystyle {\begin{aligned}&\scriptstyle \\&\textstyle f(x)={\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}.

Фу́нкция (отображе́ние, опера́тор, преобразова́ние) — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так, значение переменной x{\displaystyle x} однозначно определяет значение выражения x2{\displaystyle x^{2}}, также значение месяца однозначно определяет значение следующего за ним месяца. Другой пример функции: каждому человеку можно однозначно поставить в соответствие его биологическую мать.

Аналогично, задуманный заранее алгоритм по значению входного данного выдаёт значение выходного данного.

Часто под термином «функция» понимается числовая функция, то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представлять в виде графиков.

Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год). В свою очередь, Иоганн Бернулли в письме к тому же Лейбницу употребил этот термин в смысле, более близком к современному^[1][2].

Первоначально понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год), — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год)^[3].

К концу XIX века понятие функции переросло рамки числовых систем. Сначала понятие функции было распространено на векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение^[2].

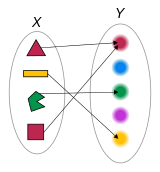Функция, сопоставляющая каждой из четырёх фигур её цвет.

Наиболее строгим является теоретико-множественное определение функции (на основе понятия бинарного отношения). Часто вместо определения функции даётся понятие функции, то есть описание математического объекта с помощью понятий обычного языка, таких как «закон», «правило» или «соответствие».

Понятие функции[править | править код]

Говорят, что на множестве X{\displaystyle X} имеется функция (отображение, операция, оператор) f{\displaystyle f} со значениями из множества Y{\displaystyle Y}, если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} по правилу f{\displaystyle f} поставлен в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}^[1].

Говорят также, что функция f{\displaystyle f} отображает множество X{\displaystyle X} в множество Y{\displaystyle Y}. Функцию обозначают также записью y=f(x){\displaystyle y=f(x)}.

Если используется термин оператор, то говорят, что оператор f{\displaystyle f} действует из множества X{\displaystyle X} в множество Y{\displaystyle Y} и добавляют запись y=fx{\displaystyle y=fx}.

Если хотят подчеркнуть, что правило соответствия считается известным, то говорят, что на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из Y{\displaystyle Y}. Если функция f{\displaystyle f} должна находиться в результате решения какого-нибудь уравнения, то говорят, что f{\displaystyle f} — неизвестная или неявно заданная функция. Но в любом случае, функция, по смыслу этого понятия, считается заданной, хотя и косвенно.

Заметим, что в формулировке понятия функции требование соответствия «по правилу» является повтором, поскольку оно содержится в понятии однозначного соответствия. Формулировка понятия функции без понятия правило и необходимости его обозначать:

Говорят, что на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из Y{\displaystyle Y}, если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} поставлен в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}^[4].

Например, функция, заданная на X{\displaystyle X} таблицей пар элементов x{\displaystyle x} и y{\displaystyle y}, содержит и правило соответствия для каждого элемента из X{\displaystyle X}, поскольку значения функции при переходе от элемента к элементу множества X{\displaystyle X} располагаются по вполне определенному правилу.

Для числовых функций, часто задаваемых формулами, понятие функции формулируется как соответствие между элементами множеств посредством правила. Правило не обозначается, чтобы избежать совпадения обозначений правила и функции:

Если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} по какому-либо правилу ставится в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}, то указанное соответствие называется функцией y=f(x){\displaystyle y=f(x)}, заданной на множестве X{\displaystyle X} со значениями из Y{\displaystyle Y}^[3][5].

Буква f{\displaystyle f} в этом обозначении — индивидуальный знак функции.

Итак, функция y=f(x){\displaystyle y=f(x)} (или кратко: функция f(x){\displaystyle f(x)} или f{\displaystyle f}) представляет собой тройку объектов: X,f,Y{\displaystyle X,f,Y}, где

Обозначенный буквой x{\displaystyle x} каждый элемент множества X{\displaystyle X} называется независимой переменной или аргументом функции. Множество X{\displaystyle X} при этом называется областью изменения переменной x{\displaystyle x}.

Элемент y{\displaystyle y}, соответствующий фиксированному элементу x{\displaystyle x} называется частным значением функции в точке x{\displaystyle x}.

Совокупность всех частных значений y{\displaystyle y}, обозначаемая символом {y}{\displaystyle \{y\}}, называется множеством значений функции.

Теоретико-множественное определение[править | править код]

Понятие множества упорядоченных пар (отношения) позволяет исключить из формулировки понятия функции не только понятие правило, но и понятие соответствие, к которому сводится понятие функции в обычных формулировках предыдущего подраздела.

Таким образом, для функции можно сформулировать определение, использующее только начальные математические понятия:

Функцией f{\displaystyle f} называется множество упорядоченных пар (x,y)∈X×Y{\displaystyle (x,y)\in X\times Y}, таких, что пары существуют для всех элементов множества X{\displaystyle X}, и, если первые элементы пар совпадают, то совпадают и вторые их элементы^[1].

При этом:

Функции f{\displaystyle f} и g{\displaystyle g} называются равными, если их графики совпадают^[6].

Поскольку равенство функций (в любой формулировке понятия функции) включает в себя не только совпадение правил соответствия между элементами множеств, но и совпадение областей задания, то функции f1(x)=x:R→R{\displaystyle f_{1}(x)=x:\mathbb {R} \to \mathbb {R} } и f2(x)=x:R+→R{\displaystyle f_{2}(x)=x:\mathbb {R} ^{+}\to \mathbb {R} }, где R{\displaystyle \mathbb {R} } — множество вещественных чисел, а R+{\displaystyle \mathbb {R} ^{+}} — множество положительных вещественных чисел, являются разными функциями.

Более общим, включающим в себя не только однозначные функции, является следующее определение функции:

Функцией f{\displaystyle f} называется любое множество упорядоченных пар (x,y)∈X×Y{\displaystyle (x,y)\in X\times Y}^{[1][нет в источнике]}.

При этом:

• Множество X{\displaystyle X} называется областью отправления функции. Множество всех элементов x∈X{\displaystyle x\in X}, для которых существует пара (x,y)∈f{\displaystyle (x,y)\in f}, называется областью задания функции;

• множество Y{\displaystyle Y} называется областью прибытия функции. Множество всех элементов y∈Y{\displaystyle y\in Y}, для которых существует пара (x,y)∈f{\displaystyle (x,y)\in f}, называется множеством значений функции.

Если на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из множества Y{\displaystyle Y}, то

• этот факт записывают в виде f:X→Y{\displaystyle f\colon X\to Y} или X⟶fY{\displaystyle X{\stackrel {f}{\longrightarrow }}Y};
• множество X{\displaystyle X} — область задания функции f{\displaystyle f} — обозначается символом D(f){\displaystyle D(f)} или domf;{\displaystyle \mathrm {dom} \,f;}
• множество Y{\displaystyle Y} — область значений^[3] функции f{\displaystyle f};
• множество значений {y}{\displaystyle \{y\}} функции f{\displaystyle f} обозначается символом E(f){\displaystyle E(f)} или codf{\displaystyle \mathrm {cod} \,f} (ranf{\displaystyle \mathrm {ran} \,f}).
• Если область значений Y{\displaystyle Y} и множество значений E(f){\displaystyle E(f)} совпадают, то говорят, что f{\displaystyle f} отображает множество X{\displaystyle X} на Y{\displaystyle Y}.
• Функция, заданная на множестве X{\displaystyle X}, наиболее часто обозначается как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:

  y=f(x){\displaystyle y=f(x)}, или кратко:f(x){\displaystyle f(x)} или f{\displaystyle f};

  x↦y{\textstyle x\mapsto y} или x↦f(x){\displaystyle x\mapsto f(x)};

• для сокращения числа обозначений знак функции, заданной на множестве X{\displaystyle X}, может обозначаться той же буквой, что и каждое значение функции:

  y=y(x){\displaystyle y=y(x)}, z=z(x){\displaystyle z=z(x)};

• функция обозначается и как функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}с обозначением соответствия между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:

  f:x↦y{\displaystyle f\colon x\mapsto y} или f:y=f(x){\displaystyle f\colon y=f(x)};

• реже используется обозначение функции как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y} без скобок: y=fx{\displaystyle y=fx}, y=f∘x{\displaystyle y=f\circ x} или y=xf{\displaystyle y=xf},
• а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками: y=(f,x){\displaystyle y=(f,x)} или y=(x,f){\displaystyle y=(x,f)};
• также существует и операторное обозначение y=xf{\displaystyle y=x^{f}}, которое можно встретить в общей алгебре.
• В лямбда-исчислении Чёрча используется обозначение λx.y{\displaystyle \lambda x.y} .

Функции нескольких аргументов[править | править код]

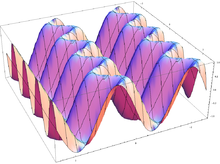График функции двух переменных f(x,y)=sin⁡(x−sin⁡(2y)){\displaystyle f(x,y)=\sin(x-\sin(2y))}

Понятие функции легко обобщается на случай функции многих аргументов.

Если множество X{\displaystyle X} представляет собой декартово произведение множеств X1,X2,…,Xn