Функции и их графики виды: Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)

Posted on by alexxlab

Содержание

Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)

Название функции Формула функции График функции Название графика Комментарий
Линейная, прямая пропорциональность y = kx Прямая Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Линейная, прямая пропорциональность со сдвигом y = kx + b Прямая Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1.
Квадратичная функция y = x2 Парабола Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат.
Квадратичная функция y = ax2 + bx + c Парабола Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа
Степенная функция y = x3 Кубическая парабола Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — корень квадратный
y = x1/2		 График функции
y = √x		 Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — обратная пропорциональность y = k/x Гипербола Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1.
Показательная функция y = ex Экспонента Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590…
Показательная функция y = ax График показательной функции а>1 Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1).
Показательная функция y = ax График показательной функции 0<a<1 Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1).
Логарифмическая функция y = ln(x) График логарифмической функции — натуральный логарифм График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой.
Логарифмическая функция y = logax График логарифмической функции — логарифм по основанию а>1 Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1).
Логарифмическая функция y = logax График логарифмической функции 0<a<1 Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1).
Синус y = sinx
Синусоида		 Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Косинус y = cosx Косинусоида Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Тангенс y = tgx Тангенсоида Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Котангенс y = сtgx Котангенсоида Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».

Урок 48. функции. свойства функций и их графики. исследование функций — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №48. Функции. Свойства функций и их графики. Исследование функций.

Перечень вопросов, рассматриваемых в теме:

  • функция, аргумент функции, значение функции
  • график функции, преобразование графика функции
  • свойства функции, исследование свойств функции

Глоссарий по теме урока

Определение

Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.

х – независимая переменная, аргумент,

у — зависимая переменная, значение функции

Определение

Множество значений аргумента функции называется областью определения функции и обозначается D(y).

Определение

Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).

Определение

Функция у = f(х) называется четной, если она обладает двумя свойствами:

  1. область определения этой функции симметрична относительно 0;
  2. для любого х из области определения выполняется равенство f(-х)=f(х).

Функция у = f(х) называется нечетной, если она обладает двумя свойствами:

  1. область определения этой функции симметрична относительно 0;

для любого х из области определения выполняется равенство f(-х)=-f(х).

Определение

Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.

Определение

Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1<х2, выполняется неравенство у1<у2.

Функция у=f(x) убывает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких что, х1<х

2, выполняется неравенство у1>у2.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н. Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.

Дополнительная литература:

Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”.

https://mathb-ege.sdamgia.ru/test?theme=177

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

1. Исследование функции и построение графика

Схема исследования функции на примере функции

1) Область определения функции

Знаменатель дроби не равен нулю:

Получили область определения

D(y)=

  1. Множество значений функции

Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).

Получили

  1. Четность / нечетность функции

D(y)= — симметрична относительно нуля

,

следовательно, функция четная и ее график симметричен относительно оси ОУ

  1. Нули функции

Для нахождения нулей функции необходимо решить уравнение

Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ

  1. Промежутки знакопостоянства

у>0 при

у<0 при

  1. Монотонность

Найдем производную

Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.

Определим знаки производной в полученных промежутках.

точки -1, 1 – выколоты, 0 — закрашена

Производная положительна, а значит, функция возрастает при .

Производная отрицательна, а значит, функция убывает при

  1. Экстремум

х=0 – стационарная точка.

В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.

Значение функции в точке максимума

  1. Дополнительные точки

у(0,5)= у(-0,5)=-5/3; у(2)=у(-2)=5/3; у(3)= у(-3)=5/4

  1. Отразим найденные свойства графически, построим график функции

2. Решение задачи на оптимизацию

Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.

В решении таких задач выделяют 3 основных этапа:

1 этап. «Перевод» задачи на язык функций:

  1. вводят независимую переменную х
  2. выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
  3. выражают у через х и другие известные величины
  4. устанавливают по условию задачи границы изменения переменной х

2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.

3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.

Рассмотрим план решения на примере задачи.

Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?

Решение:

1 этап.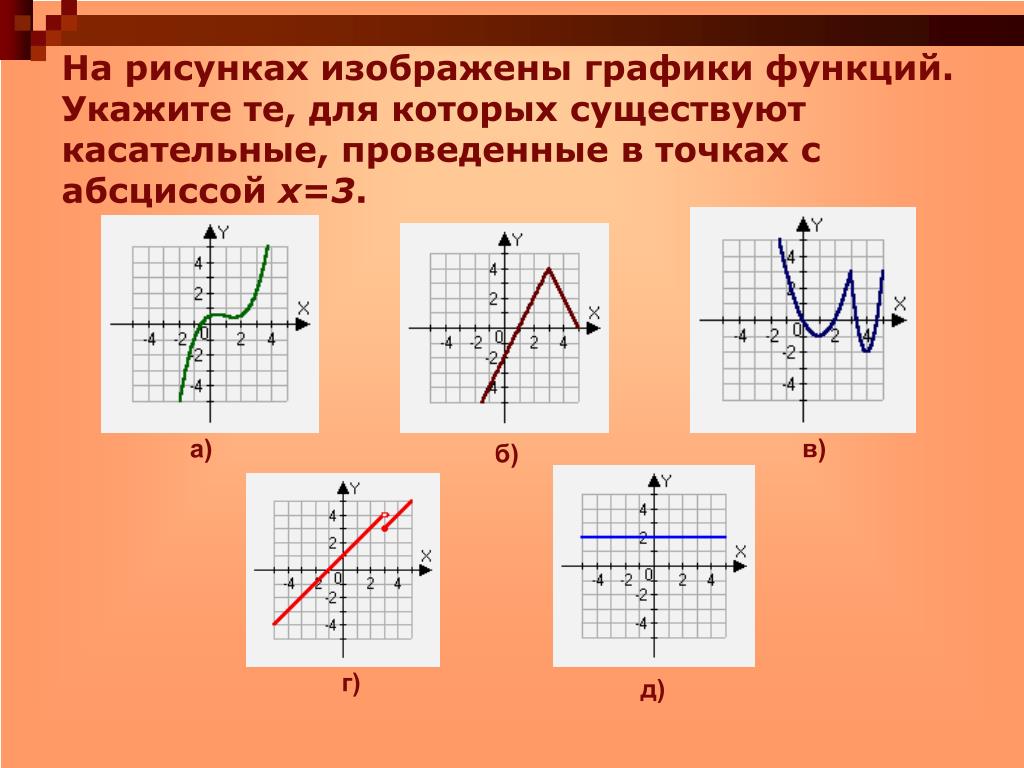 Ведем переменную, выразим нужные компоненты, составим искомую функцию.

Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x2 у.е.

Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x)2 (у.е.)

Всем рабочим нужно заплатить 4x2+(24 — x)2 = 5x2 -48x+576 (у.е.)

Причем 0≤ x ≤ 24, x ϵ N.

2 этап.

Рассмотрим функцию f(x)=5x2-48x+576.

Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x0 = 4,8 .

3 этап. Перевод на язык задачи

Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.

24-5=19 (рабочих) – на 2 объекте.

Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.

Примечание: исследовать функцию также можно было с помощью производной.

Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.

Примеры и разбор решения заданий тренировочного модуля

1. Исследуйте функции на четность.

Функции

у=0

у=sin(x+5π/2)

у=lg(x+10)

Решение:

  1. у=0

область определения – множество действительных чисел – симметрична относительно нуля

у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.

Данная функция одновременно четна и нечетна.

  1. у=sin(x+5π/2)

область определения – множество действительных чисел – симметрична относительно нуля

преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x

у= cos x – четная функция, значит, исходная функция также четная

  1. у=lg(x+10)

логарифмируемое выражение должно быть положительным

x+10>0; x>-10

D(y): x>-10

Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.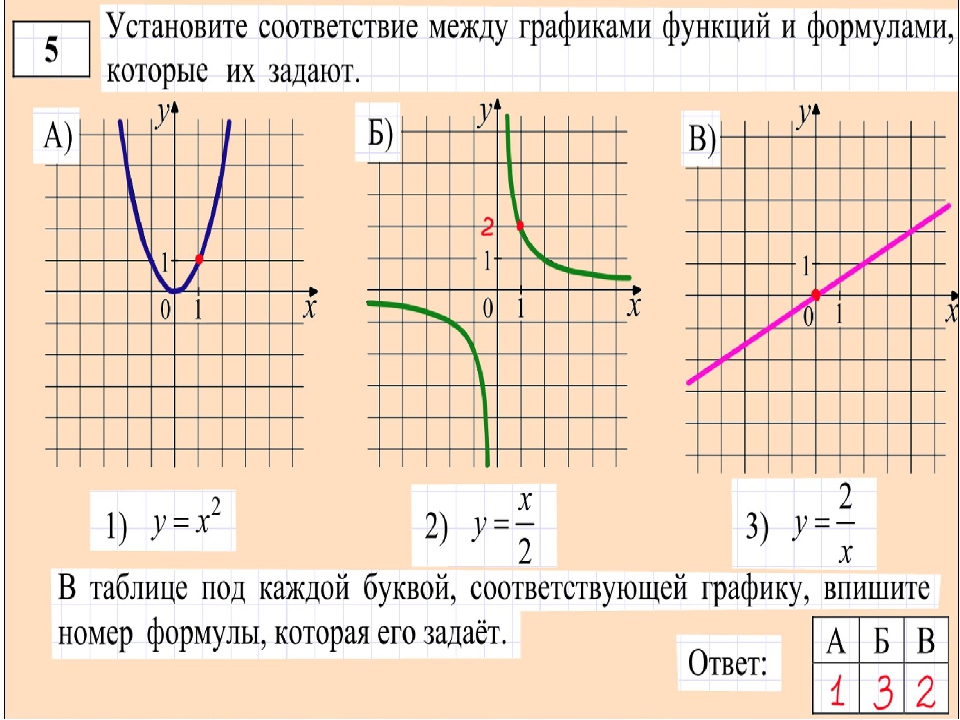

Найдем область определения D(f)

Проверим второе условие

Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.

Зайдем с другого конца, выразим -f(x):

домножим на сопряженное

Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.

Ответ:

Функции

Четность / нечетность

у=0

и четная, и нечетная

у=sin(x+5π/2)

четная

у=lg(x+10)

общего вида

нечетная

2.

Решение:

Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.

Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.

В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.

Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у<7

Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:

Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.

Выполним построения выделенных функций.

Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.

Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.

Ответ:

алгебра все о функциях

Вы искали алгебра все о функциях? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра все функции, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «алгебра все о функциях».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как алгебра все о функциях,алгебра все функции,алгебра график,алгебра графики,алгебра графики функций,алгебра функции,алгебра функции виды,алгебра функции все,алгебра функции их свойства и графики,алгебра функция,алгебра функция это,алгебра что такое функция,в алгебре функция,вид функции,виды графики функций,виды графиков все,виды графиков функции,виды графиков функций,виды графиков функций и их формулы,виды парабол и их графики,виды функции алгебра,виды функции графиков,виды функций,виды функций в математике,виды функций графики,виды функций и их графики,виды функция,все виды графиков,все виды графиков функции и их формулы,все виды функций и их графики,все графики и их функции,все графики функции,все графики функции и их формулы,все графики функций,все графики функций и их формулы,все графики функций и их формулы таблица,все о функциях алгебра,все о функциях и графиках,все функции,все функции алгебра,все функции в алгебре,все функции графики,все функции и их графики,все функции и их графики и свойства,все функции и их графики и свойства таблица,все функции и их графики и свойства таблица 9 класс,все функции и их свойства и графики,высшая математика графики функций,геометрические функции,график алгебра,график и их функции,график общего вида функции,график функции как находить,график функции как решать,график функции как читать,график функции общего вида,график функции определение,график функции примеры,график функции тема,график функции функция,график функции четверти,график функции что это,график функции это,график функции это определение,график функции это что,график функций как решать,графика простая,графика функция,графики алгебра,графики в математике,графики всех функций,графики и их названия,графики и их свойства,графики и их формулы,графики и их функции,графики и их функции и формулы,графики и их функция,графики и формулы,графики и формулы функции,графики и функции,графики и функции все,графики и функции формулы,графики как понять как,графики какие бывают,графики математика,графики математические,графики математических функций,графики основных и обратных функций,графики основных функций,графики по алгебре,графики по математике,графики пример,графики примеры,графики произвольных функций,графики простейших функций,графики простых функций,графики различных функций,графики формулы,графики функции все,графики функции и их графики таблица,графики функции и их свойства,графики функции и их формулы,графики функции и их формулы 9 класс шпаргалка,графики функции и их формулы все,графики функции и формулы,графики функции как строить,графики функции какие бывают,графики функции примеры,графики функций 9 класс и их формулы,графики функций алгебра,графики функций виды,графики функций виды функций,графики функций все,графики функций всех,графики функций высшая математика,графики функций и их,графики функций и их название,графики функций и их названия,графики функций и их свойства,графики функций и их уравнения,графики функций и их формулы,графики функций и их формулы 8 класс алгебра,графики функций и их формулы 9 класс,графики функций и их формулы все,графики функций и их формулы шпаргалка,графики функций и их формулы шпаргалка 9,графики функций и их формулы шпаргалка 9 класс,графики функций и формулы,графики функций как понять,графики функций как строить и решать,графики функций какие бывают,графики функций картинки,графики функций математика,графики функций примеры,графики функций различных,графики функций таблица,графики функций формулы,графиков примеры,графиков функций примеры,графические функции,графіки функції,графіки функцій,для функции y,как изобразить график функции,как называется функция,как найти график функции,как определить график функции по формуле,как определить по формуле график функции,как по формуле определить график функции,как понять графики функций,как решать функции,как решать функции по алгебре,как строить графики функций,как чертить графики функций,как читать график функции,как читать графики функций,как читать функцию,какая функция,какие бывают графики,какие бывают графики функции,какие бывают графики функций,какие бывают функции,какие бывают функции в алгебре,какие бывают функции в алгебре и их графики,какие графики бывают,какие графики функции бывают,какие графики функций бывают,какие есть функции,какие функции,какие функции бывают,какие функции бывают в алгебре,какие функции в,какие функции есть,какой график,какую функцию,картинки графики функций,математика высшая функции,математика графики,математика графики функций,математика функции,математика функции их свойства и графики,математика функция,математика функция это,математика что такое функция,математическая функция,математические графики,математические основные функции,математические функции,название графиков,название графиков функций,название функций,названия графиков,названия графиков функций,названия функций,названия функций графиков,названия функций и их графики,называется графиком функции,описание функций графиков,определение график функции,определение графика функции,определение по графику функции,определение функции,определение функции в алгебре,определение функции график,определение функции графика,определение функции по графику,определение что такое функция в алгебре,определения функция,основные графики и их функции,основные графики функций,основные функции и их графики,основные функции математические,парабола гипербола и другие графики,парабола гипербола и другие графики формулы,понятие графика функции,понятие функции графика функции,построить график функции что значит,приведите пример функции удовлетворяющей следующим условиям графиком является парабола,пример график,пример графика,пример функции,примеры график функции,примеры графики функции,примеры графики функций,примеры графиков,примеры графиков функций,примеры функции,примеры функций,примеры функций графиков,простая графика,простейшие графики и их функции,простейшие функции и их графики,простейшие функции их графики и свойства,простейшие функции их свойства и графики,таблица графики функций,таблица графиков функций и их формулы,таблица функций,тема график функции,типы графиков функций,укажите график функции,уравнения графиков функций,уравнения функций и их графики,формула графика прямой,формула графика функции,формула параболы на графике функции,формула прямой на графике функции,формула функции,формула функции y x,формула функции графика,формулы графики,формулы графики функций,формулы графиков функций,формулы графиков функций 9 класс,формулы и графики,формулы и графики функции,формулы и графики функций,формулы и их графики,формулы и их функции,формулы и функции графики,формулы функции,формулы функции и графики,формулы функций,формулы функций графиков,формулы функций графиков 9 класс,формулы функция,фукция,функ,функции,функции алгебра,функции алгебра все,функции в алгебре,функции в алгебре и их графики,функции в алгебре определение,функции в математике,функции в математике виды и их графики,функции виды,функции виды графиков,функции виды математика,функции все,функции все алгебра,функции геометрические,функции график формулы,функции графика,функции графики,функции графики и формулы,функции графики примеры,функции графиков и их формулы,функции графические,функции и графики,функции и графики формулы,функции и графики шпаргалка,функции и их график,функции и их графики,функции и их графики и свойства,функции и их графики и свойства таблица,функции и их свойства и графики,функции и их формулы,функции и их формулы и графики,функции и формулы,функции и формулы графики,функции их свойства и графики,функции какие есть,функции математика,функции математики,функции математические,функции название,функции определения,функции по алгебре,функции пример,функции примеры,функции таблица,функции формула,функции формулы,функции формулы и графики,функций виды в алгебре,функций их названия и графики,функция алгебра,функция алгебра это,функция в алгебре,функция в алгебре это,функция в математике,функция в математике это,функция виды,функция график функции,функция графика,функция и ее график,функция и их свойства и графики,функция и не функция картинки,функция математика,функция математика что такое,функция математика это,функция математическая,функция формулы,функция это алгебра,функция это в алгебре,функция это в математике,функция это математика,четверти график функции,четверти графика,четверти графика функции,что называется графиком функции,что называют графиком функции,что такое график функции,что такое график функции в алгебре,что такое график функций,что такое значение функции в алгебре,что такое функция в алгебре,что такое функция в алгебре определение,что такое функция в математике,что такое функция определение в алгебре,что является графиком функции. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и алгебра все о функциях. Просто введите задачу в окошко и нажмите «решить» здесь (например, алгебра график).

Где можно решить любую задачу по математике, а так же алгебра все о функциях Онлайн?

Решить задачу алгебра все о функциях вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Презентация — Функции и их графики

Слайды и текст этой презентации

Слайд 1

Функции и их графики

Слайд 2

Содержание
Теоретические сведения о функциях Преобразование графиков функций Элементарные функции и их графики Об авторе

Слайд 3

Теоретические сведения о функциях
Понятие функции Свойства функции

Слайд 4

Понятие функции
Функцией называют такую зависимость переменной У от переменной Х, при которой каждому значению переменной Х соответствует единственное значение переменной У. Х – независимая переменная (аргумент) У – зависимая переменная (значение функции) Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: у = f(х)

Слайд 5

Свойства функции
Нули функции – все значения переменной х при у = 0 Положительные значения функции — все значения переменной х при у > 0 Отрицательные значения функции — все значения переменной х при у

Слайд 6

Областью определения ( D(f) ) функции у = f(х) называется множество всех значений, которые может принимать переменная х.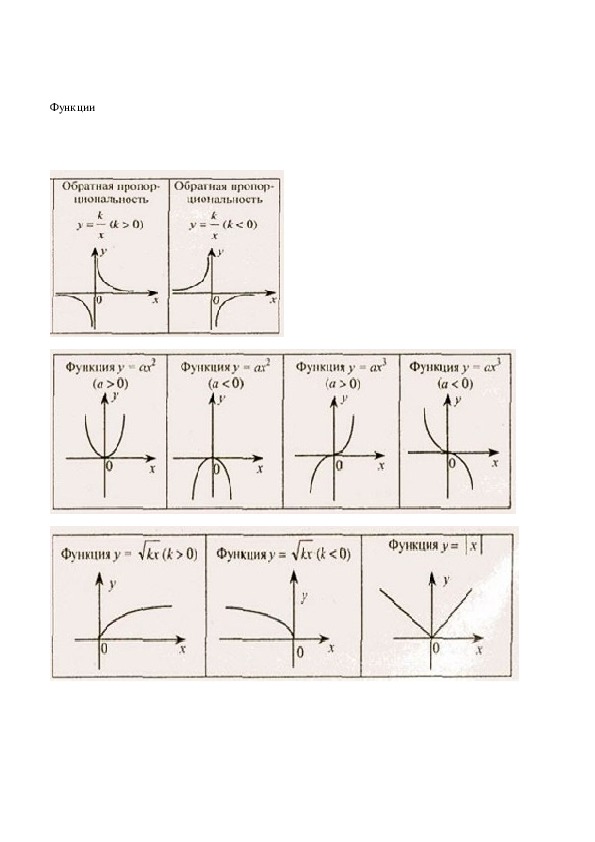 Областью значений ( E(f) ) функции у = f(х) называется множество всех значений, которые может принимать переменная у. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Понятие функции

Слайд 7

Возрастание и убывание функции
Функция называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, т. е. для любых х2 > х1, принадлежащих данному промежутку, выполняется неравенство f(х2) > f(х1) Функция называется убывающей на некотором промежутке, если меньшему значению аргумента соответствует меньшее значение функции, т. е. для любых х2 > х1, принадлежащих данному промежутку, выполняется неравенство f(х2)

Слайд 8

Четные и нечетные функции
Функция у = f(x) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство f(-x) = f(x) График любой четной функции симметричен относительно оси ординат ( оси Оу)
Функция у = g(x) называется нечетной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство g(-x) = -g(x) График любой нечетной функции симметричен относительно начала координат ( О(0,0) )

Слайд 9

Преобразование графиков функций
 Функция Преобразование графиков функции
у = f(х)+а Параллельный перенос вдоль оси OY на а единиц вверх, если а>0, и на |а| единиц вниз, если ау = f (х-а) Параллельный перенос вдоль оси OX на a единиц вправо, если a > 0, на |a| единиц влево, если a у = kf(х) Растяжение вдоль оси OY относительно оси OX в k раз, если k > 1, и сжатие в 1/k раз, если 0 у = f(kx) Сжатие вдоль оси OX относительно оси OY в k раз, если k > 1, и растяжение в 1/k раз, если 0 у = -f(х) Симметричное отражение относительно оси OX
у = |f(х)| Часть графика, расположенная ниже оси OX, симметрично отражается относительно этой оси, остальная его часть остается без изменения.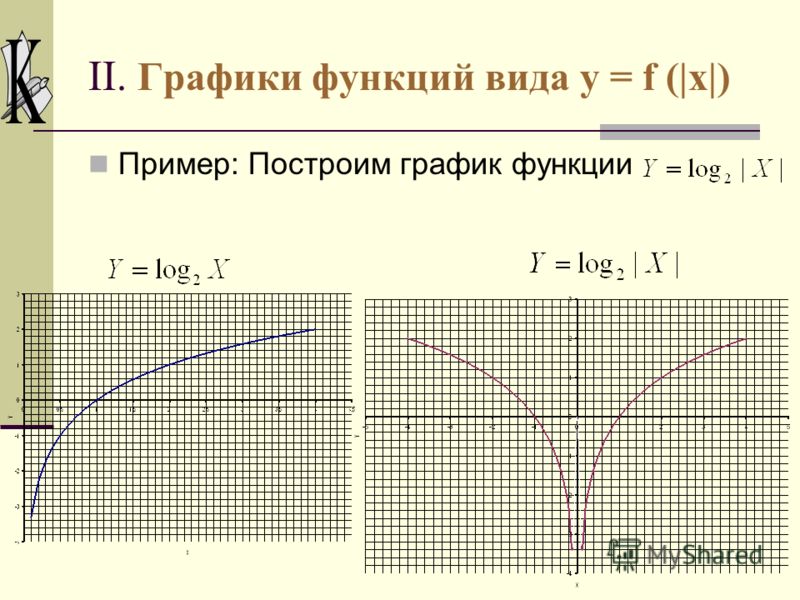
у = f(-х) Симметричное отражение относительно оси OY.
у = f(|х|) Часть графика, расположенная в области x ≥ 0, остается без изменения, а его часть для области x ≤ 0 заменяется симметричным отображением относительно оси OY части графика для x і≥0.
Посмотреть рисунки преобразований

Слайд 10

Преобразования графиков

Слайд 11

Элементарные функции и их графики
Линейная функция Прямая пропорциональность Обратная пропорциональность Квадратичная функция Кубическая функция

Слайд 12

Линейная функция
Функция у = f(х) называется линейной, если ее можно задать формулой вида у = ах+в Областью определения линейной функции является множество всех чисел Графиком линейной функции у = ах+в является прямая линия

Слайд 13

Прямая пропорциональность
Функция у = f(x) называется прямой пропорциональностью, если ее можно задать формулой вида у = kx k – коэффициент пропорциональности Областью определения прямой пропорциональности у = kx является множество всех чисел Графиком прямой пропорциональности у = kx является прямая

Слайд 14

Обратная пропорциональность
Обратной пропорциональностью называется функция, которую можно задать формулой вида у = , k ≠ 0 Область определения обратной пропорциональности состоит из всех чисел, кроме нуля Область значений обратной пропорциональности состоит из всех чисел, кроме нуля Графиком обратной пропорциональности у = является кривая, называемая гиперболой, состоящей из двух отдельных частей, симметричных относительно начала координат

Слайд 15

Квадратичная функция
Квадратичной функцией называется функция, которую можно задать формулой вида у = ах2+bх+с a,b,с – некоторые числа, причем а≠0 Областью определения квадратичной функции есть множество всех чисел Графиком квадратичной функции является кривая, которая называется параболой

Слайд 16

Преобразования графиков квадратичной функции
у = ах2 у = ах2+n у = а(х-m)2 у = а(х-m)2+n

Слайд 17

Функция у = ax2 и её график

Слайд 18

Функция у = ax2 + n и её график

Слайд 19

Функция у = a(x-m)2 и её график

Слайд 20

Функция у = a(x-m)2 + n и её график

Слайд 21

Кубическая функция
Функция вида у = х3 называется кубической Областью определения кубической функции является множество всех чисел Графиком кубической функции является кривая, которая называется гиперболой

Слайд 22

Об авторе

«Основные виды функций, их графики и свойства».

9-й класс

Предмет: Алгебра.

Класс: 9.

Тип урока: Урок повторения и обобщения.

Цель урока: Обеспечить повторение и обобщение ЗУН учащихся по теме урока, решению экзаменационных заданий данной тематики.

Задачи урока:

  1. Обеспечить в ходе урока повторение основных определений, свойств, графиков функций, их преобразований. Закрепить умения по применению данных знаний к решению некоторых типов экзаменационных заданий.
  2. Продолжить развивать умения: анализировать, сопоставлять, сравнивать, выделять главное, приводить примеры. Развивать математически грамотную речь.
  3. Воспитывать культуру учебного труда, экономного расходования времени.

Средства (оборудование):

  1. компьютер, проектор, экран;
  2. презентация: «Основные виды функций, их графики и свойства»;
  3. раздаточный материал: опорные конспекты для каждого учащегося «Схема исследования функции» и «Основные виды функций и их графики»; карты для практической работы (на 2 варианта).

Ход урока

I.

Организационный момент. (2 минуты)

Учащимся сообщается тема урока, его цель и задачи, ход урока (основные этапы). Учащиеся записывают в тетрадь дату и тему урока.

Начинается демонстрация презентации «Основные виды функций, их графики и свойства» – 1 слайд.

II.

Актуализация опорных знаний. (7 минут)

1 этап. Вспоминаем определение функции – 2 слайд.

По итогам работы с данным слайдом учащиеся повторяют определение числовой функции, вспоминают её главные особенности.

2 этап. «Разминка» – 3 слайд.

Фронтальная работа с классом, совместное решение кроссворда (некоторые названия графиков и свойств функции).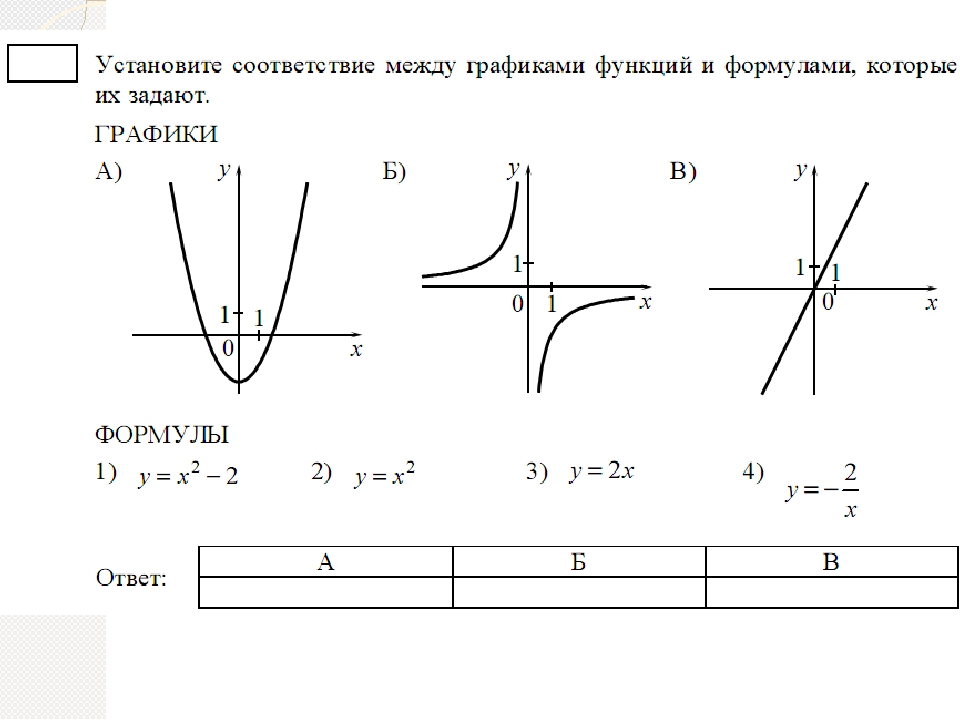 Предпочтительна работа с наиболее слабыми учащимися.

III. Повторение материала. (15 минут)

– А теперь вспомним свойства функции более детально. Достаём распечатки «Схема исследования функции» (Приложение 1) (они были розданы каждому учащемуся в процессе работы с данной темой в течение года) и с их помощью выполняем следующее задание в своих тетрадях.

4 слайд.

По окончании работы учащиеся меняются тетрадями с соседом по парте, идёт взаимопроверка выполненного задания.

– Как вам известно, заданий, связанных с основными свойствами функции, могут возникнуть и другие вопросы о ней, например, такие.

5 слайд.

– О «функциях вообще» мы с вами поговорили, пришло время вспомнить те из них, с которыми мы работали наиболее часто.

Раздаются распечатки «Основные виды функций и их графики» (Приложение 2). Параллельно идёт работа с ними и с 6 слайдом.

– Рассмотрим некоторые экзаменационные задания об этих функциях и их графиках.

7-11 слайды.

В процессе работы детально обсуждаются особенности данных функций и их графиков.

В последнем задании восстановить уравнение функции y=–2(x–2)2, соответствующее данному графику, можно несколькими способами, одним из которых является преобразование графика. Какое? (параллельный перенос на 2 единицы по оси абсцисс). Какие ещё преобразования можно совершать над графиками функций, мы с вами вспомним в процессе работы со следующим заданием.

12 слайд.

IV. Практическая работа. (12 минут)

Учащиеся выполняют задания, взятые из экзаменационных материалов прошлых лет по теме урока (2 варианта – Приложение 3, Приложение 4).

V. Подведение итогов урока. (3 минуты)

Фронтальная работа с классом:

  • Сформулируйте определение функции.
  • Какие виды функций можно назвать основными?
  • Каковы их характерные особенности?
  • Какова взаимосвязь между свойствами функции и её графиком?
  • Каковы основные преобразования графиков функций? и т.п.

Наиболее активным учащимся выставляются оценки за урок.

VI. Домашнее задание. (1 минута)
  • Повторить основные виды функций и их графики, схему исследования функции.
  • В экзаменационных вариантах прошлых лет выбрать и решить 5 заданий по теме урока.

Список литературы:

  1. Математика. 9-й класс. Подготовка к ГИА-2013: учебно-методическое пособие / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2012.
  2. ГИА 2013 г. Математика. 9-й класс. Государственная итоговая аттестация (в новой форме). Типовые тестовые задания / И.В. Ященко, С.А. Шестаков, А.С. Трепалин, А.В. Семенов, П.И. Захаров. – М.: Издательство «Экзамен», 2013.
  3. Государственная итоговая аттестация (в новой форме). Математика: сборник заданий / Л.Д. Лаппо, М.А. Попов. – М.: Издательство «экзамен», 2013.

Построение графиков функций — урок. Алгебра, 10 класс.

построить график функции y=x2&plus;4×2−4.

Решение 1. Введём обозначение: f(x)=x2&plus;4×2−4. Найдём область определения функции. Она задаётся условиями x≠2,x≠−2. Итак, D(f)=(−∞;−2)∪(−2;2)∪(2;&plus;∞).

2. Исследуем функцию на чётность:

f(−x)=−x2&plus;4−x2−4=x2&plus;4×2−4=f(x).

Функция является чётной, её график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.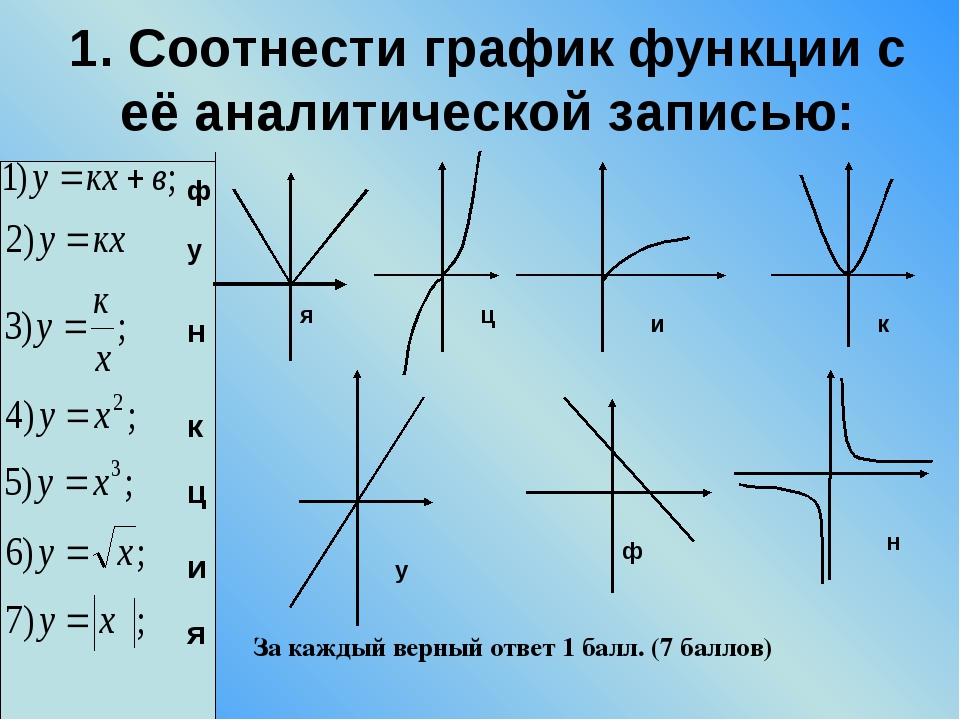

3. Определим асимптоты. Вертикальной асимптотой является прямая \(x=1\), т. к. при этом значении \(x\) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для определения горизонтальной асимптоты нужно вычислить limx→∞f(x):

limx→∞x2&plus;4×2−4=limx→∞x2x2&plus;4x2x2x2−4×2=limx→∞1&plus;4×21−4×2=1.

 Следовательно, \(y=1\) — горизонтальная асимптота.

4. Найдём стационарные и критические точки, точки экстремума и промежутки монотонности функции:

y′=x2&plus;4×2−4′=(x2&plus;4)′⋅(x2−4)−(x2&plus;4)⋅(x2−4)′x2−42=2x⋅(x2−4)−(x2&plus;4)⋅2xx2−42=2×3−8x−2×3−8xx2−42==−16xx2−42.

Производная существует на всей области определения функции, следовательно, критических точек у функции нет.

Стационарные точки определим из соотношения y′=0. Получаем: \(-16x=0\) — откуда получаем, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Таким образом, \(x=0\) — точка максимума функции, причём ymax=f(0)=02&plus;402−4=−1.

При \(x>0\) имеем: y′<0; но следует учесть наличие точки разрыва \(x=2\). Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке 0;2) функция убывает, на промежутке (2;&plus;∞) функция также убывает.

5. Найдём несколько точек, принадлежащих графику функции f(x)=x2&plus;4×2−4 при x≥0:

\(x\)

\(0\)

\(0.5\)

\(1\)

\(3\)

\(4\)

\(y\)

\(-1\)

−1715

−53

135

53

 

6. Сначала нарисуем часть графика при x≥0, потом — часть, симметричную ей относительно оси \(y\). Полученный график имеет точку максимума \((0;-2)\), горизонтальную асимптоту \(y=1\) и вертикальную асимптоту \(x=2\).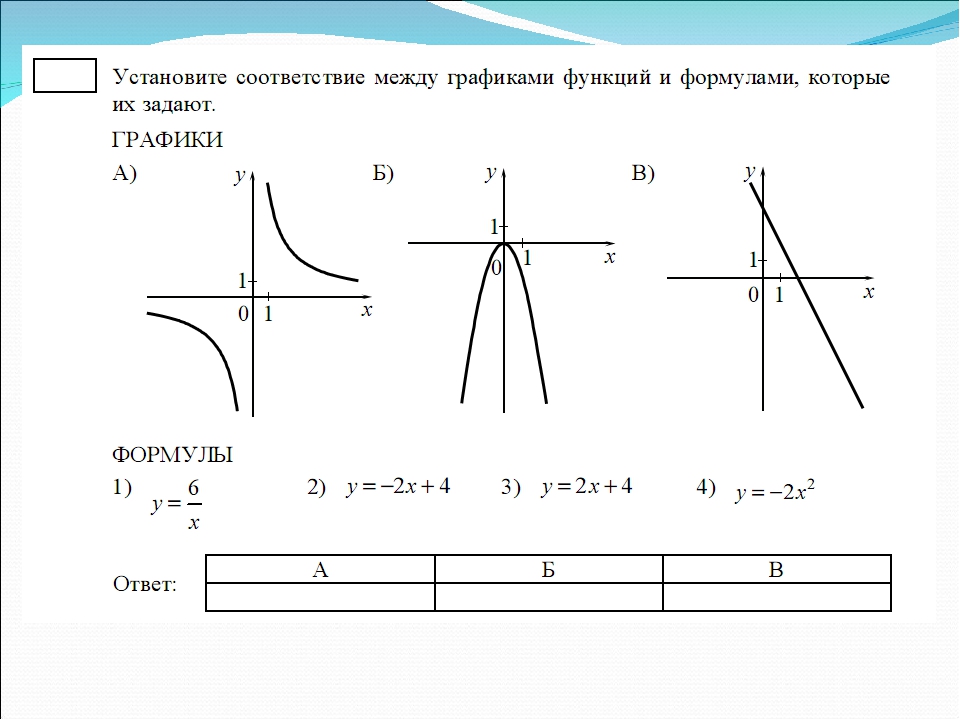 {3}}=125\)

Вот и все!

Теперь попробуй самостоятельно найти значение следующих выражений:

  1. 1

    \( \displaystyle f\left( x-9 \right)+f\left( 16-x \right)\), если \( \displaystyle f\left( x \right)=3x+2\)

  2. 2

    \( \displaystyle 3f\left( x-4 \right)-f\left( 3x \right)\), если \( \displaystyle f\left( x \right)=x-5\)

Справился? Сравним наши ответы: 

  1. 1

    \( \displaystyle 25\)

  2. 2

    \( \displaystyle -22\)

Мы привыкли, что функция имеет вид \( \displaystyle y=f\left( x \right)\), даже в наших примерах мы задаем функцию именно таким образом, однако аналитически можно задать функцию в неявном виде, например \( \displaystyle 5x+2y-3=0\). Попробуй построить эту функцию самостоятельно.

Справился?

Вот как строила ее я.

\( \displaystyle 5x+2y-3=0\)

\( \displaystyle y=\frac{3-5x}{2}\)

\( \displaystyle y=1,5-2,5x\)

Какое уравнение мы в итоге вывели? Правильно! Линейное, а это значит, что графиком будет прямая линия. Сделаем табличку, чтобы определить, какие точки принадлежат нашей прямой:

\( \displaystyle x\)

\( \displaystyle 0\)

\( \displaystyle 1\)

\( \displaystyle -1\)

\( \displaystyle 2\)

\( \displaystyle -2\)

\( \displaystyle y\)

\( \displaystyle 1.5\)

\( \displaystyle -1\)

\( \displaystyle 4\)

\( \displaystyle -3.5\)

\( \displaystyle 6.5\)

А теперь строим по данным точкам график:

функций и их графиков

Функции: \ (f \), \ (g \), \ (y \), \ (u \)
Аргумент (независимая переменная): \ (x \)
Набор натуральных чисел: \ (\ mathbb {N} \)
Набор действительных чисел: \ (\ mathbb {R} \)
Основание натурального логарифма: \ (e \)

Натуральные числа: \ (n \)
Целые числа: \ (k \)
Действительные числа: \ (a \), \ (b \), \ (c \), \ (d \)
Угол: \ (\ alpha \)
Период функции: \ (T \)

  1. Понятие функции — одно из важнейших в математике. Это определяется следующим образом. Пусть даны два множества \ (X \) и \ (Y \). Если для каждого элемента \ (x \) в множестве \ (X \) есть ровно один элемент (изображение) \ (y = f \ left (x \ right) \) в множестве \ (Y \), то говорят, что функция \ (f \) определена на множестве \ (X \). Элемент \ (x \) называется независимой переменной, и, соответственно, выход \ (y \) функции называется зависимой переменной. Если мы рассмотрим наборы чисел \ (X \ subset \ mathbb {R} \), \ (Y \ subset \ mathbb {R} \) (где \ (\ mathbb {R} \) — множество действительных чисел), тогда функция \ (y = f \ left (x \ right) \) может быть представлена ​​в виде графика в декартовой системе координат \ (Oxy \).
  2. Четная функция
    \ (f \ left ({- x} \ right) = f \ left (x \ right) \)
  3. Нечетная функция
    \ (f \ left ({- x} \ right) = -f \ left (x \ right) \)
  4. Периодическая функция
    \ (f \ left ({x + kT} \ right) = f \ left (x \ right), \)
    где \ (k \) — целое число, \ (T \) — период функция.
  5. Обратная функция
    Дана функция \ (y = f \ left (x \ right) \). Чтобы найти обратную ему функцию, необходимо решить уравнение \ (y = f \ left (x \ right) \) для \ (x \), а затем поменять местами переменные \ (x \) и \ (y \) .{- 1}} \ left (x \ right) \). Графики исходной и обратной функций симметричны относительно прямой \ (y = x \).
  6. Составная функция
    Предположим, что функция \ (y = f \ left (u \ right) \) зависит от промежуточной переменной \ (u \), которая, в свою очередь, является функцией независимой переменной \ (x \): \ (и = г \ влево (х \ вправо) \). В этом случае связь между \ (y \) и \ (x \) представляет собой «функцию функции» или составную функцию, которую можно записать как \ (y = f \ left ({g \ left (x \верно-верно)\).Двухслойные составные функции можно легко обобщить на произвольное количество «слоев».
  7. Линейная функция
    \ (y = ax + b, \) \ (x \ in \ mathbb {R} \).
    Здесь число \ (a \) называется наклоном прямой. {- x}}}}} {2} \ normalsize}, \) \ (х \ в \ mathbb {R}.{- x}}}} \ normalsize}, \) \ (x \ in \ mathbb {R}, \) \ (x \ ne 0. \)
  8. Функция обратного гиперболического синуса
    \ (y = {\ mathop {\ rm arcsinh} \ nolimits} \, x, \) \ (x \ in \ mathbb {R}. \)
  9. Функция обратного гиперболического косинуса
    \ (y = {\ mathop {\ rm arccosh} \ nolimits} \, x, \) \ (x \ in \ left [{1, \ infty} \ right). \)
  10. Обратная функция гиперболического тангенса
    \ (y = {\ mathop {\ rm arctanh} \ nolimits} \, x, \) \ (x \ in \ left ({-1,1} \ right). \)
  11. Обратная гиперболическая функция котангенса
    \ (y = {\ mathop {\ rm arccoth} \ nolimits} \, x, \) \ (x \ in \ left ({- \ infty, — 1} \ right) \ cup \ left ({1, \ infty} \ right).\)
  12. Обратная гиперболическая секущая функция
    \ (y = {\ mathop {\ rm arcsech} \ nolimits} \, x, \) \ (x \ in \ left ({0,1} \ right]. \)
  13. Обратная гиперболическая функция косеканса
    \ (y = {\ mathop {\ rm arccsch} \ nolimits} \, x, \) \ (x \ in \ mathbb {R}, \; x \ ne 0. \)

5.2 — Справочник — Графики восьми основных типов функций

5.2 — Справочник — Графики восьми основных типов функций

5.2 — Справочная информация — Графики восьми основных типов функций

Цель этого справочного раздела — показать вам графики различных типов функций для того, чтобы вы могли ознакомиться с типами.Вы обнаружите, что каждый тип имеет свой собственный отличительный граф. Показывая несколько графиков на одном графике, вы увидеть их общие черты. В этой галерее показаны примеры функций следующих типов: В каждом случае аргумент (вход) функции называется x , а значение (выход) функции называется y .

Линейные функции. Это функции формы:
y = м x + b ,
где m и b — константы.Типичное использование для линейные функции — это преобразование одной величины или набора единиц в другую. 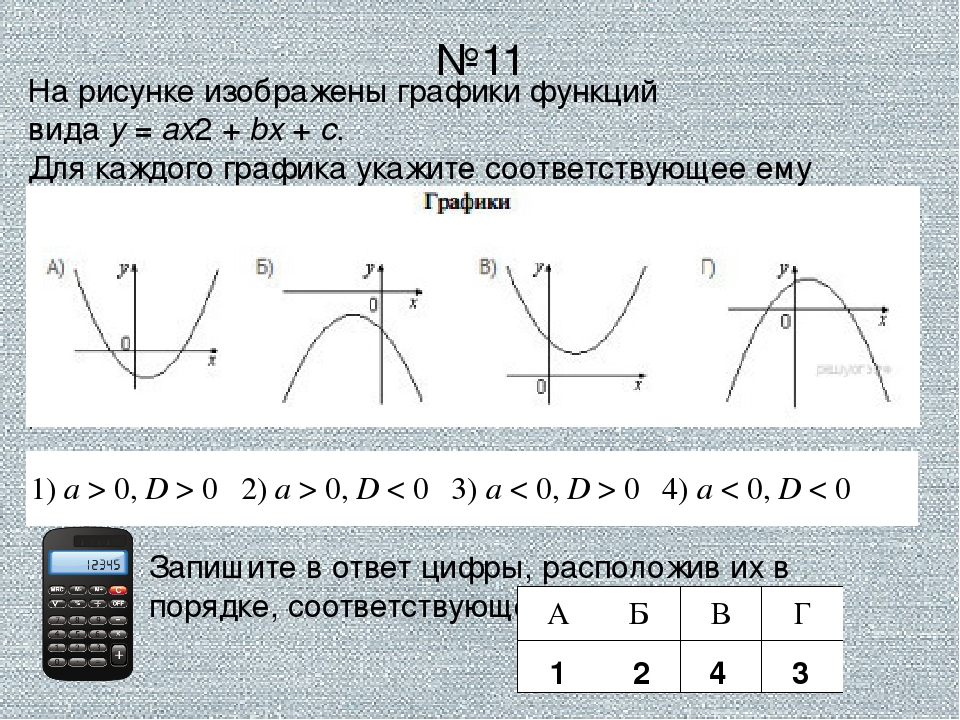Графики этих функций представляют собой прямых . м — это уклон, а b — точка пересечения y . Если м положительно, линия поднимается вправо, а если м. отрицательное, тогда линия падает вправо. Здесь подробно описаны линейные функции.

Квадратичные функции. Это функции формы:
y = a x 2 + b x + c ,
где a , b и c — константы. Их графики называются парабол . Это следующий по простоте тип функции после линейной функции. Падающие предметы движутся по параболическим траекториям. Если , а — положительное число, то парабола открывается вверх, и если a — отрицательное число, тогда парабола открывается вниз.Подробно квадратичные функции описаны здесь.

Силовые функции. Это функции формы:
y = a x b ,
где a и b — константы. Они получили свое название от факта что переменная x возведена в некоторую степень. Многие физические законы (например, гравитационная сила как функция расстояния между двумя объектами или изгиб балки в зависимости от нагрузки на нее) представлены в виде степенных функций.Предположим, что a = 1, и рассмотрим несколько случаев для b :
.
Степень b — положительное целое число. См. График справа. Когда x = 0, все эти функции равны нулю. Когда x большой и позитивные, все они большие и позитивные. Когда x большой и отрицательный тогда те, у кого четные полномочия, большие и положительные, в то время как с нечетной мощностью большие и отрицательные.

Степень b — отрицательное целое число. См. График справа. Когда x = 0, эти функции подвергаются делению на ноль и, следовательно, все бесконечны. Когда x большой и положительные они маленькие и положительные. Когда x большой и отрицательный тогда те, у кого четная степень, маленькие и положительные, а те, у кого нечетные степени малы и отрицательны.

Степень b — это дробная часть от 0 до 1. См. График справа. Когда x = 0, все эти функции равны нулю. Кривые вертикальные на origin и по мере увеличения x они увеличиваются, но изгибаются к оси x .

Здесь подробно обсуждается степенная функция.


Полиномиальные функции. Это функции формы:
y = a n · x n + a n -1 · x n -1 +… + a 2 · x 2 + a 1 · x + a 0 ,
где a n , a n −1 ,…, a 2 , a 1 , a 0 — константы.Допускаются только степени целого числа x . Наивысшая степень x , которая встречается, называется степенью полинома. На графике показаны примеры полиномов 4-й и 5-й степени. Степень дает максимальное количество « взлетов и падений, », которое многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.

Полиномы полезны для создания гладких кривых в компьютерной графике. приложений и для аппроксимации других типов функций.Здесь подробно описаны полиномы.


Рациональные функции. Эти функции представляют собой отношение двух многочленов. Одна область обучения, где они важны при анализе устойчивости механических и электрических систем. (который использует преобразования Лапласа).

Когда многочлен от знаменатель равен нулю, то рациональная функция становится бесконечной, как указано вертикальной пунктирной линией (называемой асимптотой ) на его графике. Для пример справа это происходит, когда x = −2 и когда x = 7.

Когда x становится очень большим, кривая может выровняться. Кривая справа выравнивается на y = 5.

График справа показывает еще один пример рациональной функции. У этого есть деление на ноль при x = 0. Он не выравнивается, но приближается к прямой y = x , когда x большой, как показано пунктирной линией (еще одна асимптота).


Экспоненциальные функции. Это функции формы:
y = a b x ,
где x — показатель степени (не в основании, как это было для степенных функций) и a и b — константы. (Обратите внимание, что только b возводится в степень x , а не a .) Если основание b больше 1, то результат будет экспоненциальный рост.Многие физические величины растут экспоненциально (например, популяции животных и наличные деньги). на процентном счете).

Если основание b меньше 1, то результат будет экспоненциальный спад. Многие величины убывают экспоненциально (например, солнечный свет достигает заданной глубины океана и скорость замедления объекта из-за трения).

Здесь подробно описаны экспоненциальные функции.


Логарифмические функции. Есть много эквивалентных способов определения логарифмических функций. Мы будем определите их как имеющие форму:
y = a ln ( x ) + b ,
где x — натуральный логарифм, а a и b — константы. Они определены только для положительного x . Для маленьких x они отрицательные, а для больших x положительные, но остаются маленькими.Логарифмические функции точно описывают реакцию человеческого уха на звуки различной громкости и реакция человеческого глаза на свет различной яркость. Здесь подробно описаны логарифмические функции.

Синусоидальные функции. Это функции формы:
y = a sin ( b x + c ),
где a , b и c — константы.Синусоидальные функции полезны для описания всего, что имеет форму волны относительно положение или время. Примеры: волны на воде, высота прилива во время дневной и переменный ток в электричестве. Параметр a (называется амплитудой) влияет на высоту волны, b (угловая скорость) влияет на ширину волны и c (фазовый угол) сдвигает волну влево или вправо.Здесь подробно описаны синусоидальные функции.

Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.

Характеристики функций и их графиков

Результаты обучения

  • Определите, представляет ли отношение функцию.
  • Найдите значения функции.
  • Определить, является ли функция взаимно однозначной.
  • Используйте тест вертикальной линии для определения функций.
  • Изобразите функции в библиотеке функций.

Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения.

Характеристики функций

Отношение — это набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется областью отношения, а набор вторых компонентов каждой упорядоченной пары называется диапазоном отношения. Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.

[латекс] \ влево \ {\ влево (1,2 \ вправо), \ влево (2,4 \ вправо), \ влево (3,6 \ вправо), \ влево (4,8 \ вправо), \ влево (5,10 \ вправо) \ вправо \} [/ латекс]

Домен [латекс] \ left \ {1,2,3,4,5 \ right \} [/ latex].Диапазон: [латекс] \ left \ {2,4,6,8,10 \ right \} [/ latex].

Обратите внимание, что значения в домене также известны как входные значений или значения независимой переменной и часто обозначаются строчной буквой [latex] x [/ latex]. Значения в диапазоне также известны как выходных значений или значения зависимой переменной и часто обозначаются строчной буквой [latex] y [/ latex].

Функция [latex] f [/ latex] — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене . Другими словами, значения [latex] x [/ latex] не используются более одного раза. В нашем примере, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене [latex] \ left \ {1,2,3,4,5 \ right \} [/ latex] соединяется ровно с одним элементом в диапазоне, [latex] \ left \ {2,4,6,8,10 \ right \} [/ latex].

Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами.Будет отображаться как

[латекс] \ left \ {\ left (\ text {odd}, 1 \ right), \ left (\ text {even}, 2 \ right), \ left (\ text {odd}, 3 \ right), \ left (\ text {even}, 4 \ right), \ left (\ text {odd}, 5 \ right) \ right \} [/ latex]

Обратите внимание, что каждый элемент в домене [latex] \ left \ {\ text {even,} \ text {odd} \ right \} [/ latex] равен , а не в паре с ровно одним элементом в диапазоне, [latex ] \ left \ {1,2,3,4,5 \ right \} [/ латекс]. Например, термин «нечетный» соответствует трем значениям из домена [латекс] \ left \ {1,3,5 \ right \} [/ latex], а термин «четный» соответствует двум значениям из диапазона, [латекс] \ left \ {2,4 \ right \} [/ латекс].Это нарушает определение функции, поэтому это отношение не является функцией.

На этом изображении сравниваются отношения, которые являются функциями, а не функциями.

(a) Это отношение является функцией, потому что каждый вход связан с одним выходом. Обратите внимание, что input [latex] q [/ latex] и [latex] r [/ latex] оба дают output [latex] n [/ latex]. (б) Эта взаимосвязь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Эта связь не является функцией, потому что input [latex] q [/ latex] связан с двумя разными выходами.

A Общее примечание: функции S

Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».

Входные значения составляют область , а выходные значения составляют диапазон .

Практическое руководство. Учитывая связь между двумя величинами, определите, является ли связь функцией.
  1. Определите входные значения.
  2. Определите выходные значения.
  3. Если каждое входное значение приводит только к одному выходному значению, связь является функцией. Если какое-либо входное значение приводит к двум или более выходам, связь не является функцией.

Пример: определение того, являются ли прайс-листы меню функциями

Меню кофейни состоит из позиций и их цен.

  1. Цена зависит от товара?
  2. Товар зависит от цены?
Показать решение
  1. Давайте начнем с рассмотрения ввода как пунктов меню.Выходные значения — это цены. Каждый пункт в меню имеет только одну цену, поэтому цена является функцией этого элемента.
  2. Два пункта меню имеют одинаковую цену. Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. Следовательно, товар не является функцией цены.

Пример: определение того, являются ли правила оценки класса функциями

В конкретном математическом классе общая процентная оценка соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице ниже показано возможное правило присвоения баллов.

Процентная оценка 0–56 57–61 62–66 67–71 72–77 78–86 87–91 92–100
Средний балл 0,0 1,0 1,5 2.0 2,5 3,0 3,5 4,0
Показать решение

Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.

В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3.0 может иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.

Попробуй

В таблице ниже перечислены пять величайших бейсболистов всех времен в порядке рангов.

Игрок Рейтинг
Бэйб Рут 1
Уилли Мейс 2
Тай Кобб 3
Уолтер Джонсон 4
Хэнк Аарон 5
  1. Является ли ранг функцией имени игрока?
  2. Имя игрока зависит от ранга?
Показать решение
  1. да
  2. да.(Примечание: если бы два игрока были разделены, скажем, за 4-е место, то имя не зависело бы от ранга.)

Использование обозначения функций

Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда и чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартное обозначение функции — это представление, упрощающее работу с функциями.

Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных [latex] h [/ latex] для роста и [latex] a [/ latex] для возраста. Буквы [latex] f, g [/ latex] и [latex] h [/ latex] часто используются для обозначения функций точно так же, как мы используем [latex] x, y [/ latex] и [latex] z [/ латекс] для обозначения чисел и [латекс] A, B [/ латекс] и [латекс] C [/ латекс] для представления наборов.

[латекс] \ begin {align} & h \ text {is} f \ text {of} a && \ text {Мы называем функцию} f; \ text {высота является функцией возраста}.\\ & h = f \ left (a \ right) && \ text {Мы используем круглые скобки для обозначения ввода функции} \ text {. } \\ & f \ left (a \ right) && \ text {Мы называем функцию} f; \ text {выражение читается как} » f \ text {of} a ». \ end {align} [/ latex]

Помните, мы можем использовать любую букву для названия функции; мы можем использовать обозначение [латекс] h \ left (a \ right) [/ latex], чтобы показать, что [latex] h [/ latex] зависит от [latex] a [/ latex]. Входное значение [latex] a [/ latex] должно быть помещено в функцию [latex] h [/ latex], чтобы получить выходное значение.Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.

Мы также можем дать алгебраическое выражение в качестве входных данных для функции. Например, [латекс] f \ left (a + b \ right) [/ latex] означает «сначала добавьте [latex] a [/ latex] и [latex] b [/ latex], и результат будет входом для функции [латекс] е [/ латекс] ». Мы должны выполнять операции именно в таком порядке, чтобы получить правильный результат.

A Общее примечание: обозначение функций

Обозначение [латекс] y = f \ left (x \ right) [/ latex] определяет функцию с именем [latex] f [/ latex].Это читается как [latex] «y [/ latex] является функцией [latex] x». [/ Latex] Буква [latex] x [/ latex] представляет входное значение или независимую переменную. Буква [латекс] y [/ latex] или [латекс] f \ left (x \ right) [/ latex] представляет выходное значение или зависимую переменную.

Пример: использование обозначения функций для дней в месяце

Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце в невисокосном году.

Показать решение

Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию [latex] f [/ latex], мы напишем [latex] \ text {days} = f \ left (\ text {месяц} \ справа) [/ латекс] или [латекс] d = f \ left (m \ right) [/ латекс].Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.

Например, [латекс] f \ left (\ text {April} \ right) = 30 [/ latex], потому что в апреле 30 дней. Обозначение [латекс] d = f \ left (m \ right) [/ latex] напоминает нам, что количество дней, [latex] d [/ latex] (вывод), зависит от названия месяца, [ латекс] м [/ латекс] (вход).

Анализ решения

Мы должны ограничить функцию невисокосными годами. В противном случае у февраля было бы 2 выхода, и это не было бы функцией.Также обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода. Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.

Пример: интерпретация обозначения функции

Функция [латекс] N = f \ left (y \ right) [/ latex] дает количество полицейских, [latex] N [/ latex], в городе в году [latex] y [/ latex].Что означает [латекс] f \ left (2005 \ right) = 300 [/ latex]?

Показать решение

Когда мы читаем [латекс] f \ left (2005 \ right) = 300 [/ latex], мы видим, что входным годом является 2005. Значение для выхода, количество полицейских [латекс] N [/ latex] , равно 300. Помните, [латекс] N = f \ left (y \ right) [/ latex]. Выражение [латекс] f \ left (2005 \ right) = 300 [/ latex] говорит нам, что в 2005 году в городе было 300 полицейских.

Вопросы и ответы

Вместо обозначения, такого как [латекс] y = f \ left (x \ right) [/ latex], могли бы мы использовать тот же символ для вывода, что и для функции, например [latex] y = y \ left (x \ right) [/ latex], что означает: « y является функцией x ?»

Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, например физике и инженерии.Однако, исследуя математику, нам нравится различать такую ​​функцию, как [latex] f [/ latex], которая является правилом или процедурой, и выводом [latex] y [/ latex], который мы получаем, применяя [latex ] f [/ latex] к конкретному входу [latex] x [/ latex]. Вот почему мы обычно используем такие обозначения, как [латекс] y = f \ left (x \ right), P = W \ left (d \ right) [/ latex] и так далее.

Представление функций с помощью таблиц

Общий метод представления функций — в виде таблицы. Строки или столбцы таблицы отображают соответствующие входные и выходные значения.В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.

В таблице ниже перечислены входные числа каждого месяца (январь = 1, февраль = 2 и т. Д.) И выходное значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце [latex] f [/ latex], где [latex] D = f \ left (m \ right) [/ latex] определяет месяцы целым числом. а не по имени.

Номер месяца, [латекс] м [/ латекс] (ввод) 1 2 3 4 5 6 7 8 9 10 11 12
Дней в месяце, [латекс] D [/ латекс] (вывод) 31 28 31 30 31 30 31 31 30 31 30 31

В таблице ниже определяется функция [латекс] Q = g \ left (n \ right) [/ latex].Помните, что эта запись говорит нам, что [latex] g [/ latex] — это имя функции, которая принимает входные данные [latex] n [/ latex] и выдает на выходе [latex] Q [/ latex].

[латекс] n [/ латекс] 1 2 3 4 5
[латекс] Q [/ латекс] 8 6 7 6 8

В таблице ниже показан возраст детей в годах и их рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Сразу видно, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.

Возраст в годах, [latex] \ text {} a \ text {} [/ latex] (ввод) 5 5 6 7 8 9 10
Высота в дюймах, [латекс] \ text {} h \ text {} [/ latex] (вывод) 40 42 44 47 50 52 54

Как: по таблице входных и выходных значений определить, представляет ли таблица функцию.
  1. Определите входные и выходные значения.
  2. Убедитесь, что каждое входное значение сопряжено только с одним выходным значением. Если это так, таблица представляет функцию.

Пример: определение таблиц, представляющих функции

Какая таблица, A, B или C, представляет функцию (если есть)?

Таблица A
Ввод Выход
2 1
5 3
8 6
Таблица B
Ввод Выход
–3 5
0 1
4 5
Таблица C
Ввод Выход
1 0
5 2
5 4
Показать решение

a) и b) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. c) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.

Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.

Функция, представленная a), может быть представлена ​​записью

[латекс] f \ left (2 \ right) = 1, f \ left (5 \ right) = 3, \ text {и} f \ left (8 \ right) = 6 [/ latex]

Аналогично, утверждения [латекс] g \ left (-3 \ right) = 5, g \ left (0 \ right) = 1, \ text {и} g \ left (4 \ right) = 5 [/ latex] представляют функцию в b).

c) нельзя выразить аналогичным образом, потому что он не представляет функцию.

Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.

Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа.Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.

Определить, является ли функция взаимно однозначной

Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям. Например, на следующей биржевой диаграмме цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.

Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа.Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в.

Буквенный класс Средний балл
A 4,0
B 3,0
С 2,0
D 1,0

Эта система оценок представляет собой функцию «один-к-одному», потому что каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.

Чтобы наглядно представить эту концепцию, давайте еще раз посмотрим на две простые функции, схематически изображенные в пунктах (a) и (b) ниже. {2} + 2p [/ latex], решите относительно [латекс] h \ left (p \ right) = 3 [/ latex].{2} + 2p — 3 = 0 && \ text {Вычтите по 3 с каждой стороны}. \\ & \ left (p + 3 \ text {) (} p — 1 \ right) = 0 && \ text {Factor}. \ end {align} [/ latex]

Если [латекс] \ left (p + 3 \ right) \ left (p — 1 \ right) = 0 [/ latex], либо [latex] \ left (p + 3 \ right) = 0 [/ latex] или [латекс] \ left (p — 1 \ right) = 0 [/ latex] (или оба они равны 0). Мы установим каждый коэффициент равным 0 и решим для каждого случая [латекс] p [/ латекс].

[латекс] \ begin {align} & p + 3 = 0, && p = -3 \\ & p — 1 = 0, && p = 1 \ hfill \ end {align} [/ latex]

Это дает нам два решения.Выход [латекс] h \ left (p \ right) = 3 [/ latex], когда вход либо [latex] p = 1 [/ latex], либо [latex] p = -3 [/ latex].

Мы также можем проверить, построив график, как на рисунке 5. График проверяет, что [latex] h \ left (1 \ right) = h \ left (-3 \ right) = 3 [/ latex] и [latex] h \ left (4 \ справа) = 24 [/ латекс].

Попробуй

Учитывая функцию [латекс] g \ left (m \ right) = \ sqrt {m — 4} [/ latex], решите [latex] g \ left (m \ right) = 2 [/ latex].

Вычисление функций, выраженных в формулах

Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения .Если возможно выразить выход функции с помощью формулы , включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение [латекс] 2n + 6p = 12 [/ латекс] выражает функциональную связь между [латексом] n [/ латексом] и [латексом] p [/ латексом]. Мы можем переписать его, чтобы решить, является ли [latex] p [/ latex] функцией [latex] n [/ latex].

Практическое руководство. Для данной функции в форме уравнения напишите ее алгебраическую формулу.

  1. Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а с другой стороны как выражение, которое включает только входную переменную.
  2. Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих частей уравнения на одинаковую величину.

Пример: поиск уравнения функции

Выразите отношение [латекс] 2n + 6p = 12 [/ latex] как функцию [latex] p = f \ left (n \ right) [/ latex], если это возможно.

Показать решение

Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где [latex] p [/ latex] является функцией [latex] n [/ latex], что означает запись его как [latex] p = [/ latex] выражение, включающее [latex] n [/ latex].

[латекс] \ begin {align} & 2n + 6p = 12 \\ [1mm] & 6p = 12 — 2n && \ text {Subtract} 2n \ text {с обеих сторон}. \\ [1mm] & p = \ frac {12 — 2n} {6} && \ text {Разделите обе стороны на 6 и упростите}. \\ [1 мм] & p = \ frac {12} {6} — \ frac {2n} {6} \\ [1 мм] & p = 2- \ frac {1} {3} n \ end {align} [/ latex ]

Следовательно, [латекс] p [/ latex] как функция [latex] n [/ latex] записывается как

[латекс] p = f \ left (n \ right) = 2- \ frac {1} {3} n [/ latex]

Анализ решения

Важно отметить, что не все отношения, выраженные уравнением, можно также выразить как функцию с формулой.{y} [/ latex], если мы хотим выразить [latex] y [/ latex] как функцию [latex] x [/ latex], не существует простой алгебраической формулы, включающей только [latex] x [/ latex] что равно [латекс] y [/ латекс]. Однако каждый [latex] x [/ latex] определяет уникальное значение для [latex] y [/ latex], и существуют математические процедуры, с помощью которых [latex] y [/ latex] может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex] y [/ latex] как функции [latex] x [/ latex], даже если формулу нельзя записать явно.

Оценка функции, заданной в табличной форме

Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев.И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.

Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу ниже.

ПЭТ Объем памяти в часах
Щенок 0,008
Взрослая собака 0.083
Кот 16
Золотая рыбка 2160
Бета-рыба 3600

Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию [латекс] П [/ латекс].

Домен функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память домашнего животного.Мы можем оценить функцию [latex] P [/ latex] при входном значении «золотая рыбка». Мы бы написали [латекс] P \ left (\ text {goldfish} \ right) = 2160 [/ latex]. Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex] P [/ latex] кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.

Практическое руководство. Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.


  1. Найдите данный вход в строке (или столбце) входных значений.
  2. Определите соответствующее выходное значение в паре с этим входным значением.
  3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
  4. Определите входное значение (я), соответствующее заданному выходному значению.

Пример: оценка и решение табличной функции

Используя приведенную ниже таблицу,

  1. Вычислить [латекс] g \ left (3 \ right) [/ latex].
  2. Решите [латекс] g \ left (n \ right) = 6 [/ latex].
[латекс] n [/ латекс] 1 2 3 4 5
[латекс] г (п) [/ латекс] 8 6 7 6 8
Показать решение
  • Вычисление [latex] g \ left (3 \ right) [/ latex] означает определение выходного значения функции [latex] g [/ latex] для входного значения [latex] n = 3 [/ latex].Выходное значение таблицы, соответствующее [latex] n = 3 [/ latex], равно 7, поэтому [latex] g \ left (3 \ right) = 7 [/ latex].
  • Решение [latex] g \ left (n \ right) = 6 [/ latex] означает определение входных значений, [latex] n [/ latex], которые дают выходное значение 6. В таблице ниже показаны два решения: [ латекс] n = 2 [/ латекс] и [латекс] n = 4 [/ латекс].
[латекс] n [/ латекс] 1 2 3 4 5
[латекс] г (п) [/ латекс] 8 6 7 6 8

Когда мы вводим 2 в функцию [latex] g [/ latex], на выходе получаем 6.Когда мы вводим 4 в функцию [latex] g [/ latex], наш результат также равен 6.

Попробуй

Используя таблицу из предыдущего примера, оцените [латекс] g \ left (1 \ right) [/ latex].

Показать решение

[латекс] г \ слева (1 \ справа) = 8 [/ латекс]

Поиск значений функций из графика

Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.

Пример: чтение значений функций из графика

Учитывая график ниже,

  1. Вычислить [латекс] f \ left (2 \ right) [/ latex].
  2. Решите [латекс] f \ left (x \ right) = 4 [/ latex].
Показать решение
  1. Чтобы оценить [latex] f \ left (2 \ right) [/ latex], найдите точку на кривой, где [latex] x = 2 [/ latex], затем прочтите [latex] y [/ latex] — координата этой точки.Точка имеет координаты [latex] \ left (2,1 \ right) [/ latex], поэтому [latex] f \ left (2 \ right) = 1 [/ latex].
  2. Чтобы решить [латекс] f \ left (x \ right) = 4 [/ latex], мы находим выходное значение [latex] 4 [/ latex] по вертикальной оси. Двигаясь горизонтально по линии [latex] y = 4 [/ latex], мы обнаруживаем две точки кривой с выходным значением [latex] 4: [/ latex] [latex] \ left (-1,4 \ right) [/ латекс] и [латекс] \ влево (3,4 \ вправо) [/ латекс]. Эти точки представляют два решения [латекса] f \ left (x \ right) = 4: [/ latex] [latex] x = -1 [/ latex] или [latex] x = 3 [/ latex].Это означает [латекс] f \ left (-1 \ right) = 4 [/ latex] и [latex] f \ left (3 \ right) = 4 [/ latex], или когда ввод [латекс] -1 [ / latex] или [latex] \ text {3,} [/ latex] вывод будет [latex] \ text {4} \ text {.} [/ latex] См. график ниже.

Попробуй

Используя график, решите [латекс] f \ left (x \ right) = 1 [/ latex].

Показать решение

[латекс] x = 0 [/ латекс] или [латекс] x = 2 [/ латекс]

Определение функций с помощью графиков

Как мы видели в примерах выше, мы можем представить функцию с помощью графика.Графики отображают множество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.

Наиболее распространенные графики называют входное значение [latex] x [/ latex] и выходное значение [latex] y [/ latex], и мы говорим, что [latex] y [/ latex] является функцией [latex] x [ / latex] или [latex] y = f \ left (x \ right) [/ latex], если функция называется [latex] f [/ latex].График функции — это набор всех точек [латекс] \ left (x, y \ right) [/ latex] в плоскости, которая удовлетворяет уравнению [латекс] y = f \ left (x \ right) [/ latex ]. Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующее выходное значение. Например, черные точки на графике на графике ниже говорят нам, что [латекс] f \ left (0 \ right) = 2 [/ latex] и [latex] f \ left (6 \ right) = 1 [/ latex ].Однако набор всех точек [latex] \ left (x, y \ right) [/ latex], удовлетворяющих [latex] y = f \ left (x \ right) [/ latex], является кривой. Показанная кривая включает [латекс] \ left (0,2 \ right) [/ latex] и [latex] \ left (6,1 \ right) [/ latex], потому что кривая проходит через эти точки.

Тест вертикальной линии может использоваться для определения того, представляет ли график функцию. Вертикальная линия включает все точки с определенным значением [latex] x [/ latex]. Значение [latex] y [/ latex] точки, где вертикальная линия пересекает график, представляет собой выход для этого входного значения [latex] x [/ latex].Если мы можем нарисовать любую вертикальную линию , которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что это значение [latex] x [/ latex] имеет более одного вывода. Функция имеет только одно выходное значение для каждого входного значения.

Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.

  1. Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
  2. Если такая линия есть, график не представляет функцию.
  3. Если ни одна вертикальная линия не может пересекать кривую более одного раза, график действительно представляет функцию.

Пример: применение теста вертикальной линии

Какой из графиков представляет функцию [латекс] y = f \ left (x \ right)? [/ Latex]

Показать решение

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) графика выше.Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия пересекает график более чем в одной точке.

Попробуй

Представляет ли приведенный ниже график функцию?

Тест горизонтальной линии

После того, как мы определили, что график определяет функцию, простой способ определить, является ли он взаимно однозначной функцией, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Горизонтальная линия включает все точки с определенным значением [latex] y [/ latex]. Значение [latex] x [/ latex] точки, где вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex] y [/ latex]. Если мы можем нарисовать любую горизонтальную линию , которая пересекает график более одного раза, тогда график , а не , представляет собой взаимно-однозначную функцию, потому что это значение [latex] y [/ latex] имеет более одного входа.

Как сделать. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию «один к одному».

  1. Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
  2. Если такая строка есть, функция не взаимно однозначная.
  3. Если ни одна горизонтальная линия не может пересекать кривую более одного раза, функция взаимно однозначна.

Пример: применение теста горизонтальной линии

Рассмотрим функции (a) и (b), показанные на графиках ниже.

Являются ли какие-либо функции взаимно однозначными?

Показать решение

Функция в (а) не является взаимно однозначной.Горизонтальная линия, показанная ниже, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках).

Функция в (b) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.

Определение основных функций набора инструментов

В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем.Учимся читать, начинаем с алфавита. Когда мы учимся арифметике, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать [latex] x [/ latex] в качестве входной переменной и [latex] y = f \ left (x \ right) [/ latex] в качестве выходной переменной.

Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги. Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную ниже.

Ключевые понятия

  • Отношение — это набор упорядоченных пар. Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.
  • Функциональная нотация — это сокращенный метод соотнесения ввода с выводом в форме [латекс] y = f \ left (x \ right) [/ latex].
  • В табличной форме функция может быть представлена ​​строками или столбцами, относящимися к входным и выходным значениям.
  • Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно оценить, заменив входную переменную заданным значением.
  • Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение.
  • Алгебраическая форма функции может быть записана из уравнения.
  • Входные и выходные значения функции можно определить по таблице.
  • Связь входных значений с выходными значениями на графике — еще один способ оценить функцию.
  • Функция взаимно однозначна, если каждое выходное значение соответствует только одному входному значению.
  • График представляет функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке.
  • График представляет собой взаимно однозначную функцию, если любая горизонтальная линия, проведенная на графике, пересекает график не более чем в одной точке.

Глоссарий

зависимая переменная
выходная переменная
домен
набор всех возможных входных значений для отношения
функция
отношение, в котором каждое входное значение дает уникальное выходное значение
тест горизонтальной линии
метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза
независимая переменная
входная переменная
вход
каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция
индивидуальная функция
функция, для которой каждое значение вывода связано с уникальным значением ввода
выход
каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию
диапазон
набор выходных значений, которые являются результатом входных значений в отношении
отношение
комплект заказанных пар
тест вертикальной линии
способ проверки того, представляет ли график функцию, путем определения того, пересекает ли вертикальная линия график не более одного раза

Семь элементарных функций и их графики — Концепция

В математике мы часто сталкиваемся с некоторыми элементарными функциями.Эти элементарные функции включают рациональные функции, экспоненциальные функции, основные полиномы, абсолютные значения и функцию квадратного корня. Важно распознавать графики элементарных функций и уметь строить их сами. Это будет особенно полезно при преобразовании.

Я хочу поговорить о семи действительно важных функциях, которые я называю родительскими функциями.Я их здесь нарисовал. Первый f из x равен x. Это функция идентичности. Это своего рода родитель всех линейных функций. Во-вторых, функция абсолютного значения f от x равна абсолютному значению x.
Третий, f x равняется x в квадрате, функция возведения в квадрат, ее график представляет собой параболу, и это родитель всех квадратичных функций. f x равно x в кубе, кубической функции.
Номер пять, функция извлечения квадратного корня. f из x равно квадратному корню x. Типичная экспоненциальная функция f от x равна 2 x.Обратите внимание на разницу между 2 и x и x в квадрате, очень разные формы, разные классы функций и f для x равняется 1 по x, обратной функции. Это родительские функции, и по мере того, как мы узнаем, как графически отображать функции в их преобразованиях, мы будем использовать их в качестве своих главных подопытных кроликов. Мы будем преобразовывать их и создавать из них новые функции, поэтому мы называем их родительскими функциями. Но вам важно знать эти функции. Вы, вероятно, уже узнали о большинстве из них, если не обо всех, и просто запомните их графики и узнайте их с первого взгляда, а также знаете ключевые моменты, которые есть на графиках, эти ключевые точки, которые на графике являются функцией.
Вот и все. Это семь функций. Время от времени я буду добавлять к этому списку по ходу курса.

Типы функций и их графики

Вы можете идентифицировать функцию по ее графику. В этом уроке мы исследуем различные типы функций и их графики.

Необходимые условия для изучения этой статьи перечислены ниже.

Существует связь между функцией и ее графиком. С помощью графика функций вы можете обнаружить некоторые свойства, которые не предоставляет алгебраическая форма.

График функций помогает визуализировать функцию, заданную в алгебраической форме. Взглянув на уравнение, вы можете сказать, что график будет нечетным или четным, увеличивающимся или уменьшающимся, или даже уравнение вообще представляет собой график.

  • Линейная функция
  • Функция возведения в квадрат
  • Кубическая функция
  • Функция квадратного корня
  • Взаимная функция
  • Пошаговая функция
  • Мудрая функция по частям

Линейные функции

Линейные функции — это прямые линии.Прочтите следующую статью, чтобы узнать больше о линейной функции.

Линейные уравнения

Функции возведения в квадрат

График функции возведения в квадрат обычно известен как парабола, которая представляет собой U-образную кривую. Диаграмма функции возведения в квадрат приведена ниже.

Функции возведения в квадрат

Свойства функции возведения в квадрат

Свойства функции возведения в квадрат: область определения и диапазон, точки пересечения и т. Д.

  • Область возведения в квадрат функции набора всех действительных чисел, соответствующих оси абсцисс.
  • Диапазон функции возведения в квадрат — все неотрицательные действительные числа, потому что график имеет U-образную форму.
  • Функция является четной, поскольку она симметрична по оси y.
  • Перехватчик функции возведения в квадрат находится в точке (0, 0).
  • График функции возведения в квадрат имеет относительный минимум в точке (0, 0).
  • График функции возведения в квадрат уменьшается между интервалами.
  • График увеличивается между интервалами.

График кубической функции

График кубической функции находится в положительной и отрицательной сторонах, в отличие от функции возведения в квадрат, которая находится только на положительной стороне.3 точка -2 -8 (-2, -8) -1–1 (-1, -1) 0 0 (0, 0) 1 1 (1, 1) 2 8 (2, 8)

График кубической функции выглядит следующим образом.

График кубической функции

Свойства кубической функции

Кубическая функция имеет следующие свойства.

  • Кубическая функция — это нечетная функция.
  • Кубическая функция симметрична относительно начала координат.
  • Область кубической функции задается всеми действительными числами.
  • Диапазон кубической функции состоит из всех действительных чисел, потому что функция имеет интервал между ними.
  • Пересечение графика находится в точке (0, 0).
  • Функция всегда увеличивается между интервалом -.

График функции квадратного корня

График функции

, где значение результата.

f (x) = x

Построим график функции квадратного корня, получив несколько точек. Мы использовали калькулятор для вычисления некоторых значений.

x балл
4 2 (4, 2)
3 1,73 (3, 1,73)
2 1,41 (2, 1. 41)
1 1 (1, 1)
0 0 (0, 0)

График функции возведения в квадрат представлен ниже.

График функции возведения в квадрат

Как вы можете видеть, график имеет только положительную сторону как для

, так и для.

Свойства функции возведения в квадрат

График функции возведения в квадрат представлен ниже.

График обратной функции

Пусть

— функция, тогда

f (x) = 1x

называется обратной функцией.

Чтобы построить график обратной функции, давайте сначала найдем все точки.

x f (x) = 1 / x точка
-3 -1/3 (-3, -1/3)
-2 -1/2 (-2, -1/2)
-1–1 (-1, -1)
0 undefined undefined
1 1 (1, 1)
2 1/2 (2, 1/2)
3 1/3 (3, 1/3)

График обратной связи показан ниже.

График обратной функции f (x) = 1 / x

Свойства графика обратной функции

Обратная функция симметрична вдоль начала координат, но никогда не касается самой начала координат. Свойства обратной функции приведены ниже.

График ступенчатой ​​функции

График ступенчатой ​​функции на самом деле выглядит как лестница со ступенями.

Пусть

, будет ступенчатой ​​функцией, где

[[x]] означает найти значение « больше или равно x ».

Мы должны найти точки, чтобы построить график ступенчатой ​​функции.

x f (x) = [[x]] + 1 баллов
-2–1 (-2, 1)
-1 0 (-1, 0)
0 1 (0, 1)
1 2 (1, 2)
2 3 (2, 3)

График ступенчатой ​​функции показан ниже.

График ступенчатой ​​функции

Свойства ступенчатой ​​функции

Свойства ступенчатой ​​функции приведены ниже.

  • В домене заданы все действительные числа.
  • Диапазон функции задается всеми целыми числами.
  • Отсечка по оси Y равна (0,0), а точка пересечения по оси x — [0, 1).
  • График постоянен между каждой парой целых чисел.
  • График перескакивает по вертикали на одну единицу для каждого значения y.

График кусочной функции

График кусочной функции уже обсуждался в предыдущих уроках.

Графики функций

Если вы помните эти базовые графы функций, используемые в алгебре, то легче выучить высшие и сложные графы. Позже, когда вы изучите математический анализ, визуализировать концепции будет намного проще с помощью графика функций.

Статьи по теме: —

Родительские функции — Типы, свойства и примеры

При работе с функциями и их графиками вы заметите, как графики большинства функций выглядят одинаково и следуют аналогичным шаблонам.Это потому, что функции, имеющие одинаковую степень, будут следовать аналогичной кривой и использовать одни и те же родительские функции.

Родительская функция представляет собой простейшую форму семейства функций.

Это определение прекрасно описывает родительские функции. Мы используем родительские функции, чтобы направлять нас при построении графиков функций, которые находятся в том же семействе. В этой статье мы:

  • Рассмотрим все уникальные родительские функции (возможно, вы уже сталкивались с некоторыми ранее).
  • Узнайте, как определить родительскую функцию, которой принадлежит функция.

Возможность идентифицировать и графически отображать функции с помощью их родительских функций может помочь нам лучше понять функции, так чего же мы ждем?

Что такое родительская функция?

Теперь, когда мы понимаем, насколько важно для нас овладеть различными типами родительских функций, давайте сначала начнем понимать, что такое родительские функции и как их семейства функций зависят от их свойств.

Определение родительской функции

Родительские функции — это простейшая форма данного семейства функций . Семейство функций — это группа функций, которые имеют одинаковую высшую степень и, следовательно, одинаковую форму для своих графиков .

На приведенном выше графике показаны четыре графика, которые демонстрируют U-образный график, который мы называем параболой. Поскольку все они имеют одинаковую высшую степень двойки и одинаковую форму, мы можем сгруппировать их в одно семейство функций.Сможете угадать, к какой семье они принадлежат?

Все эти четыре функции являются квадратичными, и их простейшая форма будет y = x 2 . Следовательно, родительской функцией для этого семейства является y = x 2 .

Поскольку родительские функции являются простейшей формой данной группы функций, они могут сразу дать вам представление о том, как будет выглядеть данная функция из того же семейства.

Какие бывают типы родительских функций?

Пришло время освежить наши знания о функциях, а также узнать о новых функциях.Как мы уже упоминали, знакомство с известными родительскими функциями поможет нам лучше и быстрее понять и построить графики функций.

Почему бы нам не начать с тех, которые мы, возможно, уже узнали в прошлом?

Первые четыре родительские функции содержат многочлены с возрастающей степенью. Давайте посмотрим, как ведут себя их графики, и отметим область и диапазон соответствующих родительских функций.

Функции констант

Функции констант — это функции, которые определяются своей соответствующей константой c.Все постоянные функции будут иметь горизонтальную линию в качестве графика и содержать только константу в качестве члена.

Все постоянные функции будут иметь все действительные числа в качестве домена и y = c в качестве диапазона. У каждого из них также есть точка пересечения по оси y в точке (0, c).

Движение объекта в состоянии покоя — хороший пример постоянной функции.

Линейные функции

Линейные функции имеют x как член с наивысшей степенью и общую форму y = a + bx.Все линейные функции имеют прямую линию в виде графика .

Родительская функция линейных функций — это y = x, , и она проходит через начало координат. Область и диапазон всех линейных функций: , все действительные числа .

Эти функции представляют отношения между двумя объектами, которые линейно пропорциональны друг другу.

Квадратичные функции

Квадратичные функции — это функции с высшей степенью 2 .Все квадратичные функции возвращают параболу в качестве своего графика . Как обсуждалось в предыдущем разделе, квадратичные функции имеют y = x 2 в качестве родительской функции .

Вершина родительской функции y = x 2 лежит в начале координат. Он также имеет область для всех действительных чисел и диапазон [0, ∞) . Обратите внимание, что эта функция увеличивается, когда x положительна , а уменьшается, когда x отрицательна .

Хорошим применением квадратичных функций является движение снаряда.Мы можем наблюдать за движением снаряда объекта, построив график квадратичной функции, которая его представляет.

Кубические функции

Давайте перейдем к родительской функции многочленов с 3 в качестве высшей степени . Кубические функции имеют общую родительскую функцию y = x 3 . Эта функция на увеличивается по всему домену .

Как и в случае с двумя предыдущими родительскими функциями, график y = x 3 также проходит через начало координат.Его домен и диапазон равны (-∞, ∞) или все действительные числа.

Функции абсолютного значения

Родительской функцией функций абсолютного значения является y = | x | . Как показано на графике родительской функции, ожидается, что функции абсолютного значения будут возвращать V-образных графиков .

Вершина y = | x | также находится в начале координат. Поскольку он проходит на обоих концах оси x, y = | x | имеет область в (-∞, ∞). Абсолютные значения никогда не могут быть отрицательными, поэтому родительская функция имеет диапазон [0, ∞) .

Мы используем функции абсолютного значения, чтобы подчеркнуть, что значение функции всегда должно быть положительным.

Радикальные функции

Двумя наиболее часто используемыми радикальными функциями являются функции извлечения квадратного корня и кубического корня .

Родительская функция функции извлечения квадратного корня — y = √x . Его график показывает, что его значения x и y никогда не могут быть отрицательными.

Это означает, что область и диапазон y = √x равны [0, ∞ ) . Начальная точка или вершина родительской функции также находится в точке в начале координат . Родительская функция y = √x также возрастает на во всей области .

Давайте теперь изучим родительскую функцию функций кубического корня. Подобно функции извлечения квадратного корня, ее родительская функция выражается как y = ∛ x .

На графике показано, что родительская функция имеет домен и диапазон (-∞, ∞) .Мы также можем видеть, что y = ∛x составляет , увеличиваясь во всей области .

Экспоненциальные функции

Экспоненциальные функции — это функции, в экспоненте которых есть алгебраические выражения. Их родительская функция может быть выражена как y = b x , где b может быть любой ненулевой константой. График родительской функции, y = e x , , показан ниже, и из него мы видим, что никогда не будет равно 0 .

И когда x = 0, y проходит через ось y при y = 1.Мы также можем видеть, что родительская функция никогда не находится ниже оси Y, поэтому ее диапазон равен (0, ∞ ). Его домен , однако, может быть полностью действительным числом . Мы также можем видеть, что эта функция на увеличивается во всей области.

Одним из наиболее распространенных приложений экспоненциальных функций является моделирование роста населения и сложных процентов.

Логарифмические функции

Логарифмические функции являются функциями, обратными экспоненциальным функциям. Его родительская функция может быть выражена как y = log b x , где b — ненулевая положительная константа. Рассмотрим график, когда b = 2 .

Как и экспоненциальная функция, мы можем видеть, что x никогда не может быть меньше или равным нулю для y = log 2 x. Следовательно, его область определения (0, ∞) . Однако его диапазон содержит все действительные числа . Мы также можем видеть, что эта функция на увеличивается во всей области.

Мы используем логарифмические функции для моделирования природных явлений, таких как сила землетрясения.Мы также применяем его при вычислении скорости распада периода полураспада в физике и химии.

Взаимные функции

Взаимные функции — это функции, которые содержат числитель-константу и знаменатель x. Его родительская функция — y = 1 / x .

Как видно из графика, ни x, ни y никогда не могут быть равны нулю. Это означает, что его домен и диапазон равны (-∞, 0) U (0, ∞) . Мы также можем видеть, что функция на убывает во всей области .

На протяжении всего нашего пути с функциями и графиками есть много других родительских функций, но эти восемь родительских функций относятся к , наиболее часто используемым и обсуждаемым функциям .

Вы даже можете резюмировать то, что вы узнали, создав таблицу, показывающую все свойства родительских функций.

Как найти родительскую функцию?

Что, если нам дана функция или ее график, и нам нужно идентифицировать ее родительскую функцию? Мы можем сделать это, запомнив важные свойства каждой функции и определив, какие из родительских графиков, которые мы обсуждали, соответствуют заданному.

Вот несколько наводящих вопросов, которые могут нам помочь:

  • Какая наивысшая степень функции?
  • Содержит ли он квадратный корень или кубический корень?
  • Функция находится в экспоненте или знаменателе?
  • График функции увеличивается или уменьшается?
  • Каков домен или диапазон функции?

Если мы сможем ответить на некоторые из этих вопросов путем проверки, мы сможем вывести наши варианты и в конечном итоге идентифицировать родительскую функцию.

Давайте попробуем f (x) = 5 (x — 1) 2 . Мы видим, что наивысшая степень f (x) равна 2 , поэтому мы знаем, что эта функция является квадратичной функцией. Следовательно, , его родительская функция — y = x 2 .

Почему бы нам не построить график f (x) и также не подтвердить наш ответ?

На графике мы видим, что он образует параболу, подтверждая, что его родительская функция равна y = x 2 .

Просмотрите первые несколько разделов этой статьи и свои собственные заметки, а затем давайте попробуем задать несколько вопросов, чтобы проверить наши знания о родительских функциях.

Пример 1

Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?

Решение

Функции, представленные графиками A, B, C и E, имеют аналогичную форму, но смещены вверх или вниз. Фактически, эти функции представляют собой семейство из экспоненциальных функций . Это означает, что все они имеют общую родительскую функцию: y = b x .

С другой стороны, график D представляет логарифмическую функцию, поэтому D не принадлежит к группе экспоненциальных функций.

Пример 2

Какие из следующих функций не принадлежат к данному семейству функций?

  • y = 5x 2
  • y = -2x 2 + 3x — 1
  • y = x (3x 2 )
  • y = (x — 1) (x + 1)

Решение

Функция y = 5x 2 имеет наивысшую степень двойки, поэтому она является квадратичной функцией.Это означает, что его родительская функция — y = x 2 . То же самое и для y = -2x 2 + 3x — 1. Исходя из этого, мы можем подтвердить, что рассматриваем семейство квадратичных функций.

Применяя разность полных квадратов к четвертому варианту, получаем y = x 2 — 1. Это также квадратичная функция. Остается третий вариант.

В развернутом виде y = x (3x 2 ) становится y = 3x 3, , и это показывает, что наивысшая степень равна 3.Следовательно, он не может быть частью данного семейства функций.

Пример 3

Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.

Решение

Начнем с f (x). Мы видим, что его график имеет параболу, поэтому мы можем сказать, что f (x) является квадратичной функцией .

  • Это означает, что f (x) имеет родительскую функцию y = x 2 .
  • График простирается по обе стороны от x, поэтому он имеет область из (-∞, ∞) .
  • Парабола никогда не опускается ниже оси x, поэтому ее диапазон составляет [0, ∞) .

Основываясь на графике, мы видим, что значения x и y функции g (x) никогда не будут отрицательными. Они также показывают возрастающую кривую, которая напоминает график функции квадратного корня .

  • Следовательно, родительская функция для g (x) равна y = √x .
  • График простирается до правой части x и никогда не меньше 2, поэтому он имеет область [2, ∞) .
  • Парабола никогда не опускается ниже оси x, поэтому ее диапазон составляет [0, ∞) .

График h (x) показывает, что их значения x и y никогда не будут равны 0. Симметричные кривые также похожи на график обратных функций.

  • Это означает, что h (x) имеет родительскую функцию y = 1 / x.
  • Пока x и y никогда не равны нулю, h (x) по-прежнему действителен, поэтому он имеет как домен , так и диапазон (-∞, ∞) .

Прямые линии, представляющие i (x), говорят о том, что это линейная функция.

  • Имеет родительскую функцию y = x.
  • График простирается по обе стороны от x и y, поэтому он имеет область и диапазон (-∞, ∞) .

Пример 4

Определите родительскую функцию для следующих функций.

  • f (x) = x 3 — 2x + 1
  • g (x) = 3√x + 1
  • h (x) = 4 / x
  • i (x) = e x + 1

Решение

  • Наивысшая степень f (x) равна 3, поэтому это кубическая функция.Это означает, что у него есть родительская функция y = x 3 .
  • Функция g (x) имеет радикальное выражение 3√x. Поскольку у нее есть член с квадратным корнем, функция является функцией квадратного корня и имеет родительскую функцию y = √x.
  • Мы видим, что x находится в знаменателе h (x), поэтому он обратный. Следовательно, его родительская функция — y = 1 / x .
  • Показатели степени содержат x, поэтому одно это говорит нам о том, что i (x) — экспоненциальная функция.Следовательно, его родительская функция может быть выражена как y = b x , где b — константа. Для случая i (x) у нас есть y = e x в качестве его родительской функции.

Практические вопросы

1. Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?

2. Какие из следующих функций не относятся к данному семейству функций?

  • y = 4x 3
  • y = -3x 3 + 4x 2 + 5x — 1
  • y = x (5x 2 )
  • y = (x — 1) (x + 1) (х + 2)

3.Определите родительскую функцию следующих функций.

  • f (x) = x 3 — 2x + 1
  • g (x) = 3√x + 1
  • h (x) = 1 / (x + 1)
  • i (x) = e x + 1

4. Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.

5. Опишите разницу между f (x) = -5 (x — 1) 2 и его родительской функцией. Каков домен и диапазон f (x)?

6.Пусть a и b — две ненулевые константы. Опишите разницу между g (x) = ax + b и его родительской функцией. Каков домен и диапазон f (x)?

Изображения / математические рисунки создаются с помощью GeoGebra.

функция | Определение, типы, примеры и факты

Функция , в математике выражение, правило или закон, определяющий связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной).Функции повсеместно используются в математике и необходимы для формулирования физических соотношений в естественных науках. Современное определение функции было впервые дано в 1837 году немецким математиком Петером Дирихле:

Британская викторина

Определить: математические термины

Вот ваша миссия, если вы решите принять ее: Определите следующие математические термины до того, как истечет время.

Если переменная y так связана с переменной x , что всякий раз, когда числовое значение присваивается x , существует правило, согласно которому определяется уникальное значение y , тогда y считается функцией независимой переменной x .

Это соотношение обычно обозначается как y = f ( x ). Помимо f ( x ), другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда природа функции неизвестна или не указана.

Общие функции

Многие широко используемые математические формулы являются выражениями известных функций. Например, формула для площади круга A = π r 2 дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных, также распространены в математике, что можно увидеть в формуле для площади треугольника: A = b h /2, которая определяет A как функцию от обоих b (основание) и h (высота).В этих примерах физические ограничения вынуждают независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчас

Формула площади круга является примером полиномиальной функции. Общий вид таких функций: P ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + 9 х n , где даны коэффициенты ( a 0 , a 1 , a 2 ,…, a n ), x может быть любым действительным числом, и все степени x — это счетные числа (1, 2, 3,…).(Когда степень x может быть любым действительным числом, результат известен как алгебраическая функция.) Полиномиальные функции изучались с давних времен из-за их универсальности — практически любые отношения, включающие действительные числа, можно точно аппроксимировать с помощью полиномиальная функция. Полиномиальные функции характеризуются наивысшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные имена — линейная, квадратичная, кубическая, квартичная и квинтическая.

Полиномиальным функциям можно дать геометрическое представление с помощью аналитической геометрии. Независимая переменная x нанесена вдоль оси x (горизонтальная линия), а зависимая переменная y нанесена вдоль оси y (вертикальная линия). График функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 — 3 x + 2.

График кубического уравнения f ( x ) = x 3 — 3 x + 2. Точки на графике показывают изменения кривизны.

Encyclopædia Britannica, Inc.

Другой распространенный тип функций, который изучался с древности, — это тригонометрические функции, такие как sin x и cos x , где x — это мера угла ( см. Рисунок ). Из-за своей периодической природы тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».«Негебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.

графики некоторых тригонометрических функций

Обратите внимание, что каждая из этих функций периодическая. Таким образом, функции синуса и косинуса повторяются каждые 2π, а функции тангенса и котангенса повторяются через каждые π.

Encyclopædia Britannica, Inc.

Комплексные функции

Практическое применение функций, переменные которых являются комплексными числами, не так легко проиллюстрировать, но, тем не менее, они очень обширны.Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена ​​в виде z = x + i y , где i — мнимая единица (квадратный корень из −1), а x и y — действительные переменных ( см. рисунок ), можно разделить комплексную функцию на действительную и мнимую части: f ( z ) = P ( x , y ) + i Q ( x , y ).

точка в комплексной плоскости

Точка в комплексной плоскости. В отличие от действительных чисел, которые могут быть расположены одним знаком (положительным или отрицательным) числом вдоль числовой прямой, для комплексных чисел требуется плоскость с двумя осями, одна ось для компонента действительного числа и одна ось для мнимого компонента. Хотя комплексная плоскость выглядит как обычная двумерная плоскость, где каждая точка определяется упорядоченной парой действительных чисел ( x , y ), точка x + i y является одиночным количество.

Encyclopædia Britannica, Inc.

Меняя ролями независимых и зависимых переменных в заданной функции, можно получить обратную функцию. Обратные функции делают то, что подразумевает их название: они отменяют действие функции, чтобы вернуть переменную в исходное состояние. Таким образом, если для данной функции f ( x ) существует функция g ( y ) такая, что g ( f ( x )) = x и f ( g ( y )) = y , тогда g называется обратной функцией f и обозначается как f −1 , где по соглашению переменные меняются местами.Например, функция f ( x ) = 2 x имеет обратную функцию f −1 ( x ) = x /2.

Прочие функциональные выражения

Функция может быть определена с помощью степенного ряда. Например, бесконечный ряд можно использовать для определения этих функций для всех комплексных значений x . Когда это удобно, можно использовать другие типы серий, а также бесконечное количество продуктов. Важным случаем является ряд Фурье, выражающий функцию через синусы и косинусы:

Такие представления имеют большое значение в физике, особенно при изучении волнового движения и других колебательных явлений.

Иногда функции удобнее всего определять с помощью дифференциальных уравнений. Например, y = sin x является решением дифференциального уравнения d 2 y / d x 2 + y = 0, имея y = 0, d y / d x = 1, когда x = 0; y = cos x является решением того же уравнения, имеющего y = 1, d y / d x = 0, когда x = 0.

The Editors of Encyclopaedia Britannica Эта статья была недавно отредактирована и обновлена ​​Адамом Августином, управляющим редактором, справочное содержание.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *