Онлайн урок табличный и графический способы задания функции.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.
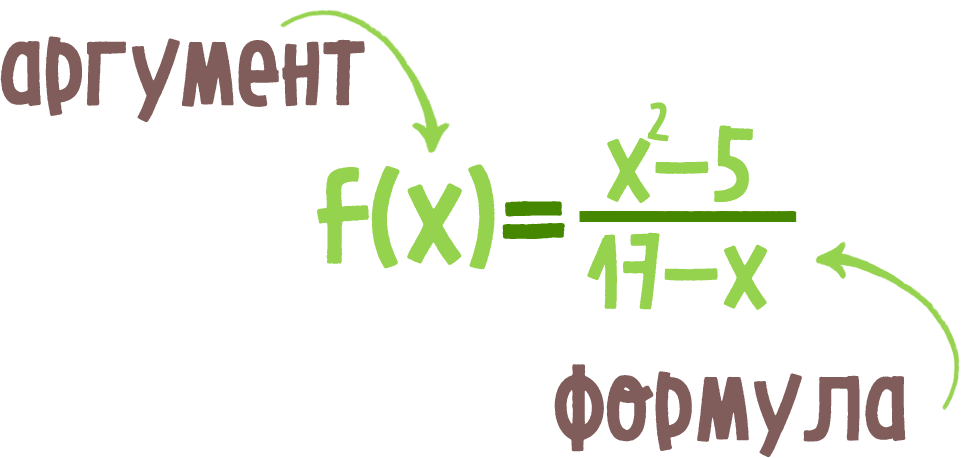
Аргумент функции — это независимая переменная, от значений которой зависят значения функции. Говорят, что функция задана аналитически, если она задана с помощью формулы.
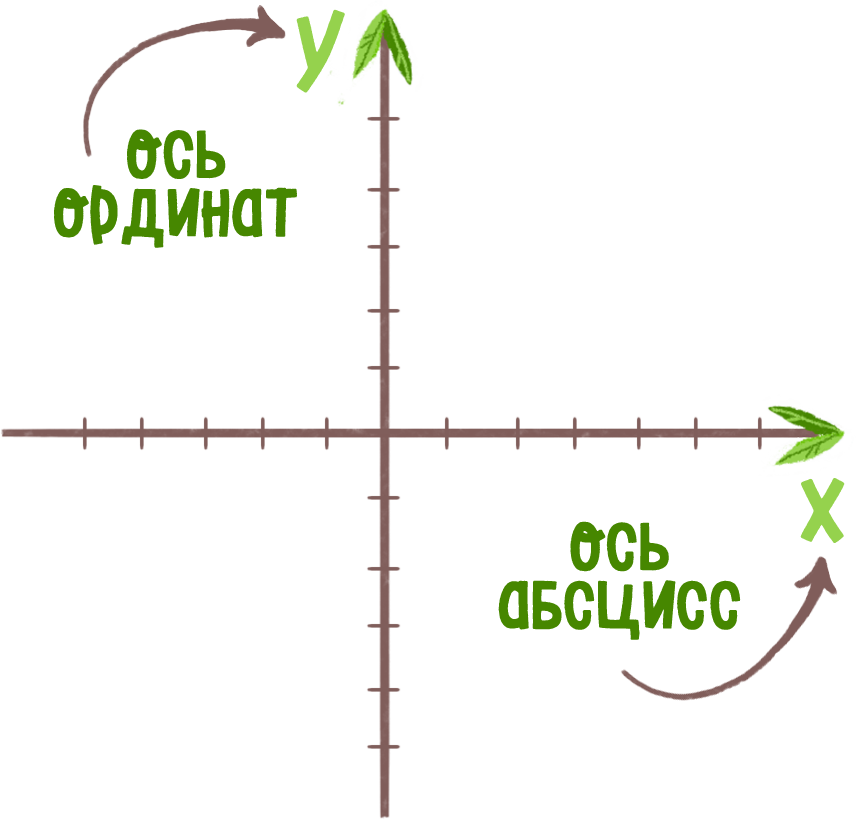
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями абсцисс и ординат на плоскости.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.
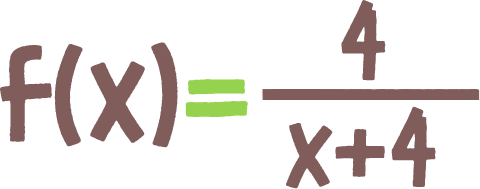
это не функцияобласть определения функцииобласть значений функциифункция задана аналитически
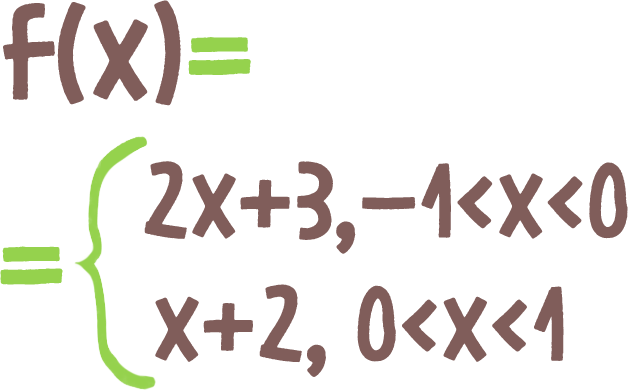
функция задана несколькими формуламиэто не функцияэто график функцииобласть определения функции — любое число
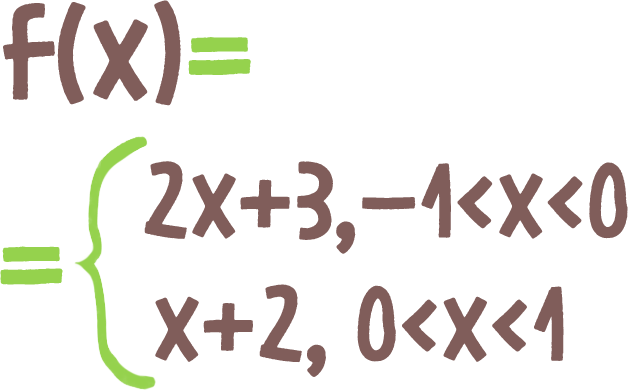
f(-1) = 2 · (-1) + 3 = -2 + 3 = 1f(1) = 2 · 1 + 3 = 2 + 3 = 5f( 0,1 ) = 0,1 + 2 = 2,1f( -0,1 ) = -0,1 + 2 = 1,9
Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Координатная плоскость.
2. Табличный способ задания функции.
3. График функции.
Урок по теме «Способы задания функции»
Технологическая карта урокаПредмет: математика
Класс: 9
Тема урока: «Способы задания функции»
Целиурока:овладеть способами задания функции: аналитический, графический, табличный, словесный; использовать эти способы в ходе выполнения заданий базового уровня.
Структура и ход урока
Актуализировать опорные знания в ходе ответов на вопросы 1.Вспомните определение функции.2.Как называется множество Х?
3.Как называется множество У?
Уметь дать определение функции;
области определения и области значения функции.
2.
Этап целеполагания
Определить тему и цели урока через ответы на вопросы. 1.Как можно представить функцию?
2.Как это можно объединить?
3.Что мы должны изучить?
4.Чего добиться? 5.Где использовать?
Выделение и формулирование учебной и познавательной цели на уроке
Планирование и выстраивание учебного сотрудничества с учителем и сверстниками;
умение полно и точно выражать свои мысли в соответствии с задачами коммуникации;
владение монологической и диалогической формами речи.
3.
Этап овладения новыми знаниями и СД
Выполнить учебные задания на определение способов задания функции по группам.
1.Найдите §9. Способы задания функции.
2.Группа №1 изучает аналитический способ задания функции.
Группа №2 — графический
Группа № 3 — табличный
Группа №4 – словесный.
3. Представьте каждая группа способ задания функции. Иметь все варианты способов задания функции.
4. Оцените, как вы поняли способы задания функции.
(на оценочном листе отметить: понял все способы; испытываю трудности в каком -то способе)
Уметь работать с учебником; уметь находить необходимый материал; уметь выделить главное; уметь привести примеры; уметь представить изученный материал.
Поиск, выделение, обработка, преобразование необходимой учебной информации;
моделирование изучаемых объектов;
осознанное построение речевого высказывания в устной и письменной форме;
умение извлекать необходимую информацию из текста,
краткое изложение содержания текста,
умение отстаивать и обосновывать свое мнение; уметь оценить себя.
.
Подбор теоретической модели для выполнения учебной задачи; составление и выполнение плана действий по решению учебной задачи, достижению учебной цели; умение оценить себя при изучении нового материала.
Постановка вопросов как выражение инициативы сотрудничества в поиске и сборе информации;
умение обоснованно формулировать свое собственное мнение и позицию, учитывать мнение и позицию других;
умение слушать и вступать в диалог, участвовать в коллективном обсуждении;работать в группе сверстников, умение договариваться и находить общее решение в совместной деятельности при наличии разных мнений.
.
4.
Этап применения новых знаний и СД
1.Через работу в группах установить связь между способами задания функции. Приложение 1.Задания для работы в группах: обсудите задание и представьте её решение
Группа №1. Функцию, заданную формулой, задайте графическим и табличным способами.
Группа №2. Функцию, заданную графически, задайте формулой и таблицей.
Группа №3.Функцию, заданную словесным способом, задайте графически.
Группа №4. Кусочную функцию, заданную графически, задайте формулой.
2.Представьте эти способы задания функции.
3.Оцените выполнение задания группы.
Уметь применить новые знания; уметь построить график функции; уметь составить формулу по заданному графику; уметь представить материал.
Применение различных видов представления информации:формулы, графики;
умение отстаивать и обосновывать свое мнение, точку зрения, позицию; понимать мнение, точку зрения, позицию другого.
Определение вариантов решения учебной задачи, выбор оптимального;
определение своего индивидуального образовательногомаршрута, учебного плана;
определение и описание результата учебной деятельности; умение дать оценку учебной деятельности.
.
Планирование и выстраивание учебного сотрудничества с учителем и сверстниками;
умение обоснованно формулировать свое собственное мнение и позицию, учитывать мнение и позицию других;
умение слушать и вступать в диалог, участвовать в коллективном обсуждении;работать в группе сверстников, строить продуктивное взаимодействие и сотрудничество со сверстниками и взрослыми;
умение договариваться и находить общее решение в совместной деятельности при наличии разных мнений;
умение полно и точно выражать свои мысли в соответствии с задачами коммуникации.
5.
Этап взаимопроверки, взаимоконтроля, самооценки
1.Выполните задания из экзаменационных работ по карточкам. Приложение 2.
2.Проверьте результаты выполнения задания.(по образцу на доске)
3.Оцените выполнение карточки. Самопроверка.
Уметь применять полученные знания при выполнении заданий из ОГЭ
Определение разных способов решения учебных задач, умение отстаивать и обосновывать свое мнение.
Определение своего индивидуального образовательногомаршрута, учебного плана;
определение и описание результата учебной деятельности;
сличение способа действия и его результата с заданным эталоном для обнаружения отклонений и отличий от эталона.
.
6.
Рефлексивный этап1.Как мы достигли поставленных целей урока?
2.Какие возникли трудности на уроке?
3.Какие пути преодоления этих трудностей вы видите?
4.Оцените свою работу на уроке.
Рефлексия способов и условий учебных действий и их результатов.
.
Определение и описание результата учебной деятельности;
оценка усвоенного;
поиск способов выхода из ситуации неуспеха.
Карточка № 1
Функция задана формулой Задайте эту функцию графическим, табличным способами.
Карточка № 2
Дан график некоторой функции. Задайте эту функцию формулой и табличным способом.
Карточка № 3
Функция у=f(x) задана с помощью следующего правила: каждому числу х ставится в соответствие наибольшее из всех целых чисел, которые не превосходят х. Задайте эту функцию графическим способом.
Дан график некоторой функции. Задайте эту функцию аналитическим способом.
КАРТОЧКА № 1
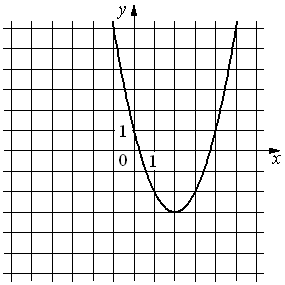
№ 1.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А)k<0, b<0
Б)k<0, b>0
В)k>0, b<0
ГРАФИКИ
1) А
АБ
В
2)

3)

4)

№ 2.Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)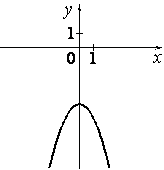
Б)

В)

ФОРМУЛЫ
1)y=− x2−4
2)y=− 2x−4
3)
4)
АБ
В
№ 1.Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)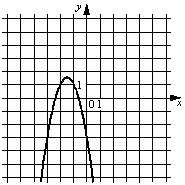
Б)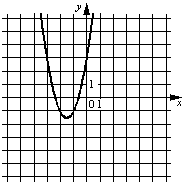
В)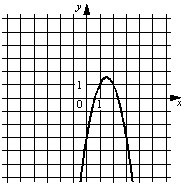
ФОРМУЛЫ
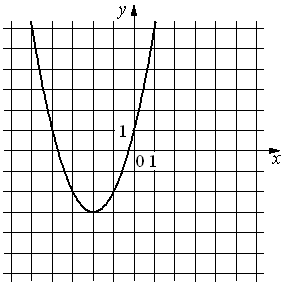
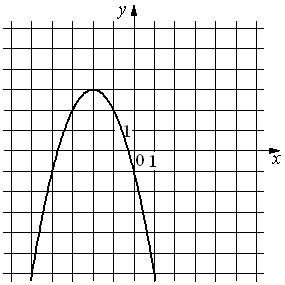
1)y=2x2+6x+3
2)y=2x2−6x+3
3)y=− 2x2−6x−3
4)y=− 2x2+6x−3
АБ
В
№ 2.Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
А)
Б)
В)
ФОРМУЛЫ
1)y=x2+2
2)y=x
3)
4)
АБ
В
КАРТОЧКА № 3
№ 1.На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)
Б)

В)

КОЭФФИЦИЕНТЫ
1)k<0, b<0
2)k<0, b>0
3)k>0, b>0
4)k>0, b<0
АБ
В
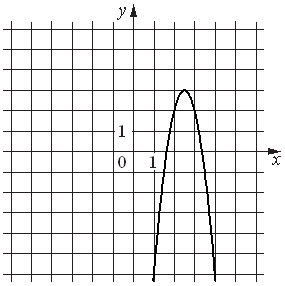
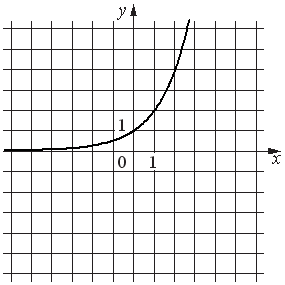
№ 2.Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А)
Б)y = − 4x2+20x−22
В)
ГРАФИКИ
1)
2)
3)
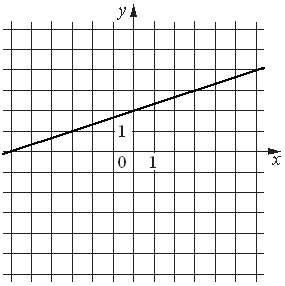
4)
А
Б
В
КАРТОЧКА № 4
№ 1.Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
- А)

Б)

В)

ФОРМУЛЫ
1)y=x2+2
2)
3)
4)
АБ
В
№ 2.Установите соответствие между функциями и их графиками.
ФУНКЦИИ
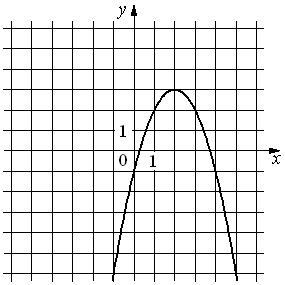
А)y=x2+4x+1
Б)y=x2−4x+1
В)y=− x2+4x−1
ГРАФИКИ
1)
2)
3)
4)
А
Б
В
Приложение №3
ОЦЕНОЧНЫЙ ЛИСТ
Фамилия, имя кадетаЭтап овладения новыми знаниями
Этап применения новых знаний
Этап взаимоконтроля
Итог
Приложение №4
Знаковые символы для постановки целей урока
Узнать!
??
?
?
Установить связь!
Применить!
ОГЭСпособы задания функции — Студопедия
Существует несколько способов задания функции.
а) Аналитический способ,если функция задана формулой вида 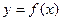 . Этот способ наиболее часто встречается на практике. Так, функция
. Этот способ наиболее часто встречается на практике. Так, функция  задана аналитически.
задана аналитически.
Не следует смешивать функцию с ее аналитическим выражением. Например, одна функция


имеет два аналитических выражения:  (при
(при 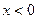 ) и
) и  (при
(при  ).
).
б) Табличный способ, если функция задана таблицей, содержащей значения аргумента х и соответствующие значения функции  , например таблица логарифмов.
, например таблица логарифмов.
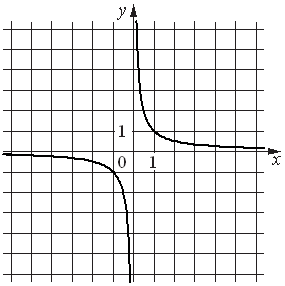
в) Графический способ, если функция изображена в виде графика – множества точек (х,у) плоскости, абсциссы которых есть значения аргумента х, а ординаты которых – соответствующие им значения функции у  f(x).
f(x).
г) Словесный способ, если функция описана правилом ее составления, например, функция Дирихле:  , если х – рационально,
, если х – рационально,  , если – х иррационально.
, если – х иррационально.
д) Функция может быть задана программой, вычисляющей ее значения с помощью компьютера.
Основные свойства функций. К ним относятся четность и нечетность, монотонность, ограниченность, периодичность.
1. Четность и нечетность. Функция 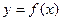 называется четной, если для любых значений х из области определения
называется четной, если для любых значений х из области определения  , и нечетной, если
, и нечетной, если  . В противном случае функция
. В противном случае функция 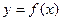 называется функцией общего вида.
называется функцией общего вида.
Например, функция  является четной, так как
является четной, так как  и
и  , а функция
, а функция  — нечетной, так как
— нечетной, так как  и
и  . В то же время, например, функция
. В то же время, например, функция  является функцией общего вида, так как
является функцией общего вида, так как  и
и  ,
,  .
.
График четной функции симметричен относительно оси ординат (см., например, график функции  на рис. 4.12), а график нечетной функции симметричен относительно начала координат (см., например, график функции
на рис. 4.12), а график нечетной функции симметричен относительно начала координат (см., например, график функции  на рис. 4.13).
на рис. 4.13).
 2. Монотонность. Функция
2. Монотонность. Функция 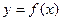 называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть  и
и  . Тогда функция возрастает на промежутке Х, если
. Тогда функция возрастает на промежутке Х, если  , и убывает, если
, и убывает, если 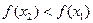 (рис. 4.8).
(рис. 4.8).
Функции, возрастающие и убывающие, называются монотонными функциями. Так, например функция  (см. рис. 4.12) при
(см. рис. 4.12) при 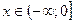 убывает и при
убывает и при  возрастает.
возрастает.
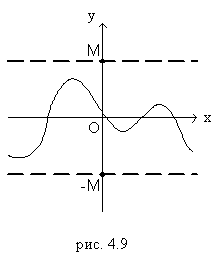
3. Ограниченность.Функция  называется ограниченнойна промежутке Х, если существует такое положительное число M>0, что
называется ограниченнойна промежутке Х, если существует такое положительное число M>0, что  для любого
для любого 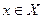 . В противном случае функция называется неограниченной. Например, функция
. В противном случае функция называется неограниченной. Например, функция  ограничена на всей числовой оси, ибо
ограничена на всей числовой оси, ибо  для любого x
для любого x 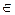 R. (рис. 4.9).
R. (рис. 4.9).
4. Периодичность. Функция 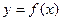 называется периодической с периодом
называется периодической с периодом  , если для любых х из области определения функций
, если для любых х из области определения функций  . Например, функция
. Например, функция  имеет период
имеет период  , так как для любых значений х
, так как для любых значений х  .
.
График периодической функции 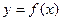 может быть получен сдвигом кривой
может быть получен сдвигом кривой 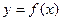 (
(  ) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).
) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).

Обратная функция.Пусть  есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому
есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому 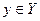 единственноезначение
единственноезначение 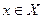 , при котором
, при котором  . Тогда полученная функция
. Тогда полученная функция  , определенная на множестве Y с областью значений Х, называется обратной.
, определенная на множестве Y с областью значений Х, называется обратной.
Так как традиционно независимую переменную обозначают через х, а функцию – через у, то функция, обратная к функции 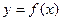 , примет вид
, примет вид  . Обратную функцию
. Обратную функцию  обозначают также в виде
обозначают также в виде  (аналогично с обозначением обратной величины). Например, для функции y
(аналогично с обозначением обратной величины). Например, для функции y  ax обратной будет функция x
ax обратной будет функция x  logay, или (в обычных обозначениях зависимой и независимой переменных)
logay, или (в обычных обозначениях зависимой и независимой переменных)  .
.
Можно доказать, что для любой строго монотонной функции  существует обратная функция.
существует обратная функция.
 Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций 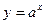 и
и  при
при  ).
).
Сложная функция. Пусть функция  есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией
есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией  от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция
от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция  называется сложной функцией (функцией от функции). Например,
называется сложной функцией (функцией от функции). Например, 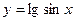 — сложная функция, так как ее можно представить в виде
— сложная функция, так как ее можно представить в виде  , где
, где 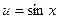 .
.
4.3. Элементарные функции. Классификация функций. Преобразования графиков.
Функция называется явной, если она задана формулой 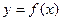 , в которой правая часть не содержит зависимой переменной. Например,
, в которой правая часть не содержит зависимой переменной. Например,  .
.
Функция у называется неявной, если она задана уравнением 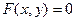 , неразрешенным относительно зависимой переменной. Например,
, неразрешенным относительно зависимой переменной. Например,  . Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например,
. Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например,  — функция задана неявно. Приведем к явному виду:
— функция задана неявно. Приведем к явному виду: 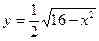 .
.
Графиком уравнения 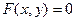 называется множество точек плоскости хОу, координаты которых удовлетворяют этому уравнению.
называется множество точек плоскости хОу, координаты которых удовлетворяют этому уравнению.
Урок игра-путешествие «Движение к знаниям» на Тему «Функция. Способы задания функции формулой и таблице». 5 класс
Нет силы более могучей, чем знание: человек, вооруженный знаниями, непобедим.
М. Горький
Урок игра-путешествие «Движение к знаниям».
Тема: Функция. Способы задания функции формулой и таблицей.
Цель урока: обобщение и контроль знаний в игровой форме.
Задачи:
Проверка и закрепление практических навыков и умений при записи и чтении функциональной зависимости, заданной табличным способом и формулой.
Активизация работы учащихся, развитие самостоятельности и умения учиться.
Воспитывать волю и настойчивость для достижения результатов учебного труда.
Ход урока.
Организационный момент.
Придумано кем-то
Просто и мудро
При встречи здороваться:
— Доброе утро!
Сегодня у нас с вами необычный урок, а урок путешествие «Движение к знаниям». Путешествовать пешком очень долго, и поэтому мы с вами отправимся в путь на автомобилях. Но никто не разрешит вам сесть за руль, пока вы не получите права. Чтобы их получить, вам необходимо сдать экзамен.
Устная работа.
Давайте, ребята, учиться считать:
Делить, умножать, прибавлять, вычитать.
Запомните все, что без устного счета
Не сдвинется с места любая работа.
Беритесь ребята, скорей за работу!
Учитесь считать, чтоб не сбиться со счету!
А). Вычислите устно цепочку действий: /работа с мультимедийной доской/
1) 26-40 2) -7-8 3) -5*3 4) 8-12
: (-7) *(-1/5) *1/15 *3/4
— 1/3 -2,5 +3/4 +2,5
* 3 * 2 *(-4) *(-6)

 -1,8 -7/8 -2/7 *1/3
-1,8 -7/8 -2/7 *1/3


? ? ? ?
Перед вами весит светофор, который задает вопросы (на красных, желтых, зеленых билетах, в зависимости от уровня знаний).
Красные:
Сформулируйте определение функциональной зависимости.
Какую переменную называют аргументом?
Что называют шагом таблицы?
Желтые:
Что такое область определения функции?
Как задаётся функция таблицей?
Что такое область значения функций?
Зеленые:
Как находят при табличном задании функции для данного значения аргумента соответствующее значение функции?
Как найти значение функции?
Как найти значение аргумента?
Б). Выберите области определения для каждой функции, заданной формулой:
/работа с мультимедийной доской или распечатать на столы карточки/.
Функция
Правильный ответ
Варианты ответов:
5
f(x)=———
х — 6
а) все де6йствительные числа, кроме 0;
в) все де6йствительные числа, кроме -1 и 1;
с) все де6йствительные числа, кроме 6;
d) множество всех действительных чисел.
9
f(x)=———
х
6
f(x)=———
х2 — 1
8 + х
f(x)=————
3
Письменная работа.
Ну вот, ребята, права мы с вами получили, теперь можно отправляться в путь. Путешествовать мы будем по карте с помощью маршрутных листов. На листах три варианта дифференцированных заданий. Задания выполняются в рабочих тетрадях, а результат записывается в лист ответов. Можно начинать работу с любого задания. Помогать мне будут консультанты из группы «Ауди» /предст. консульт./.


За каждый правильный ответ учащиеся получают по жетону, а затем по количеству набранных жетонов сами выставляют себе оценку и им присваивается одна из категорий водителей.
Категории водителей — путешественников.
1 класс
max количество баллов — 9
Категория С, Д, Е
Водитель, которому разрешены перевозки людей – АС.
2 класс
max количество баллов – 7
Категория С, Д
Любитель.
3 класс
max количество баллов — 5
Категория С
Начинающий, но подающий надежду.
Подведение итогов: выяснить, какую категорию присвоили ребята; оценить класс по данной теме /выст. оценки за урок/.
Домашнее задание.
§ 37, 38, задача д/п; индивидуальная работа по карточкам.
д/п Задание: решите задачу с помощью уравнения.
Великий ученый Ньютон в своём учебнике «Всеобщая арифметика», писал: «Чтобы решить вопрос, относящийся к числам или отвлеченным отношениям величин, нужно лишь перевести с родного языка на язык алгебраический». Один из таких переводов вы попробуете выполнить самостоятельно дома.
Задача:
На памятнике древнегреческому математику Диофанту начертано: «Прохожий! Под этим камнем покоится прах Диофанта, умершего в старости. Шестую часть его жизни заняло детство, двенадцатую – отрочество, седьмую – юность. Затем протекала половина его жизни, после чего он женился. Через пять лет у него родился сын, а когда сыну минуло четыре года, Диофант скончался». Сколько лет прожил Диофант?
Рефлексия.
9.Способы задания функции | spiruk
9.Способы задания функции
Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут , при этом x называют аргументом функции, y называют значением функции.
Существуют разные способы задания функций.
1. Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .
Рассмотрим первый пример — . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д.
Функция может быть задана на разных частях множества X разными функциями.
Например:
Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а справа формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.
Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
. То есть, значение функции при х = 3 равно -4/3.
При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,
Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.
2. Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом . Пример:
3. Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
4. Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Пример:
Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком.
Понравилось это:
Нравится Загрузка…
Похожее
Область задания функции Википедия
Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Содержание
- 1 Определение
- 2 Примеры
- 2.1 Числовые функции
- 2.1.1 Тождественное отображение
- 2.1.2 Гармоническая функция
- 2.1.3 Дробно-рациональные функции
- 2.2 Мера
- 2.3 Функционал
- 2.1 Числовые функции
- 3 См. также
- 4 Примечания
- 5 Литература
Определение[ | ]
Если на множестве X {\displaystyle X} задана функция, которая отображает множество X {\displaystyle X} в другое множество, то множество X {\displaystyle X} называется областью определения или областью задания функции.
Более формально, если задана функция f {\displaystyle f} , которая отображает множество X {\displaystyle X} в Y {\displaystyle Y} , то есть: f : X → Y {\displaystyle f\colon X\to Y} , то множество X {\displaystyle X} называется областью определения[1] или областью задания[2] функции f {\displaystyle f} и обозначается D ( f ) {\displaystyle D(f)} или d o m f {\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).
Иногда рассматриваются и функции, определённые на подмножестве D {\displaystyle D} некоторого множества X {\displaystyle X}
Использовать вложенные функции в формуле
Использование функции в качестве одного из аргументов в формуле, которая использует функцию, называется вложением, и мы будем называть эту функцию вложенной функцией. Например, вложив функции СРЕДНЕЕ и СУММ в аргументы функции ЕСЛИ, следующая формула суммирует набор чисел (G2: G5), только если среднее значение другого набора чисел (F2: F5) больше 50. В противном случае возвращается 0.
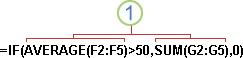
Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
В формулу можно вложить до 64 уровней функций.
Щелкните ячейку, в которую вы хотите ввести формулу.
Чтобы начать формулу с помощью функции, щелкните Вставить функцию
 в строке формул
в строке формул  .
.Excel вставляет вам знак равенства ( = ).
В поле Или выберите категорию , выберите Все .
Если вы знакомы с категориями функций, вы также можете выбрать категорию.
Если вы не уверены, какую функцию использовать, вы можете ввести вопрос, описывающий, что вы хотите сделать, в поле Искать функцию (например, «добавить числа» возвращает функцию СУММ ).
Чтобы ввести другую функцию в качестве аргумента, введите нужную функцию в поле аргумента.
Части формулы, отображаемые в диалоговом окне Аргументы функции , отражают функцию, которую вы выбрали на предыдущем шаге.
Если вы щелкнули IF , в диалоговом окне Function arguments отображаются аргументы для функции IF .Чтобы вложить другую функцию, вы можете ввести ее в поле аргумента. Например, вы можете ввести СУММ (G2: G5) в поле Value_if_true функции IF .
Введите любые дополнительные аргументы, необходимые для завершения формулы.
Вместо того, чтобы вводить ссылки на ячейки, вы также можете выбрать ячейки, на которые вы хотите ссылаться. Нажмите
 чтобы свернуть диалоговое окно, выберите ячейки, на которые вы хотите сослаться, а затем щелкните
чтобы свернуть диалоговое окно, выберите ячейки, на которые вы хотите сослаться, а затем щелкните  чтобы снова развернуть диалоговое окно.
чтобы снова развернуть диалоговое окно.Совет: Для получения дополнительных сведений о функции и ее аргументах щелкните Справка по этой функции .
После ввода аргументов формулы нажмите ОК .
Щелкните ячейку, в которую вы хотите ввести формулу.
Чтобы начать формулу с помощью функции, щелкните Вставить функцию
 в строке формул
в строке формул  .
.В диалоговом окне «Вставить функцию» в поле « Выбрать категорию» выберите Все .
Если вы знакомы с категориями функций, вы также можете выбрать категорию.
Чтобы ввести другую функцию в качестве аргумента, введите функцию в поле аргумента в построителе формул или непосредственно в ячейку.
Введите любые дополнительные аргументы, необходимые для завершения формулы.
После того, как вы введете аргументы для формулы, нажмите ENTER.
Примеры
Ниже показан пример использования вложенных функций ЕСЛИ для присвоения буквенной оценки числовому результату теста.
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Оценка | ||
|---|---|---|
45 | ||
90 | ||
78 | ||
Формула | Описание | Результат |
‘= ЕСЛИ (A2> 89, «A», IF (A2> 79, «B», IF (A2> 69, «C», ЕСЛИ (A2> 59, «D», «F»)))) | Использует вложенные условия ЕСЛИ для присвоения буквенной оценки баллу в ячейке A2. | = ЕСЛИ (A2> 89, «A», ЕСЛИ (A2> 79, «B», ЕСЛИ (A2> 69, «C», ЕСЛИ (A2> 59, «D», «F»)))) |
‘= ЕСЛИ (A3> 89, «A», IF (A3> 79, «B», IF (A3> 69, «C», IF (A3> 59, «D», «F»)))) | Использует вложенные условия ЕСЛИ для присвоения буквенной оценки баллу в ячейке A3. | = ЕСЛИ (A3> 89, «A», ЕСЛИ (A3> 79, «B», ЕСЛИ (A3> 69, «C», ЕСЛИ (A3> 59, «D», «F»)))) |
‘= ЕСЛИ (A4> 89, «A», IF (A4> 79, «B», IF (A4> 69, «C», IF (A4> 59, «D», «F»)))) | Использует вложенные условия ЕСЛИ для присвоения буквенной оценки баллу в ячейке A4. | = ЕСЛИ (A4> 89, «A», ЕСЛИ (A4> 79, «B», ЕСЛИ (A4> 69, «C», ЕСЛИ (A4> 59, «D», «F»)))) |
Нужна дополнительная помощь?
Вы всегда можете спросить эксперта в техническом сообществе Excel, получить поддержку в сообществе Answers или предложить новую функцию или улучшение в Excel User Voice.
См. Также
Видео: вложенные функции ЕСЛИ
.Справка в Интернете — Учебные пособия — Функция подгонки, определяемая пользователем
UserDef-FitFunc СводкаПомимо более 200 встроенных функций подгонки, вы также можете создавать свои собственные функции подгонки в Origin. Origin предоставляет три инструмента для настройки пользовательских функций:
Требуется минимальная версия Origin: Origin 2016 SR0 Что вы узнаетеИз этого туториала Вы узнаете, как:
ступеней Данные, которые мы собираемся подогнать, — это файл ConcentrationCurve.dat по пути Функция подгонки, которую нужно создать и использовать, показана ниже: в котором — зависимая переменная — независимая переменная и все параметры подгонки. Создание функции подгонкиВ этом разделе мы покажем, как создать определяемую пользователем функцию подгонки в конструкторе функций подгонки . Но есть альтернативный инструмент Fitting Function Organizer , который также можно использовать для создания определенных пользователем функций подгонки (откройте его, выбрав Инструменты : Органайзер функций подгонки или нажав F9 ).
Монтаж по кривой
| |||||
 в строке формул
в строке формул  .
. чтобы свернуть диалоговое окно, выберите ячейки, на которые вы хотите сослаться, а затем щелкните
чтобы свернуть диалоговое окно, выберите ячейки, на которые вы хотите сослаться, а затем щелкните  чтобы снова развернуть диалоговое окно.
чтобы снова развернуть диалоговое окно.