Функция у ах2 ее свойства и график: План-конспект урока по алгебре (9 класс) на тему: Функция у= ах2,ее график и свойства

Posted on by alexxlab

Содержание

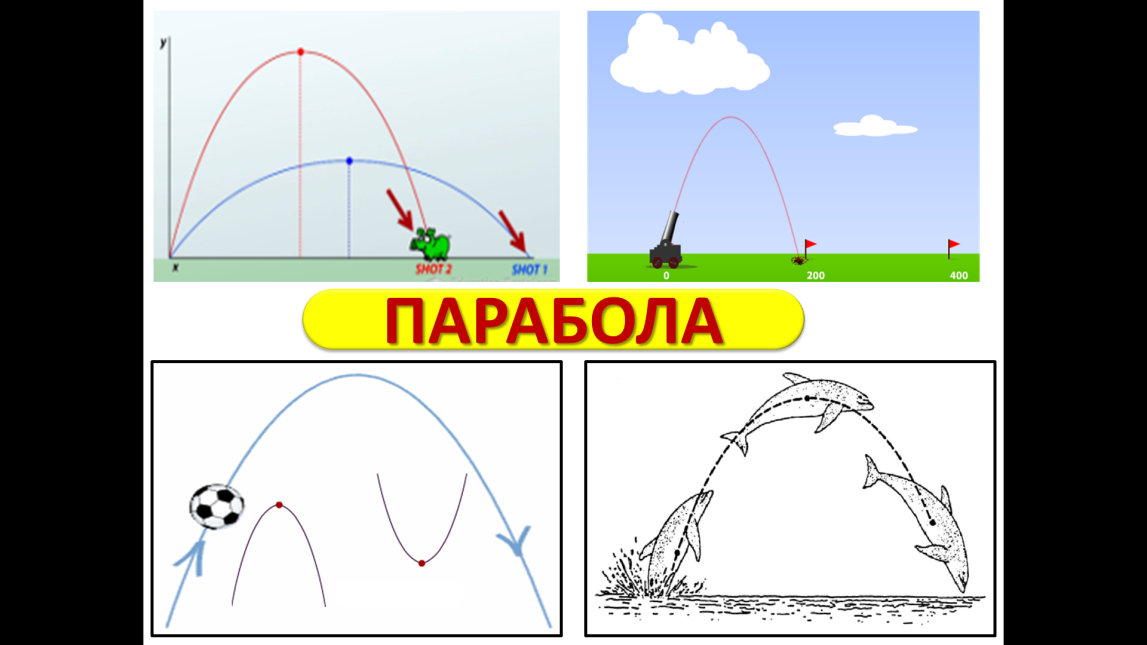
Презентация к уроку алгебры по теме»Функция у= ах², ее график и свойства». ( 7 класс)

Инфоурок › Алгебра ›Презентации›Презентация к уроку алгебры по теме»Функция у= ах², ее график и свойства». ( 7 класс) «Сотвори солнце в себе» В природе есть солнце. Оно всем светит, всех любит и...

Описание презентации по отдельным слайдам:

1 слайд «Сотвори солнце в себе» В природе есть солнце. Оно всем светит, всех любит и Описание слайда:

«Сотвори солнце в себе» В природе есть солнце. Оно всем светит, всех любит и греет. Давайте сотворим солнце в себе. Закройте глаза, представьте в своем сердце маленькую звездочку. Мысленно направляем к ней лучик, который несет любовь. Звездочка увеличилась. Направляем лучик, который несет мир. Звездочка опять увеличилась. Направляем лучик с добром, звездочка стала еще больше. Я направляю к звездочке лучики, которые несут здоровье, радость, тепло, свет, нежность, ласку. Теперь звездочка становится большой, как солнце. Оно несет тепло всем-всем.

2 слайд Удачи!!! !!! Описание слайда:

Удачи!!! !!!

3 слайд Функция у= ах², ее график и свойства. 7 класс. Описание слайда:

Функция у= ах², ее график и свойства. 7 класс.

4 слайд Цели: ввести понятие квадратичной функции; научится строить график функции у
Описание слайда:

Цели: ввести понятие квадратичной функции; научится строить график функции у=ах2 и описывать свойства данной функции по графику; установить закономерность между графиком функции у=ах2 и значением коэффициента а.

5 слайд Разминка Описание слайда:

Разминка

6 слайд 1 2 3 4 5 6 7 8
Описание слайда:

1 2 3 4 5 6 7 8

7 слайд 1 2 3 4 5 6 7 8 о с и п е р н п е д и к у л я р н н а ч а о о р д и н а т а б Описание слайда:

1 2 3 4 5 6 7 8 о с и п е р н п е д и к у л я р н н а ч а о о р д и н а т а б с с с ц к о о р и н а т ы ч е в е р т и Д е к а

8 слайд Устный счет Найдите значения функции у = 5*х+4, если х= -1 Найдите значения ф
Описание слайда:

Устный счет Найдите значения функции у = 5*х+4, если х= -1 Найдите значения функции  у = -2*х +1, если х= 3 Вычислите  (-2)², 5²

9 слайд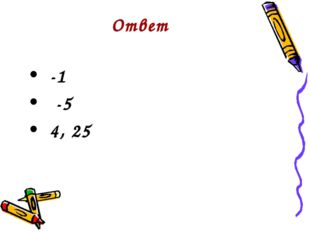 Ответ   -1    -5   4, 25 Описание слайда:

Ответ   -1    -5   4, 25

10 слайд терминологический диктант Описание слайда:

терминологический диктант

11 слайд Функция, Аргумент, Линейная, Пропорциональность, Параллельные, Пересекаются, Описание слайда:

Функция, Аргумент, Линейная, Пропорциональность, Параллельные, Пересекаются, Прямая, Коэффициент.

12 слайд Тест Описание слайда:

Тест

13 слайд
Отлично 5 Описание слайда:

Отлично 5

14 слайд Зависимость между  переменными, при которой каждому значению независимой пере Описание слайда:

Зависимость между  переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной. (Функция.) Независимая переменная. (Аргумент.) Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – значениям функции. (График.) Функция, заданная формулой y= kx + b. (Линейная.) Что служит графиком линейной функции? (Прямая.) Функция  y = x². (Квадратичная.) Название графика квадратичной функции. (Парабола.)

15 слайд Машина движется по шоссе с постоянной скоростью 70 км/ч. За время t ч машина Описание слайда:

Машина движется по шоссе с постоянной скоростью 70 км/ч. За время t ч машина проходит путь S = 70 · t км. Легко вычислить пройденный путь за любое время: Если t = 1, то Если t = 1,5, то Если t = 3, то S = 70 · 1 = 70 S = 70 · 1,5 = 105 S = 70 · 3 = 210 S = 70 · t Независимая переменная АРГУМЕНТ Зависимая переменная ФУНКЦИЯ

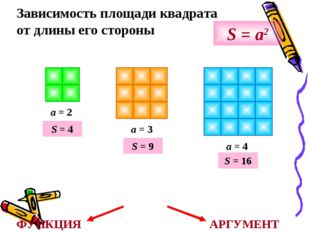
16 слайд Зависимость площади квадрата от длины его стороны a = 2 a = 3 a = 4 S = a2 S Описание слайда:

Зависимость площади квадрата от длины его стороны a = 2 a = 3 a = 4 S = a2 S = 4 S = 9 S = 16 ФУНКЦИЯ АРГУМЕНТ

17 слайд Таблица квадратов натуральных чисел: 1 4 9 16 25 36 49 64 81 100 Для каждого Описание слайда:

Таблица квадратов натуральных чисел: 1 4 9 16 25 36 49 64 81 100 Для каждого значения х можно найти единственное значение у у = х2 АРГУМЕНТ ФУНКЦИЯ х 1 2 3 4 5 у = х2

18 слайд В рассмотренных примерах каждому значению независимой переменной соответствуе Описание слайда:

В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Зависимость одной переменной от другой называют функциональной зависимостью или функцией.

19 слайд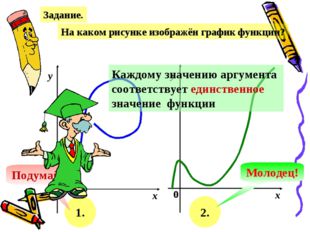 Задание. На каком рисунке изображён график функции? х у 0 х у 0 1. 2. Подумай
Описание слайда:

Задание. На каком рисунке изображён график функции? х у 0 х у 0 1. 2. Подумай! Молодец! Каждому значению аргумента соответствует единственное значение функции

20 слайд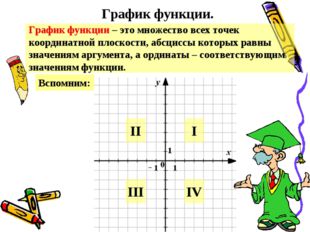 График функции. График функции – это множество всех точек координатной плоско Описание слайда:

График функции. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Вспомним: IV III II I

21 слайд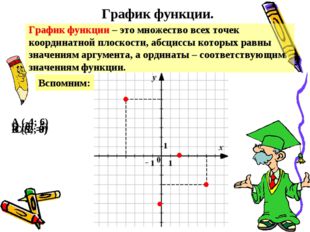 График функции. График функции – это множество всех точек координатной плоско Описание слайда:

График функции. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Вспомним: A (-4; 6) B (5; -3) C (2; 0) D (0; -5)

22 слайд Машина движется по шоссе с постоянной скоростью 70 км/ч. За время t ч машина Описание слайда:

Машина движется по шоссе с постоянной скоростью 70 км/ч. За время t ч машина проходит путь S = 70 · t км. Область значения и область определения функции. Какие значения может принимать t ? Какие значения может принимать S ? t ≥ 0 S ≥ 0 Все значения, которые принимает независимая переменная образуют область определения функции Значения зависимой переменной образуют область значений функции

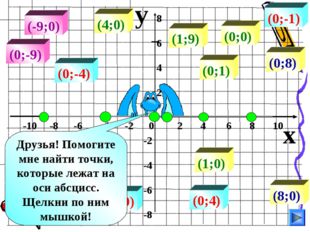23 слайд Машина движется по шоссе с постоянной скоростью 70 км/ч. За время t ч машина Описание слайда: 24 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (8;0) (-4;0) (-9;0) (4;0 Описание слайда:

y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (8;0) (-4;0) (-9;0) (4;0) (1;0) (1;9) (0;0) (0;8) (0;-1) (0;-9) (0;4) (0;-4) (0;1) Друзья! Помогите мне найти точки, которые лежат на оси абсцисс. Щелкни по ним мышкой!

25 слайд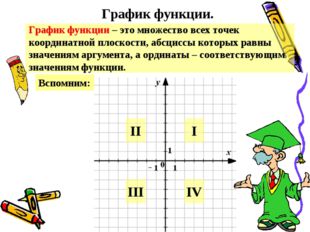 График функции. График функции – это множество всех точек координатной плоско Описание слайда:

График функции. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Вспомним: IV III II I

26 слайд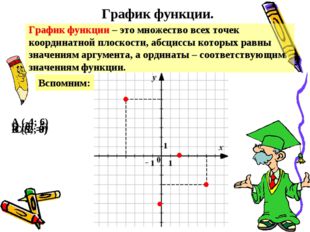 График функции. График функции – это множество всех точек координатной плоско Описание слайда:

График функции. График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Вспомним: A (-4; 6) B (5; -3) C (2; 0) D (0; -5)

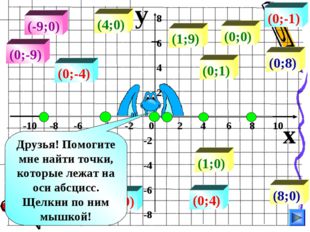27 слайд График функции. График функции – это множество всех точек координатной плоско Описание слайда: 28 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (8;0) (-4;0) (-9;0) (4;0 Описание слайда:

y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (8;0) (-4;0) (-9;0) (4;0) (1;0) (1;9) (0;0) (0;8) (0;-1) (0;-9) (0;4) (0;-4) (0;1) Друзья! Помогите мне найти точки, которые лежат на оси абсцисс. Щелкни по ним мышкой!

29 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (0;6) (0;-2) (0;-4) (0;0 Описание слайда:

y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (0;6) (0;-2) (0;-4) (0;0) (4;8) (6;0) (-23;0) (-4;0) (5;0) (-9;0) Друзья! Помогите найти точки, которые лежат на оси ординат. Щелкни по ним мышкой! (0;5) (0;-8) (-2;0)

30 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (2;8) (8;8) (5;2) (1;1) Описание слайда:

y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (2;8) (8;8) (5;2) (1;1) (-1;0) (11;1) (-1;8) (-3;-1) (2;-3) (-2;-4) (8;-4) (0;1) Друзья! Помогите найти точки, которые лежат в I четверти. Щелкни по ним мышкой! (3;4) Лишние точки удали из I четверти!

31 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (-7;6) (-10;2) (-1;4) (- Описание слайда:

y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (-7;6) (-10;2) (-1;4) (-12;4) (-1;0) (-1;1) (-1;-8) (-3;-1) (2;-3) (-2;-4) (8;-4) (0;1) Друзья! Помогите найти точки, которые лежат во II четверти. Щелкни по ним мышкой! (-3;4) Лишние точки удали из II четверти!

32 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (-7;6) (-10;2) (-1;4) (- Описание слайда: 33 слайд y x -10 -8 -6 -4 -2 0 2 4 6 8 10 8 6 4 2 -2 -4 -6 -8 (-7;6) (-10;2) (-1;4) (- Описание слайда: 34 слайд (-6 ; 0) (0 ; -6) (6 ; 0) (0 ; 6) Описание слайда:

(-6 ; 0) (0 ; -6) (6 ; 0) (0 ; 6)

35 слайд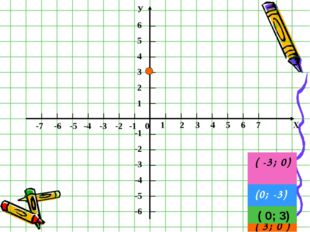 ( 0; 3) ( -3; 0) (0; -3) ( 3; 0 ) ( 0; 3) Описание слайда:

( 0; 3) ( -3; 0) (0; -3) ( 3; 0 ) ( 0; 3)

36 слайд (3;0) (0;3) (-3;0) (0;-3) Описание слайда:

(3;0) (0;3) (-3;0) (0;-3)

37 слайд Мини-исследование по таблице Описание слайда:

Мини-исследование по таблице

38 слайд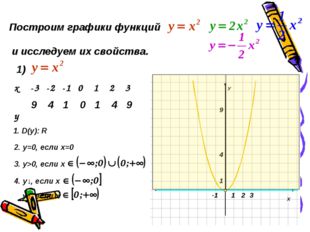 Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R Описание слайда:

Построим графики функций и исследуем их свойства. 1) 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у>0, если х 4. у↓, если х у↑, если х х -3 -2 -1 0 1 2 3 у

39 слайд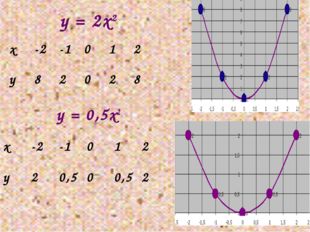 у = 2х2 у = 0,5х2 х -2 -1 0 1 2 у 8 2 0 2 8 х -2 -1 0 1 2 у 2 0,5 0 0,5 2 Описание слайда:

у = 2х2 у = 0,5х2 х -2 -1 0 1 2 у 8 2 0 2 8 х -2 -1 0 1 2 у 2 0,5 0 0,5 2

40 слайд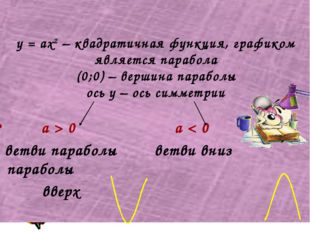 у = ах2 – квадратичная функция, графиком является парабола (0;0) – вершина па Описание слайда:

у = ах2 – квадратичная функция, графиком является парабола (0;0) – вершина параболы ось у – ось симметрии а > 0 а < 0 ветви параболы ветви вниз параболы вверх

41 слайд «Солнечный луч». Описание слайда:

«Солнечный луч».

42 слайд Работа у нас была очень напряженной, поэтому мы сейчас выполним гимнастику дл Описание слайда:

Работа у нас была очень напряженной, поэтому мы сейчас выполним гимнастику для глаз. Глубоко вдохните, зажмурьте глаза как можно сильнее. Задержите дыхание и на счет «3» быстро выдохните, широко раскрыв на выдохе глаза. (упражнение повторить 3-5 раз) Не поворачивая головы, выполняем горизонтальные движения глаз: направо-налево. Представляем, что наши глазки «катаются по оси ОХ». (упражнение повторить 3-5 раз) Не поворачивая головы, выполняем д.вижение глазными яблоками вертикально вверх-вниз. Представляем, что наши глазки «катаются по оси ОУ». (упражнение повторить 3-5 раз) Положите кончики пальцев на виски, слегка сжав их. 10 раз быстро и легко моргните. Закройте глаза и отдохните, сделав 2-3 глубоких вдоха. (упражнение повторить 3 раза)

43 слайд График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох. Описание слайда:

График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох. Если а>0, то ветви параболы направлены… Если а<0, то ветви параболы направлены…

44 слайд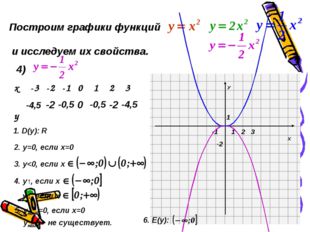 Построим графики функций и исследуем их свойства. 4) -4,5 -2 -0,5 0 -0,5 -2 - Описание слайда:

Построим графики функций и исследуем их свойства. 4) -4,5 -2 -0,5 0 -0,5 -2 -4,5 1. D(y): R 2. у=0, если х=0 3. у<0, если х 4. у↑, если х у↓, если х 5. унаиб=0, если х=0 унаим – не существует. 6. Е(y): х -3 -2 -1 0 1 2 3 у

45 слайд График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох. Описание слайда:

График функции у=ах2 симметричен графику функции у=-ах2 относительно оси Ох. Если а>0, то ветви параболы направлены… Если а<0, то ветви параболы направлены…

46 слайд У У У Установите соответствие: Описание слайда:

У У У Установите соответствие:

47 слайд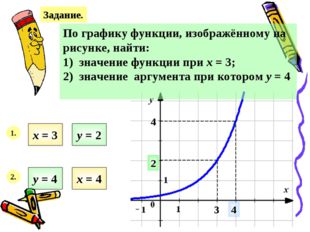 Задание. По графику функции, изображённому на рисунке, найти: 1) значение фун Описание слайда:

Задание. По графику функции, изображённому на рисунке, найти: 1) значение функции при х = 3; 2) значение аргумента при котором у = 4 1. х = 3 у = 2 3 2 2. у = 4 4 4 х = 4

48 слайд Задание. По графику функции найдите: 1) её область определения; 2) область зн Описание слайда:

Задание. По графику функции найдите: 1) её область определения; 2) область значений функции. 1. х – любое число 2. у ≥ -1

49 слайд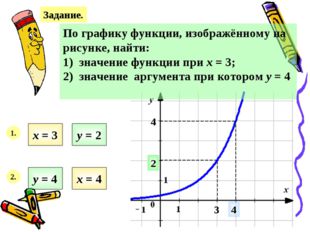 Задание. По графику функции, изображённому на рисунке, найти: 1) значение фун Описание слайда:

Задание. По графику функции, изображённому на рисунке, найти: 1) значение функции при х = 3; 2) значение аргумента при котором у = 4 1. х = 3 у = 2 3 2 2. у = 4 4 4 х = 4

50 слайд Домашнее задание Описание слайда:

Домашнее задание

51 слайд * Описание слайда:

*

52 слайд * Описание слайда: *

Курс повышения квалификации

*

Курс повышения квалификации

*

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

loading

Общая информация

Номер материала: ДA-024142

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Конспект урока «Графики функций_функция ах^2»

Раздел долгосрочного плана:

7.2А: Функция. График функции

Школа-лицей № 5

Дата:

ФИО учителя: Шайхутдинова Альфия Фауисовна

Класс: 7

Количество присутствующих: 18

отсутствующих:0

Тема урока

Функция вида у=ах2, ее график и свойства

Цели обучения, которые достигаются на данном уроке

7.5.1.10 строить график функции у=ах2 (а≠0) и знать её свойства;

Цели урока

-Будут знать определение квадратичной функции;

-будут строить график функции у=ах2 и описывать свойства данной функции по графику;

Классификация мыслительных уровней

-Знание

-Понимание

-Применение

— Анализ

Критерии оценивания

Учащийся достигнет цели урока, если:

— составляет таблицу для построения графика;

— правильно строит график;

— понимает зависимость между знаком коэффициента и графиком функции;

— определяет знак коэффициента функции по готовому графику.

Языковые цели

Предметная лексика и терминология:

  1. Парабола, вершина параболы, ветви параболы, график,

Вопросы:

  1. Какие способы задания функции вы знаете?

  2. Что будет при вращении параболы вокруг оси симметрии?

  3. Объясните, почему ось ординат является осью симметрии параболы.

Привитие ценностей

  • Независимость Казахстана и Астана; (Архитектура Астаны- Бизнес центр «Москва» и т.д.)

  • Индустриализация и экономический рост, базирующийся на инновациях (экономический рост-EXPO-2017г.)

Межпредметные связи

Предварительные знания

Функция и график функции. Линейная функция и её график. Взаимное расположение графиков линейных функций. Решение системы линейных уравнений с двумя переменными графическим способом.

ХОД УРОКА

Запланирован-ные этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

5 минут

Организационный момент.

В начале урока учитель и учащиеся приветствуют друг друга. Создание коллабаративной среды.

Позитивный настрой учащихся

І. Стадия вызова. Мотивация. Развитие критического мышления.

Задачей является актуализировать знания, пробудить познавательный интерес к вновь предложенной теме, помочь им самим определить направление в обучении.

hello_html_7e9ab1be.png

Задание: Ученики определяют лишнее фото, и определяют, что объединяет остальные картины.

Вопрос к ученикам: Какое фото тебе особенно дорого? Почему? (Астана, Моя Родина, индустриализация, EXPO-2017г)

Разбирая фотографии, учитель приводит учащихся к формированию темы урока.

hello_html_m5f1e5dde.png

Далее учитель совместно с учащимися определяет цели урока и ожидаемые результаты.

Таким образом у учащихся развивается открытость во взаимоотношениях, они осознают цели и стремятся их достичь

презентация

Середина урока

3 мин

10 минут

7 минут

1 мин

9 мин

ІІ. Стадия «Осмысление».

Задачей является содействовать активному восприятию нового материала и сопоставление имеющихся знаний с новыми.

«Мозговой штурм». Проверка пройденного материала по слайдам.11-12

hello_html_78586371.pnghello_html_m4bc75d56.png

Деление на группы.

3 группы по 6 человек. Нумерация участников такая:

2 ученик

3 ученик

4 ученик

5 ученик

6 ученик

А1

А2

А3

А4

А5

А6

В1

В2

В3

В4

В5

В6

С1

С2

С3

С4

С5

С6

(в большой группе подгруппы А-а-)

Изучение нового материала

Каждая группа открывает конверт с заданием и ресурсами.

Ученик получает лист с заданным масштабом, чтобы группы могли сравнивать графики, выводить свойства

(А)1 группа- График функции у=х2 и у= -х2

(В)2 группа- График функции у=2х2 и у=-2х2

(С)3 группа — График функции у=х2 и у=-х2

Практическая работа в группах

Учащиеся строят графики функций на постерах и отвечают на вопросы:

— Найдите области определения данных функций.

— Найдите область значений данных функций.

— Найдите значение функции при х=0.

— Найдите промежуток, когда функция возрастает.

— Найдите промежуток, когда функция убывает.

Работа продолжается в новых мозаичных группах

Мозаичная группа-2 этап: новые группы.

1.Каждый член новой группы объясняет своим новым коллегам свою часть темы, основы которой он изучил в составе предыдущей группы и отвечает на заданные вопросы.2.В заключение работы составляется резюме по предложенным вопросам

Закрепление по слайдам 14-19

ФОРМАТИВНОЕ ОЦЕНИВАНИЕ

Приготовлено 3 билета с вопросами:

1.Сравнить у=х2 и у= -х2 и ответить на вопросы

2.Сравнить у=х2 и у= 2х2 и ответить на вопросы

3. Сравнить у=х2 и у=-х2 и ответить на вопросы

(используют свои постеры)

1. и

— Есть ли различия в свойствах по сравнению с функцией?

— Чем отличается график?

Отвечая на вопросы, учащиеся самостоятельно подходят к правилу. График функции у=kx2 может быть получен из графика функции у=x2 путем растяжения его вдоль оси Оу в k раз (k-натуральное число).

2. и

— Есть ли различия в свойствах по сравнению с функцией?

— Чем отличается график?

Отвечая на вопросы, учащиеся самостоятельно подходят к правилу. График функции у= x2 может быть получен из графика функции у=x2 путем сжатия его вдоль оси Оу в k раз (k-натуральное число).

3. и

Учитель задает вопросы:

— Есть ли различия в свойствах по сравнению с функцией?

— Чем отличается график?

Отвечая на вопросы, учащиеся самостоятельно подходят к правилу.

ОЦЕНИВАНИЕ (каждый участник отмечает одного ученика, потом подсчет голосов)

РАБОТА С УЧЕБНИКОМ у доски

Решение упражнений №25.1(4,5,6)-устно, № 25.6- письменно

Самостоятельная работа. № 25,3 (3)

Самооценивание по дискрипторам

-Составил таблицу;

-Построил графики

Презентация.

11-12

Приложение-1

«Мозаичная группа»

Приложения- 2,3,4

Учебник

Проверку осуществляют сами учащиеся по готовым ответам.

на слайде

Конец урока

5 мин

Рефлексия

В конце урока учащиеся проводят рефлексию.

«Билет для выхода из класса» (Раздайте ученикам бумагу с вопросами об их учебе, они должны ответить на вопросы и сдать бумагу учителю до времени, когда разрешается выйти из класса.)

Заполняют листок обратной связи

Ф.И.___________________

Я научился…..

Затруднялся…….

У меня есть вопрос..

Я разобрался…..

Подведение итогов, домашнее задание

№25.1(1-3)-устно № 25.3(2).

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?

Здоровье и соблюдение техники безопасности

Дифференциация по уровням на уроке присутствовала во время закрепления и самостоятельной работы.

Использование открытых вопросов.

Дифференциация времени.

Дифференциация группы. 3 учащихся выбирает учитель (А1,В1,С1). Остальным ученикам в случайном порядке раздаются карточки А2,А3,…; В2,В3,…; С2,С3,…

Дифференциация заданий.

№ 25.1 (4,5,6)-устно (задание легкое, экономия времени, Устные вычисления способствуют развитию мышления учащихся, их сообразительности, ),

№ 25.6- письменно у доски.

№ 25.3 (3) – самостоятельная работа. (данное задание позволяет определить достиг ли ученик цели урока )

№ 25.9 (1,2) – задание из уровня «С», для детей с повышенной мотивацией

Дифференциация метода преподавания.

Мозаичная группа. 3 группы рассматривают 3 случая преобразования графиков. Задействован каждый ученик. Взаимообучение на уроке учащимися позволяет им усваивать до 90% информации.

Дифференциация способов оценивания.

«Мозговой штурм» — Верные ответы высвечиваются на экране (для экономии времени)

Групповая работа — Взаимооценивание. На стикерах отмечают номер лучшего спикера. (Конфедициальность и объективность оценивания)

Самостоятельная работа — Самооценивание. Сравнивают свои ответы с верными ответами представленными учителем. Каждый ученик оценивает достиг ли он цели данного урока.

После каждого этапа урока происходит оценивание работы (самооценивание, взаимооценивание или оценивание учителем).

«Мозговой штурм» — оценивание учителем

Групповая работа — Взаимооценивание.

Самостоятельная работа —

Самооценивание (по дискрипторам)

Лист обратной связи

Различные виды деятельности

Смена формы деятельности: Умственная-физическая-умственная.

«График и свойства функции y=ax^2» (7 класс)

ТЕМА: «График и свойства функции y = ax2»

Цель урока:

  1. Формирование знаний обучающихся о графике и свойствах функции у = ах2.

  2. Формирование представления о влиянии коэффициента а на свойство и вид графика у = ах2.

  3. Формирование навыков построения графиков данной функции.

  4. Воспитание сознательного отношения к учебному труду. Образовательные Задачи:

    1. Актуализировать знания по теме: «Функция у = х2«

    2. Изучить свойство функции у = ах2, при а > 0, а < 0.

    3. Рассмотреть влияние коэффициента а на свойства и вид графика у = ах2. Развивающие задачи:

1. Развивать логическое мышление через построение графиков функций. Воспитательные задачи:

1. Отрабатывать навыки аккуратности и точности построения графиков. Формы работы на уроке:

Методы обучения:

Ход урока:

      1. Организационный момент.

      2. Постановка цели урока:

Мы продолжаем изучение темы «Квадратичная функция». И сегодня мы должны с вами повторить все, что мы знаем о функции у = х2 а затем рассмотрим новую функцию у = ах2 ее свойства и график.

      1. Повторение:

(Актуализация знаний)

Среди изображенных графиков функций найдите график функции у = х2

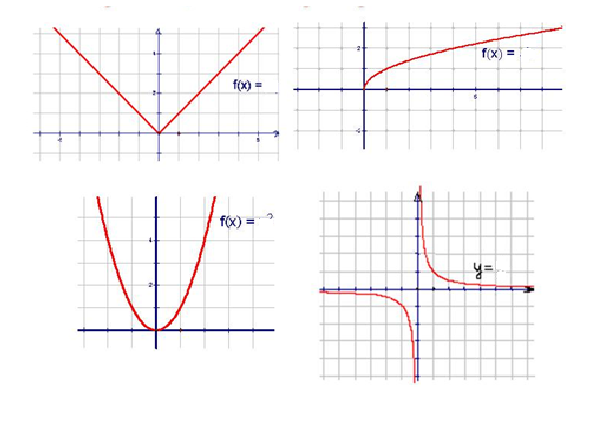
hello_html_m709dcec5.png

  • Как называется график данной функции?

  • Как называется точка пересечения графика функции с осью ординат?

  • Назовите основные свойства функции у = х2.

(Приглашается 1 ученик к доске и работает с графиком функции у =х2).

Свойства функции у = х2:

  1. При х=0, у=0

При значении х=0, значение функции равно нулю.

  1. При х > 0; х< 0; у > 0.

При любом значении х, кроме нуля значение функции положительно.

  1. График функции у = х2 симметричен относительно оси ординат. Ось ординат является осью симметрии параболы.

  2. Функция у = х2 возрастает на промежутке х ≥ 0 и убывает на промежутке х ≤ 0.

Возрастает: большему значению х соответствует большее значение у.

Убывает: большему значению х соответствует меньшее значение у.

  • Какие новые математические понятия вы узнали при изучении темы у = х2?

  • парабола;

  • ветвь параболы;

  • вершина параболы.

IV. Объяснение нового материала.

Итак, мы повторили свойства функции у = ах2.

  • Открываем тетради, записываем число, тему урока «Свойства и график функции у = ах2. «

  1. Рассмотрим график и свойства функции у = ах2, когда а > 0. Для этого в одной системе координат построим графики функций:

у = х2

у = 2х2

у = 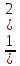hello_html_m7a13863.gifх2

Для экономии времени у вас на рабочих листах №1 и здесь на координатной плоскости построен уже график функции у = х2. Обучающиеся строят на рабочих листах графики функций у = 2х2 и у = 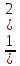hello_html_m7a13863.gifх2.

Анализ построенных графиков позволяет сделать вывод:

  1. Графиками всех трех функций является парабола.

  2. Ветви парабол направлены вверх.

  3. Вершины парабол находятся в начале координат.

  4. Графики функций симметричны оси ОУ.

Выясним, как коэффициент а влияет на вид параболы в зависимости от коэффициента а.

Сравним две функции:

у = 2х2

у = х2

При одних и тех же значениях х, значение функции у = 2х2 увеличивается в 2 раза, т.е. ординаты этой функции становятся больше в 2 раза. И наша парабола растягивается от оси ОХ вдоль оси ОУ.

А теперь сравним функции:

у = х2

у = 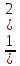hello_html_m7a13863.gifх2

При одних и тех же значениях х, значение функции у = 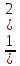hello_html_m7a13863.gifх2 уменьшается в

2 раза, а значит ординаты этой функции становятся меньше в 2 раза. И наша парабола сжимается к оси ОХ вдоль оси ОУ и становится шире. Итак, если у функции у = ах2 коэффициент а > 1 то происходит растяжение парабол от оси ОХ вдоль оси ОУ.

Если коэффициент а < 1, то происходит сжатие парабол к оси ОХ вдоль оси ОУ. А теперь по графикам данных функций запишем свойства функции у = ах2, при а > 0.

            1. х = 0; у = 0

При значении х = 0, значение функции равно 0.

            1. При х>0 и х<0, у>0. При любом значении х, кроме х = 0, функция принимает только положительные значения.

            2. График функции симметричен относительно оси ординат. Ось ординат является осью симметрии.

            3. Функция возрастает на промежутке х ≥ 0 убывает на промежутке х ≤ 0.

Рассмотрим функцию у = ах, когда а < 0.

В одной системе координат построим графики функций:

у = -х2

у = -2х2

у = 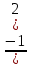hello_html_2f051a38.gifх2

После построения графиков делаем вывод: если а < 0, то

              1. Графиками этих функций является парабола.

              2. Ветви параболы направлены вниз.

              3. Вершина параболы находится в начале координат.

Рассмотрим свойства функции у = ах2 при а < 0

                1. При значении х = 0, значение функции равно 0.

                2. При любых значениях х, кроме х = 0, значение функции отрицательно. При х > 0 и х < 0, у < 0.

                3. Графики функций симметричны оси ОУ. ОУ — ось симметрии параболы.

                4. На промежутке х ≤ 0 функция возрастает, на промежутке х ≥ 0 функция убывает.

Выводы: мы рассматривали с вами функцию у = ах2, при коэффициенте а > 0 и а < 0, еще раз проговорим свойства данной функции. Если коэффициент а > 0, то

                  1. Графиком данной функции является парабола, ветви которой направлены вверх.

                  2. Вершина параболы находится в точке начала координат.

                  3. График функции симметричен оси ординат, которая является осью симметрии параболы.

                  4. Значение функции при любом значении х, кроме х = 0, положительно.

                  5. Функция возрастает на промежутке х ≥ 0 и убывает на промежутке х ≤ 0. Если коэффициент а < 0, то

                    1. 1.Графиком функции является парабола ветви которой направлены вниз.

                    2. 2.Вершина параболы находится в точке начала координат.

                    3. 3.График функции симметричен относительно оси ОУ. Ось ОУ является осью симметрии параболы.

Закрепление:

1. Определите направление ветвей параболы данных функций:

1.у = — 0,1х2 у = 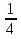hello_html_685d8d49.gifх2

у = — 2,2 х2 у = 5,7 х2

2.На каком промежутке функция у = -5х2 возрастает? (х ≤ 0)

3.На каком промежутке функция у = 7х2 убывает? (х ≤ 0)

4.Что произойдет с графиком функции у = х2, если коэффициент а увеличим в 5 раз (произойдет растяжение параболы от оси ОХ вдоль оси ОУ в 5 раз). 5.Что произойдет с графиком функции у = х2, если коэффициент а уменьшить в 5 раз? (произойдет сжатие параболы к оси ОХ вдоль оси ОУ в 5 раз).

Итоги урока.

Сегодня мы рассмотрели с вами функцию у = ах2, ее свойства и график. Выяснили как коэффициент а влияет на свойства и график функции у = ах2.

После изучения новой темы, МЫ ДОЛЖНЫ ЗНАТЬ:

  • Свойства графика функции у = ах2, при а > 0 и а < 0.

  • Направление ветвей параболы в зависимости от коэффициента а.

  • Название графика функции.

МЫ ДОЛЖНЫ УМЕТЬ:

  • По графику функции определить знак коэффициента а.

  • Определять направление ветвей параболы.

  • Строить графики функций у = ах2.

  • Определить по графику промежутки возрастания и убывания функций.

Обобщающий урок по теме «Функция у= ах2+bx+c,её свойства и график»

Обобщающий урок по теме

«Функция у= ах2+bx+c,её свойства и график»

Семенова Секинат Магомедовна,

учитель математики МКОУ « СОШ № 2 г.Усть-Джегуты»

Тип урока : Урок обобщения и систематизации знаний.

Цели урока :

Образовательные :

-обобщить и закрепить ЗУН учащихся по данной теме;

-обобщение единичных знаний в систему

Развивающие :

— научить применять теоретические знания на практике;

— развитие умений обобщать факты и делать выводы;

— развитие инициативы, уверенности в своих силах;

Воспитательные :

— привитие интереса к изучаемому предмету;

— воспитание осмысленной учебной деятельности.

Оборудование : компьютер, проектор, карточки с заданиями

Ход урока:

I.Организационный момент

II.Фронтальный опрос

-Что называется квадратным трехчленом? квадратичной функцией?

-Что является графиком квадратичной функции?

-Как получается график функции у= ах2+bx+с из параболы у= ах2?

-Что является осью параболы у= ах2+bx+с?

-По какой формуле вычисляется абсцисса х0 вершины параболы? Как вычисляется ордината вершины параболы ?

-Как определить направление ветвей параболы?

-Расскажите алгоритм построения параболы у= ах2+bx+с

III.Устная работа ( проецируется на экране)

— Из материалов открытого банка заданий ФИПИ по подготовке к ОГЭ

Задание № 1.

На рисунке изображены графики функций вида y=ax2​+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.

ГРАФИКИ

А) Б) В)

http://opengia.ru/resources/0264AFF385C6AD6B40F704459E23DB39-0264AFF385C6AD6B40F704459E23DB39-xs3qvrsrc5DA52D92B072A04A4C155040C7B9E4CF-1-1398232674/repr-0.png http://opengia.ru/resources/0264AFF385C6AD6B40F704459E23DB39-0264AFF385C6AD6B40F704459E23DB39-xs3qvrsrcD96A5EBC734AB9194825E22F8CD41B14-1-1398232676/repr-0.png http://opengia.ru/resources/0264AFF385C6AD6B40F704459E23DB39-0264AFF385C6AD6B40F704459E23DB39-xs3qvrsrc4B60E0EE437F960742C4A3600C83FDE6-1-1398232678/repr-0.png

КОЭФФИЦИЕНТЫ

1) a<0,  c>0 2) a>0,  c<0 3) a>0,  c>0

Задание № 2.

На рисунке изображён график квадратичной функции y=f(x).

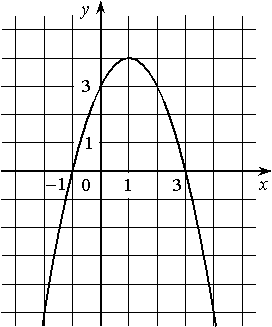
http://opengia.ru/resources/0948F5A9D3AF9AC149FEE0C5F53F2238-0948F5A9D3AF9AC149FEE0C5F53F2238-0948F5A9D3AF9AC149FEE0C5F53F2238-1-1334148029/repr-0.png

Какие из следующих утверждений о данной функции неверны? Запишите их номера.

1) f(x)<0 при x<1

2) Наибольшее значение функции равно 3

3) f(0)>f(4)

Задание № 3

На рисунке изображён график функции y=ax2​+bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.

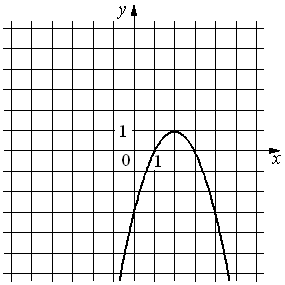
http://opengia.ru/resources/09C87CD07717A54F40F94CD13B014139-09C87CD07717A54F40F94CD13B014139-09C87CD07717A54F40F94CD13B014139-1-1398155446/repr-0.png

УТВЕРЖДЕНИЯ

А) Функция возрастает на промежутке

Б) Функция убывает на промежутке

ПРОМЕЖУТКИ

1)[0; 3]

2)[− 1; 1]

3)[2; 4]

4)[1; 4]

Задание № 4

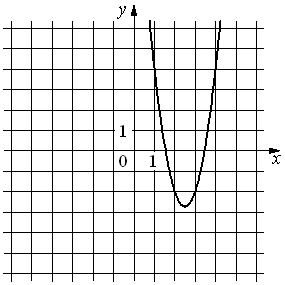
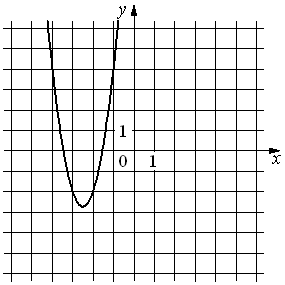
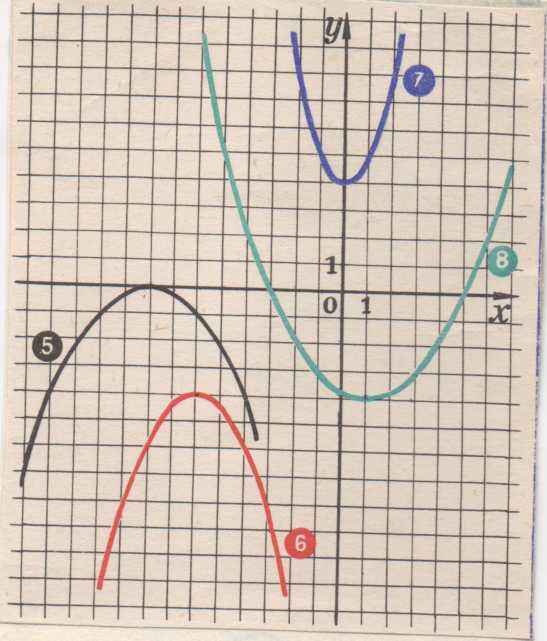
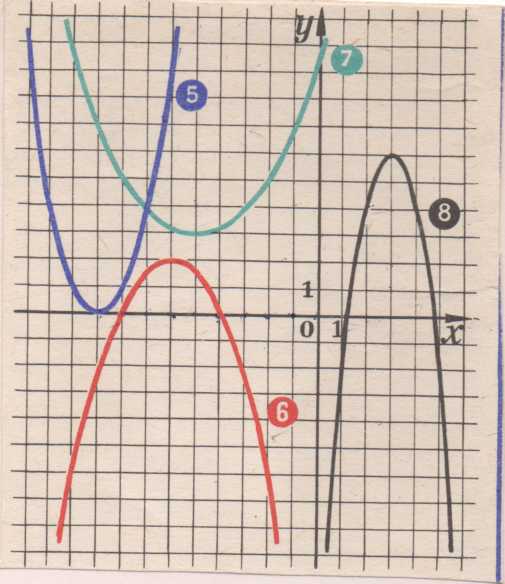
Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) y =3x2​+15x+16

Б) y =3x2​−15x+16

В) y = − 3x2​+15x−16

ГРАФИКИ

2) 3)

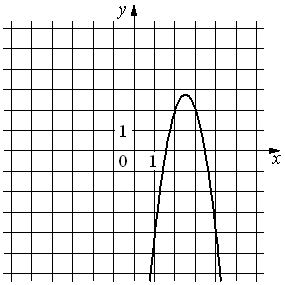
http://opengia.ru/resources/1117D10BDF7D90494B298B9E769833B1-1117D10BDF7D90494B298B9E769833B1-xs3qvrsrcEC80D2BCBDE48EBA4FE2617481BCF675-1-1398683578/repr-0.png http://opengia.ru/resources/1117D10BDF7D90494B298B9E769833B1-1117D10BDF7D90494B298B9E769833B1-xs3qvrsrc5CEB8CEC3939A8274AE036B7982E0CF9-1-1398683582/repr-0.png http://opengia.ru/resources/1117D10BDF7D90494B298B9E769833B1-1117D10BDF7D90494B298B9E769833B1-xs3qvrsrc6AD188A65404B9B441B356BABD9C5A81-1-1398683585/repr-0.png

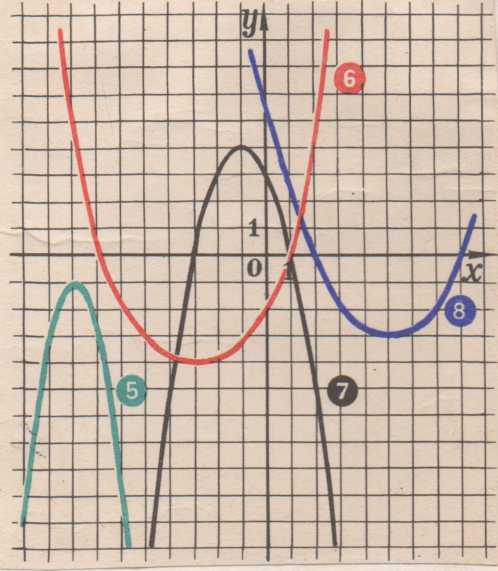
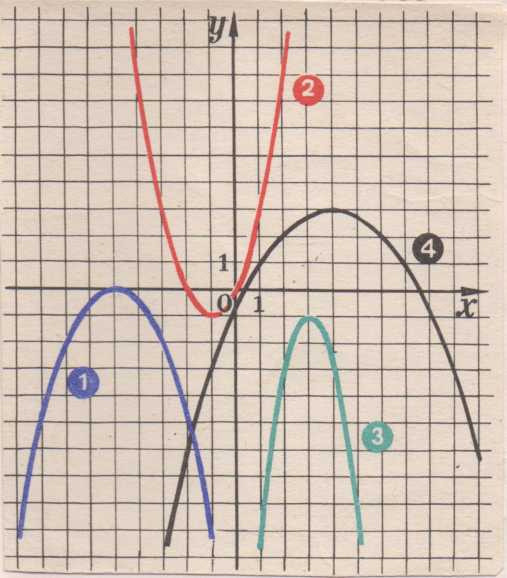
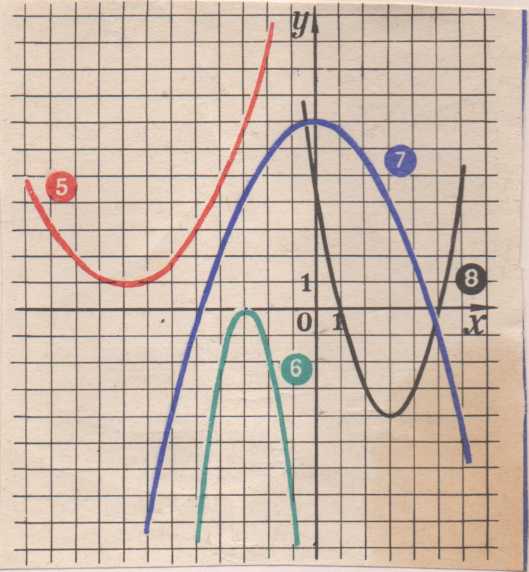
IV.Самостоятельная работа по карточкам

Задание : написать уравнение каждого графика

(Приложение 1)

V.Домашнее задание : повторить теорию п.22,№№22.17;22.21

Литература :

  1. Алгебра. 8 класс. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 12-е изд., стер. — М.: Мнемозина, 2010.

  2. Алгебра. 8 класс. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — 12-е изд., испр. и доп. — М.: Мнемозина, 2010.

  3. Материалы открытого банка заданий ФИПИ для подготовки к ОГЭ

Приложение 1( можно по вариантам)

C:\Users\Секинат\Documents\media\image6.jpegC:\Users\Секинат\Documents\media\image5.jpeg

C:\Users\Секинат\Documents\media\image8.jpegC:\Users\Секинат\Documents\media\image7.jpeg

C:\Users\Секинат\Documents\media\image1.jpegC:\Users\Секинат\Documents\media\image3.jpeg

Разработка урока по теме «Функция у=ах²+вх+с, ее свойства и график» (8 класс)

МОБУ ООШ с.СРЕДНИЕ КАРАМАЛЫ

РАЗРАБОТКА ОТКРЫТОГО

УРОКА ПО АЛГЕБРЕ

8 класса

«Функция у=ах²+вх+с, ее свойства и график»

ПРОВЕЛА: Муталова З.Х.

2017 г.

Тема урока: Функция у=ах²+вх+с, ее свойства и график

Цели урока:

Образовательные:

  • способствовать развитию у учащихся навыков чтения и построения графиков функций;

  • формировать навык простейших преобразований графиков функций;

  • формировать умения и навыки исследовать графики функций;

  • формировать умения анализировать, выделять главное, сравнивать, обобщать.

Развивающие:

  • развивать творческую сторону мыслительной деятельности учащихся,

  • развивать умение обобщать, классифицировать, проводить анализ и делать выводы;

  • развивать коммуникативную компетенцию учащихся;

  • создать условия для проявления познавательной активности учащихся;

  • показать взаимосвязь математики с окружающей действительностью

Воспитательные задачи урока:

  • воспитывать культуру умственного труда;

  • воспитывать культуру коллективной работы;

  • воспитывать информационную культуру;

  • воспитывать графическую и функциональную культуру учащихся.

Тип урока: Комбинированный.

Формы роботы: фронтальная, работа в парах, самостоятельная работа, устный счет

с использование взаимоконтроля, самоконтроль, использование

опережающих заданий.
Ход урока

I. Организационный этап

Учащимся сообщается тема урока, цели урока, формы работы на уроке.

Сегодня вам самим предстоит подвести итог изучению и получению новых знаний. Прежде, чем мы это сделаем, давайте проверим себя, готовы ли мы совершить его, всё ли было усвоено на уроках, имеются ли слабые места. Для этого проверим, как мы справились с домашним заданием..

II Проверка домашнего задания

III. Актуализация знаний

Повторение теоретического материала (фронтальная работа с классом).

Все вопросы и задания высвечиваются на слайдах.

1.Какая функция называется квадратичной?

(функция вида у = ах² + вх + с, где а, в, с — коэффициенты, х – переменная)

2. Из приведенных примеров укажите те функции, которые являются квадратичными. (слайд 1)

Примеры:

у=5х+1;

у=3х2-1;

у=-2х2+х+3;

у=x3+7x-1;

у=4х2;

у=-3х2+2х.

3. Что является графиком квадратичной функции? (парабола) (слайд 2)

4. От чего зависит направление ветвей параболы? от коэффициента а, если а>0, то ветви параболы направлены вверх, если а<0, ветви параболы — вниз)

5. Определите знак коэффициента a у парабол, изображенных на рисунке (слайд 3)

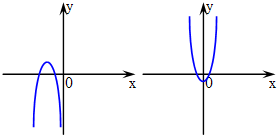
hello_html_m29166b4.png

6. Как найти координаты вершины параболы? (слайд 4)

( два способа нахождения координат вершины параболы:

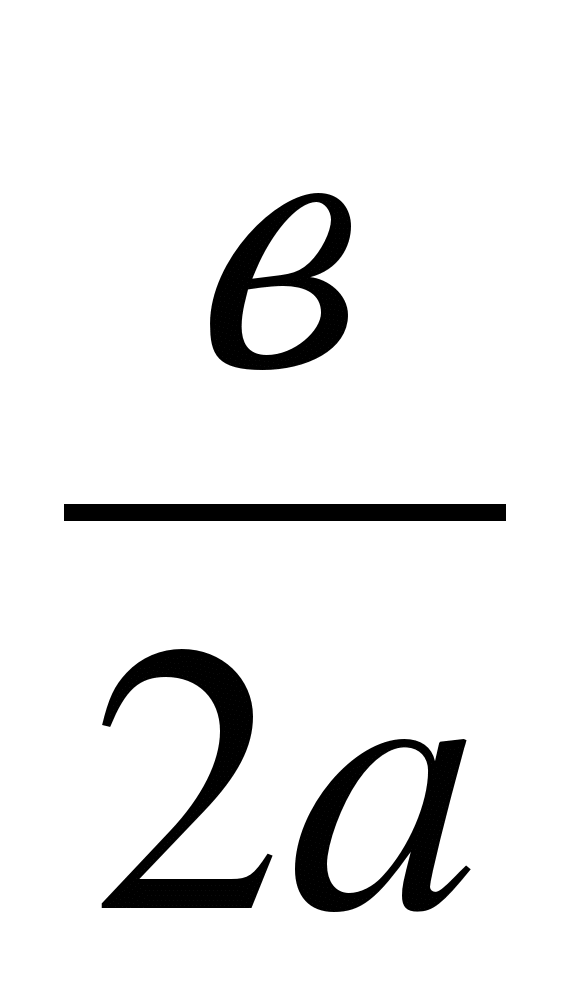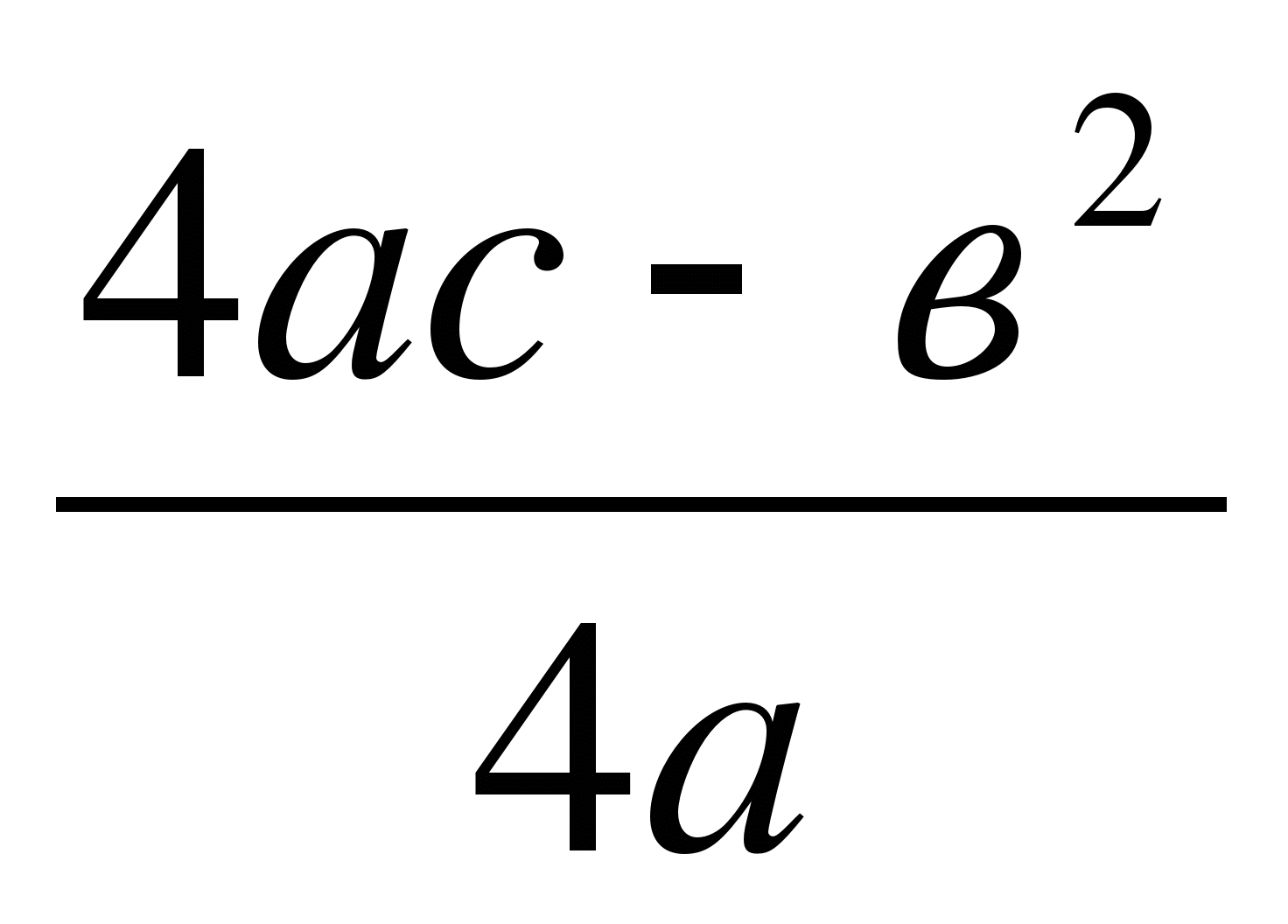— с помощью формулы координат вершины параболы – х0 = —hello_html_4afc2f9c.gif, у0 =hello_html_m34c608ae.gif,

— с помощью выделения квадрата двучлена .

7. Найдите координаты вершины параболы: (слайд 5)

а) у = х2 -4х-5 (выделим квадрат двучлена: у = (х² — 2*2*х + 4) -9 = (х – 2)² -9, А(2;-9)

б) у=-5х2+3 ( найдем координаты вершины параболы по формуле х0 = —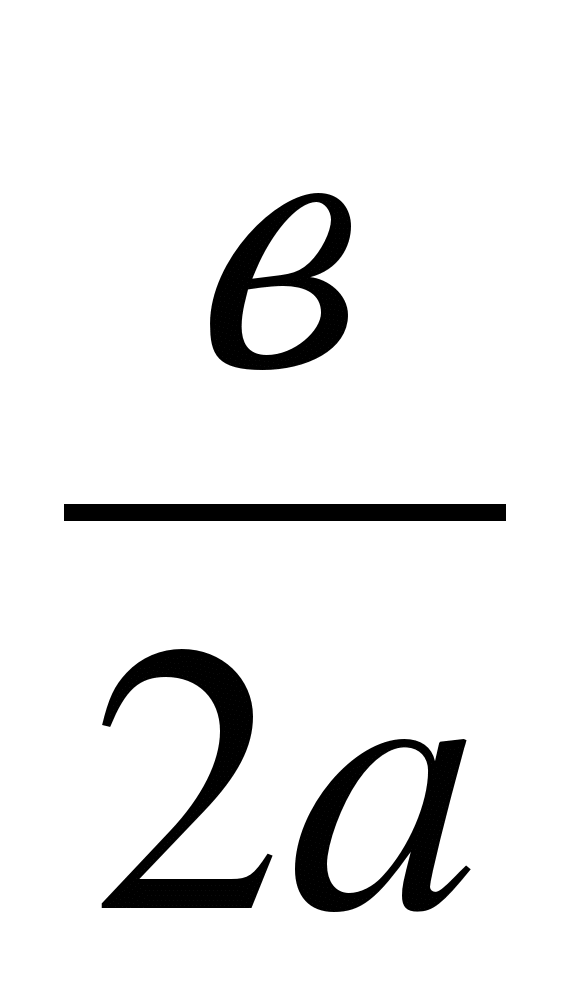hello_html_4afc2f9c.gif = 0/10 =0,

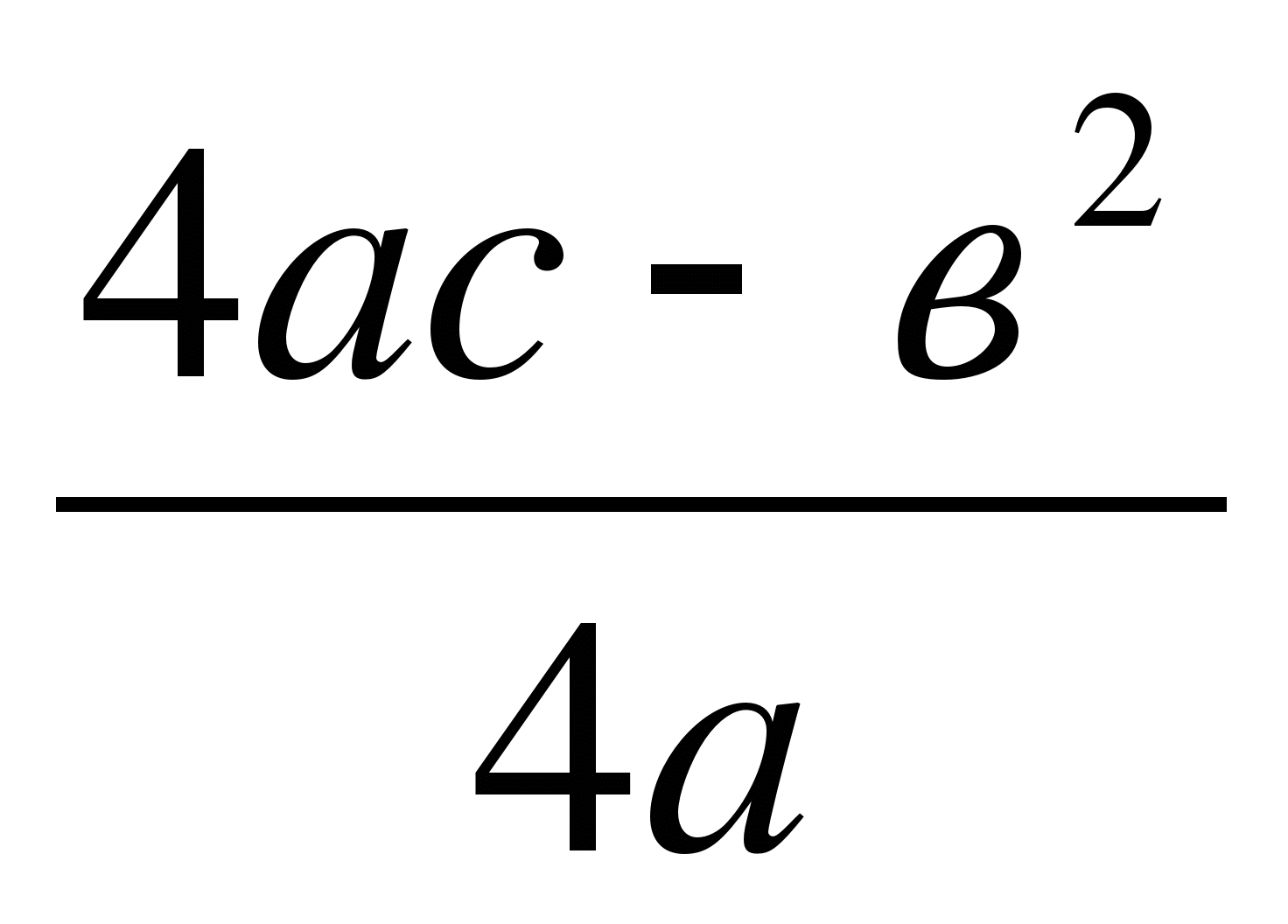у0 =hello_html_m34c608ae.gif или найдем значение функции в т. х = 0, у(0) =3, В(0;3)

8. Расскажите алгоритм построения графика квадратичной функции. (слайд 6)

(Алгоритм построения графика квадратичной функции:

— определить направление ветвей параболы;

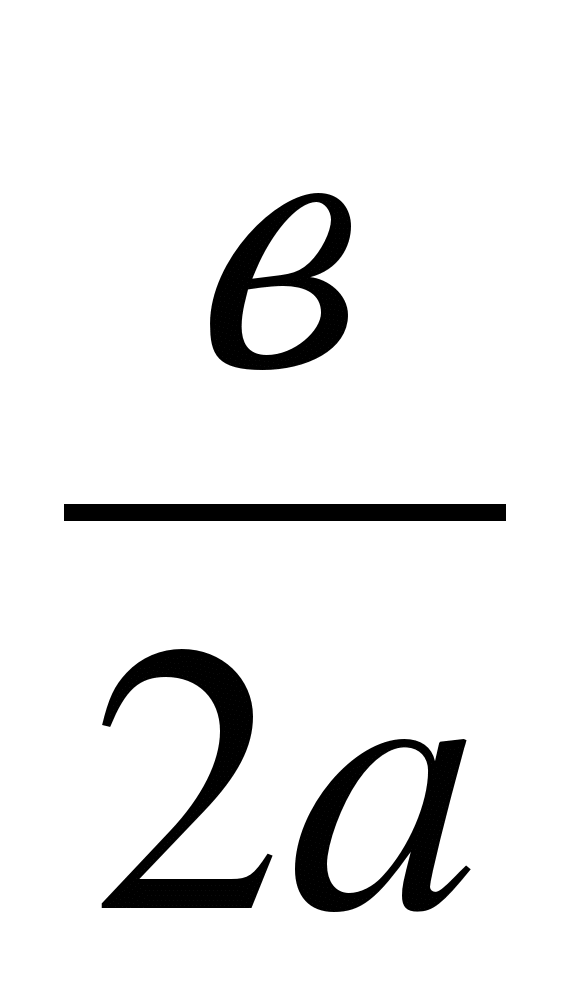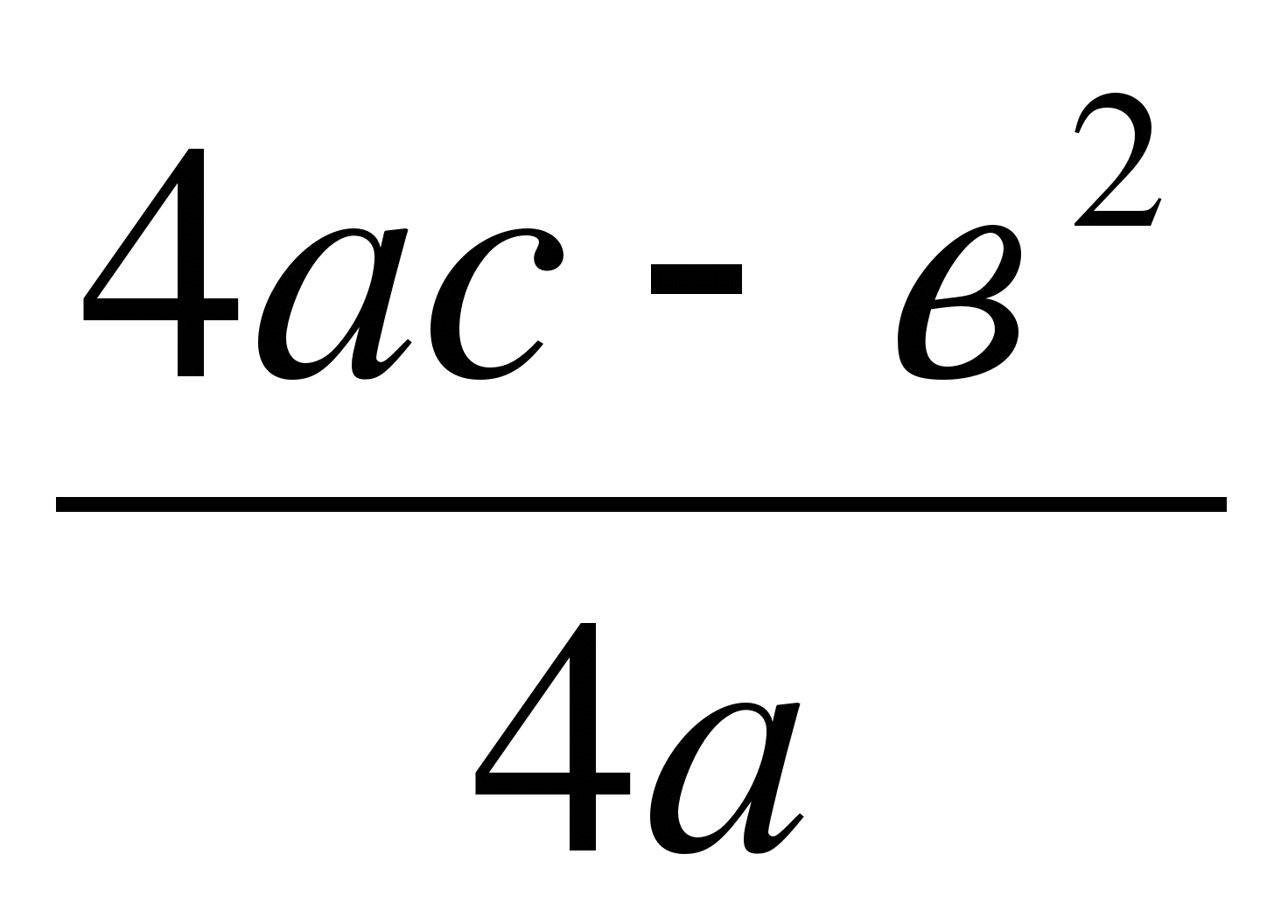— найти координаты вершины параболы по формулам: х0 = —hello_html_4afc2f9c.gif, у0 =hello_html_7ac30f4d.gif,

— отметить эту точку на координатной плоскости;

— через вершину параболы начертить ось симметрии параболы х=х0;

— найти нули функции и отметить их на числовой прямой;

— найти координты двух дополнительных точек и симметричных им;

— провести кривую параболы.

9. Постройте график функции у = 2х² + 4х -6 и опишите его свойства. (слайд 7)

Параболу  Строим и чертим 
Красивой, плавной, аккуратной 
Получился у нас график 
всем понятный 

IV.Физкультминутка.

Ребята, сейчас проверим как вы, зная преобразования графика функции, можете показать их с помощью физических упражнений.

Напомним: параллельный перенос вдоль оси ОХ – прыжки вправо или влево;

параллельный перенос вдоль оси ОУ – прыжки вверх или приседание;

коэффициент а >0 – движение рук вдоль туловища – прижимание,

а <0 – движение рук вдоль туловища – растяжение.

И так, начинаем изобразите схематически график функции

у = х2 ; у = 3х2 ; у = 1/5 х2 ;

у = (х+2)2; у = (х-1)2; у = (х+2)2— 3; у = (х-2)2 + 1; у = 2(х+3)2 .

Спасибо, молодцы. Заряд бодрости получили и присели на свои места.

Продолжаем наш урок. А сейчас проверим, как вы сами справитесь с квадратичной функцией, кто из вас сильнее и умнее. Если с заданиями справляетесь, значит, вы умнее и сильнее, если нет – то нужно еще потренироваться. Желаю вам успехов в математическом соревновании.

V Самостоятельная работа.

Работа с графиком функции (индивидуальная) .(рис распечатать)

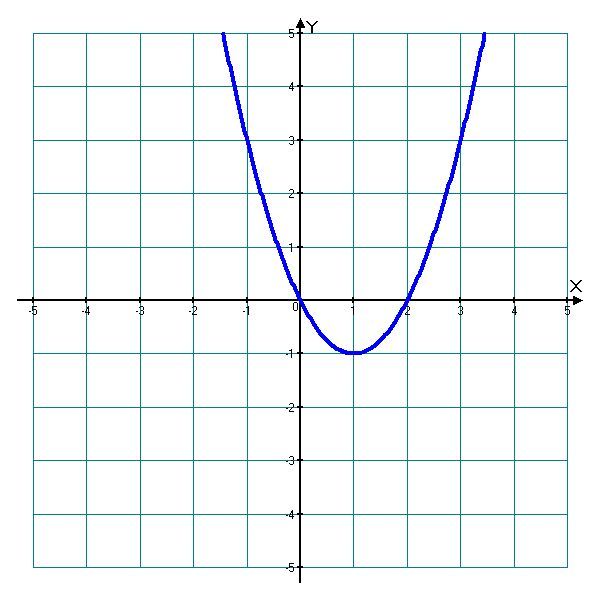
hello_html_27b05dc3.jpg

1.Определите знак коэффициента a

2. Назовите координаты вершины параболы.

3. Назовите область значений функции.

4. Назовите значения переменной х, при которых данная функция принимает:

а) значения, равные нулю;

б) при каких значениях х функция принимает

положительные значения.

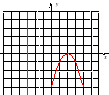
hello_html_6205dd87.gif

1.Определите знак коэффициента а.

2. Назовите координаты вершины параболы.

3. Назовите область значений функции.

4. Назовите значения переменной х, при которых данная

функция принимает: а) значения, равные нулю;

б) меньше нуля;

hello_html_m1024dd2.gif

1. Определите знак коэффициента a.

2. Назовите координаты вершины параболы.

3. Назовите область значений функции.

4. Назовите значения переменной х, при которых данная функция

принимает а) значения, равные нулю;

б) при каких значениях х функция монотонно

возрастает.

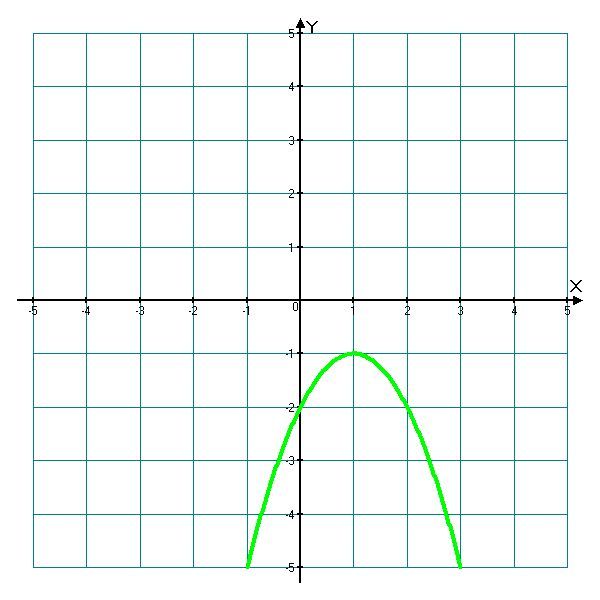
hello_html_5edeb8d7.jpg

1. Определите знак коэффициента a.

2. Назовите координаты вершины параболы.

3. Назовите область значений функции.

4. Назовите значения переменной х, при которых данная функция

принимает: а) значения, равные нулю;

б) больше нуля, меньше нуля;

в) при каких значениях х функция монотонно

убывает

Б. Работа с формулами координат вершины параболы, расчетные упражнения

(работа в парах с взаимопроверкой)

Вариант 1. Найти координаты вершины параболы:

у = х2 -4х-5;

2. Найдите область значений функции.

3. При каких значениях х функция а) принимает отрицательные значения;

Вариант 2. 1. Найти координаты вершины параболы:

у = — 5х2+3

2. Найдите область значений функции.

3. При каких значениях х функция монотонно возрастает;

Вариант 3. 1. Найти координаты вершины параболы:

. у = 5х2-3х-2.

2. Найдите координаты точек пересечения с осями координат

3. При каких значениях х функция монотонно убывает;

В. Карточка 1. Постройте график функции у = х2 – 6х +10 используя формулы координат вершины параболы. Опишите свойства графика квадратичной функции.

Карточка 2. Постройте график функции у = х2 – 6х -7 используя метод выделения квадрата двучлена. Опишите свойства графика квадратичной функции.

Г. Коллективно — индивидуальная работа

Установите соответствие между уравнением функции и ее графиком.

Из букв, оставшихся «лишними», составьте вспомогательное слово.

1. у = – х2 – 2 4. у = (х + 3)2 7. у = – (х + 2)2

2. у = (х – 3)2 5. у = – (х – 1)2 + 4 8. у = 4 – (х – 1)2

3. у = (х + 4)2 – 1 6. у = – х2 + 3 9. у = х2 + 2

1

2

3

4

5

6

7

8

9

Слово: гол

Аhello_html_m1ffd2f5f.gif

Иhello_html_m6fc766cb.gif

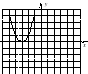
Рhello_html_m5b5e1360.gif

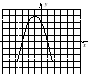
Гhello_html_m466b1c4e.gif

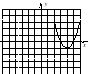
Лhello_html_m4e2cd925.gif

Сhello_html_1f47a95c.gif

Дhello_html_24b2bddb.gif

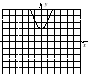
Нhello_html_1accb09f.gif

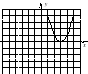
Тhello_html_m6c3f8bc5.gif

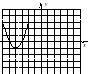
Еhello_html_2542f564.gif

Оhello_html_m4ffbd854.gif

Уhello_html_m2f34703d.gif

VI Подведение итогов урока.

VII Домашнее задание

VIII Рефлексия Мы стали друзьями, мы стали умнее,

Богаче на целый волшебный урок!

Нас знания делают выше, сильнее,

А дружба крепче и добрей.

Ты согласен, дружок?

  1. На уроке я работал активно / пассивно

  2. Своей работой на уроке я доволен / не доволен

  3. Урок для меня показался коротким / длинным

  4. За урок я не устал / устал

  5. Моё настроение стало лучше / стало хуже

  6. Материал урока мне был понятен / не понятен

полезен / бесполезен

интересен / скучен

7.Домашнее задание мне кажется лёгким / трудным

интересно / не интересно

Источники информации:

1.https://kittymcteague.files.wordpress.com/2013/05/7730_1.jpg

2. http://player.myshared.ru/547694/data/images/img25.jpg

3. http://textarchive.ru/images/836/1670841/ac145154.gif

4.http://turizm.lib.ru/img/b/bersenewa_n_b/ergakimart2010/skalaparabola.jpg

5.http://mathforum.org/mathimages/imgUpload/thumb/Fountain.jpg/400px-Fountain.jpg

6.http://www.fresher.ru/manager_content/images2/kak-otmetili-alye-parusa-2014-v-sankt-peterburge/15.jpg

7.http://images.aif.ru/006/633/def5f1e6b6cdc7208dc252436988f991.jpg

8.http://player.myshared.ru/589208/data/images/img76.jpg

9https://upload.wikimedia.org/wikipedia/commons/5/5a/Troms%C3%B8_library_-_2005-09-13.jpg

10.ttps://upload.wikimedia.org/wikipedia/commons/5/5a/Troms%C3%B8_library_-_2005-09-13.jpg

11.https://yandex.ua/images/#!/images/search?text=%

12 http://prezentacii.com/matematike/6989-kvadratichnaya-funkciya-i-ee-grafik.html слайд 7

13 http://www.uztest.ru/plugins/lessons/pazl/moe/tests/fun1/eigensch.html).

14. Алгебра 9 класс. Поурочные планы по учебнику “Алгебра 9 класс” / Ю.Н. Макарычев/ Под редакцией С.А. Теляковского . М.: Просвещение, 2002. /Сост. Д.Ф. Айвазян.– Волгоград – АСТ, 2008

15. ГИА-9. Математика. Учебно-тренировочные тесты под ред.Ф. Ф. Лысенко.

16. Шалкина С.В. «Здоровьесберегающие технологии на уроках математики»/ festival.1september.ru / Фестиваль педагогических идей«Открытый урок» 2006-2007 учебный год +

17. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений / Под ред. С.А. Теляковского. – М.: Просвещение, 2002.
18. Цукарь А.Я. Рисуем графиками функций // Математика. – 1999. – № 7, № 22, № 23, № 24, № 25.
19. Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – № 4. – С. 80-81.

20.. http://festival.1september.ru/articles/101475/img27.gifкартинка тюльпана,колокольчика

21. http://1.bp.blogspot.com/-rOOH6x_2qsg/Ta3ca_DrzEI/AAAAAAAAQRY/GVaCD0LZKls/s1600/vihmavari.jpg зонтик

22. http://4.bp.blogspot.com/-RvwIRt2MrWw/Ta3cdtIOTeI/AAAAAAAAQRc/1X7bWfaYIJ8/s1600/prillid.jpg очки

23. http://festival.1september.ru/articles/101475/img2.jpg жаба

24. http://festival.1september.ru/articles/589062/ таблица

«Функция у=ах² + вх +с, её свойства и график»

Контрольный срез № 5. Тема: «Функция у=ах² + вх +с,ее свойства и график»

Вариант 1

Время выполнение работы 15 мин.

Желаем успеха!

1. Парабола задана уравнением у= х² — 4х -5.

а) Найдите координаты вершины параболы. – 1балл

б) Определите, куда направлены ветви параболы, и объясните почему. – 1 балл

в) Постройте параболу.- 3 балла

г) Найдите координаты точек пересечения параболы с осью абсцисс. – 1 балл

2. Найдите наименьшее значение функции у= х² — 4х -5. – 1 балл

Оценка «5» — 7 баллов

Оценка «4» — 6 баллов

Оценка «3» — 5 баллов

Контрольный срез № 5. Тема: «Функция у=ах² + вх +с,ее свойства и график» Вариант 2

Время выполнение работы 15 мин.

Желаем успеха!

1. Парабола задана уравнением у= — х² +6х -5.

а) Найдите координаты вершины параболы. – 1балл

б) Определите, куда направлены ветви параболы, и объясните почему. – 1 балл

в) Постройте параболу.- 3 балла

г) Найдите координаты точек пересечения параболы с осью абсцисс. – 1 балл

2. Найдите наибольшее значение функции у= -х² +6х -5. – 1 балл

Оценка «5» — 7 баллов

Оценка «4» — 6 баллов

Оценка «3» — 5 баллов

Контрольный срез № 5. Тема: «Функция у=ах² + вх +с,ее свойства и график» Вариант 3

Время выполнение работы 15 мин.

Желаем успеха!

1. Парабола задана уравнением у= — 2х² +4х +6.

а) Найдите координаты вершины параболы. – 1балл

б) Определите, куда направлены ветви параболы, и объясните почему. – 1 балл

в) Постройте параболу.- 3 балла

г) Найдите координаты точек пересечения параболы с осью абсцисс. – 1 балл

2. Найдите наибольшее значение функции у= -2х² +4х+6. – 1 балл

Оценка «5» — 7 баллов

Оценка «4» — 6 баллов

Оценка «3» — 5 баллов

@# Федорова О.Ю. 04.01.2012 г. Ульяновск-73

{2} $$


Самая низкая или самая высокая точка параболы называется вершиной. Вершина имеет координату x

$$ x = — \ frac {b} {2a} $$

Координата Y вершины — это максимальное или минимальное значение функции.

a> 0 парабола открывает минимальное значение


<0 парабола раскрывается до максимального значения


Практическое правило напоминает нам, что когда у нас есть положительный символ перед x 2 , мы получаем счастливое выражение на графике, а отрицательный символ отображает печальное выражение.

Вертикальная линия, проходящая через вершину и разделяющая параболу пополам, называется осью симметрии. Ось симметрии имеет уравнение

$$ x = — \ frac {b} {2a} $$

Отсечка по оси Y уравнения равна c.


Когда вы хотите построить график квадратичной функции, вы начинаете с создания таблицы значений для некоторых значений вашей функции, а затем наносите эти значения на координатную плоскость и проводите плавную кривую через точки.

Пример

График

$$ x = x ^ {2} + 2x + 1 $$

Составьте таблицу значений для некоторых значений x.Используйте как положительные, так и отрицательные значения!

х y = x 2 + 2x + 1
-3 4
-2 1
-1 0
0 1
1 4
2 9
3 16

Постройте точки и проведите плавную линию через точки и продолжите ее в обоих направлениях


Обратите внимание, что у нас есть точка минимума, на которую указывает положительное значение a (a = 1).Вершина имеет координаты (-1, 0), которые вы получите, если воспользуетесь формулой для координаты x вершины

.

$$ x = — \ frac {b} {2a} = — \ frac {2} {2 \ cdot 1} = — 1 $$

и что линия имеет точку пересечения по оси y (0, 1), которая могла быть определена из значения c, равного 1.

Если у вас абсолютное значение a больше 1, парабола будет уже, чем родительская квадратичная функция. И наоборот, если у вас есть абсолютное значение a, которое меньше 1, тогда парабола будет шире, чем родительская квадратичная функция.{2} — 3х — 10 $$

.

PPT — Напомним: график квадратичной функции y = ax 2 + bx + c представляет собой параболу. Презентация PowerPoint

  • Алгебра 2cc Раздел 2.9 Используйте графический калькулятор для построения графика функций , поиска максимальных / минимальных значений, перехватов и решать квадратные уравнения Напомним: график квадратичной функции y = ax2 + bx + c представляет собой параболу

  • Используйте графический калькулятор для построения графика параболы, найдите ее максимальное / минимальное значение , а ее точку пересечения x. y = x2 + x — 6 y = -½ x2 — 3x + 4

  • Шаги для построения графика функции. • Постройте уравнение • TI 84 • Задайте окно (область и диапазон) с помощью клавиш • Масштаб • Zстандарт • Y = • Введите уравнение, используя [X, T, θ] для переменной. Нажмите • График • TI Nspire • Используйте блокнот: [B Graph] • меню • Тип графика • Функция • Введите уравнение f (x) = • Найдите максимум / минимум / ноль графика функции • TI 84 • Постройте график функции с помощью Y = клавиша (см. Инструкции по построению графиков) • 2-я • График • макс / мин / ноль • Переместите курсор влево от макс / мин / нуля и введите.Переместите курсор вправо от максимума / минимума / нуля и введите. Переместите курсор ближе к максимальному / минимальному / нулю и введите. Макс / мин / ноль отображается внизу экрана. • TI N-spire • График функции (см. Инструкции для построения графиков) • меню • Анализ графика • макс / мин / ноль • Переместите курсор влево от макс / мин / нуля и введите. Переместите курсор вправо от максимума / минимума / нуля и введите. Переместите курсор ближе к максимальному / минимальному / нулю и введите. Макс / мин / ноль отображается внизу экрана.

  • Воспользуйтесь графическим калькулятором для построения графика параболы, найдите ее максимальное / минимальное значение и пересечения по оси x.y = 2×2 + 3x + 8

  • Реальные решения квадратного уравнения ax2 + bx + c = 0 могут быть найдены с помощью графического калькулятора. Найдите все реальные решения с помощью калькулятора. 3×2 + 16x + 5 = 0 • Решите полиномиальное уравнение • TI84 (решите графически) • Изобразите уравнение как функцию. (установите его равным y) • 2nd • Trace • Zero / root • Переместите курсор в обе стороны от точки пересечения x, нажав [ввод] на левой (нижней) и правой (верхней) границах. Ноль (корень / раствор) появится внизу экрана.• TI Nspire • Используйте блокнот: [A Calculate] • Меню • алгебра • Полиномиальные инструменты • Найдите корни поли • Введите степень (2 для квадратичной). Введите тип корней (вещественные или сложные). Введите коэффициенты полиномиального уравнения.

  • Найдите реальные решения с помощью графического калькулятора. -5x = 2×2 — 7 3×2 + 5x = 2

  • Объект запускается со скоростью 19,6 метра в секунду (м / с) с платформы высотой 58,8 метра. Уравнение для высоты объекта s в момент времени t секунд после запуска: h = –4.9t2 + 19,6t + 58,8, где h в метрах. Когда объект ударяется о землю? Когда он достигает максимальной высоты? Какая максимальная высота?

  • Прямоугольный загон должен быть построен с использованием 70-метровой ограды. Если ограждение должно охватывать все четыре стороны загона, какова максимально возможная площадь загона в квадратных метрах? • Задание: рабочий лист

    • .

    Алгебра 2cc Раздел 2.7. Графики квадратичных функций в различных формах. Квадратичная функция имеет вид: y = ax 2 + bx + c. Ее график называется параболой.

    Презентация на тему: «Алгебра 2cc, раздел 2.7. Графики квадратичных функций в различных формах. Квадратичная функция имеет вид: y = ax 2 + bx + c. Ее график называется параболой». — Стенограмма презентации:

    1 Алгебра 2cc Раздел 2.7. Графики квадратичных функций в различных формах. Квадратичная функция имеет вид: y = ax 2 + bx + c. Ее график называется параболой. Если a> 0, парабола раскрывается. Если a <0, парабола открывается вниз. Значение x вершины находится по формуле x = -b / 2a. Значение y вершины находится путем подстановки значения x в уравнение. Пересечение y - это значение c. Ось симметрии - это вертикальная линия, уравнение которой x = -b / 2a. Algebra 2cc Section 2.7 Graph quadratic functions in various forms A quadratic function takes the form: y = ax 2 + bx + c Its graph is called a parabola.

    2 Найдите вершину, точки пересечения по осям x и y, уравнение оси симметрии и график.у = ½ х 2 + 2х — 1 Find the vertex, x and y intercepts, equation of axis of symmetry, and graph. y = ½ x 2 + 2x - 1

    3 Найдите вершину, точки пересечения по осям x и y, уравнение оси симметрии и график. у = -x 2 + 4x — 2 Find the vertex, x and y intercepts, equation of axis of symmetry, and graph. y = -x 2 + 4x - 2

    4 Найдите вершину, точки пересечения по осям x и y, уравнение оси симметрии и график. у = ½ х 2 + 3х + 6 Find the vertex, x and y intercepts, equation of axis of symmetry, and graph. y = ½ x 2 + 3x + 6

    5 Формы квадратичной функции Стандарт y = ax 2 + bx + c Форма вершины y = a (x-h) 2 + k vertex is (h, k) Пересечение Y находится путем замены x нулем.Forms of a quadratic function Standard y = ax 2 + bx + c Vertex form y = a(x-h) 2 + k vertex is (h,k) Y intercept is found by substituting zero in for x.

    6 Найдите вершину, пересечения x и y, ось симметрии и график. у = -1/2 (х-3) 2 + 4 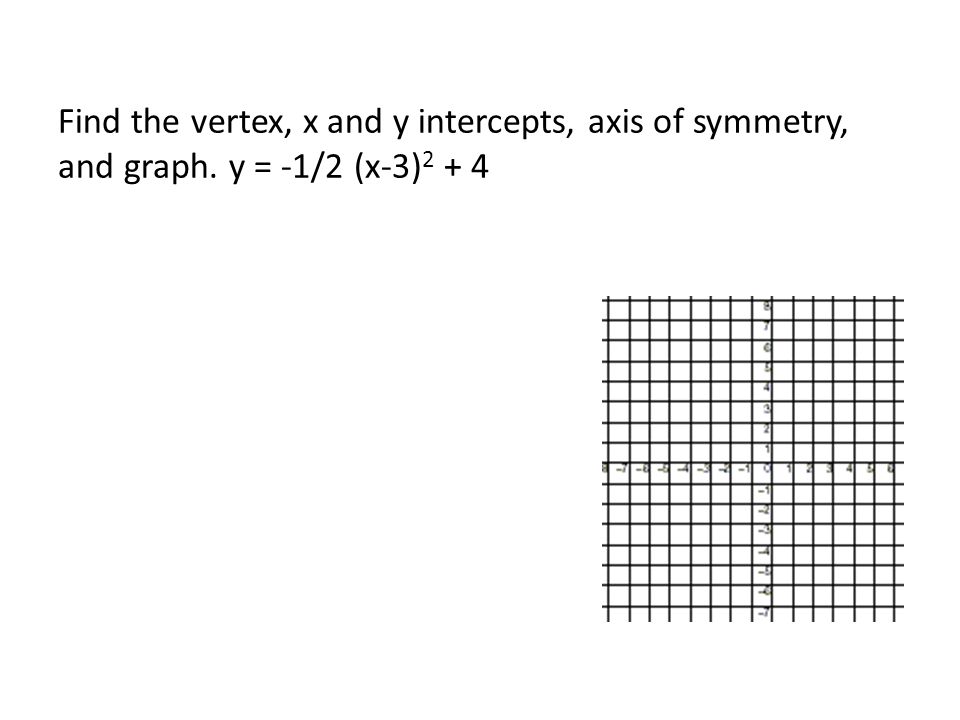Find the vertex, x and y intercepts, axis of symmetry, and graph. y = -1/2 (x-3) 2 + 4

    7 Найдите вершину, пересечения x и y, ось симметрии и график. у = 2 (х + 4) 2-3 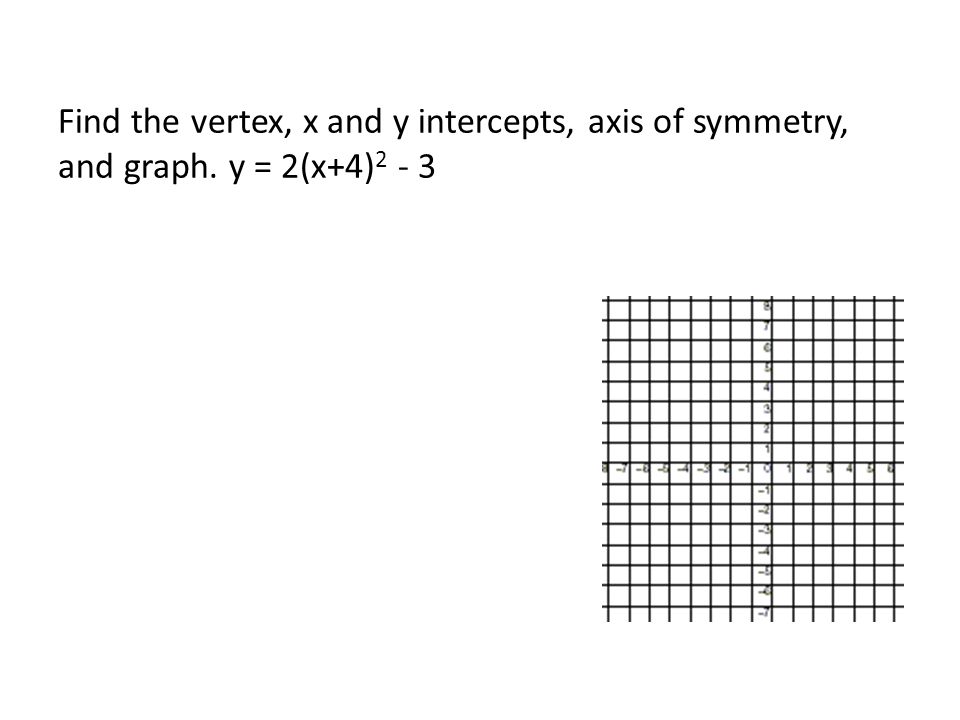Find the vertex, x and y intercepts, axis of symmetry, and graph. y = 2(x+4) 2 - 3

    8 Преобразуйте в форму вершины, заполнив квадрат.Найдите точки пересечения x и y, вершину и график y = x 2 + 6x + 2 Convert to vertex form by completing the square.

    9 Исследователи провели эксперимент, чтобы определить температуру, при которой люди чувствуют себя комфортно. Процент y испытуемых, которые чувствовали себя комфортно при температуре x, можно смоделировать следующим образом: y = -3,678x 2 + 527,3x — 18807. Какая температура обеспечивала комфорт наибольшему проценту людей? При такой температуре какой процент чувствовал себя комфортно? Researchers conducted an experiment to determine temperatures at which people feel comfortable.

    10 Количество бактерий в охлажденной пище определяется выражением N (t) = 20t 2 — 20t + 120, где -2

    11 Высота h в футах объекта над землей определяется как h = -16t 2 + 64t + 190, где t — время в секундах. Найдите время, за которое объект ударяется о землю, и найдите максимальную высоту объекта. The height, h, in feet of an object above the ground is given by h = -16t t where t is the time in seconds.

    .

    Отображение квадратичной кривой и графика (стандартная форма) — Math Open Reference

    Отображение квадратичной кривой и графика (стандартная форма) — Math Open Reference

    См. Также Общий обозреватель функций, где можно построить до трех функций в виде графиков. по вашему выбору, одновременно используя ползунки для независимых переменных, как указано выше. См. Также Linear Explorer и Cubic Explorer.

    Что попробовать

    Предполагая, что вы уже знакомы с квадратными уравнениями, следующие действия могут помочь вам получить больше интуитивно чувствуют действие трех коэффициентов a, b, c.

    Самый простой корпус. Y = постоянная. (у = с)

    1. Щелкните «ноль» под тремя ползунками

    Поскольку все a, b, c равны нулю, это график уравнения y = 0x 2 + 0x + 0. Это упрощается до y = 0 и, конечно, равно нулю для всех значений x. Следовательно, его график представляет собой горизонтальную прямую, проходящую через начало координат.

    1. Теперь переместите крайний правый ползунок для c и оставьте его, скажем, на 12.

    Это график уравнения y = 0x 2 + 0x + 12. Это упрощается до y = 12, и поэтому функция имеет значение 12 для всех значений x. Следовательно, это прямая горизонтальная линия, проходящая через 12 по оси y. Поиграйте с разными значениями c и посмотрите на результат.

    Линейные уравнения. (y = bx)

    1. Щелкните «ноль» под тремя ползунками
    2. Переместите центральный ползунок, чтобы получить разные значения b.Пусть осядет, скажем, 2.

    Это график уравнения y = 0x 2 + 2x + 0, которое упрощается до y = 2x. Это простое линейное уравнение, как и прямая линия с наклоном 2. То есть y увеличивается на 2 каждый раз, когда x увеличивается на единицу. Поскольку наклон положительный, линия идет вверх и вправо. Отрегулируйте ползунок b и наблюдайте за результатами, включая отрицательные значения.

    1. Теперь переместите оба ползунка b и c на некоторое значение.
    Это уравнение y = bx + c, объединяющее эффекты Коэффициенты b и c.Играйте с различными значениями b и c чтобы почувствовать влияние их значений на график.

    Член в квадрате. (у = ах 2 )

    1. Щелкните «ноль» под тремя ползунками
    2. Переместите левый ползунок, чтобы получить разные значения a. Пусть осядет, скажем, 3.

    Это график уравнения y = 3x 2 + 0x + 0. Это упрощается до y = 3x 2 . Уравнения такого вида и имеют форму параболы, а поскольку a положительный, он идет вверх по обе стороны от начала координат.Поиграйте с различными значениями a. По мере увеличения парабола становится круче и «уже». Когда a отрицательное, он наклоняется вниз с каждой стороны от начала координат. Обратите внимание, что корни уравнения (где y равно нулю) находятся в начале координат, поэтому оба они равны нулю.

    Полный квадратичный. (у = ах 2 + bx + с)

    1. Щелкните «ноль» под тремя ползунками
    2. Установите c на 4, линия переместится вверх
    3. Установите b на 3, наклон линии.
    4. Установите a на 2. Форма параболы добавлена.

    Это график уравнения y = 2x 2 + 3x + 4. Обратите внимание, как он сочетает в себе эффекты трех терминов. Поиграйте с различными значениями a, b и c.

    • Изменение c перемещает его вверх и вниз.
    • Изменение b изменяет наклон.
    • При изменении a изменяется кривизна параболического элемента.

    Корни

    На рисунке выше нажмите «показать корни». Играя с квадратичным, обратите внимание, что корни находятся там, где кривая пересекает ось x, где у = 0. Есть два корня, поскольку кривая дважды пересекает ось x, поэтому есть два разных значения x, где y = 0. При некоторых обстоятельствах два корня могут иметь одинаковое значение. Если кривая вообще не пересекает ось x, у квадратичной нет вещественных корней.

    Если вы сделаете b и c равными нулю, вы увидите, что оба корня находятся в одном месте. При некоторых условиях кривая никогда не пересекает ось x, поэтому уравнение не имеет действительных корней. Обратите внимание, что если b = 0, то корни равномерно расположены по обе стороны от начала координат, например +2 и -2.См. «Ось симметрии» ниже.

    При выражении в нормальной форме корни квадратичного уравнения задаются формулой, приведенной ниже. Он указывает положение двух корней по оси x и будет работать, только если a не равно нулю. Если выражение внутри квадратного корня отрицательное, кривая не пересекает ось x и действительных корней нет.

    Ось симметрии

    Нажмите «показать ось симметрии». Это вертикальная линия, проходящая через вершину кривой. Обратите внимание, как кривая является зеркальным отображением слева и справа от линии.(Мы говорим, что кривая симметрична относительно этой линии). Обратите внимание, что корни расположены на равных расстояниях с каждой стороны.

    Когда квадратичный элемент имеет нормальную форму, как здесь, мы можем найти ось симметрии по формуле ниже. Он показывает его положение по оси абсцисс. Если a равно нулю, оси симметрии нет и эта формула не будет работать, попытка разделить на ноль даст неопределенный результат. На рисунке выше установите a равным нулю и, перемещая другие ползунки, убедитесь, что не может быть оси симметрии с a = 0.

    Попробуйте сами

    1. Нажмите «сбросить», затем «скрыть детали»
    2. Отрегулируйте ползунки, пока не увидите форму, которая вам нравится
    3. Оцените значения a, b и c для этой кривой и запишите уравнение для кривой
    4. Оценить корни
    5. Нажмите «Показать подробности» и посмотрите, насколько близко вы подошли к

    Другие вопросы о квадратных уравнениях

    Обозреватель квадратичных функций

    (C) Открытый справочник по математике, 2011 г.
    Все права защищены.

    .

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *