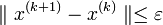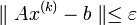Метод Гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) строки матрицы можно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) к строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х1, стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную хn. Для этого решаем элементарное уравнение А*хn = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг. К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по апробированной методике:
2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг. Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x 3 = 23, x3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x3 = 1
x2 = 3
x1 + x2 – x3 = 1, следовательно x1 + 3 – 1 = 1, x1 = –1
Ответ: x1 = –1, x2 = 3, x3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х3 = 0,96 или приблизительно 1.
х2 = 3 и х1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Метод Гаусса
Определение и описание метода Гаусса
Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.
Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.
Определение 1
Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.
После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.
Описание алгоритма метода Гаусса
Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид:
$\begin{cases} a_{11} \cdot x_1 +…+ a_{1n} \cdot x_n = b_1 \\ … \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$
Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:
$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$
Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов. Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:
$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & …\\ a_{m1} & … & a_{mn} & b_m \end{array}$
Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:
$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}…+ α_{1j_{r}} \cdot x_{j_{r}} +… α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}…+ α_{2j_{r}} \cdot x_{j_{r}} +… α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ …\\ α_{rj_{r}} \cdot x_{j_{r}} +… α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)
Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:
$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$
Для этих матриц характерен следующий набор свойств:
- Все её нулевые строки стоят после ненулевых
- Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.
После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.
Основные правила и разрешаемые преобразования при использовании метода Гаусса
При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования.
Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла:
- перестановка нескольких строк местами,
- прибавление или вычитание из одной строчки матрицы другой строчки из неё же,
- умножение или деление строчки на константу, не равную нулю,
- строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить,
- Также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами.
Все элементарные преобразования являются обратимыми.
Разбор трёх основных случаев, возникающих при решении линейных уравнений используя метод простых преобразований Гаусса
Различают три возникающих случая при использовании метода Гаусса для решения систем:
- Когда система несовместная, то есть у неё нет каких-либо решений
- У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой.
- Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов.
Исход решения с несовместной системой
Для этого варианта при решении матричного уравнения методом Гаусса характерно получение какой-то строчки с невозможностью выполнения равенства. Поэтому при возникновении хотя бы одного неправильного равенства полученная и исходная системы не имеют решений вне зависимости от остальных уравнений, которые они содержат. Пример несовместной матрицы:
$\begin{array}{ccc|c} 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end{array}$
В последней строчке возникло невыполняемое равенство: $0 \cdot x_{31} + 0 \cdot x_{32} + 0 \cdot x_{33} = 1$.
Система уравнений, у которой есть только одно решение
Данные системы после приведения к ступенчатой матрице и удаления строчек с нулями имеют одинаковое количество строк и столбцов в основной матрице. Вот простейший пример такой системы:
$\begin{cases} x_1 — x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$
Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$
Этот пример можно записать в виде системы:
$\begin{cases} x_1 — x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$
Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.
Система, обладающая множеством возможных вариантов решений
Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).
Переменные в такой системе делятся на два вида: базисные и свободные. При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.
У такой системы есть только некое общее решение.
Разберём следующую систему уравнений:
$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 — 4y_4 = 1 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$
Наша задача найти общее решение системы. Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ — так как он стоит на первом месте, а в случае $y_3$ — располагается после нулей).
В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.
Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.
Используя так называемый обратный ход, разбираем систему снизу вверх, для этого сначала выражаем $y_3$ из нижней строчки системы:
$5y_3 – 4y_4 = 1$
$5y_3 = 4y_4 + 1$
$y_3 = \frac{4/5}y_4 + \frac{1}{5}$.
Теперь в верхнее уравнение системы $2y_1 + 3y_2 + y_4 = 1$ подставляем выраженное $y_3$: $2y_1 + 3y_2 — (\frac{4}{5}y_4 + \frac{1}{5}) + y_4 = 1$
Выражаем $y_1$ через свободные переменные $y_2$ и $y_4$:
$2y_1 + 3y_2 — \frac{4}{5}y_4 — \frac{1}{5} + y_4 = 1$
$2y_1 = 1 – 3y_2 + \frac{4}{5}y_4 + \frac{1}{5} – y_4$
$2y_1 = -3y_2 — \frac{1}{5}y_4 + \frac{6}{5}$
$y_1 = -1.5x_2 – 0.1y_4 + 0.6$
Решение готово.
Пример 1
Решить слау методом Гаусса. Примеры. Пример решения системы линейных уравнений заданных матрицей 3 на 3 используя метод Гаусса
$\begin{cases} 4x_1 + 2x_2 – x_3 = 1 \\ 5x_1 + 3x_2 — 2x^3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$
Запишем нашу систему в виде расширенной матрицы:
$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.
Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
Далее к средней строчке прибавим верхнюю, умноженную на $5$, а последнюю строчку преобразуем, умножив первую строчку на 3 и сложив с последней, получаем:
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$
Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$
Далее сложим последнюю строчку с удвоенной средней:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$
И разделим последнюю строчку на $3$:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$
Получаем следующую систему уравнений, равносильную исходной:
$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$
Из верхнего уравнения выражаем $x_1$:
$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.
Пример 2
Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса
$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$
Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$
Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$
Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$
Решаем полученную систему уравнений:
$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$
$y=2$, $x = 0$.
spravochnick.ru
Описание метода Гаусса
Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований исходная система приводится к равносильной ей системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру), неизвестных находятся все остальные неизвестные. Дана система (1)
 (1)
(1)
Начинаем осуществлять прямой ход. Считаем, что коэффициент а11 ≠ 0; если же это не так, меняем местами уравнения.
Первый
шаг состоит в том, чтобы исключить
неизвестное х1 из всех уравнений, кроме первого. Для
этого ко второму уравнению прибавим
первое уравнение, умноженное на число  ,
к третьему уравнению прибавим первое
уравнение, умноженное на число
,
к третьему уравнению прибавим первое
уравнение, умноженное на число  ,
и так далее до последнего уравнения.
После первого шага получим систему:
,
и так далее до последнего уравнения.
После первого шага получим систему:

Полученная система равносильна исходной системе.
Вторым
шагом исключают неизвестное из всех
уравнений, кроме первого и второго. Для
этого повторяем все действия первого
шага для второго и последующих уравнений,
а именно: считаем, что коэффициент  ≠ 0
и так далее. Если в результате преобразований
получается нулевое уравнение, то его
удаляют, если же получается несовместное
уравнение, то решение системы закончено
– она несовместна. Процесс исключения
неизвестных продолжаем до тех пор, пока
это возможно. Обозначим количество
уравнений, оставшихся после прямого
хода, через r.
Это число равно рангу основной матрицы
системы и может быть меньше или равно n.
Рассмотрим оба случая.
≠ 0
и так далее. Если в результате преобразований
получается нулевое уравнение, то его
удаляют, если же получается несовместное
уравнение, то решение системы закончено
– она несовместна. Процесс исключения
неизвестных продолжаем до тех пор, пока
это возможно. Обозначим количество
уравнений, оставшихся после прямого
хода, через r.
Это число равно рангу основной матрицы
системы и может быть меньше или равно n.
Рассмотрим оба случая.
1) Если r = n, то система после прямого хода принимает вид:

где с11 ≠ 0, с22 ≠ 0, …, сnn ≠ 0.
Обратным
ходом,
начиная с последнего уравнения,
последовательно найдем значения xn,
(где xn =  ), xn – 1,
…, x1.
В этом случае система линейных уравнений
имеет единственное решение, то есть
является определенной.
), xn – 1,
…, x1.
В этом случае система линейных уравнений
имеет единственное решение, то есть
является определенной.
2) Если r < n, то система после прямого хода принимает вид:

где с11 ≠ 0, с22 ≠ 0, …, сrr ≠ 0. Неизвестные x1, x2, …, xr, с которых начинаются уравнения, называются главными неизвестными, а остальные xr + 1, x r + 2, …, xn – свободными. В этом случае обратным ходом, начиная с последнего уравнения, выражают главные неизвестные через свободные неизвестные. Получают следующие равенства:
x1 = k1,r + 1xr + 1 + … + k1,nxn + t1,
x2 = k2,r + 1xr + 1 + … + k2,nxn + t2,
……………………………………..
xr = kr,r + 1xr + 1 + … + kr,nxn + tr.
Определение 6.10. Общим решением системы называется выражение главных неизвестных через свободные.
Если свободным неизвестным придать какие-нибудь числовые значения, то из общего решения получим значения главных неизвестных. Таким образом, получают частное решение системы. Из способа его получения следует, что система имеет более одного решения, то есть является неопределенной.
Пример 6.3. Решить методом Гаусса систему линейных уравнений:

Решение.
Преобразования
с системой линейных удобнее производить
не с самими уравнениями, а с матрицей
их коэффициентов. Расширенная матрица
этой системы имеет вид: (А|B) =  .
.
Осуществляем
прямой ход. Первым шагом исключаем
неизвестное х1 из всех уравнений, кроме первого. Так
как а11 = 1 ≠ 0,
то переставлять уравнения местами не
нужно. Прибавим ко второму уравнению
системы первое уравнение, умноженное
на (–1), к третьему уравнению – первое,
умноженное на (–3). Получим после
преобразований следующую матрицу:  ,
в которой элемент а22 = 1.
Перестановка местами уравнений (первое
уравнение трогать не следует) не поможет,
поэтому переходим к следующему
неизвестному х3 и исключаем его из всех уравнений, кроме
первого и второго. Для этого к третьему
уравнению прибавим второе, умноженное
на (–2) и вычеркнем получившееся нулевое
уравнение. После прямого хода получаем
следующую систему:
,
в которой элемент а22 = 1.
Перестановка местами уравнений (первое
уравнение трогать не следует) не поможет,
поэтому переходим к следующему
неизвестному х3 и исключаем его из всех уравнений, кроме
первого и второго. Для этого к третьему
уравнению прибавим второе, умноженное
на (–2) и вычеркнем получившееся нулевое
уравнение. После прямого хода получаем
следующую систему:  .
Прямой ход завершен. В этом случае n = 4, r = 2, r < n,
и, следовательно, система неопределенная.
Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х1 и х3.
Неизвестные х2 и х4 – свободные.
.
Прямой ход завершен. В этом случае n = 4, r = 2, r < n,
и, следовательно, система неопределенная.
Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х1 и х3.
Неизвестные х2 и х4 – свободные.
Обратным
ходом надо выразить главные неизвестные
через свободные. Для этого в столбцах,
содержащих ведущие элементы строк,
следует получить нули. Здесь это элемент а13.
Прибавим к первому уравнению, умноженному
на 2, второе и выпишем получившуюся
матрицу коэффициентов:  ,
а затем и сами уравнения:
,
а затем и сами уравнения:  Из
этих уравнений получаем общее решение:
Из
этих уравнений получаем общее решение:

Найдем
какое-нибудь частное решение; пусть х2 = 3, х4 = 1,
тогда из общего решения получим значения х1 =  ,
и х1 = –2.
Таким образом, частное решение – вектор а = (
,
и х1 = –2.
Таким образом, частное решение – вектор а = ( ,
3, –2, 1).
,
3, –2, 1).
Ответ:
общее решение {( , х2,
, х2,  , х4)},
где х2, х4 R;
, х4)},
где х2, х4 R;
частное
решение, если х2 = 3, х4 = 1,
то (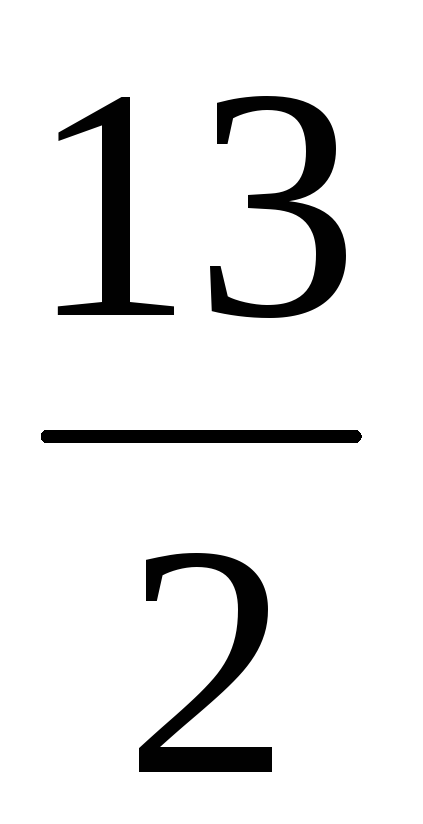 ,
3, –2, 1).
,
3, –2, 1).
studfile.net
метод Гаусса. Вычисление матрицы методом Гаусса: примеры
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.
Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
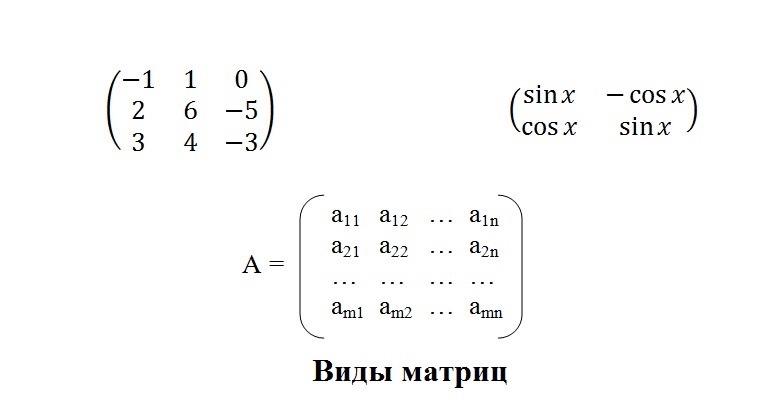
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l<j).
Теперь рассмотрим схему. Она отражает ступенчатую форму матрицы. В схеме представлено 3 вида клеток. Каждый вид обозначает определенные элементы:
- пустые клетки – нулевые элементы матрицы;
- заштрихованные клетки – произвольные элементы, которые могут быть как нулевыми, так и ненулевыми;
- черные квадратики – ненулевые элементы, которые называются угловыми элементами, «ступеньками» (в представленной рядом матрице такими элементами являются цифры –1, 5, 3, 8).
При решении матриц иногда получается такой результат, когда «длина» ступеньки оказывается больше 1. Такое допускается. Важна лишь «высота» ступенек. В матрице ступенчатого вида этот параметр должен быть всегда равным единице.
Приведение матрицы к ступенчатой форме
Любая прямоугольная матрица может быть преобразована до ступенчатого вида. Делается это благодаря элементарным преобразованиям. Они включают в себя:
- перестановку строк местами;
- прибавление к одной строке другой строки, при необходимости умноженной на какое-либо число (можно также производить операцию вычитания).
Рассмотрим элементарные преобразования в решении конкретной задачи. На рисунке ниже представлена матрица A, которую требуется привести к ступенчатому виду.

Для того чтобы решить задачу, будем следовать алгоритму:
- Удобно выполнять преобразования над такой матрицей, у которой первый элемент в верхнем углу с левой стороны (т. е. «ведущий» элемент) равен 1 или –1. В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
- Выполним операции вычитания, затронув строки № 2, 3 и 4. Мы должны получить в первом столбце под «ведущим» элементом нули. Для достижения такого результата: из элементов строчки № 2 последовательно вычтем элементы строчки № 1, умноженные на 2; из элементов строчки № 3 последовательно вычтем элементы строчки № 1, умноженные на 4; из элементов строчки № 4 последовательно вычтем элементы строчки № 1.
- Далее будем работать с укороченной матрицей (без столбца № 1 и без строки № 1). Новый «ведущий» элемент, стоящий на пересечении второго столбца и второй строки, равен –1. Переставлять строки не требуется, поэтому переписываем без изменений первый столбец и первую и вторую строки. Выполним операции вычитания, чтобы во втором столбце под «ведущим» элементом получить нули: из элементов третьей строчки последовательно вычтем элементы второй строчки, умноженные на 3; из элементов четвертой строчки последовательно вычтем элементы второй строчки, умноженные на 2.
- Осталось изменить последнюю строку. Из ее элементов вычтем последовательно элементы третьей строки. Таким образом мы получили ступенчатую матрицу.

Приведение матриц к ступенчатой форме используется в решении систем линейных уравнений (СЛУ) методом Гаусса. Перед рассмотрением этого метода давайте разберемся в терминах, имеющих отношение к СЛУ.
Матрицы и системы линейных уравнений
Матрицы применяются в разных науках. С использованием таблиц из чисел можно, например, решать линейные уравнения, объединенные в систему, методом Гаусса. Для начала давайте познакомимся с несколькими терминами и их определениями, а также посмотрим, как из системы, объединяющей несколько линейных уравнений, составляется матрица.
СЛУ – несколько объединенных алгебраических уравнений, в которых присутствуют неизвестные в первой степени и отсутствуют члены, представляющие собой произведение неизвестных.
Решение СЛУ – найденные значения неизвестных, при подстановке которых уравнения в системе становятся тождествами.
Совместная СЛУ – такая система уравнений, у которой есть хотя бы одно решение.
Несовместная СЛУ – система уравнений, которая не имеет решений.
Как же составляется матрица на основе системы, объединяющей линейные уравнения? Существуют такие понятия, как основная и расширенная матрицы системы. Для того чтобы получить основную матрицу системы, необходимо вынести в таблицу все коэффициенты при неизвестных. Расширенная матрица получается путем присоединения к основной матрице столбца свободных членов (в него входят известные элементы, к которым в системе приравнивается каждое уравнение). Понять весь этот процесс можно, изучив картинку ниже.
Первое, что мы видим на картинке, – это систему, включающую в себя линейные уравнения. Ее элементы: aij – числовые коэффициенты, xj – неизвестные величины, bi – свободные члены (где i = 1, 2, …, m, а j = 1, 2, …, n). Второй элемент на картинке – основная матрица из коэффициентов. Из каждого уравнения коэффициенты записываются в строку. В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.

Общая информация о методе Гаусса
В линейной алгебре методом Гаусса называется классический способ решения СЛУ. Он носит имя Карла Фридриха Гаусса, жившего в XVIII–XIX вв. Это один из величайших математиков всех времен. Суть метода Гаусса заключается в выполнении элементарных преобразований над системой линейных алгебраических уравнений. С помощью преобразований СЛУ приводится к равносильной системе треугольной (ступенчатой) формы, из которой можно найти все переменные.
Стоит отметить, что Карл Фридрих Гаусс не является первооткрывателем классического способа решения системы линейных уравнений. Метод был придуман намного раньше. Первое его описание встречается в энциклопедии знаний древнекитайских математиков, носящей название «Математика в 9 книгах».
Пример решения СЛУ методом Гаусса
Рассмотрим на конкретном примере решение систем методом Гаусса. Будем работать с СЛУ, представленной на картинке.
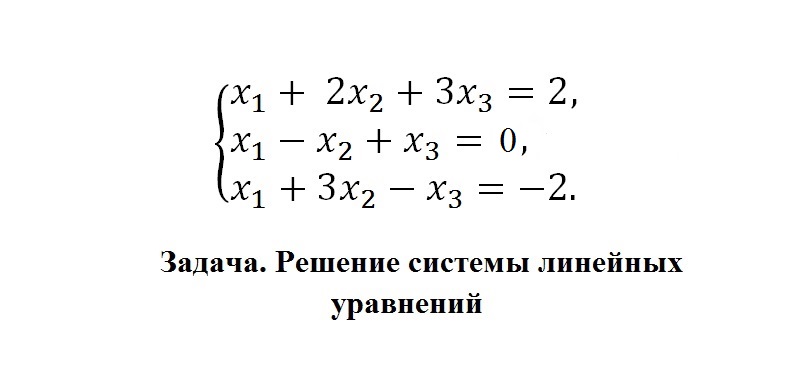
Алгоритм решения:
- Прямым ходом метода Гаусса приведем систему к ступенчатой форме, но для начала составим расширенную матрицу из числовых коэффициентов и свободных членов.
- Чтобы решить матрицу методом Гаусса (т. е. привести ее к ступенчатому виду), из элементов второй и третьей строчек последовательно вычтем элементы первой строчки. Получим в первом столбе под «ведущим» элементом нули. Далее поменяем вторую и третью строчки местами для удобства. К элементам последней строки прибавим последовательно элементы второй строчки, умноженные на 3.
- В результате вычисления матрицы методом Гаусса мы получили ступенчатый массив элементов. На его основе составим новую систему линейных уравнений. Обратным ходом метода Гаусса находим значения неизвестных членов. Из последнего линейного уравнения видно, что x3 равен 1. Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Ответ: используя матрицу, метод Гаусса, мы нашли значения неизвестных; x1 = –1, x2 = 0, x3 = 1.

Метод Гаусса – Жордана
В линейной алгебре есть еще такое понятие, как метод Гаусса – Жордана. Он считается модификацией метода Гаусса и применяется при нахождении обратной матрицы, вычислении неизвестных членов квадратных систем алгебраических линейных уравнений. Метод Гаусса – Жордана удобен тем, что он в один этап позволяет решить СЛУ (без применения прямого и обратного ходов).
Начнем с термина «обратная матрица». Допустим, у нас есть матрица A. Обратной для нее будет матрица A-1, при этом обязательно выполняется условие: A × A-1 = A-1 × A = E, т. е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
Важный нюанс: в линейной алгебре есть теорема существования обратной матрицы. Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю.
Основные шаги, на которых основывается метод Гаусса – Жордана:
- Взгляните на первую строку конкретной матрицы. Метод Гаусса – Жордана можно начинать применять, если первое значение не равно нулю. Если же на первом месте стоит 0, то поменяйте строки местами так, чтобы первый элемент имел отличное от нуля значение (желательно, чтобы число было ближе к единице).
- Разделите все элементы первой строки на первое число. У вас получится строка, которая начинается с единицы.
- Из второй строки вычтите первую строку, умноженную на первый элемент второй строки, т. е. в итоге у вас получится строка, которая начинается с нуля. Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент.
- В итоге вы получите верхнюю треугольную матрицу методом Гаусса — Жордана. В ней главная диагональ представлена единицами. Нижний угол заполнен нулями, а верхний угол – разнообразными значениями.
- Из предпоследней строки вычтите последнюю строчку, умноженную на необходимый коэффициент. У вас должна получиться строка с нулями и единицей. Для остальных строк повторите аналогичное действие. После всех преобразований получится единичная матрица.
Пример нахождения обратной матрицы методом Гаусса – Жордана
Для вычисления обратной матрицы нужно записать расширенную матрицу A|E и выполнить необходимые преобразования. Рассмотрим простой пример. На рисунке ниже представлена матрица A.

Решение:
- Для начала найдем определитель матрицы методом Гаусса (det A). Если этот параметр не окажется равным нулю, то матрица будет считаться невырожденной. Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2.
- Составим расширенную матрицу, добавив к исходной матрице единичную матрицу. Полученный массив элементов будем использовать для нахождения обратной матрицы методом Гаусса – Жордана.
- Первый элемент в первой строке равен единице. Нас это устраивает, т. к. не нужно переставлять строки и делить данную строку на какое-нибудь число. Начинаем работать со второй и третьей строками. Чтобы первый элемент во второй строке превратился в 0, отнимем от второй строки первую строчку, умноженную на 3. Из третьей строчки вычтем первую (умножения не требуется).
- В получившейся матрице второй элемент второй строчки равен –4, а второй элемент третьей строчки равен –1. Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу.
- Из второй строчки отнимем последнюю строчку, умноженную на 4, из первой строчки – последнюю строчку, умноженную на 5. Далее вычтем из первой строчки вторую строчку, умноженную на 2. С левой стороны мы получили единичную матрицу. Справа находится обратная матрица.

Пример решения СЛУ методом Гаусса – Жордана
На рисунке представлена система линейных уравнений. Требуется найти значения неизвестных переменных, используя матрицу, метод Гаусса – Жордана.

Решение:
- Составим расширенную матрицу. Для этого вынесем в таблицу коэффициенты и свободные члены.
- Решим матрицу методом Гаусса – Жордана. Из строки № 2 вычтем строку № 1. Из строки № 3 вычтем строку № 1, предварительно умноженную на 2.
- Поменяем местами строки № 2 и 3.
- От строки № 3 отнимем строку № 2, умноженную на 2. Разделим полученную третью строку на –1.
- От строки № 2 отнимем строку № 3.
- От строки № 1 отнимем строку № 2, умноженную на –1. Сбоку у нас получился столбик, состоящий из цифр 0, 1 и –1. Из этого делаем вывод, что x1 = 0, x2 = 1 и x3 = –1.

При желании можно проверить правильность решения, подставив вычисленные значения в уравнения:
- 0 – 1 = –1, первое тождество из системы является верным;
- 0 + 1 + (–1) = 0, второе тождество из системы является верным;
- 0 – 1 + (–1) = –2, третье тождество из системы является верным.
Вывод: используя метод Гаусса – Жордана, мы нашли правильное решение квадратной системы, объединяющей линейные алгебраические уравнения.
Онлайн-калькуляторы
Жизнь современной молодежи, обучающейся в вузах и изучающей линейную алгебру, значительно упростилась. Еще несколько лет назад находить решения систем методом Гаусса и Гаусса – Жордана приходилось самостоятельно. Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
В интернете есть немало ресурсов со встроенными онлайн-калькуляторами. Матрицы методом Гаусса, системы уравнений решаются этими программами за несколько секунд. Студентам требуется только указывать необходимые параметры (например, количество уравнений, количество переменных).
fb.ru
Метод Гаусса-Зейделя — это… Что такое Метод Гаусса-Зейделя?
- Метод Гаусса-Зейделя
Метод Гаусса—Зейделя[1] является классическим итерационным методом решения системы линейных уравнений.
Постановка задачи
Возьмём систему:
 , где
, где 
Или

И покажем, как её можно решить с использованием метода Гаусса-Зейделя.
Метод
Чтобы пояснить суть метода, перепишем задачу в виде:

Здесь в j-м уравнении мы перенесли в правую часть все члены, содержащие xi , для i > j. Эта запись может быть представлена:

где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули.
Итеративный процесс в методе Гаусса-Зейделя строится по формуле
 после выбора соответствующего начального приближения
после выбора соответствующего начального приближения  .
.Метод Гаусса-Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что новые значения
 используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
где

Таким образом i-тая компонента (k + 1)-го приближения вычисляется по формуле:
Условие сходимости
Приведем достаточное условие сходимости метода.
Условие окончания
Условие окончания итерационного процесса Зейделя при достижении точности
 в упрощённой форме имеет вид:
в упрощённой форме имеет вид:Более точное условие окончания итерационного процесса имеет вид
и требует больше вычислений. Хорошо подходит для разреженных матриц.
Пример алгоритма на с++
// Условие сходимости bool converge(double *xk, double* xkp) { bool b = true; for (int i = 0; i < n; i++) { if (fabs(xk[i]-xkp[i]) > eps) { b = false; break; } } return b; } while(converge(x,p)) { for(int i = 0; i < n; i++) { var = 0; for(int j = 0; j < n; j++) { if(j != i){ var += (a[i][j]*x[j]); } } p[i] = x[i]; x[i]=(b[i] - var)/a[i][i]; } }Примечания
- ↑ Людвиг Зейдель (1821—1896) — немецкий астроном и математик, Карл Фридрих Гаусс (1777—1855) — немецкий математик, астроном и физик
См. также
Wikimedia Foundation. 2010.
- Метод Гаусса-Жордана
- Метод Гаусса — Йордана
Смотреть что такое «Метод Гаусса-Зейделя» в других словарях:
Метод Гаусса — Зейделя — У этого термина существуют и другие значения, см. метод покоординатного спуска. Метод Гаусса Зейделя[1] является классическим итерационным методом решения системы линейных уравнений. Содержание 1 Постановка задачи 2 Метод … Википедия
Метод Гаусса—Зейделя — Метод Гаусса Зейделя[1] является классическим итерационным методом решения системы линейных уравнений. Содержание 1 Постановка задачи 2 Метод 3 Условие сходимости … Википедия
Метод Гаусса (оптимизация) — У этого термина существуют и другие значения, см. Метод Гаусса. Метод Гаусса[1] прямой метод решения задач многомерной оптимизации. Содержание 1 Описание 2 Примечания … Википедия
Метод Гаусса — У этого термина существуют и другие значения, см. Метод Гаусса (оптимизация). Метод Гаусса[1] классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью… … Википедия
Метод Зейделя — Метод Гаусса Зейделя[1] является классическим итерационным методом решения системы линейных уравнений. Содержание 1 Постановка задачи 2 Метод 3 Условие сходимости … Википедия
Метод Якоби — метод простой итерации для решения системы линейных алгебраических уравнений. Содержание 1 Постановка задачи 2 Описание метода … Википедия
Метод покоординатного спуска — Содержание 1 Постановка задачи решения системы уравнений в терминах методов оптимизации 2 Градиентные методы … Википедия
Метод Якоби для линейных систем — У этого термина существуют и другие значения, см. Метод Якоби. Метод Якоби метод простой итерации для решения системы линейных алгебраических уравнений. Содержание 1 Постановка задачи 2 Описание метода … Википедия
Метод простой итерации — Содержание 1 Постановка задачи 2 Численные методы решения уравнений 2.1 Метод простой итерации … Википедия
Стационарный итерационный метод — Стационарный итерационный метод это метод, который может быть представлен в следующей простой форме: , где и не зависят от номера итерации . Стационарные итерационные методы метод Якоби … Википедия
biograf.academic.ru
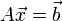 , где
, где 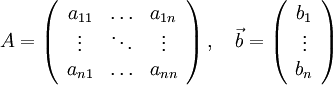
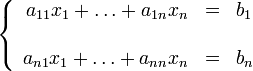
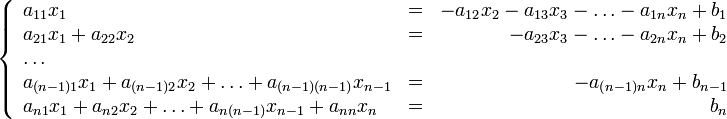
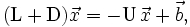
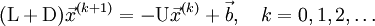 после выбора соответствующего начального приближения
после выбора соответствующего начального приближения 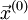 .
.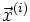 используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации: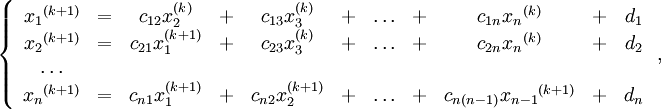
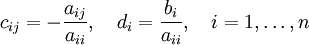
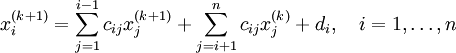
 в упрощённой форме имеет вид:
в упрощённой форме имеет вид: