Гаусс, Карл Фридрих — Википеди

ХӀара яззам Википеди чура бу — маьрша энциклопеди

Иога́нн Карл Фри́дрих Га́усс (нем. Johann Carl Friedrich Gauß; 1777 шеран 30 апрель, Брауншвейг — 1855 шеран 23 февраль, Гёттинген) — гӀарвелла немцойн математик, механик, физик, астроном^[1]. Лоруш ву массо а заманийн тоьллачарах математик, «математикийн паччахь»^[2]. Медаль Коплин лауреат (1838 шо), кхоьчу пачхьалкхара Шведийн а (1821 шо), Российн (1824 шо) а Ӏилманийн академийн декъашхо, ингалсан Лондонан паччахьан юкъараллин.

Гаусс вина цӀа (ца дисна) Брауншвейгехь йолу Гауссан памятник. Цунна тӀехь биллина бу 17 зӀенар йолу седа Гаусс а, Вебер а. Гёттингенехь йолу скульптура.

Гаусс — это… Что такое Гаусс?

        Карл Фридрих (30.4.1777, Брауншвейг, — 23.2.1855, Гёттинген), немецкий математик, внёсший фундаментальный вклад также в астрономию и геодезию. Родился в семье водопроводчика. С 1795 по 1798 учился в Гёттингенском университете. В 1799 получил доцентуру в Брауншвейге, в 1807 — кафедру математики и астрономии в Гёттингенском университете, с которой была также связана должность директора Гёттингенской астрономической обсерватории. На этом посту Г. оставался до конца жизни. Отличительными чертами творчества Г. являются глубокая органическая связь в его исследованиях между теоретической и прикладной математикой, необычайная широта проблематики. Работы Г. оказали большое влияние на развитие высшей алгебры, теории чисел, дифференциальной геометрии, теории притяжения, классической теории электричества и магнетизма, геодезии, целых отраслей теоретической астрономии. Во многих областях математики труды Г. содействовали повышению требований к логической отчётливости доказательств, однако сам Г. оставался в стороне от работ по строгому обоснованию математического анализа, которые проводил в его время О. Коши.          Первое крупное сочинение Г. по теории чисел и высшей алгебре — «Арифметические исследования» (1801) — во многом предопределило дальнейшее развитие этих дисциплин. Г. даёт здесь обстоятельную теорию квадратичных вычетов (См. Квадратичный вычет), первое доказательство квадратичного закона взаимности — одной из центральных теорем теории чисел. Г. даёт также новое подробное изложение арифметической теории квадратичных форм, до того построенной Ж. Лагранжем, в частности тщательную разработку теории композиции классов таких форм. В конце книги излагается теория уравнений деления круга (т. е. уравнений

xⁿ — 1 = 0), которая во многом была прообразом Галуа теории (См. Галуа теория). Помимо общих методов решения этих уравнений, Г. установил связь между ними и построением правильных многоугольников. Он, впервые после древнегреческих учёных, сделал значительный шаг вперёд в этом вопросе, а именно: Г. нашёл все те значения n, для которых правильный n-угольник можно построить циркулем и линейкой; в частности, решив уравнение х¹⁷—1 = 0, он дал построение правильного 17-угольника при помощи циркуля и линейки. Г. придавал этому открытию очень большое значение и завещал выгравировать правильный 17-угольник, вписанный в круг, на своём надгробном памятнике, что и было исполнено.          Астрономические работы Г. (1800—20) в основном связаны с решением проблемы определения орбит малых планет и исследованием их возмущений. Г. как астроном получил широкую известность после разработки метода вычисления эллиптических орбит планет по трём наблюдениям, успешно примененного им к первым открытым малым планетам Церера (1801) и Паллада (1802). Результаты исследований по вычислению орбит Г. опубликовал в сочинении «Теория движения небесных тел» (1809). В 1794—95 открыл и в 1821—23 разработал основной математический метод обработки неравноценных наблюдательных данных (Наименьших квадратов метод). В связи с астрономическими вычислениями, основанными на разложении интегралов соответствующих дифференциальных уравнений в бесконечные ряды, Г. занялся исследованием вопроса о сходимости бесконечных рядов [в работе, посвященной изучению гипергеометрического ряда (См. Гипергеометрический ряд) (1812)].          Работы Г. по геодезии (1820—30) связаны с поручением провести геодезическую съёмку и составить детальную карту Ганноверского королевства; Г. организовал измерение дуги меридиана Гёттинген — Альтона, в результате теоретической разработки проблемы создал основы высшей геодезии («Исследования о предметах высшей геодезии», 1842—47). Для оптической сигнализации Г. изобрёл специальный прибор — Гелиотроп. Изучение формы земной поверхности потребовало углублённого общего геометрического метода для исследования поверхностей. Выдвинутые Г. в этой области идеи получили выражение в сочинении «Общие изыскания о кривых поверхностях» (1827). Руководящая мысль этого сочинения заключается в том, что при изучении поверхности как бесконечно тонкой гибкой плёнки основное значение имеет не уравнение поверхности в декартовых координатах, а дифференциальная квадратичная форма, через которую выражается квадрат элемента длины и инвариантами которой являются все собственные свойства поверхности — прежде всего её кривизна в каждой точке. Др. словами, Г. предложил рассматривать те свойства поверхности (т. н. внутренние), которые не зависят от изгибаний поверхности, не изменяющих длин линий на ней. Созданная таким образом внутренняя геометрия поверхностей послужила образцом для создания

n-mepной римановой геометрии (См. Риманова геометрия).          Исследования Г. по теоретической физике (1830—40) являются в значительной мере результатом тесного общения и совместной научной работы с В. Вебером. Вместе с Вебером Г. создал абсолютную систему электромагнитных единиц и сконструировал в 1833 первый в Германии электромагнитный телеграф. В 1835 Г. основал магнитную обсерваторию при Гёттингенской астрономической обсерватории. В 1838 он издал труд «Общая теория земного магнетизма». Небольшое сочинение «О силах, действующих обратно пропорционально квадрату расстояния» (1834—40) содержит основы теории потенциала. К теоретической физике примыкают также разработка (1829) Г. принципа наименьшего принуждения (см. Гаусса принцип) и работы по теории капиллярности (1830). К числу физических исследований Г. относятся и его «Диоптрические исследования» (1840), в которых он заложил основы теории построения изображения в системах линз.          Очень многие исследования Г. остались неопубликованными и в виде очерков, незаконченных работ, переписки с друзьями входят в его научное наследие. Вплоть до 2-й мировой войны оно тщательно разрабатывалось Гёттингенским учёным обществом, которое издало 12 тт. сочинений Г. Наиболее интересными в этом наследии являются дневник Г. и материалы по неевклидовой геометрии и теории эллиптических функций. Дневник содержит 146 записей, относящихся к периоду от 30 марта 1796, когда 19-летний Г. отметил открытие построения правильного 17-угольника, по 9 июля 1814. Эти записи дают отчётливую картину творчества Г. в первой половине его научной деятельности; они очень кратки, написаны на латинском языке и излагают обычно сущность открытых теорем. Материалы, относящиеся к неевклидовой геометрии, обнаруживают, что Г. пришёл к мысли о возможности построения наряду с евклидовой геометрией и геометрии неевклидовой в 1818, но опасение, что эти идеи не будут поняты, и, по-видимому, недостаточное сознание их научной важности были причиной того, что Г. их не разрабатывал далее и не опубликовывал. Более того, он категорически запрещал опубликовывать их тем, кого посвящал в свои взгляды. Когда вне всякого отношения к этим попыткам Г. неевклидова геометрия была построена и опубликована Н. И. Лобачевским (См. Лобачевский), Г. отнёсся к публикациям Лобачевского с большим вниманием, был инициатором избрания его член-корреспондентом Гёттингенского учёного общества, но своей оценки великого открытия Лобачевского по существу не дал. Архивы Г. содержат также обильные материалы по теории эллиптических функций и своеобразную их теорию; однако заслуга самостоятельной разработки и публикации теории эллиптических функций принадлежит К. Якоби и Н. Абелю (См. Абель).

         Соч.: Werke, Bd 1 —, Gött., 1908 —; в рус. пер. — Общие исследования о кривых поверхностях, в сборнике: Об основаниях геометрии, 2 изд., Каз., 1895; Теоретическая астрономия. (Лекции, читанные в Гёттингене в 1820—26 гг., записанные Купфером), в кн.: Крылов А. Н., Собр. трудов, т. 6, М. — Л., 1936; Письма П. С. Лапласа, К. Ф. Гаусса, Ф. В. Бесселя и др. к академику Ф. И. Шуберту, в сборнике: Научное наследство, т 1, М. — Л., 1948, с. 801—22.

         Лит.: Клейн Ф., Лекции о развитии математики в 19 столетии, пер. с нем., ч. 1, М. — Л., 1937: Карл Фридрих Гаусс. Сб. ст., М., 1956.

        

        К. Ф. Гаусс.

Пушка Гаусса — Википедия

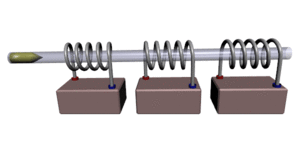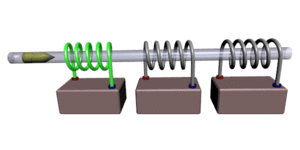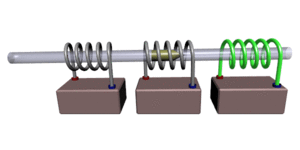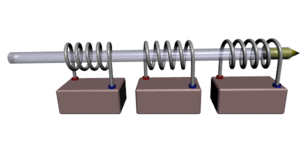Иллюстрация принципа стрельбы

Пушка Гаусса (англ. Gauss gun, Coil gun, Gauss cannon) — одна из разновидностей электромагнитного ускорителя масс. Названа по имени немецкого учёного Карла Гаусса, заложившего основы математической теории электромагнетизма. Следует иметь в виду, что этот метод ускорения масс используется в основном в любительских установках, так как не является достаточно эффективным для практической реализации. По своему принципу работы (создание бегущего магнитного поля) сходна с устройством, известным как линейный двигатель.

Пушка Гаусса состоит из соленоида, внутри которого находится ствол (как правило, из диэлектрика). В один из концов ствола вставляется снаряд, сделанный из ферромагнетика. При протекании электрического тока в соленоиде возникает электромагнитное поле, которое разгоняет снаряд, «втягивая» его внутрь соленоида. На концах снаряда при этом образуются полюса, ориентированные согласно полюсам катушки, из-за чего после прохода центра соленоида снаряд притягивается в обратном направлении, то есть тормозится. В любительских схемах иногда в качестве снаряда используют постоянный магнит, так как с возникающей при этом ЭДС индукции легче бороться. Такой же эффект возникает при использовании ферромагнетиков, но выражен он не так ярко благодаря тому, что снаряд легко перемагничивается (коэрцитивная сила).

Для наибольшего эффекта импульс тока в соленоиде должен быть кратковременным и мощным. Как правило, для получения такого импульса используются электролитические конденсаторы большой ёмкости и с высоким рабочим напряжением.

Параметры ускоряющих катушек, снаряда и конденсаторов должны быть согласованы таким образом, чтобы при выстреле к моменту подлета снаряда к соленоиду индукция магнитного поля в соленоиде была максимальна, но при дальнейшем приближении снаряда резко падала. Стоит заметить, что возможны разные алгоритмы работы ускоряющих катушек.

Кинетическая энергия снаряда

E=mv22{\displaystyle E={mv^{2} \over 2}}

m{\displaystyle m} — масса снаряда

v{\displaystyle v} — его скорость

Энергия, запасаемая в конденсаторе

E=CU22{\displaystyle E={CU^{2} \over 2}}

U{\displaystyle U} — напряжение конденсатора

C{\displaystyle C} — ёмкость конденсатора

Время разряда конденсаторов

Это время за которое конденсатор полностью разряжается:

T=πLC2{\displaystyle T={\pi {\sqrt {LC}} \over 2}}

L{\displaystyle L} — индуктивность

C{\displaystyle C} — ёмкость

Время работы катушки индуктивности

Это время, за которое ЭДС катушки индуктивности возрастает до максимального значения (полный разряд конденсатора) и полностью падает до 0. Оно равно верхнему полупериоду синусоиды.

T=2πLC{\displaystyle T=2\pi {\sqrt {LC}}}

L{\displaystyle L} — индуктивность

C{\displaystyle C} — ёмкость

Стоит заметить, что в представленном виде две последние формулы не могут применяться для расчетов пушки Гаусса, хотя бы по той причине, что по мере движения снаряда внутри катушки, её индуктивность все время изменяется.

Теоретически возможно применение пушек Гаусса для запуска лёгких спутников на орбиту, так как при стационарном использовании есть возможность иметь большой источник энергии. Основное применение — любительские установки, демонстрация свойств ферромагнетиков. Также достаточно активно используется в качестве детской игрушки или развивающей техническое творчество самодельной установки (простота и относительная безопасность)

Простейшие конструкции могут быть собраны из подручных материалов даже при школьных знаниях физики^[1]

Существует множество сайтов, в которых подробно описано, как собрать пушку Гаусса. Но стоит помнить, что создание оружия в некоторых странах может преследоваться по закону. Поэтому, перед тем, как создавать пушку Гаусса, стоит задуматься, как вы будете применять её.

Пушка Гаусса в качестве оружия обладает преимуществами, которыми не обладают другие виды стрелкового оружия. Это отсутствие гильз и неограниченность в выборе начальной скорости и энергии боеприпаса, возможность бесшумного выстрела (если скорость достаточно обтекаемого снаряда не превышает скорости звука) в том числе без смены ствола и боеприпаса, относительно малая отдача (равная импульсу вылетевшего снаряда, нет дополнительного импульса от пороховых газов или движущихся частей), теоретически, больша́я надёжность и, в теории, износостойкость, а также возможность работы в любых условиях, в том числе в космическом пространстве.

Однако, несмотря на кажущуюся простоту пушки Гаусса, использование её в качестве оружия сопряжено с серьёзными трудностями, главное из которых: большие затраты энергии.

Первая и основная трудность — низкий КПД установки. Лишь 1-7 % заряда конденсаторов переходят в кинетическую энергию снаряда. Отчасти этот недостаток можно компенсировать использованием многоступенчатой системы разгона снаряда, но в любом случае КПД редко достигает 27 %. В основном в любительских установках энергия, запасённая в виде магнитного поля, никак не используется, а является причиной использования мощных ключей (часто применяют IGBT модули) для размыкания катушки (правило Ленца).

Вторая трудность — большой расход энергии (из-за низкого КПД).

Третья трудность (следует из первых двух) — большой вес и габариты установки при её низкой эффективности.

Четвёртая трудность — достаточно длительное время накопительной перезарядки конденсаторов, что заставляет вместе с пушкой Гаусса носить и источник питания (как правило, мощную аккумуляторную батарею), а также высокая их стоимость. Можно, теоретически, увеличить эффективность, если использовать сверхпроводящие соленоиды, однако это потребует мощной системы охлаждения, что приносит дополнительные проблемы, и серьёзно влияет на область применения установки. Или же использовать заменяемые батареи-конденсаторы.

Пятая трудность — с увеличением скорости снаряда время действия магнитного поля, за время пролёта снарядом соленоида, существенно сокращается, что приводит к необходимости не только заблаговременно включать каждую следующую катушку многоступенчатой системы, но и увеличивать мощность её поля пропорционально сокращению этого времени. Обычно этот недостаток сразу обходится вниманием, так как большинство самодельных систем имеет или малое число катушек, или недостаточную скорость пули.

В условиях водной среды применение пушки без защитного кожуха также серьёзно ограничено — дистанционной индукции тока достаточно, чтобы раствор солей диссоциировал на кожухе с образованием агрессивных (растворяющих) сред, что требует дополнительного магнитного экранирования.

Таким образом, на сегодняшний день у пушки Гаусса нет перспектив в качестве оружия, так как она значительно уступает другим видам стрелкового оружия, работающего на других принципах. Теоретически, перспективы, конечно, возможны, если будут созданы компактные и мощные источники электрического тока и высокотемпературные сверхпроводники (200—300К). Однако, установка, подобная пушке Гаусса, может использоваться в космическом пространстве, так как в условиях вакуума и невесомости многие недостатки подобных установок нивелируются. В частности, в военных программах СССР и США рассматривалась возможность использования установок, подобных пушке Гаусса, на орбитальных спутниках для поражения других космических аппаратов (снарядами с большим количеством мелких поражающих деталей), или объектов на земной поверхности.

Довольно часто в литературе научно-фантастического жанра упоминается пушка Гаусса. Она выступает там в роли высокоточного смертоносного оружия.

Примером такого литературного произведения являются книги из серии «S.T.A.L.K.E.R.», написанные по серии игр S.T.A.L.K.E.R., где Гаусс-пушка была одним из мощнейших видов оружия, не считая РПГ-7.

Но первым в научной фантастике пушку Гаусса воплотил в реальность Гарри Гаррисон в своей книге «Месть Стальной Крысы». Цитата из книги: «Каждый имел при себе гауссовку — многоцелевое и особо смертоносное оружие. Его мощные батареи накапливали впечатляющий заряд. Когда нажимали на спуск, в стволе генерировалось сильное магнитное поле, разгоняющее снаряд до скорости, не уступающей скорости снаряда любого другого оружия с реактивными патронами. Но гауссовка имела то превосходство, что обладала более высокой скорострельностью, была абсолютно бесшумной и стреляла любыми снарядами, от отравленных иголок до разрывных пуль».

1. ↑ Брага Н. Создание роботов в домашних условиях. — М.: НТ Пресс, 2007. — С. 141 — ISBN 5-477-00749-4.

Проекция Гаусса — Крюгера — Википедия

Материал из Википедии — свободной энциклопедии

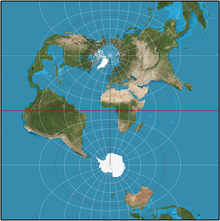
Развёртка карт проекции Гаусса-Крюгера на плоскую поверхность

Проекция Гаусса — Крюгера — поперечная цилиндрическая равноугольная картографическая проекция, разработанная немецкими учёными Карлом Гауссом и Луи Крюгером^[1]. Эта проекция является вариантом поперечной проекции Меркатора^[2].

Названия «проекция Гаусса — Крюгера» и «поперечная проекция Меркатора» также используются как взаимозаменяемые синонимы^[2][3].

Применение этой проекции даёт возможность практически без существенных искажений изобразить довольно значительные участки земной поверхности и, что очень важно, построить на этой территории систему плоских прямоугольных координат. Эта система является наиболее простой и удобной при проведении инженерных и топографо-геодезических работ^[4].

Cферическая форма поперечной проекции Меркатора

Первый вариант поперечной цилиндрической равноугольной проекции был представлен в 1772 году немецким учёным Иоганном Генрихом Ламбертом^[5]. Аналогично простейшему варианту проекции Меркатора эта проекция представляет собой проекцию сферы на цилиндр^[5], однако в отличие от классической проекции Меркатора, здесь цилиндр ориентирован продольно: не вдоль экватора, а вдоль одного из меридианов^[2].

Вариант поперечной цилиндрической равноугольной проекции основанный на проекции эллипса был опубликован в 1825 году Карлом Гауссом^[6]. Для обозначения этой проекции использовались названия: проекция Гаусса-Ламберта, конформная проекция Гаусса, а также Ганноверская проекция Гаусса, так как она использовалась при обработке данных ганноверской триангуляции 1821-1825 годов^[3][1]. Во второй половине 19 века для обозначения этой проекции также стали использовать название «поперечная проекция Меркатора» (англ. transverse Mercator projection)^[7].

Впоследствии немецкий топограф Оскар Шрайбер, основываясь на работах Гаусса, разработал новый вариант проекции, которая получила название «проекция Гаусса-Шрайбера». Эта проекция использовалась в работах над Прусским кадастром в 1876-1923 годах.^[3]

В 1912 году Луи Крюгер опубликовал труд, продолжающий работы Гаусса и Шрайбера^[8].

Шкалы географических координат и километровая сетка на карте масштабом 1:25000. Сопоставление угловых и прямоугольных координат

Пример алгоритма перевода из географических координат в прямоугольные приведен в Викиучебнике.

В результате исследований было установлено, что оптимальные размеры территории изображения должны ограничиваться меридианами, отстоящими друг от друга на 6° (хотя в принятой в Германии первоначальной версии этой проекции меридианы отстоят на 3°). Эта фигура получила название сфероидального двуугольника. Его размеры: 180° по широте (от полюса до полюса), и 6° по долготе. Несмотря на то, что площадь зоны в проекции (зоны Гаусса) будет увеличенной, относительные искажения длин в отдалённых от среднего меридиана точках экватора на границе зоны составит 1/800. Максимальные искажения длин в пределах зоны составляет +0,14 %, а площадей — +0,27 %, а в пределах России — ещё меньше (примерно 1/1400). Таким образом, искажения длин и площадей в пределах зоны меньше, чем искажения, возникающие при печати карты за счёт деформации бумаги. Изображение зоны в проекции Гаусса практически не имеет искажений и допускает любые карто- и морфометрические работы.

Точкой отсчёта принимается пересечение выбранного осевого меридиана с экватором. Для этого вся земная поверхность разбита на зоны ограниченные меридианами отстоящими друг от друга на 6°, с порядковой нумерацией начиная от Гринвичского меридиана на восток. Всего 60 зон. К примеру 8-я зона находится между меридианами 42° и 48° восточной долготы, а 58-я зона соответственно находится между меридианами 12° и 18° западной долготы.

Координаты отсчитываются от середины зоны, при этом во избежание отрицательных значений координат, к значению абсциссы прибавляются 500 км. К примеру координаты условной точки М (смотреть пример на иллюстрации) с координатами 50° 28′ 43″ с.ш. и 31° 32′ 46″ в.д. находятся в 6-й зоне (между 30° и 36° восточной долготы), приблизительно севернее на 500 метров и восточнее на 700 метров от пересечения горизонтальной километровой линии 5594 (севернее экватора на 5594 километра) и вертикальной километровой линии 6396 (западнее середины 6-й зоны на 500-396=104 км). Соответственно запись в прямоугольных координатах условной точки М будет следующей: x = 6396700 и y = 5594500^[9].

1. ↑ ^{1 2} Балис Балио Серапинас. Математическая картография. Учебник для вузов. – М.: Издательский центр «Академия», 2005. – 336 с. — М.: Издательский центр «Академия», 2005. — С. 268. — 336 с. — ISBN 5-7695-2131-7.
2. ↑ ^{1 2 3} ArcGIS 9. Картографические проекции. — Environmental Systems Research Institute, Inc. (ESRI), 2000. — 109 с.
3. ↑ ^{1 2 3} R. E. Deakin, M. N. Hunter, C. F. F. Karney. Warrnambool Conference.pdf The Gauss-Krüger projection (неопр.). Victorian Regional Survey Conference (2010). (недоступная ссылка)
4. ↑ М. В. Потокий КАРТОГРАФИЯ С ОСНОВАМИ ТОПОГРАФИИ, КОМПЛЕКС ПРОГРАММНО-МЕТОДИЧЕСКИХ МАТЕРИАЛОВ ПО ПРЕДМЕТУ, 2003
5. ↑ ^{1 2} Tobler, Waldo R, Notes and Comments on the Composition of Terrestrial and Celestial Maps, 1972 (University of Michigan Press)
6. ↑ Gauss, Karl Friedrich, 1825. «Allgemeine Auflösung der Aufgabe: die Theile einer gegebnen Fläche auf einer andern gegebnen Fläche so abzubilden, daß die Abbildung dem Abgebildeten in den kleinsten Theilen ähnlich wird» Preisarbeit der Kopenhagener Akademie 1822. Schumacher Astronomische Abhandlungen, Altona, no. 3, p. 5–30. [Reprinted, 1894, Ostwald’s Klassiker der Exakten Wissenschaften, no. 55: Leipzig, Wilhelm Engelmann, p. 57–81, with editing by Albert Wangerin, pp. 97–101. Also in Herausgegeben von der Gesellschaft der Wissenschaften zu Göttingen in Kommission bei Julius Springer in Berlin, 1929, v. 12, pp. 1–9.]
7. ↑ Snyder, John P. Flattening the Earth: Two Thousand Years of Map Projections (англ.). — University of Chicago Press (англ.)русск., 1993. — P. 82. — ISBN 978-0-226-76747-5.
8. ↑ Krüger, L. (1912). Konforme Abbildung des Erdellipsoids in der Ebene. Royal Prussian Geodetic Institute, New Series 52.
9. ↑ Военная топография. ВоенИздат. Москва 1977 год. 280 стр.

Теорема Гаусса — Ванцеля — Википедия

Материал из Википедии — свободной энциклопедии

Теоре́ма Га́усса — Ва́нцеля утверждает, что правильный n{\displaystyle n}-угольник возможно построить с помощью циркуля и линейки тогда и только тогда, когда n=2k⋅p1⋅…⋅pm{\displaystyle n=2^{k}\cdot p_{1}\cdot \ldots \cdot p_{m}}, где pi{\displaystyle p_{i}} — различные простые числа Ферма. Это условие также эквивалентно тому, что значение функции Эйлера φ(n){\displaystyle \varphi (n)} является степенью числа два.

Античным геометрам были известны способы построения правильных n{\displaystyle n}-угольников для n=2k,3⋅2k,5⋅2k{\displaystyle n=2^{k},3\cdot 2^{k},5\cdot 2^{k}} и 3⋅5⋅2k{\displaystyle 3\cdot 5\cdot 2^{k}}.

В 1796 году Гаусс показал возможность построения правильных n{\displaystyle n}-угольников при n=2k⋅p1⋯pm{\displaystyle n=2^{k}\cdot p_{1}\cdots p_{m}}, где pi{\displaystyle p_{i}} — различные простые числа Ферма. (Здесь случай m=0{\displaystyle m=0} соответствует числу сторон n=2k{\displaystyle n=2^{k}}.)

В 1837 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Конкретные реализации построения весьма трудоёмки:

Один слишком навязчивый аспирант довёл своего руководителя до того, что тот сказал ему: «Идите и разработайте построение правильного многоугольника с 65537 сторонами». Аспирант удалился, чтобы вернуться через 20 лет с соответствующим построением[2].Дж. Литлвуд