Основные свойства геометрических фигур на плоскости и в пространстве?
Ни в какой. По определению, параллельные прямые не имеют точек пересечения.
Теперь давайте по геометриям и заблуждениям. Всюду будут рассматриваться «плоскости», чтобы это ни значило.
Геометрия Евклида. То, что учили в школе, то, что привычнее и почти точно выполняется в повседневной жизни. Выделю те два факта, что будут существенны потом. Первое: в этой геометрии есть расстояние, между любыми двумя точками существует кратчайшая, и притом только одна (отрезок прямой). Второе: через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной и при том только одну.
Это соответствует какой-то паре аксиом из учебника Погорелова, поэтому мне удобнее будет на это опираться.
Геометрия Лобачевского. С расстоянием в ней все отлично, но нам его сложно представить из-за постоянной отрицательной кривизны (не поняли — не страшно). С параллельностью сложнее. Через точку вне прямой всегда можно провести не просто одну, а бесконечно много параллельных прямых.
Сферическая геометрия. Во-первых, что мы считаем «прямыми». Прямые на сфере — большие круги = круги, высекаемык на сфере плоскостью, проходящей через центр = круги радиуса равного радиусу сферы. Это прямые в том смысле, что это кратчайший путь между не очень далекими (чуть позже станет понятно, какими) точками. Некоторые могли заметить, что если города находятся на одной параллели, то самолет летит не по этой параллели, а по траектории выпуклой на север в северном полушарии. Если порисуете, то заметите, что большой круг, соединяющий две точки проходит северней параллели.
Чем же плохо расстояние на сфере? Возьмем диаметрально противоположные точки на сфере, для них существует бесконечно много кратчайших. Нагляднее: посмотрю на северный и южный полюса. Все мерилианы проходят через них, все они имеют одинаковые длины, любой другой путь будет длиннее.
Параллельных прямых при этом нет совсем, любые две прямые пересекаютсяются в диаметрально противоположных точках.
Проективная плоскость. Самое главное и первое отличие: никакого расстояния нет и быть не может. В принципе, его нельзя ввести, чтобы оно удовлетворяло каким-то естественным условиям (сохранялось при «движениях» плоскости). Таким образом, ни про какие «бесконечно удаленные прямые» сама геометрия не знает, все это придумано людьми, чтобы как-то понять проективную плоскость. Самый «простой» способ: представить привычную нам плоскость (так называемую «аффинную карту») и добавить к ней прямую, которая «бесконечно удалена», причем все прямые, которые были параллельны данной в плоскости, которую представили, пересекутся в какой-то одной точке на этой «бесконечно удаленной» прямой. Такое описание довольно просто: вот я что-то написал в два предложения, и кто-то что-то уже представил. Но оно вводит в заблуждение, никакой выделенной прямой в проективной геометрии нет. Но уже это описание показывает, что параллельных прямых
в проективной геометрии нет.
Ответы Mail.ru: Геометрия и ее разделы…
Геоме́трия (от греч. γη — Земля и μετρέω — «меряю» ) — раздел математики, изучающий пространственные структуры, отношения и их обобщения. Общепринятую в наши дни классификацию различных разделов геометрии предложил Феликс Клейн в своей «Эрлангенской программе» (1872). Согласно Клейну, каждый раздел изучает те свойства геометрических объектов, которые сохраняются (инвариантны) при действии некоторой группы преобразований, специфичной для каждого раздела. В соответствии с этой классификацией, в классической геометрии можно выделить следующие основные разделы. * Евклидова геометрия, в которой предполагается, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении. o Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости. o Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве. * Проективная геометрия, изучающую проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях. Инварианты в этой геометрии — это свойства, сохраняющиеся при замене фигур на подобные им, но другого размера. * Аффинная геометрия, использующая очень общие аффинные преобразования. В ней длины и величины углов не имеют существенного значения, но прямые переходят в прямые. Современная геометрия включает в себя следующие дополнительные разделы. * Многомерная геометрия. * Неевклидовы геометрии. o Сферическая геометрия. o Геометрия Лобачевского. * Риманова геометрия. * Геометрия многообразий. * Топология — наука о непрерывных преобразованиях самого общего вида, то есть свойства объектов, которые остаются неизменными при непрерывных деформациях. В топологии не рассматриваются никакие метрические свойства объектов. По используемым методам выделяют также такие инструментальные подразделы. * Аналитическая геометрия — геометрия координатного метода. В ней геометрические объекты описываются алгебраическими уравнениями в декартовых (иногда аффинных) координатах и затем исследуются методами алгебры и анализа. * Дифференциальная геометрия — изучает линии и поверхности, задающиеся дифференцируемыми функциями, с помощью дифференциальных уравнений.
Понятие геометрической фигуры — Студопедия.Нет
Геометрические фигуры
Из истории развития геометрии
Слово «геометрия» греческое и в переводе на русский язык означает «землемерие». Исторические памятники и археологические находки свидетельствуют о том, что задолго до нашей эры в древнем Вавилоне и Египте люди владели некоторыми геометрическими знаниями. Для решения задач, связанных с земледелием и строительством, требовались умения измерять величины (длину, площадь, объем и другие), знания законов геометрических построений и расчетов. Одно из чудес света – египетские пирамиды свидетельствуют о достижениях египтян в области геометрии.
Греки заимствовали накопленные сведения о геометрических фигурах и применяли их, например, при изучении земельных участков. Они же и придумали название науке, которое используют до сих пор во всех странах мира: «геос» — земля, «метрио» — измеряю. Геометрия, возникшая из практических потребностей человека, постепенно становилась теоретической наукой. Появились ученые, объектами, изучения которых стали не только бытовые задачи, а непосредственно, геометрические фигуры и их свойства: Фалес (624 – 547 до н.э.), Пифагор (580 – 496 до н.э.), Платон (429 – 348 до н.э.), Евклид (III в. до н.э.) и другие.
Основной заслугой Евклида является создание «Начал» — самого распространенного научного сочинения в мире. В 13 книгах им были систематизированы все предыдущие знания геометрии и арифметики. Это произведение стало образцом дедуктивного построения теории. По «Началам» Евклида многие поколения людей на протяжении двух с лишним тысячелетий изучали геометрию, которая получила название евклидовой геометрии.
Значительным событием в истории геометрии стала книга «Геометрия» (1637) французского ученого Рене Декарта (1596 – 1650) – создателя координатной системы и аналитической геометрии. Это стало возможным с развитием алгебры и математического анализа.
Перевод в геометрии произошел в начале XIX в. Некоторые ученые пришли к мысли о создании геометрии, отличной от евклидовой. Великому русскому математику Н.И. Лобачевскому (1792 – 1827) было 34 года, когда он решил «многовековую» проблему V постулата Евклида (о параллельных), построив свою, неевклидову геометрию. В геометрии, которую Лобачевский назвал «воображаемой», принята аксиома: «Через точку, не лежащую на данной прямой, можно провести более одной прямой параллельной данной», здесь сумма углов треугольника меньше 180º, нет квадратов и прямоугольников и др. Геометрия Лобачевского не была признана учеными до 1860 г., затем же нашла свое применение и сыграла огромную роль в развитии математики и физики. Позже были созданы и другие неевклидовы геометрии.
Примечание
Лекция может сопровождаться сообщениями на тему «История возникновения и развития геометрии», предварительно подготовленными студентами.
Геометрия, которую изучают в школе, строится на аксиоматической основе.
Правила построения геометрии
1. Некоторые понятия вводятся без определения, их называют основными. Например: точка, прямая, плоскость.
2. Часть свойств основных понятий раскрывается через аксиомы. Например, через две точки можно провести единственную прямую.
3. Другие понятия определяются, как правило, через род и видовое отличие, через основные понятия или уже определенные понятия. Например, окружность – это множество точек плоскости, равноудаленных от заданной точки.
4. Другие свойства понятий формулируются в виде теорем и доказываются с использованием аксиом и ранее доказанных теорем.
Задание 36
Постройте цепочку определений через род и видовое отличие: отрезок → ломаная → многоугольник → четырехугольник → прямоугольник → квадрат.
Геометрия – наука, изучающая геометрические фигуры и их свойства.
Планиметрия – часть геометрии, изучающая фигуры на плоскости.
Стереометрия – часть геометрии, изучающая фигуры в пространстве.
Дети уже в дошкольном возрасте знакомятся с фигурами на плоскости (плоскими фигурами) и в пространстве (геометрическими телами). При обучении дошкольников не дают явные определения фигурам, а знакомят с их моделями, названием, свойствами, отношением равенства и другими связями между фигурами.
Понятие геометрической фигуры
Одним из свойств окружающих предметов является форма. Форма предметов получила обобщенное отражение в таком математическом понятии, как геометрическая фигура. Геометрические фигуры являются эталонами, пользуясь которыми человек определяет форму предметов.
Дети, познавая окружающий мир, сталкиваются с разнообразием форм предметов, учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур.
— Этот платок имеет форму квадрата.
— У квадрата есть 4 стороны и 4 угла.
— Орнамент выполнен из круга и треугольников.
— Что вы про них знаете?
Рис. 43
Геометрическая фигура – это любое множество точек, поэтому отношения геометрических фигур и операции над ними определяются как отношения множеств и операции с множествами.
Точка, прямая, отрезок, круг, квадрат, треугольник, шар, куб являются геометрическими фигурами.
Примеры:
F
F
Рис. 44 Рис. 45 Рис. 46
1) Пересечение (рис. 44): 
. Вопрос детям: «Сколько вы видите треугольников?»
2) Объединение (рис. 45):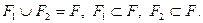 
Задание детям: «Сложи из двух (равных, прямоугольных, равнобедренных) треугольников квадрат».
3) Нахождение дополнения (рис. 46): 
Вопрос детям: «Есть квадрат. Какую фигуру можно добавить, чтобы получился домик?»
Задание 37
Определите, какие отношения между фигурами устанавливают, и какие операции над фигурами выполняют дети, получив следующие задания:
1. Нарисуй круг и квадрат так, чтобы:
— Круг находился в квадрате (рис. 47),
— Квадрат находился в круге (рис. 48),
— Квадрат и круг пересекались (рис. 49),
— Квадрат и круг не пересекались (рис. 50).
 |
Рис. 47 Рис. 48 Рис. 49 Рис. 50
2. Закрась:
— Часть фигуры между границей круга и квадрата (рис. 51),
— Общую часть фигур (рис. 52),
— Всю фигуру, которая получилась (рис. 53).
 |
Рис. 51 Рис. 52 Рис. 53
Учащиеся начальной школы определяют равенство фигур способом наложения:
Фигуры равны, если они при наложении совпадают.
Для развития глазомера дошкольникам предлагают найти одинаковые фигуры по форме и размеру и проверить правильность выбора, наложив одну фигуру на другую.
Геометрия Что изучает геометрия Слово геометрия
Геометрия
Что изучает геометрия? Слово «геометрия» – греческое , оно составлено из двух частей «гео» и «метрия» и дословно на русский язык переводится как «земле-мерие» .
Разделы геометрии Современная геометрия включает в себя следующие дополнительные разделы: Многомерная геометрия. Неевклидовы геометрии. Сферическая геометрия. Геометрия Лобачевского. Риманова геометрия. Геометрия многообразий.
«Геометрия» – это раздел математики, изучающий пространственные формы и их отношения» . «Геометрия – это наука о свойствах геометрических фигур» .
При изучении геометрии нас интересуют геометрические форма и размеры тела. Например, и деревянный, и картонный куб носят одно и тоже название-куб. Также футбольный мяч, резиновый мяч и мыльный пузырь имеют одну и ту же форму-шар.
Если не обращать внимания на свойства предмета (материал, цвет), а рассматривать только его форму и размеры, то этому предмету можно дать название геометрической фигуры или тела.
Возникновение геометрии О Зарождении геометрии около двух тысяч лет назад древнегреческий ученый Геродот писал: Египетский фараон, разделил землю, дав каждому египтянину участок по жребию и брал налог с каждого участка. Иногда Нил заливал участки земли, и пострадавшие просили землемеров перемерить участки , чтобы уменьшить налоги. Так возникла геометрия в Египте, а оттуда перешла в Грецию.
История возникновения геометрии Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т. д. А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т. д. Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов. Пирамиды – а они построены более 5 тыс. лет назад – состоят из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: «Не знающие геометрии не допускаются!» И наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э. ) в его 13 томах «Начала» . Евклид жил в Александрии, был современником царя Птоломея I и учеником Платона. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.
Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире. В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах. Ученый гордо ответил: » В геометрии нет царской дороги».
Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, т. е. логически мыслить.
В геометрии рассматриваются различные возможности расположения геометрических фигур на плоскости. Фигуры делятся на 2 класса: плоские и объемные. Геометрия Планиметрия (свойства фигур на плоскости) Точка, прямая, квадрат, круг и т. д. Стереометрия (Свойства фигур в пространстве) Плоскость, шар, пирамида и т. д.
Планиметрия — раздел евклидовой геометрии, Планиметрия исследующий фигуры на плоскости. у Аксиомой называется бесспорное утверждение, не требующее и не имеющее доказательств. Теоремой называется утверждение, правильность которого устанавливается путем логических рассуждений. Эти рассуждения называются доказательством теоремы. а В А
Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.
Виды стереометрических фигур Додекаэдр – 12 граней, 20 вершин, 30 ребер. Тетраэдр – 4 грани, 4 вершины, 6 ребер.
Виды стереометрических фигур Октаэдр – 8 граней, 6 вершин, 12 ребер. Икосаэдр – 20 граней, 12 вершин, 30 ребер
Основные геометрические понятия Геометрические предложения Определения Название Аксиомы Положение без логического доказательства Верить Теоремы Устанавливающие утверждения при помощи доказательства Доказать
классической геометрии можно выделить следующие основные разделы: Евклидова геометрия, в которой предполагается, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении. Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости. Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве. Проективная геометрия, изучающую проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях. Инварианты в этой геометрии — это свойства, сохраняющиеся при замене фигур на подобные им, но другого размера. Аффинная геометрия, использующая очень общие аффинные преобразования. В ней длины и величины углов не имеют существенного значения, но прямые переходят в прямые. Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.
Литература Каган В. Ф. Очерки по геометрии. -М. : Московский университет, 1963. Свечников А. А. Путешествия в историю математике или как люди научились считать. М. : Просвещение, 1995.
Презентацию выполнили: Ученики МБОУ гимназии № 1 7 -2 класса Момот Полина Игнатьева Анна Кичатов Игорь Рыкова Анна Мещеряков Влад Юшков Никита