Геометрия сечения – «Как строить сечения?» – Яндекс.Знатоки — Детская игровая комната «Волшебный лес»

Posted on 04.09.201821.12.2019 by alexxlab

Содержание

Стереометрия. Задачи на построение сечений

В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.

Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.

Как вы думаете — может ли восьмиугольник быть сечением куба?

И может ли правильный пятиугольник быть сечением куба?

Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.

А вообще сечение — это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.

Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.

При построении сечений мы часто используем следующие теоремы:

1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.

Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.

2. Теорема о прямой и параллельной ей плоскости:

Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.

Эта теорема помогает, например, при построении сечений пирамиды.

Разберем несколько задач на построение сечений.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.

Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.

Продлим отрезки MN и АС;

Проведем РК в плоскости нижней грани; четырехугольник — искомое сечение.

MNLK

2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре

$BC, M \in AD, K \in BD, MK \parallel AB.$

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.

Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,

Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.

3. Постройте сечение куба проходящее через вершину и середины ребер и

BC.

Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;

Треугольники АМР и KCN — прямоугольные равнобедренные, причем

Проведем — в плоскости задней грани и — в плоскости левой грани куба;

Пятиугольник — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.

4. Постройте сечение куба проходящее через вершину В и середины ребер и

CC_1.

Пусть М — середина ребра , N — середина ребра

Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб

5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.

Пусть SH — апофема грани SBC; N—середина SH.

Проведем MN в плоскости ASH;

Четырехугольник KMEF — искомое сечение.

Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.

$\left(MN\right)\cap \left(AH\right)=P;P\in \left(ABC\right).KP\cap BC=F;FN\cap SC=E;$

Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.

Из подобия треугольников SMT и SEH получим, что Значит

По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ. Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.

где — середина ;

— искомое сечение.

7. Постройте сечение куба , проходящее через точку М, лежащую на ребре и точки Т и К, принадлежащие граням АВС и .

$DCC_{1}$

Точки М и К лежат в плоскости задней грани . Соединив М и К, получим, что

Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;

. Трапеция FMEN — искомое сечение.

8. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.

$M \in \left(BB_1C_1\right),N\in \left(AA_1D_1\right),K\in \left(ABC\right)$

Пусть точки и — проекции точек M и N на плоскость нижней грани

Плоскость проходит через параллельные прямые и .

Проведем в этой плоскости MN и

Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Задачи на построение сечений в параллелепипеде . Видеоурок. Геометрия 10 Класс

В ходе урока все желающие смогут получить представление о теме «Задачи на построение сечений в параллелепипеде». Вначале мы повторим четыре основные опорные свойства параллелепипеда. Затем, используя их, решим некоторые типовые задачи на построение сечений в параллелепипеде и на определение площади сечения параллелепипеда.

Тема: Параллельность прямых и плоскостей

Урок: Задачи на построение сечений в параллелепипеде

В ходе урока все желающие смогут получить представление о теме «Задачи на построение сечений в параллелепипеде».

Рассмотрим параллелепипед АВСDА₁B₁C₁D₁(рис. 1). Вспомним его свойства.

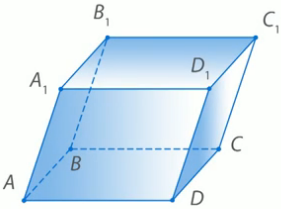
Рис. 1. Свойства параллелепипеда

1) Противоположные грани (равные параллелограммы) лежат в параллельных плоскостях.

Например, параллелограммы АВСD и А₁B₁C₁D₁равны (то есть их можно совместить наложением) и лежат в параллельных плоскостях.

2) Длины параллельных ребер равны.

Например, AD = BC = A₁D₁ = B₁C₁(рис. 2).

Рис. 2. Длины противоположных ребер параллелепипеда равны

3) Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Например, диагонали параллелепипеда BD₁ и B₁D пересекаются в одной точке и делятся этой точкой пополам (рис. 3).

Рис. 3.

4) В сечение параллелепипеда может быть треугольник, четырехугольник, пятиугольник, шестиугольник.

Задача на сечение параллелепипеда

Например, рассмотрим решение следующей задачи. Дан параллелепипед АВСDА₁B₁C₁D₁ и точки M, N, K на ребрах AA₁, A₁D₁, A₁B₁соответственно (рис. 4). Постройте сечения параллелепипеда плоскостью MNK. Точки M и N одновременно лежат в плоскости AA₁D₁ и в секущей плоскости. Значит, MN – линия пересечения двух указанных плоскостей. Аналогично получаем MK и KN. То есть, сечением будет треугольник MKN.

Рис. 4.

Построить сечение параллелепипеда AD

1 плоскостью А₁В₁М_,где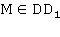

Решение (см. рис. 5)

Рис. 5.

1 способ

Соединим точки А₁ и М. Эти точки лежат одновременно в плоскости AA₁D₁ и в секущей плоскости. Значит, А₁М – линия пересечения этих плоскостей.

Если две параллельные плоскости АВВ₁ и DCC₁ рассечены третьей плоскостью (секущей плоскостью), то линии их пересечения параллельны. Поэтому, проведем прямую MN параллельно А₁В₁, 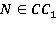. Соединим точки В₁ и N. A

1B₁NM — искомое сечение.

interneturok.ru

Сечение (геометрия) — Cross section (geometry)

Вид в поперечном разрезе уплотнения сжатия

В геометрии и науки , А сечение представляет собой непустое пересечение твердого тела в трехмерном пространстве с плоскостью , или аналог в многомерных пространствах. Режущий объект кружочков создает множество параллельных сечений. Граница поперечного сечения в трехмерном пространстве, параллельно двум из осей , то есть параллельно плоскости , определяемой осями этих, является иногда называют контурной линией ; например, если плоскость прорезает горы с рельефным рельефной карте параллельно земле, результатом является контурная линия в двумерном пространстве , показывая точек на поверхности гор одинаковой высоты .

В техническом чертеже поперечного сечения, будучи проекцию объекта на плоскость , которая пересекает ее, является обычным инструментом , используемым , чтобы изобразить внутреннее расположение 3-мерного объект в двух измерениях. Традиционно заштриховали со стилем штриховки часто с указанием типов используемых материалов.

С компьютерной аксиальной томографией , компьютеры построить поперечные сечения из рентгеновских данных.

Определение

Если плоскость пересекает твердую (3-мерный объект), то область общей плоскости , и твердое вещества называется поперечным сечением твердого вещества. Самолет , содержащий в поперечном сечении твердого вещества может упоминаться в качестве секущей плоскости .

Форма поперечного сечения твердого вещества может зависеть от ориентации плоскости резания до твердого вещества. Например, в то время как все сечения шара представляют собой диски, поперечные сечения куба зависит от того, как секущая плоскость связана с кубом. Если секущая плоскость перпендикулярна линии, соединяющей центры двух противоположных граней куба, поперечное сечение будет квадрат, однако, если секущая плоскость перпендикулярна диагонали куба присоединения противоположные вершины, перекрестная секция может быть либо точка, треугольник или шестиугольник.

разделы Plane

Связанное понятие является то , что из плоского сечения , которая является кривая пересечения плоскости с поверхностью . Таким образом, плоскость сечения является границей поперечного сечения твердого тела в плоскости резания.

Если поверхность в трехмерном пространстве определяется функцией двух переменных, т.е. г = ф ( х , у ) , секции плоскости отсекающих плоскостей, которые параллельны координатной плоскости (плоскость определяется двумя осями координат ) называются линиями уровня или изолинии . Более конкретно, отсекающие плоскости с уравнениями вида г = к (плоскости , параллельные ху плоскости) производят участки плоскости, которые часто называемые контурные линии в областях применения.

Математические примеры сечений и плоских сечений

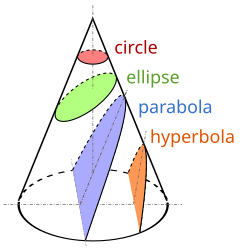Цветные области являются сечением твердого конуса. Их границы (в черном) являются названные плоскости сечения.

Поперечное сечение в многогранника является многоугольник .

В конические сечения — круги , эллипсы , параболы и гиперболы — представляют собой плоские участки в конуса с режущими плоскостями при различных разными углами, как показано на рисунке слева.

Любое поперечное сечение проходит через центр с эллипсоидом образует эллиптическую область, в то время как соответствующие плоские участки представляют собой эллипсы на его поверхность. Это вырожденный к дискам и окружностей, соответственно, когда режущие струи перпендикулярно к оси симметрии. В более общем, плоские участки на квадрике конические сечения.

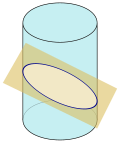Поперечное сечение сплошного цилиндра

Поперечное сечение сплошного прямого кругового цилиндра , проходящей между двумя основаниями является диском , если поперечное сечение параллельно основанию цилиндра или эллиптической области (см схему справа) , если она не является ни параллельна , ни перпендикулярно к основанию. Если секущая плоскость перпендикулярна к основанию она состоит из прямоугольника (не показано) , если это не просто касательной к цилиндру, и в этом случае это один линейный сегмент .

Термин цилиндр может также означать боковую поверхность сплошного цилиндра (см цилиндр (геометрия) ). Если цилиндр используется в этом смысле, указанное в пункте будет читать следующим образом : плоскость сечения прямого кругового цилиндра конечной длины является окружность , если секущая плоскость перпендикулярна к оси цилиндра симметрии, или эллипса , если он не является ни параллельны , ни перпендикулярно к этой оси. Если секущая плоскость параллельна оси плоскость сечения состоит из пары параллельных отрезков , если секущая плоскость не является касательной к цилиндру, и в этом случае, секция плоскость является одной отрезок.

График г = х ² + х + у ² . При частичной производной в (1, 1, 3) , что оставляет у постоянная, соответствующая касательная линия параллельно хты плоскости.

Плоская часть выше графика , показывающая кривой уровня в хтах плоскости при у = 1

Секция плоскость может быть использована для визуализации частной производной от функции по отношению к одному из его аргументов, как показано на рисунке. Пусть г = п ( х , у ) . Принимая частную производную F ( х , у ) относительно х , можно взять плоское сечение функции F при фиксированном значении у , чтобы построить кривую уровня г исключительно против х ; то частная производная по й представляет собой наклон полученного двумерный графика.

В смежных областях

Секция плоскость функции плотности вероятности двух случайных величин , в которой режущая плоскость находится на фиксированном значении одной из переменных является условной функцией плотности от другой переменной (условной на фиксированном значении , определяющей плоское сечение). Если вместо этого плоскость сечения берется при фиксированном значении плотности, результатом является контур изо-плотности . Для нормального распределения , эти контуры представляют собой эллипсы.

В экономике , А производственная функция F ( х , у ) задает выходной сигнал , который может быть получен различными величинами х и у входов, как правило , рабочей силы и физического капитала. Функция производства фирмы или общества могут быть построены в трехмерном пространстве. Если секущая плоскость берутся параллельно х плоскости, результат является изоквантом , показывающий различных комбинации труда и использования капитала , которые привели бы к уровню выхода , заданной высота сечения плоскости. В качестве альтернативы, если плоскость сечения производственной функции берется при фиксированном уровне у , то есть, параллельно XZ -плоскость-то результатом является двумерный график , показывающий , сколько выход может быть получен на каждом из различных значений использования х одного входа в сочетании с фиксированным значением другого входного у .

Кроме того, в экономике, кардинальная или порядковой функция полезности U ( ш , v ) дает степень удовлетворенности потребителя , полученному потребляя величины ш и v из двух товаров. Если плоскость сечения функции полезности принимается на заданной высоте (уровень полезности), двумерная результатом является кривая безразличия показывает различные альтернативные комбинации потребляемых количеств ш и v из двух товаров , все из которых дают указанного уровня полезности.

Площадь и объем

Принцип Кавальери утверждает , что твердые частицы с соответствующими сечениями равных областей имеют равные объемы.

Площадь поперечного сечения ( ) объекта , если смотреть с определенного угла общая площадь ортогональной проекции объекта от этого угла. Например, цилиндр высоты ч и радиус г имеет , если смотреть вдоль его центральной оси, и , если смотреть с ортогональным направления. Сфера радиуса г имеет , если смотреть с любого угла. Более обобщенно, может быть вычислена путем вычисления следующей поверхностный интеграл: A'{\ Displaystyle A ‘}A’знак равноπр2{\ Displaystyle А ‘= \ пи г ^ {2}}A’знак равно2рчас{\ Displaystyle А ‘= 2rh}A’знак равноπр2{\ Displaystyle А ‘= \ пи г ^ {2}}A'{\ Displaystyle A ‘}

A’знак равно∬TопdA⋅р^,{\ Displaystyle A ‘= \ \ IINT пределы _ {\ mathrm {сверху}} d \ mathbf {A}, \ CDOT \ mathbf {\ {г шляпы}}}

где единичный вектор направлен вдоль направления наблюдения к зрителю, представляет собой поверхность элемент с внешним указывающим нормальным, а интеграл берется только по самой верхней поверхности, что часть поверхности , которая является «видимым» из в перспективе зрителя. Для выпуклого тела , каждый луч через объект с точки зрения зрителя пересекает только две поверхности. Для таких объектов, интеграл может быть взят по всей поверхности ( ), беря абсолютное значение подынтегральной (так что «верхний» и «нижний» объекта не вычитают прочь, как это требовалось бы по дивергенции теореме применяется к постоянному векторного поля ) и разделив на две части : р^{\ Displaystyle \ mathbf {\ Шляпа {г}}}dA{\ Displaystyle д \ mathbf {A}}A{\ Displaystyle A}р^{\ Displaystyle \ mathbf {\ Шляпа {г}}}

A’знак равно12∬A|dA⋅р^|{\ Displaystyle А ‘= {\ гидроразрыва {1} {2}} \ IINT \ пределы _ {А} | d \ mathbf {A}, \ CDOT \ mathbf {\ {г шлем}} |}

В более высоких измерениях

По аналогии с поперечным сечением твердого тела, поперечное сечение п — мерного тело в п — мерном пространстве есть непустое пересечение тела с гиперплоскостью (An ( п — 1) -мерное подпространство) , Эта концепция иногда используется , чтобы помочь визуализировать аспекты более высоких размерностей пространств. Например, если четыре-мерный объект прошел через наше трехмерное пространство, мы хотели бы видеть трехмерное сечение четырехмерного объекта. В частности, 4-шарик (гиперсфера) , проходящий через 3-пространства будет выглядеть как при переходе в 3-шаре , который увеличен до максимума , а затем уменьшается в размерах. Этот динамический объект (с точки зрения 3-пространства) представляет собой последовательность поперечных сечений 4-шара.

Примеры в науке

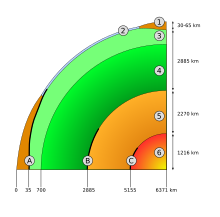Схематическое изображение поперечного сечения внутренней части Земли

Поперечное сечение среднего мозга на уровне верхнего холмика.

В геологии , структура внутренней части планеты часто иллюстрируются с помощью схемы поперечного сечения планеты , которая проходит через центр планеты, как и в поперечном сечении Земли справа.

Поперечные сечения часто используются в анатомии , чтобы проиллюстрировать внутреннюю структуру органа, как показано на рисунке слева.

Поперечное сечение дерева ствола, как показано на рисунке слева, показывает рост кольца , которые могут быть использованы , чтобы найти возраст дерева и временные свойства его среды.

Смотрите также

Викискладе есть медиафайлы по теме сечений .

Заметки

Пошаговое построение сечения параллелепипеда

Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.

Задача 1. Построить сечение параллелепипеда плоскостью, проходящей через точки T, U, V .

Задача 1. Дано

Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой – .

Задача 1. Шаг 1.

Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра – .

Задача 1. Шаг 2.

Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани. Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой – . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром BB_1 – .

Задача 1. Шаг 3.

Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.

Задача 1. Шаг 4.

Задача 2. Построить сечение параллелепипеда плоскостью, проходящей через точки T, U, V

Задача 2. Дано.

Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро BB_1 в точке .

Задача 2. Шаг 1.

Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра B_1C – .

Задача 2. Шаг 2

Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч A_1D_1 и найдем его пересечение с прямой – ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка . Точки и можно соединить отрезком.

Задача 2. Шаг 3.

Шаг 4. Находим точку пересечения отрезком ребра DD_1 – точку .

Задача 2. Шаг 4

Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.

Задача 2. Шаг 5

Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки T, U, V

Задача 3. Дано.

Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.

Задача 3. Шаг 1

Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой – .

Задача 3. Шаг 2.

Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром – точка .

Задача 3. Шаг 3.

Шаг 4. Теперь надо найти точку в плоскости передней грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую и найдем пересечение этой прямой с прямой – точка .

Задача 3. Шаг 4

Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер DD_1 – точку , и ребра A_1D_1 – точку .

Задача 3. Шаг 5.

Шаг 6. Соединяем точки и получаем многоугольник сечения.

Задача 3. Шаг 6

Окончательный вид сечения с другого ракурса:

Окончательный вид

Задача 4. Построить сечение параллелепипеда плоскостью, проходящей через точки T, U, V . Точка в задней грани.

Задача 4. Дано

Шаг 1. Проводим прямую через две точки одной плоскости – и . Определяем точку пересечения данной прямой ребра – .

Задача 4. Шаг 1.

Шаг 2. Продолжение прямой пересечется с продолжением прямой CC_1 – так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .

Задача 4. Шаг 2.

Шаг 3. Точка – точка пересечения прямой ребра D_1C_1 . Продлим также ребро и найдем пересечение прямой и прямой – точку , которая принадлежит плоскости основания.

Задача 4. Шаг 3

Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром – точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.

Задача 4. Шаг 4.

Окончательный вид сечения с другого ракурса:

Окончание построения

easy-physic.ru

Построение сечений тетраэдра и параллелепипеда в более сложных случаях

Данный урок поможет получить представление о теме «Построение сечений тетраэдра и параллелепипеда в более сложных случаях». На этом занятии мы познакомимся двумя опорными задачами на построение более сложных сечений. Затем решим несколько задач по построению сечений.

Более сложными будем называть сечения, для построения которых даны точки, лежащие не только на ребрах, но и внутри граней или самой фигуры.

Решим две стандартные задачи на построение сечений для последующего их использования в качестве опорных.

Есть плоскость α и прямая AB, которая пересекает плоскость α. Построить точку пересечения прямой AB и плоскости 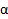(след AB на плоскости ).

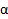1. Первый вариант решения – это когда есть удобная точка S. В этом случае следует провести прямые SB и SA до пересечения с плоскостью 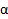в точках и 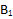. Затем провести прямые AB и 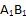, и получим точку пересечения E (рис. 1).

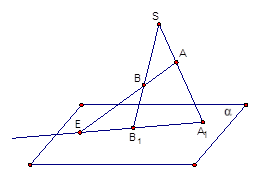
Рис. 1

2. Если точки S нет, то проведем перпендикуляры 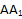и на плоскость 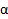. Затем проведем прямые AB и 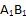и получим точку пересечения E (рис. 2).

Рис. 2

Задача №1:

Дан тетраэдр ABCD и три точки: P, лежащая на ребре DC; M, лежащая на ребре AB; точка N – внутренняя точка грани ABD. Построить сечение плоскостью () данного тетраэдра (рис. 3).

Рис. 3

Решение

Используя первую опорную задачу, найдем пересечение прямой PN и плоскости (ABC) (след прямой PN на плоскость основания). Будем использовать вспомогательную плоскость PND. Проведем прямую DN и на пересечении с AB получим точку 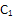. Проведем прямую 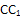и прямую PN и получим точку их пересечения E. Эта точка существует, так как обе прямые лежат в одной плоскости, и мы рассматриваем случай, когда прямые не параллельны. Проведем прямую EM и получим точку Q в месте ее пересечения с ребром AC. Линия MQ будет линией пересечения. Провести прямую MN и получить точку 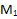в месте ее пересечения с ребром BD. Линия будет линией пересечения. Проведем последнюю линию пересечения PQ.

Можно было обойтись и без опорной задачи:

Проведем прямую NM до пересечения с прямой AD – точки 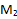, и до пересечения с прямой BD – точки 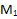. Точку 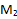соединим с точкой P и таким образом найдем точку пересечения Q. Соединив попарно точки , , 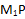PQ, QM, мы получим все линии пересечения.

Ответ: в сечении лежит четырехугольник .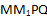

Задача №2:

Дан параллелепипед, заданы точки А и C, лежащие на ребрах, и точка B – внутренняя точка нижней грани. Построить сечение параллелепипеда плоскостью (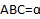) (рис. 4).

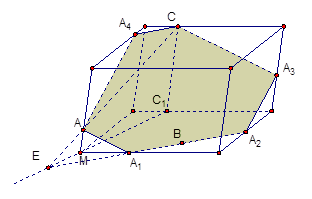
Рис. 4

Решение

Используем вторую опорную задачу. Через точку C проведем прямую, параллельную боковому ребру параллелепипеда. Она пересечется с плоскостью нижнего основания в точке 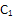, которая лежит на ребре. Проведем прямые 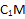и CA и получим точку их пересечения – точку E (след прямой AC на плоскость нижней грани). Точки B и E лежат и в плоскости 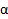, и в плоскости нижнего основания. Проведем через эти точки прямую BE и получим точки пересечения с ребрами нижнего основания – точки и . 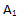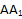Соединив точки A си с , получим две линии пересечения: и 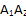. Используя свойство параллелепипеда о параллельности противоположных граней и учитывая факт того, что, при пересечении двух параллельных плоскостей третьей, линии пересечения будут параллельны, проведем линию 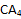, параллельную 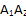. Аналогично проведем прямую 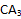параллельно 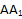. Соединим точки A с 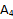и с 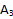и получим линии пересечения и .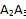

Ответ: получено сечение .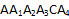

Задача №3:

Дан тетраэдр ABCD, точка P, лежащая на ребре DC и точки M и N, являющиеся внутренними точками граней ABC и ABD соответственно. Построить сечение данного тетраэдра плоскостью (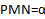) (рис. 5).

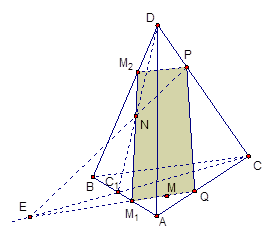
Рис. 5

Решение

Рассмотрим плоскость DNP и получим точку пересечения этой плоскости с ребром AB – точку 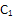. Проведем прямые 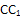и PN. Найдем точку их пересечения E. Проводим прямую EM и получаем точки ее пересечения с ребрами AB и AC – точки 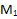и Q соответственно. Проводим линию 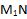и получаем точку ее пересечения с ребром BD – точку 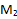. Соединяем точки P с Q и 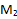с P. Получим последние линии пересечения PQ и .

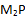Ответ: в сечении получен четырехугольник .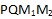

Выводы:

Были рассмотрены опорные задачи и конкретные задачи на построение сечений в тетраэдре и параллелепипеде в более сложных случаях.

Список литературы

И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Yaklass.ru (Источник).
Festival.1september.ru (Источник).
Slideshare.net (Источник).

Домашнее задание

Чем отличаются более сложные сечения от простых?
Обязательно ли использовать опорные задачи при построении сечений?
Что нужно искать для выяснения метода построения следа на плоскости?
На ребрах параллелепипеда ABCDD₁A₁B₁C₁ даны три точки: M на ребре AB, N на ребре CD, K на грани A₁B₁C₁D₁. Построить сечение параллелепипеда плоскостью (MNK).

interneturok.ru

«Построение сечений в многогранниках методом следов». 10-й класс

Девиз: “Мы одна семья, мы учимся все вместе”

Цели урока:

Формирование у учащихся навыков решения задач на построение сечений методом следов.
Формирование и развитие у учащихся пространственного воображения.
Развитие графической культуры и математической речи.

Обучающая цель: формирование умений и навыков построения сечений методом следов.

Воспитывающая цель: воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей.

Тип урока: урок формирования и совершенствования знаний.

Формы организации учебной деятельности: групповая, индивидуальная, коллективная.

Техническое обеспечение урока: мультимедийный проектор, набор геометрических тел (куб, параллелепипед, пирамида).

Структура урока:

Ход урока

Организационный момент: Рассаживаемся на 3 группы по 5 человек. На каждом столе – набор тел, памятки-опоры, карточки для индивидуальной работы по построению сечений.

Слово учителя: Вы изучили аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых и плоскостей в пространстве. При решении многих стереометрических задач используют сечение многогранника плоскостью. Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод.

Мы изучим метод следов.

1) Ребята, я предлагаю вам повторить и вспомнить некоторые геометрические понятия и определения.

Основное понятие геометрии – место пересечения двух прямых, не имеющее измерения.
Геометрическая фигура, состоящая из шести квадратных граней.
Отдельный предмет в пространстве.
Способ изображения пространственных фигур на плоскость.
Плоская фигура, образуемая пересечением тела плоскостью.
Сторона грани многогранника.
Многогранник, поверхность которого состоит из четырех треугольников.

Ответы:

Точка
Куб
Тело
Проекция
Сечение
Ребро
Тетраэдр

2) Ребята, перед вами пример неправильного построения сечения куба АС1 плоскостью, проходящей через заданные точки N, C, D1.

А рядом сечение построено верно.

На уроках черчения вы пользовались определением: Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью.

Вот таким определением мы и будем пользоваться сегодня на уроке.

В тетраэдре сечениями могут быть только треугольники или четырехугольники, а в параллелепипеде – треугольники, четырехугольники, пятиугольники или шестиугольники.

Метод следов включает три важных пункта:

Строится линия пересечения (след) секущей плоскости с плоскостью основания многогранника.
Находим точки пересечения секущей плоскости с ребрами многогранника.
Строим и заштриховываем сечение.

Рассмотрим пример (мультимедийный проектор).

Построить сечение куба, проходящее через точки М, N, L.

Алгоритм построения

3)
4)

5)

6)
7)

Задания группам построить сечение

Три ученика работают у доски (по одному ученику из каждой группы)!
Опора-памятка
Аксиома₁. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и причем только одна.

Аксиома₂. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Аксиома₃. Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом:
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Способы задания плоскости.

Итог урока: повторить алгоритм построения сечения методом следов. Оценить работу учащихся.

Домашнее задание: закончить задания по индивидуальным карточкам.
Презентация
urok.1sept.ru
Сечение геометрических тел плоскостями
Цель урока:
Познакомить студентов с методами построения усечённых геометрических тел в прямоугольных проекциях.

Изучить методы, позволяющие определять на чертеже действительную величину отрезка прямой и плоской фигуры.

Формирование пространственных представлений студентов посредством чтения и построения чертежей.

Совершенствование графической техники.

Учебные пособия и принадлежности:
Для преподавателя:
усечённые геометрические модели.

чертёжные инструменты и принадлежности.

Для студентов:
рабочая тетрадь.

чертёжные инструменты и принадлежности.

План урока:
1. Организационная часть
— приветствие, проверка присутствующих на занятии,
— объявление темы занятия, постановка целей и задач занятия,
5 мин

2. Изложение нового материала
— понятие о сечениях. Привести практические примеры на пересечение тел плоскостями;
— сечение призмы плоскостью;
— сечение кругового цилиндра плоскостью;
— сечение пирамиды плоскостью;
— сечение кругового конуса плоскостью.

40 мин

3. Закрепление новой темы
— построение профильной проекции геометрических тел;
— построение сечения на виде слева;
— построение натуральной величины сечения.

35 мин

4. Заключение
— подведение итогов по занятию,
— приведение в порядок рабочих мест.

5 мин

5. Домашнее задание
— прочитать конспект – лекцию.
— закончить и оформить построения в тетради.
— прочитать материал в учебнике стр.102 – 109.

5 мин

ПОНЯТИЕ О СЕЧЕНИЯХ ГЕОМЕТРИЧЕСКИХ ТЕЛ
Построение пересечения тел плоскостями часто встречается при изображении внешних очертаний деталей машин и приборов, при выявлении внутренних очертаний деталей и во вспомогательных построениях (нахождение точек встречи прямой с поверхностью, отыскание линий пересечения двух поверхностей и др.).
Детали машин и приборов очень часто имеют формы, представляющие собой различные геометрические поверхности. Пылесборник машины для очистки литых деталей (см. рис.1) представляет собой усеченный цилиндр. Форма крышки трубы пылесборника является фигурой сечения прямого кругового цилиндра и представляет собой эллипс. Пример сечения прямого кругового конуса приведен на рисунке 2. Колпак сепаратора представляет собой сварную конструкцию из тонкой листовой стали и состоит из двух конусов.
Рисунок 1
Рисунок 2
Кроме того, иногда необходимо выполнить развёртки поверхности полых деталей, усечённых плоскостью. Это применяется в раскрое листового материала, из которого изготовляются полые детали. Такие детали обычно представляют собой части всевозможных трубопроводов, вентиляционных устройств, кожухов для закрытия механизмов, ограждения станков и т.п. (см. рис.3).
Рисунок 3
При изучении темы «Пересечение поверхностей геометрических тел плоскостями» нужно обратить особое внимание на построение опорных точек при выполнении сечений.
«Сечение – изображение фигуры, получающеёся при мысленном рассечении предмета одной или несколькими плоскостями. На сечении показывается только то, что получается непосредственно в секущей плоскости» (ГОСТ 2.305-68).
Построения прямоугольных и аксонометрических проекций усечённых тел, а также определение истинного вида сечений и развёрток поверхностей геометрических тел часто используются на практике.
Рассекая геометрическое тело плоскостью, получают сечение – ограниченную замкнутую линию, все точки которой принадлежат как секущей плоскости, так и поверхности тела.
Нужно обратить внимание на то, что при пересечении многогранника с плоскостью в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника, а при пересечении тел вращения фигура сечения ограничена плавной кривой линией. Точки этой кривой находят с помощью вспомогательных линий, взятых на поверхности тела (например, образующих конуса и цилиндра). Точки пересечения образующих с секущей плоскостью будут принадлежать кривой линии сечения.
Для того чтобы определить действительную величину сечений, необходимо знать способы преобразования плоскостей проекций: способ вращения и способ перемены плоскостей проекций.
В качестве вспомогательных, к комплексным чертежам применяют аксонометрические проекции. Это делают в тех случаях, когда нужно дать наглядное изображение предмета.
Сечение призмы плоскостью
Из комплексного чертежа на рисунке 4, видно, что плоскость Р_v пересекает не только боковую поверхность, но и верхнее основание призмы. Поэтому фигура сечения представляет собой плоский шестиугольник 1 2 3 4 5 6. Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Р_vс ребрами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы со следом Р_v, секущей плоскости Р (точки 1` — 6`).
Горизонтальные проекции точек пересечения 1-6 совпадают с горизонтальными проекциями ребер.
Имея фронтальные и горизонтальные проекции этих точек, с помощью линий связи находят профильные проекции 1″ — 6» Полученные точки соединяют прямыми линиями и получают профильную проекцию фигуры сечения.
Действительный вид фигуры сечения можно определить любым из способов: вращения, совмещения или перемены плоскостей проекций.
В данном примере (см. рис. 4) применён способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой плоскостью, причём ось х₁, для упрощения построений, параллельна фронтальному следу плоскости Р.
Для нахождения новой горизонтальной проекции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие построения. Из точки 1′ , на фронтальном следе плоскости Р, восстанавливают перпендикуляр к новой оси х₁, и откладывают на нем расстояние от прежней оси х до прежней горизонтальной проекции точки 1, т.е. отрезок n₁. В результате получают точку 1₁. Таким же способом построения находят и остальные горизонтальные проекции точек 2₁-6₁. Соединив прямыми линиями новые горизонтальные проекции 1₁-6₁, получают натуральную величину фигуры сечения (см. рис.4).
Рисунок 4 Вы можете посмотреть здесь.
Сечение цилиндра плоскостью
Построение плоского сечения прямого кругового цилиндра аналогично построению плоского сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра.
На рисунке 5 даны три проекции прямого кругового цилиндра, пересеченного фронтально-проецирующей плоскостью Р.
Из комплексного чертежа видно, что фронтально-проецирующая плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под угломк оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса.
Натуральная величина фигуры сечения, получена способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой. Новая ось проекций выполнена совпадающей с плоскостью Р, (построение аналогично рис. 4).
Рисунок 5 Вы можете посмотреть здесь.
Сечение пятигранной пирамиды плоскостью
Правильная пятигранная пирамида, пересеченная фронтально-проецирующей плоскостью Р, показана на рисунке 7.
Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным следом P_v плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости Р с ребрами пирамиды. Натуральная величина фигуры сечения может быть найдена, например, способом совмещения.
Указание: Нахождение натуральной величины отрезка (бокового ребра пирамиды) (см. рис. 6).
Пусть требуется определить действительный вид боковых ребер пирамиды.
Рисунок 6
Как видно из рисунка, рёбра пирамиды горизонтально-проецирующие, поэтому действительный вид рёбер треугольника можно получить на плоскости V (на виде спереди) вращением любого из рёбер вокруг вертикальной оси до тех пор, пока проекция ребра не станет параллельна плоскости V.
На комплексном чертеже (см. рис.6) ось вращения 2‘S, перпендикулярная плоскости H, проведена через вершину треугольника S. Вращается вершина рёбра треугольника точка 2. После поворота, новая горизонтальная проекция ребра треугольника S 2₁ должна быть параллельна оси х. Фронтальную проекцию — точки 2₁‘ — вершины 2 после поворота находят, проводя вертикальную линию связи вверх до оси х из точки 2₁. Соединив точки 2₁‘ и S‘, получим на плоскости V (на виде спереди) действительную величину ребра S 2 треугольной пирамиды.
Рисунок 7 Вы можете посмотреть здесь.
Сечение прямого кругового конуса плоскостью
При различном расположении секущей плоскости Р по отношению к оси прямого кругового конуса получают различные фигуры сечения, ограниченные большей частью кривыми линиями.
Сечение прямого кругового конуса фронтально-проецирующей плоскостью Р рассматривается на рисунке 8. Основание конуса расположено на горизонтальной плоскости Н. Фигура сечения в данном случае будет ограничена эллипсом.
Для построения горизонтальной проекции контура фигуры сечения – горизонтальную проекцию основания конуса (окружность) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях проводят вспомогательные образующие. Сначала находят фронтальные проекции точек сечения 1` — 12`, лежащих на фронтальном следе плоскости Р_v. Затем с помощью линий связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей S2, проецируется на горизонтальную проекцию этой же образующей S2 в точку 2.
Найденные горизонтальные проекции точек контура сечения соединяют по лекалу. Действительный вид фигуры сечения в данном примере найден способом перемены плоскости проекций. Плоскость Н заменяется новой плоскостью проекции Н₁. Чтобы получить новую горизонтальную проекцию какой-либо точки проекции эллипса, например точки 2₁, из точки 2′ восстанавливают перпендикуляр и откладывают на нем отрезок равный отрезку 2′ — 2, т.е. расстояние n (см. рис.8).
Рисунок 8 Вы можете посмотреть здесь.
Самостоятельная работа по теме: «Сечение геометрических тел плоскостями» (Приложение).
Литература
Основная:
Учебники
В.Г.Григорьев, В.И.Горячев, Т.П.Кузнецова Инженерная графика/ Серия «Учебники, учебные пособия». – Ростов н/Д: Феникс, 2004.

С.К. Боголюбов Черчение – М.: Машиностроение, 2002. ил. И.С.Вышнепольский, В.И. Вышнепольский Черчение для техникумов: Учеб. для учеб. заведений нач. и сред. проф. образования – М.: ООО «ИздательствоАстрель»: ООО «Издательство АСТ», 2002., ил.

И.А.Ройтман, Я.В.Владимиров Черчение: Учеб. Пособие для уч-ся 9 кл. общеобразовательных учреждений. – М.: Гуманит. изд. центр ВЛАДОС, 2001., ил.

Р.С. Миронова, Б.Г.Миронов Инженерная графика – М.: Высш. школа, 2000., ил.

А.Потёмкин Инженерная графика. Просто и доступно – Москва: издательство «Лори», 2000.

Дополнительная:
Сборники заданий
Боголюбов С.К. Задания по курсу инженерной графики. – М.: Машиностроение, 2004.

Миронова Р.С., Миронов Б.Г. Сборник задач по инженерной графике. Учебное пособие. – М.: Высшая школа, 2000.

Пакеты прикладных программ компьютерной графики профессиональной деятельности.

urok.1sept.ru