Математическая гипербола. Как построить гиперболу?

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Математическая гипербола.

Функция заданная формулой \(y=\frac{k}{x}\), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции \(y=\frac{k}{x}\) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти

 

гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти

2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=\frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$y\neq\color{red} {\frac{1}{x}}+0$$
\(\frac{1}{x}\) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=\frac{1}{x+2}-1$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

$$y=\color{red} {\frac{1}{x+2}}-1$$

Дробь \(\color{red} {\frac{1}{x+2}}\) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Пример №3:

$$\begin{align*}
&y=\frac{2+x}{1+x} \\\\
&y=\frac{\color{red} {1+1}+x}{1+x} \\\\
&y=\frac{1}{1+x}+\frac{1+x}{1+x}\\\\
&y=\frac{1}{1+x}+1\\\\
&y=\frac{1}{\color{red} {1+x}}+1
\end{align*}$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.

1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

$$y=\color{red}{\frac{1}{1+x}}+1$$

\(\color{red}{\frac{1}{1+x}}\) Дробь убираем.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

$$y=\frac{1}{x}$$

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

$$y=\frac{1}{x}$$

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

$$f(-x)=\frac{1}{-x}=-\frac{1}{x}=-f(x)$$

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

$$y=\frac{-1}{x-1}-1$$

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.

x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

$$y=\color{red} {\frac{-1}{x-1}}-1$$

Дробь \(\color{red} {\frac{-1}{x-1}}\) удаляем.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.

8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама

Построение гиперболы, с примерами

Схема построения графика гиперболы

Функцию, которую можно задать формулой вида называют обратной пропорциональностью. Кривая, которая является графиком функции , называется гиперболой.

Гипербола состоит из двух частей – веток гиперболы. Если , то ветви гиперболы расположены в I и III координатных четвертях, а если – то в II и IV четвертях.

Областью определения и областью значений функции , где , есть все числа, кроме 0. Гипербола не имеет общих точек с осью ординат.

Функция – нечетная функция, поскольку

   

значит, график функции симметричен относительно начала координат.

Если , то функция убывает на промежутке .

Если , то функция возрастает на промежутке .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Гипербола (математика) — Википедия

У этого термина существуют и другие значения, см. Гипербола. Гипербола и её фокусы Сечения конусов плоскостью (с эксцентриситетом, большим единицы)

Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} (называемых фокусами) постоянно. Точнее,

||F1M|−|F2M||=2a,{\displaystyle {\bigl |}|F_{1}M|-|F_{2}M|{\bigr |}=2a,} причём |F1F2|>2a>0.{\displaystyle |F_{1}F_{2}|>2a>0.}

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, бо́льшим единицы.

Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Гипербола может быть определена несколькими путями.

Коническое сечение[править | править код]

Три основных конических сечения

Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.

Как геометрическое место точек[править | править код]

Через фокусы[править | править код]

Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.

Для сравнения: кривая постоянной суммы расстояний от любой её точки до фокусов — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.

Через директрису и фокус[править | править код]

Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная ε>1{\displaystyle \varepsilon >1} называется эксцентриситетом гиперболы.

Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F₁ и F₂. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D₁ и D₂. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее:

a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра к оси абсцисс, восставленного из каждой из вершин до пересечения с асимптотой
c — расстояние от центра C до любого из фокусов, F₁ и F₂,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами

• Гипербола состоит из двух отдельных кривых, которые называют ветвями.
• Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
• Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
• Середина большой оси называется центром гиперболы.
• Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
  • Обычно обозначается a.
• Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
  • Обычно обозначается c.
• Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной, или поперечной, осью гиперболы.
• Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой, или сопряжённой, осью гиперболы.
• Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
• Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
  • Обычно обозначается b.
• В задачах, связанных с движением тел по гиперболическим траекториям, расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
  • Обычно обозначается rp{\displaystyle r_{p}}.

Соотношения[править | править код]

Для характеристик гиперболы, определённых выше, существуют следующие соотношения

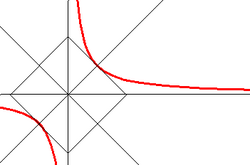Равнобочная гипербола

Гиперболу, у которой a=b{\displaystyle a=b}, называют равнобочной, или равносторонней. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением

xy=a2/2,{\displaystyle xy=a^{2}/2,}

при этом фокусы гиперболы располагаются в точках (a, a) и (−a,−a). Равнобочная гипербола является графиком обратной пропорциональности, задаваемой формулой:

y=kx,k≠0.{\displaystyle y={\frac {k}{x}},k\neq 0.}

Эксцентриситет такой гиперболы равен 2{\displaystyle {\sqrt {2}}}.

Декартовы координаты[править | править код]

Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:

Axxx2+2Axyxy+Ayyy2+2Bxx+2Byy+C=0{\displaystyle A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C\,=\,0},

где коэффициенты A_xx, A_xy, A_yy, B_x, B_y, и C удовлетворяют следующему соотношению

D=|AxxAxyAxyAyy|<0{\displaystyle D={\begin{vmatrix}A_{xx}&A_{xy}\\A_{xy}&A_{yy}\end{vmatrix}}<0}

и

Δ:=|AxxAxyBxAxyAyyByBxByC|≠0.{\displaystyle \Delta :={\begin{vmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{vmatrix}}\not =0.}

Канонический вид[править | править код]

Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду:

x2a2−y2b2=1{\displaystyle {\frac {{x}^{2}}{a^{2}}}-{\frac {{y}^{2}}{b^{2}}}=1},

где a — действительная полуось гиперболы; b — мнимая полуось гиперболы^[1]. В этом случае эксцентриситет равен

ε=1+b2a2.{\displaystyle \varepsilon ={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}.}

Полярные координаты[править | править код]

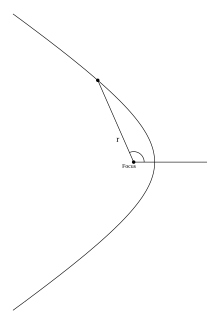Гипербола в полярных координатах

Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то

r=p1−εcos⁡φ{\displaystyle r={\frac {p}{1-\varepsilon \cos \varphi }}}

Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то

1r=ab2(1−cos⁡θ)+1bsin⁡θ{\displaystyle {\frac {1}{r}}={\frac {a}{b^{2}}}\left(1-\cos \theta \right)+{\frac {1}{b}}\sin \theta }

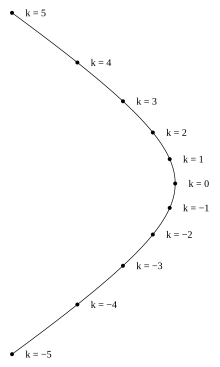
Уравнения в параметрической форме[править | править код]

Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции^[2].

{x=±ach⁡ty=bsh⁡t−∞<t<+∞.{\displaystyle {\begin{cases}x=\pm a\operatorname {ch} t\\y=b\operatorname {sh} t\end{cases}}\;\;\;-\infty <t<+\infty .}

В первом уравнении знак «+» соответствует правой ветви гиперболы, а «-» — её левой ветви.

• Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
  • Иначе говоря, если F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} фокусы гиперболы, то касательная в любой точке X{\displaystyle X} гиперболы является биссектрисой угла ∠F1XF2{\displaystyle \angle F_{1}XF_{2}}.
• Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
• Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
• Каждая гипербола имеет сопряжённую гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряжённая гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при a≠b{\displaystyle a\neq b}.
• Отрезок касательной в каждой точке гиперболы, заключенный между двумя асимптотами гиперболы, делится точкой касания пополам и отсекает от двух асимптот треугольник постоянной площади.

Асимптоты[править | править код]

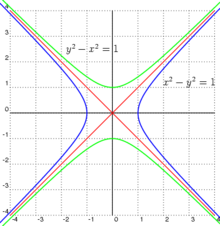Две сопряжённые гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1

Для гиперболы, заданной в каноническом виде

x2a2−y2b2=1{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}

уравнения двух асимптот имеют вид:

xa±yb=0{\displaystyle {\frac {x}{a}}\pm {\frac {y}{b}}=0}.

Диаметры и хорды[править | править код]

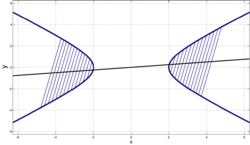Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением

k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными. Главными диаметрами называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы

Поскольку гипербола является гладкой кривой, в каждой её точке (x₀, y₀) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

xx0a2−yy0b2=1{\displaystyle {\frac {xx_{0}}{a^{2}}}-{\frac {yy_{0}}{b^{2}}}=1},

или, что то же самое,

y=y0+b2x0a2y0(x−x0){\displaystyle y=y_{0}+{\frac {b^{2}x_{0}}{a^{2}y_{0}}}\left(x-x_{0}\right)}.

Уравнение нормали к гиперболе имеет вид:

y=y0−a2b2y0x0(x−x0){\displaystyle y=y_{0}-{\frac {a^{2}}{b^{2}}}{\frac {y_{0}}{x_{0}}}\left(x-x_{0}\right)}.

Вывод уравнения нормали

Уравнение нормали произвольной плоской линии имеет вид y−y0=1y′(x0,y0)(x0−x){\displaystyle y-y_{0}={\frac {1}{y’\left(x_{0},y_{0}\right)}}\left(x_{0}-x\right)}. Каноническое уравнение гиперболы можно представить в виде пары функций y=±b2a2x2−b2{\displaystyle y=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}. Тогда производная этих функций имеет вид y′=±b2a2xb2a2x2−b2=b2a2xy{\displaystyle y’=\pm {\frac {{\frac {b^{2}}{a^{2}}}x}{\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}={\frac {b^{2}}{a^{2}}}{\frac {x}{y}}}. Подставив это уравнение в общее уравнение нормали, получим y−y0=−a2b2y0x0(x−x0){\displaystyle y-y_{0}=-{\frac {a^{2}}{b^{2}}}{\frac {y_{0}}{x_{0}}}\left(x-x_{0}\right)}.

Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в её вершине)

Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:

K=ab(a2b2y2+b2a2x2)3/2{\displaystyle K={\frac {ab}{\left({\frac {a^{2}}{b^{2}}}y^{2}+{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}}}.

Соответственно, радиус кривизны имеет вид:

R=1K=(a2b2y2+b2a2x2)3/2ab{\displaystyle R={\frac {1}{K}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}+{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab}}}.

В частности, в точке (a, 0) радиус кривизны равен

R(a,0)=b2a=p{\displaystyle R\left(a,0\right)={\frac {b^{2}}{a}}=p}.

Вывод формулы для радиуса кривизны

Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид: Rc=(x′2 +y′2)3/2|x′y″−x″y′|{\displaystyle R_{c}={\frac {\left(x’^{2}\ +y’^{2}\right)^{3/2}}{\left|x’y»-x»y’\right|}}}. Воспользуемся параметрическим представлением гиперболы: {x=a⋅ch(t)y=b⋅sh(t){\displaystyle {\begin{cases}x=a\cdot \mathrm {ch} \,(t)\\y=b\cdot \mathrm {sh} \,(t)\end{cases}}} Тогда, первая производная x и y по t имеет вид {x′=a⋅sh(t)=abyy′=b⋅ch(t)=bax{\displaystyle {\begin{cases}x’=a\cdot \mathrm {sh} \,(t)={\frac {a}{b}}y\\y’=b\cdot \mathrm {ch} \,(t)={\frac {b}{a}}x\end{cases}}}, а вторая производная — {x″=a⋅ch(t)=xy″=b⋅sh(t)=y{\displaystyle {\begin{cases}x»=a\cdot \mathrm {ch} \,(t)=x\\y»=b\cdot \mathrm {sh} \,(t)=y\end{cases}}} Подставляя эти значения в формулу для кривизны получаем: Rc=(a2b2y2 +b2a2x2)3/2|ay2b−bx2a|=(a2b2y2 +b2a2x2)3/2ab|y2b−x2a|=(a2b2y2 +b2a2x2)3/2ab{\displaystyle R_{c}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{\left|a{\frac {y^{2}}{b}}-b{\frac {x^{2}}{a}}\right|}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab\left|{\frac {y^{2}}{b}}-{\frac {x^{2}}{a}}\right|}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab}}}.

Коо

Гиперболические графики функций, общий вид гиперболической функции

Функция записывается в общем виде, как y =  или f(x) = 

y и x — это обратно пропорциональные величины, т.е. когда одна растет, другая уменьшается (проверьте, подставив числа в функцию)

В отличие от предыдущей функции, в которой x² всегда создает положительные значения, здесь мы не можем сказать, что — = , поскольку это будут совершенно противоположные числа. Такие функции называют нечетными.

Построим для примера график y = 

Естественно, x не может быть равен нулю (x ≠ 0)

Ветви гиперболы лежат в 1-й и 3-й части координат.

Они бесконечно могут приближаться к осям абсцисс и ординат и так никогда их не достигнуть, даже если «x» станет равен миллиарду. Гипербола будет бесконечно близко, но все же так и не пересечется с осями (такая вот математическая печалька).

Построим график для y = —

​​​​​​​​​​​​​​И теперь ветви гиперболы находятся во второй и 4-й четверти частях координатной плоскости.

В итоге, между всеми ветвями можно наблюдать полную симметрию.

Далее, подобным образом, вы сможете строить любые другие графики, опираясь на эти.

​​​​​​​

Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

Добавить новость и получить деньги

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников