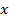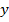Построение графиков функций — урок. Алгебра, 10 класс.
построить график функции y=x2+1×2−1.
Решение 1. Введём обозначение: f(x)=x2+1×2−1. Найдём область определения функции. Она задаётся условиями x≠1,x≠−1. Итак, D(f)=(−∞;−1)∪(−1;1)∪(1;+∞).
2. Исследуем функцию на чётность:
f(−x)=−x2+1−x2−1=x2+1×2−1=f(x).
Значит, заданная функция чётна, её график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.
3. Найдём асимптоты. Вертикальной асимптотой является прямая \(x=1\), поскольку при этом значении \(x\) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить limx→∞f(x):
limx→∞x2+1×2−1=limx→∞x2x2+1x2x2x2−1×2=limx→∞1+1×21−1×2=1.
Значит, \(y=1\) — горизонтальная асимптота графика функции.
4. Найдём стационарные и критические точки, точки экстремума и промежутки монотонности функции:
y′=x2+1×2−1′=(x2+1)′⋅(x2−1)−(x2+1)⋅(x2−1)′x2−12=2x⋅(x2−1)−(x2+1)⋅2xx2−12==−4xx2−12.
Производная существует всюду в области определения функции, значит, критических точек у функции нет.
Стационарные точки найдём из соотношения y′=0. Получаем: \(-4x=0\) — откуда находим, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Значит, \(x=0\) — точка максимума функции, причём ymax=f(0)=02+102−1=−1.
При \(x>0\) имеем: y′<0; но следует учесть наличие точки разрыва \(x=1\). Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке 0;1) функция убывает, на промежутке (1;+∞) функция также убывает.
5. Составим таблицу значений функции f(x)=x2+1×2−1 при x≥0:
\(x\) | \(0\) | \(0.5\) | \(2\) | \(3\) | \(4\) |
\(y\) | \(-1\) | −53 | 53 | 54 | 1715 |
6. Отметим найденные точки на координатной плоскости, учтя при этом, что \((0;-1)\) — точка максимума, что \(y=1\) — горизонтальная асимптота, что \(x=1\) — вертикальная асимптота, построим ветви искомого графика при x≥0. Добавив ветви, симметричные построенным относительно оси ординат, получим весь график.
www.yaklass.ru
Тема урока «Функции и их графики». 10-й класс
1. Введение
Цели урока:
Повторить графики базовых функций и их преобразования: сдвиги по осям координат. Научиться строить графики функций с модулями. Целью урока также является развитие внимания, памяти, логического мышления и повышение интереса к предмету.
Вступительное слово учителя:
Сегодня мы закрепим ваши знания и умения строить графики функций, в частности путём преобразования графиков базовых функций, научимся строить графики функций, содержащих модули, и напишем самостоятельную работу для проверки полученных знаний.
2. Повторение пройденного материала.
2.1. Графики базовых функций.
Линейная функция
y = kx
при k > 0; k < 0.
<Рисунок 1>
y = kx + b
при k > 0 и b > 0; k > 0 и b < 0; k < 0 и b > 0; k < 0 и b < 0.
<Рисунок 2>
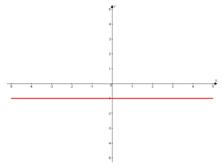
y = b
при b > 0; b < 0.
<Рисунок 3>
x = p
при p > 0; p < 0.
<Рисунок 4>
Степенная функция
<Рисунок 5>
<Рисунок 6>
<Рисунок 7>
<Рисунок 8>
Обратная пропорциональность
<Рисунок 9>
<Рисунок 10>
Функция арифметического квадратного корня
<Рисунок 11>
<Рисунок 12>
Модуль
<Рисунок 13>
<Рисунок 14>
2.2. Преобразование графиков базовых функций.
y = x
- y = x + 3 – сдвиг на 3 единицы вверх по оси Oy
- y = x – 4 – сдвиг на 4 единицы вниз по оси Oy
<Рисунок 15>
y = x2
а) y = (x – 5)2 – сдвиг на 5 единиц вправо по оси Ox
б) y = (x + 3)2 – сдвиг на 3 единицы влево по оси Ox
<Рисунок 16>
y = – (x – 4)2 + 2
а) y = (x – 4)
2<Рисунок 17>
б) y = – (x – 4)2 – симметричное отображение графика относительно оси Ox
<Рисунок 18>
в) y = – (x – 4)2 + 2 – сдвиг на 2 единицы вверх по оси Oy
<Рисунок 19>
3. Объяснение нового материала. Графики функций, содержащие модули.
<Рисунок 20>
<Рисунок 21>
<Рисунок 22>
Оставить без изменения ту часть графика функции y = x – 4, точки которой находятся на оси Ox и выше этой оси, и симметрично относительно оси Ox отобразить ту часть графика, которая находится ниже оси Ox.
<Рисунок 23>
<Рисунок 24>
<Рисунок 25>
Оставить без изменения ту часть графика функции y = x2 – 6x + 5, которая находится на оси Ox и выше этой оси, и симметрично относительно оси Ox отобразить ту часть графика, которая находится ниже оси Ox.
<Рисунок 26>
Оставить без изменения ту часть графика функции y = |x
<Рисунок 27>
<Рисунок 28>
4. Подготовка к самостоятельной работе.
№1
<Рисунок 29>
<Рисунок 30>
№2
y = (x – 3)2 + 4
- y = x2
- y = (x – 3)2
- y = (x – 3)2 + 4
<Рисунок 31>
№3
<Рисунок 32>
- y = x2 – 2x – 3
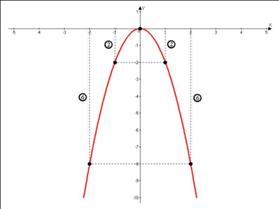
<Рисунок 33>
x1, x2 – нули функции y = x2 – 2x – 3:
x2 – 2x – 3 = 0
x1 = 3, x2 = –1
(x0; y0) – координаты вершины параболы
<Рисунок 34>
(1; –4) – вершина параболы
<Рисунок 35>
<Рисунок 36>
<Рисунок 37>
<Рисунок 38>
5. Самостоятельная работа с самопроверкой с помощью проектора.
№1
<Рисунок 39>
<Рисунок 40>
№2
y = (x + 4)2 – 3
<Рисунок 41>
№3
<Рисунок 42>
<Рисунок 43>
6. Закрепление пройденного материала.
№1
Предварительный разбор и самостоятельное повторение графика функции
<Рисунок 44>
<Рисунок 45>
№2
<Рисунок 46>
<Рисунок 47>
№3
<Рисунок 48>
<Рисунок 49>
<Рисунок 50>
№4
<Рисунок 51>
<Рисунок 52>
<Рисунок 53>
<Рисунок 54>
<Рисунок 55>
<Рисунок 56>
<Рисунок 57>
<Рисунок 58>
<Рисунок 59>
<Рисунок 60>
urok.1sept.ru
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Практика
Подготовка к ЕГЭ по математике
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
Практика
Конспект урока
Сначала разберем примеры на построение графиков основных функций.
Задача №1. Построить графики функций: а) 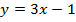 ; б)
; б) 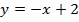 ; в)
; в) 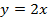
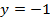 .
.Решение. Воспользуемся методом построения линейных функций «по точкам».
а) 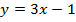
|
|
|
|
0 |
-1 |
|
1 |
2 |
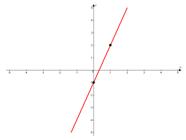
Как видим, 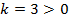 и угол наклона к оси
и угол наклона к оси 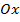 острый,
острый, 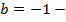 смещение по оси
смещение по оси 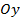 .
.
б) 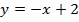
|
|
|
|
0 |
2 |
|
1 |
1 |
 и
и 
в) 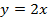
|
|
|
|
0 |
0 |
|
1 |
2 |
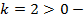 угол наклона к оси
угол наклона к оси острый,
острый, 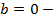 график проходит через начало координат.
график проходит через начало координат.
г) 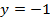
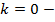 константная функция, прямая проходит через точку
константная функция, прямая проходит через точку 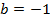
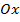 .
.Задача №2. Построить графики функций: а) 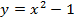 ; б)
; б) 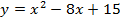 ; в)
; в) 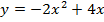 .
.
Решение. Воспользуемся методом построения квадратичных функций «по вершине».
а) 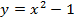
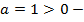 ветки параболы направлены вверх,
ветки параболы направлены вверх, 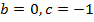 .
.
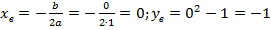
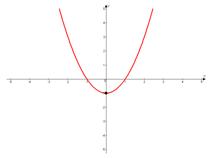
Если возникает вопрос, как точно строится парабола, т.е. с какой именно скоростью растут и убывают ее ветки, то можно запомнить следующий факт: если старший коэффициент 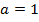 или
или 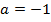 , как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.
, как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.
Например, в нашем графике:
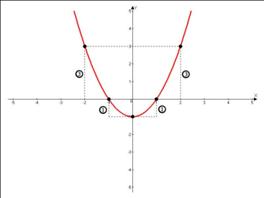
Для функций, у которых старший коэффициент 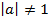 , значения изменений функции умножаются на это «
, значения изменений функции умножаются на это «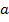 ». Например, построение функции
». Например, построение функции 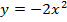 выглядит так:
выглядит так:
Но, как правило такая точность построения не важна, а нужен только эскиз графика, поэтому в дальнейшем мы не будем это учитывать.
б) 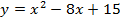
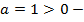 ветки параболы направлены вверх,
ветки параболы направлены вверх, 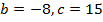 .
.
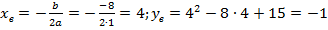
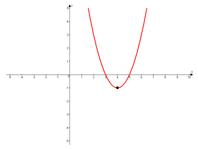
в) 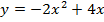
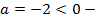 ветки параболы направлены вниз,
ветки параболы направлены вниз, 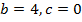 .
.
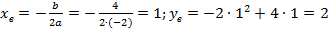
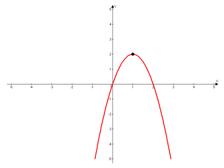
Кстати, график проходит через ноль, что легко проверить подстановкой в функцию точки 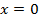 или обратив внимание на то, что
или обратив внимание на то, что 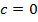 .
.
Задача №3. Построить графики функций: а) 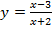 ; б)
; б) 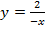 ; в)
; в) 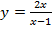 .
.
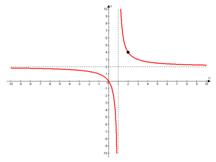
Решение. Воспользуемся нашим методом построения дробно-рациональных функций «по асимптотам».
а) 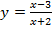
Вертикальная асимптота определяется решением уравнения, которое показывает, что знаменатель дроби равен нулю: 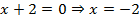 .
.
Горизонтальную асимптоту определим по тому быстрому способу, который мы указали в лекции. Она определяется отношением коэффициентов при иксах в числителе и знаменателе: 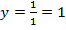 .
.
Для определения расположения веток гиперболы подставим в функцию любую точку из области определения, т.е. кроме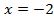 , например,
, например, 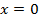 :
: 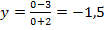 , т.е. координаты этой точки
, т.е. координаты этой точки 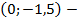 через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
Теперь строим гиперболу, прижимая ее к асимптотам:
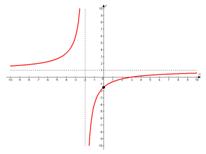
Остальные пункты строим аналогично.
б) 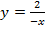
Вертикальная асимптота: 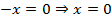 .
.
Горизонтальная асимптота: 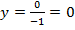 , т.е. асимптотами являются оси координат.
, т.е. асимптотами являются оси координат.
Проверочная точка: 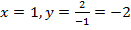 .
.
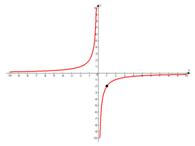
в) 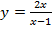
Вертикальная асимптота: 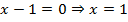 .
.
Горизонтальная асимптота: 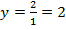 .
.
Проверочная точка: 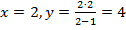 .
.
Задача №4. Построить графики функций: а) 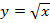 , б)
, б)  , в)
, в) 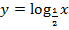 .
.
Решение. По сути дела, указаны функции, которые не имеют особых методов построения их графиков. Поэтому если необходимо изобразить их эскиз, то просто вспоминаем теорию, а если необходимо построить графики более точно, то следует подставить несколько контрольных точек, так и поступим.
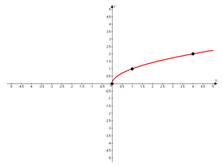
а) 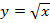
Подставим полные квадраты, чтобы вычислить из них целые значения корня.
|
|
|
|
0 |
0 |
|
1 |
1 |
|
4 |
2 |
б) 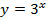
Подставим несколько значений и учтем общий вид графика.
|
|
|
|
0 |
1 |
|
1 |
3 |
|
2 |
9 |
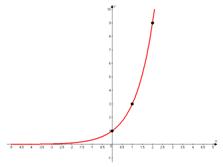
Т.к. основание степени 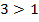 , то функция растет.
, то функция растет.
в) 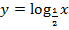
Подставим такие значения аргумента, при которых значения логарифма будут целыми. При построении учтем общий вид графика.
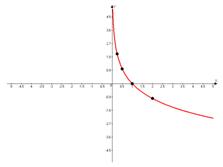
Т.к. основание логарифма 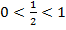 , то функция убывает.
, то функция убывает.
Теперь давайте попробуем научиться решать обратную задачу – по изображенному графику исследовать функцию.
Задача №5. По виду графика определить знаки коэффициентов общего вида функции 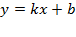 :
:
а) 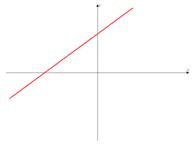
б) 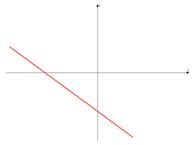
в) 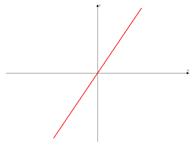
г) 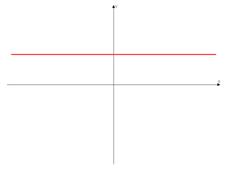
Решение. Для определения знаков коэффициентов  и
и  вспомним, как от них зависят формы графиков.
вспомним, как от них зависят формы графиков.
а) Острый угол наклона прямой к оси 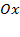 (функция возрастает) – это
(функция возрастает) – это 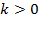 . Точка пересечения с осью
. Точка пересечения с осью  — это
— это 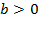 .
.
Далее аналогичные рассуждения.
б) 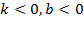
в) 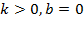
г) Константная функция, т.к. график параллелен оси 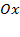 , т.е.
, т.е. 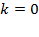 , а
, а 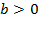 .
.
Задача №6. По виду графика определить знаки коэффициентов общего вида функции 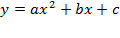 :
:
а) 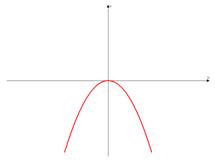
б) 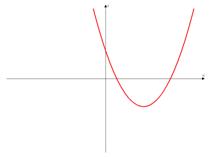
в) 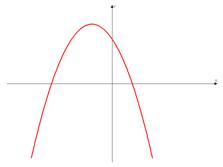
Решение. Вспомним, как параметры 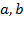 и
и  определяют положение параболы.
определяют положение параболы.
а) Ветви вниз, следовательно, 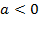 .
.
Точка пересечения с осью 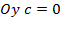 .
.
Иксовая координата вершины 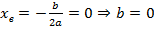 .
.
б) Ветви вверх, следовательно, 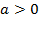 .
.
Точка пересечения с осью 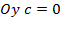 .
.
Иксовая координата вершины 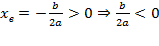 , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно,
, т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, 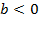 .
.
в) Ветви вниз, следовательно, 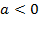 .
.
Точка пересечения с осью 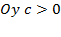 .
.
Иксовая координата вершины 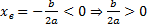 , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно,
, т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, 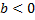 .
.
И теперь переходим к рассмотрению примеров на преобразование графиков функций.
Задача №7. Построить графики функций: а) 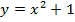 ; б)
; б) 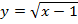 ; в)
; в) 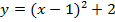 ; г)
; г) 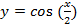 ; д)
; д) 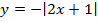 .
.
Решение. Когда сложная функция получена из простейшей путем нескольких преобразований, то преобразования графиков выполняются в порядке арифметических действий с аргументом, например, умножение идет до сложения и т.п.
а) 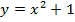
Преобразование в одно действие типа 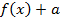 .
.
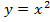
Сдвигаем график вверх на 1: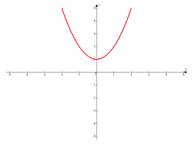
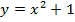
б) 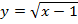
Преобразование в одно действие типа 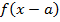 .
.
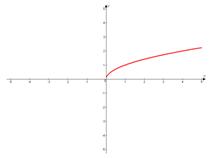
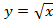
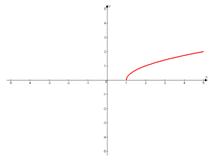
Сдвигаем график вправо на 1:
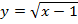
в) 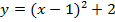
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках 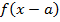 , затем сложение
, затем сложение 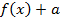 .
.
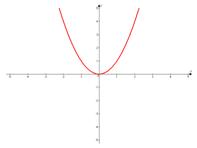
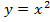
Сдвигаем график вправо на 1:
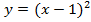
Сдвигаем график вверх на 2:
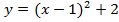
Конечно же, можно построить эту функцию как квадратичную после раскрывания скобок. Проверьте это самостоятельно.
г)
interneturok.ru
Урок алгебры «Функции. Графики функций». 10-й класс
| Цели урока: | – восстановление в памяти понятие
функции, свойства функции, виды функций, графики
функций; – развитие навыков построения графиков функций, применяя преобразования графиков, и решения параметрического уравнения с помощью графиков функций; – развитие умений анализировать собственные потребности, выбора соответствующей позиции на каждый этап урока с последующим анализом своей деятельности. |
| Название урока: | Моя позиция на уроке |
| Оборудование: | Презентация, папка с заданиями, карточки «Моя позиция на уроке» |
| Формы работы: | – групповая – индивидуальная – фронтальная с использованием ИКТ |
| Развитие специальных умений: | – развитие навыков построения
графиков; – развитие навыков преобразования графиков; – решение параметрических уравнений; – работа с модулями. |
| Развитие учебно-организационных умений: | – развитие умений анализировать
собственные потребности; – выбор соответствующей позиции на каждый этап урока; – развитие умений анализа своей деятельности. |
| Развитие учебно-интеллектуальных умений: | – умение использовать знания графиков
основных функций для построения графиков более
сложных функций; – умения решать уравнения с помощью графиков. |
| Развитие учебно-информационных умений: | – умение выделять главные свойства
основных функций при построении графиков более
сложных функций; – умение применять графики для решения уравнений. |
| Развитие учебно-коммуникативных умений: | – обсуждение задания и планирования
путей выполнения задания; – взаимопомощь при работе в группе; – выбор представителя результата работы группы. |
| Структура урока: |
|
| Список литературы | 1. Никольский С.М., Потапов М.К.,
Решетников Н.Н., Шевкин А.В. Алгебра и начала
математического анализа. 10 класс. М. :
Просвещение, 2010. 2. Потапов М.К., Шевкин А.В. Алгебра и начала математического анализа. 10 класс. Дидактические материалы. М. : Просвещение, 2010. |
ХОД УРОКА
1. Организационный момент
Учащиеся сидят группами. Сообщается тема урока и цели 1 и 2.
2. Выбор «Моя позиция на уроке» 1 этап (Презентация. Слайд 2)
Учитель. Но, кроме чисто
математических целей, предлагаю каждому из вас
поставить перед собой личностную цель.
Психолог Антон Григорьевич Рубинштейн писал:
«Личность – это человек со своей четко
выработанной жизненной позицией…»
Вот я вам и предлагаю сегодня на уроке
проконтролировать собственный выбор той или
иной позиции на уроке.
Итак, название нашего урока «Моя позиция на
уроке» (Презентация.
Слайд 3)
Из папки достаньте карточки «Моя позиция на
уроке», на которой указаны варианты возможных
позиций: лидер, ведомый, слушатель, критик,
помощник, творческая личность, исследователь,
зритель… или можете предложить свой вариант.
Отметьте, пожалуйста, каким-либо значком
выбранную позицию в I столбце. Отложите в сторону
карточки, приступаем к работе.
3. Фронтальная работа (повторение)
– Предлагаю вам ответить на вопросы:
- Что называется функцией? (Презентация. Слайд 4)
- Свойства функции: (используя презентацию) (Презентация. Слайд 5)
а) область определения; (Презентация.
Слайд 6)
б) область значений функции; (Презентация.
Слайд 7)
в) нули функции; (Презентация.
Слайд 8)
г) характер монотонности; (Презентация.
Слайд 9)
д) график функции. (Презентация.
Слайд 10)
– А теперь по графику функции попытаемся назвать функцию и вспомнить её свойства (используя презентацию) (Презентация. Слайды 11-20)
Ответы:
1) Прямая пропорциональность y = kx ;
2) Линейная функция y = ax + b;
3) Квадратичная функция y = ax2 + bx + c;
4) Обратная пропорциональность ;
5) Дробно-линейная функция .
4. Самоанализ своей деятельности на 1 этапе урока.
– Предлагаю вернуться к карточкам «Моя
позиция на уроке». (Презентация.
Слайд 21)
Придерживались ли вы ранее выбранной позиции?
Если «да», то подтвердите это во II столбце. Если
«нет», то укажите знаком во II столбце, какой
позиции вы придерживались.
Как вы считаете, готовы ли мы, используя ранее
полученные знания, строить графики более сложных
функций.
5. Задание для работы в группах. (Презентация. Слайд 22)
Переходим к следующему этапу урока: работа в группах.
Построить график функции: (Презентация. Слайд 23)
В каждой папке есть лист А 4 в клетку. Вы должны выбрать в группе человека, который будет строить график на этом листе, остальные – работают в тетради.
6. Выбор «Моя позиция на уроке» 2 этап (Презентация. Слайд 24)
– Задание знаете, оцените свои силы и настроение и выберите свою позицию на следующий этап урока и отметьте её знаком в III столбце карточки «Моя позиция на уроке».
7. Практическая работа в группах (Презентация. Слайд 25)
Ребята работают, помогая друг другу, при необходимости учитель может оказать помощь или посоветовать, на какие моменты при выполнении задания обратить внимание.
Графики построены. От каждой группы лист А 4 с графиком на доске (при помощи магнитов). Оценим творчество каждой группы и уровень выполнения задания.
Учитель: График любой функции можно построить в программе Excel. Показываю график, построенный в программе Excel. (Презентация. Слайд 26)
Второе задание. Используя построенный график, для каждого значения параметра m определить количество решений уравнения: (Презентация. Слайд 27)
Каждая группа записывает ответ, затем проверяем: (Презентация. Слайд 28)
- если , то уравнение имеет одно решение;
- если , то уравнение имеет два решения;
- если , то уравнение имеет три решения;
- если m = 5, то уравнение не имеет решений;
8. Самоанализ своей деятельности на 2 этапе урока (Презентация. Слайд 29)
– Предлагаю вернуться к карточкам «Моя позиция на уроке». Придерживались ли вы ранее выбранной позиции? Если «да», то подтвердите это в IV столбце. Если «нет», то укажите знаком в IV столбце, какой позиции вы придерживались.
9. Образовательный итог урока (Презентация. Слайд 30)
– Какие проблемы возникли при построении
графика функции?
– Какие вопросы требуют дополнительной
отработки?
Учитель дает словесную оценку работе групп, учеников.
– Каждый из вас сегодня попытался контролировать свою позицию на уроке. Если хотите, подпишите свою карточку «Моя позиция на уроке». Все карточки положите в папку, мне хотелось бы знать, какую позицию на каждом этапе урока вы выбирали, и что из этого получилось.
10. Домашнее задание. (Слайд 31)
- Построить график функции:
- Определить для каждого значения параметра m количество решений уравнения:
Дополнительное задание: построить график в программе Excel.
Список литературы:
1. Никольский С.М., Потапов М.К., Решетников Н.Н.,
Шевкин А.В. Алгебра и начала математического
анализа. 10 класс. М. : Просвещение, 2010.
2. Потапов М.К., Шевкин А.В. Алгебра и начала
математического анализа. 10 класс. Дидактические
материалы. М. : Просвещение, 2010.
urok.1sept.ru
Построение графиков функции. Алгебра, 10 класс: уроки, тесты, задания.
| 1. |
Вертикальная асимптота
Сложность: лёгкое |
1 |
| 2. |
Горизонтальная асимптота
Сложность: лёгкое |
1 |
| 3. |
Выпуклости графика функции
Сложность: лёгкое |
2 |
| 4. |
Построение графика дробной функции
Сложность: среднее |
8 |
| 5. |
Точки перегиба функции
Сложность: среднее |
2 |
| 6. |
Доказательство выпуклости функции
Сложность: среднее |
4 |
| 7. |
Исследование и построение графика сложной функции, содержащей квадратный корень
Сложность: сложное |
6 |
| 8. |
Уравнение с параметром
Сложность: сложное |
4 |
| 9. |
Определение количества корней
Сложность: сложное |
3 |
www.yaklass.ru
Свойства функции — Математика — 10 класс

Что такое функция.
Определение. Соответствия, при которых каждому элементу одного множества сопоставляется единственный элемент другого множества называются функциями.
Пишут: у = f(x), x Є X.
Переменную х называют независимой переменной или аргументом.
Множество всех допустимых значений независимой переменной является областью определения функции и обозначается D(y).
Переменную у – зависимой переменной .
Множество всех значений зависимой переменной является областью значений функции и обозначается Е(у ).

Способы задания функции
Существуют 4 способа задания функции.
1.Табличный способ. Удобен тем, что позволяет найти значения функции имеющихся в таблице значений аргумента без вычислений.
Х
2
У
4
3
4
6
5
8
10
2.Аналитический способ. Функция задается одной или несколькими формулами. Этот способ незаменим для исследования функции, установления ее свойств.
У=2х+5, у= х² -5х+1, у= |х+5|.
3. Графический способ . Функция задается своей геометрической моделью на координатной плоскости.
4. Описательный способ . Удобно использовать тогда, когда задание другими способами затруднительно.

§3
Свойства
функции
четность
нечетность
Монотонность:
непрерывность
Возрастание;
убывание
выпуклость
нули функции
( значения аргумента,
в которых значение
Функции равно нулю)
Наибольшее и
наименьшее
значения
функции
периодичность
Промежутки
знакопостоянства
(промежутки, в которых функция
принимает только положительные
или только отрицательные значения)
Экстремумы:
точка максимума,
точка минимума

Линейная функция.
О. Функция вида y=kx+b называется линейной.
Т. Графиком линейной функции y=kx+b, при k ≠0 является прямая, пересекающая
ось ординат в точке (0; b), ось абсцисс в точке (-b/ k; 0)
k0 k=0
D(f) = R
E(f) = R

- О. Функция вида у=к/х, где к ≠0, называется обратной пропорциональностью.
- График обратной пропорциональности (гипербола) получается из графика функции у=1/х с помощью растяжения (а при к
- D(f) = (-∞;0) U (0;+∞)
- E(f) = (-∞;0) U (0;+∞)

Степенная функция с целым показателем .
О. Функция вида у=х ⁿ , где n- натуральное число, называется степенной .
О. График степенной функции с показателем n называется параболой степени n.
n- четное число n- нечетное число
D(f) = (-∞;∞) D(f) = (-∞;∞)
E(f) = [0;∞) E(f) = (-∞;∞)

Функция у = ах² +вх+с

О.Функцией «корень n степени» называется функция вида
Т. Графики функций и у = хⁿ симметричны относительно прямой у = х
D(f) = (-∞;∞) E(f) = (-∞;∞)

Функция у = |х|
у= |х |= х, если х≥0
-х, если х Функция задается кусочно.
х
Т. Область определения функции
D( y)= (-∞; + ∞)
Множество значений функции
Е(у)= [0; + ∞)
Т. Функция у = |х | убывает
при х Є(-∞; 0]
возрастает при х Є [0; + ∞)
 0. О. График дробно-линейной функции- гипербола , получаемая из графика обратной пропорциональности с помощью сдвига. «
0. О. График дробно-линейной функции- гипербола , получаемая из графика обратной пропорциональности с помощью сдвига. «
Дробно-линейная функция
О. Функция вида называется дробно-линейной , где с 0.
О. График дробно-линейной функции- гипербола , получаемая из графика обратной пропорциональности с помощью сдвига.

Нахождение области определения функции
1.
2.
3.
![Функция задана графиком. Укажите область определения. Ответ: X Є [-1;8] Ответ: X Є [1;5]](/800/600/https/fsd.multiurok.ru/html/2017/05/05/s_590c31a04897f/img11.jpg)
Функция задана графиком. Укажите область определения.
Ответ:
X Є [-1;8]
Ответ:
X Є [1;5]

Множество значений функции
Решение: 2sin²x-cos2x=2sin²x-(1-2sin²x)=4sin²x-1
0 ≤ Sin²x ≤ 1, -1 ≤ 4sin²x-1 ≤ 3
Ответ: -1 ≤ у ≤ 3
Решение: -1 ≤ cosx ≤ 1 , 0 ≤ |cosx| ≤ 1 , -1 ≤ 1 — 2 |cosx| ≤ 1 ≤ 1
Ответ: -1 ≤ у ≤ 1
3.Функция задана графиком. Укажите множество значений этой функции.
E(f)=(-2;2] E(f)= [-3;1] E(f)= (-∞;4]
![Решение неравенств На рисунке изображены графики функций y= f (x) и y= g (x), заданных на промежутке. Укажите те значения х, для которых выполняется неравенство f(x) ≤ g(x) Ответ: f(x)≤ g(x) на отрезке [-3;2]](/800/600/https/fsd.multiurok.ru/html/2017/05/05/s_590c31a04897f/img13.jpg)
Решение неравенств
На рисунке изображены графики функций y= f (x) и y= g (x), заданных на промежутке. Укажите те значения х, для которых выполняется неравенство f(x) ≤ g(x)
Ответ: f(x)≤ g(x) на отрезке [-3;2]
![На рисунке изображен график функции у =f(x), заданной на отрезке [-4;7]. Укажите те значения х, для которых выполняется неравенство f(x)≤-2 Ответ: [0; 2]](/800/600/https/fsd.multiurok.ru/html/2017/05/05/s_590c31a04897f/img14.jpg)
На рисунке изображен график функции у =f(x), заданной на отрезке [-4;7]. Укажите те значения х, для которых выполняется неравенство f(x)≤-2
Ответ: [0; 2]

Какие из данных линий являются функцией?
multiurok.ru
Основные правила преобразования графиков функций. Видеоурок. Алгебра 9 Класс
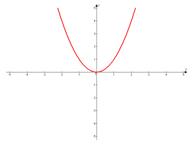
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции 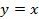 – это прямая, а график функции
– это прямая, а график функции 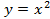 – это парабола. Но как построить, например, график функции
– это парабола. Но как построить, например, график функции 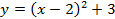 , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
, не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Предположим, что у нас есть функция 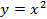 (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 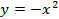 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола (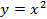 ) зеркально отобразится относительно оси
) зеркально отобразится относительно оси 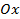 (см. Рис. 1).
(см. Рис. 1).
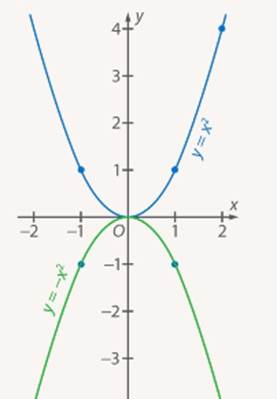
Рис. 1. Графики функций 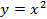 и
и 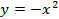
Таким образом, если у нас есть произвольный график  , то для построения графика
, то для построения графика 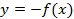 необходимо график
необходимо график 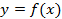 симметрично отразить относительно оси
симметрично отразить относительно оси  (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси
(см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси  .
.
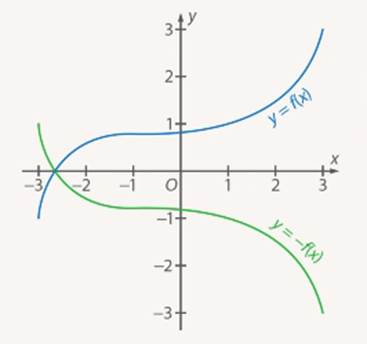
Рис. 2. Преобразование симметрии относительно оси 
Преобразование симметрии – зеркальное отражение относительно прямой. График  получается из графика функции
получается из графика функции  преобразованием симметрии относительно оси
преобразованием симметрии относительно оси  .
.
На рисунке 3 показаны примеры симметрии относительно оси 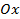 .
.
Рис. 3. Симметрия относительно оси Ox
Предположим, что у нас есть функция 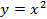 (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 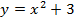 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 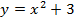 больше на 3 единицы. Графически это означает, что график функции
больше на 3 единицы. Графически это означает, что график функции 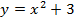 находится на 3 единицы выше, чем график функции
находится на 3 единицы выше, чем график функции 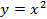 (см. Рис. 4).
(см. Рис. 4).
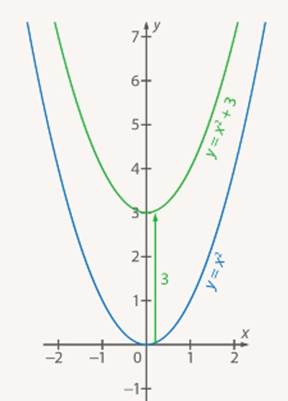
Рис. 4. Графики функций 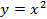 и
и 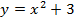
График 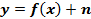 получается из графика функции
получается из графика функции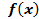 параллельным переносом последнего вдоль оси ординат на
параллельным переносом последнего вдоль оси ординат на 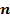 единиц вверх, если
единиц вверх, если 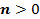 , и на
, и на 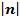 единиц вниз, если
единиц вниз, если 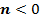 (см. Рис. 5, 6).
(см. Рис. 5, 6).
Рис. 5. Параллельный перенос вдоль оси  (при
(при  )
)
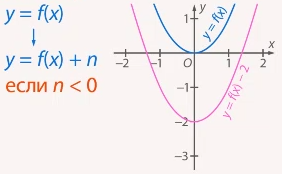
Рис. 6. Параллельный перенос вдоль оси  (при
(при  )
)
Предположим, что у нас есть функция  (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 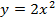 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 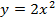 больше в 2 раза. Графически это означает, что график функции
больше в 2 раза. Графически это означает, что график функции 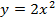 сужается по сравнению с графиком функции
сужается по сравнению с графиком функции 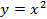 (см. Рис. 7).
(см. Рис. 7).
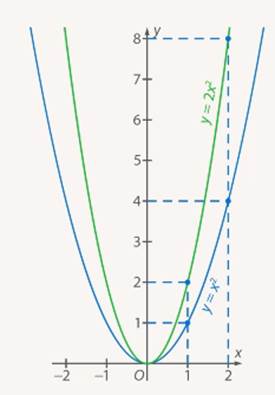
Рис. 7. Графики функций 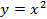 и
и 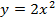
Если необходимо построить график функций 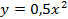 , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика
, то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 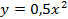 меньше в 2 раза, чем у
меньше в 2 раза, чем у 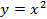 . Графически это означает, что график функции
. Графически это означает, что график функции 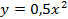 расширяется по сравнению с графиком функции
расширяется по сравнению с графиком функции 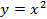 (см. Рис. 8).
(см. Рис. 8).
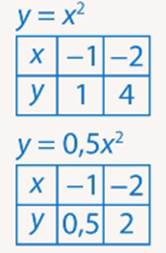
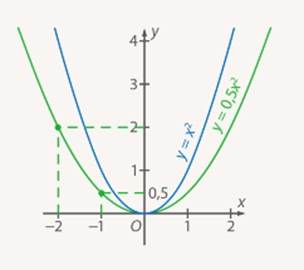
Рис. 8. Графики функций 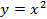 и
и 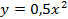
Чтобы построить график функции 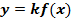 , где
, где 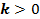 и
и 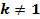 , нужно ординаты точек заданного графика умножить на
, нужно ординаты точек заданного графика умножить на 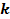 . Такое преобразование называется растяжением от оси
. Такое преобразование называется растяжением от оси 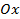 с коэффициентом
с коэффициентом 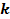 , если
, если 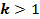 , и сжатием к оси
, и сжатием к оси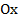 , если
, если 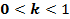 (см. Рис. 9, 10).
(см. Рис. 9, 10).
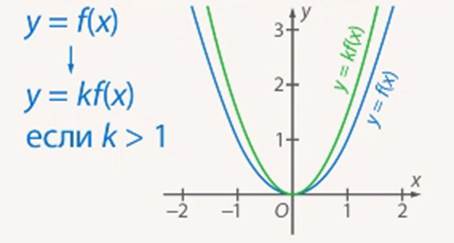
Рис. 9. Растяжение от оси 
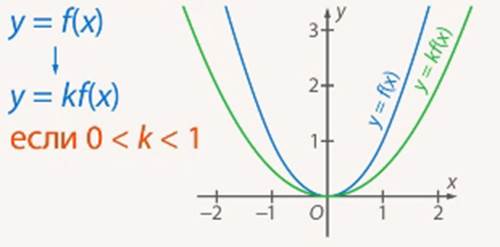
Рис. 10. Сжатие к оси 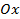
Предположим, что у нас есть функция 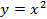 , необходимо построить график функции
, необходимо построить график функции 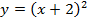 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:
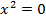 , при
, при 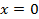
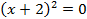 при
при 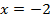
Следовательно, если необходимо было построить график функции 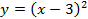 , то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции
, то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции 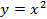 ) (см. Рис. 11).
) (см. Рис. 11).
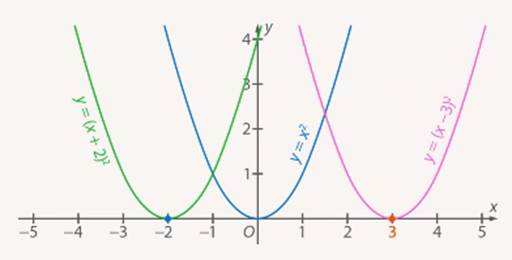
Рис. 11. Графики функций 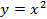 ,
, 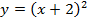 и
и 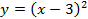
График 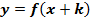 получается из графика функции
получается из графика функции 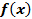 параллельным переносом последнего на
параллельным переносом последнего на 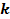 единиц влево, если
единиц влево, если 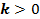 , и на
, и на  единиц вправо, если
единиц вправо, если  (см. Рис. 12, 13).
(см. Рис. 12, 13).
Рис. 12. Параллельный перенос влево при 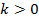
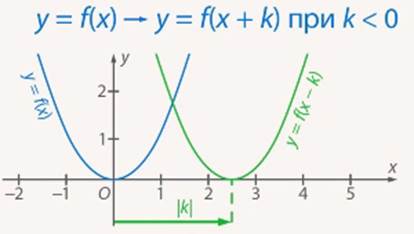
Рис. 13. Параллельный перенос вправо при 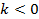
Обратите внимание на то, что по этому принципу из графика 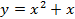 не построить график
не построить график 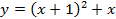 , ведь мы добавили 1 не ко всем вхождениям
, ведь мы добавили 1 не ко всем вхождениям 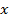 в это выражение. А вот график
в это выражение. А вот график 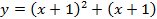 построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
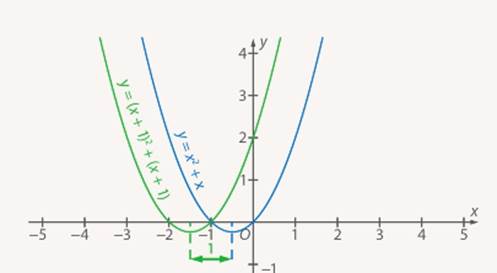
Рис. 14. Графики функции 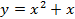 и
и 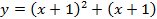
График функции 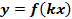 , где
, где 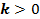 и
и 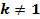 , получается из графика функции
, получается из графика функции 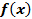 сжатием с коэффициентом
сжатием с коэффициентом 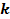 к оси
к оси 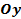 (если
(если  указанное «сжатие» фактически является растяжением с коэффициентом
указанное «сжатие» фактически является растяжением с коэффициентом  ) (см. Рис. 15, 16).
) (см. Рис. 15, 16).
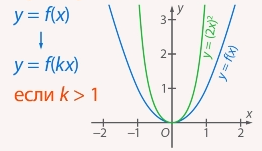
Рис. 15. Сжатие к оси 
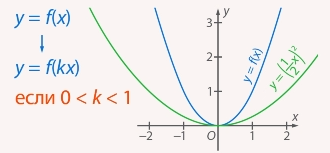
Рис. 16. Растяжение от оси 
Подобное преобразование мы уже рассматривали в случае построения графика функции 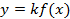 .
.
Ранее мы рассматривали преобразование симметрии относительно оси Ox, то есть функция умножалась на (-1). Рассмотрим случай, когда на (-1) умножается только аргумент.
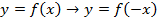
В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента:
для функции 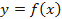 :
:
при 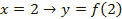
при 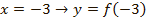
для функции 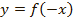 :
:
при 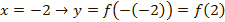
при 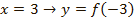
График 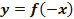 получается из графика функции
получается из графика функции 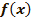 преобразованием симметрии относительно оси
преобразованием симметрии относительно оси 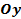 (см. Рис. 17).
(см. Рис. 17).
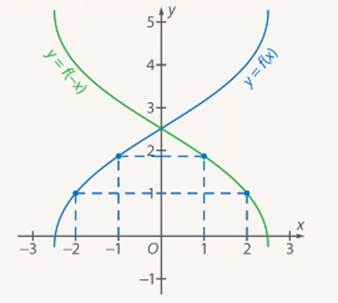
Рис. 17. Преобразование симметрии относительно оси Oy
Построение графиков 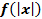 и
и 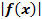
Пусть дан график 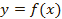 , построим график
, построим график 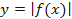 . Для начала раскроем модуль по определению:
. Для начала раскроем модуль по определению:
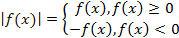
Следовательно, те точки, в которых значения функции положительны или равны 0, остаются на месте, а все точки, в которых значения отрицательны, – отражаются относительно оси 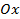 (см. Рис. 18).
(см. Рис. 18).
interneturok.ru