Построение графика функции y=mf(x) по графику функции y=f(x) при m>0
На этом уроке мы будем изучать модификацию графика вида у=m∙f(x) при m>0.
Вначале вспомним, как мы строим модификации графиков вида у=f(x+a) и y=f(x)+b. Далее рассмотрим, как строить график при m=2 и роль этого коэффициента. Построим графики известных нам функций при коэффициенте, равном двум. И сформулируем общее правило для построения подобных кривых при положительных m.
Тема: Числовые функции
Урок: Построение графика функции 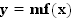 по графику функции
по графику функции 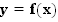
На этом уроке мы рассмотрим, каким образом, зная график функции 
 , где
, где 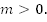
Вспомним, как из кривой 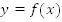 построить кривые
построить кривые
1. 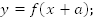
2. 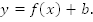
Ответ: Сдвигом кривой 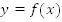
На 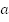
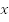 ;
;На 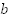 единиц вдоль оси
единиц вдоль оси 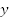 .
.
Рассмотрим конкретные примеры:
Пример 1. Дан график функции 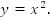 Необходимо получить графики функций
Необходимо получить графики функций 
Решение:
Кривая 
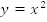 на 1 вправо по оси x, кривая
на 1 вправо по оси x, кривая 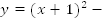 сдвигом на 1 влево по оси x (Рис. 1).
сдвигом на 1 влево по оси x (Рис. 1).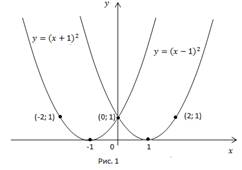
Пример 2. Построить график функции 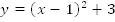 .
.
Решение:
Параболу 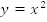 необходимо сдвинуть на 1 вправо по оси x и на 3 вверх по оси y (Рис. 2).
необходимо сдвинуть на 1 вправо по оси x и на 3 вверх по оси y (Рис. 2).
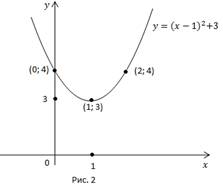
Рассмотрим, как из кривой  получить кривую
получить кривую 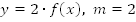 .
.
Дана кривая 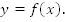 Чтобы получить кривую
Чтобы получить кривую 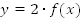 , необходимо каждую ординату умножить на 2. Точки пересечения кривой с осью ox остаются без изменения, т.к. их ординаты равны нулю (Рис. 3).
, необходимо каждую ординату умножить на 2. Точки пересечения кривой с осью ox остаются без изменения, т.к. их ординаты равны нулю (Рис. 3).
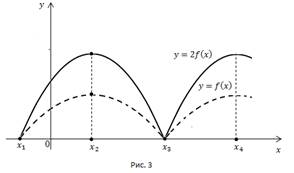
Применим полученное правило к конкретным кривым:
Пример 3. Дана кривая 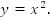 Построить кривую
Построить кривую 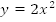 (Рис. 4).
(Рис. 4).
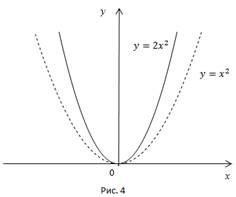
В точке 2 значение функции было 4, стало 8.
Произошло растяжение кривой 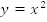 от оси x в два раза.
от оси x в два раза.
Пример 4. Дана кривая 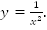 Построить кривую
Построить кривую 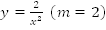
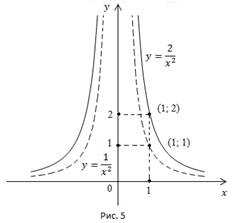
В точке 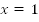 значение функции было равно 1, теперь станет равно 2.
значение функции было равно 1, теперь станет равно 2.
Происходит растяжение исходной кривой в два раза от оси x.
Асимптоты останутся прежними.
Рассмотрим случай, когда 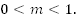
Пример 5. Дана кривая 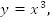 необходимо построить кривую
необходимо построить кривую 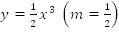
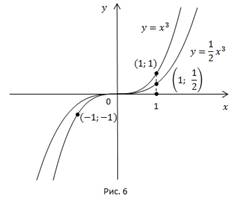
При 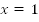 значение функции было равно 1, станет равным
значение функции было равно 1, станет равным 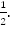
Произошло сжатие кривой 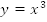 к оси x в два раза.
к оси x в два раза.
Пример 6. Дана кривая  Построить график функции
Построить график функции 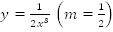
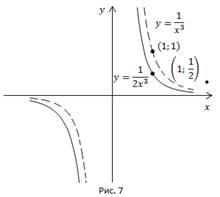
Точка 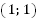 перейдет в точку
перейдет в точку 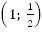 и т.д.
и т.д.
Искомый график получаем сжатием графика функции 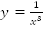 в 2 раза к оси x.
в 2 раза к оси x.
Мы рассмотрели, каким образом по графику функции 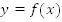 получить график функции
получить график функции 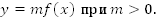

Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 352(б,в), 353(а,г), 357.
Алгоритмы построения графиков функции. 8–9-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Урок алгебры в 9 классе по теме «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины» был построен на основе компьютерных технологии, применяя исследовательскую деятельность обучения.
Цели урока: Обучающая: Наглядно продемонстрировать учащимся возможности использования компьютера при построении графиков функции с модулями; для самоконтроля, экономии времени при построении графиков функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |.
Развивающая: Развитие интеллектуальных умений и мыслительных операций — анализ и синтез сравнение, обобщение. Формирование ИКТ компетентности учащихся.
Воспитывающая: Воспитание познавательного интереса к предмету путем введения новейших технологий обучения. Воспитание самостоятельности при решении учебных задач.
Оборудование: Оборудование: компьютерный класс, интерактивная доска, презентация на тему «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины», раздаточный материал: карточки для работы с графической моделью функций, листы для фиксирования результатов исследования функций, персональные компьютеры. Лист самоконтроля.
Программное обеспечение: презентация Microsoft PowerPoint «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины»
Ход урока
1. Организационный момент
2. Повторение, обобщение и систематизация. Это этап урока сопровождается компьютерной презентацией.
Слайд 2.
График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f(х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f(х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
Рис.1
Рис.2
1. Исследование графика функции у= |х|
- Если х 0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.
- Если х<0, то |х|= -х и у= -х. При отрицательных значениях аргумента х график данной функции - прямая у= -х, т.е. биссектриса второго координатного угла.
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Рис. 3
Из сопоставления двух графиков: у=х и у= |х|, учащиеся сделают вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Из сопоставления двух графиков: у = х и у = -х, сделают вывод: функции у = f(|х|) получается из графика у = f (x) при х 0 симметричным отображением относительно оси ОУ.
Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину?
Слайд 3 и 4.
1. Построите график функции у=0,5 х2 — 2|х| — 2,5
1) Поскольку |х| = х при х 0, требуемый график совпадает с параболой у=0,5 х2 — 2х — 2,5 . Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,5 х2 + 2х — 2,5.
2) Если рассмотрим график у=0,5 х2 -2х — 2,5 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график.
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину?
2. Например: у=х2 — |х| -3
1) Поскольку |х| = х при х 0, требуемый график совпадает с параболой у=0,25 х2 — х — 3. Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,25 х2 + х — 3.
2) Если рассмотрим график у=0,25 х2 — х — 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график.
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
у =0, х2 -х -3 = 0
х2 -4х -12 = 0
Имеем, х1= — 2; х2 = 6.
(-2; 0) и (6; 0) — координаты точки пересечения графика функции с осью ОХ.
Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной |х|. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4).
Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0.
б) Поэтому достраиваю для х<0 часть графика, симметричную построенной относительно оси ОУ.
Рис. 4
На тетрадях ученики доказывают, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.
Доказательство: Если х 0, то f |(х)|= f (х), т.е. на множестве неотрицательных значений аргумента графики функции у = f (х) и у = f |(х)| совпадают. Так как у = f |(х)| — чётная функция, то её график симметричен относительно ОУ.
Таким образом, график функции у = f |(х)| можно получить из графика функции у = f (х) следующим образом:
1. построить график функции у = f(х) для х>0;
2. Для х<0, симметрично отразить построенную часть относительно оси ОУ.
Вывод: Для построения графика функции у = f |(х)|
1. построить график функции у = f(х) для х>0;
2. Для х<0, симметрично отразить построенную часть
относительно оси ОУ.
Слайд 5
4. Исследовательская работа по построению графика функции у = | f (х)|
Построить график функции у = |х2 — 2х|
Освободимся от знака модуля по определению
Если х2 — 2х0, т.е. если х 0 и х2, то |х2 - 2х|= х2 — 2х
Если х2 — 2х<0, т.е. если 0<х< 2, то |х2 — 2х|=- х2 + 2х
Видим, что на множестве х 0 и х2 графики функции
у = х2 — 2х и у = |х2 — 2х|совпадают, а на множестве (0;2)
графики функции у = -х2 + 2х и у = |х2 — 2х| совпадают. Построим их.
График функции у = | f (х)| состоит из части графика функции у = f(х) при у ?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ.
Слайд 6
Построить график функции у = |х2 — х —6|
1) Если х2 — х -6 0, т.е. если х-2 и х3, то |х2 — х -6|= х2 — х -6.
Если х2 — х -6<0, т.е. если -2<х< 3, то |х2 — х -6|= -х2 + х +6.
Построим их.
2) Построим у = х2 — х -6 . Нижнюю часть графика
симметрично отбражаем относительно ОХ.
Сравнивая 1) и 2), видим что графики одинаковые.
Работа на тетрадях.
Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у <0 относительно оси ОХ.
Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у = f(х), если f(х) 0; у = — f(х), если f(х) <0
Для любой функции у = f(х), если f(х) >0, то
| f (х)| = f(х), значит в этой части график функции
у = | f (х)| совпадает с графиком самой функции
у = f(х).
Если же f(х) <0, то | f (х)| = — f(х),т.е. точка (х; — f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика у = f(х).
Слайд 7
Вывод: действительно для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5)
Рис.5
Вывод: Для построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строим кривые, симметричные построенным графикам относительно оси абсцисс.
(Рис.6, 7.)
Слайды 8-13.
5. Исследовательская работа по построению графиков функции у=|f |(х)| |
Применяя определение абсолютной величины и ранее рассмотренные примеры, построим графиков функции:
у = |2|х| — 3|
у = |х2 — 5|х||
у = | |х2| — 2| и сделал выводы.
Для того чтобы построить график функции у = | f |(х)| надо:
1. Строить график функции у = f(х) для х>0.
2. Строить вторую часть графика, т. е. построенный график симметрично отражать относительно ОУ, т.к. данная функция четная.
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Построить график функции у = | 2|х | — 3| (1-й способ по определению модуля)
1. Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5
а) у = 2х — 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Строим у = —2 |х| + 3, для 2|х | — 3 < 0. т.е. -1,5<х<1,5
а) у = —2х + 3, для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
У = | 2|х | — 3|
1) Строим у = 2х-3, для х>0.
2) Строим прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.
Сравнивая оба графика, видим, что они одинаковые.
2.
у = | х2 — 5|х| |
1. Строим у = х2 — 5 |х|, для х2 — 5 |х| > 0 т.е. х >5 и х<-5
а) у = х2 — 5 х, для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Строим у = — х2 + 5 |х| , для х2 — 5 |х| < 0. т.е. -5х5
а) у = — х2 + 5 х , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
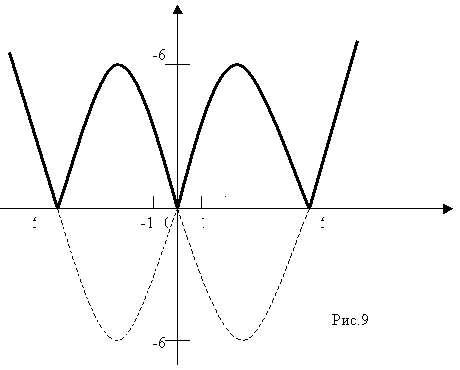
У = | х2 — 5|х| |
а) Строим график функции у = х2 — 5 х для х>0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.9)
3. у =| |х|2 — 2 |
1). Строим у = |х|2 — 2 , для |х|2 — 2 > 0, x> и x< —
а) у = х2 — 2, для х>0
б) для х<0, симметрично отражаю построенную часть относительно оси ОУ.
2). Строим у = — |х|2 + 2 , для |х|2 — 2 < 0. т.е. — < x<
а) у = —х2 + 2 , для х>0
б) для х<0, симметрично отражаю построенную часть относительно оси ОУ.
У = ||х|2 — 2 |
а) Строим у = х2 -2 для х > 0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.10)
3. Подведение итогов урока.
14,15 слайды.
Алгоритм построения графика функции у=f |(х)|
1.Построить график функции у=f(х) для х>0;
2.Построить для х<0 часть графика, симметричную построенной относительно оси ОУ.
Алгоритм построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строить кривые, симметричные построенным графикам относительно оси абсцисс.
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
urok.1sept.ru
«Построение графиков функции» ( 9 класс )
Урок алгебры в 9 классе по теме «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины».
Цели урока: Обучающая: Наглядно продемонстрировать учащимся возможности использования компьютера при построении графиков функции с модулями; для самоконтроля, экономии времени при построении графиков функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |.
Развивающая: Развитие интеллектуальных умений и мыслительных операций — анализ и синтез сравнение, обобщение. Формирование ИКТ компетентности учащихся.
Воспитывающая: Воспитание познавательного интереса к предмету путем введения новейших технологий обучения. Воспитание самостоятельности при решении учебных задач.
Оборудование: Оборудование: компьютерный класс, интерактивная доска, презентация на тему «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины», раздаточный материал: карточки для работы с графической моделью функций, листы для фиксирования результатов исследования функций, персональные компьютеры. Лист самоконтроля.
Ход урока
1. Организационный момент
2. Повторение, обобщение и систематизация.
График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f(х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f(х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
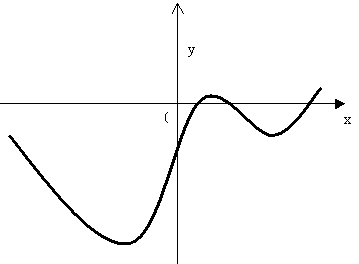
Рис.1
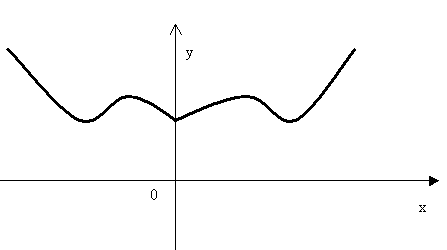
Рис.2
1. Исследование графика функции у= |х|
Если х
 0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.
0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.Если х<0, то |х|= -х и у= -х. При отрицательных значениях аргумента х график данной функции — прямая у= -х, т.е. биссектриса второго координатного угла.
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
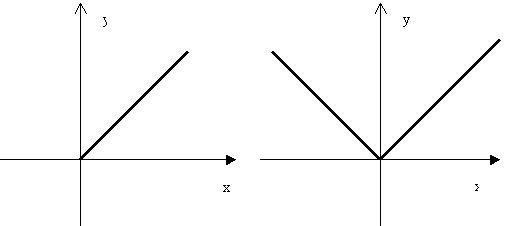
Рис. 3
Из сопоставления двух графиков: у=х и у= |х|, учащиеся сделают вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Из сопоставления двух графиков: у = х и у = -х, сделают вывод: функции у = f(|х|) получается из графика у = f (x) при х  0 симметричным отображением относительно оси ОУ.
0 симметричным отображением относительно оси ОУ.
Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину?
1. Построите график функции у=0,5 х2 — 2|х| — 2,5
1) Поскольку |х| = х при х  0, требуемый график совпадает с параболой у=0,5 х2 — 2х — 2,5 . Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,5 х2 + 2х — 2,5.
0, требуемый график совпадает с параболой у=0,5 х2 — 2х — 2,5 . Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,5 х2 + 2х — 2,5.
2) Если рассмотрим график у=0,5 х2 -2х — 2,5 при х  0 и отобразить его относительно оси ОУ мы получим тот же самый график.
0 и отобразить его относительно оси ОУ мы получим тот же самый график.
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину?
2. Например: у=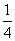 х2 — |х| -3
х2 — |х| -3
1) Поскольку |х| = х при х  0, требуемый график совпадает с параболой у=0,25 х2 — х — 3. Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,25 х2 + х — 3.
0, требуемый график совпадает с параболой у=0,25 х2 — х — 3. Если х<0, то поскольку х2 = |х|2, |х|=-х и требуемый график совпадает с параболой у=0,25 х2 + х — 3.
2) Если рассмотрим график у=0,25 х2 — х — 3 при х  0 и отобразить его относительно оси ОУ мы получим тот же самый график.
0 и отобразить его относительно оси ОУ мы получим тот же самый график.
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
у =0, 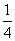 х2 -х -3 = 0
х2 -х -3 = 0
х2 -4х -12 = 0
Имеем, х1= — 2; х2 = 6.
(-2; 0) и (6; 0) — координаты точки пересечения графика функции с осью ОХ.
Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной |х|. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4).
Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0.
б) Поэтому достраиваю для х<0 часть графика, симметричную построенной относительно оси ОУ.
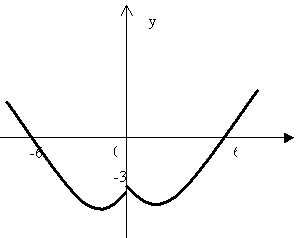
Рис. 4
На тетрадях ученики доказывают, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.
Доказательство: Если х 0, то f |(х)|= f (х), т.е. на множестве неотрицательных значений аргумента графики функции у = f (х) и у = f |(х)| совпадают. Так как у = f |(х)| — чётная функция, то её график симметричен относительно ОУ.
Таким образом, график функции у = f |(х)| можно получить из графика функции у = f (х) следующим образом:
1. построить график функции у = f(х) для х>0;
2. Для х<0, симметрично отразить построенную часть относительно оси ОУ.
Вывод: Для построения графика функции у = f |(х)|
1. построить график функции у = f(х) для х>0;
2. Для х<0, симметрично отразить построенную часть
относительно оси ОУ.
4. Исследовательская работа по построению графика функции у = | f (х)|
Построить график функции у = |х2 — 2х|
Освободимся от знака модуля по определению
Если х2 — 2х 0, т.е. если х
0, т.е. если х 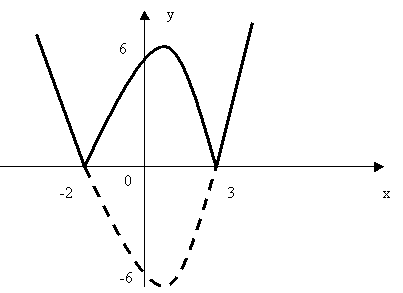 0 и х
0 и х 2, то |х2 — 2х|= х2 — 2х
2, то |х2 — 2х|= х2 — 2х
Если х2 — 2х<0, т.е. если 0<х< 2, то |х2 — 2х|=- х2 + 2х
Видим, что на множестве х 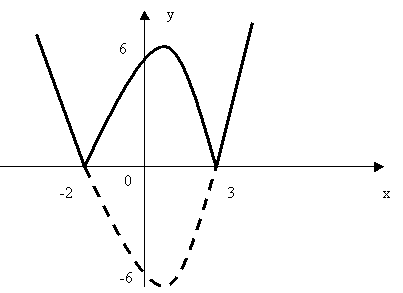 0 и х
0 и х 2 графики функции
2 графики функции
у = х2 — 2х и у = |х2 — 2х|совпадают, а на множестве (0;2)
графики функции у = -х2 + 2х и у = |х2 — 2х| совпадают. Построим их.
График функции у = | f (х)| состоит из части графика функции у = f(х) при у ?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ.
Построить график функции у = |х2 — х —6|
1) Если х2 — х -6  0, т.е. если х
0, т.е. если х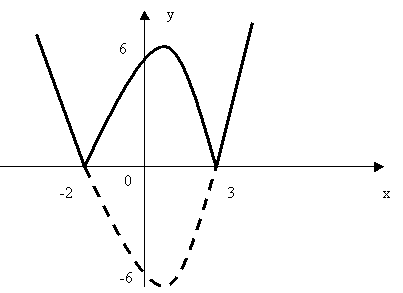 -2 и х
-2 и х 3, то |х2 — х -6|= х2 — х -6.
3, то |х2 — х -6|= х2 — х -6.
Если х2 — х -6<0, т.е. если -2<х< 3, то |х2 — х -6|= -х2 + х +6.
Построим их.
2) Построим у = х2 — х -6 . Нижнюю часть графика
симметрично отбражаем относительно ОХ.
Сравнивая 1) и 2), видим что графики одинаковые.
Работа на тетрадях.
Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у <0 относительно оси ОХ.
Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у = f(х), если f(х)  0; у = — f(х), если f(х) <0
0; у = — f(х), если f(х) <0
Для любой функции у = f(х), если f(х) >0, то
| f (х)| = f(х), значит в этой части график функции
у = | f (х)| совпадает с графиком самой функции
у = f(х).
Если же f(х) <0, то | f (х)| = — f(х),т.е. точка (х; — f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика у = f(х).
Вывод: действительно для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5)
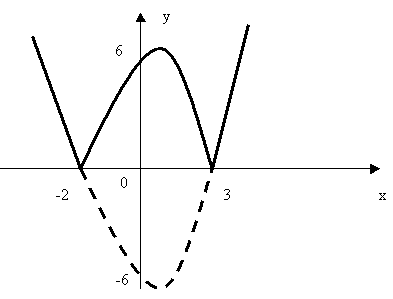
Рис.5
Вывод: Для построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строим кривые, симметричные построенным графикам относительно оси абсцисс.
(Рис.6, 7.)
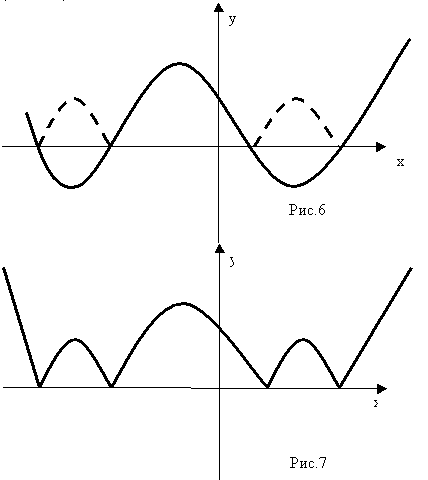
5. Исследовательская работа по построению графиков функции у=|f |(х)| |
Применяя определение абсолютной величины и ранее рассмотренные примеры, построим графиков функции:
у = |2|х| — 3|
у = |х2 — 5|х||
у = | |х2| — 2| и сделал выводы.
Для того чтобы построить график функции у = | f |(х)| надо:
1. Строить график функции у = f(х) для х>0.
2. Строить вторую часть графика, т. е. построенный график симметрично отражать относительно ОУ, т.к. данная функция четная.
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
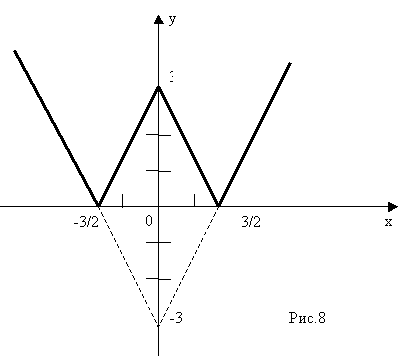
Построить график функции у = | 2|х | — 3| (1-й способ по определению модуля)
1. Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5
а) у = 2х — 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Строим у = —2 |х| + 3, для 2|х | — 3 < 0. т.е. -1,5<х<1,5
а) у = —2х + 3, для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
У = | 2|х | — 3|
1) Строим у = 2х-3, для х>0.
2) Строим прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.
Сравнивая оба графика, видим, что они одинаковые.
2.
у = | х2 — 5|х| |
1. Строим у = х2 — 5 |х|, для х2 — 5 |х| > 0 т.е. х >5 и х<-5
а) у = х2 — 5 х, для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Строим у = — х2 + 5 |х| , для х2 — 5 |х| < 0. т.е. -5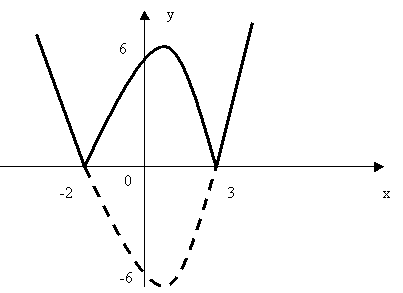 х
х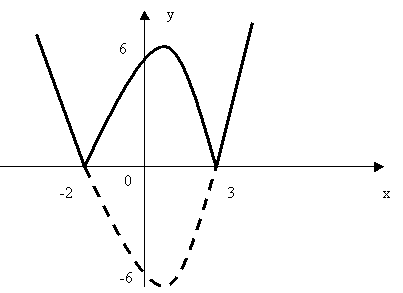 5
5
а) у = — х2 + 5 х , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
У = | х2 — 5|х| |
а) Строим график функции у = х2 — 5 х для х>0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.9)
3. у =| |х|2 — 2 |
1). Строим у = |х|2 — 2 , для |х|2 — 2 > 0, x> 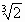 и x< —
и x< —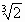
а) у = х2 — 2, для х>0
б) для х<0, симметрично отражаю построенную часть относительно оси ОУ.
2). Строим у = — |х|2 + 2 , для |х|2 — 2 < 0. т.е. — 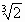 < x<
< x<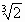
а) у = —х2 + 2 , для х>0
б) для х<0, симметрично отражаю построенную часть относительно оси ОУ.
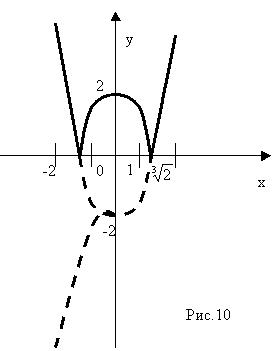
У = ||х|2 — 2 |
а) Строим у = х2 -2 для х > 0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.10)
3. Подведение итогов урока.
Алгоритм построения графика функции у=f |(х)|
1.Построить график функции у=f(х) для х>0;
2.Построить для х<0 часть графика, симметричную построенной относительно оси ОУ.
Алгоритм построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строить кривые, симметричные построенным графикам относительно оси абсцисс.
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
infourok.ru
Урок математики в 9 классе по теме»Графики функций»

Тест — игра
Кто хочет стать отличником?
Тема: Графики функций
Начало игры

ОТБОРОЧНЫЙ ТУР
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
5
Баллы за вопрос
0
4
0
3
0
2
0
1
0
B )
А)
D )
C )

Вопрос 1
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
0
1
0
B)
А )
C)
D)

Вопрос 1
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
0
1
0
B)
А )
C)
D)

Вопрос 2
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
1
0
1
B)
А )
D)
C)

Вопрос 2
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
1
0
0
B)
А )
D)
C)

Вопрос 3
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
1
1
1
А )
B)
C)
D)

Вопрос 3
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
0
1
1
А )
B)
C)
D)

Вопрос 3
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
1
1
0
А )
B)
C)
D)

Вопрос 3
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
0
1
0
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
1
1
1
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
1
2
1
1
1
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
1
2
0
1
1
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
0
1
1
А )
B)
D)
C)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
1
2
1
1
0
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
1
1
0
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
1
2
0
1
0
А )
B)
C)
D)

Вопрос 4
График какой из приведенных ниже
функций изображен на рисунке
№ вопроса
Баллы за вопрос
5
0
4
0
3
0
2
0
1
0
А )
B)
C)
D)

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
1
2
1
1
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
1
2
1
1
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
0
2
1
1
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
0
2
1
1
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
1
2
1
0
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
1
2
1
0
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
0
2
1
0
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
0
2
1
0
1
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
1
2
1
1
0
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
1
2
1
1
0
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
0
2
1
1
0
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
0
2
1
1
0
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
1
2
1
0
0
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
1
2
1
0
0
А ) -1
B) 2
C) 1
D )3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
1
3
0
2
1
0
0
А ) -1
B) 2
C) 1
D) 3

Вопрос 5
Найдите значение коэффициента а
по графику функции
№ вопроса
5
Баллы за вопрос
0
4
0
3
0
2
1
0
0
А ) -1
B) 2
D) 3
C) 1

Вы набрали 0 баллов
Закончить игру
Начать игру

Вы набрали 1 балл
Закончить игру
Начать игру

Вы набрали 2 балла
Закончить игру
Начать игру

Вы набрали 3 балла
Закончить игру
Начать игру

Вы набрали 4 балла
Закончить игру
Начать игру

Вы набрали 5 баллов
Закончить игру
Начать игру

multiurok.ru
Построение графика квадратичной функции. 9-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
“Мало иметь хороший ум, главное – уметь его применять”. Рене Декарт
Цели урока:
- формирование у учащихся умения строить график квадратичной функции в соответствии со схемой, приведенной в учебнике на с.41 учебника “Алгебра, 9 класс” под редакцией Теляковского А.С.;
- научить учащихся определять основные свойства квадратичной функции.
Задачи урока.
обучающие:
знать: алгоритм построения графика квадратичной функции;
уметь: строить график любой квадратичной функции, определять основные свойства функции по графику.
развивающие: развивать навыки самостоятельной работы, самоконтроля и взаимоконтроля.
воспитательные: воспитывать самостоятельность, настойчивость для достижения конечных результатов, способствовать развитию интереса к математике через различные формы работы.
Оборудование: мультимедийный проектор, интерактивная доска, презентация Power Point, тетрадь с печатной основой.
Ход урока
1. Организационный момент.
2. Устная работа. Повторение ранее изученного материала.
1) Повторить, как найти координаты вершины параболы, что является осью симметрии параболы, куда направлены ветви параболы, что такое нули функции.
(Вопросы задаются всему классу, после ответов к доске приглашаются три ученика работать по карточкам)
Карточка №1.
Найти координаты вершины параболы:
a) x2-8x+7=0; б) 9x2-6x+1=0; в) 7x-2x2=0
Карточка №2.
Найти нули функции:
a) x2-8x+7=0; б) 9x2-6x+1=0; в) 7x-2x2=0
Карточка №3.
Найдите координаты вершины параболы:
а)y=5(x-7)2+9 x0=______, y0= ______
б)y=-4(x+3)2-5 x0=______, y0= ______
в)y=x2— 16 x0=______, y0= ______
г)y=(x-4)2 +10 x0=______, y0= ______
2) запись темы урока (Слайд 2), сообщение целей и задач урока (Слайд 3-4).
3) проверка домашнего задания с помощью тестового задания (учащиеся выполняют задание по вариантам в течение 5 минут, у каждого ученика на столе текст задания и чистый лист). Текст задания на экране (Слайд 5-6).
Учитель в это время проверяет работы учащихся у доски. Затем проверка тестовых заданий (взаимопроверка — ученики обменялись вариантами). (Слайд 7)
Работы сданы учителю для выставления оценок.
4) а) повторение (устно) преобразований графика квадратичной функции с помощью слайдов, учащиеся при этом комментируют свои ответы (Слайды 9-13):
График функции, симметричен оси Оу;
График функции симметричен оси Ох;
Сжатие или растяжение;
График функции y=|f(x)|;
График функции у =f(x)+A, y=f(x)-A.
Итак, можно показать, что любую квадратичную функцию у =ax2+вх +с
с помощью выделения полного квадрата можно записать в виде у = a(x-x0)2 +y0 , где х0= — b/(2a) , y0= y(x0)= — (b2-4ac)/(4a).
Графиком функции у =a(x-x0)2 +y0 является парабола, получаемая сдвигом параболы у = ax2:
вдоль оси абсцисс вправо на x0, если x0 > 0,влево на |x0|, если х0 < 0.
вдоль оси ординат вверх на y0, если y0 >0, вниз на |y0|, если y0 < 0.
(Слайды 14-15)
б) Рассмотрим несколько примеров, как определить координаты вершины параболы, заданной уравнением у = (х – а)2+в и у = ( х +а)2-в. (Слайд 16)
в) найти координаты вершины параболы: (Слайд 17), учащиеся записывают и называют координаты вершин заданных графиков параболы (красная, синяя, фиолетовая, желтая, зеленая) и проверка ответов из слайда.
Выставление оценок за устно — письменную работу на уроке на данном этапе.
5) Повторить этапы построения параболы, заданной уравнениями:
y = (x+7)2 -6; y= (x-4)2 +3. (Слайд 18-19)
Затем построить график у = (х-4)2 -8 в тетради с помощью шаблона y = x2 с последующей проверкой (Слайд 21).
(Выставление оценок за устно-письменную работу)
3. Объяснение нового материала.
Беседа. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи, и порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. Находясь на выставке картин, мы рассматриваем произведения искусств и обращаем внимание на то, сумел ли художник передать глубину, завершенность образного содержания. Картина является итогом длительных наблюдений и размышлений художника над жизнью. Представьте, что мы находимся на выставке картин, выполненных с помощью компьютера. В компьютерном “изобразительном искусстве” мы можем увидеть не что иное, как графики функций. Чтобы научиться видеть в таких картинах действительно графики функций, научиться создавать самим такие картины, необходимо знать основные функции их свойства. Можно привести множество примеров, как важно уметь строить графики и описывать их свойства.
Ученый-сейсмолог, анализируя сейсмограмму, узнает, когда было землетрясение, где оно произошло, определяет силу и характер толчков. Врач, исследующий больного, может по кардиограмме судить о нарушениях сердечной деятельности: изучение кардиограммы помогает правильно поставить диагноз заболевания. Инженер- радиоэлектроник по характеристике полупроводникового элемента выбирает наиболее подходящий режим его работы. Более того, по мере развития математики растет проникновение графического метода в самые различные области
жизни человека. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике. Значит, растет и важность изучения рассматриваемого раздела математики в школе, в вузе, и особенно - важности самостоятельной работы над ним. (Слайд 22)
Итак, тема урока: “Построение графика квадратичной функции” (Слайд 23-24). Работа учеников в тетради по заданному алгоритму.
В результате выполнения работы, учащиеся приходят к выводу, что для построения любой квадратичной функции необходимо использовать схему: (Слайд 25)
4. Закрепление учебного материала.
Ученики работают в рабочих тетрадях с печатной основой самостоятельно, используя полученные знания, затем тетради сдают на проверку учителю. (Тетрадь с печатной основой прилагается)
5. Подведение итогов урока. Выставление оценок.
Домашнее задание: п.7, №125 (в), 126 (б, в), 132 (а, б). (Слайды 26-27)
Приложение
urok.1sept.ru