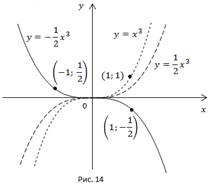
Построение графика функции y=mf(x) по графику функции y=f(x) при m
На этом уроке мы продолжим изучение построения модификаций графиков. Здесь мы рассмотрим построение графика функции вида у=m∙f(x) для m<0.
Вначале вспомним правило для построения графика функции у=m∙f(x) для m>0. Далее мы рассмотрим, как выглядят графики для коэффициентов m, равных –1 и –2, и сформулируем общее правило для построения подобных графиков. В конце решим несколько примеров на построение графиков и сопутствующие задачи.
Тема: Числовые функции
Урок: Построение графика функции  по графику функции
по графику функции  при
при 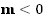
На прошлом уроке мы рассмотрели соответствующую задачу для 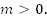 Теперь рассмотрим, как построить график функции
Теперь рассмотрим, как построить график функции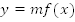 по графику функции
по графику функции 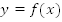 при
при 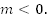
Вспомним известную задачу. Дан график функции 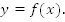 Построить график функции
Построить график функции 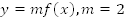
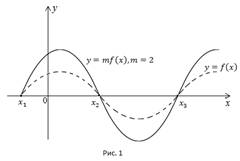
Точки пересечения с осью x остаются без изменения. Все ординаты умножаются на 2.
Если 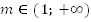 происходит растяжение вдоль оси y от оси x.
происходит растяжение вдоль оси y от оси x.
Если 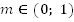 происходит сжатие вдоль оси y к оси x.
происходит сжатие вдоль оси y к оси x.
Рассмотрим случай, когда  . Дан график функции
. Дан график функции 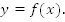
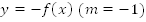 .
.Точки  остаются без изменений. В точке
остаются без изменений. В точке 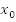 значение функции было равно
значение функции было равно 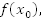 станет равным
станет равным 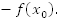 Мы симметрично отображаем каждую точку графика относительно оси x (Рис. 2).
Мы симметрично отображаем каждую точку графика относительно оси x (Рис. 2).
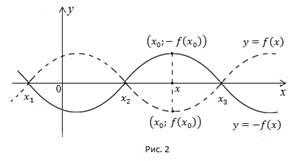
Для того, чтобы получить график функции 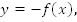 необходимо график
необходимо график 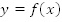 симметрично отобразить относительно оси x.
симметрично отобразить относительно оси x.
Пример 1. Дан график функции 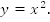 Необходимо получить график функции
Необходимо получить график функции  .
.
Решение.
Рис. 3.
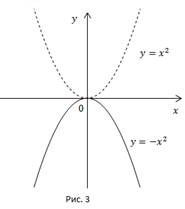
Симметрично отображая кривую 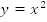
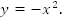
Рассмотрим случай  .
.
Дана кривая 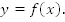 Построить кривую
Построить кривую .
.
План построения:
1. Построить кривую 
2. Построить кривую 
Растяжением в два раза вдоль оси y получаем кривую  Симметричным отображением относительно оси x получим кривую
Симметричным отображением относительно оси x получим кривую  (Рис. 4).
(Рис. 4).
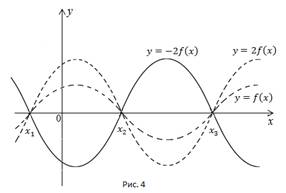
Сформулируем план построения графика функции  по графику
по графику 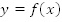 для любого
для любого 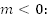
1. 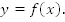
2. 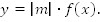
3. 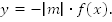
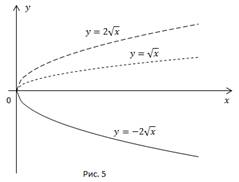
Пример 2. Построить кривую 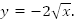
План построения:
1. 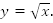
2. 
3. 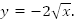
Рис. 5.
Пример 3. Построить график функции 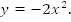
План построения:
1. 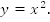
2. 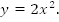
3. 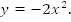
Рис. 6, 7, 8.

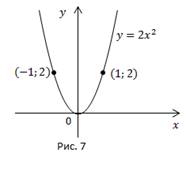
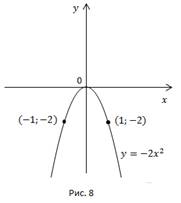
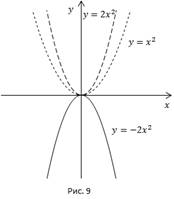
Также полезно построить все три кривые в одних координатных осях (Рис. 9).
Пример 4. Построить график функции 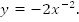
План построения:
1. 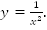
2. 
3. 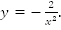
Рис. 10, 11, 12.
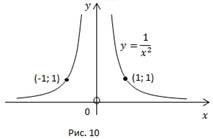
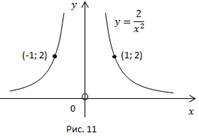

Построим все три кривые в одних осях (Рис. 13).

Пример 5. Построить график функции 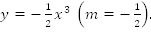
План построения:
1. 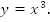
2. 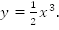
3. 
Мы научились получать график функции 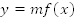 при
при 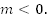 На следующем уроке будет подробно рассмотрен графический метод решения уравнений и неравенств.
На следующем уроке будет подробно рассмотрен графический метод решения уравнений и неравенств.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 352(а,г), 353(б,в), 358.
interneturok.ru
График функции y=kf(x) | Алгебра
График функции y=kf(x) (k>1) можно получить из графика функции y=f(x) растяжением от оси Ox в k раз. При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; ky) графика функции y=kf(x):
(x; y) → (x; ky)
(то есть абсцисса (x) каждой точки начального графика остаётся без изменений, а ордината (y) увеличивается в k раз).
При растяжении от оси Ox точки графика y=f(x), лежащие на оси абсцисс, остаются на месте, так как k∙0=0.
Примеры.
1) График функции y=3x² получен из графика функции y=x² растяжением в 3 раза от оси Ox.
При растяжении графика от оси абсцисс нужно ординату каждой точки увеличить в 3 раза.
Для построения графика отмечаем базовые точки графика y=x². Для каждой точки координату x оставляем неизменной, значение координаты y умножаем на 3. Таким образом, каждая точка нового графика располагается строго над соответствующей точкой графика y=x², в 3 раза дальше от оси Ox.
Вершина параболы y=x², точка O (0; 0), остаётся на месте (так как 3∙0=0).
График y=3x² из y=x²
(1; 1) → (1; 3),
(-1; 1) → (-1; 3),
(2; 4) → (2; 12),
(-2; 4) → (-2; 12)
и т. д.
2) График функции y=2|х| можно получить из графика функции y=|х| растяжением от оси абсцисс в 2 раза.
Точка O (0; 0) остаётся на месте. В I и II координатных четвертях берём по одной точке графика y=|х|, например, (5; 5) и (-5; 5). Их абсциссы оставляем без изменений, а ординаты удваиваем:
График y=2|х| из y=|х|
(5; 5)→ (5; 10),
(-5; 5)→ (-5; 10).
Через эти точки из точки O проводим лучи.
Получаем график функции y=2|х|
3) График функции y=4√x можно получить из графика функции y=√x растяжением от оси Ox в 4 раза.
Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y увеличиваем в 4 раза. Точка O (0; 0) при этом остаётся на месте.
Через полученные точки проводим новый график:
График y=4√x из y=√x
(0; 0) → (0; 0),
(1; 1) → (1; 4),
(4; 2) → (4; 8),
(9; 3) → (9; 12),
и т. д.
Преобразование графиков может быть использовано для построения графиков функций в ходе решения примеров из разных разделов алгебры.
www.algebraclass.ru
График функции y=f(x)+b | Алгебра
График функции y=f(x)+b (b>0) можно получить из графика функции y=f(x) с помощью параллельного переноса (сдвига) вдоль оси Oy на b единиц вверх.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y+b) графика функции y=f(x)+b (то есть абсцисса (координата x) каждой точки остается без изменения, а ордината (координата y ) увеличивается на b.
Один из вариантов преобразования — осуществить параллельный перенос начала отсчёта, точки O(0;0), в точку O1(0;b) и построить график y=f(x) с началом отсчёта от точки O1.
Примеры.
1) График функции y=x²+3 может быть получен из графика функции y=x² с помощью параллельного переноса вдоль оси Oy на 3 единицы вверх.
Строим параболу y=x². Затем переносим каждую из основных точек на 3 единицы вверх.
y=x²+3 из y=x²
Можно перенести только вершину параболы, точку (0; 0), на 3 единицы вверх, в точку (0; 3), и от новой вершины строить параболу y=x² (1 единица вправо, 1 — вверх; 1 единица влево, 1 — вверх; 2 единицы вправо, 2 — вверх и т.д.). (Фактически, в этом случае осуществляется параллельный перенос начала отсчёта из точки O(0; 0) в точку O1(0; 3), и строится график y=x² с новым началом отсчёта от точки O1).
1) График функции y=x³+2 может быть получен из графика функции y=x³ с помощью параллельного переноса вдоль оси Oy на 2 единицы вверх.
Можно обойтись без построения начального графика y=x³, достаточно обозначить его основные точки, и выполнить параллельный перенос каждой из них на 2 единицы вверх.
y=x³+2 из y=x³
3) График функции y=√x+4 может быть получен из графика функции y=√x параллельным переносом на 4 единицы вверх вдоль оси Oy.
Строим график функции y=√x по основным точкам. Затем переносим каждую из этих точек вверх на 4 единицы.
Через полученные точки проводим ветвь параболы:
В следующих раз рассмотрим рассмотрим построение графиков вида y=f(x)-b.
Преобразование графиков позволяет на основе графиков элементарных функций получать графики сложных функций. Умение преобразовывать графики в алгебре пригодится не только при изучении функций, но и при решении уравнений и неравенств, в частности, при решении заданий с параметрами.
www.algebraclass.ru
| 1. | Вспомогательная система координат | 1 вид — рецептивный | лёгкое | 1 Б. | Записать координаты новой начальной точки. |
| 2. | Параллельный перенос графика функции | 1 вид — рецептивный | лёгкое | 2 Б. | Вставить пропущенные числа в предложение. |
| 3. | Направление сдвига графика функции | 1 вид — рецептивный | лёгкое | 2 Б. | Определить направление сдвига графика функции. |
| 4. | Формула функции | 2 вид — интерпретация | среднее | 2 Б. | Необходимо записать формулу функции. |
| 5. | Уравнение параболы | 2 вид — интерпретация | среднее | 2 Б. | Необходимо написать уравнение параболы. |
| 6. | Значение функции | 2 вид — интерпретация | среднее | 2 Б. | Необходимо вычислить значение функции. |
| 7. | Построение графика квадратичной функции вида y = (x + a)² + b | 1 вид — рецептивный | среднее | 3 Б. | Построение графика квадратичной функции вида y = (x + a)^2 + b. |
| 8. | Метод выделения полного квадрата | 3 вид — анализ | сложное | 3 Б. | Необходимо записать формулу функции. |
| 9. | Функции | 3 вид — анализ | сложное | 3 Б. | Вычислить значение функций, вычислить сумму. |
| 10. | Графическое решение системы уравнений | 3 вид — анализ | сложное | 3 Б. | Необходимо графически решить систему уравнений. |
www.yaklass.ru
График функции y=f(|x|) | Алгебра
График функции y=f(|x|) может быть получен из графика функции y=f(x).
Для этого ту часть графика, которая лежит левее оси Oy, отбрасываем. Часть графика, расположенную правее оси ординат, сохраняем, и её же отображаем симметрично относительно оси Oy.
Точка, лежащая на оси Oy, при таком преобразовании остаётся на месте.
Примеры.
1) Построить график функции y= -x²+2|x|+8.
Решение:
Так как x²=|x|², запишем формулу функции в виде y= —|x|²+2|x|+8.
График функции y= —|x|²+2|x|+8 можно получить из графика функции y= -x²+2x+8. Для этого часть графика, лежащую слева от оси Oy, отбрасываем. Правее оси ординат график сохраняем и это же часть отображаем симметрично относительно оси Oy:
(1; 9) → (-1; 9),
(2; 8) → (-2; 8),
(3; 5) → (-3; 5),
(4; 0) → (-4; 0).
График y= -|x|²+2|x|+8 из графика y= -x²+2x+8.
2) График функции
получен из графика функции y=-4/(x-2).
Всё, что лежит левее оси Oy, отбрасываем, всё, что правее — отображаем симметрично относительно оси ординат:
3) График функции
получен из графика y=√x.
Отбрасывать здесь нечего, поскольку график полностью расположен правее оси ординат. Весь график сохраняем, и его же отображаем симметрично относительно оси Oy:
Геометрические преобразования — быстрый и удобный способ построения графиков на основе графиков элементарных функций. Поскольку в алгебре строить графики приходится достаточно часто, важно вовремя научиться пользоваться этим инструментом.
www.algebraclass.ru