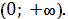Логарифмическая функция. Преобразования графика логарифмической функции(11 класс)

Разработка урока обобщения и систематизации знаний в 11 классе по теме « Логарифмическая функция. Преобразования графика логарифмической функции»

Этап урока

Время, мин.

Приёмы и методы

Содержание деятельности

Организация начала урока

1

словесный

Приветствует, проверяет готовность к уроку, организует внимание

Подготовка учащихся: сообщение темы (проблемы). Исторический материал и связь с окружающим миром – для развития интереса к предмету

5

Словесный, фронтальная беседа, словесно-наглядный с применением презентаций учащегося

Предлагает план работы на уроке.

Учащиеся с помощью презентации рассказывают о связи логарифмической функции с окружающим миром

Проверка готовности к уроку по материалу предыдущего урока (самими учащимися)

5

Индивидуальный интерактивный тест с последующей самопроверкой

Предъявляет задания. Организует и корректирует работу обучающихся

Обобщение отдельных фактов, понятий

Построение графика логарифмической функции путем несложных преобразований

5

Фронтальный анализ, словесно-наглядный с применением презентаций Самостоятельная работа с проверкой

Предъявляет задания. Организует и корректирует работу обучающихся, организует проверку, демонстрируя параллельный перенос с помощью презентации

Обобщение отдельных фактов, понятий

Построение графика логарифмической функции путем сложных преобразований

10

Фронтальный анализ и обобщение

Самостоятельная работа с проверкой

Предъявляет задания. Организует и корректирует работу обучающихся, организует проверку с помощью документ- камеры

Применение построений графиков при решении уравнений и неравенств

12

Работа у доски, самостоятельная работа

Предъявляет задания. Организует и корректирует работу обучающихся, организует проверку

Подведение итогов урока. Рефлексия

2

Словесный анализ, фронтальная

Задает вопросы, отвечая на которые учащиеся анализируют свою работу

Тема урока

Логарифмическая функция. Преобразования графика логарифмической функции

Цель урока (учебная, развивающая, воспитательная)

Образовательные: совершенствовать навыки построения графиков сложных логарифмических функций; уметь применять их при графическом решении уравнений и неравенств.

Развивающие:

• Развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизаций

• Сознательного восприятия учебного материала

• Развитие математической речи учащихся, потребности к самообразованию

• Способствовать развитию исследовательской деятельности учащихся

Воспитательные:

• Чувства ответственности, уверенности в себе, воспитание культуры общения

Тип урока

Комбинированный

Основные термины и понятия для изучения

Логарифм, свойства логарифма, логарифмическая функция, ее свойства

Оборудование

Ноутбуки персональные, документ-камера, карточки с заданиями, листы оценивания, презентации, интерактивный тест.

Формы работы

Фронтальная, индивидуальная.

Методические приемы мотивации обучения

Использование ИКТ, презентации составленные учащимися

Методические приемы проверки домашнего задания

Интерактивный тест

Межпредметные связи

Выступление ученика с демонстрацией материала по презентации «Логарифмическая функция в окружающем нас мире»

Тема: Логарифм, его свойства, логарифмическая функция, ее свойства и график

«В науке нет широкой столбовой дороги, и только тот достигнет ее сияющих вершин, кто, не страшась усталости, карабкается по ее каменистым тропам»

(Маркс)

Цели урока:

Образовательные: совершенствовать навыки построения графиков логарифмических функций; уметь применять их при графическом решении уравнений и неравенств.

Развивающие:

• Развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, конкретизаций

• Сознательного восприятия учебного материала

• Развитие математической речи учащихся, потребности к самообразованию

• Способствовать развитию исследовательской деятельности учащихся

Воспитательные:

• Воспитание познавательной активности

• Чувства ответственности, уверенности в себе, воспитание культуры общения

Ресурсы урока: Карточки с заданиями, интерактивный тест, презентации, лист оценивания.

Тип урока: Комбинированный

Форма урока: Классно-урочная

Форма работы: фронтальная, индивидуальная.

Технология: Личностно-ориентированная; информационно-коммуникативная

План урока:

1. Организационный момент (сообщение темы урока, цель урока, что должны знать и уметь).

2. Осуществление межпредметных связей (сообщение учащегося)

3. Обобщение ранее изученного материала. Проверка готовности к изучению материала (индивидуальное тестирование).

4. Изучение и закрепление нового материала

5. Применение нового материала

6. Подведение итогов.

Ход урока:

1. Организационный момент (приветствие, проверка готовности учащихся к уроку).

• • Тема сегодняшнего нашего урока «Логарифмическая функция. Преобразование графика».

  • Наша цель научиться строить графики логарифмических функций с помощью преобразований и применять их в решении уравнений и неравенств.

  • Будем работать по следующему плану:

1. Узнаем о связи логарифмической функции с окружающим миром.

2. Проверка готовности к уроку с помощью тестирования

3. Построение графиков логарифмической функции +самостоятельная работа

4. Графическое решение уравнений и неравенств + самостоятельная работа

На уроке вы должны быть активными, так как ваша оценка за урок будет складываться из количества баллов набранных вами за урок. Критерии оценок посмотрите в листах оценивания.

2. Осуществление межпредметных связей (сообщение учащегося)

3. Обобщение ранее изученного материала. Проверка готовности к изучению материала (индивидуальное тестирование). Вопросы по тестированию есть? При рассмотрении примеров были ли у вас трудности?

4. Изучение и закрепление нового материала

Напомните как построить график графики функций y = log ₃(x), y = log _0,3(x)

Как получить графики функции y = log ₃(x – 1) , y = log _0,3(x)+3. Учитель обсуждает с учащимися сделанные выводы и дает задание построить самостоятельно графики функций y = log ₃(x-3), y = log ₃(x)+2, y = log ₃(x +4) – 2. Ученики комментируют построение и проверяют с помощью презентации.

А как построить графики следующих функций y = log ₃(ǀxǀ), y =ǀlog ₃(ǀxǀ)ǀ, y = ǀlog ₃(ǀxǀ)ǀ

Обсуждается способ построения каждой функции, общие и отличительные черты в построении. Строятся графики на доске. Учитель предлагает учащимся самостоятельно построить графики следующих функций по выбору y = log

3(ǀx-2ǀ),, y = ǀ-log ₃(ǀ-xǀ)ǀ-2. Комментируют построение и проверяют с помощью документ-камеры.

5. Применение нового материала

Выполнение у доски №29(а), 30(б), 31(б), 47(а), 48(б). Учащиеся обсуждают, делают выводы и выполняют самостоятельно на выбор задания

(x + 3) ²= log ₂(x-2), ^{(x + 3) 2˃ log ₂(x-2), (x + 3) 2≥log ₂(x-2)}

или 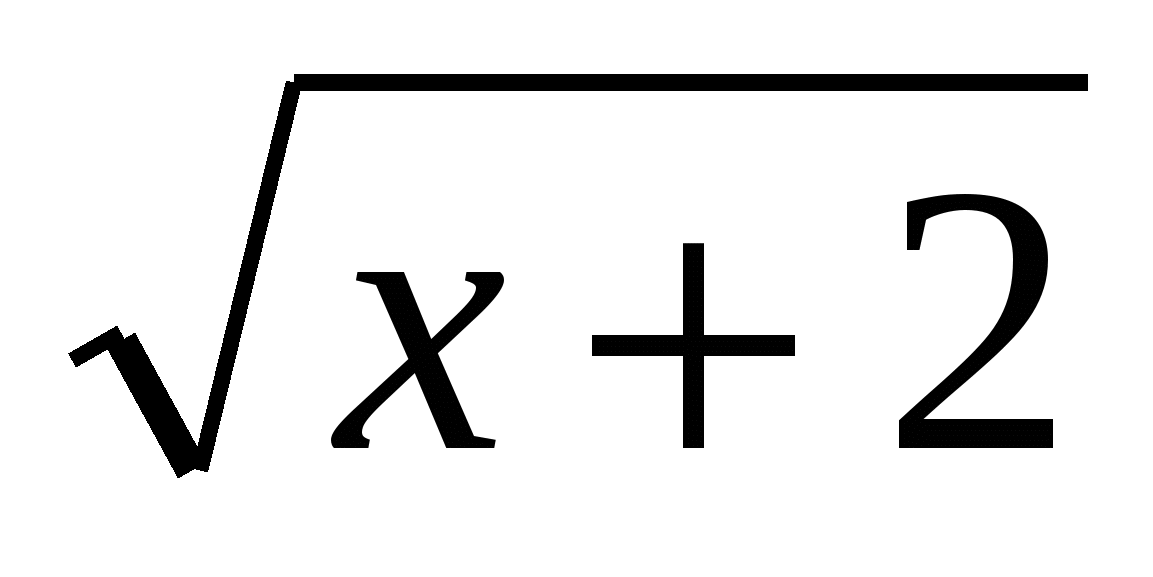-2= log ₂(x-2), 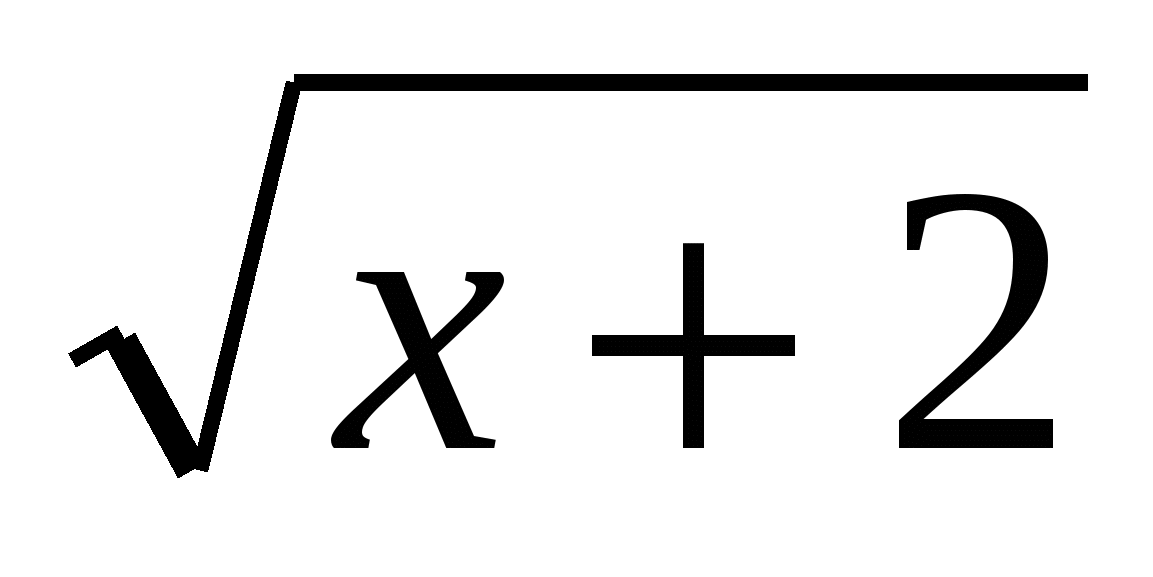-2 ˃ log ₂(x-2),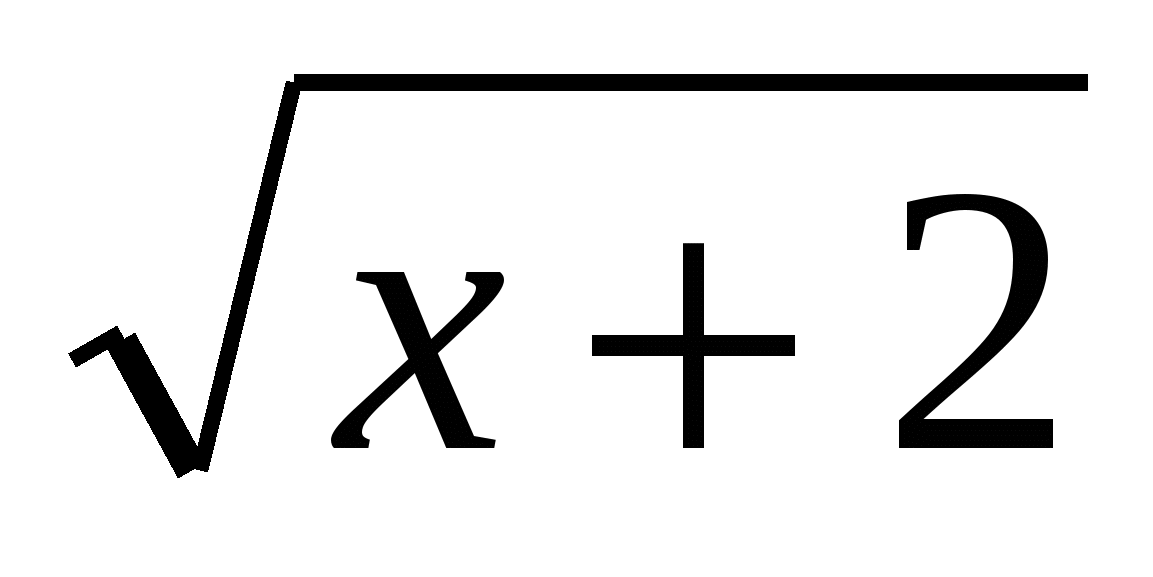

-2≥ log ₂(x-2). Комментируют решение и проверяют с помощью документ-камеры.

6. Подведение итогов. Объявление оценок.

Методическая разработка «Логарифмическая функция. Свойства и график»

Министерство образования и молодежной политики Чувашской Республики

Государственное автономное профессиональное

образовательное учреждение Чувашской Республики

«Чебоксарский техникум транспортных и строительных технологий»

(ГАПОУ «Чебоксарский техникум ТрансСтройТех»

Минобразования Чувашии)

Методическая разработка

ОДП. 01 Математика

«Логарифмическая функция. Свойства и график»

Разработал: преподаватель математики М.В. Дмитриева

 

Чебоксары – 2016

Оглавление

Пояснительная записка……………………………………………………………………………………………….….…3

Теоретическое обоснование и методическая реализация…………….……………………………..4-10

Заключение…………………………………………………………………………………………………………………….11

Список использованной и рекомендованной литературы………………………………………..………12

Приложения………………………………………………………………………………………………………….…………13

 

Пояснительная записка

Методическая разработка модуля занятия по дисциплине «Математика» на тему «Логарифмическая функция. Свойства и график» из раздела «Корни, степени и логарифмы» составлена на основе Рабочей программы по математике и календарно-тематического плана. Темы занятия взаимосвязаны содержанием, основными положениями.

Цель изучения данной темы узнать понятие логарифмической функции, изучить её основные свойства, научиться строить график логарифмической функции и научиться видеть логарифмическую спираль в окружающем нас мире.

Программный материал данного занятия базируется на знаниях математики. Методическая разработка модуля занятия составлена для проведения теоретических занятий по теме: «Логарифмическая функция. Свойства и график» –1 час. В процессе практического занятия студенты закрепляют полученные знания: определения функций, их свойства и графики, преобразования графиков, непрерывные и периодические функции, обратные функции и их графики, логарифмические функции.

Методическая разработка предназначена для оказания методической помощи студентам при изучении модуля занятий по теме «Логарифмическая функция. Свойства и график». В качестве внеаудиторной самостоятельной работы студенты могут подготовить с помощью дополнительных источников сообщение на тему, «Логарифмы и их применение в природе и технике», кроссворды и ребусы. Учебные знания и профессиональные компетенции, полученные при изучении темы «Логарифмические функции, их свойства и графики» будут применены при изучении следующих разделов: «Уравнения и неравенства» и «Начала математического анализа».

 

Дидактическая структура урока:

Тема: «Логарифмическая функция. Свойства и график»

Тип занятия: Комбинированный.

Цели занятия:

Образовательные – формирование знаний в усвоении понятия логарифмической функции, свойства логарифмической функции; применять графики при решении задач.

Развивающие – развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.

Воспитательные – воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения; воспитание сознательного отношения и заинтересованности к учебе.

Средства обучения:

— методическая разработка по теме;

— персональный компьютер;

— учебник Ш.А Алимов«Алгебра и начала анализа» 10-11 класс. Издательство «Просвещение».

Внутрипредметные связи: показательная функция и логарифмическая функция.

Межпредметные связи: алгебра и математический анализ.

Студент должен знать:

определение логарифмической функции;

свойства логарифмической функции;

график логарифмической функции.

Студент должен уметь:

выполнять преобразования выражений, содержащих логарифмы;

находить логарифм числа, применять свойства логарифмов при логарифмировании;

определять положение точки на графике по ее координатам и наоборот;

применять свойства логарифмической функции при построении графиков;

Выполнять преобразования графиков.

План занятия

1. Организационный момент (1 мин).

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся (1 мин).

3. Этап актуализации опорных знаний и умений (3 мин).

4. Проверка домашнего задания (2 мин).

5. Этап усвоения новых знаний (10 мин).

6. Этап закрепления новых знаний (15 мин).

7. Контроль усвоенного на уроке материала (10 мин).

8. Подведение итогов (2 мин).

9. Этап информирования учащихся о домашнем задании (1 мин).

 

Ход урока:

1. Организационный момент.

Включает в себя приветствие учителем класса, подготовку помещения к уроку, проверку отсутствующих.

2. Постановка целей и задач урока.

Сегодня мы с вами поговорим о понятии логарифмической функции, нарисуем график функции, изучим его свойства.

3. Этап актуализации опорных знаний и умений.

Проводится в форме фронтальной работы с классом.

Какую последнюю функцию мы изучали? Схематично изобразить на доске.

Дайте определение показательной функции.

Что является корнем показательного уравнения?

Дайте определение логарифма?

Назовите свойства логарифмов?

Назовите основное логарифмическое тождество?

4. Проверка домашнего задания.

Студенты открывают тетради и показывают решенные упражнения. Задают вопросы, которые возникли при выполнении домашнего задания.

5. Этап усвоения новых знаний.

Учитель: Открывайте тетради, записывайте сегодняшнее число и тему урока «Логарифмическая функция, ее свойства и график».

Учитель:

Определение: Логарифмической функцией называется функция вида

, где – заданное число, .

Рассмотрим построение графика данной функции на конкретном примере.

Построим графики функций и .

        Примечание 1: Логарифмическая функция  является обратной по отношению к показательной функции , где . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 1).

Рис. 1

Опираясь на определение логарифма и вид графиков, выявим свойства логарифмической функции:

1)    Область определения: , т.к. по определению логарифма х>0.

2)    Область значений функции: .

3)    Логарифм единицы равен нулю, логарифм основания равен единице: , .

4)    Функция ,  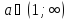возрастает в промежутке  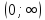(рис. 1).

5)    Функция ,   убывают в промежутке 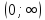  (рис. 1).

6) Промежутки знакопостоянства:

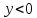Если , то при ; при ;

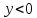Если , то при при ;

Примечание 2: График любой логарифмической функции всегда проходит через точку (1; 0).

Теорема: Если , где , то .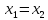

6. Этап закрепления новых знаний.

Учитель: Решаем задания № 318 –№322 (нечётные) (§18Алимов Ш.А. «Алгебра и начала анализа» 10-11 класс).

№ 318

1) т.к функция возрастает.

3) , т.к функция убывает.

 

№ 319

1) , т.к и .

3) , т.к и .

№ 320

1) , т.к , , то .

3) , т.к 10> 1, , то .

№ 321

1)убывает

3)возрастает.

№ 322

7. Подведение итогов.

—Сегодня мы с вами хорошо поработали на уроке! Что нового вы узнали сегодня на уроке?

(Новый вид функции — логарифмическая функция)

— Сформулируйте определение логарифмической функции.

(Функцию y = logax, (a > 0, a ≠ 1) называют логарифмической функцией)

-Молодцы! Верно! Назовите свойства логарифмической функции.

(область определения функции, множество значений функции, монотонность, знакопостоянства)

8. Контроль усвоенного на уроке материала.

Учитель: Выясним, насколько хорошо вы усвоили тему «Логарифмическая функция. Свойства и график». Для этого напишем проверочную работу (Приложение 1). Работа состоит из четырех заданий, которые необходимо решить, применяя свойства логарифмической функции. На выполнение проверочной работы вам дается 10 минут.

 

9. Этап информирования учащихся о домашнем задании.

Запись на доске и в дневниках: Алимов Ш.А. «Алгебра и начала анализа» 10-11 класс. §18 №318 — №322 (четные)

 

Заключение

В ходе использования методической разработки мы добились всех поставленных целей и задач. В данной методической разработке были рассмотрены все свойства логарифмической функции, благодаря которым студенты научились выполнять преобразования выражений, содержащих логарифмы и строить графики логарифмических функций. Выполнение практических задач способствует закреплению изученного материала, а контроль проверки знаний и умений поможет преподавателям и студентам выяснить насколько эффективной была их работа на уроке. Методическая разработка позволяет студентам получить интересную и познавательную информацию по теме, обобщить и систематизировать знания, применять свойства логарифмов и логарифмической функции при решении различных логарифмических уравнений и неравенств.

Список использованной и рекомендованной литературы

Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В., Фёдорова Н. Е., Шабунин М. И. под научным руководством академика Тихонова А. Н. Алгебра и начала математического анализа 10 — 11кл. – М. Просвещение, 2011.

Никольский С. М., Потапов М. К., Решетников Н. Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2006.

Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2005.

Лисичкин В. Т. Математика в задачах с решениями : учеб.пособие / В. Т. Лисичкин, И. Л. Соловейчик. — 3-е изд., стер. — СПб. [и др.] : Лань, 2011 (Архангельск). — 464 с.

Интернет-ресурсы:

http://school- collection.edu.ru – Электронный учебник «Математика в

школе, XXI век».

http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.

www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов.

 

 

 

 

 

Приложения

Вариант 1.

Вариант 2.

 

Критерии оценки:

Отметка «3» (удовлетворительно) ставится за любые 2 верно выполненных примера.

Отметка «4» (хорошо) ставится при верном выполнении любых 3 примеров.

Отметка «5» (отлично) ставится за все 4 верно выполненных примеров.

 

» Логарифмическая функция и ее приложения»

Тема урока: «Логарифмическая функция и ее приложения»

Цель урока:

расширять представления учащихся о логарифмической функции, применении ее свойств в нестандартных ситуациях;

развивать интерес к истории математики и ее практическим приложениям, логическое мышление, математическую грамотность речи;

воспитывать познавательную активность, чувство ответственности, культуру общения, культуру диалога.

Оборудование: компьютер, мультимедийная презентация.

« СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ УСВОИЛ НИЧЕГО НОВОГО И НИЧЕГО НЕ ПРИБАВИЛ К СВОЕМУ ОБРАЗОВАНИЮ.»

Я. А. КОМЕНСКИЙ

ХОД УРОКА

I. Организационный момент

Приветствие. Сообщение темы и цели урока. Подготовка учащихся к работе на уроке.

II. Актуализация опорных знаний.

1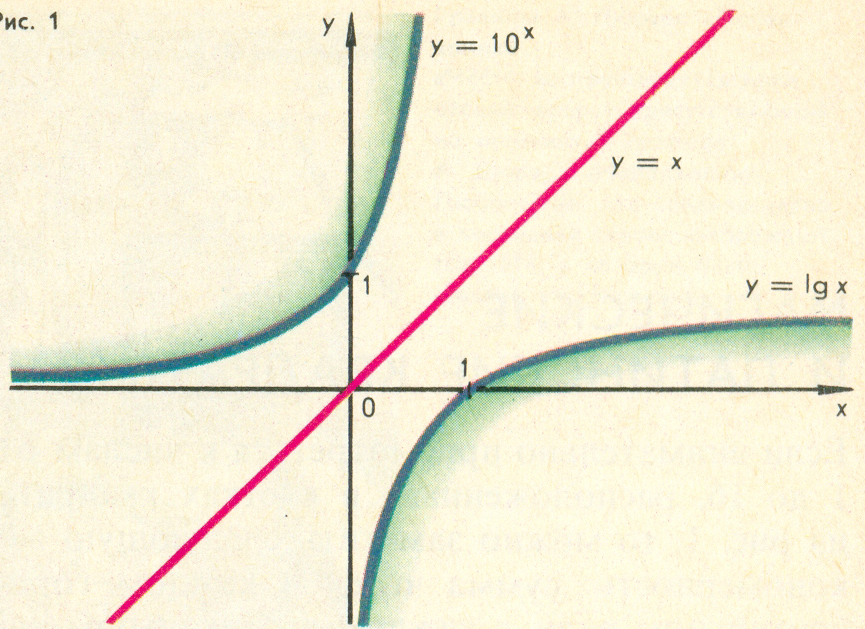 студент:

Друзья, поверьте: самая интересная, полезная и лирическая

Это – функция логарифмическая.

Спросите вы: «А чем интересна?»

А тем, что обратна она показательной

И относительно прямой y = x, как известно,

Симметричны их графики обязательно.

2 студент:

Проходит график через точку (1;0)

И в том еще у графика соль,

Что в правой полуплоскости он «стелется»,

А в левую попасть и не надеется.

3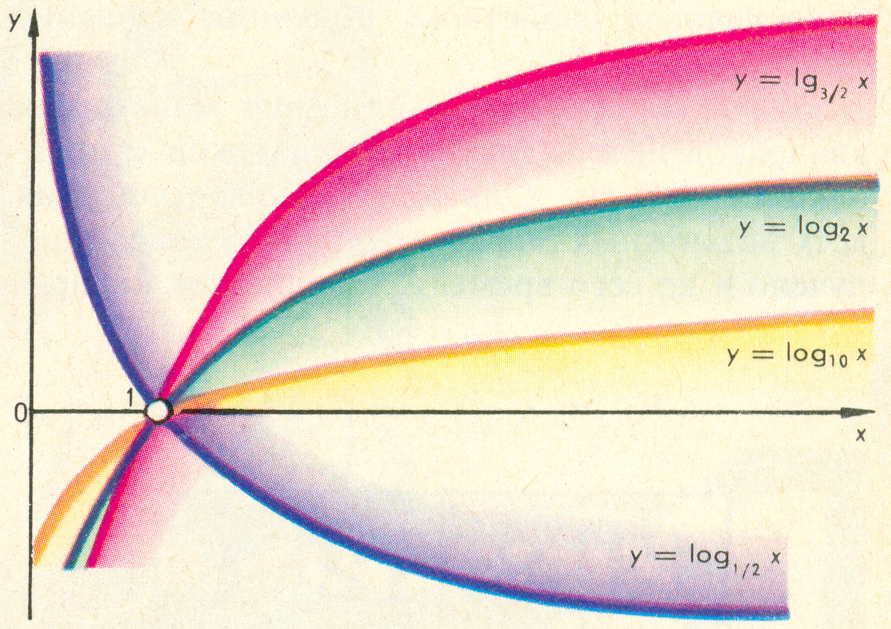 студент:

Но, если аргументы поменяем,

Тогда по правилам кривую мы сдвигаем,

Растягиваем, если надо, иль сжимаем

И относительно осей отображаем.

Сама же функция порою убывает,

Порою по команде возрастает.

А командиром служит ей значенье α,

И подчиняется она ему всегда.

2. Устные упражнения.

Вопрос №1

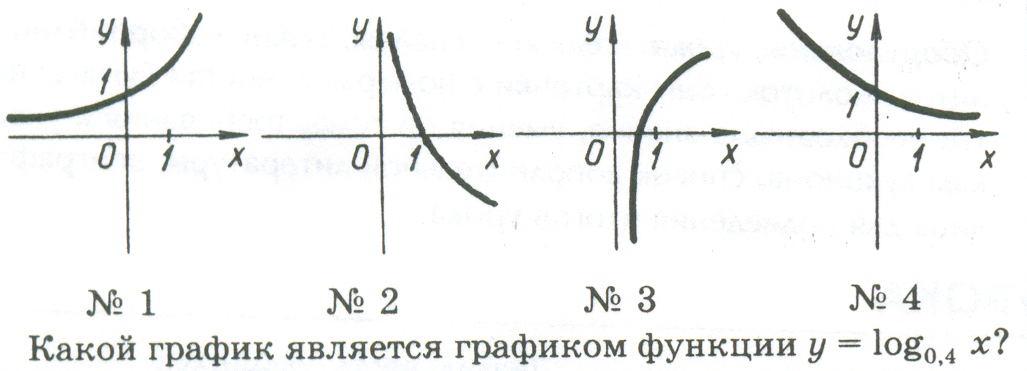
Вопрос №2

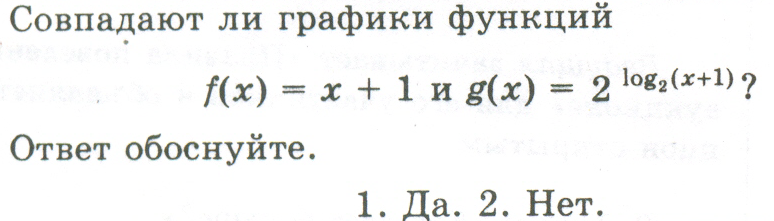
Вопрос №3

Вопрос №4

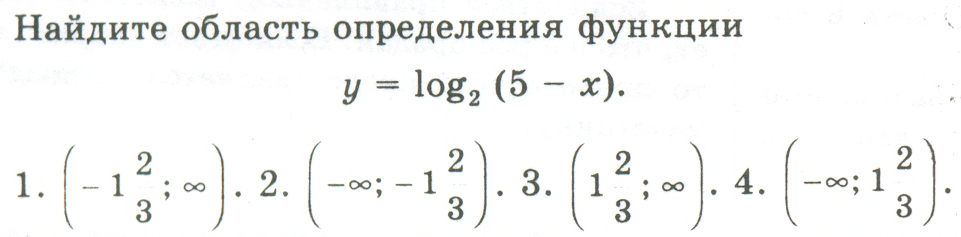
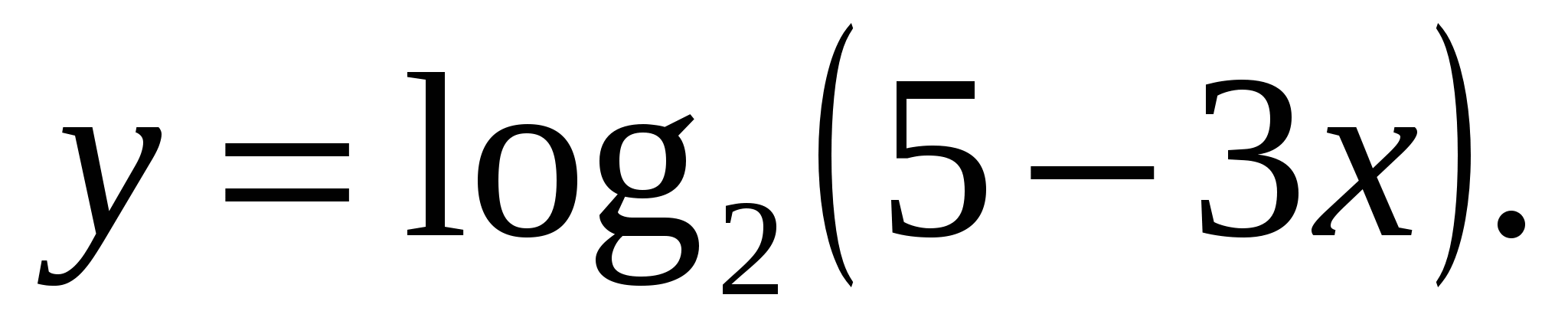
Учитель: Итак, мы повторили свойства логарифмической функции.

Расширим наши представления о логарифмической функции и применим ее свойства в нестандартных ситуациях.

III. Сообщения студентов по теме урока и решение нестандартных заданий:

1.Немного из истории.

Поистине безграничны приложения показательной и логарифмической фун­кций в самых различных областях на­уки и техники, а ведь придумывали логарифмы для облегчения вычислений. Более трех столетий прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, со­ставленные Джоном Непером. Они помогли астрономам и инженерам, сокра­щая время на вычисления, и тем самым, как сказал знаменитый французский ученый Лаплас, «удлиняли жизнь вычислителям»,

Еще недавно трудно было представить инженера без логарифмической линейки в кармане; изобретенная через десяток лет после появления логарифмов Непера английским математиком Гунтером, она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь ее из инженерного обихода вытеснили микрокалькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы.

Задание классу

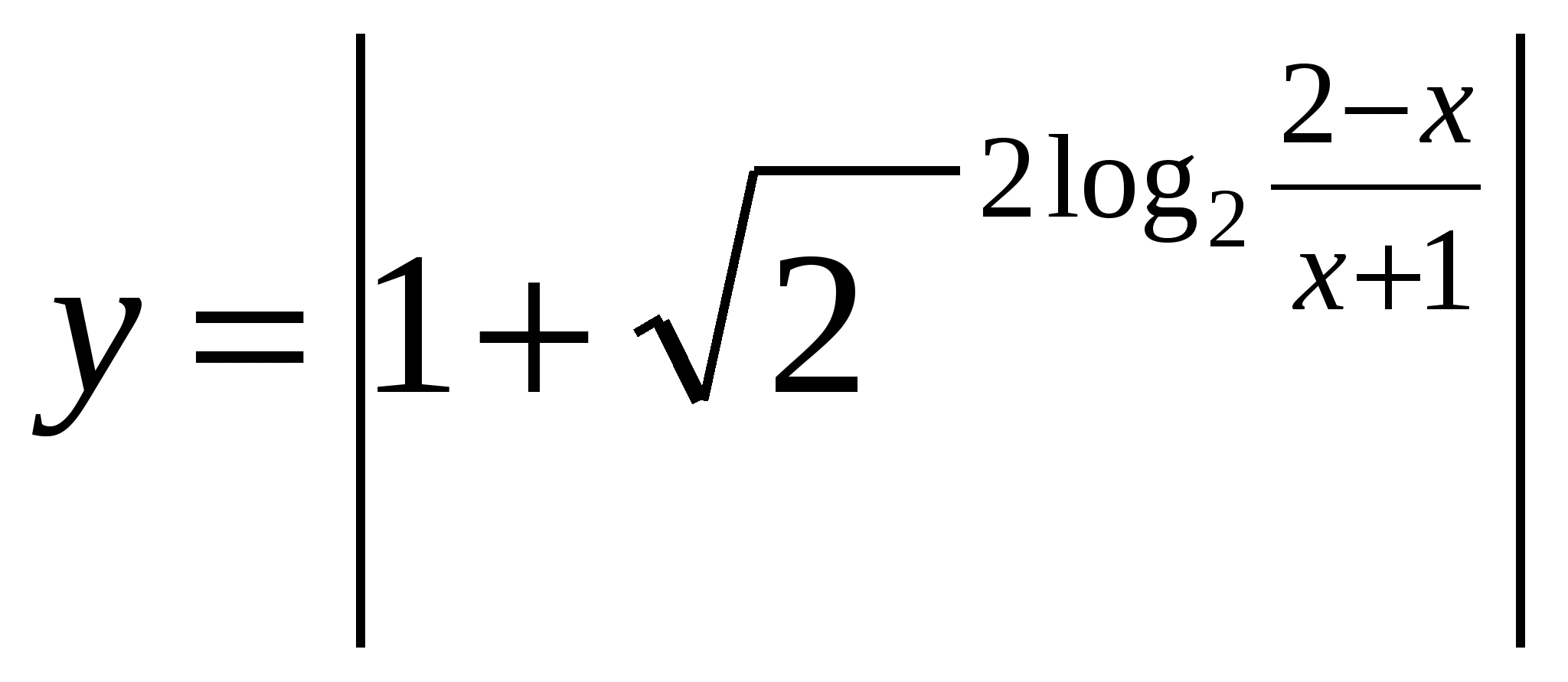
Построить график функции:

2. Звезды, шум и логарифмы.

Этот заголовок связывает столь, казалось бы, несоеди­нимые вещи. Шум и звезды объединяются здесь потому, что громкость шума и яркость звезд оцениваются одина­ковым образом — по логарифмической шкале.

Астрономы делят звезды по степени яркости на ви­димые и абсолютные звезд­ные величины — звезды пер­вой величины, второй, тре­тьей и т. д. Последователь­ность видимых звездных ве­личин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая их яр­кость изменяется по иному закону: яркости звезд составляют геометрическую прогрес­сию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой логарифм ее физической ярко­сти. Короче говоря, оценивая яркость звезд, астроном оперирует таблицей логарифмов, составленной при основа­нии 2,5.

Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приемы точной числовой оценки громкости шума. Единицей гром­кости звука служит «бел», но практически используются единицы громкости, равные его десятой доле, — так назы­ваемые «децибелы». Последовательные степени громко­сти 1 бел, 2 бела и т.д. составляют арифметическую прогрессию… Физические же величины, характеризующие шумы (энергия, интенсивность звука и др.), составляют геометрическую прогрессию со знаменателем 10. Гром­кость, выраженная в белах, равна десятичному логариф­му соответствующей физической величины.

3. Логарифмическая комедия.

Логарифмическая «комедия 2 > 3»

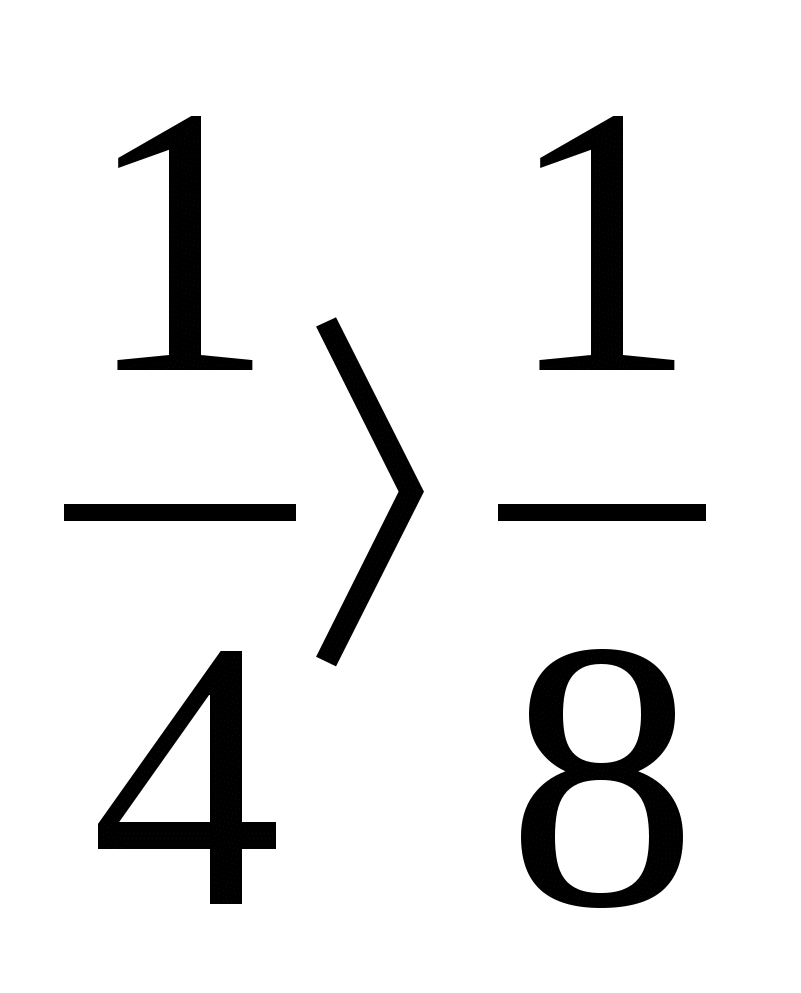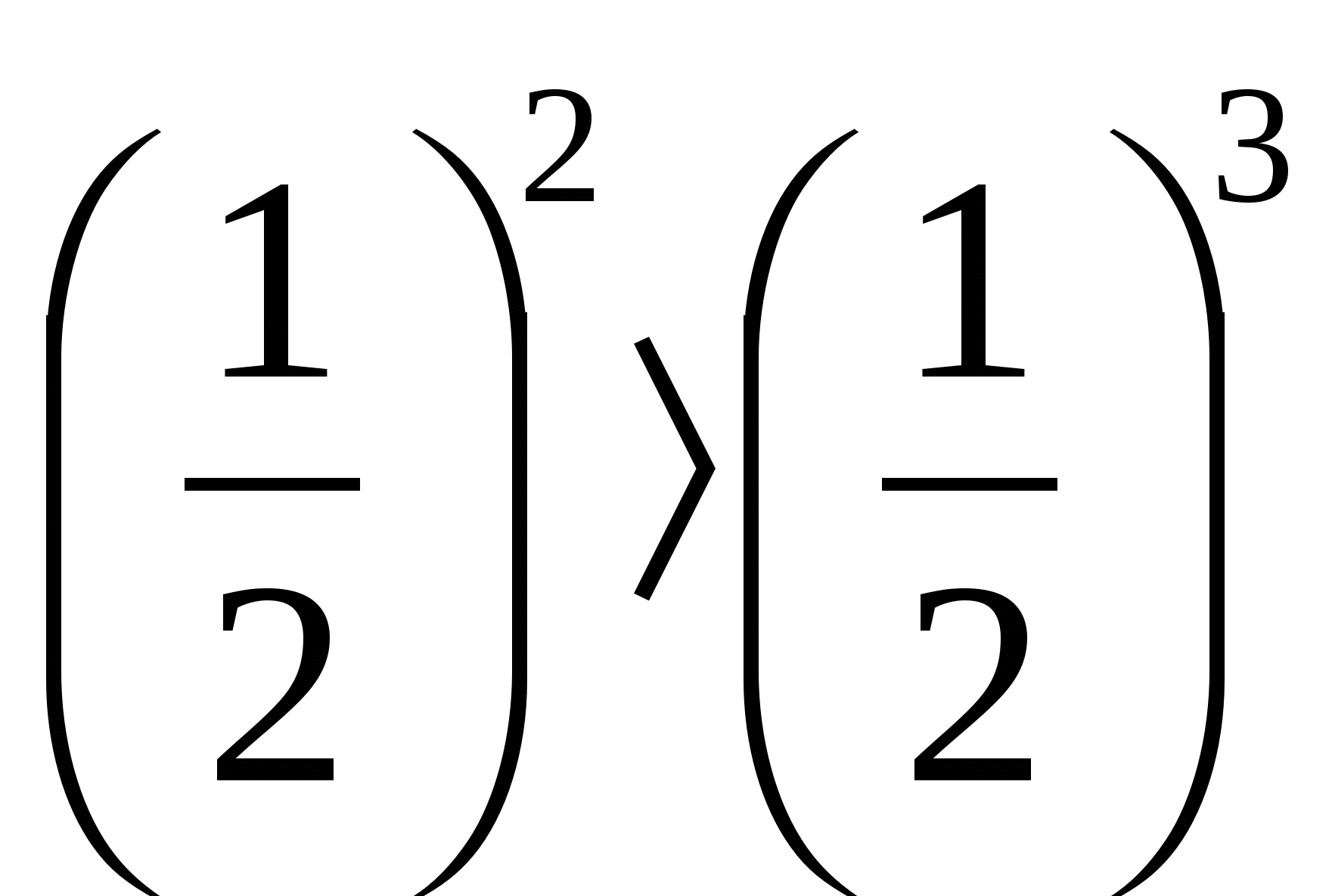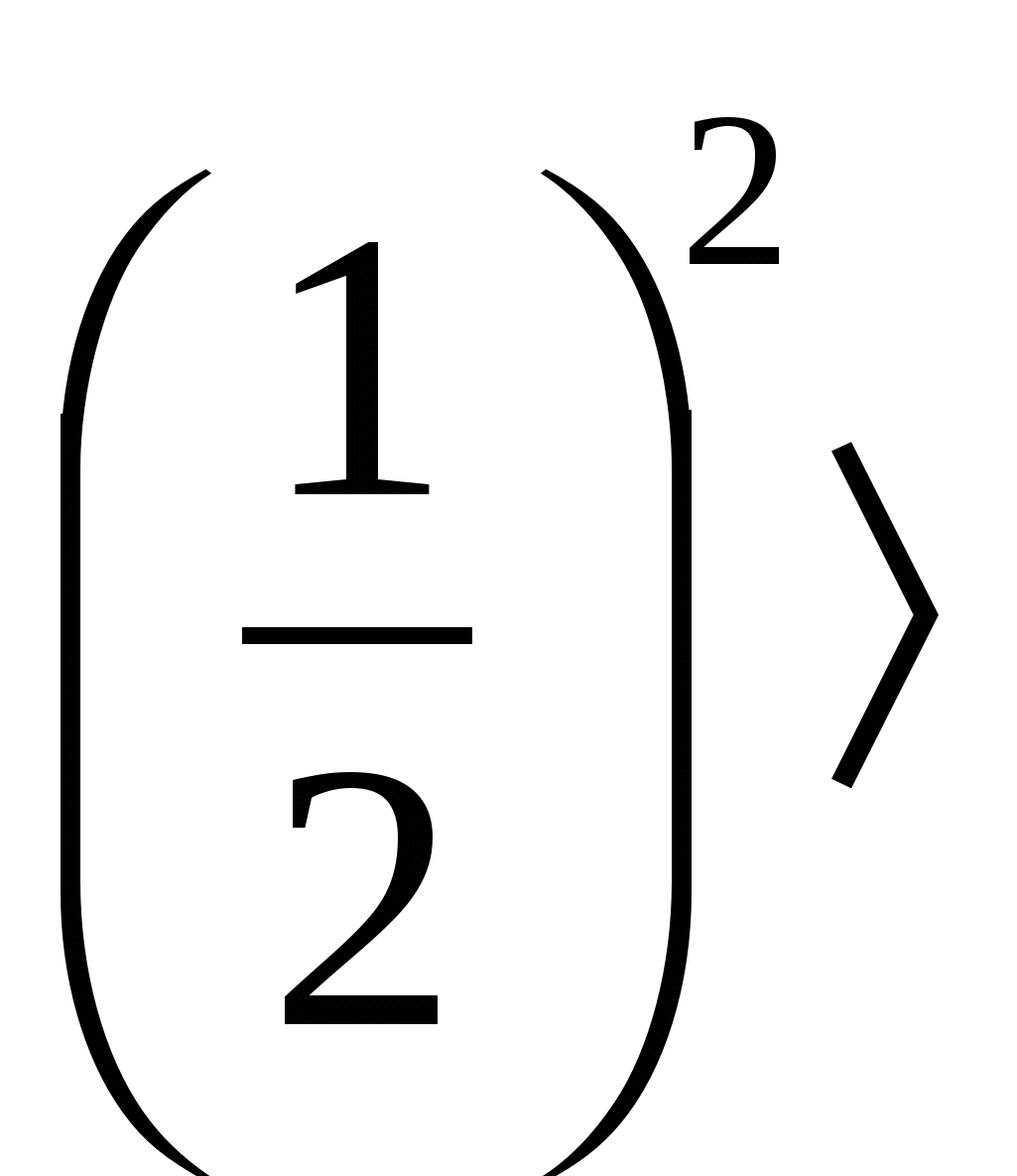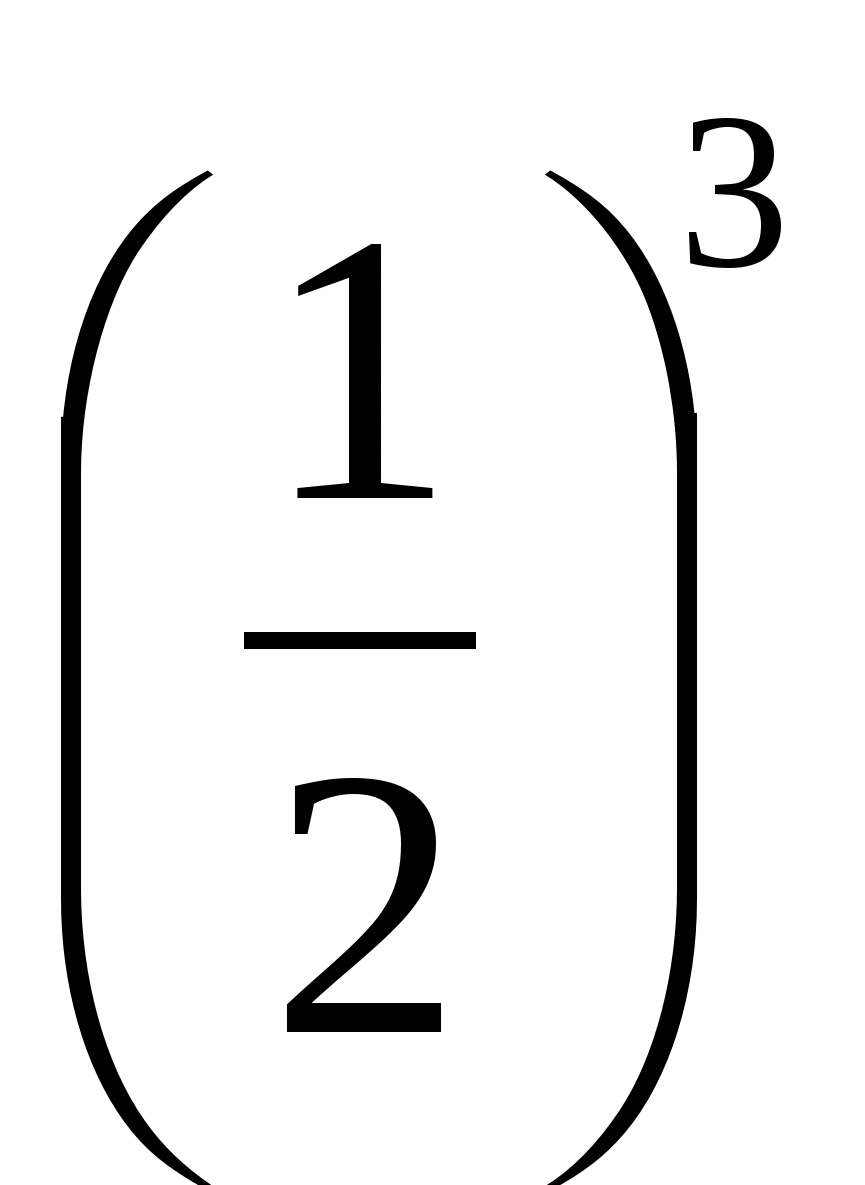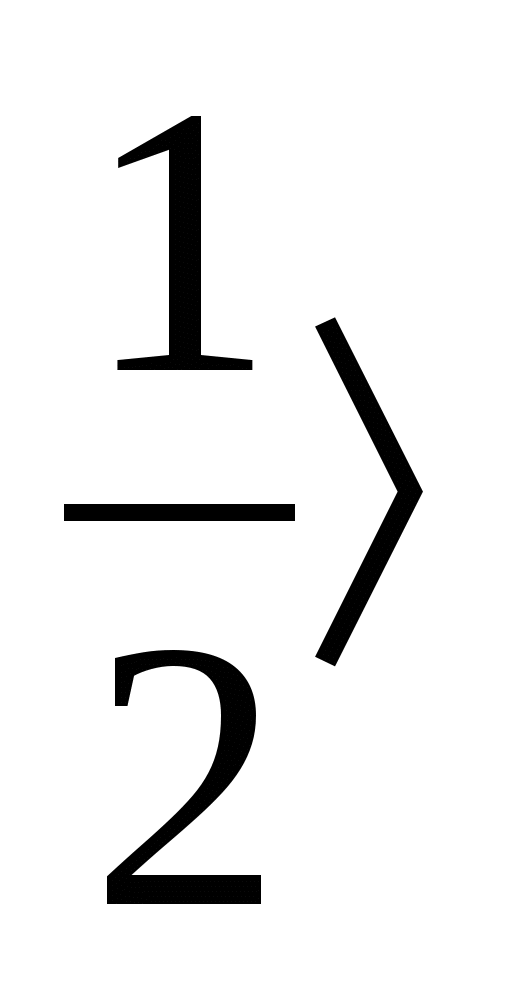Комедия начинается с неравенства , бесспорно правильного. Затем следует преобразование , тоже не внушающее сомнения. Большему числу соответствует больший логарифм, значит, lg lg , 2lg 3lg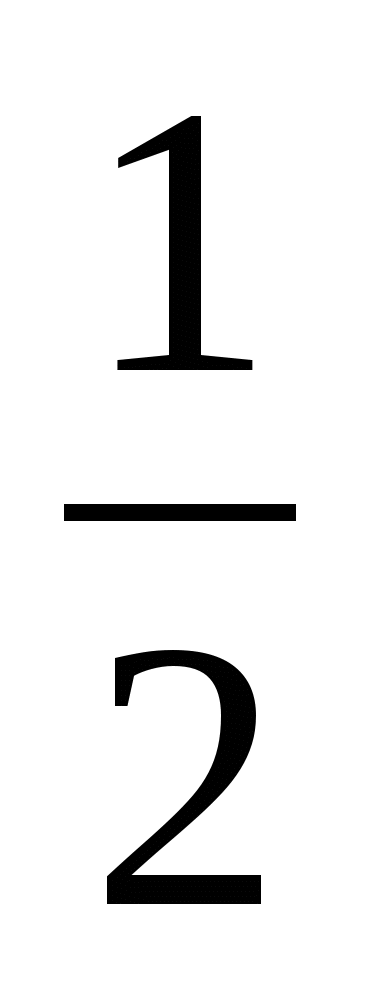

После сокращения на lg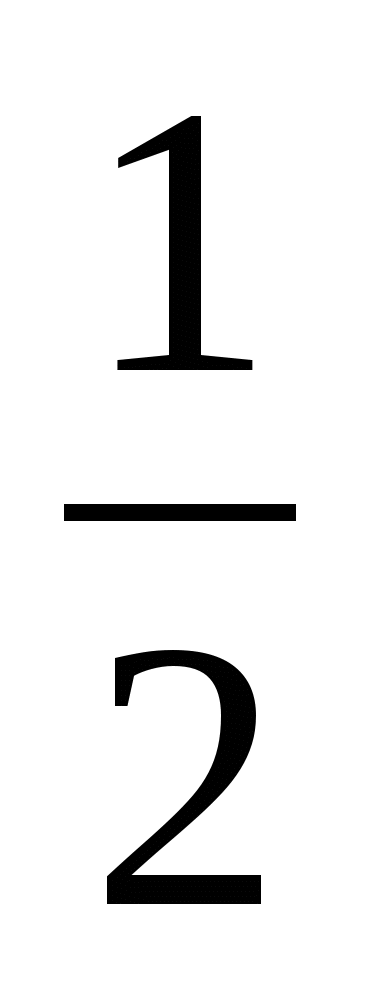 имеем 2 > 3

В чем ошибка этого доказательства?

4. Любое число — тремя двойками.

Творческое задание.

Учитель: Продолжим урок остроумной алгебраической голово­ломкой, которой развлекались участники одного съезда физиков в Одессе. Предлагается задача: любое данное чис­ло, целое и положительное, изобразить с помощью трех двоек и математических символов, например, пусть дан­ное число 3.

З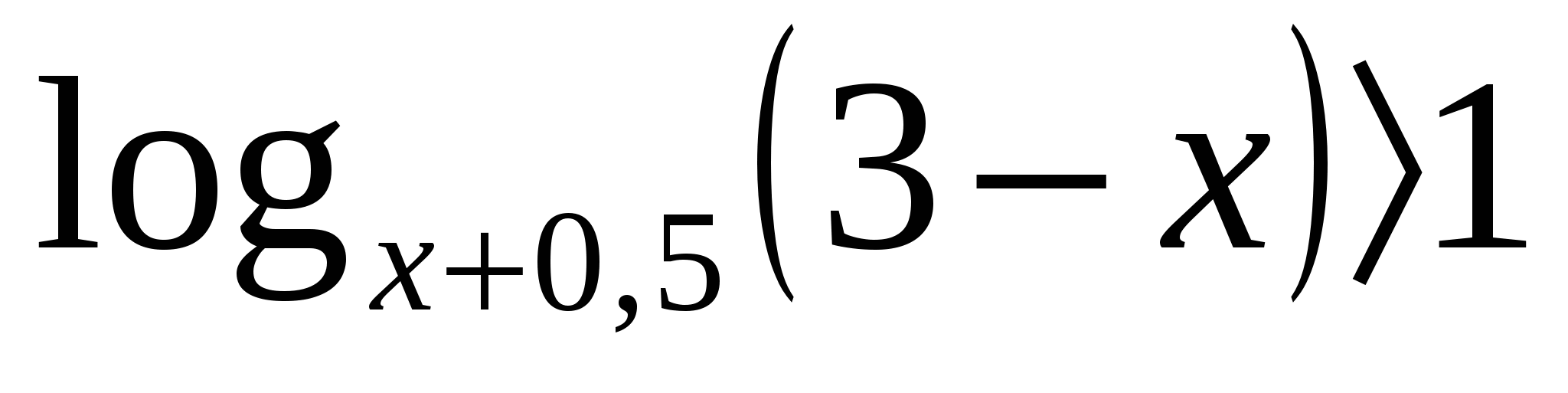адание

Решить неравенство:

5. Задание . Постройте графики функций: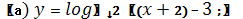

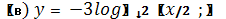
6. Подведение итогов и результатов работы на уроке.

Учитель предлагает учащимся блиц — опрос, чтобы проверить себя, на сколько каждый понял изученный материал . Необходимо ответить только «да» или «нет». Проверяется сразу.

Вопросы:

1. Ось у является вертикальной асимптотой графика логарифмической функции.

2. Графики показательной и логарифмической функций симметричны относительно прямой у = х.

3. Область определения логарифмической функции – вся числовая прямая, а область значений этой функции – промежуток

4. Монотонность логарифмической функции зависит от основания логарифма.

5. Не каждый график логарифмической функции проходит через точку с координатами (1; 0).

6. Логарифмическая кривая это та же экспонента, только по-другому расположенная в координатной плоскости.

7. Выпуклость логарифмической функции не зависит от основания логарифма.

8. Логарифмическая функция не является ни чётной, ни нечётной.

9. Логарифмическая функция имеет наибольшее значение и не имеет наименьшего значения при а > 1 и наоборот при 0 < a < 1.

Проверка: да, да, нет, да, нет, да, нет, да, нет.

IV. Итог урока.

Рефлексия

• Что нового вы узнали о логарифмической функции и ее приложениях?

• Какая информация вас заинтересовала?

• С какими трудностями вы столкнулись при решении нестандартных заданий?

• Понравился ли вам сегодняшний урок?

V. Домашнее задание (из вариантов ЕГЭ)

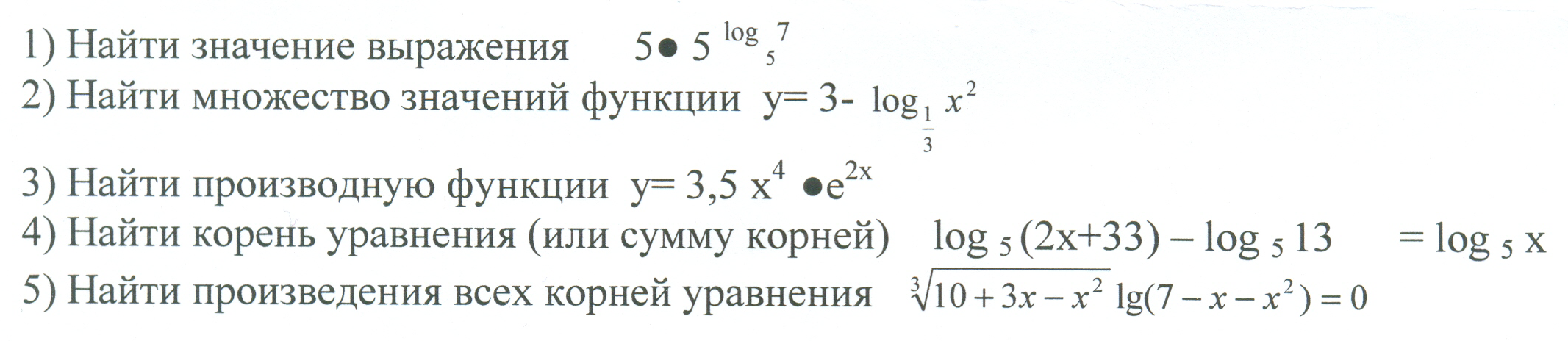
Логарифмической функцией называется функция

Свойства логарифмической функции

1. Область определения:

2. Множество значений:

3. Четность и нечетность: функция не обладает свойством четности.

4. Периодичность функции: непериодическая.

5. Нули: функция обращается в нуль при X = 1.

6. Промежутки знакопостоянства: Если то функция положительна для отрицательна для если то функция положительна для отрицательна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: если функция убывает для если возрастает для

9. Асимптоты: прямая X = 0 (ось Oy) – вертикальная асимп­тота.

10. График функции для изображен на рис. 6.9, а для на рис. 6.10.

 

Рис. 6.9 Рис. 6.10

Из свойств функции следует: тогда и только тогда, когда

или

Функция если является обратной для функции при

Функция если является обратной для функции при

Пример 1. Определить знак числа:

1) 2) 3) 4)

Решение. 1) Поскольку основание логарифма больше 1 (А = 7) и значение, стоящее под знаком логарифма, больше 1 (B = 35), то из свойств логарифмической функции

2) Для основания логарифма имеем и для выражения, стоящего под знаком логарифма, выполняется Поэтому

3) Так как основание логарифма 5 и 5 > 1, а выражение, стоящее под знаком логарифма, равно и то

4) Для основания логарифма выполняется а под знаком логарифма число 19 (19 > 1). Поэтому

Пример 2. Сравнить числа:

1) и 2) и

3) и 3.

Решение. 1) Используем тот факт, что логарифмические функции с основанием 11 и 13 монотонно возрастают. Поэтому

Тогда

2) Рассмотрим числа и Так как

и

то

следовательно,

3) Известно, что или

Если A ³ 0, B ³ 0.

В нашем случае тогда

Т. е.

Пример 3. Установить, между какими последовательными целыми числами находится число

Решение. Поскольку логарифмическая функция с основанием 7 монотонно возрастает, то

Пример 4. Найти функцию, обратную функции Построить графики обеих функций в одной системе координат.

Решение. Найдем функцию, обратную данной:

Построим графики функций:

А) строим график функции график функции переносим параллельно на две единицы вправо по оси Ox и на две единицы вниз по оси Oy;

Б) график обратной функции симметричен графику данной функции относительно прямой (рис. 6.11).

Рис. 6.11

< Предыдущая		Следующая >

Логарифмическая функция, формула и примеры

Определение и формулы логарифмической функции

ОПРЕДЕЛЕНИЕ Логарифмической функцией называется функция .

Замечание. Показательная и логарифмическая функции являются взаимно обратными. Их графики симметричны относительно прямой — биссектрисы первой и третьей координатных четвертей.

Свойства логарифмической функции

1) Область определения: .

2) Множество значений: .

3) Четность/нечетность: функция общего вида.

4) Период: функция непериодическая.

5) Точки пересечения графика функции с координатными осями:

• с осью абсцисс: точка ;
• с осью ординат точек пересечения нет.

6) Промежутки знакопостоянства:

• : для и для ;
• для и для .

7) Монотонность:

• : функция убывает для любого ;
• : функция возрастает для любого .

8) Точек минимума/максимума нет.

9) График

Примеры решения задач

ПРИМЕР 1

Задание	Среди приведенных функций а)-в) указать убывающие: а) ; б) ; в)
Решение	Согласно свойствам логарифмической функции, такая функция является убывающей, если ее основание удовлетворяет условию , и возрастает для : а) для данной функции основание , то есть первая функция является строго возрастающей; б) , то есть функция убывает; в) , следовательно, и эта функция является убывающей.
Ответ	б), в).

логарифмическая функция и ее свойства и графики

1 y = log a х, 0 а у у 1 0 0 1 «

х

х

y = log a x ,

а 1

y = log a х,

0 а

у

у

1

0

0

1

Содержание

• Сведения из истории
• Понятие логарифма
• Свойства логарифмов
• Примеры
• Понятие функции у = log a x
• Свойства логарифмической функции
• График логарифмической функции
• Свойства сравнения логарифмов
• Логарифмические уравнения
• Логарифмические неравенства

Сведения из истории

Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц

геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, а извлечение корня степени n сводится к делению логарифма подкоренного выражения на n . Первым эту идею опубликовал в своей книге « Arithmetica integra » Михаэль Штифель , который, впрочем, не приложил серьёзных усилий для реализации своей идеи.

.

Сведения из истории

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием « Описание удивительной таблицы логарифмов ». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером , утвердился в науке. Теорию логарифмов Непер изложил в другой своей книге «Построение удивительной таблицы логарифмов», изданной посмертно в 1619 году его сыном.

Слово логарифм происходит от греческого λόγοφ (число) и αρινμοφ (отношение) и переводится, следовательно, как отношение чисел.

«Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать».

Сведения из истории

Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство – таблицы логарифмов, – резко повысившее производительность труда вычислителей. Добавим, что уже в 1623 г., т. е. всего через 9 лет после издания первых таблиц, английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений.

Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж. Непером (1550 — 1617) и швейцарцем И. Бюрги (1552 — 1632).

Логарифмическая линейка

Часы Breitling Navitimer

Круговая логарифмическая линейка (логарифмический круг)

0 , b 0 log a b a = b — основное логарифмическое тождество «

Понятие логарифма

Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а , чтобы получить число b

.

log a b = c , a c = b ; а ≠ 1 , a 0 , b 0

log a b

a = b

— основное логарифмическое тождество

Примеры

• log 2 8 =
• log 3 729 =
• log 0,2 25 =
• log 4 8 =
• log 2 2 =
• log 10 1 =
• log 49 1/7 =
• log 0,1 10000 =

3 , 2 3 = 8 ;

6 , 3 6 = 729 ;

-2 , (0, 2 ) -2 = 25 ;

1,5 , 4 1,5 = 8 ;

1 , 2 1 = 2 ;

0 , 10 0 = 1 ;

-0,5 , 49 -0,5 = 1/7 ;

-4 , 0,1 -4 = 10000 .

Основные свойства логарифмов

• log a b m =
• log a k b m =
• log a b =
• log a b =
• log a b ∙ log c d =

=

• log a 1 =
• log a a =
• log a =
• log a k a =
• log a a m =
• log a k a m =
• log a bc =
• log a =
• log a k b =

m log a b ;

0 ;

m

log a b ;

1 ;

k

log с b

1

-1 ;

;

a

log с а

1

;

1

k

;

log b а

m ;

m

;

k

log c b ∙ log a d

log a b + log a c ;

b log c a

b

log a b − log a с ;

c

1

log a b ;

k

0 , х 0 называют логарифмической функцией . «

Понятие логарифмической функции

Функцию вида

y = log a х , где а ≠ 1 , a 0 , х 0

называют

логарифмической функцией

.

0 D(y) = ( 0; +∞), E(y) = (-∞; +∞) . а) Нули функции: у = 0 при х = 1 ; б) точек пересечения с осью ординат нет . а) При а 1 функция возрастает на ( 0; +∞) ; б) при 0 функция убывает на ( 0; +∞). Ни четная функция, ни нечетная. Не ограничена сверху, не ограничена снизу. Не имеет ни наибольшего, ни наименьшего значений. Непрерывна. а) При а 1 функция выпукла вверх; б) при 0 функция выпукла вниз. Ось у является вертикальной асимптотой графика логарифмической функции. «

Свойства логарифмической функции y = log а х, а ≠ 1, a 0

E(y) = (-∞; +∞) .

• а) Нули функции: у = 0 при х = 1 ;

б) точек пересечения с осью ординат нет .

• а) При а 1 функция возрастает на ( 0; +∞) ;

б) при 0 функция убывает на ( 0; +∞).

• Ни четная функция, ни нечетная.

• Не ограничена сверху, не ограничена снизу.

• Не имеет ни наибольшего, ни наименьшего значений.

• а) При а 1 функция выпукла вверх;

б) при 0 функция выпукла вниз.

• Ось у является вертикальной асимптотой графика логарифмической функции.

0 y = log а х, 0 а y = log a х, а 1 у у х х 0 0 1 1 «

График логарифмической функции y = log а х, а ≠ 1, a 0

y = log а х, 0 а

y = log a х, а 1

у

у

х

х

0

0

1

1

0 «

Графики логарифмической функции y = log а х, а ≠ 1, a 0

0 Если 0 и 0 1 2 , то log a x 1 log a x 2 . Если а 1 и 0 1 2 , то log a x 1 a x 2 . Если 1 а и x 1 , то log a x log b x . Если 0 а и x 1 , то log a x log b x . Если 1 а и 0 , то log a x b x . Если 0 а и 0 , то log a x b x . log a b 0 ⟺ a 0, b 0 и (a – 1)(b – 1 ) 0 ( если положительные числа a и b лежат “ по одну сторону от единицы ”) log a b 0 ⟺ a 0, b 0 и (a – 1)(b – 1 ) ( если положительные числа a и b лежат “ по разные стороны от единицы ”) «

Свойства сравнения логарифмов при а ≠ 1, a 0

• Если 0 и 0 1 2 , то log a x 1 log a x 2 .

• Если а 1 и 0 1 2 , то log a x 1 a x 2 .

• Если 1 а и x 1 , то log a x log b x .

• Если 0 а и x 1 , то log a x log b x .

• Если 1 а и 0 , то log a x b x .

• Если 0 а и 0 , то log a x b x .

• log a b 0 ⟺ a 0, b 0 и (a – 1)(b – 1 ) 0 ( если положительные числа a и b лежат “ по одну сторону от единицы ”)

• log a b 0 ⟺ a 0, b 0 и (a – 1)(b – 1 ) ( если положительные числа a и b лежат “ по разные стороны от единицы ”)

0 называют логарифмическими уравнениями log a f(x) = log a h( х ) f(x) = h( х ) f(x) 0 h( х ) 0 Методы решения логарифмических уравнений: Функционально-графический метод. Метод потенцирования. Метод введения новой переменной. «

⟺

Логарифмические уравнения

Уравнения вида log a f(x) = log а h( х ) , где а ≠ 1 , a 0

называют логарифмическими уравнениями

log a f(x) = log a h( х )

f(x) = h( х )

f(x) 0

h( х ) 0

Методы решения логарифмических уравнений:

• Функционально-графический метод.
• Метод потенцирования.
• Метод введения новой переменной.

Логарифмические уравнения. Примеры

Пример 1

Пример 2

Ответ: -3.

Логарифмические уравнения. Примеры

Пример 3



x = 2



Ответ: 2 .

Логарифмические уравнения. Примеры

Пример 4

Ответ: 100.

Логарифмические уравнения. Примеры

Пример 5

Логарифмические уравнения. Примеры

Пример 5

Логарифмические уравнения. Примеры

Пример 6

Т.к. обе части равенства принимают только положительные значения, прологарифмируем их по основанию 5:

Ответ: 0,2; 25.

Логарифмические уравнения. Примеры

Пример 7

Логарифмические уравнения. Примеры

Пример 8

log а g( х ) , где а ≠ 1 , a 0 называют логарифмическими неравенствами log a f(x) log а g( х ) 0 а 1 или «

Логарифмические неравенства

Неравенства вида log a f(x) log а g( х ) , где а ≠ 1 , a 0

называют логарифмическими неравенствами

log a f(x) log а g( х )

0

а 1

или

Логарифмические неравенства. Примеры

Пример 1

Пример 2

+

+

−

х

х

4

0

2

1 4

6

Ответ: [ 0 ; 4] .

Ответ: (6; 14) .

Логарифмические неравенства. Примеры

Пример 3

Пример 4

+

+

−

t

1

1

4

−

+

+

х

5

4 5

0

4 0

Ответ: (0; 5) ∪ (40; 45) .

Логарифмические неравенства. Примеры

Пример 5

х

х

2

1,5

4

3

1,5

3,375

4

3

3,375

x ∈ (3,375; 4)

x ∈ (2; 3)

Ответ: (2; 3) ∪ (3,375; 4) .

Используемые материалы

• Алгебра и начала анализа. 11 класс. В 2 ч. Ч. 1. Учебник для общеобразоват. учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. 2-е изд., стер. – М.: Мнемозина, 2008

• http://ru.wikipedia.org/wiki — логарифмические линейки
• http://ru.wikipedia.org/wiki — логарифм

Комплексный логарифм

(мнимая часть)

Логарифмическая функция: основные свойства и графики

 

Функцию вида y = log_a(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: log_a(b) — данная запись будет обозначать логарифм b по основанию а.

Основные свойства логарифмической функции:

1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.

2. Областью значения логарифмической функции будет являться все множество вещественных чисел.

3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a

4. График логарифмической функции всегда проходит через точку (1;0).

5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.

6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:

На следующем рисунке представлен график убывающей логарифмической функции — (0<a<1):

7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.

8. Функция не имеет точек максимума и минимума.

Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.

Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций. Рассмотрим пример: найти область определения логарифмической функции f(x) = log₈(4 — 5*x).

Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 — 5*x>0. Решаем это неравенство и получаем x<0.8.

Таким образом, получается, что областью определения функции f(x) = log₈(4 — 5*x) будет являться промежуток (-∞;0.8)

Нужна помощь в учебе?

Предыдущая тема: Логарифмы и их свойства: определение и алгоритм решения
Следующая тема:&nbsp&nbsp&nbspПонятие об обратной функции: график функции и теорема

Все неприличные комментарии будут удаляться.