Функция y=k/х, ее свойства и график (продолжение 1). Видеоурок. Алгебра 8 Класс
Тема: Квадратичная функция. Функция 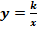
Урок: Функция 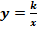 , её свойства и график (продолжение 1)
, её свойства и график (продолжение 1)
На этом уроке мы продолжим изучение функции 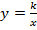 , её графика и свойств, а также научимся решать типовые задачи.
, её графика и свойств, а также научимся решать типовые задачи.
Напомним, как выглядит график данной функции.
В случае, если  , то ветви гиперболы расположены в
, то ветви гиперболы расположены в 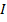
 координатных четвертях, а если
координатных четвертях, а если  , то –
, то –  ,
,  . (Рис. 1,2 соответственно).
. (Рис. 1,2 соответственно).
Рис. 1.

Рис. 2.
Перечислим теперь основные свойства функции 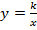
1) Область определения: 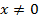 .
.
2) Монотонность на промежутках 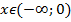 и
и  .
.
3) Асимптоты: координатные оси 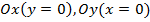 .
.
4) Центр симметрии  .
.
Вспомним также о влиянии коэффициента 
 – чтобы получить из первого графика второй, необходимо растянуть его в 2 раза от оси
– чтобы получить из первого графика второй, необходимо растянуть его в 2 раза от оси  .
.
Рис. 3.
Повторив все основные свойства гиперболы, перейдём к решению типовых задач.
Задача 1
Гипербола 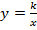 проходит через точку
проходит через точку 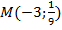
а) коэффициент  , изобразить схематически график функции;
, изобразить схематически график функции;
б) найти пределы изменения функции на луче  ;
;
в) установить: проходит ли гипербола через точки  ,
,  .
.
Решение:
а) при 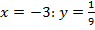 , так как график функции проходит через точку
, так как график функции проходит через точку 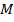
 . Получаем, что график имеет вид:
. Получаем, что график имеет вид:  . Его схематический вид следующий:
. Его схематический вид следующий: 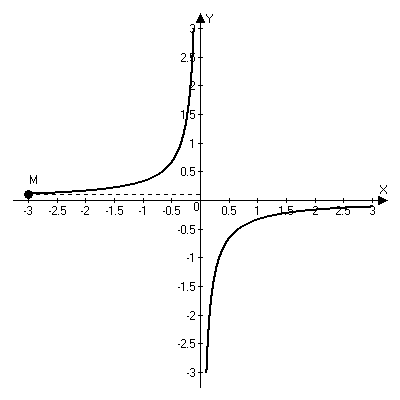
Рис. 4.
б) Рассмотрим поведение гиперболы при  . Воспользуемся монотонностью функции на этом промежутке. Данная гипербола на этом промежутке монотонно возрастает. Значит, её максимальное значение будет достигаться на правом конце промежутка:
. Воспользуемся монотонностью функции на этом промежутке. Данная гипербола на этом промежутке монотонно возрастает. Значит, её максимальное значение будет достигаться на правом конце промежутка: 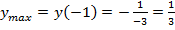
 , но не будет его достигать.
, но не будет его достигать.Значит, при  :
:  .
.

Рис. 5.
в)  проходит через точку
проходит через точку 
 . Поясним это: чтобы точка лежала на графике, её координаты должны удовлетворять уравнению этого графика.
. Поясним это: чтобы точка лежала на графике, её координаты должны удовлетворять уравнению этого графика.  – верно, значит, точка
– верно, значит, точка 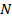 лежит на графике. С другой стороны,
лежит на графике. С другой стороны,  – неправильное равенство, значит, точка
– неправильное равенство, значит, точка 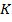 не лежит на графике.
не лежит на графике.
Рис. 6.
Задача 2
Определите с помощью графиков число решений системы уравнений:
 .
.
Решение:
 – гипербола (
– гипербола (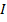 и
и  координатные четверти).
координатные четверти).
 – прямая (
– прямая (
 :
: 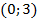 ).
).Построим эти графики в одной системе координат:

Рис. 7.
Как видно из рисунка, графики этих функций пересекаются в двух точках. Значит, данная система имеет два решения.
Ответ: 2 решения.
Задача 3
Построить график функции: 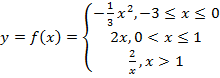 .
.
Найти: а) 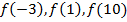
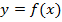 ; в) перечислите свойства этой функции.
; в) перечислите свойства этой функции.Решение:
Начнём с построения графика этой функции. Данная функция называется кусочной.
Первая часть графика – это кусок параболы 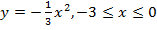 (рис.8.).
(рис.8.).
Вспомнив, свойства параболы с отрицательным коэффициентом, получаем, что на указанном промежутке функция возрастает, причём её значения меняются от  до
до 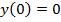 .
.
Вторая часть графика – это часть прямой (отрезок) 
 положителен), причём её значения меняются от
положителен), причём её значения меняются от 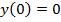 до
до  . (рис. 9.).
. (рис. 9.).Третья часть графика – это часть гиперболы 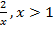 . (рис. 10.).
. (рис. 10.).
Зная свойства гиперболы, получаем, что на этом промежутке функция убывает, причём максимальное значение достигается на левом конце:  (хотя эта точка не принадлежит этой части графика).
(хотя эта точка не принадлежит этой части графика).

Рис. 8.
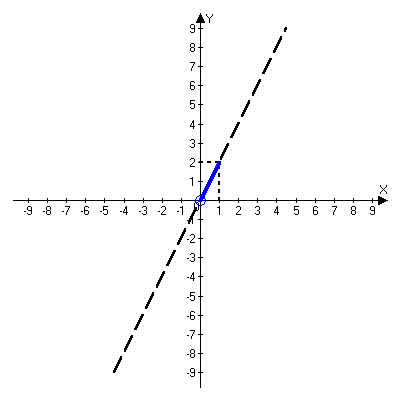
Рис. 9.
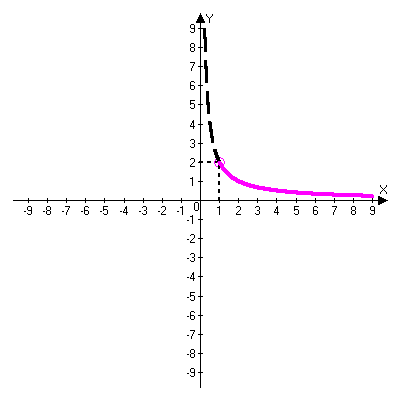
Рис. 10.
Следующий шаг – это объединение всех трёх графиков на одном рисунке. В результате получается следующий график:

Рис. 11.
Вернёмся теперь к пункту а). Теперь мы легко можем посчитать значения:  ,
, 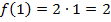 ,
,  .
.
Теперь осталось сформулировать ответ на пункт в): функция определена на промежутке 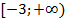 . Кроме того, она принимает все значения на промежутке
. Кроме того, она принимает все значения на промежутке  . Также функция является непрерывной. При этом на промежутке:
. Также функция является непрерывной. При этом на промежутке: 
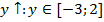 . На промежутке
. На промежутке 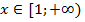
 .
.
Мы рассмотрели типовые задачи. Теперь рассмотрим задачи, которые могут сопутствовать этим задачам.
Задача 4
Найти все значения параметра 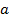 , при каждом из которых уравнение
, при каждом из которых уравнение  имеет хотя бы 1 решение (корень), где
имеет хотя бы 1 решение (корень), где  – функция из предыдущей задачи.
– функция из предыдущей задачи.
Решение:
Методика решения подобных задач:
1) Вначале необходимо изобразить график функции.
Мы воспользуемся графиком из предыдущей задачи:

Рис. 12.
2) Найти множество значений функции:  . Для этого используем определение и свойство функции: функция – это зависимость
. Для этого используем определение и свойство функции: функция – это зависимость  от
от  , при которой каждому допустимому значению
, при которой каждому допустимому значению  соответствует ровно одно значение
соответствует ровно одно значение  . А свойство функции: каждое значение
. А свойство функции: каждое значение  достигается хотя бы при одном значении
достигается хотя бы при одном значении  .
.
3) Выписать ответ:  . Это следует из того, что уравнение
. Это следует из того, что уравнение 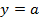 может иметь решения только в случае, если
может иметь решения только в случае, если 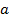 принадлежит множеству значений функции. Действительно, если провести прямую
принадлежит множеству значений функции. Действительно, если провести прямую  , то она не пересечёт график функции, то есть корней не будет. А если провести прямую
, то она не пересечёт график функции, то есть корней не будет. А если провести прямую  , то будут точки пересечения, значит, будут и решения соответствующего уравнения.
, то будут точки пересечения, значит, будут и решения соответствующего уравнения.

Рис. 13.
Ответ: .
.
Задача 5
Для каждого значения параметра 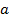 найти число решений уравнения
найти число решений уравнения  (функция
(функция  из предыдущей задачи).
из предыдущей задачи).
Решение:
Фактически нам необходимо перебрать все значения 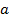 и указать ответ.
и указать ответ.
Методика решения подобных задач:
1) Вначале необходимо изобразить график функции (см. рис. 12).
2) Рассечь его семейством прямых 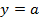 при разных значениях параметра
при разных значениях параметра 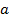 .
.

Рис. 14.
3) Определить количество точек пересечения прямых с графиком функции при различных значениях параметра 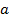 .
.
Мы видим, что при  – решений нет; при
– решений нет; при  – 1 решение; при
– 1 решение; при  – 2 решения; при
– 2 решения; при  – 1 решение; при
– 1 решение; при  – решений нет.
– решений нет.
4) Выписать ответ.
Ответ: при  – решений нет; при
– решений нет; при 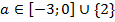 – 1 решение; при
– 1 решение; при  – 2 решения.
– 2 решения.
Итак, мы повторили свойства функции 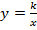 при различных значениях
при различных значениях  , а также разобрали ряд типовых задач, которые связаны со свойствами и графиками данной функции.
, а также разобрали ряд типовых задач, которые связаны со свойствами и графиками данной функции.
На следующем уроке мы перейдём к изучению новой темы: «Квадратный корень».
Список рекомендованной литературы
1. Башмаков М.И. Алгебра 8 класс. М.: Просвещение. 2004 г.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Фестиваль педагогических идей «Открытый урок» (Источник).
2. Алгебра и начала анализа – 10 кл (Источник).
3. Вся элементарная математика (Источник).
Рекомендованное домашнее задание
1. № 826, 827 Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
2. Исследуйте количество корней уравнения  , в зависимости от значений параметра
, в зависимости от значений параметра 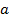 .
.
3. Решите графически уравнения: а)  , б)
, б)  .
.
interneturok.ru
ее график и свойства при k0
Рассмотрим функцию y=k/y. Графиком этой функции является линия, называемая в математике гиперболой. Общий вид гиперболы, представлен на рисунке ниже. (На графике представлена функция y равно k разделить на x, у которой k равно единице.)
Видно, что график состоит из двух частей. Эти части называют ветвями гиперболы. Стоит отметить также, что каждая ветвь гиперболы подходит в одном из направлений все ближе и ближе к осям координат. Оси координат в таком случае называют асимптотами.
Вообще любые прямые линии, к которым бесконечно приближается график функции, но не достигает их, называются асимптотами. У гиперболы, как и у параболы, есть оси симметрии. Для гиперболы, представленной на рисунке выше, это прямая y=x.
Теперь разберемся с двумя общими случаями гипербол. Графиком функции y = k/x, при k ≠0, будет являться гипербола, ветви которой расположены либо в первом и третьем координатных углах, при k>0, либо во втором и четвертом координатных углах, при k<0.
Основные свойства функции y = k/x, при k>0
График функции y = k/x, при k>0
1. Точка (0;0) центр симметрии гиперболы.
2. Оси координат – асимптоты гиперболы.
3. Прямая y=x ось симметрии гиперболы.
4. Область определения функции все х, кроме х=0.
5. y>0 при x>0; y6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
7. Функция не ограничена ни снизу, ни сверху.
8. У функции нет ни наибольшего, ни наименьшего значений.
9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Основные свойства функции y = k/x, при k<0
График функции y = k/x, при k<0
1. Точка (0;0) центр симметрии гиперболы.
2. Оси координат – асимптоты гиперболы.
3. Прямая y=-x ось симметрии гиперболы.
4. Область определения функции все х, кроме х=0.
5. y>0 при x0.
6. Функция возрастает как на промежутке (-∞;0), так и на промежутке (0;+∞).
7. Функция не ограничена ни снизу, ни сверху.
8. У функции нет ни наибольшего, ни наименьшего значений.
9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Нужна помощь в учебе?
Предыдущая тема: Преобразование рациональных выражений: способы преобразований и примеры
Следующая тема:   Рациональные числа: определение, сумма, разность, умножение, деление
Все неприличные комментарии будут удаляться.
www.nado5.ru
График функции y=f(x)/k | Алгебра
График функции y=f(x)/k (где k>1) может быть получен из графика функции y=f(x) с помощью сжатия к оси Ox в k раз.
При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; y/k) графика функции y=f(x)/k:
(x; y) → (x; y/k)
(то есть абсцисса (x) каждой точки начального графика остаётся неизменной, а ордината (y) уменьшается в k раз).Точки, лежащие на оси Ox при сжатии к оси абсцисс остаются на месте (так как 0/k=0).
Примеры.
1) График функции y=x²/3 можно получить из графика функции y=x² сжатием к оси Ox в 3 раза.
Строим параболу y=x² (достаточно отметить базовые точки). Координату x каждой точки оставляем без изменения, координату y делим на 3.
(1; 1) → (1; 1/3),
(-1; 1) → (-1; 1/3),
(2; 4) → (2; 4/3),
(-2; 4) → (-2; 4/3),
(3; 9) → (3; 3),
(-3; 9) → (-3; 3).
Таким образом, каждая точка нового графика соответственно располагается под точкой первоначального графика, но в 3 раза ближе к оси абсцисс.
Вершина параболы при сжатии к оси Ox остаётся на месте (0:3=0).
2) График функции y=x³/4 может быть получен из графика функции y=x³ сжатием к оси абсцисс в 4 раза.
Для построения графика абсциссы базовых точек графика кубической функции оставляем неизменными, а каждую ординату делим на 4:
(1; 1) → (1; 1/4),
(-1; -1) → (-1; -1/4),
(2; 8) → (2; 8/3),
(-2; 8) → (-2; -8/3).
Точка (0; 0) при таком преобразовании остаётся на месте.
3) График функции y=(1/2)√x можно получить сжатием к оси Ox графика функции y=√x.
Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y делим на 2:
(0; 0) → (0; 0),
(1;1) → (1; 1/2),
(4; 2) → (4; 1),
(9; 3) → (9; 9/2) и т. д.
Геометрические преобразования дают возможность на основании графиков элементарных функций строить многие другие графики. Умение строить графики функций востребовано при решений заданий из различных разделов алгебры.
www.algebraclass.ru
| 1. | Коэффициент обратной пропорциональности | 1 вид — рецептивный | лёгкое | 1 Б. | Записать коэффициент обратной пропорциональности. |
| 2. | Расположение графика функции | 1 вид — рецептивный | лёгкое | 1 Б. | Определить, в каких четвертях расположен график функции. |
| 3. | Построение графика функции | 1 вид — рецептивный | лёгкое | 1 Б. | Необходимо построить график функции и ответить на вопрос. |
| 4. | Обратно пропорциональные величины | 1 вид — рецептивный | лёгкое | 1 Б. | Определение обратно пропорциональных велиин. |
| 5. | Гипербола | 1 вид — рецептивный | лёгкое | 1 Б. | Определение вида функции, графиком которой является гипербола. |
| 6. | Значение обратной пропорциональности | 1 вид — рецептивный | лёгкое | 1 Б. | Вычисление значения обратной пропорциональности, если известен аргумент. |
| 7. | Принадлежность точки графику обратной пропорциональности | 1 вид — рецептивный | лёгкое | 2 Б. | Определение координаты точки, принадлежащей графику обратной пропорциональности. |
| 8. | Определение формулы обратной пропорциональности | 1 вид — рецептивный | лёгкое | 2 Б. | Определение формулы обратной пропорциональности, если известны координаты точки, через которую проходит график данной функции. |
| 9. | Задача на обратную пропорциональность | 1 вид — рецептивный | среднее | 2 Б. | Решение задачи на обратную пропорциональность, выбор графика, описывающего данную в задаче ситуацию. |
| 10. | Задача на обратную пропорциональность (количество и стоимость товара) | 1 вид — рецептивный | среднее | 2 Б. | Решение задачи на обратную пропорциональность (стоимость и количество товара). |
| 11. | Построение графика обратной пропорциональности | 1 вид — рецептивный | среднее | 4 Б. | Построение графика обратной пропорциональности. |
| 12. | Аргумент обратной пропорциональности | 1 вид — рецептивный | среднее | 3 Б. | Вычисление аргумента обратной пропорциональности (y = k/x + b), если дано значение функции. |
| 13. | Экономическая задача | 2 вид — интерпретация | среднее | 4 Б. | Решение экономической задачи. |
| 14. | Принадлежность точки графику | 2 вид — интерпретация | среднее | 2 Б. | Без построения графика определить, принадлежит ли точка графику функции. |
| 15. | Обратная пропорциональность | 2 вид — интерпретация | среднее | 2 Б. | Задать формулой обратную пропорциональность. |
| 16. | Вычисление значения | 2 вид — интерпретация | среднее | 2 Б. | Вычислить значение функции. |
| 17. | Нахождение значения | 3 вид — анализ | сложное | 3 Б. | Найти значение функции. |
| 18. | Значение функции | 3 вид — анализ | сложное | 3 Б. | Вычислить значение функции. |
| 19. | Значение аргумента | 3 вид — анализ | сложное | 3 Б. | Необходимо найти значение аргумента. |
www.yaklass.ru
| 1. |
Ветви параболы
Сложность: лёгкое |
1 |
| 2. |
Свойства функции (коэффициент больше нуля)
Сложность: лёгкое |
1 |
| 3. |
Свойства функции (коэффициент меньше нуля)
Сложность: лёгкое |
1 |
| 4. |
Значение квадратичной функции
Сложность: лёгкое |
1 |
| 5. |
Коэффициент k в уравнении параболы
Сложность: среднее |
1 |
| 6. |
Вычисление значения функции
Сложность: среднее |
2 |
| 7. |
Принадлежность точки графику функции
Сложность: среднее |
2 |
| 8. |
Вычисление значения
Сложность: сложное |
3 |
| 9. |
Вычисления
Сложность: сложное |
3 |
| 10. |
Решение уравнения
Сложность: сложное |
3 |
www.yaklass.ru
| 1. |
Вспомогательная система координат
Сложность: лёгкое |
1 |
| 2. |
Параллельный перенос графика функции
Сложность: лёгкое |
2 |
| 3. |
Направление сдвига графика функции
Сложность: лёгкое |
2 |
| 4. |
Формула функции
Сложность: среднее |
2 |
| 5. |
Уравнение параболы
Сложность: среднее |
2 |
| 6. |
Значение функции
Сложность: среднее |
2 |
| 7. |
Построение графика квадратичной функции вида y = (x + a)² + b
Сложность: среднее |
3 |
| 8. |
Метод выделения полного квадрата
Сложность: сложное |
3 |
| 9. |
Функции
Сложность: сложное |
3 |
| 10. |
Графическое решение системы уравнений
Сложность: сложное |
3 |
www.yaklass.ru