Методы построения графиков функций содержащих модуль
Цель урока:
- повторить построение графиков функций содержащих знак модуля;
- познакомиться с новым методом построения графика линейно-кусочной функции;
- закрепить новый метод при решении задач.
Оборудование:
- мультимедиа проектор,
- плакаты.
Ход урока
Актуализация знаний
На экране слайд 1 из презентации.
Что является графиком функции y=|x| ? (слайд 2).
(совокупность биссектрис 1 и 2 координатных углов)
Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).
Рисунок 1
y=| x+3|
y=| x| +3
y=-2| x| -2
y=6-| x-5|
y=1/3| x-6| -3
Расскажите алгоритм построения графиков функций вида y=|f(x)| на примере функции y=|x2-2x-3| (слайд 4)
Ученик: чтобы построить график данной функции нужно
— построить параболу y=x2-2x-3
— часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)
Рисунок 2
Рисунок 3
Расскажите алгоритм построения графиков функций вида y=f(|x|) на примере функции y=x2-2|x|-3 (слайд 6).
Ученик: Чтобы построить график данной функции нужно:
— построить параболу.
— часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)
Рисунок 4
Расскажите алгоритм построения графиков
функций вида y=|f(|x|)| на примере функции y=|x 2-2|x|-3|
(слайд 8).
Ученик: Чтобы построить график данной функции нужно:
— нужно построить параболу у=x2-2x-3
— строим у= x2-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ
— часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)
Рисунок 5
Следующее задание выполняем письменно в тетрадях.
1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|
Ученик на доске с комментарием:
— находим нули подмодульных выражений х1=-2, х2=1, х3=3
— разбиваем ось на промежутки
— для каждого промежутка запишем функцию
при х < -2, у=-х-4
при -2 х<1, у=х
при 1 х<3, у = 3х-2 при х 3, у = х+4
— строим график линейно-кусочной функции.
Мы с вами построили график функции используя определение модуля (слайд 10).
Рисунок 6
Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.
Метод вершин
Алгоритм:
- Найдем нули каждого подмодульного выражения
- Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
- Нанесем точки на координатную плоскость и соединим последовательно
2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|
Учитель на доске, дети в тетрадях.
Метод вершин:
— найдем нули каждого подмодульного выражения;
— составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
х -3 -2 1 3 4
у -1 -2 1 7 8
— нанесем точки на координатную плоскость и
соединим последовательно.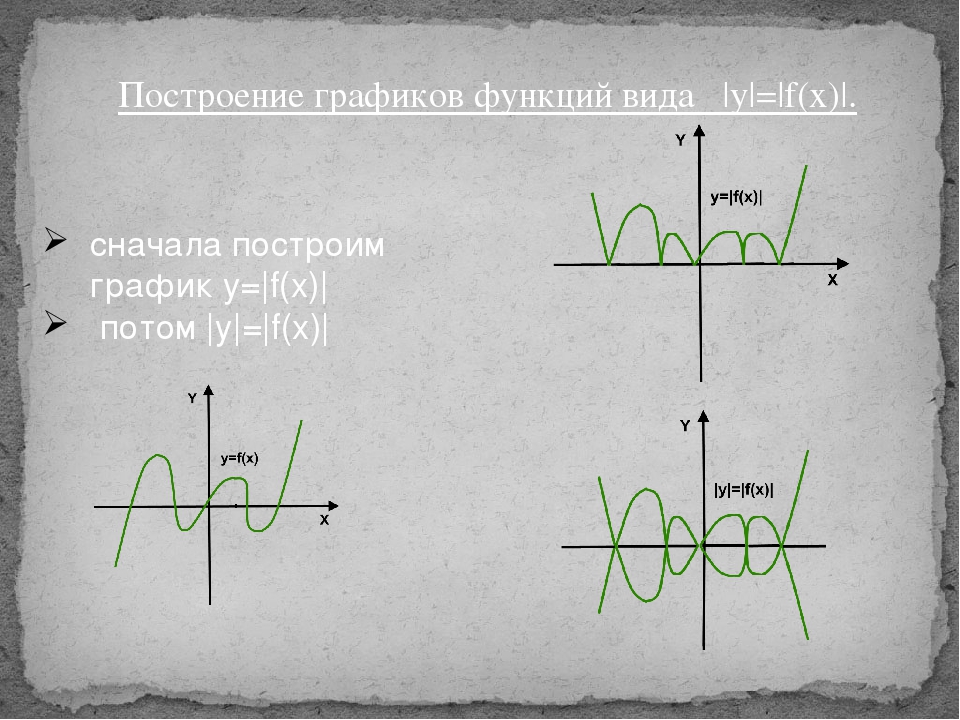
Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .
Рисунок 7
Каким же методом график получается быстрее и легче?
3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:
При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.
Следуем алгоритму; ученик на доске.
у=|х-2|-|х+1|
х1=2, х2=-1
у(-2)=4-1=3
у(-1)=3
у(2)=-3
у(3)=1-4=3, соединяем последовательно точки.
унаиб
4. Дополнительное задание
При каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.
5. Домашняя работа
а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.
б) Построить график функции y=||x-1|-2|-3| .
§ 10. Построение графиков функций, содержащих модуль
По определению . Исходя из этого, получаем, что график функции состоит из двух лучей: при неотрицательных X и при отрицательных X. Построение этого графика можно проводить также, используя преобразование симметрии относительно оси ОХ.
Так как модуль любого выражения неотрицателен, то все точки графика расположены выше оси абсцисс, или на оси абсцисс. Из этого следует, что для получения графика функции все точки графика функции , лежащие выше или на оси ОХ, нужно оставить на месте, а все точки, лежащие ниже оси ОХ, отобразить симметрично относительно этой оси.
Пример 12.
Постройте график функции.Решение. Построение графика будем выполнять последовательно. Сначала строим график функции . Затем сдвигаем его на 3 единицы вправо и на 4 единицы вниз. Заметим, что при этом вершина графика окажется в точке с координатами и (рис. 35).
Пример 13. Постройте график функции .
Постройте график функции .
Решение. Построение графика будем выполнять последовательно. Сначала строим график функции как параболу с вершиной в точке , и ветвями, направленными вверх. Затем точки графика, расположенные ниже оси ОХ, – это точки, у которых координата X принадлежит интервалу , – отображаем симметрично относительно этой оси (рис. 36).
Пример 14. Постройте график функции .
Решение. Функция – четная. Ее график симметричен относительно оси OY, причем при неотрицательных X он совпадает с параболой , имеющей вершину , и ветви, направленные вверх. Сначала построим часть данной параболы при неотрицательных
Упражнения
12. Постройте графики функций:
А) ; б) ;
В) ; г) ;
Д) ; е) .
13. Постройте графики функций:
А) ; б) ;
В) ; г) ;
Д) ; е) .
14. Постройте графики функций:
А) ; б) ;
В) ; г) ;
Д) ; е) .
15. Постройте графики функций:
А) ; б) ;
В) ; г) ;
Д) ; е) .
| < Предыдущая | Следующая > |
|---|
Постройте график функции y = |-2
Задание.
Постройте график функции y = |-2 – |x + 5||.
Решение.
Страшная на первый взгляд функция на самом деле строиться не так уж сложно.
Чтобы разобраться в ее построении вспомним, что представляет собой модуль. Как известно из алгебры, модулем любого числа (то ли оно положительное, то ли отрицательное) всегда будет положительное число. Также модуль называют расстоянием, а как известно, расстояние не может быть отрицательным – это всегда положительное число.
 Поэтому для построения графика этой функции нужно рассмотреть обе возможности.
Поэтому для построения графика этой функции нужно рассмотреть обе возможности.Пусть сумма (х + 5) будет положительным числом. Тогда, при открытии знака модуля, функция примет следующий вид:
y = |–2 – |x + 5|| = |-2 – x – 5| = |– x – 7|
Здесь также возможны два варианта:
1) –х – 7 – положительное, тогда у = –х – 7
2) –х – 7 – отрицательное, тогда у = х + 7
Таким образом, при х > –5:
1) –х – 7 > 0
При x < –7 функция существовать не будет
При x > –7 функция будет существовать для х > –5, а тогда:
у (–4) = –4 + 7 = 3 – точка (–4; 3)
у (0) = 0 + 7 = 7 – точка (0; 7)
Пусть сумма (х + 5) будет отрицательным числом. Тогда, открыв знак модуля, получим:
y = |–2 – |x + 5|| = |-2 + x + 5| = |x + 3|
Здесь также возможны два варианта:
1) х + 3 – положительное, тогда у = х + 3
2) х + 3 – отрицательное, тогда у = – х – 3
Таким образом, при х < –5:
3) х + 3 > 0
При x > –3 функция у = х + 3 существовать не будет
4) х + 3 < 0
При x < –3 функция будет существовать для х < –5. Тогда:
у (–6) = –(–6) – 3 = 3 – точка (–6; 3)
у (–10) = –(–10) – 3 = 7 – точка (–10; 7)
Нанесем полученные точки на плоскость.
Графические функции абсолютных значений | Purplemath
Purplemath
Принятие абсолютного значения отрицательного числа делает его положительным. По этой причине графики функций абсолютных значений имеют тенденцию не совсем походить на графики линейных функций, которые вы уже изучили. Однако из-за того, как ведут себя абсолютные значения, важно включать отрицательные входные данные в вашу Т-диаграмму при построении графиков функций абсолютных значений.Если вы не выберете значения x , которые поместят отрицательные значения внутри абсолютного значения, вы обычно будете вводить себя в заблуждение относительно того, как выглядит график.
Например, предположим, что ваш класс проходит следующую викторину:
MathHelp.com
Затем он наносит на график свои очки:
Эти очки хороши, насколько они идут, но их недостаточно; они не дают точного представления о том, как должен выглядеть график.В частности, они не включают никаких «минусовых» входов, поэтому легко забыть, что эти столбцы абсолютных значений означают что-то . В результате ученик забывает учесть эти столбцы и рисует ошибочный график:
НЕПРАВИЛЬНЫЙ ОТВЕТ!
Аааааа … он просто завалил викторину.
Но вы более осторожны.Вы помните, что графики абсолютных значений включают абсолютные значения, и что абсолютные значения влияют на «минусовые» входные данные. Итак, вы выбираете значения x , которые ставят «минус» внутри абсолютного значения, и выбираете еще несколько точек. Ваш T-график выглядит примерно так:
Затем вы наносите свои очки:
. .. и, наконец, вы соединяете свои точки:
.. и, наконец, вы соединяете свои точки:
У вас есть правильный график:
Правильный ответ!
Ааааанд… вы только что успешно прошли викторину. Хорошая работа!
Хотя графики абсолютных значений имеют тенденцию выглядеть так, как показано выше, с «локтем» посередине, это не всегда так. Однако, если вы видите график с таким изгибом, вы должны ожидать, что уравнение графика, вероятно, включает в себя абсолютное значение. Во всех случаях вы должны позаботиться о том, чтобы выбрать хороший диапазон значений x , потому что три соседних значения x почти наверняка не дадут вам достаточно информации, чтобы нарисовать достоверную картину.
Примечание. Полосы абсолютных значений позволяют оценивать введенные значения как всегда неотрицательные (то есть положительные или нулевые). В результате буква «V» на приведенном выше графике появилась там, где знак внутри был равен нулю. Когда x было меньше –2, выражение x + 2 было меньше нуля, и столбцы абсолютных значений перевернули эти «минусовые» значения из-под оси x вверх. Когда x равняется –2, аргумент (то есть выражение внутри столбцов) равен нулю.Для всех значений x справа от –2 аргумент был положительным, поэтому столбцы абсолютных значений ничего не меняли.
Другими словами, графически столбцы абсолютных значений занимают этот график:
… и перевернул «минус» (зеленый на графике) снизу оси x на верхнюю. Замечание, где аргумент столбцов абсолютного значения будет равен нулю, может быть полезным для проверки правильности построения графика.
Эта функция почти такая же, как и предыдущая.
Однако аргумент предыдущего выражения абсолютного значения был x + 2. В этом случае только x находится внутри столбцов абсолютного значения. Этот аргумент будет равен нулю, когда x = 0, поэтому я должен ожидать увидеть локоть в этой области. Кроме того, поскольку «плюс два» находится за пределами столбцов абсолютных значений, я ожидаю, что мой график будет выглядеть как обычный график абсолютных значений (представляющий собой «V» с изгибом в начале координат), но смещенный вверх на две единицы .
Сначала я заполню свою Т-диаграмму, выбирая по ходу несколько отрицательных значений x :
Затем нарисую точки и заполню график:
Партнер
Поскольку столбцы абсолютных значений всегда показывают неотрицательные значения, может возникнуть соблазн предположить, что графики абсолютных значений не могут опускаться ниже оси x .Но могут:
График
y = — | x + 2 |
Эта функция является своего рода противоположностью первой функции (выше), потому что в выражении абсолютного значения в правой части уравнения стоит «минус». Из-за этого «минуса» все положительные значения, предоставленные столбцами абсолютных значений, будут переключены на отрицательные значения.Другими словами, я должен ожидать, что этот график будет иметь изгиб в точке (–2, 0), как и первый график выше, но остальная часть графика будет перевернута вверх дном, чтобы оказаться ниже оси x .
Сначала я заполню свою Т-диаграмму:
Затем делаю свой график:
Также не предполагайте, что какой-либо график абсолютных значений всегда будет находиться только на одной стороне оси x .Графики могут пересекаться:
График
y = — | x | + 2
Моя Т-диаграмма:
… и мой график:
URL: https: // www.purplemath.com/modules/graphabs.htm
Обработка графиков
Многие модули обработки данных Gwyddion выдают на выходе графики. Графики можно экспортировать в текстовые файлы или проанализировать в дальнейшем. Gwyddion несколькими модулями обработки графиков. Эти модули можно найти в меню График в главном окне Gwyddion. Обратите внимание, что количество Графические модули сейчас довольно ограничены и состоят из базовых модулей для делать то, что очень часто встречается при анализе данных SPM.Для большего аналитические инструменты, вы можете использовать вашу любимую программу обработки графиков.
В этом разделе кратко описаны графические модули, присутствующие в Gwyddion. представлен.
Основные операции
Прежде всего, доступны функции масштабирования и чтения данных. в окне графика:
- Логарифмические оси — можно переключать горизонтальные и вертикальные оси
между линейным и логарифмическим значениями с помощью кнопок логарифмической шкалы.
 Переключение
в логарифмическом масштабе возможно только для положительных значений (либо на
абсцисса или ордината).
Переключение
в логарифмическом масштабе возможно только для положительных значений (либо на
абсцисса или ордината). - Увеличение и уменьшение масштаба — после выбора увеличения просто нарисуйте область это должно быть увеличено с помощью мыши. Уменьшение восстанавливает состояние, в котором все данные можно увидеть.
- Измерение расстояний — позволяет пользователю выбрать несколько точек в пределах график и отображает их расстояния и углы между ними.
Вырезать график
График — это очень простой модуль, который обрезает кривые графика до выбранных диапазон (численно или на графике с помощью мыши) и создает новый график.Если вырезать все кривые, все кривые вырезать и поставить на новый граф; в противном случае только одна выбранная кривая.
Уровень графика
Уровень графика — это также простой модуль, который в настоящее время выполняет линейную аппроксимацию каждую кривую графика и вычитает из них подогнанные линейные функции.
Выровнять график
Выравнивание графика сдвигает кривые графиков по горизонтали, чтобы максимально увеличить их взаимные корреляции, т. е. совпадение общих черт на кривых.Это полезно, в частности, для сравнения профилей, снятых в разных локации.
Элементы управления окном графика позволяют переключаться между линейным и логарифмическим
топоры. Однако для подгонки степенных зависимостей это
часто полезно для физического преобразования данных путем логарифмирования
значения. Функция графа преобразования логарифмической шкалы выполняет такие
трансформация. Вы можете выбрать, какую ось преобразовать
(x, y или оба),
что делать с неположительными значениями, если они встречаются, и основанием логарифма.Затем создается новый график со всеми кривыми, преобразованными в соответствии с запросом.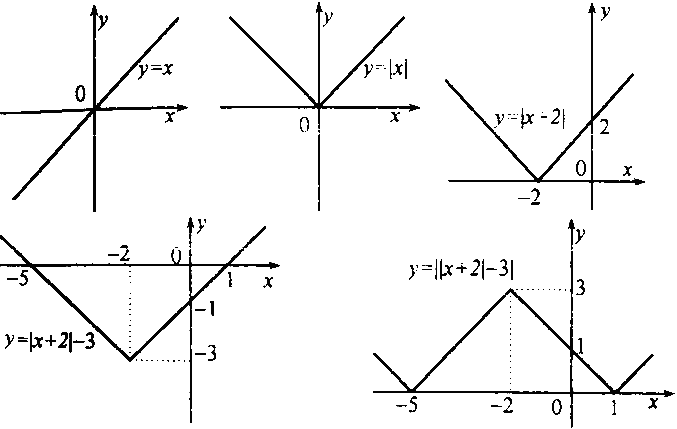
Данные кривой графика можно экспортировать в текстовые файлы с помощью . Диалог экспорта позволяет выбор нескольких вариантов стиля, которые может найти другое программное обеспечение легче читать. Параметры Экспорт этикеток, Экспортные единицы и Экспорт метаданных позволяют добавлять информационные строки перед фактическими данными. Это может быть очень полезно для напоминания о том, что содержит файл, но может вызвать проблемы когда файл читается в другом программном обеспечении.
Вариант числового формата POSIX обеспечивает соблюдение стандарта машиночитаемый формат научных чисел с десятичной точкой. Иначе значения записываются в соответствии с настройками локали (в офисном стиле ПО может это понравиться; научного софта вообще нет).
Другой важный параметр, влияющий на структуру всего файл — единая объединенная абсцисса. По умолчанию отдельные кривые записываются в файл последовательно, разделенные пустые строки.Когда этот флажок установлен, экспорт кривой записывает одна многоколоночная таблица с данными всех кривых и одной абсциссой в первый столбец. Если кривые выбраны не одинаково, некоторые строки конечно, будет содержать значения только для некоторых кривых. Экспортированный файл с две отдельные кривые могут выглядеть как
0,1 3,32e6 0,2 3.80e6 0,4 4,15e6 0,0 11,1 0,3 9,66 0,4 9,70
в то время как с одной объединенной абсциссой будут сохранены те же данные
0.0 --- 11,1 0,1 3,32e6 --- 0,2 3.80e6 --- 0,3 --- 9,66 0,4 4,15e6 9,70
Также можно экспортировать векторную (EPS) или растровую (PNG) визуализацию.
графика с помощью или
. Однако эти варианты
довольно примитивно. Gwyddion не является специализированным программным обеспечением для построения графиков и
если вам нужны красивые графики, используйте их вместо них — например
гнуплот
или же
matplotlib.
Статистика
Статистика графика отображает сводную информацию обо всех кривых графика или выбранные диапазоны.В диалоговом окне отображаются две основные группы величин. которые рассчитываются по-разному.
Простые параметры рассчитываются из набора значения ординат без учета абсцисс. Это важно для имейте в виду, когда кривая выбирается неравномерно, то есть интервалы между абсциссами различаются, возможно, много. Часть кривой, которая более плотная выборка содержит относительно больше точек и, следовательно, также больше влияет на результат.Доступные параметры включают элементарные характеристики с тем же значением, что и для двумерные данные. Некоторые из них также совпадают с рассчитанными основными параметрами шероховатости. инструментом Шероховатость.
С другой стороны, интегралы получаются интегрирование с использованием правила трапеций (или аналогичного приближения). Следовательно, более длительные интервалы способствуют большему результату. Имеется в наличии количество включает:
- Проектная длина
- Длина выбранного интервала (или всего диапазона абсцисс если интервал не выбран).
- Развернутая длина
- Сумма длин линейных отрезков, соединяющих точки кривой.
- Вариант
- Интеграл от модуля производной — рассчитывается как сумма абсолютных значений разностей ординат.
- Среднее значение
- Площадь под кривой, разделенная на предполагаемую длину.
- Площадь под кривой
- Общий интеграл (сумма положительной и отрицательной площади).
- Положительная область
- Интеграл участков кривой, где он положительный.
- Отрицательная зона
- Интеграл участков кривой, где он отрицательный.

- Среднеквадратичное значение
- Интеграл квадратов значений, деленный на прогнозируемую длину.
Одномерные статистические функции рассчитываются для графиков с использованием те же определения, что и для изображений.Они описаны в Инструмент статистических функций документация. Доступные функции включают высота и угол дистрибутивы, автокорреляционная функция, соотношение высота-высота функция и спектральная плотность. Их можно рассчитать для выбранной кривой или сразу для всех кривых. если включен параметр Все кривые.
Основное различие между изображениями и графиками заключается в том, что кривые графиков не необходимо иметь равномерно разнесенные значения абсцисс (равномерная выборка).В в таком случае кривая повторно дискретизируется в рамках расчета статистические функции для единой выборки. Шаг выборки по умолчанию такое, что количество точек сохраняется. Однако его можно изменить по передискретизации, которая дает, на сколько точек больше кривая передискретизации должна сравниваться с кривой графика. Иногда это может быть полезно использовать передискретизацию больше 1 даже для регулярных выборочные графические кривые.
Функция Фитинг
Подгонка кривой предназначена именно для подбора статистических функции, используемые при оценке параметров шероховатости.Поэтому большинство доступные функции в настоящее время являются различными статистическими функциями поверхности с гауссовыми или экспоненциальными автокорреляционными функциями. Тем не менее, он также предлагает несколько обычных универсальных функции. Увидеть список фитинговых функций.
В модуле подгонки вы можете выбрать область, которая должна быть подогнана.
(с помощью мыши или численно), попробуйте некоторые начальные параметры или позвольте
модуль, чтобы угадать их, а затем подогнать данные с помощью Марквардта-Левенберга
алгоритм.
В результате вы получаете подогнанную кривую и набор ее параметров. Отчет о соответствии можно сохранить в файл, используя Кнопка «Сохранить». Нажатие Кнопка OK добавляет подобранную кривую к графику, если это нежелательно, прекратите диалог с Отмена.
Подгонка кривой силы-расстояния
Модуль для построения кривых сила-расстояние очень похож на модуль подгонки общей кривой, он просто специализирован для кривые сила-расстояние.В настоящее время модуль служит для установки врезного часть кривой сила-расстояние (представляющая силы притяжения) с использованием разные модели:
- сила Ван-дер-Ваальса между полусферой и полупространством
- сила Ван-дер-Ваальса между пирамидой и полупространством
- сила Ван-дер-Ваальса между усеченной пирамидой и полупространством
- сила Ван-дер-Ваальса между сферой и полупространством
- сила Ван-дер-Ваальса между двумя сферами
- сила Ван-дер-Ваальса между конусом и полупространством
- сила Ван-дер-Ваальса между цилиндром и полупространством
- сила Ван-дер-Ваальса между параболоидом и полупространством
Обратите внимание, что аппроксимируемая кривая должна быть реальной кривой силы-расстояния, а не кривая смещения-расстояния или сенсора-расстояния.Пересчет прогиб кантилевера в силу должен быть выполнен до вызова этого модуль.
Также обратите внимание, что для небольших консольных пружин количество используемых данные в привлекательной области ограничены эффектом прыжка в контакт.
Критическое измерение
Модуль критических размеров может использоваться для некоторых
«Типовые» объекты, которые часто встречаются при анализе
профили, извлеченные из микрочипов и связанных поверхностей. Эти объекты
расположены на графике и оцениваются их свойства.
Эти объекты
расположены на графике и оцениваются их свойства.
Пользовательский интерфейс этого модуля практически такой же, как и у модуль подгонки графа.
DOS Spectrum
Модуль спектра DOS, предназначенный для получения спектров плотности состояний из I-V СТМ спектроскопии. Он рассчитывает
и строит его в виде графика.
Найти пики
Наиболее заметные пики на графиках могут быть автоматически обнаружены. с точностью до подвыборки.Вы можете указать количество наиболее видные пики как количество пиков и функция отметим их на графике. Высота пика зависит от его высоты, площадь и удаленность от других вершин. Обычно функция представляет, что наиболее заметные вершины вполне согласуются с человеческой оценкой. Если вы не согласны с выбором, вы можете попросить больше пиков и проигнорировать те, которые вам не нравятся. Также возможно найти отрицательные пики, то есть долины, включив опцию Инвертировать (найти долины).
В левой части отображается таблица всех пиков, отсортированных по Заказать козырьки по. Сортировка по позиции означает пики перечислены так, как они отображаются на графике слева направо. Порядок заметности означает, что более значимые пики перечислены первыми.
Для каждого пика отображается несколько основных характеристик:
позиция (абсцисса) x,
высота h,
площадь А,
и ширина (или дисперсия) w.
Положение рассчитывается квадратичным субпиксельным уточнением пика.
максимум.Остальные количества зависят от того, каков фон пика.
определенный. Возможные варианты включают нулевое значение
база пиков всегда считается нулевой, а двусторонняя
минимум означает, что фон пика является ступенчатой функцией
проходя через ближайшие минимумы кривой слева и справа от
Пик.
Террасы
Структуры, похожие на террасы или амфитеатры, можно измерить с помощью одномерные профили, аналогично тому, как они измеряются по данным изображения в Террасах.График и изображение модули практически идентичны. Поэтому следующие лишь основные моменты основные отличия:
Ядро обнаружения ступеней и уширение одномерны. Они есть все еще измеряется в пикселях, что соответствует среднему интервалу между точками кривой. Минимальная площадь террасы заменена на минимальную. длина, измеренная как доля от полного диапазона абсцисс.
Варианта маскировки нет.Вместо этого террасы можно разметить вручную на графике с помощью мыши при выборе регионов вручную включен.
В меню Display есть дополнительный выбор, Обнаружение шагов. Он показывает результаты обнаружение края фильтрует и отмечает выбранный порог с помощью пунктирная красная линия. Это один из самых полезных графиков для настройка параметров.
Площадь пикселя A пикселей заменяется на N пикселей , количество кривых указывает на терраса состоит из.
| Графический модуль отображает ваше выбранный набор данных в виде графика, что дает вам возможность визуализировать ваши данные. В этом модуле у вас есть следующие варианты выбора: | |
Выбрать субмодуль | |
Внутри графического модуля есть два разных подмодуля: в первом (« одна переменная — несколько стран, »)
у вас есть возможность легко сравнивать эволюцию и тенденции для пары стран на основе предварительно выбранной переменной.Второй (« One Country
— Несколько переменных «) предлагает вам обратную возможность: сравнить различные переменные для данной страны. Поскольку эти модули уже есть Если у вас сложный анализ и функции отображения, вам следует потратить несколько минут, чтобы понять, как работают модули. | |
Выбрать тип графика | |
| Базовый Инструменты : Это основные функции отображения для навигации по карте: После того, как вы выбрали свой подмодуль, вы должны решить, какой тип графика вы хотите использовать.Наиболее типичными являются Line — и Бар — Графики . Третья возможность — это Накопленный линейный график . | |
| | |
Выберите страны / суб- / регионы | |
| В зависимости от подмодуля, в котором вы находитесь, вы можете выбрать одну страну / суб- / регион (для «Одна страна — несколько переменных») или несколько. Максимальное значение установлено для семи стран, поскольку при отображении большего количества стран различить их будет практически невозможно.Удерживайте кнопку Ctrl для множественного выбора страны / субрегионы / регионы, не смежные друг с другом в списке или иным образом кнопка Shift. | |
Выбрать годы | |
| В этом поле вы можете выбрать несколько или все годы для отображения. Удерживайте нажатой кнопку Ctrl или кнопку Shift, чтобы выбрать пару или ряд лет. Или просто нажмите «Все годы», чтобы выбрать все доступные годы за один шаг. | |
Go — создать новый график | |
| Нажмите эту кнопку, когда будете готовы.Готово, и через несколько секунд вы получите свой график. | |
Дополнительные опции | |
Под заголовком «Дополнительные параметры» вы можете найти еще два параметра, которые вы можете выбрать. Поскольку они не нужны
для корректного отображения графика они «прогнаны» в нижнюю область. Параметр «Изменить размещение легенды» позволяет перемещать
легенда (т.е. поле, показывающее выбранные вами страны и цвет линии / столбца на графике).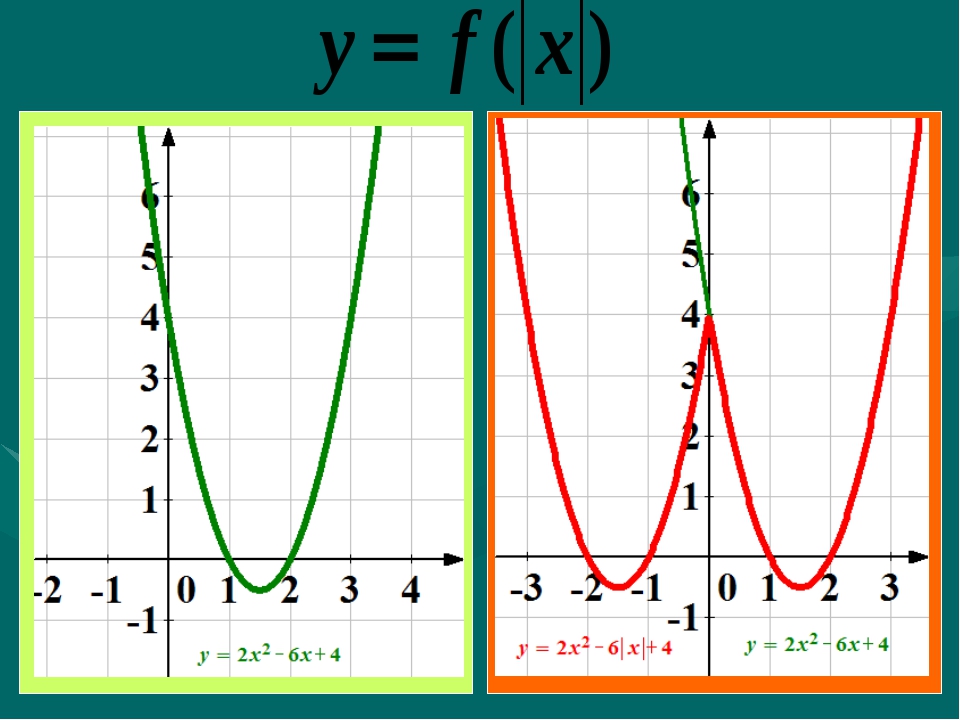 Опция «Показать глобальные значения»
добавляет на график глобальное среднее значение выбранной переменной. Опция «Показать глобальные значения»
добавляет на график глобальное среднее значение выбранной переменной. | |
Графики — PyX 0.15 Руководство
Введение
PyX можно использовать для построения графиков данных и функций. В настоящее время x-y-графы и Поддерживаются только графики x-y-z. Однако компонентная архитектура Графическая система, описанная в разделе Компонентная архитектура, допускает дополнительные геометрии графа при повторном использовании большинства существующих компонентов.
Создание графика разбивается на два основных шага.Сначала вам нужно создать график пример. Самая простая форма будет выглядеть так:
из импорта pyx * g = graph.graphxy (ширина = 8)
Экземпляр графика g , созданный в этом примере, может затем использоваться для
нанести что-нибудь на график. Предположим, у вас есть данные в файле graph.dat , который вы хотите построить. Содержимое файла может выглядеть так:
1 2 2 3 3 8 4 13 5 18 6 21
Чтобы отобразить эти данные на графике g , необходимо выполнить:
г.график (graph.data.file ("graph.dat", x = 1, y = 2))
Метод plot () принимает данные для построения графика и, возможно, список
стили графиков, которые будут использоваться для построения данных. Если стили не указаны, по умолчанию
используется стиль, определенный экземпляром данных. Для данных, считанных из файла
экземпляр graph.data.file , по умолчанию используются символы. Когда
создавая экземпляр graph.data.file , вы не только указываете имя файла, но и
также сопоставление столбцов с именами осей и другой информацией, которую стили могут
использовать ( e.грамм. данных для полос ошибок, которые будут использоваться в стиле полосы ошибок).
Хотя граф уже создан этим, нам все еще нужно выполнить запись
результат в файл. Поскольку экземпляр графа является холстом, мы можем просто вызвать
его метод writeEPSfile () .
Результат graph.eps показан на рисунке Минималистичный график для данных из файла graph.dat ..
Минималистичный график для данных из файла graph.dat .
Вместо вывода данных из файла доступен и другой источник данных.Например, данные функции создаются и помещаются в plot () с помощью
следующая строка:
g.plot (graph.data.function ("y (x) = x ** 2"))
Вы можете построить разные данные на одном графике, вызвав plot () несколько
раз перед записью вывода в файл. Обратите внимание, что вызывающий график () завершится ошибкой, если график был вынужден «закончить» сам себя. Это случилось
автоматически, когда график записывается в файл. Таким образом, это не вариант
вызовите plot () после записи вывода.Тема доработки
Граф более подробно рассматривается в разделе graph.graph . Как вы видете
на рисунке Отображение данных из файла вместе с функцией., по умолчанию функция отображается в виде линии.
Отображение данных из файла вместе с функцией.
Хотя в предыдущем примере диапазоны осей настраивались автоматически, они может быть исправлено параметрами ключевого слова в конструкторах осей. Построение только функции потребуется такая настройка хотя бы в переменной координате.Следующий код также показывает, как установить логатмическую ось в направлении y:
из импорта pyx *
g = graph.graphxy (ширина = 8, x = graph.axis.linear (min = -5, max = 5),
y = graph.axis.logarithmic ())
g.plot (graph.data.function ("y (x) = exp (x)"))
g.writePDFfile ()
Результат показан на рисунке. Построение функции для заданного диапазона осей с использованием логарифмической оси Y ..
Построение функции для заданного диапазона осей с использованием логарифмической оси y.
Компонентная архитектура
Создание графика включает в себя множество задач, которые, таким образом, можно разделить на
комплектующие без значительных дополнительных затрат. Эта структура проявляется
также в источнике PyX, где есть разные модули для разных
задачи. Они взаимодействуют через некоторые четко определенные интерфейсы. Они обязательно должны быть
завершены и стабилизированы в деталях, но основная структура возникла в
непрерывное развитие совершенно ясно. Основные части графика:
Эта структура проявляется
также в источнике PyX, где есть разные модули для разных
задачи. Они взаимодействуют через некоторые четко определенные интерфейсы. Они обязательно должны быть
завершены и стабилизированы в деталях, но основная структура возникла в
непрерывное развитие совершенно ясно. Основные части графика:
- график
Определяет геометрию графика с помощью координат графика с диапазоном [0: 1]. Хранит списки нанесенных данных, осей и т. Д.
- data
Производит или подготавливает данные для отображения в виде графиков.
- style
Выполняет нанесение данных на график. Он получает данные, конвертирует их через оси в координаты графика и использует график для окончательного построения данных относительно методов геометрии графа.
- ключ
Ответственный за ключи графика.
- ось
Создает оси для графика, которые обеспечивают отображение значений данных в координаты графика.Поскольку оси также отвечают за создание тиков и метки, отображаемые на самом графике и другие вещи, эта задача разделен на несколько независимых подзадач. Оси обсуждаются отдельно в Глава
ось.
Модуль
graph.graph : Геометрия графа Классы graphxy и graphxyz являются частью модуля граф. Граф . Однако есть ярлыки для доступа к классам через график.graphxy и graph.graphxyz соответственно.
- класс
граф. Граф.graphxy( xpos = 0 , ypos = 0 , width = None , height = None , ratio = goldenmean , key = None , backgroundattrs = None dist = 0,8 * ед.в_см , xaxisat = Нет , yaxisat = Нет , ** оси ) Этот класс предоставляет график x-y.Экземпляр графа также является полностью функциональным холст.

Положение графика на собственном холсте определяется значениями xpos и ypos . Размер графика определяется шириной , высотой и соотношением . Эти параметры определяют размер области графика без учета дополнительное место, необходимое для осей. Обратите внимание, что вы должны указать как минимум ширина или высота . Соотношение будет использоваться как соотношение между шириной и высота , если предоставляется только один из них.
ключ может быть установлен на экземпляр
graph.key.keyдля создания автоматического ключ графика.Нетпропускает ключ графика.backgroundattrs — это список атрибутов для рисования фона график. Допускаются декораторы, мазки и заливки.
Нетотключает фоновый рисунок.axisdist — это расстояние между осями, нарисованными на одной стороне графика.
xaxisat и yaxisat задают значение по осям y и x, где необходимо переместить соответствующую ось.Это ярлык для соответствующих звонков от
axisatv (), описанный ниже. Перемещение оси на xaxisat или yaxisat отключает автоматическое создание связанной оси на противоположной стороне график.** оси получает экземпляры осей. Допустимые ключевые слова (названия осей):
x,x2,x3, и т. Д. иy,y2,y3, и т. Д. При отсутствииxилиy, экземпляры линейных осей будут использоваться автоматически.Когда нет обеспечивая осьx2илиy2, связанные оси с осямиxиyсоздается автоматически и наоборот . В виде исключения связанная ось не создается автоматически, когда ось помещается в определенное положение с помощью xaxisat или yaxisat . Вы можете отключить автоматическое создание осей,
установка связанных осей на
Вы можете отключить автоматическое создание осей,
установка связанных осей на Нет. Оси с четными номерами нанесены на сверху (осиx) и справа (осиy), а остальные нанесены на снизу (осиx) и слева (осиy) в порядке возрастания.
Некоторые атрибуты экземпляра могут быть полезны для внешнего доступа для чтения. Это:
-
графокси.оси Словарь, отображающий имена осей на экземпляры
anchoredaxis.
Чтобы отобразить что-либо на графике, следующий метод экземпляра участок () предоставляется:
-
графокси.график( данных , стилей = нет ) Добавляет данных в список данных для построения графика.Устанавливает стилей , которые будут использоваться для построение графика данных. Когда стилей равно
Нет, стили по умолчанию для данных как по данным используется .данных должен быть экземпляром любых данных, описанных в разделе
граф. Данные.Когда используется одна и та же комбинация стилей (, т.е. одинаковых ссылок) несколько раз в одном и том же экземпляре графа стили любезно запрашиваются график для повторения их внешнего вида.Это зависит от стилей, как это выполняется.
Вместо того, чтобы вызывать метод построения несколько раз с разными данными , но в том же стиле вы можете использовать список (или что-то повторяемое) для данных .
Хотя экземпляр графика собирает данные только первоначально, в определенный момент он должен
создать весь сюжет. Как только это будет сделано, дальнейшие вызовы plot () будут
неудача. Обычно о доработке графика не нужно заботиться,
потому что это происходит автоматически, когда вы записываете сюжет в файл. Тем не мение,
иногда методы позиционирования (описанные ниже) удобны, если они доступны. Для
что, по крайней мере, макет графика должен быть завершен. Тем не менее
порядок рисования основан на слоях холста и, следовательно, в порядке, в котором
Тем не мение,
иногда методы позиционирования (описанные ниже) удобны, если они доступны. Для
что, по крайней мере, макет графика должен быть завершен. Тем не менее
порядок рисования основан на слоях холста и, следовательно, в порядке, в котором вызываемые методы do () не изменяют вывод. Множественные звонки на
любой из методов do () не имеет никакого эффекта (учитывается только первый вызов).
Первоначальный порядок, в котором вызываются методы do () , следующий:
-
графокси.dolayout() Исправляет макет графика. В рамках этой работы диапазоны осей адаптированы к данным, когда диапазонам осей разрешено подстраиваться под диапазоны данных. Другие методы
do ()гарантируют, что этот метод всегда позвонил первым.
-
графокси.dobackground() Рисует фон.
-
графокси.доакси() Вставляет оси.
-
графокси.doplotitem( plotitem ) Строит элемент графика, возвращенный методом построения графиков.
-
графокси.доплот() Графики всех (оставшихся) участков.
-
графокси.dokeyitem() Вставляет элемент графика в ключ графика, возвращенный методом построения графика.
-
графокси.dokey() Вставляет ключ графика.
-
графокси.отделка() Завершает построение графика вызовом всех ожидающих выполнения
do ()-методов. Закончено автоматически при создании вывода.
График предоставляет несколько методов для доступа к его геометрии:
-
графокси.
pos( x , y , xaxis = None , yaxis = None ) Возвращает заданную точку в x и y как кортеж
(xpos, ypos)на графике холст. x и y являются экземплярами якорной оси для двух осей x и ось . Когда xaxis или yaxis равныNone, оси с именамиxиyиспользуются. Этот метод не работает, если вызывается доdolayout ().
-
графокси.vpos( vx , vy ) Возвращает заданную точку в vx и vy как кортеж
(xpos, ypos)в графическое полотно. vx и vy — координаты графика с диапазоном [0: 1].
-
графокси.vgeodesic( vx1 , vy1 , vx2 , vy2 ) Возвращает геодезические между точками vx1 , vy1 и vx2 , vy2 как путь. Все параметры находятся в координатах графика в диапазоне [0: 1]. Для
graphxyэто прямая линия.
-
графокси.vgeodesic_el( vx1 , vy1 , vx2 , vy2 ) Как
vgeodesic (), но этот метод возвращает элемент пути для подключения два очка.
Дополнительная информация о геометрии доступна с помощью переменной экземпляра осей ,
with — словарь, отображающий имена осей на экземпляров оси привязки .
Ярлыки методов позиционирования с привязкой для осей x и y становятся доступными после dolayout () как методы graphxy Xbasepath , Xvbasepath , Xgridpath , Xvgridpath , Xtickpoint , Xvtickpoint , Xtickdirection и Xvtickdirection , где префикс X обозначает x и y .
-
графокси.axistrafo( ось , т ) Этот метод можно использовать для применения преобразования t к
anchoredaxisinstance axis для изменения положения оси и т.п. Этот метод не работает при вызове на еще не завершенной оси, т.е. его следует использовать послеdolayout ().
-
графокси.axisatv( ось , v ) Этот метод вызывает
axistrafo ()с преобразованием для перемещения оси ось в положение графика v (в координатах графика).
Класс graphxyz очень похож на класс graphxy ,
за исключением его дополнительного измерения. В следующей документации только
описаны отличия от класса graphxy .
- класс
граф. Граф.graphxyz( xpos = 0 , ypos = 0 , size = None , xscale = 1 , yscale = 1 , zscale = 1 / goldenmean , xy12axesat, 0006 xy12axesatname = «z» , проектор = центральный (10 , -30 , 30) , ключ = нет , ** оси ) Этот класс предоставляет график x-y-z.
Положение графика на собственном холсте определяется значениями xpos и ypos . Размер графика определяется размером и коэффициентом длины xscale , yscale и zscale . Окончательный размер графика зависит от проектора. проектор , который вызывается со значениями
x,yиzдо xscale , yscale и zscale соответственно и масштабирование результата на размер .Для изменение размера параллельного проектора , таким образом, идентично изменению xscale , yscale и zscale с тем же коэффициентом. Для центрального проектора
внутреннее расстояние проекторов также должно быть изменено этим фактором. Таким образом size изменяет размер всего графика без изменения проекции.
Для центрального проектора
внутреннее расстояние проекторов также должно быть изменено этим фактором. Таким образом size изменяет размер всего графика без изменения проекции.xy12axesat перемещает плоскость xy осей
x,x2,y,y2к заданное значение на оси xy12axesatname .проектор определяет преобразование трехмерных координат в двумерные координаты. Может быть экземпляром
центральногоилипараллельного, описанного ниже.** оси получают экземпляры осей, как для
graphxy. Graphxyz позволяет для 4 осей на размер графикаx,x2,x3,x4,y,y2,y3,y4,z,z2,z3иz4.X-Y-плоскость — это горизонтальная плоскость внизу и осиx,x2,yиy2размещается на границе этой плоскости сxиyвсегда впереди.x3,x4,y3иy4обрабатываются аналогично, но для верхней плоскости график. Осьzпомещается в начало координатxиyразмер, тогда какz2помещается в конечную точку размераx,z3в конечной точке измеренияyиz4в конечной точке размеромxиyвместе.
-
graphxyz.центральный Центральным атрибутом graphxyz является класс
central. Увидеть описание класса ниже.
-
graphxyz.параллельно Параллельный атрибут graphxyz — это класс
parallel. Увидеть описание класса ниже.
Что касается преобразования 3d в 2d, то методы pos () , vpos () , vgeodesic () и vgeodesic_el () доступны как для класса graphxy и просто возьмите дополнительный аргумент для измерения.Примечание
что аналогичный метод преобразования (3d в 2d) доступен как часть
проектор тоже уже, но только график признает его размер, масштаб
и внутреннее преобразование координат графика в масштабированный
координаты. Поскольку проектор также реализует zindex (), и angle () метод, они также доступны на уровне графика в графике
вариант с координатами (то есть с дополнительным v в его имени и с использованием значений
от 0 до 1 для каждого измерения).
-
graphxyz.vzindex( vx , vy , vz ) Глубина точки, заданной параметрами vx , vy и vz , масштабирована до диапазона [-1: 1] где 1 ближе всего к зрителю. Все аргументы, переданные методу, представлены на графике. координаты с диапазоном [0: 1].
-
graphxyz.vangle( vx1 , vy1 , vz1 , vx2 , vy2 , vz2 , vx3 , vy3 ,96 vz) Косинус угла обзора луча через точку
(vx1, vy1, vz1)и плоскость, определяемая точками(vx1, vy1, vz1),(vx2, vy2, vz2)и(vx3, vy3, vz3).Все аргументы, переданные методу, находятся в координатах графика с диапазоном [0: 1].
Существует два класса проекторов: центральный и параллельный :
- класс
граф. Граф.центральный( расстояние , phi , theta , anglefactor = math.pi / 180 ) Экземпляры этого класса реализуют центральную проекцию для заданных параметров.

расстояние — это расстояние наблюдателя от исходной точки.Обратите внимание, что Класс
graphxyzиспользует диапазон от-xscale отдоxscale,-yscale отдоyscaleи-zscale отдоzscaleдля координатx,yииз. Поскольку эти масштабы имеют порядок единицы (по умолчанию), расстояние должно быть порядка 10 для получения хороших результатов. Меньшие расстояния увеличивают характер центральной проекции, в то время как для больших расстояний центральная проекция становится идентичным параллельной проекции.phi— угол наблюдателя в плоскости x-y, аtheta— угол зрителя в плоскость x-y. Стандартные обозначения сферических координат используются. Углы умножаются на anglefactor , который инициализируется для выполнения степень трансформации излучения, позволяющая указатьphiитетав градусах, в то время как внутренние вычисления всегда выполняются в радиантах.
- класс
график.график.параллельно( phi , theta , anglefactor = math.pi / 180 ) Экземпляры этого класса реализуют параллельную проекцию для данного параметры. Для этого преобразования нет расстояния (по сравнению с центральная проекция). Все остальные параметры идентичны
центральномукласс.
Следующие классы предоставляют данные для метода графика plot () . В
классы реализованы в графе .данные .
- класс
граф. Данные.файл( имя_файла , commentpattern = defaultcommentpattern , columnpattern = defaultcolumnpattern , stringpattern = defaultstringpattern , skiphead = 0 , skiptail = 0 , title = , context = {} , copy = 1 , replaceollar = 1 , columncallback = «__ column__» , ** columns ) Этот класс считывает данные из файла и делает их доступными для системы графиков.
 имя_файла — это имя файла для чтения. Данные должны быть организованы в
столбцы.
имя_файла — это имя файла для чтения. Данные должны быть организованы в
столбцы.Аргументы commentpattern , columnpattern и stringpattern являются отвечает за идентификацию данных в каждой строке файла. Соответствие строк шаблон комментария игнорируются, за исключением поиска имени столбца последнего не- пустая строка комментария перед данными. По умолчанию строка, начинающаяся с одного из символы
'#','%'или'!', а также пустая строка рассматривается как комментарий.Строка без комментариев анализируется путем многократного сопоставления строкового шаблона и, всякий раз, когда шаблон строки не совпадает, на шаблон столбца . Когда stringpattern совпадений, результат принимается как значение для следующего столбца без дальнейших преобразований. Когда columnpattern совпадает, выполняется попытка преобразовать результат в число с плавающей запятой. Когда это не удается, результат принимается как строка также. По умолчанию вы можете писать строки с пробелами, окруженными
'"'сразу окруженный пробелами или началом / концом строки в файле данных.В противном случае'"'не считается особенным.skiphead и skiptail — это номера строк данных, которые следует игнорировать на начало и конец файла, а каждые выбирает только каждые каждые строк из данные.
заголовок — заголовок данных, которые будут использоваться в ключе графика. Заголовок по умолчанию состоит из имя_файла и ** столбцов . Вы можете установить заголовок на
Нетчтобы отключить заголовок.Наконец, столбцов определяют столбцы из существующих столбцов файла с помощью номер столбца или математическое выражение (см. ниже). Когда копия установлена, имена столбцов в файле (имена столбцов файла) и только что созданных столбцы, имеющие имена ключа словаря (имена столбцов данных), передаются как данные к стилям графиков.
 Столбцы данных могут скрывать столбцы файлов, если имена
равный. Для снятой копии столбцы файла недоступны для стилей графиков.
Столбцы данных могут скрывать столбцы файлов, если имена
равный. Для снятой копии столбцы файла недоступны для стилей графиков.Имена столбцов файла появляются, когда файл данных сразу содержит строку комментария. перед данными (кроме пустых или пустых строк комментариев). Эта линия будет анализировать, пропуская соответствующий идентификатор комментария, как если бы строка была обычные данные, но они не будут преобразованы в числа с плавающей запятой, даже если они будут возможно преобразовать предметы. Результат принимается как имена столбцов файла, , то есть . строковое представление столбцов в файле.
Значения ** столбцов могут относиться к номерам столбцов в файле, начиная с
1.Столбец0также доступен и содержит номер строки, начинающейся из1без учета строк комментариев, но строк, пропущенных skiphead , скиптейл и каждые . Кроме того, значения ** столбцов могут быть строками: имена столбцов файла или сложные математические выражения. Для ссылки на столбцы в математических выражениях вы также можете использовать имена столбцов файлов, если они допустимые идентификаторы переменных. После этого элементы с одинаковыми именами в контексте будут скрыты.В качестве альтернативы столбцы могут быть доступны с помощью синтаксиса$, когда Установлен замененный воротник . Они будут переведены в вызовы функций для columncallback , который является функцией для доступа к данным столбца по индексу или имени.контекст позволяет получить доступ к внешним переменным и функциям при оценке математические выражения для столбцов. Дополнительно к идентификаторам в контекст , имена столбцов файла, функция обратного вызова столбца и функции, указанные в таблице «Встроенные математические выражения» в конце раздел доступны.
Пример:
graph.data.
 file ("test.dat", a = 1, b = "B", c = "2 * B + $ 3")
file ("test.dat", a = 1, b = "B", c = "2 * B + $ 3")
с
test.datвыглядит так:# A B C 1,234 1 2 5,678 3 4
Столбцы с именем
"a","b","c"станут"[1.234, 5.678] "," [1.0, 3.0] "и" [4.0, 10.0] "соответственно. Столбцы"A","B","C"также будут доступны, так как копия включена По умолчанию.При создании нескольких экземпляров данных, обращающихся к одному и тому же файлу, файл читается только один раз. Имеется встроенное кеширование содержимого файла.
Для полноты перечислим шаблоны по умолчанию:
re.compile (r "(# + |! + |% +) \ S *")
-
файл.шаблон столбца по умолчанию re.compile (r "\" (. *?) \ "(\ S + | $)")
-
файл.шаблон строки по умолчанию re.compile (r "(. *?) (\ S + | $)")
- класс
граф. Данные.функция( выражение , title = notitle , min = None , max = None , баллов = 100 , context = {} ) Этот класс создает данные графика из функции. выражение — математическое выражение функции.Он также должен содержать имя переменной результата включая переменную, от которой функция зависит от присвоения. Типичный пример выглядит как
"y (x) = sin (x)".заголовок — заголовок данных, которые будут использоваться в ключе графика. По умолчанию используется выражение . Вы можете установить заголовок на
Нет, чтобы отключить заголовок.мин. и макс. задают диапазон переменной. Если не установлен, диапазон охватывает весь диапазон оси.
 Диапазон оси может быть задан явно или неявно по диапазонам.
других данных. точек — количество точек, для которых функция
рассчитано. Точки выбираются линейно по координатам графика.
Диапазон оси может быть задан явно или неявно по диапазонам.
других данных. точек — количество точек, для которых функция
рассчитано. Точки выбираются линейно по координатам графика.контекст позволяет получить доступ к внешним переменным и функциям. Дополнительно к идентификаторы в контексте , имя переменной и функции, показанные в таблица «встроенные в математические выражения» в конце раздела доступна.
- класс
график.данные.paramfunction( varname , min , max , expression , title = notitle , points = 100 , context = {} ) Этот класс создает данные графика из параметрической функции. varname — это параметр функции. мин. и макс. дают диапазон для этой переменной. точек — количество точек, для которых вычисляется функция. В точки выбираются линейно по параметру.
выражение — математическое выражение для параметрической функции. Это содержит присвоение набора функций набору переменных. А типичный пример выглядит как
"x, y = cos (k), sin (k)".заголовок — заголовок данных, которые будут использоваться в ключе графика. По умолчанию используется выражение . Вы можете установить заголовок на
Нет, чтобы отключить заголовок.контекст позволяет получить доступ к внешним переменным и функциям.Дополнительно к идентификаторы в контексте , varname и функции, показанные в таблице Доступны «встроенные в математические выражения» в конце раздела.
- класс
граф. Данные.значений( title = «пользовательские значения» , ** столбцы ) Этот класс создает данные графика из данных, предоставленных извне. Каждый столбец представляет собой список значений, которые будут использоваться для этого столбца.

заголовок — заголовок данных, которые будут использоваться в ключе графика.
- класс
граф. Данные.баллов( данных , title = «баллы, предоставленные пользователем» , дополнительных номеров = 1 , ** столбцы ) Этот класс создает данные графика из данных, предоставленных извне. data — это список строки, где каждая строка представляет собой список значений данных для столбцов.
заголовок — заголовок данных, которые будут использоваться в ключе графика.
Ключевые слова ** столбцов становятся именами столбцов данных. Ценности номера столбцов, начинающиеся с единицы, при включении доп. номера (нулевой столбец добавляется, чтобы содержать номер строки в этом случае), а номера столбцов начинается с нуля, когда дополнительных номеров выключено.
- класс
граф. Данные.data( data , title = notitle , context = , copy = 1 , replaceollar = 1 , columncallback = «__ column__» , ** columns ) Этот класс предоставляет данные графика из других данных графика. данных является источником данные. Все остальные параметры работают как равнозначно вызываемые параметры в
файл графических данных. Действительно, последний построен на вершине этого класса благодаря чтение файла и кеширование его содержимого вgraph.data.listпример.
- класс
граф. Данные.conffile( filename , title = notitle , context = , copy = 1 , replaceollar = 1 , columncallback = «__ column__» , ** columns ) Этот класс считывает данные из файла конфигурации с именем файла имя файла .
 В
формат файла конфигурации описан в документации к
В
формат файла конфигурации описан в документации к ConfigParserмодуль стандартной библиотеки Python.Каждый раздел файла конфигурации становится строкой данных. Опции в разделе столбцы. Имя параметров будет использоваться в качестве имен столбцов файла. Все остальные параметры работают как в graph.data.file и graph.data.data , поскольку они все используют один и тот же код.
- класс
график.данные.cbdfile( имя_файла , minrank = Нет , maxrank = Нет , title = notitle , context = , copy = 1 , replaceollar = 1 column, __ столбец = столбец __callback , ** столбцы ) Это экспериментальный класс для чтения картографических данных из файлов cbd. Видеть http://sepwww.stanford.edu/ftp/World_Map/ для получения некоторых данных карты мира.
Встроенные функции в математических выражениях перечислены в следующей таблице:
имя | значение |
|---|---|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| см. Описание |
| |
| |
математика относится к математическому модулю Pythons . Функция splitatvalue имеет вид
определяется как:
-
graph.data.splitatvalue( значение , * количество точек разделения ) Этот метод возвращает кортеж
(раздел, значение). Сечение рассчитывается по сравнение значения со значениями точек разделения. Если точек разделения содержит только
один элемент,
Если точек разделения содержит только
один элемент, разделравен0, когда значение меньше или равно этому элементу и1остальное.Для нескольких точек разделенияразделравен0, когда его нижняя или равен первому элементу,Нет, если он больше первого элемента, но ниже или равен второму элементу,1, когда он даже больше второго элемента, но ниже или равен третьему пункту. Он продолжает меняться междуНети2,3, пр.
Обратите внимание, что здесь мы говорим о стилях графиков. Те несут ответственность для нанесения на график символов, линий, полос и всего остального.Не смешивайте это вверх со стилями пути, такими как толщина линии, стиль линии (сплошная, пунктирная, пунктирная и др. ) и др.
Следующие классы предоставляют стили для использования в методе plot () график. Метод plot принимает список стилей. Тем самым вы можете совместить несколько
стили одновременно.
Некоторые из приведенных ниже стилей являются скрытыми. Они не создают никакого вывода, но они выполняют внутреннюю обработку данных и, таким образом, помогают модульности стили.Обычно видимый стиль зависит от данных, предоставленных одним или несколькими скрытые стили, но в большинстве случаев указывать скрытые стили вручную. Скрытые стили регистрируются по умолчанию для предоставление определенных внутренних данных.
- класс
граф. Стиль.pos( имен пользователей = {} , epsilon = 1e-10 ) Этот класс представляет собой скрытый стиль, определяющий позицию на графике. Нужны данные столбец для каждого измерения графика.Для этого имена столбцов должны быть равны имя оси или перевод имени из имен осей в имена столбцов должны быть задано именами . Точки данных считаются вне графика, если их позиция в координатах графика превышает диапазон [0: 1] более чем на эпсилон .

- класс
граф. Стиль.диапазон( имен пользователей = {} , эпсилон = 1e-10 ) Этот класс представляет собой скрытый стиль, обеспечивающий диапазон шкалы ошибок.Нужен столбец данных имена, составленные из имени оси
Xдля данных каждой шкалы ошибок измерения должен быть предоставлен следующим образом:имя данных
описание
Xminминимальное значение
Xmaxмаксимальное значение
dXминимальная и максимальная дельта
dXminминимальная дельта
dXmaxмаксимальная дельта
Если предоставлены данные дельты, стиль также будет считывать данные столбца для оси название
Xсам. имен пользователей позволяет вставить словарь перевода из имена осей к идентификаторамX.epsilon - это точность сравнения при проверке недопустимых диапазонов шкалы ошибок.
- класс
граф. Стиль.символ( символ = changecross , размер = 0,2 * unit.v_cm , symbolattrs = [] ) Этот класс представляет собой стиль для нанесения символов на график. символ относится к (изменяемая) символьная функция с прототипом символа
(c, x_pt, y_pt, size_pt, attrs)и рисует символ на холстеcв позиции(x_pt, y_pt)с размеромsize_ptи атрибутамиattrs.Некоторые предопределенные символы доступны в переменных-членах, перечисленных ниже. Символ нарисован в размере размером с использованием символов и атрибутов . символов объединены с
Символ нарисован в размере размером с использованием символов и атрибутов . символов объединены с символами по умолчаниюкоторый представляет собой список, содержащий декораторdeco.stroked. Экземпляр Символgraph.dataкроме функцииПараметры.
Символ класса предоставляет некоторые функции символа в качестве переменных-членов,
а именно:
-
символ.крест Крест. Следует использовать только для поглаживания.
-
символ.плюс Плюс. Следует использовать только для поглаживания.
-
символ.квадрат А кв. Можно погладить или набить, или и то, и другое.
-
символ.треугольник Треугольник. Можно погладить или набить, или и то, и другое.
-
символ.круг Круг. Можно погладить или набить, или и то, и другое.
-
символ.алмаз Бриллиант. Можно погладить или набить, или и то, и другое.
символ предоставляет некоторые изменяемые символьные функции в качестве переменных-членов,
а именно:
-
символ.changecross аттр.список изменений ([крестик, плюс, квадрат, треугольник, круг, ромб])
-
символ.changeplus attr.changelist ([плюс, квадрат, треугольник, круг, ромб, крест])
-
символ.см. Квадр. attr.changelist ([квадрат, треугольник, круг, ромб, крест, плюс])
-
символ.
изменяемый треугольник аттр.список изменений ([треугольник, круг, ромб, крест, плюс, квадрат])
-
символ.изменить круг attr.changelist ([круг, ромб, крест, плюс, квадрат, треугольник])
-
символ.заменен алмаз attr.changelist ([ромб, крест, плюс, квадрат, треугольник, круг])
-
символ.сменить дважды аттр.список изменений ([квадрат, квадрат, треугольник, треугольник, круг, круг, ромб, алмаз])
-
символ.чейнджетрианглет дважды attr.changelist ([треугольник, треугольник, круг, круг, ромб, ромб, квадрат, квадрат])
-
символ.изменить круг дважды attr.changelist ([круг, круг, ромб, ромб, квадрат, квадрат, треугольник, треугольник])
-
символ.заменен алмаз дважды attr.changelist ([ромб, ромб, квадрат, квадрат, треугольник, треугольник, круг, круг])
Символ класса предоставляет два сменных декоратора для чередующихся
начинка и поглаживание. Это особенно полезно в сочетании с изменить () - дважды () -символьные методы выше. Их:
-
символ.чередовано заполнено аттр.список изменений ([deco.stroked, deco.filled])
-
символ.замена заполнено ходом attr.changelist ([deco.filled, deco.stroked])
- класс
граф. Стиль.строка( lineattrs = [] , epsilon = 1e-10 ) Этот класс представляет собой стиль обводки линий на графике.
 lineattrs объединяется с
lineattrs объединяется с defaultlineattrs, который представляет собой список, содержащий переменную-членchangelinestyle, как описано ниже.Экземпляр строки, функцияи Параметрописан в разделеgraph.data. epsilon - это точность координат графика для отсечения линии.
Линия класса обеспечивает изменяемый стиль линии. Его определение:
-
линия.чейнджелинстайл attr.changelist ([style.linestyle.solid, style.linestyle.dashed, style.linestyle.dotted, style.linestyle.dashdotted])
- класс
граф. Стиль.импульсов( lineattrs = [] , fromvalue = 0 , frompathattrs = [] , valueaxisindex = 1 ) Этот класс представляет собой стиль для построения импульсов. lineattrs объединяется с
defaultlineattrs, который представляет собой список, содержащий переменную-членchangelinestyleиз линейкикласса. от значения является базовым. значение импульсов. Если установлено значениеНет, импульсы начнутся с исходный уровень. Если задано значение fromvalue, frompathattrs являются используемыми атрибутами штриха. для отображения базовой линии импульсов.
- класс
граф. Стиль.errorbar(размер = 0,1 * unit.v_cm , errorbarattrs = [] , epsilon = 1e-10 ) Этот класс представляет собой стиль для обводки полос ошибок на графике. размер - размер колпачки полос ошибок и индикаторы ошибок - атрибуты штрихов. Полосы ошибок а предельные значения ошибок считаются за пределами графика, если их положение в координаты графика превышают диапазон [0: 1] более чем на эпсилон .
 Вне графика
заглавные буквы опущены, а полосы ошибок обрезаются до допустимого диапазона графика.
Вне графика
заглавные буквы опущены, а полосы ошибок обрезаются до допустимого диапазона графика.
- класс
граф. Стиль.текст( textname = "text" , dxname = None , dyname = None , dxunit = 0.3 * unit.v_cm , dyunit = 0,3 * unit.v_cm , textdx = 0 * unit.v_cm , textdy = 0,3 * unit.v_cm , textattrs = [] ) Этот класс представляет собой стиль обводки текста на графике. Текст для написания должен быть предоставлено в столбце данных с именем
текстовое имя. textdx и textdy являются положение текста по отношению к положению на графике. Альтернативно вы можете указатьdxnameиdynameи предоставить соответствующие данные в эти столбцы следует брать в единицах dxunit и dyunit , чтобы указать положение текста по каждому пункту отдельно. textattrs - текстовые атрибуты для вывода текста. Эти атрибуты объединены со значениями по умолчанию атрибутыtextmodule.halign.centerиtextmodule.vshift.mathaxis.
- класс
граф. Стиль.стрелка(длина линии = 0,25 * unit.v_cm , размер стрелки = 0,15 * unit.v_cm , lineattrs = [] , arrowattrs = [] , arrowpos = 0,5 , epsilon = 1e- 10 , декоратор = деко.ухо ) Этот класс представляет собой стиль для построения коротких линий со стрелками в двухмерном график в заданную позицию графика. Параметры стрелки определяются двумя дополнительные столбцы данных с именами
размериуголопределяют размер и угол для каждой стрелки.размерпринимается как коэффициент , размер стрелки и длина линии , размер стрелки и длина линии, на которой отображается стрелка.угол- это угол, на который указывает стрелка относительно горизонтальной линии. Угол
Угол 0,5означает центрирование на графике. позиции, тогда как0и1создает стрелки для начала или конца в положение графика соответственно. epsilon используется в качестве отсечки для коротких стрелок в чтобы предотвратить численные нестабильности. декоратор определяет декоратор для быть добавленным в строку.
- класс
граф. Стиль.rect( colorname = "color" , gradient = color.gradient.Grey , coloraxis = None , keygraph = _autokeygraph ) Этот класс представляет собой стиль для построения двухмерных графиков из цветных прямоугольников. Размер прямоугольников взят из данных, предоставленных диапазоном
xопределяет преобразование цвета и coloraxis игнорируется.
- класс
граф. Стиль.гистограмма( lineattrs = [] , шагов = 0 , fromvalue = 0 , frompathattrs = [] , fillable = 0 , rectkey = 0 , autodegramaxisin точка автогистограммы pos = 0,5 , эпсилон = 1e-10 ) Этот класс представляет собой стиль для построения гистограмм.
 lineattrs объединяется с
lineattrs объединяется с defaultlineattrs, который равен[deco.гладил]. Когда установлено шагов , гистограмма отображается в виде шагов вместо гистограммы по умолчанию. fromvalue - это базовое значение гистограммы. Если установлено значениеНет, гистограмма начнется с базовой линии. Когда задано значение from, frompathattrs являются атрибуты штриха, используемые для отображения пути базовой линии гистограммы.Заполняемый Флаг изменяет сток-линию гистограммы, чтобы сделать ее заполняемой. должным образом.Это важно для гистограмм без пошагового сканирования или для гистограмм, которые граница графа. rectkey можно настроить для создания прямоугольной области вместо линии в ключе графика.
В самом общем случае гистограмма определяется спецификацией диапазона (например, для панели ошибок) в одном измерении графика (скажем, по оси x) и значение для другое измерение графика. Это позволяет ширину полей гистограммы быть переменным. Однако часто все диапазоны бинов гистограммы имеют одинаковый размер, и вместо того, чтобы передавать диапазон, позиция бункера по оси x полностью указывает гистограмму - при условии, что имеется как минимум два интервала.Этот общий case поддерживается двумя параметрами: autohistogramaxisindex , который определяет индекс оси независимой гистограммы (в только что описанном случае это будет
0, обозначающее ось x). точка автогистограммы pos , определяет относительное положение центра ячейки гистограммы:0,5означает, что ячейка центрируется по значениям, переданным в стиль,0(1) означает, что корзина выравнивается по правой (левой) стороне.XXX описывает, как задать общие гистограммы с различной шириной бина
Позиции гистограмм считаются вне графика, если они превышают диапазон координат графика [0: 1] более чем на эпсилон .

- класс
граф. Стиль.barpos( fromvalue = None , frompathattrs = [] , epsilon = 1e-10 ) Этот класс представляет собой скрытый стиль, предоставляющий информацию о положении в виде гистограммы.Эти графики должны содержать специальную ось, а именно ось столбцов. Данные столбец для этой оси стержней называется
Xname, гдеX- имя оси. в в другом измерении графика имя столбца данных должно совпадать с именем оси. К построить несколько столбцов на одном графике рядом, вам понадобится вложенная полоса оси и предоставить кортеж в качестве данных для оси вложенных столбцов.Полосы начинаются с от значения , если оно предусмотрено. от значения отмечен значком линия сетки, начерченная с использованием отpathattrs .Таким образом, этот скрытый стиль может на самом деле создать некоторый вывод. Значение оси столбца считается вне графика когда его положение в координатах графика превышает диапазон [0: 1] более чем на эпсилон .
- класс
граф. Стиль.stackedbarpos( stackname , addontop = 0 , epsilon = 1e-10 ) Этот класс представляет собой скрытый стиль, предоставляющий информацию о положении на гистограмме с помощью укладывание нового бара поверх другого бара.Значение нового бара берется из столбец данных с именем имя стека . При установке addontop значения принимаются относительно предыдущей вершины полосы.
- класс
граф. Стиль.бар( бар = [] , эпсилон = 1e-10 , gradient = color.gradient.RedBlack ) Этот класс рисует столбцы на гистограмме. Бары заполнены с использованием баррелей . баратров объединяется с
баратрами по умолчанию, который представляет собой список, содержащий[цвет.. gradient.Rainbow, deco.stroked ([color.grey.black])]
gradient.Rainbow, deco.stroked ([color.grey.black])] Стиль столбца имеет ограниченную поддержку трехмерных графиков: окклюзия не работает правильно для составленных столбцов или нескольких наборов данных. epsilon используется в 3D для предотвращения числовые нестабильности на стержнях без высоты. Когда градиент не
Нетиспользуется для расчета расцветки освещения с учетом угла между лучом обзора и полосой и расстоянием между зрителем и полосой. В точное преобразование определяется в методеlighting ().
- класс
граф. Стиль.сменный стержень( бар = [] ) Этот стиль работает аналогично стилю
бара, но вместо бар к быть измененным в последующих экземплярах данных, баратров изменяются для каждого значение в одном экземпляре данных. В результате стиль нельзя применить к несколько экземпляров данных и не поддерживает 3D. Стиль вызывает ошибку вместо.
- класс
граф. Стиль.gridpos( index1 = 0 , index2 = 1 , gridlines1 = 1 , gridlines2 = 1 , gridattrs = [] , epsilon = 1e-10 ) Этот класс представляет собой скрытый стиль, предоставляющий информацию о прямоугольной сетке вне графика. позиции для измерений графика index1 и index2 . Точки данных считаются быть вне графика, когда их положение в координатах графика превышает диапазон [0: 1] более чем на эпсилон .Точки данных объединены в единый график значение координаты, когда их разница в координатах графика меньше эпсилон .
- класс
граф. Стиль.сетка( линий сетки1 = 1 , линий сетки2 = 1 , линий сетки = [] , эпсилон = 1e-10 ) Обводит прямоугольную сетку в первом направлении сетки, если установлено линий сетки1 и во втором направлении сетки, когда установлено линий сетки2 .
 gridattrs есть
объединен с
gridattrs есть
объединен с defaultgridattrs, который представляет собой список, содержащий переменную-членchangelinestyleиз линейкикласса. epsilon - точность на графике координаты для обрезки линии.
- класс
граф. Стиль.поверхность( линий сетки1 = 0,05 , линий сетки2 = 0,05 , цвета сетки = Нет , backcolor = color.gray.black , ** kwargs ) Рисует поверхность прямоугольной сетки.Каждый прямоугольник разделен на 4 треугольники.
Если установлен цвет сетки , прямоугольная сетка помечается маленькими полосами относительный (по сравнению с каждым прямоугольником) размер линий сетки1 и линий сетки2 для первое и второе направление сетки соответственно.
backcolor используется для заливки треугольников, показанных сзади. Если установлен backcolor до
Нет, обратная сторона не прорисовывается иначе, чем лицевая сторона.Поверхность кодируется с использованием одной сетки. Хотя это довольно компактно, это имеет следующие последствия:
Все цвета должны использовать одно и то же цветовое пространство.
- Цвета HSB не допускаются, тогда как серый, RGB и CMYK разрешены. Вы можете
преобразовать цвета HSB в другое цветовое пространство с помощью
rgbgradientи class: cmykgradient перед передачей в стиль поверхности.
- Сама сетка также построена из треугольников. Сетка преобразуется ,
- ,
вместе с треугольниками, таким образом, выглядит совсем не так, как штриховая сетка (как сделано по стилю сетки).
Окклюзия устраняется в надлежащем порядке покраски.
Изменение цвета непрерывно (в выбранном цветовом пространстве) для каждого треугольника.

Дальнейшие аргументы идентичны графику
.style.rectстиль. Тем не мение, если столбец colorname не существует, стиль поверхности возвращается к освещению раскраска с учетом угла между лучом обзора и треугольником и расстояние между зрителем и треугольником. Точное преобразование определено в метод освещения().
-
плотность (epsilon = 1e-10, ** kwargs): Графики плотности могут быть созданы с помощью стиля плотности. Это похоже на поверхность график в 2d, но вместо него используется не сетка, а растровое представление.Из-за этой разницы размер файла меньше, а цветовая интерполяция отсутствует. происходит. Кроме того, этот стиль можно использовать с данными, расположенными на одинаковом расстоянии. только (после преобразования по оси, поэтому логарифмические исходные данные и тому подобное возможно с использованием соответствующих осей). Дальнейшие аргументы идентичны
graph.style.rectstyle.
Модуль
graph.key : Клавиши графика Следующий класс предоставляет ключ, экземпляры которого могут быть переданы в
аргумент ключевого слова конструктора ключ графа.Класс реализован в граф. Ключ .
- класс
граф. Ключ.ключ( dist = 0,2 * unit.v_cm , pos = "tr" , hpos = None , vpos = None , hinside = 1 , vinside = 1 , hdist = 0,6 * unit.v_cm , vdist = 0,4 * unit.v_cm , ширина символа = 0,5 * unit.v_cm , высота символа = 0,25 * unit.v_cm , символов = 0,2 * unit.v_cm , textattrs = [] , столбцов = 1 , столбцов = 0.5 * unit.v_cm , border = 0.3 * unit.v_cm , keyattrs = Нет ) Этот класс записывает заголовок данных в график вместе с небольшим иллюстрация стиля.
 Стиль отвечает за его иллюстрацию.
Стиль отвечает за его иллюстрацию.dist - визуальная длина и расстояние между ключевыми записями. поз. - это положение ключа относительно графика. Допустимые значения - это комбинации
"т"(вверху),"м"(в центре) и"б"(внизу) с"л"(слева),"c"(в центре) и"r"(справа).В качестве альтернативы вы можете использовать hpos и vpos , чтобы указать относительное положение в диапазоне [0: 1]. hdist и vdist - расстояния от указанного угла графика. хинсайд и vinside - это числа, которые нужно установить на 0 или 1, чтобы определить, должен ли ключ быть размещены горизонтально и вертикально внутри графика или нет.Ширина символа и высота символа передаются в style для управления размером иллюстрация стиля. пространство символов - это пространство между иллюстрацией и текст. textattrs - атрибуты для создания текста. Они сливаются с
[text.vshift.mathaxis].столбцов - это количество столбцов ключа графика, а столбец - это расстояние между этими столбцами.
Когда keyattrs настроен на то, чтобы содержать некоторые атрибуты рисования, ключ графика увеличена на граница , а ключевая область нарисована с использованием keyattrs .
Graphing With Excel - Главное меню
Ниже приведен список учебных модулей доступны для справки по визуализации данных в Excel. Вся продвинутая техника модули предполагают, что вы усвоили материал раздела «Основы». В остальном модули Advanced Techniques независимы друг от друга.Основы
Ввод данных в ячейки
Ввод значений данных в ячейки, выбор и указание диапазонов ячеек, создание формул для обработки данных и форматирования значений данных для отображения.
Создание точечной диаграммы и линейного графика
Основы создания графика из набора данных. В этом примере создается диаграмма рассеяния и простой линейный график.
Продвинутые методы
Гистограммы и гистограммы
Создание одиночных и множественных гистограмм. Справочная информация о том, для чего используется гистограмма. Также подробности о том, как использовать функцию ЧАСТОТА для создания набора данных и преобразования его в гистограмму.
Импорт текстовых файлов
Перенос необработанных данных в Excel через текстовый файл, созданный другой программой или лабораторным прибором.
Окончательное форматирование
Отформатируйте элементы графика, скрывая или отображая их, а также изменяя их размер, цвет и ориентация. Новые элементы, такие как опорные линии, можно добавлять с помощью инструментов рисования.
Линии регрессии
Обобщение тенденции набора данных с помощью линии регрессии.Показывает, как рассчитать и отобразить уравнение. для линии регрессии и ее коэффициента корреляции, R-квадрат.
Наложение графиков
Объединение данных из двух графиков в один график, как правило, для изображения второй независимой переменной. Включает информация о переформатировании графика для правильного отображения новой переменной.
Создание планок погрешностей
Предоставляет информацию о суммировании данных с средние значения и представляющие экспериментальную неопределенность с планками ошибок.
Выбор данных для отображения
Выборочное отображение только части вашего набора данных. Включает использование графиков для идентификации и удаление точек выброса.
Благодарности
matplotlib - Экспоненциальные графики в Python без использования NumPy
Конечно, и я надеюсь, что вы понимаете мои сомнения, я предпочитаю оставить свой ответ как можно более общим, пытаясь помочь вам.
Если вы не можете использовать Numpy 1 , вы должны использовать математический модуль и старые добрые списки.
Вы начинаете импортировать math из стандартной библиотеки и модуль pyplot из Matplotlib:
импорт математики
импортировать matplotlib.pyplot как plt
Вы сами выбираете интервал, в котором вы строите свою функцию, и сколько точек вам нужно для вашего графика
х_0, х_N = 0, 12
N = 120
N лучше всего подходит как количество интервалов между N + 1 точками, так что мы пишем
dx = (x_N-x_0) / N
Теперь мы можем сказать x_i = x_0 + dx × i , но мы должны сохранить наши результаты, чтобы их можно было использовать повторно.Теперь нам нужно использовать список, и у нас есть два варианта: ① начать с пустого списка и добавить к нему все x_i , используя для цикла
xs = []
для i в диапазоне (N + 1): xs.append (x_0 + dx * i)
и ② понимание списка
xs = [x_0 + dx * i для i в диапазоне (N + 1)]
(результат идентичный).
Теперь вы устранили проблему абсцисс, теперь очередь ординат; опять же, мы можем использовать добавление или понимание списка
лет = []
для i в диапазоне (N + 1):
x = xs [i]
у = математика.грех (х / 3.805)
ys.append (y)
или
ys = [math.sin (xs [i] /3.805) для i в диапазоне (N + 1)]
Теперь вы можете построить функцию
plt.plot (xs, ys, label = 'sin (%. 3fx)'% (1 / 3.805))
plt.legend ()
plt.grid ()
plt.show ()
(1) Вы не можете использовать Numpy, но, но Matplotlib будет использовать Numpy за кулисами ...
Списки, которые вы передаете в plt.plot , сразу же конвертируются в массивы Numpy! и только позже обрабатываются сложным оборудованием графического модуля.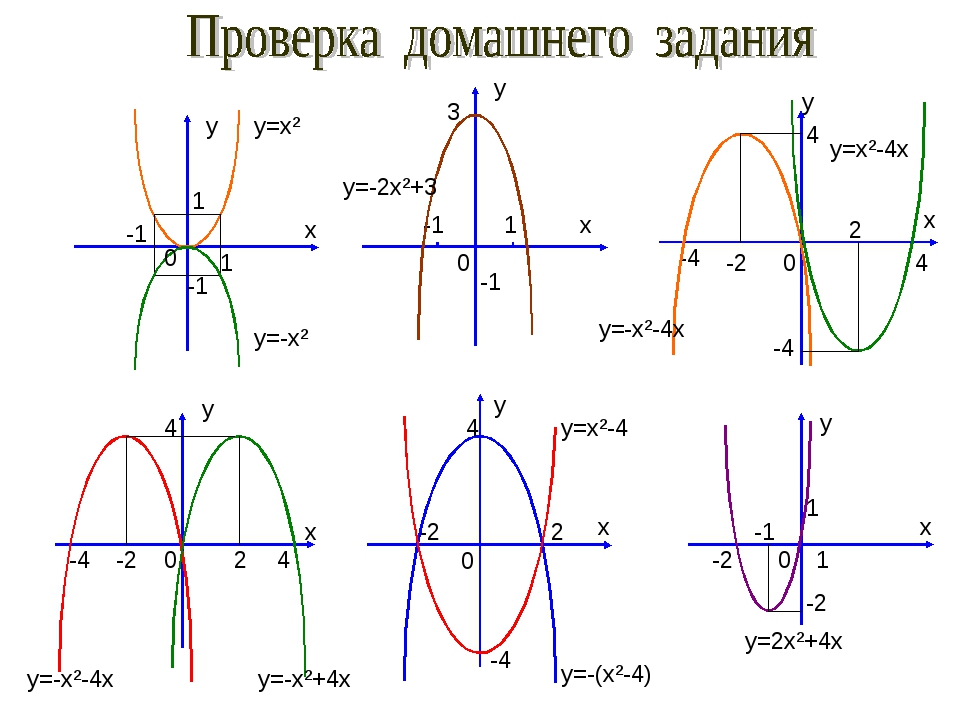
| Категория | Описание | Разрешить |
|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | |
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей.Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | |
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи для обеспечения расширенной функциональности, в том числе более персонализированного и актуального опыта на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. | |
| Файлы cookie социальных сетей | Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей. |
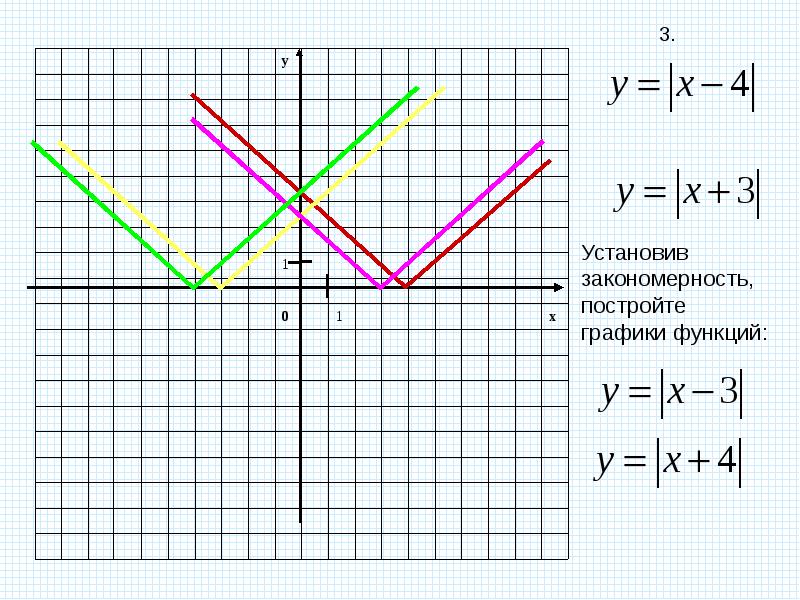 Переключение
в логарифмическом масштабе возможно только для положительных значений (либо на
абсцисса или ордината).
Переключение
в логарифмическом масштабе возможно только для положительных значений (либо на
абсцисса или ордината).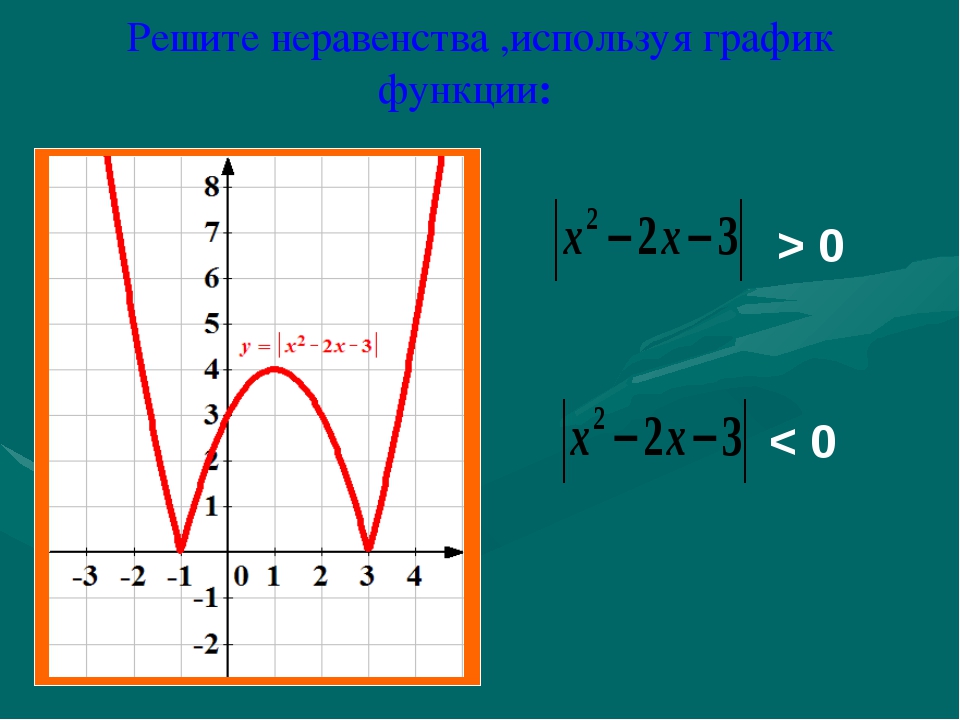
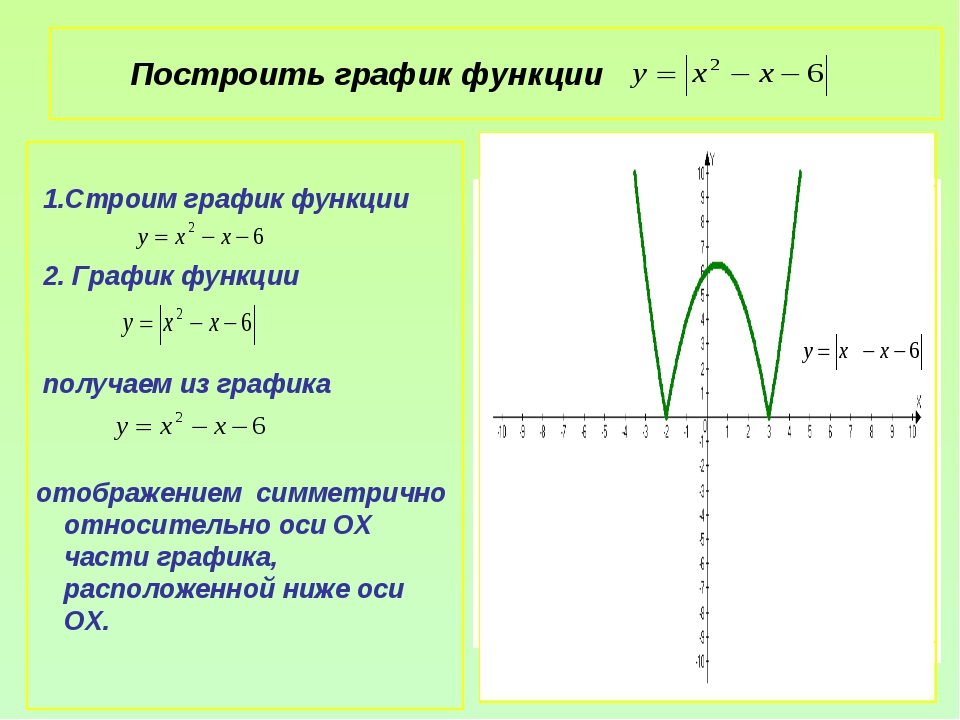
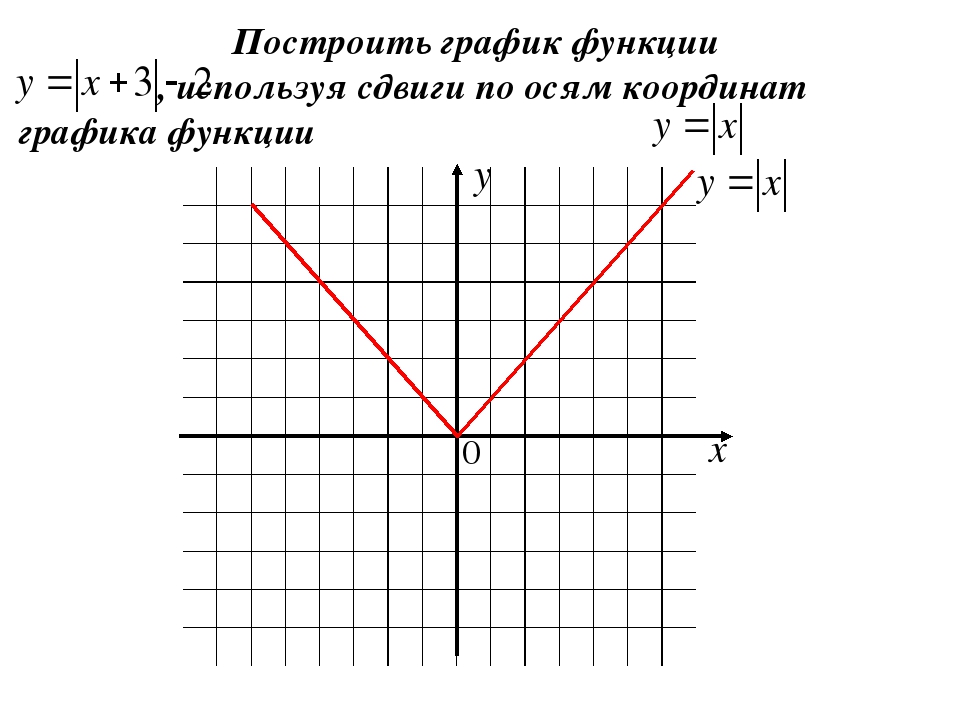 Вы можете отключить автоматическое создание осей,
установка связанных осей на
Вы можете отключить автоматическое создание осей,
установка связанных осей на 
 Для центрального проектора
внутреннее расстояние проекторов также должно быть изменено этим фактором. Таким образом size изменяет размер всего графика без изменения проекции.
Для центрального проектора
внутреннее расстояние проекторов также должно быть изменено этим фактором. Таким образом size изменяет размер всего графика без изменения проекции.
 имя_файла — это имя файла для чтения. Данные должны быть организованы в
столбцы.
имя_файла — это имя файла для чтения. Данные должны быть организованы в
столбцы. Столбцы данных могут скрывать столбцы файлов, если имена
равный. Для снятой копии столбцы файла недоступны для стилей графиков.
Столбцы данных могут скрывать столбцы файлов, если имена
равный. Для снятой копии столбцы файла недоступны для стилей графиков. file ("test.dat", a = 1, b = "B", c = "2 * B + $ 3")
file ("test.dat", a = 1, b = "B", c = "2 * B + $ 3")
 Диапазон оси может быть задан явно или неявно по диапазонам.
других данных. точек — количество точек, для которых функция
рассчитано. Точки выбираются линейно по координатам графика.
Диапазон оси может быть задан явно или неявно по диапазонам.
других данных. точек — количество точек, для которых функция
рассчитано. Точки выбираются линейно по координатам графика.
 В
формат файла конфигурации описан в документации к
В
формат файла конфигурации описан в документации к  загар
загар  Если точек разделения содержит только
один элемент,
Если точек разделения содержит только
один элемент, 
 Символ нарисован в размере размером с использованием символов и атрибутов . символов объединены с
Символ нарисован в размере размером с использованием символов и атрибутов . символов объединены с 
 lineattrs объединяется с
lineattrs объединяется с 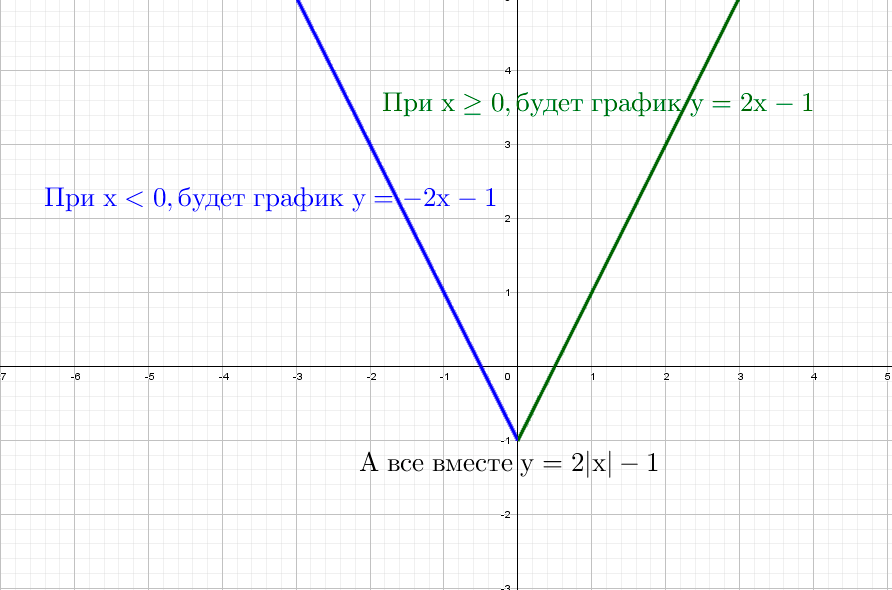 Вне графика
заглавные буквы опущены, а полосы ошибок обрезаются до допустимого диапазона графика.
Вне графика
заглавные буквы опущены, а полосы ошибок обрезаются до допустимого диапазона графика. Угол
Угол 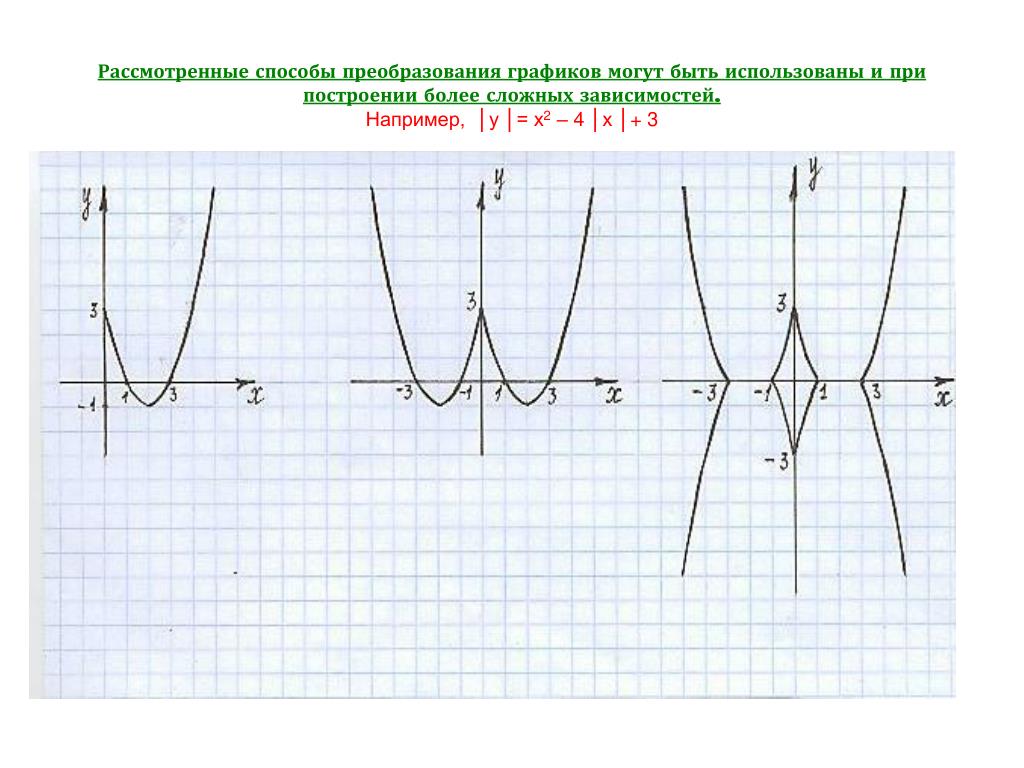 lineattrs объединяется с
lineattrs объединяется с 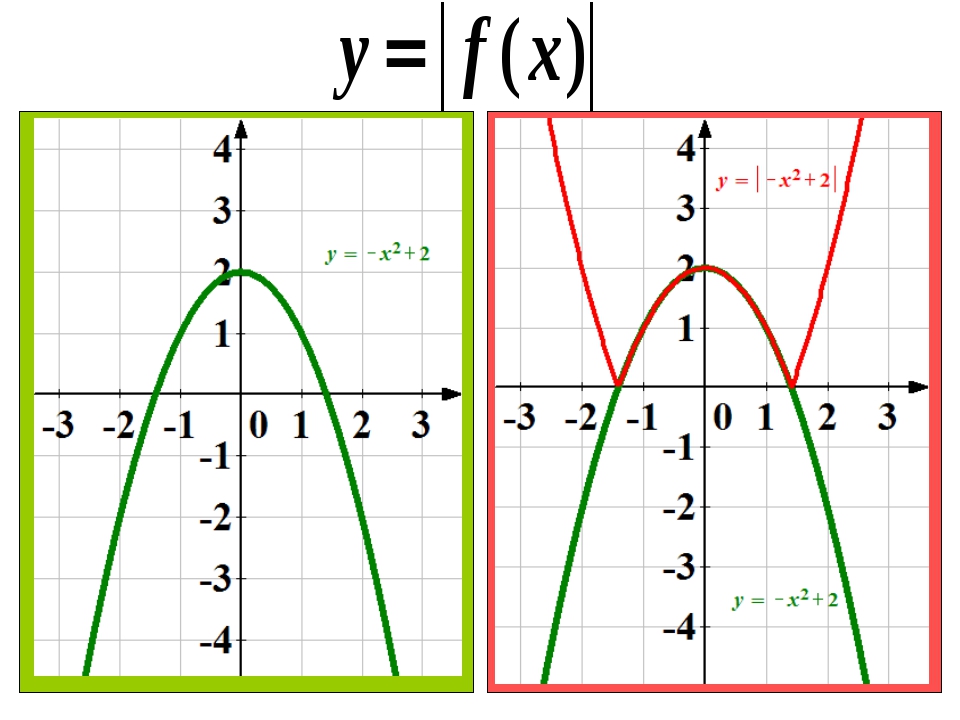
 gradient.Rainbow, deco.stroked ([color.grey.black])]
gradient.Rainbow, deco.stroked ([color.grey.black])]  gridattrs есть
объединен с
gridattrs есть
объединен с 
 Стиль отвечает за его иллюстрацию.
Стиль отвечает за его иллюстрацию.