| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. | |
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа.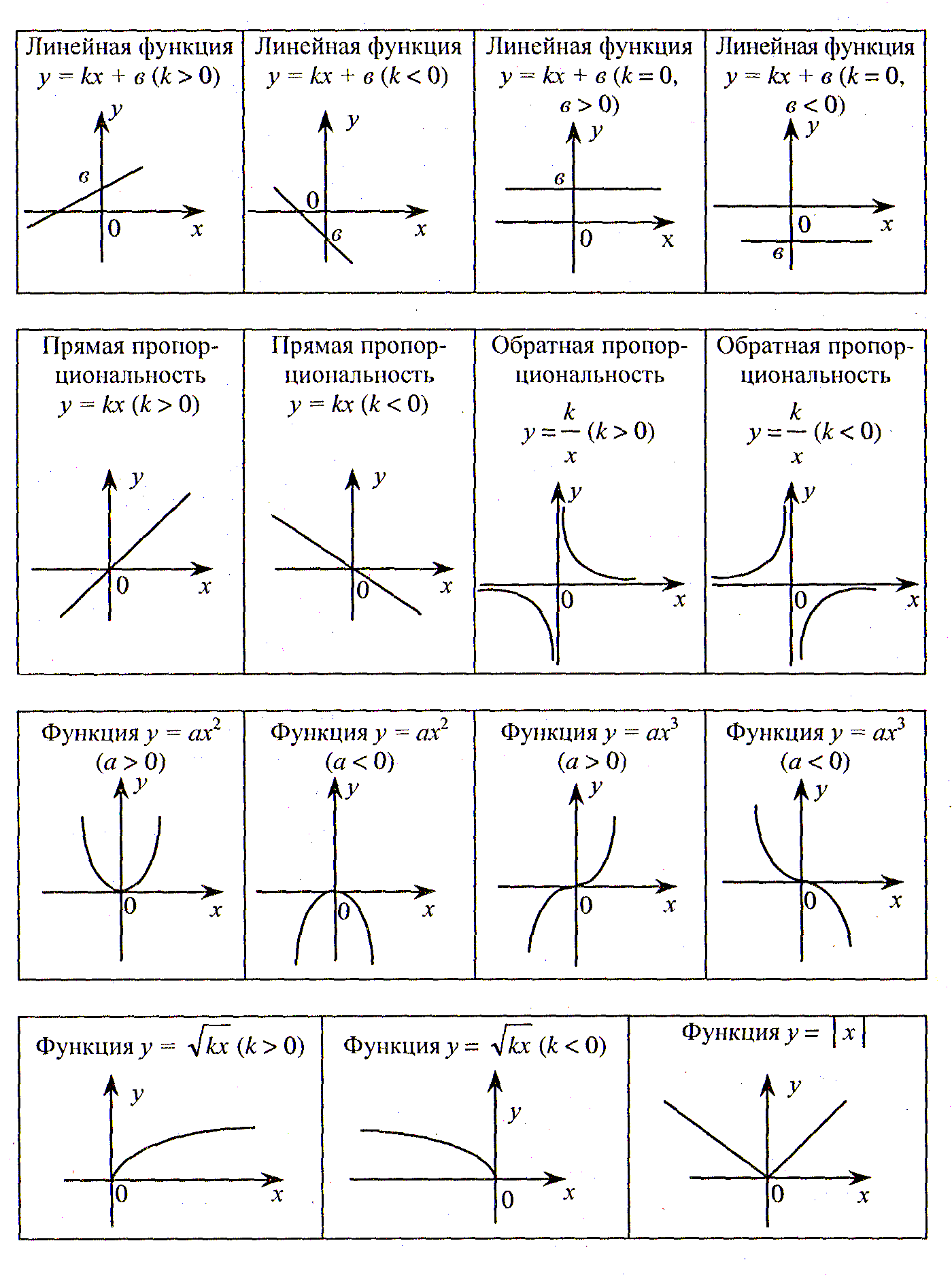 |
|
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — корень квадратный | y = x1/2 | График функции y = √x |
Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
|
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590… | |
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). Здесь пример для y = 2x (a = 2 > 1). |
|
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. | |
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). |
|
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a |
|
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
|
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
Графики функций и их модификация
Графиком функции у=f(х), где , называется множество всех точек координатной плоскости хОу вида (х;f(х)) или графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Параллельный перенос (сдвиг) вдоль оси абсцисс
График функции у=f(х+а) получаем с помощью
параллельного переноса (сдвига) последнего вдоль
оси Ох на |а| единиц масштаба в
направлении, имеющем знак, противоположный знаку
числа а.
Например, для построения графика функции у=f(х+2) вспомогательную ось ординат графика функции у=f(х) переносим параллельно вдоль оси абсцисс на две единицы масштаба вправо или сам график переносим на две единицы влево.
Параллельный перенос (сдвиг) вдоль оси ординат
График функции у=f(х+b) получаем из графика функции у=f(х) с помощью параллельного переноса (сдвига) последнего вдоль оси Оу на |b| единиц масштаба в направлении, имеющем знак числа b.
Например, для построения графика функции у=f(х)-4 вспомогательную ось абсцисс графика функции у=f(х) поднимаем вдоль оси ординат на четыре единицы или сам график переносим на 4 единицы вниз.
Растяжение или сжатие по оси абсцисс
График функции у=f(kх) получаем из графика
функции у=f(х ) с помощью сжатия по оси абсцисс
исходного графика пропорционально коэффициенту k
при аргументе: если k>1, то график сжимается в k
раз, а если 0<k<1, то график растягивается в раз.
Построим графики функций у=f(2х) и
Растяжение или сжатие по оси ординат
График функции у=mf(х) получаем из графика функции у=f(х) с помощью растяжения этого графика по оси ординат пропорционально m при функции (если m>1, то график растягивается в m раз, если 0<m<1, то график сжимается в раз).
Построим графики функций у=3f(х) и у=f(х).
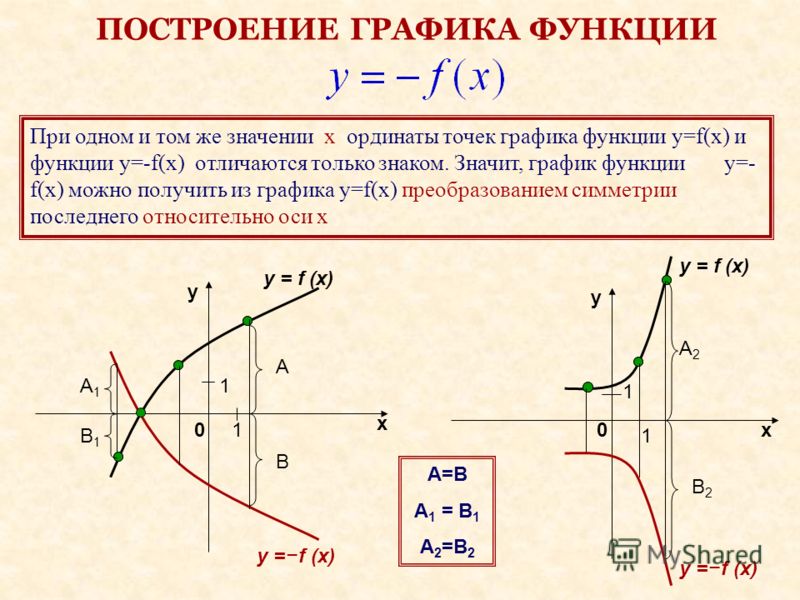
Построение графика функции у=-f(х)
График функции у=-f(х) получаем из графика функции у=f(х) с помощью симметрии относительно оси абсцисс.
Построим график этой функции.
Построение графика функции у=f(-х)
График функции у=f(-х) получаем из графика
функции у=f(х) с помощью симметрии
относительно оси ординат.
Построим график этой функции.
Построение графика функции у=|f(х)|
Для построения графика функции у=|f(х)|, надо построить график функции у=f(х), далее оставить без изменения все части построенного графика, которые лежат выше оси абсцисс или на оси, а части, расположенные ниже её, отобразить симметрично относительно этой оси.
Строим график этой функции:
Построение графика функции у= f(|х|)
Для построения графика функции у=f(|х|), надо построить график функции у=f(х) для х?0, а затем отобразить построенную часть симметрично относительно оси ординат. Обе части в совокупности дадут график функции у=f(|х|).
Построение графика функции y=-f(-х)
Для построения графика функции y=-f(-х), надо
построить график функции у = f(х), затем
выполнить симметрию относительно начала
координат. В результате получим график заданной
функции.
В результате получим график заданной
функции.
Открытая Математика. Функции и Графики. Линейная функция
Функция y = kx + b называется линейной функцией. Ее график получается путем параллельного переноса графика функции
Графики всех линейных функций, имеющих один и тот же угловой коэффициент, параллельны друг другу. Графики функций, коэффициенты k1 и k2 которых связаны соотношением k1k2 = –1, перпендикулярны друг другу.
График линейной функции является прямой.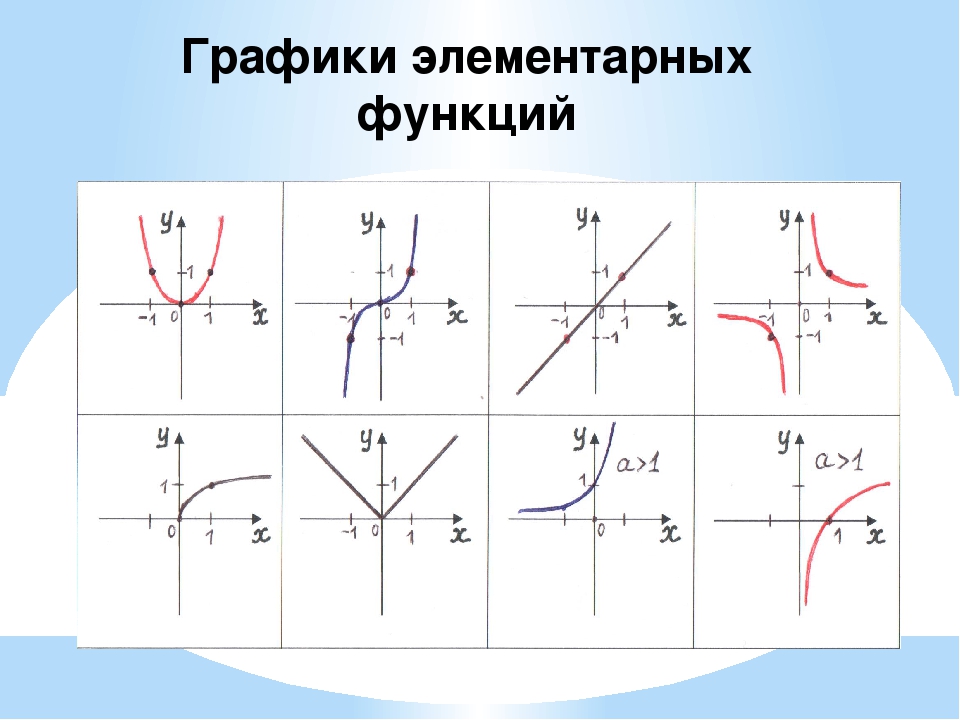 Его можно построить несколькими способами.
Его можно построить несколькими способами.
- По двум точкам. Выберем произвольные (удобные для построения) значения абсцисс x1 и x2, найдем соответствующие им ординаты y1 = k x1 + b, y2 = k x2 + b. Построим на координатной плоскости точки (x1; y1), (x2; y2) и проведем через них прямую. Это и будет искомый график.
- По пересечениям с осями. Решим уравнение y = k x + b, подставив в него сначала x1 = 0, а затем y2 = 0. Получим две точки (0; y1), (x2; 0). Построим их на координатной плоскости и проведем через них прямую.
- По угловому коэффициенту. Построим на координатной плоскости произвольную точку прямой. Проведем через эту точку прямую, образующую с осью OX угол, тангенс которого равен k.
 ,её свойства и график
,её свойства и график[музыка] тема урока функция y равно k x в квадрате ее свойства и график на этом уроке мы познакомимся с квадратичной функции вида y равняется к x в квадрате и и свойствами рассмотрим принципиальные примеры когда k меньше 0 и к больше 0 и увидим закономерность построения графиков функций для таких двух случаев рассмотрим функцию y равняется к x в квадрате при значениях к равно единице к равно 2 и к равно 1 2 составим таблицу значений для каждой функции y равняется x в квадрате y равняется 2 x в квадрате y равняется 1 2 x в квадрате из таблицы легко заметить такую закономерность для всех значений аргумента x значение функции y равно 2x в квадрате в два раза больше чем значение функция y равняется x в квадрате а значение функция y равняется 1 2 x в квадрате в два раза меньше чем у функции y равняется x в квадрате изобразим в одной системе координат графики всех трех функций y равняется x в квадрате y равняется 2 x в квадрате y равняется 1 2 x в квадрате очевидно графики рассматриваемых функций похожий каждый из них называются параболой при этом точку с координатами 00 называют вершины параболы а ось y осью симметрии параболы также для любой другой функции вида y равняется к x в квадрате при значении к больше нуля графиком является парабола с вершины в начале координат ветви которой направлены вверх причем тем круче чем больше коэффициент к то есть коэффициент к показывает степень кривизны во сколько раз растягивается или сжимается график функции y равняется к x в квадрате ось y является осью симметрии параболы кратко осью парабола выясним как обстоит дело в случае отрицательного коэффициента к построим например график функции y равняется минус x в квадрате к равно минус единица и график функции y равняется x в квадрате к равно единице в одной системе координат составим таблицу значений этих двух функций как видим из таблицы значение функция y равняется минус x в квадрате отличаются от значений функция y равняется x в квадрате только знаком это говорит о симметрии графиков функций относительно оси x поэтому график y равняется минус x в квадрате получаем из графика y равняется x в квадрате отражая его симметрично относительно оси x вообще график функции y равняется минус f от x симметричен графику функции y равняется f от x относительно оси абсцисс на рисунке видно что построены график функции y равняется минус x в квадрате это тоже парабола с вершиной в точке 0 0 ось y и ось симметрии параболы но ветви ее направлены вниз так же обстоит дело для любой другой функции вида y равняется к x в квадрате при отрицательных значениях коэффициента к и так графиком функции y равняется к x в квадрате при значениях к не равна нулю является парабола с вершины в начале координат ось y является осью параболы ветви параболы направлены вверх при к больше 0 и вниз при k меньше 0 опишем свойства функции y равняется к x в квадрате приказ больше нуля опираясь на график парабола с ветвями направленными вверх касающаяся оси x в точке 0 0 область определения функции вся числовая прямая то есть x принадлежит от минус бесконечности до плюс бесконечности действительно любое число можно возвести в квадрат y больше 0 3x не равным нулю весь график расположен выше оси x y равно нулю при x равно нулю точка касания графика с осью x вершина параболы функция убывает при x меньше или равно нулю функция возрастает при x больше или равно нулю наибольшее значение функции не существует наименьшее значение функции достигается при x равно нулю функция непрерывна функция ограничено снизу и не ограничена сверху функцию называют ограниченной снизу если все ее значения больше некоторого числа или геометрически график функции расположен выше некоторые прямой параллельной оси x область значений функции луч от 0 до плюс бесконечности или y больше или равно нулю функция выпукло вниз на примере один найдем наибольшее и наименьшее значение функции y равняется 2 x в квадрате на отрезке от минус 2 до минус единицы для удобства изобразим график данной функции на отрезке от минус 2 до минус единицы функция монотонно убывает в диапазоне от in greek равно 8 до y равно 2 то есть наименьшее значение y при минус единица равно 2а наибольшая y при минус 2 равно 8 выделим теперь основные свойства функции y равняется к x в квадрате при k меньше 0 опираясь на ее график парабола с ветвями направленными вниз касающиеся оси x в точке 0 0 область определения функции вся числовая прямая то есть x принадлежит от минус бесконечности до плюс бесконечности y меньше 0 когда x не равно нулю весь график расположен ниже оси x функция равна нулю при x равном нулю функция возрастает при всех не положительных значениях функция убывает при всех неотрицательных значениях x наименьшее значение функции не существует наибольшее значение функция достигается при x равном нулю y наибольшее равно y от 0 равно нулю функция непрерывна функция ограничена сверху и неограниченно снизу функцию называют ограниченной сверху если все ее значения меньше некоторого числа или геометрически график функции расположен ниже некоторые прямой параллельной оси x область значений функции луч от минус бесконечности до 0 функция выпукло верха решим пример 2 необходимо изобразить схематически графики функций y равняется минус x в квадрате где k равно минус единица y равняется минус 4 умноженное на x в квадрате где k равно -4 и y равняется -1 4 умноженное на x в квадрате где k равно минус 1 4 построим указанные графике это параболы а так как их коэффициенты отрицательны ветви их направлены вниз мы знаем что коэффициент к показывает степень крутизны параболы получаем что относительно графика функции y равняется минус x в квадрате степени крутизны графика функции y равняется минус 4 на x в квадрате выше в 4 раза аналогично для графика функции y ровняя минус 1 4 умноженное на x в квадрате степень крутизны в 4 раза меньше относительно графика функции y равняется минус x в квадрате и так мы изучили свойства функции при отрицательных и при положительных значениях к построили графики соответствующих функций и выяснили что от коэффициента к зависит скорость устремления ветвей параболы вверх к больше нуля или вниз к меньше 0 [музыка]
Линейная функция, график — прямая.
 Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты
Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. ТестыТестирование онлайн
Линейная функция
Определение. График
Линейной функцией называется функция вида
где k, b — некоторые числа.
Функция вида называется прямой пропорциональностью, является частным случаем линейной зависимости.
Графиком линейной функции является прямая линия.
Для построения графика достаточно знать координаты двух точек.
Свойства линейной функции
1) Область определения функции — множество всех действительных чисел
2) Множеством значений функции является множество всех действительных чисел
3) Функция не имеет ни наибольшего, ни наименьшего значений.
4) Функция не является ни четной, ни нечетной (кроме особых случаев).
5) Функция непериодическая.
6) График функции пересекает ось Ох в точке , а ось Оу — в точке (0; b).

7) — является нулем функции.
8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k.
9) При k>0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
При k: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
10) Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом. Если k>0, то этот угол острый, если k — тупой, если k=0, то прямая совпадает с осью Ох.
Для построения графика функции — прямой линии, очевидно, достаточно двух точек.
Особые случаи
1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.
2) Если k=0, получим уравнение y=b.
 Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).
Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).Ссылка на экспоненциальную функцию
Это общая экспоненциальная функция (см. Ниже e x ):
f (x) = a x
a — любое значение больше 0
Свойства зависят от значения «а»
- Когда a = 1 , график представляет собой горизонтальную линию при y = 1 .
- Кроме того, есть два случая, на которые стоит обратить внимание:
a от 0 до 1
Пример: f (x) = (0.5) хДля a от 0 до 1
a выше 1
Пример: f (x) = (2) xДля и и выше 1:
Постройте график здесь (используйте ползунок «a»)
В общем:
- Это всегда больше 0 и никогда не пересекает ось x
- Он всегда пересекает ось y при y = 1 .
 .. другими словами, он проходит через (0,1)
.. другими словами, он проходит через (0,1) - При x = 1 , f (x) = a … другими словами он проходит через (1, а)
- Это инъективная (однозначная) функция
Его домен — вещественные числа:
Его диапазон — положительные действительные числа: (0, + ∞)
Обратный
Таким образом, экспоненциальная функция может быть «обращена» с помощью логарифмической функции.
Естественная экспоненциальная функция
Это экспоненциальная функция «Natural «:
f (x) = e x
Где e — «Число Эйлера» = 2.718281828459 … и т. Д.
График f (x) = e xЗначение e важно, поскольку оно создает следующие полезные свойства:
В любой момент наклон e x равен значению e x :
, когда x = 0, значение e x = 1 и наклон = 1
при x = 1 значение e x = e и наклон = e
и т. Д…
Д…В области от до любое значение x также равно e x :
5.2 — Справочник — Графики восьми основных типов функций
5.2 — Справочник — Графики восьми основных типов функций5.2 — Справочная информация — Графики восьми основных типов функций
Цель этого справочного раздела — показать вам графики различных типов функций для того, чтобы вы могли ознакомиться с типами.Вы обнаружите, что каждый тип имеет свой собственный отличительный граф. Показывая несколько графиков на одном графике, вы сможете увидеть их общие черты. В этой галерее показаны примеры функций следующих типов: В каждом случае аргумент (вход) функции называется x , а значение (выход) функции называется y .
Линейные функции. Это функции формы:y = m x + b ,
где m и b — постоянные.Типичное использование для линейные функции — это преобразование одной величины или набора единиц в другую. Графики этих функций представляют собой прямых . м, — это уклон, а b — точка пересечения y .
Если м положительно, линия поднимается вправо, а если м. отрицательное, тогда линия падает вправо.
Здесь подробно описаны линейные функции.
Графики этих функций представляют собой прямых . м, — это уклон, а b — точка пересечения y .
Если м положительно, линия поднимается вправо, а если м. отрицательное, тогда линия падает вправо.
Здесь подробно описаны линейные функции.
Квадратичные функции. Это функции формы:y = a x 2 + b x + c ,
где a , b и c — константы. Их графики называются парабол . Это следующий по простоте тип функции после линейной функции. Падающие предметы движутся по параболическим траекториям. Если , а — положительное число, то парабола открывается вверх, и если a — отрицательное число, тогда парабола открывается вниз.Подробно квадратичные функции описаны здесь.
Силовые функции. Это функции формы:y = a x b ,
где a и b — константы. Они получили свое название от факта
что переменная x возведена в некоторую степень.
Многие физические законы (например, гравитационная сила как функция расстояния
между двумя объектами или изгиб балки в зависимости от нагрузки на нее)
представлены в виде степенных функций.Предположим, что a = 1, и рассмотрим несколько случаев для b :
Они получили свое название от факта
что переменная x возведена в некоторую степень.
Многие физические законы (например, гравитационная сила как функция расстояния
между двумя объектами или изгиб балки в зависимости от нагрузки на нее)
представлены в виде степенных функций.Предположим, что a = 1, и рассмотрим несколько случаев для b :
Степень b — целое положительное число. Смотрите график справа. Когда x = 0, все эти функции равны нулю. Когда x большой и позитивные, все они большие и позитивные. Когда x большой и отрицательный тогда те, у кого четные полномочия, большие и положительные, в то время как с нечетной мощностью большие и отрицательные.Степень b — отрицательное целое число. Смотрите график справа. Когда x = 0, эти функции подвергаются делению на ноль и, следовательно, все бесконечны. Когда x большой и положительные они маленькие и положительные.
 Когда x большой и отрицательный
тогда те, у кого четная степень, маленькие и положительные, а те, у кого
нечетные степени малы и отрицательны.
Когда x большой и отрицательный
тогда те, у кого четная степень, маленькие и положительные, а те, у кого
нечетные степени малы и отрицательны.Степень b — это дробная часть от 0 до 1. Смотрите график справа. Когда x = 0, все эти функции равны нулю. Кривые вертикальные на origin и по мере увеличения x они увеличиваются, но изгибаются к оси x .
Здесь подробно обсуждается степенная функция.
Полиномиальные функции. Это функции формы:y = a n · x n + а n -1 · x n -1 +… + а 2 · x 2 + a 1 · x + a 0 ,
где a n , a n −1 ,…, a 2 , a 1 , a 0 — константы. Допускаются только степени целого числа x .
Наивысшая степень x , которая встречается, называется степенью полинома .
На графике показаны примеры полиномов 4-й и 5-й степени.
Степень дает максимальное количество « взлетов и падений, », которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.
Допускаются только степени целого числа x .
Наивысшая степень x , которая встречается, называется степенью полинома .
На графике показаны примеры полиномов 4-й и 5-й степени.
Степень дает максимальное количество « взлетов и падений, », которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.Полиномы полезны для создания гладких кривых в компьютерной графике. приложений и для аппроксимации других типов функций.Здесь подробно описаны полиномы.
Рациональные функции. Эти функции представляют собой отношение двух многочленов. Одна область обучения, где они важны при анализе устойчивости механических и электрических систем. (который использует преобразования Лапласа).Когда многочлен от знаменатель равен нулю, то рациональная функция становится бесконечной, как указано вертикальной пунктирной линией (называемой асимптотой ) на его графике.Для пример справа это происходит, когда x = −2 и когда x = 7.

Когда x становится очень большим, кривая может выровняться. Кривая справа выравнивается на y = 5.
График справа показывает еще один пример рациональной функции. Здесь деление на ноль равно x = 0. Он не выравнивается, но приближается к прямой y = x , когда x большой, как показано пунктирной линией (еще одна асимптота).
Показательные функции. Это функции формы:y = a b x ,
где x — показатель степени (не в основании, как это было для степенных функций) и a и b — константы. (Обратите внимание, что только b возводится в степень x , а не a .) Если основание b больше 1, то результат будет экспоненциальный рост.Многие физические величины растут экспоненциально (например, популяции животных и наличные деньги). на процентном счете).Если основание b меньше 1, то результат будет экспоненциальный спад.
 Многие величины убывают экспоненциально
(например, солнечный свет достигает заданной глубины океана и
скорость замедления объекта из-за трения).
Многие величины убывают экспоненциально
(например, солнечный свет достигает заданной глубины океана и
скорость замедления объекта из-за трения).Здесь подробно описаны экспоненциальные функции.
Логарифмические функции. Есть много эквивалентных способов определения логарифмических функций. Мы будем определите их как имеющие форму:y = a ln ( x ) + b ,
где x — натуральный логарифм, а a и b — константы. Они определены только для положительных x . Для маленьких x они отрицательные, а для больших x положительные, но остаются маленькими.Логарифмические функции точно описывают реакцию человеческого уха на звуки различной громкости и реакция человеческого глаза на свет различной яркость. Здесь подробно описаны логарифмические функции.
Синусоидальные функции. Это функции формы:y = a sin ( b x + c ),
где a , b и c — константы. Синусоидальные функции
полезны для описания всего, что имеет форму волны относительно
положение или время.
Примеры: волны на воде, высота прилива в течение
дневной и переменный ток в электричестве. Параметр a (называется амплитудой) влияет на высоту волны, b (угловая скорость)
влияет на ширину волны и c (фазовый угол) сдвигает волну
влево или вправо.Здесь подробно описаны синусоидальные функции.
Синусоидальные функции
полезны для описания всего, что имеет форму волны относительно
положение или время.
Примеры: волны на воде, высота прилива в течение
дневной и переменный ток в электричестве. Параметр a (называется амплитудой) влияет на высоту волны, b (угловая скорость)
влияет на ширину волны и c (фазовый угол) сдвигает волну
влево или вправо.Здесь подробно описаны синусоидальные функции.
Если вы нашли эту страницу в ходе веб-поиска, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.графиков: типы, примеры и функции — видео и стенограмма урока
Линейные графики
Линейные графики создаются линейными функциями этой формы:
Линейная функция Линейные функции имеют переменные первой степени и две константы, определяющие положение графика.
 Эти функции всегда отображаются в виде графика. Константа м определяет наклон линии вниз или вверх. Если он положительный, линия будет наклоняться вверх, а если отрицательная, то линия будет наклоняться вниз.
Эти функции всегда отображаются в виде графика. Константа м определяет наклон линии вниз или вверх. Если он положительный, линия будет наклоняться вверх, а если отрицательная, то линия будет наклоняться вниз.Линейный график Графики мощности
Графики мощности создаются функциями только с одним членом и степенью. Мощность может быть положительной, отрицательной или даже дробной.
Степенная функция Графики, создаваемые этими функциями, зависят от мощности.Если степень положительная, график меняет направление в зависимости от числа степеней. Если степень четная, у графа оба ребра будут идти в одном направлении. Если степень нечетная, у графа одно ребро поднимается вверх, а другое опускается. Если мощность отрицательная, она будет состоять из двух частей.
 Каждая часть будет избегать строки x = 0, потому что это приведет к делению на ноль. Когда степень является дробной, график идет вверх при x = 0, а затем, когда y положительное, он начинает изгибаться к оси x.
Каждая часть будет избегать строки x = 0, потому что это приведет к делению на ноль. Когда степень является дробной, график идет вверх при x = 0, а затем, когда y положительное, он начинает изгибаться к оси x.График мощности Квадратичные графики
Квадратичные — это функции, в которых максимальная степень равна двум.
Квадратичная функция Они построены на параболах. Константы a , b, и c определяют положение параболы на графике. Модель a сообщает вам, будет ли парабола открываться вверх или вниз.Если положительный, он откроется и улыбнется. Если он отрицательный, он откроется и нахмурится.
Квадратичный граф Полиномиальные графы
Полиномы являются более общей функцией, чем квадратичная, и позволяют использовать более высокие степени, которые по-прежнему являются целыми числами.

Полиномиальная функция Эти функции создают более интересные графики с большим количеством кривых.Наивысшая степень функции показывает, сколько кривых или подъемов и падений может иметь график.
Полиномиальный граф Rational Graphs
Графики Rational взяты из функций, которые являются делением двух многочленов. Когда они построены, вы увидите, что график разделен на части. Области, которых избегает график, — это те места, где происходит деление на ноль.
Рациональный граф Экспоненциальные графики
Показатели — это степень, в которой переменная x является степенью.
Экспоненциальная функция Когда b больше единицы, вы увидите экспоненциальный рост.
 Если он меньше единицы, но больше нуля, вы увидите экспоненциальный спад. Рост — это когда график поднимается вправо. Распад — это когда он падает вправо.
Если он меньше единицы, но больше нуля, вы увидите экспоненциальный спад. Рост — это когда график поднимается вправо. Распад — это когда он падает вправо.Экспоненциальный график Логарифмические графики
Логарифмические функции включают построение логарифмов.
Логарифмическая функция Эти графики похожи на экспоненты, за исключением того, что они растут раньше и растут медленнее.
Логарифмический график Синусоидальный
Синусоидальный график использует функции, которые имеют внутри синусоидальную функцию.
Синусоидальная функция На графике отображается волновая картина.

Синусоидальный график Краткое содержание урока
Различные типы графиков зависят от типа отображаемой функции. Восемь наиболее часто используемых графиков: линейные, степенные, квадратичные, полиномиальные, рациональные, экспоненциальные, логарифмические и синусоидальные. У каждого есть уникальный график, который легко визуально отличить от остальных.
Вы можете увидеть другие типы графиков, которых здесь нет. Это потому, что существует много разных типов функций, и чем больше вы продолжаете изучать математику, тем больше вы будете сталкиваться с ними.То, что вы узнали в этом уроке, является хорошей начальной основой для типов графиков, которые вы увидите.
Результат обучения
После того, как вы закончите этот урок, вы сможете назвать и определить восемь наиболее часто используемых графиков.
Исчисление I — Общие графы
Большинство людей вышли из класса алгебры, способного работать с функциями в форме \ (y = f (x) \).
 Однако многие функции, с которыми вам придется иметь дело в классе Calculus, имеют форму \ (x = f (y) \), и с ними легко работать только в этой форме.2} + на + c \]
Однако многие функции, с которыми вам придется иметь дело в классе Calculus, имеют форму \ (x = f (y) \), и с ними легко работать только в этой форме.2} + на + c \]Это общая форма этого вида параболы, и это будет парабола, которая открывается влево или вправо в зависимости от знака \ (a \). \ (Y \) — координата вершины задается как \ (y = — \ frac {b} {{2a}} \), и мы находим \ (x \) — координату, подставляя это в уравнение. Итак, вы можете видеть, что это очень похоже на тип параболы, с которым вы уже привыкли иметь дело.
А теперь вернемся к примеру. Наша функция — парабола, которая открывается вправо (\ (a \) положительно) и имеет вершину в \ (\ left (-4,3 \ right) \).2} — 6y + 5 & = 0 \\ \ left ({y — 5} \ right) \ left ({y — 1} \ right) & = 0 \ end {align *} \]
Итак, наша парабола будет иметь \ (y \) — точки пересечения в точках \ (y = 1 \) и \ (y = 5 \). Вот набросок графика.
Типы функций и их графики
Вы можете идентифицировать функцию по ее графику.
 В этом уроке мы исследуем различные типы функций и их графики.
В этом уроке мы исследуем различные типы функций и их графики.Необходимые условия для изучения этой статьи перечислены ниже.
Существует связь между функцией и ее графиком. С помощью графика функций вы можете обнаружить некоторые свойства, которые не предоставляет алгебраическая форма.
График функций помогает визуализировать функцию, заданную в алгебраической форме. Посмотрев на уравнение, вы можете сказать, что график будет нечетным или четным, увеличивающимся или уменьшающимся, или даже уравнение вообще представляет собой график.
- Линейная функция
- Функция возведения в квадрат
- Кубическая функция
- Функция квадратного корня
- Взаимная функция
- Пошаговая функция
- Мудрая функция по частям
Линейные функции
Линейные функции — это прямые линии.Прочтите следующую статью, чтобы узнать больше о линейной функции.
Линейные уравнения
Функции возведения в квадрат
График функции возведения в квадрат обычно известен как парабола, которая представляет собой U-образную кривую.
Функции возведения в квадрат Диаграмма функции возведения в квадрат приведена ниже.
Диаграмма функции возведения в квадрат приведена ниже.Свойства функции возведения в квадрат
Свойства функции возведения в квадрат: область определения и диапазон, точки пересечения и т. Д.
- Область возведения в квадрат всех действительных чисел, соответствующая оси абсцисс.
- Диапазон функции возведения в квадрат — все неотрицательные действительные числа, потому что график имеет U-образную форму.
- Функция является четной, потому что она симметрична по оси y.
- Перехватчик функции возведения в квадрат находится в точке (0, 0).
- График функции возведения в квадрат имеет относительный минимум в точке (0, 0).
- График функции возведения в квадрат уменьшается между интервалами.
- График увеличивается между интервалами.
График кубической функции
График кубической функции имеет положительную и отрицательную стороны, в отличие от функции возведения в квадрат, которая находится только на положительной стороне.
 3
3 точка -2 -8 (-2, -8) -1 –1 (-1, -1) 0 0 (0, 0) 1 1 (1, 1) 2 8 (2, 8) График кубической функции выглядит следующим образом.
График кубической функцииСвойства кубической функции
Кубическая функция имеет следующие свойства.
- Кубическая функция — нечетная функция.
- Кубическая функция симметрична относительно начала координат.
- Область кубической функции задается всеми действительными числами.
- Диапазон кубической функции состоит из всех действительных чисел, потому что функция имеет интервал между ними.
- Пересечение графика находится в точке (0, 0).
- Функция всегда увеличивается между интервалом -.

График функции квадратного корня
График функции
, где значение результата.f (х) = х
Построим график функции квадратного корня, получив несколько точек. Мы использовали калькулятор для вычисления некоторых значений.
x точка 4 2 (4, 2) 3 1,73 (3, 1,73) 2 1,41 (2, 1. 41) 1 1 (1, 1) 0 0 (0, 0) График функции возведения в квадрат представлен ниже.
График функции возведения в квадратКак вы можете видеть, график имеет только положительную сторону как для
, так и для.Свойства функции возведения в квадрат
График функции возведения в квадрат представлен ниже.
График обратной функции
Пусть
— функция, тогдаf (x) = 1x
называется обратной функцией.

Чтобы построить график обратной функции, давайте сначала найдем все точки.
x f (x) = 1 / x точка -3 -1/3 (-3, -1/3) -2 -1/2 (-2, -1/2) -1 –1 (-1, -1) 0 undefined undefined 1 1 (1, 1) 2 1/2 (2, 1/2) 3 1/3 (3, 1/3) График обратной связи показан ниже.
График обратной функции f (x) = 1 / xСвойства графика обратной функции
Обратная функция симметрична вдоль начала координат, но никогда не касается самой начала координат. Свойства обратной функции приведены ниже.
График ступенчатой функции
График функции ступени на самом деле выглядит как лестница со ступенями.

Пусть
, будет ступенчатой функцией, где[[x]] означает найти значение « больше или равно x ».
Мы должны найти точки, чтобы построить график ступенчатой функции.
x f (x) = [[x]] + 1 баллов -2 –1 (-2, 1) -1 0 (-1, 0) 0 1 (0, 1) 1 2 (1, 2) 2 3 (2, 3) График ступенчатой функции показан ниже.
График ступенчатой функцииСвойства ступенчатой функции
Свойства ступенчатой функции приведены ниже.
- В домене заданы все действительные номера.
- Диапазон функции задается всеми целыми числами.
- Пересечение по оси Y равно (0,0), а точка пересечения по оси x — [0, 1).

- График постоянен между каждой парой целых чисел.
- График перескакивает по вертикали на одну единицу для каждого значения y.
График кусочной функции
График кусочной функции уже обсуждался в предыдущих уроках.
Графики функций
Если вы помните эти основные графы функций, используемые в алгебре, то легче выучить высшие и сложные графы. Позже, когда вы изучите математический анализ, визуализировать концепции будет намного проще с помощью графика функций.
Статьи по теме: —
Описание графика функции
Иногда вам нужно описать график функции несимвольным образом. Например, вас могут спросить
- увеличивается или уменьшается функция;
- имеет ли он одно минимальное значение или максимальное значение, или несколько таких значений
- линейно это или нет
- будь то скорость изменения постоянно, увеличивается или уменьшается
- имеет ли он верхнюю или нижнюю границу.

Пример 1:
Опишите две функции ж ( Икс ) и г ( Икс ) , используя термины «возрастание», «убывание», «максимум» и «минимум».
График ж ( Икс ) периодический. Он уменьшается для — 3 < Икс < - 1 , то увеличивается при - 1 < Икс < 1 , затем снова уменьшается при 1 < Икс < 3 , и т.д.Имеет максимальное значение 1 и минимальное значение — 1 , и он многократно достигает этих максимумов и минимумов. Верхняя граница функции равна 1 и нижняя оценка — 1 .
График г ( Икс ) увеличивается для — ∞ < Икс < - 1 и уменьшается для - 1 < Икс < ∞ .
 График принимает максимальное значение
3
в
Икс
знак равно
—
1
. У него нет минимума.
График принимает максимальное значение
3
в
Икс
знак равно
—
1
. У него нет минимума.Пример 2:
Какой график имеет более высокую скорость изменения?
Оба графика начинаются вместе в ( 0 , 0 ) . Сначала линейная функция, г ( Икс ) , имеет более высокую скорость изменения.
Но ж ( Икс ) скоро догоняет и превосходит г ( Икс ) в ( 8 , 16 ) , и продолжает увеличиваться более быстрыми темпами.
: основы работы с графами — Справка | Документация
Визуальные и аналитические преимущества графика можно улучшить, добавив функцию.
 Функция применяет определенную математическую или статистическую операцию к значениям в серии данных и отображает результат в виде линии на графике.
Функция применяет определенную математическую или статистическую операцию к значениям в серии данных и отображает результат в виде линии на графике.Категории функций
В графических инструментах приложений ArcGIS Desktop доступны 16 типов функций. Они делятся на две большие категории: описательные и трендовые.
Описательная
Описательная функция — это функция, в которой одно значение вычисляется из всех значений в серии. Этот тип функции отображается в виде прямой линии на графике, представляющей вычисленное значение.
Описательные типы функций
Тип функции Описание Среднее
Простое среднее (среднее) значений.
Счетчик
Количество значений в серии ( n ).

Высокий
Наибольшее значение в серии.
Низкий
Наименьшее значение в серии.
Медиана
Среднее значение ряда.
Режим
Значение режима серии.
RMS
Среднеквадратичное значение для ряда. Общая формула для RMS:
RMS = Sqrt (Sum (Sqr (x [i]))) / nСтандартное отклонение
Мера разброса значений в серии.
 Общая используемая формула:
Общая используемая формула:StDev = Sqrt (((n * Sum (y * y)) - Sqr (Sum (y))) / Sqrt (n))Дисперсия
Дисперсия — это разброс распределения значений в ряду, вычисляемый как среднее квадратичное отклонение каждого числа от его среднего.
Типы описательной функции (где n — количество значений)
Тренд
Трендовые функции показывают направление изменения значений.Функции трендов могут быть локальными или глобальными, и при добавлении к графику они действуют как глобальная сводка по диапазону значений данных.
Типы функций Описание Тренд
Линейная зависимость, отображаемая в виде прямой линии с определенным уклоном.

Экспоненциальный тренд
Изогнутая линия, представляющая экспоненциальную зависимость.
Типы функций тренда Другие тренды вычисляют локальную сводку для обобщения или сглаживания значений.
Типы локальных сводок Описание Скользящее среднее
Для каждого значения в серии среднее (простое или взвешенное) вычисляется для подмножества смежных значений. Это помогает лучше отличать долгосрочные тенденции от циклических.
Экспоненциальное скользящее среднее
Подобно скользящему среднему, за исключением того, что оно взвешено, так что значениям в подмножестве, близком к вычисляемому, дается больший вес.

Подгонка кривой
Сглаженная кривая генерируется из значений в серии путем применения полиномиальной функции Гаусса. Степень полинома используется для управления порядком (количеством коэффициентов) используемого полинома.
Сглаживание
Сглаженная кривая создается из значений в ряду путем применения сплайн-функции к значениям. Чем выше коэффициент, тем более гладкой станет кривая (на основе компонента B-сплайна Мартин ван Энгеланд).
Типы локальной сводки тренда Другой тип тенденции — Накопительный, который показывает совокупное количество значений:
Накопительное
Каждое значение добавляется к предыдущему значению.

 ,её свойства и график
,её свойства и график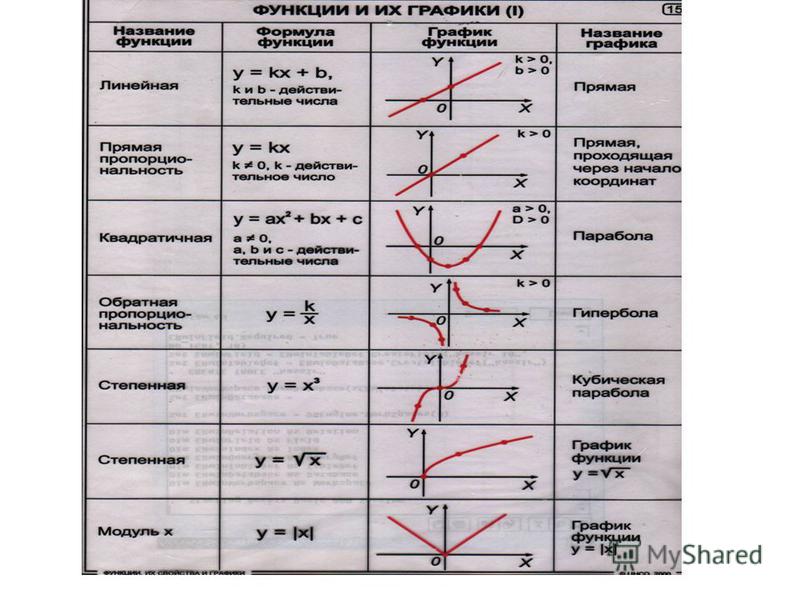 Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты
Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты
 Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).
Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b). .. другими словами, он проходит через (0,1)
.. другими словами, он проходит через (0,1)  Д…
Д… Графики этих функций представляют собой прямых . м, — это уклон, а b — точка пересечения y .
Если м положительно, линия поднимается вправо, а если м. отрицательное, тогда линия падает вправо.
Здесь подробно описаны линейные функции.
Графики этих функций представляют собой прямых . м, — это уклон, а b — точка пересечения y .
Если м положительно, линия поднимается вправо, а если м. отрицательное, тогда линия падает вправо.
Здесь подробно описаны линейные функции. Они получили свое название от факта
что переменная x возведена в некоторую степень.
Многие физические законы (например, гравитационная сила как функция расстояния
между двумя объектами или изгиб балки в зависимости от нагрузки на нее)
представлены в виде степенных функций.Предположим, что a = 1, и рассмотрим несколько случаев для b :
Они получили свое название от факта
что переменная x возведена в некоторую степень.
Многие физические законы (например, гравитационная сила как функция расстояния
между двумя объектами или изгиб балки в зависимости от нагрузки на нее)
представлены в виде степенных функций.Предположим, что a = 1, и рассмотрим несколько случаев для b :  Когда x большой и отрицательный
тогда те, у кого четная степень, маленькие и положительные, а те, у кого
нечетные степени малы и отрицательны.
Когда x большой и отрицательный
тогда те, у кого четная степень, маленькие и положительные, а те, у кого
нечетные степени малы и отрицательны. Допускаются только степени целого числа x .
Наивысшая степень x , которая встречается, называется степенью полинома .
На графике показаны примеры полиномов 4-й и 5-й степени.
Степень дает максимальное количество « взлетов и падений, », которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.
Допускаются только степени целого числа x .
Наивысшая степень x , которая встречается, называется степенью полинома .
На графике показаны примеры полиномов 4-й и 5-й степени.
Степень дает максимальное количество « взлетов и падений, », которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.
 Многие величины убывают экспоненциально
(например, солнечный свет достигает заданной глубины океана и
скорость замедления объекта из-за трения).
Многие величины убывают экспоненциально
(например, солнечный свет достигает заданной глубины океана и
скорость замедления объекта из-за трения). Синусоидальные функции
полезны для описания всего, что имеет форму волны относительно
положение или время.
Примеры: волны на воде, высота прилива в течение
дневной и переменный ток в электричестве. Параметр a (называется амплитудой) влияет на высоту волны, b (угловая скорость)
влияет на ширину волны и c (фазовый угол) сдвигает волну
влево или вправо.Здесь подробно описаны синусоидальные функции.
Синусоидальные функции
полезны для описания всего, что имеет форму волны относительно
положение или время.
Примеры: волны на воде, высота прилива в течение
дневной и переменный ток в электричестве. Параметр a (называется амплитудой) влияет на высоту волны, b (угловая скорость)
влияет на ширину волны и c (фазовый угол) сдвигает волну
влево или вправо.Здесь подробно описаны синусоидальные функции.  Эти функции всегда отображаются в виде графика. Константа м определяет наклон линии вниз или вверх. Если он положительный, линия будет наклоняться вверх, а если отрицательная, то линия будет наклоняться вниз.
Эти функции всегда отображаются в виде графика. Константа м определяет наклон линии вниз или вверх. Если он положительный, линия будет наклоняться вверх, а если отрицательная, то линия будет наклоняться вниз. Каждая часть будет избегать строки x = 0, потому что это приведет к делению на ноль. Когда степень является дробной, график идет вверх при x = 0, а затем, когда y положительное, он начинает изгибаться к оси x.
Каждая часть будет избегать строки x = 0, потому что это приведет к делению на ноль. Когда степень является дробной, график идет вверх при x = 0, а затем, когда y положительное, он начинает изгибаться к оси x.
 Если он меньше единицы, но больше нуля, вы увидите экспоненциальный спад. Рост — это когда график поднимается вправо. Распад — это когда он падает вправо.
Если он меньше единицы, но больше нуля, вы увидите экспоненциальный спад. Рост — это когда график поднимается вправо. Распад — это когда он падает вправо.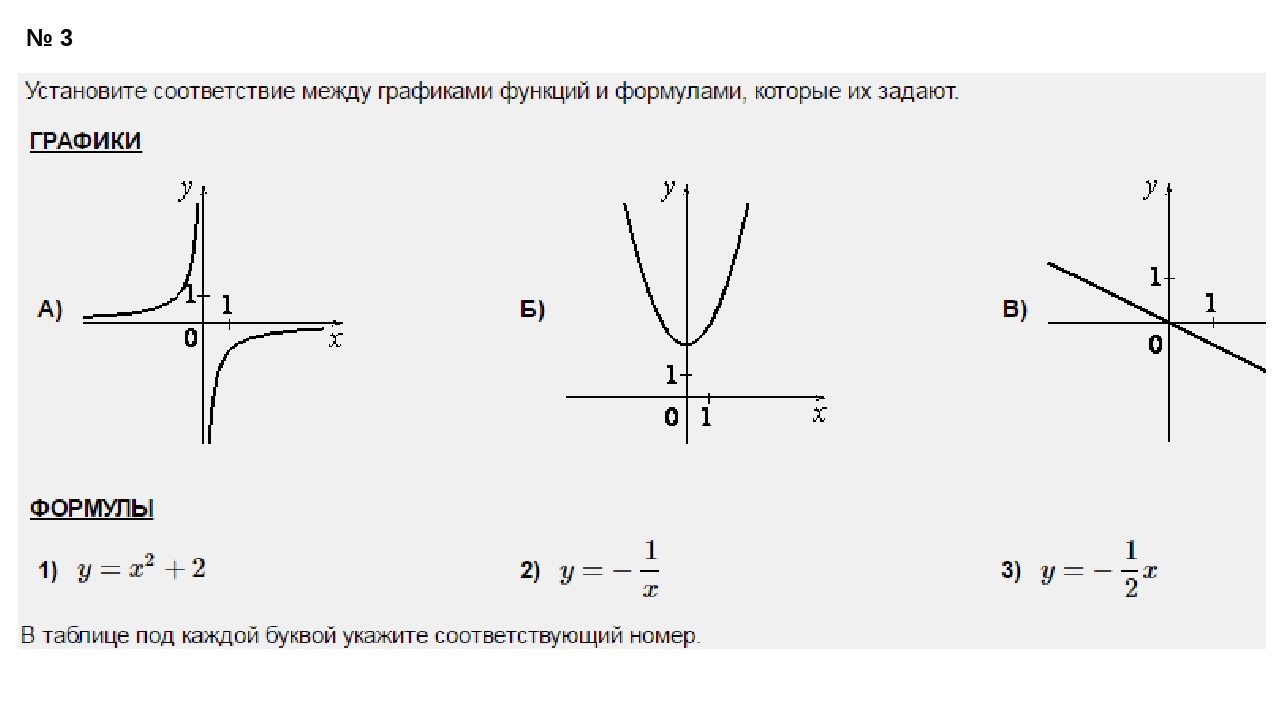
 Однако многие функции, с которыми вам придется иметь дело в классе Calculus, имеют форму \ (x = f (y) \), и с ними легко работать только в этой форме.2} + на + c \]
Однако многие функции, с которыми вам придется иметь дело в классе Calculus, имеют форму \ (x = f (y) \), и с ними легко работать только в этой форме.2} + на + c \] В этом уроке мы исследуем различные типы функций и их графики.
В этом уроке мы исследуем различные типы функций и их графики. Диаграмма функции возведения в квадрат приведена ниже.
Диаграмма функции возведения в квадрат приведена ниже.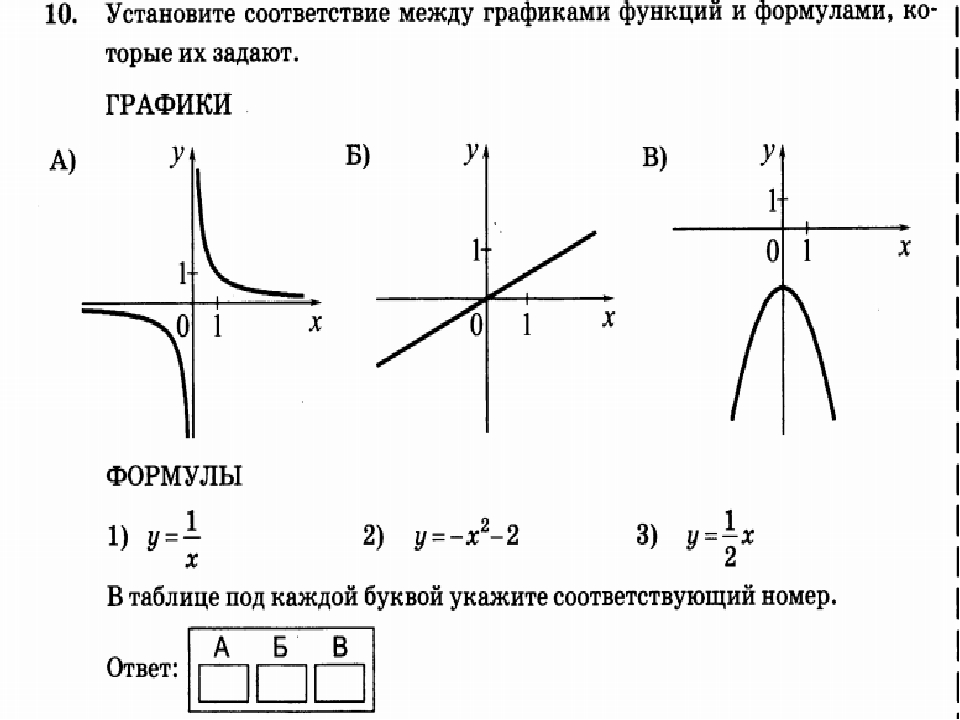 3
3 




 График принимает максимальное значение
3
в
Икс
знак равно
—
1
. У него нет минимума.
График принимает максимальное значение
3
в
Икс
знак равно
—
1
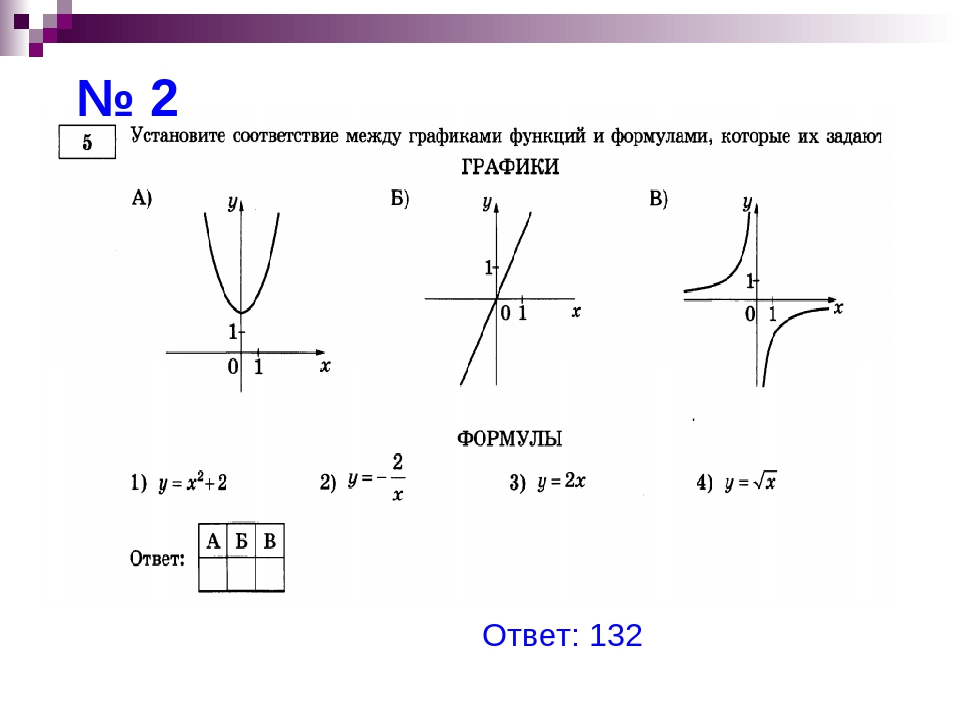
. У него нет минимума. Функция применяет определенную математическую или статистическую операцию к значениям в серии данных и отображает результат в виде линии на графике.
Функция применяет определенную математическую или статистическую операцию к значениям в серии данных и отображает результат в виде линии на графике.
 Общая используемая формула:
Общая используемая формула: