Степенная функция, линейная функция, квадратичная, кубическая и y=1/х 9 класс онлайн-подготовка на Ростелеком Лицей |
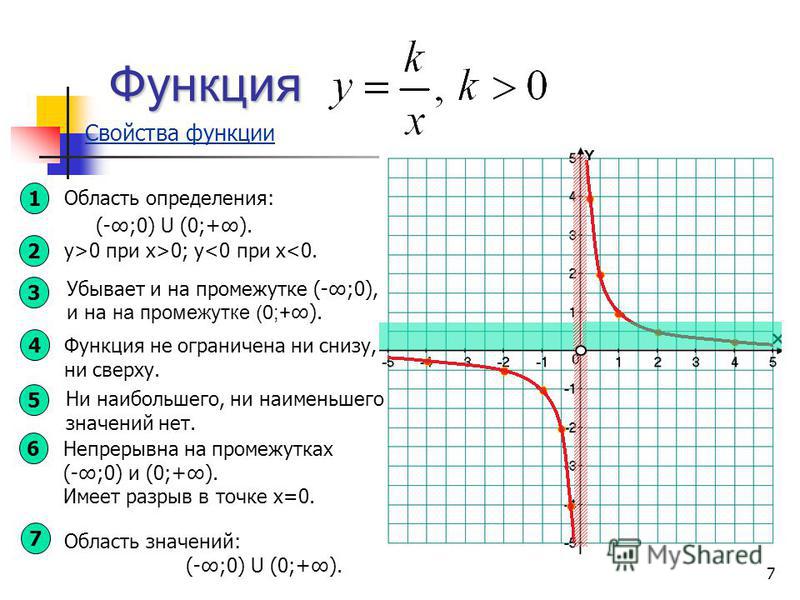
Тема 14.
Функция y=xn , четные и нечетные функции.
Сравним значения функции fx=18×4-x2 при двух противоположных значениях аргумента, например x=3 и x=-3:
f3=18∙34-32=18∙81-9=118
f-3=18∙(-3)4-(-3)2=18∙81-9=118
Получим f3=f-3. Значения этой функции равны и при любых других противоположных значениях аргумента. Действительно,
f-x=18∙(-x)4-(-x)2=18∙x4-x2, то есть
f-x=fx
При этом рассматриваемая функция такова, что для каждого значения аргумента х противоположное ему число (–х) так же принадлежит ее области определения. В таких случаях говорят, что область определения функции симметрична относительно нуля.
Функции, обладающие такими свойствами, называют четными функциями.
Определение: Функция y=fx называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство
f-x=fx
График любой четной функции симметричен относительно оси ординат.
Определение: Функция y=fx называется нечетной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство
f-x=-fx
Заметим, что не всякая функция является четной или нечетной.
График любой нечетной функции симметричен относительно начала координат.
Давай проверим на четность и нечетность функции:
fx=3×4-x2+5
Для этого подставим в нашу функцию вместо переменной х (-х), получим:
f-x=3(-x)4—x2+5=3×4-x2+5
Значит, f-x=fx, следовательно, функция является четной.
fx=x2+x+1
f-x=(-x)2+(-x)+1=x2-x+1
Эта функция является ни четной, ни нечетной.
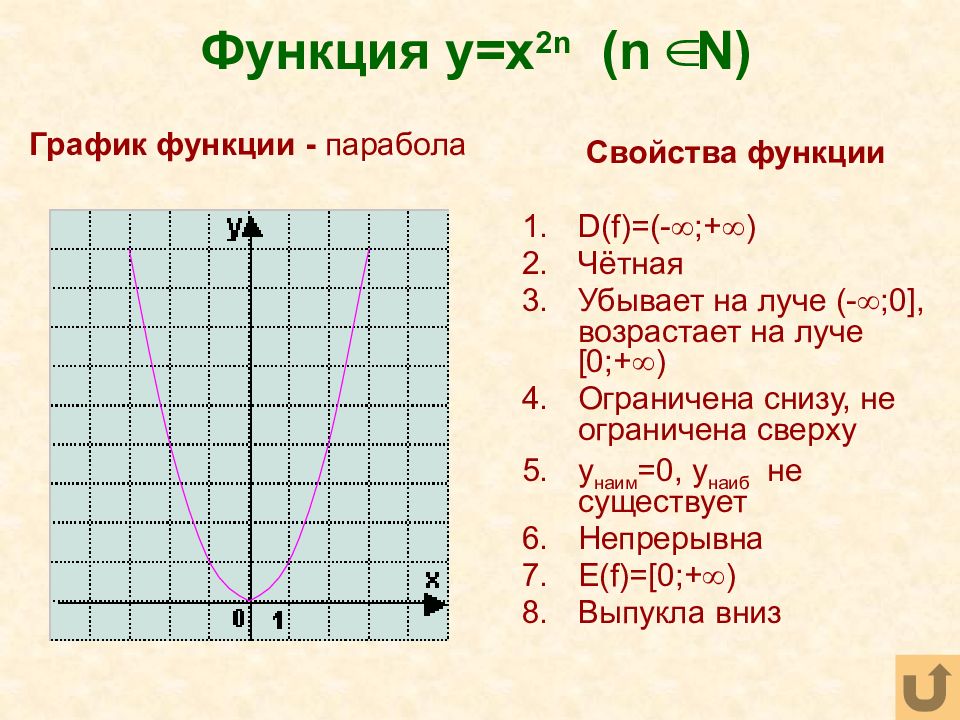
Свойства функции y = x
n при четном n аналогичны свойствам функции y = x2.Степенные функции при n=1, 2 и 3, то есть функции y=x, y = x2, y = x3 тебе уже знакомы. Их свойства и графики нам известны.
Их свойства и графики нам известны.
Выясним теперь свойства степенной функции и особенности ее графика при любом натуральном n.
Рассмотрим случай, когда n – четное число.
Свойства функции y = xn при четном n аналогичны свойствам функции y = x2.
- Выражение xn, где n – натуральное число, имеет смысл при любом x. Поэтому областью определения функции является множество всех действительных чисел.
- Область значений функции есть множество неотрицательных чисел.
- Если х=0, то
- Если Если x ≠ 0, то y > 0. Это следует из того, что четная степень как положительного, так и отрицательного числа положительна. График функции расположен в первой и второй координатных четвертях.
- Функция является четной, график функции симметричен относительно оси ординат.

- Функция возрастает в промежутке 0;+∞) и убывает в промежутке (-∞;0.
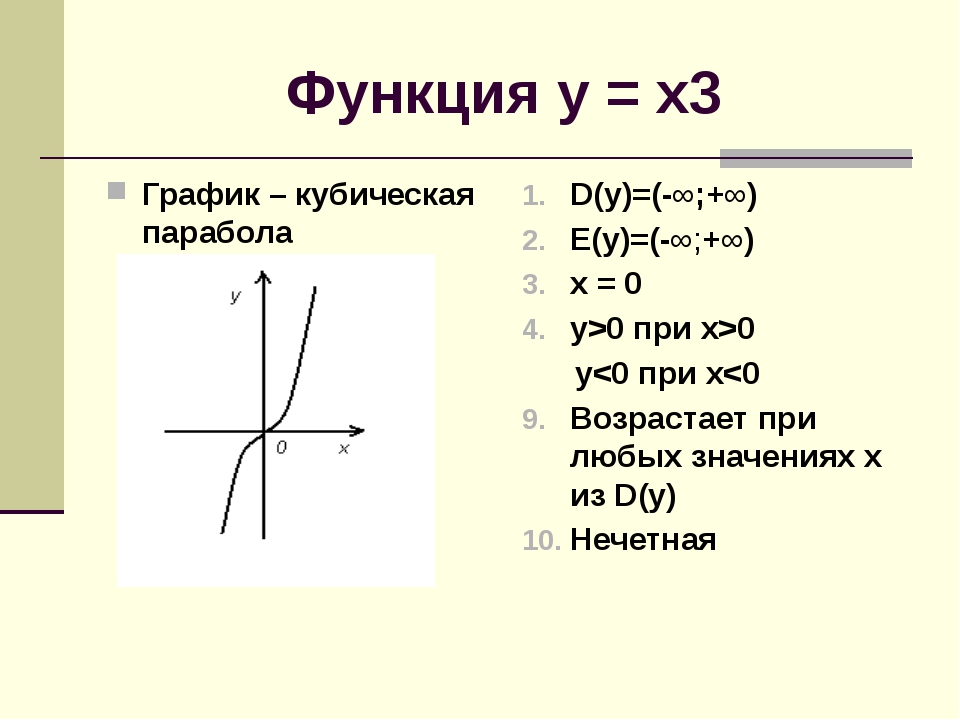
Рассмотрим теперь случай, когда n – нечетное число.
Свойства функции y = xn при нечетном n аналогичны свойствам функции y = x3.
По графику этой функции перечислим ее свойства.
- Выражение xn, где n – натуральное число, имеет смысл при любом x. Поэтому областью определения функции является множество всех действительных чисел.
- Область значений функции есть множество всех действительных чисел.
- Если х=0, то у=0. График функции проходит через начало координат.
- Если x > 0, то y > 0, если x < 0, то y < 0 График функции расположен в первой и третьей координатных четвертях
- Функция является нечетной. График функции симметричен относительно начала координат.
 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
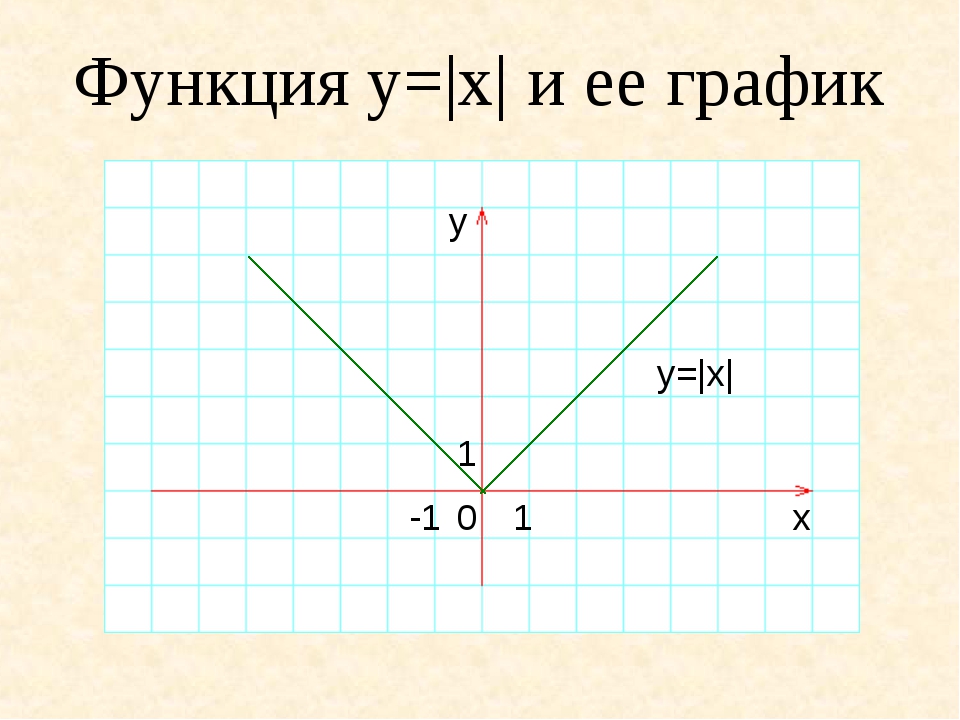
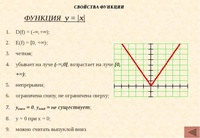
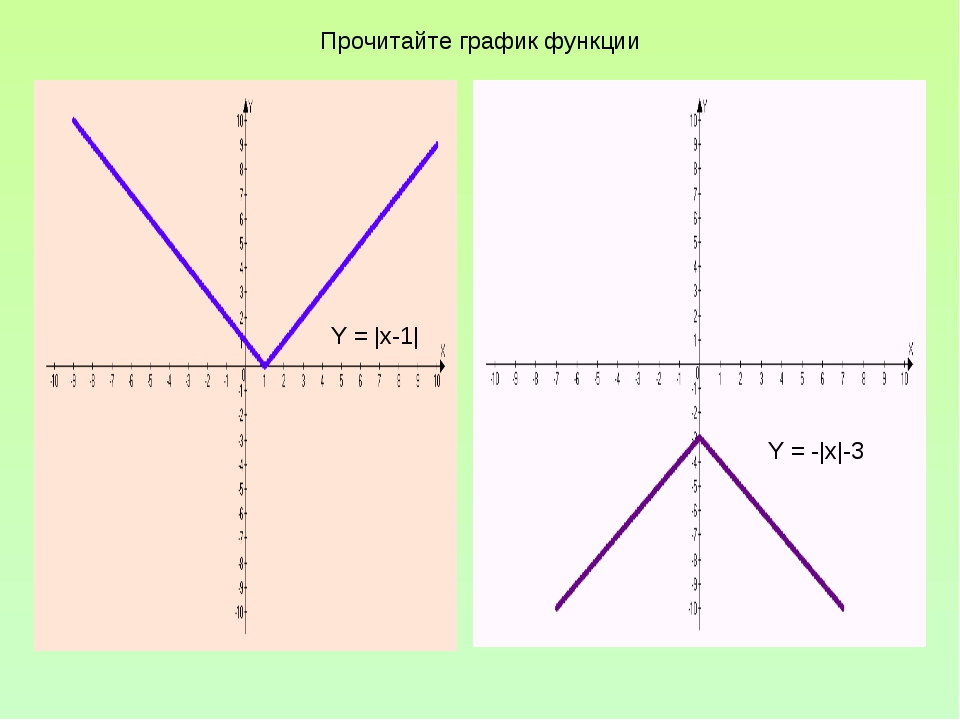
Пример. Построить график функции \(y=\left|x \right|\).Решение. Рассмотрим функцию: \(f\left(x \right)=\left|x \right|\) и подставим вместо \(x \) противоположное \(-x \). В результате не сложных преобразований получим: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части).
 Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Пример. Построить график функции \(y=x\left|x \right|\).Решение. Выполним проверку так же как в предыдущем примере: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right)$$ Это означает, что исходная функция является нечетной (знак функции поменялся на противоположный).
Вывод: функция симметрична относительно начала координат. Можно строить только одн половину, а вторую рисовать симметрично.
 2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.

x −2 −1 0 1 2 3 y −4 −3 −2 −1 0 1 Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy .
 {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0 тогда, когда у функции f(x) , что дифференцируема в точке x_{0} , появится экстремум в этой точке.

Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Tesla отзовет более 570 000 автомобилей в США из-за проблем со звуковой системой
Американский производитель электрокаров Tesla отзовет 578 607 автомобилей из-за возможной проблемы со звуковой системой, сообщает Reuters со ссылкой на отчет Национального управления безопасности дорожного движения (NHTSA) США.

Отзыву подлежат некоторые автомобили Model S, Model X и Model Y 2020-2022 гг. выпуска и Model 3 2017-2022 гг. «Функция Boombox позволяет воспроизводить звук через внешний динамик во время движения автомобиля, она может заглушать звуки системы предупреждения о пешеходах», — говорится в отчете регулятора. Эксперты NHTSA также заявили, что транспортные средства с такой функцией не соответствуют федеральному стандарту безопасности транспортных средств, в котором обозначены минимальные требования к звуку для электромобилей. В компании в свою очередь пообещали усовершенствовать функцию и обновить программное обеспечение, однако им неизвестно о каких-либо авариях или травмах, связанных с этой проблемой.
Tesla впервые представила Boombox в декабре 2020 г. В январе 2021 г. регулятор отправил несколько информационных запросов производителю, после чего состоялся ряд виртуальных совещаний. В октябре того же года Tesla предоставила регулятору дополнительную информацию и результаты тестирований, чтобы обосновать использование Boombox в своих электрокарах.

Это уже четвертый отзыв автомобилей Tesla в США в 2022 г. В начале января компания обязалась отозвать 53 822 автомобиля из-за ошибки в программе автономного вождения. Тогда отзыву подлежали некоторые автомобили марок Model S и Model X 2016-2022 гг. выпуска, Model 3 2017-2022 гг. выпуска и Model Y 2020-2022 гг. Второй раз компания обещала отозвать 817 000 автомобилей из-за проблемы со срабатыванием звукового сигнала, оповещающего о непристегнутом ремне безопасности. Это коснулось электрокаров Model S и Model X выпуска 2021-2022 гг., Model 3 2017-2022 гг. и Model Y 2020-2022 гг. 9 февраля стало известно, что производитель отзовет еще 26 681 автомобиль из-за возможной проблемы с обогревом лобового стекла. Это коснется некоторых автомобилей Model S и Model Y 2020-2022 гг. выпуска, Model 3 2021-2022 гг. и Model X 2021-2022 гг. выпуска. По подсчетам NHTSA, за последние четыре месяца Tesla отзовет около 1,5 млн автомобилей в США.
Если f(x,y,z) = z•х+у и рекурсия проводится по переменной z, то функция h(х,у,z,m) равна
Дедуктивные рассуждения преобладают в науках, которые принято называть
(*ответ*) точными
гуманитарными
естественно–научными
техническими
Для вещественныех чисел x,y,z утверждению х Î[y,z] эквивалентна запись
(*ответ*) $t (x+t=z) Ù (y+t=x)
«t (x+t=z) Ù (y+t=x)
$t (x+t=z) Ú (y+t=x)
$t (y+t=z) Ù (y+t=x)
Для вещественныех чисел x,y,z утверждению х £y эквивалентна запись
(*ответ*) $z (x+z=y)
«z (x+z=y)
$z (y+z=x)
«x (x+z=y)
Для обозначения какой–либо связи между предметами или понятиями используется математический термин, который называется
(*ответ*) отношением
суждением
выражением
выводом
Для однозначной записи алгоритмов существует формализованный язык, который называется языком
(*ответ*) алгоритмическим
метаязыком
регулярным
автоматным
Для присвоения, хранения, обработки и передачи информации используется способ обозначения определенного понятия, предмета, свойства, который называется
(*ответ*) языком
словом
списком
выражением
Единственным неопределимым отношением в системе арифметики натуральных чисел Пеано является
(*ответ*) y = x/
у ÷ x
у + х
у – х
Если f(n) = cos(pn), то функция h(n,m) в рекуррентной формуле равна
(*ответ*) –m
sin(pn)
1– cos(pn)
m+1
Если f(n)=n!, то функция h(n,m) в рекуррентной формуле равна
(*ответ*) m(n+1)
m+1
m+n+1
m!
Если f(x,y) = х + у и рекурсия проводится по переменной y, то функция h(х,у,m) равна
(*ответ*) m+1
m+у
m+x
2+m
Если f(x,y) = х • у и рекурсия проводится по переменной x, то функция h(x,y,m) равна
(*ответ*) m+y
1
m+x
х + у
Если f(x,y) = х+у и рекурсия проводится по переменной у, то функция g(x) равна
(*ответ*) x
2x
x+1
x+2
Если f(x,y,z) = z•х+у и рекурсия проводится по переменной z, то функция h(х,у,z,m) равна
(*ответ*) m+x
mx
my
m+х+у+zTesla отзывает более 578 тыс.
 машин из-за проблем со звуковым оповещением пешеходов
машин из-за проблем со звуковым оповещением пешеходовФото из архива
10 февраля, Минск /Корр. БЕЛТА/. Tesla отзовет более 578 тыс. своих электромобилей из-за проблем с функцией Boombox, которая мешает работе так называемой системы предупреждения пешеходов. Об этом сообщает ТАСС со ссылкой на документы, обнародованные Национальным управлением дорожной безопасности США.
Отзываются Model S, Model X, Model 3 и Model Y 2017-2022 годов выпуска.
 Как установили в управлении, функция Boombox, позволяющая воспроизводить мелодии через внешний динамик этих автомобилей во время движения, может заглушать звуки системы предупреждения пешеходов.
Как установили в управлении, функция Boombox, позволяющая воспроизводить мелодии через внешний динамик этих автомобилей во время движения, может заглушать звуки системы предупреждения пешеходов.Ранее американский регулятор начал проверку в отношении Boombox на предмет ее соответствия стандартам безопасности. Tesla будет обязана обновить программное обеспечение своих автомобилей, чтобы принудительно отключить возможность использовать функцию во время движения.
Согласно информации на сайте автопроизводителя, система оповещения пешеходов встроена в указанные модели электрокаров и заставляет их издавать определенный звук при движении со скоростью ниже 24 км/ч. Этот звук служит оповещением для пешеходов о приближении автомобиля, что позволяет избежать столкновений.-0-
Таблица функций (2 переменные) Калькулятор
- Цель использования
- определить, является ли y функция от x и если функция взаимно однозначна.

[1] 2022/02/07 06:43 Младше 20 лет / Высшая школа/ Университет/ Аспирант / Очень /
- Цель использования
- Я пытался выяснить, linear
xy
—
00
11
24
[2] 20.11.2021 10:34 Младше 20 лет / Начальная школа/ Учащийся средней школы / Совсем нет /
- 0 Назначение использования Чтобы создать функцию для скрипта python, где он обратно отсчитывал вниз или вверх в каждом столбце по строкам.
- Комментарий/Запрос
- Очень полезно, спасибо!
[3] 2021/09/30 02:34 20-летний уровень / Офисный работник / Государственный служащий / Очень /4
- Цель использования
- попытка найти функцию с помощью таблицы без уравнения
[4] 2021/09/09 09:32 Младше 20 лет / Старшая школа/ Университет/ Аспирант / Немного /
- Назначение
- Функция Назначение
[5] 2021/08/16 19:58 До 20 лет / Высшая школа/ Университет/ Аспирант / Очень /
- Цель использования
- Мне нужно было быстро найти шаблон для [более сложных] линейных функций, чтобы работать с уравнением быстрее/больше точно
- Комментарий/Запрос
- что-то более четкое
[6] 07/2021 02 18:54 Младше 20 лет / Старшая школа/ Университет/ Аспирант / Вовсе нет /
- Назначение
- Чтобы найти необходимое уравнение с таблицей
- Комментарий/Запрос st
- Направления должны быть более точными, и должно быть больше вариантов, если мы хотим уравнение или что это такое.

[7] 2021/05/03 18:18 Младше 20 лет / Начальная школа / Младший школьник / Совсем нет /
- Цель использования
- Чтобы мои вычисления выполнялись быстрее при выполнении домашних заданий.
[8] 2021/04/27 20:25 Младше 20 лет / Старшая школа / Университет / Аспирант / Совсем нет /
- Назначение
- Для завершения таблицы математических парабол
- Комментарий /Запрос
- Меньше требований к калькулятору, хочу найти у не выражение
[9] 2021/04/25 15:22 Младше 20 лет / Начальная школа/ Ученик младших классов средней школы / Совсем нет /
- Назначение
- Нужна помощь с домашним заданием по математике.
- Комментарий/Запрос
- Необходимо иметь уравнение таблицы функций.
[10] 2021/04/20 17:30 Младше 20 лет / Начальная школа/ Младший школьник / Немного /
Функции
Что такое функция?
А функция это способ борьбы с «Вход» , применяя некоторые «правило» (функция), а затем получить «вывод» .

А функция представляет собой набор упорядоченные пары в котором никакие две различные упорядоченные пары не имеют одинаковых Икс -координата.Уравнение, которое производит такой набор упорядоченных пар, определяет функцию.
В чем подвох? Для каждого входа может быть не более одного выхода. Входные данные, которые имеют «смысл», формируют домен функции, а ответы или выходные данные образуют диапазон .
Обозначение функции
Мы можем назвать ввод Икс , правило ф , а затем вывод ф ( Икс ) , читать » ф из Икс «.
Это НЕ означает » ф раз Икс «, это просто устройство записи для записи ввода и вывода.
Например, найти выход функции ф ( Икс ) знак равно Икс 2 когда ввод, Икс знак равно 3 .

Чтобы найти выходное значение, когда Икс знак равно 3 , заменять 3 за Икс в функции.
ф ( 3 ) знак равно 3 2
3 2 означает 3 раз 3 .
ф ( 3 ) знак равно 3 × 3 знак равно 9
(Примечание: ф ( 3 ) не является ф раз 3 )
Думать о ф ( Икс ) знак равно Икс 2 в виде ф ( ) знак равно ( ) 2 ; таким образом вы можете безопасно вставлять отрицательные числа или даже другие выражения:
ф ( − 5 ) знак равно ( − 5 ) 2 знак равно 25
ф ( Икс + час ) знак равно ( Икс + час ) 2
Функции и отношения
Функция – это особый вид связь .
 Отношение — это просто набор упорядоченных пар
(
Икс
,
у
)
. На формальном математическом языке функция — это отношение, для которого:
Отношение — это просто набор упорядоченных пар
(
Икс
,
у
)
. На формальном математическом языке функция — это отношение, для которого:если ( Икс 1 , у ) и ( Икс 2 , у ) оба находятся в отношении, то Икс 1 знак равно Икс 2 .
Это просто говорит о том, что в функции не может быть двух упорядоченных пар с одинаковыми Икс -значение, но другое у -ценности.
Если у вас есть график отношения, вы можете использовать тест вертикальной линии выяснить, является ли отношение функцией.
Создание точечной диаграммы xy в Microsoft Excel и OpenOffice.org Calc 2.0
Создание точечной диаграммы xy в Microsoft Excel и OpenOffice.org Calc 2. 0
0Создание точечной диаграммы xy в Microsoft Excel
Создание точечной диаграммы xy в OpenOffice.org Calc 2.0Создание точечной диаграммы xy в Microsoft Excel
- Выберите данные и нажмите кнопку мастера построения диаграмм:
- Выберите диаграмму разброса x-y:
- Выберите отделку:
- Щелкните точку на диаграмме, чтобы выделить точки данных:
- Выберите Диаграмму: Добавить линию тренда
- Выберите линейную регрессию, а затем перейдите на вкладку «Параметры»
- Выберите и Отображать уравнение на диаграмме, и Отображать значение R-квадрата на диаграмме (на изображении показан только первый выбранный элемент.
- Результат:
Чтобы получить наклон и точку пересечения в Excel для приведенных выше данных, используйте следующие функции:
= наклон (c2: c8, b2: b8)
= точка пересечения (c2: c8, b2: b8) точка с запятой. В Excel по умолчанию используется запятая, в OpenOffice 2. 0 — точка с запятой. OpenOffice.org 3.0 и 3.1 в Ubuntu 9.04 и 9.10 соответственно используют запятую. В дистрибутивах OpenOffice.org 3.0 и 3.1 для Windows по-прежнему используется точка с запятой.
0 — точка с запятой. OpenOffice.org 3.0 и 3.1 в Ubuntu 9.04 и 9.10 соответственно используют запятую. В дистрибутивах OpenOffice.org 3.0 и 3.1 для Windows по-прежнему используется точка с запятой.Excel 2007 использует разные экраны для получения линейной регрессии.
Создание точечной диаграммы xy в OpenOffice.org Calc 2.0
Следующие инструкции относятся к OpenOffice.org Calc версий 2.0, 2.1 и 2.2. В версии 2.3 мастер диаграмм был изменен. Начиная с версии 2.3, мастер диаграмм не ждет, пока пользователь использует мышь для перетаскивания местоположения диаграммы. Инструкции по использованию версии 2.3 см. в примечаниях к версии 2.4.
- Выберите данные и щелкните мастер диаграмм
- Перетащите, чтобы указать, где должен располагаться график и насколько большим должен быть график
- Нажмите далее
- Выберите диаграмму xy
- В этом курсе лучше всего работает первый вариант
- Выберите «Создать» (можно указать различные заголовки)
- Выберите статистику вставки
- Выберите линейную регрессию, нажмите OK
- На графике будет отображаться линия наилучшего соответствия, но не функция.

Чтобы отобразить наклон и точку пересечения в OpenOffice для вышеуказанных данных, используйте следующие функции:
= наклон (c2: c8; b2: b8)
= точка пересечения (c2: c8; b2: b8) точка с запятой. В Excel по умолчанию используется запятая, в OpenOffice — точка с запятой.Однородные уравнения первого порядка
Однородные уравнения первого порядка
Функция f ( x,y ) называется однородной степени n , если уравнение
справедливо для всех x,y и z (для которых определены обе стороны).
Пример 1 : Функция f ( x,y ) = x 2 + y 2 является однородной степени 2, так как
Пример 2 : Функция является однородной степени 4, так как
Пример 3 : Функция f ( x,y ) = 2 x + y является однородной степени 1, так как
Пример 4 : Функция f ( x,y ) = x 3 – y 2 неоднородна, так как
, который не равен z n f ( x,y ) для любого n .

Пример 5 : Функция f ( x,y ) = x 3 sin ( y/x ) является однородной степени 3, так как
Дифференциальное уравнение первого порядка называется однородным , если M ( x,y ) и N ( x,y ) являются однородными функциями одной и той же степени.
Пример 6 : Дифференциальное уравнение
однородный, потому что оба м ( x, y ) = x 2 2 2 и n ( x, y ) = xy — это однородные функции того же степень (а именно, 2).
Из этого факта следует метод решения однородных уравнений:
Замена y = xu (и, следовательно, dy = xdu + udx ) превращает однородное уравнение в разделимое.
Пример 7Это уравнение является однородным, как видно из примера 6.
 Таким образом, чтобы решить ее, сделайте замены y = xu и dy = x dy + u dx :
Таким образом, чтобы решить ее, сделайте замены y = xu и dy = x dy + u dx :Это последнее уравнение теперь разделимо (что и было задумано). Приступая к решению,
Следовательно, решение разделимого уравнения, включающего x и v , можно записать как
Чтобы получить решение исходного дифференциального уравнения (которое включало переменные x и y ), просто заметьте, что
Замена v на y / x в предыдущем решении дает окончательный результат:
Это общее решение исходного дифференциального уравнения.
Пример 8: Решение IVP
Так как функции
оба однородны степени 1, дифференциальное уравнение однородно. Подстановки y = xv и dy = x dv + v dx преобразуют уравнение в
.
, что упрощается следующим образом:
Теперь уравнение разделимо. Разделение переменных и интегрирование дает
Интеграл левой части вычисляется после разложения на неполные дроби:
Следовательно,
Правая часть (†) сразу интегрируется в
Следовательно, решение разделимого дифференциального уравнения (†) равно
Теперь, заменив v на y / x , вы получите
.как общее решение данного дифференциального уравнения.Применение начального условия y (1) = 0 определяет значение константы c :
Таким образом, частным решением IVP является
, который можно упростить до
как вы можете проверить.
Техническое примечание: на этапе разделения (†) обе части были разделены на ( v + 1)( v + 2), а v = –1 и v = –2 были потеряны как решения .
 Однако их не нужно рассматривать, потому что хотя эквивалентные функции y = – x и y = –2 x действительно удовлетворяют данному дифференциальному уравнению, они несовместимы с начальным условием.
Однако их не нужно рассматривать, потому что хотя эквивалентные функции y = – x и y = –2 x действительно удовлетворяют данному дифференциальному уравнению, они несовместимы с начальным условием.График уравнения
Пример графика функцииКак нарисовать график функции
Во-первых, начните с пустой диаграммы, подобной этой. У него значения x идут слева направо, а значения y идут снизу вверх:
Оси x и y пересекаются с
, где x и y равны нулю.Точки построения
Простой (но не идеальный) подход состоит в том, чтобы вычислить функцию в некоторых точках и затем построить их.
График функции представляет собой набор точек значений, принимаемых функцией.
Пример: у = х
2 — 5Вычислим несколько точек :
х у = х 2 −5 −2 −1 0 −5 1 −4 3 4 И начертите их так:
Пока не очень полезно.
 Добавим еще точек :
Добавим еще точек :Выглядит лучше!
Теперь мы можем предположить, что построение всех точек будет выглядеть так:
Красивая парабола.
Мы должны попытаться нанести достаточно точек, чтобы быть уверенными в том, что происходит!
Пример: у = х
3 — 5хС этими расчетными точками:
х у = х 3 -5х −2 2 0 0 2 −2 Можно подумать, что это график:
Но это реальный график:
Так что «нанесение некоторых точек» полезно, но может привести к ошибкам .Полный график
Чтобы график был «полным», нам нужно показать все важные функции:
- Пункты пересечения
- Пики
- Долины
- Плоские поверхности
- Асимптоты
- Любые другие особенности
Это часто означает тщательное обдумывание функции.

Пример: (x−1)/(x
2 −9)На странице Rational Expressions мы делаем некоторую работу, чтобы обнаружить, что функция:
- пересекает ось x в точке 1,
- пересекает ось Y в точке 1/9,
- имеет вертикальные асимптоты (где оно направлено к минус/плюс бесконечности) при −3 и +3
В результате мы можем сделать этот эскиз:
Набросок (x−1)/(x 2 −9) из Rational Expressions.2=9″ (что означает x 2 +y 2 =9 ).
Но помните, что они только помогают! Это всего лишь компьютерные программы, и мог легко пропустить что-то важное на графике, или не построить что-то правильно.
Примечание: вы можете услышать фразу «удовлетворить уравнению», что означает, что уравнение верно .
БиоМатематика: тригонометрические функции
В этом разделе мы рассмотрим графики шести тригонометрических функций, начиная с графика функции косинуса.
График y = cos x
Чтобы нарисовать график y = cos x , мы можем составить таблицу значений, которые мы можем вычислить точно:
Мы можем нанести эти точки и начертить плавную кривую, проходящую через них:
Поскольку областью определения функции косинуса являются все действительные числа, мы помещаем стрелки на
график, чтобы указать, что график повторяется точно в обоих направлениях.Тот факт, что функция косинуса повторяется, означает, что она является периодической . В
в частности, y = cos x периодично с периодом 2π . Это означает, что если точка
( x , y ) лежит на графике, то точка ( x +2 k π, y ) также будет лежать на графике, где k — любое целое число. Например, ( x + 2π, y ) и ( x — 2π, y ) оба будут лежать на графике.
Например, ( x + 2π, y ) и ( x — 2π, y ) оба будут лежать на графике.
Графики y = sin x
Чтобы нарисовать график y = sin x , мы можем составить таблицу значений, которые мы можем вычислить точно:
Мы можем нанести эти точки и начертить плавную кривую, проходящую через них:
Поскольку областью определения синуса являются все действительные числа, мы помещаем стрелки на график, чтобы указать, что график повторяется точно в обоих направлениях.Нравится функция косинуса, функция синуса также 2π-периодична.
Графики y = tan x
Чтобы нарисовать график y = tan x , мы можем составить таблицу значений, которые мы можем вычислить точно:
Обратите внимание, что теперь у нас есть некоторые неопределенные функциональные значения; графически эти
соответствуют вертикальным асимптотам.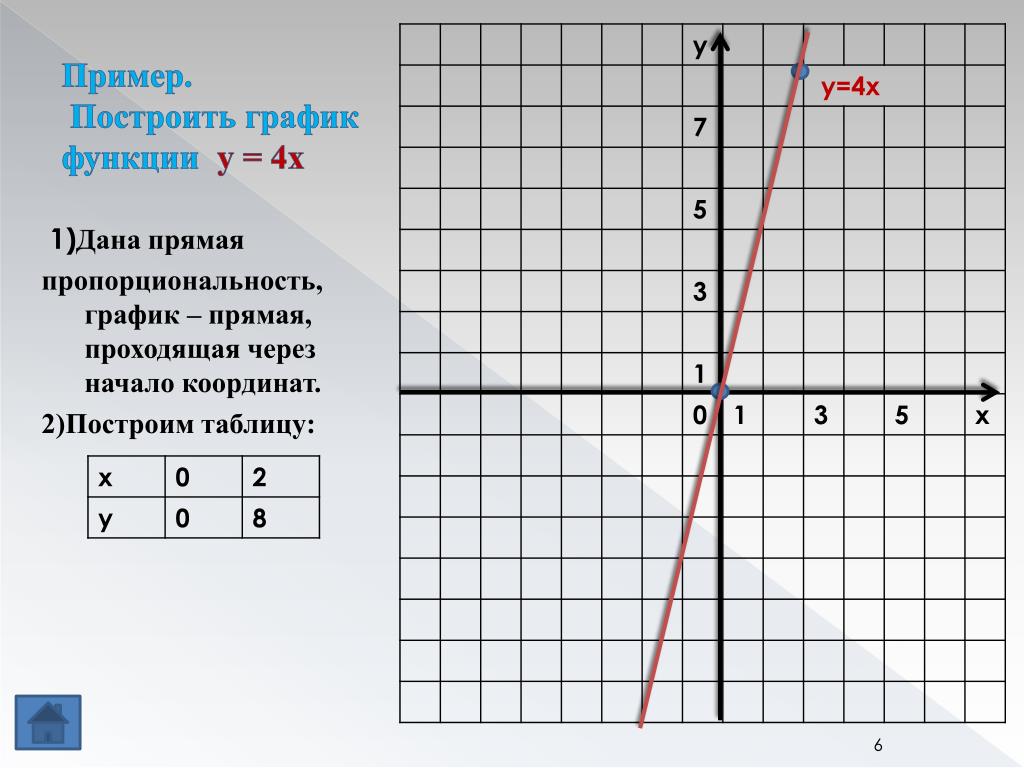 Мы можем сделать набросок y = tan x следующим образом:
Мы можем сделать набросок y = tan x следующим образом:
На приведенном выше графике пунктирные линии обозначают вертикальные асимптоты. Мы размещаем стрелки на графике указывают на то, что функция возрастает до ∞. Например, tan x → ∞ как x → (π/2) — (т. е. когда x приближается к π/2 слева) и тангенс x → −∞, поскольку x → (π/2) — (т.е. поскольку x приближается к π/2 справа). В отличие от синуса и косинуса, тангенс функция является π-периодической. То есть, если точка ( x , y ) лежит на графике y = tan x , то и точка ( x + k π , y 90 ) где любое целое число.
Графика y = sec x , y = csc x, и y = кроватка x
Напомним, что функции секанса, косеканса и котангенса являются обратными функциями косинуса, синуса и тангенса соответственно. Вы вряд ли столкнетесь с этими графиками при изучении наук о жизни. Мы включаем эти графики для полноты.
Вы вряд ли столкнетесь с этими графиками при изучении наук о жизни. Мы включаем эти графики для полноты.
Преобразование y = cos x и y = sin x
Теперь мы рассмотрим графические преобразования y = cos x и y = sin x .Мы можно записать преобразованную функцию косинуса и синуса следующим образом:
y = a cos ( b ( x − d )) + c ,
y = a sin ( b ( x − d )) + c .
Звоним | и | амплитуда функции. Амплитуда – это расстояние от
от минимального функционального значения до максимального функционального значения, деленного на 2. То
период вышеуказанных функций равен 2π/ b (обратите внимание, когда b = 1, период равен 2π). Когда
моделирование определенной величины или явления с использованием функции синуса или косинуса,
амплитуда и период являются двумя важными характеристиками, определяющими поведение. Ты
можно обратиться к разделу преобразований, чтобы изучить другие преобразования
ближе.
То
период вышеуказанных функций равен 2π/ b (обратите внимание, когда b = 1, период равен 2π). Когда
моделирование определенной величины или явления с использованием функции синуса или косинуса,
амплитуда и период являются двумя важными характеристиками, определяющими поведение. Ты
можно обратиться к разделу преобразований, чтобы изучить другие преобразования
ближе.
*****
В следующем разделе мы представим тригонометрические тождества.
Личности
Глава 13. Обратные функции
Глава 13. Обратные функцииГлава 13. Обратные функции
Во второй части этой книги, посвященной
Исчисление, мы посвятим наше исследование другому типу функций,
экспоненциальная функция и ее близкая родственница функция синуса. Прежде чем мы
погрузиться в это сложное и аналитическое исследование, нам сначала нужно
понять кое-что об обратных функциях.
Обратная функция определение функции, выход которой становится входом или зависимым Переменная становится независимой переменной.Например, учитывая функцию:
Что такое Второй закон Ньютона, или сила, действующая на тело массой m, представляет собой функция придаваемое ему ускорение. Мы вольны вводить любое значение a и то, что мы получаем вне сила. Обратная этой силовой функции, согласно определение, даст нам ускорение как функцию Силы. Это делается просто решение для независимой переменной, a:
Теперь я могу позволить F быть чем угодно, а затем найти ускорение как функцию от него.
Обратной функцией f(x) является
обычно пишется как, . Теперь рассмотрим более общий случай построения графика.
функция и обратная ей функция в одних и тех же координатных плоскостях. Учитывая
функция , чтобы вычислить его обратную, нам нужно решить это только для x
получить . Обратите внимание, что мы вообще не изменили функцию,
мы решили только для независимой переменной. График этих двух
функции будут точно такими же. Наше определение обратного
функция
поэтому придется немного изменить.После нахождения обратного
функция
мы просто меняем местами x и y, чтобы получить:
График этих двух
функции будут точно такими же. Наше определение обратного
функция
поэтому придется немного изменить.После нахождения обратного
функция
мы просто меняем местами x и y, чтобы получить:
Что это делает с обратной функцией? Это существенно переворачивает график f (x) вокруг линии y = x так, что для каждый точки (x,y) есть соответствующая точка (y,x) на графике обратный функция. Теперь обе функции можно изобразить в одной плоскости x-y.
Помните, что если мы просто решим для зависимого, мы не меняем уравнение, а просто переписываем его. За по этой причине его график такой же.Поменяв местами x и y, мы получим еще один функция x, отношение которой к f(x) состоит в том, что она была представлена на графике как хотя ось x была осью y и наоборот. Лучше всего мы посмотрим на два графики:
Обратите внимание, как каждый точка (x, y) имеет соответствующую точку (y, x) на обратной функции. То график обратная функция точно такая же, как исходная функция за исключением того, что оси x и y поменялись местами:
Так как каждая точка (x, y) имеет соответствующую точку (y,x), то любую точку y из обратной функции, когда введенный в исходную функцию должен дать x:
Запомнить
функция и ее обратная функция. с х. Как они
связанный
что обратная функция представляет исходную функцию, просто имея
это
зависимая и независимая переменная поменялись местами. Как вы можете видеть из
в
первый график, когда две функции изображены вместе, обратная
функция
содержит все точки (x, y) первой функции, представленные как (y, x)
с участием
за исключением того, что y задается как функция x. По этой причине
с х. Как они
связанный
что обратная функция представляет исходную функцию, просто имея
это
зависимая и независимая переменная поменялись местами. Как вы можете видеть из
в
первый график, когда две функции изображены вместе, обратная
функция
содержит все точки (x, y) первой функции, представленные как (y, x)
с участием
за исключением того, что y задается как функция x. По этой причине
Что такое Важно понимать об обратной функции то, что она получается от найти независимую переменную, а затем заменить ее на y, чтобы создать а функция, которая также является функцией x и может быть изображена на графике вместе с оригинальная функция.
Теперь, когда мы знаем, как работает функция и его обратная функция тесно связана, это приводит нас к вопросу, как производные связаны? Логика подскажет нам, что вместо мы должны просто найти взяв обратная производная. Например, если бы у нас было:
Производная обратной функции может быть:
Или
производная от составляет 1/2x. Но это не так, производная:
Но это не так, производная:
Давайте рассмотрим график f(x) и его обратной функции, чтобы увидеть, что именно происходит на.
Обратите внимание, что в x=2, наклоны не обратны, а обратны только при значениях y на обратную функцию или через (x, f(x)) и (f -1 (f(x)), x). Или точка (3,9) будет иметь обратный наклон в точке (9,3), так как в этой точке x и ты меняются местами, поэтому наклон становится обратным или Это важный момент, чтобы понять о функции и ее обратной, они Только ведут себя как противоположности в точках (a,b) и (b,a). Это означает, что в точке а происходит что-то другое.Тогда возникает вопрос, как мы можем найти производная обратной функции по оси x? Ищу снова по адресу:
Путем замены x с y и y с x в этом последнем выражении мы получаем:
Что у нас есть только что сделано вычисление производной обратной функции только по Ищу на исходную функцию и ее производную. Причина, по которой производная была нет просто обратное значение y=2x было потому, что мы забыли сделать следующие два шагов:
1) Замените x его эквивалентом
выражение через y.
Уклон в следующий график при x=2 наклон равно (2)(2)=4
Путем замены x с участием мы можем найти производная по отношению к же ось x , но вместо этого со значением y .
При y=4 наклон является какой ответ вместо этого мы использовали x=2.
Поскольку обратная функция нарисован в той же плоскости xy, что и , мы можем найти производную обратной функции с относительно оси, взяв обратное выражение а затем замена каждый y с x и наоборот.
Последний выражение является производной функции, обратной по отношению к в ось х.
Подводя итог, можно констатировать следующая теорема:
Чтобы найти производная обратной функции,
1) Помните, обратная функция связана с основной функцией в том смысле, что если вы отразите ее над линией y=x, вы приземлитесь на основную функцию.
2) Первая находка производная f(x)
3) Заменить любой x
в производной с ее y-эквивалентом, чтобы иметь возможность найти
производная с любым заданным значением y.

 3 симметрична относительно начала координат.
3 симметрична относительно начала координат. Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.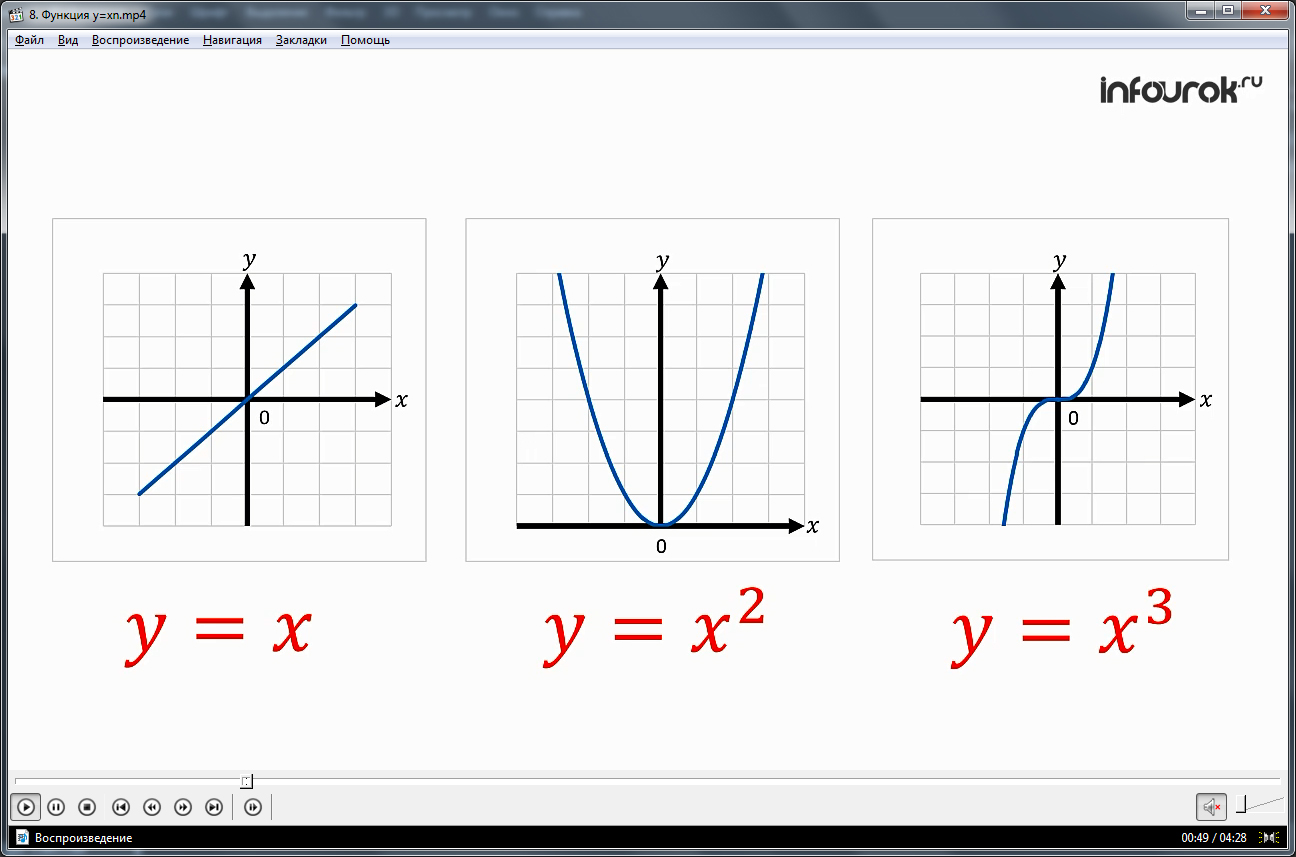 2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
 {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.


 машин из-за проблем со звуковым оповещением пешеходов
машин из-за проблем со звуковым оповещением пешеходов Как установили в управлении, функция Boombox, позволяющая воспроизводить мелодии через внешний динамик этих автомобилей во время движения, может заглушать звуки системы предупреждения пешеходов.
Как установили в управлении, функция Boombox, позволяющая воспроизводить мелодии через внешний динамик этих автомобилей во время движения, может заглушать звуки системы предупреждения пешеходов.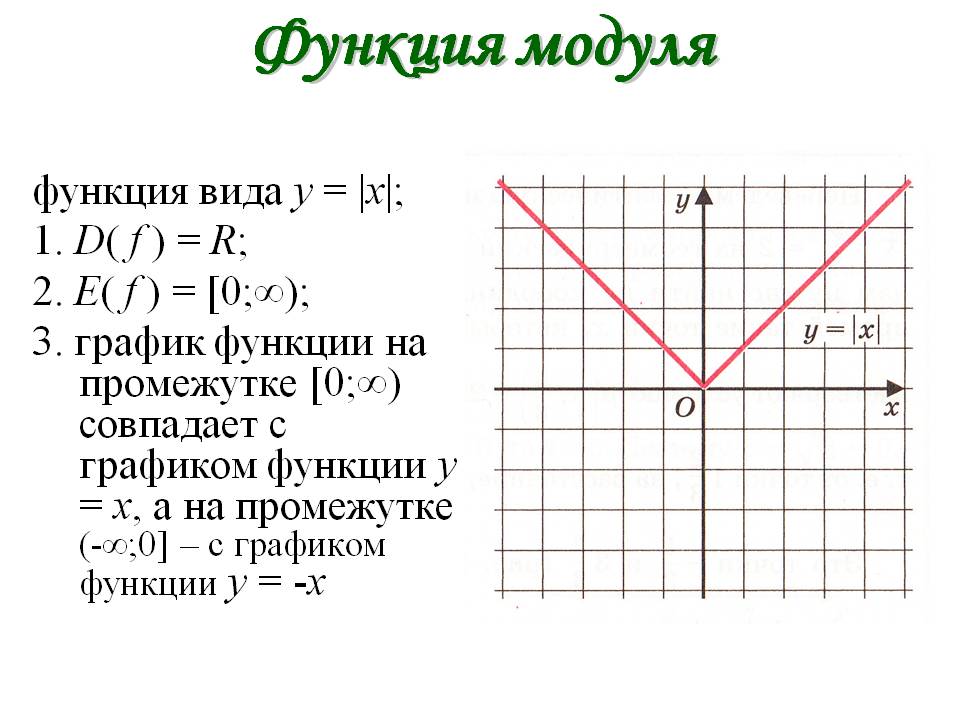


 Отношение — это просто набор упорядоченных пар
(
Икс
,
у
)
. На формальном математическом языке функция — это отношение, для которого:
Отношение — это просто набор упорядоченных пар
(
Икс
,
у
)
. На формальном математическом языке функция — это отношение, для которого: 0
0 0 — точка с запятой. OpenOffice.org 3.0 и 3.1 в Ubuntu 9.04 и 9.10 соответственно используют запятую. В дистрибутивах OpenOffice.org 3.0 и 3.1 для Windows по-прежнему используется точка с запятой.
0 — точка с запятой. OpenOffice.org 3.0 и 3.1 в Ubuntu 9.04 и 9.10 соответственно используют запятую. В дистрибутивах OpenOffice.org 3.0 и 3.1 для Windows по-прежнему используется точка с запятой.
 Таким образом, чтобы решить ее, сделайте замены y = xu и dy = x dy + u dx :
Таким образом, чтобы решить ее, сделайте замены y = xu и dy = x dy + u dx :
 Однако их не нужно рассматривать, потому что хотя эквивалентные функции y = – x и y = –2 x действительно удовлетворяют данному дифференциальному уравнению, они несовместимы с начальным условием.
Однако их не нужно рассматривать, потому что хотя эквивалентные функции y = – x и y = –2 x действительно удовлетворяют данному дифференциальному уравнению, они несовместимы с начальным условием.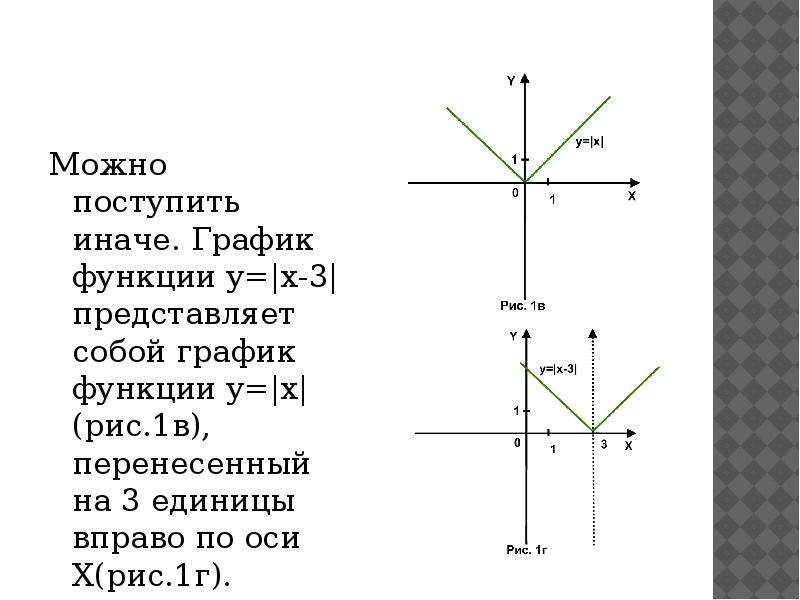 Добавим еще точек :
Добавим еще точек :