Метод математической индукции — это… Что такое Метод математической индукции?
- Метод математической индукции
-

Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:

Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений
 . Допустим, что
. Допустим, что- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все
 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда

 ,
,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Метод лактационной аменореи
- Метод реплик
Смотреть что такое «Метод математической индукции» в других словарях:
Принцип математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
Метод индукции — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Индуктивный метод — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
ГЕНЕТИЧЕСКИЙ МЕТОД — способ задания содержания и сущности исследуемого предмета не путем конвенции, идеализации или логического вывода, а с помощью изучения его происхождения (опираясь на изучение причин, приведших к его возникновению, механизм становления). Широко… … Философия науки: Словарь основных терминов
Аксиоматический метод — способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) аксиомы (См. Аксиома), или Постулаты, из которых все остальные утверждения этой науки (теоремы (См. Теорема)) должны выводиться… … Большая советская энциклопедия
аксиоматический метод — АКСИОМАТИЧЕСКИЙ МЕТОД (от греч. axioma) принятое положение способ построения научной теории, при котором в доказательствах пользуются лишь аксиомами, постулатами и ранее выведенными из них утверждениями. Впервые ярко продемонстрирован… … Энциклопедия эпистемологии и философии науки
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Индуктивное умозаключение — У этого термина существуют и другие значения, см. Индукция. Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки… … Википедия
Математическая индукция — Википедия. Что такое Математическая индукция

Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Формулировка
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: P1,P2,…,Pn,Pn+1,…{\displaystyle P_{1},P_{2},\ldots ,P_{n},P_{n+1},\ldots }.
Допустим, что
Тогда все утверждения нашей последовательности верны. |
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом непустом подмножестве натуральных чисел существует минимальный элемент.
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}}, P3{\displaystyle P_{3}}, …{\displaystyle \ldots }. Если для любого натурального n{\displaystyle n} из того, что истинны все P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}}, P3{\displaystyle P_{3}}, …{\displaystyle \ldots }, Pn−1{\displaystyle P_{n-1}}, следует также истинность Pn{\displaystyle P_{n}}, то все утверждения в этой последовательности истинны, то есть (∀n∈N)((∀i∈{1;…;n−1})Pi⟶Pn)⟶(∀n∈N)Pn{\displaystyle (\forall n\in {\mathbb {N} }){\Big (}(\forall i\in \{1;\dots ;n-1\})P_{i}\longrightarrow P_{n}{\Big )}\longrightarrow (\forall n\in {\mathbb {N} })P_{n}}. |
В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при n=1{\displaystyle n=1} импликация (∀i∈{1;…;n−1})Pi⟶Pn{\displaystyle (\forall i\in \{1;\dots ;n-1\})P_{i}\longrightarrow P_{n}} эквивалентна P1{\displaystyle P_{1}}. Принцип полной математической индукции является прямым применением более сильной трансфинитной индукции.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
История
Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида[1]. Современное название метода было введено де Морганом в 1838 году.
Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
- 1+q+q2+⋯+qn=1−qn+11−q.{\displaystyle 1+q+q^{2}+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}}.}
Доказательство. Индукция по n.
База, n = 1:
- 1+q=(1−q)(1+q)1−q=1−q1+11−q.{\displaystyle 1+q={\frac {(1-q)(1+q)}{1-q}}={\frac {1-q^{1+1}}{1-q}}.}
Переход: предположим, что
- 1+q+⋯+qn=1−qn+11−q,{\displaystyle 1+q+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}},}
тогда
- 1+q+⋯+qn+qn+1=1−qn+11−q+qn+1={\displaystyle 1+q+\cdots +q^{n}+q^{n+1}={\frac {1-q^{n+1}}{1-q}}+q^{n+1}=}
- =1−qn+1+(1−q)qn+11−q=1−qn+1+qn+1−q(n+1)+11−q=1−q(n+1)+11−q{\displaystyle ={\frac {1-q^{n+1}+(1-q)q^{n+1}}{1-q}}={\frac {1-q^{n+1}+q^{n+1}-q^{(n+1)+1}}{1-q}}={\frac {1-q^{(n+1)+1}}{1-q}}},
что и требовалось доказать.
Комментарий: истинность утверждения Pn{\displaystyle P_{n}} в этом доказательстве — то же, что истинность равенства
- 1+q+⋯+qn=1−qn+11−q.{\displaystyle 1+q+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}}.}
Вариации и обобщения
Примечания
- ↑ Nachum L. Rabinovih. Раби Леви бен Гершом и происхождение метода математической индукции = Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — Вып. 6. — С. 237-248.
Литература
Ссылки
- Видео по методу математической индукции
Математическая Индукция — Математическая энциклопедия
Метод доказательства математич. утверждений, основанный на принципе математической индукции: утверждение (х), зависящее от натурального параметра х, считается доказанным, если доказано А(1) и для любого натурального пиз предположения, что верно (п), выведено, что верно также А(n+1). Доказательство утверждения А(1) составляет первый шаг (или базис) индукции, а доказательство А(n+1)в предположении, что верно (п), наз. индукционным переходом. При этом хназ. параметром индукции, а предположение (п).при доказательстве А(n+1) наз. индуктивным предположением. Принцип М. и. является также основанием для индуктивных определений. Простейшим примером такого определения является определение свойства: «быть словом длины n в данном алфавите Базис индукции: каждая буква алфавита (*) есть слово длины 1. Индукционный переход: если Е — слово длины п, то каждое слово Еai, где есть слово длины n+1. Индукция может начинаться с нулевого шага. Часто бывает так, что А(1) и А(n+1) доказываются аналогичными рассуждениями. В таких случаях удобно пользоваться следующей эквивалентной формой принципа М. и. Если для всякого пиз предположения: (х).верно при любом натуральном x<n — следует, что (х).верно также при х=п, то утверждение (х).верно при любом натуральном х. В такой форме принцип М. и. может быть применен для доказательства утверждений (х), в к-рых параметр хпробегает то пли иное множество, вполне упорядоченное по нек-рому трансфинитному типу (трансфинитная индукция). В качестве простых примеров трансфинитной индукции отметим индукцию по параметру, пробегающему множество всех слов в данном алфавите, упорядоченное лексикографически, и индукцию по построению формул в данном логико-математич. исчислении. Иногда для доказательства нек-рого утверждения А(n) индукцией по пприходится одновременно с (п).доказывать индукцией по пряд других утверждений, без к-рых индукцию для (п).не удается провести. В формальной арифметике можно указать такие утверждения (п), для к-рых в рамках рассматриваемого исчисления индукция не может быть проведена без добавления новых вспомогательных утверждений, зависящих от п(см. [3]). В таких случаях мы имеем дело с доказательством ряда утверждений совместной математической индукцией. Все эти утверждения формально можно объединить в одну конъюнкцию, однако практически такое объединение только усложнило бы рассмотрение, т. к. при этом исчезла бы возможность неформальных осмысленных ссылок на определенные индуктивные предположения. В нек-рых конкретных математич. исследованиях число понятий и утверждений, определяемых и доказываемых сложной совместной индукцией, исчисляется трехзначной цифрой (см. [4]). В этом случае ввиду наличия в индуктивном доказательстве большого числа перекрестных ссылок на индуктивные предположения, для содержательного (неформального) понимания любого (даже самого простого) определения или утверждения при данном достаточно большом значении параметра индукции читатель должен быть знаком с содержанием всех вводимых совместной индукцией понятий и многих свойств этих понятий для меньших значений параметра индукции. По-видимому, единственным корректным с логич. точки зрения выходом из возникающего здесь логич. круга является аксиоматич. изложение всей рассматриваемой системы понятий. Таким образом, большое число понятий, определяемых совместной индукцией, приводит к необходимости применения аксиоматического метода в индуктивном определении и доказательстве. Это — наглядный пример необходимости аксиоматич. метода для решения конкретных математич. задач, а не только вопросов, относящихся к основаниям математики. Лит.:[1] Гильберт Д., Б е р н а й с П., Основания математики. Логические исчисления и формализация арифметики, пер. с нем., М., 1979; [2] К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Ц и н м а н Л. Л., «Матем. сб.», 1968, т. 77, №1, с. 71-104; [4] Адян С. И., Проблема Бернсайда и тождества в группах, М., 1975. С. И. Адян.
Источник: Математическая энциклопедия на Gufo.me
Значения в других словарях
- МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ, метод, доказывающий, что математическое утверждение верно для любого положительного целого числа п, если выполняются два условия: 1) оно верно для основной величины, например, 1, и 2) если оно верно для значения k… Научно-технический словарь
- Математическая индукция — Весьма общий способ математических доказательств и определений. Индуктивные доказательства основаны на так называемом принципе М. и., являющемся одной из основных математических аксиом. Большая советская энциклопедия
- МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — общий способ математического доказательства или определения некоторого свойства А для всех натуральных n, основанный на заключении от n к n+1. Большой энциклопедический словарь

Метод математической индукции — это… Что такое Метод математической индукции?
- Метод математической индукции
Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:
Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений . Допустим, что
- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда
- ,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Метод лактационной аменореи
- Метод реплик
Смотреть что такое «Метод математической индукции» в других словарях:
Принцип математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
Метод индукции — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Индуктивный метод — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
ГЕНЕТИЧЕСКИЙ МЕТОД — способ задания содержания и сущности исследуемого предмета не путем конвенции, идеализации или логического вывода, а с помощью изучения его происхождения (опираясь на изучение причин, приведших к его возникновению, механизм становления). Широко… … Философия науки: Словарь основных терминов
Аксиоматический метод — способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) аксиомы (См. Аксиома), или Постулаты, из которых все остальные утверждения этой науки (теоремы (См. Теорема)) должны выводиться… … Большая советская энциклопедия
аксиоматический метод — АКСИОМАТИЧЕСКИЙ МЕТОД (от греч. axioma) принятое положение способ построения научной теории, при котором в доказательствах пользуются лишь аксиомами, постулатами и ранее выведенными из них утверждениями. Впервые ярко продемонстрирован… … Энциклопедия эпистемологии и философии науки
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Индуктивное умозаключение — У этого термина существуют и другие значения, см. Индукция. Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки… … Википедия
Метод математической индукции — это… Что такое Метод математической индукции?
- Метод математической индукции
-

Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:

Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений
 . Допустим, что
. Допустим, что- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все
 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда

 ,
,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Метод лактационной аменореи
- Метод реплик
Смотреть что такое «Метод математической индукции» в других словарях:
Принцип математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
Метод индукции — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Индуктивный метод — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
ГЕНЕТИЧЕСКИЙ МЕТОД — способ задания содержания и сущности исследуемого предмета не путем конвенции, идеализации или логического вывода, а с помощью изучения его происхождения (опираясь на изучение причин, приведших к его возникновению, механизм становления). Широко… … Философия науки: Словарь основных терминов
Аксиоматический метод — способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) аксиомы (См. Аксиома), или Постулаты, из которых все остальные утверждения этой науки (теоремы (См. Теорема)) должны выводиться… … Большая советская энциклопедия
аксиоматический метод — АКСИОМАТИЧЕСКИЙ МЕТОД (от греч. axioma) принятое положение способ построения научной теории, при котором в доказательствах пользуются лишь аксиомами, постулатами и ранее выведенными из них утверждениями. Впервые ярко продемонстрирован… … Энциклопедия эпистемологии и философии науки
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Индуктивное умозаключение — У этого термина существуют и другие значения, см. Индукция. Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки… … Википедия

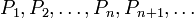
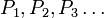 . Допустим, что
. Допустим, что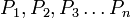 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)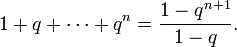
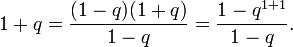
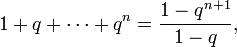
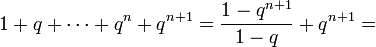
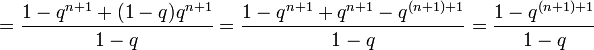 ,
,
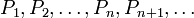
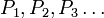 . Допустим, что
. Допустим, что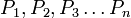 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)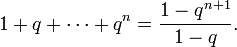
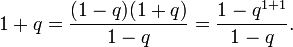
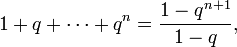
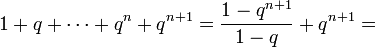
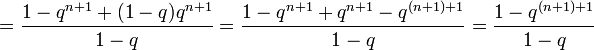 ,
,