Нескучные интегралы / Habr

Некоторые из вас, вероятно, видали на просторах сети эту задачку: какое число продолжает следующий ряд?

Предлагался такой очевидный правильный ответ:

Для тех, кому неочевидно, как он получен, предлагалось объяснение. Пусть (ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке:

Пока всё идёт хорошо, но тут внезапно:

В принципе, этого достаточно, чтобы повеселить друзей-математиков, но мне захотелось узнать, как вообще считаются такие интегралы и почему получается такой смешной результат. Если кому-то ещё охота тряхнуть стариной и вспомнить матан с функаном, прошу читать дальше.

Начинает сказка сказываться

Для начала отдельно посмотрим на первый интеграл:

Некоторое время назад я подумал: «Эй, я ещё не совсем забыл матан! Дайте-ка я возьму этот интеграл как неопределённый, а потом подставлю пределы. Наверняка пару раз по частям, и дело в шляпе. Вот сейчас на бумажке всё решу без посторонней помощи». Хочу предостеречь вас: не повторяйте моей ошибки. Вас ждёт бессонная ночь, а потом вы заглянете в справочник и узнаете, что неопределённый интеграл не берётся в элементарных функциях. Для него даже специальную функцию ввели.

Однако с данными конкретными пределами взять интеграл можно разными способами. Мы пойдём путём, который требует минимум базовых знаний (самое суровое — то же интегрирование по частям). Для начала сделаем внезапную замену:

Вы спросите: откуда вообще это взялось и зачем нам ещё один интеграл, мало что ли? Спокойно, так надо (знакомые со свойствами преобразования Лапласа весело ухмыляются). Подставим замену в исходную формулу и поменяем порядок интегрирования:

Внутри получился почти классический интеграл по dx, которым всех пугали у нас в физматшколе. Его можно взять и как неопределённый, дважды использовав формулу интегрирования по частям. Тогда справа получится какая-то муть и ещё раз тот же самый интеграл, домноженный на что-то, и в результате можно будет решить уравнение относительно этого интеграла и получить ответ, а потом подставить пределы. Кому интересно, проделайте это сами, а я лениво запишу готовый результат:

Ну а теперь совсем всё просто: это табличный интеграл из средней школы, который равен арктангенсу. В бесконечности пи-пополам, в нуле — ноль, вот мы и получили ответ.
Интеграл, кстати, настолько хорош, что у него есть своё имя — интеграл Дирихле. По ссылке вы можете найти другие способы взять его.

Скоро сказка сказывается, а не скоро дело делается

Для следующего путешествия нам понадобятся четыре вещи: прямоугольная функция, косинусное преобразование Фурье, свёртка и теорема Парсеваля. Сперва скажу пару слов об этих замечательных штуках.

Прямоугольная функция — это у нас будет такая ступенька вокруг нуля:

Значение 1/2 в точках разрыва нужно в основном для соблюдения свойств преобразования Фурье, в целом для нашей задачи оно непринципиально.

Косинусное преобразование Фурье

. Для простоты мы немного отступим от математической точности и сформулируем грубовато. Для достаточно хорошей чётной функции f(x) выполняются такие соотношения:

Функция и называется косинусным преобразованием Фурье (FCT) от f(x) (её ещё называют образом f). То есть, косинусное преобразование от косинусного преобразования даёт снова исходную функцию f(x)!

Людям, знакомым с обработкой сигналов, хорошо известно, что FCT от прямоугольной функции — это . Это легко доказать, пользуясь вышеприведёнными формулами и школьными знаниями. Так как прямоугольная функция за пределами промежутка [-a, a] равна нулю, то можно просто интегрировать cos(xt) dt по этому промежутку, тут простая замена переменной и табличный интеграл. Приведённое выше свойство говорит, что FCT от — это прямоугольная функция.

Свёртка — это ещё одна прекрасная штука, без которой не обходится обработка сигналов. Для двух функций f₁(x) и f₂(x) можно определить функцию-свёртку (обозначается звёздочкой) вот так:

У свёртки есть прекрасное свойство, за которое её любят: преобразование Фурье превращает её в умножение, а умножение — в свёртку. Если точнее, косинусное преобразование произведения двух хороших чётных функций есть свёртка их образов, делённая на корень из двух пи: .

Теорема Парсеваля — это очень крутое утверждение о равенстве энергии сигнала и его спектра, которое записывают по-разному в разных целях. Нам потребуется такая версия: для чётных и достаточно хороших функций .

Доселева Макар огороды копал, а нынече Макар в воеводы попал

Возьмём второй интеграл из нашей чудесной последовательности. Как многие уже догадались, мы воспользуемся теоремой Парсеваля и заменим множители на их FCT-образы:

Первая прямоугольная функция под интегралом равна единице для аргументов меньше единицы и нулю для аргументов больше единицы. Поэтому ничто нам не мешает убрать её из интеграла, откорректировав пределы интегрирования:

Под интегралом осталась ступенька высотой 3 и шириной 1/3. Такой интеграл возьмёт даже третьеклассник: надо всего лишь умножить 3 и 1/3. От интеграла остаётся единица, и мы имеем искомое пи-пополам! Таким образом мы почти честно взяли второй интеграл из ряда. Кто желает сделать это совсем честно, тому придётся разобраться, что же такое хорошесть функции, и доказать, что наши функции хорошие.

Чтобы дальше было проще, обозначим эту ступеньку под интегралом как F₁(x) и нарисуем её график:

Пойдём веселиться дальше и посмотрим на интеграл с тремя множителями. Чтобы применить теорему Парсеваля, мы теперь все множители со второго будем считать одним множителем: . С образом первого множителя всё уже понятно, а образ второго множителя, выражается через свёртку:

На первый взгляд жутковато. Но можно кое-чего повыносить, кое-чего посокращать и подставить нашу F₁(x). Тогда получим:

Внутренний интеграл — это просто прямоугольный фильтр, эдакий «блюр» для функции

F₁(x): мы просто для каждой точки усредняем все значения в окрестности плюс-минус одна пятая. Можно опять же избавиться от прямоугольной функции, подшаманив пределы интегрирования. И со внешним интегралом сделаем такую же процедуру. Вот что получится в итоге:


Слева график функции F₂(x), которая на самом деле — сглаженная F₁(x). Нетрудно доказать, что после сглаживания функции по нормированному ядру её интеграл не меняется. Ну, вообще-то речь об интеграле от -∞ до +∞, но для чётной функции это верно и для интеграла от нуля. В данном случае ядром была ступенька от -1/5 до +1/5, умноженная на 5/2. Площадь под ступенькой единица, значит, ядро нормировано. Тут тоже можно сравнить с блюром в фотошопе: после применения блюра картинка в целом не становится светлее или темнее. А раз так, то интеграл F₂(x) в точности равен интегралу F₁(x), то есть единице, поэтому и третий интеграл равен пи-пополам!

Дальше процедура во многом похожая. Четвёртый интеграл сгруппируем так: . Сначала теорему Парсеваля, для скобок свёртку, причём мы уже умеем выразить образ внутренней скобки через F₂(x). Дальше всё то же самое, что в прошлый раз, и в результате получим:

Теперь мы уже имеем F₃(x), которая на самом деле — сглаженная F₂(x) с ядром шириной 2/7. Ядро нормировано, значит, интеграл F₃(x) равен интегралу F₂(x), то есть единице, и мы снова имеем пи-пополам!

Отлично, мы теперь щёлкаем эти интегралы как орехи. Но по идее, если так и дальше пойдёт, они все до бесконечности будут равны пи-пополам? Давайте смотреть дальше. Пятый интеграл:

Вроде всё то же самое. Ладно, шестой интеграл:

И здесь никаких проблем. Хорошо, берём седьмой:

Ничего нового! Ладно, а восьмой?

Стоп-стоп-стоп! Здесь нам не обойтись без команды CSI!

Функция протекла через единицу! Интеграл F₇(x) всё ещё равен единице, но это если интегрировать от 0 до ∞. А мы-то интегрируем до единицы! До сих пор все функции были нулевыми при x больше единицы, но рано или поздно это должно было кончиться.

А как понять, когда наступает конец? Это очень просто. F₁(x) была ненулевой при x<1/3. F₂(x) сглаживала её по ±1/5, значит, была ненулевой при x<1/3+1/5. Аналогичным образом можно найти границу ненулевых значений для всех этих функций, и для F₇(x) эта граница впервые превышает единицу:

Несложно даже посчитать, сколько конкретно утекло, и тем самым вычислить точное значение восьмого интеграла. Заметим, что слева от границы F₁(x) — это константа 3. F₂(x) — минус интеграл этой константы с коэффициентом 5/2, то есть прямая с коэффициентом 3×5/2. F₃(x) в достаточной близости к границе 1/3+1/5+1/7 — это интеграл той прямой с коэффициентом 7/2, то есть что-то вроде . Продолжая аналогичные рассуждения, получим формулу для

F₇(x) в окрестности границы:

Собственно, обычная парабола шестой степени, сдвинутая и домноженная. Если проинтегрировать её от единицы и до границы 1/3+1/5+1/7+1/9+1/11+1/13+1/15, то мы узнаем, сколько функции утекло за пределы единицы. Можно решить эту задачу целиком в обыкновенных дробях. Получится вот сколько:

Если эту цифру вычесть из единицы и домножить на пи-пополам, мы получим окончательное значение восьмого интеграла:

Такие интегралы называются борвейновскими интегралами в честь Давида и Джонатана Борвейнов, которые их описали. Если вы хотите строгие математические доказательства (без всяких «хороших функций») и другие свойства этих замечательных интегралов, почитайте статью авторов.

Заключение: троллинг восьмидесятого уровня

Открыв эти интегралы, Джонатан Борвейн ввёл их в программный пакет Maple и, убедившись, что Maple корректно берёт все восемь интегралов, сообщил разработчикам о «баге»: мол, восьмой интеграл тоже должен быть пи-пополам, а у вас получается чёрт-те-что. Три дня и три ночи убил Жак Каретт, один из разработчиков Maple, в поисках ошибки, пока не понял, что над ним жестоко пошутили. А ещё говорят, что математики — скучные люди!

habr.com

Интеграл от дроби, все формулы и примеры

Нужно запомнить, что интеграл от дроби не равен интегралу числителя, деленному на интеграл знаменателя:

   

Для интегрирования подобных выражений существует несколько методов, которые зависят от вида подынтегральной функции.

Первый метод вычисления интеграла от дроби

Подынтегральная функция является отношением двух многочленов и представляет собою неправильную дробь (степень числителя больше или равна степени знаменателя). Тогда нужно выделить целую часть, для этого в числителе либо нужно выделить выражение, стоящее в знаменателе, либо поделить числитель на знаменатель в столбик.

Замечание. Если степень многочлена, стоящего в числителе, большее степени многочлена, стоящего в знаменателе, то рациональнее для выделения целой части делить числитель на знаменатель в столбик.

Второй метод

Для дробей типа

   

применяется метод замены переменной или заданный интеграл сводится к табличным.

Третий метод вычисления интеграла от дроби

Интегралы вида

   

находятся с помощью выделения полного квадрата в знаменателе, что позволит свести их к табличным интегралам.

Четвертый метод

Для интегралов вида

   

применяется следующий подход. В числителе выделяется производная знаменателя, далее дробь почленно делится: получаем сумму двух интегралов, в числителе одного из них стоит производная знаменателя, а второго – константа. Первый из интегралов находится методом замены, метод нахождения второго описан выше.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Что такое интеграл? Интегралы с подробным решением. Таблица интегралов :: SYL.ru

Слово «интеграл» происходит от латинского integralis – целостный. Это название предложил в 17 в. ученик великого Лейбница (и также выдающийся математик) И. Бернулли. А что такое интеграл в современном понимании? Ниже мы постараемся дать всесторонний ответ на этот вопрос.

Исторические предпосылки возникновения понятия интеграла

В начале 17 в. в рассмотрении ведущих ученых находилось большое число физических (прежде всего механических) задач, в которых нужно было исследовать зависимости одних величин от других. Самыми наглядными и насущными проблемами были определение мгновенной скорости неравномерного движения тела в любой момент времени и обратная этой задача нахождения величины пути, пройденного телом за определенный промежуток времени при таком движении. Сегодня мы уже знаем, что такое интеграл от скорости движения – это и есть пройденный путь. Но понимание того, как его вычислять, зная скорость в каждый момент времени, появилось не сразу.

Поначалу из рассмотрения таких зависимостей физических величин, например, пути от скорости, было сформировано математическое понятие функции y = f(x). Исследование свойств различных функций привело к зарождению математического анализа. Ученые активно искали способы изучения свойств различных функций.

Как возникло вычисление интегралов и производных?

После создания Декартом основ аналитической геометрии и появления возможности изображать функциональные зависимости графически в осях декартовой системы координат, перед исследователями встали две крупные новые задачи: как провести касательную к кривой линии в любой ее точке и как найти площадь фигуры, ограниченной сверху этой кривой и прямыми, параллельными осям координат. Неожиданным образом оказалось, что первая из них эквивалентна нахождению мгновенной скорости, а вторая – нахождению пройденного пути. Ведь он при неравномерном движении изображался в декартовых осях координат «расстояние» и «время» некоторой кривой линией.

Гением Лейбница и Ньютона в середине 17 в. были созданы методы, позволившие решать обе эти задачи. Оказалось, что для проведения касательной к кривой в точке нужно найти величину так называемой производной от функции, описывающей эту кривую, в рассматриваемой ее точке, и эта величина оказывается равной скорости изменения функции, т. е. применительно к зависимости «путь от скорости» собственно мгновенной скоростью тела.

Для нахождения же площади, ограниченной кривой линией, следовало вычислить определенный интеграл, который давал ее точную величину. Производная и интеграл – основные понятия дифференциального и интегрального исчисления, являющихся базисом современного матанализа – важнейшего раздела высшей математики.

Площадь под кривой линией

Итак, как же определить ее точную величину? Попробуем раскрыть процесс ее вычисления через интеграл подробно, с самых азов.

Пусть f является непрерывной на отрезке [ab] функцией. Рассмотрим кривую у = f(x), изображенную на рисунке ниже. Как найти площадь области, ограниченной кривой ), осью х, и линиями х = а и х = b? То есть площадь заштрихованной фигуры на рисунке.

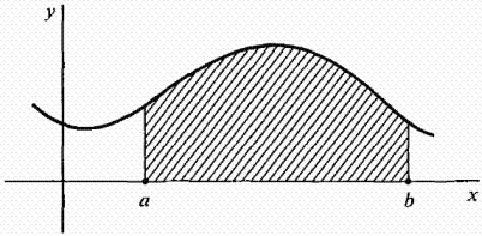
Самый простой случай, когда f является постоянной функцией; то есть, кривая есть горизонтальная линия f(X) = k, где k постоянная и k ≥ 0, как показано на рисунке ниже.

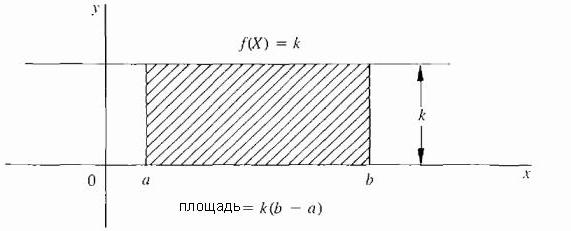В этом случае область под кривой — всего лишь прямоугольник с высотой k и шириной (b – a), так что площадь определяется как: k · (b — а).

Области некоторых других простых фигур, таких как треугольник, трапеция и полуокружность, даются формулами из планиметрии.

Площадь под любой непрерывной кривой у = f(х) дается определенным интегралом, который записывается так же, как обычный интеграл.

Риманова сумма

Прежде чем погрузиться в подробный ответ на вопрос, что такое интеграл, выделим некоторые основные идеи.

Во-первых, область под кривой делится на некоторое число n вертикальных полос достаточно малой ширины Δx. Далее каждая вертикальная полоса заменяется вертикальным прямоугольником высотой f(х), шириной Δx, и площадью f(х)dx. Следующим шагом является формирование суммы площадей всех этих прямоугольников, называемой Римановой суммой (смотрите рисунки ниже).

Рисуя наши прямоугольники шириной Δx, мы можем брать их высоту, равную значению функции на левом краю каждой полоски, т. е. на кривой будут лежать крайние левые точки их верхних коротких сторон шириной Δx. При этом на участке, где функция растет, и ее кривая является выпуклой, все прямоугольники оказываются ниже этой кривой, т. е. их сумма будет заведомо меньшей точной величины площади под кривой на этом участке (см. рисунок ниже). Такой способ аппроксимации называется левосторонним.

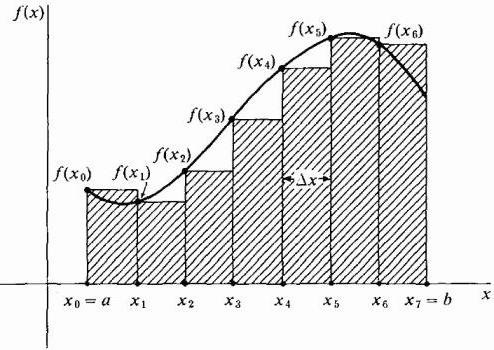
В принципе, можно нарисовать аппроксимирующие прямоугольники таким образом, чтобы на кривой лежали крайние правые точки их верхних коротких сторон шириной Δx. Тогда они будут выше кривой, и приближение площади на этом участке окажется больше ее точной величины, как показано на рисунке ниже. Этот способ носит название правостороннего.

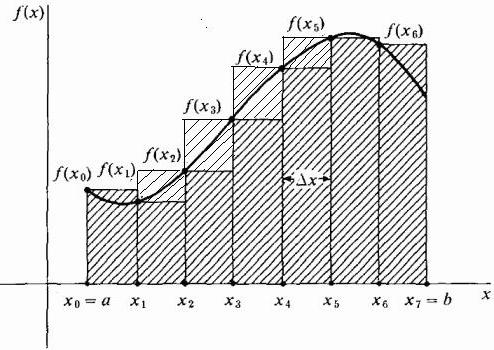
Но мы можем также взять высоту каждого из аппроксимирующих прямоугольников, равной просто некоторому значению функции в произвольной точке x*_i внутри соответствующей полоски Δx_i (смотри рис. ниже). При этом мы даже можем не брать одинаковую ширину всех полосок.

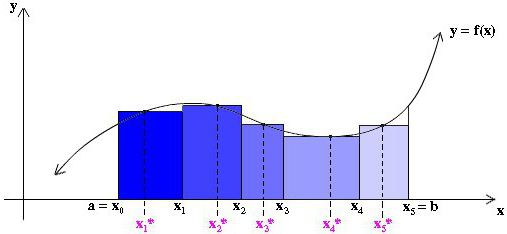
Составим Риманову сумму:

Переход от Римановой суммы к определенному интегралу

В высшей математике доказывается теорема, которая гласит, что если при неограниченном возрастании числа n аппроксимирующих прямоугольников наибольшая их ширина стремится к нулю, то Риманова сумма A_n стремится к некоторому пределу A. Число A – одно и то же при любом способе образования аппроксимирующих прямоугольников и при любом выборе точек x*_i.

Наглядное пояснение теоремы дает рисунок ниже.

Из него видно, что, чем уже прямоугольники, тем ближе площадь ступенчатой фигуры к площади под кривой. При числе прямоугольников n→∞ их ширина Δx_i→0, а предел A суммы A_n численно равен искомой площади. Этот предел и есть определенный интеграл функции f (х):

Символ интеграла, представляющий собой видоизмененную курсивную литеру S, был введен Лейбницем. Ставить сверху и снизу обозначения интеграла его пределы предложил Ж. Б. Фурье. При этом ясно указывается начальное и конечное значение x.

Геометрическое и механическое истолкование определенного интеграла

Попробуем дать развернутый ответ на вопрос о том, что такое интеграл? Рассмотрим интеграл на отрезке [a,b] от положительной внутри него функции f(х), причем считаем, что верхний предел больше нижнего a<b. Как мы уже видели выше, в этом случае площадь, находящаяся между графиком y= f(х) и осью абсцисс в пределах отрезка [a,b], численно равна интегралу от a до b.

Если ординаты функции f(х) отрицательны внутри [a,b], то абсолютное значение интеграла равно площади между осью абсцисс и графиком y=f(х), сам же интеграл отрицателен.

В случае же однократного или неоднократного пересечения графиком y=f(х) оси абсцисс на отрезке [a,b], как показано на рисунке ниже, для вычисления интеграла нужно определить разность, в которой уменьшаемое будет равно суммарной площади участков, находящихся над осью абсцисс, а вычитаемое – суммарной площади участков, находящихся под ней.

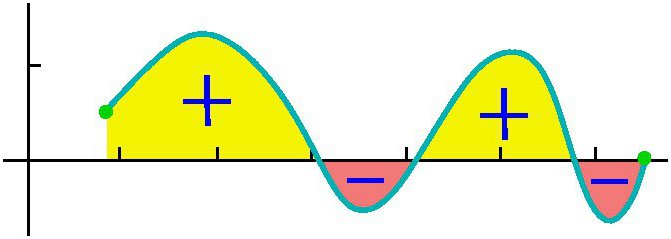Так, для функции, показанной на рисунке выше, определенный интеграл от a до b будет равен (S1 + S3) – (S2+S4).

Механическое истолкование определенного интеграла тесно связано с геометрическим. Вернемся к разделу «Риманова сумма» и представим, что приведенный на рисунках график выражает функцию скорости v=f(t) при неравномерном движении материальной точки (ось абсцисс является осью времени). Тогда площадь любого аппроксимирующего прямоугольника шириной Δt, который мы строили при формировании Римановой суммы, будет выражать приближенно путь точки за время Δt, а именно v(t*)Δt.

Полная сумма площадей прямоугольников на отрезке от t₁=a до t₂=b выразит приближенно путь s за время t₂– t₁ , а предел ее, т. е. интеграл (определенный) от a до b функции v = f(t) по dt даст точное значение пути s.

Дифференциал определенного интеграла

Если вернуться к его обозначению, то вполне можно предположить, что a = const, а b является конкретным значением некоторой независимой переменной x. Тогда определенный интеграл с верхним пределом x̃ из конкретного числа превращается в функцию от x̃. Такой интеграл равен площади фигуры под кривой, обозначенной точками aABb на рисунке ниже.

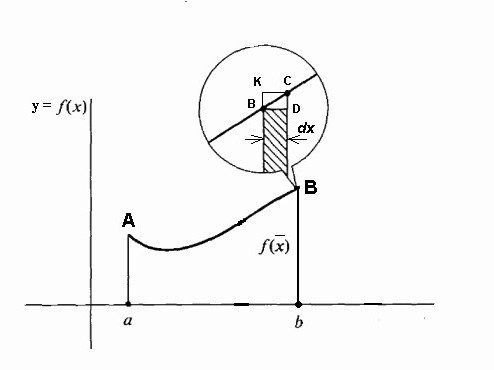При неподвижной линии aA и подвижной Bb эта площадь становится функцией f(x̃), причем приращения Δx̃ по-прежнему откладываются вдоль оси х, а приращением функции f(x̃) являются приращения площади под кривой.

Предположим, что мы дали переменной x̃ = b некоторое малое приращение Δx̃. Тогда приращение площади фигуры aABb складывается из площади прямоугольника (заштрихован на рисунке) Bb∙Δx̃ и площади фигуры BDC под кривой. Площадь прямоугольника равна Bb∙Δx̃ = f(x̃)Δx̃, т.е она является линейной функцией приращения независимой переменной. Площадь же фигуры BDC заведомо меньше, чем площадь прямоугольника BDCK = Δx̃∙Δy, и при стремлении Δx̃ →0 она уменьшается еще быстрее него. Значит, f(x̃)Δx̃ = f(x̃)dx̃ есть дифференциал переменной площади aABb, т. е. дифференциал определенного интеграла

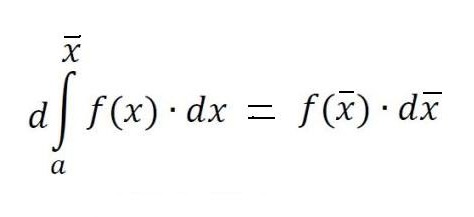
Отсюда можно заключить, что вычисление интегралов заключается в разыскании функций по заданным выражениям их дифференциалов. Интегральное исчисление как раз и представляет собой систему способов разыскания таких функций по известным их дифференциалам.

Фундаментальное соотношение интегрального исчисления

Оно связывает отношения между дифференцированием и интегрированием и показывает, что существует операция, обратная дифференцированию функции, — ее интегрирование. Оно также показывает, что если любая функция f(х) непрерывна, то применением к ней этой математической операции можно найти целый ансамбль (совокупность, множество) функций, первообразных для нее (или иначе, найти неопределенный интеграл от нее).

Пусть функция F(x) является обозначением результата интегрирования функции f(х). Соответствие между этими двумя функциями в результате интегрирования второй из них обозначается следующим образом:

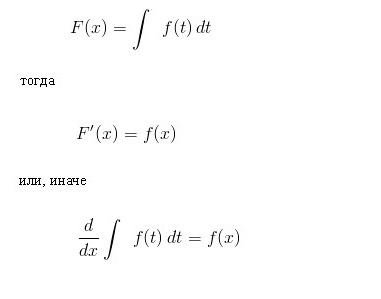
Как видно, при символе интеграла отсутствуют пределы интегрирования. Это означает, что из определенного он преобразован в неопределенный интеграл. Слово «неопределенный» означает, что результатом операции интегрирования в данном случае является не одна, а множество функций. Ведь, кроме собственно функции F(x), последним выражениям удовлетворяет и любая функция F(x)+С, где С = const. При этом подразумевается, что постоянный член в ансамбле первообразных можно задавать по произволу.

Следует подчеркнуть, что, если интеграл, определенный от функции, является числом, то неопределенный есть функция, точнее, их множество. Термин «интегрирование» применяется для определения операции разыскания обоих видов интегралов.

Основное правило интегрирования

Оно представляет собой полную противоположность соответствующему правилу для дифференцирования. Как же берутся неопределенные интегралы? Примеры этой процедуры мы рассмотрим на конкретных функциях.

Давайте посмотрим на степенную функцию общего вида:

f(х) = cxⁿ

После того как мы сделали это с каждым слагаемым в выражении интегрируемой функции (если их несколько), мы добавляем постоянную в конце. Напомним, что взятие производной от постоянной величины уничтожает ее, поэтому взятие интеграла от любой функции даст нам восстановление этой постоянной. Мы обозначаем ее С, так как постоянная неизвестна — это может быть любое число! Поэтому мы можем иметь бесконечно много выражений для неопределенного интеграла.

Давайте рассмотрим простые неопределенные интегралы, примеры взятия которых показаны ниже.

Пусть нужно найти интеграл от функции:

f(х) = 4x² + 2x – 3.

Начнем с первого слагаемого. Мы смотрим на показатель степени 2 и увеличиваем его на 1, затем делим первый член на результирующий показатель 3. Получаем: 4(x³) / 3.

Затем мы смотрим на следующий член и делаем то же самое. Так как он имеет показатель степени 1, то результирующий показатель будет 2. Таким образом, мы разделим это слагаемое на 2: 2(x²) / 2 = x².

Последний член имеет множитель х, но мы просто не видим его. Мы можем представить себе последнее слагаемое как (-3x⁰). Это эквивалентно (-3)∙(1). Если мы используем правило интегрирования, мы добавим 1 к показателю, чтобы поднять его до первой степени, а затем разделим последний член на 1. Получим 3x.

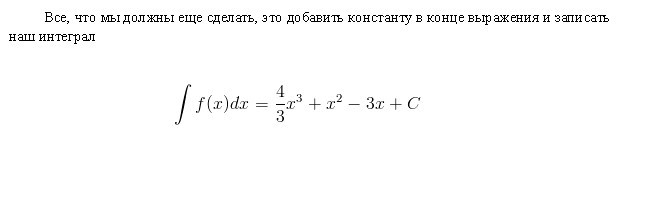
Это правило интегрирования работает для всех значений n, кроме n = – 1 (потому что мы не можем разделить на 0).

Мы рассмотрели самые простой пример нахождения интеграла. Вообще же решение интегралов является делом непростым, и в нем хорошим подспорьем является уже накопленный в математике опыт.

Таблицы интегралов

В разделе выше мы видели, что из каждой формулы дифференцирования получается соответствующая формула интегрирования. Поэтому все возможные их варианты уже давно получены и сведены в соответствующие таблицы. Нижеприведенная таблица интегралов содержит формулы интегрирования основных алгебраических функций. Эти формулы нужно знать на память, заучивая их постепенно, по мере их закрепления упражнениями.

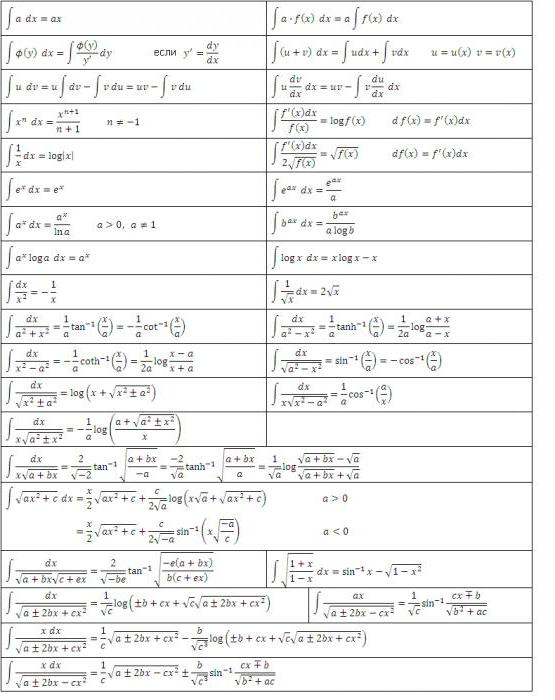
Еще одна таблица интегралов содержит основные тригонометрические функции:

Как же вычислить определенный интеграл

Оказывается, сделать это, умея интегрировать, т. е. находить неопределенные интегралы, очень просто. И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница

Согласно ей, вычисление искомого интеграла состоит на первом этапе в нахождении неопределенного, последующем вычислении значения найденной первообразной F(x) при подстановке x, равного сначала верхнему пределу, затем нижнему и, наконец, в определении разности этих значений. При этом константу С можно не записывать. т.к. она пропадает при выполнении вычитания.

Рассмотрим некоторые интегралы с подробным решением.

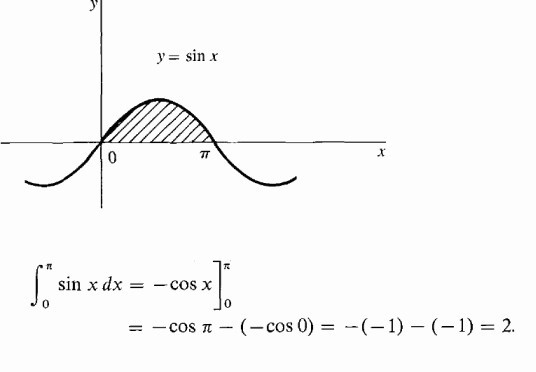
Найдем площадь участка под одной полуволной синусоидой.

Вычислим заштрихованную площадь под гиперболой.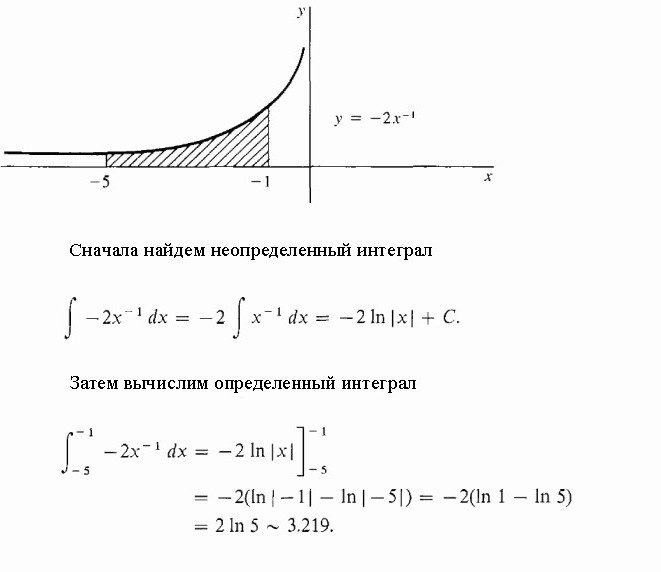

Рассмотрим теперь интегралы с подробным решением, использующим в первом примере свойство аддитивности, а во втором — подстановку промежуточной переменной интегрирования. Вычислим определенный интеграл от дробно-рациональной функции:

y=(1+t)/t³ от t=1 до t=2.

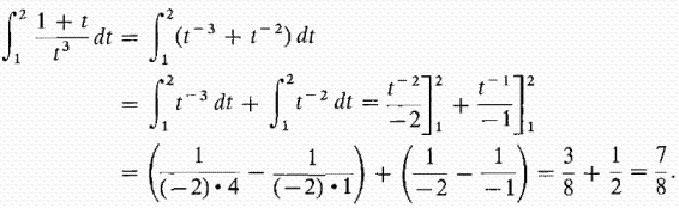
Теперь покажем, как можно упростить взятие интеграла введением промежуточной переменной. Пусть нужно вычислить интеграл от (x+1)².

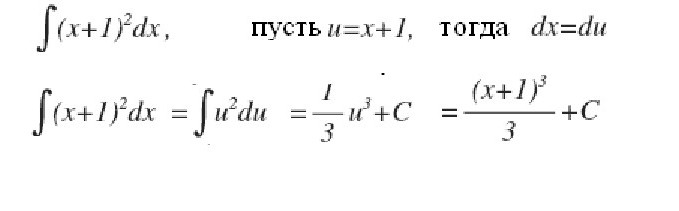
О несобственных интегралах

Мы говорили об определенном интеграле для конечного промежутка [a,b] от непрерывной на нем функции f(х). Но ряд конкретных задач приводит к необходимости расширить понятие интеграла на случай, когда пределы (один или оба) равны бесконечности, или при разрывной функции. Например, при вычислении площадей под кривыми, асимптотически приближающимися к осям координат. Для распространения понятия интеграла на этот случай, кроме предельного перехода при вычислении Римановой суммы аппроксимирующих прямоугольников, выполняется еще один. При таком двукратном переходе к пределу получается несобственный интеграл. В противоположность ему все интегралы, о которых говорилось выше, называются собственными.

www.syl.ru

11-а, Решение интегралов

Решение интегралов. Рассказываем, как решать интегралы.

Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое. Решение интегралов (интегрирование) есть операция обратная диференциированию. Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему. В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .

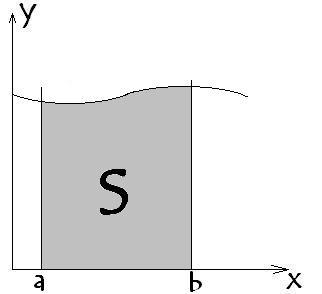
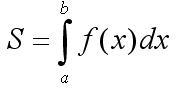Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b. Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим: 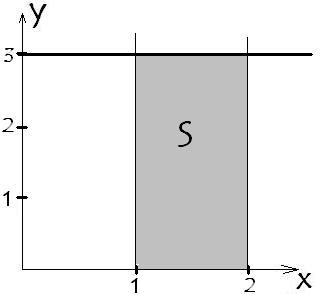Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3. Попробуем решить тоже самое не прибегая к построению, используя интегрирование: 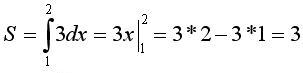Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными. Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной. F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением. Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов: Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду. Сначала следует запомнить основные свойства интегралов: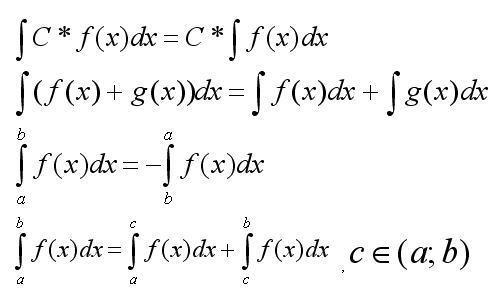

Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные примеры решения интегралов. Приемы будет даны для общего ознакомления без примеров решения, чтобы не перегружать статью. Нужно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной. Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой. 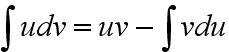Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

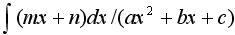3. Интегрирование дробно-рациональных функций.  — разложить дробь на простейшие  — выделить полный квадрат.  — создать в числителе дифференциал знаменателя.

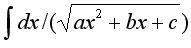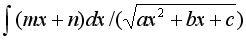4. Интегрирование дробно-иррациональных функций.  — выделить под корнем полный квадрат  — создать в числителе дифференциал подкоренного выважения. 5. Интегрирование тригонометрических функций.  При интегрировании выражений вида применяет формулы разложения для произведения. Для выражений 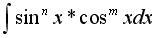 m-нечетное, n –любое, создаем d(cosx). 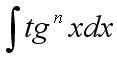Используем тождество sin²+cos²=1 m,n – четные, sin²x=(1-cos2x)/2 и cos²x=(1+cos2x)/2 Для выражений вида:  — Применяем свойство tg²x=1/cos²x – 1

1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию. 2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен. 3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя. Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом. Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1: Решить интеграл: Интеграл неопределенный. Находим первообразную. Для этого интеграл суммы разложим на сумму интегралов. 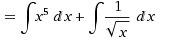Каждый из интегралов табличного вида. Смотрим первообразные по таблице. Решение интеграла: Проверим решение(найдем производную):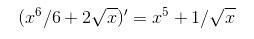

Пример 2. Решаем интеграл 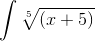Интеграл неопределенный. Находим первообразную. Сравниваем с таблицей. В таблице нет. Разложить, пользуясь свойствами, нельзя. Смотрим приемы. Наиболее подходит замена переменной. Заменяем х+5 на t⁵. t⁵ = x+5 . Получаем. 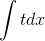Но dx нужно тоже заменить на t. x= t⁵ — 5, dx = (t⁵ — 5)’ = 5t⁴. Подставляем: 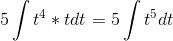Интеграл из таблицы. Считаем: 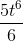Подставляем в ответ вместо t , 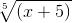Решение интеграла: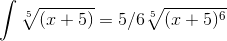

Пример 3. Решение интеграла: 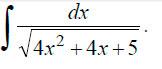Для решения в этом случае необходимо выделить полный квадрат. Выделяем:

В данном случае коэфециент ½ перед интегралом получился в результате замены dx на ½*d(2x+1). Если вы найдете производные x’ = 1 и ½*(2x+1)’= 1, то поймете почему так. В результате мы привели интеграл к табличному виду. Находим первообразную. 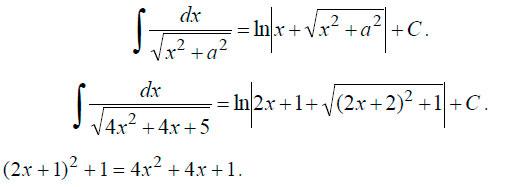В итоге получаем: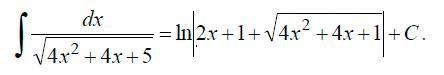

studfile.net