Интеграл Римана — Википедия

Геометрический смысл интеграла Римана

Интегра́л Ри́мана — одно из важнейших понятий математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.

Неформальное геометрическое описание[править | править код]

Риманова сумма (суммарная площадь прямоугольников) в пределе, при измельчении разбиения, дает площадь подграфика.

Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс).

Для этого он рассмотрел фигуры, состоящие из некоторого количества вертикальных прямоугольников, основания которых составляют вместе отрезок интегрирования и получаются при разбиении отрезка (см. рисунки) на соответствующее количество маленьких отрезков.

Площадь S такой фигуры при конкретном разбиении на отрезки длинами Δxi{\displaystyle \Delta x_{i}} будет интегральной суммой:

S=∑if(xi)Δxi.{\displaystyle S=\sum _{i}f(x_{i})\Delta x_{i}.}

Если существует предел, к которому сходится площадь S (интегральная сумма) для каждого разбиения — при хорошем «размельчении» разбиения (когда наибольшее из Δxi{\displaystyle \Delta x_{i}} стремится к нулю), этот предел называется интегралом Римана функции на отрезке.

Через интегральные суммы[править | править код]

Пусть на отрезке [a,b]{\displaystyle [a,b]} определена вещественнозначная функция f{\displaystyle f}.

Рассмотрим разбиение отрезка a=x0<x1<x2<⋯<xn−1<xn=b{\displaystyle a=x_{0}<x_{1}<x_{2}<\dots <x_{n-1}<x_{n}=b} — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок [a,b]{\displaystyle [a,b]} на n отрезков [xi−1,xi],i=1…n{\displaystyle [x_{i-1},x_{i}],\;i=1\dots n}. Длина наибольшего из отрезков δR=max(Δxi){\displaystyle \delta R=\max(\Delta x_{i})} называется

шагом разбиения, где Δxi=xi−xi−1{\displaystyle \Delta x_{i}=x_{i}-x_{i-1}} — длина элементарного отрезка.

Отметим на каждом отрезке разбиения по точке ξi∈[xi−1,xi]{\displaystyle \xi _{i}\in [x_{i-1},x_{i}]}. Интегральной суммой называется выражение σx=∑i=1nf(ξi)Δxi{\displaystyle \sigma _{x}=\sum \limits _{i=1}^{n}{f(\xi _{i})\Delta x_{i}}}.

Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора ξi∈[xi−1,xi]{\displaystyle \xi _{i}\in [x_{i-1},x_{i}]}, то это число называется интегралом функции f{\displaystyle f} на отрезке [a,b]{\displaystyle [a,b]}, то есть ∫abf(x)dx=limδR→0σx{\displaystyle \int \limits _{a}^{b}f(x)\,dx=\lim \limits _{\delta R\to 0}\sigma _{x}}.

В этом случае, сама функция f{\displaystyle f} называется интегрируемой (по Риману) на [a,b]{\displaystyle [a,b]}; в противном случае f{\displaystyle f} является неинтегрируемой (по Риману) на отрезке [a,b]{\displaystyle [a,b]}.

Через суммы Дарбу[править | править код]

1. Невырожденность: ∫ab1dx=b−a{\displaystyle \int \limits _{a}^{b}1\,dx=b-a}.
2. Положительность: Если интегрируемая функция f{\displaystyle f} неотрицательна, то её интеграл на отрезке [a,b]{\displaystyle [a,b]} также неотрицателен.
3. Линейность: Если функции f{\displaystyle f} и g{\displaystyle g} интегрируемы, и α,β∈R{\displaystyle \alpha ,\beta \in \mathbb {R} }, то функция αf+βg{\displaystyle \alpha f+\beta g} тоже интегрируема, и ∫ab(αf(x)+βg(x))dx=α∫abf(x)dx+β∫abg(x)dx{\displaystyle \int \limits _{a}^{b}(\alpha f(x)+\beta g(x))\,dx=\alpha \int \limits _{a}^{b}f(x)\,dx+\beta \int \limits _{a}^{b}g(x)\,dx}.
4. Непрерывность: Если интегрируемые функции fi{\displaystyle f_{i}} равномерно сходятся на отрезке [a,b]{\displaystyle [a,b]} к функции f{\displaystyle f}, то f{\displaystyle f} интегрируема, и limi→∞∫abfi(x)dx=∫abf(x)dx{\displaystyle \lim _{i\to \infty }\int \limits _{a}^{b}f_{i}(x)\,dx=\int \limits _{a}^{b}f(x)\,dx}. (Последняя формула может быть получена уже как формальное следствие свойств 1-3 и интегрируемости предельной функции).
5. Аддитивность при разбиениях отрезка: Пусть a<b<c{\displaystyle a<b<c}. Функция f{\displaystyle f} интегрируема на отрезке [a,c]{\displaystyle [a,c]}, тогда и только тогда, когда она интегрируема на каждом из отрезков [a,b]{\displaystyle [a,b]} и [b,c]{\displaystyle [b,c]}, при этом ∫acf(x)dx=∫abf(x)dx+∫bcf(x)dx{\displaystyle \int \limits _{a}^{c}f(x)\,dx=\int \limits _{a}^{b}f(x)\,dx+\int \limits _{b}^{c}f(x)\,dx}.
6. Если функция F{\displaystyle F} является первообразной непрерывной функции f{\displaystyle f}, то интеграл функции f{\displaystyle f} на отрезке [a,b]{\displaystyle [a,b]} может быть вычислен по формуле Ньютона-Лейбница: он равен F(b)−F(a){\displaystyle F(b)-F(a)}. (Это — общее свойство любых интегралов, удовлетворяющих свойствам 1-5, а не только интеграла Римана). Непрерывная на отрезке функция f{\displaystyle f} всегда имеет первообразную, и каждая первообразная имеет вид: F(x)=∫axf(t)dt+C{\displaystyle F(x)=\int \limits _{a}^{x}f(t)dt+C}, где C{\displaystyle C} — произвольная константа.

Условия существования интеграла Римана[править | править код]

Непрерывная на отрезке функция всегда интегрируема по Риману (следствие свойств 1—5). Разрывные функции могут быть интегрируемы, но могут и не быть; примером функции, не интегрируемой по Риману, является всюду разрывная функция Дирихле.

Критерий Лебега интегрируемости функции по Риману[править | править код]

Функция интегрируема по Риману на отрезке [a,b]{\displaystyle [a,b]}, тогда и только тогда, когда на этом отрезке она ограничена, и множество точек, где она разрывна, имеет нулевую меру (то есть может быть покрыто счётным семейством интервалов со сколь угодно малой суммарной длиной).

Другой критерий[править | править код]

Для того, чтобы функция f(x){\displaystyle f(x)} была интегрируемой на отрезке [a,b]{\displaystyle [a,b]}, необходимо и достаточно, чтобы сумма ∑i=1nωiΔi{\displaystyle \sum _{i=1}^{n}\omega _{i}\Delta _{i}} стремилась к нулю вместе с диаметром разбиения d{\displaystyle d}.

Здесь ωi{\displaystyle \omega _{i}} — колебание функции f(x){\displaystyle f(x)} в сегменте Δi=[xi−1,xi]{\displaystyle \Delta _{i}=[x_{i-1},x_{i}]},

колебание ω{\displaystyle \omega } функции f{\displaystyle f} на множестве E{\displaystyle E} — разность supEf(x)−infEf(x){\displaystyle \sup _{E}f(x)-\inf _{E}f(x)},

диаметр разбиения d=supi(xi−xi−1){\displaystyle d=\sup _{i}(x_{i}-x_{i-1})}^[1].

Некоторые классы функций, интегрируемых по Риману[править | править код]

Ниже перечислены некоторые классы функций, для которых значение интеграла Римана всегда существует и конечно^[2].

Приведенное выше определение интеграла дано Коши^[3], оно применялось только для непрерывных функций.

Риман в 1854 году (опубликовано в 1868 году^[4]:101-103, на русском языке впервые в 1914 году^[5][6]) дал это же определение без предположения непрерывности. Современный вид теории Римана придал Дарбу (1879).

1. ↑ Песин И. Н. Развитие понятия интеграла. — М.: Наука. — С. 17
2. ↑ Фихтенгольц, 1966, с. 101—103.
3. ↑ Cauchy A. L., Sur la mécanique céleste et sur un nouveau calcul appelé calcul des limites, Turin 1831
4. ↑ Riemann В. Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe // Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen. — 1868. — Vol. 13. — P. 87-132.
5. ↑ Риманн Б. О возможности выражения функции при помощи тригонометрического ряда // Разложение функций в тригонометрические ряды / Лежен-Дирикле, Риманн, Липщиц; Пер. Г.А. Грузинцева и С.Н. Бернштейна. — Харьков: Харьковское математическое общество, 1914. — (Харьковская математическая библиотека. Серия В; № 2).
6. ↑ Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу / Под ред. В. А. Садовничего. — 2-е изд. — М.: Высшая школа, 2000. — С. 186. — ISBN 5-06-003955-2.

• В.А. Ильин, В.А. Садовничий, Бл. Х. Сендов. Математический анализ. Начальный курс. — 2-е, переработанное. — М.: Издательство Московского Университета, 1985. — Т. 1. — 660 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в трёх томах. — Изд. 6-е. — М.: Наука, 1966. — Т. 2. — 800 с.

Интегральное исчисление — Википедия

Интегральное исчисление — раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений^[1].

В сочинении Архимеда «Об измерении длины окружности» рассматривается вопрос об определении площади и длины окружности круга, а в трактате «О шаре и цилиндре» — о поверхностях и объёмах тел, ограниченных кривыми поверхностями; эти вопросы представляют первые геометрические задачи, относящиеся к исчислению. И в настоящее время основной задачей исчисления является нахождение площадей криволинейных фигур. Под площадью криволинейной фигуры S{\displaystyle S} (черт. 1) подразумевается предел, к которому стремится площадь вписанного в фигуру многоугольника по мере увеличения числа его сторон, причём эти стороны могут быть сделаны меньше всякого заранее заданного произвольно малого числа.

Основная идея вычисления площади произвольных геометрических фигур состоит в следующем. Для начала, как посчитать площадь прямоугольника, то есть как доказать, что его площадь — это произведение длины на ширину. Если речь идёт о геометрии, где все построения нужно делать с помощью циркуля и линейки, то в такой геометрии, отношение длины к ширине есть число рациональное (см. Учебник Погорелова), то есть если длину принять за единицу, то ширина может быть выражена в качестве дроби m/n{\displaystyle m/n}, где m{\displaystyle m} и n{\displaystyle n} натуральные числа. Для такого прямоугольника можно подобрать такой «единичный квадратик», который полностью покроет такой прямоугольник. Сторону «единичный квадратик» можно подобрать как

d = НОД(m, n), где d{\displaystyle d} — натуральное число. Например, если мы имеем прямоугольник длиной 10 см и шириной 14 см, то такой прямоугольник может быть построен при помощи циркуля и линейки (если длину принять за единицы, его ширина будет 14 / 10 = 7/5). В качестве стороны «единичного квадратика» можно взять d = НОД(14, 10) = 2 см. Этот квадратик войдёт 5 раз в длину и 7 в ширину, всего нужно 5 × 7 = 35 таких «единичных квадратиков». Можно взять квадраты со стороной 1 см. Этот квадратик войдёт 10 раз в длину и 14 в ширину, всего нужно 10 × 14 = 140 таких «единичных квадратиков». Из этого построения видно, что размерность (см.) не играет никакой существенной роли при таком построении.

Площадь прямоугольного треугольника можно посчитать если заметить, что если отложить точно такой же треугольник рядом, то получится прямоугольник. Так как мы удвоили площадь треугольника, то площадь треугольника является половиной площади прямоугольника. Площадь параллелограмма определяется аналогичным, чуть более сложным образом, через площади прямоугольника и треугольника. Площадь многоугольников определяется при помощи площади треугольников.

Как определить площадь произвольной кривой? Например, кривой, являющиеся непрерывной функцией ограниченная прямыми x=a{\displaystyle x=a} и x=b{\displaystyle x=b}?

Геометрический смысл интеграла Римана

Если попытаться разбить такую фигуру на «единичные квадратики», то будут оставаться незаполненные «дыры» (как и в случае прямоугольников со сторонами отношение, которых не равно рациональному числу). В таком случае пытаются сделать два покрытия: прямоугольниками «сверху» и «снизу», то есть построить прямоугольники таким образом, чтобы они включали график функции или не включали. Здесь существенным является каким именно образом мы будем разбивать на прямоугольники (см. ниже). Второй момент заключается в том, что если мы будем брать разбиения всё мельче и мельче, то площадь покрытия «сверху» и площадь покрытия «снизу» должны сходиться и сходиться к какому-то конечному значению. Третий момент заключается в том, что площадь покрытия «сверху» и площадь покрытия «снизу» должны сходиться к одному и тому же числу.

Вернёмся к способу разбиения на прямоугольники. Существует как минимум два распространённых способа.

Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке. См. подробнее Интеграл Римана.

Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.

Вернёмся к определению интеграла по Риману.

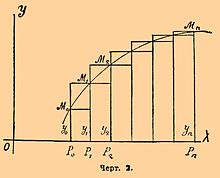
Указанная задача решается при помощи интегрального исчисления, если криволинейный контур фигуры S{\displaystyle S} задан уравнением, как это делается в аналитической геометрии (см. Аналитическая геометрия и Дифференциальное исчисление). Пусть уравнение заданной кривой S{\displaystyle S} (черт. 2) есть y=f(x){\displaystyle y=f(x)}.

Определим площадь P0M0MnPn{\displaystyle P_{0}M_{0}M_{n}P_{n}}, образованную отрезком оси x{\displaystyle x}-ов P0Pn{\displaystyle P_{0}P_{n}}, двумя ординатами M0P0{\displaystyle M_{0}P_{0}} и MnPn{\displaystyle M_{n}P_{n}} и дугой M0Mn{\displaystyle M_{0}M_{n}} кривой S{\displaystyle S}. Ясно, что нахождение площади всякой криволинейной фигуры может быть сведено к нахождению площадей такого вида (то есть ограниченным тремя прямыми и дугой кривой). Проведем между крайними ординатами M0P0{\displaystyle M_{0}P_{0}} и MnPn{\displaystyle M_{n}P_{n}} n−1{\displaystyle n-1} ординат M1P1{\displaystyle M_{1}P_{1}}, M2P2{\displaystyle M_{2}P_{2}} …, соответствующих точкам деления P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}} … отрезка оси P0Pn{\displaystyle P_{0}P_{n}}. Эти точки выберем произвольно, с тем лишь ограничением, чтобы по мере увеличения числа n{\displaystyle n} наибольший из отрезков был бесконечно мал (напр. точки P1,P2{\displaystyle P_{1},P_{2}}… можно выбрать на равных расстояниях друг от друга). Предполагая, как это имеет место на черт. 2, что ординаты кривой во все время при переходе от M0{\displaystyle M_{0}} к Mn{\displaystyle M_{n}} возрастают, легко видеть, что криволинейная площадь фигуры S{\displaystyle S} будет заключаться между следующими двумя суммами:

Sn=f(x0)(x1−x0)+f(x1)(x2−x1)+…+f(xn−1)(xn−xn−1){\displaystyle S_{n}=f(x_{0})(x_{1}-x_{0})+f(x_{1})(x_{2}-x_{1})+…+f(x_{n-1})(x_{n}-x_{n-1})}

и Sn′=f(x1)(x1−x0)+f(x2)(x2−x1)+…+f(xn)(xn−xn−1){\displaystyle S’_{n}=f(x_{1})(x_{1}-x_{0})+f(x_{2})(x_{2}-x_{1})+…+f(x_{n})(x_{n}-x_{n-1})}

где x0=OP0{\displaystyle x_{0}=OP_{0}}, x1=OP1{\displaystyle x_{1}=OP_{1}}, x2=OP2{\displaystyle x_{2}=OP_{2}}, …, xn=OPn{\displaystyle x_{n}=OP_{n}},

a f(x0)=M0P0{\displaystyle f(x_{0})=M_{0}P_{0}}, f(x1)=M1P1{\displaystyle f(x_{1})=M_{1}P_{1}}, f(x2)=M2P2{\displaystyle f(x_{2})=M_{2}P_{2}}, …, f(xn)=MnPn{\displaystyle f(x_{n})=M_{n}P_{n}}.

Знак интеграла — Википедия

Знак	Юникод		Название	HTML-представление			LaTeX
	Позиция	Название		Шестнадцатеричное	Десятичное	Мнемоника
∫	U+222B	integral	Интеграл	∫	∫	∫	\int
∬	U+222C	double integral	Двойной интеграл	∬	∬		\iint
∭	U+222D	triple integral	Тройной интеграл	∭	∭		\iiint
∮	U+222E	contour integral	Интеграл по контуру	∮	∮		\oint
∯	U+222F	surface integral	Интеграл по поверхности	∯	∯		\oiint (требуется пакет esint)
∰	U+2230	volume integral	Интеграл по объёму	∰	∰		\oiiint (требуется пакет esint)
∱	U+2231	clockwise integral	Интеграл с правым обходом	∱	∱
∲	U+2232	clockwise contour integral	Интеграл по контуру с правым обходом	∲	∲		\ointclockwise (требуется пакет esint)
∳	U+2233	anticlockwise contour integral	Интеграл по контуру с левым обходом	∳	∳		\ointctrclockwise (требуется пакет esint)
⨋	U+2A0B	summation with integral		⨋	⨋
⨌	U+2A0C	quadruple integral operator	Четырёхкратный интеграл	⨌	&#;
⨍	U+2A0D	finite part integral		⨍	⨌
⨎	U+2A0E	integral with double stroke		⨎	⨍
⨏	U+2A0F	integral average with slash		⨏	⨎
⨐	U+2A10	circulation function		⨐	⨏
⨑	U+2A11	anticlockwise integration	Интеграл с левым обходом	⨑	⨐
⨒	U+2A12	line integration with rectangular path around pole		⨒	⨑
⨓	U+2A13	line integration with semicircular path around pole		⨓	⨒
⨔	U+2A14	line integration not including the pole		⨔	⨓
⨕	U+2A15	integral around a point operator		⨕	⨔
⨖	U+2A16	quaternion integral operator		⨖	⨕
⨗	U+2A17	integral with leftwards arrow with hook		⨗	⨖
⨘	U+2A18	integral with times sign		⨘	⨗
⨙	U+2A19	integral with intersection		⨙	⨘
⨚	U+2A1A	integral with union		⨚	⨙
⨛	U+2A1B	integral with overbar	Верхний интеграл Дарбу	⨛	⨚
⨜	U+2A1C	integral with underbar	Нижний интеграл Дарбу	⨜	⨛

Обсуждение:Интеграл — Википедия

Материал из Википедии — свободной энциклопедии

Об объединении со знаком интеграла[править код]

На мой взгляд, интеграл это (многозначное) математическое понятие, а знак интеграла это скорее типографский символ. Объединять статьи нет особого смысла. Лучше статью про сам интеграл привести в божеский вид. Mir76 12:02, 5 февраля 2007 (UTC)

«любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.» — неправда! как же функция дирихле?

---

правда, правда… Ну функция Дирихле…. Ну и что?.. Интеграл Ньютона-Лейбница не существует. Интеграл Римана не существует. Интеграл Лебега существует. И? —91.193.127.47 23:02, 31 января 2008 (UTC) Waterlaz

Пустая секция это не заготовка, удаляю —Тоша 17:11, 22 февраля 2008 (UTC)

Она здесь не столько как секция предполагается, сколько как один из пунктов списка типов. Просто в виде секций удобно оформление. infovarius 21:08, 22 февраля 2008 (UTC)

Не просветите что такое «интеграл Ньютона-Лейбница»?

Florian Cajori: A history of mathematical notations

kakoye s — ſ zdes?: http://www.worldcat.org/title/geometriae-speciosae-elementa/oclc/23618844?title=&detail=&page=frame&url=http://www.mdz-nbn-resolving.de/urn/resolver.pl%3Furn%3Durn:nbn:de:bvb:12-bsb10053678-9%26checksum%3Da0a921c80af8b3e1bfffe319fbafcc17&linktype=digitalObject

То я с Вами месяц назад за эту же long s бодался? Сразу бы Cajori в статье указали и ни у кого б вопросов не возникло. Поправил в Вашей реплике ссылку на более читабельный вид. —Alex-engraver 20:59, 17 октября 2011 (UTC)

Главным врагом женщин на пути к карьере в науке оказался интеграл – курсы по основам интегрального счисления в 1,5 раза чаще заставляют их отказываться от дальнейшего изучения инженерного дела и науки, чем мужчин. http://ria.ru/studies/#ixzz4EPabkTjq

Как правильно:∫ba{\displaystyle \int _{b}^{a}} или ∫ba{\displaystyle \int \limits _{b}^{a}}? —88.81.37.24 11:49, 8 марта 2012‎ (UTC)

И так и так правильно. Первый вариант обычно используют, когда есь недостаток свободного места по вертикали, в сплошном тексте. В этом случае сам знак интеграла уменьшают, и пределы размещают сбоку (заметьте, они занимают отдельное горизонтальное место). А второй вариант для отдельных формул, где много вертикального простанства. Также часто используют и при ручном письме. В русской традиции обычно второе начертание, в английской первое. (In English: [1], [2] или английскую версию статьи; на русском языке: [3] или любой другой учебник). Интересно, что для интегралов по контуру всё ж таки и в англоязычной литературе иногда встречается второе начертание. —Zorgit 19:25, 8 марта 2012 (UTC)

Неопределённый и определённый интегралы[править код]

По-моему, нет смысла разделять интегралы на эти два вида. Считаю, что это разделение на категории является обыкновенным пережитком математики, всё ещё не исправленным. И считать, что любой интеграл всегда определён (даже если пределы не указаны из соображений краткой записи) Так, согласно формулы Ньютона-Лейбница, вместо записи первообразной:

F(x)=∫f(x)dx{\displaystyle F(x)=\int f(x)dx}

лучше использовать более ясную запись:

F(x)=∫x0xf(x)dx+F(x0){\displaystyle F(x)=\int \limits _{x_{0}}^{x}f(x)dx+F(x_{0})}

А неопределённые интегралы, представленные списком в справочниках, считать определёнными с обязательным указанием нижнего предела интегрирования, выбранным таким образом, чтобы запись была наиболее краткой, исключая произвол постоянной C. Для краткости верхний предел x можно не писать, например:

∫b1−adxx(ax+b)=−1bln⁡|ax+bx|{\displaystyle \int \limits _{\frac {b}{1-a}}^{}{\frac {dx}{x(ax+b)}}=-{\frac {1}{b}}\ln \left|{\frac {ax+b}{x}}\right|}

Таким образом, интеграл это одна из первообразных, другая имеет иное значение в точке x0{\displaystyle x_{0}} Dorogusha-w (обс.) 13:35, 30 апреля 2018 (UTC)

Это предложение не для Википедии. Мы пишем то, что написано в учебниках, а не пытаемся изменить стандарты. — Алексей Копылов 13:41, 30 апреля 2018 (UTC)

Функциональный интеграл — Википедия

Функциональный интеграл (континуальный интеграл, интеграл по траекториям, фейнмановский интеграл по траекториям, интеграл Фейнмана) — запись или результат функционального интегрирования (интегрирования по траекториям). Находит наибольшее применение в квантовой физике (квантовой теории поля, теории струн и т. д.) и статистической физике, а также при изучении ряда классов стохастических процессов вообще.

Под функциональным интегрированием формально имеется в виду вычисление интеграла некоторого функционала Ф по пространству функций x(t) или какому-то подмножеству^[1] такого пространства:

∫DxΦ[x],{\displaystyle \int Dx\,\Phi [x],}

который определяется как предел (конечномерного) интеграла по пространству неких конечномерных аппроксимаций функций x(t) при стремлении размерности этих аппроксимаций к бесконечности; обычный и наиболее простой способ заключается в рассмотрении функции x на конечном множестве точек t1,t2,…,tN{\displaystyle t_{1},t_{2},\dots ,t_{N}}, определяя тогда функциональный интеграл в простейшем случае равномерного разбиения, которым можно и ограничиться, как

limN→∞∫∫…∫dx1dx2…dxNΦ[x1,x2,…,xN],{\displaystyle \lim _{N\to \infty }\int \int \dots \int dx_{1}\,dx_{2}\dots dx_{N}\,\Phi [x_{1},x_{2},\dots ,x_{N}],}

где под Φ[x1,x2,…,xN]{\displaystyle \Phi [x_{1},x_{2},\dots ,x_{N}]} имеется в виду соответствующая аппроксимация функционала Ф[x], интегрирование же подразумевается отдельно по x1,x2,…,xN{\displaystyle x_{1},x_{2},\dots ,x_{N}} от −∞{\displaystyle -\infty } до +∞{\displaystyle +\infty } (в случае фиксированных x1{\displaystyle x_{1}} и xN{\displaystyle x_{N}} по ним интегрировать не нужно).

Корректность уже этого определения находится под вопросом в том смысле, что не доказано даже для многих из тех случаев, которые представляют физический интерес, не говоря уж о более общей постановке вопроса, само существование предела (в частности, его одинаковость при выборе разных типов разбиения; более того, в ряде примеров разные типы дают разный результат) и нет во многих случаях способа указания чётких критериев выбора «правильного» типа разбиения, который приведёт именно к нужному результату, а значит корректность определения меры интегрирования не доказана даже для многих из тех случаев, которые представляют физический интерес, по крайней мере в обычном смысле.

Также серьёзную трудность представляет точное вычисление таких интегралов (за исключением гауссова случая).

Тем не менее, уже то, что точно вычисляются хотя бы интегралы гауссова типа, дает очень много для применения метода функционального интегрирования. В частности, этот результат можно принять за определение функционального интеграла для этого случая и доказать, что, будучи так определённым, он действительно обладает свойствами интеграла: допускает интегрирование по частям, замены переменных и т. д.^[2]

Физический смысл функционального интеграла сводится обычно к тому, чтобы вычислить сумму (суперпозицию) некоторой величины (обычно это вероятность для классической статфизики или амплитуда вероятности для квантовой механики) по «всем» траекториям (то есть по всем доступным классической частице в случае броуновского движения и по всем, какие можно вообразить, в случае квантовой механики).

Обычное случайное блуждание способно порождать при переформулировке интеграл по траекториям с определённым действием. Это в общем-то сравнительно очевидно в простых случаях.

Было показано, что подобный способ порождения континуального интеграла с обычным действием работает и в двумерном случае — для получения действия для струны (двумерного объекта, учитывая временное измерение).

Аналогией интеграла по траекториям для точечной частицы является статистическая сумма (статистический вес) для полимерной нити^[3].

Точное вычисление[править | править код]

Как уже упоминалось выше, точное вычисление функционального интеграла вида

∫DxekS[x],{\displaystyle \int Dx\,e^{kS[x]},}

где k может быть чисто мнимым в квантовом случае или действительным в случае классической диффузии, возможно лишь в случае, когда он относится к гауссовскому типу, то есть, когда действие S квадратично по x (лагранжиан квадратичен по x и его производным, или, может быть, ещё в некоторых подобных случаях: главное, чтобы S было квадратичной формой, в вещественном случае отрицательно определенной).

Способ сводится к написанию дискретного варианта, в соответствии с определением в начале статьи. Затем (обычные) интегралы, входящие в формулу, точно берутся (как гауссовы), и тогда можно перейти к пределу.

Приближенное вычисление[править | править код]

Численные методы[править | править код]

Вычислительные методы, связанные с нахождением значений континуальных интегралов при помощи ЭВМ, в том числе квадратурные формулы типа формул Симпсона и другие методы к 2010 году разработаны довольно обширно, хотя используются в основном лишь узкими специалистами и в большинстве своём не известны физикам.

Первое появление интегралов по траекториям относится, по-видимому, к работам Эйнштейна и Смолуховского^{[уточнить]} по теории броуновского движения.

Основы математической теории таких интегралов связаны с работами Винера 1920-х годов. Однако до сих пор строгая и достаточно полная их математическая теория встречается с существенными трудностями (связанными с вопросом корректного введения меры на пространстве функций, с проблемой доказательства независимости предела от типа разбиения в достаточно общем случае).

В 1933 году (в работе «Лагранжиан в квантовой механике») Дирак предложил идею использования интеграла по траекториям в квантовой механике.

Фейнман в конце 1940-х годов реализовал эту программу, разработав формализм континуального интеграла, оказавшийся крайне плодотворным в теоретической физике. Это означало появление технически нового (имевшего — кроме чисто технических — к тому же ряд интуитивных преимуществ) метода построения квантовых теорий, ставшего впоследствии едва ли не самым популярным среди теоретиков. Уже сам Фейнман на основе формализма континуального интеграла построил такую базовую технику квантовой теории поля, как диаграммы Фейнмана.

С помощью использования континуального интеграла были получены такие фундаментальные результаты, как, например, доказательство перенормируемости теории Янга — Миллса (Фаддеевым и Поповым).

1. ↑ Наиболее типичный пример области интегрирования в пространстве функций является множество всех функций заданного пространства, удовлетворяющих условию фиксирования их значения в двух точках (на концах отрезка).
2. ↑ Статья в Физической энциклопедии (А. А. Славнов).
3. ↑ Поляков, 1999.

• Simon B. Functional Integration and Quantum Physics. — Academic Press, 1979.
• Березин Ф. А. Метод вторичного квантования. — М.: Наука, 1986. — 320 с.
• Зинн-Жюстен Ж. Континуальный интеграл в квантовой механике. — М.: Физматлит, 2010. — 360 с.
• Лобанов Ю. Ю. Методы приближенного функционального интегрирования для численного исследования моделей в квантовой физике (диссертация на соискание ученой степени доктора физико-математических наук). — М., 2009.
• Поляков А. М. Калибровочные поля и струны. — Ижевск: РХД, 1999. — 316 с.
• Попов В. Н. Континуальные интегралы в квантовой теории поля и статистической механике. — М.: Атомиздат, 1976. — 256 с.
• Славнов А. А., Фаддеев Л. Д. Введение в квантовую теорию калибровочных полей. — М.: Наука, 1988. — 272 с.
• Смолянов О. Г., Шавгулидзе Е. Т. Континуальные интегралы. — М.: Наука, 1990. — 150 с.
• Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. — М.: Мир, 1968. — 384 с.
• Шестакова Т. П. Метод континуального интеграла в квантовой теории поля. — Ижевск: ИКИ, 2005. — 228 с.

Определённый интеграл — это… Что такое Определённый интеграл?

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Определение

Пусть определена на . Разобьём на части с несколькими произвольными точками . Тогда говорят, что произведено разбиение отрезка Далее выберем произвольную точку , ,

Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю , если он существует независимо от разбиения и выбора точек , то есть

Если существует указанный предел, то функция называется интегрируемой на по Риману.

Обозначения

Свойства

Если функция интегрируема по Риману на , то она ограничена на нем.

Геометрический смысл

Определённый интеграл как площадь фигуры

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми и и графиком функции .

Формула Ньютона — Лейбница

См. также

Первый интеграл — Википедия

Материал из Википедии — свободной энциклопедии

Пе́рвый интегра́л системы обыкновенных дифференциальных уравнений

{x1′=a1(x)…xn′=an(x),x∈U{\displaystyle \left\{{\begin{matrix}{x_{1}}’&=&a_{1}(x)\\\dots &&\\{x_{n}}’&=&a_{n}(x)\end{matrix}}\right.,\quad x\in U}

— дифференцируемая функция f:U→R{\displaystyle f:U\to \mathbb {R} }, U⊆Rn{\displaystyle U\subseteq \mathbb {R} ^{n}}, такая, что её производная по направлению векторного поля A(x)=(a1(x),…,an(x)){\displaystyle A(x)=(a_{1}(x),\ldots ,a_{n}(x))}

LAf=a1(x)∂f∂x1+⋯+an(x)∂f∂xn=0{\displaystyle L_{A}f=a_{1}(x){\frac {\partial f}{\partial x_{1}}}+\dots +a_{n}(x){\frac {\partial f}{\partial x_{n}}}=0}

для всех x{\displaystyle x} из области U{\displaystyle U}. Другими словами, функция f{\displaystyle f} постоянна на любом решении системы, содержащемся в области U{\displaystyle U}.

Первые интегралы используются при изучении автономных систем дифференциальных уравнений и решении дифференциальных уравнений в частных производных.

Пусть U{\displaystyle U} — область в Rn{\displaystyle \mathbb {R} ^{n}}, A(x)=(a1(x),…,an(x)){\displaystyle A(x)=(a_{1}(x),\ldots ,a_{n}(x))} — дифференцируемое векторное поле в U{\displaystyle U}, x0∈U{\displaystyle x_{0}\in U}, A(x0)≠0{\displaystyle A(x_{0})\neq 0}. Тогда существует такая окрестность точки x0{\displaystyle x_{0}}, что система дифференциальных уравнений

{x1′=a1(x)…xn′=an(x){\displaystyle \left\{{\begin{matrix}{x_{1}}’&=&a_{1}(x)\\\dots &&\\{x_{n}}’&=&a_{n}(x)\end{matrix}}\right.}

имеет в этой окрестности ровно n−1{\displaystyle n-1} функционально независимых первых интегралов.

Для уравнения x″+V(x)=0{\displaystyle x»+V(x)=0} относительно функции x(t){\displaystyle x(t)} первым интегралом является функция E=12x′2+∫x0xV(z)dz{\displaystyle E={\frac {1}{2}}x’^{2}+\int \limits _{x_{0}}^{x}V(z)dz} (полная энергия в физических приложениях).

• Арнольд В. И. «Обыкновенные дифференциальные уравнения». М.: Наука, 1966.