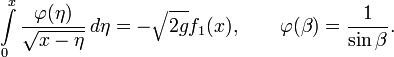Интегральное уравнение — Википедия
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
Классификация интегральных уравнений[править | править код]
Линейные интегральные уравнения[править | править код]
Это интегральные уравнения, в которые неизвестная функция входит линейно:
- φ(x)=λ∫abK(x,s)φ(s)ds+f(x){\displaystyle \varphi (x)=\lambda \int \limits _{a}^{b}K(x,\;s)\varphi (s)\,ds+f(x)}
где φ(x){\displaystyle \varphi (x)} — искомая функция, f(x){\displaystyle f(x)}, K(x,s){\displaystyle K(x,\;s)} — известные функции, λ{\displaystyle \lambda } — параметр. Функция K(x,s){\displaystyle K(x,\;s)} называется ядром интегрального уравнения. В зависимости от вида ядра и свободного члена линейные уравнения можно разделить ещё на несколько видов.
Уравнения Фредгольма[править | править код]
Уравнения Фредгольма 2-го рода[править | править код]
Уравнения Фредгольма 2-го рода — это уравнения вида:
- φ(x)=λ∫abK(x,s)φ(s)ds+f(x).{\displaystyle \varphi (x)=\lambda \int \limits _{a}^{b}K(x,\;s)\varphi (s)\,ds+f(x).}
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: a⩽x,s⩽b{\displaystyle a\leqslant x,\;s\leqslant b}, а ядро и свободный член должны быть непрерывными: K(x,s)∈C(a⩽x,s⩽b),f(x)∈C([a,b]){\displaystyle K(x,\;s)\in C(a\leqslant x,\;s\leqslant b),\;f(x)\in C([a,\;b])}, либо удовлетворять условиям:
- ∫ab∫ab|K(x,s)|2dxds<+∞,∫ab|f(x)|2dx<+∞.{\displaystyle \int \limits _{a}^{b}\int \limits _{a}^{b}|K(x,\;s)|^{2}\,dx\,ds<+\infty ,\qquad \int \limits _{a}^{b}|f(x)|^{2}\,dx<+\infty .}
Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если f(x)≡0{\displaystyle f(x)\equiv 0} на [a,b]{\displaystyle [a,\;b]}, то уравнение называется однородным, иначе оно называется неоднородным интегральным уравнением.
Уравнения Фредгольма 1-го рода[править | править код]
Уравнения Фредгольма 1-го рода выглядят так же, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
- ∫abK(x,s)φ(s)ds=f(x),{\displaystyle \int \limits _{a}^{b}K(x,\;s)\varphi (s)\,ds=f(x),}
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 2-го рода.
Уравнения Вольтерры[править | править код]
Уравнения Вольтерры 2-го рода[править | править код]
Уравнения Вольтерры отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
- φ(x)=λ∫axK(x,s)φ(s)ds+f(x),a⩽x⩽b.{\displaystyle \varphi (x)=\lambda \int \limits _{a}^{x}K(x,\;s)\varphi (s)\,ds+f(x),\qquad a\leqslant x\leqslant b.}
Уравнения Вольтерры 1-го рода[править | править код]
Также, как и для уравнений Фредгольма, в уравнениях Вольтерры 1-го рода отсутствует неизвестная функция вне интеграла:
- ∫axK(x,s)φ(s)ds=f(x).{\displaystyle \int \limits _{a}^{x}K(x,\;s)\varphi (s)\,ds=f(x).}
В принципе, уравнения Вольтерры можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
- K(x,s)={K(x,s),a⩽s⩽x,0,x<s⩽b.{\displaystyle {\mathcal {K}}(x,\;s)={\begin{cases}K(x,\;s),&a\leqslant s\leqslant x,\\0,&x<s\leqslant b.\end{cases}}}
Однако некоторые свойства уравнений Вольтерры не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения[править | править код]
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона[править | править код]
- φ(x)=∫abK(x,s,φ(s))ds,K(x,s,φ)∈C(a⩽x,s⩽b;−M⩽φ⩽M).{\displaystyle \varphi (x)=\int \limits _{a}^{b}K(x,\;s,\;\varphi (s))\,ds,\qquad K(x,\;s,\;\varphi )\in C(a\leqslant x,\;s\leqslant b;\;-M\leqslant \varphi \leqslant M).}
Постоянная M{\displaystyle M} — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна[править | править код]
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
- φ(x)=∫abK(x,s)F(s,φ(s))ds,{\displaystyle \varphi (x)=\int \limits _{a}^{b}K(x,\;s)F(s,\;\varphi (s))\,ds,}
где K(x,s){\displaystyle K(x,\;s)} — фредгольмово ядро.
Уравнения Ляпунова — Лихтенштейна[править | править код]
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
- φ(x)=f(x)+λ∫abK[1](x,s)φ(s)ds+μ∫ab∫abK[1,1](x,s,z)φ(x)φ(z)dsdz+…{\displaystyle \varphi (x)=f(x)+\lambda \int \limits _{a}^{b}K_{[1]}(x,\;s)\varphi (s)\,ds+\mu \int \limits _{a}^{b}\int \limits _{a}^{b}K_{[1,\;1]}(x,\;s,\;z)\varphi (x)\varphi (z)\,ds\,dz+\ldots }
Нелинейное уравнение Вольтерры[править | править код]
- φ(x)=∫axF(x,s,φ(s))ds,{\displaystyle \varphi (x)=\int \limits _{a}^{x}F(x,\;s,\;\varphi (s))\,ds,}
где функция F(x,s,φ){\displaystyle F(x,\;s,\;\varphi )} непрерывна по совокупности своих переменных.
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений, не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа[править | править код]
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
- ∫0xf(x−t)g(t)dt≓F(p)G(p),{\displaystyle \int \limits _{0}^{x}f(x-t)g(t)\,dt\risingdotseq F(p)G(p),}
то есть, когда ядро является функцией разности двух переменных:
- φ(x)=f(x)+∫0xK(x−s)φ(s)ds.{\displaystyle \varphi (x)=f(x)+\int \limits _{0}^{x}K(x-s)\varphi (s)\,ds.}
Например, дано такое уравнение:
- φ(x)=sinx+2∫0xcos(x−s)φ(s)ds.{\displaystyle \varphi (x)=\sin x+2\int \limits _{0}^{x}\cos(x-s)\varphi (s)\,ds.}
Применим преобразование Лапласа к обеим частям уравнения:
- φ(x)≓Φ(p),{\displaystyle \varphi (x)\risingdotseq \Phi (p),}
- Φ(p)=11+p2+2p1+p2Φ(p)⇒Φ(p)=1(p−1)2.{\displaystyle \Phi (p)={\frac {1}{1+p^{2}}}+2{\frac {p}{1+p^{2}}}\Phi (p)\Rightarrow \Phi (p)={\frac {1}{(p-1)^{2}}}.}
Применяя обратное преобразование Лапласа, получим:
- φ(x)=resp=11(p−1)2epx=(epx)p′|p=1=xex.{\displaystyle \varphi (x)={\underset {p=1}{\mathrm {res} }}\,{\frac {1}{(p-1)^{2}}}e^{px}=(e^{px})’_{p}{\Big |}_{p=1}=xe^{x}.}
Метод последовательных приближений[править | править код]
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
- |λ||b−a|maxa⩽x,s⩽b|K(x,s)|<1.{\displaystyle |\lambda ||b-a|\max _{a\leqslant x,\;s\leqslant b}|K(x,\;s)|<1.}
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
- φ(x)=∑k=0∞λk(Kkf)(x),{\displaystyle \varphi (x)=\sum _{k=0}^{\infty }\lambda ^{k}(K^{k}f)(x),}
который и является решением уравнения. (Kkf)(x){\displaystyle (K^{k}f)(x)} — k{\displaystyle k}-ая степень интегрального оператора (Kf)(x){\displaystyle (Kf)(x)}:
- (Kf)(x)=∫abK(x,s)f(s)ds.{\displaystyle (Kf)(x)=\int \limits _{a}^{b}K(x,\;s)f(s)\,ds.}
Впрочем, такое решение является хорошим приближением лишь при достаточно малых |λ|{\displaystyle |\lambda |}.
Этот метод применим также и при решении уравнений Вольтерры 2-го рода. В таком случае ряд Лиувилля — Неймана сходится при любых значениях |λ|{\displaystyle |\lambda |}, а не только при малых.
Метод резольвент[править | править код]
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
- K0(x,t)=K(x,t),K1(t,s)=K(t,s),{\displaystyle {\begin{aligned}K_{0}(x,\;t)=K(x,\;t),\\K_{1}(t,\;s)=K(t,\;s),\end{aligned}}}
то повторными ядрами ядра K(x,s){\displaystyle K(x,\;s)} будут ядра Kp(x,s){\displaystyle K_{p}(x,\;s)}:
- Kp(x,s)=∫abK(x,t)Kp−1(t,s)dt.{\displaystyle K_{p}(x,\;s)=\int \limits _{a}^{b}K(x,\;t)K_{p-1}(t,\;s)\,dt.}
Ряд, составленный из повторных ядер,
- R(x,s,λ)=∑k=0∞λkKk+1(x,s),{\displaystyle {\mathcal {R}}(x,\;s,\;\lambda )=\sum _{k=0}^{\infty }\lambda ^{k}K_{k+1}(x,\;s),}
называется резольвентой ядра K(x,s){\displaystyle K(x,\;s)} и является регулярно сходящимся при a⩽x{\displaystyle a\leqslant x}, s⩽b{\displaystyle s\leqslant b} и вышеупомянутому условию сходимости ряда Лиувилля — Неймана. Решение интегрального уравнения представляется по формуле:
- φ(x)=f(x)+λ∫abR(x,s,λ)f(s)ds.{\displaystyle \varphi (x)=f(x)+\lambda \int \limits _{a}^{b}{\mathcal {R}}(x,\;s,\;\lambda )f(s)\,ds.}
Например, для интегрального уравнения
- φ(x)=f(x)+λ∫01xsφ(s)ds{\displaystyle \varphi (x)=f(x)+\lambda \int \limits _{0}^{1}xs\varphi (s)\,ds}
повторными будут следующие ядра:
- K0(x,s)=xs,{\displaystyle K_{0}(x,\;s)=xs,}
- K1(x,t)=xt,{\displaystyle K_{1}(x,\;t)=xt,}
- K2(x,t)=∫01xsstds=xt3,{\displaystyle K_{2}(x,\;t)=\int \limits _{0}^{1}xs\,st\,ds={\frac {xt}{3}},}
- K3(x,t)=∫01xsst3ds=xt9,{\displaystyle K_{3}(x,\;t)=\int \limits _{0}^{1}xs{\frac {st}{3}}\,ds={\frac {xt}{9}},}
- …{\displaystyle \ldots }
- Kn+1=xt3n,{\displaystyle K_{n+1}={\frac {xt}{3^{n}}},}
а резольвентой — функция
- R(x,t,λ)=∑n=0∞λnKn+1=∑n=0∞λnxt3n=xt11−λ3=3xt3−λ.{\displaystyle {\mathcal {R}}(x,\;t,\;\lambda )=\sum _{n=0}^{\infty }\lambda ^{n}K_{n+1}=\sum _{n=0}^{\infty }\lambda ^{n}{\frac {xt}{3^{n}}}=xt{\frac {1}{1-{\dfrac {\lambda }{3}}}}={\frac {3xt}{3-\lambda }}.}
Тогда решение уравнения находится по формуле:
- φ(x)=f(x)+λ∫013xt3−λf(t)dt.{\displaystyle \varphi (x)=f(x)+\lambda \int \limits _{0}^{1}{\frac {3xt}{3-\lambda }}f(t)\,dt.}
Метод сведения к алгебраическому уравнению[править | править код]
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть K(x,s)=∑i=1Nfi(x)gi(s){\displaystyle K(x,\;s)=\sum _{i=1}^{N}f_{i}(x)g_{i}(s)}, само интегральное уравнение можно свести к системе алгебраических уравнений. Действительно, в этом случае уравнение можно переписать так:
- φ(x)=λ∑i=1Nfi(x)∫abgi(s)φ(s)ds+f(x)=λ∑i=1Ncifi(x)+f(x),{\displaystyle \varphi (x)=\lambda \sum _{i=1}^{N}f_{i}(x)\int \limits _{a}^{b}g_{i}(s)\varphi (s)\,ds+f(x)=\lambda \sum _{i=1}^{N}c_{i}f_{i}(x)+f(x),}
где ci=∫abφ(s)gi(s)ds{\displaystyle c_{i}=\int \limits _{a}^{b}\varphi (s)g_{i}(s)\,ds}. Умножив предыдущее равенство на gi(x){\displaystyle g_{i}(x)} и проинтегрировав его по x{\displaystyle x} на отрезке [a,b]{\displaystyle [a,\;b]}, приходим к системе алгебраических уравнений для неизвестных чисел ci{\displaystyle c_{i}}:
- ci=λ∑k=0Naikck+bi,i=1,…,N,{\displaystyle c_{i}=\lambda \sum _{k=0}^{N}a_{ik}c_{k}+b_{i},\qquad i=1,\;\ldots ,\;N,}
где aik=∫abgi(x)fk(x)dx{\displaystyle a_{ik}=\int \limits _{a}^{b}g_{i}(x)f_{k}(x)\,dx} и bi=∫abgi(x)f(x)dx{\displaystyle b_{i}=\int \limits _{a}^{b}g_{i}(x)f(x)\,dx} — числовые коэффициенты.
Приближённо этим методом можно решить интегральное уравнение Фредгольма с любым ядром, если в качестве вырожденного ядра, близкого к действительному, взять отрезок ряда Тейлора для функции K(x,s){\displaystyle K(x,\;s)}
Интегральные уравнения и их решение
Определения и формулы интегральных уравнений
Например.
Например.
Здесь — неизвестная функция, относительно которое ищется решение, — заданные функции; — параметр. Функция называется ядром, а функция — свободным членом интегрального уравнения.
Если , то интегральное уравнение называется однородным; в противном случае — неоднородным.
В зависимости от вида ядра и свободного члена линейные уравнения можно разделить на несколько видов.
Интегральные уравнения Фредгольма
Уравнения Фредгольма первого рода называется интегральное уравнение вида
Например.
Интегральным уравнением Фредгольма второго рода называется уравнение вида
Пределы интегрирования — и — могут быть как конечными, так и бесконечными.
Например. }
Интегральные уравнения Вольтерра
Уравнения Вольтерра первого рода — это интегральное уравнение вида
Например.
Интегральным уравнением Вольтерра второго рода называется уравнение
Например.
Следующие уравнения относятся к нелинейным интегральным уравнениям.
Интегральным уравнением Урысона называется уравнение
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
Уравнением Ляпунова-Лихтенштейна принято называть уравнение, содержащее существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерры — это уравнение
где функция непрерывна по совокупности своих переменных.
Интегральные уравнения — это… Что такое Интегральные уравнения?
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.Классификация интегральных уравнений
Линейные интегральные уравнения
Это интегральные уравнения, в которые неизвестная функция входит линейно:
где 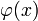 — искомая функция, f(x),
— искомая функция, f(x), 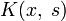 — известные функции, λ — параметр. Функция
— известные функции, λ — параметр. Функция 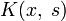
Уравнения Фредгольма
Уравнения Фредгольма 2-го рода
Уравнения Фредгольма 2-го рода — это уравнения вида:
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: 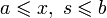 , а ядро и свободный член должны быть непрерывными:
, а ядро и свободный член должны быть непрерывными: ![K(x,\;s)\in C(a\leqslant x,\;s\leqslant b),\;f(x)\in C([a,\;b])](/800/600/https/dic.academic.ru/pictures/wiki/files/51/33aa54d6203d2f6dd5f0fca7afede0ce.png) , либо удовлетворять условиям:
, либо удовлетворять условиям:
Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если 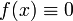 на
на ![[a,\;b]](/800/600/https/dic.academic.ru/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) , то уравнение называется однородным, иначе оно называется неоднородным интегральным уравнением.
, то уравнение называется однородным, иначе оно называется неоднородным интегральным уравнением.
Уравнения Фредгольма 1-го рода
Уравнения Фредгольма 1-го рода выглядят также, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 1-го рода.
Уравнения Вольтерра
Основная статья: Интегральное уравнение Вольтерра
Уравнения Вольтерра 2-го рода
Уравнения Вольтера отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
Уравнения Вольтерра 1-го рода
Также, как и для уравнений Фредгольма, в уравнениях Вольтерра 1-го рода отсутствует неизвестная функция вне интеграла:
В принципе, уравнения Вольтерра можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
Однако некоторые свойства уравнений Вольтерра не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона
Основная статья: Интегральное уравнение Урысона
Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
где 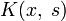 — фредгольмово ядро.
— фредгольмово ядро.
Уравнения Ляпунова — Лихтенштейна
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерра
где функция 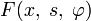 непрерывна по совокупности своих переменных.
непрерывна по совокупности своих переменных.
Методы решения
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
то есть, когда ядро является функцией разности двух переменных:
Например, дано такое уравнение:
Применим преобразование Лапласа к обеим частям уравнения:
Применяя обратное преобразование Лапласа, получим:
Метод последовательных приближений
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
который и является решением уравнения. (Kkf)(x) — k-ая степень интегрального оператора (Kf)(x):
Впрочем, такое решение является хорошим приближением лишь при достаточно малых | λ | .
Метод резольвент
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
то повторными ядрами ядра 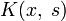 будут ядра
будут ядра  :
:
Ряд, составленный из повторных ядер,
называется резольвентой ядра 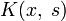 и является регулярно сходящимся при
и является регулярно сходящимся при 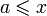 ,
,  и вышеупомянутому условию сходимости ряда Лиувилля — Неймана. Решение интегрального уравнения представляется по формуле:
и вышеупомянутому условию сходимости ряда Лиувилля — Неймана. Решение интегрального уравнения представляется по формуле:
Например, для интегрального уравнения
повторными будут следующие ядра:
а резольвентой — функция
Тогда решение уравнения находится по формуле:
Метод сведения к алгебраическому уравнению
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть  , само интегральное уравнение можно свести к системе алгебраических уравнений. Действительно, в этом случае уравнение можно переписать так:
, само интегральное уравнение можно свести к системе алгебраических уравнений. Действительно, в этом случае уравнение можно переписать так:
где  . Умножив предыдущее равенство на gi(x) и проинтегрировав его по x на отрезке
. Умножив предыдущее равенство на gi(x) и проинтегрировав его по x на отрезке ![[a,\;b]](/800/600/https/dic.academic.ru/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) , приходим к системе алгебраических уравнений для неизвестных чисел ci:
, приходим к системе алгебраических уравнений для неизвестных чисел ci:
где 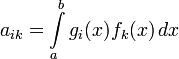 и
и 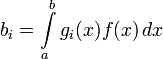 — числовые коэффициенты.
— числовые коэффициенты.
Приложения
Термин «интегральное уравнение» ввёл в 1888 году Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.
Формула обращения Фурье
Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x):
Фурье получил выражение для функции f(y):
Сведение задачи Коши к интегральному уравнению
К нелинейным интегральным уравнениям Вольтерра приводит задача Коши для обыкновенных дифференциальных уравнений:
В самом деле, это уравнение можно проинтегрировать по t от a до t:
Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерра 2-го рода. Этим еще в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:
Для уравнения с постоянными коэффициентами с теми же начальными условиями:
- x»(t) + λ2x(t) = g(t)
решение может быть найдено методом вариации постоянных и представлено в виде:
Тогда для исходного уравнения получается:
— интегральное уравнение Вольтерра 2-го рода.
Линейное дифференциальное уравнение n-го порядка
также может быть сведено к интегральному уравнению Вольтерра 2-го рода.
Задача Абеля
Основная статья: Задача о таутохроне
Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:
где f(x) — заданная функция, а 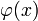 — искомая. Это уравнение есть частный случай линейного интегрального уравнения Вольтерра 1-го рода. Уравнение Абеля интересно тем, что к нему непосредственно приводит постановка той или иной конкретной задачи механики или физики (минуя дифференциальные уравнения).
— искомая. Это уравнение есть частный случай линейного интегрального уравнения Вольтерра 1-го рода. Уравнение Абеля интересно тем, что к нему непосредственно приводит постановка той или иной конкретной задачи механики или физики (минуя дифференциальные уравнения).
У Абеля формулировка задачи выглядела примерно так:
Материальная точка под действием силы тяжести движется в вертикальной плоскости
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x, достигла оси Oξ за время t = f1(x), где f1(x) — заданная функция.
Если обозначить угол между касательной к траектории и осью Oξ как β и применить законы Ньютона, можно прийти к следующему уравнению:
См. также
Литература
- М. Л. Краснов. Интегральные уравнения: введение в теорию. — М.: Наука, 1975.
- В. С. Владимиров, В. В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
Wikimedia Foundation. 2010.
интегральное уравнение — Integral equation
В математике , интегральные уравнения являются уравнениями , в которых неизвестная функция появляется под интегралом знака.
Существует тесная связь между дифференциалом и интегральными уравнениями, и некоторые проблемы могут быть сформулированы так или иначе. Смотрите, например, функция Грина , теория Фредгольма и уравнения Максвелла .
обзор
Самый основной тип интегрального уравнения называется уравнением Фредгольма первого типа ,
- е(Икс)знак равно∫aбК(Икс,T)φ(T)dT,{\ Displaystyle F (X) = \ Int _ {а} ^ {Ь} К (х, т) \, \ varphi (т) \, дт.}
Обозначения следующим образом Arfken . Здесь φ является неизвестной функцией, е является известной функцией, а K является еще одной известной функцией двух переменных, часто называют ядром функции. Обратите внимание , что пределы интегрирования постоянны: это то , что характеризует уравнение Фредгольма.
Если неизвестная функция происходит как внутри , так и за ее пределы интеграла, уравнение известно как уравнение Фредгольма второго типа ,
- φ(Икс)знак равное(Икс)+λ∫aбК(Икс,T)φ(T)dT,{\ Displaystyle \ varphi (х) = Р (х) + \ Lambda \ Int _ {A} ^ {B} К (х, т) \, \ varphi (T) \, дт.}
Параметр λ является неизвестным фактором, который играет ту же роль, что и собственное значение в линейной алгебре .
Если один предел интегрирования является переменной, уравнение называется уравнением Вольтерра . Называются следующие уравнения Вольтерра первого и второго типов , соответственно,
- е(Икс)знак равно∫aИксК(Икс,T)φ(T)dT{\ Displaystyle F (X) = \ Int _ {а} ^ {х} К (х, т) \, \ varphi (т) \, дт}
- φ(Икс)знак равное(Икс)+λ∫aИксК(Икс,T)φ(T)dT,{\ Displaystyle \ varphi (х) = Р (х) + \ Lambda \ Int _ {A} ^ {х} К (х, т) \, \ varphi (T) \, дт.}
Во всех выше, если известная функция F тождественно равна нулю, то уравнение называется однородным интегральное уравнение . Если е не равен нулю, то она называется неоднородным интегральное уравнение .
Численное решение
Стоит отметить , что интегральные уравнения часто не имеют аналитического решения, и должны быть решены численно. Пример этого является оценка интегрального уравнения электрического поля (EFIE) или магнитного поле интегрального уравнения (MFIE) над произвольной формой объектом в электромагнитной задаче рассеяния.
Один из методов численного решения требует дискретизацию переменных и замены интеграла квадратурного правила
- ΣJзнак равно1NвесJК(sя,TJ)U(TJ)знак равное(sя),язнак равно0,1,⋯,N,{\ Displaystyle \ сумма _ {= 1} ^ {п} w_ {J} К \ влево (S_ {I}, T_ {J} \ справа) и (T_ {J}) = F (S_ {я}) , \ qquad I = 0,1, \ cdots, п.}
Тогда мы имеем систему с п уравнений и п переменных. Решая ее , мы получаем значение из п переменных
- U(T0),U(T1),⋯,U(TN),{\ Displaystyle и (Т_ {0}), и (T_ {1}), \ cdots, и (T_ {п}).}
классификация
Интегральные уравнения классифицируются по трем различным дихотомии, создавая восемь различных видов:
- Пределы интегрирования
- Размещение неизвестной функции
- только внутри интеграла: первого рода
- как внутри , так и вне интеграла: второго рода
- Характер известной функции F
- тождественно нулю: однородная
- не тождественно равна нулю: неоднородное
Интегральные уравнения имеют важное значение во многих приложениях. Задачи , в которых встречаются интегральные уравнения включают перенос излучения , а также колебания строкового, мембраны или оси. Проблемы Осцилляционных также могут быть решены в дифференциальных уравнениях .
Оба Фредгольмовы и вольтерровы уравнения являются линейными интегральными уравнениями, из — за линейное поведение ф ( х ) под знаком интеграла. Нелинейное интегральное уравнение Вольтерра имеет общий вид:
- φ(Икс)знак равное(Икс)+λ∫aИксК(Икс,T)F(Икс,T,φ(T))dT,{\ Displaystyle \ varphi (х) = Р (х) + \ Lambda \ Int _ {а} ^ {х} К (х, т) \, Р (х, т, \ varphi (т)) \, дт, }
где Р является известной функцией.
Винера-Хопфа интегральные уравнения
- Y(T)знак равноλИкс(T)+∫0∞К(T-s)Икс(s)ds,0≤T<∞,{\ Displaystyle у (г) = \ лямбда х (т) + \ Int _ {0} ^ {\ infty} к (ц) х (з) аз, \ qquad 0 \ Leq т <\ infty.}
Первоначально, были изучены такие уравнения в связи с проблемами переноса излучения, а в последнее время, они были связаны с решением граничных интегральных уравнений для плоских задач, в которых граница является только кусочно-гладким.
Степенные ряды решение интегральных уравнений
Во многих случаях, если ядро интегрального уравнения имеет вид К ( хгу ) и Меллин из К ( т ) существует, мы можем найти решение интегрального уравнения
- г(s)знак равноs∫0∞dTК(sT)е(T){\ Displaystyle г (з) = s \ Int _ {0} ^ {\ infty} DTK (й) е (т)}
в виде степенного ряда
- е(T)знак равноΣNзнак равно0∞aNM(N+1)TN{\ Displaystyle е (т) = \ сумма _ {п = 0} ^ {\ infty} {\ гидроразрыва {а_ {п}} {М (п + 1)}} т ^ {п}}
где
- г(s)знак равноΣNзнак равно0∞aNs-N,M(N+1)знак равно∫0∞dTК(T)TN{\ Displaystyle г (з) = \ сумма _ {п = 0} ^ {\ infty} а_ {п} с ^ {- п}, \ qquad М (п + 1) = \ Int _ {0} ^ {\ infty} DTK (т) т ^ {п}}
являются Z — преобразование функции г ( ов ) , а М ( п + 1) , представляет собой преобразование Меллина ядра.
Интегральные уравнения как обобщение собственных значений уравнений
Некоторые однородные линейные интегральные уравнения можно рассматривать как предел континуального собственных значений уравнений . Используя индекс обозначения , собственное уравнение может быть записано в виде
- ΣJMя,JvJзнак равноλvя{\ Displaystyle \ сумма _ {j} M_ {I, J} V_ {j} = \ лямбда V_ {я}}
где М = [ М I, J ] представляет собой матрицу, v является одним из его собственных векторов, и λ является ассоциированным собственным значением.
Переходя к пределу континуума, то есть, заменив дискретные индексы я и J с непрерывными переменными х и у , урожайность
- ∫К(Икс,Y)φ(Y)dYзнак равноλφ(Икс),{\ Displaystyle \ Int К (х, у) \ varphi (у) \ mathrm {д} у = \ Lambda \ varphi (х),}
где сумма по J была заменена на интеграл по у и матрица М , а вектор v были заменены на ядре К ( х , у ) и собственная функции ф ( у ) . (Пределы интеграла фиксированы, аналогично ограничениям на сумму свыше J ) . Это дает линейное однородное уравнение Фредгольма второго типа.
В общем, К ( х , у ) может быть распределение , а не функция в строгом смысле этого слова. Если распределение К имеет поддержку только в точке х = у , то интегральное уравнение сводится к уравнению дифференциальной собственной функции .
В общем, вольтерровы и фредгольмов интегральные уравнения могут возникать из одного дифференциального уравнения, в зависимости от того, какого вида условий применяются на границе области ее решения.
Смотрите также
Рекомендации
- Kendall Е. Аткинсон Численное решение интегральных уравнений второго рода . Cambridge Монографии по прикладной и вычислительной математики, 1997.
- Джордж Arfken и Ганс Вебер. Математические методы для физиков . Харкорт / Academic Press, 2000.
- Гарри Bateman (1910) История и современное состояние теории интегральных уравнений , отчет о Британской ассоциации .
- А. Д. Полянин и Александр Manzhirov В. Справочник по интегральным уравнениям . CRC Press, Boca Raton, 1998. ISBN 0-8493-2876-4 .
- ET Уиттакер и Г. Н. Ватсон . Курс современного анализа Кембриджской математической библиотеки.
- М. Краснов, А. Киселев, Г. Макаренко, Проблемы и упражнения в интегральных уравнений , Мир Издатели, Москва, 1971
- Нажмите, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). «Глава 19. Интегральные уравнения и теория обратной задачи» . Числовые Рецепты: Искусство научных вычислений (3 — е изд.). Нью — Йорк: Cambridge University Press. ISBN 978-0-521-88068-8 .
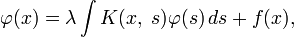

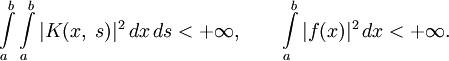
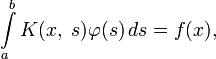
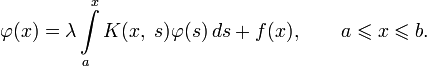

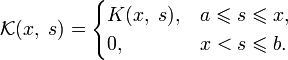

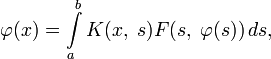
![\varphi(x)=f(x)+\lambda\int\limits_a^b K_{[1]}(x,\;s)\varphi(s)\,ds+\mu\int\limits_a^b\int\limits_a^b K_{[1,\;1]}(x,\;s,\;z)\varphi(x)\varphi(z)\,ds\,dz+\ldots](/800/600/https/dic.academic.ru/pictures/wiki/files/98/b7119825c8fddf18017b640e05cd33be.png)
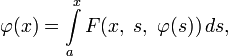
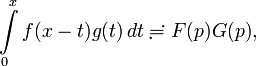
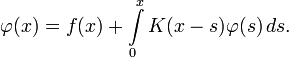
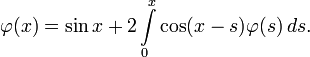
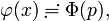


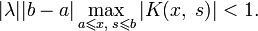
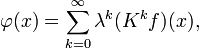
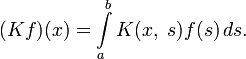
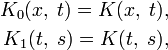
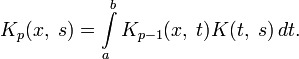

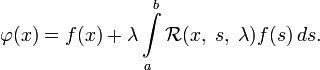
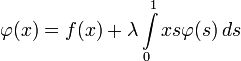
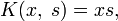
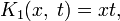


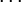
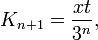
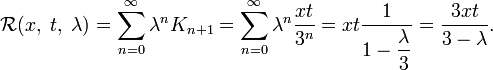
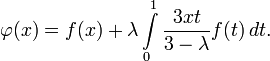
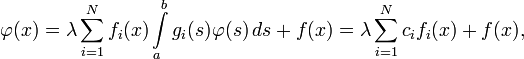

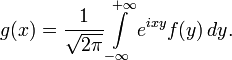
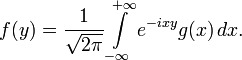
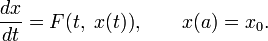

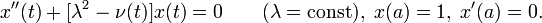
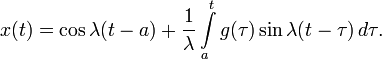
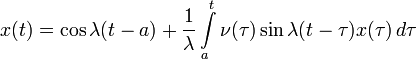
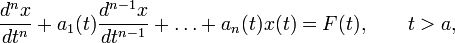


 по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x, достигла оси Oξ за время t = f1(x), где f1(x) — заданная функция.
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x, достигла оси Oξ за время t = f1(x), где f1(x) — заданная функция.