Интегрирование по частям в определенном интеграле
ТЕОРЕМА 6. Пусть функции и(х) и v(x) имеют непрерывные производные на отрезке [а, b]; тогда справедлива формула

Равенство (7.13) называется формулой интегрирования по частям в определенном интеграле. Рассмотрим ряд примеров вычисления определенных интегралов методом интегрирования по частям.

Решение. Положим здесь и = х, v = e-x, тогда dv = -e-xdx и
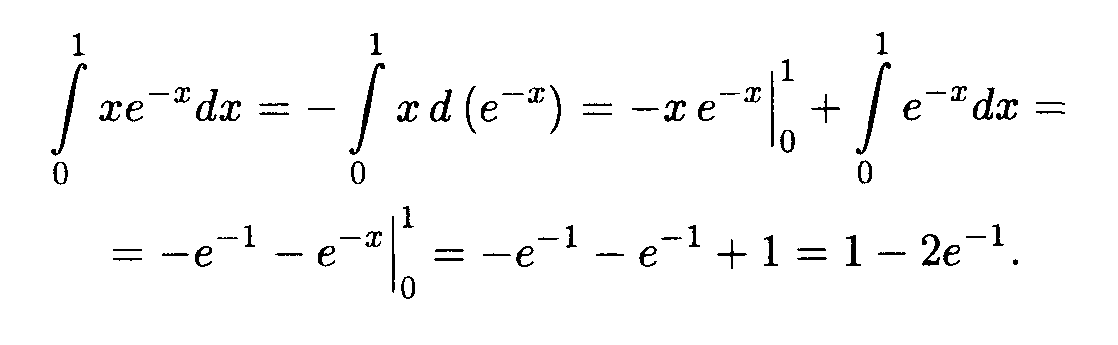

Решение. Здесь и = х, sin x dx = dv или v = — cos x; далее по формуле (7.13) имеем

7.5. Геометрические приложения определенного интеграла Площадь плоской фигуры
Рассмотрим на плоскости Оху фигуру, ограниченную графиком непрерывной и положительной функции f(x) на отрезке [а, b], отрезком [а, b] и вертикальными прямыми х = а и х = b (рис. 7.2). Эту фигуру будем называть криволинейной трапецией.

Величина площади криволинейной трапеции равна определенному интегралу от функции
f(x) на отрезке [а, b]: 
Если фигура ограничена сверху и снизу неотрицательными функциями f(x) и g(х) соответственно, непрерывными на отрезке [а, b], то площадь S криволинейной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху графиками f(x) и g(х):
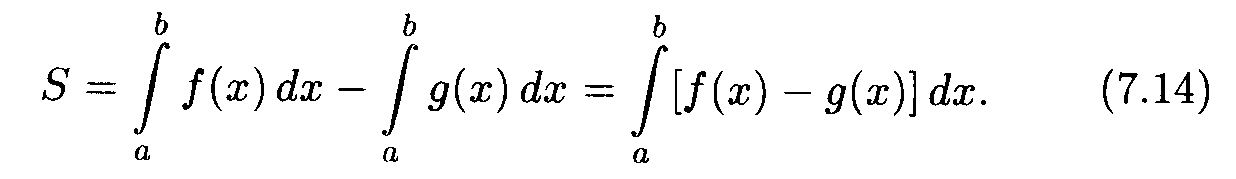
Рассмотрим задачи на вычисление площадей фигур.
Пример 1. Найти площадь фигуры, ограниченной графиком функции у = ln x ≥ 0, осью Ох и прямой х = 2.
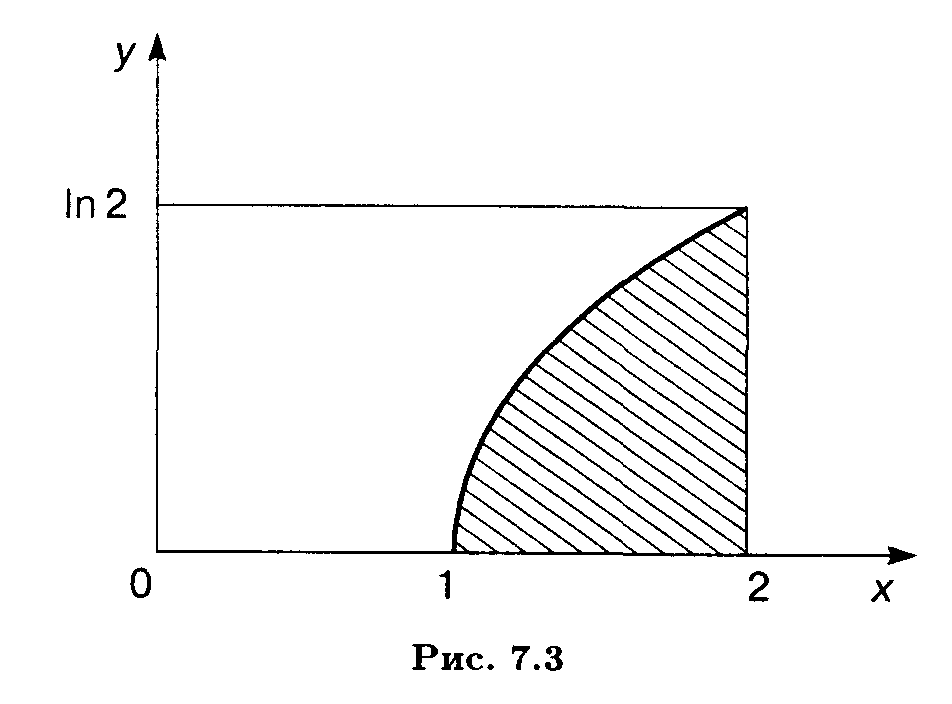
Решение. Отрезок интегрирования: 1 ≤ х ≤ 2 (рис. 7.3), так что искомая площадь согласно формуле (7.14) равна:

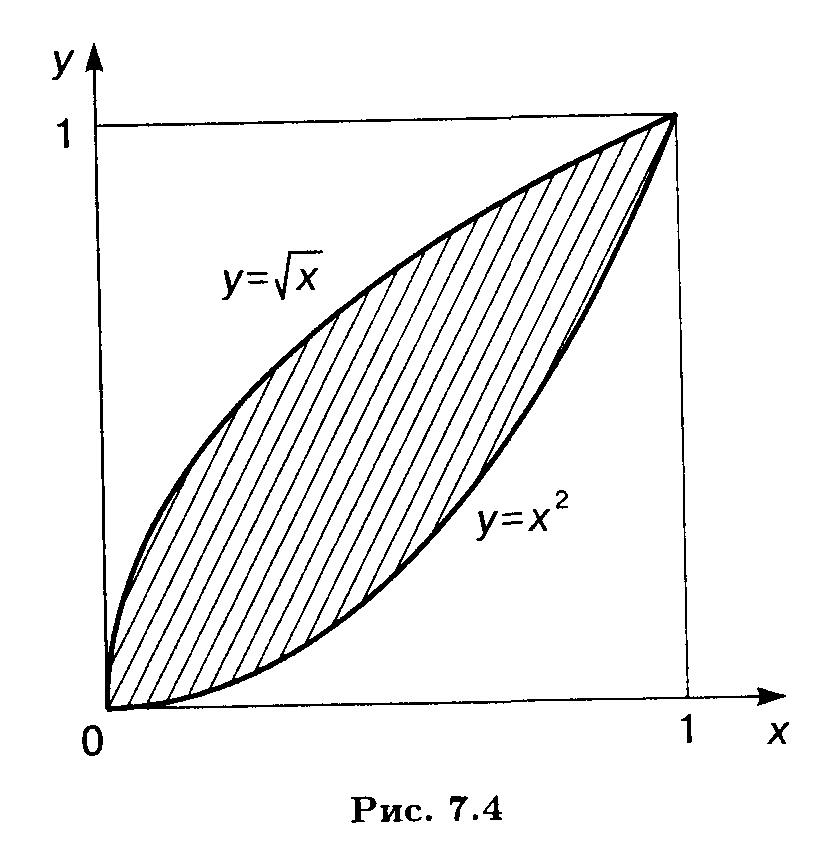
Пример 2. Найти площадь фигуры, ограниченной
линиями у =  ,
у = х2.
,
у = х2.
Решение.
Вычислим абсциссы точек пересечения
указанных кривых, для чего приравняем
правые части этих уравнений: х2 =  . Корни этого уравнения суть x1 = 0, x2 = 1. Следовательно, площадь фигуры,
ограниченной сверху функцией у =
. Корни этого уравнения суть x1 = 0, x2 = 1. Следовательно, площадь фигуры,
ограниченной сверху функцией у =  и снизу функцией у = x2 (рис. 7.4), дается определенным интегралом
на отрезке [0,1]:
и снизу функцией у = x2 (рис. 7.4), дается определенным интегралом
на отрезке [0,1]:

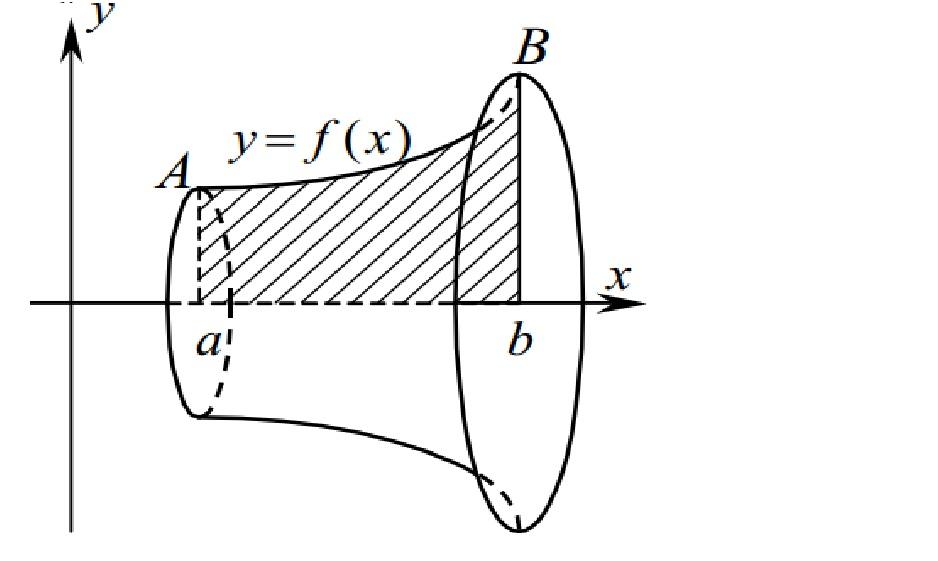
Объем тела вращения
Рассмотрим тело, которое образуется при вращении вокруг оси Ох криволинейной трапеции, ограниченной сверху непрерывной и положительной на отрезке [а, b] функцией f(x) (рис. 7.5). Объем этого тела вращения определяется формулой


Если тело образовано вращением криволинейной трапеции вокруг оси

где [c, d] — область изменения функции у = f(x).
Рассмотрим примеры вычисления объемов тел, образованных вращением фигур, ограниченных следующими линиями.
Пример 3. у = х2,
у =  вокруг оси Ох.
вокруг оси Ох.
Решение.
Искомый объем вращения равен разности
объемов, образованных вращением
криволинейных трапеций с верхними
границами соответственно у =  и у = х2. Пределы интегрирования определяются
по точкам пересечения этих кривых: а = 0 и b =
1.
По формуле
(7.15) получаем
и у = х2. Пределы интегрирования определяются
по точкам пересечения этих кривых: а = 0 и b =
1.
По формуле
(7.15) получаем

Пример 4. у = eх, х = 0, х = 1, у = 0 вокруг оси Оу.
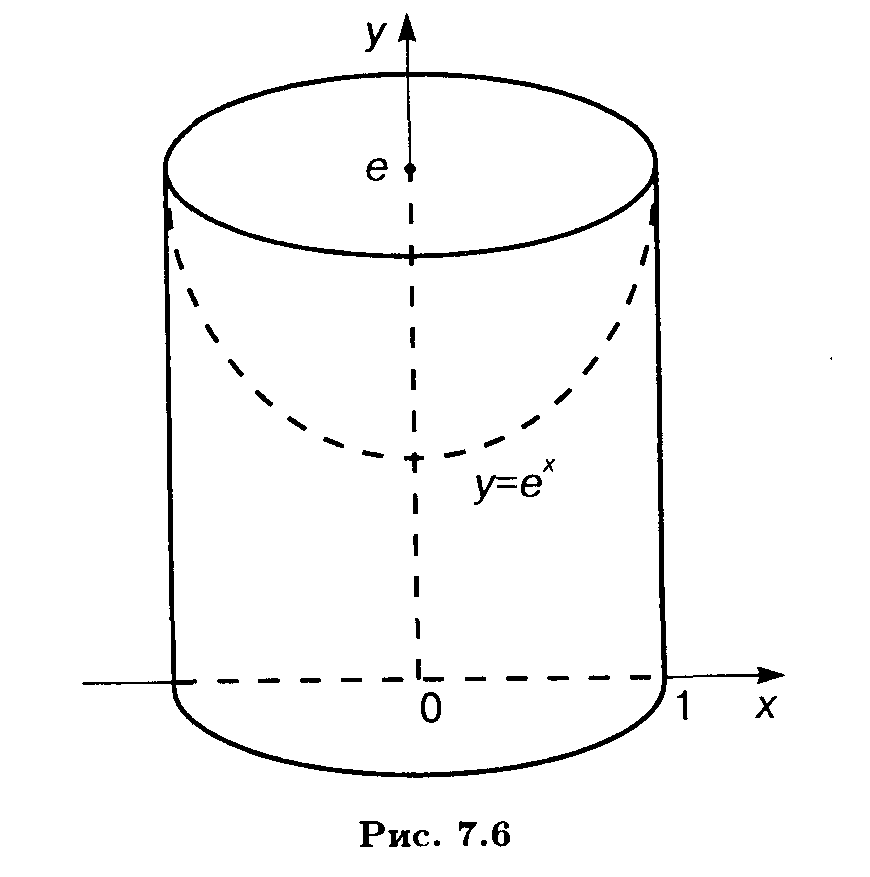
Ррешение. Выражаем х через у: х = ln у; промежуток интегрирования [1, е] определяется очевидным образом. Объем тела вращения (рис. 7.6) равен разности объемов соответственно цилиндра радиуса 1 и высоты е и тела вращения вокруг оси Оу криволинейной трапеции, ограниченной сверху кривой х = ln
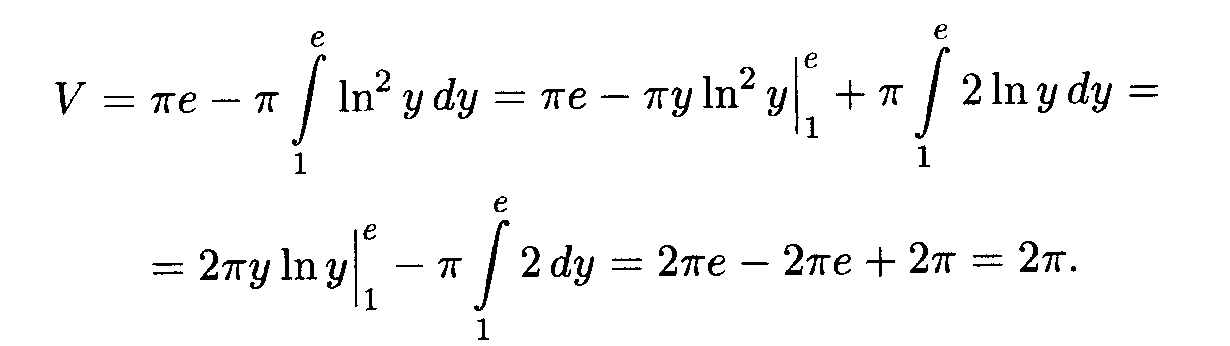
studfile.net
4. Интегрирование подстановкой.
Теорема: Имеет место равенство

где
функция  непрерывно дифференцируема на
непрерывно дифференцируема на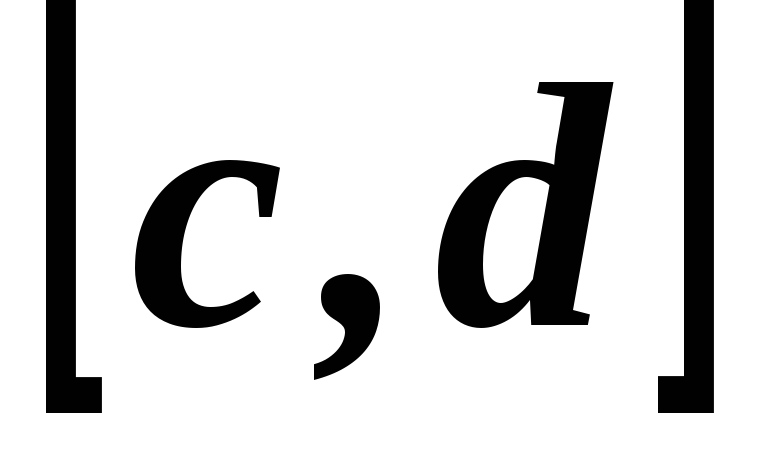 ,
, ,
,
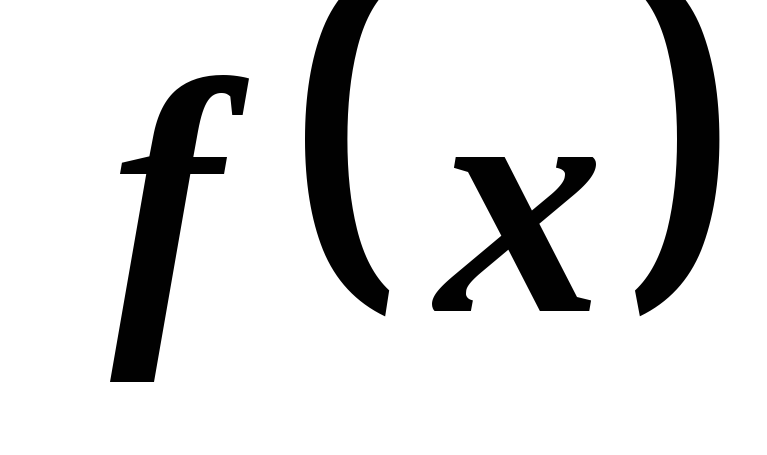 непрерывна на
непрерывна на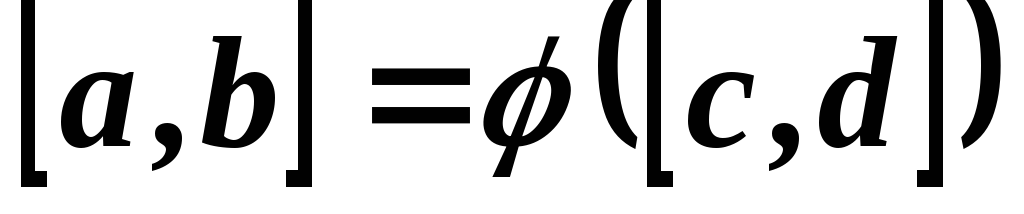 — образе отрезка
— образе отрезка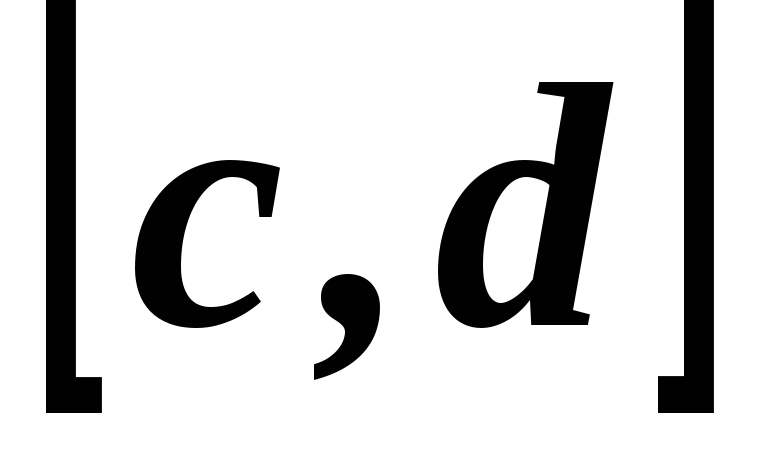 при помощи функции
при помощи функции .
. Доказательство.
Пусть  и
и — первообразные функции соответственно
— первообразные функции соответственно и
и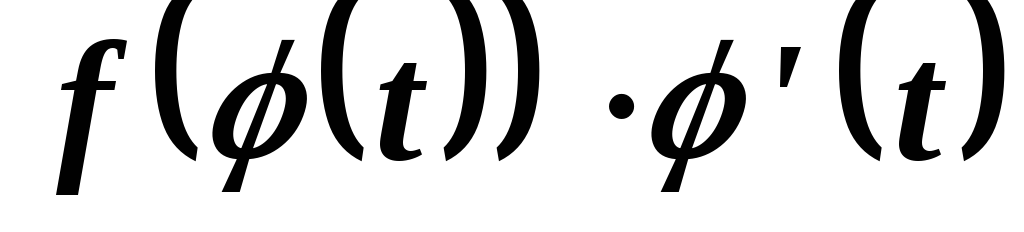 .
Тогда справедливо тождество
.
Тогда справедливо тождество

где  — некоторая постоянная. Поэтому
— некоторая постоянная. Поэтому

На основании формулы Ньютона-Лейбница, левая часть этого равенства равна левой части равенства теоремы, соответственно и правые части, что доказывает теорему.
Пример 1.
Найти интеграл  .
.
Сделаем замену
переменных:  .
Найдем дифференциал
.
Найдем дифференциал :
: .
В результате наш интеграл примет вид:
.
В результате наш интеграл примет вид:
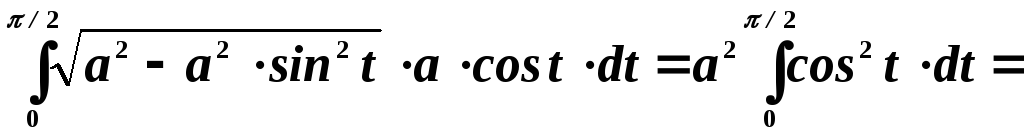
Преобразуем подынтегральное выражение:
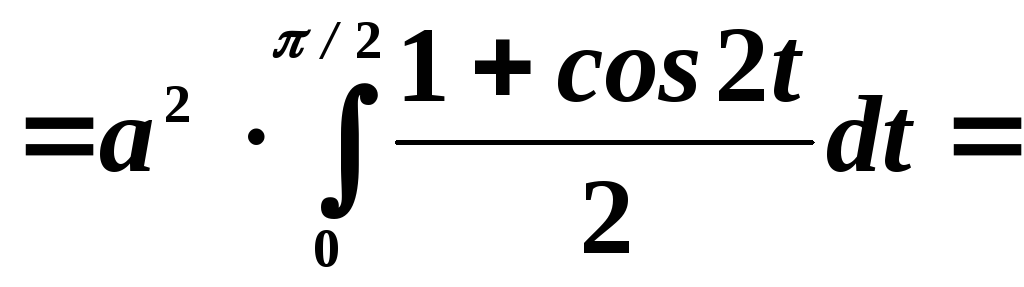
Взяв этот интеграл, получим:
 .
.
5. Интегрирование по частям в определенном интеграле.
Теорема. Справедлива формула интегрирования по частям для определенного интеграла

где  и
и — непрерывно дифференцируемые на
— непрерывно дифференцируемые на
Доказательство.
Произведение  имеет на
имеет на непрерывную производную
непрерывную производную
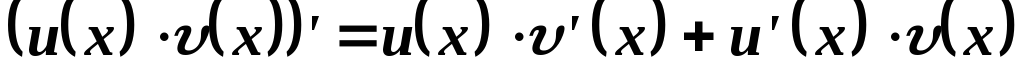
Поэтому по теореме Ньютона-Лейбница

Этим теорема доказана.
Например, найти
интеграл  .
.
Обозначим 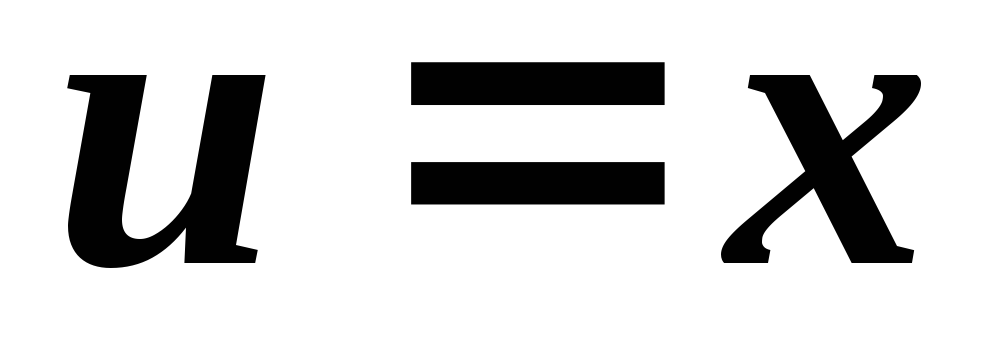 и
и .
Тогда
.
Тогда .
Поэтому
.
Поэтому

Или, окончательно
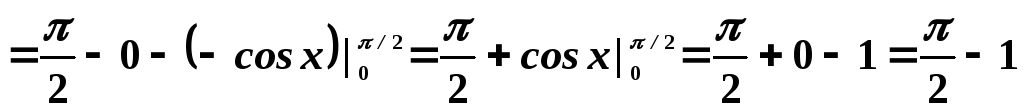 .
.
Если  — четная функция
— четная функция ,
то
,
то
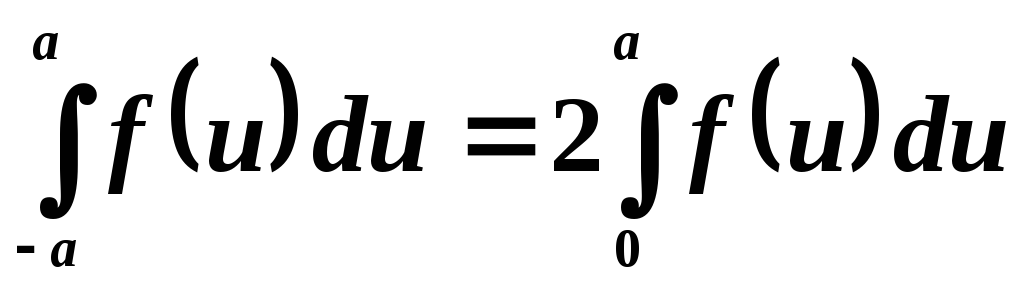
Пример 2. Найти
интеграл 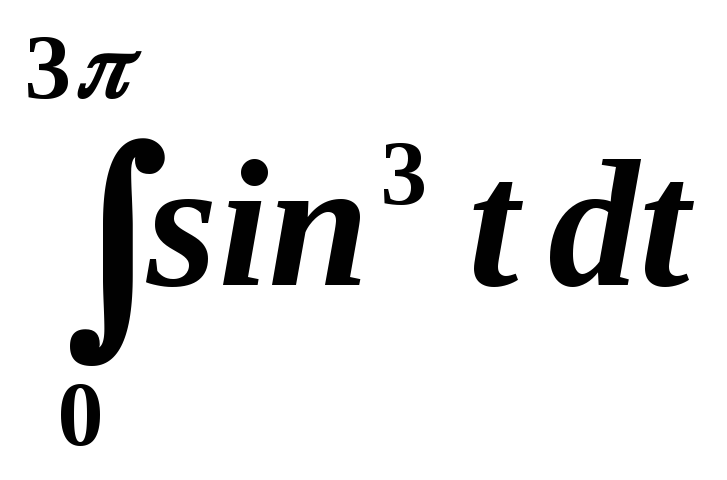 .
.
Преобразуем этот интеграл к виду

Сделаем замену  .
В результате пределы интегрирования
изменятся:
.
В результате пределы интегрирования
изменятся: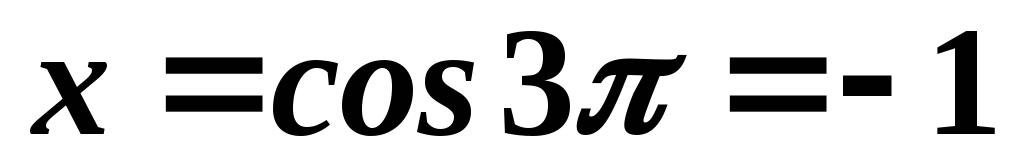 и
и .
В результате получим:
.
В результате получим:


Далее,
если  — нечетная функция
— нечетная функция ,
то
,
то
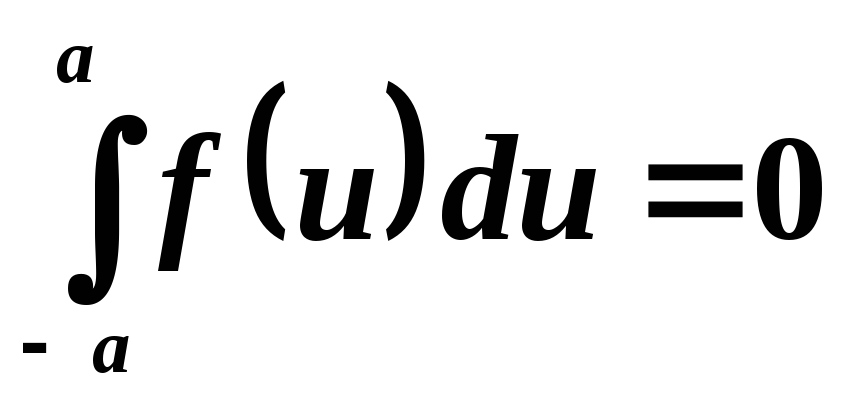 .
.
Если  — периодическая функция периода
— периодическая функция периода —
— ,
то
,
то
 .
.
Такие особенности в некоторых случаях упрощают процесс интегрирования.
Пример 3. Вычислить
интеграл  .
.
Преобразуем этот интеграл к виду:
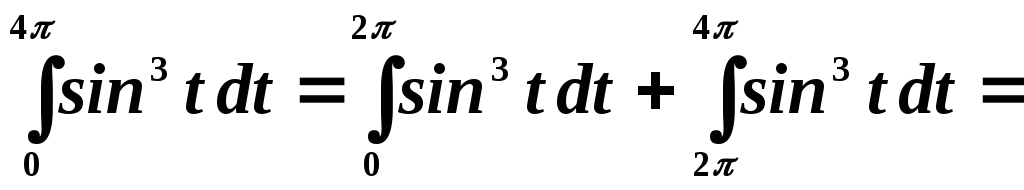
Пределы интегрирования во втором интеграле представим как:

Согласно свойству периодической функции, перепишем это выражение:
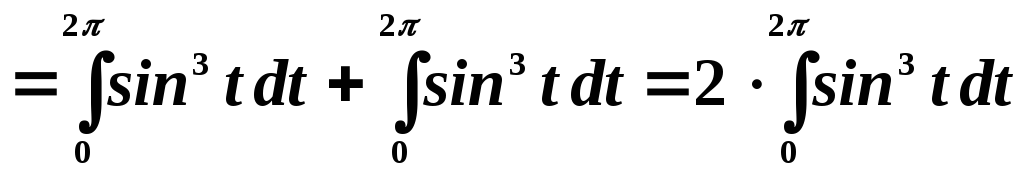
Преобразуем далее
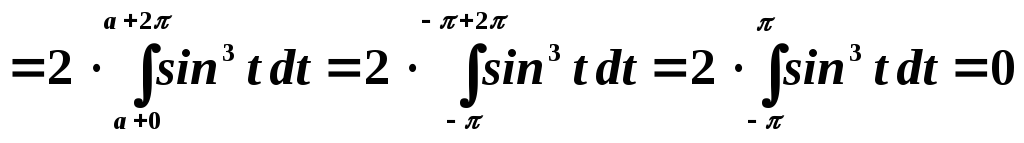
Пример
4. Определить
объем продукции, произведенной рабочим
за третий час рабочего дня, если
производительность труда характеризуется
функцией  .
.
График этой функции имеет вид, изображенный на рисунке.

Решение. Если
непрерывная функция 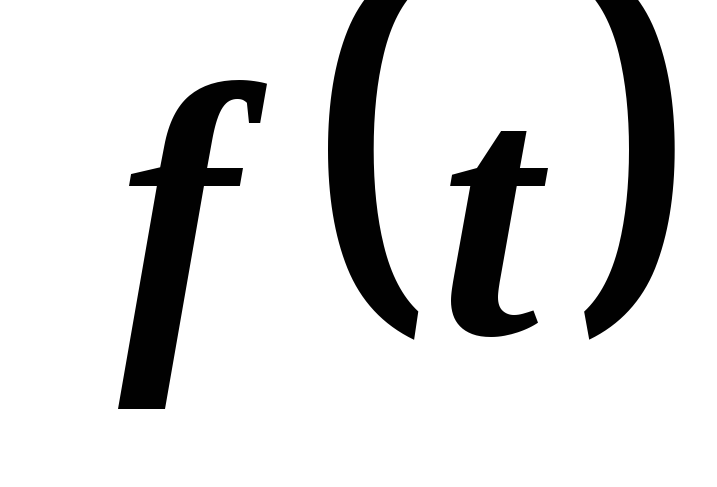 характеризует производительность труда
рабочего в зависимости от времени
характеризует производительность труда
рабочего в зависимости от времени ,
то объем продукции, произведенной
рабочим за промежуток времени от
,
то объем продукции, произведенной
рабочим за промежуток времени от до
до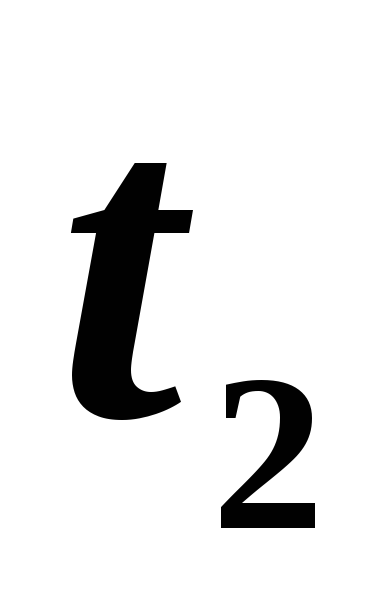 будет выражаться формулой:
будет выражаться формулой:

В нашем случае:
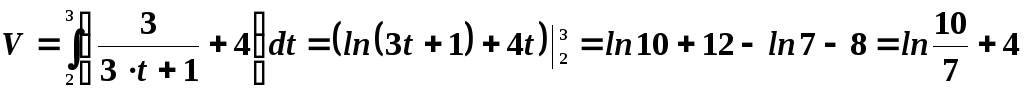
Пример
5. Определить
запас товаров в магазине, образуемый
за три дня, если поступление товаров
характеризуется функцией  .
.
Решение. Имеем:
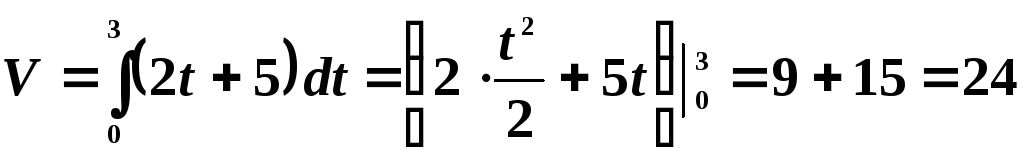
6. Несобственные интегралы.
Пусть
на конечном полуинтервале
задана функция такая, что она интегрируема (т.е. конечна)
на любом интервале
такая, что она интегрируема (т.е. конечна)
на любом интервале ,
где
,
где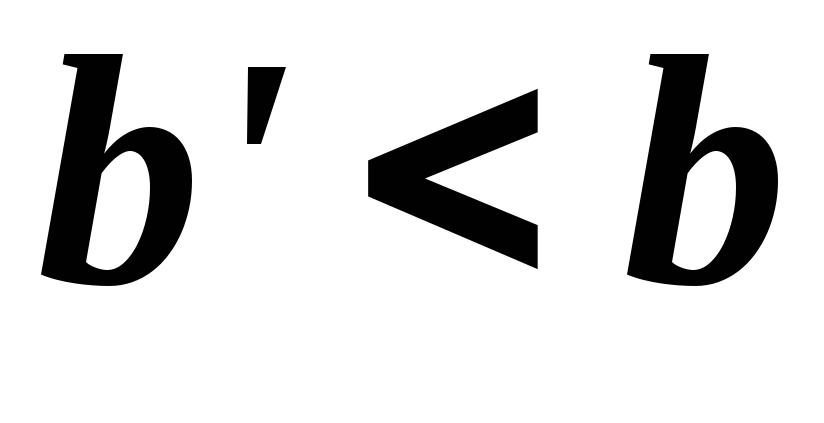 ,
но неограниченна в окрестности точки
,
но неограниченна в окрестности точки .
Тогда ее интеграл на
.
Тогда ее интеграл на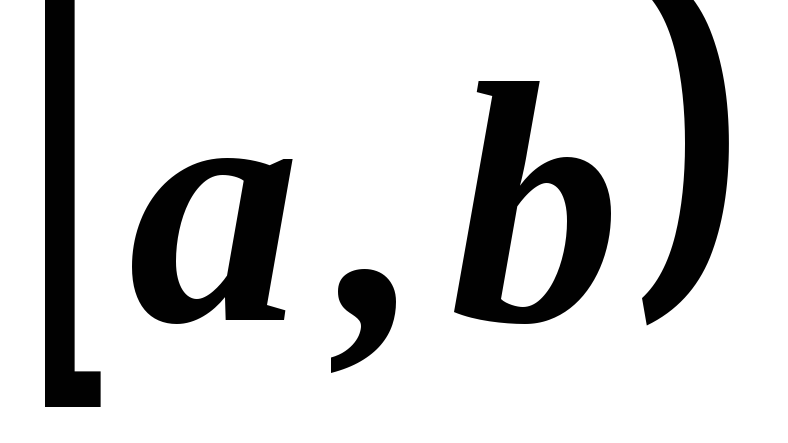 ,
или, что то же самое, на
,
или, что то же самое, на не может существовать, так как интегрируемая
функция должна быть ограничена.
не может существовать, так как интегрируемая
функция должна быть ограничена.
Однако может случиться так, что существует конечный предел

То
есть функция не ограничена, а ее интеграл
ограничен. В этом случае записанный
предел называют несобственным
интегралом от  на отрезке
на отрезке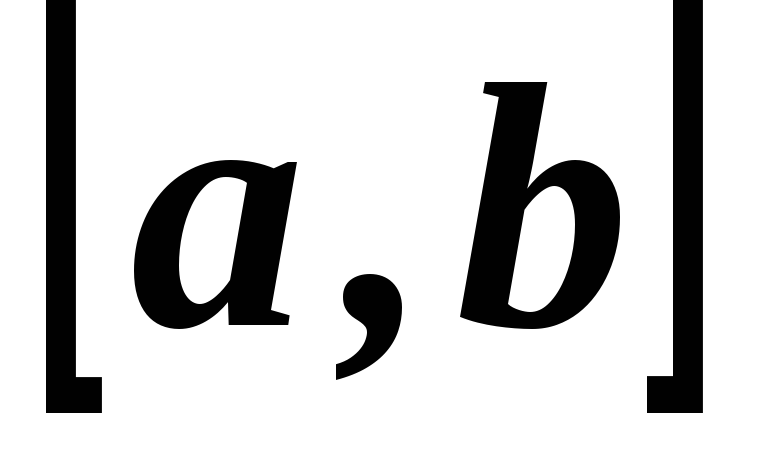 и записывают в виде
и записывают в виде

В таком
случае говорят, что интеграл  сходится. В противном случае говорят,
что он расходится или не существует как
несобственный риманов интеграл.
сходится. В противном случае говорят,
что он расходится или не существует как
несобственный риманов интеграл.
Аналогично
и на полуинтервале 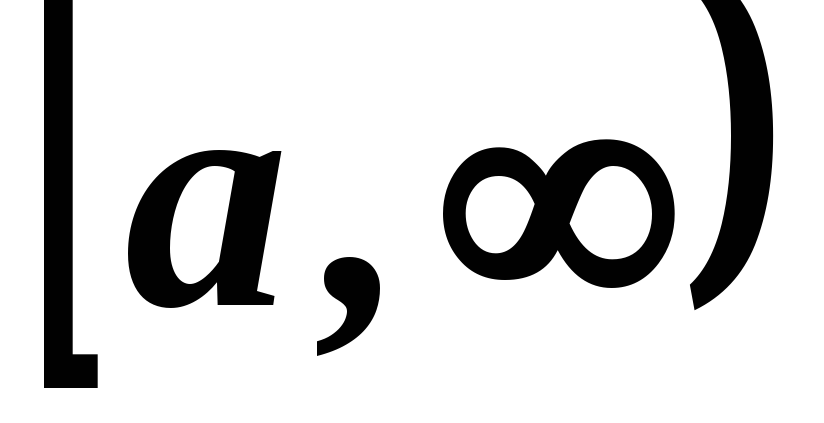

В связи с этим выражение

называется
интегралом от 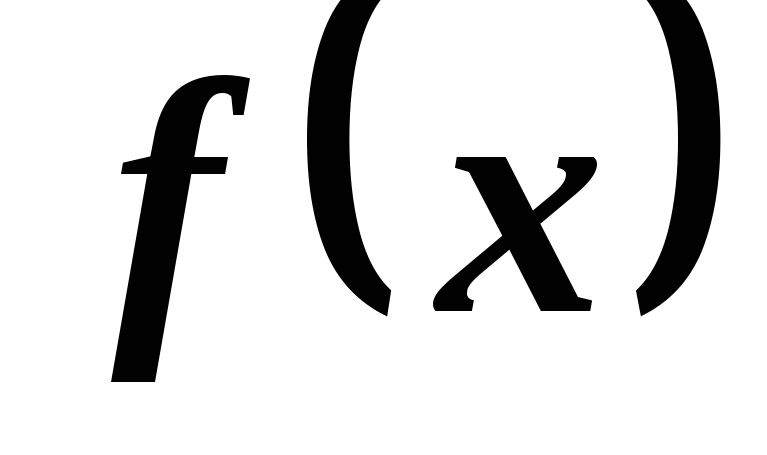 с единственной особенностью в точке
с единственной особенностью в точке ,
если выполняется следующее условие:
если
,
если выполняется следующее условие:
если конечная точка, то функция
конечная точка, то функция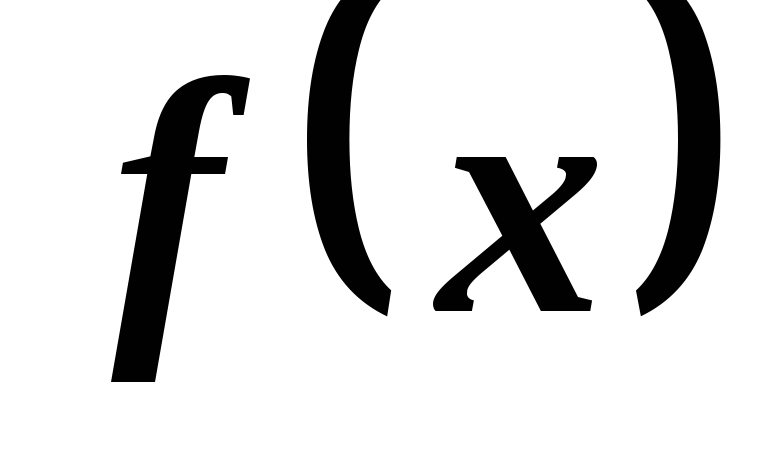 интегрируема на
интегрируема на при любом
при любом удовлетворяющим неравенствам
удовлетворяющим неравенствам ,
и, кроме того, не ограничена в точке
,
и, кроме того, не ограничена в точке .
Если же
.
Если же ,
то про функцию
,
то про функцию предполагается лишь, что она интегрируема
на
предполагается лишь, что она интегрируема
на при любом конечном
при любом конечном .
.
Также различают несобственные интегралы первого типа (с одним или двумя бесконечными пределами) и несобственные интегралы второго типа (от разрывных функций).
Несобственный интеграл первого рода, вычисляется обычно как

Например,
найти  .
.
Имеем  .
.
При
это выражение имеет предел .
Значит
.
Значит .
.
Или,
найти 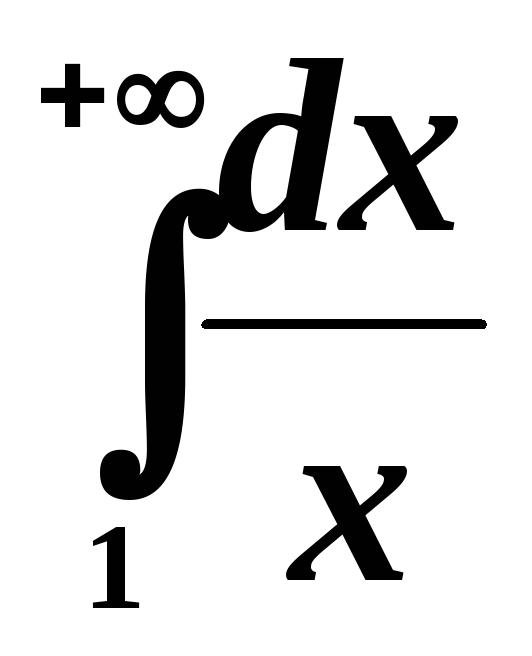 .
.
Имеем 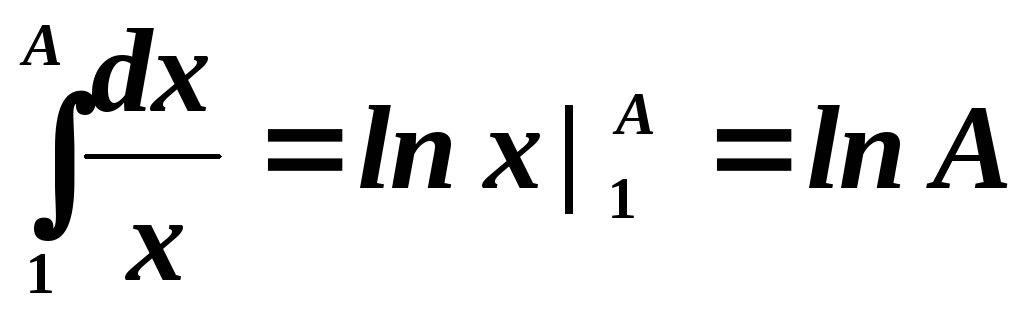 . Этот интеграл расходится.
. Этот интеграл расходится.
П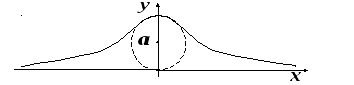 ример
6. Найти
площадь бесконечной полосы
ример
6. Найти
площадь бесконечной полосы  (верзьера Аньези).
(верзьера Аньези).
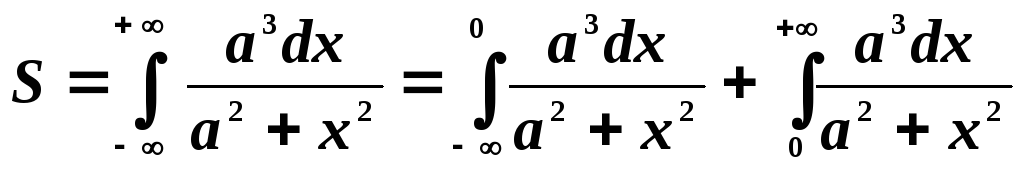 .
.
Далее, имеем  .
.
Отсюда  .
.
Аналогично вычисляется и первое слагаемое. В итоге получим:
 .
.
Пример 7. Найти  .
.
Данный интеграл
— несобственный, так как подынтегральная
функция терпит разрыв в точке  .
Однако этот интеграл сходится, так как
.
Однако этот интеграл сходится, так как

studfile.net
Некоторые типы интегралов, берущиеся посредством формулы интегрирования по частям:
где
| |
| |
| |
Интегрирование рациональных функций.
А) Метод
неопределенных коэффициентов:
Интегрирование рациональной функции
после выделения целой части сводится
к интегрированию правильной рациональной
дроби  ,
где
,
где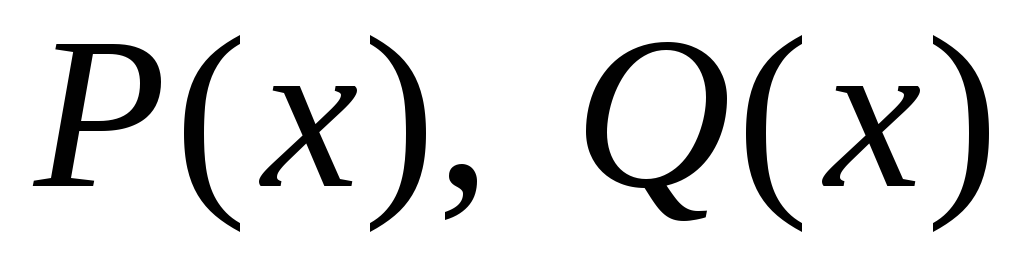
целые многочлены, причем степень
числителя
целые многочлены, причем степень
числителя  ниже степени знаменателя
ниже степени знаменателя .
Если,
то справедливо следующее разложение:
.
Если,
то справедливо следующее разложение:
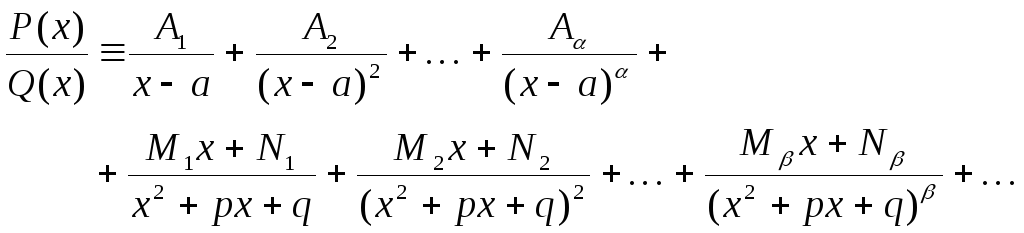
Для
вычисления неопределенных коэффициентов  ,
, ,
,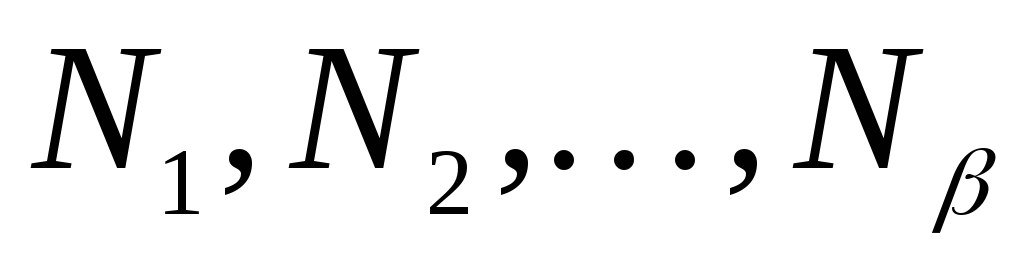 обе части тождества приводят к целому
виду, а затем приравнивают коэффициенты
при одинаковых степенях
обе части тождества приводят к целому
виду, а затем приравнивают коэффициенты
при одинаковых степенях .
.
Пример. Найти  .
.
Б) Метод
Остроградского:
Если  имеет кратные корни, то
имеет кратные корни, то ,
где
,
где
общий наибольший делитель многочлена
общий наибольший делитель многочлена 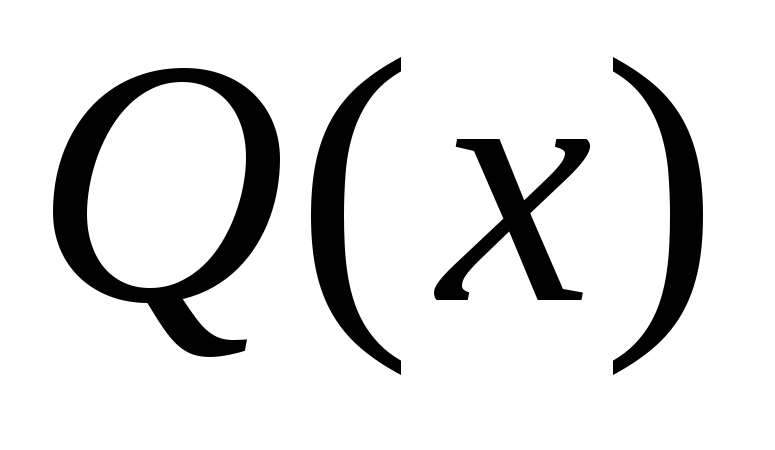 и его производной;
и его производной; ;
;
многочлены с неопределенными
коэффициентами, степени которых
соответственно на единицу меньше
степеней
многочлены с неопределенными
коэффициентами, степени которых
соответственно на единицу меньше
степеней  и
и .
.
Пример. Найти  .
.
Интегрирование иррациональных функций.
А) Интегралы
вида 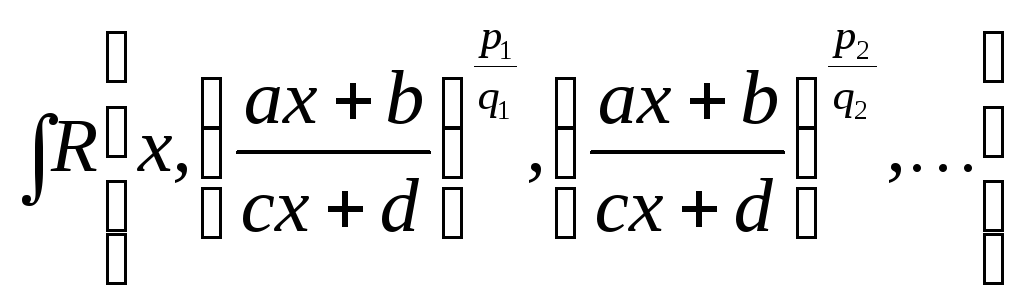 ,
где
,
где
 рациональная
функция,
рациональная
функция, 
целые числа, находятся с помощью
подстановки
целые числа, находятся с помощью
подстановки  ,
где
,
где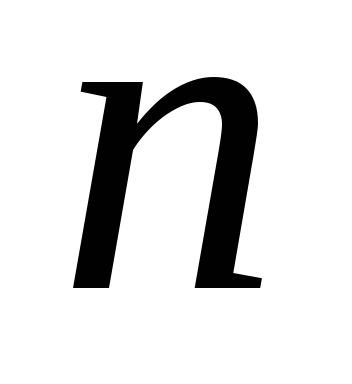
общее наименьшее кратное чисел
общее наименьшее кратное чисел 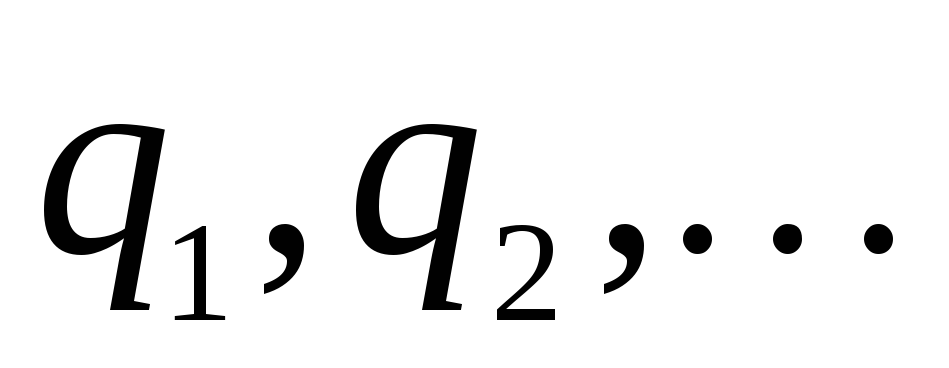 .
.
Пример. Найти 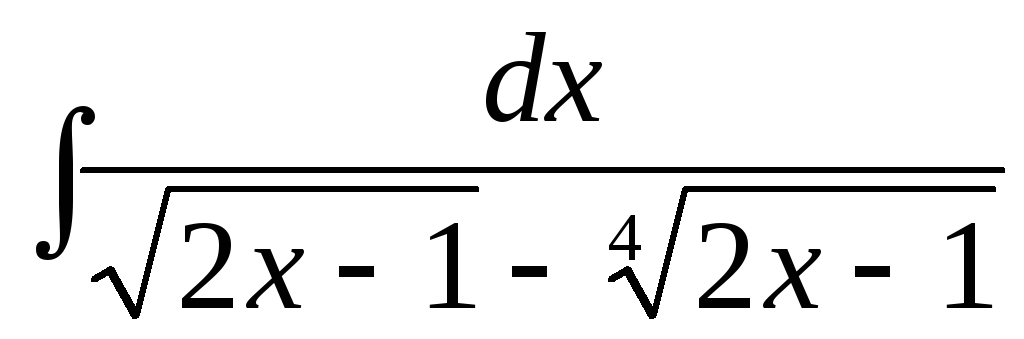 .
.
Б) Интегралы
вида  ,
где
,
где
многочлен степени
многочлен степени  ,
полагают равными
,
полагают равными ,
где
,
где
многочлен степени
многочлен степени  с неопределенными коэффициентами;
с неопределенными коэффициентами;
число. Коэффициенты
число. Коэффициенты  и число
и число находят с помощью дифференцирования
тождества
находят с помощью дифференцирования
тождества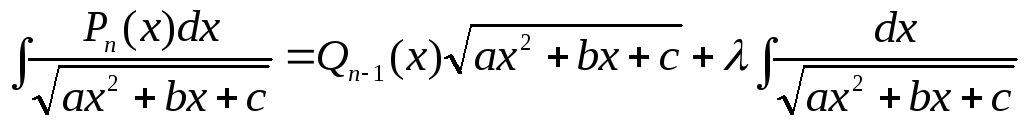 .
.
Пример. Найти 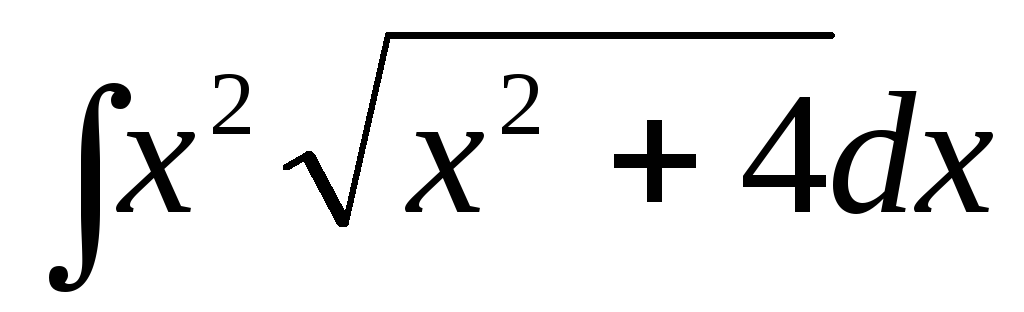 .
.
В) Интеграл
вида  с помощью подстановки
с помощью подстановки приводят к интегралам вида Б).
приводят к интегралам вида Б).
Пример. Найти 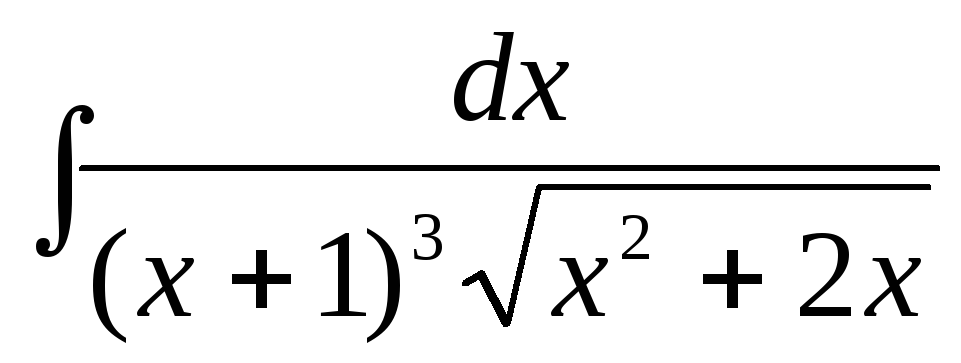 .
.
Г) Интегралы
вида 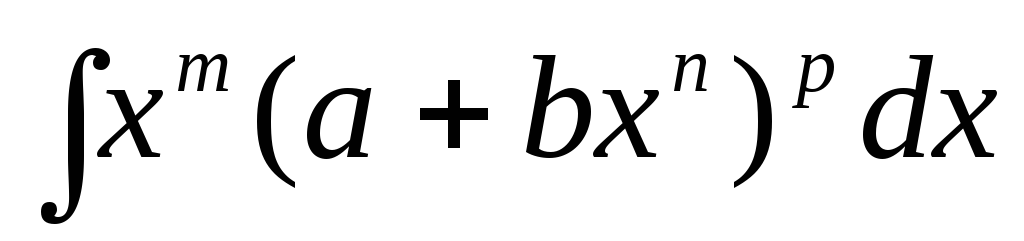 ,
где
,
где
рациональные числа, выражаются через
конечную комбинацию элементарных
функций лишь в случаях:
рациональные числа, выражаются через
конечную комбинацию элементарных
функций лишь в случаях:
Пример. Найти 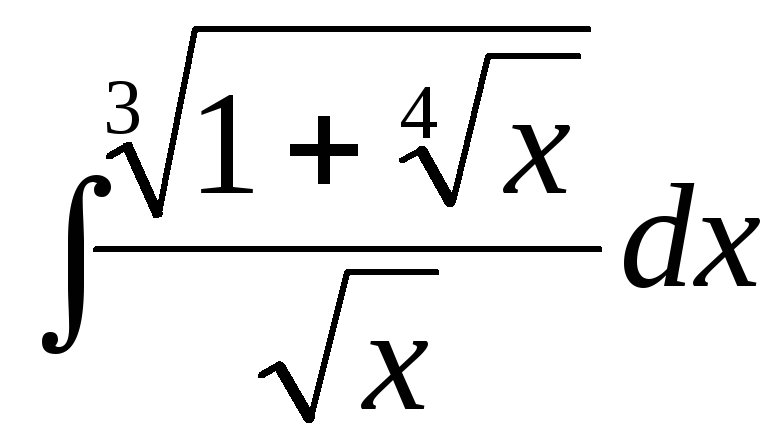 .
.
Интегрирование тригонометрических функций.
А)
Для интегралов
вида  ,
где
,
где
целые числа, возможны случаи:
целые числа, возможны случаи:
1)
Если 
нечетное число, то
нечетное число, то

Аналогично,
если 
нечетное число.
нечетное число.
Пример. Найти  .
.
2)
Если  и
и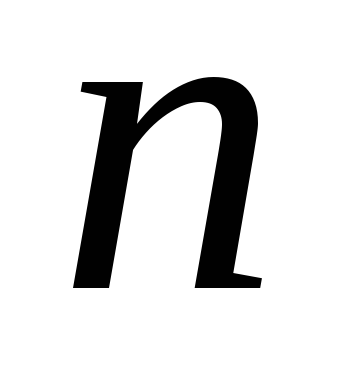 четные положительные числа, то
подынтегральные выражения преобразуются
с помощью формул:
четные положительные числа, то
подынтегральные выражения преобразуются
с помощью формул: ,
, ,
, .
.
Пример. Найти 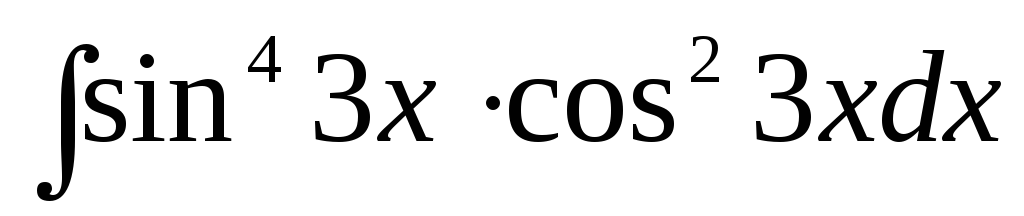 .
.
3)
Если  и
и
целые отрицательные числа одинаковой
четности, то
целые отрицательные числа одинаковой
четности, то  ,
,
в
частности,  ,
, .
.
Пример. Найти  .
.
Б) Интегралы
вида  ,
, ,
, преобразуются с помощью формул:
преобразуются с помощью формул:
 ,
,
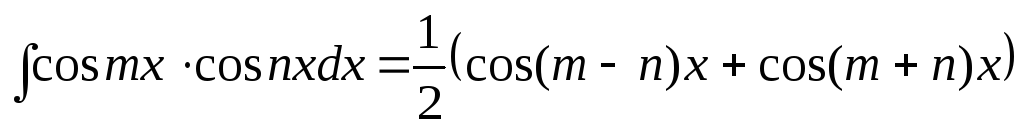 ,
,
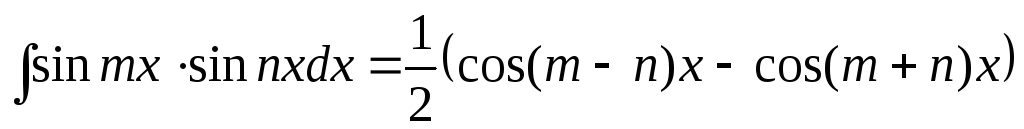 .
.
Пример. Найти  .
.
В)
Для вычисления интегралов
вида  ,
где
,
где
рациональная функция, можно использовать
подстановку
рациональная функция, можно использовать
подстановку 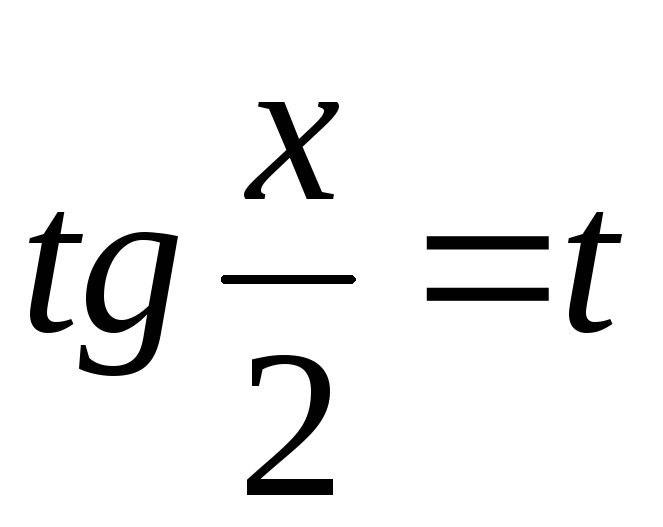 ,
откуда
,
откуда .
.
Пример.
Найти  .
.
Если 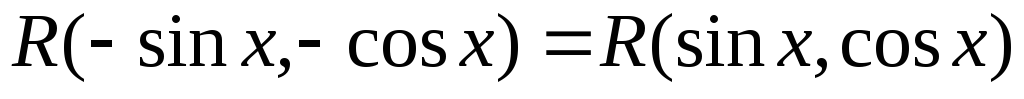 ,
то можно применить замену переменной
,
то можно применить замену переменной ,
где
,
где .
.
Пример. Найти 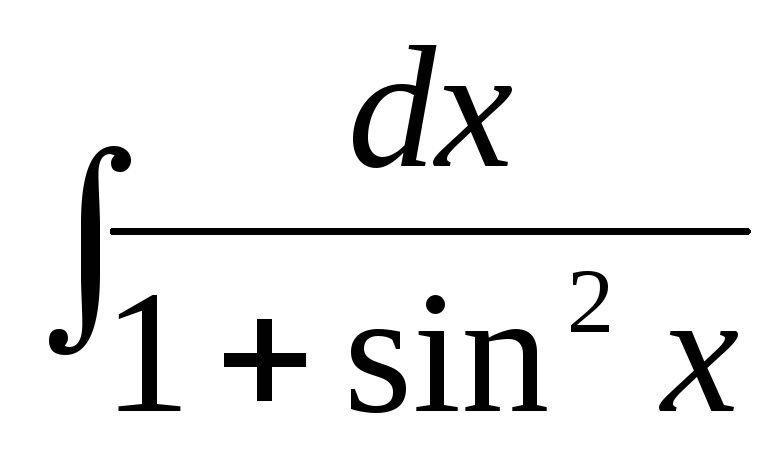 .
.
Определенный интеграл.
Пусть
на отрезке  задана функция
задана функция (рис.
1).
Разобьем отрезок
(рис.
1).
Разобьем отрезок  на
на элементарных отрезков точками,
где
элементарных отрезков точками,
где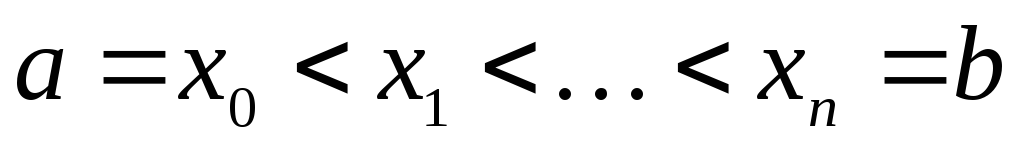 .
На каждом отрезке разбиения выберем
некоторую точку
.
На каждом отрезке разбиения выберем
некоторую точку и положим
и положим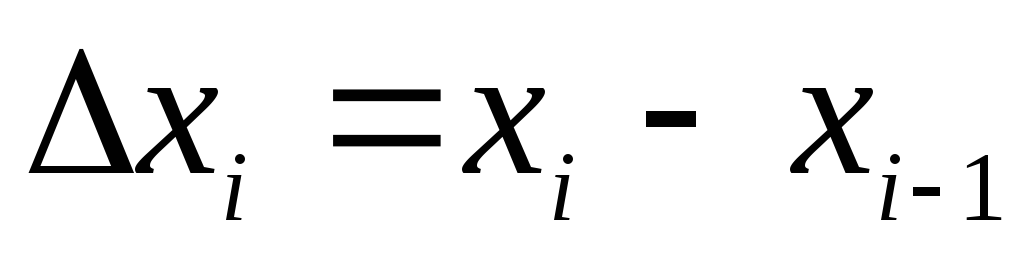 ,
где
,
где .
.

Рис. 1.
Сумму
вида 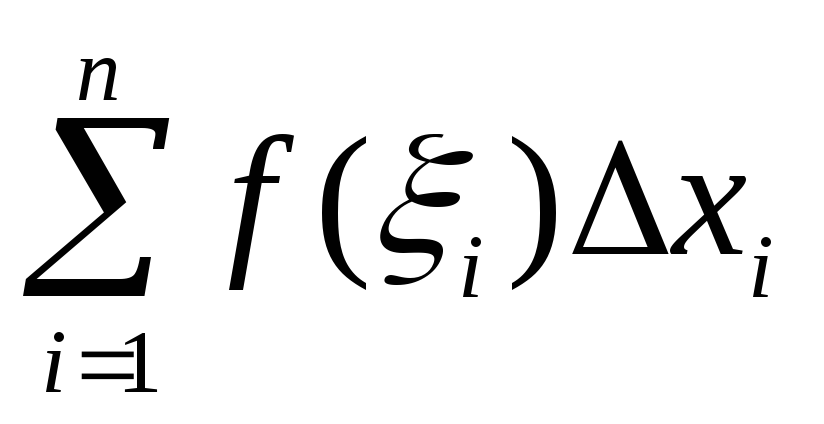 будем называтьинтегральной
суммой для функции
будем называтьинтегральной
суммой для функции  на
отрезке
на
отрезке  .
.
Обозначим
через  максимальную из длин отрезков
максимальную из длин отрезков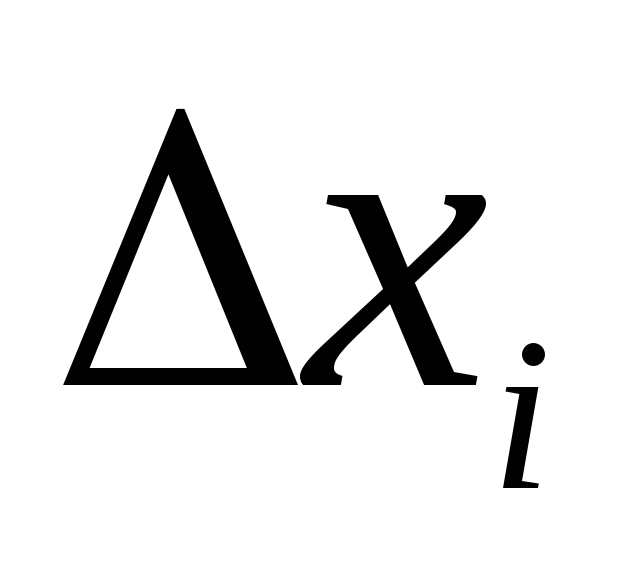 ,
т.е.
,
т.е. .
.
Определенным
интегралом от функции 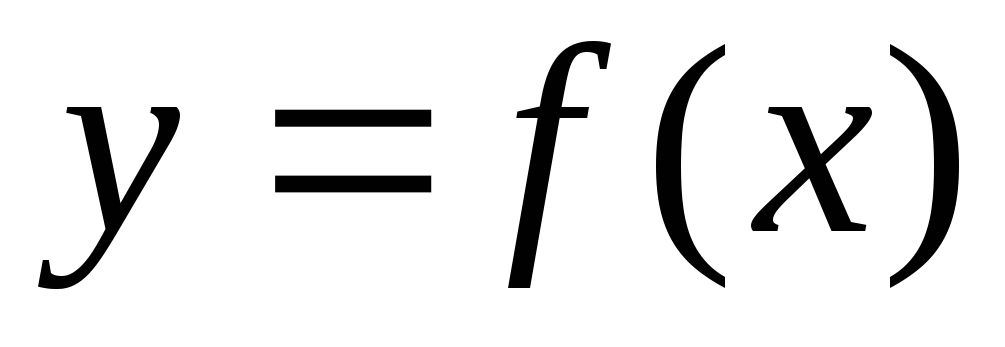 на отрезке
на отрезке называется предел интегральной суммы
при
называется предел интегральной суммы
при ,
т.е.
,
т.е.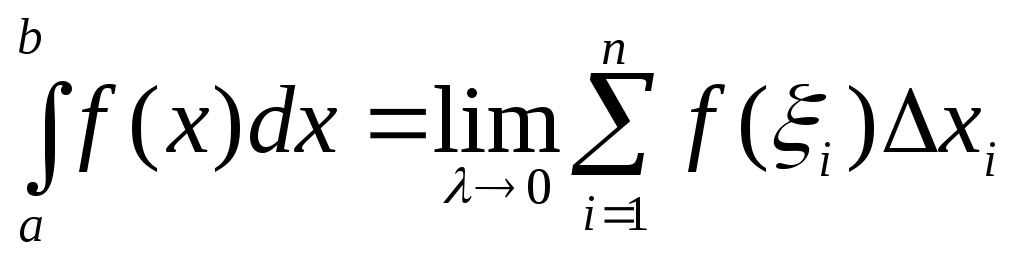 ,
,
нижний предел,
нижний предел, 
верхний предел,
верхний предел, 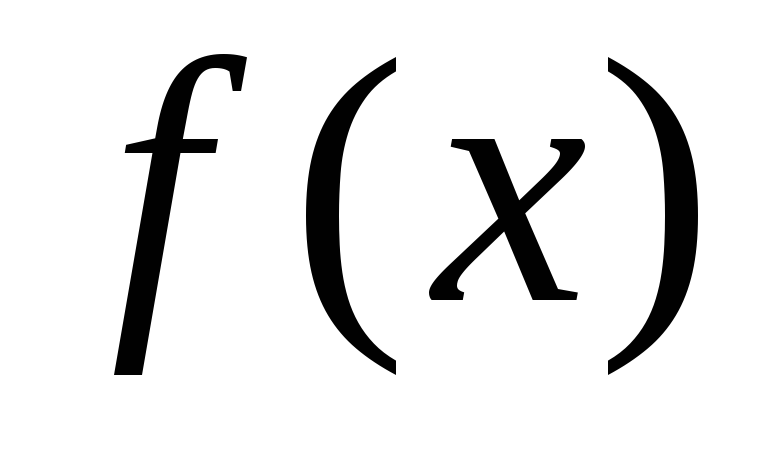
подынтегральная функция,
подынтегральная функция, 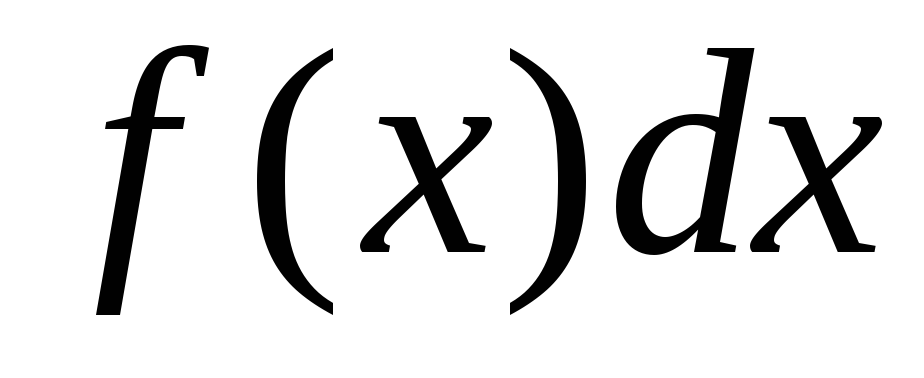
подынтегральное выражение.
подынтегральное выражение.
Замечание
1. Переменную под знаком интеграла можно
обозначать любой буквой:  и т. д.
и т. д.
Замечание
2. В отличие от неопределенного интеграла  ,
который представляет семейство функций
(первообразных), определенный интеграл
,
который представляет семейство функций
(первообразных), определенный интеграл есть определенное число.
есть определенное число.
Теорема
(достаточное условие существования
определенного интеграла). Если функция 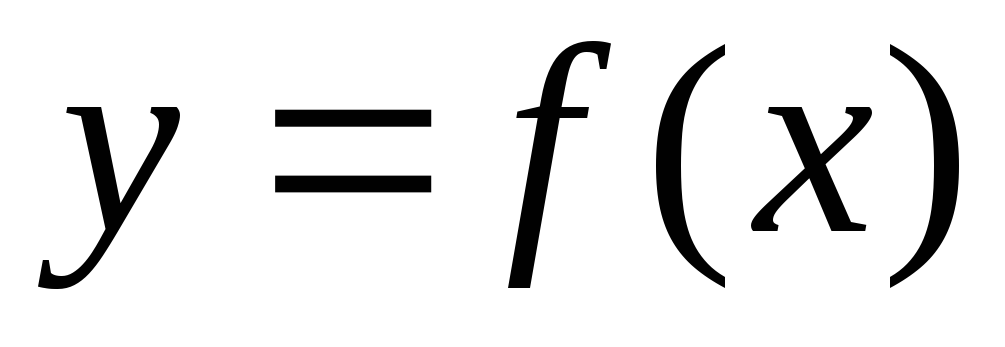 непрерывна на отрезке
непрерывна на отрезке ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
Свойства определенного интеграла:
Постоянный множитель можно выносить за знак интеграла:
 .
.Интеграл от алгебраической суммы 2х функций равен такой же сумме интегралов от этих функций:
 .
.При перестановке пределов интегрирования знак определенного интеграла меняется на противоположный:
 .
.Если пределы интегрирования равны
 ,
то интеграл равен нулю:
,
то интеграл равен нулю: .
.Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей:
 .
.Если на отрезке
 ,
где
,
где ,
, ,
то и
,
то и ,
т.е. обе части неравенства можно почленно
интегрировать.
,
т.е. обе части неравенства можно почленно
интегрировать.Если
 на отрезке
на отрезке ,
то
,
то .
.Если
 интегрируема на отрезке
интегрируема на отрезке ,
то
,
то .
.Теорема о среднем. Если функция
 непрерывна на отрезке
непрерывна на отрезке ,
то найдется такое значение
,
то найдется такое значение ,
что
,
что .
Т.о. теорема о среднем утверждает, что
найдется такая точка
.
Т.о. теорема о среднем утверждает, что
найдется такая точка из отрезка
из отрезка ,
что площадь под кривой
,
что площадь под кривой равна площади прямоугольника со
сторонами
равна площади прямоугольника со
сторонами и
и .
.
Пусть 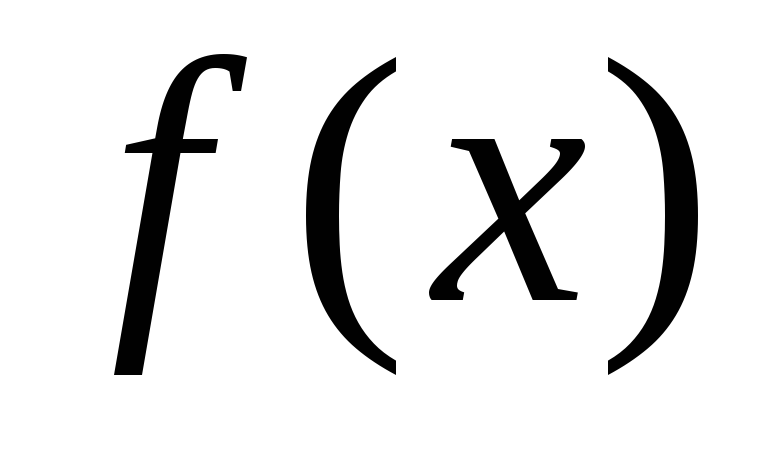
непрерывная на отрезке
непрерывная на отрезке 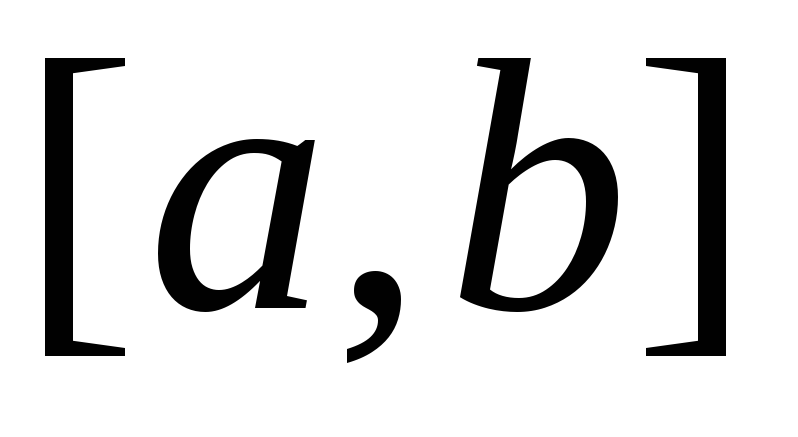 функция, а
функция, а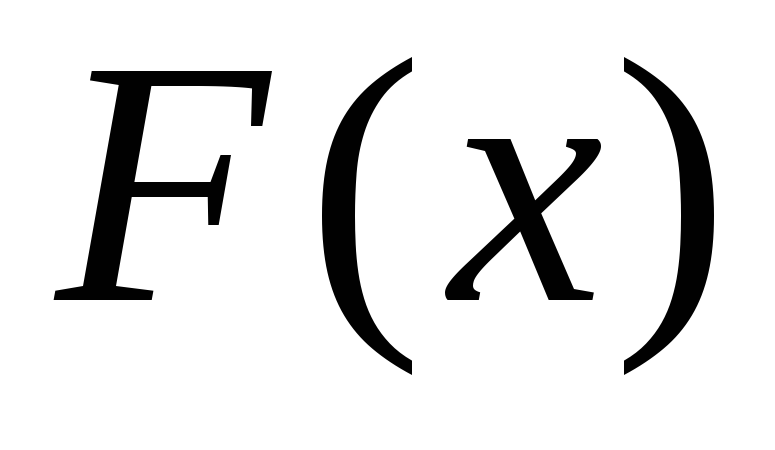
ее первообразная. Рассмотрим определенный
интеграл
ее первообразная. Рассмотрим определенный
интеграл  ,
где
,
где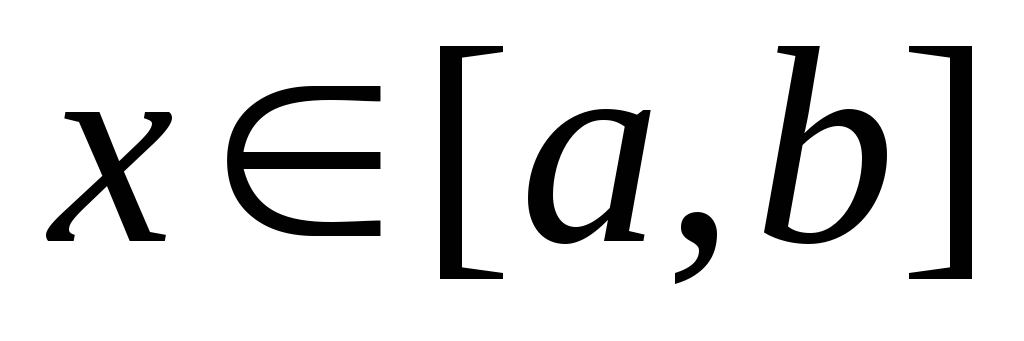 .
При изменении
.
При изменении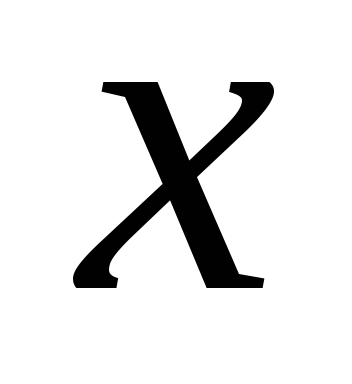 меняется
и определенный интеграл
меняется
и определенный интеграл  ,
т.е. он является функцией верхнего
предела интегрирования
,
т.е. он является функцией верхнего
предела интегрирования ,
которую обозначим через
,
которую обозначим через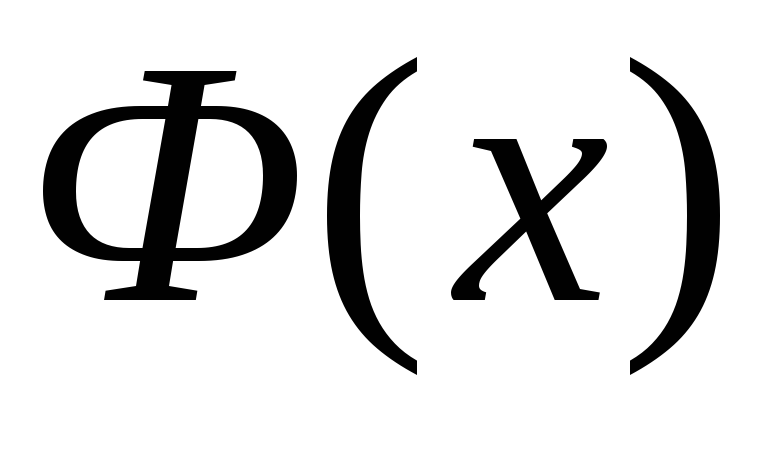 :
: .
Функция
.
Функция называетсяинтегралом
с переменным верхним пределом (с открытым
верхним пределом).
называетсяинтегралом
с переменным верхним пределом (с открытым
верхним пределом).
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке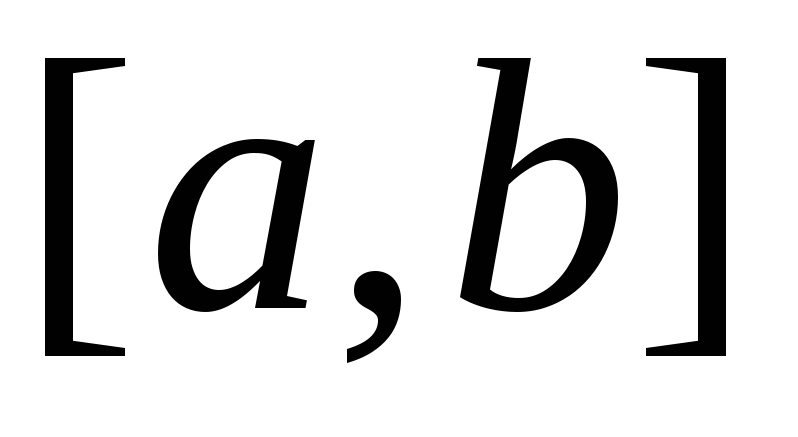 ,
то функция
,
то функция так же непрерывна на
так же непрерывна на .
.
Теорема
о производной интеграла по верхнему
пределу. Пусть функция  непрерывна на отрезке
непрерывна на отрезке .
Тогда в каждой точке
.
Тогда в каждой точке отрезка
отрезка производная функции
производная функции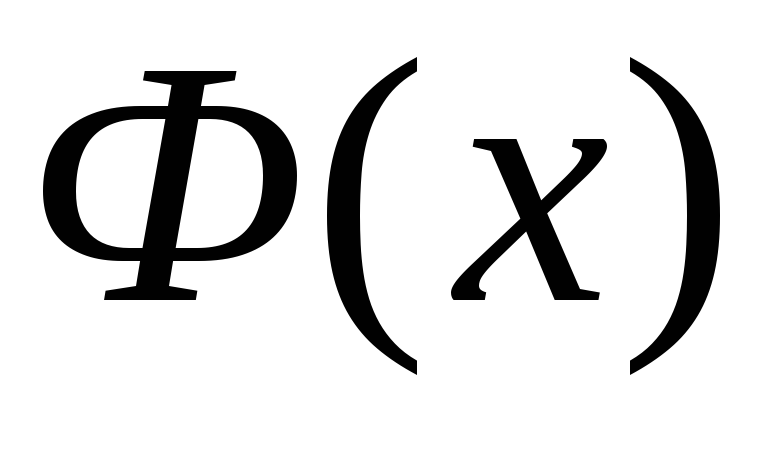 по переменному верхнему пределу равна
подынтегральной функции
по переменному верхнему пределу равна
подынтегральной функции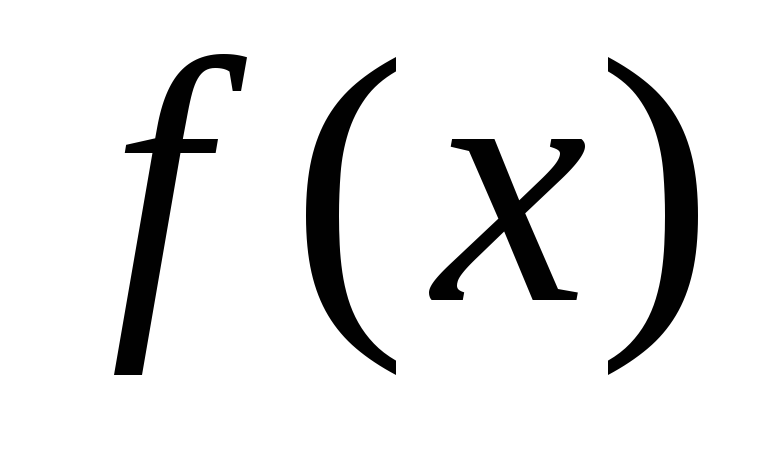 на верхнем пределе, т.е.
на верхнем пределе, т.е. .
.
Теорема. Пусть функция 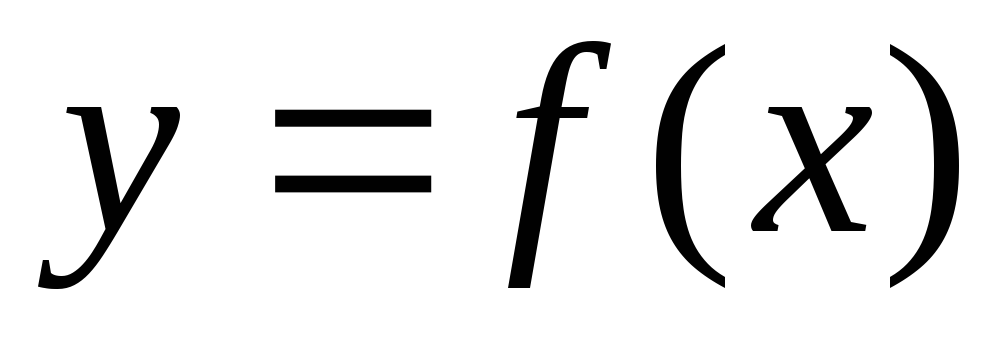 непрерывна на отрезке
непрерывна на отрезке и
и
любая первообразная для
любая первообразная для  на
на .
Тогда определенный интеграл от функции
.
Тогда определенный интеграл от функции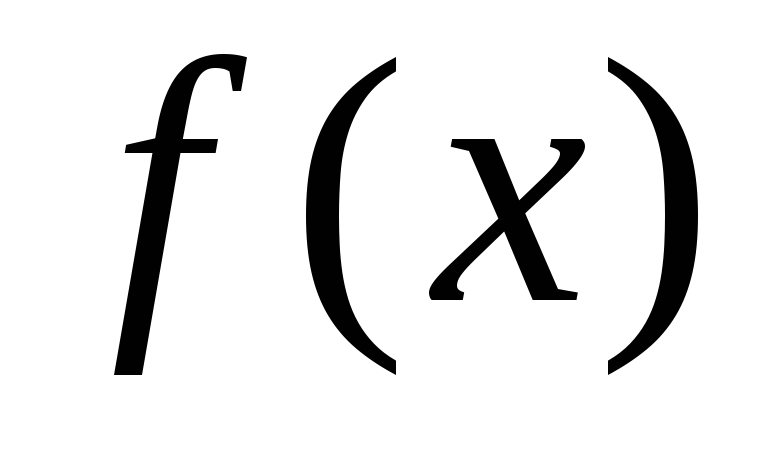 на отрезке
на отрезке равен приращению первообразной
равен приращению первообразной на этом отрезке:
на этом отрезке:
это формула Ньютона-Лейбница или основная
формула интегрального исчисления.
это формула Ньютона-Лейбница или основная
формула интегрального исчисления.
Формула Ньютона-Лейбница позволяет находить определенный интеграл, обходя суммирование, при помощи первообразных функций.
Пример. Вычислите  и
и .
.
Методы вычисления определенного интеграла:
Метод замены переменной (метод подстановки). Данный метод основан на следующей теореме: Пусть дан интеграл
 ,
где функция
,
где функция  непрерывна на отрезке
непрерывна на отрезке .
Введем новую переменную равенством
.
Введем новую переменную равенством ,
где: 1) между переменными
,
где: 1) между переменными  и
и  существует взаимно-однозначное
соответствие; 2)
существует взаимно-однозначное
соответствие; 2)  непрерывна на отрезке
непрерывна на отрезке  ;
3)
;
3)  ;
4)
;
4)  непрерывна на
непрерывна на  .
Тогда
.
Тогда  .
.
Пример.
Вычислите  .
.
Интегрирование по частям. Теорема. Пусть функции
 ,
, имеют непрерывные производные на
отрезке
имеют непрерывные производные на
отрезке .
Тогда имеет место равенство:
.
Тогда имеет место равенство:
эта формула называется формулой
интегрирования по частям для
определенного интеграла.
эта формула называется формулой
интегрирования по частям для
определенного интеграла.
Пример. Вычислить 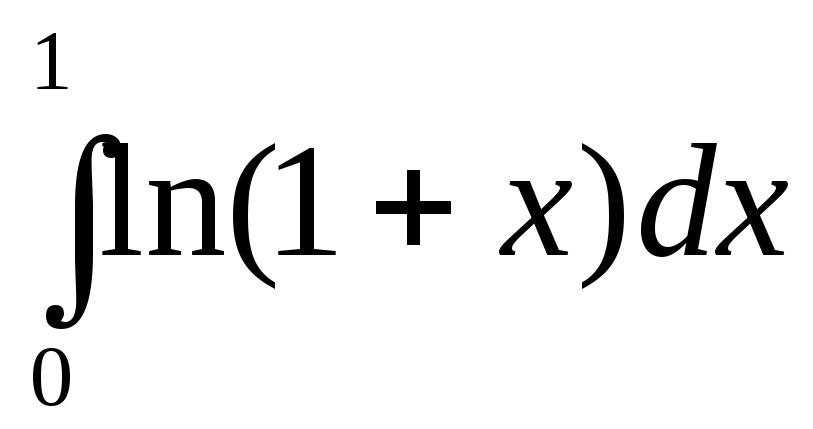 .
.
Геометрические приложения определенного интеграла:
Площадь плоской фигуры.
А)
Пусть на отрезке  задана неотрицательная функция
задана неотрицательная функция .
Тогда площадь
.
Тогда площадь криволинейной трапеции, ограниченной
кривой
криволинейной трапеции, ограниченной
кривой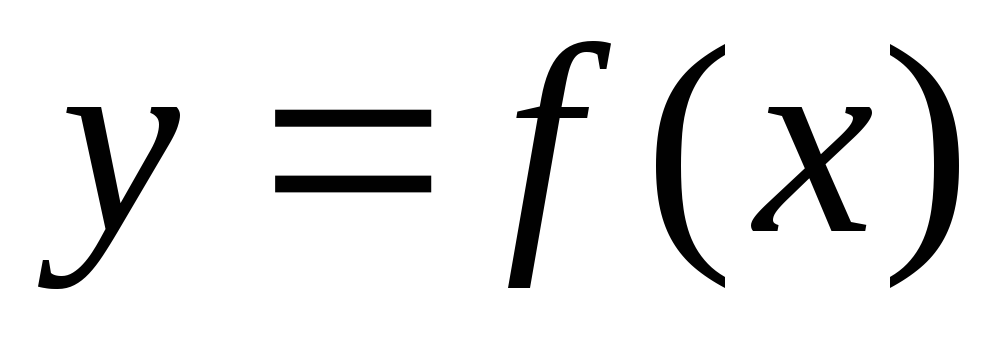 ,
прямыми
,
прямыми и осью абсцисс
и осью абсцисс (рис.
2)
численно равна определенному интегралу
от функции
(рис.
2)
численно равна определенному интегралу
от функции  на
на ,
т.е.
,
т.е. .
.

Рис. 2.
Пример. Найти площадь фигуры, ограниченной
линиями  .
.
Б)
Если функция 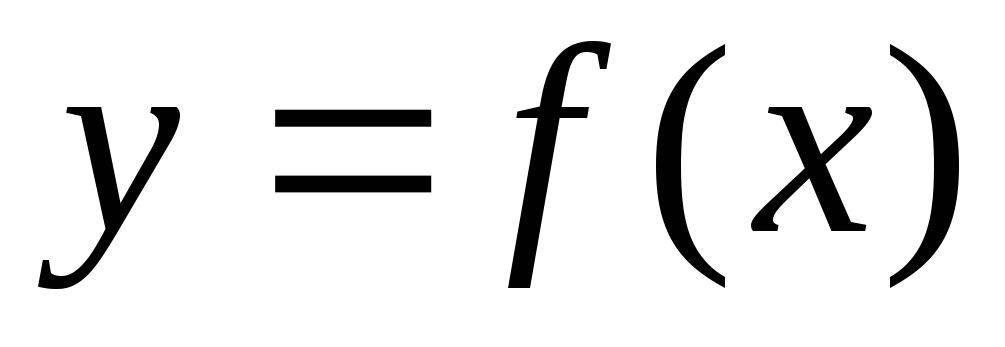 неположительная и непрерывна на отрезке
неположительная и непрерывна на отрезке (рис.
3),
то площадь
(рис.
3),
то площадь 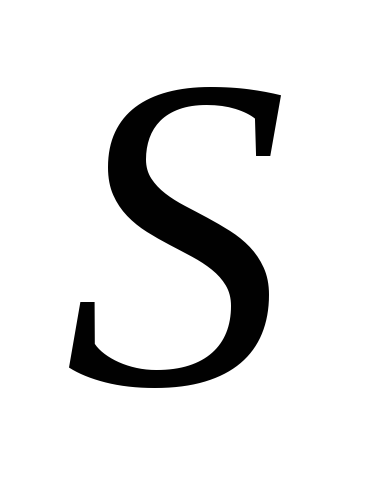 над кривой
над кривой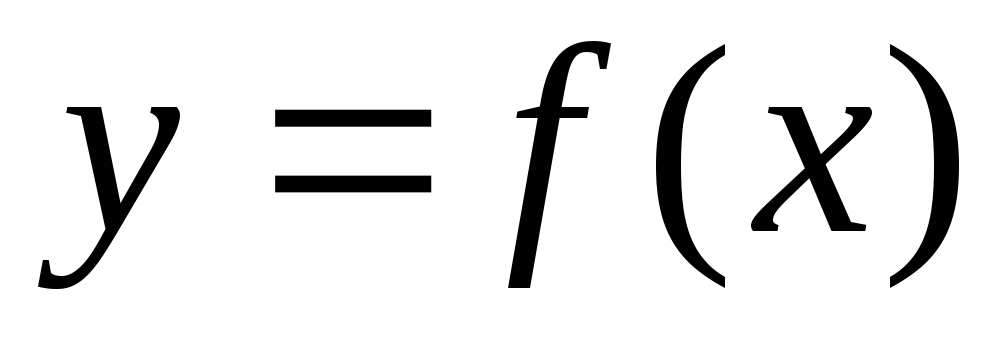 на
на отличается знаком от определенного
интеграла
отличается знаком от определенного
интеграла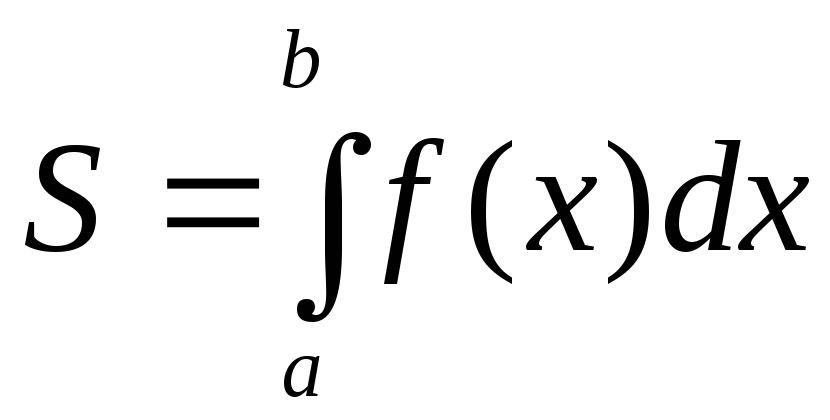 ,
т.е.
,
т.е.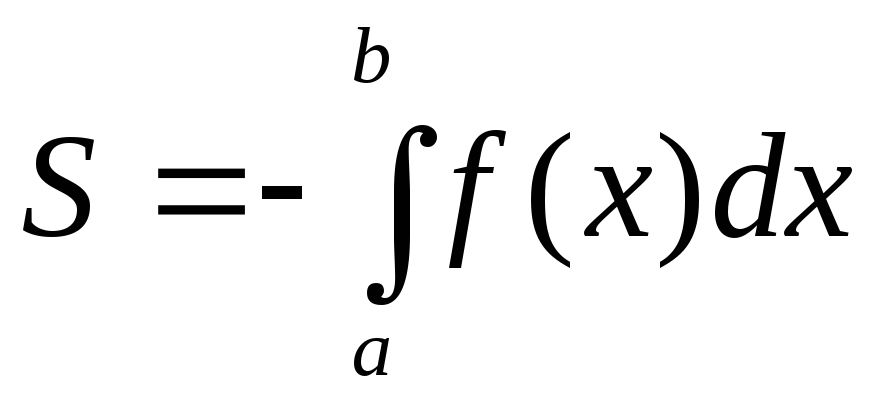
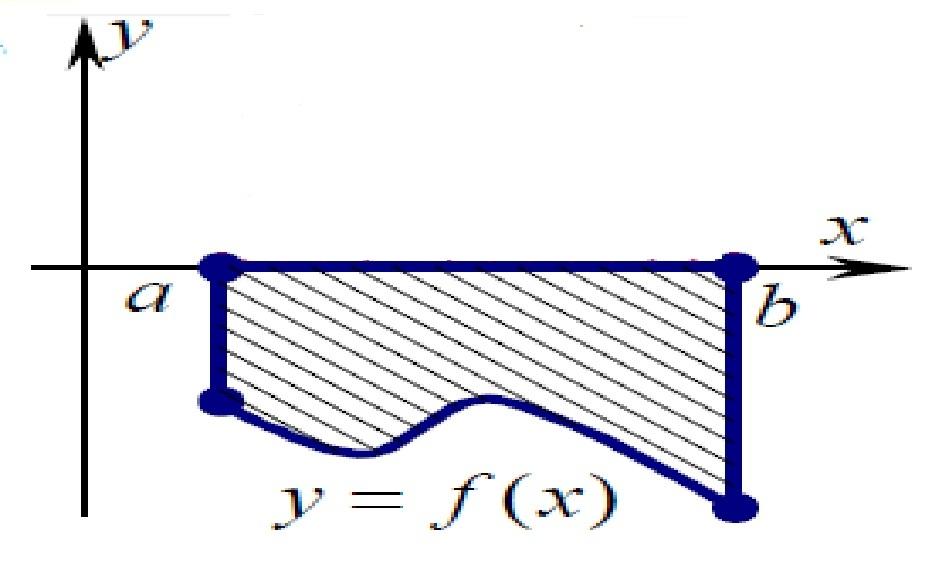
Рис. 3.
Пример. Найти площадь фигуры, ограниченной
кривой  и осью абсцисс.
и осью абсцисс.
В) Теорема. Если
на отрезке 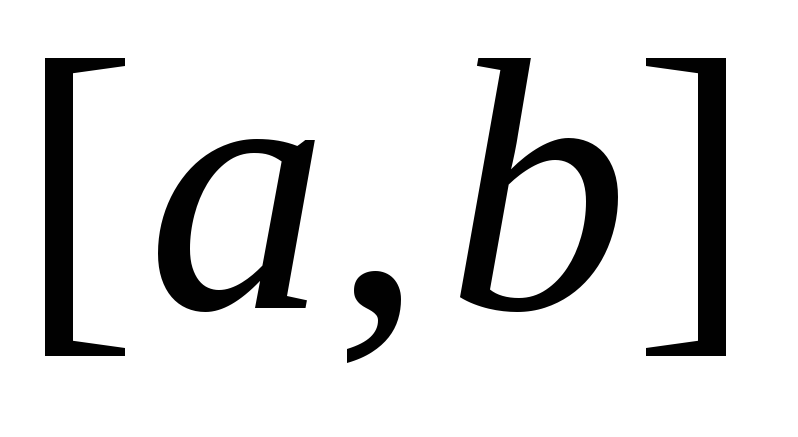 заданы непрерывные функции
заданы непрерывные функции и
и такие, что
такие, что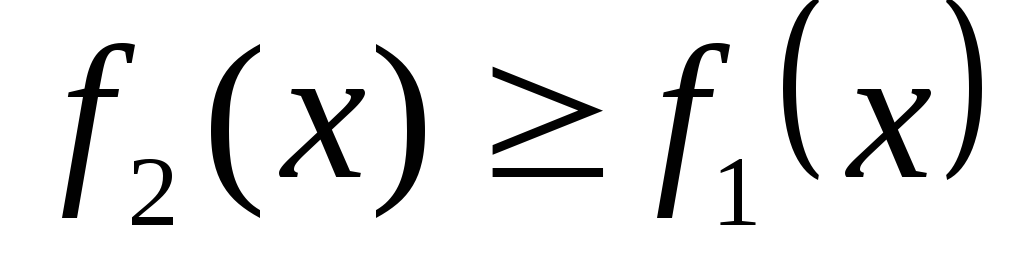 (рис.
5).
(рис.
5).
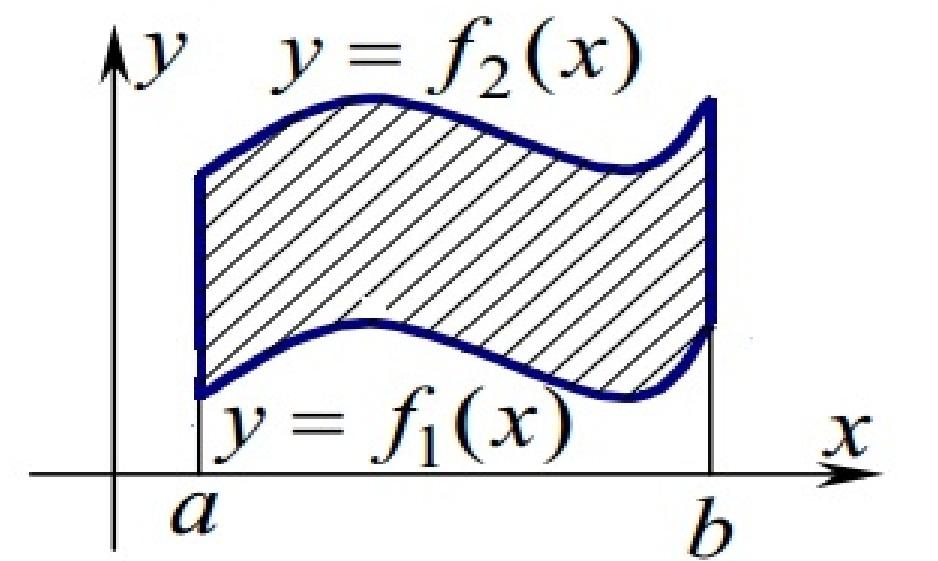
Рис. 5.
Тогда
площадь 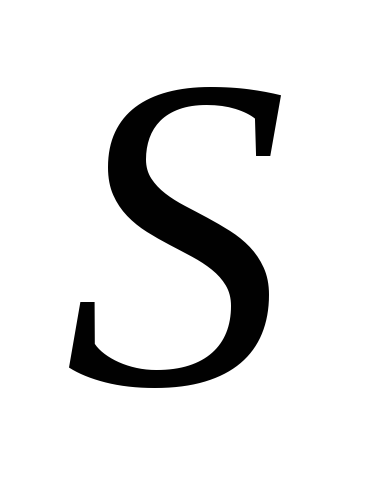 фигуры, заключенной между кривыми
фигуры, заключенной между кривыми и
и на отрезке
на отрезке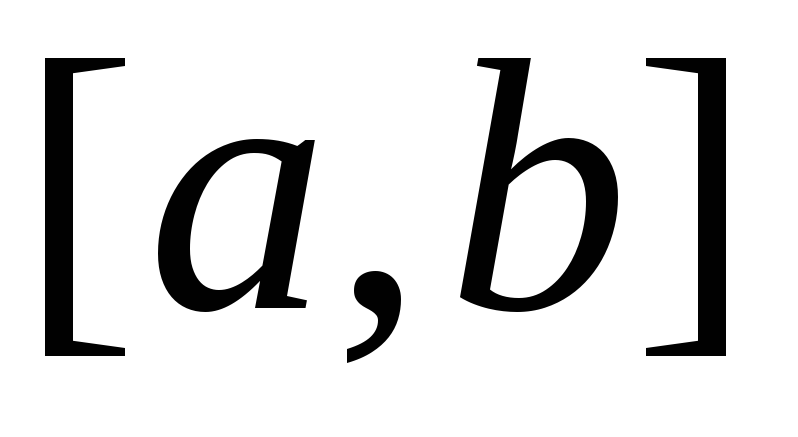 ,
вычисляется по формуле:
,
вычисляется по формуле: .
.
Пример. Найти площадь фигуры, ограниченной
линиями:  .
.
Объем тела вращения:
А)
вокруг оси  :
: .
.
Б)
вокруг оси  :
: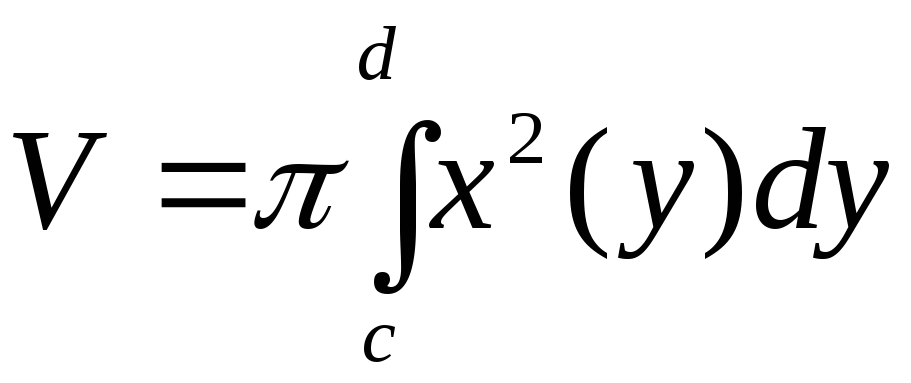 .
.
Вычисление длины дуги кривой
 на отрезке
на отрезке  :
:  .
.Вычисление площади поверхности вращения вокруг оси
 :
: .
.
Экономический
смысл определенного интеграла. Пусть
функция  описывает изменение производительности
некоторого производства с течением
времени. Тогда объем продукции
описывает изменение производительности
некоторого производства с течением
времени. Тогда объем продукции ,
произведенной за промежуток времени
,
произведенной за промежуток времени ,
равен
,
равен .
.
Физические приложения определенного интеграла:
Пройденный путь. Пусть точка движется вдоль некоторой кривой со скоростью
 .
Тогда путь
.
Тогда путь ,
пройденный точной за время
,
пройденный точной за время ,
равен
,
равен .
.Масса отрезка. Пусть
 – плотность распределения массы на
отрезке
– плотность распределения массы на
отрезке .
Тогда масса отрезка равна:
.
Тогда масса отрезка равна: .
.Работа переменной силы. Пусть под действием некоторой силы
 материальная точка
материальная точка движется по прямой в направлении оси
движется по прямой в направлении оси из точки
из точки в точку
в точку .
Тогда работа, произведенная силой
.
Тогда работа, произведенная силой при перемещении точки
при перемещении точки из положения
из положения в положение
в положение равна
равна .
.
studfile.net
Способы вычисления определенного интеграла Интегрирование по частям
Пусть  и
и — дифференцируемая функция от
— дифференцируемая функция от .
Тогда
.
Тогда
 (8.21)
(8.21)
Проинтегруем
тождество (8.21) в границах от  до
до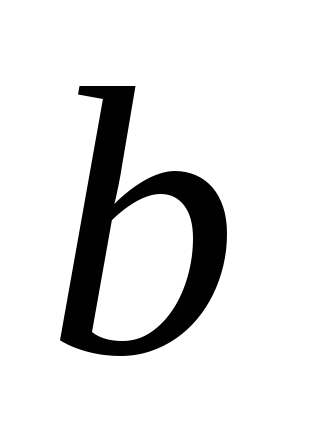 ,
получим
,
получим
 (8.22)
(8.22)
Поскольку 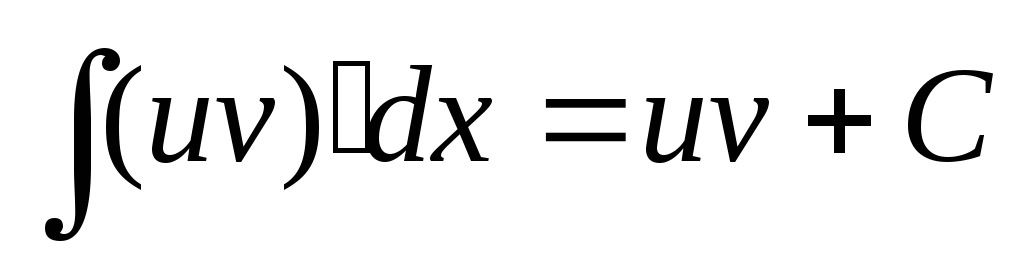 ,
то
,
то и равенство (8.22) приобретает вид
и равенство (8.22) приобретает вид

или
окончательно 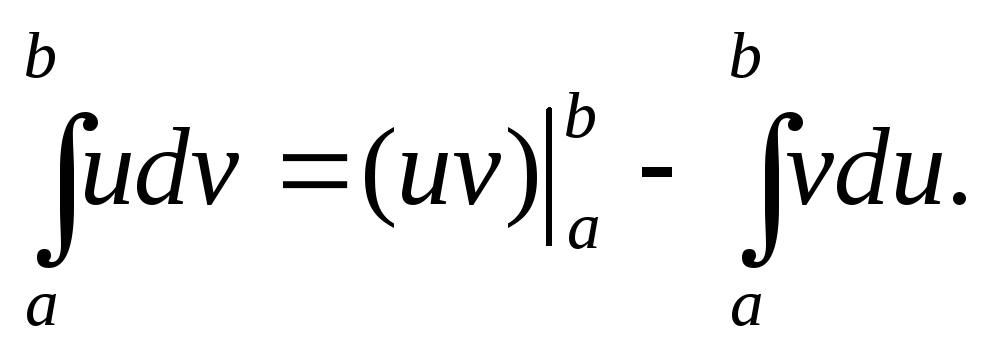 (8.23)
(8.23)
Формула (8.23) и выражает способ интегрирования по частям определенного интеграла. Видно, что она подобна формуле (7.12) интегрирования по частям неопределенного интеграла.
Пример.1. Вычислить 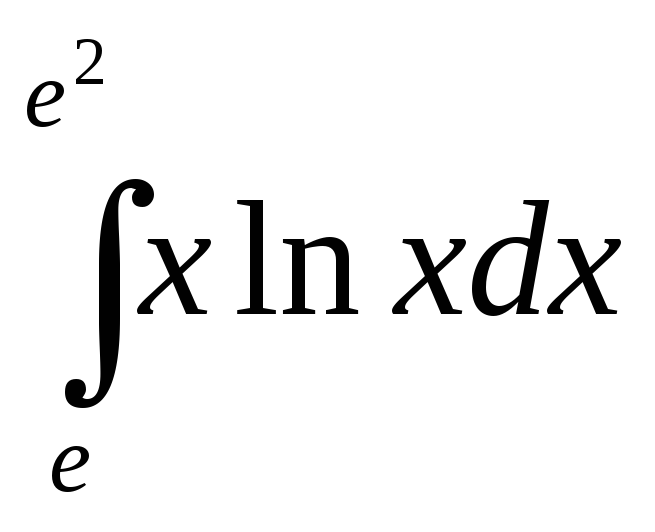 .
.
Решение
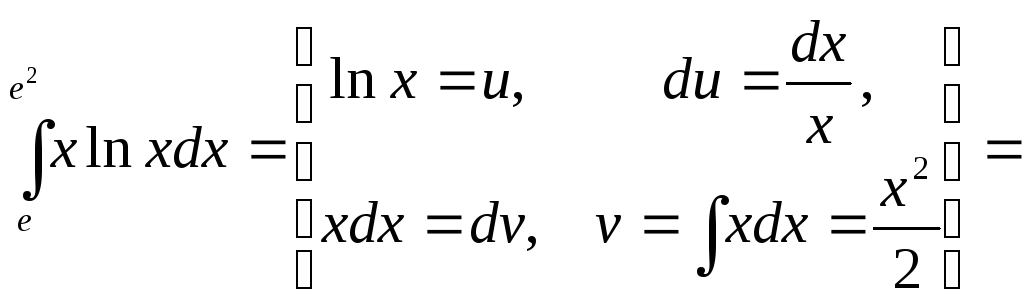
Пример 2. Вычислить  .
.
Решение.
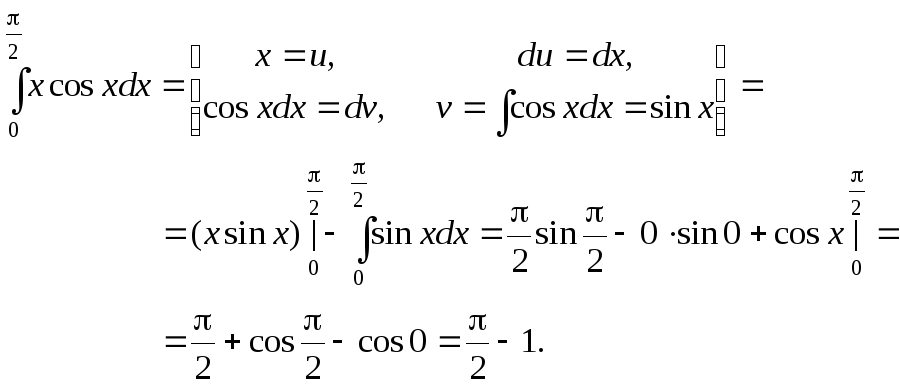
Интегрирование подстановкой
Пусть
надо вычислить определенный интеграл 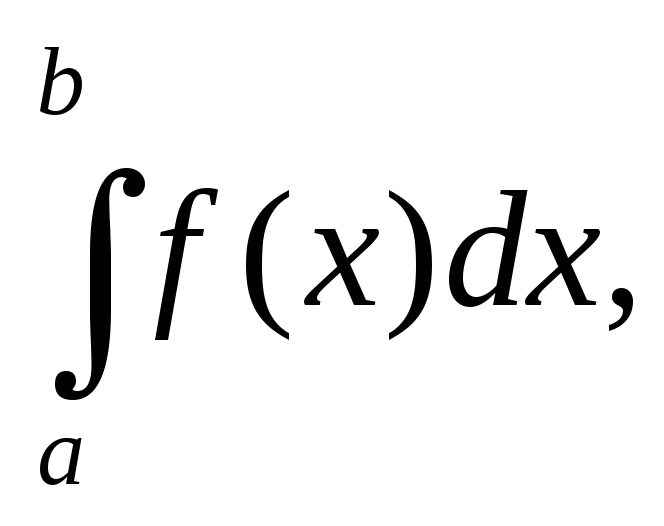
где  — непрерывная на
— непрерывная на функция, а первообразной для нее нет в
таблице простейших интегралов. Тогда
произведем замену переменной, а именно,
введем новую переменную
функция, а первообразной для нее нет в
таблице простейших интегралов. Тогда
произведем замену переменной, а именно,
введем новую переменную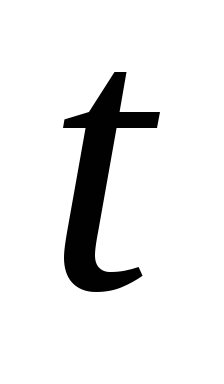 таким образом:
таким образом: ,
где
,
где — непрерывно дифференцируема на
— непрерывно дифференцируема на функция.
функция.
Если при этом будут выполняться такие условия:
при изменении
 от
от до
до переменная
переменная изменяется от
изменяется от до
до ,
то есть
,
то есть
 . (8.24)
. (8.24)
сложная функция
 определена и непрерывна на отрезке
определена и непрерывна на отрезке ,
то справедлива такая формула
,
то справедлива такая формула
 (8.25)
(8.25)
Формула (8.25) и выражает собою суть метода подстановки.
Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к старой переменной (как это нужно было делать при вычислении неопределенного интеграла) достаточно лишь учесть границы интегрирования соответственно (8.24).
Пример 8.3. Вычислить 
Решение
Введем
новую переменную  .
Тогда
.
Тогда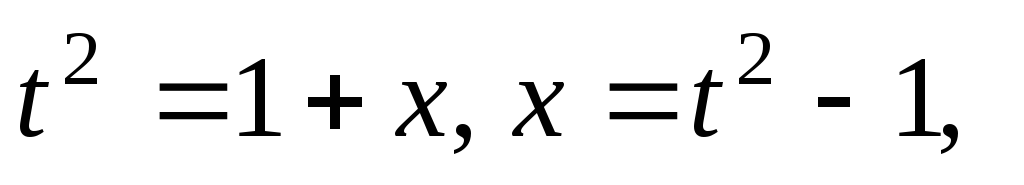
 .
Вычислим границы интегрирования и
результат представим в виде табл. 1.
Таблица 1
.
Вычислим границы интегрирования и
результат представим в виде табл. 1.
Таблица 1
из
которой видно, что при 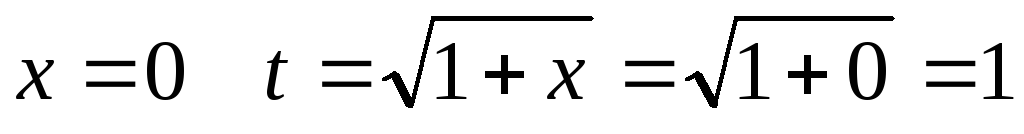 ,
а при
,
а при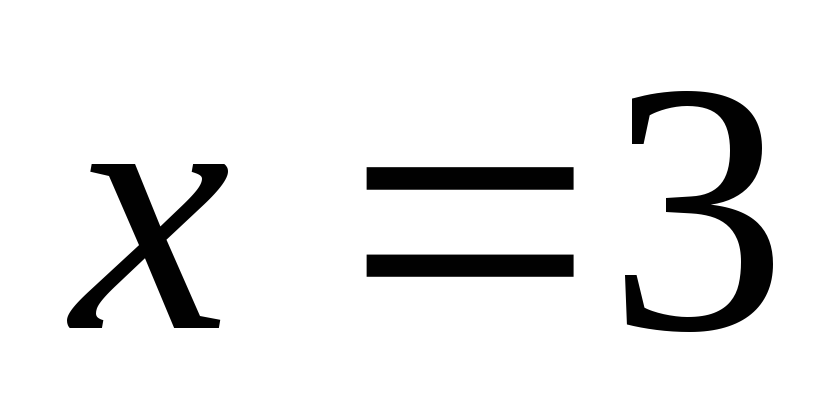
 .
Итак, после введении новой переменной
получим
.
Итак, после введении новой переменной
получим
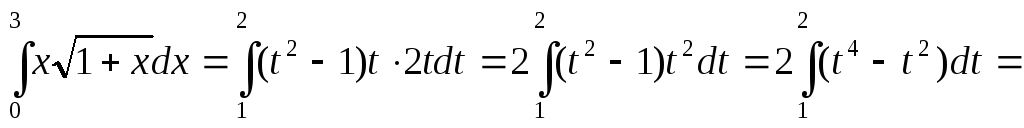



Пример 4.Вычислить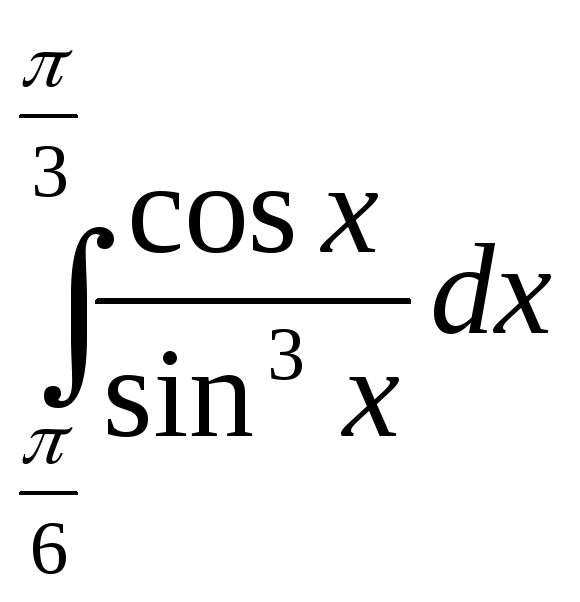 .
.
Решение.
Произведем
замену переменной:  .
Тогда
.
Тогда ,
а границы интегрирования приобретают
значения: при
,
а границы интегрирования приобретают
значения: при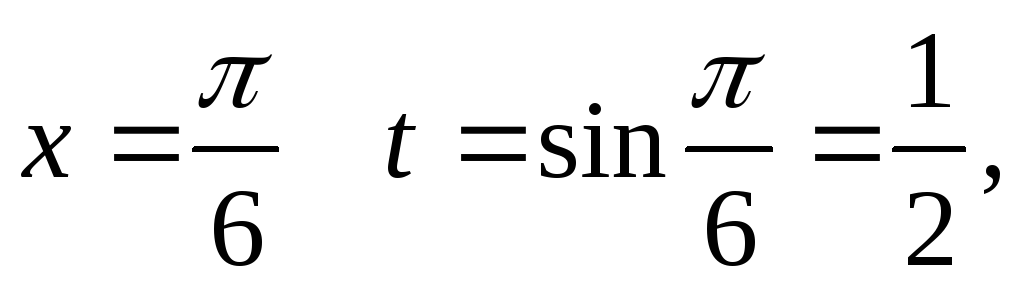
при 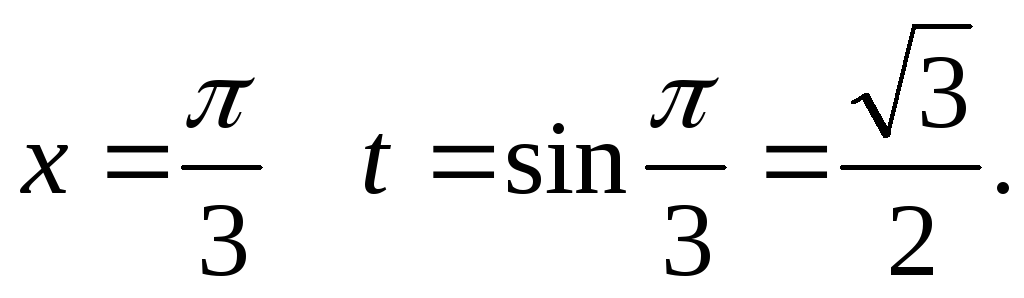
Итак, получаем

Таким образом, видим, что различие в применении метода замены переменной в неопределенном и определенном интеграле состоит в том, что в втором случае не надо возвращаться к старой переменной, поскольку при замене переменной изменяются также и границы интегрирования.
Приближенное вычисление определенного интеграла
Пусть
надо вычислить 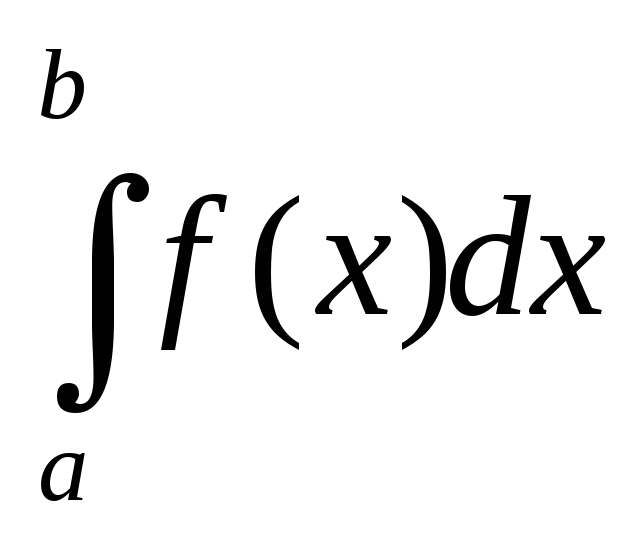 ,
но первообразная для функции
,
но первообразная для функции не выражается через элементарные
функции. Тогда применить формулу
Ньютона-Лейбница невозможно. В таких
случаях применяются методы приближенного
вычисления определенных интегралов.
Рассмотрим их, используя определение
интеграла как границы интегральной
суммы. Разделим отрезок
не выражается через элементарные
функции. Тогда применить формулу
Ньютона-Лейбница невозможно. В таких
случаях применяются методы приближенного
вычисления определенных интегралов.
Рассмотрим их, используя определение
интеграла как границы интегральной
суммы. Разделим отрезок точками
точками на
на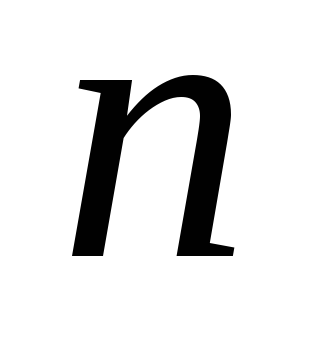 частичных отрезков равной длины.
Обозначим длину каждый из них через
частичных отрезков равной длины.
Обозначим длину каждый из них через .
Тогда
.
Тогда
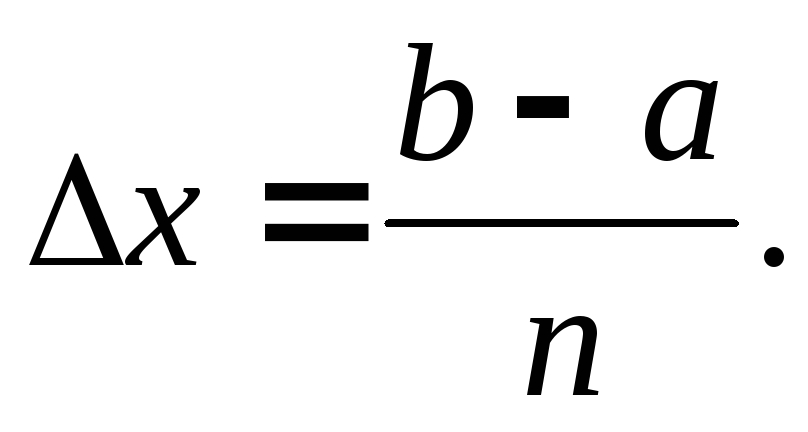
Обозначим
через 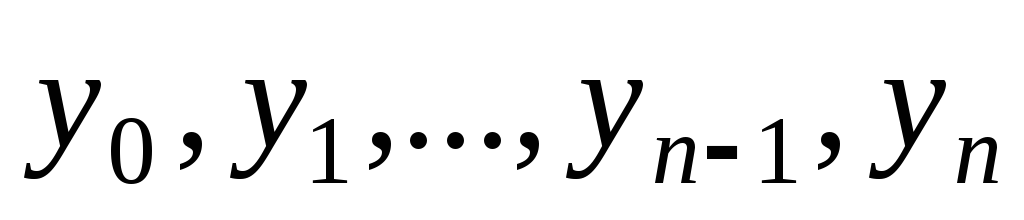 значения функции
значения функции в точках
в точках ,
то есть
,
то есть
 .
.
Составим суммы:
 ,
,
 .
.
Каждая
из этих сумм представляет собой
интегральную сумму для  на отрезке
на отрезке и поэтому приближенно выражает интеграл
и поэтому приближенно выражает интеграл

 , (8.26)
, (8.26)
 .
(8.27)
.
(8.27)
Из
рис. 8.7 видно, что формула (8.26) выражает
площадь ступенчатой фигуры, составленной
из прямоугольников, вписанных в
криволинейную трапецию, а формула (8.27)
выражает площадь ступенчатой фигуры,
составленной из прямоугольников,
описанных вокруг криволинейной трапеции.
Поэтому формулы (8.26; 8.27) называются
формулами прямоугольников. Погрешность
при вычислении интегралов за формулами
прямоугольников будет тем меньше, чем
больше число n. Она выражается формулой
где -максимальное значение
абсолютной величиныпроизводной
-максимальное значение
абсолютной величиныпроизводной на
на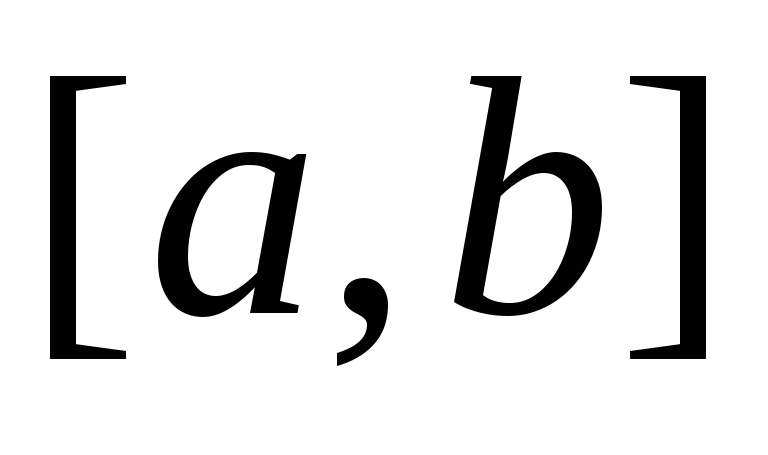 .
.
Более точное значение определенного интеграла получим, если данную кривую заменим не ступенчатой линией, как это делается в формуле прямоугольников, а вписанной ломаной (рис. 8.8).
 Тогда
площадь криволинейной трапеции
Тогда
площадь криволинейной трапеции  заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
 Поскольку площадь первой из
этих трапеций равна
Поскольку площадь первой из
этих трапеций равна  ,
площадь второй равняется
,
площадь второй равняется ,
то
,
то
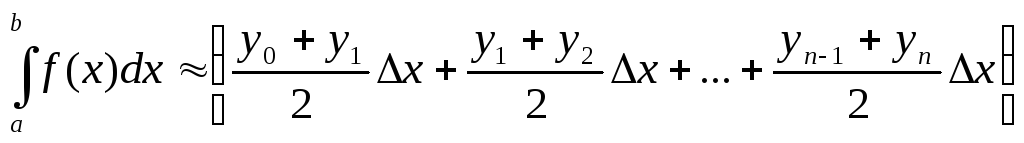
или
 . (8.28)
. (8.28)
Легко
видеть, что она дает среднее арифметическое
из формул (8.26 и 8.27). Формула (8.28) называется
формулой трапеций. В этом случае
погрешность вычисляется по формуле 
где  — минимальное значение абсолютной
величины второй производной
— минимальное значение абсолютной
величины второй производной на
на .
.
Более точные результаты можно получить по формуле Симпсона (или формуле парабол), которая имеет вид:
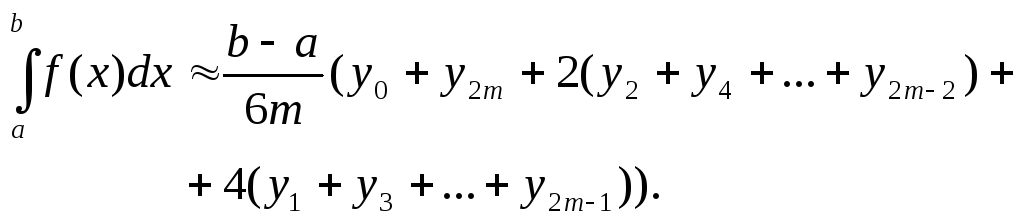 (8.29)
(8.29)
При
этому надо обратить внимание на то, что
число 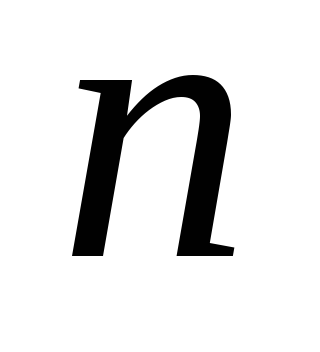 частичных отрезков, на которые разбивается
отрезок
частичных отрезков, на которые разбивается
отрезок ,
должно быть обязательно четным, то есть
,
должно быть обязательно четным, то есть .
Тогда каждые две соседних криволинейных
трапеции, на которые разбилась вся
криволинейная трапеция
.
Тогда каждые две соседних криволинейных
трапеции, на которые разбилась вся
криволинейная трапеция (рис. 8.8), заменяютсяпараболической
трапецией, площадь
которой исчисляется по формуле
(рис. 8.8), заменяютсяпараболической
трапецией, площадь
которой исчисляется по формуле  ,
,
г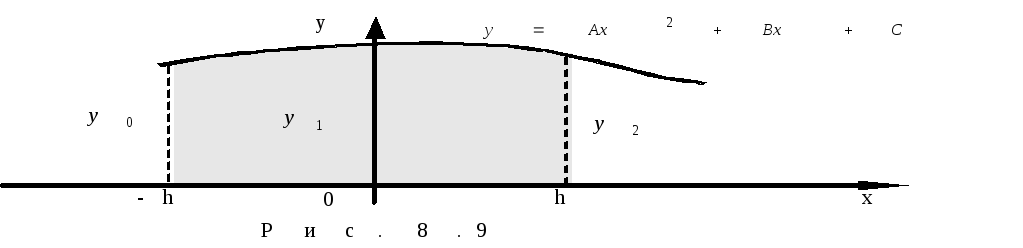 деи
деи —
крайние ординаты,
—
крайние ординаты,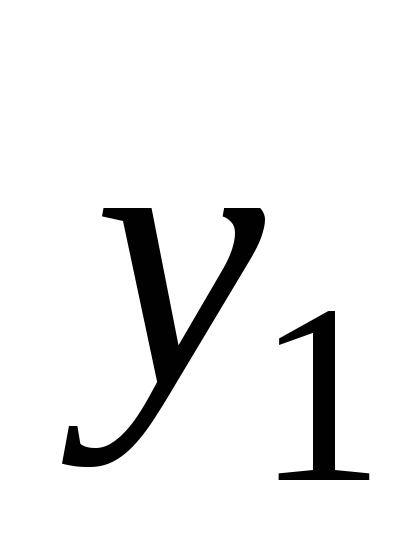 —
ордината кривой в середине отрезка, а
—
ордината кривой в середине отрезка, а — расстояние между ординатами
— расстояние между ординатами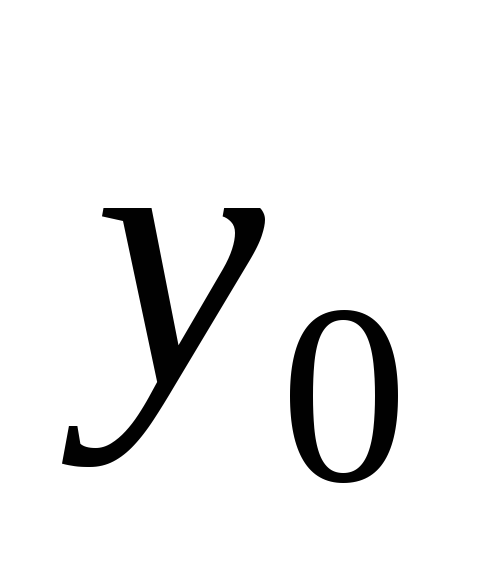 и
и (рис. 8.9).
(рис. 8.9).
Погрешность при этом может быть вычислена по формуле
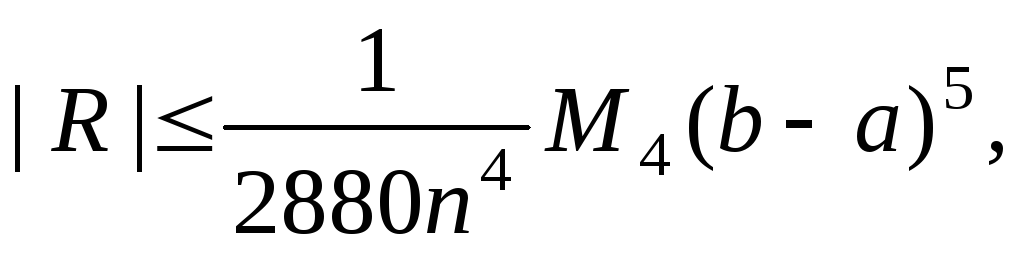
где 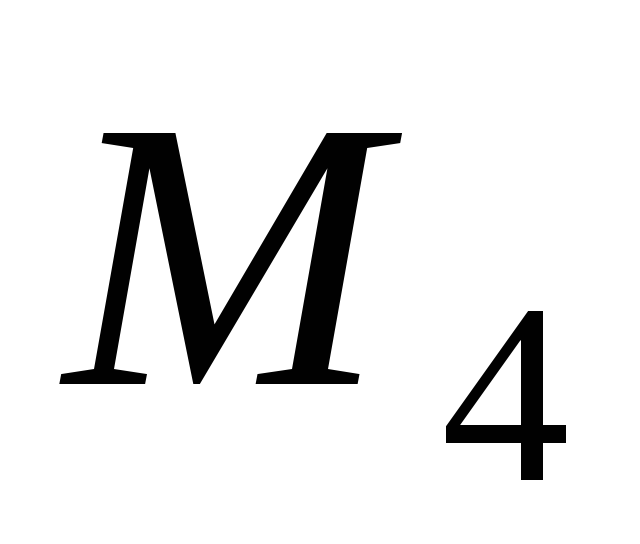 — максимальное значение абсолютной
величины производной
— максимальное значение абсолютной
величины производной на отрезке
на отрезке .
.
Пример.5. Вычислить приближенно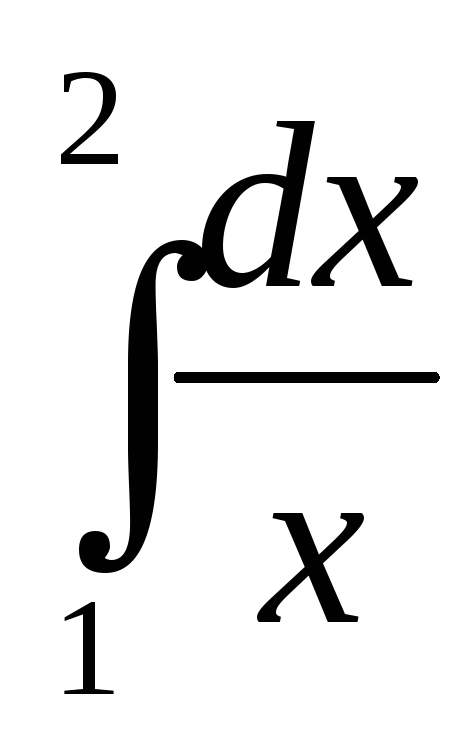 .
.
Точное
значение его 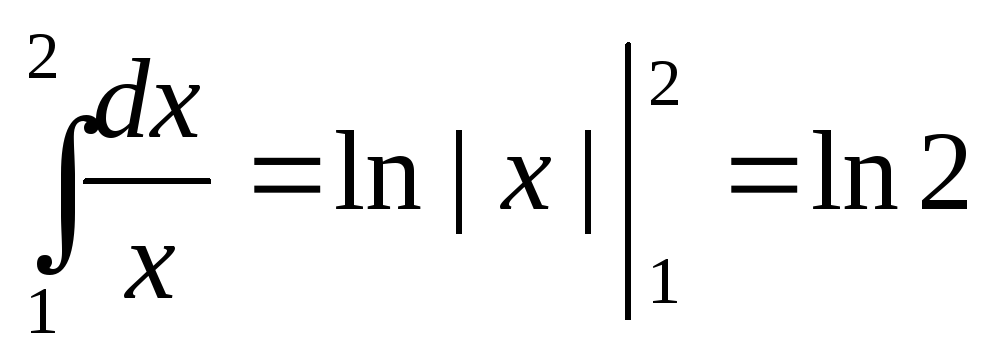 .
З точностью до седьмого знака
.
З точностью до седьмого знака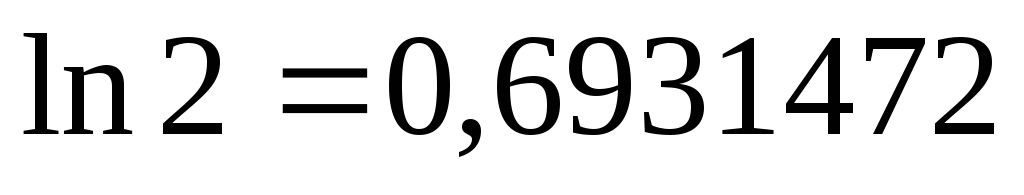 .
Вычислим теперь его значение, пользуясь
формулами (8.26-8.29). Для этого разделим
отрезок
.
Вычислим теперь его значение, пользуясь
формулами (8.26-8.29). Для этого разделим
отрезок на 10 равных отрезков. Тогда длина каждого
из них будет
на 10 равных отрезков. Тогда длина каждого
из них будет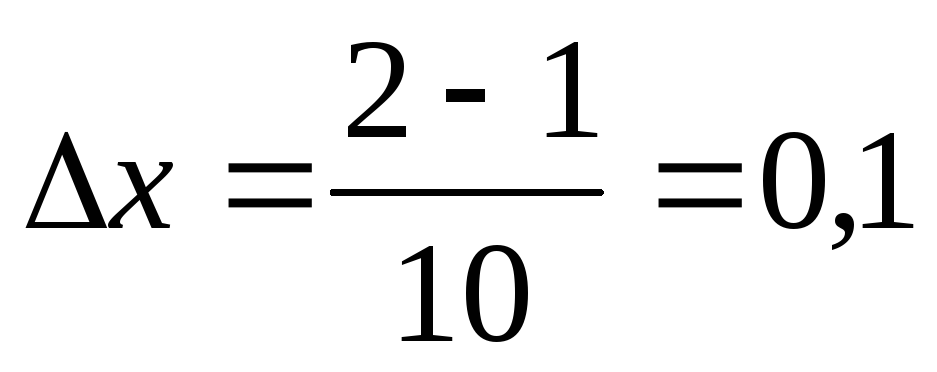 .
.
Составим
табл. 2 значений подынтегральной функции
в точках разбиения 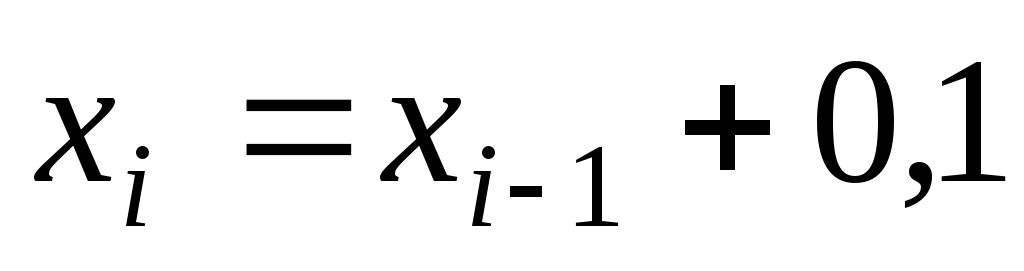 .
.
Таблица 2
Тогда
по формуле (8.26) получим .
.
По
формуле (8.27)  .
.
По
формуле (8.28)  .
.
По формуле Симпсона (8.29)

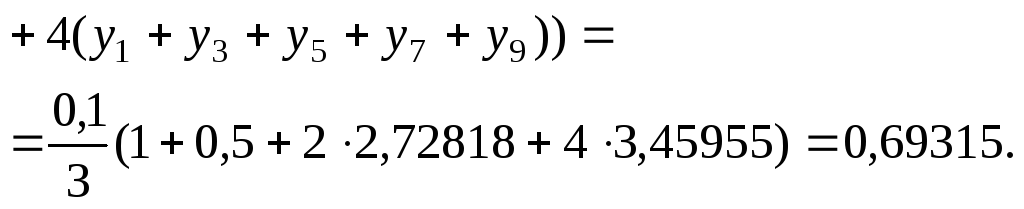
Таким
образом, по формуле Симпсона при  получили 5 верных знаков, по формуле
трапеций — лишь три верных знака, за
формулами прямоугольников мы можем
быть уверены только в одном знаке.
получили 5 верных знаков, по формуле
трапеций — лишь три верных знака, за
формулами прямоугольников мы можем
быть уверены только в одном знаке.
studfile.net
4. Интегрирование подстановкой.
Теорема: Имеет место равенство
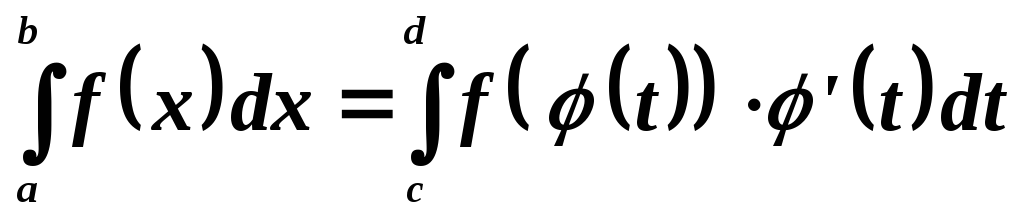
где
функция 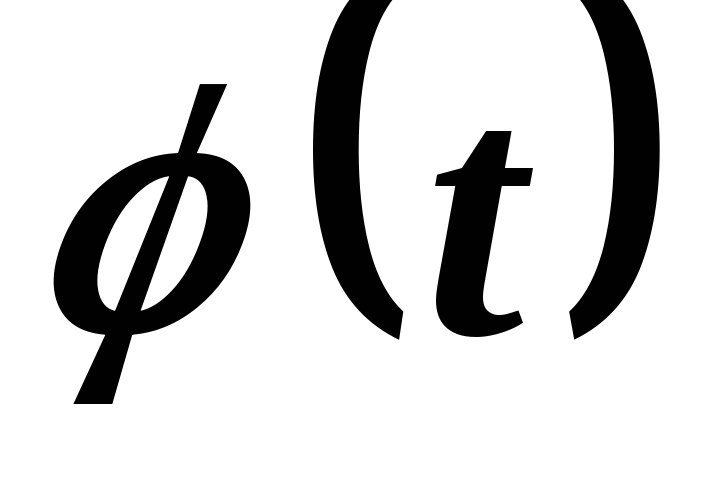 непрерывно дифференцируема на
непрерывно дифференцируема на ,
, ,
, и
и непрерывна на
непрерывна на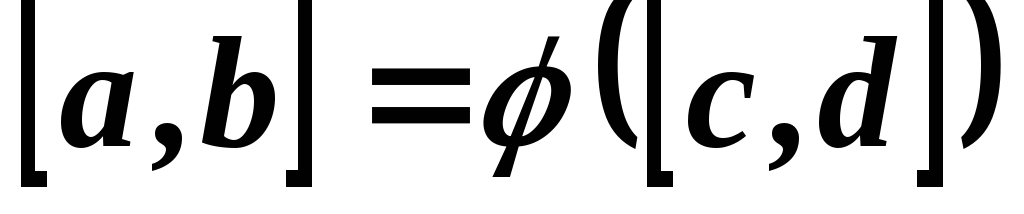 — образе отрезка
— образе отрезка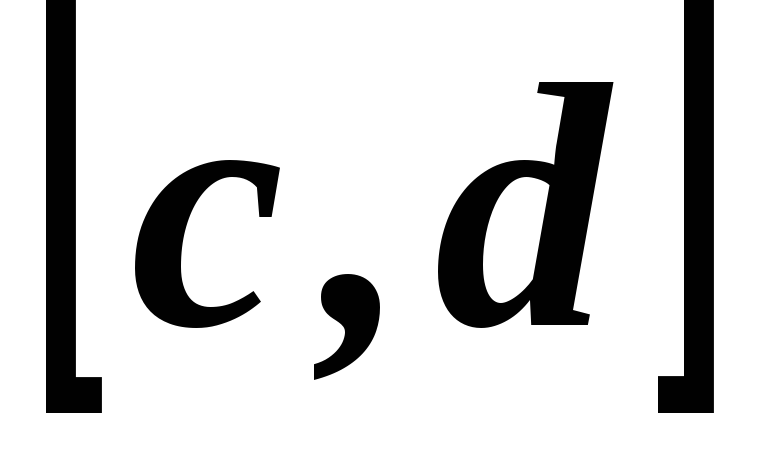 при помощи функции
при помощи функции .
.
Доказательство.
Пусть 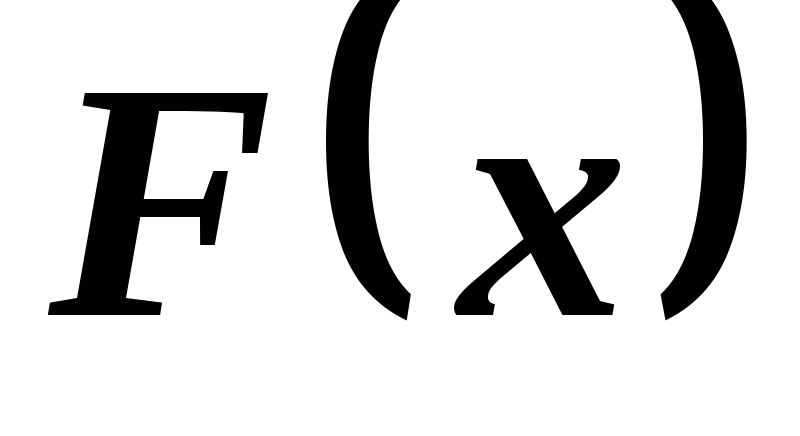 и
и — первообразные функции соответственно
— первообразные функции соответственно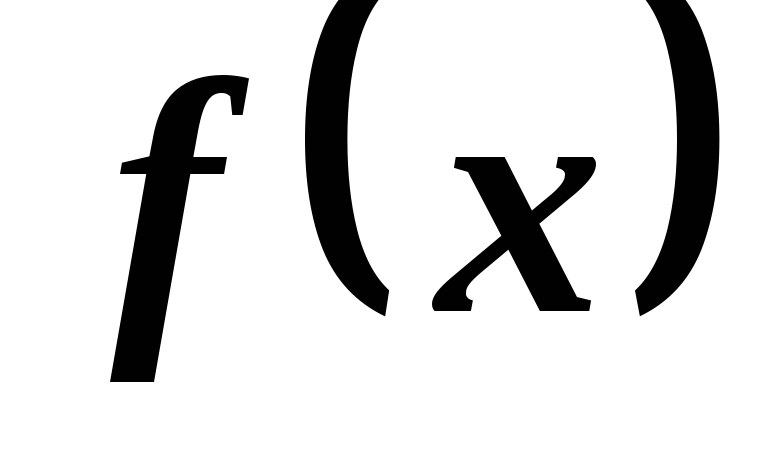 и
и .
Тогда справедливо тождество
.
Тогда справедливо тождество

где  — некоторая постоянная. Поэтому
— некоторая постоянная. Поэтому

На основании формулы Ньютона-Лейбница, левая часть этого равенства равна левой части равенства теоремы, соответственно и правые части, что доказывает теорему.
Пример 1.
Найти интеграл  .
.
Сделаем замену
переменных:  .
Найдем дифференциал
.
Найдем дифференциал :
: .
В результате наш интеграл примет вид:
.
В результате наш интеграл примет вид:

Преобразуем подынтегральное выражение:

Взяв этот интеграл, получим:
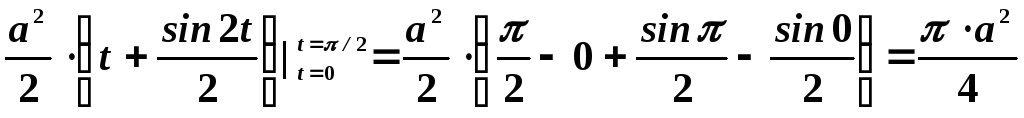 .
.
5. Интегрирование по частям в определенном интеграле.
Теорема. Справедлива формула интегрирования по частям для определенного интеграла

где  и
и — непрерывно дифференцируемые на
— непрерывно дифференцируемые на функции.
функции.
Доказательство.
Произведение  имеет на
имеет на непрерывную производную
непрерывную производную
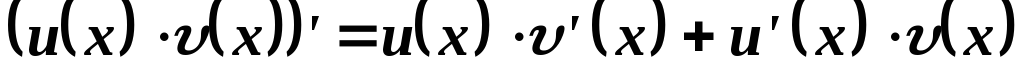
Поэтому по теореме Ньютона-Лейбница

Этим теорема доказана.
Например, найти
интеграл  .
.
Обозначим 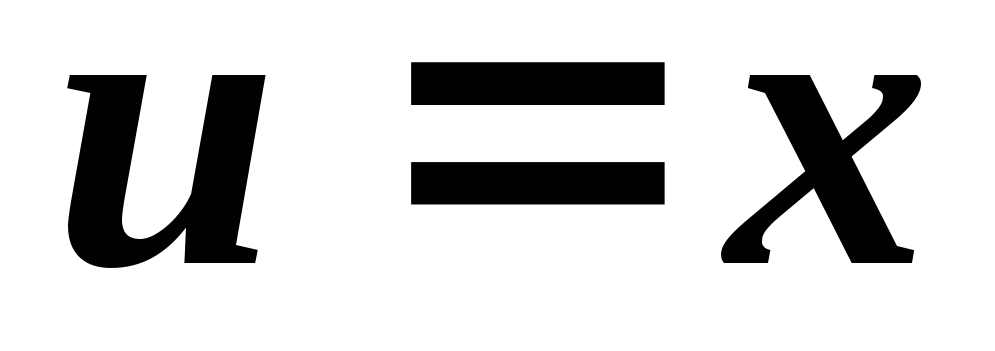 и
и .
Тогда
.
Тогда .
Поэтому
.
Поэтому

Или, окончательно
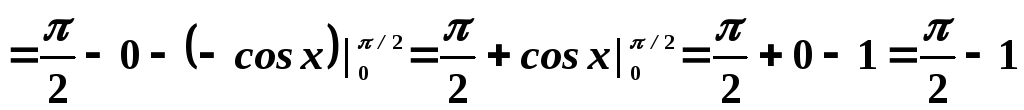 .
.
Если  — четная функция
— четная функция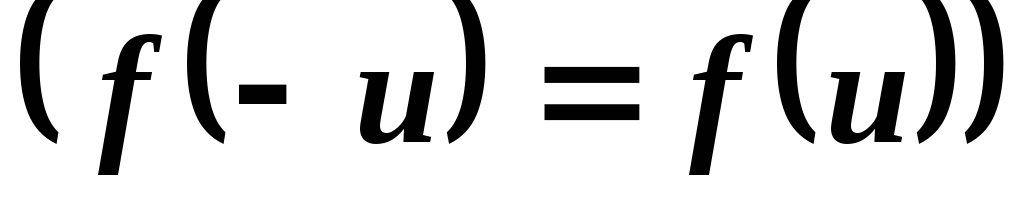 ,
то
,
то
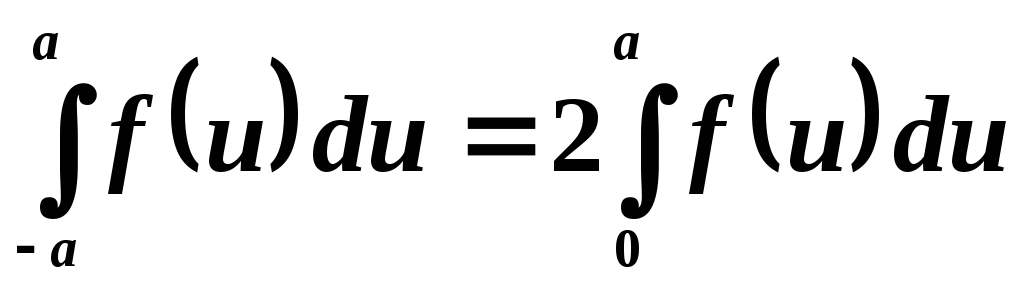
Пример 2. Найти
интеграл 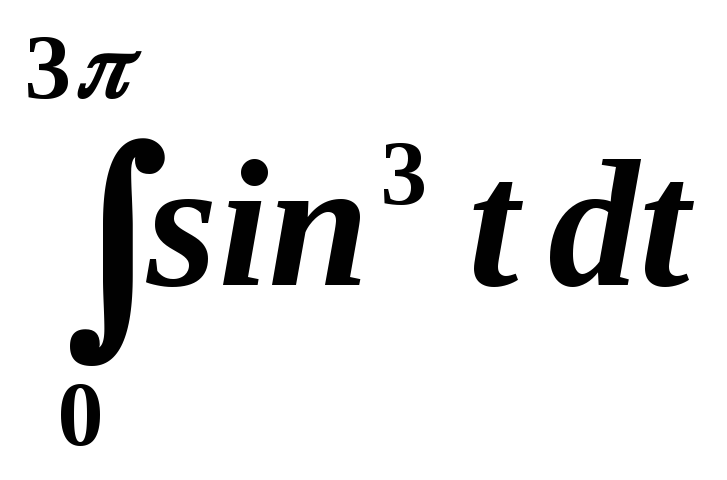 .
.
Преобразуем этот интеграл к виду

Сделаем замену  .
В результате пределы интегрирования
изменятся:
.
В результате пределы интегрирования
изменятся: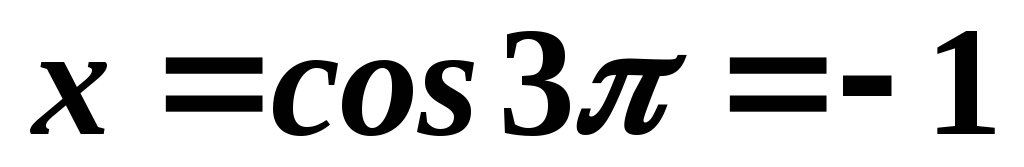 и
и .
В результате получим:
.
В результате получим:

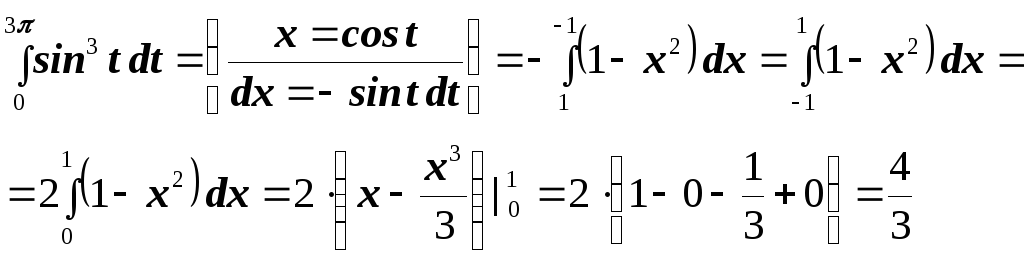
Далее,
если  — нечетная функция
— нечетная функция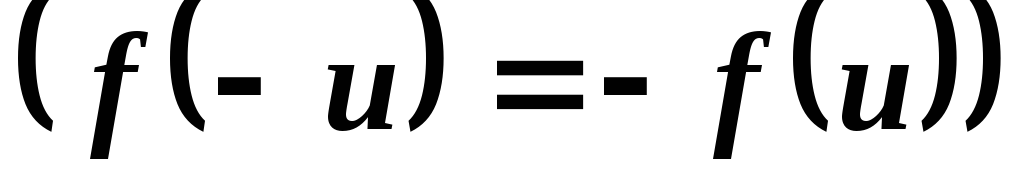 ,
то
,
то
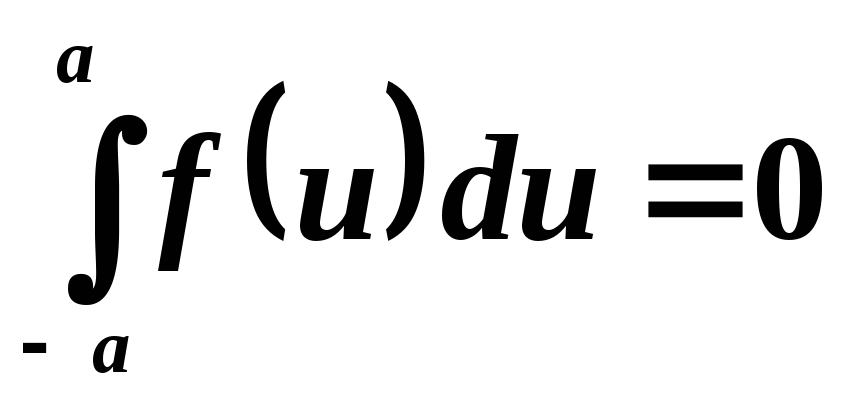 .
.
Если  — периодическая функция периода
— периодическая функция периода —
— ,
то
,
то
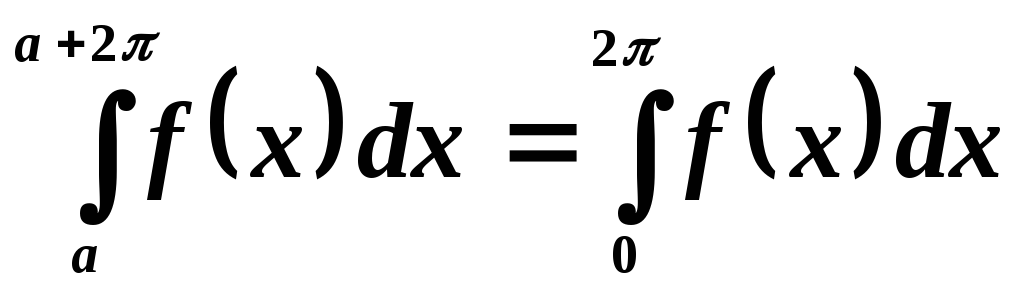 .
.
Такие особенности в некоторых случаях упрощают процесс интегрирования.
Пример 3. Вычислить
интеграл 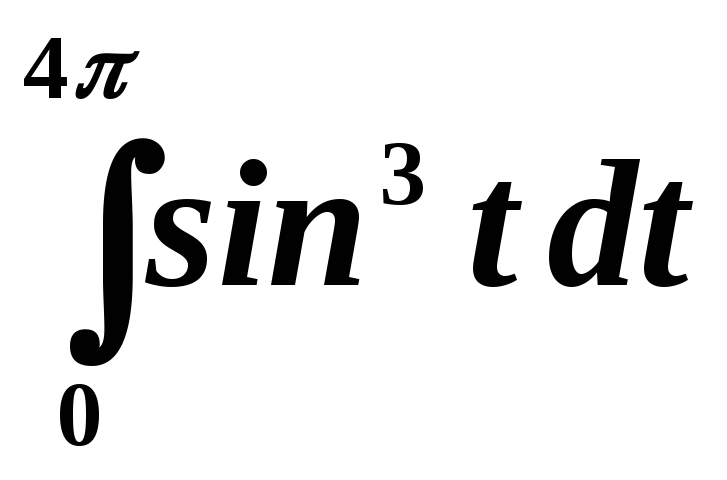 .
.
Преобразуем этот интеграл к виду:
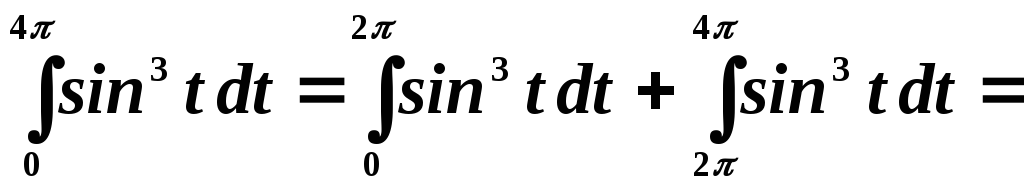
Пределы интегрирования во втором интеграле представим как:
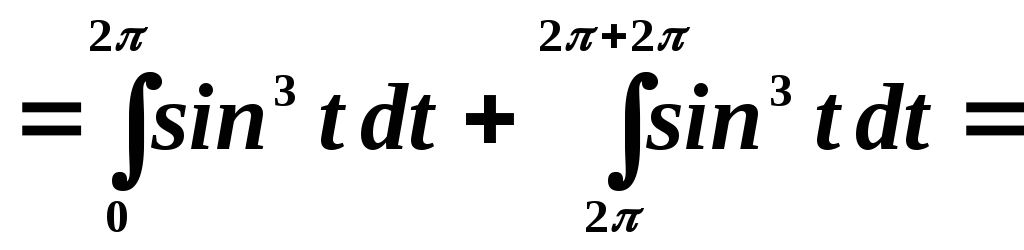
Согласно свойству периодической функции, перепишем это выражение:
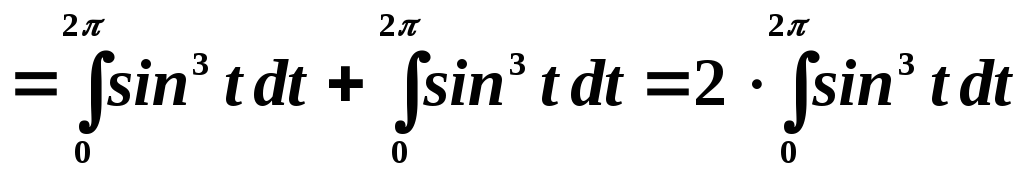
Преобразуем далее
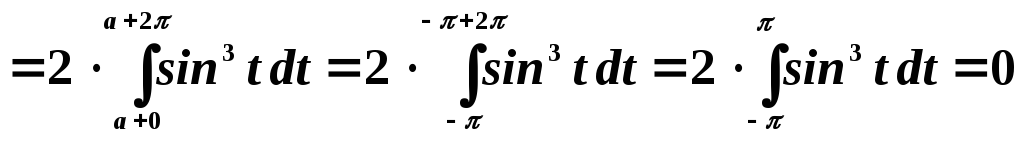
Пример
4. Определить
объем продукции, произведенной рабочим
за третий час рабочего дня, если
производительность труда характеризуется
функцией 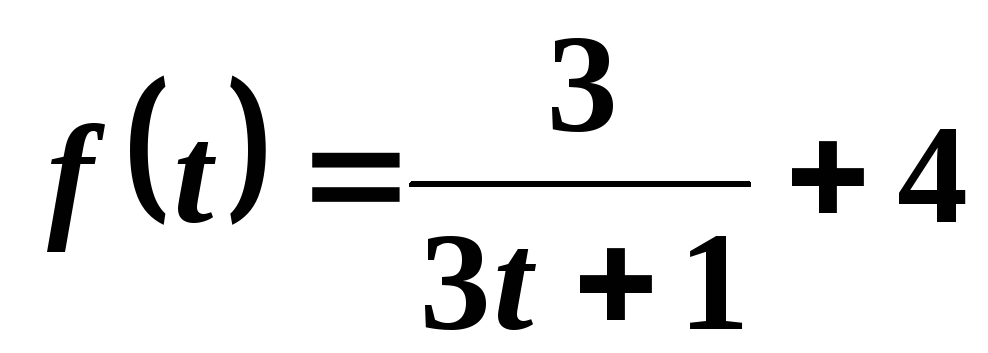 .
.
График этой функции имеет вид, изображенный на рисунке.

Решение. Если
непрерывная функция  характеризует производительность труда
рабочего в зависимости от времени
характеризует производительность труда
рабочего в зависимости от времени ,
то объем продукции, произведенной
рабочим за промежуток времени от
,
то объем продукции, произведенной
рабочим за промежуток времени от до
до будет выражаться формулой:
будет выражаться формулой:

В нашем случае:

Пример
5. Определить
запас товаров в магазине, образуемый
за три дня, если поступление товаров
характеризуется функцией  .
.
Решение. Имеем:
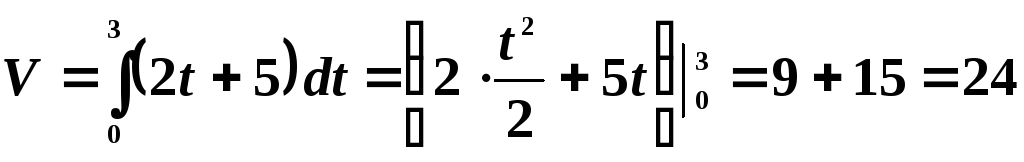
6. Несобственные интегралы.
Пусть
на конечном полуинтервале  задана функция
задана функция такая, что она интегрируема (т.е. конечна)
на любом интервале
такая, что она интегрируема (т.е. конечна)
на любом интервале ,
где
,
где ,
но неограниченна в окрестности точки
,
но неограниченна в окрестности точки .
Тогда ее интеграл на
.
Тогда ее интеграл на ,
или, что то же самое, на
,
или, что то же самое, на не может существовать, так как интегрируемая
функция должна быть ограничена.
не может существовать, так как интегрируемая
функция должна быть ограничена.
Однако может случиться так, что существует конечный предел
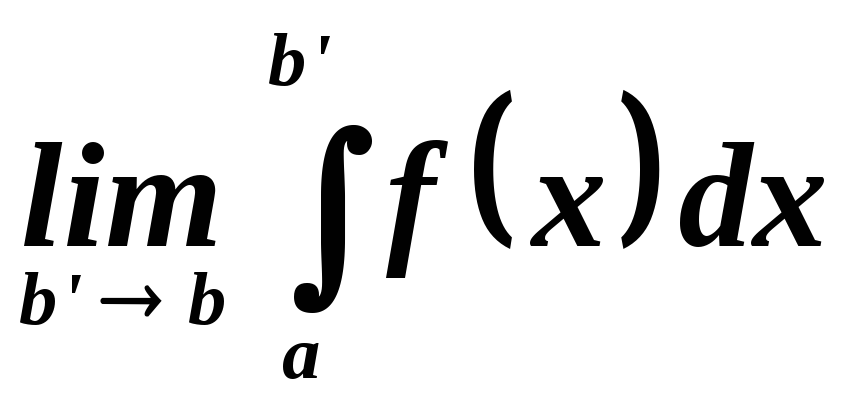
То
есть функция не ограничена, а ее интеграл
ограничен. В этом случае записанный
предел называют несобственным
интегралом от 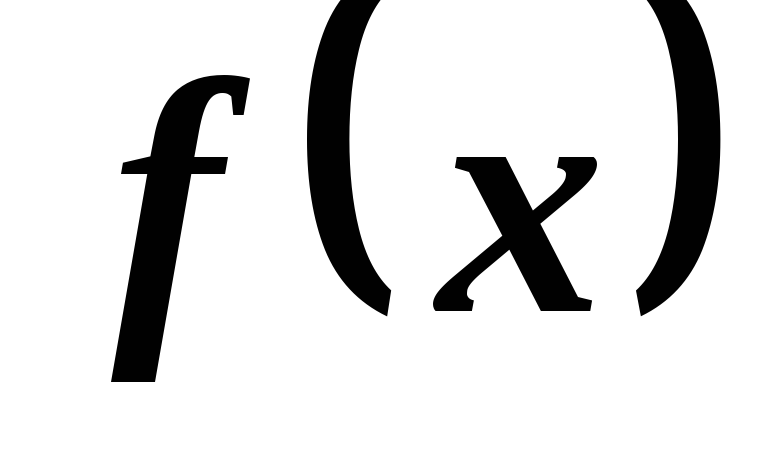 на отрезке
на отрезке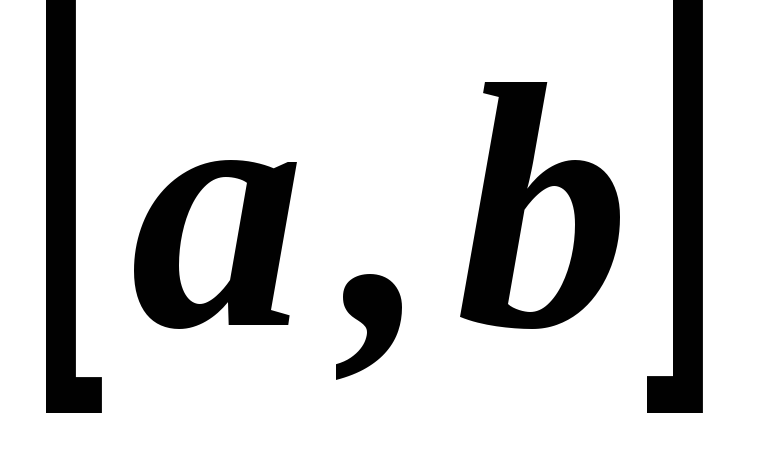 и записывают в виде
и записывают в виде
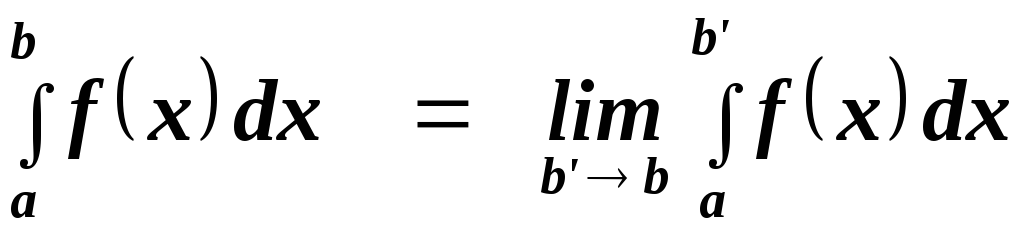
В таком
случае говорят, что интеграл  сходится. В противном случае говорят,
что он расходится или не существует как
несобственный риманов интеграл.
сходится. В противном случае говорят,
что он расходится или не существует как
несобственный риманов интеграл.
Аналогично
и на полуинтервале 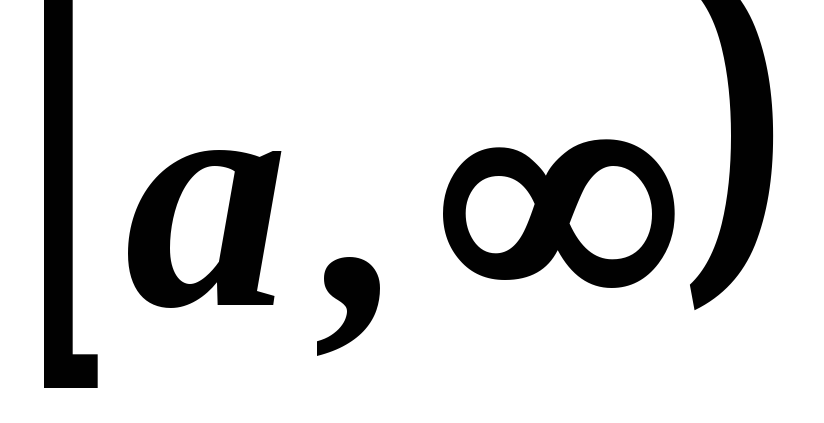
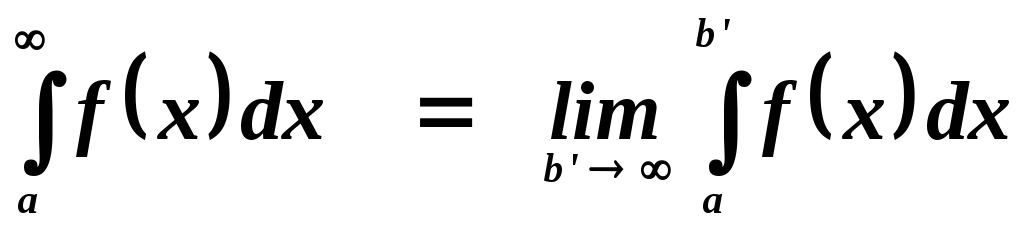
В связи с этим выражение
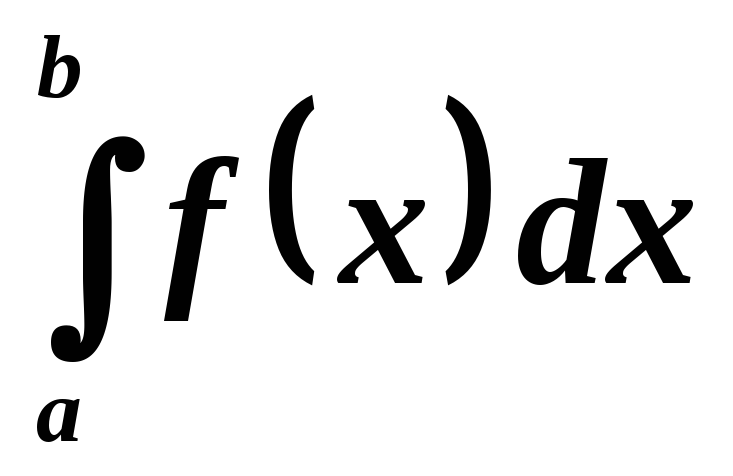
называется
интегралом от  с единственной особенностью в точке
с единственной особенностью в точке ,
если выполняется следующее условие:
если
,
если выполняется следующее условие:
если конечная точка, то функция
конечная точка, то функция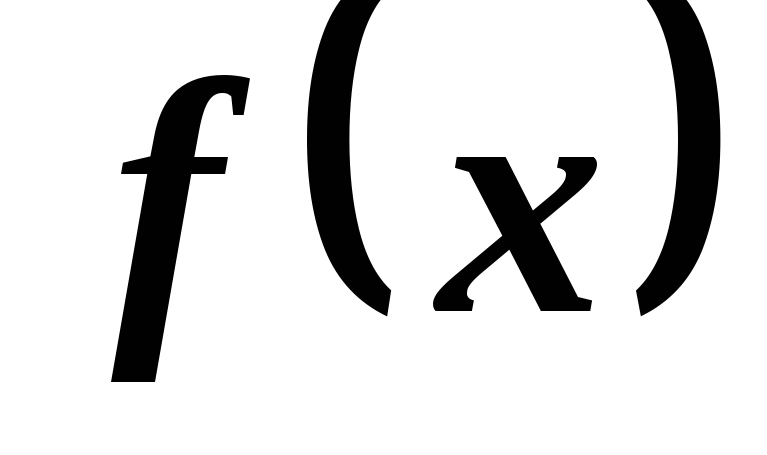 интегрируема на
интегрируема на при любом
при любом удовлетворяющим неравенствам
удовлетворяющим неравенствам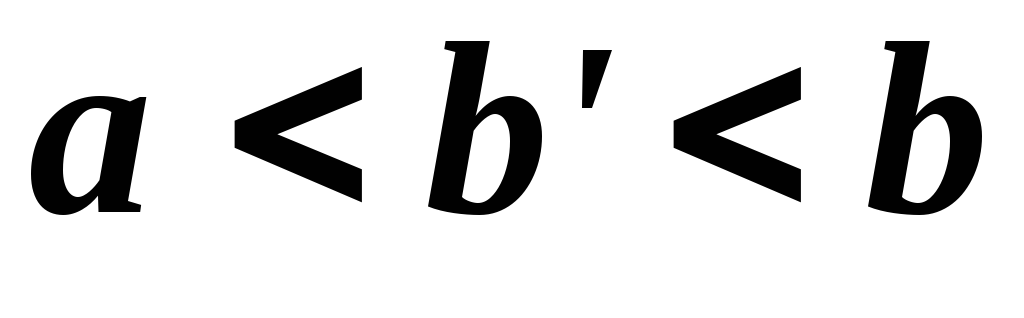 ,
и, кроме того, не ограничена в точке
,
и, кроме того, не ограничена в точке .
Если же
.
Если же ,
то про функцию
,
то про функцию предполагается лишь, что она интегрируема
на
предполагается лишь, что она интегрируема
на при любом конечном
при любом конечном .
.
Также различают несобственные интегралы первого типа (с одним или двумя бесконечными пределами) и несобственные интегралы второго типа (от разрывных функций).
Несобственный интеграл первого рода, вычисляется обычно как

Например,
найти  .
.
Имеем 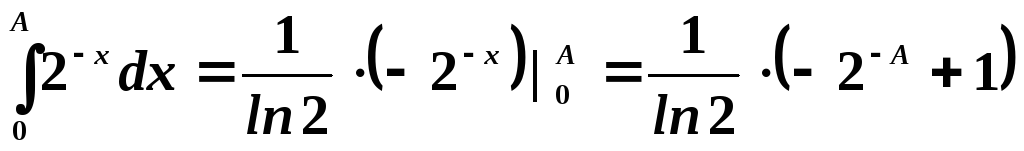 .
.
При  это выражение имеет предел
это выражение имеет предел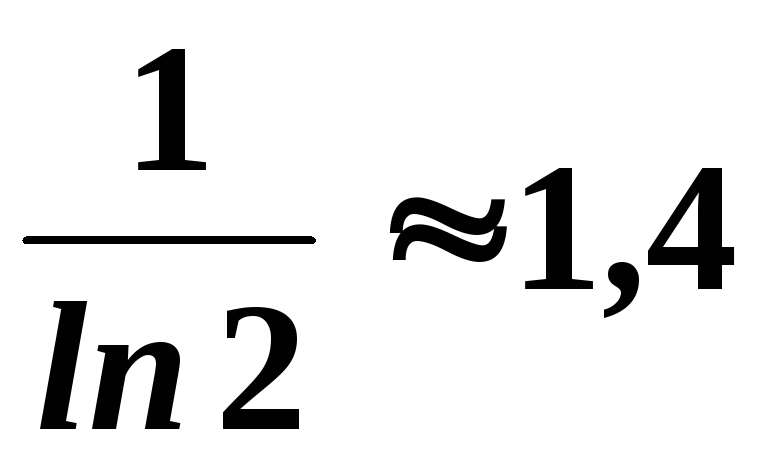 .
Значит
.
Значит .
.
Или,
найти 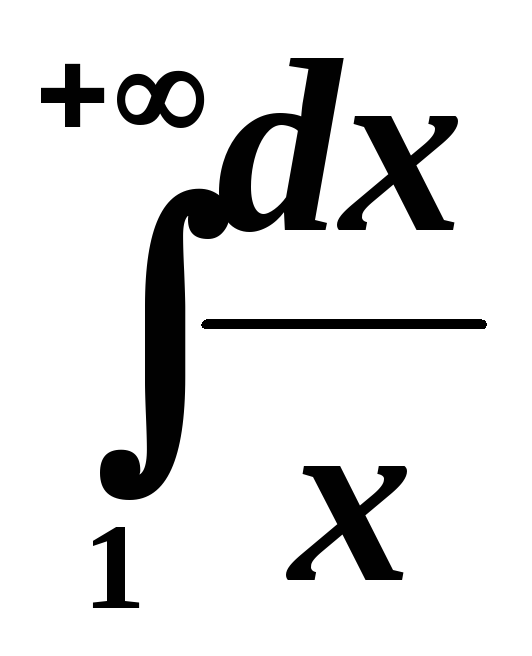 .
.
Имеем 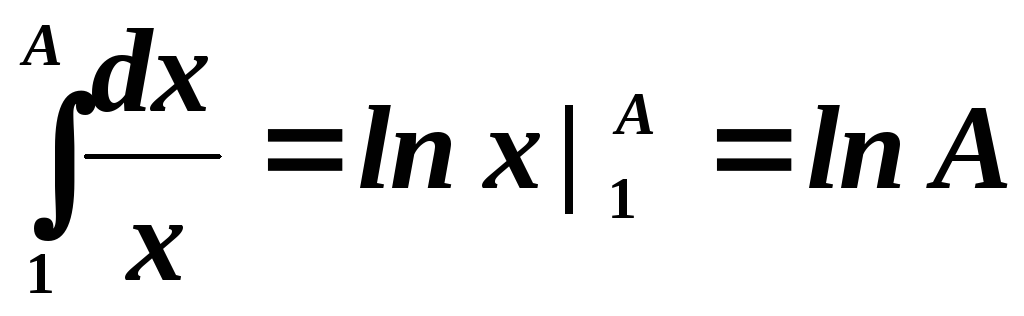 . Этот интеграл расходится.
. Этот интеграл расходится.
П ример
6. Найти
площадь бесконечной полосы
ример
6. Найти
площадь бесконечной полосы  (верзьера Аньези).
(верзьера Аньези).
 .
.
Далее, имеем 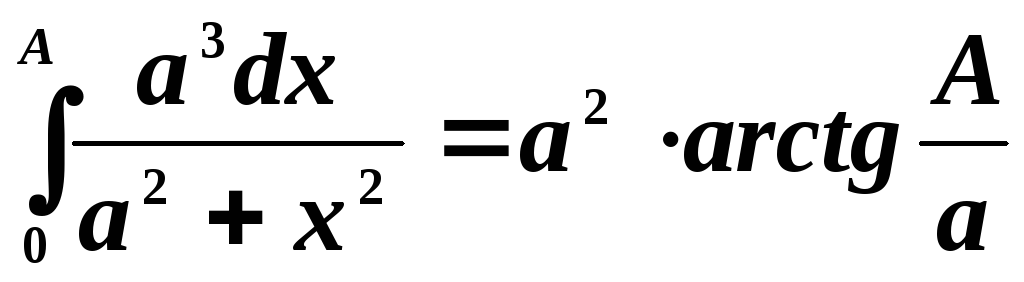 .
.
Отсюда  .
.
Аналогично вычисляется и первое слагаемое. В итоге получим:
 .
.
Пример 7. Найти  .
.
Данный интеграл
— несобственный, так как подынтегральная
функция терпит разрыв в точке  .
Однако этот интеграл сходится, так как
.
Однако этот интеграл сходится, так как

studfile.net
2.2. Методы вычисления определенного интеграла
Вычисление определенных интегралов как пределов интегральных сумм связано в большими трудностями даже в тех случаях, когда подынтегральные функции являются простыми. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов.
Ниже будет сформулирована теорема Ньютона-Лейбница, позволяющая сводить вычисления определенного интеграла к неопределенному. Эта теорема играет фундаментальную роль в математическом анализе (см.подробнее [1] с.397).
2.2.1. Теорема Ньютона-Лейбница
Пусть f(x) непрерывна на сегменте [a,b] и F(x) одна из ее первообразных, тогда справедлива формула

Пример 34.
Вычислить 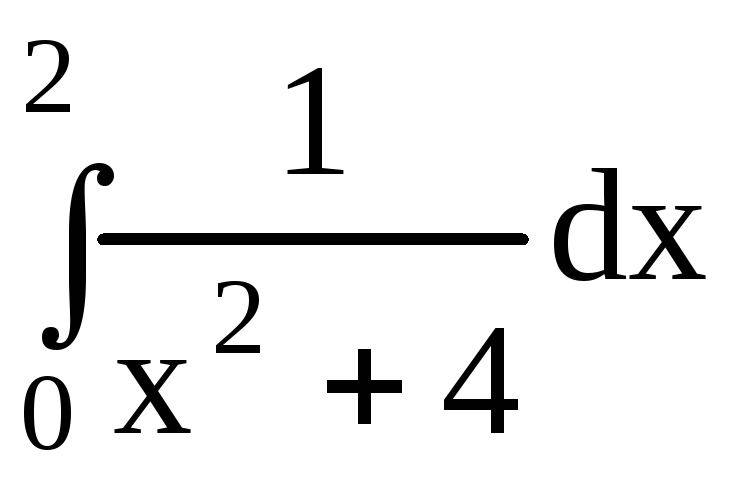 .
.
Решение. Используя формулу Ньютона-Лейбница, а также табличный интеграл 16, получим
 .
.
2.2.2. Методы замены переменной в определенном интеграле
а) Необходимо
вычислить интеграл  ,
,
где f(x) непрерывная функция на [a,b].
Перейдем к новой
переменной t,
полагая  .
Пусть
.
Пусть ,
кроме того, при измененииt
от
до
значения функции
,
кроме того, при измененииt
от
до
значения функции  не выходят за пределы сегмента [a,b].
Предположим, что функция
не выходят за пределы сегмента [a,b].
Предположим, что функция 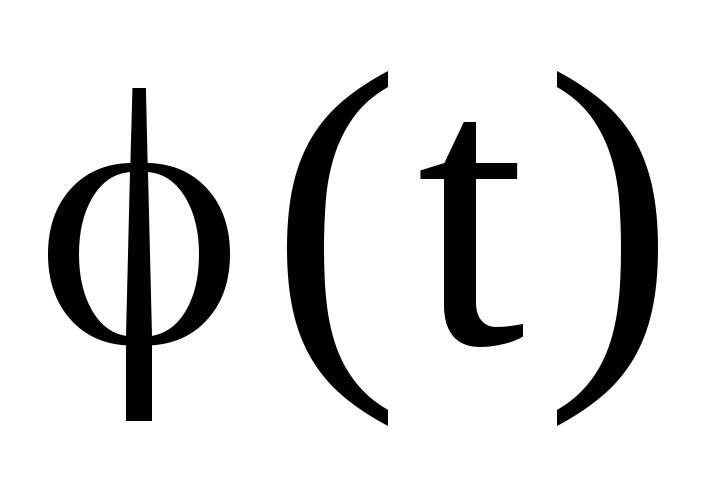 непрерывно дифференцируема на промежутке
[,],
то справедлива следующая формула замены
переменной
непрерывно дифференцируема на промежутке
[,],
то справедлива следующая формула замены
переменной
 .
.
Пример 35. Вычислить 
Решение. Преобразуем подкоренное выражение, выделив полный квадрат
 .
.
Введем новую
переменную:  тогда
тогда ,
,
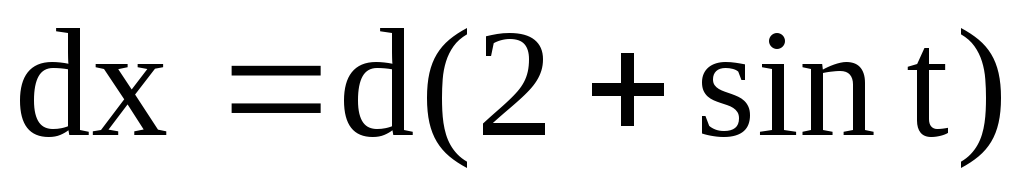 или
или 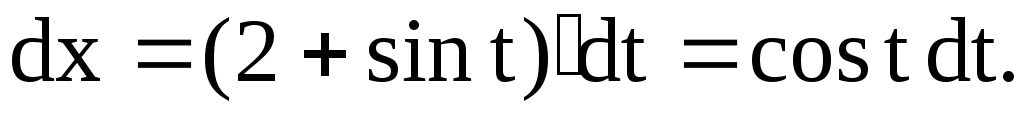
Найдем пределы интегрирования новой переменной t:
если  ,
то
,
то
если  ,
то
,
то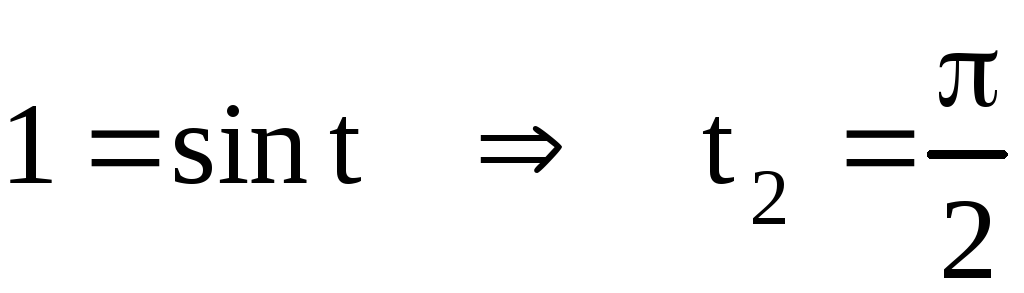 .
.
Воспользуемся формулой замены переменной в определенном интеграле, получим


Заметим, что в данном случае при применении формулы замены переменной отпадает необходимость возвращения к старой переменной х по сравнению с неопределенным интегралом. Это вполне объяснимо, ибо определенный интеграл есть некоторое постоянное число, в то время как неопределенный интеграл от той же самой функции есть некоторая функция.
б) Часто вместо
замены переменной 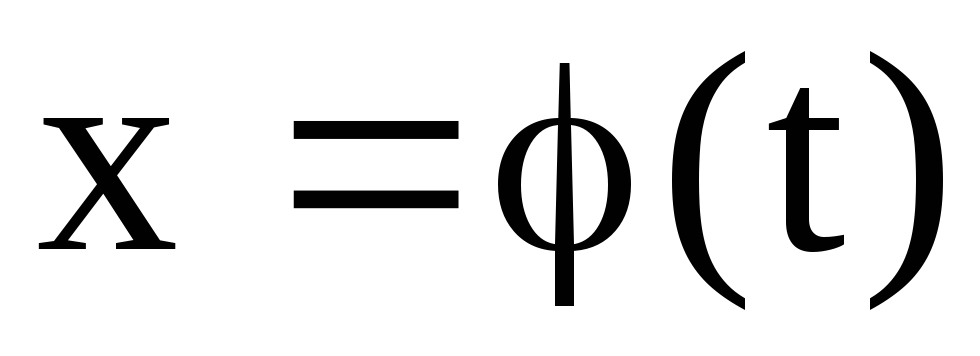 употребляют обратную замену переменной
употребляют обратную замену переменной .
На конкретном примере покажем, как это
делается.
.
На конкретном примере покажем, как это
делается.
Покажем это на конкретном примере.
Пример 36. Вычислить  .
.
Решение. Пусть 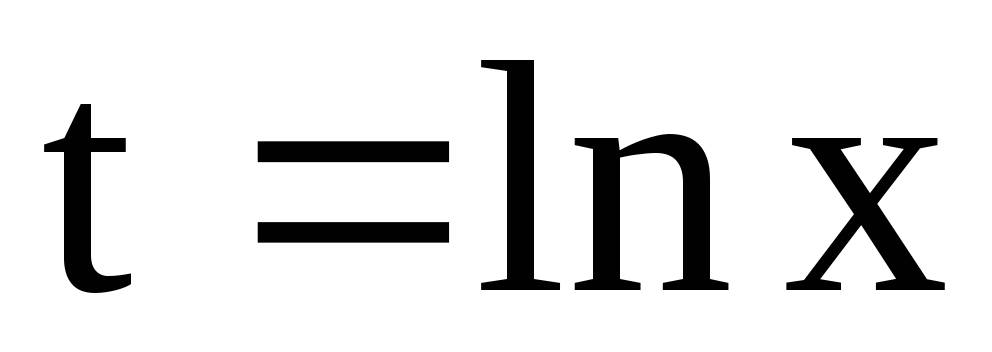 ,
тогда
,
тогда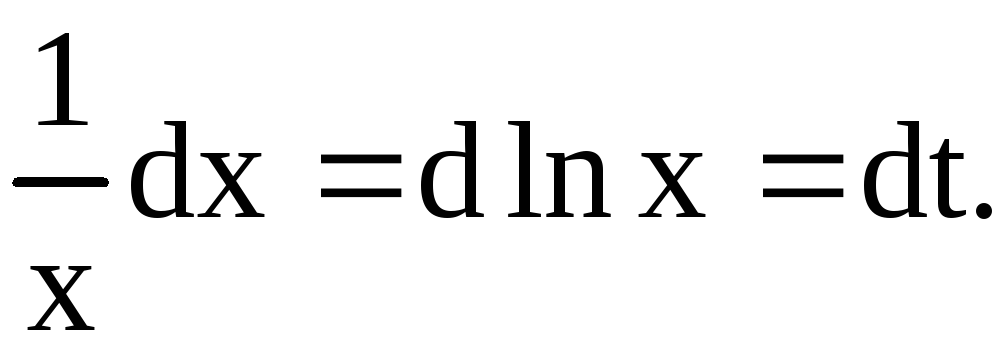
Если 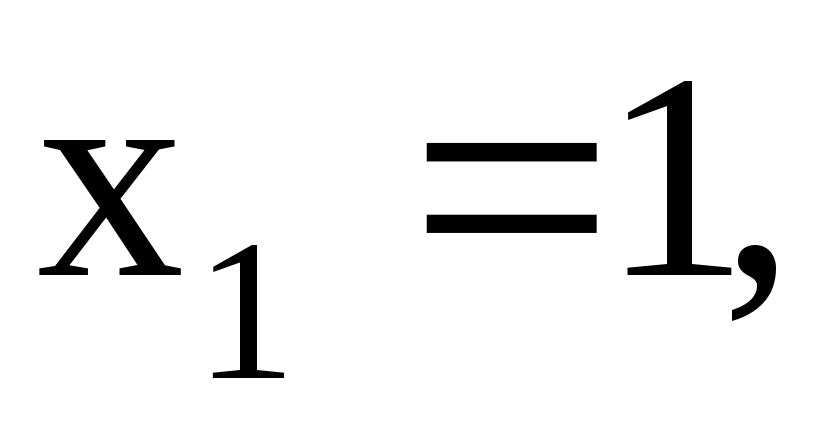 то
то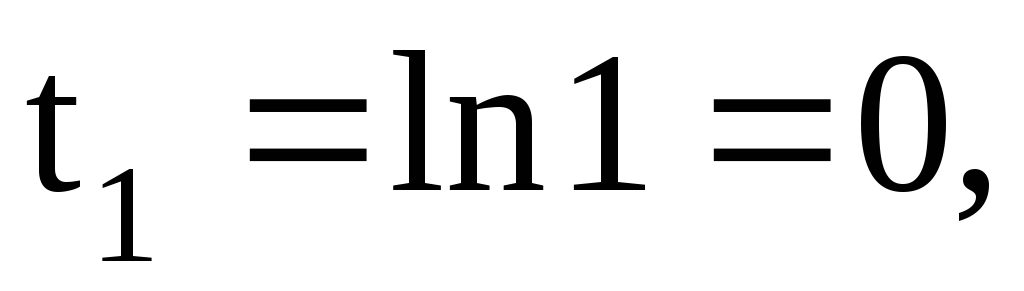 если
если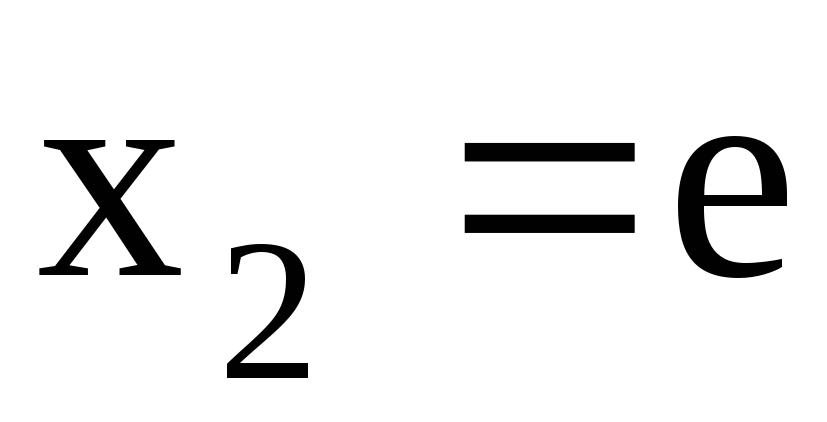 ,
то
,
то
Следовательно,

2.2.3. Формула интегрирования по частям в определенном интеграле
Пусть  и
и
непрерывные функции вместе со своими
первыми производными на [a,b],
тогда справедлива формула интегрирования
по частям:
непрерывные функции вместе со своими
первыми производными на [a,b],
тогда справедлива формула интегрирования
по частям:
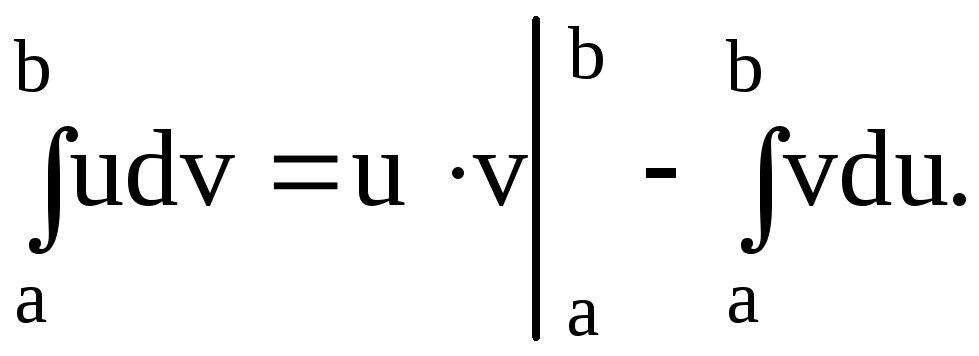
Пример 37. Вычислить интеграл  .
.
Решение. Применим полученную формулу
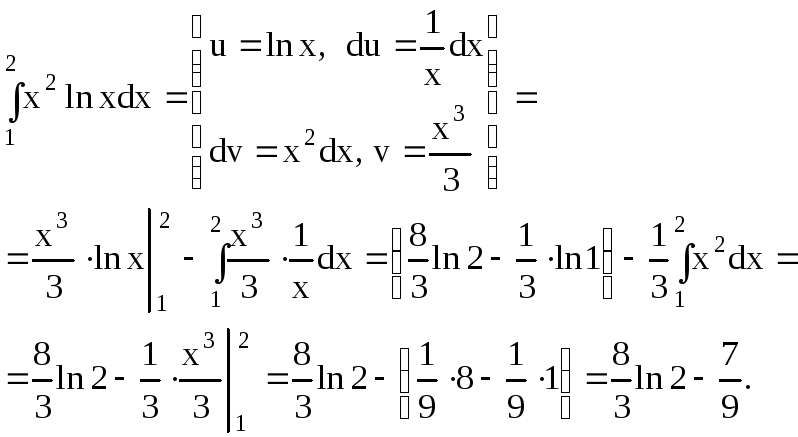
Подробнее о методах интегрирования в определенном интеграле см.[1] с.399-403.
3. Несобственные интегралы
Определение определенного интеграла, его свойства и методы интегрирования рассматривались в предположении, что промежуток интегрирования [a,b] конечен и функция f(x) непрерывна на нем.
Иногда приходится отказываться от одного или обоих этих предположений. В этом случае мы приходим к понятию несобственного интеграла.
3.1. Несобственные интегралы с бесконечными пределами интегрирования
Рассмотрим функцию  ,
непрерывную на бесконечном промежутке
,
непрерывную на бесконечном промежутке .
.
Несобственным
интегралом от функции f(x)
по промежутку 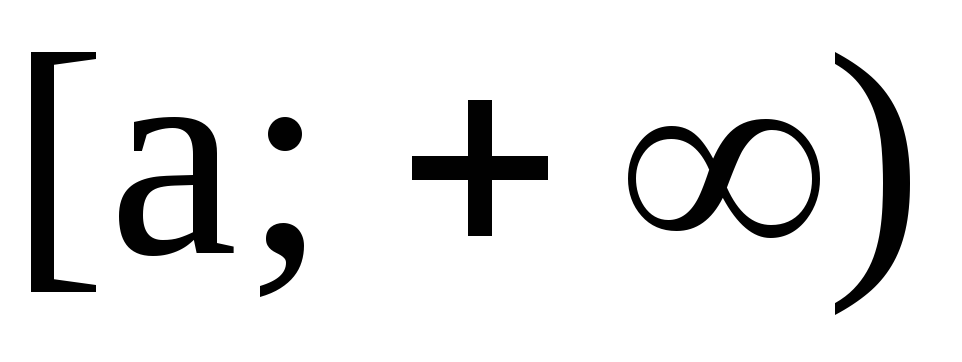 называется
называется :
:
 .
.
Если указанный предел существует и конечен, то несобственный интеграл с бесконечным пределом интегрирования называется сходящимся, в противном случае расходящимся.
Если  на
на и
и ,
то данный интеграл представляет собой
площадь бесконечной криволинейной
трапеции, ограниченной кривой
,
то данный интеграл представляет собой
площадь бесконечной криволинейной
трапеции, ограниченной кривой ,
прямой
,
прямой и бесконечным интервалом
и бесконечным интервалом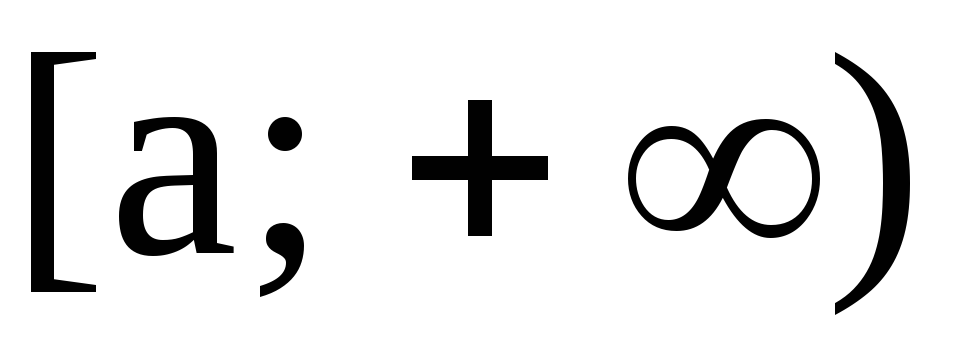 .
.

Аналогично
определяется несобственный интеграл
на промежутке  :
:

а на интервале 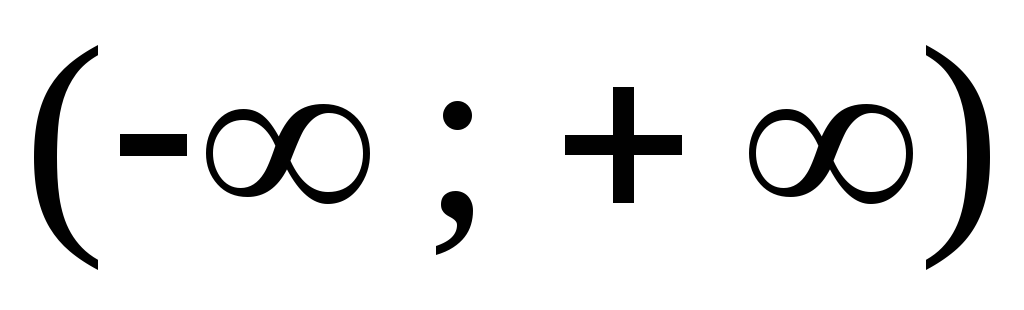 определяется формулой
определяется формулой
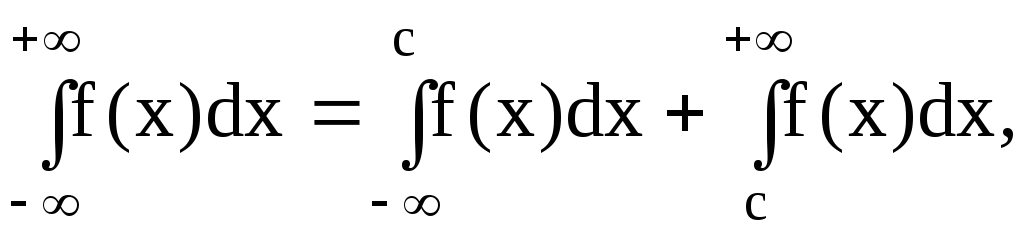
где с любое действительное число.
Если сравнить две
криволинейные трапеции на рис.3.1, то
конечность или бесконечность их
соответствующих несобственных интегралов
зависит от скорости убывания функции  и
и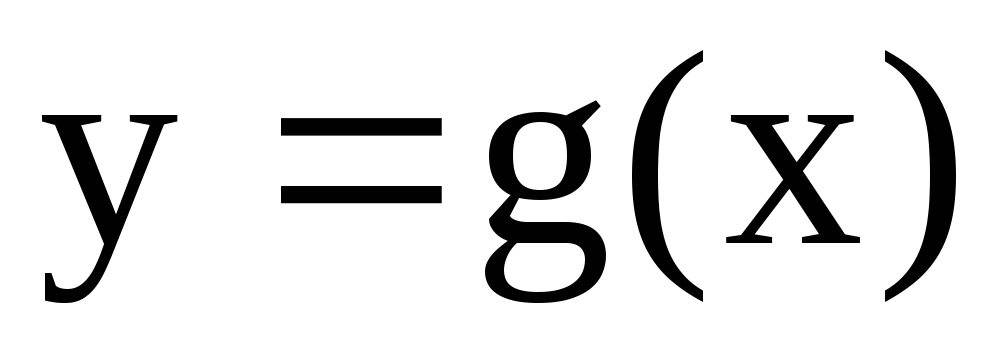 при
при .
.
Так, например, 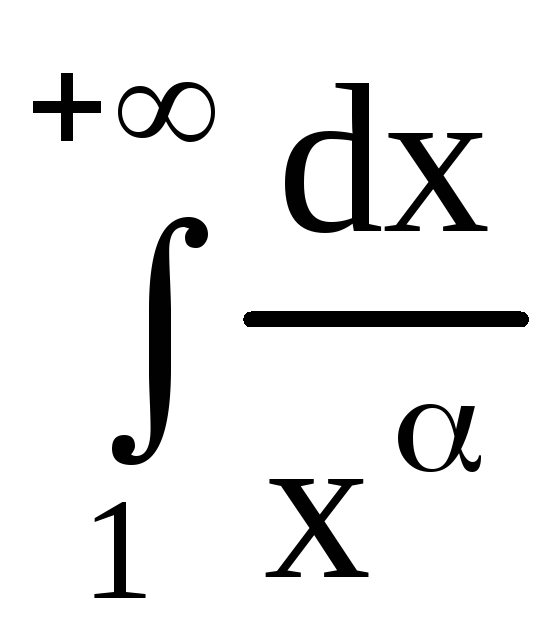 сходится при
сходится при и расходится при
и расходится при .
.
В этом легко
убедится, вычислив  ,
если
,
если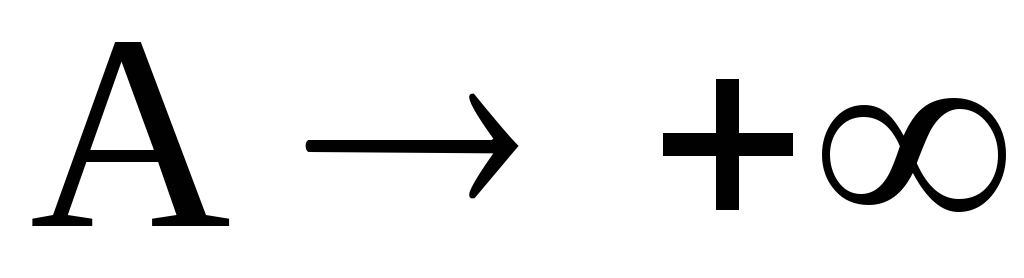 .
.
Если 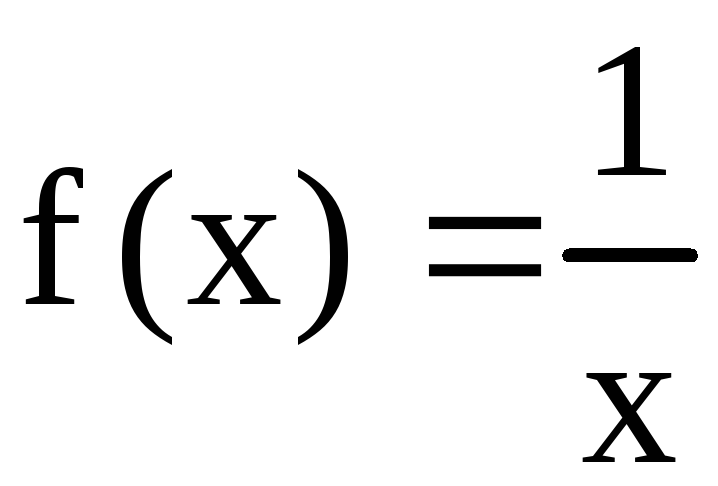 ,
то
,
то при
при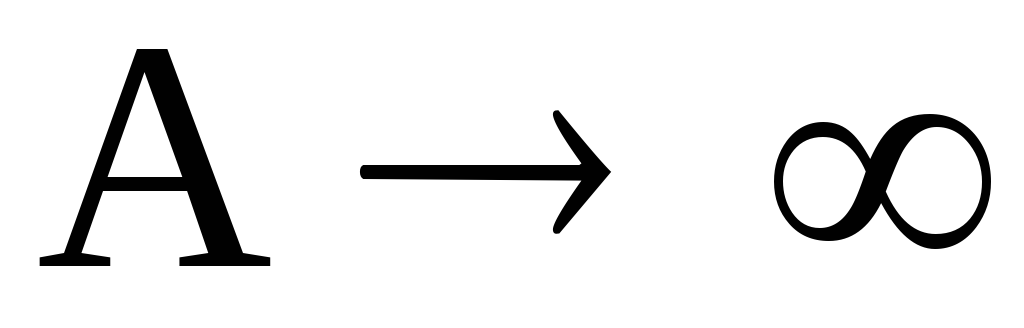 ,
поэтому
,
поэтому
расходится, следовательно, и площадь
соответствующей криволинейной трапеции
бесконечна.
расходится, следовательно, и площадь
соответствующей криволинейной трапеции
бесконечна.

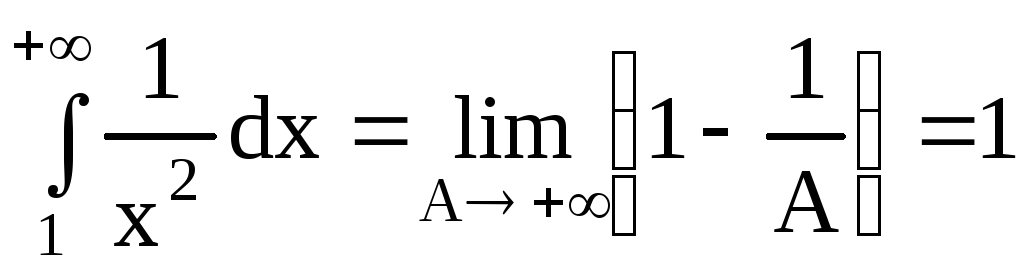 несобственный
интеграл сходящийся, следовательно,
площадь криволинейной трапеции,
ограниченной линиями
несобственный
интеграл сходящийся, следовательно,
площадь криволинейной трапеции,
ограниченной линиями  и бесконечным промежутком
и бесконечным промежутком ,
является конечной и равна 1.
,
является конечной и равна 1.
Пример 38. Исследовать на сходимость несобственный
интеграл 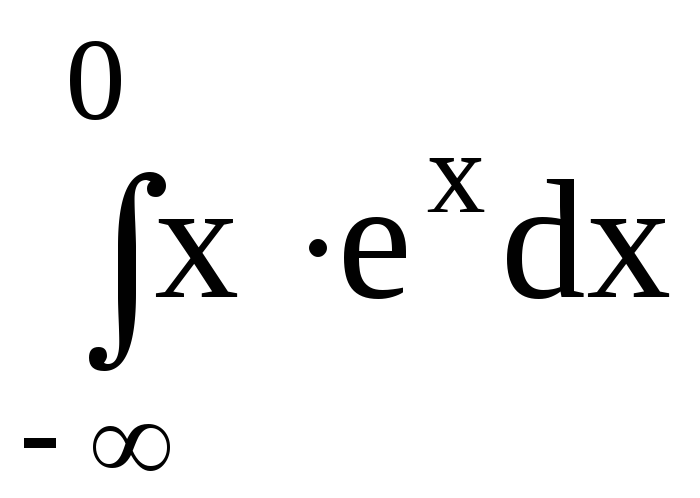 .
.
Решение. Воспользуемся определением несобственного интеграла с бесконечным нижним пределом интегрирования и далее формулой интегрирования по частям

 .
.
Несобственный интеграл сходится.
Пример 39.
Вычислить несобственный интеграл или
установить его расходимость 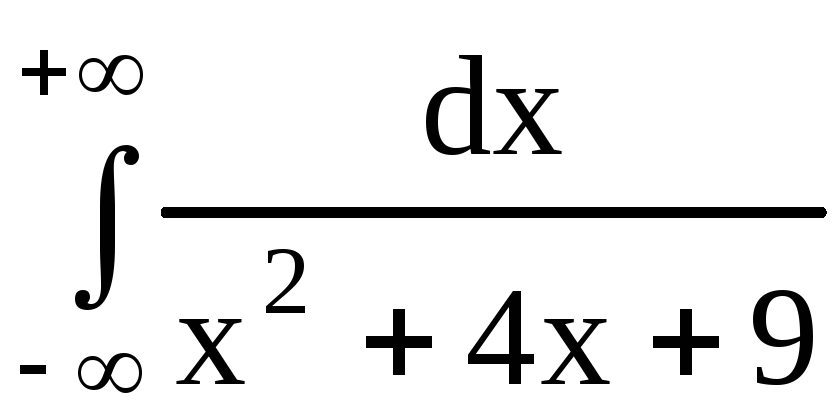 .
.
Решение. Воспользуемся определением несобственного
интеграла с бесконечными пределами
интегрирования. Полагаем  .
.

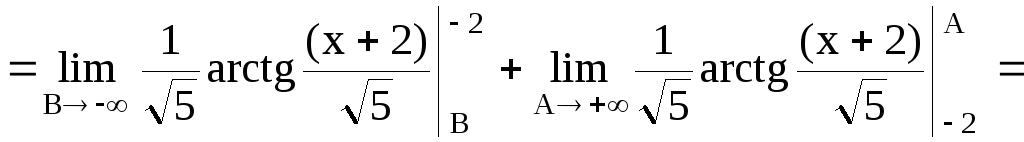

Признак
сравнения. Пусть в промежутке 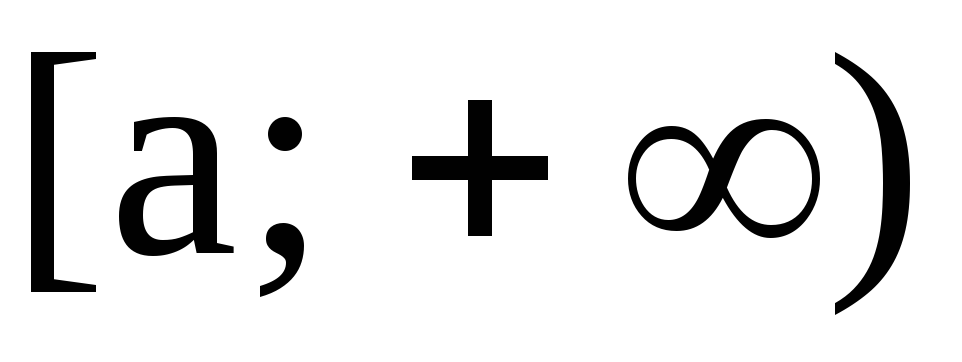 функцииf(x)
и g(x)
непрерывны и
функцииf(x)
и g(x)
непрерывны и  .
Если
.
Если сходится, то сходится и интеграл
сходится, то сходится и интеграл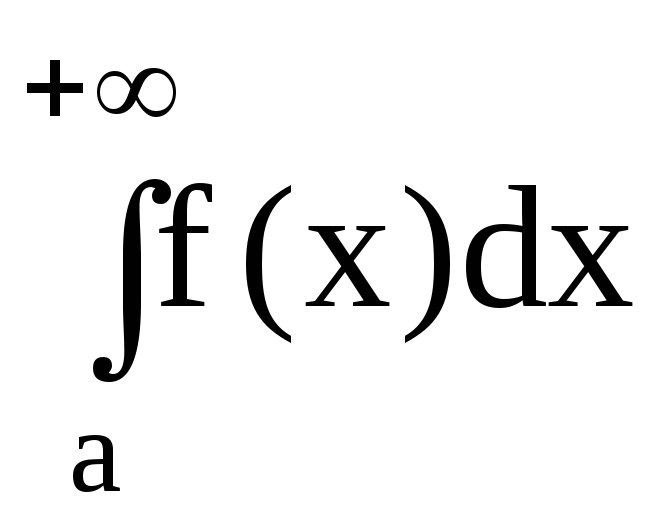 .
Если интеграл
.
Если интеграл расходится, то и
расходится, то и также расходится.
также расходится.
Замечание. Аналогичное утверждение верно для несобственных интегралов и по другим бесконечным пределам интегрирования.
Пример 40.
Исследовать на сходимость несобственный
интеграл  .
.
Решение. Проведем сравнительный анализ
подынтегральной функции при  .
.
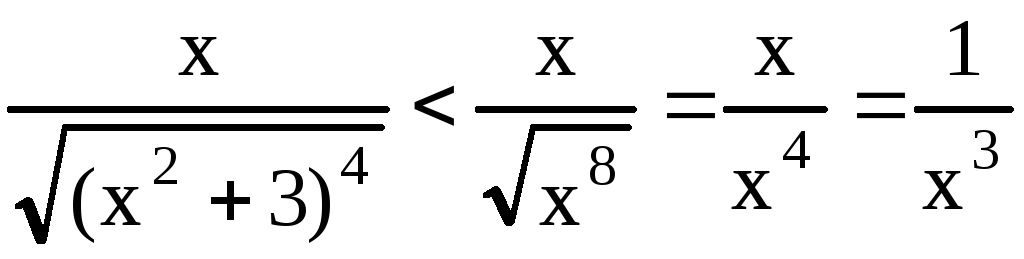
 .
.
Но  сходится, т.к.
сходится, т.к.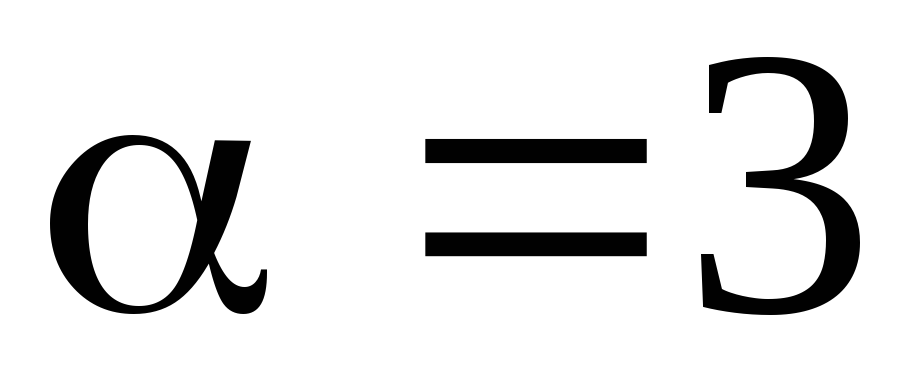 (см. рассуждения выше). Следовательно,
по признаку сравнения сходится и данный
интеграл.
(см. рассуждения выше). Следовательно,
по признаку сравнения сходится и данный
интеграл.
studfile.net
77. Докажите формулу интегрирования по частям для неопределенного интеграла.
Теорема: пусть U(x) и V(x) – две дифференцируемые функции на промежутке X. Тогда на этом промежутке выполняется формула интегрирования по частям: ∫udv=uv-∫vdu
Доказательство. Имеем формулу дифференциала произведения функций uv:
d(uv)=udv+vdu
Интегрируя обе части равенства, получим:
uv=∫udv+∫vdu
Откуда ∫udv=uv-∫vdu.
78. Докажите формулу замены переменной для неопределенного интеграла.
Теорема:.пусть
функция x=φ(t) определена и дифференцируема
на промежутке T и X – множество ее
значений, на котором определена функция
f(x). Тогда если F(x) – первообразная для
f(x) на X, то F(φ(t)) – первообразная для
f(φ(t)φ’(t)) на T, т.е. на множестве T выполняется
равенство: 
Доказательство: По правилу дифференцирования сложной функции производная левой части равенства равна F’t(φ(t))=Fx’(φ(t)) φ’(t)=f(φ(t))φ’(t), что совпадает с подынтегральной функцией в правой части равенства.
79. Дайте определение функции f (x), интегрируемой на отрезке [a,b].Докажите, исходя из определения, что постоянная функция f (x) = 9 интегрируема на любом отрезке.
Функция y=f(x), ограниченная на отрезке [a;b], называется интегрируемой на этом отрезке, если существует единственное число I, разделяющее множества нижних и верхних сумм Дарбу для всевозможных разбиений отрезка [a;b]. Если функция y=f(x) интегрируема на отрезке [a;b], то единственное число, разделяющее эти два множества, называют определенным интегралом функции y=f(x) по отрезку [a;b] и обозначают следующим образом: I=a∫bf(x)dx
81. Докажите, что если функция f (x) непрерывна на отрезке [a,b], то функция = .xaF(x) f (t) dt, x .[a,b], является ее первообразной на этом отрезке.
если функция y=f(x) непрерывна на отрезке [a;b], то функция F(x) =a∫xf(t)dt дифференцируема в любой внутренней точке этого отрезка, причем F’(x)=f(x).
Доказательство:
F’(x)=lim∆x→0 (F(x+∆x)-F(x))/∆x
Для xє(a;b) выберем ∆x столь малым, чтобы точка x+∆x лежала внутри [a;b], тогда
F(x+∆x)=a∫ x+∆xf(t)dt
F(x+∆x)-F(x)= a∫ x+∆xf(t)dt — a∫xf(t)dt= x∫ x+∆xf(t)dt + a∫xf(t)dt — a∫xf(t)dt= x∫ x+∆xf(t)dt
Применим теорему о среднем
F(x+∆x)-F(x)= x∫ x+∆xf(t)dt=f(c)*∆x x<c<x+∆x
(F(x+∆x)-F(x))/∆x=(f(c)*∆x)/∆x=f(c)
Так как функция f(x) непрерывна и c→x при ∆x→0, то lim∆x→0f(c)=f(x)
F’(x)= lim∆x→0(F(x+∆x)-F(x))/∆x= lim∆x→0f(c)=f(x)
Значит f(x) непрерывна на [a;b] и F(x)=a∫xf(t)dt
82. Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона — Лейбница для определенного интеграла.
Пусть функция y=f(x) непрерывна на [a;b] и F(x) – первообразная для f(x), тогда: интеграл f(x)dx=F(b)-F(a), т.е. значение определенного интеграла равно приращению любой из первообразных подынтегральной функции на отрезке интегрирования.
Доказательство: Поскольку функция F(x) непрерывна на отрезке [a;b], то она интегрируема на этом отрезке и имеет первообразную на этом отрезке.
По теореме о производной интеграла по переменному верхнему пределу F(t)=a∫t f(x)dx=f(t)
Но первообразные отличаются на c-const
a∫t f(x)dx=F(t)+c (*)
1) t=a, значит a∫af(x)dx=F(a)+c=0 F(a)=-c подставим это выражение в уравнение (*) и получим:
a∫t f(x)dx=F(t)-F(a)
2) t=b, значит a∫b f(x)dx=F(b)-F(a)
studfile.net
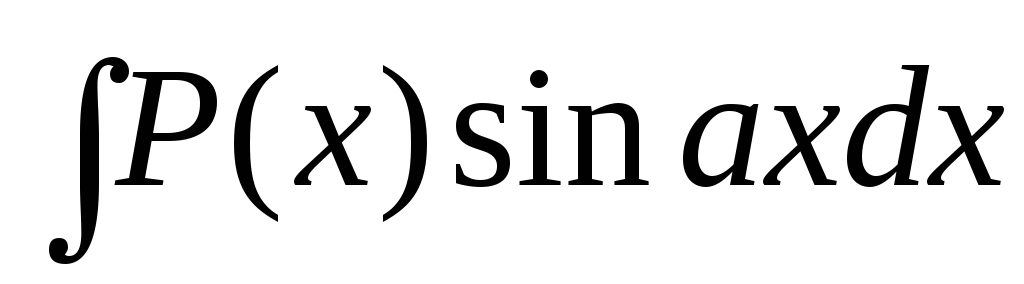
 ,
,
многочлен,
многочлен, действительное
число
действительное
число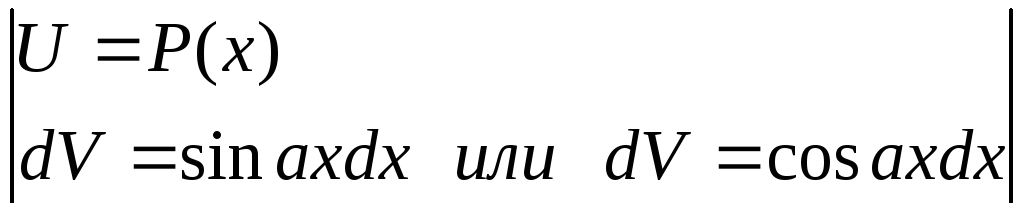


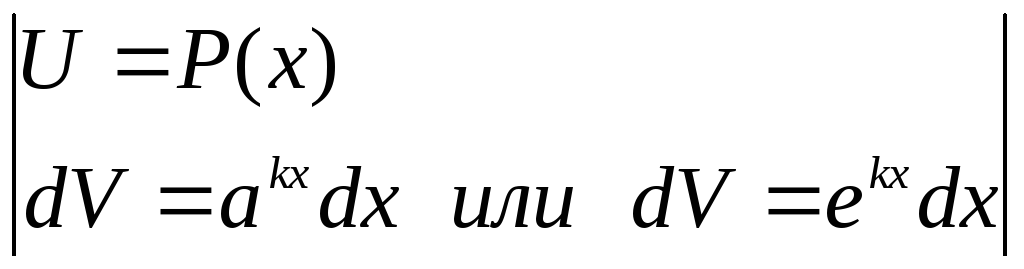


 .
. .
.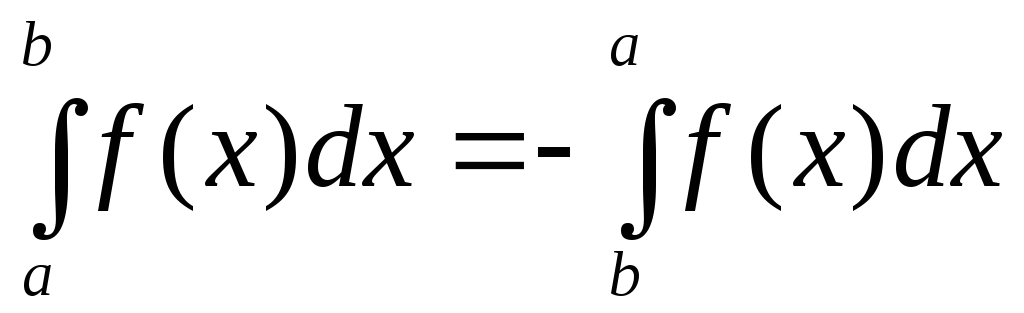 .
. ,
то интеграл равен нулю:
,
то интеграл равен нулю: .
.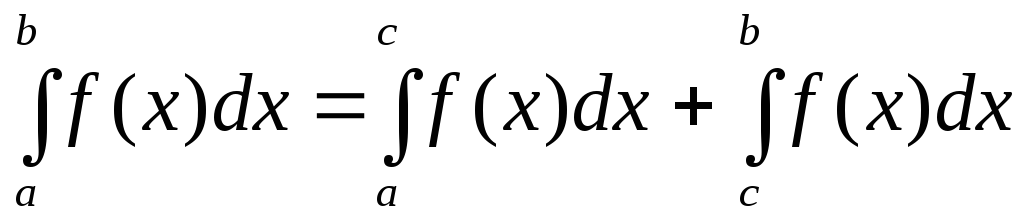 .
. ,
где
,
где ,
,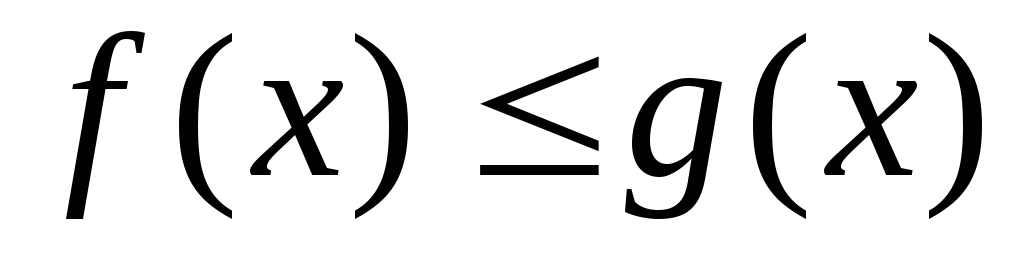 ,
то и
,
то и ,
т.е. обе части неравенства можно почленно
интегрировать.
,
т.е. обе части неравенства можно почленно
интегрировать. на отрезке
на отрезке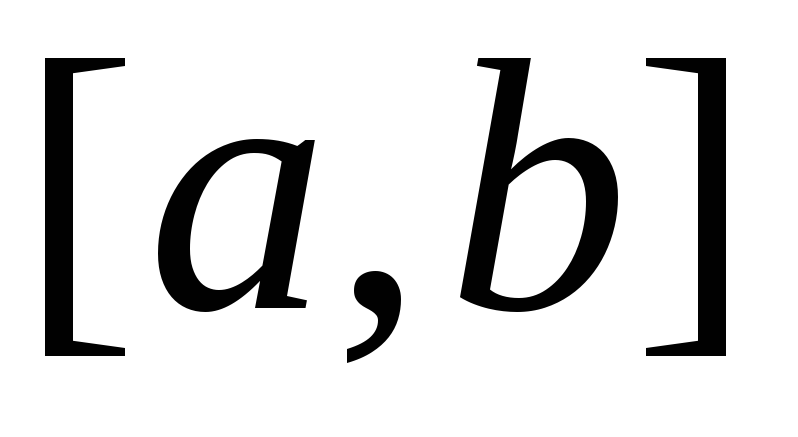 ,
то
,
то .
. интегрируема на отрезке
интегрируема на отрезке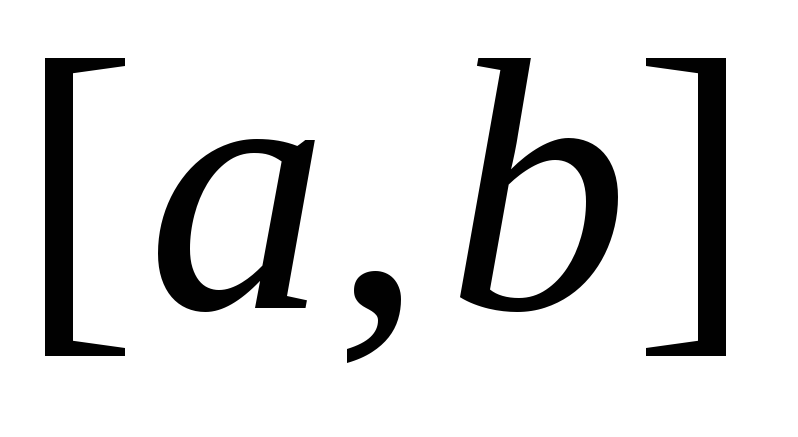 ,
то
,
то .
. непрерывна на отрезке
непрерывна на отрезке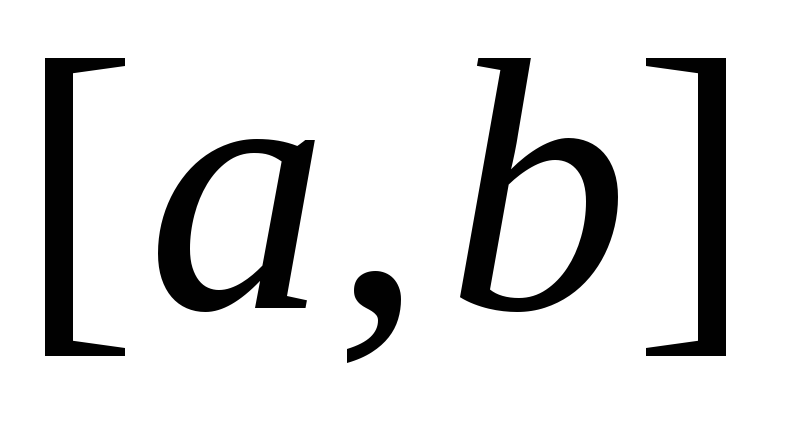 ,
то найдется такое значение
,
то найдется такое значение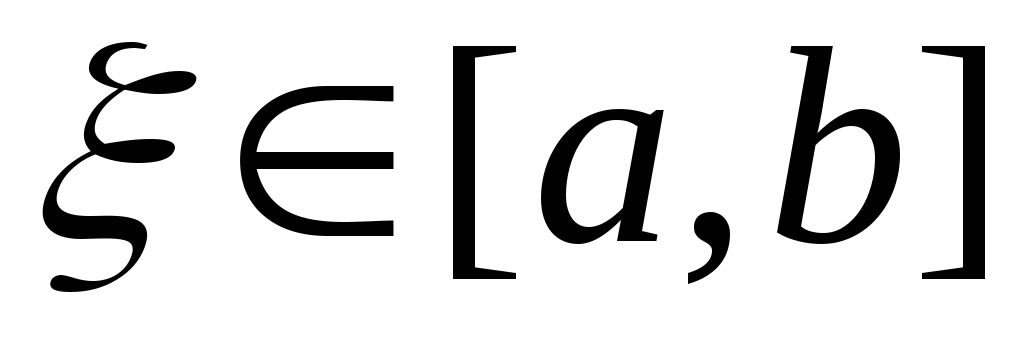 ,
что
,
что .
Т.о. теорема о среднем утверждает, что
найдется такая точка
.
Т.о. теорема о среднем утверждает, что
найдется такая точка из отрезка
из отрезка ,
что площадь под кривой
,
что площадь под кривой равна площади прямоугольника со
сторонами
равна площади прямоугольника со
сторонами и
и .
.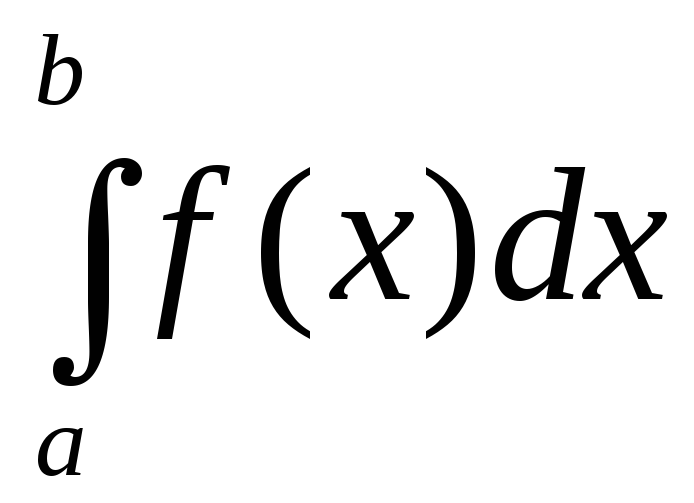 ,
где функция
,
где функция  непрерывна на отрезке
непрерывна на отрезке .
Введем новую переменную равенством
.
Введем новую переменную равенством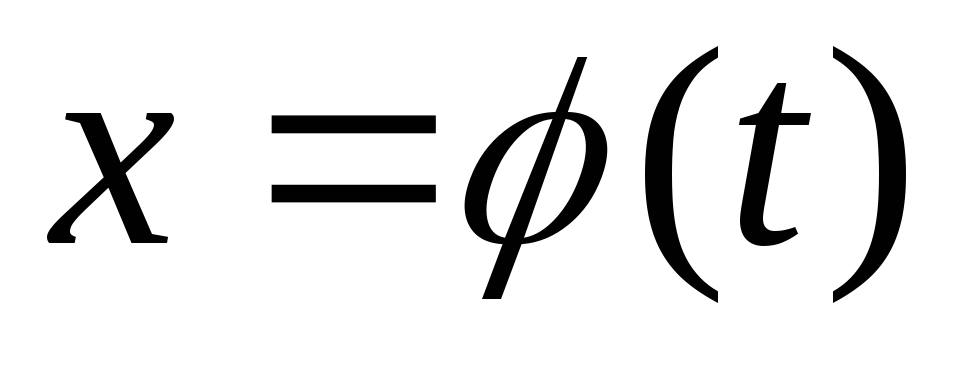 ,
где: 1) между переменными
,
где: 1) между переменными  и
и  существует взаимно-однозначное
соответствие; 2)
существует взаимно-однозначное
соответствие; 2)  непрерывна на отрезке
непрерывна на отрезке  ;
3)
;
3)  ;
4)
;
4)  непрерывна на
непрерывна на 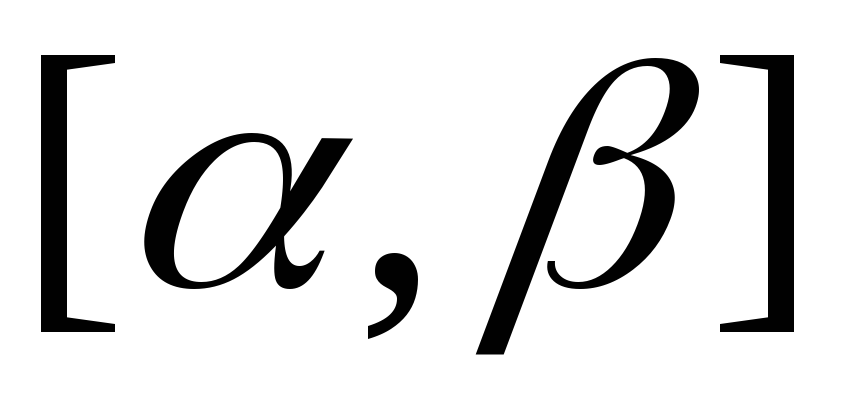 .
Тогда
.
Тогда  .
. ,
, имеют непрерывные производные на
отрезке
имеют непрерывные производные на
отрезке .
Тогда имеет место равенство:
.
Тогда имеет место равенство:
эта формула называется формулой
интегрирования по частям для
определенного интеграла.
эта формула называется формулой
интегрирования по частям для
определенного интеграла.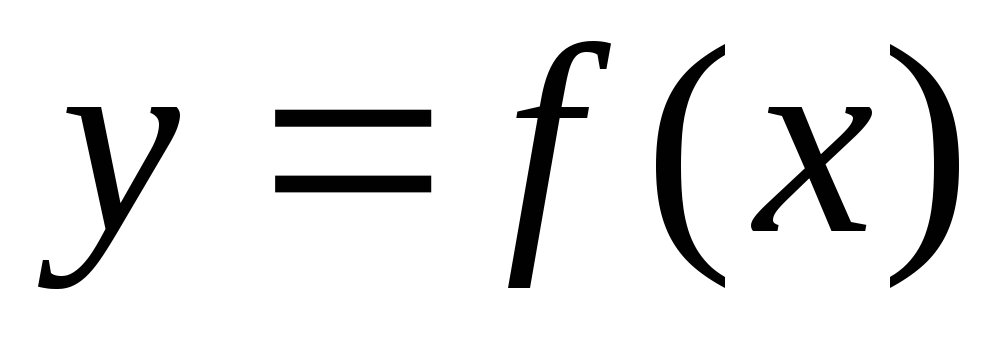 на отрезке
на отрезке  :
:  .
. :
: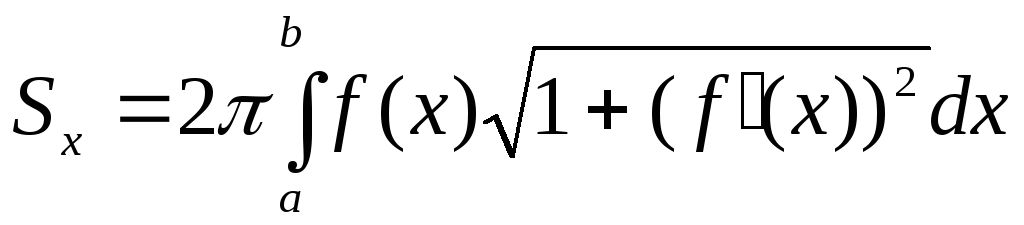 .
. .
Тогда путь
.
Тогда путь ,
пройденный точной за время
,
пройденный точной за время ,
равен
,
равен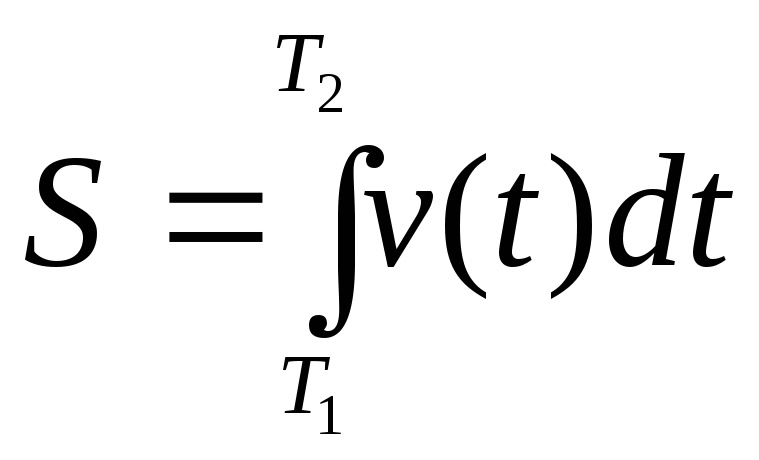 .
.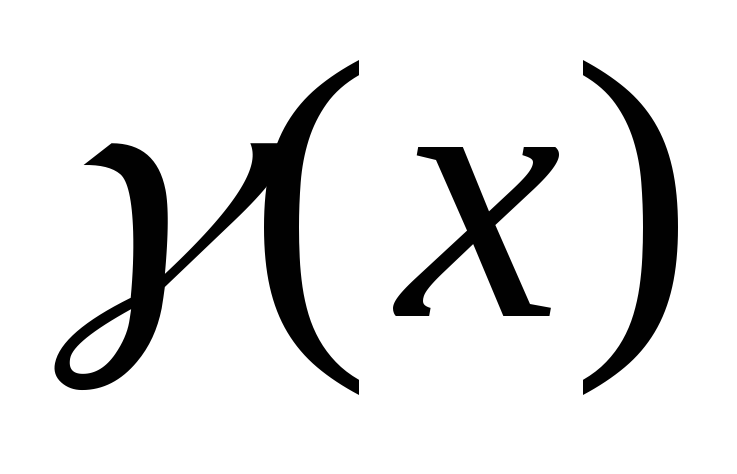 – плотность распределения массы на
отрезке
– плотность распределения массы на
отрезке .
Тогда масса отрезка равна:
.
Тогда масса отрезка равна: .
. материальная точка
материальная точка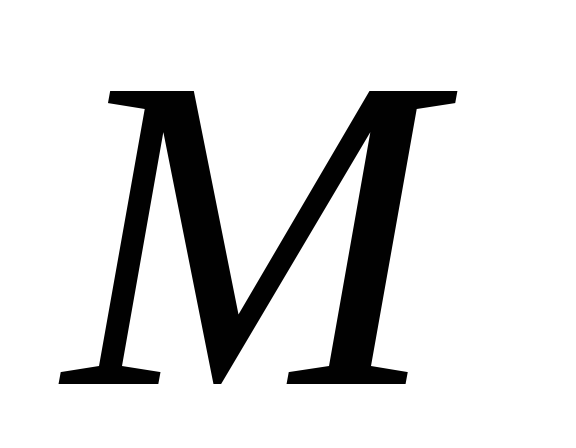 движется по прямой в направлении оси
движется по прямой в направлении оси из точки
из точки в точку
в точку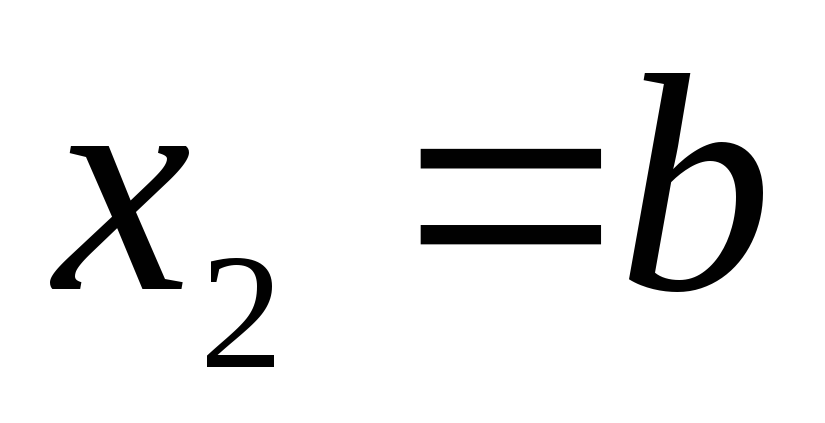 .
Тогда работа, произведенная силой
.
Тогда работа, произведенная силой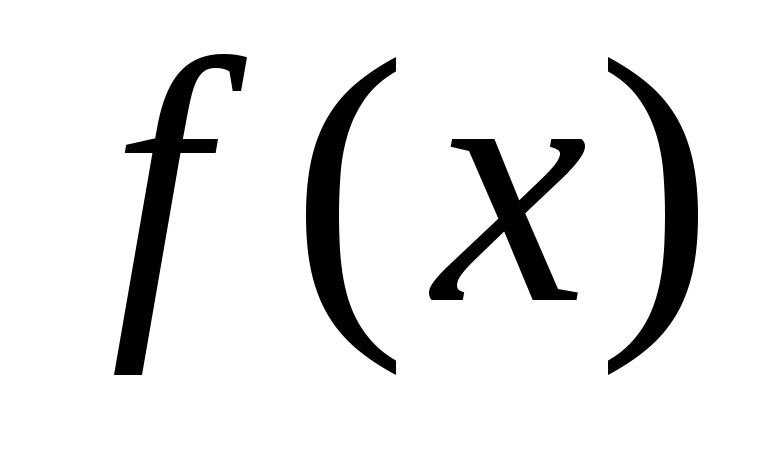 при перемещении точки
при перемещении точки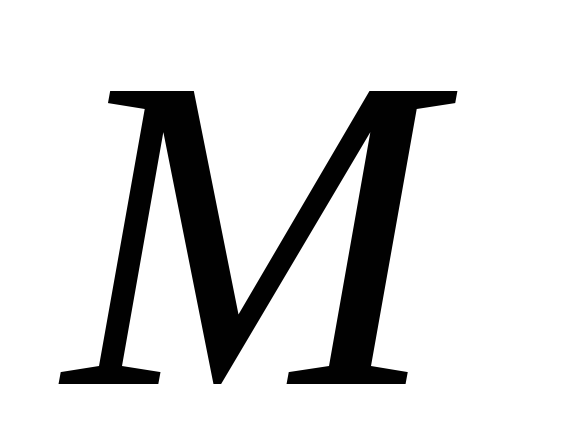 из положения
из положения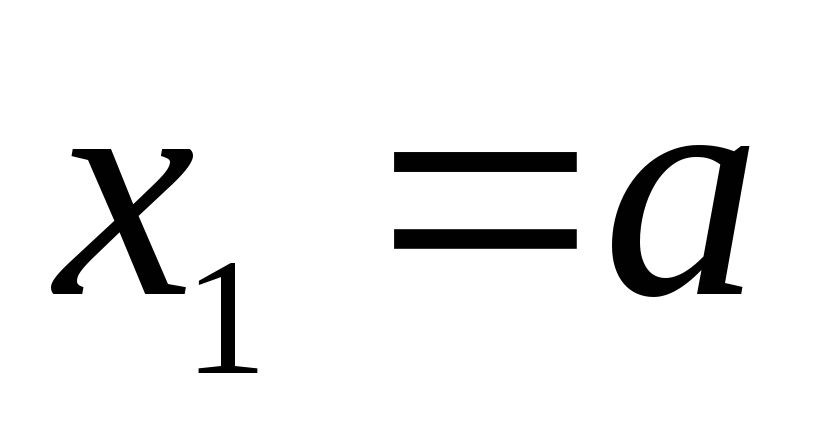 в положение
в положение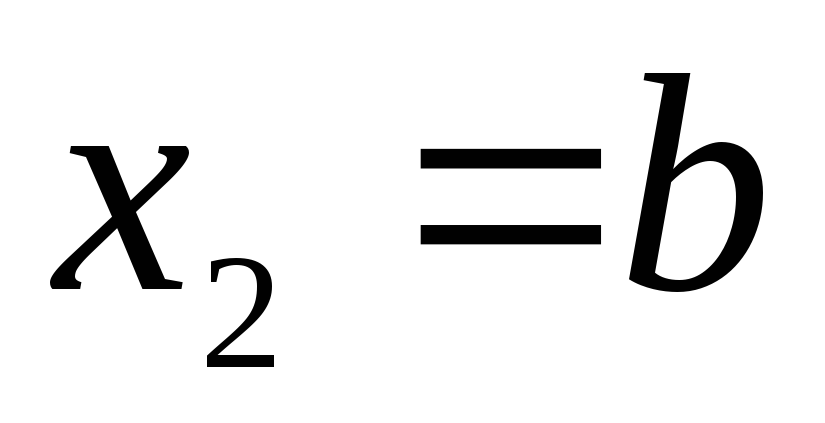 равна
равна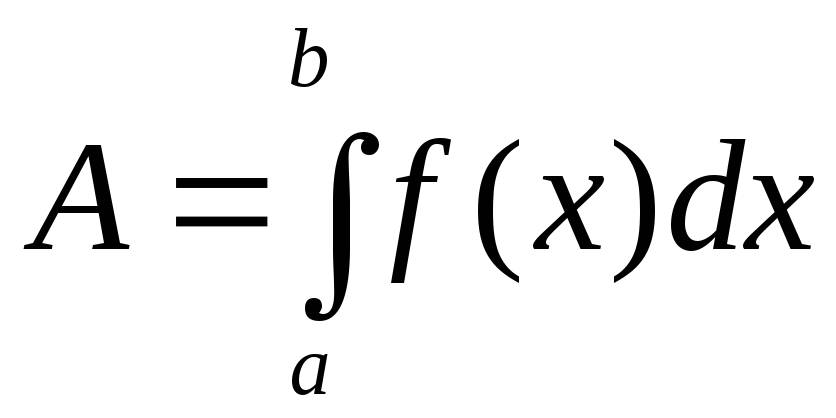 .
. от
от до
до переменная
переменная изменяется от
изменяется от до
до ,
то есть
,
то есть определена и непрерывна на отрезке
определена и непрерывна на отрезке ,
то справедлива такая формула
,
то справедлива такая формула