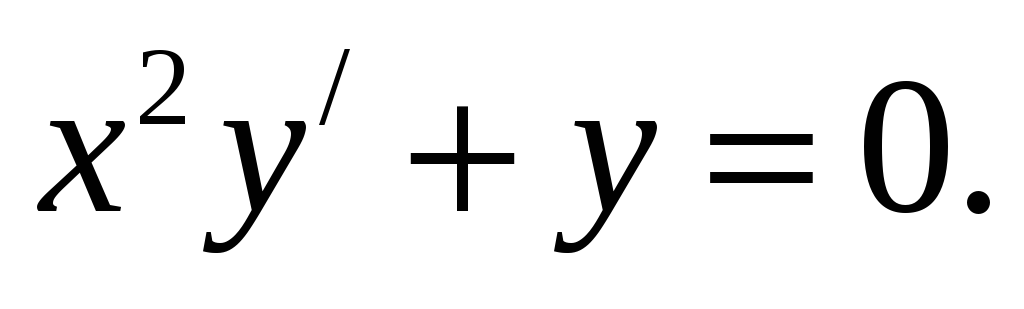2 Метод включений и исключений
Известно, что из 100 студентов живописью увлекаются 28, спортом – 42, музыкой – 30, живописью и спортом – 10, живописью и музыкой – 8, спортом и музыкой – 5, живописью, спортом и музыкой – 3. Определить: количество студентов, увлекающихся только спортом; ничем не увлекающихся.
В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. Шестеро знают английский, шестеро – немецкий, семеро – французский. Четверо знают английский и немецкий, трое – немецкий и французский, двое – французский и английский. Один человек знает все три языка. Сколько человек работают в отделе? Сколько из них знают только английский язык? Только французский?
На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек, и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?
Сколько неотрицательных целых чисел, меньших, чем миллион, содержат все цифры 1, 2, 3, 4? Сколько чисел состоит только из этих цифр?
Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?
Сколько можно сделать перестановок из п элементов, в которых данные два элемента а иb не стоят рядом? Данные три элементаa,b, с не стоят рядом (в любом порядке)? Никакие два из элементова, b, с не стоят рядом?
Сколько пятизначных чисел можно составить из цифр числа 12312343 так, чтобы три цифры 3 не шли друг за другом?
Сколькими способами можно переставить цифры числа 12341234 так, чтобы никакие две одинаковые цифры не шли друг за другом?
Сколькими способами можно переставить цифры числа 1234114546 так, чтобы три одинаковые цифры не шли друг за другом?
Сколькими способами можно переставить цифры числа 1234114546 так, чтобы две одинаковые цифры не шли друг за другом?
Найти число способов разложения nшаров поmящикам так,
чтобыr(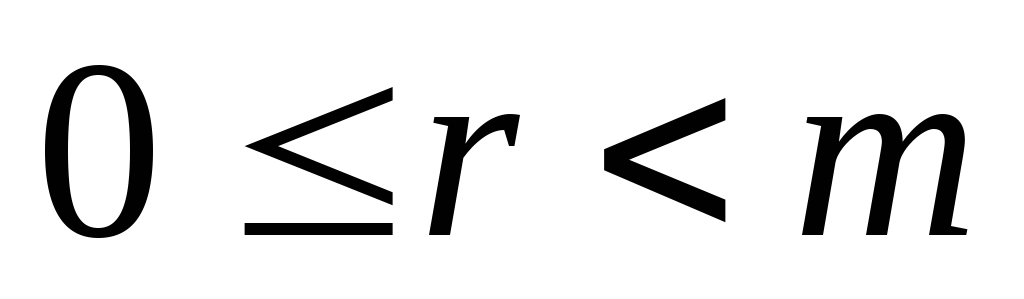 )
ящиков остались пустыми.
)
ящиков остались пустыми.
Из урны, содержащей mразличных шаров, одновременно извлекаютs( )
шаров, записывают их номера, а затем
шары возвращают обратно в урну. Можно
составить
)
шаров, записывают их номера, а затем
шары возвращают обратно в урну. Можно
составить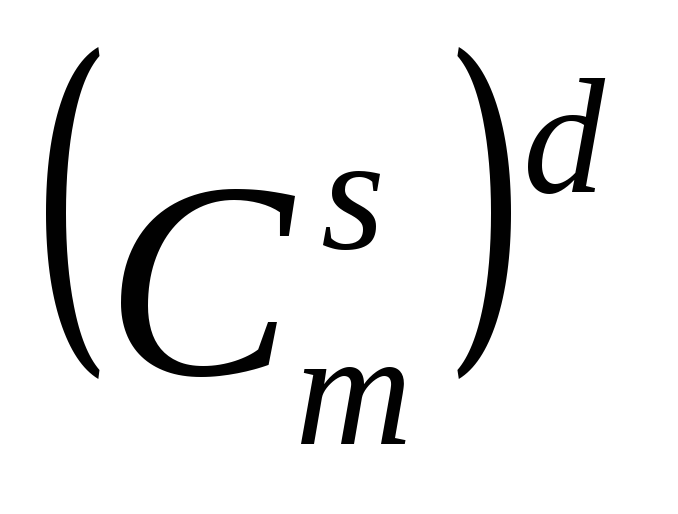 различных наборов, получающихся в
результатеdизвлечений.
Найти число наборов, в которых а)
встречаются все шары; б) ровноr(
различных наборов, получающихся в
результатеdизвлечений.
Найти число наборов, в которых а)
встречаются все шары; б) ровноr(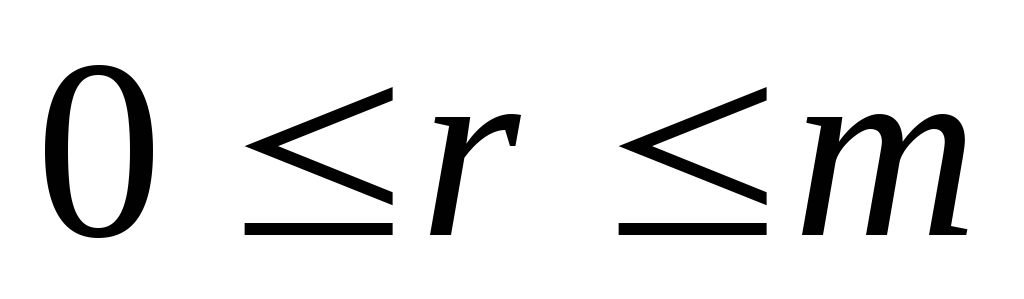 )
шаров не встречаются.
)
шаров не встречаются.
Вычислить  ,
где суммирование производится по всем
натуральнымk, не
кратным 2, 3 и 5.
,
где суммирование производится по всем
натуральнымk, не
кратным 2, 3 и 5.
1. Доказать, что
1.1 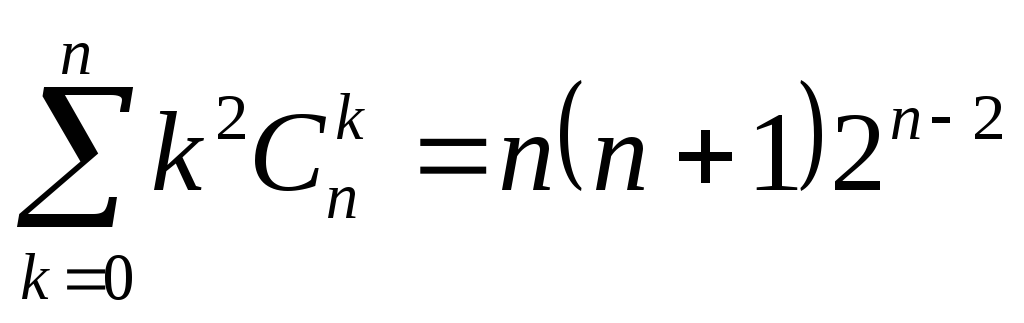 .
.
1.2 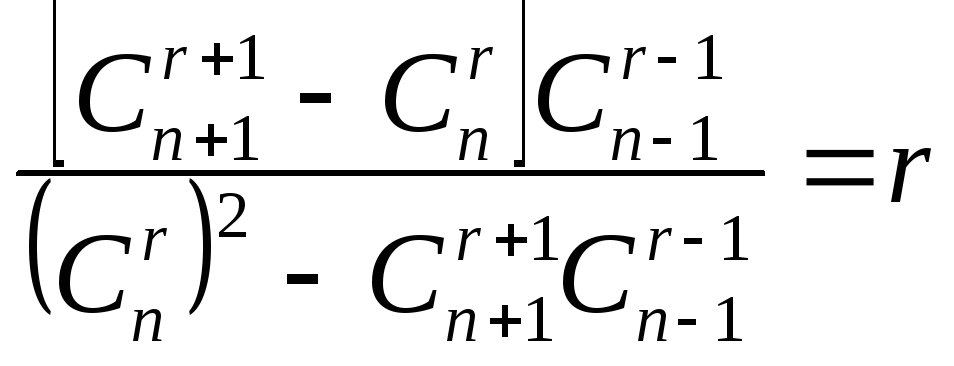 .
.
1.3 при m>n 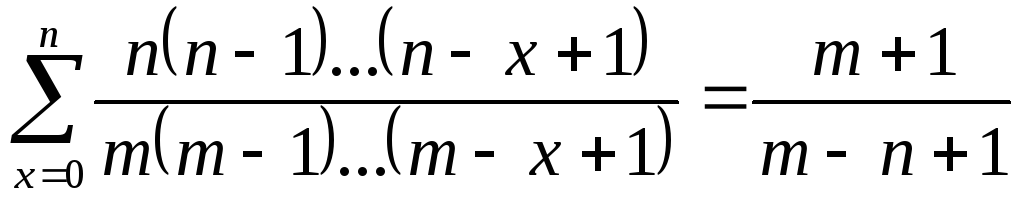 и
и .
.
1.4 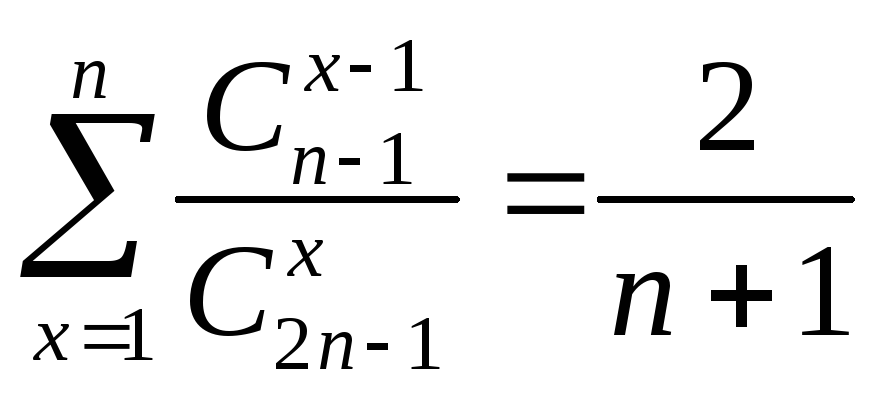 .
.
1.5  .
.
1.6 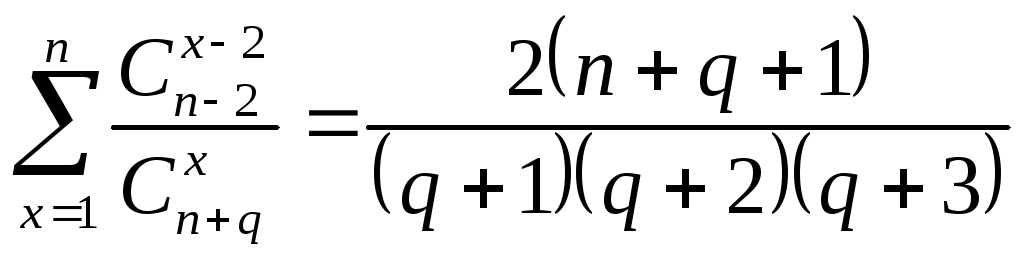 .
.
1.7 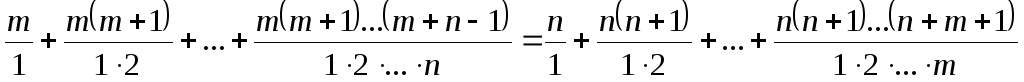 .
.
2. Используя биномиальную теорему, получить формулу для расчета
2.1 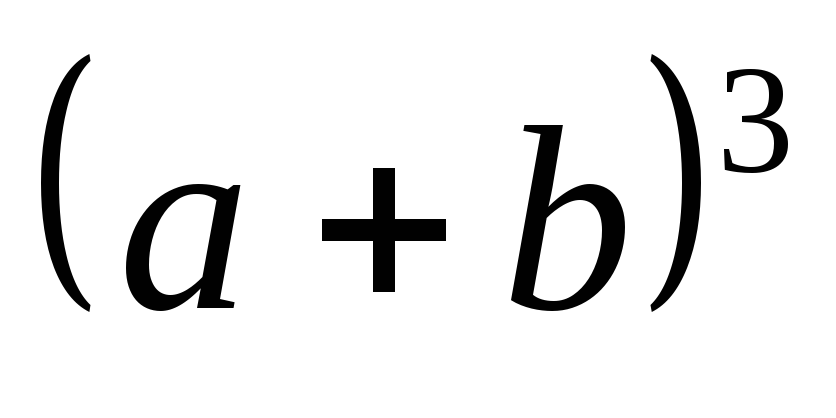 .
2.2
.
2.2 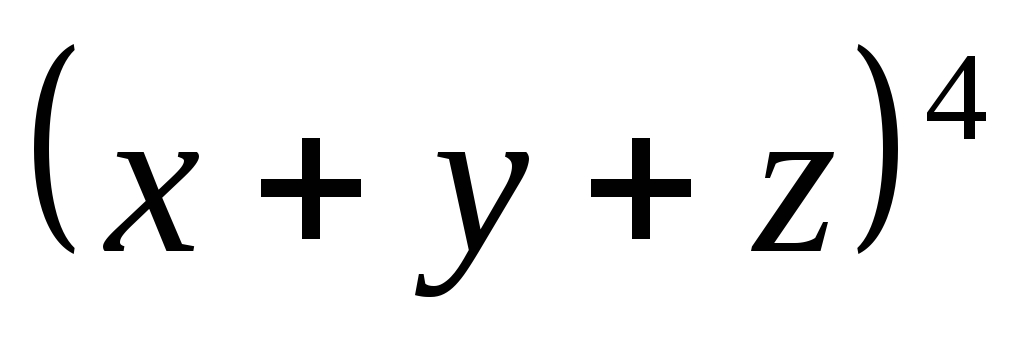
3.1 С каким коэффициентом входит в
разложение 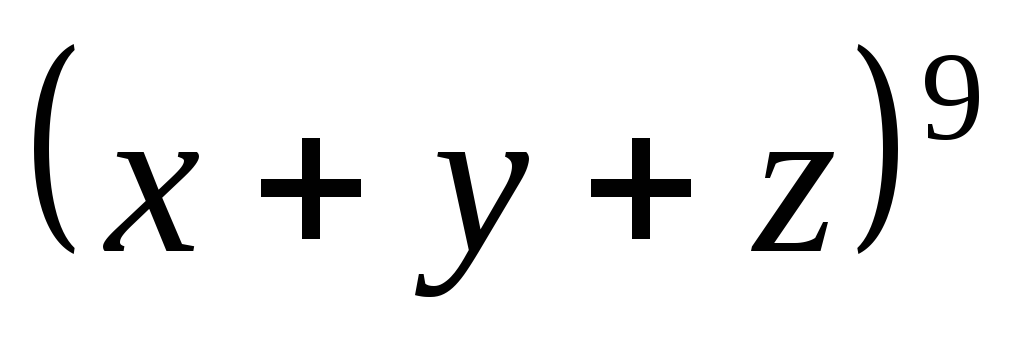 член
член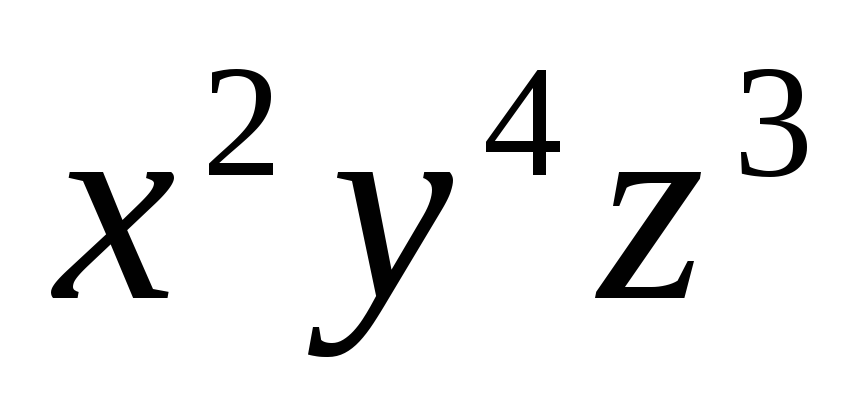 .
.
3.2 Найти коэффициент при х8в разложении (1 +x2–x3)9.
3.3 Найти коэффициент при хmв разложении (1 +x)k+ (1 +x)k+1 + … + (1 +x)nпо степенямх. Разобрать отдельно
случаи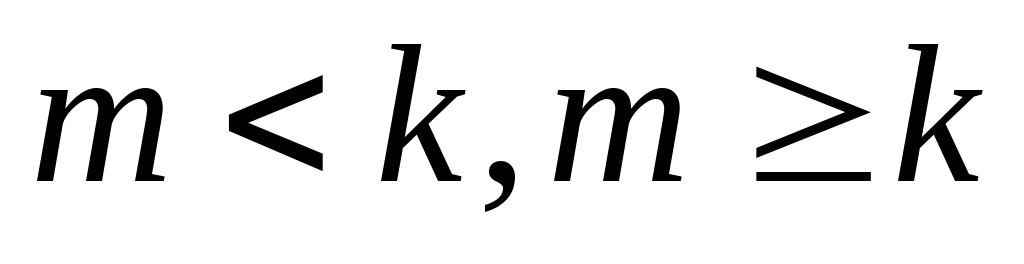 .
.
3.4 Найти коэффициенты при х17их18после раскрытия скобок и приведения подобных членов в выражении (1 +x5+x
7)20.3.5 В каком из выражений (1 + x2–x3)1000 или (1 –x2+x3)1000будет после раскрытия скобок и приведения подобных членов больший коэффициент прих17?
4. Вычислить следующие суммы:
4.1 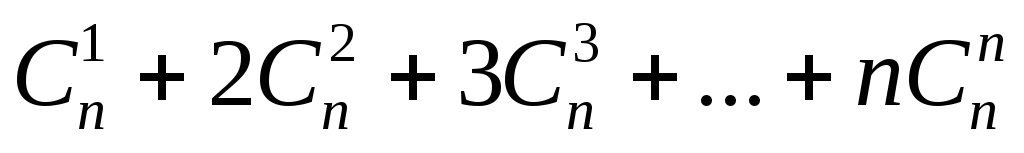 . 4.2
. 4.2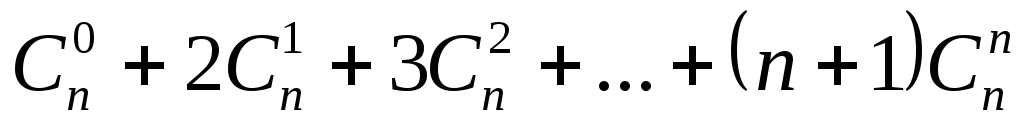 .
.
4.3  . 4.4
. 4.4 .
.
4.5 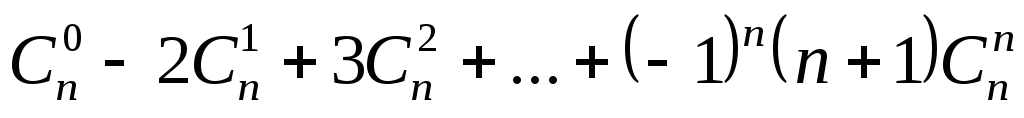 . 4.6
. 4.6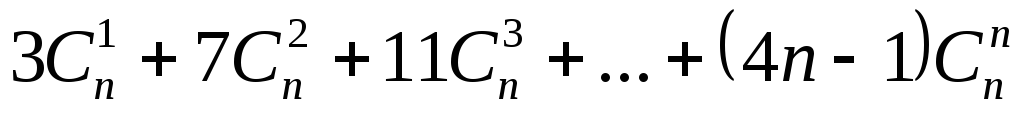 .
.
4.7 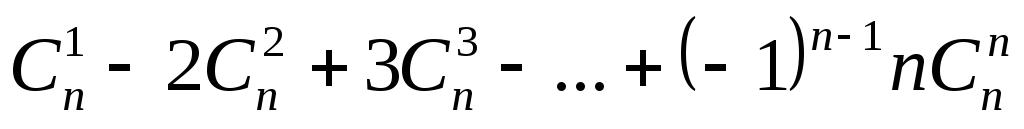
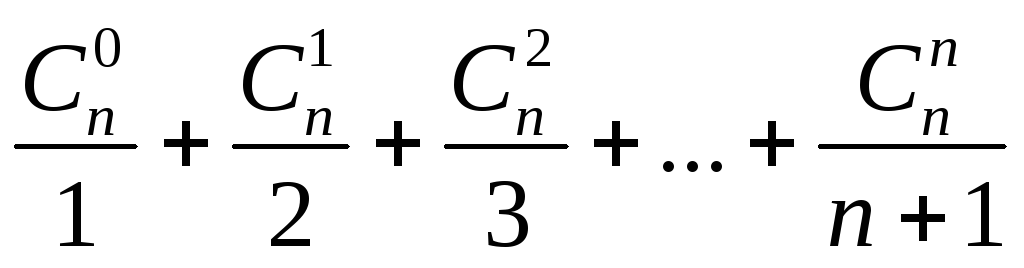 .
. 5.1 При каком значении (значениях) kвеличина максимальна, еслиn–
заданное положительное число.
максимальна, еслиn–
заданное положительное число.
5.2 Найти наибольший коэффициент в
разложениях 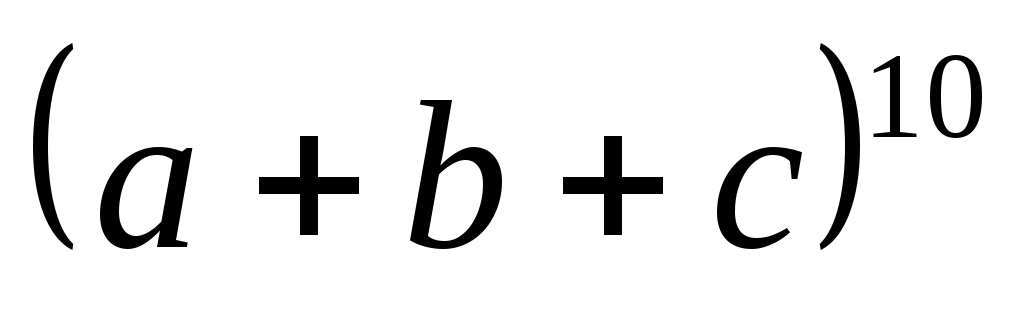 и
и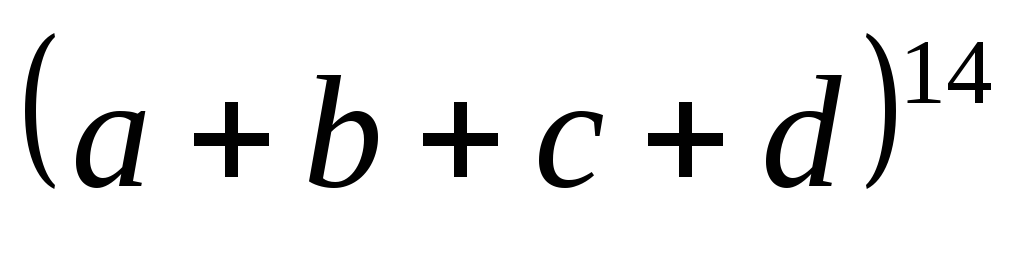 .
.
6. Чему равно число 114? Используйте результат биномиальной теоремы.
2 5-30(1курс
Вариант 25
Контрольная работа по курсу « Математический анализ»
I. Множества
Среди абитуриентов, выдержавших экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 человек, по физике – 37,по языку – 42, по математике или физике – 75, математике или языку – 76, по физике или языку – 66 человек. По трём предметам получили отличную оценку 4 человека.
Сколько абитуриентов получили хотя бы одну пятёрку?
Сколько среди них получивших только одну пятёрку?
Сколько человек не получили пятёрку по языку?
Задать множество перечислением его элементов:
исчисле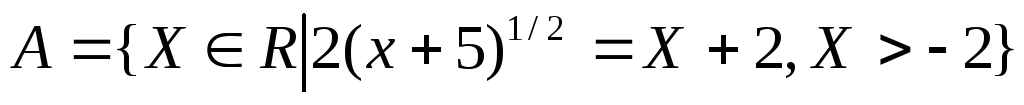
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) 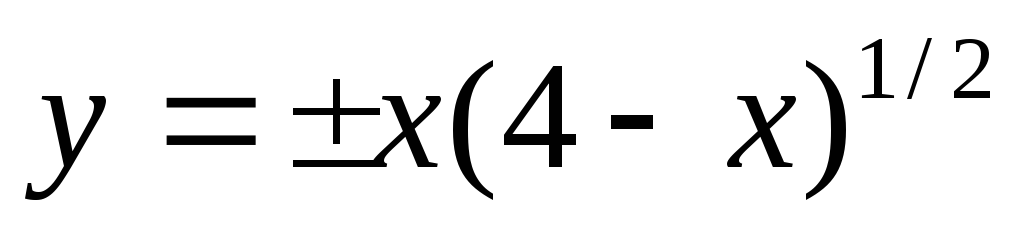 ;
б)
;
б) 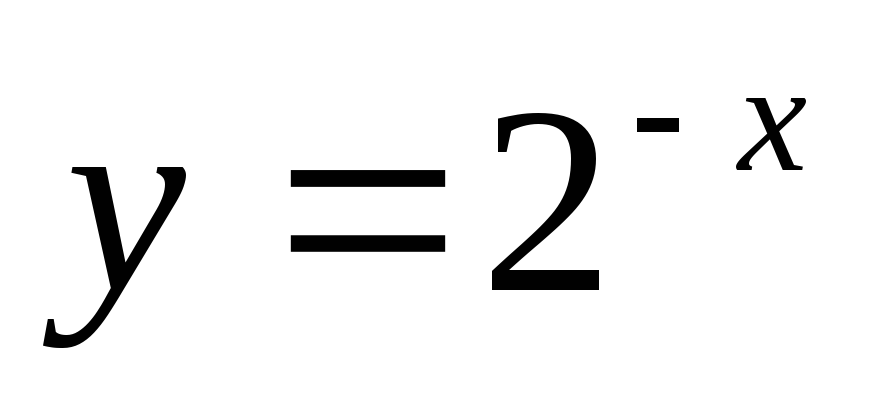 ;
в)
;
в) 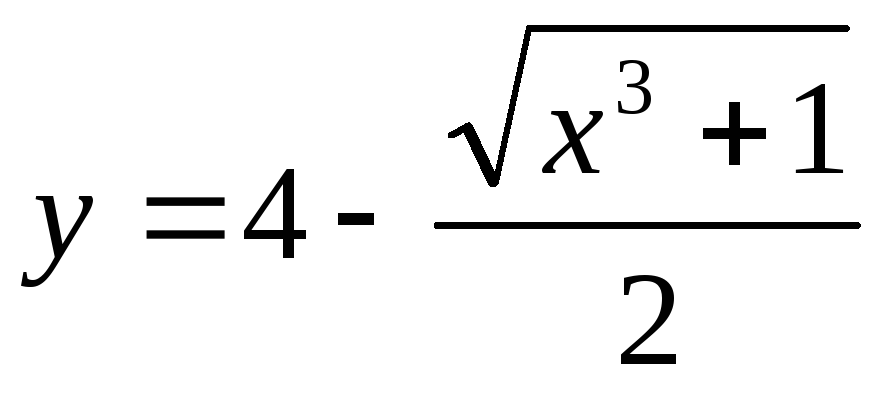 .
.
2) Найти пределы:
а) 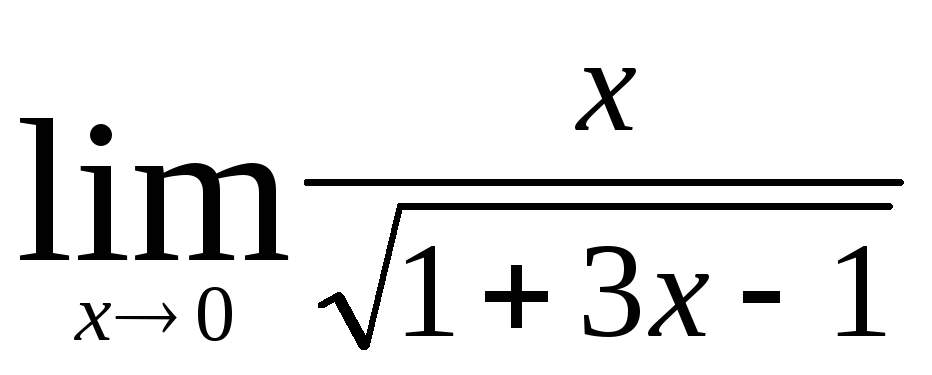 ;
б)
;
б) 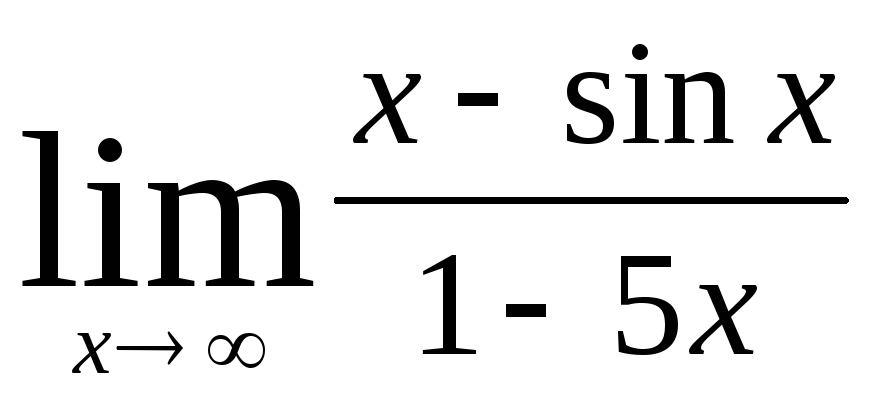 ;
в)
;
в) 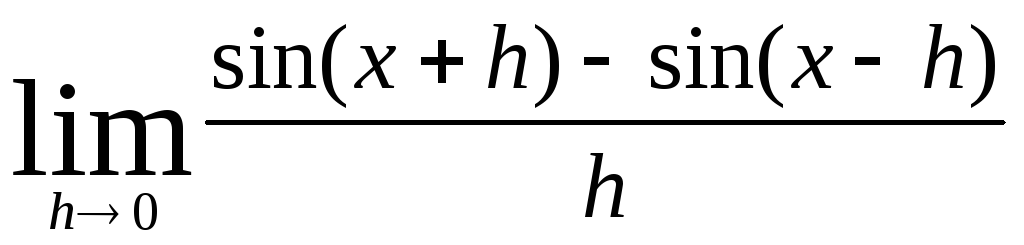 ;
;
г) 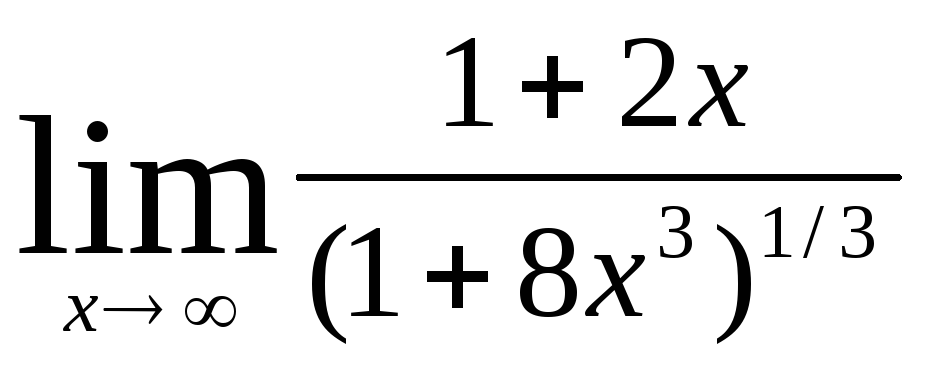 .
.
3) Найти производные функций:
а) 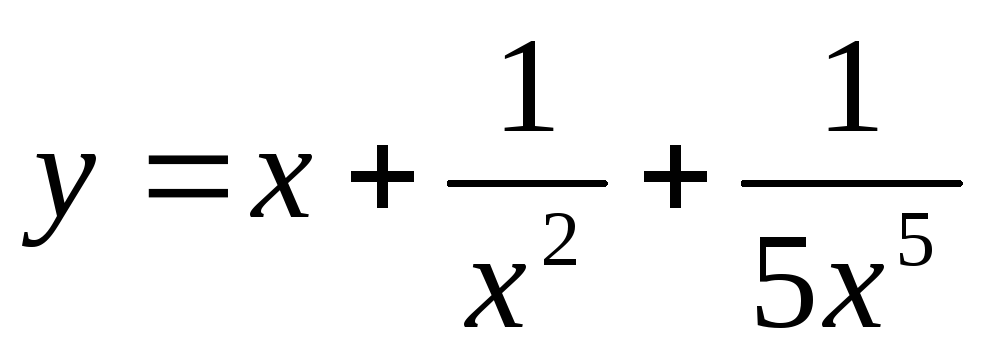 ;
б)
;
б) 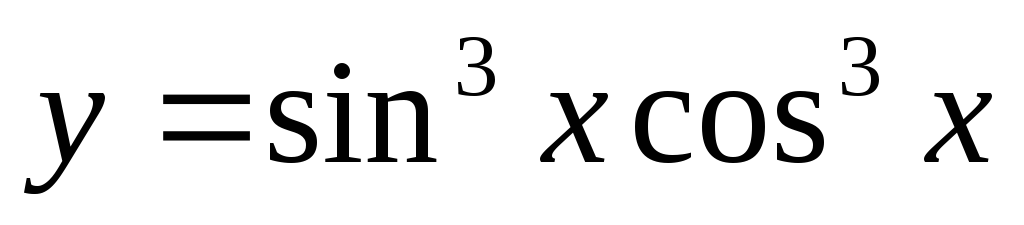
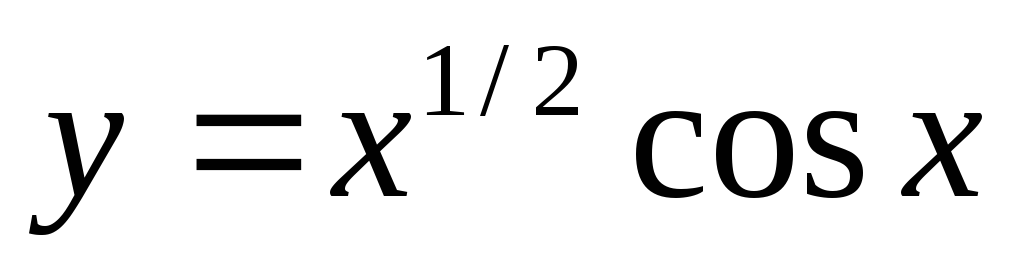 ;
; г) 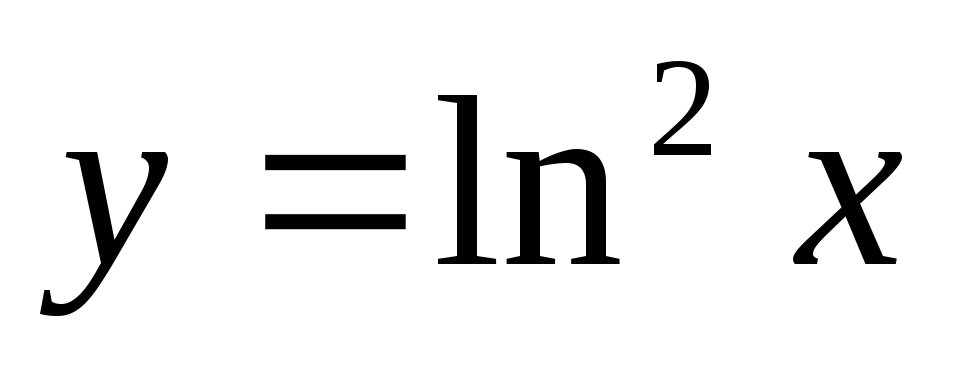 .
.
4) Найти пределы, используя правило Лопиталя:
а) 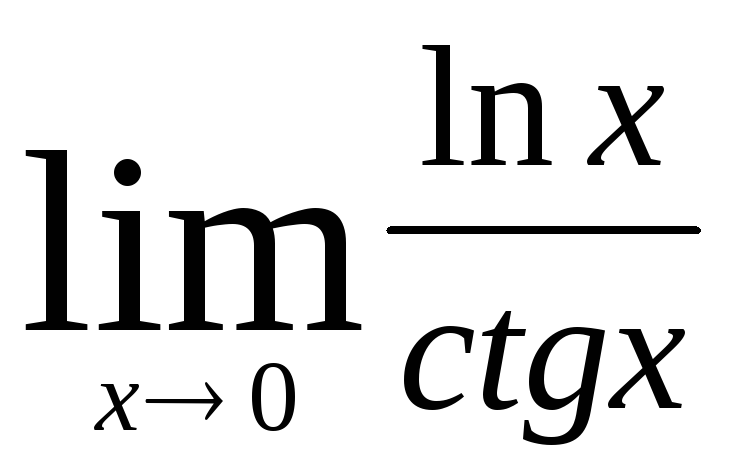 ;
б)
;
б) 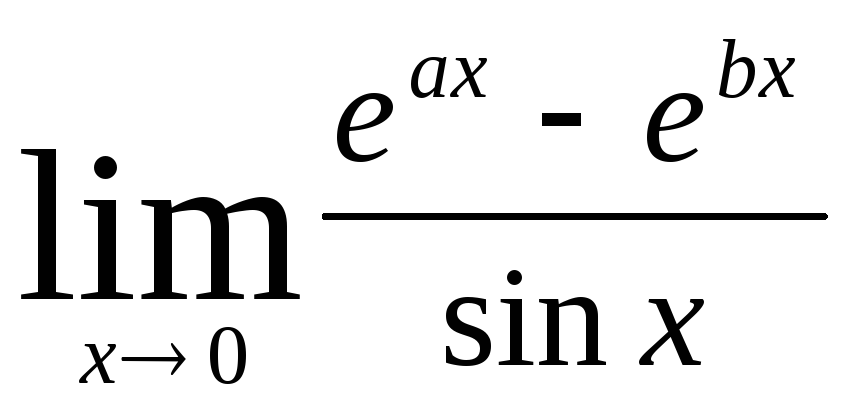 .
.
5) Выполнить полное исследование функции о построить её график:
а) 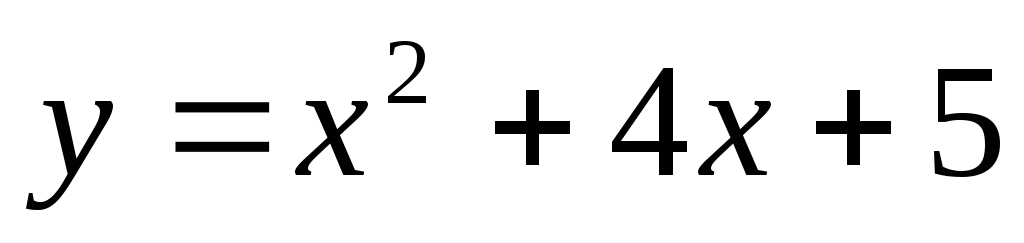 ;
б)
;
б) 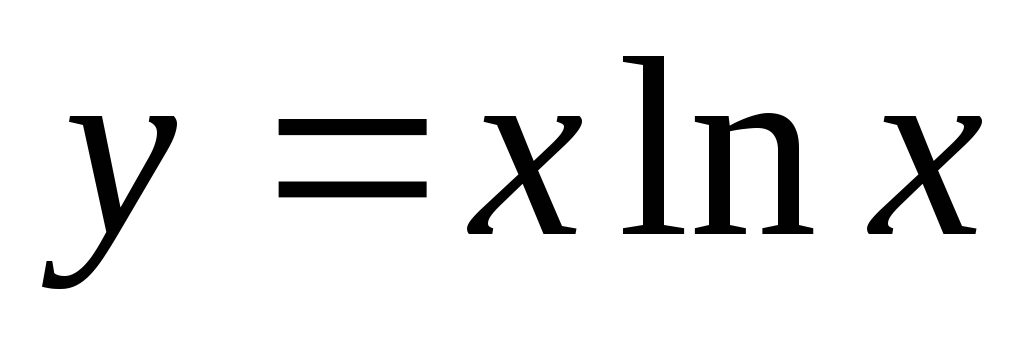 .
.
6) Для функций многих переменных:
а) Указать область определения
функции: 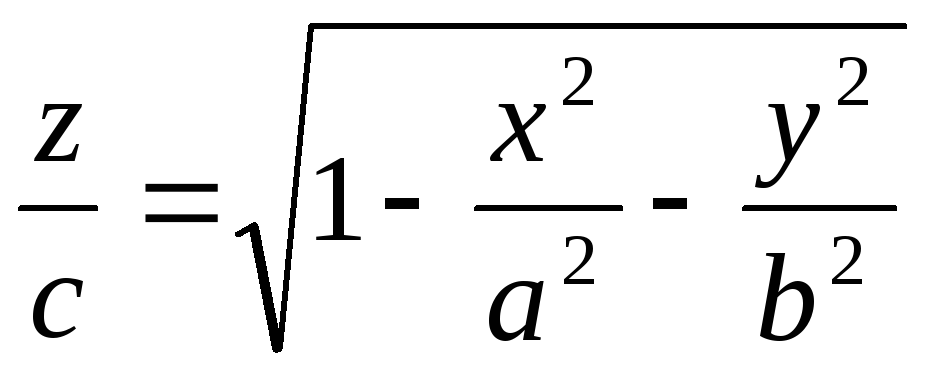
б) Найти частные производные
функции:  ;
;
в) Исследовать на экстремум функцию: 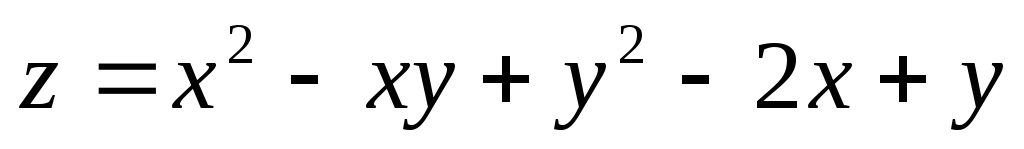 .
.
III. Интегральное исчисление и ряды
Найти интегралы:
а) 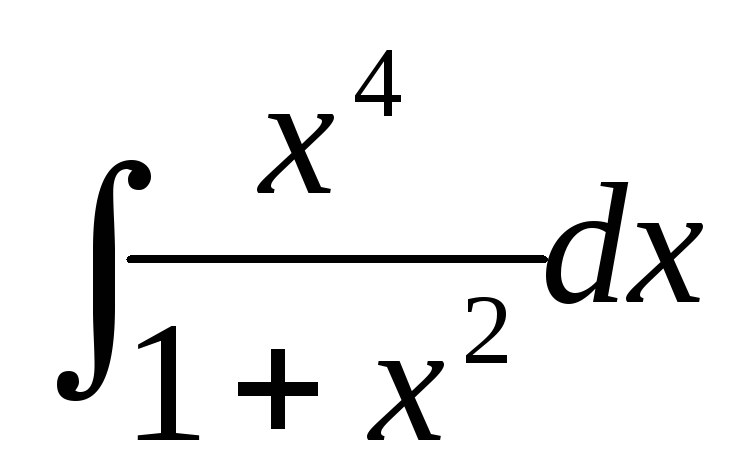 ;
б)
;
б) 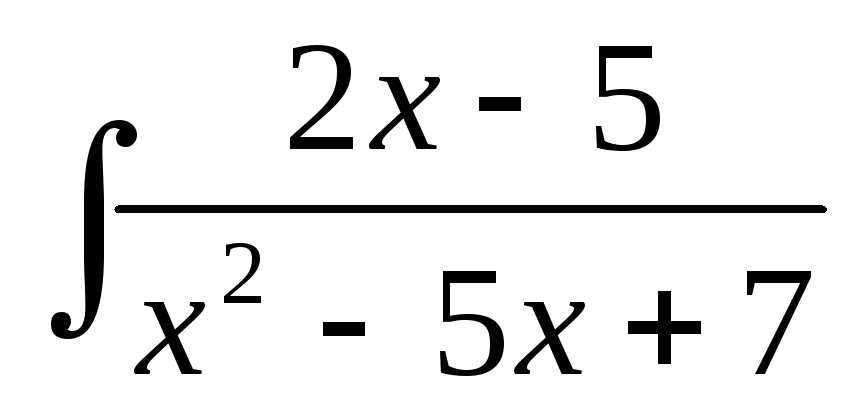 ;
в)
;
в) 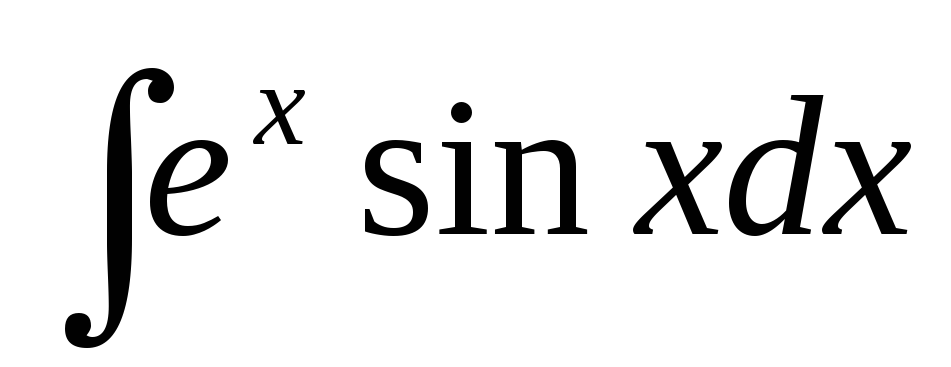 .
.
2) Вычислить интегралы:
а) 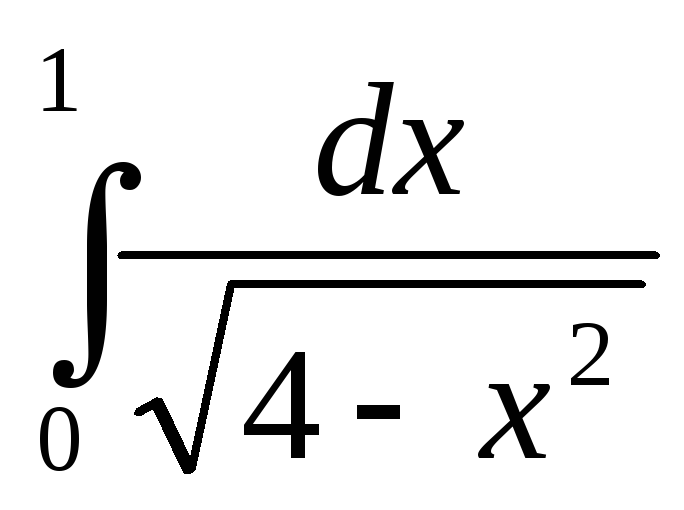 ;
б)
;
б)  .
.
3) Найти общий интеграл:  .
.
4) Исследовать сходимость числовых рядов:
а) 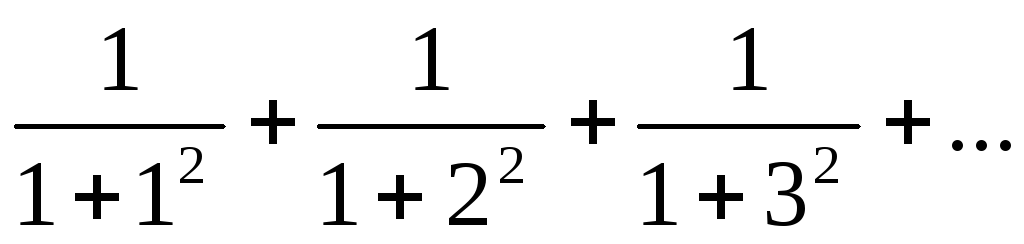 ;
б)
;
б) 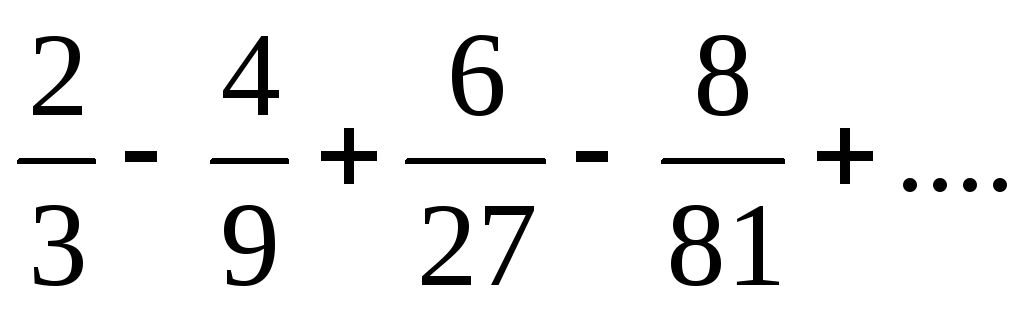
Вариант 26
Контрольная работа по курсу «Математический анализ»
I. Множества.
М – подмножество множества натуральных чисел N. Каждый элемент множества М есть число кратное или 2 или 3. Найти число элементов во множестве М, если среди них имеются: 70 чисел, кратных 2; 60 чисел, кратных 3; 32 числа, кратных 6. Сколько элементов множества М кратны только 2?
Задать множество перечислением его элементов:
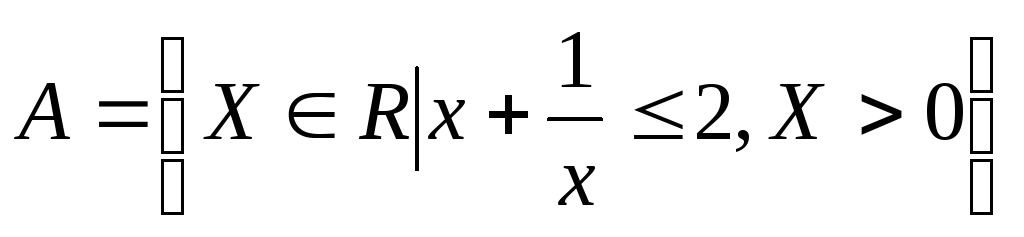
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) 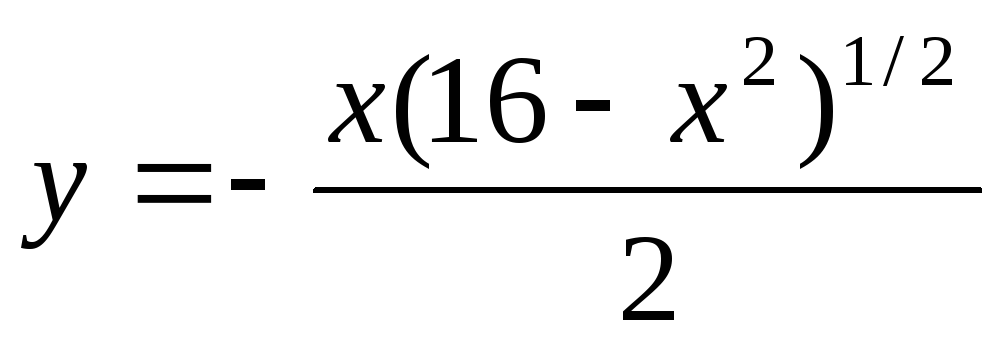 ;
б)
;
б) 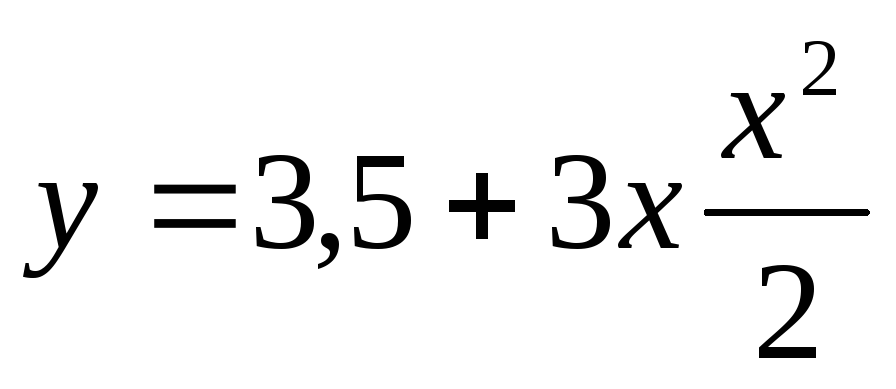 ;
в)
;
в) 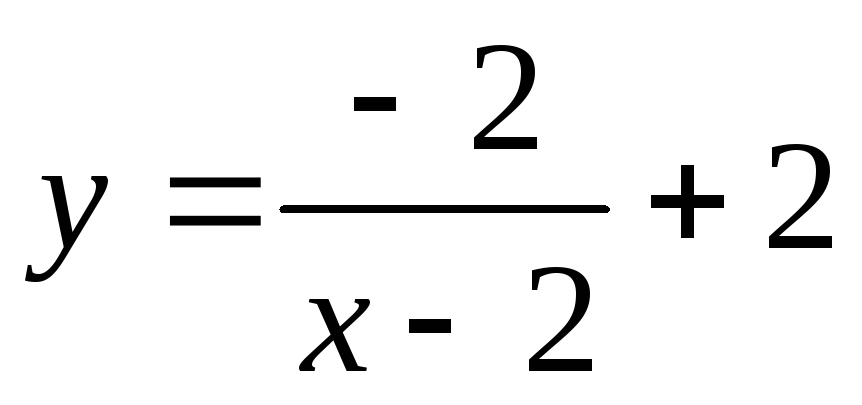
Найти пределы:
а)  ;
б)
;
б) 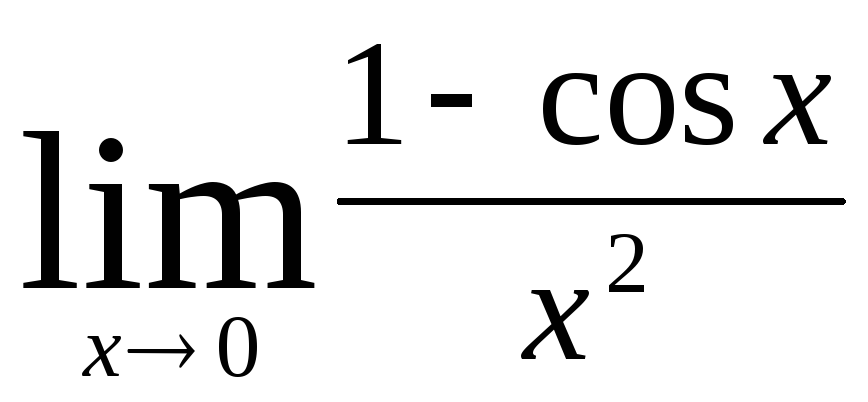 ; в)
; в) 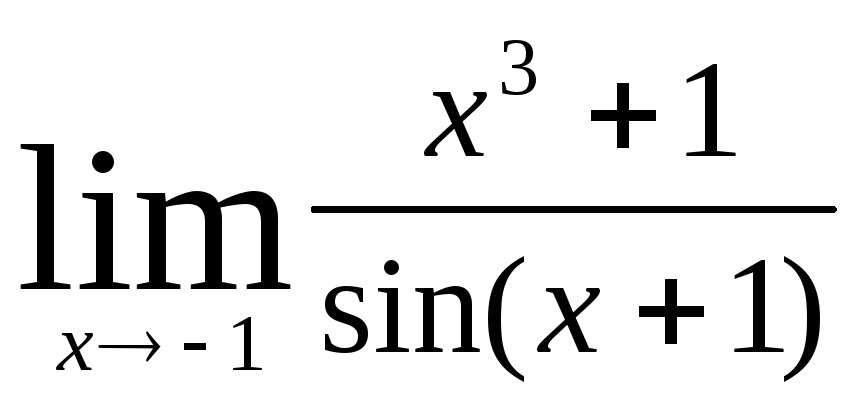 ;
г)
;
г) 
 .
.
3) Найти производные функций:
а) 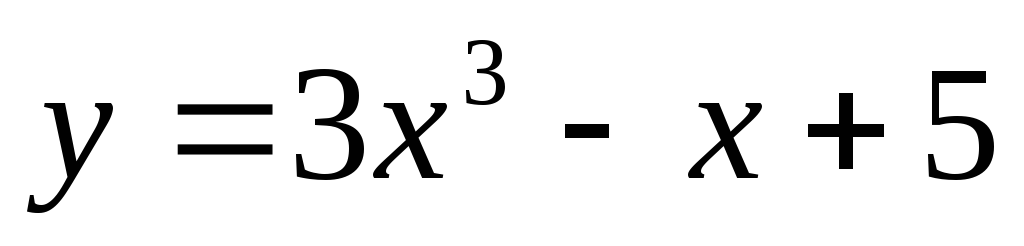 ;
б)
;
б) 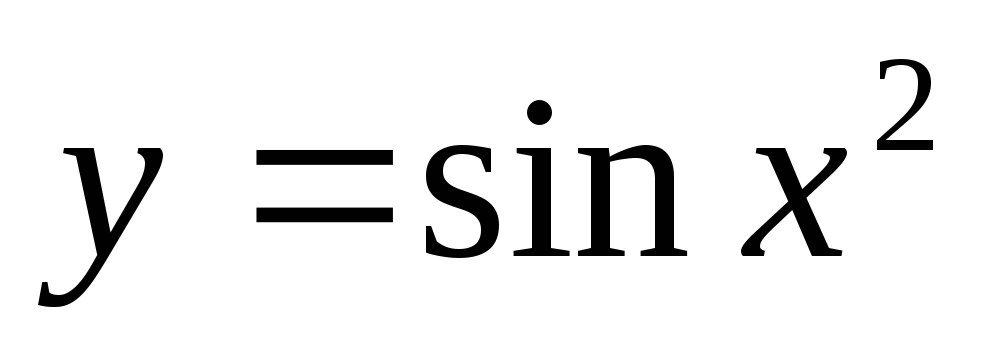 ;
в)
;
в) 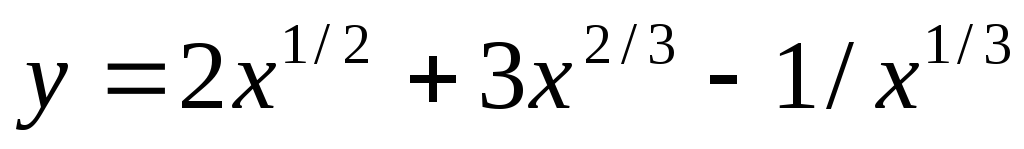 ;
г)
;
г) 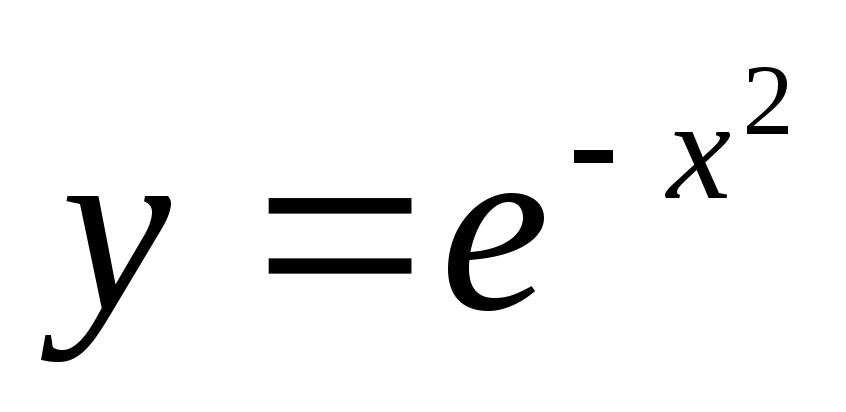
4) Найти пределы, используя правило Лопиталя:
а)  ;
б)
;
б) 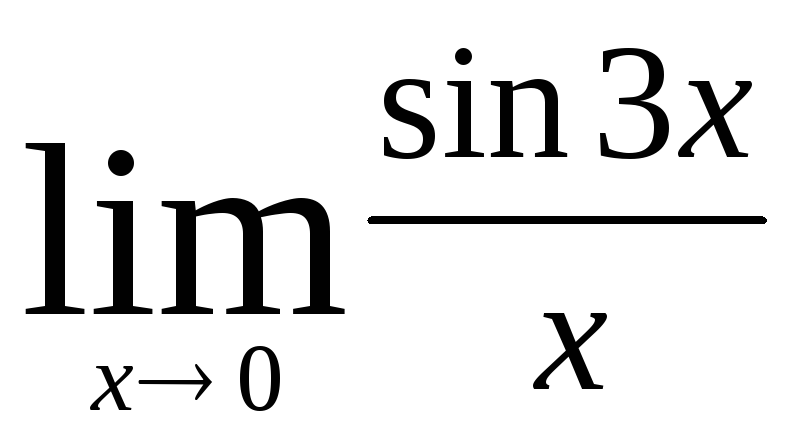 .
.
5) Выполнить полное исследование функции и построить график:
а) 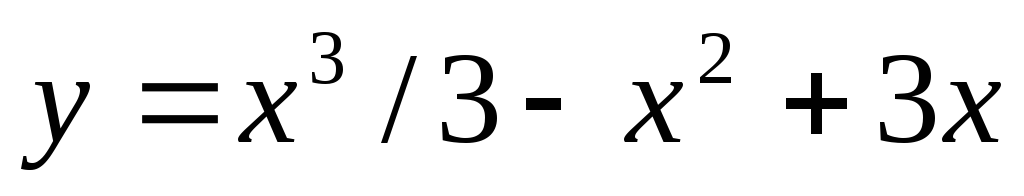 ;
б)
;
б) 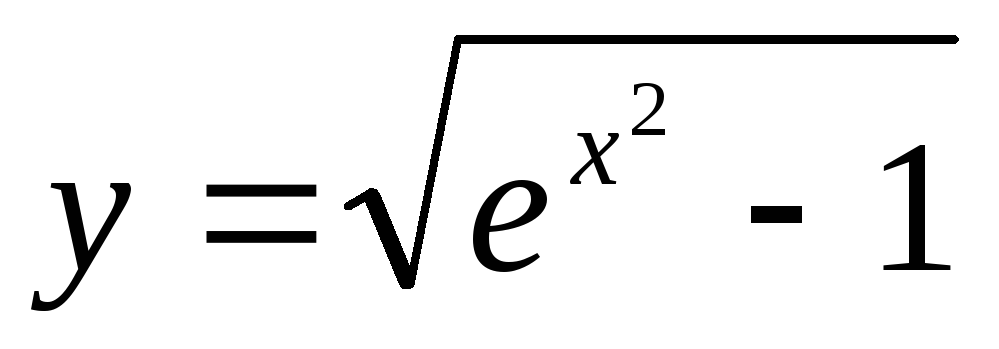 .
.
6) Для функций многих переменных:
а) Указать область
определения функции:  ;
;
б) Найти частные производные
функции: 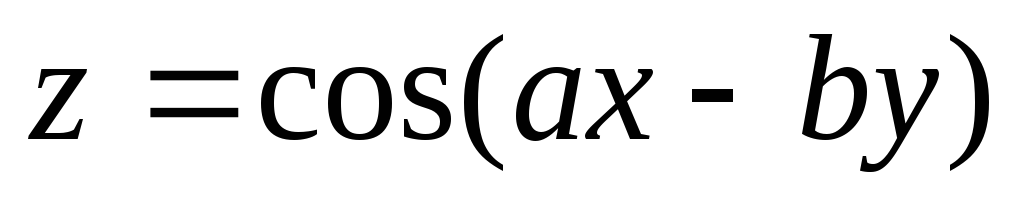 ;
;
в) Исследовать на экстремум
функцию: 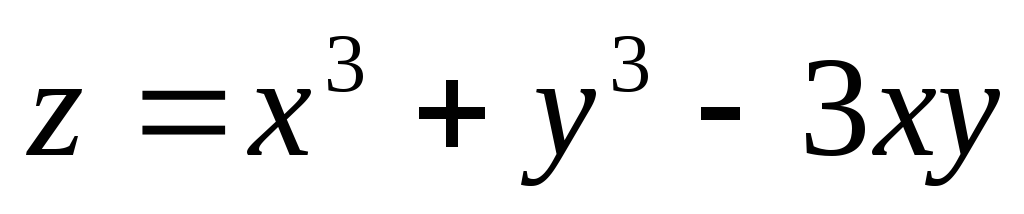 .
.
III. Интегральное исчисление и ряды
Найти интегралы:
а) 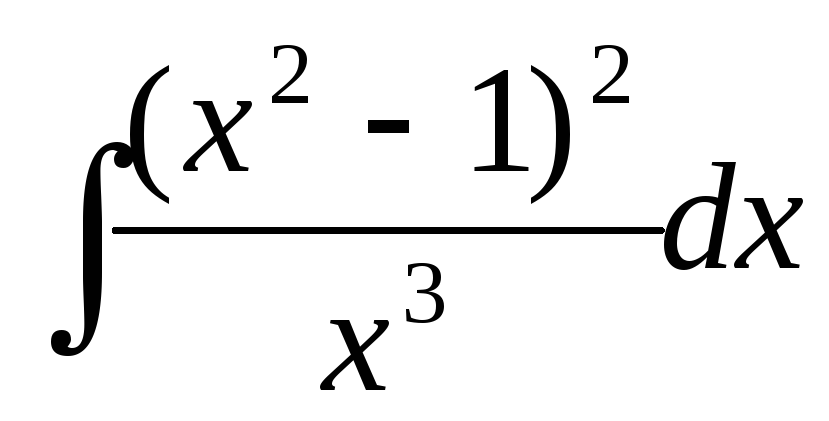 ;
б)
;
б) 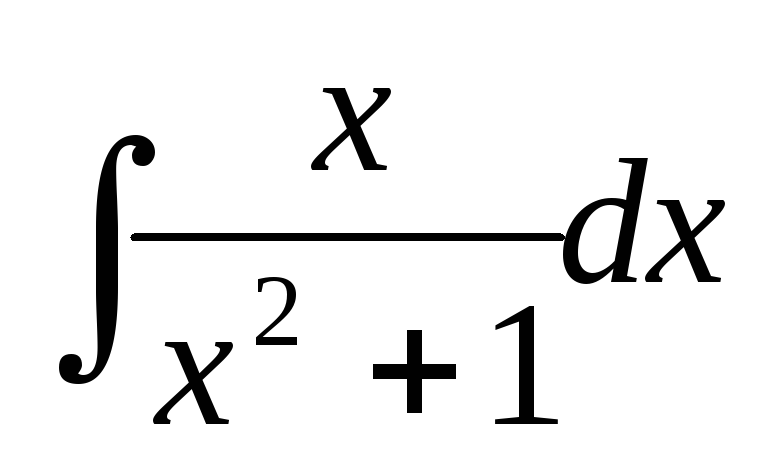 ;
в)
;
в)  .
.
2) Вычислить интегралы:
а) 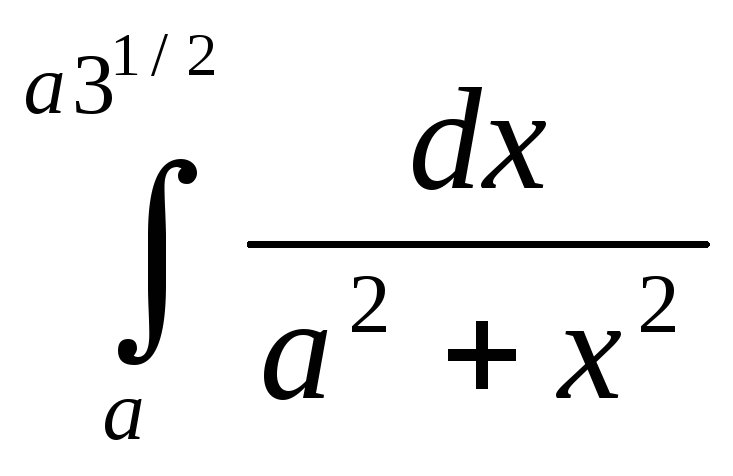 ;
б)
;
б) 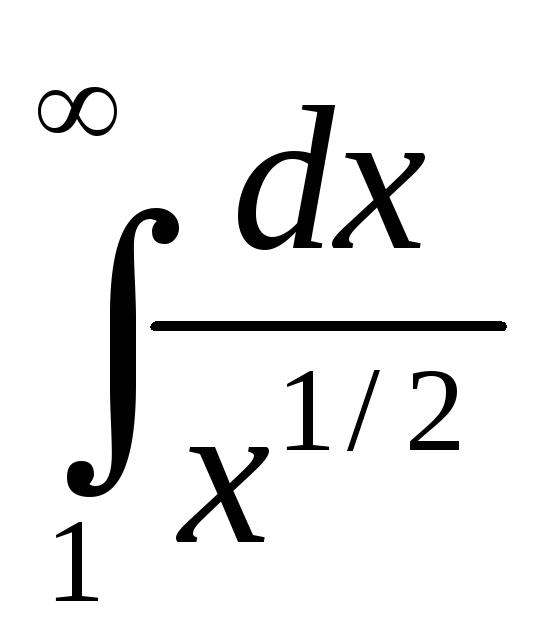 .
.
3) Найти общий интеграл: 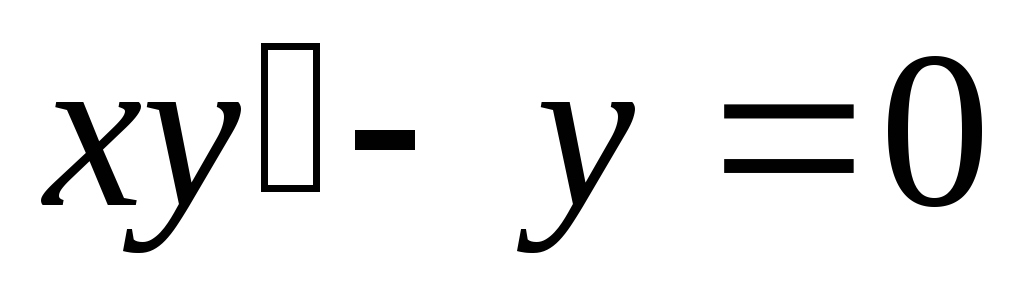 .
.
4) Исследовать сходимость числовых рядов:
а) 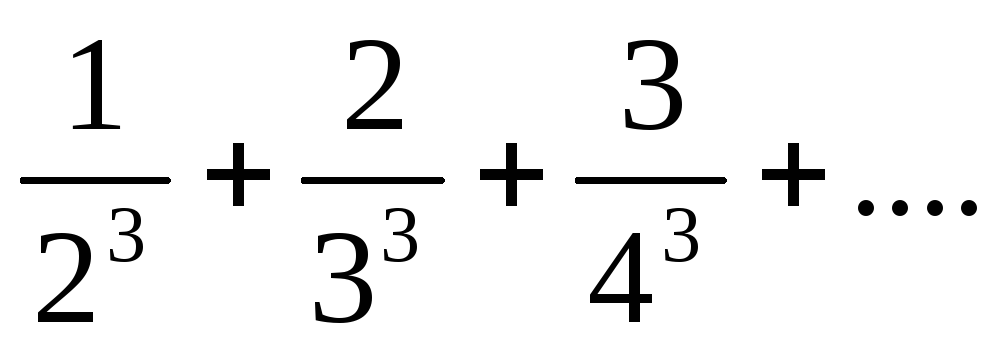 ;
б)
;
б) 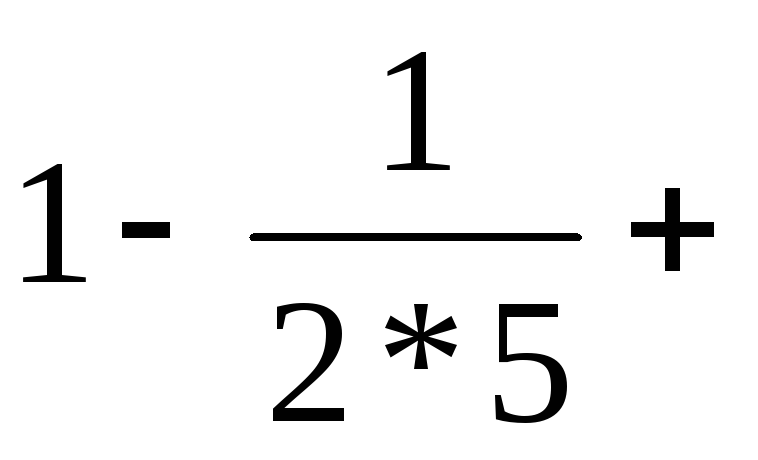
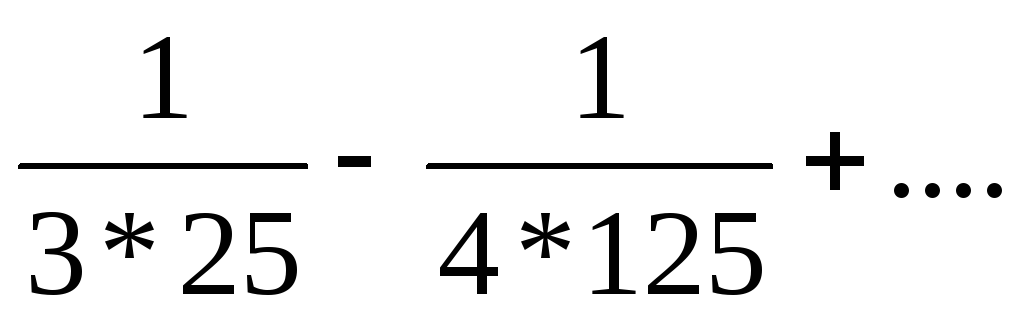
Вариант 27
Контрольная работа по курсу «Математический анализ»
I . Множества
1) В группе из 50 студентов 40 человек сдали экзамен по математике, 27 студентов сдали экзамен по экономике, 5 человек не сдали ни того, ни другого экзамена.
Сколько студентов сдали оба экзамена?
Сколько студентов сдали только экономику?
2) Задать множество перечислением его элементов:
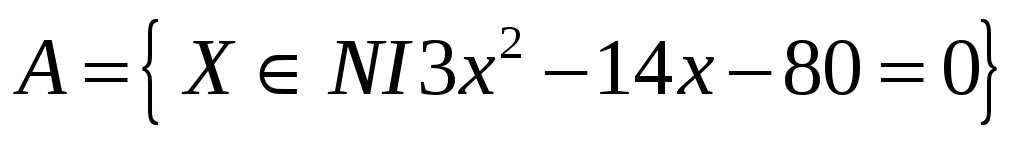
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) y= 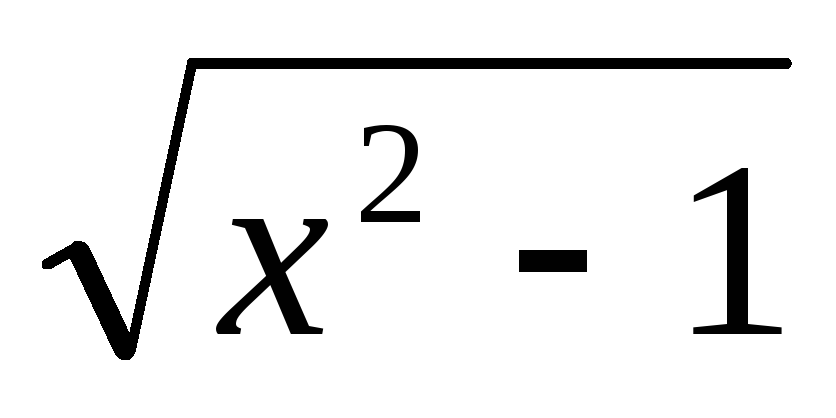 б)
б)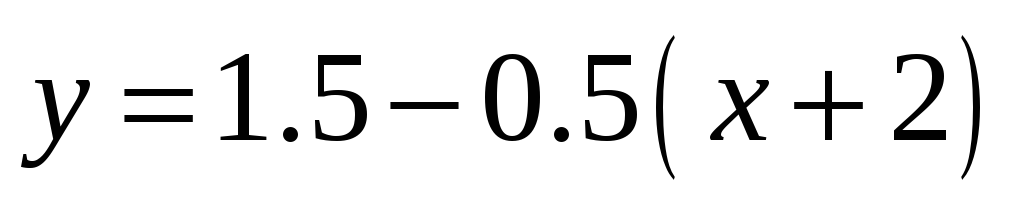 2;в)y = lg
(10x-1).
2;в)y = lg
(10x-1).
2) Найти пределы:
а)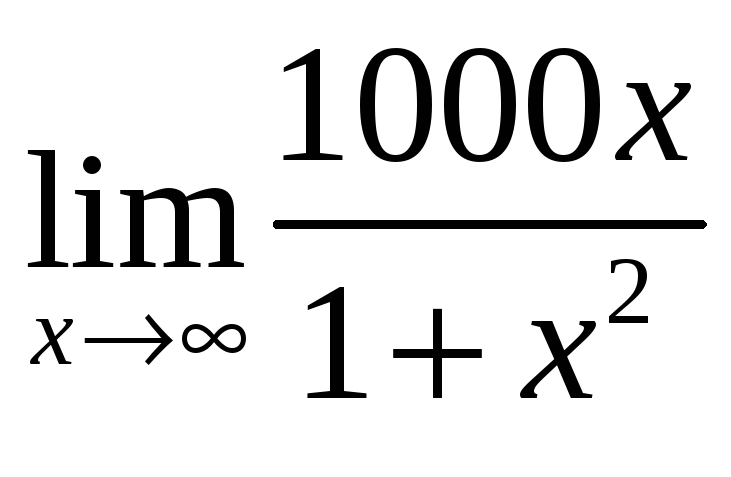 ;
б)
;
б) ;
в)
;
в) 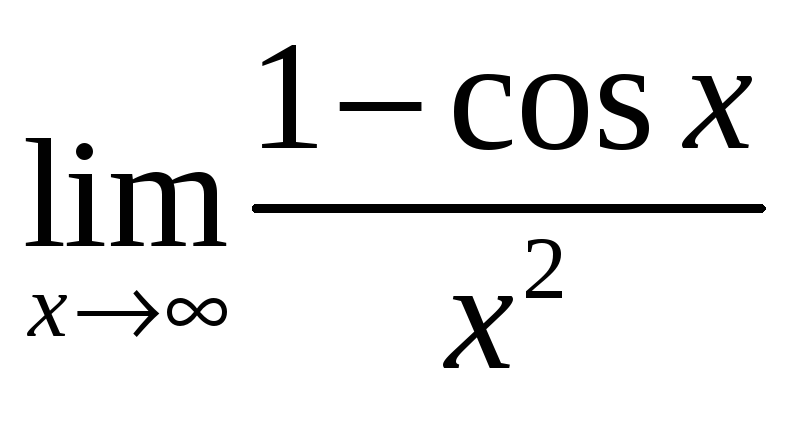 ;
г)
;
г) 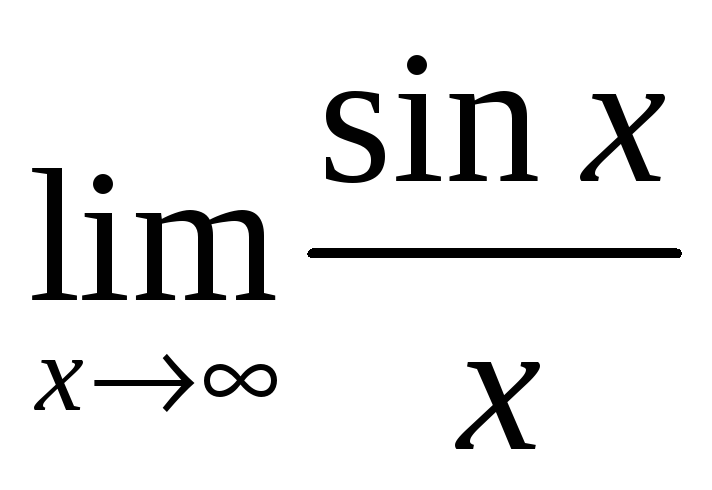
3) Найти производные функций:
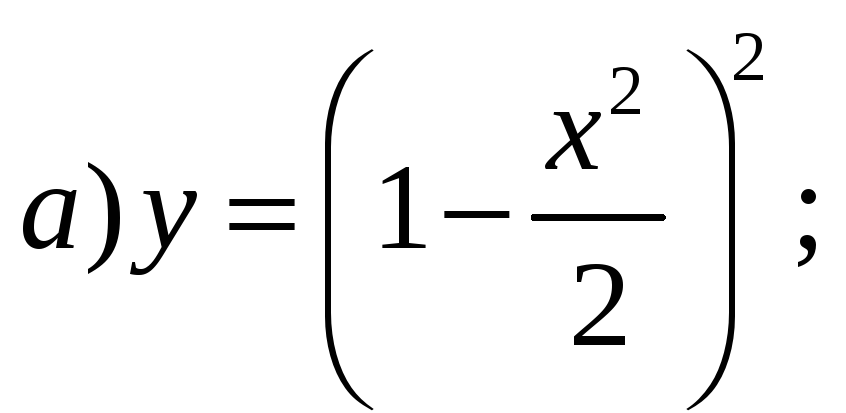

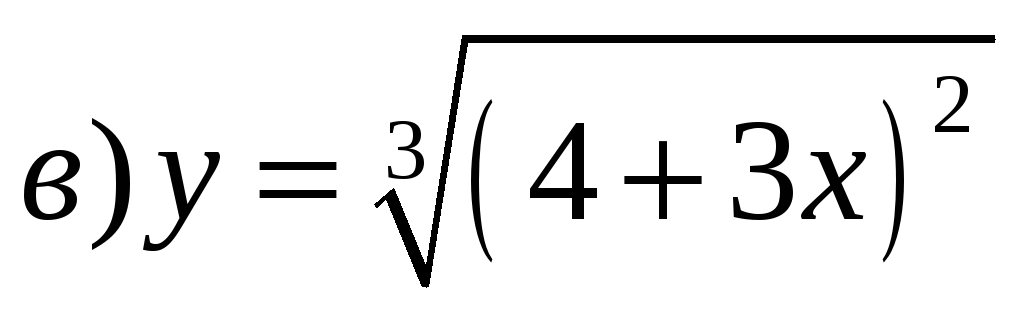 ;
г)
;
г) 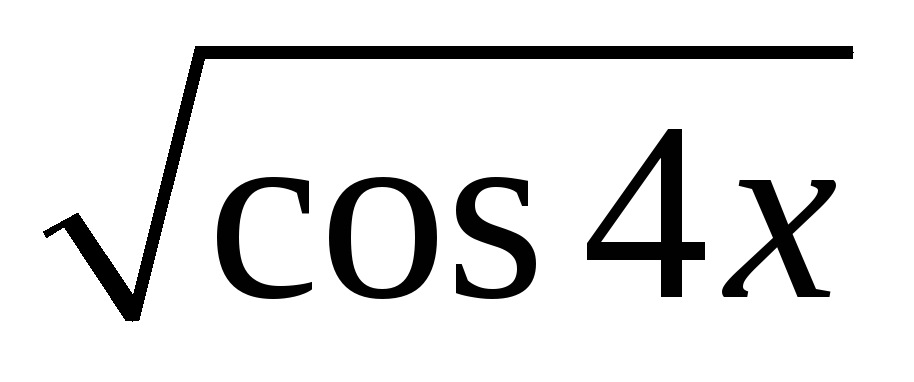
Найти пределы, используя правило Лопиталя:
а) 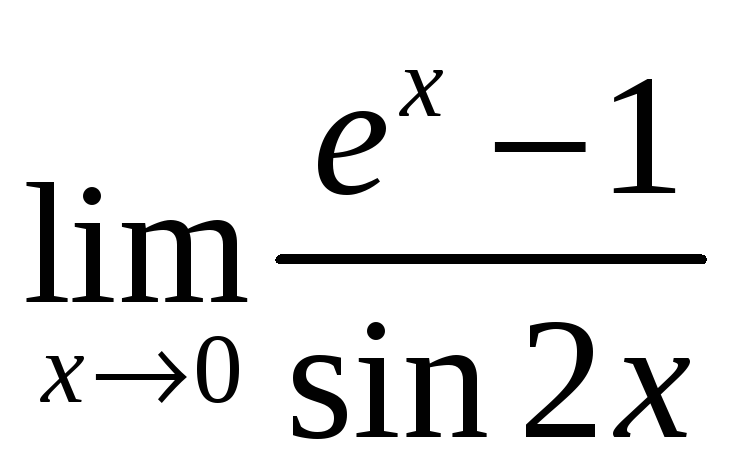 ;
б)
;
б) 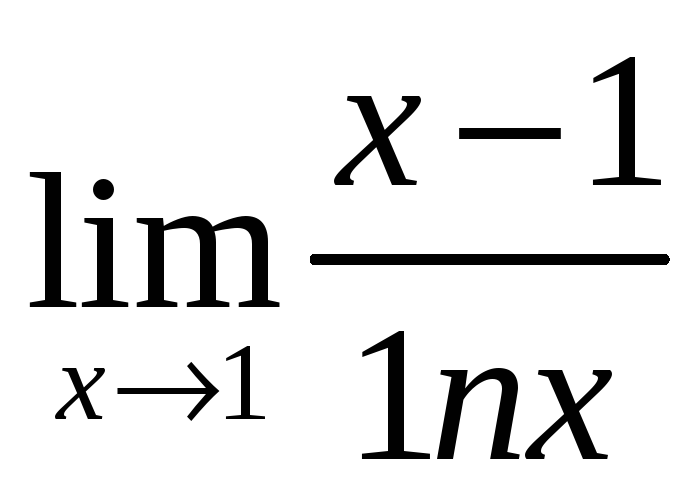
Выполнить полное исследование функции и построить ее график:
а)y=x/2+2/x; б)y=1+2x2-x4/4
Для функций многих переменных:
а) Указать область определения
функции: 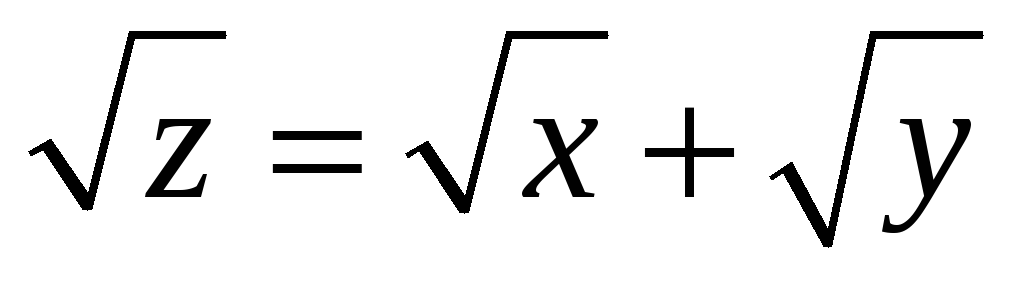 ;
;
б) Найти частные производные функции: z = x2 y-3;
в) Исследовать на экстремум функцию : z = x4 + y4 — x2 — 2xy -y2
Интегральное исчисление и ряды
Найти интегралы:
а)  (x2+2x+1/
x)dx; б)
(x2+2x+1/
x)dx; б) 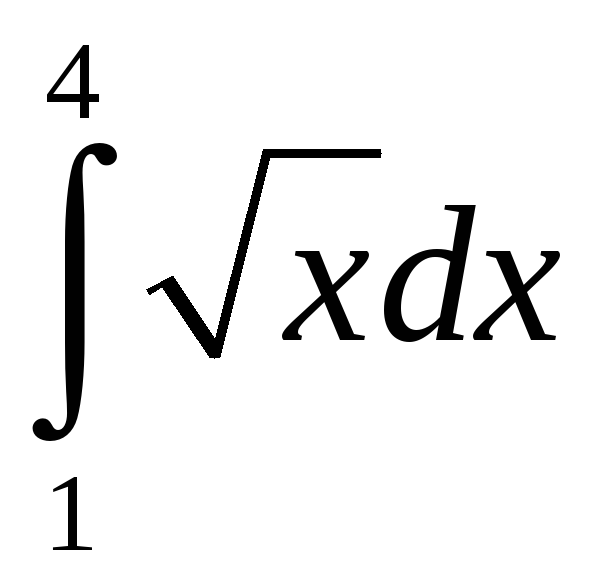 ;
в)
;
в) x2 cos xdx.
x2 cos xdx.
Вычислить интегралы:
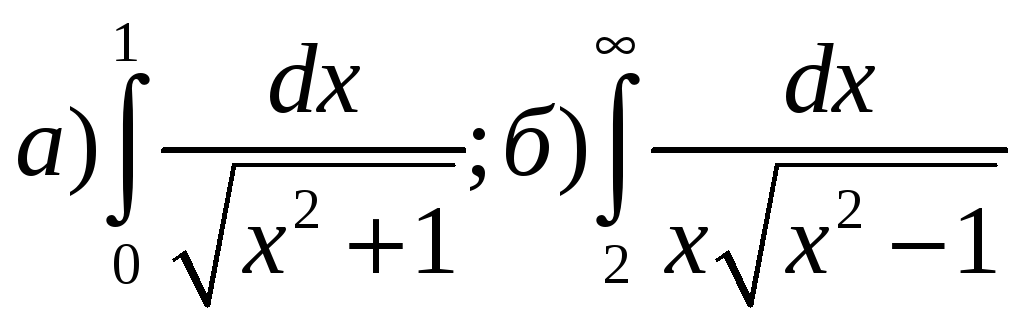
Найти общий интеграл:
(x2+x)y/= 2y+1
Исследовать сходимость числовых рядов:
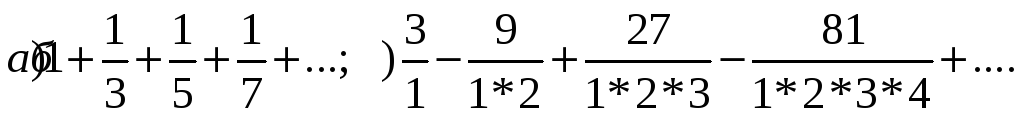
Контрольная работа по курсу «Математический анализ» Вариант 28
I. Множества
1) Известно, что из 100 студентов увлекаются живописью 28 человек, спортом 42, музыкой30; живописью и спортом 10; живописью и музыкой 5; спортом и музыкой 8; и живописью и спортом и музыкой 3 человека.
Сколько студентов увлекаются только живописью?
Сколько студентов ничем не увлекаются?
Сколько человек не увлекаются музыкой?
2) Указать штриховкой множества:
 ;
; 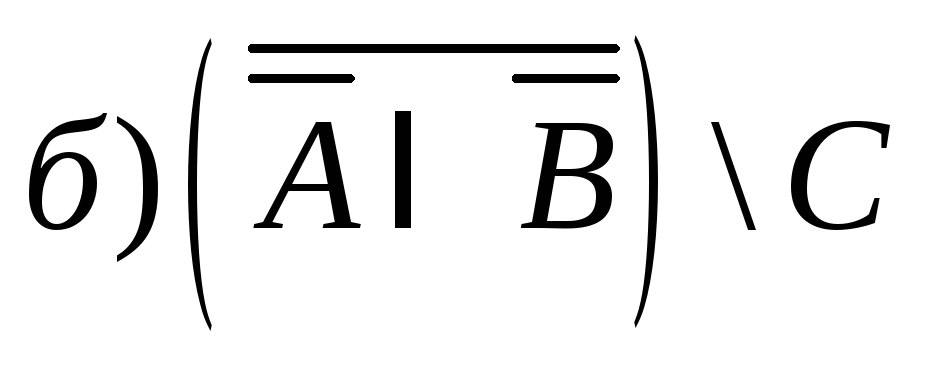
II. Дифференциальное исчисление
Найти область определения действительных значений функций:
а) y=x-4+Ix-2I;
б) y=1-cosx;
в) 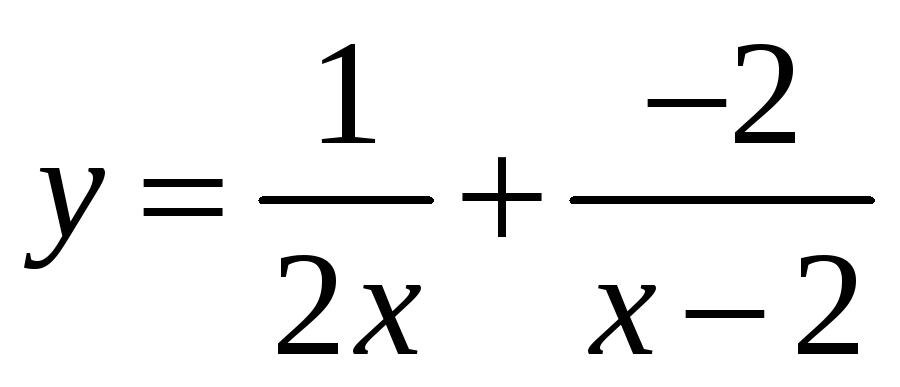 ;
;
2) Найти пределы:
а) 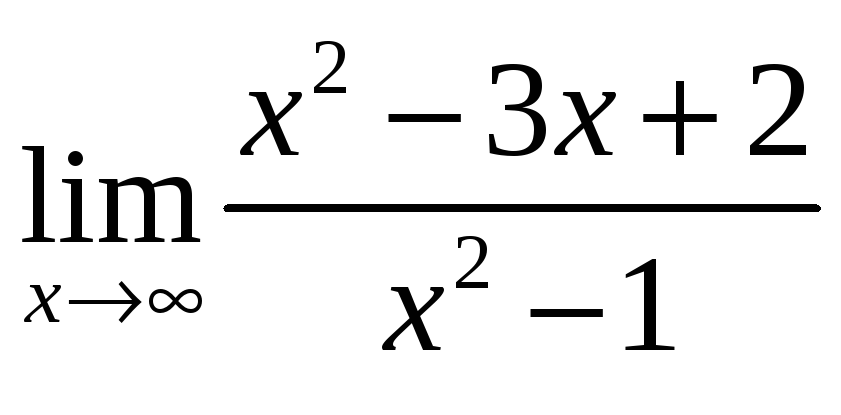 ;
б)
;
б) 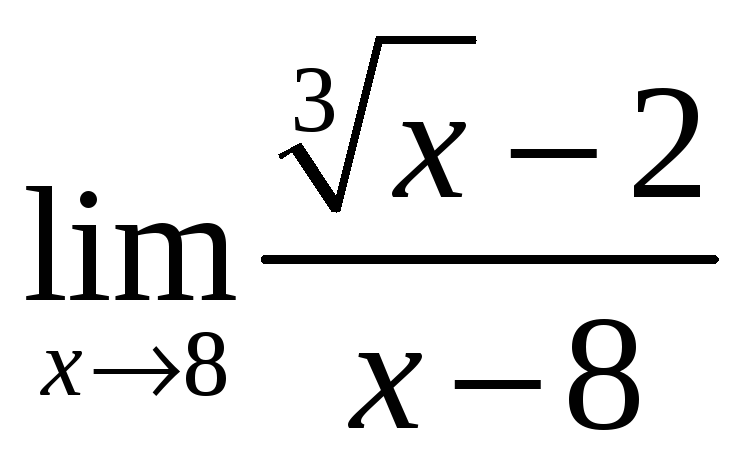 ;
в)
;
в)  ;
г)
;
г) 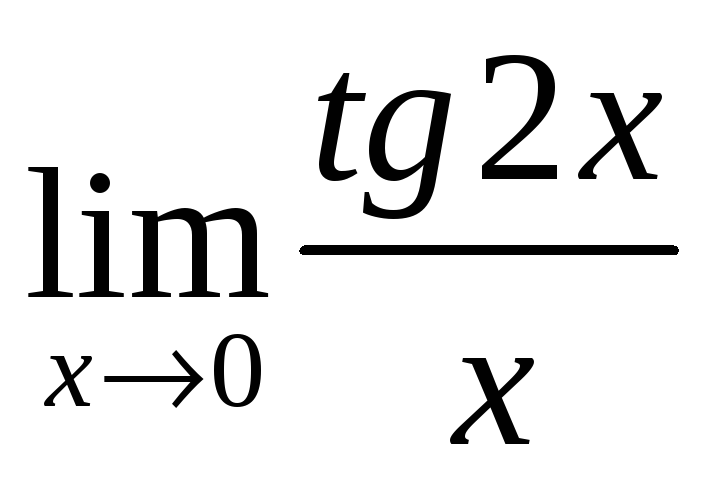 ;
;
3) Найти производные функций:
а) ;
б) y=sin 6x;
в)
;
б) y=sin 6x;
в) 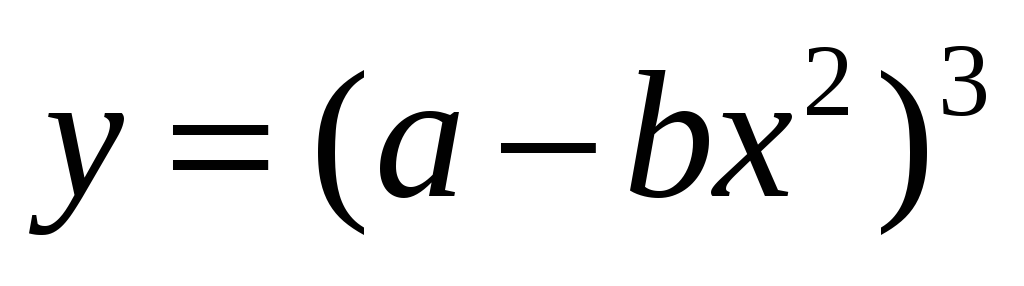 ;
г)
;
г) 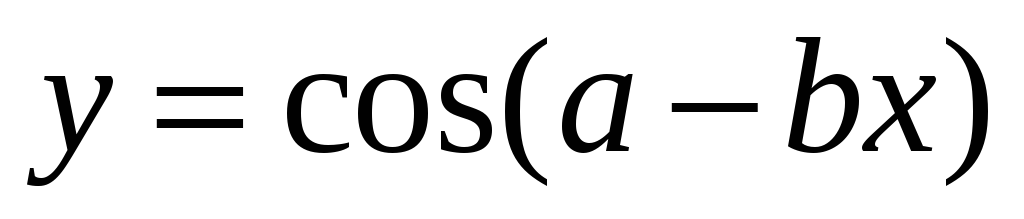 ;
;
4) Найти пределы, используя правило Лопиталя:
а) 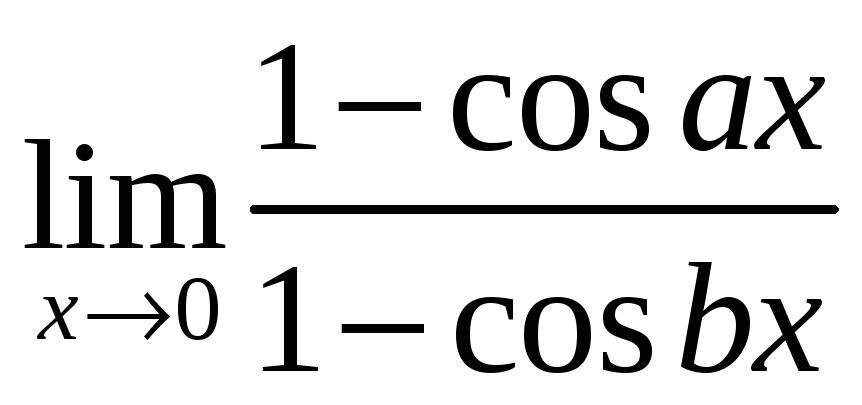 ;
б)
;
б) 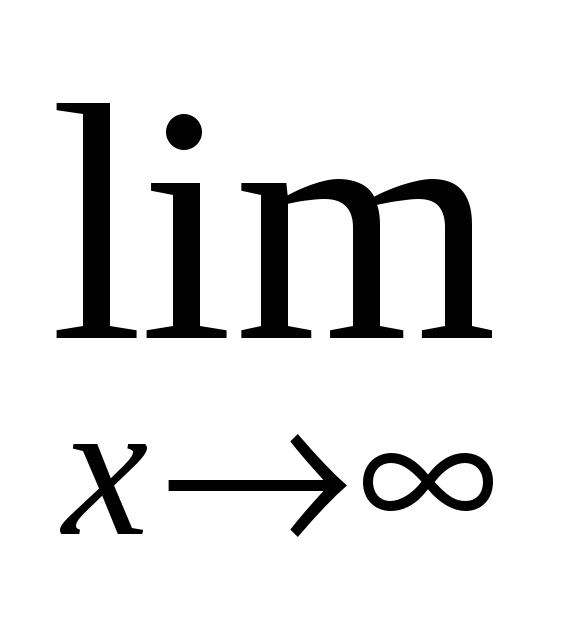 xne—x
xne—x
5) Выполнить полное исследование функции и построить ее график:
а) y=x 4 /4-x3; б) 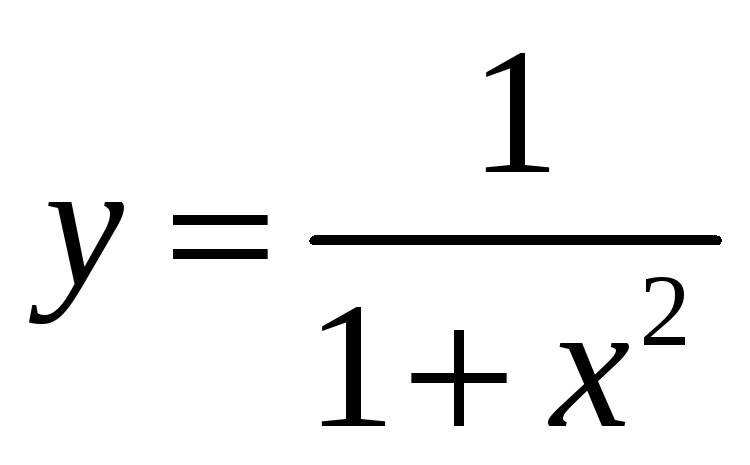 ;
;
6) Для функций многих переменных:
а) Указать область
определения функции: 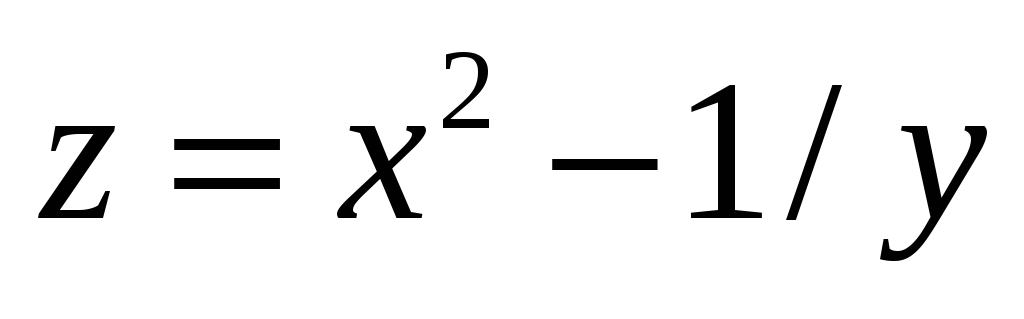 ;
;
б) Найти частные производные
функции:  ;
;
в) Исследовать на экстремум
функцию: 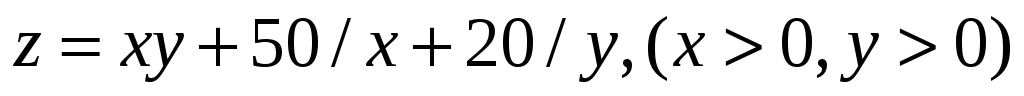
III. Интегральное исчисление и ряды
1) Найти интегралы:
а) 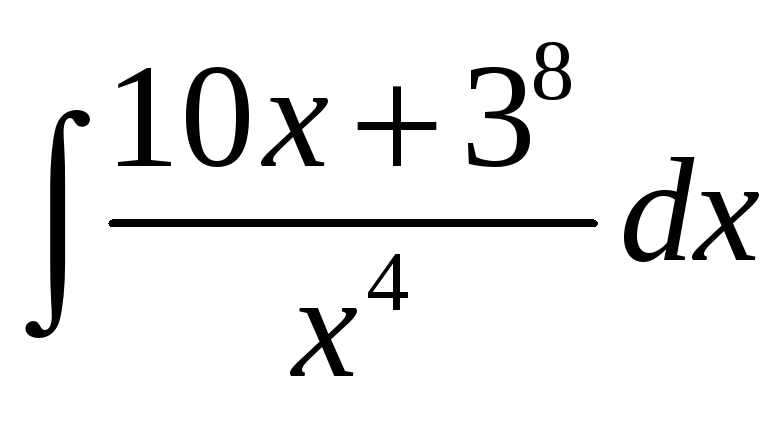 ;
б)
;
б) 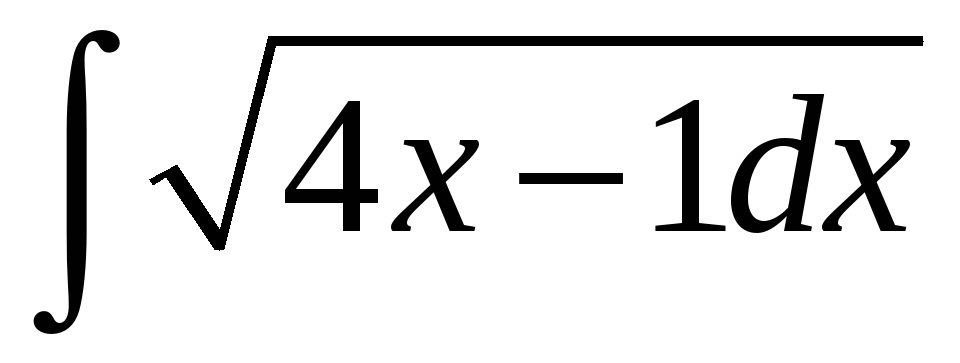 ;
в)
;
в) 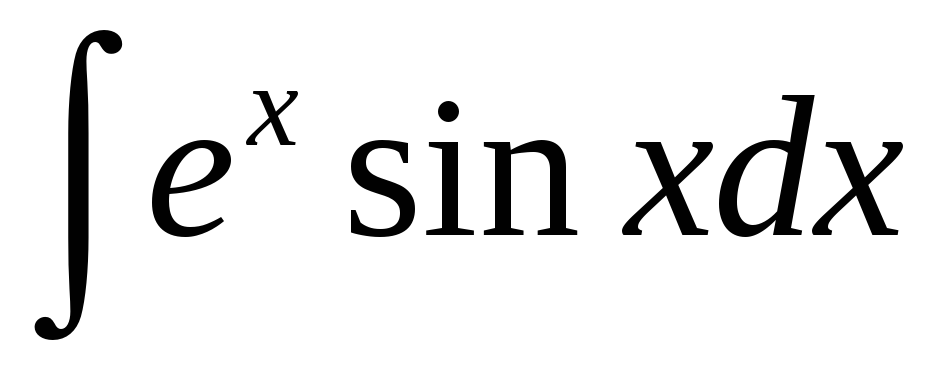 ;
;
Вычислить интегралы:
а)  ;
б)
;
б) 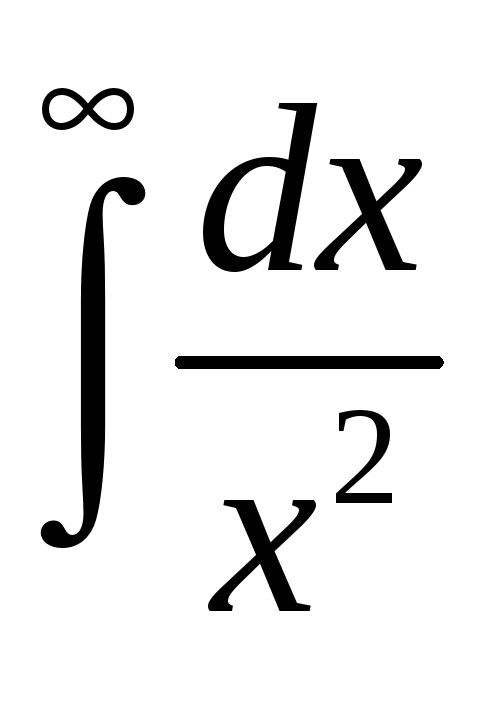
Найти общий интеграл:
yy/+x=0
Исследовать сходимость числовых рядов:
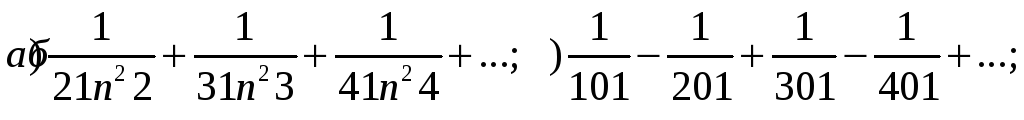
Вариант29
Контрольная работа по курсу «Математический анализ»
I. Множества
1) В коллоквиуме по математике приняло участие 40 студентов. Им были предложены задачи из 3-х разделов: по множествам, по алгебре, по анализу. По множествам решили задачу 20 человек, по алгебре-18, По матем. анализу-18. Не решили ни одной задачи 3 человека. По анализу и по алгебре справились с заданием 7 человек, по множествам и анализу- 8 , по алгебре и анализу – 9 чел..
Сколько студентов решили все задачи?
Сколько студентов решили ровно 2 задачи?
Сколько человек решили задачу только по множествам?
2) Задать множество перечислением его элементов.
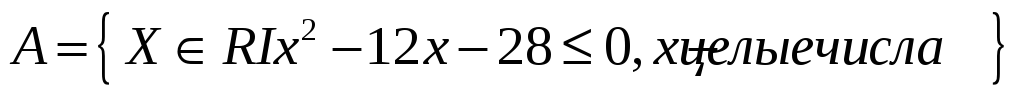
II. Дифференциальное исчисление
1) Найти область определения действительных значений функций:
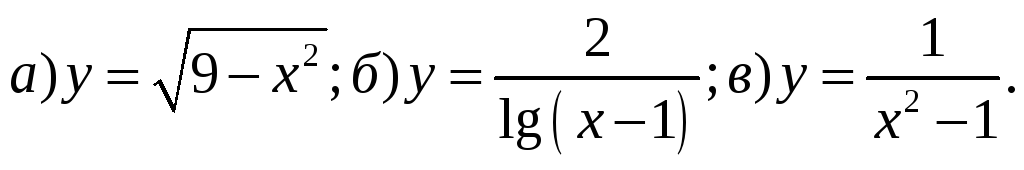
2) Найти пределы:
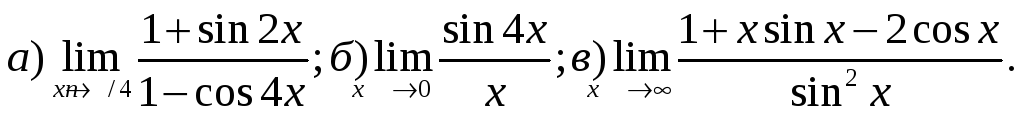
3) Найти производные функций:
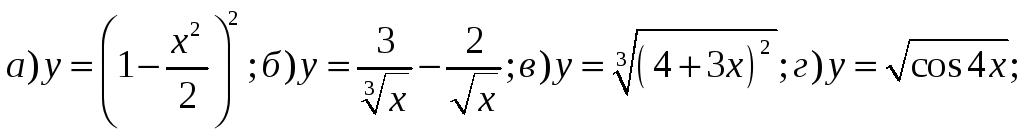
4) Найти пределы, используя правило Лопиталя:
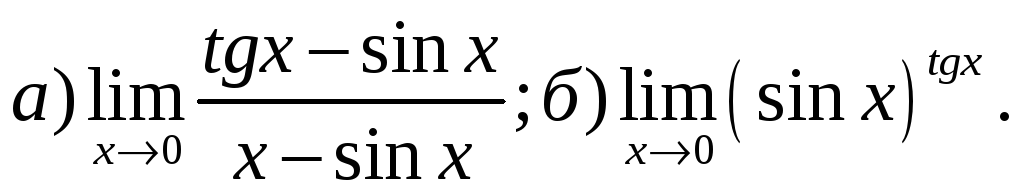
5) Выполнить полное исследование функции и построить ее график:

6) Для функций многих переменных:
а) Указать область
определения функции: 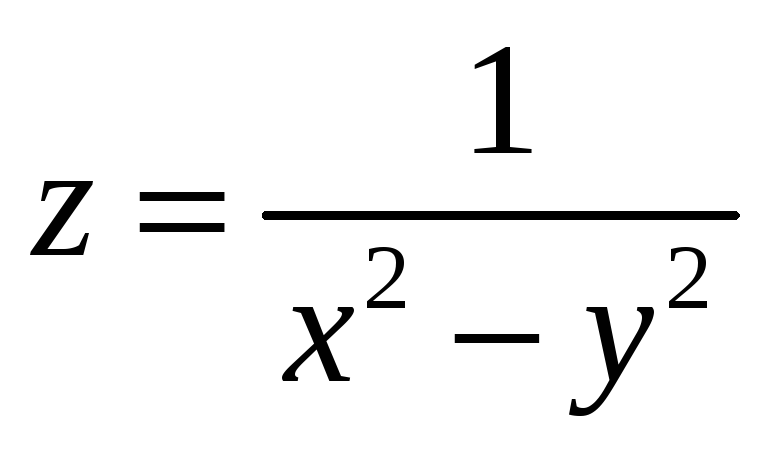 ;
;
б) Найти частные производные
функции: 
в) Исследовать на экстремум
функцию: 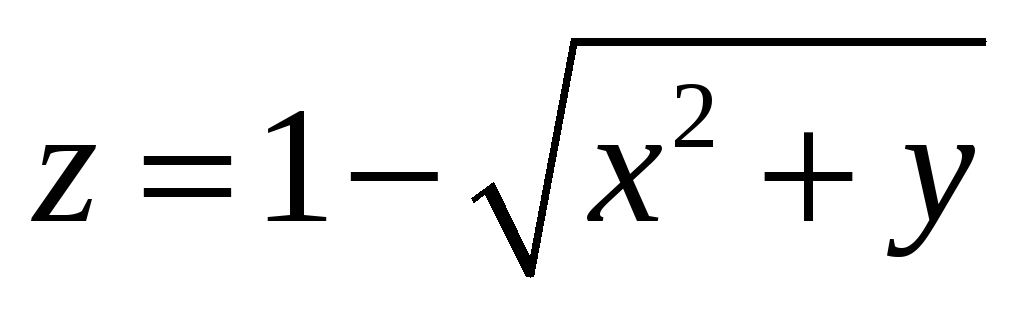 ;
;
III. Интегральное исчисление и ряды
1) Найти интегралы:

2) Вычислить интегралы:
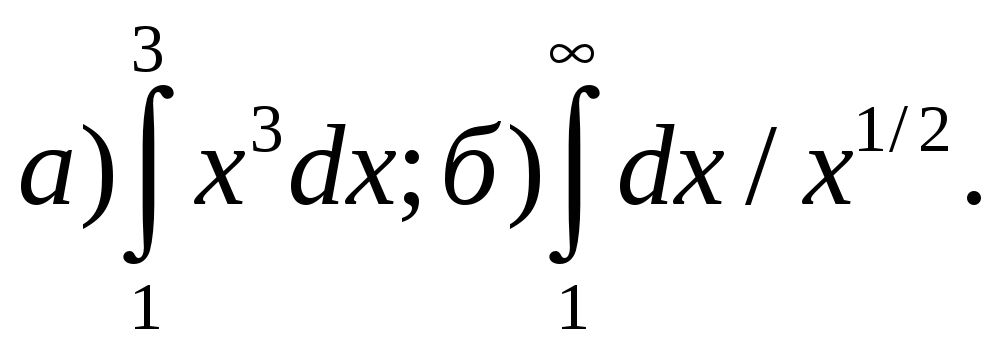
Найти общий интеграл:

Исследовать сходимость числовых рядов:

Вариант 30
Контрольная работа по курсу «Математический анализ»
Множества
1) Среди абитуриентов, выдержавших экзамены в ВУЗ, оценку «отлично» получили: по матеметике-48 человек, по физике-37, по языку-42. по математике или физике-75, математике или языку-76, по физике или языку-66 человек. По всем трем предметам получили отличную оценку 4 человека.
Сколько абитуриентов получили хотя бы одну пятерку?
Сколько среди них получивших только одну пятерку?
Сколько человек не получили пятерку по языку?
2) Задать множество перечислением его элементов:
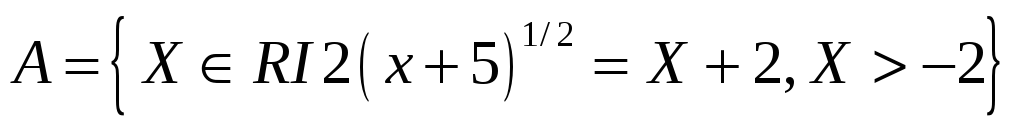
II. Дифференциальное исчисление
1) Найти область определения действительных значений функций:
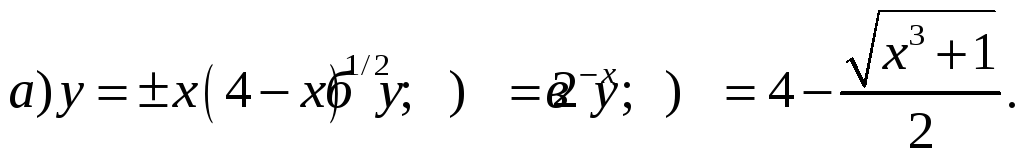
2) Найти пределы:
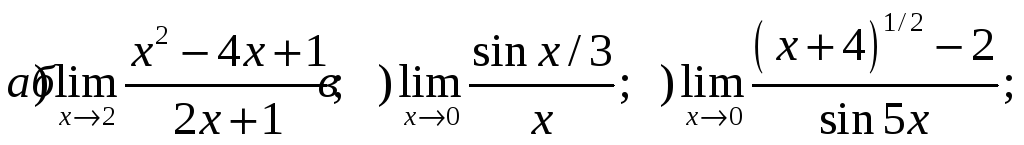
3) Найти производные функций:
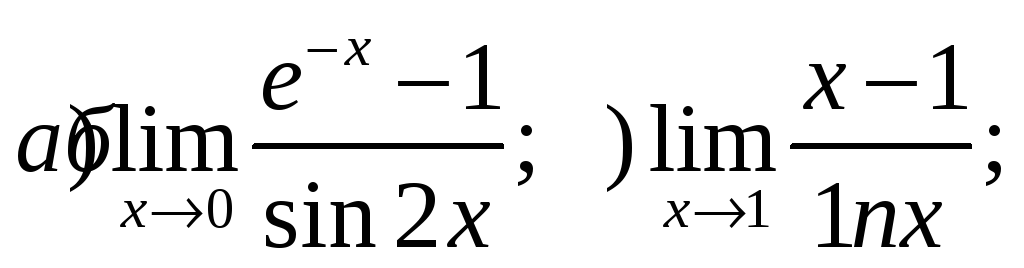
4) Найти пределы, используя правило Лопиталя:
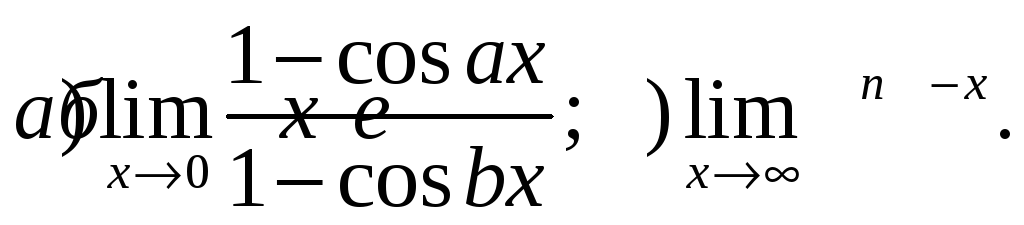
Выполнить полное исследование функции и построить ее график:
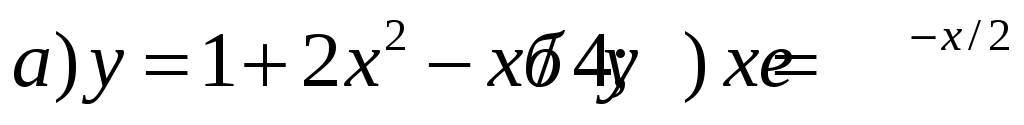
Для функций многих переменных:
а) Указать область
определения функции: 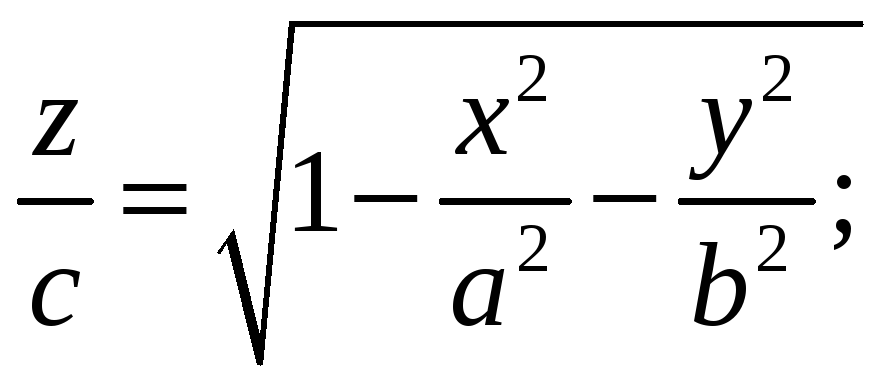
б) Найти частные производные
функции: 
в) Исследовать на экстремум
функцию: 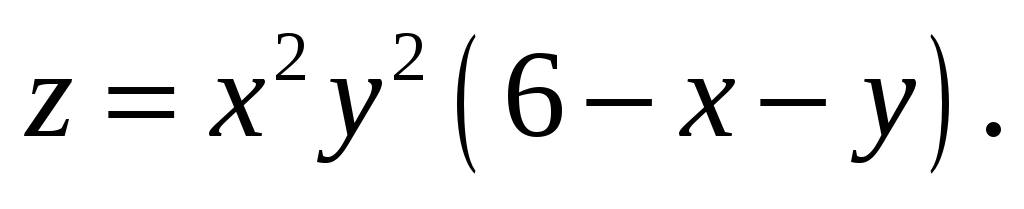
III. Интегральное исчисление и ряды
Найти интегралы:
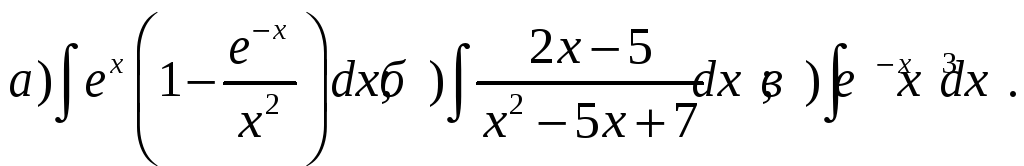
Вычислить интегралы:
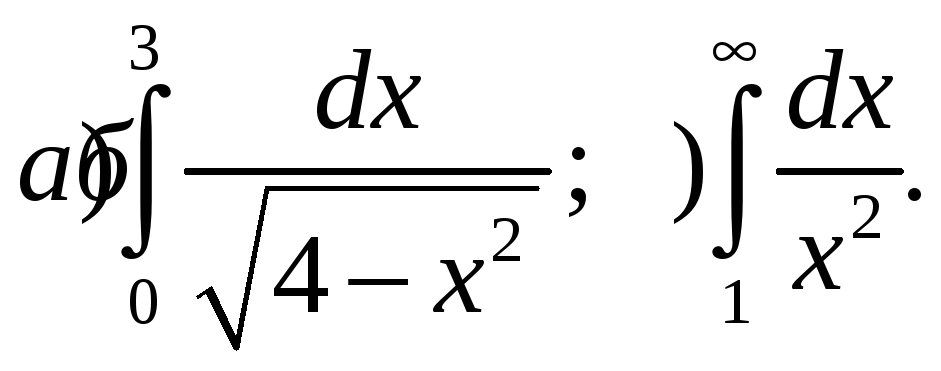
Найти общий интеграл:
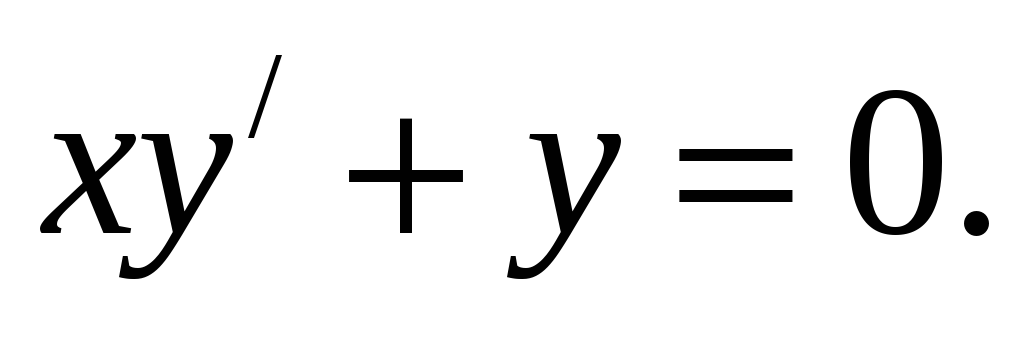
Исследовать сходимость числовых рядов:
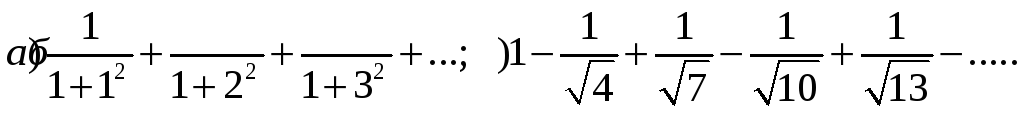
I. Множества
1. В группе из 50 студентов 40 человек сдали экзамен по математике, 27 студентов сдали экзамен по экономике, 5 человек не сдали ни того, ни другого экзамена. Сколько человек сдали оба экзамена?
Сколько человек сдали только 1 экзамен по экономике?
2. Задать множества перечислением элементов: А = {xN I 3х²-14х-80=0}.
II. Дифференциальное исчисление
1. Найти область определения действительных значений функций:
1). у = Ιх²-1I; 2). у =1,5 -0,5(х+2)²;3). у = lg(10x-l)
2. Найти пределы:
1).lim 1000x 2).lim √x-3 3). lim 1-cosx; 4). lim sinx;
x→∞ 1+x² х→9 х-9 x→0 х² x→∞ x
3. Найти пределы, используя правило Лопиталя:
1).lim ex-1 2) lim x-1
x→0 sin2x x→1 lnx
4. Найти производные функции:
1).
у=(1-x²/2)²;2).
у=3/ ³ √x
; 3). y=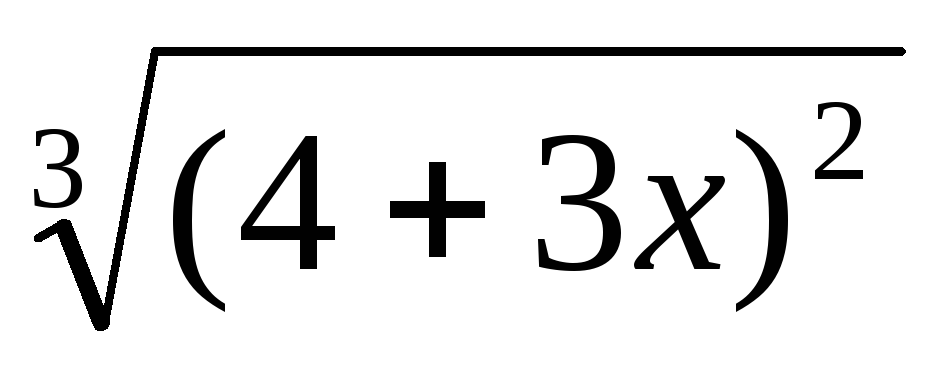 ;4). y=√cos4x
;4). y=√cos4x
5. Выполнить полное исследование функции и построить ее график:
1).
у=х/2 + 2/х;
2). у=√ e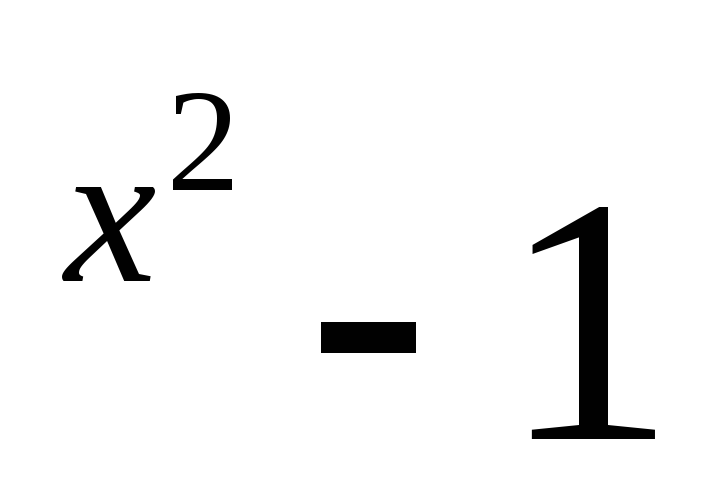
6. Для функций нескольких переменных:
1). Указать область определения функции: √z = √x+√y.;
2). Найти частные производные функции: z = х² ∙ y─3;
3). Исследовать на экстремум функцию:
z
= х²- xy+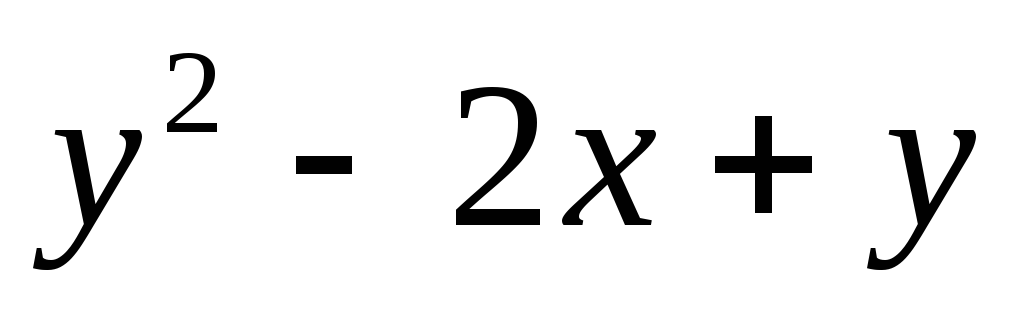
‘»
III. Интегральное исчисление и ряды
1. Найти интегралы:
1) ∫ (x²+2x+1/x)dx;
2) ∫ 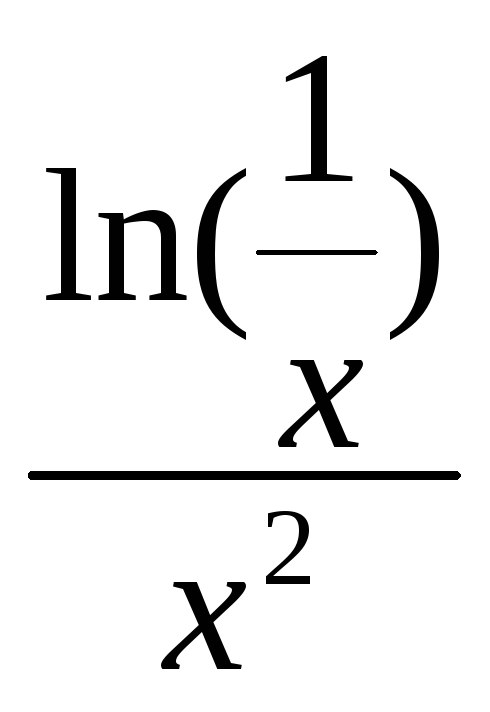 dx;
3) ∫
x²cosx
dx
dx;
3) ∫
x²cosx
dx
2.Вычислить интегралы:
1 ∞
1) ∫dx/√x²+1; 2) ∫dx/x√x²-1
0 2
3. Найти общий интеграл: (x²+x)y′ = 2y+1
4. Исследовать сходимость числовых рядов:
1) 1+1/3+1/5+1/7+…
2) 1-1/4+1/9-1/16+1/25-…
Вариант 12
Вариант 13Контрольная работа по курсу «Математический анализ»
I. Множества.
1. Известно, что из 100 студентов увлекаются живописью 28;спортом 42;музыкой 30;живописью и спортом 10; живописью и музыкой 5; спортом и музыкой 8; живописью, спортом и музыкой 3 человека.
Определить:
1). Количество студентов, увлекающихся только живописью;
2). Количество студентов, ничем не увлекающихся.
3). Сколько человек имеет ровно два увлечения?
2. Множества A, B, С являются подмножествами u
Указать штриховкой
множества: 1) 
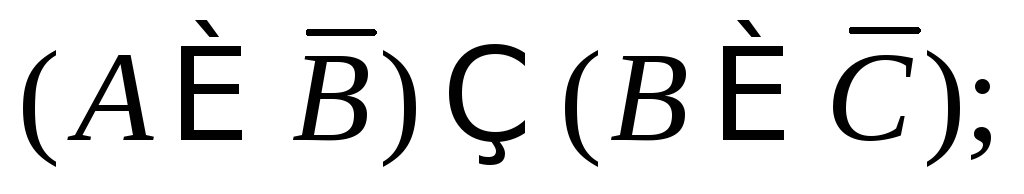
2) 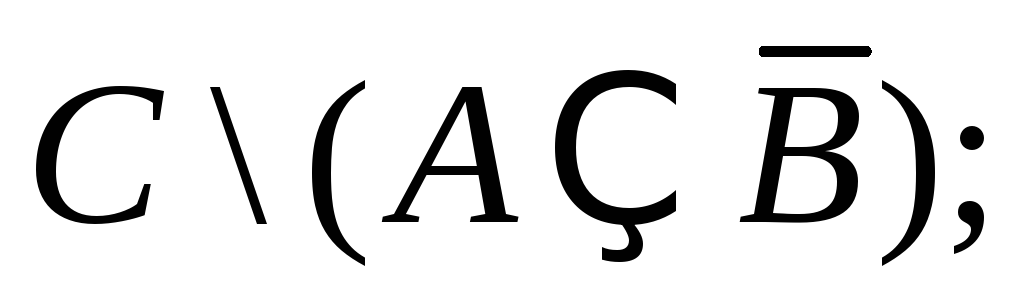
Упростить выражение
Выполнить над множествами следующие операции и дать графическую интерпретацию.
· `A È C Ç B для варианта множеств а).
· B D A Ç C для варианта множеств b).
· C \ `B Ç A для варианта множеств c).
2. Выяснить выполняется ли соотношение (графически):
A\(C È B)=(A\B)\C.
3. Найдите произведение множеств A ´ C, B ´ A и C2 и их мощности для варианта множеств c).
4. Найдите проекцию множеств A ´ C´ B на 2, 3 составляющие, то есть Пр2,3 A ´ C´ B для варианта множеств a).
5. Дано множество M={m: m =x+y, x ‘ A, y ‘ B} для варианта множеств а). и отношение R={(a, b): a, b ‘ M, a+b — нечетное}
· записать отношение в явном виде, найти обратное отношение R-1 .
· представить R линейным способом,
· выяснить какими свойствами обладает данное отношение,
6. Известно, что из 100 студентов живописью увлекаются 28 чел., спортом – 42 чел., музыкой – 30 чел., живописью и спортом – 10 чел., живописью и музыкой — 8 чел., спортом и музыкой – 5 чел., живописью, спортом и музыкой –3 чел. Определить a). сколько человек увлекается только музыкой, b). сколько человек ничем не увлекается, c). сколько человек увлекается хотя бы живописью и музыкой ?
7. Надо послать 7 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно послать 3 курьеров и каждое письмо можно дать любому из 3 курьеров?
y(a,b,c ) = (aÚ bc)ac Ú b®c
9. Минимизировать функции по картам Карно и найти сложность по Квайну:
а) Найти мин. сумму б) Найти мин произведение
Сборник задач на решение задач при помощи кругов Эйлера с ссылками на интерактивный ресурс LearningApps.org
5 класс, задачи на круги Эйлера
В классе 25 учащихся. Из них 5 человек не умеют играть ни в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 — в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы?
A+B+C+D=25
A+B=18
B+C=20
D=5
B-?
A=25-(B+C+D)= 25- (20+5)=0
A+B=18
B=18-A=18-0=18
Ответ: 18 учащихся.
Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский язык изучают 25 человек, французский — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?
A+B=25
B+C=27
B=18
A+B+C-?
C=27-B=27-18=9
A=25-B=25-18=7
7+18+9=34
Ответ: 34 учащихся.
В детском саду 52 ребенка. Каждый из них любит либо пирожное, либо мороженое, либо и то, и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое?
A+B+C=52
A+B=26
B=20
B+C-?
C=52-(A+B)=52-26=26
B+C=20+26=46
Ответ: 46 детей любит мороженое.
Сколько в классе учащихся, если известно, что лыжным спортом увлекаются 28 человек, отличников в классе — 12, причем отличников-спортсменов, увлекающихся лыжами, — 10?

A+B=28
B+C=12
B=10
A+B+C=?
C=12-B=12-10=2
A+B+C=28+2=30
Ответ: 30 человек
37 школьников из ученической производственной бригады изъявили желание летом работать на уборке зерновых. Каждый из них имеет права для работы на тракторе или на комбайне, а некоторые могут работать и на тракторе, и на комбайне. Сколько школьников могут работать и на тракторе, и на комбайне, если известно, что трактором хорошо овладели 23 человека, а комбайном — 31 человек?
A+B+C=37
A+B=23
B+C=31
B-?
C=37-(A+B)=37-23= 14
B=31-C=31-14=17
Ответ: 17 человек могут работать на тракторе и комбайне.
В ученической производственной бригаде 86 старшеклассников. 8 из них не умеют работать ни на тракторе, ни на комбайне. 54 ученика хорошо овладели трактором, 62 — комбайном. Сколько человек из этой бригады могут работать и на тракторе, и на комбайне?
A+B+C+D=86
D=8
A+B=54
B+C=62
B-?
C=86-(A+B+D)=86-(54+8)=24
B=62-C=62-24=38
Ответ: 38 человека могут работать на тракторе и комбайне.
Формула включений и исключений — 7 Июля 2016 — Примеры решений задач
Пусть задано конечное множество А. Число его элементов обозначим n(А). Найдем сколько элементов содержится в множестве А ∪ В. Основная формула нахождения числа элементов суммы двух множеств
n(А ∪ В) = n(А) + n(В) – n(А ∩ В) (1)
Действительно, n(А ∪ В) — это сумма числа элементов множеств А и В, но при подсчете элементы, принадлежащие А ∩ В учитывались дважды. С помощью формулы (1) можно получить формулы для определения числа элементов суммы любого числа множеств. Например,
n(А ∪ В ∪ С) = n(А ∪ (В ∪ С)) = n(А) + n(В ∪ С) – n(А ∩ (В ∪ С)) =
= n(А) + n(В) + n(С) – n(В ∩ С) – n((А ∩ В) ∪ (А ∩ С)) =
= n(А) + n(В) + n(С) – n(В ∩ С) – (n(А ∩ В) + n(А ∩ С) – n((А ∩ В) ∩ (А ∩ С))) =
=n(А) + n(В) + n(С) – n(В ∩ С) – n(А ∩ В) – n(А ∩ C) + n(А ∩ В ∩ С).
n(А ∪ В ∪ С) = n(А) + n(В) + n(С) – n(А ∩ В) – n(В ∩ С) – n(А ∩ C) + n(А ∩ В ∩ С) (2)
Формулы (1) и (2) называют формулами включений и исключений.
Примеры с подробным решением.
Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?
Решение. I способ.
Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.
Тогда n(A) = 42, n(N) = 30, n(F) = 28, n(A ∩ N) = 5,
n(A ∩ F) = 10, n(N ∩ F) = 8, n(A ∩ N ∩ F) = 3.
Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.
n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =
= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =
= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.
Следовательно, не знают ни одного иностранного языка:
100 – 80 = 20 школьников.
II способ.
Эту же задачу можно решить с помощью диаграммы Эйлера–Венна (рис. 1).
Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,
немецкий и французский — 8 – 3 = 5 школьников.
Только английский знают 42 –(2 + 3 + 7) = 30,
только немецкий — 30 – (2 + 3 + 5) = 20,
только французский — 28 – (3 + 5 + 7) = 13 школьников.
Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.
Задача 2. Сколько двузначных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 11?
Решение. Обозначим: А — множество двузначных чисел, делящихся на 2;
В — множество двузначных чисел, делящихся на 3;
С — множество двузначных чисел, делящихся на 5;
D — множество двузначных чисел, делящихся на 11.
n(A ∪ B ∪ C ∪ D) — количество двузначных чисел, делящихся хотя бы на одно из чисел 2; 3; 5; 11.
n(A ∪ B ∪ C ∪ D) = n(A) + n(B) + n(C) + n(D) –
– n(A ∩ B) – n(A ∩ C) – n(A ∩ D) – n(B ∩ C) –
– n(B ∩ D) – n(C ∩ D) + n(A ∩ B ∩ C) + n(A ∩ B ∩ D) +
+ n(A ∩ C ∩ D) + n(B ∩ C ∩ D) – n(A ∩ B ∩ C ∩ D).
n(A) = 45, n(B) = 30, n(C) = 18, n(D) = 9,
n(A ∩ B) = 15, n(A ∩ C) = 9, n(A ∩ D) = 4, n(B ∩ C) = 6,
n(B ∩ D) = 3, n(C ∩ D) = 1, n(A ∩ B ∩ C) = 3,
n(A ∩ B ∩ D) = 1, n(A ∩ C ∩ D) = n(B ∩ C ∩ D) = n(A ∩ B ∩ C ∩ D) = 0.
Итак, n(A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 – 15 – 9 – 4 – 6 – 3 – 1 + 3 + 1 = 68.
Так как всего 90 двузначных чисел, то чисел, не делящихся ни на одно из заданных чисел:
90 – 68 = 22.
Задача 3. Известно, что из n учеников спортом увлекаются a учеников, программированием b, математикой c, спортом и программированием d, спортом и математикой e, программированием и математикой f , спортом, математикой и программированием g учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?
Вариант | n | a | b | c | d | e | f | g |
14 | 70 | 32 | 21 | 23 | 8 | 12 | 4 | 3 |
Решение. Пусть A —множество учеников, которые увлекаются спортом,
B — программированием, С — математикой.
Тогда |A| = 32, |B| = 21, |C| = 23, |A ∩ B| = 8, |A ∩ C| = 12, |B ∩ C| =4 |A ∩ B ∩ C| = 3
|(A ∩ B) ∪ ( B ∩ C) | = |A ∩ B| + |B ∩ C| − |A ∩ B ∩ C| = 8 + 4 – 3 = 9
Тогда, только программированием занимается 21 – 9 = 12 учеников.
|(A ∩ C) ∪ ( B ∩ C) | = |A ∩ C| + |B ∩ C| − |A ∩ B ∩ C| = 12 + 4 – 3 = 13
Тогда, только математикой занимается 23 – 13 = 10 учеников.
По формуле включений и исключений для трёх множеств находим число учеников увлекающихся спортом, программированием или математикой:
|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B∩ C| = =32+21+23-8-12-4+3 = 55
Значит, ничем не увлекается 70 − 55 = 15 человек. Ответ: 15.
Упражнения
1. В спортивном классе обучаются 24 человека. Каждый учащийся занимается хотя бы одним видом спорта (баскетболом или волейболом), из них баскетболом и волейболом занимаются 12 человек. Сколько человек занимается только волейболом, если их в 3 раза больше, чем тех, кто занимается только баскетболом?
2. В одном украинском городе все жители говорят на русском или украинском языке. По-украински говорят 80 % всех жителей, а по-русски — 75 %. Сколько процентов всех жителей говорят на обоих языках?
3. Группа ребят отправилась в поход. Семеро из них взяли с собой бутерброды, шестеро — фрукты, пятеро — печенье. Четве- ро ребят взяли с собой бутерброды и фрукты, трое — бутерброды и печенье, двое — фрукты и печенье, а один — и бутерброды, и фрукты, и печенье. Сколько ребят пошли в поход?
4. Староста класса, в котором 40 человек, подводил итоги по успеваемости группы за I полугодие. Получилась следующая картина: из 40 учащихся не имеют троек по русскому языку 25 человек, по математике — 28 человек, по русскому языку и мате- матике — 16 человек, по физике — 31 человек, по физике и ма- тематике — 22 человека, по физике и русскому языку 16 человек. Кроме того, 12 человек учатся без троек по всем трем предметам. Классный руководитель, просмотрев результаты, сказал: «В тво- их расчетах есть ошибка». Составьте диаграмму Эйлера–Венна и объясните, почему это так.
5. В лаборатории института работают несколько человек. Каждый из них знает хотя бы один иностранный язык. 7 человек знают английский, 7 — немецкий, 8 — французский, 5 знают английский и немецкий, 4 — немецкий и французский, 3 — французский и английский, 2 человека знают все три языка. Сколько человек работает в лаборатории? Сколько из них знает только французский язык? Сколько человек знает ровно 1 язык?
6. Сколько целых чисел от 0 до 999 не делятся ни на 5, ни на 7, ни на 11?
Ответы: 1. 9. 2. 55 %. 3. 10. 4. Если на диаграмме Эйлера– Венна отметить данные в непересекающихся множествах класса, то общее число учащихся класса получится равным 42, а не 40, как сказано в условии. 5. 12; 3; 4. 6. 376.
Ответы@Mail.Ru: вопрос по математике
к сожалению все решения предыдущих авторов безосновательны и следовательно неверны. решение проведем при помощи диаграмм если всего 100 человек и количество языков 3,то существует несколько множеств, множество не изучающих ничего, изучающих 2 языка, изучающих 3 языка. на рисунке а-английский, н-немецкий, ф- французский языки<img src=»//otvet.imgsmail.ru/download/37dc536b1342562a51b401a6fbceb7a7_i-105.jpg» > надеюсь идея понятна, сначала 3 -пересечение всех 3 языков, а другие пересечения 2 языков соответственно 8,10 и 5 человек. вычтем студентов изучающих несколько языков и получимизучающих только 1 язык, а если вычесть всех что-то изучающих от 100,то получим 29
Только французский — 32 Не изучающих ничего — 30
Ни одного — 26 Только французкий — 24
28 англичан 30 немцев 42 француза итого 100человек т. е. все что то да изучают = ничего не изучающих 0 студентов. французов изучающих еще что то 10 + 5 + 3 (8 тут не при чем) . = 18 человек. или 42 — 18 = 24 человека учат только французский. так как то…