Как из смешанной дроби сделать натуральное число: Как перевести смешанную дробь в натуральное число — Детская игровая комната «Волшебный лес»

Posted on 22.06.202029.05.2021 by alexxlab

Содержание

Как перевести смешанную дробь в натуральное число

У господарки був відріз тканини довжиною 3 м 60 см і шириною 1 м 50 см. Спочатку вона пошила з нього дві скатертини квадратної форми найбільшого розмі … ру. Із тканини, що залишилася, господарка пошила дві квадратні серветки максимального розміру, а з решти — дві квадратні носові хустинки. Визнач розмір носових хустинок? Помогите пожалуйста записать решение и объяснение к ним!!!!!

Как рєшить ×-1/3=2целі2/3

Туристы отправились в трёхдневный поход. За первые два дня они прошли 35 км, после чего им осталось преодалеть 2/7 пути. Сколько км составлял весь мар … шрут?

Пасажирка запізнилася на потяг,щоб його наздогнати вона бігла1 год зі швидкістю 13,7 км/год,їхала 3 год на скутері зі швидкістю 28,6км/год і 1 год їха … ла на таксі зі швидкстю 105,8км/год.Знайти середню швидкість пасажирки,з якою вона наздоганяла потяг?

Какое число надо дописать в клетку, чтобы равенство □+600=7900-900 стало верным Решите пожалуйста

(2:3):(4:15) решение

решите примеры и перемножте ответы 1) 3. 1/2 + 4.5/6 2) 6. 1\15-4.2\3 3) 11/5 : 3.2\3 4) 4.1\2*2/21

Как решаются примеры столиком 234÷6 158÷2

Помогите пожалуйста

Решите задачу.3) Площадь, занятая овощами, должна быть удобрена из расчёта 100 гудобрения на каждые 10м. Сколько денег потребуется для покупки удоб-ре … ния, если 1 кг удобрения стоит 0,8 манат?4) Ильгар предложил отцу всю площадь дачи засадить газоном. Цена га-зонных семян на 1м? стоит 55 гяпик. Сколько денег необходимо для по-кулки газонных семян на всю площадь дачного участка?5) Чтобы взрыхлить дачный участок Аян и её брат поделили участок на 2равные части. Сколькими способами они могут это сделать? Выполнитезадание схематически. Это же задание выполните на примере дачногоучастка Ильгара,6) Каждый метр дачного забора обошёлся семье Ильгарав 8,5 манат, а семье Аян — 6,5 манат. Сколько денег былопотрачено на ограждение каждого участка?7) Вдоль всего забора Ильгар выложил дорожку (см. рис.)в ширину одной каменной плитки размером 50 см х 50 см.

Сколько ка-менных плиток потребовалось для укладки дорожки? (Обратите особоевнимание на плиты, уложенные в углах участка).8) Сколько денег необходимо на покупку всех плиток, если 1 плитка стоит76 манат?Помогите прошу❤Если не поймёте во картинкаТам первое,второе задание не делайте☻

Урок 71. понятие смешанной дроби — Математика — 5 класс

Математика

5 класс

Урок № 71

Понятие смешанной дроби

Перечень рассматриваемых вопросов:

– введение понятий «смешанная дробь», «целая часть смешанной дроби», «дробная часть смешанной дроби»;

– правило преобразования неправильных дробей в смешанные дроби;

– правило преобразования смешанных дробей в неправильные дроби;

– отработка правил преобразования неправильных и смешанных дробей;

– сравнение смешанных дробей.

Тезаурус

Правильная дробь – дробь, числитель которой меньше знаменателя.

Неправильная дробь – дробь, числитель которой больше знаменателя.

Смешанная дробь – сумма натурального числа и правильной дроби, записанная без знака плюс;

Целая часть смешанной дроби – натуральное число в смешанной дроби.

Дробная часть смешанной дроби – правильная дробь в смешанной дроби.

Обязательная литература

Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

Дополнительная литература

Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Вы уже знакомы с обыкновенными дробями. Умеете выполнять с ними все арифметические действия. Знаете, что обыкновенные дроби бывают правильными – это те дроби, числитель которых меньше знаменателя, и неправильными – дроби, у которых числитель больше знаменателя.

Если числитель неправильной дроби делится на знаменатель без остатка, то такая неправильная дробь равна частному от деления числителя на знаменатель.

Сумму натурального числа три и правильной дроби две пятых, записанную сокращённо, без знака плюс, называют смешанной дробью.

Натуральное число «три» в смешанной дроби «три целых две пятых» называют целой частью, а правильную дробь «две пятых» – дробной частью смешанной дроби.

Чтобы правильно назвать дробную часть смешанной дроби поступаем так: называя числитель, отвечаем на вопрос: «сколько долей взято?» – две. Называя знаменатель, отвечаем на вопрос: «две каких?» – пятых.

Научимся записывать неправильные дроби, числитель которых не делится на знаменатель нацело, в виде смешанных дробей.

Каждую смешанную дробь можно представить в виде неправильной дроби.

Для этого надо:

• знаменатель дробной части умножить на целую часть,

• прибавить к этому числу числитель дробной части,

• полученное число записать в числитель искомой неправильной дроби,

• знаменатель оставить прежним.

Так как у этих дробей целые части одинаковые, то сравнивать мы будем дробные части. Но дробные части данных дробей имеют разные знаменатели. Чтобы сравнить дроби с разным знаменателем, нужно привести их сначала к общему знаменателю. Меньшей из них будет та дробь, числитель которой меньше.

А можно ли сравнить эти дроби, не приводя их к общему знаменателю? Можно. И даже не одним способом.

Тренировочные задания

Преобразуем каждую смешанную дробь в неправильную, пользуясь правилом:

– знаменатель умножить на целую часть,

– прибавить его к дробной части,

– полученное число записать в числитель,

– знаменатель останется прежним.

Для того чтобы выбрать равные дроби, нужно привести их к одинаковому виду: или все дроби сделать неправильными, или все дроби – смешанными.

Преобразуем первые четыре неправильные дроби в смешанные числа.

Как разделить натуральное число на обыкновенную дробь

В данной публикации мы рассмотрим, каким образом можно натуральное число разделить на обыкновенную дробь: правильную, неправильную и смешанную. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

Деление числа на правильную/неправильную дробь

Чтобы разделить натуральное число n на обыкновенную дробь (правильную или неправильную), последнюю следует перевернуть (т.е. поменять числитель и знаменатель местами) и далее умножить на это число n.

n :

a/b

= n ⋅

b/a

n ⋅ b/a

Примечание: если в результате деления получится новая дробь, проверяем, можно ли ее сократить.

Деление числа на смешанную дробь

Чтобы найти частное от деления числа n на смешанную дробь, последнюю для начала необходимо представить в виде неправильной дроби. Затем делим число на полученную дробь.

n : X

a/b

= n :

X ⋅ b + a/b

= n ⋅

b/X ⋅ b + a

n ⋅ b/X ⋅ b + a

Примеры задач

Задание 1

Разделите число 6 на дробь

7/12

Решение

6 :

7/12

= 6 ⋅

12/7

6 ⋅ 12/7

72/7

=10

2/7

Задание 2

Разделите число 3 на дробь 2

7/11

Решение

Сначала представим смешанную дробь в виде неправильной, затем выполним деление.

3 : 2

7/11

= 3 :

2 ⋅ 11 + 7/11

= 3 :

29/11

= 3 ⋅

11/29

3 ⋅ 11/29

33/29

= 1

4/29

Как перевести обыкновенную дробь в десятичную?

Что такое дробь: понятие

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 5/9 или (1,5 — 0,2)/15.

Алгебраические — состоят из переменных. Например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.

Приходите закреплять теорию на увлекательных задачках с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Что такое десятичная дробь

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

0,600 = 0,6
21,10200000 = 21,102

Основные свойства десятичных дробей

Дробь не имеет значения, при условии, если делитель равен нулю.

Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.

Две дроби a/b и c/d называются равными, если a * d = b * c.

Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Как перевести обычную дробь в десятичную

Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.

Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей:

Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:

Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.

Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.

А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.

Способ 1. Превращаем знаменатель в 10, 100 или 1000

Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т. д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.

Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.

Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.

Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.

Еще пример:

Способ 2. Делим числитель на знаменатель

Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.

Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.

Делим столбиком числитель на знаменатель — преобразование готово:

Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).

Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:

Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Еще алгоритм: как преобразовать десятичную дробь в обыкновенную

Посчитать, сколько цифр стоит после запятой. Например, у дроби 0,25 таких цифр две, а у 1,0211 — четыре. Обозначим это количество буквой n.

Переписать исходное число в виде дроби вида a/10ⁿ, где a — это все цифры исходной дроби, а n — количество цифр после запятой, которое мы посчитали в первом шаге. Другими словами, нужно разделить цифры исходной дроби на единицу с n нулями.

Сократить полученную дробь, если это возможно.

Вот и всё! Эта схема значительно проще и быстрее. Проверим:

Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5. Поэтому n = 2. Если убрать запятую и нули слева, то получим число 55. Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит 100. Остается сократить числитель и знаменатель. Вот и ответ: 11/20.

Как перевести периодическую десятичную дробь в обыкновенную

Любую бесконечную периодическую десятичную дробь можно перевести в обыкновенную. Разберем на примерах.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

Вот и ответ!

Если период дроби отличен от нуля — рассматриваем периодическую часть как сумму членов геометрический прогрессии, которая убывает. Поясним на примере:

0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q).

Переведем периодическую дробь 0,(7) в обыкновенную.

Запишем: 0,(7) = 0,7 + 0,07 + 0,007 + .. Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1. Применим формулу: 0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 — 0,1) = 0,7/0,9 = 7/9.

Смешанные числа

В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.

Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.

Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.

Сложение целого числа и правильной дроби

Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:

А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.

Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.

Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.

Значит значение выражения равно

Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:

Пример 2. Найти значение выражения

Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:

Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:

Пример 3. Найти значение выражения

Можно записать вместе число 2 и дробь , но этот ответ не будет окончательным, поскольку в дроби можно выделить целую часть.

Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:

Теперь в главном выражении вместо дроби запишем смешанное число

Получили новое выражение . В этом выражении смешанное число запишем в развёрнутом виде:

Применим сочетательный закон сложения. Сложим две двойки, получим 4:

Теперь свернём полученное смешанное число:

Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:

Сложение смешанных чисел

Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.

Для начала запишем смешанные числа в развёрнутом виде:

Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:

Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:

Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:

Получили . Теперь в главном выражении заменяем дробные части на полученную дробь

Теперь свернем полученное смешанное число:

Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:

Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:

Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.

Пример 2. Найти значение выражения

Запишем смешанные числа в развёрнутом виде:

Сгруппируем целые и дробные части по отдельности:

Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8

Теперь вычислим дробные части:

Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число

Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:

Сложим целые части. Получаем 9

Сворачиваем готовый ответ:

Таким образом, значение выражения равно .

Полное решение этого примера выглядит следующим образом:

Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:

Чтобы сложить смешанные числа, надо:

привести дробные части этих чисел к общему знаменателю;
отдельно выполнить сложение целых и дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.

Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.

Пример 3. Найти значение выражения

Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:

Сложение целого и смешанного числа

Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:

Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .

Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:

Пример 2. Найти значение выражения

В этом примере, как и в предыдущем, нужно сложить целые части:

Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:

Вычитание дроби из целого числа

Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:

Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:

Пример 2. Найти значение выражения .

Представим число 2 в виде дроби , и выполним вычитание дробей с разными знаменателями:

Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:

Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.

Представим, что число 3 это три пиццы:

Нужно вычесть из них . Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось (две целых и две трети пиццы).

Чтобы убедиться в правильности решения, можно найти значение выражения обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:

Пример 3. Найти значение выражения

Представим число 3 в виде дроби .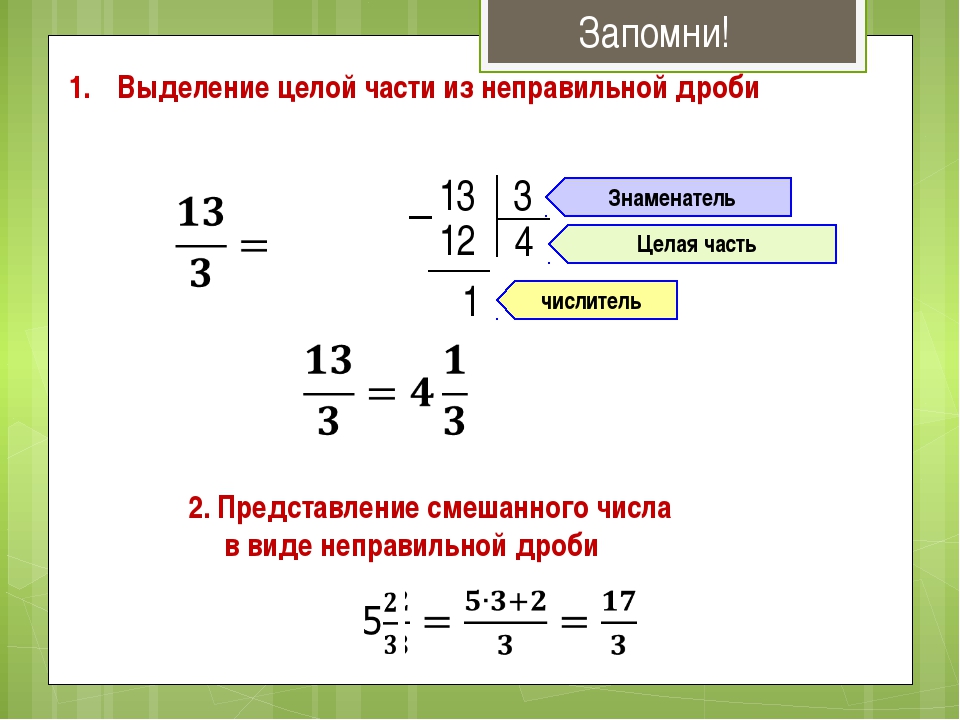 Затем выполним вычитание дробей с разными знаменателями:

Вычитание смешанного числа из целого числа

Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .

Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:

Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:

Пример 2. Найти значение выражения

Представим 6 в виде дроби , а смешанное число , в виде неправильной дроби. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:

Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.

К примеру, если нужно быстро найти значение выражения , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:

Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.

Вычитание смешанных чисел

Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:

Чтобы решить этот пример, нужно смешанные числа и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:

Если от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:

Пример 2. Найти значение выражения

Переводим смешанные числа и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:

К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.

А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.

Умножение целого числа на дробь

Любое целое число можно умножить на дробь. Для этого достаточно умножить это число на числитель дроби.

Например, умножим число 5 на дробь . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:

Пример 2. Найти значение выражения

Умножим число 3 на числитель дроби

В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.

Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:

Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:

Пример 3. Найти значение выражения

Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:

Пример 4. Найти значение выражения

Умножим число 3 на числитель дроби

Умножение смешанного числа на дробь

Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.

Пример 1. Найти значение выражения

Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на

Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:

Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:

Поэтому значение выражения было равно 1

Умножение смешанных чисел

Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:

Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:

Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.

С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:

Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:

Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:

А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:

Деление целого числа на дробь

Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.

Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь — делитель.

Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь

Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».

Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:

Поэтому значение выражения равно 6.

Пример 2. Найти значение выражения

Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь

Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим

Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».

Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам.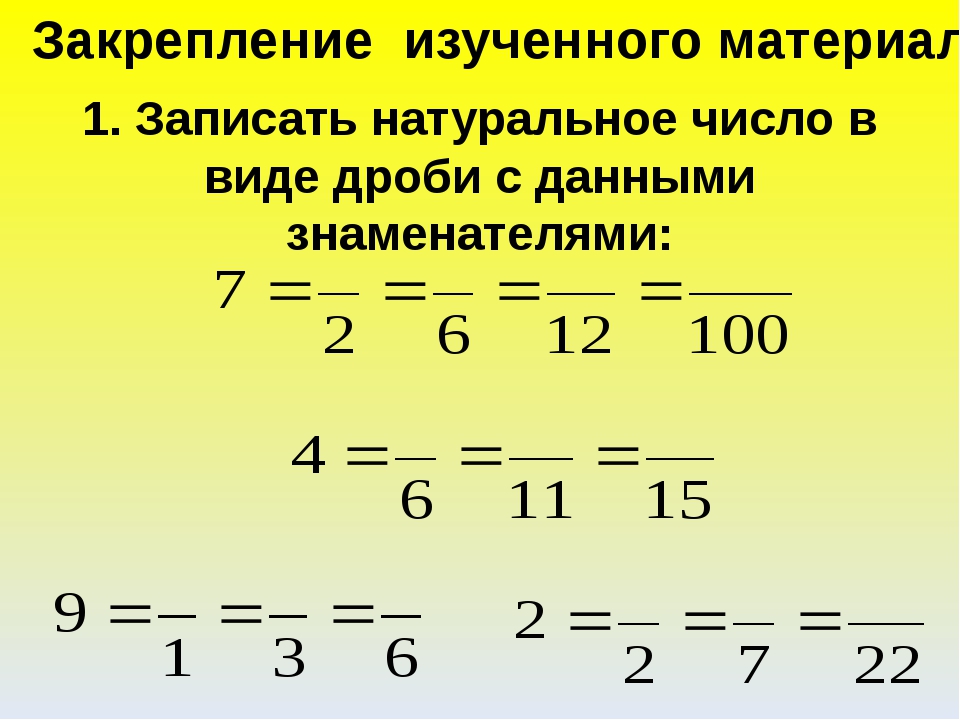 Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения равно

Пример 3. Найти значение выражения

Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на

Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:

А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .

То есть пиццы содержится в пяти целых пиццах раза.

Давайте нащупаем в пяти пиццах два раза по

Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:

Поэтому значение выражения равно

Деление дроби на целое число

Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.

Пример 1. Разделим дробь на число 2

Чтобы разделить дробь на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь

Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь

Пример 3. Найти значение выражения

Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь

Деление целого числа на смешанное число

Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .

Чтобы решить этот пример, нужно делитель перевести в неправильную дробь.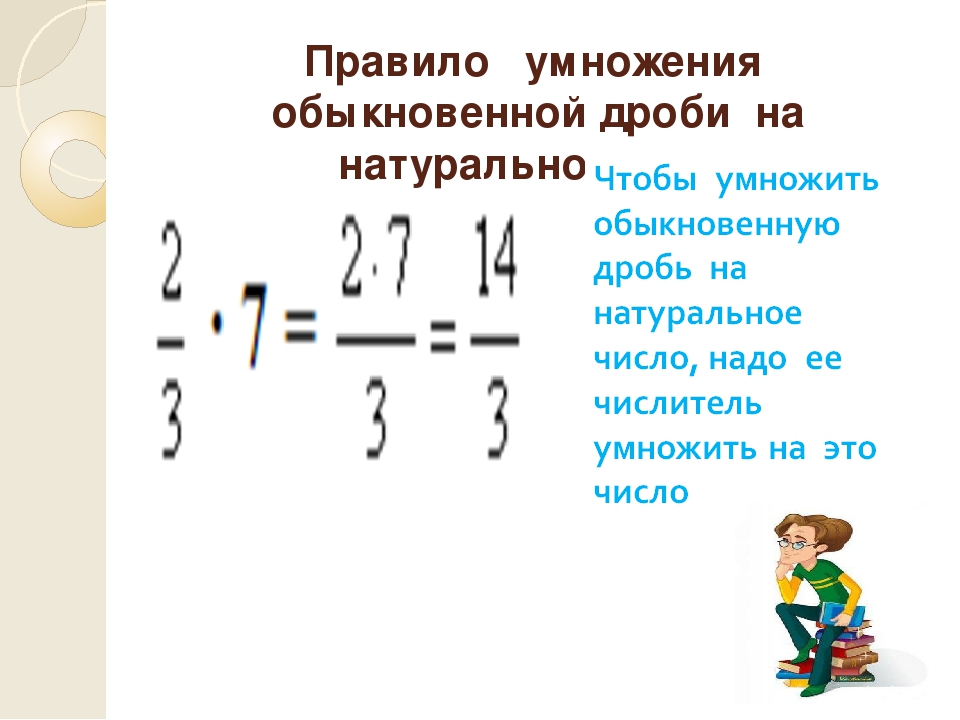 Затем умножить число 2 на дробь, обратную делителю.

Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь

Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Переводим делитель в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь

Сначала мы получили ответ , затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ

Деление смешанного числа на целое число

Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.

Например, разделим на 2. Чтобы решить этот пример, нужно делимое перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.

Переведём смешанное число в неправильную дробь, получим .

Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь

Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Переведём делимое в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .

Деление смешанных чисел

Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.

Пример 1. Найти значение выражения

Переведём смешанные числа в неправильные дроби. Получим следующее выражение:

Как решать дальше мы уже знаем. Первую дробь нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь .

Дорешаем данный пример до конца:

Допустим, имеются две целые и половина пиццы:

Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:

Пример 2. Найти значение выражения

Переведём смешанные числа в неправильные дроби. Получим следующее выражение:

Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь

Сначала мы получили дробь. Эту дробь мы сократили на 9. В результате получили дробь , но такой ответ нас тоже не устроил и мы выделили в дроби целую часть. В результате получили окончательный ответ .

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Задание 2. Найдите значение выражения:

Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Калькулятор онлайн — Сокращение дробей

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби $ \frac{m}{n} $, где числитель m — делимое, а знаменатель п — делитель:
$ m:n = \frac{m}{n} $

Верны следующие правила:

Чтобы получить дробь $ \frac{m}{n} $, надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь $ \frac{m}{n} $, надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
$ \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} $

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
$ \large \frac{a}{b} = \frac{a : m}{b : m} $
Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь $ \frac{3}{4} $ означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, $ \frac{5}{5} $ или $ \frac{8}{5} $? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями.

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:
$ 5:3 = 1\frac{2}{3} $ : 1 — целая часть, а $ \frac{2}{3} $ — дробная часть.

Если числитель дроби $ \frac{a}{b} $ делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
$ \large \frac{a}{b} : n = \frac{a:n}{b} $

Если числитель дроби $ \frac{a}{b} $ не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
$ \large \frac{a}{b} : n = \frac{a}{bn} $

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму $ \frac{2}{7} $ и $ \frac{3}{7} $. Легко понять, что $ \frac{2}{7} + \frac{2}{7} = \frac{5}{7} $

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
$ \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} $

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
$ \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} $

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как $ 2\frac{2}{3} $, называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число $ \frac{2}{3} $ — ее дробной частью. Запись $ 2\frac{2}{3} $ читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: $ \frac{8}{3} $ и $ 2\frac{2}{3} $. Они выражают одно и то же дробное число, т.е $ \frac{8}{3} = 2 \frac{2}{3} $

Таким образом, неправильная дробь $ \frac{8}{3} $ представлена в виде смешанной дроби $ 2\frac{2}{3} $. В таких случаях говорят, что из неправильной дроби выделили целую часть.

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
$ \frac{8}{9}-\frac{1}{9} = \frac{7}{9} $ так как $ \frac{7}{9}+\frac{1}{9} = \frac{8}{9} $

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
$ \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} $

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
$ \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} $

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь $ \frac{2}{3} $ и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь $ \frac{3}{2} $. Эту дробь называют обратной дроби $ \frac{2}{3} $.

Если мы теперь «перевернем» дробь $ \frac{3}{2} $, то получим исходную дробь $ \frac{2}{3} $. Поэтому такие дроби, как $ \frac{2}{3} $ и $ \frac{3}{2} $ называют взаимно обратными.

Взаимно обратными являются, например, дроби $ \frac{6}{5} $ и $ \frac{5}{6} $, $ \frac{7}{18} $ и $ \frac{18}{7} $.

С помощью букв взаимно обратные дроби можно записать так: $ \frac{a}{b} $ и $ \frac{b}{a} $

Понятно, что произведение взаимно обратных дробей равно 1. Например: $ \frac{2}{3} \cdot \frac{3}{2} =1 $

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
$ \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} $

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

что это значит в математике, правила, как решать, формулы и примеры

Что такое смешанная дробь

Определение

Число, содержащее в себе целую и дробную части, называется смешанной дробью.

По сути, данное понятие представляет собой сумму целого числа и правильной дроби:

$a\frac bc\;=\;a+\frac bc$

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Пример:

$7\frac34\;=\;7+\frac34$

Превращение смешанной дроби в неправильную

Любое смешанное число можно преобразовать в неправильную дробь. Для этого необходимо к произведению целой части и знаменателя дробной части прибавить числитель. Полученная сумма будет числителем неправильной дроби, а знаменатель останется прежним.

Преобразование смешанной дроби в неправильную можно записать в виде формулы:

$a\frac bc\;=\;\frac{a\times c+b}c$

Пример:

$15\frac89\;=\;\frac{15\times9+8}9\;=\;\frac{143}9$

Выполнение действий со смешанными дробями, формулы и примеры

Сложение

Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.

Формульное выражение сложения смешанных чисел:

$a\frac bc+d\frac ef=\left(a+d\right)+\left(\frac bc+\frac ef\right)$

Пример:

$2\frac13+5\frac47\;$

Вычисляем наименьший общий знаменатель дробных слагаемых:

3×7=21

$2\frac13+5\frac47=2+5+\frac13+\frac47\;=7+\frac7{21}+\frac{12}{21}=7+\frac{7+12}{21}=7\frac{19}{21}$

Вычитание

Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.

Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:

$a\frac bc-d\frac ef=\left(a+\frac bc\right)-\left(d+\frac ef\right)\;=\left(a-d\right)+\left(\frac bc-\frac ef\right)$

В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:

$a\frac bc-d\frac ef=\left(\left(a-d\right)-\frac ef\right)+\frac bc$

Пример:

$13\frac38-6\frac12$

Для решения этого выражения найдем наименьший общий знаменатель:

8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.

$13\frac38-6\frac12=13\frac38-6\frac48=\left(12+1+\frac38\right)-6\frac48=\left(12+\frac{1\times8+3}8\right)-6\frac48=12\frac{11}8-6\frac48=\left(12-6\right)+\left(\frac{11}8-\frac48\right)=6+\frac{11-4}8=6\frac78$

Умножение и деление

Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.

Формула умножения смешанных чисел выглядит так:

$a\frac bc\times d\frac ef=\frac{a\times c+b}c\times\frac{d\times f+e}f=\frac{\left(a\times c+b\right)\times\left(d\times f+e\right)}{c\times f}=\frac{\left(ac+b\right)\left(df+e\right)}{cf}$

Формула деления смешанных дробей:

$a\frac bc\div d\frac ef=\frac{a\times c+b}c\div\frac{d\times f+e}f=\frac{a\times c+b}c\times\frac f{d\times f+e}=\frac{\left(a\times c+b\right)\times f}{c\times\left(d\times f+e\right)}=\frac{f\left(ac+b\right)}{c\left(df+e\right)}$

Пример 1:

$5\frac2{19}\times2\frac79=\frac{5\times19+2}{19}\times\frac{2\times9+7}9=\frac{97}{19}\times\frac{25}9=\frac{97\times25}{19\times9}=\frac{2425}{171}=14\frac{31}{171}$

Пример 2:

$4\frac23\div3\frac57=\frac{4\times3+2}3\div\frac{3\times7+5}7=\frac{14}3\div\frac{26}7=\frac{14}3\times\frac7{26}=\frac{14\times7}{3\times26}=\frac{98}{78}=\frac{98\div2}{78\div2}=\frac{49}{39}=1\frac{10}{39}$

При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно.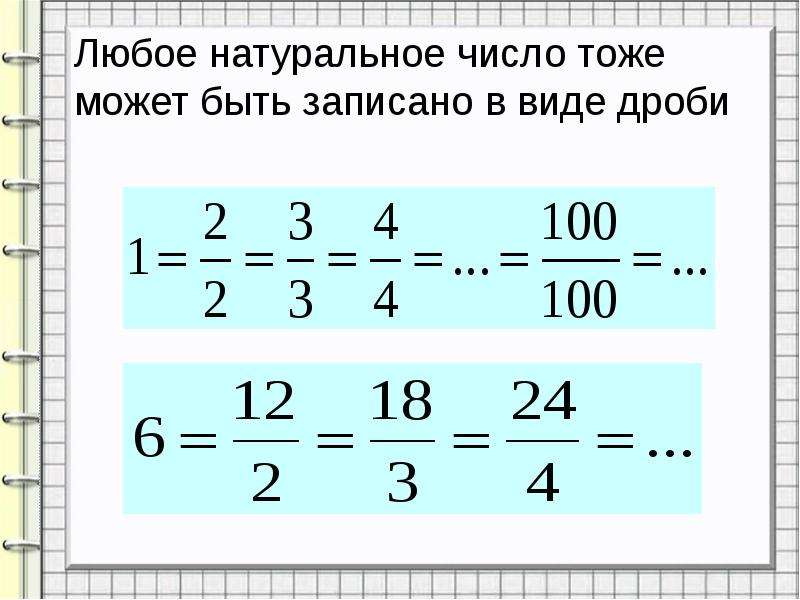 Такого рода вычисления производятся с помощью распределительного закона умножения.

Пример 3:

$3\frac56\times4=\left(3+\frac56\right)\times4=3\times4+\frac56\times4=12+\frac{5\times4}6=12+\frac{20\div2}{6\div2}=12+\frac{10}3=12+3\frac13=15\frac13$

Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.

Пример 4:

$5\div3\frac27=\frac51\div\frac{3\times7+2}7=\frac51\div\frac{23}7=\frac51\times\frac7{23}=\frac{5\times7}{1\times23}=\frac{35}{23}=1\frac{12}{23}$

Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.

Пример 5:

$\frac34\div6\frac12=\frac34\div\frac{6\times2+1}2=\frac34\div\frac{13}2=\frac34\times\frac2{13}=\frac{3\times1}{2\times13}=\frac3{26}$

Как преобразовать смешанные числа в целые

Технически смешанное число, такое как 2 и 3/4, уже содержит целое число — в данном случае 2. (Целые числа — это числа, с помощью которых вы научились считать: ноль, один, два, три и так далее, а в смешанном числе они всегда пишутся слева от дроби.) Преобразование смешанного числа в целое не имеет особого смысла, потому что целое число уже есть. Но есть два случая, в которых вы могли бы оправдать это преобразование: если дробная часть смешанного числа является неправильной дробью, вы можете извлечь из нее другое смешанное число или вы можете преобразовать смешанное число в целое число с десятичной дробью. после него вместо дроби.

Преобразование смешанных чисел в десятичные

Если вам нужно преобразовать смешанное число в целое число, за которым следует десятичная дробь, просто сохраните целое число, затем выполните деление, указанное дробью, чтобы выяснить, что идет вправо десятичной запятой. Используя пример 2 и 3/4, вы должны оставить 2, а затем разделить 3 на 4, чтобы выяснить, что идет справа от десятичной точки: 0,75, что дает окончательный ответ 2,75.

Другой сценарий для нахождения целых чисел в смешанных числах

При использовании предыдущего смешанного числа в качестве примера — 2 и 3/4 — числитель дроби или числа наверху меньше знаменателя, число внизу дроби.Это означает, что 3/4 — правильная дробь, или, другими словами, она представляет собой количество меньше единицы, и в ней больше нет целых чисел. Но если после 2 следует неправильная дробь с большим числом в числителе, чем в знаменателе, то иногда из этой дроби можно извлечь целое число.

Извлечение целого числа из неправильной дроби

Вместо 2 и 3/4 вы можете оказаться с такими числами, как 2 и 12/4. Поскольку дробная часть этого смешанного числа является неправильной дробью, ее значение больше единицы, это позволяет вам извлечь из нее смешанное число, равное единице (или, возможно, большее). Просто вычислите деление, представленное дробью: 12 ÷ 4 = 3, и у вас останется целое число вместо дроби 12/4. Поскольку смешанное число 2 и 12/4 означает 2 + 12/4, вы можете переписать смешанное число как 2 + 3 (заменив 3 на дробь 12/4) и упростить это до 5 в качестве окончательного ответа.

Неправильная дробь с остатком

В некоторых случаях неправильная дробь не сводится к истинному целому числу и вместо этого содержит оставшийся дробный остаток.Рассмотрим смешанные числа 2 и 13/4. Если вы выполните деление, представленное этой дробью, 13 ÷ 4, чтобы найти, что у вас осталось целое число 3 плюс остаток, выраженный в виде дроби 1/4 или десятичной дроби 0,25. Помните, что соединяйте каждый термин в смешанном количестве с другими добавочными знаками, чтобы сложить все термины вместе. 2 + 3 + 1/4 и упростите результат до нового смешанного числа: 5 и 1/4. Хотя в результате у вас все еще остается смешанное число, можно сказать, что вы изменили часть дроби на целое число.

Правильные дроби | Неправильные дроби

Из неправильной фракции в смешанное число

Разделите числитель на знаменатель.
Например: Преобразовать 5/4 в смешанное число
`1`
`4` `5`
`4`
`1`
Используйте частное как целое число.
в нашем примере частное 1.
Используйте остаток как числитель правильной дроби.
в нашем примере остаток равен 1.
Знаменатель останется прежним.
в нашем примере знаменатель равен 4.
Следовательно, требуемое смешанное число — `1 1 / 4`

Смешанное число в неправильную фракцию

Умножьте целое число на знаменатель.
Например: Преобразовать 2 1/4 в неправильную дробь
В нашем примере целое число — 2 , а знаменатель — 4
.
, следовательно, 2 x 4 = 8

Добавьте произведение к числителю правильной дроби. Сумма является числителем неправильной дроби.
Здесь числитель 1
сложив числитель и произведение получим, числитель
= 8 + 1 = 9

Знаменатель останется прежним.Знаменатель
= 4
Следовательно, неправильная дробь — `9/4`

Как вычитать дроби из целых чисел — Видео и стенограмма урока
Целые числа минус дроби
Давайте сформулируем нашу математическую задачу:
3 — 1/16 =?
Чтобы решить эту проблему, мы будем использовать следующие шаги.
Шаг 1: Преобразуйте целое число в дробь.
Любое целое число можно преобразовать в дробь, используя целое число в качестве числителя и число 1 в качестве знаменателя.В нашем примере три — это целое число, что дает нам 3/1. Теперь имеем:
3/1 — 1/16 =?
Шаг 2. Найдите общий знаменатель.
Другими словами, нижнее число двух дробей должно быть одинаковым. Здесь мы изменим знаменатель в 3/1 на 16, умножив знаменатель на 16. Когда мы это сделаем, нам также придется умножить числитель на 16. На этом этапе очень важно всегда помнить, что то, что мы делаем со знаменателем, мы должны делать и с числителем.Итак, 3 * 16 = 48. Теперь имеем:
48/16 — 1/16 =? (как показано на изображении для шага 2)
Шаг 2
Прежде чем мы продолжим, важно понять, что 48/16 — это просто еще один способ записать число 3 (48/16 = 3).
Шаг 3: Вычтите числители (но не знаменатели).
48/16 — 1/16 = 47/16
Пробежка на 47/16 миль каждый день не так уж и впечатляет, но 47, разделенное на 16, равно 2.9, что довольно близко к 3 милям.
Вот еще пара практических задач:
Не забудьте преобразовать целое число в дробь, знаменатель которой совпадает с дробью. Для первой задачи замените 4 на дробь, сделав 4 числителем и 1 знаменателем: 4/1. Теперь превратите 4/1 в дробь со знаменателем 8, умножив знаменатель и числитель на 8. Помните, 32/8 = 4. Теперь вычтите числители:
32/8 — 5/8 = 27/8
Во второй задаче заменим 10 на дробь с тем же знаменателем, что и дробь 3/4.Здесь 10 = 10/1. Затем сделайте знаменатель 4 (не забудьте также умножить числитель): 40/4. Теперь вычтите:
40/4 — 3/4 = 37/4
Целые числа минус смешанные числа
Теперь мы обсудили, как вычитать дроби из целых чисел. Давайте вычтем смешанные числа из целых чисел. Допустим, вы изменили маршрут бега, вычтя 1 и 5/6 из бега на 3 мили. Как далеко ты сейчас бежишь? Зададим нашу задачу:
3 — 1 и 5/6 =?
Шаг 1. Измените целое число на смешанное.
Здесь 3 = 2 и 6/6. Помните, что 6/6 — это то же самое, что 1, поэтому 2 и 6/6 = 3. Мы выбрали 6/6, потому что нам нужен тот же знаменатель, что и дробь.
Шаг 2: Вычтите недробные части смешанных чисел.
В задаче 2 и 6/6 — 1 и 5/6. Здесь 2 — 1 = 1.
Шаг 3: Вычтите дроби.
6/6 — 5/6 = 1/6 (помните, что мы вычитаем только числитель)
Наш ответ — 1 и 1/6. Ух ты, правда, сейчас не так уж и далеко, не так ли?
Давайте попробуем еще две практические задачи:
6 — 4? знак равно
9 — 8¼ =?
В первой задаче замените целое число на смешанное:
6 = 5 и 8/8 (знаменатель совпадает со знаменателем смешанного числа).
Это дает нам:
5 и 8/8 — 4 и 1/8 =?
Сначала вычтите целые числа:
5 — 4 = 1
Теперь вычтите дробную часть:
8/8 — 1/8 = 7/8
Итак, наш ответ — 1 и 7/8.
Во второй задаче замените 9 на смешанное число с тем же знаменателем, что и дробь в смешанном числе. Здесь 9 = 8 и 4/4. Это дает нам:
8 и 4/4 — 8 и 1/4
Сначала вычтите целые числа:
8-8 = 0
Теперь вычтите дроби:
4/4 — 1/4 = 3 / 4
Это дает нам 0 3/4 или только 3/4.
Краткое содержание урока
Теперь, когда вы являетесь экспертом как в вычислении дробей и смешанных чисел, так и в их вычитании из целых чисел, все готово! Перед тем, как вы снова отправитесь на пробежку, почему бы нам не пройтись по основным моментам урока.
Целые числа — это числа без дробей или десятичных знаков и не отрицательные, тогда как дроби являются частями целого числа. Дроби содержат числителей (верхние числа) и знаменателей (нижние числа).Наконец, смешанных чисел представляют собой комбинацию двух. Они содержат целое число и дробь.
При вычитании дробей из целых чисел преобразуйте целое число в дробь, затем составьте общий знаменатель и вычтите два числителя.
При вычитании смешанных чисел из целых чисел замените целое число на смешанное, убедившись, что дроби имеют одинаковый общий знаменатель. Наконец, вычтите целые числа друг из друга и числитель дробей друг из друга.
Теперь, когда мы закончили наш обзор, наслаждайтесь пробежкой!
Как складывать дроби и смешанные дроби
Дроби являются частью повседневной жизни. Их используют во всех сферах, от статистики до кулинарии. От оценки количества осадков до определения времени — они являются мерой различных величин, связанных с любым измеряемым веществом.
Проще говоря, дроби являются частью поровну разделенного сегмента. В более точных математических терминах дробь используется для представления равных частей коллекции.
Например, давайте представим, что мальчик ест 3/4 часть торта. Это означает, что торт делится на четыре равные части, и мальчик съедает три части или порции торта.
Как представлены дроби
Дробь обычно представлена двумя числами, разделенными линией. Число, которое написано над линией, называется числителем. Знаменатель — это число под чертой. Знаменатель используется для представления общего количества равных частей коллекции.Числитель используется для представления частей или частей коллекции.
Смешанные фракции
Смешанную дробь также иногда называют смешанным числом. Смешанная дробь состоит из двух частей: целой части и дробной части, т. Е. 3 1/4.
Неправильная дробь образуется, если число в знаменателе меньше числа в числителе, то есть 3/4.
Обычно неправильную дробь переводят в смешанную. Например, 23/4 — неправильная дробь.При преобразовании в смешанную фракцию получается 5 ¾.
шагов для преобразования неправильной фракции в смешанную фракцию
Возьмите числитель дроби (число над чертой) на и разделите его на знаменатель неправильной дроби (число под чертой).
Знаменатель считается делителем, а числитель — делимым.
Частное деления, выполненного на «этапе 1», записывается как целочисленная часть смешанной дроби.
Запишите делитель в качестве знаменателя, а остаток в качестве числителя смешанной дроби.
Пример
Преобразовать 9/4 в смешанную фракцию. Вы можете преобразовать неправильную дробь 9/4 в смешанную, выполнив следующие действия.
Числитель здесь 9, а знаменатель 4. Итак, разделив 9 на 4
После деления 9 на 4 получается 2 в качестве частного.
При делении 9 на 4 получается остаток 1.
Полученная смешанная дробь будет 2 ¼.
шагов для преобразования смешанной фракции в неправильную фракцию
Умножьте знаменатель на целое число, затем сложите полученное произведение с числителем.
Запишите ответ, полученный на шаге 1, в числитель дроби. Знаменатель оставьте неизменным.
Пример
Давайте рассмотрим смешанную дробь, 2 ¾, и преобразуем ее в неправильную дробь. Чтобы разбить это, знаменатель смешанной дроби равен 4, а числитель равен 3.Целая числовая часть смешанной дроби равна 2. Выполните следующие действия:
Умножьте знаменатель 4 на целое число 2. Результат: 8. Затем к 8 прибавьте числитель 3.
Запишите 11 в числитель дроби. Оставьте тот же знаменатель. В результате получается неправильная дробь 11/4.
Добавление фракции и смешанной фракции
Сложение дробей со смешанными дробями — это, по сути, нахождение суммы обеих дробей. Шаги, чтобы найти добавление смешанной фракции к фракции, обсуждаются ниже:
Преобразование смешанных фракций в неправильную дробь.
Проверьте знаменатели дроби и найдите НОК (наименьшее общее кратное).
Разделите результат НОК на знаменатель каждой дроби и умножьте числитель на частное.
Сложите сумму произведения и поместите НОК в знаменатель.
[(Числитель дроби 1 * (НОК / знаменатель дроби 1)] + [Числитель дроби 2 * (НОК / знаменатель дроби 2)] / НОК
Пример
Нахождение суммы ¼ + 3 ½.Вы можете сложить две дроби, ¼ и 3 ½, выполнив следующие действия:
Есть только одна смешанная дробь из двух операндов, равных 3 ½. После преобразования 3 ½ в неправильную дробь результат становится 7/2.
Знаменатели двух дробей — 2 и 4. НОК 2 и 4 равно 4.
Результатом НОК будет 4. Разделите НОК со знаменателем ¼, так что 4 разделится на знаменатель 4. В результате получится 1, которую вы умножите на числитель, 1, в результате получится сумма 1.
Аналогично, тот же шаг необходимо выполнить во второй дроби. Сумма будет равна 14. Наконец, вы можете сложить сумму произведения и поместить НОК в знаменатель.
([Числитель дроби 1 * (НОК / знаменатель дроби 1)] + [Числитель дроби 2 * (НОК / знаменатель дроби 2)]) / НОК
= ([1 * (4/4)] + [7 * (4/2)]) / 4
= (1 + 14) / 4 = 15/4
После сложения результат будет 15/4, что является неправильной дробью.Однако его можно было преобразовать в смешанную фракцию. Действия по преобразованию неправильной фракции в смешанные описаны выше.
Заключение
Дроби очень важны не только для математики, но и в нашей повседневной жизни. Вычисление с использованием дробей требуется практически во всех областях, поэтому понимание того, как преобразовывать смешанные и неправильные дроби, сэкономит ваше время и поможет обеспечить точность результатов.
Оставьте первый комментарий ниже.
Классификация действительных чисел — ChiliMath
Схема «стопки воронок» ниже поможет нам легко классифицировать любые заданные действительные числа. Но сначала нам нужно описать, какие элементы входят в каждую группу чисел. Каждая группа или набор чисел представлены воронкой.
Описание каждого набора действительных чисел
Натуральные числа (также известные как счетные числа) — это числа, которые мы используем для счета. Он начинается с 1, затем с 2, затем с 3 и так далее.
Целые числа представляют собой небольшую «модернизацию» натуральных чисел, потому что мы просто добавляем элемент ноль к текущему набору натуральных чисел.Думайте о целых числах как о натуральных числах вместе с нулем.
Целые числа включают все целые числа вместе с «отрицательными» натуральными числами.
Рациональные числа — это числа, которые можно выразить как отношение целых чисел. Это означает, что если мы можем записать данное число в виде дроби, где числитель и знаменатель являются целыми числами; тогда это рациональное число.
Условно мы можем записать рациональное число как:
Внимание: знаменатель не может быть равен нулю.
Рациональные числа могут также отображаться в десятичной форме . Если десятичное число завершается или повторяется, то его можно записать как дробь с целым числителем и знаменателем. Таким образом, это тоже рационально.
Иррациональные числа — это все числа, которые при записи в десятичной форме не повторяются и не заканчиваются.
Реальные числа включают как рациональные, так и иррациональные числа. Помните, что под набором рациональных чисел у нас есть подкатегории или подмножества целых чисел, целых чисел и натуральных чисел.
Классификация примеров действительных чисел
Пример 1 : Натуральное число также является целым числом.
Набор целых чисел включает в себя ноль и все натуральные числа. Это верное заявление.
Пример 2 : Целое число всегда является целым числом.
Набор целых чисел состоит из числа ноль, натуральных чисел и «минусов» натуральных чисел. Это означает, что некоторые целые числа являются целыми числами, но не все.
Например, — 2 — целое, а не целое число. Это утверждение неверно.
Пример 3 : Каждое рациональное число также является целым.
Слово «каждый» означает «все». Можете ли вы придумать рациональное число, не являющееся целым? Достаточно одного контрпримера, чтобы показать, что это утверждение неверно.
Дробь \ Large {1 \ over 2} является примером рационального числа, которое НЕ является целым. Итак, это утверждение неверно.
Пример 4 : Каждое целое число является рациональным числом.
Это верно, потому что каждое целое число можно записать как дробь со знаминателем 1.
Пример 5 : Каждое натуральное число представляет собой целое, целое и рациональное число.
Рассматривая приведенные выше описания, можно сказать, что натуральные числа находятся в наборах целых, целых и рациональных чисел. Это делает его истинным заявлением.
Мы также можем использовать приведенную выше схему воронок, чтобы ответить на этот вопрос. Если мы наливаем воду в «воронку натуральных чисел», вода также должна течь через все воронки под ней.Таким образом, проходя по воронкам целых чисел, целых чисел и рациональных чисел.
Пример 6 : Каждое целое число является натуральным, целым и рациональным числом.
Используя ту же аналогию с «воронкой»; если мы нальем немного жидкости в воронку целых чисел, она должна пройти через воронки целых и рациональных чисел, пока спускается вниз. Поскольку последовательность натуральных чисел находится над набором целых чисел, с которого мы начали, мы не можем включить эту воронку в группу.
Это ложное утверждение, поскольку целые числа принадлежат множеству целых и рациональных чисел, но не множеству натуральных чисел.
Пример 7 : Классифицируйте число ноль, 0.
Определенно не натуральное число, но целое, целое, рациональное и действительное число. Может быть неочевидно, что ноль также является рациональным числом. Однако запись его в виде дроби с ненулевым знаменателем ясно показывает, что это действительно рациональное число.
Пример 8 : Классифицируйте число 5.
Это натуральное или счетное число, целое число и целое число. Поскольку мы можем записать его в виде дроби со знаминателем 1, то есть \ Large {5 \ over 1}.
Это также делает его рациональным числом. И конечно, это реальная цифра.
Пример 9 : Классифицируйте число 0,25.
Данное десятичное число завершается, и поэтому мы можем записать его в виде дроби, которая является характеристикой рационального числа.Это число также является действительным числом.
\ Large {0,25 = {{25} \ over {100}} = {1 \ over 4}}
Пример 10 : Классифицируйте число {\ rm {2}} {1 \ over 5}.
Мы можем переписать эту смешанную дробь как неправильную дробь, чтобы было ясно, что у нас есть отношение двух целых чисел.
\ Large {{\ rm {2}} {1 \ over 5} = {{11} \ over 5}}
Это действительное и рациональное число.
Пример 11 : Классифицируйте число {\ rm {5.241879132…}}.
Десятичное число не является завершающим и неповторяющимся, что делает это число иррациональным. Конечно, любое иррациональное число также является действительным числом.
Пример 12 : Классифицируйте число 1.7777….
Поскольку десятичная дробь повторяется, получается рациональное число. Любое рациональное число также является действительным числом.
Пример 13 : Классифицируйте число \ sqrt 2.
Это иррациональное число, потому что в десятичной форме оно не завершается и не повторяется.Это тоже реальное число.
Пример 14 : Классификация числа — \ sqrt {16}.
Во-первых, нам нужно упростить это радикальное выражение, которое дает нам — \ sqrt {16} = — \, 4. Число — \, 4 — целое, рациональное и действительное число.
Пример 15 : Классифицируйте номер — 8.123123….
Десятичное число не является окончательным, однако число 123 после десятичной точки продолжает повторяться.Мы можем переписать десятичное число с «полосой» поверх повторяющихся чисел.
Это делает его рациональным числом. Не забывайте, что это тоже реальное число.
Практика с рабочими листами
Умножение дроби на целое число
Чтобы умножить дробь на целое число, помните, что умножение — это повторное сложение.
Пример 1:
Умножить 1 7 ⋅ 3 .
Запишите умножение в виде сложения. Добавлять 1 7 три раза.
1 7 ⋅ 3 знак равно 1 7 + 1 7 + 1 7
Теперь нам просто нужно добавить дроби с одинаковыми знаменателями. Знаменатели оставьте неизменными, а числители сложите.
знак равно ( 1 + 1 + 1 ) 7 знак равно 3 7
Пример 2:
Умножить 5 ⋅ 3 16 .
5 ⋅ 3 16 знак равно 3 16 + 3 16 + 3 16 + 3 16 + 3 16 знак равно 5 ⋅ 3 16 знак равно 15 16
Другой способ подумать об этом — переписать целое число в виде дроби со знаменателем 1 .
5 ⋅ 3 16 знак равно 5 1 ⋅ 3 16
Затем умножьте числители а также знаменатели , согласно обычным правилам для умножение дробей .
знак равно 5 ⋅ 3 1 ⋅ 16 знак равно 15 16
В некоторых случаях ваш ответ может быть больше, чем 1 , поэтому вы захотите переписать его как смешанное число .Вам также может потребоваться уменьшить фракцию чтобы получить его в простейшем виде.
Пример 3:
Умножить 1 4 ⋅ 10 .
1 4 ⋅ 10 знак равно 10 4
И числитель, и знаменатель имеют общий множитель: 2 . Разделите оба на 2 .
знак равно 5 2
Перепишите эту неправильную дробь как смешанное число.
знак равно 2 1 2
Иллюстративная математика
Задача
Бен записал смешанное число как дробь 7 $ \ frac {1} {3} $. Вот его работа:
$$ \ begin {align} 7 \ frac {1} {3} & = \ frac {7} {1} + \ frac {1} {3} & \ text {(Шаг 1)} \\ & = \ frac {(7 \ times 3) +1} {3} & \ text {(Шаг 2)} \\ & = \ frac {21 + 1} {3} & \ text {(Шаг 3)} \\ & = \ frac {22} {3} & \ text {(Шаг 4)} \ end {align} $$
Объясните, что Бен делал на каждом этапе.
Комментарий IM
Эта задача относится к одному аспекту 4.NF3.c, а именно к записи смешанного числа как эквивалентной дроби; другие задачи иллюстрируют другие аспекты этого стандарта. Цель этого задания — помочь студентам понять и сформулировать причины шагов в обычном алгоритме преобразования смешанного числа в эквивалентную дробь, то есть
$$ A \ frac {B} {C} = \ frac {(A \ times C) + B} {C} $$
Шаг второй показывает, что алгоритм — это просто сокращение для нахождения общего знаменателя между двумя дробями. Эта концепция является важным предшественником сложения смешанных чисел и дробей с одинаковыми знаменателями, и поэтому шаг 2 должен быть основным.
Эта задача подходит либо для обучения, либо для формирующего оценивания, и хорошо согласуется с MP 3, Создание жизнеспособных аргументов и критика рассуждений других. Если цель состоит в том, чтобы заставить учащихся объяснять шаги с помощью картинок, могут потребоваться дополнительные инструкции.
Естественным продолжением или дополнением к этой задаче было бы выполнение и обоснование обратного действия этих шагов, то есть перехода от дроби больше 1 к смешанному числу.
Решения
Решение: Душа 1
Напомним, что 7 $ \ frac {1} {3} $ — это сокращение от $ 7 + \ frac {1} {3} $ и что $ 7 = \ frac {7} {1} $.
Итак, на шаге 1 Бен записывает $ 7 \ frac {1} {3} $ как $ 7 + \ frac {1} {3} $, а затем записывает 7 как $ \ frac {7} {1} $.
На шаге 2 Бен нашел эквивалентную дробь для $ \ frac {7} {1} $, чтобы у нее был тот же знаменатель, что и у $ \ frac {1} {3} $:
$$ \ frac {7} {1} + \ frac {1} {3} = \ frac {(7 \ times 3)} {(1 \ times 3)} + \ frac {1} {3} = \ frac {(7 \ times 3)} {3} + \ frac {1} {3} $$
, а затем сложил их вместе
$$ \ frac {(7 \ times 3)} {3} + \ frac {1} {3} = \ frac {(7 \ times 3) +1} {3} $$
На шаге 3 Бен нашел произведение $ (7 \ times 3) = 21 $.
На шаге 4 он добавил 21 и 1 в числитель.
Решение: Решение 2
Решение Бена также может быть представлено заштрихованной частью рисунков ниже:
На первой картинке у нас есть 7 целых вместе с $ \ frac {1} {3} $ целым. Это представляет собой $ 7 \ frac {1} {3} $, но также может интерпретироваться как $ \ frac {7} {1} + \ frac {1} {3} $ и таким образом иллюстрирует то, что Бен написал на шаге 1.
На следующем рисунке каждое из 7 целых разделено на три равные части, что дает нам $ (7 \ times 3) $ третей вместе с 1 дополнительной третью.Это иллюстрирует Шаг 2 работы Бена: $$ 7 \ frac {1} {3} = \ frac {(7 \ times 3) +1} {3} $$
Наконец, на третьем рисунке мы можем подсчитать все трети и увидеть, что у нас есть 21 из 7 целых и еще 1, что в сумме составляет 22 трети. Итак, наш окончательный ответ — $ \ frac {22} {3} $. Правильно интерпретируя изображения, мы можем понять Шаг 3 и Шаг 4 Бена.
.