Уравнение и его корни с примерами
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x — 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x \in \Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x — (3 — 2x) = 9
Решение:
x-(3-2x)=9 $\iff$ x-3+2x=9 $\iff$ x+2x=9+3 $\iff$ 3x=12 $\iff$ x=4
Проверка:
$4 -(3 — 2 \cdot 4)=9 \implies 4 — 3 + 8 = 9 \implies 9 \equiv 9$
Ответ: x = 4
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
Решение:
7(x + 3)=56 |:7 $\iff$ x + 3 = 8 $\iff$ x = 8 — 3 $\iff$ x=5
Проверка:
$7(5 + 3) = 56 \implies 7 \cdot 8 = 56 \implies 56 \equiv 56$
Ответ: x = 5
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
Решение:
(3x + 4) : 2=14 |$\times$2 $\iff$ 3x + 4 = 28 $\iff$ 3x = 28 — 4 $\iff$ 3x = 24 $\iff$ x=8
Проверка:
$(3 \cdot 8 + 4) : 2 = 14 \implies (24 + 4) : 2 = 14 \implies 28 : 2 = 14 \implies 14 \equiv 14$
Ответ: x = 8
Пример 4. Решите уравнение $ \frac{3x-7}{3} — \frac {5x-11}{5} = 0$
Решение:
$\frac {3x-7}{3} — \frac {5x-11}{5} = 0 | \times 15 \iff5(3x-7)-3(5x-11)=0 \iff$
$ \iff 15x-35-15x+33=0 \iff 0x=2 \iff x \in \varnothing $
Решений нет.
Ответ: $x \in \varnothing $
Пример 5. Решите уравнение $\frac {2x — 7}{2} = \frac {3x+6}{3}$
Решение:
$\frac {2x-7}{2}=\frac {x+6}{3} | \times 6 \iff 3(2x-7)=2(x+6) \iff 6x-21=2x+12 \iff $
$\iff 6x-2x=12+21 \iff 4x=33 \iff x= \frac {33}{4} =8 \frac 14$
Ответ: $8 \frac 14$
Пример 6. Решите уравнение |x+1|=5
Решение:
$$|x+1|=5 \iff \left[ \begin{array}{cc} {x+1=-5}\\ {x+1=5} \end{array} \right. \iff \left[ \begin{array}{cc} {x=-5-1}\\ {x=5-1} \end{array} \right. \iff \left[ \begin{array}{cc} {x_1=-6}\\ {x_2=4} \end{array} \right. $$
Ответ: $ x_1=-6, x_2=4$
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
Решение:
$$ |x + 1| = x + 3 \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x+1 \ge 0 \\ x+1=x+3 \end{array} \right.}\\ {\left\{ \begin{array}{c} x+1<0 \\ -(x+1)=x+3 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \ge -1 \\ 1=3 \end{array} \right.}\\ {\left\{ \begin{array}{c} x<-1 \\ -x-1=x+3 \end{array} \right.} \end{array} \right. \iff $$
$$ \iff \left[ \begin{array}{cc} {\emptyset}\\ {\left\{ \begin{array}{c} x<-1 \\ -x-x=3+1 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {x<-1}\\ {-2x=4} \end{array} \right. \iff \left[ \begin{array}{cc} {x<-1}\\ {x=-2} \end{array} \right. \iff x=-2 $$
Проверка:
$$|-2+1|=-2+3 \implies |-1|=1\implies 1 \equiv 1$$
Ответ: x = -2
Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Решение:
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $\cdot$ (-3) + 18 = 3 $\iff$ -15a = 3 — 18 $\iff$ -15a = -15 $\iff$ a = -15:(-15)=1
a=1
Ответ: a = 1
Основные правила математики. 7 класс алгебра – Сайт учителя математики Косыхиной Н.В.
Основные правила математики. 7 класс алгебра
Содержание
Уравнения. Равносильные уравнения. Свойства
Корень уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение означает найти все его корни или убедиться, что их вообще нет. Также можно сказать, что решить уравнение — это значит найти множество его корней.
Равносильные уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
Линейное уравнение
Уравнение вида  , где
, где  — переменная,
— переменная, 
 некоторые числа, называют линейным уравнением с одной переменной.
некоторые числа, называют линейным уравнением с одной переменной.Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
- Одночлены, из которых состоит многочлен, называют членами многочлена.
- Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
Формулы
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Сумма и разность кубов двух выражений
Многочлен  называют неполным квадратом разности.
называют неполным квадратом разности.
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
Многочлен  называют неполным квадратом суммы.
называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого  и любых целых
и любых целых  выполняются равенства:
выполняются равенства:
Для любых  ,
,  и любого целого
и любого целого  выполняются равенства:
выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают  , зависимую обозначают
, зависимую обозначают  , функцию(правило) –
, функцию(правило) –  .
.
Независимую переменную  называют аргументом функции. Значение зависимой переменной
называют аргументом функции. Значение зависимой переменной  называют значением функции.
называют значением функции.
Тогда функциональную зависимость обозначают  .
.
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными – значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.
Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.
Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
как найти корень уравнения 7 класс
Вы искали как найти корень уравнения 7 класс? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти корень уравнения 7 класс алгебра, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как найти корень уравнения 7 класс».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как найти корень уравнения 7 класс,как найти корень уравнения 7 класс алгебра. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как найти корень уравнения 7 класс. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти корень уравнения 7 класс).
Где можно решить любую задачу по математике, а так же как найти корень уравнения 7 класс Онлайн?
Решить задачу как найти корень уравнения 7 класс вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| 1. |
Составление уравнения
Сложность: лёгкое |
1 |
| 2. |
Уравнение
Сложность: лёгкое |
1 |
| 3. |
Количество корней уравнения
Сложность: лёгкое |
1 |
| 4. |
Решение уравнения
Сложность: среднее |
1 |
| 5. |
Линейное уравнение
Сложность: среднее |
1 |
| 6. |
Нахождение корней уравнения
Сложность: среднее |
1 |
| 7. |
Графическое решение системы уравнения
Сложность: сложное |
3 |
| 8. |
Решение задачи
Сложность: сложное |
3 |
| 9. |
Графическое решение уравнения
Сложность: сложное |
3 |
java — Поиск корней квадратного уравнения с использованием определенного класса
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
- Авторизоваться зарегистрироваться
Где вам нужны математика, квадратные корни или алгебра?
Вы здесь: Главная → Статьи → Зачем нужны квадратные корниСтуденты часто задаются вопросом, понадобятся ли им математические навыки в реальной жизни. Вероятно, они осознают необходимость в простой математике, такой как сложение, умножение, дроби и проценты, но в средней школе некоторые ученики начинают задаваться вопросом, зачем вообще изучать определенные понятия, такие как квадратные корни или целые числа. Затем, в 8 или 9 классе, когда они изучают алгебру, многие подростки начинают задавать извечный вопрос: « Где мне когда-нибудь понадобится алгебра? »
Ответ заключается в том, что вам нужна алгебра в любой профессии, требующей высшего образования , такой как информатика, электроника, инженерия, медицина (врачи), торговля, коммерческие аналитики, ВСЕ ученые, и т. Д. .Короче говоря, если кто-то хочет даже получить высшее образование, он должен изучать алгебру. Вам также понадобится алгебра, чтобы сдать тест SAT или GED.
Изучение алгебры также дает преимущество для развития логического мышления и навыков решения проблем . Алгебра может повысить ваш интеллект! (На самом деле, изучение любой математической темы — даже элементарной математики — может сделать это, если она представлена и преподается таким образом, чтобы развить мышление человека.)
Вы можете признаться своим ученикам, что многие математические понятия, изучаемые в старших классах алгебры, исчисления и других дисциплин, не нужны для каждой профессии.Понятия геометрии очень полезны практически для всех. Никогда не знаешь, сможешь ли ты построить дом или сарай!
Однако решение НЕ изучать алгебру представляет собой большую проблему, потому что большинство подростков в средней школе не уверены, что они собираются делать во взрослом возрасте. В таком случае, , им лучше изучать алгебру и выучить всю математику, которую они могут, чтобы их не остановили в карьере из-за того, что не изучили ее. Было много учеников, которые были горько разочарованы, когда после школы они не могли (по крайней мере, не сразу) перейти на интересующую их сферу обучения из-за отсутствия математических навыков.
И даже если студенты думают, что они знают, кем они хотят быть, сколько раз молодые люди меняли свое мнение? Даже мы, взрослые, не всегда знаем, какие изменения в работе или карьере нас ждут. В прошлом вы вполне могли рассчитывать либо на то, что станете домохозяйкой (девочкой), либо продолжите заниматься отцовской деятельностью (мальчик). В современном мире это не так. У молодых людей больше свободы выбора, но с другой стороны, им нужно учиться намного больше, чтобы получить хорошее образование.Поскольку они не знают всего о своем будущем, гораздо лучше изучать, даже математику.
Чтобы в дальнейшем помочь студентам увидеть, как математика и алгебра используются в реальном мире, ознакомьтесь с бесплатными образцами рабочих листов из учебников Make It Real Learning. Эти книги сосредоточены на ответе на вопрос: «Когда я когда-нибудь собираюсь это использовать?» и использовать данные РЕАЛЬНОЙ ЖИЗНИ в задачах.
Пример: где нужны квадратные корни?
Допустим, ваши ученики задаются вопросом: «Зачем мне нужно знать, как вычислять квадратный корень из числа? Действительно ли квадратные корни нужны в реальной жизни за пределами урока математики?»
Вот одна идея, которая демонстрирует важное практическое применение квадратного корня и в то же время позволяет студентам задуматься, где нужна математика.Эта идея будет работать лучше всего после того, как вы уже изучили концепцию квадратных корней, но еще не коснулись теоремы Пифагора.
- Нарисуйте на доске или бумаге квадрат и начертите в нем одну диагональ . Сделайте стороны квадрата равными, скажем, 5 единицам. Затем сделайте картинку прямоугольным треугольником, удалив две стороны квадрата. Затем спросите учащихся , как найти длину самой длинной стороны треугольника.
Студенты, вероятно, не смогут найти длину, если они еще не изучили теорему Пифагора — но это часть «игры».Вы когда-нибудь видели рекламу, в которой нельзя было сказать, что они рекламировали? Затем, через несколько недель реклама изменится и раскроет, о чем идет речь. Это вызывает любопытство.
Итак, дайте им подумать об этом несколько минут (сначала не говорите им ответ). Надеюсь, это вызовет их интерес. Скоро вы, вероятно, все равно будете изучать теорему Пифагора, поскольку она часто следует за квадратными корнями в учебной программе.
- Затем переходите к вопросу: В каких профессиях или ситуациях вам нужно будет найти самую длинную сторону прямоугольного треугольника , если вы знаете две другие стороны? Это может их вовлечь!
Ответ: в любой работе, связанной с треугольниками.Например, он нужен плотникам, инженерам, архитекторам, строителям, тем, кто измеряет и маркирует землю, художникам и дизайнерам.
Однажды я наблюдал за строителями, которые измеряли и отмечали на земле, где будет строиться здание. У них были отмечены стороны, и у них была рулетка для измерения диагоналей, и они спросили МЕНЯ, какой должна быть мера, потому что они не могли точно вспомнить, как это делать. Эта диагональная проверка предназначена для того, чтобы убедиться, что здание действительно будет прямоугольником, а не трапецией или какой-либо другой формой.
Теперь, помимо этого простого примера, учащихся должны понять КОНЦЕПЦИЮ квадратного корня, чтобы понять других математических концепций . Изучение математики похоже на постройку стены из блоков или здания: вам нужны блоки в нижней части, чтобы вы могли строить на них, и если вы оставите отверстия, вы не сможете строить на них.
Концепция квадратного корня является предпосылкой и связана со многими другими концепциями в математике:
- квадратный корень → уравнения 2-й степени → функции и графики
- квадратный корень → теорема Пифагора → тригонометрия
- корень квадратный → дробные показатели → функции и графики
- квадратный корень → иррациональные числа → действительные числа
См. Также:
Онлайн-ресурсы по математике в реальной жизни — существует множество веб-сайтов, посвященных этому вопросу!
Где вам нужны экспоненты в повседневной жизни?
Комментарии
Я всегда ненавидел математику, но никогда не думал, что она помешает мне получить образование в колледже.Мне было так трудно пройти, что я просто бросил. Я еще не закончил …
Вам нужна математика, чтобы вы могли закончить школу и поступить в колледж.
Эм
Какие математические навыки необходимы, чтобы работать на стройке?
Дэвид Куц
Я считаю, что строителям в первую очередь необходимо хорошо знать свою геометрию и все, что касается измерения, площади и объема.
Тогда вы, вероятно, будете
.Решайте линейные и квадратные уравнения с помощью программы «Пошаговое решение математических задач»
Введите уравнение вместе с переменной, для которой вы хотите его решить, и нажмите кнопку «Решить».
Решение уравнений — центральная тема алгебры. В этой главе мы изучим некоторые методы решения уравнений с одной переменной. Для этого мы будем использовать навыки, полученные при работе с числами и символами алгебры, а также операции с целыми числами, десятичными и дробями, которые вы изучили в арифметике.
УСЛОВНЫЕ И ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Классифицирует уравнение как условное или тождественное.
- Решите простые уравнения мысленно.
- Определите, эквивалентны ли определенные уравнения.
Уравнение — это указание в символах того, что два числовых выражения равны.
Уравнения можно разделить на два основных типа:
1.Идентификатор верен для всех значений буквальных и арифметических чисел в нем.
Пример 1 5 x 4 = 20 — это идентификатор.
Пример 2 2 + 3 = 5 — это идентификатор.
Пример 3 2x + 3x = 5x — это тождество, поскольку любое значение, замененное на x, приведет к равенству.
2. Условное уравнение верно только для определенных значений буквальных чисел в нем.
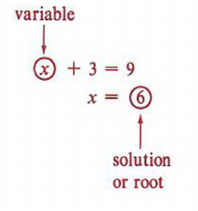
Пример 4 x + 3 = 9 истинно, только если буквальное число x = 6.
Пример 5 3x — 4 = 11 верно, только если x = 5.
Буквальные числа в уравнении иногда называют переменными .
Поиск значений, которые делают условное уравнение истинным, является одной из основных целей этого текста.
Решение или корень уравнения — это значение переменной или переменных, которые делают уравнение истинным.
Говорят, что решение или корень для удовлетворяет уравнению .
Решение уравнения означает нахождение решения или корня.
Многие уравнения можно решить мысленно. Умение мысленно решить уравнение будет зависеть от умения манипулировать числами в арифметике. Чем лучше вы знаете факты умножения и сложения, тем более искусными вы будете в решении уравнений в уме.
Пример 6 Решить относительно x: x + 3 = 7
Решение
Чтобы получить истинное утверждение, нам нужно значение x, которое при добавлении к 3 даст 7.Наши знания арифметики показывают, что 4 — это необходимое значение. Следовательно, решение уравнения x = 4.
| Какое число, добавленное к 3, равно 7? |
Пример 7 Решить относительно x: x — 5 = 3
Решение
Из какого числа вычитаем 5, чтобы получить 3? Снова наш опыт с арифметикой говорит нам, что 8 — 5 = 3. Следовательно, решение x = 8.
Пример 8 Решить относительно x: 3x = 15
Решение
Какое число нужно умножить на 3, чтобы получить 15? Наш ответ — x = 5.
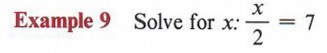
Решение
На какое число разделим 2, чтобы получить 7? Наш ответ — 14.
Пример 10 Решить относительно x: 2x — 1 = 5
Решение
Мы бы вычли 1 из 6, чтобы получить 5. Таким образом, 2x = 6. Тогда х = 3.
Независимо от того, как решается уравнение, решение всегда следует проверять на правильность.
Пример 11 Студент решил уравнение 5x — 3 = 4x + 2 и нашел ответ x = 6.Это правильно или неправильно?
Решение
Удовлетворяет ли x = 6 уравнению 5x — 3 = 4x + 2? Чтобы проверить, мы подставляем 6 вместо x в уравнение, чтобы увидеть, получим ли мы истинное утверждение.

Это неверное утверждение, поэтому ответ x = 6 неверен.
Другой студент решил то же уравнение и нашел x = 5.
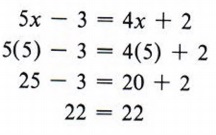
Это верное утверждение, поэтому x = 5 верно.
| Многие студенты думают, что, когда они нашли решение уравнения, проблема решена. Не так! Последним шагом всегда должна быть проверка решения. |
Не все уравнения можно решить мысленно. Теперь мы хотим представить идею, которая является шагом к упорядоченному процессу решения уравнений.
| Является ли x = 3 решением x — 1 = 2? Является ли x = 3 решением 2x + I = 7? Что можно сказать об уравнениях x — 1 = 2 и 2x + 1 = 7? |
Два уравнения эквивалентны , если они имеют одно и то же решение или решения
Пример 12 3x = 6 и 2x + 1 = 5 эквивалентны, потому что в обоих случаях x = 2 является решением.
Методы решения уравнений включают процессы преобразования уравнения в эквивалентное уравнение. Если сложное уравнение, такое как 2x — 4 + 3x = 7x + 2 — 4x, можно заменить на простое уравнение x = 3, а уравнение x = 3 эквивалентно исходному уравнению, то мы решили уравнение.
Два вопроса теперь становятся очень важными.
- Эквивалентны ли два уравнения?
- Как мы можем заменить уравнение другим уравнением, которое ему эквивалентно?
Ответ на первый вопрос находится с использованием принципа подстановки.
Пример 13 Являются ли 5x + 2 = 6x — 1 и x = 3 эквивалентными уравнениями?
Решение

Ответ на второй вопрос включает в себя методы решения уравнений, которые будут обсуждаться в следующих нескольких разделах.
| Чтобы правильно использовать принцип подстановки, мы должны подставить цифру 3 вместо x везде, где x появляется в уравнении. |

ПРАВИЛО ПОДРАЗДЕЛЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Используйте правило деления для решения уравнений.
- Решите несколько основных прикладных задач, решение которых связано с использованием правила деления.
Как упоминалось ранее, мы хотим представить упорядоченную процедуру решения уравнений. Эта процедура включает четыре основных операции, первая из которых представлена в этом разделе.
Если каждый член уравнения представляет собой деление на одно и то же ненулевое число, результирующее уравнение будет эквивалентно исходному уравнению.
Чтобы подготовиться к использованию правила деления для решения уравнений, мы должны обратить внимание на следующий процесс:

(Обычно мы пишем 1x как x с пониманием коэффициента 1.)
Пример 1 Решить относительно x: 3x = 10
Решение
Наша цель — получить x = некоторое число. Правило деления позволяет нам разделить каждый член 3x = 10 на одно и то же число, и наша цель найти значение x будет означать, что мы делим на 3. Это дало бы нам коэффициент 1 для x.
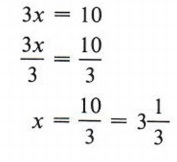
Проверить: 3x = 10 и x = 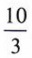 эти эквивалентные уравнения?
эти эквивалентные уравнения?
Заменим 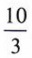 вместо x в первом уравнении, получив
вместо x в первом уравнении, получив
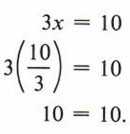
Уравнения эквивалентны, поэтому решение верное.
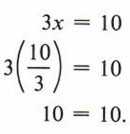
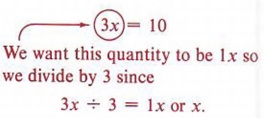
Пример 2 Решить относительно x: 5x = 20
Решение
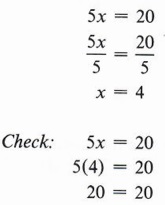
Обратите внимание, что правило деления не позволяет нам делить на ноль. Поскольку деление на ноль запрещено в математике, такие выражения, как 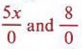 бессмысленны. бессмысленны. |
Пример 3 Решить относительно x: 8x = 4
Решение

| Ошибки иногда допускаются в очень простых ситуациях.Не обращайте внимания на эту проблему и приходите к x = 2! Обратите внимание, что правило деления позволяет разделить каждый член уравнения на любое ненулевое число, и полученное уравнение эквивалентно исходному уравнению. Таким образом, мы можем разделить каждую часть уравнения на 5 и получить  , что эквивалентно исходному уравнению. , что эквивалентно исходному уравнению. Однако деление на 5 не помогает найти решение. На какое число нужно разделить, чтобы найти решение? |
Пример 4 Решить относительно x: 0.5x = 6
Решение
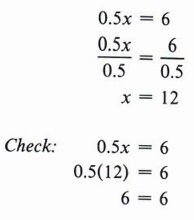

Пример 6 Формула для определения длины окружности (C) круга: C = 2πr, где π представляет радиус круга, и он составляет приблизительно 3,14. Найдите радиус круга, если измеренная длина окружности равна 40,72 см. Дайте правильный ответ с точностью до двух десятичных знаков.
Решение
Чтобы решить задачу, связанную с формулой, мы сначала используем принцип подстановки.

| Окружность означает «расстояние вокруг».»Это периметр круга. Радиус — это расстояние от центра до круга. |

ПРАВИЛО ВЫЧИСЛЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете использовать правило вычитания для решения уравнений.
В этом разделе будет обсуждаться второй шаг к упорядоченной процедуре решения уравнений. Вы будете использовать свои знания одинаковых терминов из главы 1, а также методы из раздела ПРАВИЛО ПОДРАЗДЕЛЕНИЯ .Обратите внимание, как новые идеи в алгебре основываются на предыдущих знаниях.
Если та же величина равна , вычитая из обеих частей уравнения, полученное уравнение будет равно , эквивалентному исходному уравнению.
Пример 1 Решить относительно x, если x + 7 = 12.
Решение
Хотя это уравнение легко решить в уме, мы хотим проиллюстрировать правило вычитания. Мы должны думать так:
«Я хочу решить относительно x, поэтому мне нужно, чтобы x был сам по себе на одной стороне уравнения.Но у меня x + 7. Так что, если я вычту 7 из x + 7, у меня будет только x с левой стороны ». (Помните, что величина, вычтенная из себя, дает ноль.) Но если мы вычтем 7 из одной стороны от числа. уравнение требует, чтобы мы вычли 7 и из другой стороны. Итак, мы действуем следующим образом:
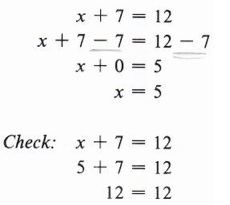
| Обратите внимание, что x + 0 можно записать просто как x, поскольку ноль, добавленный к любому количеству, равен самому количеству. |
Пример 2 Решить относительно x: 5x = 4x + 3
Решение
Здесь наше мышление должно развиваться таким же образом.«Я хочу получить все неизвестные величины с одной стороны уравнения и все арифметические числа с другой, поэтому у меня есть уравнение в форме x = некоторое число. Таким образом, мне нужно вычесть Ax из обеих сторон».
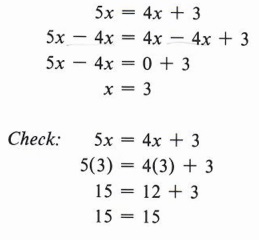
| Наша цель — получить x = некоторое число. Помните, что проверка вашего решения — важный шаг в решении уравнений. |
Пример 3 Решить относительно x: 3x + 6 = 2x + 11
Здесь у нас более сложная задача.Сначала вычтите 6 с обеих сторон.
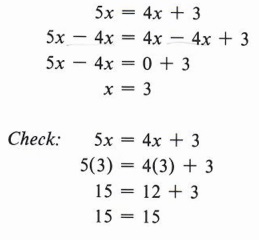
Теперь мы должны исключить 2x с правой стороны, вычтя 2x с обеих сторон.
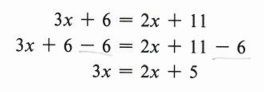
Теперь мы рассмотрим решение, которое требует использования как правила вычитания, так и правила деления.
| Обратите внимание, что вместо первого вычитания 6 мы могли бы также сначала вычесть 2x с обеих сторон, получив 3x — 2x + 6 = 2x — 2x + 11 x + 6 = 11. Затем, вычитая 6 из обеих сторон, мы имеем х + 6-6 = 11-6 х = 5. Имейте в виду, что наша цель — x = некоторое число. |
Пример 4 Решить относительно x: 3x + 2 = 17
Решение
Сначала мы используем правило вычитания, чтобы вычесть 2 из обеих сторон, получая
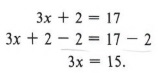
Затем мы используем правило деления, чтобы получить
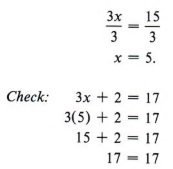
Пример 5 Решить относительно x: 7x + 1 = 5x + 9
Решение
Сначала воспользуемся правилом вычитания.
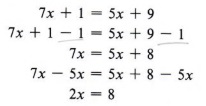
Тогда правило деления дает нам
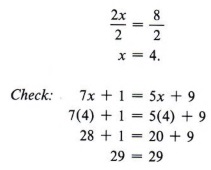
Пример 6 Периметр (P) прямоугольника находится по формуле P = 2l + 2w, где l обозначает длину, а w обозначает ширину.Если периметр прямоугольника 54 см, а длина 15 см, какова ширина?
Решение
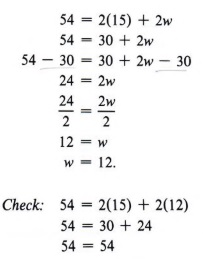
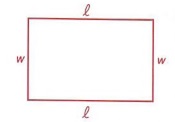
| Периметр — это расстояние вокруг. Вы понимаете, почему формула P = 2l + 2w? |
ДОПОЛНИТЕЛЬНОЕ ПРАВИЛО
ЗАДАЧИ
По завершении этого раздела вы сможете использовать правило сложения для решения уравнений.
Теперь мы переходим к следующей операции в нашей цели разработки упорядоченной процедуры решения уравнений.Еще раз будем полагаться на предыдущие знания.
Если одна и та же величина равна и прибавляется к обеим сторонам уравнения, полученное уравнение будет равно , эквивалентному исходному уравнению.
Пример 1 Решить относительно x, если x — 7 = 2.
Решение
Как всегда, при решении уравнения мы хотим прийти к форме «x = некоторое число». Мы замечаем, что 7 было вычтено из x, поэтому, чтобы получить только x в левой части уравнения, мы добавляем 7 к обеим частям.

| Не забывайте всегда проверять свое решение. |
Пример 2 Решить относительно x: 2x — 3 = 6
Решение
Помня о нашей цели получить только x, мы замечаем, что, поскольку 3 было вычтено из 2x, мы добавляем 3 к обеим частям уравнения.
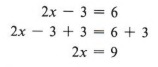
Теперь мы должны использовать правило деления.
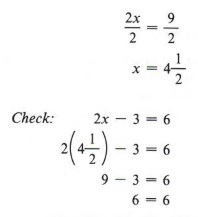
| Почему мы добавляем 3 к обеим сторонам? Обратите внимание, что в примере просто использование правила сложения не решает проблему. |
Пример 3 Решить относительно x: 3x — 4 = 11
Решение
Сначала воспользуемся правилом сложения.
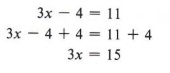
Затем, используя правило деления, получаем

| Здесь снова нам нужно было использовать как правило сложения, так и правило деления для решения уравнения. |
Пример 4 Решите относительно x: 5x = 14 — 2x
Решение
Здесь наша цель получить только x с одной стороны предполагает, что мы удалим 2x справа, поэтому мы добавляем 2x к обеим сторонам уравнения.
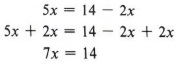
Далее мы применим правило деления.
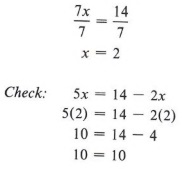
| Здесь снова нам нужно было использовать как правило сложения, так и правило деления для решения уравнения. Обратите внимание, что мы проверяем, всегда подставляя решение в исходное уравнение. |
Пример 5 Решить относительно x: 3x — 2 = 8 — 2x
Решение
Здесь наша задача более сложная. Мы должны подумать об удалении числа 2 из левой части уравнения, а также lx из правой части, чтобы получить только x с одной стороны.Сначала мы можем сделать что-то из этого. Если мы выберем сначала прибавить 2x к обеим сторонам, мы получим
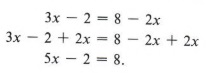
Теперь прибавляем 2 к обеим сторонам.
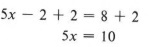
Наконец, правило деления дает
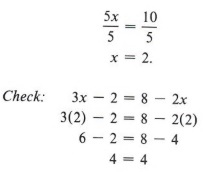
| Можем ли мы сначала добавить 2 к обеим сторонам? Попытайся! |
ПРАВИЛО УМНОЖЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Используйте правило умножения для решения уравнений.
- Решите пропорции.
- Решите основные прикладные задачи с помощью правила умножения.
Теперь мы подошли к последней из четырех основных операций при разработке нашей процедуры решения уравнений. Мы также введем соотношение и пропорции и воспользуемся правилом умножения для решения пропорций.
Если каждый член уравнения равен , умноженному на на такое же ненулевое число, полученное уравнение будет равно , эквивалентному исходному уравнению.
В элементарной арифметике одни из самых сложных операций с дробями. Правило умножения позволяет избежать этих операций при решении уравнения, содержащего дроби, путем нахождения эквивалентного уравнения, содержащего только целые числа.
Помните, что когда мы умножаем целое число на дробь, мы используем правило 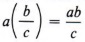
Теперь мы готовы решить уравнение, содержащее дроби.
| Обратите внимание, что в каждом случае только числитель дроби умножается на целое число. |
Пример 4 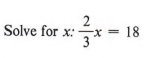
Решение
Имейте в виду, что мы хотим получить только x на одной стороне уравнения. Мы также хотели бы получить уравнение в целых числах, которое эквивалентно данному уравнению. Чтобы исключить дробь в уравнении, нам нужно умножить на число, которое делится на знаменатель 3. Таким образом, мы используем правило умножения и умножаем каждый член уравнения на 3.
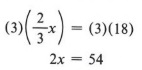
Теперь у нас есть эквивалентное уравнение, которое содержит только целые числа.Используя правило деления, получаем
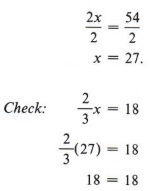
| Чтобы исключить дробь, нам нужно умножить ее на число, которое делится на знаменатель. В этом примере нам нужно умножить на число, которое делится на 3. Мы могли бы умножить обе стороны на 6, 9, 12 и так далее, но уравнение проще и легче работать, если мы используем наименьшее несколько. |
Пример 5 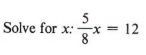
Решение

| Посмотрите, получите ли вы такое же решение, умножив каждую часть исходного уравнения на 16. Всегда проверяйте исходное уравнение. |
Пример 6 
Решение
Здесь наша задача такая же, но немного сложнее. Нам нужно исключить две фракции. Мы должны умножить каждый член уравнения на число, которое делится на 3 и 5. Лучше всего использовать наименьшее из таких чисел, которое, как вы помните, — это наименьшее общее кратное . Поэтому мы умножим на 15.
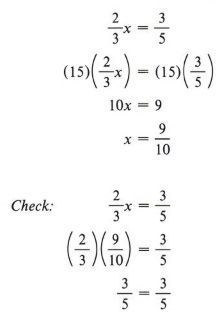
| В арифметике вы могли использовать наименьшее общее кратное как «наименьший общий знаменатель».» |
Пример 7 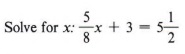
Решение
Наименьшее общее кратное для 8 и 2 равно 8, поэтому мы умножаем каждый член уравнения на 8.

Теперь воспользуемся правилом вычитания.
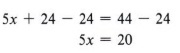
Наконец, правило деления дает нам

Перед умножением замените смешанные числа на неправильные дроби. В этом примере измените 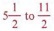 . . Помните, что каждый член нужно умножить на 8. Обратите внимание, что в этом примере мы использовали три правила для поиска решения. |
Решение простых уравнений путем умножения обеих частей на одно и то же число часто встречается при изучении соотношения и пропорции.
Соотношение — это частное двух чисел.
Отношение числа x к числу y можно записать как x: y или 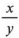 . В общем, дробная форма более значима и полезна. Таким образом, мы запишем отношение 3 к 4 как
. В общем, дробная форма более значима и полезна. Таким образом, мы запишем отношение 3 к 4 как 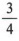 .
.
Пропорция — это утверждение, что два соотношения равны.
Пример 8 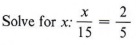
Решение
Нам нужно найти такое значение x, чтобы отношение x к 15 было равно отношению 2 к 5.
Умножая каждую часть уравнения на 15, получаем
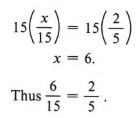
Решение вопросов Word
МНОГО примеров!
В алгебре мы часто задаем вопросы, например:
Пример: Сэм и Алекс играют в теннис.
В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как мы их решаем?
Уловка состоит в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Как английский язык превращается в алгебру
Превратить английский в алгебру помогает:
- Прочтите сначала все
- Сделайте набросок , если возможно
- Назначьте букв для значений
- Найдите или обработайте формул
Вам также следует записать , что на самом деле требуется для , чтобы вы знали, куда вы собираетесь и когда вы прибыли!
Также ищите ключевые слова:
| Когда вы видите | Думаю | |
|---|---|---|
сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более | + | |
минус, меньше, разница, меньше, уменьшилось, уменьшилось | – | |
умноженное на произведение, множитель | × | |
разделенное, частное, на, из, соотношение, соотношение, процент, ставка | ÷ | |
| увеличить или уменьшить | геометрия формулы | |
| Скорость, скорость | расстояние формулы | |
| Сколько дней, часов, минут, секунд | время |
Ясное мышление
Некоторые формулировки могут быть сложными, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.Как нам записать это в виде уравнения?
- Пусть S = долларов У Сэма
- Пусть A = долларов У Алекса
Теперь … вот что: S — 2 = A
или должно быть: S = A — 2
или должно быть: S = 2 — A
Правильный ответ: S = A — 2
( S — 2 = A — распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек.Как нам записать это в виде уравнения?
- Пусть D = количество собак
- Пусть C = количество кошек
Теперь … это то, что: 2D = C
или должно быть: D = 2C
Подумайте внимательно!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как в вопросе написано «дважды … собаки … кошки»)
Примеры
Давайте начнем с очень простого примера , чтобы увидеть, как это делается:
Пример. Прямоугольный сад размером 12 х 5 м. Какова его площадь?
Превратите английский в алгебру:
Эскиз:
.Письма:
- Используйте w для ширины прямоугольника: w = 12 м
- Используйте h для высоты прямоугольника: h = 5 м
Формула для площади прямоугольника: A = w × h
Нас спрашивают о Районе.
Решить:
A = ш × в = 12 × 5 = 60 м 2
Площадь 60 кв.м .
Теперь давайте попробуем пример сверху страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?
Превратите английский в алгебру:
Письма:
- Используйте S , чтобы узнать, сколько игр сыграл Сэм.
- Используйте A , сколько игр сыграл Алекс
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
И мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр сыграл Алекс: A
Решить:
Начать с: S + A = 12
S = A + 4 , поэтому мы можем
заменить S на «A + 4»: (A + 4) + A = 12
Упростить: 2A + 4 = 12
Вычтем 4 с обеих сторон: 2A = 12 — 4
Упростить: 2A = 8
Разделите обе части на 2: A = 4
Это означает, что Алекс сыграл 4 игры в теннис.
Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!
Пример посложнее:
Пример: Алекс и Сэм также создают таблицы.
Вместе они делают 10 столов за 12 дней.
Алекс, работая один, может заработать 10 за 30 дней.
Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?
Превратите английский в алгебру:
Письма:
- Используйте a для скорости работы Алекса
- Используйте с для скорости работы Сэма
12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10
30 дней одного Алекса — это тоже 10 столов: 30a = 10
Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.
Решить:
30a = 10 , поэтому ставка Алекса (столов в день) будет: a = 10/30 = 1/3
Начать с: 12a + 12s = 10
Положите «1/3» для a: 12 (1/3) + 12s = 10
Упростить: 4 + 12s = 10
Вычтем 4 с обеих сторон: 12s = 6
Разделите обе стороны на 12: s = 6/12
Упростить: с = 1/2
Это означает, что ставка Сэма составляет половину стола в день (быстрее, чем у Алекса!).
Итак, 10 столов займет у Сэма всего 20 дней.
Интересно, стоит ли Сэму платить больше?
И еще пример «подстановки»:
Пример: Дженна тренируетесь, чтобы претендовать на национальные игры.
У нее обычный еженедельный распорядок дня: в одни дни тренируется по пять часов в день, а в другие — по 3 часа в день.
В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?
Письма:
- Количество «5 часовых» дней: d
- Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, с d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d
Решить:
d + e = 7
Итак: e = 7 — d
Положим в 5d + 3e = 27 5d + 3 (7 − d) = 27
Упростить: 5d + 21 — 3d = 27
Вычтем 21 с обеих сторон: 5d — 3d = 6
Упростить: 2d = 6
Разделим обе стороны на 2: d = 3
Количество «5 часовых» дней — 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Некоторые примеры из Geometry:
Пример: круг имеет площадь 12 мм 2 , каков его радиус?
Письма:
- Используйте A для площади: A = 12 мм 2
- Используйте r для радиуса
И формула для площади: A = π r 2
У нас спрашивают радиус.
Решить:
Нам нужно переставить формулу, чтобы найти площадь
Начать с: A = π r 2
Поменять местами стороны: π r 2 = A
Разделите обе стороны на π : r 2 = A / π
Извлечь квадратный корень из обеих частей: r = √ (A / π)
Теперь мы можем использовать формулу: r = √ (12/ π)
И получаем: r = 1.954 (до 3-х мест)
Пример: куб имеет объем 125 мм 3 , какова его площадь поверхности?
Сделайте быстрый набросок:
Письма:
- Используйте В для объема
- Используйте A для Area
- Используйте s для длины стороны куба
Формулы:
- Объем куба: В = с 3
- Площадь куба: A = 6s 2
У нас спрашивают площадь.
Решить:
Первая тренировка с по формуле объема:
Начать с: В = с 3
Поменять местами стороны: с 3 = V
Извлечь кубический корень с обеих сторон: s = ∛ (V )
И получаем: с = ∛ (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
Начать с: A = 6s 2
И получаем: А = 6 (5) 2
A = 6 × 25 = 150 мм 2
Пример о деньгах:
Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.
Одну неделю Джоэл работал 40 часов по обычной ставке, а также работал сверхурочно по 12 часов. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?
Письма:
- Обычная ставка оплаты труда Джоэла: N $ в час
Формулы:
- Джоэл работает 40 часов по цене N $ в час = 40N
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.25N в час
- Джоэл работает 12 часов по цене 1,25 доллара США в час = (12 × 1 доллар США) = 15 долларов США долларов США
- А вместе он заработал 660 долларов, итак:
40N + $ (12 × 1¼N) = 660 $
У нас спрашивают нормальную ставку заработной платы Джоэла N $.
Решить:
Начните с $ 40N + $ (12 × 1¼N) = 660 $
Упростить: 40 долларов + 15 долларов = 660 долларов
Упростите еще: 55 долларов США = 660 долларов США
Разделим обе стороны на 55: N = 12 долларов
Итак, обычная ставка оплаты труда Джоэла составляет 12 долларов в час.
Чек
Нормальная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная работа составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная зарплата 40 × 12 = 480 долларов плюс его сверхурочная работа в размере 12 × 15 долларов = 180 долларов дает нам в общей сложности 660 долларов
.Подробнее о деньгах с этими двумя примерами, включающими сложный процент
Пример: Алекс кладет 2000 долларов в банк под 11% годовых. Сколько это будет стоить через 3 года?
Это формула сложных процентов:
Итак, мы будем использовать эти буквы:
- Текущая стоимость PV = 2000 долларов США
- Процентная ставка (десятичная дробь): r = 0.11
- Количество периодов: n = 3
- Будущая стоимость (значение, которое мы хотим): FV
Нас спрашивают о будущей стоимости: FV
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) 3
Вычислить: FV = $ 2000 × 1,367631
Вычислим: FV = 2735 долларов.26 (с точностью до цента)
Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
.