Теорема косинусов для треугольника, формула и примеры
ТЕОРЕМА Для произвольного треугольника квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.То есть для треугольника , изображенного на рисунке 1, имеют место следующие соотношения:
Следствие из теоремы косинусов
Косинус любого угла треугольника , при условии, что известны все его стороны, можно найти из соотношений
Примеры решения задач
ПРИМЕР 1| Задание | В треугольнике стороны см и см, угол между ними . Найти неизвестную сторону . |
| Решение | Запишем для неизвестной стороны теорему косинусов:
Подставляя известные значения сторон и угла, получим:
(см) |
| Ответ | см |
| Задание | Стороны треугольника равны соответственно 3, 7 и 8 см. Найти угол, лежащий против стороны длинной 7 см. |
| Решение | Обозначим стороны треугольника: ; а против стороны лежит . По следствию из теоремы косинусов, косинус выражается через стороны треугольника следующим образом:
Подставим известные значения длин сторон, получим
|
| Ответ |
ru.solverbook.com
Теорема косинусов

Теорема косинусов и теорема Пифагора. В этой статье мы рассмотрим теорему косинусов и как она используется для нахождения элементов треугольника. А так же разберём её взаимосвязь с теоремой Пифагора.



Знать эту теорему НЕОБХОДИМО. Что мы можем найти, используя её?
Если нам будут известны две стороны и угол между ними, мы без труда найдём третью сторону. Для этого нужно просто подставить в формулу известные величины. Для других сторон всё то же самое:

Можно ли использовать теорему косинусов для нахождения третьей стороны, если известны любые две стороны и угол, не лежащий между этими сторонами? Например, нам известны стороны a и b и угол альфа. Тогда из формулы

мы можем найти сторону «с». Приводим к виду:

То есть, мы получаем квадратное уравнение с переменной «с» (все остальные величины нам известны). Решив его, получим искомую сторону.
Мы можем найти любой угол, если нам известны все три стороны треугольника:

Разумеется, что учить все эти формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А косинус любого угла не трудно выразить используя простые алгебраические преобразования.
*Если вы вычисляете косинус тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах получите положительное значение, то ищите ошибку.
Следующий вопрос: а если нам дана сторона и любые два угла, что делать? В этом случае теорема косинусов не используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из следующих статей, не пропустите!
Если вы будете в совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением треугольников (в большинстве задач).
Следующий факт знают все, но всё же о взаимосвязи теоремы косинусов с теоремой Пифагора сказать стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то получим:

То есть, по сути, теорема Пифагора это как бы частный случай теоремы косинусов.
Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями:

По теореме косинусов:

Так как угол С равен 90, то

Напомню, что зная любые две стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без труда можем найти значение любой тригонометрической функции острого угла в нём. Можете изучить статью об этом.
Получить материал статьи в формате PDF
На этом всё. Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Теорема косинусов для треугольника
При решении задач по геометрии из ЕГЭ и ОГЭ по математике довольно часто возникает необходимость, зная две стороны треугольника и угол между ними, найти третью сторону. Или же, зная все стороны треугольника, найти его углы. Для решение этих задач вам потребуется значение теоремы косинусов для треугольника. В данной статье репетитор по математике и физике рассказывает о том, как формулируется, доказывается и применяется на практике при решении задач данная теорема.
Формулировка теоремы косинусов для треугольника
Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами  ,
, 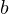 и
и 
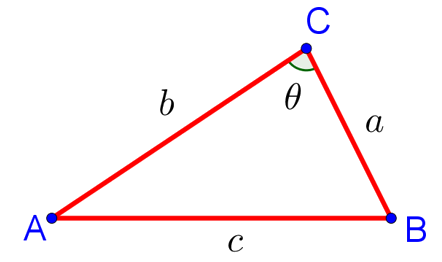
Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:
![Rendered by QuickLaTeX.com \[ c^2 = a^2+b^2-2ab\cos\angle C. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-86ee22b6e143dc86a1ea1c4d4b817ee4_l3.png)
На рисунке для удобства дальнейших рассуждений угол С обозначен углом 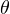 . Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
. Словами это можно сформулировать следующим образом: «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.»
Понятно, что если бы вы выражали другую сторону треугольника, например, сторону  , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны
, то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны 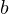 и
и  . Выражение для квадрата стороны
. Выражение для квадрата стороны 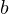 получается аналогично:
получается аналогично:
![Rendered by QuickLaTeX.com \[ a^2 = b^2+c^2-2bc\cos\angle A, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3e0142c4e326dd16341d954ebf819037_l3.png)
![Rendered by QuickLaTeX.com \[ b^2 = a^2+c^2-2ac\cos\angle B. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-245b80b13c75a7f7b01a7f756f7ebbaa_l3.png)
Доказательство теоремы косинусов для треугольника
Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.
Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне всё же пересиливает. Тем более, что доказательство в результате получается удивительно простым и запоминающимся. Сейчас вы в этом убедитесь.
Заменим стороны нашего треугольника следующими векторами:

Согласно правилам сложения векторов имеем: 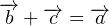 . Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим
. Действительно, по правилу треугольника вектор, равный сумме двух векторов, отложенных последовательно один за другим, — это вектор с началом в начале первого вектора и концом в конце второго. Переносим 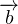 в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение:
в правую часть равенства с противоположным знаком, в результате чего получаем следующее векторное выражение: 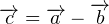 .
.
Теперь возьмём скалярный квадрат обеих частей полученного выражения. В результате чего получим:
![Rendered by QuickLaTeX.com \[ \overrightarrow{c}^2=\left(\vec{a}-\vec{b}\right)^2=\overrightarrow{a}^2-2\overrightarrow{a}\overrightarrow{b}+\overrightarrow{b}^2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a0a0a9d541cc4b5b56a6f29b724b2003_l3.png)
Я напоминаю, что по определению скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Из этого определения также следует, что скалярный квадрат вектора равен квадрату его длины. Действительно, ведь угол между вектором и им же самим равен нулю, то есть соответствующих косинус равен 1. То есть остаётся только квадрат длины вектора. Исходя из этого мы сразу получаем выражение для теоремы косинусов:
![Rendered by QuickLaTeX.com \[ c^2 = a^2+b^2-2ab\cos\theta. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2993092fc0ffed816c9d6e35a30639b9_l3.png)
Что и требовалось доказать. Причём данное доказательство хорошо ещё тем, что позволяет лучше запомнить саму формулу. Ведь теперь становится понятным, откуда берётся этот хвост 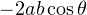 . Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол
. Как раз из скалярного произведения. Ну и, как я уже говорил, это доказательство справедливо для любых треугольников: остроугольных, тупоугольных и прямоугольных. То есть угол 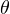 может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
может быть острым, тупым или прямым. И не требуется рассматривать доказательство для каждого из этих случаев, что не может не радовать.
Кстати, в случае, когда угол 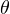 прямой, мы получаем
прямой, мы получаем 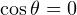 , и выражение принимает следующий вид:
, и выражение принимает следующий вид: 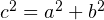 . Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.
. Что мы получили? Правильно! Это запись теоремы Пифагора. Квадрат гипотенузы равен сумме квадратов катетов. Так что ниточки постепенно сплетаются. То есть, как обычно говорят, теорема косинусов для треугольника есть обобщение теоремы Пифагора на случай произвольного треугольника, не обязательно прямоугольного.
Примеры решения задач с использованием теоремы косинусов для треугольника
Надо сказать, что даже если вы не поняли приведённое выше доказательство, это не страшно, если ваша цель состоит в сдаче ЕГЭ или ОГЭ по математике. Специфика этих экзаменов состоит в том, что само доказательство теоремы косинусов у вас никто на них не спросит. Эти экзамены фактически вообще не проверяют знание теоретического материла из школьного курса математики. Важно лишь, чтобы вы знали, как эта теорема формулируется и умели применять её на практике для решения задач.
Используя теорему косинусов для треугольника, можно найти третью сторону, зная две стороны треугольника и угол между ними. Или же, зная длины всех сторон треугольника, найти величину всех его углов. Рассмотрим на примерах, как это делается.
| Пример 1. В треугольнике ABC сторона AC равна 3, сторона CB равна 2, а угол C равен 60°. Найдите длину стороны AB. |
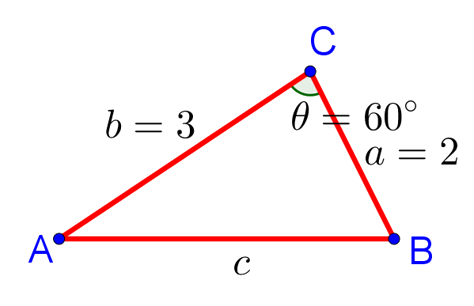
Используем теорему косинусов для треугольника ABC. Квадрат стороны  равен сумме квадратов сторон
равен сумме квадратов сторон  и
и 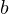 за вычетом удвоенного произведения этих сторон на косинус угла между ними:
за вычетом удвоенного произведения этих сторон на косинус угла между ними:
![Rendered by QuickLaTeX.com \[ c^2 = a^2+b^2-2ab\cos\theta. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2993092fc0ffed816c9d6e35a30639b9_l3.png)
Поскольку 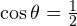 , то в результат получаем:
, то в результат получаем:
![Rendered by QuickLaTeX.com \[ c^2=2^2+3^2-2\cdot 2\cdot 2\cdot 3\frac{1}{2} = 7. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-34f665757fa3673f532d8e689b4ac70c_l3.png)
Значит, 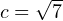 . Понятно, что отрицательное решение мы не берём, потому что длина отрезка — это число положительное.
. Понятно, что отрицательное решение мы не берём, потому что длина отрезка — это число положительное.
Пример 2. В треугольнике ABC сторона AB равна 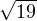 , сторона AC равна 5, сторона BC равна 3. Найдите угол C. , сторона AC равна 5, сторона BC равна 3. Найдите угол C. |
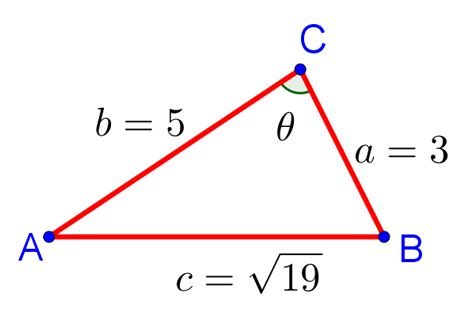
Искомый угол на рисунке обозначен 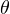 . Вновь запишем теорему косинусов для треугольника ABC. Поскольку все обозначения у нас сохранились, то и формула, выражающая теорему косинусов для этого треугольника, останется прежней:
. Вновь запишем теорему косинусов для треугольника ABC. Поскольку все обозначения у нас сохранились, то и формула, выражающая теорему косинусов для этого треугольника, останется прежней:
![Rendered by QuickLaTeX.com \[ c^2 = a^2+b^2-2ab\cos\theta. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2993092fc0ffed816c9d6e35a30639b9_l3.png)
Подставим теперь в эту формулу все величины, которые даны. В результате получаем следующее выражение:
![Rendered by QuickLaTeX.com \[ \left(\sqrt{19}\right)^2 = 3^2+5^2-2\cdot 3\cdot 5\cos\theta. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0c8c6dace9d97176093cf09526685a11_l3.png)
После всех вычислений и преобразований получаем следующее простое выражение:
![Rendered by QuickLaTeX.com \[ -15=-30\cos\theta\Leftrightarrow \cos\theta = \frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-54394a2f536abb5ca257b906d5598c99_l3.png)
Какой должна быть величина острого угла 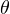 , чтобы его косинус был равен
, чтобы его косинус был равен 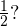 Смотрим в таблицу, которую можно найти в этой статье, и получаем ответ:
Смотрим в таблицу, которую можно найти в этой статье, и получаем ответ:  .
.
Вот так решаются задачи по геометрии с использованием теоремы косинусов для треугольника. Если вы собираетесь сдавать ОГЭ или ЕГЭ по математике, то этот материал вам нужно освоить обязательно. Соответствующие задачи почти наверняка будут на экзамене. Потренируйтесь самостоятельно в их решении. Выполните следующие задания:
- В треугольнике ABC сторона AB равна 4 см, сторона BC равна 6 см, угол B равен 30°. Найдите сторону AC.
- В треугольнике ABC сторона AB равна 10, сторона BC равна 8, сторона AC равна 9. Найдите косинус угла A.
Свои ответы и варианты решения пишите в комментариях. Удачи вам!
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
yourtutor.info
Теорема косинусов. Следствия из теоремы косинусов
Цель урока:
- Повторить ранее изученный теоретический материал, изучить теорему косинусов и её следствия, учить делать теоретические обобщения.
- Развивать логику мышления при решении специально подобранных задач.
- Воспитывать потребность в доказательстве высказанной гипотезы.
Тип урока: урок ознакомления с новым материалом.
Оборудование урока: ноутбук, мультимедийный проектор, интерактивная доска.
Ход урока
I. Сообщение темы, цели и задач урока. Мотивация учебной деятельности.
II. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний
(Фронтальная работа с классом)
III. Изучение нового материала.
Учащимся предлагается задача на готовом чертеже. Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол.
Первый способ решения задачи. (Устно)
Дано: ABC, AC = b, AB = c. A __________________ Найти: BC = a = ? |
Проведём CH – высоту. 1) Прямоугольный ACH: AH = bcosA, CH = или CH = bsinA BH = AB – AH. CB2 = a2 = CH2 + BH2 a = . |
Рис. 4 |
Второй способ решения задачи. Координатный метод.
| 1. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату.
Решение записывают все учащиеся. |
|
2. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA). 3. Найдём квадрат стороны BC:
|
Рис. 5 |
Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
По теореме косинусов можно найти любую сторону треугольника, зная длины двух других сторон и угол между ними.
Теорему косинусов иногда называют обобщённой теоремой Пифагора. Почему? Объясните.
Если С = 90°, то cosC = 0 и 2abcosC = 0, тогда c2 = a2 + b2.
Вывод: Теорема Пифагора является частным случаем теоремы косинусов.
Рассмотрим следствия из теоремы косинусов.
| 1 следствие. | ||
| Дано:
ABC AC = b, AH = bc __________________ Найти: a |
Решение:
Возможны 2 случая: а) A – острый, то cosA > 0, б) A – тупой, то cosA < 0, а) Если A – острый, тогда по теореме косинусов a2 = b2 + c2 – 2bccosA |
Рис. 6 |
В прямоугольном ACH: bc = bcosA. Так как A – острый, то cosA > 0, тогда a2 = b2 + c2 – 2bcc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой. Случай, когда угол, лежащий против неизвестной стороны тупой рассмотреть самостоятельно. Следующий урок начнём с проверки этого задания. (т.к. cosA < 0, то a 2 = b2 + c2 + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой. |
||
| 2 следствие. | ||
Дано: ABCD – параллелограмм, AB = CD =a, BC = AD = b. __________________ Найти: d12 + d22 . |
Решение: ABC: d12 = a2 + b2 – 2abcosB. ABD: d22 = a2 + b2 – 2abcosA = a2 + b2 – 2abcos(180° — B) = a2 + b2 + 2abcosB. d12 + d22 = 2 a2 + 2 b2. |
Рис. 7 |
Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. |
||
| 3 следствие. | ||
Дано: ABC, AB = c, AC = b, BC = a. __________________ Найти: ma |
Решение: Достроим ABC до параллелограмма ABA 1C.AA12 + BC2 = 2b2 + 2c2 . BC = a, 2ma = AA1. (2ma)2 + a2 = 2b2 + 2c2 4ma2 = 2(b2 + c2) – a2 ma2 = ma = mb = mc = |
Рис. 8 |
Вывод: В любом треугольнике со сторонами a, b и c длины медиан ma, mb, mc вычисляются по формулам: ma = , mb = , mc = . |
||
IV. Первичное осмысление и закрепление связей и отношений в объектах изучения.
Задача: В треугольнике две стороны равны 20 см и 21 см, а синус угла между ними равен 0,6. Найти третью сторону. Сколько решений имеет задача?
V. Домашняя работа:
п. 98 №1025(б, в, г).
VI. Подведение итогов урока.
urok.1sept.ru
Теорема косинусов. Решение задач.





 Теорема косинусов. Решение задач.
Теорема косинусов. Решение задач.Цели: научить учащихся применять теорему косинусов и следствия из неё
при решении задач.
Ход урока
Организационный момент.
Актуализация опорных знаний
1. Сформулировать теорему о площади треугольника (вычисление площади по двум сторонам и углу между ними).
2. Сформулировать теорему синусов.
3. Сформулировать теорему косинусов.
4. При решении, каких задач, мы уже использовали теорему косинусов? (Нахождение стороны по двум другим заданным сторонам и углу между ними; нахождение угла треугольника по трём известным сторонам.)Решение задач и создание проблемных ситуаций при их решении.
№ 1. Найдите неизвестную сторону и площадь треугольника АВС,
№ 2. Найдите угол А треугольника АВС, если АВ =АС =1 м, ВС = 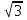 м. Решение.
м. Решение.
Пользуясь теоремой косинусов, получаем: 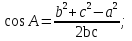 так как AC = b = 1 м, AB = c = 1м , BC = а =
так как AC = b = 1 м, AB = c = 1м , BC = а = 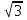 м, то
м, то
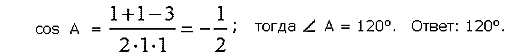
№ 3. Решить задачу № 1031 (в). Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны:
9, 5, 6. (По ходу решения учитель задаёт наводящие вопросы.)
Решение. Пусть 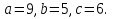
Все ли углы нужно находить?
( Достаточно найти наибольший угол — он лежит против большей из сторон, то есть в данной задаче это угол А.)

Можно ли определить вид треугольника, не вычисляя углы треугольника?
(Вариантов ответа только два: «нет» и «да». Но объяснить почему можно иначе — не могут.)
Рассмотрим теорему косинусов и проведём её исследование при различных значениях угла между сторонами a и b:
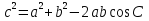
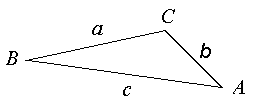
Если угол С острый, то
 следовательно,
следовательно,  .
.Если угол С прямой, то
 следовательно,
следовательно,  .
.Если угол С тупой, то
 следовательно,
следовательно,  .
.
Воспользуемся полученными следствиями из теоремы косинусов при решении следующих задач.
№ 4. Решить задачу № 1031(б). Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны: 17, 8, 15.
Решение.
Пусть 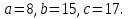

Наибольшая сторона треугольника с, поэтому сравним её квадрат с суммой квадратов двух других сторон.
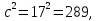
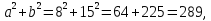 то есть
то есть 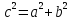 , следовательно, угол С прямой.
, следовательно, угол С прямой.
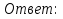 треугольник прямоугольный.
треугольник прямоугольный.
№ 5. В треугольнике АВС угол С равен 45о, АС = 5 см, ВС = 9 см. Найдите угол А.
Решение.
Найдём сторону АВ по теореме косинусов:
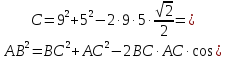
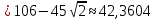 ;
;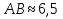 .
.
Как будем искать угол А? (Мнения разделились: одни предлагают по теореме синусов, другие – по теореме косинусов. Предлагаю решить 1 варианту по теореме косинусов, а варианту 2 – по теореме синусов.) Двое учащихся у доски воспроизводят свои варианты решений.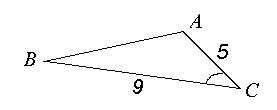
Решение 1 варианта.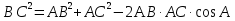 , тогда
, тогда
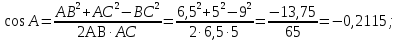
угол А – тупой, А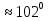 .
.
Решение 2 варианта.
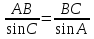 ; тогда
; тогда 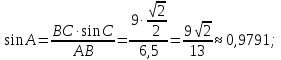
А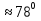
Почему получились разные значения одного и того же угла? Задача имеет несколько решений? (Некоторые из учащихся заметили, что сумма получившихся значений угла А равна 180о и сообщили, что во 2-ом варианте надо было брать угол не 78о , а 102о , так как их синусы равны.)
При решении по теореме синусов необходимо было вначале выяснить вид угла А, воспользовавшись следствиями из теоремы косинусов. В нашем случае: 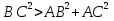 , т.к.
, т.к. 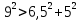 ;
; 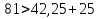 ,
,
следовательно угол А – тупой.
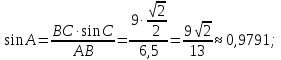 тогда А
тогда А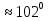 .
.
Подведение итогов урока.
Домашнее задание: выучить материал пунктов 100-102 (стр. 252-254), решить задачи № 1031(а), 1025(е).
infourok.ru
КОСИНУСОВ ТЕОРЕМА — это… Что такое КОСИНУСОВ ТЕОРЕМА?
- КОСИНУСОВ ТЕОРЕМА
квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними, т. е.

где а, 6, с- стороны треугольника, а С — угол между сторонами аи b.
Ю.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- КОСИНУС ГИПЕРБОЛИЧЕСКИЙ
- КОСИНУС-ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Смотреть что такое «КОСИНУСОВ ТЕОРЕМА» в других словарях:
КОСИНУСОВ ТЕОРЕМА — теорема тригонометрии, устанавливающая соотношения между сторонами a, b, c произвольного треугольника и косинусом угла С между сторонами a и b: c2 = a2 + b2 2abcosC … Большой Энциклопедический словарь
косинусов теорема — теорема тригонометрии, устанавливающая соотношения между сторонами а, b, с произвольного треугольника и косинусом угла C между сторонами а и b: с2 = a2 + b2 – 2ab cos C. * * * КОСИНУСОВ ТЕОРЕМА КОСИНУСОВ ТЕОРЕМА, теорема тригонометрии,… … Энциклопедический словарь
Косинусов теорема — Теорема косинусов обобщение теоремы Пифагора. Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними. Для плоского треугольника со сторонами a,b,c и углом α… … Википедия
Косинусов теорема — теорема тригонометрии, утверждающая, что квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними; c2 =а2 + b2 2ab cos α, где а, b, с… … Большая советская энциклопедия
КОСИНУСОВ ТЕОРЕМА — теорема тригонометрии, устанавливающая соотношения между сторонами а, b, с произвольного треугольника и косинусом угла С между сторонами а и b: с2 = а2 + b2 2ab cos С … Естествознание. Энциклопедический словарь
Теорема Лежандра (сферическая тригонометрия) — Теорема Лежандра в сферической тригонометрии позволяет упростить решение сферического треугольника, если известно, что его стороны достаточно малы по сравнению с радиусом сферы, на которой он расположен. Формулировка … Википедия
Теорема косинусов — Теорема косинусов теорема евклидовой геометрии, обобщающая теорему Пифагора: Для плоского тре … Википедия
Теорема Пифагора — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 … Википедия
Теорема тангенсов — Рис. 1. Треугольник В тригонометрии, теорема тангенсов[1] это теорема, связывающая между собой тангенсы двух углов треуг … Википедия
Теорема синусов (сферическая геометрия) — Сферическая теорема синусов устанавливает пропорциональность между синусами сторон a, b, c и синусами противолежащих этим сторонам углов A, B, C сферического треугольника: Сферическая теорема синусов является аналогом плоской теоремы синусов и… … Википедия
dic.academic.ru
Теорема синусов | Формулы и расчеты онлайн
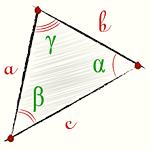
Теорема синусов гласит
Стороны треугольника пропорциональны синусам противолежащих углов
\[ \frac{a}{\sin(α)} = \frac{b}{\sin(β)} = \frac{c}{\sin(γ)} \]
Также отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.
\[ \frac{a}{\sin(α)} = \frac{b}{\sin(β)} = \frac{c}{\sin(γ)} = 2R \]
Вычислить, найти сторону треугольника по теореме синусов
Пусть известно: две стороны a, b и угол между ними γ. Нужно найти сторону c и недостающие углы α и β. Используем то, что сумма углов треугольника 180°
\[ β = (180° — (α + γ)) \]
\[ \frac{a}{\sin(α)} = \frac{b}{\sin(180° — (α + γ))} \]
По формулам приведения
\[ \sin(180° — (α + γ)) = \sin(α + γ) \]
Подставим в (4)
\[ \frac{a}{\sin(α)} = \frac{b}{\sin(α + γ)} \]
по формуле синуса суммы углов разделим углы
\[ \sin(α + γ) = \sin(α)·\cos(γ) + \cos(α)·\sin(γ) \]
Получим
\[ \frac{b}{a} = \frac{\sin(α)·\cos(γ) + \cos(α)·\sin(γ)}{\sin(α)} \]
\[ \frac{b}{a} = \cos(γ) + \ctg(α)·\sin(γ) \]
Отсюда найдутся все углы треугольника α и β (см. формула (3)):
\[ \ctg(α) = \frac{\frac{b}{a} — \cos(γ)}{\sin(γ)} \]
Далее теорема синусов позволит найти оставшуюся сторону c
\[ с = b\frac{\sin(γ)}{\sin(β)} = a\frac{\sin(γ)}{\sin(α)} \]
Вычислить, найти две стороны треугольника по теореме синусов
Пусть известно: одна сторона с, и два прилегающих к ней угла α и β. Нужно найти угол γ и стороны a и b. Используем то, что сумма углов треугольника 180°
\[ γ = (180° — (α + β)) \]
Теперь когда все углы треугольника известны, а также известна одна сторона, теорема синусов позволит легко найти недостающие стороны:
\[ a = c \frac{\sin(α)}{\sin(γ)} \]
\[ b = c \frac{\sin(β)}{\sin(γ)} \]
В помощь студенту
Теорема синусов |
стр. 238 |
|---|
www.fxyz.ru

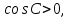 следовательно,
следовательно, 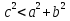 .
.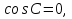 следовательно,
следовательно, 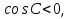 следовательно,
следовательно, 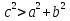 .
.