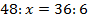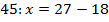Нахождение неизвестного слагаемого, множителя, и т.п.: правила, примеры, решения

Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.

Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.

Нахождение неизвестного слагаемого

Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9. Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x. Согласно первоначальному условию, это число вместе с 4 образуют 9, значит, можно записать уравнение 4+x=9. Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x? Для этого надо использовать правило:

Определение 1

Для нахождения неизвестного слагаемого надо вычесть известное из суммы.

В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a+b=c, то c−a=b и c−b=a, и наоборот, из выражений c−a=b и c−b=a можно вывести, что a+b=c.

Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.

Пример 1

Возьмем то уравнение, что у нас получилось выше: 4+x=9. Согласно правилу, нам нужно вычесть из известной суммы, равной 9, известное слагаемое, равное

zaochnik.com

46. Видеоурок. Математика 4 Класс

На этом уроке мы рассмотрим решение уравнений с неизвестным делимым и неизвестным делителем. Повторим, что такое уравнение и что такое «решить уравнение». Вспомним компоненты деления и их связи между собой. Решим несколько уравнений на нахождение неизвестного делимого и нахождение неизвестного делителя.

Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают любой латинской буквой.

Рассмотрите данные записи: только одна из них является уравнением, скажите какая.

· 

·

·

·

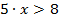
Конечно же, это первая запись. Частное неизвестного числа и числа 6 равно разности чисел 18 и 5. На уроке мы научимся решать уравнения данного вида.

Решить уравнение – это найти значение неизвестного, при котором равенство будет верным (или доказать, что таких значений не существует).

Пример 1

Решите уравнение:

 

Решение

Упростим уравнение, для этого найдем значение выражения в правой части. Значение разности чисел 18 и 5 равно 13, левую часть переписываем так, как она есть, а справа записываем 13:

 

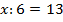
Пример 1

Решите уравнение:

 

Решение

Упростим уравнение, для этого найдем значение выражения в правой части. Значение разности чисел 18 и 5 равно 13, левую часть переписываем так, как она есть, а справа записываем 13:

 

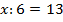
Для того чтобы найти неизвестное делимое, надо частное умножить на делитель.

 

 – это корень уравнения.

Проверка

Значение корня 78 подставим вместо неизвестного числа.

 

Вычислим левую и правую часть. Значение частного – 13, значение разности – тоже 13. Значит, уравнение решено верно.

Ответ: .

Решите уравнение:

 

Решение

Частное неизвестного числа и числа 5 равно сумме чисел 49 и 11. Сначала упростим уравнение, вычислим значение правой части: . Левую часть от знака равно переписываем, а справа запишем значение суммы:

 

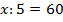
Чтобы найти делимое, нужно значение частного умножить на делитель.

 

 – это корень уравнения.

Проверка

Подставим значение корня вместо неизвестного числа.

 

Выполним вычисления:

, то есть значение частного равно значению суммы.

Ответ: .

Решите уравнение:

 

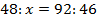
Решение

Частное чисел 48 и неизвестного числа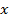

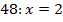
 равно частному чисел 92 и 46. Упростим уравнение. Левую часть переписываем, а в правой произведем вычисления:

Чтобы найти делитель, нужно значение делимого разделить на значение частного.

 

 – корень уравнения.

Проверка

Подставим найденное значение неизвестного числа в уравнение:

 

 

Уравнение решено верно.

Ответ: .

Сравним все уравнения.

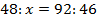
В одних мы искали неизвестный делитель, в других – неизвестное делимое. Но каждый раз мы следовали некому алгоритму:

1. Упростить уравнение: найти значение правой части.

2. Использовать знания о связи компонентов при делении.

3. Сделать проверку

 

Список литературы

1. Петерсон Л.Г. Математика. 4 класс. Учебник в 3 ч. – М.: 2013. – 96 с. + 128 с. +96 с.
2. Математика: учеб. для 4-го кл. общеобразоват. учреждений с рус. яз. обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.Л. Дрозд, А.А. Столяр; пер. с бел. яз. Л.А. Бондаревой. – 3-е изд., перераб. – Минск: Нар. асвета, 2008. – 134 с.: ил.
3. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2010.

 

Домашнее задание

1. Решите уравнения:
   
   
   
   
   

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Interneturok.ru (Источник).
2. Интернет-портал Interneturok.ru  (Источник).
3. Интернет-портал Interneturok.ru  (Источник).
4. Интернет-портал Math-prosto.ru (Источник).
5. Интернет-портал Goncharova-potter71.blogspot.com (Источник).

interneturok.ru

«Как найти неизвестное слагаемое. Решение уравнений с неизвестным слагаемым»

Конспект урока математики 2 класс

16 марта 2017 год

Цель урока: создать необходимые условия для вывода обучающимися правила нахождения неизвестного слагаемого.

Задачи урока:

• формировать понятия «уравнение», «корень уравнения»;

• составлять алгоритм решения уравнения;

• закреплять умение составлять уравнения, находить корень уравнения и выполнять проверку правильности вычисления;

• совершенствовать вычислительные навыки, математическую речь, развивать логическое мышление;

• формировать навыки самоконтроля, умение работать в паре;

• формировать умение работать по плану, алгоритму.

Планируемые результаты:

Предметные:

• знать и применять правило нахождения неизвестного слагаемого при решении простых уравнений;

• уметь записывать и решать простые уравнения на нахождение неизвестного слагаемого.

• правильно употреблять в речи математические термины.

Метапредметные:

• познавательные: поиск и выделение необходимой информации; осознанное и произвольное построение речевого высказывания; установление причинно-следственных связей.

• регулятивные: выделение и осознание обучающимися того, что уже усвоено и что ещё подлежит усвоению, сличение способа действия и его результата с заданным эталоном.

• коммуникативные: эмоционально позитивное отношение к процессу сотрудничества, умение слушать собеседника, учёт разных мнений и умение обосновать собственное, уважение иной точки зрения.

• личностные: формирование адекватной позитивной осознанной самооценки, развитие познавательных интересов, учебных мотивов.

• Методы:

Технологическая карта урока

I.

Организация класса. Мотивация учебной деятельности.

Цель: формировать умения производить рефлексию своей деятельности

Сегодня у нас открытый урок. К нам на урок пришли гости, повернитесь к ним, поприветствуем их. Тихо садитесь.

Я рада, что вновь вижу ваши милые лица на нашем очередном уроке математики. Урок сегодня – волнительный, вы встревожены. Давайте попробуем поднять своё настроение, повернитесь друг другу, улыбнитесь, поддержите друг друга:

Ты сегодня не грусти,

Вместе будем мы в пути!

-Молодцы! Изменилось ли ваше настроение? Какое оно стало?

-Посмотрите на доску и выберите себе установку на урок:

Я буду:

— внимательным

-старательным

-трудолюбивым

-любознательным

— В конце урока скажете, выполнили ее или это не удалось. Приступаем к работе.

Запись числа. Классная работа.

Представим число 16 в виде суммы двух чисел, разности двух чисел, в виде произведения двух чисел, в виде разности и произведения чисел.

Да. Спокойное, радостное, исчезли страх и волнение.

II.

Актуализация опорных знаний

Цель: совершенствование вычислительных навыков, повторение состава чисел

1. Поставьте знаки «+» или «–»

2. Заполним таблицу:

Вывод:

3. Задача

От куска ткани длиной 24 м отрезали сначала 6 м, а потом ещё 4 м. Сколько метров ткани осталось в куске?

4. Разгадайте ребус.

5.

На какие группы можно разбить эти математические записи?

Дополни …

Уравнение – это равенство, содержащее … неизвестное число

Неизвестное число в уравнении называется … корнем уравнения

Корень уравнения превращает уравнение в верное… равенство

Числовые равенства, числовые неравенства, уравнения, корни уравнений

Уравнение.

— Равенство, содержащее неизвестное, называется уравнением.

— Корень уравнения – это число, при подстановке которого в уравнение вместо х получается верное числовое равенство.

III.

Выявление места и причины затруднения

Цель: Создание условий для выделения уравнения с неизвестным вычитаемым;

-выявить место затруднения;

-зафиксировать во внешней речи причину затруднения

IV. Формулирование темы и цели урока

— Каждый из вас должен вспомнить, как решаются уравнения.

– Рассмотрите схемы на доске.

— Как вы думаете, открытию, какой закономерности будет посвящён урок?

— Откройте учебник (с.77), отметьте закладкой страницу учебника и прочитайте тему урока.

— Определите цель урока.

Мы, пока плохо можем объяснить, как найти неизвестное слагаемое

Научиться решать уравнения с неизвестным слагаемым.

Решение уравнений с неизвестным слагаемым

V. Открытие новых знаний.

Цель: выделение правила нахождения неизвестного вычитаемого.

Работа в группах

Найдите уравнение, в котором нужно найти неизвестное первое слагаемое, придумайте алгоритм его решения.

Алгоритм на слайде.

— Назовите компоненты при сложении.

— Какой компонент неизвестен? (- Как его найти, используя «Целое» и «Часть».

— Замените «Целое» и «Часть» на название компонентов действий при сложении.

— Как найти неизвестное слагаемое?

Где мы можем найти подтверждение нашим предположениям?

Сравните ваши выводы с тем, что предлагают авторы учебника с.79

Сформулировать правило нахождения неизвестного слагаемого.

Чтобы найти неизвестную часть, надо из целого вычесть известную часть.

VI.Физкультминутка

VII. Первичное закрепление с проговариванием во внешней речи.

Цель: применение правила при решении уравнений

Работа у доски

Страница 79 №6,7

Выполняют задание, проговаривают новое понятие.

VIII. Самостоятельная работа в парах с самопроверкой в классе.

Цель: формирование умения работать в парах, проявлять ответственность за собственный выбор и результаты своей деятельности.

Страница 79. № 8

Умение работать в паре, используя алгоритм

Правило нахождения неизвестного слагаемого.

IX. Систематизация и повторение.

Цель: организовать повторение умений находить все способы решения задач

Где мы можем применить уравнение на уроках математики?

В решении задач.

Решение задачи с объяснением.

На одной полке стояло 32 книги, на другой – 8, сколько книг стоит на третьей полке, если на трех полках 100 книг.

Резерв. Работа по индивидуальным карточкам.

Работа с информацией

Уметь высказывать своё предположение на основе работы с материалом учебника

Х.Рефлексия

Цель: формировать умения производить рефлексию своей деятельности

-Чему новому вы научились сегодня на уроке?

-Какую цель ставили? Достигли цели?

-Какая тема была урока?

Оценивать правильность выполнения действия на уровне адекватной оценки

Способность к самооценке на основе критерия успешности учебной деятельности

Приложение

Лист самоконтроля ______________________________________

На каждом этапе оцени свою работу, выбрав в нужной строке знак «+».

Этап

Учебная деятельность

Выполнил(а) безошибочно

Выполнил (а) с ошибками

Испытывал (а) большие затруднения

Начало урока

Настрой на урок

1 шаг

Повторение пройденного материала. Устный счет

2 шаг

Постановка учебной задачи, цели урока

3 шаг

Работа в группе

4 шаг

Первичное закрепление

Работа по учебнику с.79 №6,7

5 шаг

Самостоятельная работа

с.79 №6,7

6 шаг

Решение задачи.

7 шаг

Применение нового материала в системе знаний

Х + ^{120 = 220}

у – 19= 78

infourok.ru

Урок 26. уравнение. решение уравнений подбором неизвестного числа — Математика — 2 класс

Математика, 2 класс

Урок №26. Уравнение. Решение уравнений подбором неизвестного числа

Перечень вопросов, рассматриваемых в теме:

— Что такое уравнение, корень уравнения?

— Как решить уравнение?

Глоссарий по теме:

Уравнение – равенство, содержащее неизвестное число, которое надо найти.

Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.

Решить уравнение, значит найти его корни.

Основная и дополнительная литература по теме урока

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – С. 80-81.

2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1. – 6-е изд., дораб. – М.: Просвещение, 2016. – С. 60.

3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.

Теоретический материал для самостоятельного изучения

Вы умеете читать буквенные выражения. Например:

Вы уже знаете, что равенства бывают верные и неверные.

Рассмотрим верное равенство с окошком: + 4 = 12

Запишем вместо окошка маленькую латинскую букву , как в буквенное выражение. Какое число надо поместить вместо буквы х, чтобы равенство стало верным?

Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.

х + 4 = 12

х = 8

8 + 4 = 12

Равенство с буквой , которое мы записали – это уравнение.

Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.

Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется корень уравнения.

Решим уравнение 10 – d = 6 способом подбора.

Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим d в уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.

Попробуем взять другое число. Например, 4. При подстановке его вместо d получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.

Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число 20, вторая «часть» – это число х.

20 х

27

Воспользуемся правилом,

ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ

Запишем равенства:

20 + x = 27

27 – x = 20

Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: х — это «целое», а 30 и 6 – это части.

30 6

х

Воспользуемся правилом,

Вывод: Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Когда решение уравнения находится легко, пользуются способом подбора. Нужно подобрать такое число, чтобы получилось верное равенство.

Тренировочные задания.

1. Соедините уравнение с его решением.

Правильные ответы:

2. Выберите и подчеркните среди математических записей уравнения.

15 + 6 = 21

17 – d

b + 3 = 12

3 + 5 > 6

48 – a = 8

9 + e < 39

k – 4 = 10

Правильные ответы:

15 + 6 = 21

17 – d

b + 3 = 12

3 + 5 > 6

48 – a = 8

9 + e < 39

k – 4 = 10

resh.edu.ru

Вычислите неизвестные числа

Если в задании говорится «вычислите неизвестные числа», речь идет определенно о вычислении неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого или делителя.
Решение таких заданий начинается с самых простых вариантов уравнений, у которых в одной части уравнения находится частное, произведение, разность или сумма двух чисел, одно из которых является неизвестным, а в другой — числовое значение.
Очень важно научиться безошибочно находить решение таких уравнений, так как в последствии они начинают усложняться, состоят из большего количества чисел, содержать не одну, а несколько арифметических операций скобки и т.д.
Рассмотрим задания самые простые и чуть более сложные.
 
Пример 1.
Вычислим неизвестные числа:
1) 2784 — х = 579;
2) у: 17=1524;
3) с — 987 = 64432.
 
Решение.
1) 2784 — х = 579;
х = 2784 — 579;
х = 2205.
 
2) у: 17=1524;
у = 1524 * 17;
у = 25908.
 
3) с — 987 = 64432;
с = 64432 + 987;
с = 65419.
 
Ответ. 2205; 25908; 65419.
 
Пример 2.
Вычислим неизвестное число:
23 * (х — 19) = 414.
 
Решение.
Проанализируем данное уравнение. Первой выполняется операция умножения, поэтому неизвестным у нас является втором множитель (х — 19), который в свою очередь состоит из уменьшаемого и вычитаемого.
Первое, что мы должны сделать — это найти неизвестный множитель:
х — 19 = 414 : 23;
х — 19 = 18.
Мы пришли к простейшему уравнению, в котором неизвестным является уменьшаемое:
х = 18 + 19;
х = 37.
 
Ответ. 37.
Если в задании говорится «вычислите неизвестные числа», речь идет определенно о вычислении неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого или делителя.
Решение таких заданий начинается с самых простых вариантов уравнений, у которых в одной части уравнения находится частное, произведение, разность или сумма двух чисел, одно из которых является неизвестным, а в другой — числовое значение.
Очень важно научиться безошибочно находить решение таких уравнений, так как в последствии они начинают усложняться, состоят из большего количества чисел, содержать не одну, а несколько арифметических операций скобки и т.д.
Рассмотрим задания самые простые и чуть более сложные.
 
Пример 1.
Вычислим неизвестные числа:
1) 2784 — х = 579;
2) у: 17=1524;
3) с — 987 = 64432.
 
Решение.
1) 2784 — х = 579;
х = 2784 — 579;
х = 2205.
 
2) у: 17=1524;
у = 1524 * 17;
у = 25908.
 
3) с — 987 = 64432;
с = 64432 + 987;
с = 65419.
 
Ответ. 2205; 25908; 65419.
 
Пример 2.
Вычислим неизвестное число:
23 * (х — 19) = 414.
 
Решение.
Проанализируем данное уравнение. Первой выполняется операция умножения, поэтому неизвестным у нас является втором множитель (х — 19), который в свою очередь состоит из уменьшаемого и вычитаемого.
Первое, что мы должны сделать — это найти неизвестный множитель:
х — 19 = 414 : 23;
х — 19 = 18.
Мы пришли к простейшему уравнению, в котором неизвестным является уменьшаемое:
х = 18 + 19;
х = 37.
 
Ответ. 37.
 

ru.solverbook.com

Алгебраические уравнения с одним неизвестным, линейные уравнения

Уравнение с неизвестным может быть изначально равно нулю, если в нем отсутствуют степени, то оно линейное и выглядит так:

ax + b = 0

«a» и «b» — это любые числа, но обычно a ≠ 0 («a» не может быть нулем, иначе неизвестного тоже не будет)

Пример:

3x — 2 + 9 — 2x = 0

Сводим ближе соответствующие части:

3x — 2x + 9 — 2= 0

Считаем их:

x + 7 = 0

Как видите, «a» — коэффициент для x равен «1», «b» — число равно «7», а неизвестное x = -7 (если мы переставим цифру в правую часть).

При этом, для удобства решения таких уравнений мы можем также что-то прибавлять в обе части, умножать, делить и т.д.

Например, вот так вполне можно:

(x + 7) + 6 = 0 + 6

так как обе части, по сути, не изменились, мы просто сделали это для удобства расчетов, а потом в нужный момент вычтем эти шестерки:

(x + 7) = 0 + 6 — 6

И снова:

x + 7 = 0

Очень удобно использовать умножение при дробных уравнениях:

Если умножить это уравнение на 12, то мы сократим первую и вторую дробь, т.к. 3*4 = 12. Сделаем это:

16x — (3x + 15) = 24

Раскроем скобки:

16x — 3x — 15 = 24

13x — 15 = 24

13x = 39

x = 3

Подставляем в уравнение:

4 — 8/4 = 2

2 = 2

Тождество!

Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

Добавить новость и получить деньги

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

uchilegko.info