Решение задач №8 Найти общее решение дифференциального уравнения. | Vseznayka

Доброго времени суток. Сегодня будем разбираться с довольно простеньким примерчиком. Нужно ведь хоть когда-то отдыхать. Решать будем линейное дифференциальное уравнение с разделяющимися переменными. С разделяющимися переменными оно называется, потому что можно переменные разделить (очевидно). Именно перенести всё что зависит от одной переменной в одну сторону, а от другой в другую. Запишем сам пример собственно говоря.

Уравнение с разделяющимися переменными.

Уравнение с разделяющимися переменными.

На первый взгляд похоже больше на уравнение в полных дифференциалах. Но это не так. Проведём элементарные преобразования. Для начала перенесём что-нибудь в правую часть.

Далее отправим y из правой части в знаменатель в левую часть уравнения и распишем y’.

Воу! Мы на половине пути. Перенесём dy в знаменатель в левую часть. (a+1)/(a+1). a в нашем интеграле это квадратный корень. Запишем решённый интеграл в левую часть дифференциального уравнения (разумеется без константы), а правую часть диффура проинтегрируем по таблице (запишем с константой). В итоге получим такую картину:

Получили общее решение в неявном виде. Остаётся выразить y в левой части и мы получим общее решение. Возведём левую и правую части в квадрат, дабы избавиться от корня. Четвёрку переносим в правую часть и выражаем игрек. Нельзя забывать про плюс-минус, ведь значение под корнем всегда больше нуля и при избавлении от него, появляется модуль. Записываем общее решение:

Общее решение.

Общее решение.

Сегодня был разминочный пример однако. Ну ничего, в следующие разы отыграемся. Если вам было слишком просто, попрошу ознакомиться с другим диффуром (ЛНДУ), решали мы его двумя разными способами методом Бернулли (Решение задач № 6) и методом вариации произвольной постоянной (Решение задач № 7). А на сегодня всё. Спасибо за внимание.

Другие темы:

Неоднородное дифференциальное уравнение третьего порядка

Неоднородное дифференциальное уравнение по сложности вычислений можно разделить на два типа: первый имеет неоднородную функцию, которая не связана с решением однородного уравнения. Второй тип предполагает, что неоднородная часть ДУ может содержать экспоненту, синусы и косинусы или произведения экспонент на синусы и косинусы. Первый из вариантов ДУ подробно рассмотрен на предыдущих уроках. Далее будут проанализированы готовые ответы на сложные неоднородные ДУ 3 порядка: в этой статье задания, содержащие экспоненту, в последующих — тригонометрические функции.
Сразу хочу обратить Ваше внимание что на важных моментах при вычислениях отмечено и их следует заучить или выписать. В общем материал должен Вам понравиться и помочь в учебе!

Как решить неоднородное дифференциальное уравнение?

Пример 1. (10.16) Найти общее решение дифференциального уравнения:

Решение. Имеем неоднородное дифференциальное уравнение третьего порядка — одно из сложных в данном разделе. Его решение ищем через сумму решений однородного и неоднородно диф. уравнений . Найдем каждый из корней, для этого выполняем анализ однородного дифференциального уравнения

Его решение ищем в виде суммы экспоненциальных функций
y=exp(k*x).
При подстановке в однородное уравнение и делении на exp(k*x) (всегда больше нуля) получим характеристическое уравнение

Поскольку уравнение кубическое то один из корней ищем среди простых множителей свободного члена другие два — с неполной квадратного уравнения, которое останется
(k²-1)(k-3)=0.
В результате получим следующие значения

Так как корни характеристического уравнения различны действительные числа то решение имеет вид суммы произведения констант на экспоненты в соответствующих степенях

Правая часть дифференциального уравнения (4-8x)e^xимеет вид полинома умноженного на степенную зависимость экспоненты P(x)e^x, причем коэффициент в показательной функции является корнем характеристического уравнения (k=1),поэтому частичное решение запишем в виде

Определим А и В, входящие в формулу функции. Для этого подставим y в дифференциальное уравнение и приравняем коэффициенты при одинаковых степенях x. Вычисляем производные до третьего порядка

и подставляем в исходное дифференциальное уравнение. После объединения подобных слагаемых получим зависимость

Отсюда при одинаковых степенях переменной определяем сталые A=1, B=-1.
Таким образом частичное решение ДУ можем записать формулой

Общее решение дифференциального уравнения находим суммированием функций

Здесь С₁, С₂, С₃ – сталые, которые принимают произвольные значения. Доопределить их можем только при наличии условия Коши для функции.
Теперь Вы знаете, как решить неоднородное дифференциальное уравнение 3 порядка и как составить характеристическое уравнение.

 

Пример 2. (10.22) Найти общее решение дифференциального уравнения

Решение:Решим неоднородное дифференциальное уравнение третьего порядка через суперпозицию двух корней. .
Опуская выкладки которые можно прочитать с предыдущей задачи запишем характеристическое уравнение для однородного диф. уравнения и найдем его корни

Поскольку два корни одинаковы то общий интеграл однородного ДУ имеет вид

Правая часть данного уравнения 4x*e^x имеет вид полинома первой степени P(x) умноженного на экспоненциальную функцию exp(x),поэтому и частичное решение уравнения ищем в таком же виде

Находим производные до третьего порядка

и подставляем в исходное ДУ. После объединения подобных слагаемых получим

Отсюда находим сталые – А=1; В=0. Можем записать явный вид частного решения ДУ

Общий интеграл дифференциального уравнения находим как сумму найденных функций

На этом задача решена.

 

Пример 3.(10.24) Найти общее решение дифференциального уравнения:

Решение:Корни неоднородного дифференциальное уравнение третьего порядка по известной Вам схеме ищем в виде суммы
Для однородного дифференциального уравнения характеристическое уравнение имеет вид

Решив его, получим три корня, причем один кратности 2

В таких случаях ответ записываем формулой

Правая часть неоднородного диф. уравнение -(8x+4)*e^x имеет вид P(x)e^x, при этом степень экспоненты не совпадает с характеристическими корнями, поэтому в аналогичном виде ищем частичное решение

Находим производные до третьего порядка

Подставляем их в дифференциальное уравнение и группируем общие слагаемые, в результате получим

откуда, приравняв коэффициенты при одинаковых степенях аргумента, определяем стали A=1; B=0.
Таким образом частичное решение уравнения можем записать зависимости

Далее суммированием находим общее решение дифференциального уравнения

Как можно убедиться из приведенных задач вычисления не слишком сложные. Если есть задачи которые трудно самостоятельно решить — просьба присылать их нам на почту. Мы постоянно ищем и подбираем задачи которые научат Вас нового и в полной мере раскроют тему.
Во время учебы Вам приходилось брать куда сложные производные и интегралы, схема решения неоднородных уравнений довольно простая и ее под силу запомнить каждому.
Чтобы материал Вам лучше запомнился найдите в методичках по которым учитесь похожие дифференциальные уравнения и решите самостоятельно. Поверьте — это намного больше Вам поможет, чем прочитать на сайте и сказать — «Я все понял!». Чтобы потом не было на модули или контрольной вопросов «Как решить неоднородное дифференциальное уравнение?»
И знайте — в случае проблем при решении мы готовы Вам помочь.

Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»

I. Обыкновенные дифференциальные уравнения

1.1. Основные понятия и определения

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

F(x,y,y’)=0, F(x,y,y»)=0, F(x,y,y’,y»,. ., y⁽ⁿ⁾)=0

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Решением дифференциального уравнения называется такая функция , которая обращает это уравнение в тождество.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение

Примеры.

1. Рассмотрим дифференциальное уравнение первого порядка

Решением этого уравнения является функция y = 5 ln x. Действительно, , подставляя y’ в уравнение, получим – тождество.

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.

2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция – решение этого уравнения.

Действительно, .

Подставляя эти выражения в уравнение, получим: , – тождество.

А это и значит, что функция – есть решение этого дифференциального уравнения.

Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.

Общим решением дифференциального уравнения

называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

Примеры

1.Найти частное решение дифференциального уравнения первого порядка

xdx + ydy = 0, если y = 4 при x = 3.

Решение. Интегрируя обе части уравнения, получим

Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .

— общее решение дифференциального уравнения.

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3² + 4²= C²; C=5.

Подставляя С=5 в общее решение, получим x² +y² = 5².

Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.

2. Найти общее решение дифференциального уравнения

Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .

Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .

Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y)  удовлетворяющее начальному условию y(x₀) = y₀, называется задачей Коши.

Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x₀) = y₀, называется решением задачи Коши.

Решение задачи Коши имеет простой геометрический смысл.

Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y)  при условии y(x₀) = y₀,, означает найти интегральную кривую уравнения y’ = f(x,y)  которая проходит через заданную точку M₀(x₀,y₀).

II. Дифференциальные уравнения первого порядка

2.1. Основные понятия

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.

В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.

Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.

Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.

Пример. Рассмотрим дифференциальное уравнение первого порядка .

Решением этого уравнения является функция .

Действительно, заменив в данном уравнении, его значением, получим

то есть 3x=3x

Следовательно, функция является общим решением уравнения при любом постоянном С.

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1  в общее решение уравнения , получим откуда C = 0.

Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.

2.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x)  и g(y)– заданные функции.

Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».

Уравнение вида называется уравнением с разделёнными переменными.

Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и

f(x), C произвольная постоянная.

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными

1. Производную функции переписать через её дифференциалы
2. Разделить переменные.
3. Проинтегрировать обе части равенства, найти общее решение.
4. Если заданы начальные условия, найти частное решение.

Пример 1

Решить уравнение y’ = xy

Решение. Производную функции y’ заменим на

разделим переменные

проинтегрируем обе части равенства:

Ответ:

Пример 2

Найти частное решение уравнения

2yy’ = 1- 3x², если y₀ = 3

при x₀ = 1

Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда

Интегрируя обе части последнего равенства, найдем

Подставив начальные значения x₀ = 1, y₀ = 3 найдем С 9=1-1+C, т.е. С = 9.

Следовательно, искомый частный интеграл будет или

Пример 3

Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом

Решение. Согласно условию

Это уравнение с разделяющимися переменными. Разделив переменные, получим:

 Проинтегрировав обе части уравнения, получим:

Используя начальные условия, x = 2

  и y = — 3 найдем C:

Следовательно, искомое уравнение имеет вид

2.3. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)

где f(x) и g(x) — некоторые заданные функции.

Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид:  y’ = f(x)y

Если то уравнение y’ = f(x)y + g(x) называется неоднородным.

Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.

В частности, если С =0, то решением является  y = 0

Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: .

Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,

т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.

Для линейного неоднородного уравнения вида y’ = kx + b,

где k и b— некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .

Пример. Решить уравнение y’ + 2y +3 = 0

Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .

Следовательно, где С – произвольная постоянная.

Ответ:

2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.

 Алгоритм решения линейного дифференциального уравнения первого порядка

y’ = f(x)y + g(x)

1. Ввести подстановку y=uv.

2. Продифференцировать это равенство y’ = u’v + uv’

3. Подставить y и y’ в данное уравнение:   u’v + uv’ = f(x)uv + g(x) или u’v + uv’ +  f(x)uv = g(x).

4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:

5. Из скобки, приравняв ее к нулю, найти функцию

Это уравнение с разделяющимися переменными:

Разделим переменные и получим:

Откуда . .

6. Подставить полученное значение v в уравнение (из п.4):

и найти функцию Это уравнение с разделяющимися переменными:

7. Записать общее решение в виде: , т.е. .

Пример 1

Найти частное решение уравнения y’ = -2y +3 = 0  если y =1  при x = 0

Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’

Подставляя y и y’ в данное уравнение, получим

Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки

Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)

Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:

Подставим полученное значение v в уравнение Получим:

Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:

Ответ:

III. Дифференциальные уравнения высших порядков

3.1. Основные понятия и определения

Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0

Общим решением дифференциального уравнения второго порядка называется функция вида , в которую входят две произвольные постоянные C₁ и C₂.

Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C₁ и C₂.

3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.

Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.

2. Составить его характеристическое уравнение, обозначив y» через r², y’  через r, yчерез 1:r² + pr +q = 0

3. Вычислить дискриминант  D = p² -4q и найти корни характеристического уравнения; при этом если:

а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C₁ и C₂ — произвольные постоянные.

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде

в) D < 0; следовательно, характеристическое уравнение имеет комплексные корни, Общее решение дифференциального уравнения выражается, в виде 

Примеры.

1. Найти частное решение дифференциального уравнения

Решение. Составим характеристическое уравнение

D>0,

Общее решение

Дифференцируя общее решение, получим

Составим систему из двух уравнений

Подставим вместо ,и заданные начальные условия:

Таким образом, искомым частным решением является функция

.

2. Найти частное решение уравнения

Решение

<0,

Общее решение

— частное решение.

IV. Практическая работа

Вариант 1

1. Составить уравнение кривой, проходящей через точку M(1;2) и имеющей угловой коэффициент .

2. Найти частные решения дифференциальных уравнений:

а)

б)

в)

г)

Вариант 2

1. Составить уравнение кривой, проходящей через точку M(2;1) и имеющей угловой коэффициент

2. Найти частные решения дифференциальных уравнений:

а)

б)

в)

г)

V. Ответы

Вариант 1	Вариант 2
1.	1.
2. а)	2. а)
б)	б)
в)	в)
г)	г)

Дифференциальные уравнения — Неопределенные коэффициенты

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-9: Неопределенные коэффициенты

В этом разделе мы рассмотрим первый метод, который можно использовать для нахождения частного решения неоднородного дифференциального уравнения.

\[y» + p\left( t \right)y’ + q\left( t \right)y = g\left( t \right)\]

Одним из основных преимуществ этого метода является то, что он сводит задачу к задаче по алгебре. Иногда алгебра может запутаться, но для большинства задач она не будет слишком сложной. Еще одна приятная особенность этого метода заключается в том, что дополнительное решение не требуется явно, хотя, как мы увидим, в некоторых случаях потребуется знание дополнительного решения, и поэтому мы обычно находим и это.

Этот метод имеет два недостатка. Во-первых, это будет работать только для довольно небольшого класса \(g(t)\). Класс \(g(t)\), для которых работает этот метод, включает в себя некоторые из наиболее распространенных функций, однако существует множество функций, для которых неопределенные коэффициенты просто не будут работать. Во-вторых, это обычно полезно только для дифференциальных уравнений с постоянными коэффициентами.

Метод достаточно прост. Все, что нам нужно сделать, это посмотреть на \(g(t)\) и сделать предположение о форме \(Y_{P}(t)\), оставив коэффициент(ы) неопределенным (и, следовательно, имя метод).Подставьте предположение в дифференциальное уравнение и посмотрите, сможем ли мы определить значения коэффициентов. Если мы можем определить значения коэффициентов, значит, мы угадали правильно, если мы не можем найти значения коэффициентов, значит, мы угадали неправильно.

Обычно легче увидеть этот метод в действии, чем пытаться описать его, поэтому давайте перейдем к некоторым примерам. {5t}}\] Показать решение

Суть здесь в том, чтобы найти частное решение, однако первое, что мы собираемся сделать, это найти дополнительное решение этого дифференциального уравнения.{6т}}\]

На данный момент причина, по которой нужно сделать это в первую очередь, не будет очевидной, однако мы хотим, чтобы вы привыкли находить ее до того, как мы начнем работу по поиску конкретного решения. В конце концов, как мы увидим, полезно иметь под рукой дополнительное решение, и поэтому лучше иметь привычку сначала находить его, прежде чем выполнять работу с неопределенными коэффициентами.

Теперь приступим к поиску конкретного решения. Как упоминалось перед началом этого примера, нам нужно сделать предположение о форме конкретного решения этого дифференциального уравнения.{5t}}\end{выравнивание*}\]

Итак, чтобы наша догадка была решением, нам нужно выбрать \(A\) так, чтобы коэффициенты экспонент по обе стороны от знака равенства были одинаковыми. {5t}}\]

Прежде чем двигаться дальше, давайте еще раз отметим, что мы начали с решения выше, найдя дополнительное решение.Технически это не является частью метода неопределенных коэффициентов, однако, как мы в конечном итоге увидим, наличие этого метода до того, как мы сделаем предположение о конкретном решении, может сэкономить нам много работы и / или головной боли. Поиск дополнительного решения первым — это просто хорошая привычка, поэтому мы постараемся выработать у вас эту привычку в ходе следующих нескольких примеров. На данный момент не беспокойтесь о том, почему это хорошая привычка. Со временем мы поймем, почему это хорошая привычка.

Теперь вернемся к работе.Обратите внимание, что в последнем примере мы все время говорили «конкретное решение», а не «конкретное решение». Это потому, что есть и другие возможности для конкретного решения, которое нам только что удалось найти. Любой из них будет работать, когда дело доходит до записи общего решения дифференциального уравнения.

Говоря об этом… Этот раздел посвящен поиску частных решений, и большинство примеров будут посвящены поиску только частных решений.{5t}}\hspace{0.25in}\hspace{0.25in}y\left( 0 \right) = \frac{{18}}{7}\hspace{0.25in}y’\left( 0 \right) = — \фракция{1}{7}\] Показать решение

Мы знаем, что общее решение будет иметь вид

\[y\left( t \right) = {y_c}\left( t \right) + {Y_P}\left( t \right)\]

, и у нас уже есть как дополнительное, так и частное решение из первого примера, поэтому нам не нужно выполнять дополнительную работу для этой задачи.

Одна из наиболее распространенных ошибок в этих задачах состоит в том, чтобы найти дополнительное решение, а затем, поскольку мы, вероятно, привыкли это делать, применить начальные условия к дополнительному решению, чтобы найти константы.Однако это неверно. Дополнительное решение — это только решение однородного дифференциального уравнения, и мы ищем решение неоднородного дифференциального уравнения, и начальные условия должны удовлетворять этому решению, а не дополнительному решению. {5t}}\]

Это будет единственная IVP в этом разделе, поэтому не забывайте, как это делается для неоднородных дифференциальных уравнений!

Давайте посмотрим на другой пример, который даст второй тип \(g(t)\), для которого будут работать неопределенные коэффициенты.

Пример 3. Найдите частное решение следующего дифференциального уравнения. \[y» — 4y’ — 12y = \sin \left( {2t} \right)\] Показать решение

Опять же, давайте отметим, что нам, вероятно, следует найти дополнительное решение, прежде чем мы перейдем к угадыванию конкретного решения. Однако, поскольку однородное дифференциальное уравнение для этого примера такое же, как и для первого примера, мы не будем здесь этим заниматься.

Теперь давайте возьмем опыт из первого примера и применим его здесь.В первом примере была экспоненциальная функция в \(g(t)\), и наше предположение было экспоненциальным. Это дифференциальное уравнение имеет синус, поэтому давайте попробуем следующее предположение для конкретного решения.

\[{Y_P}\left( t \right) = A\sin \left( {2t} \right)\]

Дифференцирование и подстановка в дифференциальное уравнение дает,

\[ — 4A\sin \left( {2t} \right) — 4\left( {2A\cos \left( {2t} \right)} \right) — 12\left( {A\sin \left( { 2t} \right)} \right) = \sin \left( {2t} \right)\]

Сбор одинаковых терминов дает

\[ — 16A\sin \left( {2t} \right) — 8A\cos \left( {2t} \right) = \sin \left( {2t} \right)\]

Нам нужно выбрать \(A\) так, чтобы мы получили одну и ту же функцию по обе стороны от знака равенства.Это означает, что коэффициенты синусов и косинусов должны быть равны. Или

\[\begin{align*}& \cos \left( {2t} \right)\,: & — 8A & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}A = 0\\ & \ sin \left( {2t} \right)\,:& — 16A & = 1\hspace{0. 25in} \Rightarrow \hspace{0.25in}A = — \frac{1}{{16}}\end{align *}\]

Обратите внимание на две вещи. Во-первых, поскольку в правой части нет косинуса, это означает, что коэффициент должен быть равен нулю на этой стороне.Что еще более важно, у нас есть серьезная проблема здесь. Чтобы косинус выпадал, как и должно быть, чтобы догадка удовлетворяла дифференциальному уравнению, нужно положить \(A = 0\), но если \(A = 0\), синус тоже выпадет выходит, и этого не может быть. Аналогичным образом, выбор \(A\) для сохранения синуса также сохранит косинус.

Это означает, что наша первоначальная догадка была неверной. Если мы получаем несколько значений одной и той же константы или не можем найти значение константы, значит, мы ошиблись.

Одним из приятных аспектов этого метода является то, что когда мы ошибаемся, наша работа часто предлагает исправление. В данном случае проблема заключалась в возникшем косинусе. Итак, чтобы противостоять этому, давайте добавим косинус к нашему предположению.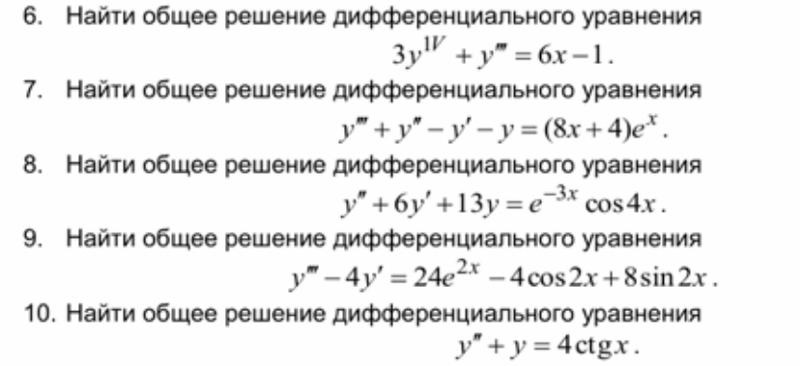 Наша новая догадка —

. \[{Y_P}\left( t \right) = A\cos \left( {2t} \right) + B\sin \left( {2t} \right)\]

Подставляя это в дифференциальное уравнение и собирая подобные члены, получаем,

\[\begin{align*} — 4A\cos \left( {2t} \right) — 4B\sin \left( {2t} \right) — 4\left( { — 2A\sin \left( {2t} \right) + 2B\cos \left( {2t} \right)} \right) — \\ 12\left( {A\cos \left( {2t} \right) + B\sin \left( {2t} \right)} \right) & = \sin \left( {2t} \right)\\ \left( { — 4A — 8B — 12A} \right)\cos \left( {2t} \right) + \left ( { — 4B + 8A — 12B} \right)\sin \left( {2t} \right) & = \sin \left( {2t} \right)\\ \left( { — 16A — 8B} \right) \cos \left( {2t} \right) + \left( {8A — 16B} \right)\sin \left( {2t} \right) & = \sin \left( {2t} \right)\end{ выровнять*}\]

Теперь установим коэффициенты равными

\[\begin{align*} & \cos \left( {2t} \right)\,: &- 16A — 8B & = 0\\ & \sin \left( {2t} \right)\,: & 8A — 16В & = 1\конец{выравнивание*}\]

Решение этой системы дает нам

\[A = \frac{1}{{40}}\hspace{0. 25 дюймов}\hspace{0,25 дюйма}B = — \frac{1}{{20}}\]

Мы нашли константы и на этот раз угадали правильно. Тогда частным решением дифференциального уравнения будет

\[{Y_P}\left( t \right) = \frac{1}{{40}}\cos \left( {2t} \right) — \frac{1}{{20}}\sin \left( {2t} \справа)\]

Обратите внимание: если бы в последнем примере у нас был косинус вместо синуса, то наше предположение было бы таким же. На самом деле, если появились и синус, и косинус, мы увидим, что то же самое предположение также будет работать.3} — т + 3\] Показать решение

Еще раз, опять же, мы обычно сначала хотим получить дополнительное решение, но опять же мы работаем с одним и тем же однородным дифференциальным уравнением (в конце концов вы поймете, почему мы продолжаем работать с одной и той же однородной задачей), поэтому мы снова будем просто ссылаться к первому примеру.

В этом примере \(g(t)\) — кубический многочлен. {n — 1}} + \cdots {A_1}t + {A_0}\)

Обратите внимание, что на самом деле существует только три типа функций, приведенных выше.Если вы думаете об этом, функции одиночного косинуса и одиночного синуса — это действительно частные случаи случая, когда присутствуют и синус, и косинус. Кроме того, мы еще не обосновали догадку для случая, когда присутствуют и синус, и косинус. Мы обосновываем это позже.

Теперь нам нужно перейти к более сложным функциям. Более сложные функции получаются путем произведения и суммы основных видов функций. Давайте сначала посмотрим на продукты.

Пример 5. Найдите частное решение следующего дифференциального уравнения.{4т}}\] Показать решение

Вы, вероятно, устали от вступительного комментария, но опять же, найти дополнительное решение сначала действительно хорошая идея, но опять же, мы уже сделали работу в первом примере, поэтому мы не будем делать это снова здесь. Мы обещаем, что со временем вы поймете, почему мы продолжаем использовать одну и ту же однородную задачу и почему мы считаем хорошей идеей иметь в запасе дополнительное решение. {4t}}\left( {ACt + BC} \ правильно)\]

Если мы умножим \(C\) на одно целое, мы увидим, что догадка может быть записана таким образом, что в действительности есть только две константы.{4т}}\]

Этот последний пример иллюстрирует общее правило, которому мы будем следовать, когда произведения содержат экспоненту. Когда произведение включает экспоненту, мы сначала удаляем экспоненту и записываем предположение для части функции без экспоненты, затем мы вернемся назад и добавим экспоненту без какого-либо ведущего коэффициента.

Давайте посмотрим еще на некоторые продукты. В интересах краткости мы просто запишем догадку для конкретного решения и не будем вдаваться во все подробности нахождения констант.{7t}}\sin \left( {10t} \right)\) Показать решение

Итак, у нас есть экспонента в функции. Помните правило. Мы проигнорируем экспоненту и запишем предположение для \(16\sin\left({10t}\right)\), а затем вернем экспоненту.

Предположение для синуса

\[A\cos \left( {10t} \right) + B\sin \left( {10t} \right)\]

Теперь в качестве фактического предположения для конкретного решения мы возьмем указанное выше предположение и прикрепим к нему экспоненту.2} + BEt + CE} \right)\sin t\end{массив}\]

Обратите внимание, что везде, где встречается одна из неизвестных констант, она находится в произведении неизвестных констант. Это означает, что если бы мы прошли и использовали это как наше предположение, система уравнений, которую нам нужно было бы решить для неизвестных констант, содержала бы в себе произведения неизвестных. Такие типы систем, как правило, очень трудно решить.

Итак, чтобы избежать этого, мы сделаем то же самое, что и в предыдущем примере.{ — 2t}}\left( {3 — 5t} \right)\cos \left( {9t} \right)\) Показать решение

Эта заключительная часть состоит из всех трех частей. Во-первых, мы проигнорируем экспоненту и запишем предположение для.

\[ — \left( {3 — 5t} \right)\cos \left( {9t} \right)\]

Знак минус также можно игнорировать. Предположение для этого

\[\left( {At + B} \right)\cos \left( {9t} \right) + \left( {Ct + D} \right)\sin \left( {9t} \right)\]

Теперь верните экспоненту обратно, и все готово.{ — 2t}}\left( {Ct + D} \right)\sin \left( {9t} \right)\]

Обратите внимание, что мы поставили экспоненту на оба члена.

Есть несколько общих правил, которые нужно помнить для продуктов.

1. Если \(g(t)\) содержит экспоненту, игнорируйте ее и запишите предположение для остатка. Затем верните экспоненту обратно без ведущего коэффициента.
2. Для произведения полиномов и тригонометрических функций сначала запишите предположение только для полинома и умножьте его на соответствующий косинус. Затем добавьте новое предположение для многочлена с другими коэффициентами и умножьте его на соответствующий синус.

Если вы помните эти два правила, вы не ошибетесь с продуктами. Записывать догадки по продуктам обычно не так уж и сложно. Трудность возникает, когда вам действительно нужно найти константы.

Теперь давайте посмотрим на суммы основных компонентов и/или произведения основных компонентов. Для этого нам понадобится следующий факт.

Факт

Если \(Y_{P1}(t)\) является частным решением для

\[y» + p\left( t \right)y’ + q\left( t \right)y = {g_1}\left( t \right)\]

и если \(Y_{P2}(t)\) является частным решением для

\[y» + p\left( t \right)y’ + q\left( t \right)y = {g_2}\left( t \right)\]

, то \(Y_{P1}(t)\) + \(Y_{P2}(t)\) является частным решением для

\[y» + p\left( t \right)y’ + q\left( t \right)y = {g_1}\left( t \right) + {g_2}\left( t \right)\]

Этот факт можно использовать как для нахождения частных решений дифференциальных уравнений, в которых есть суммы, так и для записи предположений для функций, в которых есть суммы. { — 3t}}\cos \left( {6t} \справа) — \sin\слева( {6t} \справа)\) Показать все решения Скрыть все решения a \(g\left( t \right) = 4\cos \left( {6t} \right) — 9\sin \left( {6t} \right)\) Показать решение

Этот первый мы уже рассказали вам, как это сделать.Это в таблице основных функций. Однако мы хотели обосновать догадку, которую мы там изложили. Используя факт о суммах функций, у нас возникло бы искушение записать предположение для косинуса и предположение для синуса. Это даст.

\[\ underbrace {A\cos \left( {6t} \right) + B\sin \left( {6t} \right)}_{{\mbox{угадай косинус}}} + \ underbrace {C\ cos \left( {6t} \right) + D\sin \left( {6t} \right)}_{{\mbox{угадай синус}}}\]

Итак, мы получили бы косинус от каждого предположения и синус от каждого предположения.Проблема с этим предположением заключается в том, что мы собираемся решить только два уравнения после подключения к дифференциальному уравнению, и все же у нас есть 4 неизвестных. Мы никогда не сможем решить для каждой из констант.

Чтобы исправить это замечание, мы можем объединить некоторые термины следующим образом.

\[\left( {A + C} \right)\cos \left( {6t} \right) + \left( {B + D} \right)\sin \left( {6t} \right)\]

После этого мы видим, что у нас действительно есть один косинус с коэффициентом и один синус с коэффициентом, поэтому мы можем просто использовать

\[{Y_P}\left( t \right) = A\cos \left( {6t} \right) + B\sin \left( {6t} \right)\]

Общее эмпирическое правило записи предположений для функций, включающих суммы, состоит в том, чтобы всегда объединять одинаковые члены в отдельные члены с одиночными коэффициентами.Это значительно упростит работу по нахождению коэффициентов.

b \(g\left( t \right) = — 2\sin t + \sin \left( {14t} \right) — 5\cos \left( {14t} \right)\) Показать решение

Для этого мы получим два набора синусов и косинусов. { — 8t} }\]

Обратите внимание, что это произошло из-за того, что у нас было два члена в нашем \(g(t)\), единственным отличием которых был многочлен, стоявший перед ними.{ — 3t}}\left( {B\cos \left( {6t} \right) + C\sin \left( {6t} \right)} \right) + D\cos \left( {6t} \right ) + E\sin\left( {6t} \right)\]

Мы можем комбинировать предположения только в том случае, если они идентичны с точностью до константы. Итак, мы не можем объединить первую экспоненту со второй, потому что вторая на самом деле умножается на косинус и синус, и поэтому две экспоненты на самом деле являются разными функциями. Точно так же последний синус и косинус не могут быть объединены с синусом и косинусом в среднем члене, потому что синус и косинус в среднем члене на самом деле умножаются на экспоненту и поэтому различны.

Итак, при работе с суммами функций убедитесь, что вы ищете идентичные догадки, которые могут содержаться или не содержаться в других догадках, и комбинируете их. {6t}}\]

Теперь, не беспокоясь о дополнительном решении еще пару секунд, давайте приступим к работе над конкретным решением.{6t}}\end{выравнивание*}\]

Хммм…. Что-то здесь кажется неправильным. Ясно, что экспонента не может быть равна нулю. Итак, что пошло не так? Наконец, нам нужно дополнительное решение. Обратите внимание, что второй член в дополнительном решении (перечисленном выше) является в точности нашим предположением о форме частного решения, а теперь вспомним, что обе части дополнительного решения являются решениями однородного дифференциального уравнения

. \[у» — 4у’ — 12у = 0\]

Другими словами, лучше бы мы получили ноль, подставив наше предположение в дифференциальное уравнение, это решение однородного дифференциального уравнения!

Итак, как нам это исправить? Мы исправим это, добавив \(t\) к нашему предположению следующим образом.{6т}}\]

Итак, что мы узнали из этого последнего примера. Хотя технически нам не нужно дополнительное решение для неопределенных коэффициентов, вы можете проделать большую работу только для того, чтобы в конце выяснить, что вам нужно добавить \(t\) к предположению, потому что оно появилось в комплементарное решение. Этой работы можно избежать, если мы сначала найдем дополнительное решение, сравним наше предположение с дополнительным решением и посмотрим, не появится ли какая-либо часть вашего предположения в дополнительном решении.

Если часть вашего предположения появляется в дополнительном решении, нам нужно изменить эту часть предположения, добавив \(t\) к той части предположения, которая вызывает проблемы. Однако нам нужно быть немного осторожными и убедиться, что мы добавляем \(t\) в правильном месте. Следующий набор примеров покажет вам, как это сделать.

Пример 10 Запишите предположение для частного решения данного дифференциального уравнения.{10t}} + \left( {Et + F} \right)\cos t + \left( {Gt + H} \right)\sin t\]

Обратите внимание, что если мы умножим экспоненциальный член на круглые скобки, мы в конечном итоге получим часть дополнительного решения. Поскольку проблемная часть возникает из первого члена, целых первого члена будут умножены на \(t\). Со вторым и третьим терминами все в порядке.

Правильное предположение о форме частного решения в этом случае.{ — 2t}}\left( {A\cos \left( {\frac{t}{2}} \right) + B\sin \left({\frac{t}{2}} \right)} \ справа) + \ слева ( {Ct + D} \ справа) \ соз \ слева ( {\ гидроразрыва {t} {2}} \ справа) + \ слева ( {Et + F} \ справа) \ грех \ слева ( { \frac{t}{2}} \right)\]

В этом случае и второе, и третье слагаемые содержат части дополнительного решения. Однако первый член этого не делает, поскольку при умножении и синус, и косинус будут иметь экспоненту с ними, а это не является частью дополнительного решения.{ — 2t}}\left( {A\cos \left( {\frac{t}{2}} \right) + B\sin \left({\frac{t}{2}} \right)} \ справа) + \ слева ( {Ct + D} \ справа) \ соз \ слева ( {\ гидроразрыва {t} {2}} \ справа) + \ слева ( {Et + F} \ справа) \ грех \ слева ( { \frac{t}{2}} \right)\]

Однако на этот раз проблемы вызывает первый термин, а не второй или третий. На самом деле первое слагаемое — это в точности дополнительное решение, поэтому для него потребуется \(t\). Напомним, что у нас будет проблема с членом в нашем предположении только в том случае, если оно отличается от дополнительного решения только на константу.{ — 4t}}\]

После умножения ни один из членов не окажется в дополнительном решении, так что все будет в порядке.

Как показал этот последний набор примеров, мы действительно должны иметь на руках дополнительное решение, прежде чем даже записывать первое предположение для конкретного решения. Делая это, мы можем сравнить наше предположение с дополнительным решением, и если какой-либо из терминов из вашего конкретного решения появится, мы будем знать, что у нас будут проблемы.Как только проблема определена, мы можем добавить \(t\) к термину(ам) проблемы и сравнить наше новое предположение с дополнительным решением. Если проблем нет, мы можем перейти к проблеме, если есть проблемы, добавить еще одну \(t\) и снова сравнить.

Можете ли вы увидеть общее правило относительно того, когда потребуется \(t\) и когда потребуется t ² для дифференциальных уравнений второго порядка?

Дифференциальные уравнения — Линейные уравнения

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-1: Линейные дифференциальные уравнения

Первым частным случаем дифференциальных уравнений первого порядка, который мы рассмотрим, является линейное дифференциальное уравнение первого порядка.В этом случае, в отличие от большинства случаев первого порядка, которые мы рассмотрим, мы действительно можем вывести формулу для общего решения. Общее решение выводится ниже. Однако мы бы посоветовали вам не запоминать саму формулу. Вместо того, чтобы запоминать формулу, вы должны запомнить и понять процесс, который я собираюсь использовать для вывода формулы. На самом деле с большинством задач проще работать, используя процесс, а не формулу.

Итак, давайте посмотрим, как решить линейное дифференциальное уравнение первого порядка.Помните, что по мере прохождения этого процесса цель состоит в том, чтобы прийти к решению в форме \(y = y\left( t \right)\). Иногда легко упустить цель из виду, когда мы впервые проходим через этот процесс.

Чтобы решить линейное дифференциальное уравнение первого порядка, мы ДОЛЖНЫ начать с дифференциального уравнения в форме, показанной ниже. Если дифференциальное уравнение не в такой форме, то процесс, который мы собираемся использовать, не будет работать.

\[\begin{equation}\frac{{dy}}{{dt}} + p\left( t \right)y = g\left( t \right) \label{eq:eq1} \end{equation} \]

Где обе \(p(t)\) и \(g(t)\) являются непрерывными функциями.Напомним, что быстрое и грязное определение непрерывной функции заключается в том, что функция будет непрерывной при условии, что вы можете рисовать график слева направо, даже не поднимая карандаш/ручку. Другими словами, функция непрерывна, если в ней нет дыр и разрывов.

Теперь предположим, что где-то в мире существует некая волшебная функция \(\mu \left( t \right)\), называемая интегрирующим фактором . На данный момент не беспокойтесь о том, что это за функция или откуда она взялась.Мы выясним, что такое \(\mu \left( t \right)\), когда получим формулу общего решения.

Итак, теперь, когда мы предположили существование \(\mu \left( t \right)\), умножьте все в \(\eqref{eq:eq1}\) на \(\mu \left( t \right) \). Это даст.

\[\begin{equation}\mu \left( t \right)\frac{{dy}}{{dt}} + \mu \left( t \right)p\left( t \right)y = \mu \left( t \right)g\left( t \right) \label{eq:eq2} \end{equation}\]

Теперь в игру вступает магия \(\mu \left( t \right)\).Мы собираемся предположить, что чем бы ни было \(\mu \left( t \right)\), оно удовлетворяет следующему.

\[\begin{equation}\mu \left( t \right)p\left( t \right) = \mu ‘\left( t \right) \label{eq:eq3} \end{equation}\]

Снова не беспокойтесь о том, как мы можем найти \(\mu \left( t \right)\), который будет удовлетворять \(\eqref{eq:eq3}\). Как мы увидим, если \(p(t)\) непрерывно, мы можем его найти. Итак, заменив \(\eqref{eq:eq3}\), мы теперь приходим к.

\[\begin{equation}\mu \left( t \right)\frac{{dy}}{{dt}} + \mu ‘\left( t \right)y = \mu \left( t \right) g\left( t \right) \label{eq:eq4} \end{equation}\]

На данный момент мы должны признать, что левая часть \(\eqref{eq:eq4}\) не что иное, как следующее правило произведения.\prime}\,dt}} = \int{{\mu \left( t \right)g\left( t \right)\,dt}}\] \[\begin{equation}\mu \left( t \right)y\left( t \right) + c = \int{{\mu \left( t \right)g\left( t \right)\, dt}} \label{eq:eq6} \end{уравнение}\]

Обратите внимание, что сюда включена постоянная интегрирования \(c\) из левой части интегрирования. Очень важно, чтобы это было включено. Если его не указать, вы каждый раз будете получать неправильный ответ.

Последним шагом является некоторое алгебраическое решение для решения \(y(t)\).

\[\ begin{align*}\mu \left(t\right)y\left(t\right) & = \int{{\mu \left(t\right)g\left(t\right)\, dt}} — c\\ y\left( t \right) & = \frac{{\int{{\mu \left( t \right)g\left( t \right)\,dt}} — c} }{{\ mu \left( t \right)}}\end{align*}\]

Теперь, с точки зрения записи, мы знаем, что константа интегрирования \(c\) является неизвестной константой, и поэтому, чтобы облегчить нашу жизнь, мы включим знак минус перед ней в константу и вместо этого будем использовать плюс . Это НЕ повлияет на окончательный ответ для решения. Итак, с этим изменением мы имеем.

\[\ begin{equation}y\left(t\right) = \frac{{\int{{\mu \left(t\right)g\left(t\right)\,dt}} + c}} {{\mu \left( t \right)}} \label{eq:eq7} \end{equation}\]

Опять же, изменение знака константы не повлияет на наш ответ. Если вы решите сохранить знак минус, вы получите то же значение \(c\), что и мы, за исключением того, что оно будет иметь противоположный знак. При подключении \(c\) мы получим точно такой же ответ.

В этом разделе много быстрых и лузовых игр с константами интегрирования, так что вам нужно будет к этому привыкнуть. Когда мы делаем это, мы всегда стараемся четко объяснить, что происходит, и пытаемся оправдать, почему мы сделали то, что сделали.

Итак, теперь, когда у нас есть общее решение \(\eqref{eq:eq1}\), нам нужно вернуться и определить, что представляет собой эта волшебная функция \(\mu \left( t \right)\) . На самом деле это более простой процесс, чем вы думаете. \prime} = p\left( t \right)\]

Как и в случае с процессом, все, что нам нужно сделать, это объединить обе стороны, чтобы получить.

\[\begin{align*}\ln \mu \left( t \right) + k &= \int{{p\left( t \right)\,dt}}\\ \ln \mu \left( t \right) & = \int{{p\left( t \right)\,dt}} + k\end{align*}\]

Вы заметите, что постоянная интегрирования из левой части, \(k\), была перемещена в правую часть, и в нее снова был включен знак минус, как мы делали ранее.{\ int {{p \ left ( t \ right) \, dt}}}} \ label {eq: eq8} \ end {equation} \]

Итак, теперь у нас есть формула для общего решения, \(\eqref{eq:eq7}\), и формула для интегрирующего множителя, \(\eqref{eq:eq8}\). Однако у нас есть проблема. У нас есть две неизвестные константы, и чем больше у нас неизвестных констант, тем больше проблем у нас будет позже. Поэтому было бы неплохо, если бы мы могли найти способ устранить один из них (не будем быть в состоянии устранить оба….).

На самом деле это довольно легко сделать. {\int{{p\left(t\right)\,dt}}}}\label {eq:eq10}\end{уравнение}\]

Реальность такова, что \(\eqref{eq:eq9}\) не так полезен, как может показаться.Часто бывает проще просто запустить процесс, который привел нас к \(\eqref{eq:eq9}\), чем использовать формулу. Мы не будем использовать эту формулу ни в одном из наших примеров. Нам нужно будет регулярно использовать \(\eqref{eq:eq10}\), так как эту формулу проще использовать, чем процесс ее получения.

Процесс решения

Процесс решения линейного дифференциального уравнения первого порядка выглядит следующим образом.

1. Приведите дифференциальное уравнение к правильной начальной форме \(\eqref{eq:eq1}\).
2. Найдите коэффициент интегрирования, \(\mu \left( t \right)\), используя \(\eqref{eq:eq10}\).
3. Умножьте все в дифференциальном уравнении на \(\mu \left( t \right)\) и убедитесь, что левая часть становится правилом произведения \(\left( {\mu \left( t \right)y\left( t \right)} \right)’\) и напишите так.
4. Интегрируйте обе стороны, убедитесь, что вы правильно работаете с константой интегрирования.
5. Найдите решение \(y(t)\).

Давайте рассмотрим пару примеров. Начнем с решения дифференциального уравнения, которое мы вывели в разделе «Поле направлений».

Пример 1 Найдите решение следующего дифференциального уравнения. \[\frac{{dv}}{{dt}} = 9,8 — 0,196v\] Показать решение

Во-первых, нам нужно получить дифференциальное уравнение в правильной форме.

\[\frac{{dv}}{{dt}} + 0,196v = 9.{ — 0,196т}}\]

Из решения этого примера мы теперь можем понять, почему постоянная интегрирования так важна в этом процессе. Без него в этом случае мы получили бы единственное постоянное решение \(v(t)=50\). С константой интегрирования мы получаем бесконечно много решений, по одному для каждого значения \(с\).

Вернувшись к разделу поля направления, где мы впервые вывели дифференциальное уравнение, используемое в последнем примере, мы использовали поле направления, чтобы помочь нам набросать некоторые решения. Посмотрим, правильно ли мы их поняли. Все, что нам нужно сделать, чтобы набросать некоторые решения, это выбрать различные значения \(c\), чтобы получить решение. Некоторые из них показаны на графике ниже.

Итак, похоже, мы неплохо нарисовали графики в разделе поля направления.

Теперь вспомните из раздела «Определения», что начальное условие (условия) позволит нам сосредоточиться на конкретном решении. Решения дифференциальных уравнений первого порядка (не только линейных, как мы увидим) будут содержать единственную неизвестную константу, поэтому нам потребуется ровно одно начальное условие, чтобы найти значение этой константы и, следовательно, найти решение, которое мы искали.Начальное условие для дифференциальных уравнений первого порядка будет иметь вид

\[y\влево( {{t_0}} \вправо) = {y_0}\]

Напомним также, что дифференциальное уравнение вместе с достаточным количеством начальных условий называется начальной задачей (IVP). { — 0.{\ пер \, \, \ сек \ влево ( х \ вправо)}} = \ сек \ влево ( х \ вправо) \]

Вы можете сделать интеграл? Если нет, перепишите тангенс обратно в синусы и косинусы, а затем используйте простую замену. Обратите внимание, что мы можем опустить столбцы абсолютных значений секанса из-за ограничений на \(x\). Собственно, в этом и причина ограничений на \(x\). Отметим также, что есть две формы ответа на этот интеграл. Они эквивалентны, как показано ниже. То, что вы используете, действительно вопрос предпочтений.{\ln f\left(x\right)}} = f\left(x\right) \label{eq:eq11}\end{equation}\]

Это важный факт, который вы всегда должны помнить при возникновении этих проблем. Мы хотим максимально упростить интегрирующий фактор во всех случаях, и этот факт поможет в этом упрощении.

Теперь вернемся к примеру. Умножьте интегрирующий коэффициент через дифференциальное уравнение и убедитесь, что левая часть является правилом произведения. Также обратите внимание, что мы умножаем интегрирующий коэффициент на переписанное дифференциальное уравнение, а НЕ на исходное дифференциальное уравнение.2}\left( x \right)\,dx}}\\ \sec \left( x \right)y\left( x \right) & = — \frac{1}{2}\cos \left( { 2x} \right) — \tan \left( x \right) + c\end{align*}\]

Обратите внимание на использование тригонометрической формулы \(\sin\left({2\theta} \right) = 2\sin\theta\cos\theta\), которая упростила вычисление интеграла. Далее ищите решение.

\[\begin{align*}y\left( x \right) & = — \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) — \cos \left( x \right)\tan \left( x \right) + c\cos \left( x \right)\\ & = — \frac{1}{2}\cos \left( x \right)\ cos \left( {2x} \right) — \sin \left( x \right) + c\cos \left( x \right)\end{align*}\]

Наконец, примените начальное условие, чтобы найти значение \(c\).

\[\ begin{align*}3\sqrt 2 = y\left( {\frac{\pi} {4}} \right) & = — \frac{1}{2}\cos \left({\frac {\pi} {4}} \right)\cos \left( {\frac{\pi} {2}} \right) — \sin \left({\frac{\pi} {4}} \right) + c \ cos \ left ( {\ frac {\ pi} {4}} \ right) \\ 3 \ sqrt 2 & = — \ frac {{\ sqrt 2}} {2} + c \ frac {{\ sqrt 2 }}{2}\\ c & = 7\end{align*}\]

Тогда решение есть.

\[y\left( x \right) = — \frac{1}{2}\cos \left( x \right)\cos \left( {2x} \right) — \sin \left( x \right) + 7\cos\влево(х\вправо)\]

Ниже приведен график решения.2}\]

Ниже приведен график решения.

Давайте разработаем последний пример, в котором больше рассматривается интерпретация решения, чем поиск решения.

Пример 6. Найдите решение следующего IVP и определите все возможные варианты поведения решения как \(t \to \infty \). Если это поведение зависит от значения \(y_{0}\), укажите эту зависимость. \[2y’ — y = 4\sin \left( {3t} \right)\hspace{0.{\ гидроразрыва {т} {2}}} \ конец {выровнять *} \]

Примените начальное условие, чтобы найти значение \(c\) и обратите внимание, что оно будет содержать \(y_{0}\), так как у нас нет значения для этого.

\[{y_0} = y\left( 0 \right) = — \frac{{24}}{{37}} + c\hspace{0,25 дюйма}\,\,\,\, \Rightarrow \hspace{0,25 in}\,\,c = {y_0} + \frac{{24}}{{37}}\]

Итак, решение

\[y\left( t \right) = — \frac{{24}}{{37}}\cos \left( {3t} \right)\, — \frac{4}{{37}}\sin \left( {3t} \right)\, + \left( {{y_0} + \frac{{24}}{{37}}} \right){{\bf{e}}^{\frac{t {2}}}\]

Теперь, когда у нас есть решение, давайте посмотрим на долгосрочное поведение ( i. е. \(t\to\infty\)) раствора. Первые два члена решения останутся конечными при всех значениях \(t\). Именно последнее слагаемое будет определять поведение решения. Экспонента всегда будет стремиться к бесконечности как \(t \to \infty\), однако в зависимости от знака коэффициента \(c\) (да, мы уже нашли это, но для простоты этого обсуждения мы продолжим назвать его \(с\)). В следующей таблице показано долгосрочное поведение решения для всех значений \(c\).

Диапазон \(с\)	Поведение решения как\(t\to\infty\)
\(с\) < 0	\(у\влево(т\вправо) \к — \infty\)
\(с\) = 0	\(y\left( t \right)\) остается конечным
\(с\) > 0	\(у\влево(т\вправо) \в\infty\)

Такое поведение также можно увидеть на следующем графике нескольких решений.

Теперь, поскольку мы знаем, как \(c\) связано с \(y_{0}\), мы можем связать поведение решения с \(y_{0}\). В следующей таблице показано поведение решения с точки зрения \(y_{0}\) вместо \(c\).

Диапазон \(y_{0}\)	Поведение решения как\(t\to\infty\)
\({y_0} < - \frac{{24}}{{37}}\)	\(у\влево(т\вправо) \к — \infty\)
\({y_0} = — \frac{{24}}{{37}}\)	\(y\left( t \right)\) остается конечным
\({y_0} > — \frac{{24}}{{37}}\)	\(у\влево(т\вправо) \в\infty\)

Обратите внимание, что при \({y_0} = — \frac{{24}}{{37}}\) решение останется конечным.Это не всегда будет происходить.

Изучение долгосрочного поведения решений иногда важнее, чем само решение. Предположим, что приведенное выше решение дало температуру в металлическом стержне. В этом случае мы хотели бы, чтобы решение (решения) оставалось конечным в долгосрочной перспективе. Благодаря этому исследованию у нас теперь будет значение начального условия, которое даст нам это решение, и, что более важно, значения начального условия, которых нам нужно избегать, чтобы не расплавить брусок.

17.2: Неоднородные линейные уравнения — Математика LibreTexts

В этом разделе мы рассмотрим, как решать неоднородные дифференциальные уравнения. Терминология и методы отличаются от тех, которые мы использовали для однородных уравнений, поэтому давайте начнем с определения некоторых новых терминов.

Общее решение неоднородного линейного уравнения

Рассмотрим неоднородное линейное дифференциальное уравнение

\[a_2(x)y″+a_1(x)y′+a_0(x)y=r(x).\номер\]

Ассоциированное однородное уравнение

\[a_2(x)y″+a_1(x)y′+a_0(x)y=0 \не число\]

называется дополнительным уравнением . Мы увидим, что решение дополнительного уравнения является важным шагом в решении неоднородного дифференциального уравнения.

Определение: частный раствор

Решение \(y_p(x)\) дифференциального уравнения, не содержащее произвольных констант, называется частным решением уравнения.

ОБЩЕЕ РЕШЕНИЕ НЕОДНОРОДНОГО УРАВНЕНИЯ

Пусть \(y_p(x)\) — любое частное решение неоднородного линейного дифференциального уравнения

\[a_2(x)y″+a_1(x)y′+a_0(x)y=r(x).\]

Также пусть \(c_1y_1(x)+c_2y_2(x)\) обозначает общее решение дополнительного уравнения. Тогда общее решение неоднородного уравнения имеет вид

\[y(x)=c_1y_1(x)+c_2y_2(x)+y_p(x).\]

Доказательство

Чтобы доказать, что \(y(x)\) является общим решением, мы должны сначала показать, что оно является решением дифференциального уравнения, и, во-вторых, что любое решение дифференциального уравнения может быть записано в этой форме.Подставляя \(y(x)\) в дифференциальное уравнение, мы имеем

\[\begin{align*}a_2(x)y″+a_1(x)y′+a_0(x)y &=a_2(x)(c_1y_1+c_2y_2+y_p)″+a_1(x)(c_1y_1+ c_2y_2+y_p)′  \\ &\;\;\;\; +a_0(x)(c_1y_1+c_2y_2+y_p)  \\[4pt] &=[a_2(x)(c_1y_1+c_2y_2)″+a_1(x)(c_1y_1+c_2y_2)′+a_0(x)(c_1y_1+c_2y_2 )] \\ &\;\;\;\; +a_2(x)y_p″+a_1(x)y_p′+a_0(x)y_p \\[4pt] &=0+r(x) ​​\\[4pt] &=r(x). \конец{выравнивание*}\]

Итак, \(y(x)\) является решением.

Теперь пусть \(z(x)\) будет любым решением \(a_2(x)y»+a_1(x)y’+a_0(x)y=r(x).\) Тогда

\[\ begin{align*}a_2(x)(z−y_p)″+a_1(x)(z−y_p)′+a_0(x)(z−y_p) &=(a_2(x)z″+ a_1(x)z′+a_0(x)z) \\ &\;\;\;\;−(a_2(x)y_p″+a_1(x)y_p′+a_0(x)y_p)  \\[4pt ] &=r(x)−r(x) \\[4pt] &=0, \end{align*}\]

, поэтому \(z(x)−y_p(x)\) является решением дополнительного уравнения. Но \(c_1y_1(x)+c_2y_2(x)\) является общим решением дополнительного уравнения, поэтому существуют константы \(c_1\) и \(c_2\), такие что

\[z(x)−y_p(x)=c_1y_1(x)+c_2y_2(x). \номер\]

Отсюда мы видим, что

\[z(x)=c_1y_1(x)+c_2y_2(x)+y_p(x).\номер\]

Пример \(\PageIndex{1}\): Проверка общего решения

Учитывая, что \(y_p(x)=x\) является частным решением дифференциального уравнения \(y″+y=x,\), напишите общее решение и проверьте, что решение удовлетворяет уравнению.

Раствор

Дополнительное уравнение \(y″+y=0,\), которое имеет общее решение \(c_1 \cos x+c_2 \sin x. \) Таким образом, общее решение неоднородного уравнения равно

\[y(x)=c_1 \cos x+c_2 \sin x+x.\номер\]

Чтобы убедиться, что это решение, подставьте его в дифференциальное уравнение. У нас есть

\[y′(x)=−c_1 \sin x+c_2 \cos x+1 \номер\]

и

\[y″(x)=-c_1 \cos x-c_2 \sin x. \номер\]

Затем

\[\begin{align*} y″(x)+y(x) &=−c_1 \cos x−c_2 \sin x+c_1 \cos x+c_2 \sin x+x \\[4pt] &= х.\конец{выравнивание*} \]

Итак, \(y(x)\) является решением \(y″+y=x\).

Упражнение \(\PageIndex{1}\)

Учитывая, что \(y_p(x)=−2\) является частным решением \(y″−3y′−4y=8,\), напишите общее решение и убедитесь, что оно удовлетворяет уравнению.{4x}−2\)

В предыдущем разделе мы научились решать однородные уравнения с постоянными коэффициентами. Поэтому для неоднородных уравнений вида \(ay″+by′+cy=r(x)\) мы уже знаем, как решать дополнительное уравнение, и задача сводится к нахождению частного решения неоднородного уравнения. Рассмотрим теперь для этого два приема: метод неопределенных коэффициентов и метод вариации параметров.

Неопределенные коэффициенты

Метод неопределенных коэффициентов включает обоснованные предположения о форме конкретного решения на основе формы \(r(x)\).Когда мы берем производные полиномов, показательных функций, синусов и косинусов, мы получаем многочлены, показательные функции, синусы и косинусы. Поэтому, когда \(r(x)\) имеет одну из этих форм, возможно, что решение неоднородного дифференциального уравнения может принять ту же форму. Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает.

Пример \(\PageIndex{2}\): неопределенные коэффициенты, когда \(r(x)\) является полиномом

Найдите общее решение \(y″+4y′+3y=3x\).{−3x}\). Поскольку \(r(x)=3x\), конкретное решение может иметь вид \(y_p(x)=Ax+B\). Если это так, то мы имеем \(y_p′(x)=A\) и \(y_p″(x)=0\). Чтобы \(y_p\) было решением дифференциального уравнения, мы должны найти такие значения для \(A\) и \(B\), что

\[\begin{align*} y″+4y′+3y &=3x \\[4pt] 0+4(A)+3(Ax+B) &=3x  \\[4pt] 3Ax+(4A+3B ) &=3x. \номер\конец{выравнивание*} \]

Приравняв коэффициенты подобных членов, получим

\[\begin{align*} 3A &=3 \\ 4A+3B &=0.{−3x}+x−\frac{4}{3}. \номер\]

Обратите внимание, что в примере \(\PageIndex{2}\) хотя \(r(x)\) не содержит постоянного члена, нам необходимо было включить постоянный член в наше предположение. Если бы мы приняли решение в виде \(y_p=Ax\) (без постоянного члена), мы бы не смогли найти решение. (Проверьте это!) Если функция \(r(x)\) является полиномом, наше предположение о конкретном решении должно быть полиномом той же степени, и оно должно включать все члены более низкого порядка, независимо от того, являются ли они присутствует в \(r(x)\).{2t}+ \sin t+ \cos t \)

В предыдущей контрольной точке \(r(x)\) включала как синус, так и косинус. Однако, даже если \(r(x)\) включает только синус или только косинус, в предположении должны присутствовать оба члена. Метод неопределенных коэффициентов также работает с произведениями многочленов, экспонент, синусов и косинусов. αx sin βx,” in the second column.»> Таблица \(\PageIndex{1}\): ключевые формы для метода неопределенных коэффициентов \(г(х)\) Начальное предположение для \(y_p(x)\) \(k\) (константа) \(А\) (константа) \(ах+б\) \(Ax+B\) ( Примечание : Предположение должно включать оба термина, даже если \(b=0\).{−2x}\).

СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ: МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ

1. Решите дополнительное уравнение и запишите общее решение. {−3x}\)(шаг 1).Основываясь на форме \(r(x)=−6 \cos 3x,\), наше начальное предположение для конкретного решения: \(y_p(x)=A \cos 3x+B \sin 3x\) (шаг 2) . Ни одно из условий в \(y_p(x)\) не решает дополнительное уравнение, так что это правильное предположение (шаг 3).
   Теперь мы хотим найти значения для \(A\) и \(B,\), поэтому подставим \(y_p\) в дифференциальное уравнение. У нас есть

   \[y_p′(x)=−3A \sin 3x+3B \cos 3x \text{ и } y_p″(x)=−9A \cos 3x−9B \sin 3x, \nonumber\]

   поэтому мы хотим найти значения \(A\) и \(B\) такие, что

   \[\begin{align*}y″−9y &=−6 \cos 3x \\[4pt] −9A \cos 3x−9B \sin 3x−9(A \cos 3x+B \sin 3x) &= −6 \cos 3x \\[4pt] −18A \cos 3x−18B \sin 3x &=−6 \cos 3x.2+Bt\) (шаг 3). Проверяя это новое предположение, мы видим, что ни одно из условий в \(y_p(t)\) не решает дополнительное уравнение, поэтому это верное предположение (снова шаг 3). Теперь нам нужно найти значения для \(A\) и \(B,\), поэтому мы подставляем \(y_p\) в дифференциальное уравнение. У нас есть \(y_p′(t)=2At+B\) и \(y_p″(t)=2A\), поэтому мы хотим найти такие значения AA и BB, что

   \[\begin{align*}y″−3y′ &=−12t \\[4pt] 2A−3(2At+B) &=−12t \\[4pt] −6At+(2A−3B) &=− 12т. \конец{выравнивание*}\]

   Следовательно,

   \[\begin{align*}−6A &=−12 \\[4pt] 2A−3B &=0.{2t}−5 \cos 2t+ \sin 2t\)

   Изменение параметров

   Иногда \(r(x)\) не является комбинацией полиномов, экспонент или синусов и косинусов. В этом случае метод неопределенных коэффициентов не работает, и приходится использовать другой подход для нахождения частного решения дифференциального уравнения. Мы используем подход, называемый методом вариации параметров .

   Чтобы немного упростить наши вычисления, мы разделим дифференциальное уравнение на \(a,\), чтобы получить старший коэффициент, равный 1.Тогда дифференциальное уравнение имеет вид

   \[y″+py’+qy=r(x),\]

   , где \(p\) и \(q\) — константы.

   Если общее решение дополнительного уравнения задается выражением \(c_1y_1(x)+c_2y_2(x)\), мы будем искать частное решение вида

   \[y_p(x)=u(x)y_1(x)+v(x)y_2(x). \]

   В этом случае мы используем два линейно независимых решения дополнительного уравнения для формирования нашего частного решения. Однако мы предполагаем, что коэффициенты являются функциями \(x\), а не константами.Мы хотим найти функции \(u(x)\) и \(v(x)\) такие, что \(y_p(x)\) удовлетворяет дифференциальному уравнению. У нас есть

   \[\begin{align*}y_p &=uy_1+vy_2 \\[4pt] y_p’ &=u’y_1+uy_1’+v’y_2+vy_2′ \\[4pt] y_p″ &=(u’y_1 +в’у_2)’+у’у_1’+уу_1″+в’у_2’+вы_2″. \конец{выравнивание*}\]

   Подставляя в дифференциальное уравнение, получаем

   \[\begin{align*}y_p″+py_p′+qy_p &=[(u′y_1+v′y_2)′+u′y_1′+uy_1″+v′y_2′+vy_2″] \\ &\ ;\;\;\;+p[u′y_1+uy_1′+v′y_2+vy_2′]+q[uy_1+vy_2] \\[4pt] &=u[y_1″+p_y1′+qy_1]+v [y_2″+py_2′+qy_2] \\ &\;\;\;\; +(u′y_1+v′y_2)′+p(u′y_1+v′y_2)+(u′y_1′+v′y_2′).\конец{выравнивание*}\]

   Обратите внимание, что \(y_1\) и \(y_2\) являются решениями дополнительного уравнения, поэтому первые два члена равны нулю. Таким образом, у нас есть

   \[(u′y_1+v′y_2)′+p(u′y_1+v′y_2)+(u′y_1′+v′y_2′)=r(x). \]

   Если мы упростим это уравнение, наложив дополнительное условие \(u′y_1+v′y_2=0\), первые два члена равны нулю, и это сводится к \(u′y_1′+v′y_2′=r( Икс)\). Итак, при этом дополнительном условии имеем систему двух уравнений с двумя неизвестными:

   \[\begin{align*} u′y_1+v′y_2 &= 0 \\[4pt] u′y_1′+v′y_2′ &=r(x).\конец{выравнивание*}\]

   Решение этой системы дает нам \(u′\) и \(v′\), которые мы можем интегрировать, чтобы найти \(u\) и \(v\).

   Тогда \(y_p(x)=u(x)y_1(x)+v(x)y_2(x)\) является частным решением дифференциального уравнения. Решение этой системы уравнений иногда бывает сложной задачей, поэтому давайте воспользуемся этой возможностью, чтобы рассмотреть правило Крамера, которое позволяет нам решать систему уравнений с помощью определителей.

   ПРАВИЛО

   : ПРАВИЛО КРАМЕРА

   Система уравнений

   \[\begin{align*} a_1z_1+b_1z_2 &=r_1 \\[4pt] a_2z_1+b_2z_2 &=r_2 \end{align*}\]

   имеет единственное решение тогда и только тогда, когда определитель коэффициентов отличен от нуля. 2 \\[4pt] r_1(x) &=0 \\[4pt] r_2(x) &=2x.2}\),\( z_2=\frac{2x+2}{11x}\)

   СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ: МЕТОД ВАРИАЦИИ ПАРАМЕТРОВ

   1. Решите дополнительное уравнение и запишите общее решение \[c_1y_1(x)+c_2y_2(x).\]
   2. Используйте правило Крамера или другой подходящий метод, чтобы найти функции \(u′(x)\) и \(v′(x)\), удовлетворяющие \[\begin{align*} u′y_1+v′y_2 &=0 \ \[4pt] u′y_1′+v′y_2′ &=r(x). \конец{выравнивание*}\]
   3. Интегрируйте \(u′\) и \(v′\), чтобы найти \(u(x)\) и \(v(x)\).т \лн |т| \тег{шаг 5}\]

   4. Дополнительное уравнение имеет вид \(y″+y=0\) с соответствующим общим решением \(c_1 \cos x+c_2 \sin x\). Итак, \(y_1(x)= \cos x\) и \(y_2(x)= \sin x\) (шаг 1). Затем мы хотим найти функции \(u′(x)\) и \(v′(x)\) такие, что

      \[\begin{align*} u′ \cos x+v′ \sin x &=0 \\[4pt] −u′ \sin x+v′ \cos x &=3 \sin _2 x \end{ выровнять*}.\]

      Применяя правило Крамера, мы имеем

      \[u′= \dfrac{\begin{array}{|cc|}0 \sin x \\ 3 \sin ^2 x \cos x \end{array}}{ \begin{array}{|cc| } \cos x \sin x \\ − \sin x \cos x \end{array}}=\dfrac{0−3 \sin^3 x}{ \cos ^2 x+ \sin ^2 x}=−3 \sin^3 x \номер\]

      и

      \[v′=\dfrac{\begin{array}{|cc|} \cos x 0 \\ — \sin x 3 \sin^2 x \end{array}}{ \begin{array}{|cc |} \cos x \sin x \\ − \sin x \cos x \end{array}}=\dfrac{ 3 \sin^2x \cos x}{ 1}=3 \sin^2 x \cos x( \text{шаг 2}). т \лн|т| \)

      4.1 Основы дифференциальных уравнений. Расчет, том 2

      Цели обучения

      • 4.1.1 Определите порядок дифференциального уравнения.
      • 4.1.2 Объясните, что понимается под решением дифференциального уравнения.
      • 4.1.3 Различают общее решение и частное решение дифференциального уравнения.
      • 4.1.4 Определите проблему начального значения.
      • 4.1.5 Определите, является ли данная функция решением дифференциального уравнения или задачи с начальным значением.

      Исчисление — это математика изменений, а скорости изменений выражаются производными. Таким образом, одним из наиболее распространенных способов использования исчисления является составление уравнения, содержащего неизвестную функцию y=f(x)y=f(x) и ее производную, известное как дифференциальное уравнение . Решение таких уравнений часто дает информацию о том, как изменяются величины, и часто дает представление о том, как и почему происходят изменения.

      Методы решения дифференциальных уравнений могут принимать различные формы, включая прямое решение, использование графиков или компьютерные вычисления.Мы вводим основные идеи в этой главе и опишем их более подробно позже в ходе курса. В этом разделе мы изучаем, что такое дифференциальные уравнения, как проверять их решения, некоторые методы, которые используются для их решения, и некоторые примеры распространенных и полезных уравнений.

      Общие дифференциальные уравнения

      Рассмотрим уравнение y′=3×2,y′=3×2, которое является примером дифференциального уравнения, поскольку оно включает производную. Существует связь между переменными xx и y:yy:y — неизвестная функция x.Икс. Кроме того, левая часть уравнения является производной от y.y. Поэтому мы можем интерпретировать это уравнение следующим образом: начнем с некоторой функции y=f(x)y=f(x) и возьмем ее производную. Ответ должен быть равен 3×2,3×2. Какая функция имеет производную, равную 3×2?3×2? Одной из таких функций является y=x3,y=x3, поэтому эта функция считается решением дифференциального уравнения.

      Определение

      Дифференциальное уравнение – это уравнение, включающее неизвестную функцию y=f(x)y=f(x) и одну или несколько ее производных.Решением дифференциального уравнения является функция y=f(x)y=f(x), которая удовлетворяет дифференциальному уравнению, когда ff и его производные подставляются в уравнение.

      Некоторые примеры дифференциальных уравнений и их решений приведены в таблице 4.1.

      Уравнение	Решение
      у’=2xy’=2x	у=х2у=х2
      у’+3у=6х+11у’+3у=6х+11	у=е-3х+2х+3у=е-3х+2х+3
      y′′−3y′+2y=24e−2xy′′−3y′+2y=24e−2x	y=3ex-4e2x+2e-2xy=3ex-4e2x+2e-2x

      Таблица 4. 1 Примеры дифференциальных уравнений и их решений

      Обратите внимание, что решение дифференциального уравнения не обязательно уникально, прежде всего потому, что производная константы равна нулю. Например, y=x2+4y=x2+4 также является решением первого дифференциального уравнения в таблице 4.1. Мы вернемся к этой идее немного позже в этом разделе. А пока давайте сосредоточимся на том, что означает, что функция является решением дифференциального уравнения.

      Пример 4.1

      Проверка решений дифференциальных уравнений

      Убедитесь, что функция y=e−3x+2x+3y=e−3x+2x+3 является решением дифференциального уравнения y′+3y=6x+11.y′+3y=6x+11.

      Решение

      Чтобы проверить решение, мы сначала вычисляем y′y′, используя цепное правило для производных. Это дает y′=−3e−3x+2.y′=−3e−3x+2. Затем подставляем yy и y′y′ в левую часть дифференциального уравнения:

      (-3e-3x+2)+3(e-3x+2x+3). (-3e-3x+2)+3(e-3x+2x+3).

      Полученное выражение можно упростить, сначала убрав круглые скобки, что даст

      −3e−3x+2+3e−3x+6x+9.−3e−3x+2+3e−3x+6x+9.

      Объединение одинаковых членов приводит к выражению 6x+11,6x+11, равному правой части дифференциального уравнения. Этот результат подтверждает, что y=e−3x+2x+3y=e−3x+2x+3 является решением дифференциального уравнения.

      Контрольно-пропускной пункт 4.1

      Убедитесь, что y=2e3x−2x−2y=2e3x−2x−2 является решением дифференциального уравнения y′−3y=6x+4.у’-3у=6х+4.

      Удобно определять характеристики дифференциальных уравнений, чтобы было легче говорить о них и классифицировать их. Наиболее основной характеристикой дифференциального уравнения является его порядок.

      Определение

      Порядок дифференциального уравнения — это наивысший порядок любой производной неизвестной функции, входящей в уравнение.

      Пример 4.2

      Определение порядка дифференциального уравнения

      Каков порядок каждого из следующих дифференциальных уравнений?

      1. у’-4у=х2-3х+4у’-4у=х2-3х+4
      2. x2y‴−3xy″+xy′−3y=sinxx2y‴−3xy″+xy′−3y=sinx
      3. 4xy(4)−6x2y″+12x4y=x3−3×2+4x−124xy(4)−6x2y″+12x4y=x3−3×2+4x−12

      Решение

      1. Старшая производная в уравнении равна y′,y′, поэтому порядок равен 1. 1.
      2. Старшая производная в уравнении равна y‴,y‴, поэтому порядок равен 3,3.
      3. Наибольшая производная в уравнении равна y(4),y(4), поэтому порядок равен 4,4.

      Контрольно-пропускной пункт 4.2

      Каков порядок следующего дифференциального уравнения?

      (x4−3x)y(5)−(3×2+1)y′+3y=sinxcosx(x4−3x)y(5)−(3×2+1)y′+3y=sinxcosx

      Общие и частные решения

      Мы уже отмечали, что дифференциальное уравнение y′=2xy′=2x имеет по крайней мере два решения: y=x2y=x2 и y=x2+4.у=х2+4. Единственная разница между этими двумя решениями заключается в последнем члене, который является константой. Что, если последний член является другой константой? Будет ли это выражение по-прежнему решением дифференциального уравнения? На самом деле любая функция вида y=x2+C,y=x2+C, где CC представляет любую константу, также является решением. Причина в том, что производная x2+Cx2+C равна 2x,2x, независимо от значения C.C. Можно показать, что любое решение этого дифференциального уравнения должно иметь вид y=x2+C. y=x2+C.Это пример общего решения дифференциального уравнения. График некоторых из этих решений приведен на рис. 4.2. ( Примечание : на этом графике мы использовали четные целые значения для CC в диапазоне от −4−4 до 4,4. Фактически, нет ограничений на значение C;C; оно может быть целым числом или нет.)

      Фигура 4.2 Семейство решений дифференциального уравнения y′=2x.y′=2x.

      В этом примере мы можем выбрать любое желаемое решение; например, y=x2−3y=x2−3 является членом семейства решений этого дифференциального уравнения.Это называется частным решением дифференциального уравнения. Конкретное решение часто может быть однозначно идентифицировано, если нам предоставляется дополнительная информация о проблеме.

      Пример 4.3

      Поиск частного решения

      Найдите частное решение дифференциального уравнения y′=2xy′=2x, проходящее через точку (2,7).(2,7).

      Решение

      Любая функция вида y=x2+Cy=x2+C является решением этого дифференциального уравнения. Чтобы определить значение C,C, мы подставляем значения x=2x=2 и y=7y=7 в это уравнение и решим для C:C:

      y=x2+C7=22+C=4+CC=3.y=x2+C7=22+C=4+CC=3.

      Следовательно, частное решение, проходящее через точку (2,7)(2,7), равно y=x2+3.y=x2+3.

      Контрольно-пропускной пункт 4.3

      Найдите частное решение дифференциального уравнения

      , проходящий через точку (1,7),(1,7), при условии, что y=2×2+3x+Cy=2×2+3x+C является общим решением дифференциального уравнения.

      Проблемы с начальным значением

      Обычно данное дифференциальное уравнение имеет бесконечное число решений, поэтому естественно спросить, какое из них мы хотим использовать. Чтобы выбрать одно решение, необходимо больше информации. Некоторая конкретная информация, которая может быть полезна, — это начальное значение, представляющее собой упорядоченную пару, которая используется для поиска определенного решения.

      Дифференциальное уравнение вместе с одним или несколькими начальными значениями называется начальной задачей. Общее правило состоит в том, что количество начальных значений, необходимых для начальной задачи, равно порядку дифференциального уравнения.Например, если у нас есть дифференциальное уравнение y′=2x,y′=2x, то y(3)=7y(3)=7 является начальным значением, и вместе эти уравнения образуют начальную задачу. Дифференциальное уравнение y″−3y′+2y=4exy″−3y′+2y=4ex имеет второй порядок, поэтому нам нужны два начальных значения. В задачах с начальным значением порядка больше единицы для независимой переменной следует использовать одно и то же значение. Примером начальных значений для этого уравнения второго порядка могут быть y(0)=2y(0)=2 и y′(0)=−1.y′(0)=−1. Эти два начальных значения вместе с дифференциальным уравнением образуют начальную задачу.Эти проблемы названы так потому, что часто независимой переменной в неизвестной функции является t, t, которая представляет время. Таким образом, значение t=0t=0 представляет собой начало проблемы.

      Пример 4.4

      Проверка решения задачи с начальным значением

      Проверить, что функция y=2e−2t+ety=2e−2t+et является решением задачи с начальным значением

      y′+2y=3et,y(0)=3. y′+2y=3et,y(0)=3.

      Решение

      Чтобы функция удовлетворяла начальной задаче, она должна удовлетворять как дифференциальному уравнению, так и начальному условию.Чтобы показать, что yy удовлетворяет дифференциальному уравнению, мы начнем с вычисления y′.y′. Это дает y′=−4e−2t+et.y′=−4e−2t+et. Затем мы подставляем как yy, так и y′y′ в левую часть дифференциального уравнения и упрощаем:

      y′+2y=(−4e−2t+et)+2(2e−2t+et)=−4e−2t+et+4e−2t+2et=3et.y′+2y=(−4e−2t+et )+2(2e-2t+et)=-4e-2t+et+4e-2t+2et=3et.

      Это равно правой части дифференциального уравнения, поэтому y=2e−2t+ety=2e−2t+et решает дифференциальное уравнение. Далее мы вычисляем y(0):y(0):

      у(0)=2е-2(0)+е0=2+1=3.у(0)=2е-2(0)+е0=2+1=3.

      Этот результат подтверждает начальное значение. Следовательно, данная функция удовлетворяет начальной задаче.

      Контрольно-пропускной пункт 4.4

      Убедитесь, что y=3e2t+4sinty=3e2t+4sint является решением задачи с начальным значением

      y′−2y=4cost−8sint,y(0)=3. y′−2y=4cost−8sint,y(0)=3.

      В примере 4.4 начальная задача состояла из двух частей. Первая часть представляла собой дифференциальное уравнение y′+2y=3ex,y′+2y=3ex, а вторая часть представляла собой начальное значение y(0)=3.у(0)=3. Эти два уравнения вместе образуют начальную задачу.

      То же самое в целом. Начальная задача будет состоять из двух частей: дифференциального уравнения и начального условия. Дифференциальное уравнение имеет семейство решений, а начальное условие определяет значение C.C. Семейство решений дифференциального уравнения в примере 4.4 задается формулой y=2e−2t+Cet.y=2e−2t+Cet. Это семейство решений показано на рис. 4.3, где конкретное решение y=2e−2t+ety=2e−2t+et помечено.

      Фигура 4.3 Семейство решений дифференциального уравнения y′+2y=3et.y′+2y=3et. Частное решение y=2e−2t+ety=2e−2t+et помечено.

      Пример 4,5

      Решение задачи с начальным значением

      Решите следующую задачу с начальными значениями:

      y′=3ex+x2−4,y(0)=5. y′=3ex+x2−4,y(0)=5.

      Решение

      Первым шагом в решении этой задачи с начальными значениями является поиск общего семейства решений. Для этого найдем первообразную обеих частей дифференциального уравнения

      ∫y′dx=∫(3ex+x2−4)dx,∫y′dx=∫(3ex+x2−4)dx,

      а именно

      у+С1=3ех+13х3-4х+С2.у+С1=3ех+13х3-4х+С2.

      (4.1)

      Мы можем интегрировать обе стороны, потому что термин и появляется сам по себе. Обратите внимание на две константы интегрирования: C1C1 и C2.C2. Решение уравнения 4.1 для yy дает

      y=3ex+13×3−4x+C2−C1.y=3ex+13×3−4x+C2−C1.

      Поскольку C1C1 и C2C2 являются константами, C2-C1C2-C1 также является константой. Таким образом, мы можем определить C=C2−C1,C=C2−C1, что приводит к уравнению

      y=3ex+13×3−4x+C.y=3ex+13×3−4x+C.

      Далее мы определяем значение C.C. Для этого подставим x=0x=0 и y=5y=5 в уравнение 4.1 и решим для C:C:

      . 5=3e0+1303−4(0)+C5=3+CC=2,5=3e0+1303−4(0)+C5=3+CC=2.

      Теперь подставим значение C=2C=2 в уравнение 4.1. Решение начальной задачи: y=3ex+13×3−4x+2.y=3ex+13×3−4x+2.

      Анализ

      Разница между общим решением и частным решением состоит в том, что общее решение включает в себя набор функций независимой переменной, определенных явно или неявно.Начальное значение или значения определяют, какое конкретное решение в семействе решений удовлетворяет желаемым условиям.

      Контрольно-пропускной пункт 4,5

      Решить задачу с начальным значением

      y’=x2-4x+3-6ex,y(0)=8.y’=x2-4x+3-6ex,y(0)=8.

      В физике и инженерных приложениях мы часто рассматриваем силы, действующие на объект, и используем эту информацию для понимания результирующего движения, которое может произойти. Например, если мы начнем с объекта на поверхности Земли, основной силой, действующей на этот объект, будет гравитация.Физики и инженеры могут использовать эту информацию вместе со вторым законом движения Ньютона (в форме уравнения F=ma, F=ma, где FF представляет силу, mm представляет массу, а aa представляет собой ускорение), чтобы вывести уравнение, которое можно решить. .

      Фигура 4.4 Для бейсбольного мяча, падающего в воздухе, на него действует только сила тяжести (без учета сопротивления воздуха).

      На рис. 4.4 мы предполагаем, что единственная сила, действующая на бейсбольный мяч, — это сила тяжести. Это предположение игнорирует сопротивление воздуха.(Сила, вызванная сопротивлением воздуха, будет рассмотрена позже.) Ускорение силы тяжести на поверхности Земли, g, g, составляет приблизительно 9,8 м/с2,9,8 м/с2. Введем систему отсчета, где поверхность Земли находится на высоте 0 метров. Пусть v(t)v(t) представляет собой скорость объекта в метрах в секунду. Если v(t)>0,v(t)>0, мяч поднимается, а если v(t)<0,v(t)<0, мяч падает (рис. 4.5).

      Фигура 4,5 Возможные скорости подъема/падения бейсбольного мяча.

      Наша цель — определить скорость v(t)v(t) в любой момент времени t.t. Для этого поставим задачу с начальным значением. Предположим, что масса мяча равна m,m, где mm измеряется в килограммах. Мы используем второй закон Ньютона, который гласит, что сила, действующая на объект, равна его массе, умноженной на его ускорение (F=ma).(F=ma). Ускорение является производной скорости, поэтому a(t)=v′(t).a(t)=v′(t). Следовательно, сила, действующая на бейсбольный мяч, определяется выражением F=mv′(t).F=mv′(t). Однако эта сила должна быть равна силе тяжести, действующей на объект, которая (опять же с использованием второго закона Ньютона) определяется формулой Fg=-mg, Fg=-mg, поскольку эта сила действует в направлении вниз.Поэтому мы получаем уравнение F=Fg,F=Fg, которое становится mv′(t)=−mg.mv′(t)=−mg. Разделив обе части уравнения на мм, мы получим уравнение

      . v'(t)=-g.v'(t)=-g.

      Обратите внимание, что это дифференциальное уравнение остается неизменным независимо от массы объекта.

      Теперь нам нужно начальное значение. Поскольку мы ищем скорость, в контексте задачи имеет смысл предположить, что мы знаем начальную скорость или скорость в момент времени t=0.t=0. Это обозначается как v(0)=v0. v(0)=v0.

      Пример 4.6

      Скорость движущегося бейсбольного мяча

      Бейсбольный мяч брошен вверх с высоты 33 метра над поверхностью Земли с начальной скоростью 10 м/с, 10 м/с, и единственная сила, действующая на него, — сила тяжести. Мяч имеет массу 0,15 кг 0,15 кг на поверхности Земли.

      1. Найдите скорость v(t)v(t) бейсбольного мяча в момент времени t.t.
      2. Какова его скорость через 22 секунды?

      Решение

      1. Из предыдущего обсуждения дифференциальное уравнение, которое применимо в этой ситуации, имеет вид
         . v'(t)=-g,v'(t)=-g,
         где г=9.8 м/с2.g=9,8 м/с2. Начальное условие: v(0)=v0,v(0)=v0, где v0=10м/с, v0=10м/с. Следовательно, начальная задача имеет вид v′(t)=−9,8 м/с2, v(0)=10 м/с. v′(t)=−9,8 м/с2, v(0)=10 м/с.
         Первым шагом в решении этой задачи с начальными значениями является получение первообразной обеих частей дифференциального уравнения. Это дает
         ∫v′(t)dt=∫−9,8dtv(t)=−9,8t+C.∫v′(t)dt=∫−9,8dtv(t)=−9,8t+C.
         Следующим шагом является решение для C.C. Для этого подставьте t=0t=0 и v(0)=10:v(0)=10:
         v(t)=-9,8t+Cv(0)=-9.8(0)+C10=C.v(t)=-9,8t+Cv(0)=-9,8(0)+C10=C.
         Следовательно, C=10C=10, а функция скорости определяется выражением v(t)=-9,8t+10,v(t)=-9,8t+10.
      2. Чтобы найти скорость через 22 секунды, подставьте t=2t=2 в v(t).v(t).
         v(t)=-9,8t+10v(2)=-9,8(2)+10v(2)=-9,6.v(t)=-9,8t+10v(2)=-9,8(2)+10v( 2)=-9,6.
         Единицы скорости — метры в секунду. Поскольку ответ отрицательный, объект падает со скоростью 9,6 м/с. 9,6 м/с.

      Контрольно-пропускной пункт 4.6

      Предположим, что камень падает из состояния покоя с высоты 100100 метров, и единственная сила, действующая на него, — сила тяжести.Найдите уравнение для скорости v(t)v(t) как функции времени, измеряемой в метрах в секунду.

      Естественный вопрос, который возникает после решения задачи такого типа, заключается в том, на какой высоте объект будет находиться над поверхностью Земли в данный момент времени. Пусть s(t)s(t) обозначает высоту объекта над поверхностью Земли, измеряемую в метрах. Поскольку скорость является производной положения (в данном случае высоты), это предположение дает уравнение s′(t)=v(t).s′(t)=v(t). Необходимо начальное значение; в этом случае хорошо работает начальная высота объекта.Пусть начальная высота задана уравнением s(0)=s0.s(0)=s0. Вместе эти предположения дают начальное значение задачи

      s′(t)=v(t),s(0)=s0.s′(t)=v(t),s(0)=s0.

      Если известна функция скорости, то можно найти и функцию положения.

      Пример 4.7

      Высота движущегося бейсбольного мяча

      Бейсбольный мяч брошен вверх с высоты 33 метра над поверхностью Земли с начальной скоростью 10 м/с, 10 м/с, и единственная сила, действующая на него, — сила тяжести.Мяч имеет массу 0,150,15 кг на поверхности Земли.

      1. Найдите положение s(t)s(t) бейсбольного мяча в момент времени t.t.
      2. Какова его высота через 22 секунды?

      Решение

      1. Мы уже знаем, что функция скорости для этой задачи равна v(t)=−9,8t+10,v(t)=−9,8t+10. Начальная высота бейсбольного мяча 33 метра, поэтому s0=3.s0=3. Следовательно, задача с начальным значением для этого примера равна
         . Чтобы решить начальную задачу, мы сначала находим первообразные:
         ∫s′(t)dt=∫−9.8t+10dts(t)=-4,9t2+10t+C.∫s'(t)dt=∫-9,8t+10dts(t)=-4,9t2+10t+C.
         Затем мы подставляем t=0t=0 и находим C:C:
         . s(t)=-4,9t2+10t+Cs(0)=-4,9(0)2+10(0)+C3=Cs(t)=-4,9t2+10t+Cs(0)=-4,9(0) )2+10(0)+С3=С.
         Следовательно, функция положения равна s(t)=−4,9t2+10t+3.s(t)=−4,9t2+10t+3.
      2. Высота бейсбольного мяча после 2s2s определяется выражением s(2):s(2):
         s(2)=-4,9(2)2+10(2)+3=-4,9(4)+23=3,4.s(2)=-4,9(2)2+10(2)+3=-4,9 (4)+23=3,4.
         Следовательно, бейсбольный мяч находится на высоте 3,43,4 метра над поверхностью Земли через 22 секунды.Стоит отметить, что в процессе решения задачи масса шара полностью нейтрализовалась.

      Раздел 4.1 Упражнения

      Определите порядок следующих дифференциальных уравнений.

      2 .

      (у’)2=у’+2у(у’)2=у’+2у

      3 .

      y‴+y″y′=3x2y‴+y″y′=3×2

      4 .

      y′=y″+3t2y′=y″+3t2

      6 .

      dyx+d2ydx2=3x4dydx+d2ydx2=3×4

      7 .

      (dydt)2+8dydt+3y=4t(dydt)2+8dydt+3y=4t

      Убедитесь, что следующие функции являются решениями данного дифференциального уравнения.

      8 .

      y=x33y=x33 решает y′=x2y′=x2

      9 .

      y=2e−x+x−1y=2e−x+x−1 решает y′=x−yy′=x−y

      10 .

      y=e3x−ex2y=e3x−ex2 решает y′=3y+exy′=3y+ex

      11 .

      y=11−xy=11−x решает y′=y2y′=y2

      12 .

      y=ex2/2y=ex2/2 решает y′=xyy′=xy

      13 .

      y=4+lnxy=4+lnx решает xy′=1xy′=1

      14 .

      y=3−x+xlnxy=3−x+xlnx решает y′=lnxy′=lnx

      15 .

      y=2ex−x−1y=2ex−x−1 решает y′=y+xy′=y+x

      16 .

      y=ex+sinx2−cosx2y=ex+sinx2−cosx2 решает y′=cosx+yy′=cosx+y

      17 .

      y=πe-cosxy=πe-cosx решает y′=ysinxy′=ysinx

      Проверьте следующие общие решения и найдите конкретное решение.

      18 .

      Найдите частное решение дифференциального уравнения y′=4x2y′=4×2, которое проходит через (−3,−30),(−3,−30), учитывая, что y=C+4x33y=C+4×33 является общим решением .

      19 .

      Найдите частное решение дифференциального уравнения y′=3x3y′=3×3, которое проходит через (1,4.75),(1,4.75), при условии, что y=C+3x44y=C+3×44 является общим решением.

      20 .

      Найдите частное решение дифференциального уравнения y′=3x2yy′=3x2y, которое проходит через (0,12),(0,12), учитывая, что y=Cex3y=Cex3 является общим решением.

      21 .

      Найдите частное решение дифференциального уравнения y′=2xyy′=2xy, которое проходит через (0,12),(0,12), при условии, что y=Cex2y=Cex2 является общим решением.

      22 .

      Найдите частное решение дифференциального уравнения y′=(2xy)2y′=(2xy)2, которое проходит через (1,−12),(1,−12), учитывая, что y=−3C+4x3y=−3C +4×3 — это общее решение.

      23 .

      Найдите частное решение дифференциального уравнения y′x2=yy′x2=y, которое проходит через (1,2e),(1,2e), при условии, что y=Ce−1/xy=Ce−1/x является общее решение.

      24 .

      Найдите частное решение дифференциального уравнения 8dxdt=−2cos(2t)−cos(4t)8dxdt=−2cos(2t)−cos(4t), которое проходит через (π,π),(π,π), учитывая, что x=C−18sin(2t)−132sin(4t)x=C−18sin(2t)−132sin(4t) является общим решением.

      25 .

      Найдите частное решение дифференциального уравнения dudt=tanududt=tanu, которое проходит через (1,π2),(1,π2), при условии, что u=sin−1(eC+t)u=sin−1(eC+t ) является общим решением.

      26 .

      Найдите частное решение дифференциального уравнения dydt=e(t+y)dydt=e(t+y), которое проходит через (1,0),(1,0), при условии, что y=−ln(C−et )y=−ln(C−et) является общим решением.

      27 .

      Найдите частное решение дифференциального уравнения y′(1−x2)=1+yy′(1−x2)=1+y, которое проходит через (0,−2),(0,−2), при условии, что y =Cx+11−x−1y=Cx+11−x−1 является общим решением.

      Для следующих задач найдите общее решение дифференциального уравнения.

      29 .

      y′=lnx+tanxy′=lnx+tanx

      30 .

      y’=sinxecosxy’=sinxecosx

      32 .

      у’=sin-1(2x)y’=sin-1(2x)

      34 .

      x’=кот+lnt+3t2x’=кот+lnt+3t2

      Решите следующие начальные задачи, начиная с y(0)=1y(0)=1 и y(0)=−1.y(0)=−1. Нарисуйте оба решения на одном графике.

      Решите следующие задачи с начальными значениями, начиная с y0=10.y0=10. В какой момент yy увеличивается до 100 100 или падает до 1–1?

      Напомним, что семейство решений включает в себя решения дифференциального уравнения, отличающиеся на константу.Для следующих задач используйте свой калькулятор, чтобы построить график семейства решений данного дифференциального уравнения. Используйте начальные условия от y(t=0)=-10y(t=0)=-10 до y(t=0)=10y(t=0)=10, увеличивая на 2,2. Есть ли критическая точка, в которой поведение решения начинает меняться?

      51 .

      [T] y’=x+yy’=x+y ( Подсказка: y=Cex-x-1y=Cex-x-1 является общим решением)

      52 .

      [T] y′=xlnx+sinxy′=xlnx+sinx

      53 .

      Найдите общее решение, описывающее скорость мяча массой 1 фунт 1 фунт, брошенного вверх со скоростью aa фут/сек.

      54 .

      В предыдущей задаче, если начальная скорость мяча, брошенного в воздух, равна a=25a=25 футов/с, запишите частное решение скорости мяча. Решите, чтобы найти время, когда мяч коснется земли.

      55 .

      Вы подбрасываете вверх в воздух два объекта с разными массами m1m1 и m2m2 с одинаковой начальной скоростью aa фут/с. Как изменится их скорость через 11 секунд?

      56 .

      [T] Вы бросаете мяч массой 11 кг со скоростью a=25a=25 м/с на Марс, где сила тяжести g=−3.711g=-3,711 м/с ² . С помощью калькулятора вычислите, насколько дольше мяч находится в воздухе на Марсе, чем на Земле, где g=-9,8 м/с2g=-9,8 м/с2.

      57 .

      [T] В предыдущей задаче с помощью калькулятора вычислите, насколько выше поднялся мяч на Марсе, где g=-9,8 м/с2g=-9,8 м/с2.

      58 .

      [T] Автомобиль на автостраде ускоряется по закону a=15cos(πt),a=15cos(πt), где tt измеряется в часах. Составьте и решите дифференциальное уравнение, чтобы определить скорость автомобиля, если его начальная скорость равна 5151 миля в час.Какова скорость водителя после 4040 минут вождения?

      59 .

      [T] Для автомобиля из предыдущей задачи найдите выражение для расстояния, пройденного автомобилем за время t,t, при условии, что начальное расстояние равно 0,0. За какое время автомобиль проедет 100100 км? Округлите ответ до часов и минут.

      60 .

      [T] В предыдущей задаче найдите общее расстояние, пройденное за первый час.

      61 .

      Подставьте y=Be3ty=Be3t в y′−y=8e3ty′−y=8e3t, чтобы найти конкретное решение.

      62 .

      Подставьте y=acos(2t)+bsin(2t)y=acos(2t)+bsin(2t) в y′+y=4sin(2t)y′+y=4sin(2t), чтобы найти конкретное решение.

      63 .

      Подставьте y=a+bt+ct2y=a+bt+ct2 в y′+y=1+t2y′+y=1+t2, чтобы найти конкретное решение.

      64 .

      Подставьте y=aetcost+betsinty=aetcost+betsint в y′=2etcosty’=2etcost, чтобы найти конкретное решение.

      65 .

      Решить y′=ekty′=ekt с начальным условием y(0)=0y(0)=0 и решить y′=1y′=1 с тем же начальным условием.Когда kk приближается к 0,0, что вы замечаете?

      Общие и частные решения

      
      Общие и частные решения

             

      Здесь мы научимся находить общее решение дифференциального уравнения, и использовать это общее решение, чтобы найти частное решение. Мы будем также применим это к задачам ускорения, в которых мы используем ускорение и начальные условия объекта, чтобы найти положение функция.

      Пример 1: Поиск частного решения

             Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

             Сначала нам нужно найти общее решение.Для этого нам нужно интегрировать обе стороны, чтобы найти y:

      Это дает нам общее решение. Чтобы найти конкретное решение, нам нужно применить начальные условия, заданные для нас (y = 4, x = 0) и решить для C:

             После того, как мы решим для C, мы получим частное решение.

      Пример 2. Поиск частного решения

             Найдите частное решение дифференциального уравнения, которое удовлетворяет заданному начальному условию: Теперь мы применяем начальные условия (x = 1, y = 4) и находим C, который мы используем для создания нашего частного решения:

      Пример 3. Поиск частного решения уравнение, удовлетворяющее заданному начальному условию:

             Сначала находим общее решение, интегрируя обе части:

      Теперь, когда у нас есть общее решение, мы можем применить начальные условия и найти частное решение:

      Скорость и ускорение

             Здесь мы будем применять конкретные решения, чтобы найти функции скорости и положения по ускорению объекта.

      Пример 4: Функция поиска позиции

      Найдите функцию положения движущейся частицы с заданным ускорением, начальным положением и начальной скоростью:

      У нас есть функция ускорения, начальная скорость 10 и начальное положение 5, и ищут функция положения. Мы знаем, что интеграл ускорения равен скорость, так что давайте начнем с этого:

      Теперь мы имеем общее решение скорости функция.Чтобы получить частное решение, нам нужна начальная скорость. Поскольку это начальная скорость, это скорость в момент времени t = 0; поэтому наше начальное условие v = 10, t = 0:

             Теперь, когда у нас есть частное решение скорости, мы можем интегрировать его, чтобы найти положение:

      Теперь мы можем применить наши начальные условия к этому общее решение, чтобы получить частное решение, которое является положением функцию, которую мы хотим.Как и раньше, x ₀ — это начальное положение
      , что означает, что время t = 0, а x = 5:

             Это функция положения частицы.

      Пример 5: Функция поиска положения

      Найдите функцию положения движущейся частицы с заданным ускорением, начальным положением и начальной скоростью:

      У нас есть уравнение для ускорения, начальное скорость 7 и начальное положение 0. Первый шаг — найти частное решение скорости частицы:

      Теперь мы можем использовать функцию скорости, чтобы найти функция положения. Помните, нам нужно будет найти конкретное решение функции положения, а не только общее решение:

      Пример 6: Применение дифференциального уравнения

      Здесь мы будем использовать пример из реальной жизни, чтобы применить то, что мы только что узнали.

      Мяч бросают прямо вниз с начальной со скоростью 20 футов/с с вершины здания высотой 300 футов.Пренебрегая трением воздуха, доу через какое время мяч достигнет земли и с какой скоростью он попал?

             Чтобы решить эту проблему, нам нужно положить в терминах, которые мы можем понять. Единицы даны в футах и футов/секунду; ускорение свободного падения в этих единицах равно -32 фут/с ² .

             Мы знаем, что мяч был брошен вниз с начальной скоростью (t = 0) 20 футов/с; поскольку он идет вниз, скорость будет отрицательной (v ₀ = -10).

      Наконец, здание достигает 300 футов в высоту, и мяч брошен сверху. Поскольку мяч начинается с места вверх от уровня земли, начальное положение будет положительным 300 (x ₀ = 300). Подставим все это в уравнение, аналогичное предыдущим примерам:

      Теперь мы получаем где-то! Вопрос задает о мяче, когда он падает на землю. Чтобы быть в состоянии выяснить информация о том, когда он упадет на землю, нам нужно знать, который час хиты.Уравнение, связывающее положение со временем, есть положение функция, которую мы уже знаем, как получить из предыдущих примеров:

      Теперь, когда у нас есть функция положения, мы можем начните вычислять время, за которое мяч коснется земли, и скорость, с которой он попадает. Для каждого из этих уравнений необходимо знать время; например, если мы подставим 2 вместо t в функцию скорости, это даст нам скорость в момент t = 2, или 2 секунды после броска мяча.Нам нужно знать, который час мяч падает на землю; для этого нам нужно задать позицию функцию, равную 0, и решить для t. Мяч стартовал в 300 футах от земли, и мы использовали 300 в качестве исходное положение. Если мы установим нашу позицию равной 0, это скажет нам когда мяч коснется земли:

             Мы получаем два значения для t: -5 и 3,75. Мы можем выбросить -5, так как у нас не может быть отрицательного ценность для времени. Следовательно, время, за которое мяч достигнет земля 3.75 секунд. Чтобы найти скорость в момент удара мяча о земли, мы просто подставим 3,75 вместо t в наше уравнение скорости и решим:

             Скорость мяча при ударе о землю составляет -140 фут/с

      Пример 7. Применение дифференциального уравнения

      Тормоза автомобиля включаются, когда он движется со скоростью 60 км/ч, обеспечивая постоянное замедление 12 м/с ² . Какое расстояние проезжает автомобиль до остановки и сколько времени это занимает?

            Хорошо, давайте разберемся.Мы знаем, что ускорение равно -12 м/с ² . Начальная скорость 60 км/ч; это нужно будет преобразовать в м/с (у нас не может быть проблем с разными единицами измерения):

             Начальная скорость автомобиля составляет 16,7 м/с. Мы также можем назвать начальное положение x = 0, так как это когда автомобиль начинает замедляться. Собираем все вместе:

      Мы знаем, что нам понадобится функция положения в в какой-то момент, так как нам нужно выяснить, какое расстояние проедет машина до подходит к остановке, так что давайте уберем это с дороги:

      Теперь нам нужно выяснить, в какое время машина подходит к остановке.Мы не знаем, в каком положении будет машина. этой точке, но мы знаем, что скорость будет равна 0. Чтобы узнать когда скорость равна 0, нам нужно установить скорость равной 0 и решить:

      Автомобиль останавливается через 1,4 секунды после подачи тормоза. Какое расстояние он проходит до остановки? Нам нужно подставить t = 1,4 к функции положения, чтобы узнать:

             Автомобиль проезжает 11,6 метра до остановки предполагают скорость изменения – так часто появляются в инженерном или научном контексте.
      Решение уравнения включает интегрирование.

       

      Задан порядок дифференциального уравнения по наибольшей используемой производной.

      Дана степень дифференциального уравнения по степени могущества высшей используется производная.

       
      Примеры: —

         

      Типы дифференциальных уравнений: —

       

       

      Дифференциальные уравнения первого порядка

      Решение прямым интегрированием

      Общее решение дифференциальных уравнений вида
      можно найти с помощью прямого интегрирования.
      Подстановка значений начальных условий даст
      

      Пример

      Решить уравнение

       

       

       Найти частное решение
      дифференциальное уравнение

      
      учитывая  y = 5, когда x = 3

       

       

      Пример

       Прямая линия с уклоном 2 проходит через
      . точка (1,3).Найдите уравнение прямой.

        

       

      Разделяемые переменные

      Дифференциальное уравнение с разделяемыми переменными равно одному
      в котором уравнение может быть записано со всеми членами
      для одной переменной в одной части уравнения, а в другой
      термины с другой стороны.

      Пример

      Найдите общее решение дифференциального уравнения

                 

        

      Пример

       Найти общее решение дифференциального уравнения

            

       

      Пример

       Найти частное решение дифференциального уравнения

           

        при y = 2 при x = 1

        

      Частичные дроби необходимы, чтобы преобразовать левую часть уравнения в форму, которую можно проинтегрировать.

      так

      , который интегрируется в общее решение

      замещающие значения для конкретного решения

       

      Линейные дифференциальные уравнения

       Это дифференциальные уравнения первой степени.

         описывает общее линейное дифференциальное уравнение порядка n,
      где a _n (x), a _n-1 (x) и т. д. и f(x) — заданные функции x или константы.

       Луи Арбогаст представил дифференциальный оператор
      . D = d/dx, что упрощает общее уравнение до

      .

       

      или

       
      

      Если f(x) = 0, уравнение называется однородным.
      Если f(x) ≠0, уравнение неоднородно

       

      Линейные дифференциальные уравнения первого порядка

      Для решения уравнений вида

      1) Экспресс по стандартной форме

      
      где P и Q являются функциями x или константами

      .

      2) Умножьте обе части на Интегрирующий коэффициент
      

      3) Напишите

       

      4) Интегрировать правую сторону,

      при необходимости использовать интеграцию по частям

       

      5) Разделите обе части на интегрирующий коэффициент.
      Это дает общее решение.

      6) Используйте любые начальные условия, чтобы найти
      частные решения.

       

       Пример

      Найдите общее решение уравнения

          

          

        

      так

       

      Пример

      Найдите общее решение уравнения

       

         где x ≠2 , и, следовательно, найти частное решение
      для y = 1, когда x=-1

       

       

      Линейные дифференциальные уравнения второго порядка

      Решить уравнения вида

      
      

      1) Запишите вспомогательное уравнение
      am ² +bm + c = 0         

            (почему это работает, UCL.ac.uk)

      2) Проверить дискриминант вспомогательное уравнение.

      3) Для вещественных и различных корней m ₁ и m ₂ ,

      общее решение

      
      

      4) Для действительных и равных корней,
      общее решение

       

      5)Для комплексно-сопряженных корней,
      m ₁ = p + iq и m ₂ = p — iq ,
      общее решение

      6) Используйте любые начальные условия, чтобы найти конкретное решение.

       

      Пример

       Найти общее решение уравнения

       

       и конкретное решение, для которого
      y = 7, когда x=0 и dy/dx = 7

        

      Пример

        Найти общее решение уравнения

        

      и конкретное решение для
      y=0 и dy/dx = 3, когда x=0

         

          

      Пример

       Найти общее решение уравнения

       

         

       

      Неоднородные дифференциальные уравнения второго порядка

            Решение уравнений вида

           

                состоит из двух частей: дополнительная функция (CF)
      и частный интеграл (PI).

      , поэтому Q(x) = CF +PI

      CF является общим решением, как описано выше
      для решения однородных уравнений.

       Частный интеграл находится путем подстановки
      форма, аналогичная Q (x), в уравнение левой части, 90 184 и приравнивающие коэффициенты.

      • Если Q(x) является линейной функцией, попробуйте y = Cx +D
      • Если Q(x) является квадратичным, попробуйте Cx ² +Dx +E
      • Если Q(x) является волновой функцией, попробуйте CSinx +Dcosx
      • Если Q(x) является константой, попробуйте y = C
      • Если Q(x) равно e ^kx , попробуйте y = Ce ^kx

      PI не может иметь ту же форму, что и любой из терминов в CF,
      , поэтому необходимо соблюдать осторожность чтобы убедиться, что это не так.
      В такой ситуации обычно используется дополнительный член x. познакомился с ИП.

       Частное решение находится путем замены начальные условия в общее решение. Не используйте только CF!!!

      Пример

      Найдите общее решение уравнения

          

       

           

      Пример

        Найти общее решение уравнения

          

      и конкретное решение для
      y=0 и dy/dx = 5, когда x=0

       

      Теперь подставьте их обратно в исходное уравнение

       

      Теперь найдите частное решение

       

      Фу!!

       

      Подробнее

      http://en. wikipedia.org/wiki/Дифференциальное_уравнение
      http://en.wikipedia.org/wiki/Обычное_дифференциальное_уравнение
      http://en.wikipedia.org/wiki/Линейное_дифференциальное_уравнение
      http://en.wikipedia.org/wiki/Superposition_principle
      http://en.wikipedia.org/wiki/Интегрирующий_фактор

      Некоторые примеры дифференциальных уравнений

       

      http://en.wikipedia.org/wiki/Примеры_дифференциальных_уравнений
      http://en.wikipedia.org/wiki/RC_circuit
      http://en.wikipedia.org/wiki/Classical_mechanics
      http://en.wikipedia.org/wiki/Dynamic_systems
      http://en.wikipedia.org/wiki/Numerical_methods
      http://en.wikipedia.org/wiki/Newton% 27s_Laws
      http://en.wikipedia.org/wiki/Radioactive_decay
      http://en.wikipedia.org/wiki/Wave_equation
      http://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation
      http: //en.wikipedia.org/wiki/Shallow_water_equations
      http://en.wikipedia.org/wiki/Maxwell%27s_equations
      http://en. wikipedia.org/wiki/Harmonic_oscillator
      http://en.wikipedia.org/wiki/Vector_space
      http://en.wikipedia.org/wiki/Method_of_undetermined_coefficients
      http://en.wikipedia.org/wiki/Euler%27s_formula
      http://en.wikipedia.org/wiki/Poisson%27s_equation
      http://en.wikipedia.org/wiki/Quantum_mechanics
      http://en.wikipedia.org/wiki/Verhulst_equation

      Линейные дифференциальные уравнения первого порядка

      Определение линейного уравнения первого порядка

      Дифференциальное уравнение типа

      \[y’ + a\влево( x \вправо)y = f\влево( x \вправо),\]

      , где \(a\left( x \right)\) и \(f\left( x \right)\) — непрерывные функции \(x,\), называется линейным неоднородным дифференциальным уравнением первого порядка.Рассмотрим два метода решения линейных дифференциальных уравнений первого порядка:

      • С использованием интегрирующего коэффициента;
      • Метод вариации константы.

      Использование коэффициента интегрирования

      Если линейное дифференциальное уравнение записано в стандартной форме:

      \[y’ + a\влево( x \вправо)y = f\влево( x \вправо),\]

      интегрирующий коэффициент определяется по формуле

      \[и \ влево ( х \ вправо) = \ ехр \ влево ( {\ int {а \ влево ( х \ вправо) dx}} \ вправо). \]

      Умножение левой части уравнения на интегрирующий множитель \(u\left( x \right)\) преобразует левую часть в производную от произведения \(y\left( x \right) u\left( x \ справа).\)

      Общее решение дифференциального уравнения выражается следующим образом:

      \[y = \frac{{\int {u\left(x\right)f\left(x\right)dx} + C}}{{u\left(x\right)}},\]

      , где \(С\) — произвольная константа.

      Метод вариации константы

      Этот метод аналогичен предыдущему подходу.Сначала необходимо найти общее решение однородного уравнения:

      \[у’ + а\влево( х \вправо)у = 0.\]

      Общее решение однородного уравнения содержит постоянную интегрирования \(С.\) Заменим постоянную \(С\) некоторой (пока неизвестной) функцией \(С\слева( х \справа).\) По формуле подставляя это решение в неоднородное дифференциальное уравнение, мы можем определить функцию \(C\left( x \right).\)

      Описанный алгоритм называется методом вариации константы.Конечно, оба метода приводят к одному и тому же решению.

      Проблема начального значения

      Если кроме дифференциального уравнения имеется еще начальное условие в виде \(y\left( {{x_0}} \right) = {y_0},\), то такая задача называется начальной задачей (НЗП) или задача Коши.

      Частное решение для ИВП не содержит константы \(C,\), которая определяется подстановкой общего решения в начальное условие \(y\left( {{x_0}} \right) = {y_0}.3}.\]

      Раствор.

      Мы решим эту задачу методом вариации постоянной. Сначала найдем общее решение однородного уравнения:

      \[ху’ = у,\]

      , которое можно решить, разделив переменные:

      \[x\frac{{dy}}{{dx}} = y,\;\; \Rightarrow \frac{{dy}}{y} = \frac{{dx}}{x},\;\; \Rightarrow \int {\frac{{dy}}{y}} = \int {\frac{{dx}}{x}} ,\;\; \стрелка вправо \ln \влево| у \ справа | = \ln \влево| х \ справа | + \ln С,\;\; \Стрелка вправо у = Сх,\]

      , где \(C\) — положительное действительное число.3} + {С_1}х.\]

      Дополнительные проблемы см.