Как найти радиус трапеции описанной около окружности – Радиус описанной окружности трапеции | Формулы и расчеты онлайн

Posted on by alexxlab

Все формулы для радиуса описанной окружности

Все формулы для радиуса описанной окружности

радиус описанной окружности треугольника

 

a , b , c blue    —  стороны треугольника

s12 black  — полупериметр

s (abc)2

O black  — центр окружности

 

Формула радиуса описанной окружности треугольника ( R  ) :

Формула радиуса описанной окружности треугольника

 

 

радиус описанной окружности равностороннего треугольника

 

сторона

— сторона треугольника

высота — высота

радиус — радиус описанной окружности

 

 

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Формула радиуса описанной окружности равностороннего треугольника через сторону

 

Формула радиуса описанной окружности равностороннего треугольника через высоту:

Формула радиуса описанной окружности равностороннего треугольника через высоту

 

 

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

радиус описанной окружности равнобедренного треугольника

 

a, b — стороны треугольника

 

 

 

Формула радиуса описанной окружности равнобедренного треугольника(

R):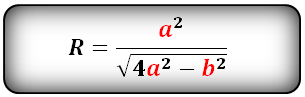

Формула радиуса описанной окружности равнобедренного треугольника

 

 

 

Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

радиус описанной окружности прямоугольного треугольника

 

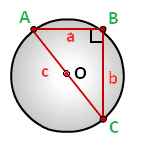
a, b — катеты прямоугольного треугольника

c — гипотенуза

 

 

 

Формула радиуса описанной окружности прямоугольного треугольника (R):

Формула радиуса описанной окружности прямоугольного треугольника

 

 

 

 

Радиус описанной окружности трапеции

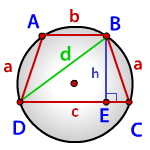
a — боковые стороны трапеции

c — нижнее основание

b — верхнее основание

d — диагональ

p — полупериметр треугольника DBC

p = (a+d+c)/2

 

Формула радиуса описанной окружности равнобокой трапеции, (R)

Формула радиуса описанной окружности равнобокой трапеции

 

 

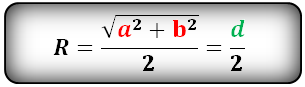
Радиус описанной окружности квадрата равен половине его диагонали

радиус описанной окружности около квадрата

 

 

a — сторона квадрата

d — диагональ

 

 

Формула радиуса описанной окружности квадрата (R):

Формула радиуса описанной окружности квадрата

 

 

 

 

Радиус описанной окружности прямоугольника равен половине его диагонали

Радиус описанной окружности прямоугольника

 

 

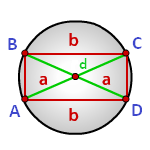
a, b — стороны прямоугольника

d — диагональ

 

 

 

Формула радиуса описанной окружности прямоугольника (R):

Формула радиуса описанной окружности прямоугольника

 

 

 

 

Радиус описанной окружности правильного многоугольника

 

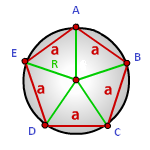
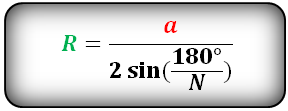
a — сторона многоугольника

N — количество сторон многоугольника

 

 

 

Формула радиуса описанной окружности правильного многоугольника, (R):

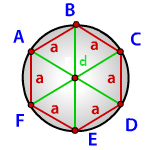
Формула радиуса описанной окружности правильного многоугольника

 

 

 

 

Формула радиуса описанной окружности правильного многоугольника

 

 

a

— сторона шестиугольника

d — диагональ шестиугольника

 

 

 

Радиус описанной окружности правильного шестиугольника (R):

Формула радиуса описанной окружности правильного многоугольника

 

Радиус описанной окружности

Наверх

© 2011-2019   Все права защищены.

При использовании материалов данного сайта обязательно указывать ссылку на источник.

www-formula.ru

Ответы@Mail.Ru: помогите, пожалуйста! Геометрия!

треугольник СОД-прямоугольный т. к. CO^2+OD^2=CD^2 15^2+20^2=625; СД=25;проводим высоту ОН на СД в итоге получим подобные тр-ки СОН и СОД по трем углам СД: ОД=СО: ОН; 25:20=15:ОН; ОН=12см и одновременно является радиусом окр, Зная, что у описанной трапеции СД+АВ=ВС+АД находим величину средней линии=(25+24):2=24,5см т. к. АВ=2R; площадь =24,5*24=588кв. см. Находим основания в равнобедренном тр-ке ВОС ОЕ=ОН=12-высота ;по т. Пифагора CE^2=CO^2-OE^2; СЕ=V81=9; ВС=18;АД=49-18=31см

Отрезки этих заданных рассстояний взаимно перпендикулярны. Боковая сторона равна 25. Найти радиус окружности — это половина высоты трапеции. Зная радиус — определить верхнее и нижнее основание. Дальше все просто. Если бы выкладывал чертеж к задаче с обозначениями можно было бы подсказать более подробно.

Все верно, кроме нахождения оснований. Ошибка в предпоследней строке треугольник ВОС не является равнобедренным! Основания находятся так: Продолжая рассматривать подобные треугольники СОН и СОД находим СН СН: СО=СО: СД ==> СН: 15=15:25 ==> CН=9см Основание ВС = СН+ОН = 12+9 = 21 см Основание АД = 49-ВС = 49-21 = 28 см ——————————————————— Проверено построением, Ответы правильные.

touch.otvet.mail.ru

Окружность описанная около трапеции

Добрый вечер! Ох уж эти описанные, или вписанные окружности, геометрические фигуры. Так сложно запутаться. что да когда.

Давайте попробуем разобраться для начала с формулировкой. Нам дана окружность описанная около трапеции. Иными словами — данная трапеция вписана в окружность.

Давайте вспомним, что описать окружность мы можем только вокруг равнобедренной трапеции. А равнобедренная трапеция в свою очередь — это трапеция, у которой боковые стороны равны.

Давайте попробуем решить задачку. Нам известно, что основания равнобедренной трапеции ADCB равны 6 (DC) и 4 (AB). А радиус описанной окружности равен 4. Нужно найдите высоту трапеции FK.

FK — высота трапеции. её нам нужно найти, но перед этим вспомним, что точка О — это центр окружности. А ОС, ОD, OA, OB — известные радиусы окружности.

В прямоугольном треугольнике OFC нам известна гипотенуза, которая является радиусом окружности, а катет FC = половине основания DC = 3 см (так как DF = FC).

Теперь по теореме Пифагора найдём OF:

   

   

   

   

А в прямоугольном треугольнике OKB нам тоже известна гипотенуза, так как это радиус окружности. А KB равняется половине AB; KB = 2 см. И, используя теорему Пифагора вычислим отрезок OK: 

   

 

   

 

   

 

   

 

   

Теперь мы с Вами можем найти высоту FK: 

   

 

   

Ответ:  см

ru.solverbook.com

Задачи В8 ЕГЭ по математике. Многоугольник и окружность

гнПродолжаем решать простейшие геометрические задачки. Разбираем Задачи №6 ЕГЭ по математике.

Сегодня работаем с окружностью, вписанной в многоугольник и описанной около многоугольника.

Вы можете пройти автотренинг «Планиметрия»

В категорию «Задачи №6» входят  также задачи следующих типов + показать

Окружность, вписанная в многоугольник

Задача 1.

Найдите радиус окружности, вписанной в квадрат со стороной 16. ьи

Решение: + показать

Задача 2.

Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба. lkj

Решение: + показать

Задача 3.

Найдите высоту трапеции, в которую вписана окружность радиуса 14.

бь

Решение: + показать

Высота трапеции  – есть диаметр вписанной окружности в трапецию.

14=r=\frac{h}{2} => h=28.

Ответ: 28. 

Задача 4.

Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции. бь

Решение: + показать

Задача 5.

Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности.

шр

Решение: + показать

Задача 6.

В четырехугольник ABCD вписана окружность,  AB=52, CD=53. Найдите периметр четырехугольника.

л

Решение: + показать

Раз в выпуклый четырехугольник ABCD вписана окружность, то AB+CD=BC+AD  (ранее эту формулу применяли для трапеции (что являлось частным случаем применения формулы).

P_{ABCD}=2(AB+CD)=2(52+53)=210.

Ответ: 210. 

Задача 7.

Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.

ьт

Решение: + показать

Задача 8.

Около окружности, радиус которой равен 3\sqrt2, описан квадрат. Найдите радиус окружности, описанной около этого квадрата. gf

Решение:  + показать

увСторона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому сторона квадрата равна 6\sqrt2. Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому радиус описанной окружности есть \sqrt{(3\sqrt2)^2+(3\sqrt2)^2}=6;

Ответ: 6.

Задача 9.

Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 33\sqrt3.

щоРешение:  + показать

Окружность, описанная около многоугольника

 

Задача 1. 

Угол A четырехугольника ABCD, вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах. ы

Решение: + показать

Задача 2.

Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах. uy

Решение: + показать

Вписанный угол C опирается на дугу BAD, равную 78˚+136˚=214˚.

Значит сам угол равен \frac{214^{\circ}}{2}=107^{\circ}.

Ответ: 107. 

Задача 3.

Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.

dc

Решение: + показать

Задача 4.

Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD. Ответ дайте в градусах.

f

Решение: + показать

Задача 5.

Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и \sqrt{155}. d

Решение: + показать

Задача 6.

Найдите сторону квадрата, вписанного в окружность радиуса 45\sqrt2.

g

Решение: + показать

Диагональ BD квадрата – диаметр окружности.

Обозначим сторону квадрата за  x.

Из треугольника ABD по т. Пифагора x^2+x^2=(90\sqrt2)^2;

2x^2=90^2\cdot 2;

x^2=90^2;

x=90;

Ответ: 90. 

Задача 7.

Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.

f

Решение: + показать

Диагонали прямоугольника – диаметры окружности.

Треугольник ABO – равносторонний, так как \angle O=60^{\circ},\;AO=BO=R.

Значит,  R=16.

Ответ: 16. 

Задача 8.

Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.

к

Решение: + показать

Задача 9.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции. lk

Решение: + показать

Задача 10.

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции. iuy

Решение: + показать

Задача 11.

Два угла вписанного в окружность четырехугольника равны  56˚ и 99˚. Найдите больший из оставшихся углов. Ответ дайте в градусах.

s

Решение: + показать

Данные два угла не могут быть противоположными, так как иначе их сумма должна была бы быть 180˚ (так как они опираются на дополняющие друг друга дуги до окружности).

Если  \angle A=99^{\circ}, то \angle C=180^{\circ}-99^{\circ}=81^{\circ};

 Если  \angle B=56^{\circ}, то \angle D=180^{\circ}-56^{\circ}=124^{\circ};

Угол D и есть наибольший.

Ответ: 124. 

Задача 12.

Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.

esd

Решение: + показать

Диаметр описанной окружности около прямоугольника – диагональ прямоугольника.

R=\frac{BD}{2}=2,5.

Ответ: 2,5. 

Задача 13.

Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

ув

Решение: + показать

Задача 14.

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен  72˚. Найдите n.

rf

Решение: + показать

Задача 15.

Около окружности, радиус которой равен \frac{3\sqrt3}{2}, описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.

d

Решение: + показать

Самое время отдохнуть! –>+ показать

Кто-то развлекается так. А вы как?

е

тест

Вы можете пройти тест по теме «Окружность и многоугольник».

egemaximum.ru

Свойства трапеции описанной около окружности

Доброй ночи! Очень хороший и популярный вопрос, который часто начинает вызывать трудности, так как речь идёт не об одной геометрической фигуре, а о двух, и тут очень легко запутаться, что как и с чем. Для начала мы с вами должны коротко вспомнить, что такое трапеция и какие понятия с ней могут быть связаны, чтоб не запутаться в дальнейшем.
Итак, трапеция – это геометрическая фигура, четырехугольник, две стороны которой параллельны друг другу (их называют основаниями). И две не параллельны – это, так называемые, боковые стороны.
В трапеции может быть опущена высота (иными словами, перпендикуляр  проведённый к основаниям). А так же могут быть проведены средняя линия и диагонали трапеции. А из любого угла трапеции можно провести биссектрису.
А теперь разберёмся с вопросом, какие свойства трапеции описанной около окружности существуют. Это должно помочь нам в дальнейшем правильно находить, как  решение задачу:
1. Если в трапецию мы вписали окружность,  то мы можем легко найти длину ее средней линии. Для этого нам потребуется сложить длины боковых сторон и разделить полученную сумму пополам:
2. У трапеции АFCD, которая описана около окружности, сумма длин оснований равняется сумме длин боковых сторон: AF + CD = FC + AD.
3. Окружность можно вписать лишь только в ту трапецию, сумма оснований которой равна сумме боковых сторон;
4. При таком условии задачи можно вычислить радиус окружности, который будет равняться:  , где   — это отрезки, которые получились вследствие деления радиусом боковой стороны трапеции.

ru.solverbook.com

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *