Как найти длину отрезка зная координаты точек. Нахождение координат середины отрезка, примеры, решения
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.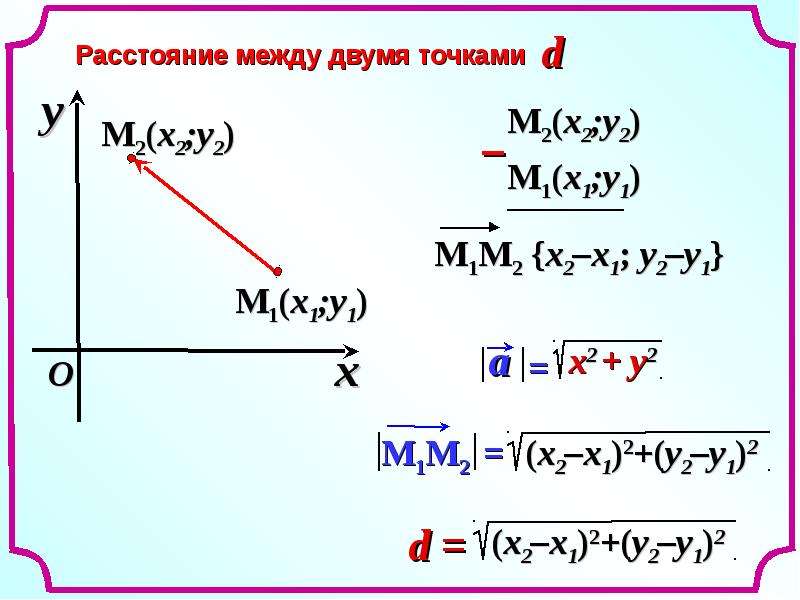
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам.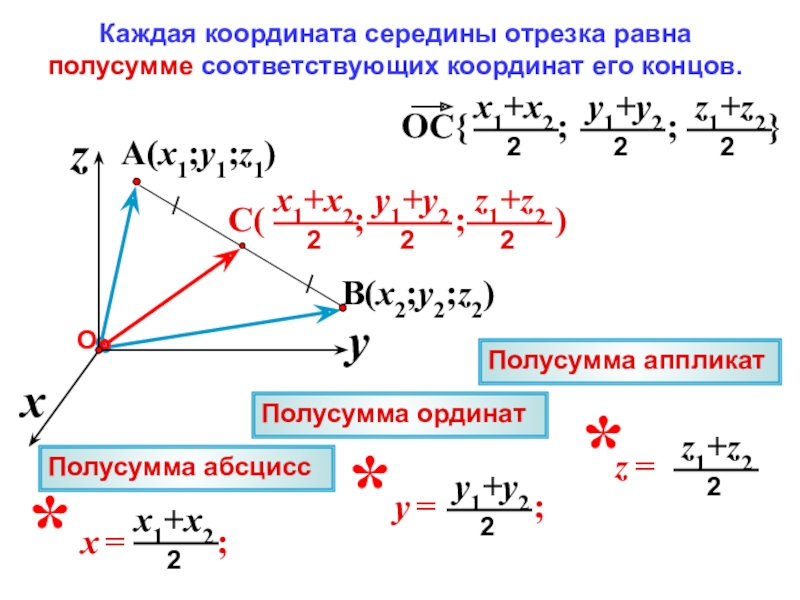 Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
(рис. 3
).
Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком .
Точка и отрезок − примеры геометрических фигур .
Точки A и B называют концами отрезка .
Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.
Также принято говорить: «отрезок MN
равен 3
см», «отрезок EF
равен 4
см». Пишут: MN =
3
см, EF =
4
см.
Длины отрезков MN и EF мы измерили единичным отрезком , длина которого равна 1 см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1 мм, 1 дм, 1 км. На рисунке 7 длина отрезка равна 17 мм. Он измерен единичным отрезком, длина которого равна 1 мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7 ).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .
Длина отрезка обладает следующим свойством.
Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).
Пишут: AB = AC + CB.
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB и CD равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB называют расстоянием между точками A и B.
Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).
Длиной ломаной называют сумму длин всех ее звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.
Решение. Имеем: BC =
8
− 3
= 5
(см).
Имеем: BC =
8
− 3
= 5
(см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC = 8 + 5 = 13 (см).
Ответ: 13 см.
Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN = 50 − 32 = 18 (см).
Имеем: NK = MK − MN.
Отсюда NK = 24 − 18 = 6 (см).
Ответ: 6 см.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z.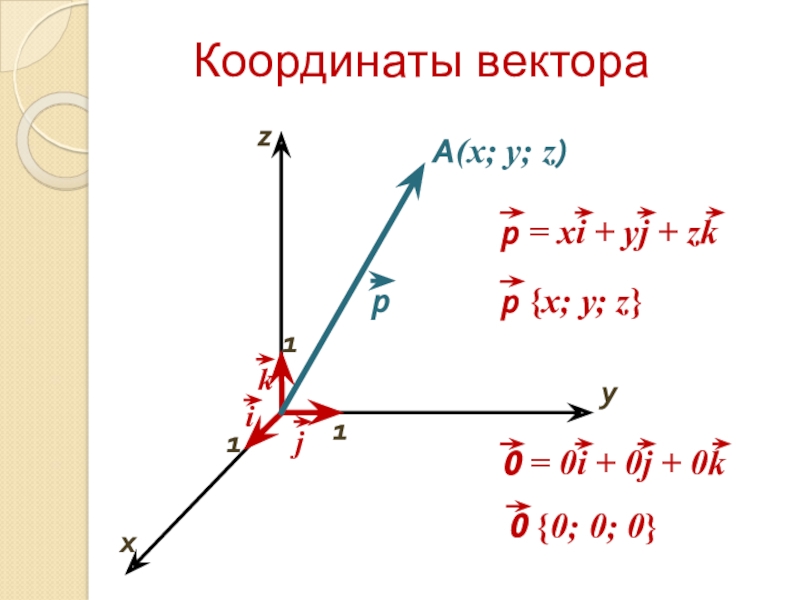 2))
2))
Видео по теме
Простейшие задачи в координатах / Метод координат / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Простейшие задачи в координатах
Метод координат — это подход к изучению свойств геометрических фигур, используя методы алгебры.
Задачи
1. Координаты середины отрезка.
Дано: система координат , А(1; 1), В(2; 2), С середина отрезка АВ.
Выразить: координаты С(; ) через координаты концов отрезка АВ.
Решение:
С — середина отрезка АВ, поэтому . (1)
(1)
(Доказательство утверждения (1) приведено в разделе «Применение векторов к решению задач»).
Координаты векторов , и равны соответствующим координатам точек С, А и В:
, и .
Записывая равенство (1) в координатах, получим:
, следовательно, и .
Вывод:
| Каждая координата середины отрезка равна полусумме соответствующих координат его концов. |
2. Вычисление длины вектора по его координатам.
Дано: .
Доказать: .
Доказательство:
1. и .
Отложим от начала координат вектор и проведем через точку А перпендикуляры АА1 и АА2 к осям и .
Координаты точки А равны координатам вектора , т.е. (; ). Поэтому . По теореме Пифагора: .
Но , следовательно, . Что и требовалось доказать.
2. и .
Отложим от начала координат вектор , учитывая то, что .
.
Но , следовательно, . Что и требовалось доказать.
3. и .
Отложим от начала координат вектор , учитывая то, что .
.
Но , следовательно, . Что и требовалось доказать.
Вывод:
| Длина вектора равна квадратному корню из суммы квадратов координат данного вектора. |
3. Расстояние между двумя точками.
Дано: М1(1; 1), М2(2; 2), — расстояние между М1 и М2.
Выразить: через координаты М1 и М2.
Решение:
Рассмотрим вектор , каждая его координата равна разности соответствующих координат его конца и начала, т.е. . Следовательно, длина этого вектора: .
Но , значит, расстояние между точками М1(1; 1) и М2(2; 2) выражается формулой:
.
Вывод:
| Расстояние между двумя данными точками равно корню квадратному из суммы квадратов разностей соответствующих координат данных точек. |
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Координаты вектора
Связь между координатами вектора его начала и конца
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 936, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 947, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 953, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 957, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 969, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 990, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 993, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1048, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1065, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2022
com, 2022
Пользовательское соглашение
Copyright
Найти середину отрезка по координатам точек. Координаты середины отрезка. Примеры решения задач на нахождение координат середины отрезка
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Ответ : K = (0,5; 0; 1)
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .
Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .
Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:
Ответ : L = (0,5; 0,5; 1)
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
По той причине, что все формулы… сами увидите.
Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:
Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.
Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.
Решение.
Используем рассмотренную выше формулу:
Ответ . М (5; 14).
С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.
Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.
Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:
Подставим известные координаты и вычислим отдельные координаты:
примеры, решения. Определение координат середины отрезка через координаты радиус-векторов его концов
После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении , и, как частный случай, о делении отрезка пополам .
Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.
Нередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек и, очевидное невероятное – отрезок :
Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок делится на две части с помощью некоторой точки , которая, понятно, расположена прямо на нём:
В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .
На сухом математическом языке этот факт записывают следующим образом: , или чаще в виде привычной пропорции: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .
Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .
Пропорцию несложно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:
Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .
После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.
Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.
урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.
Пример 1
Найти координаты точки , делящей отрезок в отношении , если известны точки
Решение : В данной задаче . По формулам деления отрезка в данном отношении, найдём точку :
Ответ :
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.
В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:
Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Равноценен второй способ решения : в нём отсчёт начинается с точки и справедливым является отношение: (человеческими словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:
По формулам деления отрезка в данном отношении:
Ответ :
Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё.
Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок , то предполагается, что вы составите пропорцию , если дан отрезок , то «негласно» подразумевается пропорция .
А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.
Пример 2
Даны точки . Найти:
а) точку , делящую отрезок в отношении ;
б) точку , делящую отрезок в отношении .
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Полное решение и ответ в конце урока.
Иногда встречаются задачи, где неизвестен один из концов отрезка:
Пример 3
Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если .
Решение : Из условия следует, что точка делит отрезок в отношении , считая от вершины , то есть, справедлива пропорция: . По формулам деления отрезка в данном отношении:
Сейчас нам неизвестны координаты точки : , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
Ответ :
Для проверки можно взять концы отрезка и, пользуясь формулами в прямом порядке, убедиться, что при соотношении действительно получится точка . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
Пример 4
Точка . Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .
Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .
Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.
Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.
Если известны две точки пространства , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
.
Пример 5
Даны точки . Найти координаты точки , принадлежащей отрезку , если известно, что .
Решение : Из условия следует отношение: . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: .
По формулам координат середины отрезка:
Ответ :
Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.
Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.
Разминочная задача для самостоятельного решения:
Пример 6
Даны точки . Найти координаты точки , если известно, что она делит отрезок в отношении .
Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.
В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.
Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:
Формулы координат середины отрезкаДаже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы чудесным образом преображаются в нечто знакомое и простое:
Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:
В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.
Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины выражаются формулами:
Пример 7
Параллелограмм задан координатами своих вершин . Найти точку пересечения его диагоналей.
Решение : Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.
По известному свойству, диагонали параллелограмма своей точкой пересечения делятся пополам, поэтому задачу можно решить двумя способами.
Способ первый : Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :
Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:
Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.
Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.
Решение.
Используем рассмотренную выше формулу:
Ответ . М (5; 14).
М (5; 14).
С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.
Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.
Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:
Подставим известные координаты и вычислим отдельные координаты:
Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.
Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т. п.
п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пример.
Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).
Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:
Следовательно, середина МО будет иметь координаты К (3,5; 5,5).
Ответ. К (3,5; 5,5).
Найти координаты середины вектора. Формулы деления отрезка в данном отношении. Формулы координат середины отрезка. Формула нахождения координаты середины отрезка
Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:
Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:
Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.
Задача.
Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.
Решение.
Используем рассмотренную выше формулу:
Ответ . М (5; 14).
С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.
Задача.
Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.
Решение.
Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:
Перепишем формулу с учетом новых названий:
Подставим известные координаты и вычислим отдельные координаты:
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Решение . Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:
Ответ : K = (0,5; 0; 1)
· Задача . Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .
Решение . Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:
Ответ : L = (0,5; 0,5; 1)
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть , даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек.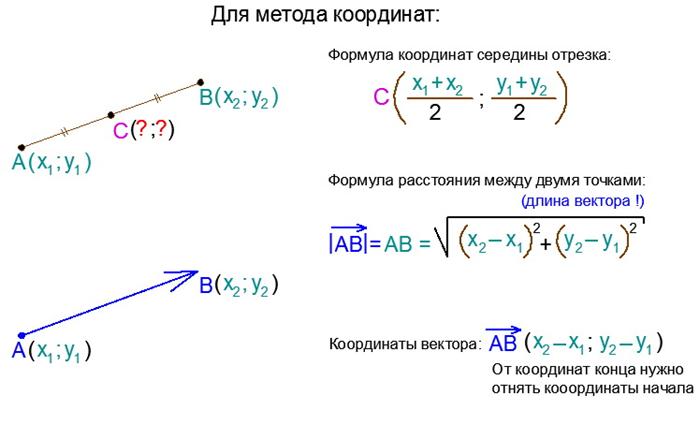 Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении , и, как частный случай, о делении отрезка пополам .
Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.
Формулы деления отрезка в данном отношении Понятие деления отрезка в данном отношенииНередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек и, очевидное невероятное – отрезок :
Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок делится на две части с помощью некоторой точки , которая, понятно, расположена прямо на нём:
В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .
На сухом математическом языке этот факт записывают следующим образом: , или чаще в виде привычной пропорции: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .
Пропорцию несложно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:
Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .
После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.
Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.
Пример 1
Найти координаты точки , делящей отрезок в отношении , если известны точки
Решение : В данной задаче . По формулам деления отрезка в данном отношении, найдём точку :
По формулам деления отрезка в данном отношении, найдём точку :
Ответ :
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.
В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:
Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Равноценен второй способ решения : в нём отсчёт начинается с точки и справедливым является отношение: (человеческими словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:
Ответ :
Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё.
Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок , то предполагается, что вы составите пропорцию , если дан отрезок , то «негласно» подразумевается пропорция .
А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.
Пример 2
Даны точки . Найти:
а) точку , делящую отрезок в отношении ;
б) точку , делящую отрезок в отношении .
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Иногда встречаются задачи, где неизвестен один из концов отрезка:
Пример 3
Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если .
Найти точку , если .
Решение : Из условия следует, что точка делит отрезок в отношении , считая от вершины , то есть, справедлива пропорция: . По формулам деления отрезка в данном отношении:
Сейчас нам неизвестны координаты точки : , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
Ответ :
Для проверки можно взять концы отрезка и, пользуясь формулами в прямом порядке, убедиться, что при соотношении действительно получится точка . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
Пример 4
Точка . Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .
Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.
Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.
Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.
Если известны две точки пространства , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
.
Пример 5
Даны точки . Найти координаты точки , принадлежащей отрезку , если известно, что .
Решение : Из условия следует отношение: . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: .
По формулам координат середины отрезка:
Ответ :
Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.
Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.
Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.
Разминочная задача для самостоятельного решения:
Пример 6
Даны точки . Найти координаты точки , если известно, что она делит отрезок в отношении .
Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.
В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.
Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:
Формулы координат середины отрезкаДаже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы чудесным образом преображаются в нечто знакомое и простое:
Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:
В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.
Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины выражаются формулами:
Пример 7
Параллелограмм задан координатами своих вершин . Найти точку пересечения его диагоналей.
Решение : Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.
По известному свойству, диагонали параллелограмма своей точкой пересечения делятся пополам, поэтому задачу можно решить двумя способами.
Способ первый : Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :
Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.
Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Тогда координаты середины отрезка РН рассчитываются по формуле:
Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пример.
Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).
Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:
Следовательно, середина МО будет иметь координаты К (3,5; 5,5).
Ответ. К (3,5; 5,5).
Найдите координату точки которая является серединой отрезка: Найдите координату точки которая является серединой отрезка с концами в точках А(2) и В(8) — ЭкоДом: Дом своими руками
примеры, решения, как найти середину отрезка по координатам
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.
Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.
Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = |СВ|. Расстояние между точками определяется модулем разницы их координат, т.е.
|АС| = |СВ|⇔xC-xA=xB-xC
Тогда возможно два равенства: xC-xA=xB-xC и xC-xA=-(xB-xC)
Из первого равенства выведем формулу для координаты точки C : xC=xA+xB2 (полусумма координат концов отрезка).
Из второго равенста получим: xA=xB , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка AB с концами A(xA) и B(xB):
xA+xB2
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости Оxy, две произвольные несовпадающие точки с заданными координатами AxA, yA и BxB, yB . Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
Точка C – середина отрезка AB. Необходимо определить координаты xC и yC для точки C.
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей.Ax, Ay ; Bx, By и Cx ,Cy — проекции точек A, B и C на оси координат (прямые Ох и Оy).
Согласно построению прямые AAx, BBx, CCx параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства АС = СВ следуют равенства: АxСx = СxВx и АyСy = СyВy, и они в свою очередь свидетельствуют о том, что точка Сx – середина отрезка АxВx, а Сy – середина отрезка АyВy. И тогда, опираясь на полученную ранее формулу, получим:
xC=xA+xB2 и yC=yA+yB2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка AB на плоскости с координатами концов A (xA,yA) и B (xB, yB) определяются как:
(xA+xB2, yA+yB2)
Середина отрезка в пространстве
Исходные данные: система координат Оxyz и две произвольные точки с заданными координатами A(xA, yA, zA) и B (xB, yB, zB). Необходимо определить координаты точки C, являющейся серединой отрезка AB.
Необходимо определить координаты точки C, являющейся серединой отрезка AB.
Ax, Ay, Az ; Bx, By,Bz и Cx, Cy, Cz — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: AxCx=CxBx, AyCy=CyBy,AzCz=CzBz
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Следовательно, точки Cx, Cy,Cz являются серединами отрезков AxBx, AyBy, AzBz соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
xC=xA+xB2, yc=yA+yB2, zc=zA+ZB2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат Oxy, точки с заданными координатами A(xA,yA) и B(xB, xB) . Точка C – середина отрезка AB.
Согласно геометрическому определению действий над векторами верным будет равенство: OC→=12·OA→+OB→ . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов OA→ и OB→ , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: OA→=(xA, yA), OB→=(xB,yB) . Выполним некоторые операции над векторами в координатах и получим:
OC→=12·OA→+OB→=xA+xB2, yA+yB2
Следовательно, точка C имеет координаты:
xA+xB2, yA+yB2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C(xA+xB2, yA+yB2, zA+zB2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (-7,3) и В (2,4). Необходимо найти координаты середины отрезка АВ.
Решение
Обозначим середину отрезка AB точкой C. Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B.
xC=xA+xB2=-7+22=-52yC=yA+yB2=3+42=72
Ответ: координаты середины отрезка АВ-52, 72.
Пример 2
Исходные данные: известны координаты треугольника АВС: А (-1,0), В (3,2), С (9,-8). Необходимо найти длину медианы АМ.
Решение
- По условию задачи AM – медиана, а значит M является точкой середины отрезка BC. В первую очередь найдем координаты середины отрезка BC, т.е. точки M:
xM=xB+xC2=3+92=6yM=yB+yC2=2+(-8)2=-3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы АМ:
AM=(6-(-1))2+(-3-0)2=58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед ABCDA1B1C1D1 . Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка АС1. Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: xM=xA+xC12 ⇒xA=2·xM-xC1=2·4-1+7yM=yA+yC12⇒yA=2·yM-yC1=2·2-1=3zM=zA+zC12⇒zA=2·zM-zC1=2·(-4)-0=-8
Ответ: координаты точки А (7,3,-8).
Расстояние между точками на координатной прямой
Расстояние между двумя точками на координатной прямой равно модулю разности их координат.
Формула расстояния между точками на координатной прямой:
AB = |a — b|,
где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.
Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:
|-3 — 5| = |-8| = 8
или
|5 — (-3)| = |5 + 3| = 8.
Ответ. Расстояние между точками L и M равно 8.
Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).
Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:
Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:
AB = |-5 — 5| = |-10| = 10;
10 : 2 = 5, значит |AC| = |CB| = 5.
Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:
-5 + 5 = 0
или
5 — 5 = 0.
Ответ. Координата середины отрезка C(0).
Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).
Решение.
AB = |7 — 25| = |-18| = 18;
AC = CB = 18 : 2 = 9;
7 + 9 = 16
или
25 — 9 = 16.
Ответ. Координата точки C — 16.
Формула нахождения координаты середины отрезка
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Помощь со студенческой работой на тему
Формула нахождения координаты середины отрезка
Рисунок 1. Отрезок. Автор24 — интернет-биржа студенческих работ
Отрезок. Автор24 — интернет-биржа студенческих работ
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Рисунок 2. Середина отрезка. Автор24 — интернет-биржа студенческих работ
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
Рисунок 5. Отрезки на плоскости. Автор24 — интернет-биржа студенческих работ
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
Ответы:
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Пример 3
Точка $B$ — середина отрезка $AC$. $AC = 8,4$ см. Какая длина $AB$?
Так как т. $B$ делит $AC$ пополам, то $AB = \frac{8,4}{2}$ см. Значит, $AB = 4,2$ см.
Ответ: 4,2 см.
Если в очередной задаче возникают трудности с пониманием её решения (например, нетипичные случаи с несколькими отрезками, образующими углами и прочими усложнениями), то лучше рассмотреть задачу, сделав по её условию рисунок. Наглядность способствует лучшему пониманию и более скорому нахождению решения.
Теперь решим задачи по аналитической геометрии.
Пример 4
Даны точки $T_1(7,11)$ и $T_2(1,23)$. Требуется найти координаты середины отрезка $T_1T_2$.
Абсцисса середины отрезка: $x=\frac{7+1}{2}=4$.
Ордината: $y=\frac{11+23}{2}=17$.
Ответ: $(4,17)$.
Пример 5
Даны точки $T(6,-1)$ и $S(-4,-8)$. Точка $S$ — середина $TK$. Найти координаты $K$.
Подставим значения и получим уравнения:
$-4=\frac{6+x_2}{2}, -8=\frac{-1+y_2}{2}.$
Найдём координаты:
$-2=6+x_2, -4=-1+y_2; x_2=-8, y_2=-3$.
Ответ: $K(-8,-3)$.
Урок – лекция по геометрии в 10 классе по теме «декартовы координаты в пространстве»
Урок – лекция по
геометрии в 10 классе по теме
«Декартовы
координаты в пространстве»
Учитель: Макеева О. В.
Цели урока:
Повторить
введение и применение координат на
прямой и на плоскости; формулы координат
середины отрезка и расстояния между
точками.Ввести
декартовы координаты в пространстве.Развивать
интерес к истории математики.
Оборудование:
Таблица
«Декартовы координаты в пространстве».
Модель
трёхмерной системы координат.Чертежные
инструменты.Портрет
Р. Декарта.
Ход урока
I.
Введение
В 1637 г. во Франции вышла книга,
которая принесла её автору невероятную
известность. По обычаям того времени
она имела довольно длинное название:
«Рассуждение о методе, позволяющем
направлять разум и отыскивать истину
в науках. Кроме того, Диоптрика, Метеоры
и Геометрия, которые являются приложениями
этого метода». Автор книги Рене Декарт
(1596 – 1650 г.). В ней он ввел прямоугольную
систему координат, поставил каждой
точке в соответствие пару чисел – её
координаты. Этот прогрессивный метод
позволил решить ряд геометрических
задач алгебраическим методом, что
оказалось очень удобным.
Главные правила метода гласят:
Не принимать за истинное что бы
то ни было, прежде чем не признал это
несомненно истинным, т. е. старательно
е. старательно
избегать поспешности и предубеждения
и включить в свои рассуждения только
то, что представляется уму так ясно и
отчетливо, что никоим образом не может
дать повод к сомнению.Делить каждую из рассматриваемых
трудностей на столько частей, на сколько
требуется, чтобы лучше их разрешить.Руководить ходом своих мыслей,
начиная с предметов простейших и легко
познаваемых, и восходить мало – помалу,
как по ступеням, до познания наиболее
сложных, допуская существования порядка
даже среди тех, которые в естественном
порядке вещей не предшествуют друг
другу.Делать всюду настолько полные
перечни и такие общие обзоры, чтобы
быть уверенным, что ничего не пропущено.
Руководствуясь этими правилами,
начнем с ранее изученного материала.
II.
Повторение. Актуализация знаний
Актуализация знаний
1.
Сначала координаты точки ввели на луче,
потом на прямой.
Координатная прямая – это прямая
с выбранными на ней направлением, началом
отсчета и единичным отрезком.
О А(х)
= ОА
0 1
х
Координатой точки А
называют число, абсолютная
величина которого равна расстоянию от
начала отсчета до точки А.
Если точка расположена справа
от точки О, то её координата положительная,
если слева – то отрицательная.
2. Для определения положения
точки на плоскости одной координаты
недостаточно. Поэтому по примеру
географических координат Декартом были
введены координаты на плоскости, добавив
к оси х перпендикулярную ось и выбрав
на ней направление и единичный отрезок.
y
О – начало
отсчета.
(Повторить
определение абсциссы и
Аy
А(х,y)
ординаты точки на плоскости).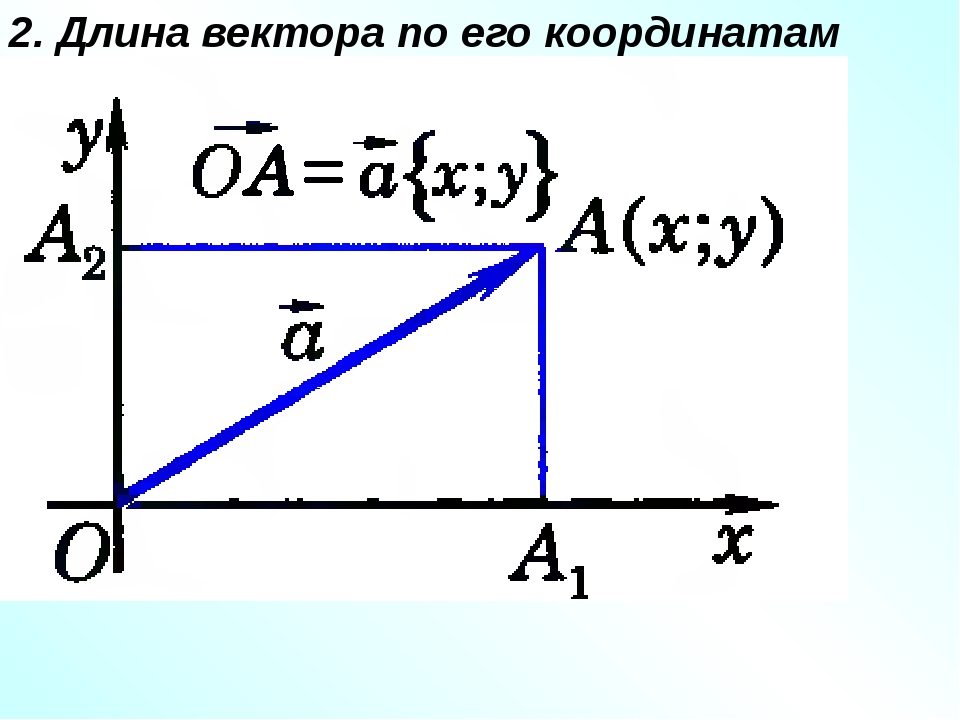
ОАх
=
,
ОАy =
,
1 А
(х;y),
Ах (х;0), Аy
(0;y
)
О
1 Ах
х
III.
Введение координат в пространстве
Первое определение IX
книги «Начала» Евклида гласит: «Тело
есть то, что имеет длину, ширину и
глубину». Тем не менее есть основание
полагать, что в древности нашего понятия
о трехмерном пространстве не существовало.
У Декарта имелись лишь далекие намеки
на возможность распространения метода
координат с двумерного пространства
(плоскости) на трехмерное. Потребовалось
ещё почти 100 лет, чтобы идея пространственных
координат была сформирована, постоянно
и и широко использовалась.
z
(Объяснение с
опорой на трехмерную модель и
Аz
Ayz
таблицу №21).
Система
координат в пространстве представляет
Axz
A
собой три взаимно
перпендикулярные прямые
х, y,
z,
пересекающиеся в одной точке.
О – начало отсчета,
О Ау
у x,
y,
z –
координатные оси,
Ax
Axy
xy,
yz,
xy
– координатные плоскости.
x
Координатные
плоскости делят все пространство
на 8
октантов.
Определим координаты
точки А на плоскости.
Через точку А проведем плоскость,
параллельную плоскости yz.
Она пересекает ось x
в точке Аx
. Координатой х точки А
называется число, равное по абсолютной
величине длине отрезка ОАх
. Аналогично определяются и другие
координаты. Таким образом, точке А в
пространстве ставится в соответствие
тройка чисел – её координаты.
Обозначение: А(x;
y;
z).
(Название координаты z
найти самостоятельно).
Рассмотрим координаты частного
расположения точек в пространстве.
Ах
(х;0;0) Ахy
(х;y;0) О
(0;0;0)
Аy
(0;y;0) Аyz
(0;y;z)
Аz
(0;0;z) Ахz
(х;0;z)
Задача
1. Дан куб с ребром,
равным 4. Определите координаты его
вершин.
z
В1
С1
Ответы:
А1
D1
А (4;0;0) А1
(4;0;4)
В (0;0;0) В1
(0;0;4)
В С y С
(0;4;0) С1
(0;4;4)
D
(4;4;0) D1
(4;4;4)
А D
x
Задача 2.
Дан прямоугольный параллелепипед,
измерения которого равны 6;4;4. Определите
координаты его вершин.
В1
z
С А1
D1
Ответы:
А1
D1
А (2;-3;0) А1
(2;-3;4)
В
С В (-2;-3;0) В1
(-2;-3;0)
А D
y С (-2;3;0) С1
(-2;3;4)
D
(2;3;0) D1
(2;3;4)
x
IV.
Приложение метода координат
В качестве иллюстрации приложения
метода координат рассмотрим алгебраические
равенства, имеющие простые геометрические
истолкования. Это формулы координат
середины отрезка и расстояния между
точками.
Задача на повторение.
Найдите координаты середины отрезка
АВ и длину отрезка АВ, если:
1 вариант – А (3;-1), В (-2;4)
2 вариант – А (3;4), В (2; -1)
(Проверку работ осуществить на
боковых досках).
Аналогичные формулы применяются
в пространстве. По учебнику прочитать
п.153, 154 и выписать формулы в тетрадь. Два
ученика получают на дом задание — вывод
формул.
Задача №3.
Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты
середины отрезка АВ и его длину.
Решение:
1). Пусть С – середина отрезка
АВ, тогда С (;
;
),
С (2;0;0)
2). АВ =
АВ =
=
= 2.
V.
Подведение итогов урока
VI.
Домашнее задание: п.
152 – 154, вопросы № 1 – 3, № 3, 9.
Два ученика получают индивидуальное
задание: вывод формул.
Самостоятельная работа по теме: «Простейшие задачи в координатах» I вариант 1.Найдите координаты вектора АВ, если А (-7; 6), В (-1; 2). 2.Найдите длину вектора , если А(-7; 6), В(-1; 2). 3.Найдите координаты точки К, которая является серединой отрезка MN ,если М(6; -5), N(3; -9) 4.Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9) 5.Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4) | Самостоятельная работа по теме: «Простейшие задачи в координатах» II вариант 1. 2.Найдите длину вектора, если M(4; -5), N(7; -9). 3.Найдите координаты точки C, которая является серединой отрезка AB ,если A(-2; 1), B(-10; -5) 4.Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1), B(-10; -5) 5.Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1) | Самостоятельная работа по теме: «Простейшие задачи в координатах» I вариант 1.Найдите координаты вектора АВ, если А (-7; 6), В (-1; 2). 2.Найдите длину вектора , если А(-7; 6), В(-1; 2). 3.Найдите координаты точки К, которая является серединой отрезка MN ,если М(6; -5), N(3; -9) 4.Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9) 5.Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4) | Самостоятельная работа по теме: «Простейшие задачи в координатах» II вариант 1. 2.Найдите длину вектора, если M(4; -5), N(7; -9). 3.Найдите координаты точки C, которая является серединой отрезка AB ,если A(-2; 1), B(-10; -5) 4.Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1), B(-10; -5) 5.Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1) | Самостоятельная работа по теме: «Простейшие задачи в координатах» I вариант 1.Найдите координаты вектора АВ, если А (-7; 6), В (-1; 2). 2.Найдите длину вектора , если А(-7; 6), В(-1; 2). 3.Найдите координаты точки К, которая является серединой отрезка MN ,если М(6; -5), N(3; -9) 4.Найдите расстояние между точками M и N, т.е. длину отрезка MN, если М(6; -5), N(3; -9) 5.Найдите медиану CD треугольника АВС, вершины которого имеют координаты: А(-1; 2), В(5; -6), С(6; 4) | Самостоятельная работа по теме: «Простейшие задачи в координатах» II вариант 1. 2.Найдите длину вектора, если M(4; -5), N(7; -9). 3.Найдите координаты точки C, которая является серединой отрезка AB ,если A(-2; 1), B(-10; -5) 4.Найдите расстояние между точками A и B, т.е. длину отрезка AB, если A(-2; 1), B(-10; -5) 5.Найдите медиану BD треугольника АВС, вершины которого имеют координаты: А(-2; -3), В(-3; 5), С(4; 1) |
Координаты симметричных точек | Треугольники
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
биссектрисы I и II координатных четвертей (прямой y=x) | A3(y;x) |
биссектрисы I b II координатных четвертей (прямой y= -x) | A4(-y;-x) |
ПРОВЕРЬТЕ ПОЖАЛУЙСТА ) — @дневники: асоциальная сеть
пятница, 11 ноября 2011
№1 Даны точки A(-2;3;4) и B(4;-1;6)
а) Найдите координаты середины отрезка АВ
б) Найдите координаты точки С , если точка В — середина отрезка АС.
в) Найдите расстояние от точки В до плоскости Oyz.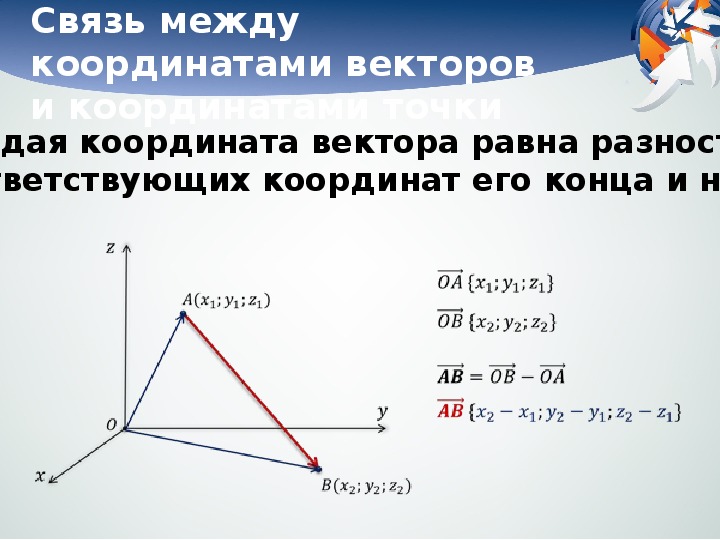
Ответы : а) М — середина АВ. М(1;1;5)
б) С(10;-5;8)
в) ответ = 2
№2
vec(a){2;-6;3} и vec(b){-1;2;-2}
Ответы : |vec(a)|-|vec(b)|=4 ?
|vec(a)-vec(b)|= 7 корней из 2. ?
№3
Даны точки А(-1;5;3) , В(-3;7;-5) , С(3;1;-5)
Найти среднюю линию треугольника АВС .
MN — СРЕДНЯЯ ЛИНИЯ ,
Ответ : MN=2 корня из 6 .
№4
Даны точки А(3;-2;5) и В(-1;4;3)
а) Найти координаты точки С — середины отрезка АВ
б) Найти координаты точки D если отрезок АD делится точками В и С ни три равные части .
Ответы : а) С(1;1;4)
б) D(1;-2;5)
№5
Дан вектор vec(a){-6;4;12}
Найдите координаты vec(b) , если |vec(b)|= 28 , а vec(a) и vec(b) противоположно направлены .
Ответ : vec(b){12;-8;-24}
№6
Даны точки А(-1;5;3) , В(-1;-3;9) , С(3;-2;6)
Найдите длину медиану треугольника АВС.
Ответ : МЕДИАНА = 13 .
№7
Найдите координаты четвертой вершины параллелограма ABCD
если B(-7;6;7) , С(4;-2;-3) , D(-3;8;-5)
Ответ : А(0;-4;9)
@темы:
Аналитическая геометрия
Векторная алгебра
- ← Предыдущая запись
- Следующая запись →
Этот пост будет безвозвратно удален:
Вы уверены в том, что действительно хотите это сделать?
Да
Нет
Калькулятор средней точки
Калькулятор средней точки берет две координаты в декартовой системе координат и находит точку прямо между ними. Этот момент часто бывает полезен в геометрии. В качестве дополнения к этому калькулятору мы написали статью ниже, в которой обсуждается, как найти среднюю точку и что такое формула средней точки.
Этот момент часто бывает полезен в геометрии. В качестве дополнения к этому калькулятору мы написали статью ниже, в которой обсуждается, как найти среднюю точку и что такое формула средней точки.
Как найти середину
- Обозначьте координаты
(x₁, y₁) и (x₂, y₂). - Введите значения в формулу.
- Сложите значения в скобках и разделите каждый результат на 2.
- Новые значения образуют новые координаты средней точки.
- Проверьте свои результаты с помощью калькулятора средней точки.
Предположим, у нас есть отрезок прямой, и мы хотим разрезать его на две равные части. Для этого нам нужно знать центр. Мы можем добиться этого, найдя середину. Вы можете измерить с помощью линейки или просто использовать формулу, включающую координаты каждой конечной точки сегмента.Средняя точка — это просто среднее значение каждой координаты сечения, образующее новую координатную точку. Мы проиллюстрируем это ниже.
Формула средней точки
Если у нас есть координаты (x₁, y₁) и (x₂, y₂) , то середина этих координат определяется как (x₁ + x₂) / 2, (y₁ + y₂) / 2 . Это формирует новую координату, которую вы можете назвать
Это формирует новую координату, которую вы можете назвать (x₃, y₃) . Калькулятор средней точки решит эту проблему мгновенно, если вы введете координаты. При вычислении вручную следуйте приведенным выше инструкциям.
Для небольших чисел легко вычислить среднюю точку вручную, но для больших и десятичных значений калькулятор является самым простым и удобным способом вычисления средней точки.
Как найти среднюю точку часто требуется в геометрии, так и расстояние между двумя точками. Расстояние между двумя точками на горизонтальной или вертикальной линии легко вычислить, но процесс усложняется, если точки не выровнены как таковые. Это часто бывает при работе со сторонами треугольника.Поэтому калькулятор расстояний — удобный инструмент для этого.
В некоторых геометрических случаях мы хотим вписать треугольник в другой треугольник, где вершины вписанного треугольника лежат в середине исходного треугольника. Калькулятор средней точки чрезвычайно полезен в таких случаях.
Как найти середину треугольника?
Чтобы найти середину треугольника, технически известную как его центроид , выполните следующие действия:
- Найдите середину сторон треугольника.Если вы знаете, как это сделать, переходите к шагу 5 .
- Измерьте расстояние между двумя конечными точками и разделите результат на 2. Это расстояние от обоих концов является средней точкой этой линии.
- Либо сложите две координаты x конечных точек и разделите на 2. Сделайте то же самое для координат y. В результате вы получите координаты средней точки.
- Проведите линию между средней точкой и ее противоположным углом.
- Повторите это действие по крайней мере для одной другой пары средней точки и угла или для обеих для наивысшей степени точности .
- Место пересечения всех линий — это центр тяжести треугольника.
Что такое середина круга?
Чтобы найти середину или центр круга, следуйте этим инструкциям:
- Найдите две точки на окружности, которые полностью противоположны друг другу , т.
 Е. Разделены диаметром окружности.
Е. Разделены диаметром окружности. - Если вы знаете их координаты, сложите две координаты x и разделите результат на 2.Это координата x центра.
- Проделайте то же самое с координатами 2 y, что даст вам координату y.
- Объедините эти два значения, чтобы получить координаты центроида .
- Если вы не знаете координаты, измерьте расстояние между двумя точками вдвое.
- Эта половина расстояния между одной конечной точкой и другой является средней точкой.
Как найти середину квадрата?
Чтобы найти середину или центроид квадрата, следуйте этому простому руководству:
- Если у вас есть координаты двух противоположных углов квадрата, сложите 2 x координаты и разделите результат на 2.
- Проделайте то же самое с координатами y.
- Используйте эти два вычисленных числа, чтобы найти центр квадрата, так как они являются его координатами x и y соответственно.

- В качестве альтернативы, проведите линию от одного угла до противоположного угла и другую для оставшейся пары.
- Место пересечения этих двух точек — центр тяжести квадрата.
Вы округляете средние точки?
Как правило, не округляет средние точки . определенно не подходит для непрерывных данных , поскольку эта точка является реальной точкой в наборе данных.Для дискретных данных вы обычно не используете , вместо этого отметив, что средняя точка — это значение обоих значений по обе стороны от вычисления средней точки.
Какая средняя точка 0 и 5?
2,5 . Чтобы найти середину любого диапазона, сложите два числа и разделите на 2. В этом случае 0 + 5 = 5, 5/2 = 2,5.
Как найти середину трапеции?
Вы можете найти середину или центроид трапеции одним из двух способов:
- Проведите линию от одного угла трапеции к противоположному углу.

- Проделайте то же самое с оставшейся парой углов.
- На пересечении этих двух линий находится центр тяжести .
- Идеально сбалансируйте трапецию по ее центру!
Альтернативно:
- Возьмем координаты двух противоположных сторон.
- Сложите координаты x этих точек вместе и разделите на 2. Это координата x средней точки .
- Повторите эти действия для координат 2 y, получив координату y средней точки .
Какая средняя точка 30 и 60?
45 . Чтобы найти середину любых двух чисел, найдите среднее значение этих двух чисел, сложив их вместе и разделив на 2. В этом случае 30 + 60 = 90. 90/2 = 45.
Как найти середину между двумя координатами
Какова формула средней точки?
Иногда вам может понадобиться найти середину между двумя точками. Обычно это вступает в игру, когда в вопросе вас просят разделить строку на две равные половины, или в задачах со словами, когда вас просят найти середину.
Если задуматься, идея найти число, лежащее между набором чисел, довольно проста. Что ты обычно делаешь? Вы возьмете среднее из них. Сначала сложите их, затем разделите на два. Формула средней точки аналогична, и вместо того, чтобы брать среднее значение только числа, вам придется взять среднее значение x и y по двум точкам отдельно.
Средняя точка значения x находится на полпути между значениями x двух точек. Средняя точка значения y находится на полпути между значениями y двух точек.В этом есть смысл, правда?
Конечно, это означает, что вам нужно знать координаты двух рассматриваемых точек, прежде чем вы сможете найти их среднюю точку. Но как только вы знаете конечные точки отрезка линии, вы можете легко найти среднюю точку.
Все это хорошо суммируется с формулой средней точки, которая выглядит следующим образом:
M = (x1 + x22, y1 + y22) M = (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2}) M = (2×1 + x2, 2y1 + y2)
Как найти среднюю точку
Чтобы увидеть, как используется формула средней точки, давайте рассмотрим пример.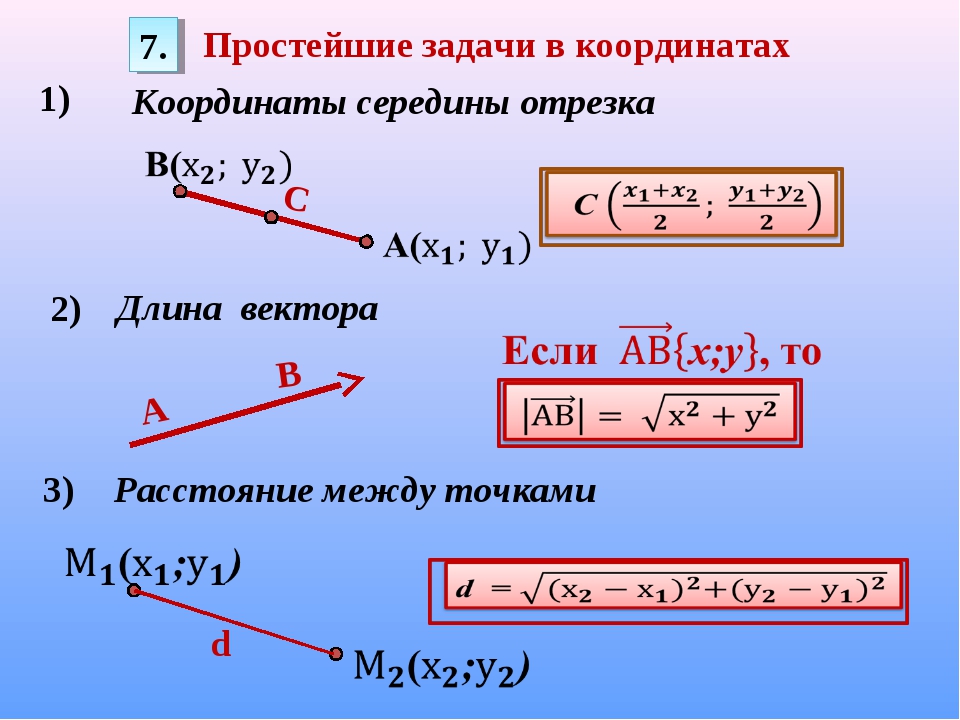
Вопрос:
Определите среднюю точку линейного сегмента с заданными конечными точками.
A (3,7), B (9,1) A (3, 7), B (9, 1) A (3,7), B (9,1)
Решение:
Мы можем использовать формулу для средней точки, чтобы определить среднюю точку: M = (x1 + x22, y1 + y22) M = (\ frac {x_1 + x_2} {2}, \ frac {y_1 + y_2} {2}) M = (2×1 + x2, 2y1 + y2)
Сначала подставьте значения x и y в формулу:
M = (3 + 92,7 + 12) M = (\ frac {3 + 9} {2}, \ frac {7 + 1} {2}) M = (23 + 9, 27 + 1)
Затем мы можем вычислить среднюю точку:
(6,4) (6, 4) (6,4)
шаги вычисления средней точки
Давайте подробнее рассмотрим шаги из приведенного выше примера.Во-первых, нам даются координаты двух точек, для которых мы должны найти середину отрезка. Это все, что вам нужно, чтобы использовать формулу средней точки.
Во-первых, мы сначала извлечем x-координаты, чтобы мы могли работать над поиском x-координаты средней точки. У нас есть 3 и 9, взятые из точек A и B соответственно. Просто сложите два вместе, а затем разделите на 2, чтобы получить среднее значение, также известное как средняя точка для значения x.
У нас есть 3 и 9, взятые из точек A и B соответственно. Просто сложите два вместе, а затем разделите на 2, чтобы получить среднее значение, также известное как средняя точка для значения x.
Затем проделайте то же самое с координатами y.У нас 7 и 1 снова из точек A и B соответственно. Сложив это вместе, мы получим 8, а разделив на два, мы получим 4.
Мы определили, что средняя точка между двумя точками лежит точно в координатах (6,4) с помощью правила средней точки с использованием уравнения средней точки. Если вы нанесли линейный сегмент на график, а затем опустили точку на (6,4), вы действительно увидите, что это точка, которая разделяет сегмент на две равные части.
Другое слово, обозначающее точку, разделяющую линию на два равных отрезка, называется биссектрисой.Некоторые вопросы могут попросить вас найти биссектрису линии, которая в основном запрашивает у вас середину. Вы также можете столкнуться с вопросами, спрашивающими, является ли определенная координата биссектрисой, и вам нужно будет определить с помощью формулы средней точки, получите ли вы указанные средние точки. Если нет, то это не биссектриса.
Если нет, то это не биссектриса.
Проверьте, правильно ли вы ответили, обратившись к этому калькулятору средней точки, если вы застряли.
Формула средней точки | Purplemath
Purplemath
Иногда нужно найти точку, которая находится точно посередине между двумя другими точками.Например, вам может потребоваться найти линию, которая делит пополам (делит на две равные половины) данный отрезок линии. Эта средняя точка называется «серединой». Идея возникает нечасто, но формула довольно проста и очевидна, так что вы легко сможете запомнить ее на будущее.
Подумайте об этом так: если вам даны два числа, вы можете найти точное число между ними, усреднив их, сложив их вместе и разделив на два. Например, число, находящееся точно посередине между 5 и 10, будет:
.
MathHelp.com
Формула средней точки работает точно так же. Если вам нужно найти точку, которая находится точно посередине между двумя заданными точками, просто усредните значения x и значения y .
Сначала я применяю формулу средней точки; тогда я упрощу:
Итак, ответ: P = (1, –2).
Формула средней точки выглядит следующим образом:
Формула средней точки: средняя точка двух точек ( x 1 , y 1 ) и ( x 2 , y 2 ) — точка M , найденная следующая формула:
Но если вы помните, что вы усредняете значения двух точек: x и y , у вас все в порядке.Неважно, какую точку вы выберете в качестве «первой» точки, которую вы подключаете. Просто убедитесь, что вы добавляете x к x и y к y .
Я применяю формулу средней точки и упрощаю:
Итак, ответ: P = (–2.15, 3.5).
Найдите значение
p так, чтобы (–2, 2,5) было средней точкой между ( p , 2) и (–1, 3).
Я использую формулу средней точки:
Координаты y уже совпадают.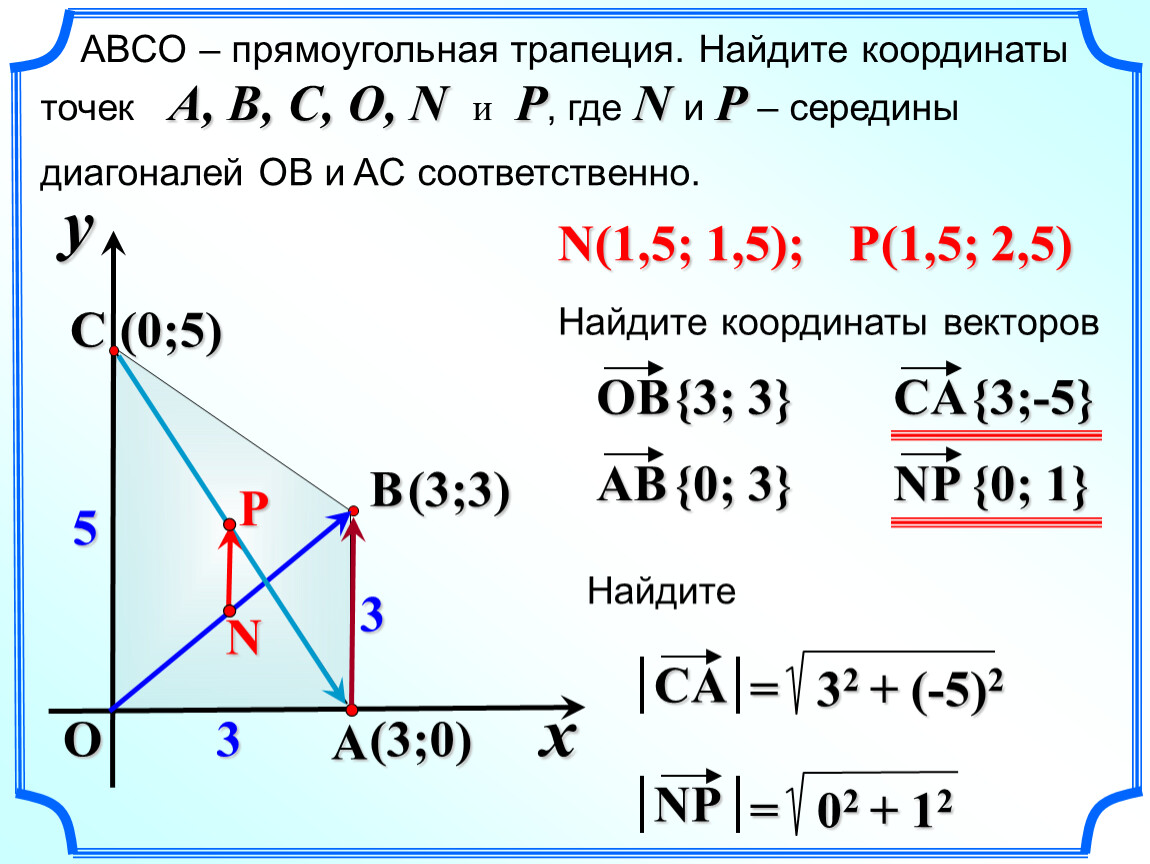 Это сводит проблему к необходимости сравнивать координаты x , «приравнивать» их (то есть устанавливать их равными, потому что они должны быть одинаковыми) и решать полученное уравнение, чтобы выяснить, что такое p . Это даст мне значение, необходимое для совпадения значений x . Итак:
Это сводит проблему к необходимости сравнивать координаты x , «приравнивать» их (то есть устанавливать их равными, потому что они должны быть одинаковыми) и решать полученное уравнение, чтобы выяснить, что такое p . Это даст мне значение, необходимое для совпадения значений x . Итак:
Итак, ответ: p = –3.
Давайте еще несколько примеров ….
URL: https://www.purplemath.com/modules/midpoint.htm
Вычисление средней точки — задача 2
Вы можете найти среднюю точку линейного сегмента, если заданы координаты его конечных точек с помощью формулы средней точки.Конечные точки линейного сегмента задаются (x 1 , y 1 ) и (x 2 , y 2 ). Чтобы найти координату x средней точки, используйте формулу: x = (x 1 + x 2 ) / 2. Чтобы найти координату y, используйте ту же формулу, но на этот раз, используя координаты y конечных точек: y = (y 1 + y 2 ) / 2. Объединяя эти два результата вместе, средняя точка отрезка линии находится в точке (x, y).
Объединяя эти два результата вместе, средняя точка отрезка линии находится в точке (x, y).
Сегмент и координатная плоскость иногда могут быть десятичными.Итак, давайте посмотрим на пример. Здесь у нас есть точки в (5, -2) и (-8,1). Как хороший изучающий геометрию, я сначала нарисую картинку, чтобы иметь представление о том, какой ответ является разумным.
Итак, 5 и -2, я собираюсь перейти от 5 до 2 вниз, так что это будет моя первая точка, мои следующие точки — -8 и +1. Итак, если я соединю эти два, я вижу в средних точках, это может быть где-то во втором или третьем квадранте, но не совсем уверен, где.
Итак, если наша средняя точка находится в (x, y), я говорю, что эта точка здесь, которую я обведу, находится в x и y, вычисляется путем взятия среднего значения ваших X, среднего значения ваших Y, поэтому x1 плюс x2 на 2, и наши x равны 5 и -8.Таким образом, x равно 5 плюс -8 разделить на 2, 5 и -8 равно -3 разделить на 2, и если вы хотите, вы можете преобразовать это в десятичное число, сказав, что это -1,5.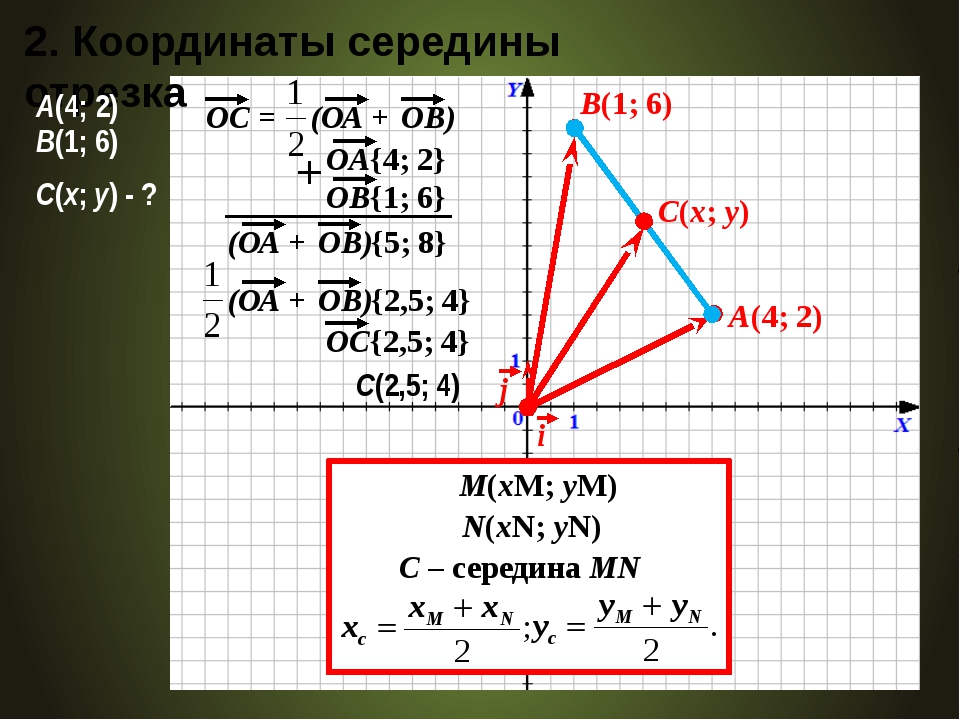
Итак, я сотру этот x и знаю, что наша координата x равна -1,5. Сделайте то же самое, чтобы найти свои Ys. Y равно среднему значению ваших двухлетних координат. У нас есть -2 и +1, поэтому y равно -2 плюс 1, деленное на 2. -2 и 1 равно -1, деленному на 2 и -1/2, мы можем записать как десятичную дробь как -0,5. Итак, сотрите y, и мы знаем, что это -0,5, и рисуем на нем рамку, чтобы сообщить нашему учителю, что это наш ответ.Наша средняя точка находится в диапазоне -1,5 и -0,5, что соответствует нашему третьему квадранту.
Формула средней точки
| Как найти уравнение средней точки // Tutors.com
Содержание
- Определение средней точки
- Формула средней точки
- Как найти среднюю точку
Определение средней точки
Для любых двух упорядоченных пар существует средняя точка , которая находится точно посередине между каждой упорядоченной парой. Это верно для двух измерений (координаты x и y) и трех измерений (координаты x, y и z).
Это верно для двух измерений (координаты x и y) и трех измерений (координаты x, y и z).
В двух измерениях у вас есть только две конечные точки, поэтому средняя точка (или среднее значение) также является медианной, что упрощает вашу математику.
Формула средней точки
Формула средней точки используется для нахождения точной центральной точки между двумя определенными точками на отрезке линии. Используйте эту формулу для вычисления точки, которая делит пополам отрезок линии
.
средняя точка = x1 + x22, y1 + y22
Как найти среднюю точку
В координатной сетке отрезки прямых линий могут быть горизонтальными (плоскими, как горизонт, вдоль оси X), вертикальными (прямо вверх и вниз, вдоль оси Y) или диагональными (под наклоном).Вы можете найти только средние точки сегментов линии, но не линии, поскольку линии не имеют конца.
Вам нужно:
- Обе конечные точки, чтобы найти среднюю точку
- Одна конечная точка и средняя точка для поиска другой конечной точки
Как найти середину отрезков горизонтальной линии
Чтобы вычислить среднюю точку сегмента горизонтальной линии, сфокусируйтесь на значениях x, сложите их и разделите на два:
8 + 22
102 = 5
Среднее значение и медиана и, следовательно, середина или середина линии, имеют значение x, равное 5.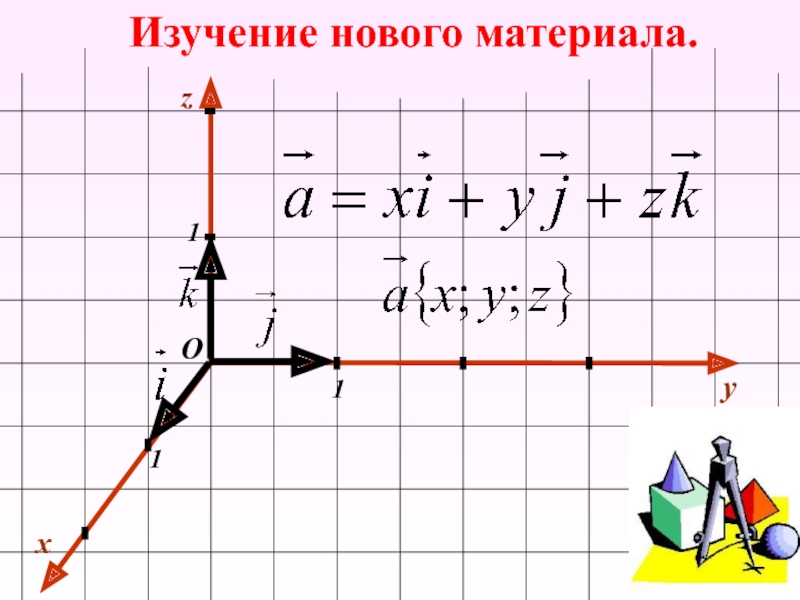 Середина — (5, 4).
Середина — (5, 4).
Как найти середину вертикальных отрезков линии
Чтобы рассчитать длину вертикального отрезка, сконцентрируйтесь на значениях y:
10 + 32
132 = 6,5
Средняя точка находится в (2, 6.5).
Как найти середину сегментов диагональной линии
Сегменты диагональной линии намного сложнее, чем найти середину вертикальных или горизонтальных сегментов линии. Вот идеальное место для формулы средней точки, которая, по сути, находит среднее из значений x и значений y:
средняя точка = x1 + x22, y1 + y22
Вы видите, как вы складываете два значения x, а затем делите их на 2? Это находит среднее значение, которое является средней точкой для значения x.Повторите эти действия для значений y, и вместе у вас будет упорядоченная пара средней точки.
Примеры формул средней точки
Формула средней точки работает с линейными сегментами во всех квадрантах. Предположим, у вас есть это:
Подключите конечные точки, обращая внимание на отрицательные числа:
-2 + -82
-102 = -5
Затем подключите, чтобы найти y
-1 + -42
-52 = -2,5
Средняя точка находится в (-5, -2. 5)
5)
Как найти середину между двумя точками
Не расстраивайтесь, когда ваш отрезок линии пересекает один квадрант в другой. Формула средней точки все еще работает. Вы должны быть осторожны со своими значениями x и y, но просто вставьте числа, разделите, и вы получите среднюю точку.
Подключите две конечные точки:
-2 + 22
02 = 0
Теперь займемся второй конечной точкой:
4 + -42
02 = 0
Средняя точка — это (0, 0) , начало координатной сетки!
Найдите координаты средней точки
Иногда вы получаете очень мало информации, например о конечной точке и средней точке.Вас попросят найти другую конечную точку. Ты можешь сделать это!
Помните, что средняя точка — это среднее значение только двух наборов чисел. Используйте это, чтобы помочь вам найти недостающее значение x и значения y, вторую конечную точку (x2, y2).
Вам даны (-7, -3) как одна конечная точка (x1, y1) и (0, -1) как средняя точка.
Вам нужно найти эти значения:
Для x:
(-7 + x2) 2 = 0
Умножить обе стороны на 2
((-7 + x2) 2) × 2 = 0 × 2
Упростить
-7 + x2 = 0
х2 — 7 = 0
Добавить 7 к обеим сторонам
x2 = 7
для у:
(-3 + y2) 2 = -1
Умножить обе стороны на 2
((-3 + y2) 2) × 2 = -1 × 2
Упростить
-3 + y2 = -2
y2 — 3 = -2
Добавить 3 к обеим сторонам
y2 = 1
Это дает конечную точку (x2, y2) (7, 1) .
Краткое содержание урока
Теперь, когда вы дошли до этого места, вы можете определить формулу средней точки и определить ее подходящее использование, объяснить себе и другим, как найти среднюю точку вертикального или горизонтального отрезка линии на координатной сетке. Вы также можете использовать формулу средней точки для вычисления конечной точки диагональной линии с учетом средней точки и одной конечной точки и использовать ту же формулу для вычисления средней точки диагональной линии с учетом двух конечных точек.
Вы также можете использовать формулу средней точки для вычисления конечной точки диагональной линии с учетом средней точки и одной конечной точки и использовать ту же формулу для вычисления средней точки диагональной линии с учетом двух конечных точек.
Следующий урок:
Теорема о средней точке
Калькулятор средней точки — поиск средней точки
Формула средней точки
Уравнение средней точки может быть выражено как:
(x1 + x2) / 2, (y1 + y2) / 2
Где x и y представляют точки в декартовой координатной плоскости .
Калькулятор средней точки — отличная утилита для поиска средней точки сегмента с заданными конечными точками. Мы обсудим, как найти середину отрезка линии, формулу средней точки и многое другое в этом пространстве.
Что такое средняя точка?
Средняя точка — это точка на отрезке прямой, которая делит его на две равные части. Она также известна как середина отрезка линии.
Проще говоря, точка в центре или около центра или рядом с ними называется средней точкой.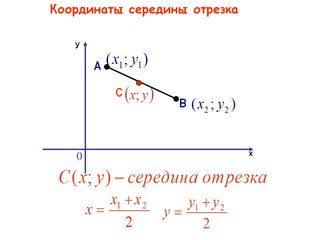 Он также определяется как точка, линия или плоскость, которая делит линию пополам.
Он также определяется как точка, линия или плоскость, которая делит линию пополам.
Как найти середину прямой?
Выполните следующие действия, чтобы найти среднюю точку без калькулятора .
Пример:
Найдите координаты средней точки линии, соединяющей (1, -3), (-5, 7).
Шаг 1: Определите и запишите значения.
x1 = 1, y1 = -3
x2 = -5, y2 = 7
Шаг 2: Примените формулу средней точки.
(x1 + x2) / 2, (y1 + y2) / 2
= ((1 + (-5)) / 2), (-3 +7) / 2
= (-4/2 , 4/2)
= -2, 2
Помимо ручного метода поиска средней точки, искатель средней точки может упростить весь процесс, если вы торопитесь.
Часто задаваемые вопросы
Как найти среднюю точку между двумя местоположениями?
Середину между двумя местоположениями можно найти с помощью следующего уравнения:
M = (x 1 + x 2 ) / 2, (y 1 + y 2 ) / 2
Поместите координаты обоих местоположений в уравнение, чтобы получить среднюю точку.
Как найти конечную точку по средней?
Конечная точка может быть рассчитана с помощью следующего уравнения:
(x 2 , y 2 ) = (2m 1 — x 1 , 2m 2 — y 1 )
Где, x 2 , y 2 — неизвестные конечные точки, м 1 , m 2 — средние точки, а x 1 , x 2 — заданные конечные точки.Более того, вы также можете найти конечную точку с помощью калькулятора конечных точек.
Как найти среднюю точку в статистике?
Средняя точка в статистике может быть рассчитана по следующей формуле:
Средняя точка = (нижний предел класса + верхний предел класса) / 2
Ссылки:
- Stapel, E. (2021). Формула средней точки | Purplemath.

- Формула средней точки | Аналитическая геометрия (статья) | Ханская академия.
Координаты точки, компоненты вектора и середина отрезка
Координаты точки на плоскости
Давайте посмотрим, как векторы используются для присвоения координат точкам на плоскости.
Мы рассматриваем фиксированную точку на плоскости $$ O $$ (известную как начало координат) и базис $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$ из $$ V_2 $$. (Космический вектор размерности $$ 2 $$).
Напомним, что в основе $$ V_2 $$ лежат два линейно независимых вектора. Набор, образованный $$ O $$ и $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$, составляет систему отсчета на плоскости, поскольку позволяет нам определять положение любой другой точки на плоскости.
Это потому, что любые другие точки $$ P $$ на плоскости определяют вместе с точкой $$ O $$ вектор $$ \ overrightarrow {OP} $$.Пусть $$ (p_1, p_2) $$ — компоненты вектора в базисе $$ B $$. Тогда $$ (p_1, p_2) $$ — координаты точки $$ P $$ в системе отсчета $$ R = \ {O; \ overrightarrow {u}, \ overrightarrow {v} \} $$ и запишем $$ P = (p_1, p_2) $$.
Тогда $$ (p_1, p_2) $$ — координаты точки $$ P $$ в системе отсчета $$ R = \ {O; \ overrightarrow {u}, \ overrightarrow {v} \} $$ и запишем $$ P = (p_1, p_2) $$.
Процедура определения координат точки $$ P $$ в заданной системе отсчета следующая:
Из точек $$ O $$ и $$ P $$ определяем вектор $$ \ overrightarrow {OP} $$
Мы выражаем вектор $$ \ overrightarrow {OP} $$ как линейную комбинацию векторов базиса $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$, то есть , $$ \ overrightarrow {OP} = p_1 \ cdot \ overrightarrow {u} + p_2 \ cdot \ overrightarrow {v} $$
- $$ P = (p_1, p_2) $$
Экспресс-точка $$ P $$ чертежа в системе отсчета $$ R = \ {O; \ overrightarrow {u}, \ overrightarrow {v} \} $$.
- Рисуем вектор $$ \ overrightarrow {OP} $$:
- Выразим вектор $$ \ overrightarrow {OP} $$ как линейную комбинацию векторов базиса $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$:
- Получаем $$ \ overrightarrow {OP} = \ overrightarrow {u} +2 \ overrightarrow {v} $$ и поэтому координаты точки $$ P $$ равны $$ P = (1, 2) $$
С этого момента мы будем рассматривать в качестве системы отсчета $$ R $$ систему, образованную началом координат $$ O = (0, 0) $$ и каноническим базисом $$ V_2 $$ $$ B = \ {\ overrightarrow {i}, \ overrightarrow {j} \} $$.
Составляющие вектора, определяемые двумя точками
Давайте теперь посмотрим, как определить компоненты вектора, если мы знаем координаты его конечных точек:
Пусть $$ P = (p_1, p_2) $$ и $$ Q = (q_1, q_2) $$ — две точки плоскости, а $$ \ overrightarrow {PQ} $$ вектор, идущий от $$ P От $$ до $$ Q $$. Тогда компоненты вектора $$ \ overrightarrow {PQ} $$ равны $$ \ overrightarrow {PQ} = (q_1-p_1, q_2-p_2) $$.
Дано $$ P = (2, 6) $$ и $$ Q = (-3, 9) $$. Компоненты вектора $$ \ overrightarrow {PQ} $$: $$ \ overrightarrow {PQ} = (-3 — 2, 9 — 6) = (-5, 3) $$
Применение вектора к точке
Для данной точки $$ P $$ и вектора $$ \ overrightarrow {v} $$ результатом применения вектора к точке будет новая точка $$ Q $$, помещенная в направлении $$ \ overrightarrow { v} $$ и на расстоянии $$ | \ overrightarrow {v} | $$.(модуль вектора $$ \ overrightarrow {v} $$)
Координаты этой новой точки $$ Q $$ вычисляются из координат $$ P = (p_1, p_2) $$ и $$ \ overrightarrow {v} = (v_1, v_2) $$, таким образом, $$$ Q = P + \ overrightarrow {v} = (p_1 + v_1, p_2 + v_2) $$$
ПРИМЕЧАНИЕ. Очень важно помнить, что эта операция сложения имеет смысл только между точкой и вектором. Мы никогда не должны складывать две точки, и результатом сложения двух векторов будет другой вектор, а не точка!
Очень важно помнить, что эта операция сложения имеет смысл только между точкой и вектором. Мы никогда не должны складывать две точки, и результатом сложения двух векторов будет другой вектор, а не точка!
Рассматривая следующий рисунок, определите координаты точки $$ P $$ фигуры, результат применения вектора $$ \ overrightarrow {v} $$ к точке $$ A $$.
Начнем с вычисления компонентов вектора $$ \ overrightarrow {v} $$: $$$ \ overrightarrow {v} = (2 — (-1), 4-2) = (3, 2) $$$
Поскольку $$ P $$ является результатом применения вектора $$ \ overrightarrow {v} $$ к имеющейся у нас точке $$ A $$, $$$ P = A + \ overrightarrow {v} = (0,4) + (3,2) = (3,6) $$$
Середина сегмента
Рассмотрим теперь сегмент с конечными точками $$ A = (a_1, a_2) $$ и $$ B = (b_1, b_2) $$. Пусть $$ M = (m_1, m_2) $$ — середина указанного выше отрезка.Очевидно, что вышеупомянутый пункт удовлетворяет тому, что $$ \ overrightarrow {AB} = 2 \ cdot \ overrightarrow {AM} $$, или что $$ (b_1-a_1, b_2-a_2) = 2 \ cdot (m_1-a_1, m_2- а_2) $$
Разделив компонент на компонент, получим:
$$$ \ begin {array} {rcl} b_1-a_1 & = & 2 \ cdot (m_1-a_1) \\ b_2-a_2 & = & 2 \ cdot (m_2-a_2) \ end {array} $$$
и изолируя мы имеем:
$$$ \ begin {array} {rcl} m_1 & = & \ displaystyle \ frac {a_1 + b_1} {2} \\ m_2 & = & \ displaystyle \ frac {a_2 + b_2} {2} \ end {array} $$$
Чтобы мы могли вычислить координаты средней точки сегмента по координатам его конечных точек.
Рассматривая точки $$ A = (-3, 7) $$ и $$ B = (1, 2) $$, найдите среднюю точку отрезка, который они определяют.
Применяя предыдущие формулы, получаем:
$$$ \ begin {array} {rcl} m_1 & = & \ displaystyle \ frac {a_1 + b_1} {2} = \ frac {-3 + 2} {2} = — 1 \\ m_2 & = & \ displaystyle \ frac {a_2 + b_2} {2} = \ frac {7 + 2} {2} = \ frac {9} {2} \ end {array} $$$
Следовательно, середина сегмента $$ AB $$ равна $$ M = (-1, \ displaystyle \ frac {9} {2}) $$
.
Формула нахождения координат середины отрезка. Как найти координаты середины отрезка
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Определение 1
Отрезок — часть прямой, ограниченная двумя точками (концами).
Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.
Определение 2
Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.
Если это точка $C$, то $AC=CB$.
Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
Определение 3
Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.
Таким образом, оси определяют плоскость $XOY$.
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Определение 4
Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Пример 1
Имеем рисунок:
На рисунке отрезки $AC, CD, DE, EB$ равны.
- Серединой каких отрезков является точка $D$?
- Какая точка является серединой отрезка $DB$?
- точка $D$ является серединой отрезков $AB$ и $CE$;
- точка $E$.
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Пример 2
Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?
Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.
Ответ: 18 см.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении , и, как частный случай, о делении отрезка пополам .
Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.
Нередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек и, очевидное невероятное – отрезок :
Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.
Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок делится на две части с помощью некоторой точки , которая, понятно, расположена прямо на нём:
В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .
На сухом математическом языке этот факт записывают следующим образом: , или чаще в виде привычной пропорции: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .
Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .
Пропорцию несложно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.
Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:
Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .
После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.
Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.
урок Линейная (не) зависимость векторов. Базис векторов ). Такая вот универсальная задача.
Пример 1
Найти координаты точки , делящей отрезок в отношении , если известны точки
Решение : В данной задаче . По формулам деления отрезка в данном отношении, найдём точку :
Ответ :
Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.
В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:
Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.
Равноценен второй способ решения : в нём отсчёт начинается с точки и справедливым является отношение: (человеческими словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:
По формулам деления отрезка в данном отношении:
Ответ :
Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё.
Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок , то предполагается, что вы составите пропорцию , если дан отрезок , то «негласно» подразумевается пропорция .
А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.
Пример 2
Даны точки . Найти:
а) точку , делящую отрезок в отношении ;
б) точку , делящую отрезок в отношении .
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Полное решение и ответ в конце урока.
Иногда встречаются задачи, где неизвестен один из концов отрезка:
Пример 3
Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если .
Решение : Из условия следует, что точка делит отрезок в отношении , считая от вершины , то есть, справедлива пропорция: . По формулам деления отрезка в данном отношении:
Сейчас нам неизвестны координаты точки : , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:
Ответ :
Для проверки можно взять концы отрезка и, пользуясь формулами в прямом порядке, убедиться, что при соотношении действительно получится точка . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:
Пример 4
Точка . Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .
Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .
Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.
Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.
Если известны две точки пространства , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
.
Пример 5
Даны точки . Найти координаты точки , принадлежащей отрезку , если известно, что .
Решение : Из условия следует отношение: . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: .
По формулам координат середины отрезка:
Ответ :
Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.
Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.
Разминочная задача для самостоятельного решения:
Пример 6
Даны точки . Найти координаты точки , если известно, что она делит отрезок в отношении .
Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.
В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.
Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:
Формулы координат середины отрезкаДаже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:
В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы чудесным образом преображаются в нечто знакомое и простое:
Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:
В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.
Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины выражаются формулами:
Пример 7
Параллелограмм задан координатами своих вершин . Найти точку пересечения его диагоналей.
Решение : Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.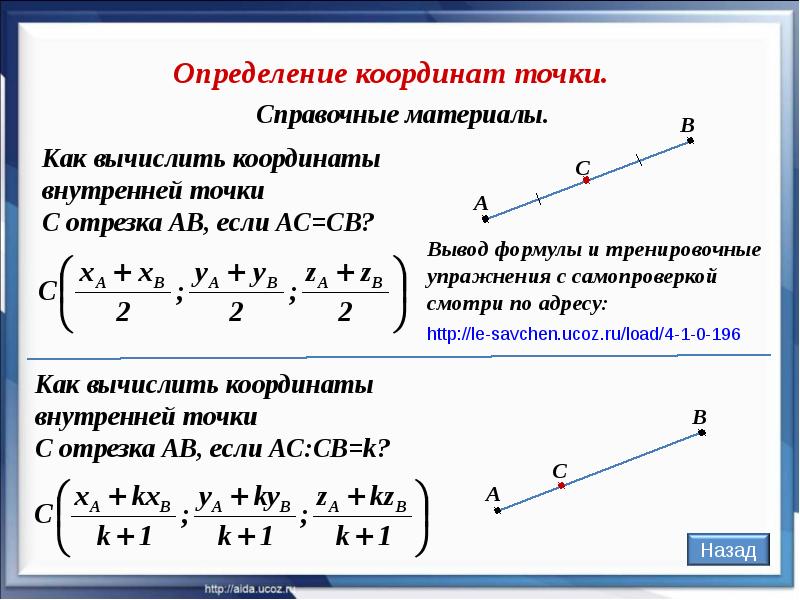
По известному свойству, диагонали параллелограмма своей точкой пересечения делятся пополам, поэтому задачу можно решить двумя способами.
Способ первый : Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y .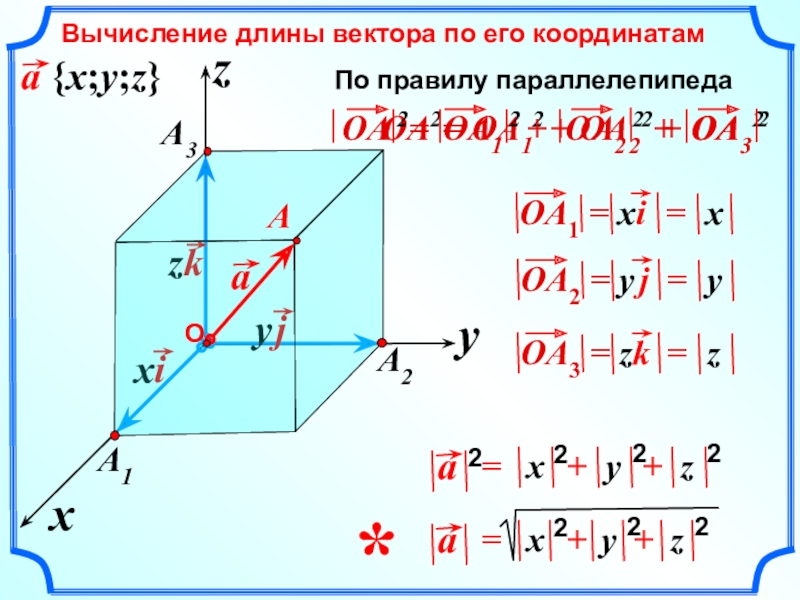 И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т. е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как найти координаты середины отрезка
Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.
Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:
Пример.
Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).
Решение.
Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:
Используем соответствующие формулы:
Следовательно, середина МО будет иметь координаты К (3,5; 5,5).
Ответ. К (3,5; 5,5).
Поделитесь статьей с друзьями:
Похожие статьи
MathScene — Векторы — Урок 3
MathScene — Векторы — Урок 32008 Расмус Эф и Джанн Сак |
Урок 3
Векторы в системе координат
Пример 1
То точка А имеет координаты (2, 2), а точка В — координаты (6, 5) (см. схему).Координаты вектора
Мы
можно использовать формулу расстояния между двумя точками, чтобы найти расстояние
между A и B, то есть длина вектора
(см. Правило Пифагора в уроке 2). Формула выглядит следующим образом:
Правило Пифагора в уроке 2). Формула выглядит следующим образом:
Подставляя заданные координаты в формулу получаем:
Мы видим, что числа под квадратным корнем — это просто координаты вектор.Это, конечно, потому, что длина вектора — это просто гипотенуза в прямоугольном треугольнике с более короткими сторонами 3 и 4.
Формула длины вектора, начинающегося в точке
A = (x 1 , y 1 ) и заканчивается на B = (x 2 ,
у 2 ) равно:
Если координаты вектора то имеем следующее правило:
Пример 2
Найдите вектор что параллельно и который имеет длину 2 единицы
(видеть
диаграмму).
Два треугольника на диаграмме подобны, поэтому соответствующие
стороны находятся в одинаковом соотношении.
||
= т∙||. Число t есть отношение между соответствующими сторонами. Отношение такое.
Мы можем найти координаты как
следует:
Если векторы и являются параллельно, то существует число t такое, что:
= т∙ |
Пример 3
Какие из следующих векторов параллельны и .
Если векторы и являются параллельно, то существует число t такое, что = т∙. Если векторы и являются параллельно существует число r такое, что знак равно р∙.
Мы можно найти числа t и r, используя координаты x, а затем проверить, чтобы увидеть найдены ли те же значения, когда мы используем координаты y.
= т∙
3 = t∙13 дает t = 3/13 = 2/9
4 = t∙18 также дает t = 4/18 = 2/9
То
векторы и есть
параллель .
= р∙
3 = r∙6 дает r =
4 = r∙9 дает r = 4/9
То векторы и есть не параллельно (Это означает, что и являются тоже не параллельно).
Вектор на диаграмме имеет координаты . То вектор начинается в точке (0, 0) и заканчивается в (3, 2), поэтому координаты конечная точка совпадает с координатами самого вектора.Это относится к все векторы, которые начинаются в начале системы координат, то есть в точка (0, 0).
Вектор, который начинается в точке (0, 0), имеет те же координаты, что и его конечная точка. Этот вектор называется вектором положения для A. |
Каждая точка в системе координат может быть представлена своим вектором положения. Координаты точки и вектор ее положения совпадают.Это может быть очень полезно при просмотре переводов в системе координат.
Пример 4
Треугольник, показанный на диаграмме, должен быть переведен вектором
.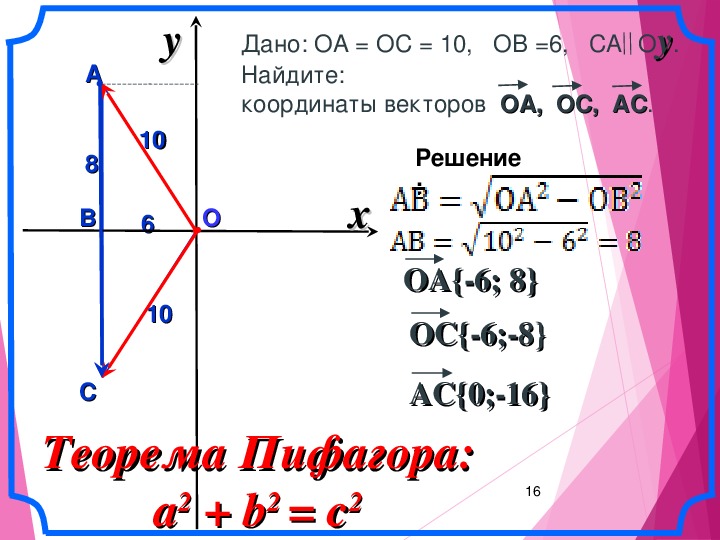
Мы используем векторы положения вершинных точек (−3, 0),
(2, −2) и (3, 1) и добавляем вектор
каждому из них.
Это дает нам новый вектор положения каждой вершины.Диаграмма ниже показывает перевод.
Пример 5
Теперь мы будем использовать векторы положения, чтобы найти середину отрезка AB, если А = (1, 2) и В = (4, 3).
Как обычно, точка O является началом системы координат. Если M середина AB тогда:
знак равно + ∙
Вектор является вектор положения точки M и, следовательно, имеет те же координаты, что и точку М, которую мы хотим вычислить.Вектор – это вектор положения A. Чтобы достичь середины M, нам нужно добавить половину вектор . Нарисуйте схему, чтобы увидеть это.
Сначала нам нужно найти вектор .
Теперь мы можем найти .
знак равно + ∙
Координаты M такие же, как у вектора положения или (2, 2) .
Легко найти формулу, по которой можно найти координаты точки. середина отрезка АВ.
2 = + ∙ + — ∙
Мы видим, что вектор положения середины отрезка представляет собой своего рода
среднее значение векторов положения конечных точек. Поэтому мы можем найти
координаты средней точки, найдя среднее значение координат x и y
координаты соответственно.
Это приводит нас к правилу, которое мы называем правилом средней точки.
Середина M отрезка AB задается правилом: При использовании координат правило: |
Пример 6
Вершинами треугольника ABC являются A = (1, 2), B = (4, 3) и C = (3, 0).
Найдите длину прямой, проведенной от А до середины стороны ВС (медиану стороны ВС).
треугольник АВС).
Мы начнем с нахождения середины BC, используя приведенное выше правило.
Назовем середину M и найдем ее вектор положения (видеть схему).
Следовательно, M, середина ВС, имеет координаты
М = (3, 1).
Далее находим координаты вектора .
Наконец, мы можем найти длину вектора как обязательный.
≈ 2,55
= + ∙
= + ∙ — ∙
= — ∙ — ∙
Когда мы сложим их вместе, выходит и мы получаем:
3= + +
Чтобы найти координаты T, мы берем среднее значение x и y координаты вершин соответственно. |
Таким образом, мы находим точку пересечения T медиан треугольника путем нахождения своего рода среднего векторов положения вершины. Таким образом, это правило является расширением правила средней точки.
Пример 7
Найдите точку пересечения Т медиан треугольника АВС (
центр ) при условии, что A = (1, 2), B = (4, 3) и C = (3, 0) (см. |
Центр Т = (2, 1) .
Попробуйте Викторина
3
на Векторы.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Формула средней точки
В одном измерении
На числовая линия , число на полпути между Икс 1 и Икс 2 является
Икс 1 + Икс 2 2
Пример 1:
Найдите середину между − 1 и 4 .
Используйте формулу. Середина
−
1
+
4
2
знак равно
3
2
знак равно
1,5
.
Пример 2:
Если 0,5 это середина п р ¯ и координата п является − 4 , найти координату р .
Используйте формулу.
− 4 + Икс 2 2 знак равно 0,5
Для начала умножьте обе части на 2 .
− 4 + Икс 2 знак равно 1
Затем добавьте 4 в обе стороны.
Икс 2 знак равно 5
Итак, координата р является 5 .
В двух измерениях
Предположим, вы получаете две точки в плоскости ( Икс 1 , у 1 ) и ( Икс 2 , у 2 ), И попросил, чтобы найти точку на полпути между ними. Координаты этой медианы будут:
( Икс 1 + Икс 2 2 , у 1 + у 2 2 )
Простой способ думать об этом является то, что Икс координата середины среднее из Икс -координаты из двух точек, а также с у -координаты.
Пример 1:
Найдите середину между ( − 2 , 5 ) и ( 7 , 7 ) .
Используйте формулу. Координаты середины:
( − 2 + 7 2 , 5 + 7 2 )
Упрощать.
( 2,5 , 6 )
Пример 2:
Если Вопрос ( 2 , − 2 ) это середина п р ¯ и п имеет координаты ( − 6 , − 6 ) , найти координаты р .
С помощью формулы напишите и решите два уравнения для координат точки. р .
Вопрос ( 2 , − 2 ) знак равно ( − 6 + Икс 2 2 , − 6 + у 2 2 )
Сначала найдите Икс -координата.
2 знак равно − 6 + Икс 2 2 4 знак равно − 6 + Икс 2 10 знак равно Икс 2
Затем найдите у -координата.
− 2 знак равно − 6 + у 2 2 − 4 знак равно − 6 + у 2 2 знак равно у 2
Итак, координаты г. р являются ( 10 , 2 ) .
В трех измерениях
Это довольно легко догадаться, основываясь на формуле для двух измерений!
В 3 -мерное пространство, середина между ( Икс 1 , у 1 , г 1 ) и ( Икс 2 , у 2 , г 1 ) является
( Икс 1 + Икс 2 2 , у 1 + у 2 2 , г 1 + г 2 2 )
Формулы средней точки и расстояния в 3D — Концепция
Есть две формулы, которые важно помнить при рассмотрении векторов или положений в трехмерной системе координат.Формула средней точки и формула расстояния в 3D. Формула средней точки и расстояния в 3D может быть получена с помощью метода сложения геометрического представления векторов. Чтобы понять вывод формулы расстояния в 3D, мы должны понимать трехмерные векторные операции.
Я хочу вывести формулу средней точки для трех измерений. Формула средней точки поможет мне найти среднюю точку между точками a с координатами x1, y1 и z1 и b с координатами x2, y2 и z2.Итак, у меня есть отрезок ab, нарисованный здесь, и я обозначил свою середину m, и я надеюсь найти формулу для ее координат. Я также добавил вектор положения oa для точки a и вектор положения om для точки m. Теперь давайте найдем компоненты для вектора положения oa, и давайте вспомним, что компоненты вектора положения — это в точности координаты конечной точки этого вектора, поэтому будут x1, y1, z1, и мне также понадобится вектор ab, чтобы найти m, и каковы компоненты ab? Ну, так как вектор абы идут из точки А в точку Б и компонента x2-x1, y2-y1 и z2-z1 хорошо, как мы собираемся, чтобы получить вектор положения ом от оа и аб?
Итак, давайте сделаем наблюдение, что вектор, который начинается в точке а и заканчивается в точке m, является половиной вектора, идущего из точки а в точку, так что это вектор ab этот вектор, начинающийся здесь и заканчивающийся здесь, является половиной ab скаляра кратное ohe половине ab, поэтому мне нужно добавить это к oa, чтобы получить om.Итак, вектор om=oa плюс половина a b, так что он будет состоять из компонентов x1, y1, z1 плюс половина этого, половина x2-x1, y2-y1 и z2-z1. Итак, давайте посмотрим, сможем ли мы объединить это в один шаг для первого компонента. Я собираюсь получить x1 плюс половина x2 минус половина x1, поэтому половина x1 плюс половина x2 теперь я получу y1 плюс половина y2 минус половина y1 это половина y1 плюс половина y2, и аналогичным образом я получаю половину z1 плюс одну половину z2.
Каждая из них является средним значением компонентов x и y этих двух точек, поэтому я могу записать это как x1+x2 по 2, y1+y2 по 2 и z1+z2 по 2, это компоненты вектора om, которые идет из начала координат в точку m и, следовательно, координаты точки m таковы.Таким образом, середина m отрезка, соединяющего x1, y1, z1 и x2, y2, z2, равна x1+x2 над 2, y1+y2 над 2 и z1+z2 над 2, и это формула средней точки.
Координаты точки, компоненты вектора и середины отрезка
Координаты точки на плоскости
Давайте посмотрим, как векторы используются для присвоения координат точкам на плоскости.
Рассмотрим фиксированную точку на плоскости $$O$$ (известную как начало координат) и базис $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$ $$V_2$$ (пространственный вектор размерности $$2$$).
Вспомним, что в основе $$V_2$$ лежат два линейно независимых вектора. Множество, образованное $$O$$ и $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, образует систему отсчета на плоскости, поскольку позволяет определить положение любых других точки на плоскости.
Это связано с тем, что любые другие точки $$P$$ на плоскости вместе с точкой $$O$$ определяют вектор $$\overrightarrow{OP}$$. Пусть $$(p_1,p_2)$$ — компоненты вектора в базисе $$B$$. Тогда $$(p_1,p_2)$$ — это координаты точки $$P$$ в системе отсчета $$R=\{O;\overrightarrow{u}, \overrightarrow{v}\}$$, и мы пишем $$P=(p_1,p_2)$$.
Процедура нахождения координат точки $$P$$ в заданной системе отсчета следующая:
Из точек $$O$$ и $$P$$ определяем вектор $$\overrightarrow{OP}$$
Выразим вектор $$\overrightarrow{OP}$$ в виде линейной комбинации векторов базиса $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$, т. е. , $$\overrightarrow{OP}=p_1 \cdot \overrightarrow{u}+p_2 \cdot \overrightarrow{v}$$
- $$P=(p_1,p_2)$$
Выразите точку $$P$$ чертежа в системе отсчета $$R =\{O;\overrightarrow {u}, \overrightarrow{v}\}$$.
- Рисуем вектор $$\overrightarrow{OP}$$:
- Выразим вектор $$\overrightarrow{OP}$$ в виде линейной комбинации векторов базиса $$B=\{\overrightarrow{u}, \overrightarrow{v}\}$$:
- Получаем $$\overrightarrow{OP}=\overrightarrow{u}+2\overrightarrow{v}$$ и, следовательно, координаты точки $$P$$ равны $$P = (1 , 2)$$
В дальнейшем в качестве системы отсчета $$R$$ будем рассматривать систему, образованную началом координат $$O = (0, 0)$$ и каноническим базисом $$V_2$$ $$B = \{\overrightarrow{i},\overrightarrow{j}\}$$.
Компоненты вектора, определяемого двумя точками
Давайте теперь посмотрим, как определить компоненты вектора, если мы знаем координаты его концов:
Пусть $$P =(p_1,p_2)$$ и $$Q = (q_1,q_2)$$ — две точки плоскости, а $$\overrightarrow{PQ}$$ — вектор, исходящий из $$P от $$ до $$Q$$. Тогда компоненты вектора $$\overrightarrow{PQ}$$ равны $$\overrightarrow{PQ}=(q_1-p_1,q_2-p_2)$$.
Учитывая $$P = (2, 6)$$ и $$Q = (-3, 9)$$. Компоненты вектора $$\overrightarrow{PQ}$$ таковы: $$\overrightarrow{PQ}= (-3 — 2, 9 — 6) = (-5, 3)$$
Применение вектора к точке
Для заданной точки $$P$$ и вектора $$\overrightarrow{v}$$ результатом применения вектора к точке является новая точка $$Q$$, расположенная в направлении $$\overrightarrow{ v}$$ и на расстоянии $$|\overrightarrow{v}|$$.(модуль вектора $$\overrightarrow{v}$$)
Координаты этой новой точки $$Q$$ вычисляются из координат $$P =(p_1,p_2)$$ и $$\overrightarrow{v}=(v_1,v_2)$$, таким образом, $$$Q = P +\overrightarrow{v}=(p_1+v_1,p_2+v_2)$$$
ПРИМЕЧАНИЕ. Очень важно помнить, что эта операция сложения имеет смысл только между точкой и вектором. Мы никогда не должны складывать две точки, а результатом сложения двух векторов будет другой вектор, а не точка!
Рассмотрев следующий рисунок, определите координаты точки $$P$$ на рисунке, результат применения вектора $$\overrightarrow{v}$$ к точке $$A$$.
Начнем с вычисления компонент вектора $$\overrightarrow{v}$$:$$$\overrightarrow{v} = (2 — (-1), 4-2) = (3, 2)$$$ Поскольку $$P$$ является результатом применения вектора $$\overrightarrow{v}$$ к точке $$A$$, имеем $$$P=A+\overrightarrow{v}=(0,4) +(3,2)=(3,6)$$$
Середина сегмента
Теперь рассмотрим отрезок с концами $$A = (a_1,a_2)$$ и $$B = (b_1,b_2)$$. Пусть $$M =(m_1,m_2)$$ — середина указанного выше отрезка.Очевидно, что указанная выше точка удовлетворяет тому, что $$\overrightarrow{AB}=2\cdot \overrightarrow{AM}$$, или что $$(b_1-a_1,b_2-a_2)=2\cdot (m_1-a_1,m_2- а_2)$$
Разделяя компонент на компонент получаем: $$$\begin{массив}{rcl} b_1-a_1 & = & 2 \cdot (m_1-a_1) \\ b_2-a_2 &=& 2\cdot (m_2-a_2) \end{массив}$$$ и изолируя имеем: $$$\begin{array}{rcl} m_1 & = & \displaystyle \frac{a_1+b_1}{2}\\ m_2 &=& \displaystyle \frac{a_2+b_2}{2} \end{array} $$$ Так что мы можем вычислить координаты середины отрезка по координатам его концов.
По точкам $$A = (-3, 7)$$ и $$B = (1, 2)$$ найдите середину отрезка, который они определяют.
Применяя предыдущие формулы, имеем: $$$\begin{array}{rcl} m_1 & = & \displaystyle \frac{a_1+b_1}{2}= \frac{-3+2}{2}=-1\\ m_2 &=& \displaystyle \frac{a_2+b_2}{2}=\frac{7+2}{2}=\frac{9}{2} \end{array}$$$ Следовательно, середина отрезка $$AB$$ равна $$M = (-1, \displaystyle \frac{9}{2})$$
Формула средней точки | Пурпурная математика
Пурпурная математика
Иногда вам нужно найти точку, которая находится ровно посередине между двумя другими точками.Например, вам может понадобиться найти линию, которая делит пополам (делит на две равные половины) заданный отрезок. Эта средняя точка называется «средней точкой». Эта концепция не часто всплывает, но формула довольно проста и очевидна, так что вы легко сможете запомнить ее на потом.
Подумайте об этом так: если вам даны два числа, вы можете найти число точно между ними, усредняя их, складывая их вместе и разделив на два. Например, число ровно посередине между 5 и 10:
.Справка по математике.ком
Формула средней точки работает точно так же. Если вам нужно найти точку, которая находится точно посередине между двумя заданными точками, просто усредните значения x и значения y .
Найдите середину
P между (–1, 2) и (3, –6).
Сначала я применяю формулу средней точки; тогда я упрощу:
Итак, ответ P = (1, –2).
Технически формула средней точки выглядит следующим образом:
Средняя формула средней точки: средняя точка двух очков, ( x 1 , y 1 ) и ( x 2 , y 2 ) — это точка м следующая формула:
Но пока вы помните, что вы усредняете значения двух точек x и y , все будет в порядке.Неважно, какую точку вы выберете в качестве «первой» для подключения. Просто убедитесь, что вы добавляете 90 501 x 90 502 к 90 501 x 90 502 и 90 501 и 90 502 к 90 501 и 90 502.
Найдите середину
P между (6.4, 3) и (–10.7, 4).
Я применю формулу средней точки и упрощу:
Итак, ответ P = (–2.15, 3.5).
Найдите значение
p так, чтобы (–2, 2,5) было средней точкой между ( p , 2) и (–1, 3).
Я применю формулу средней точки:
Координаты и уже совпадают.Это сводит проблему к необходимости сравнивать координаты x , «приравнивая» их (то есть приравнивая их, потому что они должны быть одинаковыми) и решать полученное уравнение, чтобы выяснить, что такое p . Это даст мне значение, необходимое для совпадения значений x . Итак:
Итак, ответ p = –3.
Давайте сделаем еще несколько примеров….
URL: https://www.purplemath.com/modules/midpoint.htm
Как найти середину между двумя координатами
Что такое формула средней точки?
Иногда вам может понадобиться найти среднюю точку между двумя точками.Это обычно вступает в игру, когда в вопросе вас просят разделить линию на две равные половины или в задачах со словами, когда вас просят найти середину.
Если подумать, найти число, лежащее между набором чисел, довольно просто. Что ты обычно делаешь? Вы возьмете среднее из них. Сначала сложите их вместе, а затем разделите на два. Формула средней точки аналогична, и вместо того, чтобы брать среднее значение только числа, вам придется взять среднее значение значений x и y из двух точек по отдельности.
Средняя точка значения x находится посередине между значениями x двух точек. Средняя точка значения y находится на полпути между значениями y двух точек. Это имеет большой смысл, верно?
Конечно, это означает, что вам нужно знать координаты двух рассматриваемых точек, прежде чем вы сможете найти их середину. Но как только вы узнаете конечные точки отрезка, вы сможете легко найти его середину.
Все это хорошо резюмируется формулой средней точки, которая выглядит следующим образом:
M=(x1+x22,y1+y22)M=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})M=(2×1+x2,2y1+ у2)
Как найти середину
Чтобы увидеть, как работает формула средней точки, давайте рассмотрим пример.
Вопрос:
Определить середину отрезка с заданными конечными точками.
А(3,7),В(9,1)А(3,7), В(9,1)А(3,7),В(9,1)
Решение:
Мы можем использовать формулу для средней точки, чтобы определить среднюю точку: M=(x1+x22,y1+y22)M=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})M =(2×1+x2,2y1+y2)
Сначала подставьте значения x и y в формулу:
M=(3+92,7+12)M=(\frac{3+9}{2}, \frac{7+1}{2})M=(23+9,27+1)
Затем мы можем вычислить среднюю точку:
(6,4)(6, 4)(6,4)
этапы вычисления средней точкиДавайте подробнее рассмотрим шаги из приведенного выше примера.Во-первых, нам даны координаты двух точек, для которых мы должны найти середину отрезка. Это все, что вам нужно, чтобы использовать формулу средней точки.
Во-первых, сначала мы возьмем координаты x, чтобы мы могли работать над поиском координаты x средней точки. У нас есть 3 и 9, взятые из точек A и B соответственно. Просто сложите их вместе, а затем разделите на 2, чтобы получить среднее значение, то есть среднюю точку для значения x.
Затем сделайте то же самое с координатами y.У нас есть 7 и 1 из, опять же, точек A и B соответственно. Сложив это вместе, мы получим 8, а разделив на два, получим 4.
Мы определили, что середина между двумя точками лежит точно в координатах (6,4) по правилу средней точки, используя уравнение средней точки. Если вы начертите отрезок на графике, а затем перетащите точку вниз на (6,4), вы действительно увидите, что это точка, которая разделяет отрезок на две равные части.
Другое слово для точки, которая делит прямую на два равных сегмента, называется биссектрисой.Некоторые вопросы могут потребовать от вас найти биссектрису линии, что в основном требует от вас средней точки. Вы также можете столкнуться с вопросами о том, является ли определенная координата биссектрисой, и вам придется определить с помощью формулы средней точки, получаете ли вы указанные средние точки. Если нет, то это не биссектриса.
Если вы застряли, проверьте, получили ли вы правильные ответы, обратившись к этому калькулятору средней точки.
Вектор положения – объяснение и примеры
Мы можем использовать вектор положения , чтобы сообщить нам положение одного объекта относительно другого.В частности, вектор положения:
«Вектор, который указывает местоположение или положение данной точки относительно произвольной контрольной точки, такой как начало координат».
В этом разделе мы обсудим следующие аспекты векторов положения:
- Что такое вектор положения?
- Как найти вектор положения
Что такое вектор положения?
Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения.Они используются для определения положения точки относительно начала координат.
Направление вектора положения указывает от начала координат к заданной точке. В декартовой системе координат, если точка O является началом координат, а Q является некоторой точкой (x1, y1), то вектор положения, направленный из точки O в точку Q, представляется как OQ . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представляется следующим образом:
r = x1i + y1j + z1k
Предположим, у нас есть два вектора, A и B, с векторами положения a = (2,4) и b = (3, 5) соответственно.Тогда мы можем записать координаты векторов A и B как:
A = (2,4), B = (3, 5)
определяя вектор положения точки, нам сначала нужно определить координаты этой точки. Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Далее мы хотим найти вектор положения из точки M в точку N, вектор
MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :MN = (x2-x1, y2-y1)
Формула вектора положения
Используя приведенную выше информацию, мы можем обобщить формула, которая будет определять вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy.
Например, рассмотрим точку P с координатами (xk, yk) в плоскости xy и другую точку Q с координатами (xk+1, yk+1). Формула для определения вектора положения от P до Q:
PQ = ((xk+1)-xk, (yk+1)-yk)
Помните вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q. Аналогично, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
QP = (xk – (xk+1), yk – (yk+1))
Примеры
В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения.Это поможет глубже понять векторы положения.
Пример 1
Для двух точек A = (-4, 6) и B = (5, 12) определите вектор положения AB. Затем , вычисляют модуль вектора AB .
Решение
Имея две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения AB :
AB = (x2-x1, y2-y1)
6
66
AB x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Таким образом, просто подставив значения точек A и B в приведенное выше уравнение, мы можем найти вектор положения AB :
AB = (5-(-4), 12-6)
AB = ((5+ 4), 12-6)
AB = (9, 6)
Таким образом, вектор положения AB эквивалентен вектору, начинающемуся в начале координат и направленному в точку на расстоянии 9 единиц от вправо по оси x и на 6 единиц вверх по оси y.2
| АБ | = √81 + 36
| АБ | = √117
| АБ | = 3√13
Пример 2
Имея две точки A = (-4, 6) и B = (5, 12), определите вектор положения BA. Затем вычислите модуль вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :
BA = (x1-x2, y1-y2)
6
66
BA x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто поместив значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:
BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y.2
| ВА | = √81 + 36
| ВА | = √117
| ВА | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, соотношение между ними:
BA = -1*(9, 6)
BA = -1* AB
BA = – Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они являются негативами друг друга.
Пример 3
Учитывая, что вектор положения точки S1 равен OS1 = (2, 3) и что вектор точка S2, OS2 .
Решение
Сначала мы наносим вектор OS1 с начальной точкой в начале координат (0,0) и конечной точкой в (2,3). Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает отношение между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. На изображении ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило пропорциональности) сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Подставляя данные значения в это уравнение, получаем:
OS2 = (-3, 6) – (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 =(-5, 3) есть вектор положения точки S2.
Пример 4
Имея две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Имея две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2
| Р | = √100 + 25 + 9
| Р | = √100 + 25 + 9
| Р | = √134
Пример 6
Учитывая точки c = 5i + 6j +3k и d = 2i +5j – 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Имея две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросы - Пусть u = (-1, 4 , 5).Определите вектор положения, представленный UV .
- Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный ВУ .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- При заданном b = (3,2,5) определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается в точке a = (1, 2) и заканчивается в точке б = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается в точке o = (0,0) и заканчивается в точке b = (-2, 6). Определите вектор его положения.
Ответы
- УФ = (3,1). Направление UV составляет 3 единицы вправо по оси X и 1 единицу вверх.
- ВУ = (-3,-1). Направление ВУ на 3 единицы влево по оси абсцисс и на 1 единицу вниз. Два вектора УФ и ВУ, противоположны по направлению.
6
BA x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто поместив значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:
BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y.2
| ВА | = √81 + 36
| ВА | = √117
| ВА | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, соотношение между ними:
BA = -1*(9, 6)
BA = -1* AB
BA = – Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они являются негативами друг друга. Пример 3 Учитывая, что вектор положения точки S1 равен OS1 = (2, 3) и что вектор точка S2, OS2 . Решение Сначала мы наносим вектор OS1 с начальной точкой в начале координат (0,0) и конечной точкой в (2,3). Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает отношение между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. На изображении ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило пропорциональности) сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Подставляя данные значения в это уравнение, получаем:
OS2 = (-3, 6) – (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 =(-5, 3) есть вектор положения точки S2.
Пример 4
Имея две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Имея две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2
| Р | = √100 + 25 + 9
| Р | = √100 + 25 + 9
| Р | = √134
Пример 6
Учитывая точки c = 5i + 6j +3k и d = 2i +5j – 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Имея две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросы- Пусть u = (-1, 4 , 5).Определите вектор положения, представленный UV .
- Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный ВУ .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- При заданном b = (3,2,5) определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается в точке a = (1, 2) и заканчивается в точке б = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается в точке o = (0,0) и заканчивается в точке b = (-2, 6). Определите вектор его положения.
Ответы
- УФ = (3,1). Направление UV составляет 3 единицы вправо по оси X и 1 единицу вверх.
- ВУ = (-3,-1). Направление ВУ на 3 единицы влево по оси абсцисс и на 1 единицу вниз. Два вектора УФ и ВУ, противоположны по направлению.


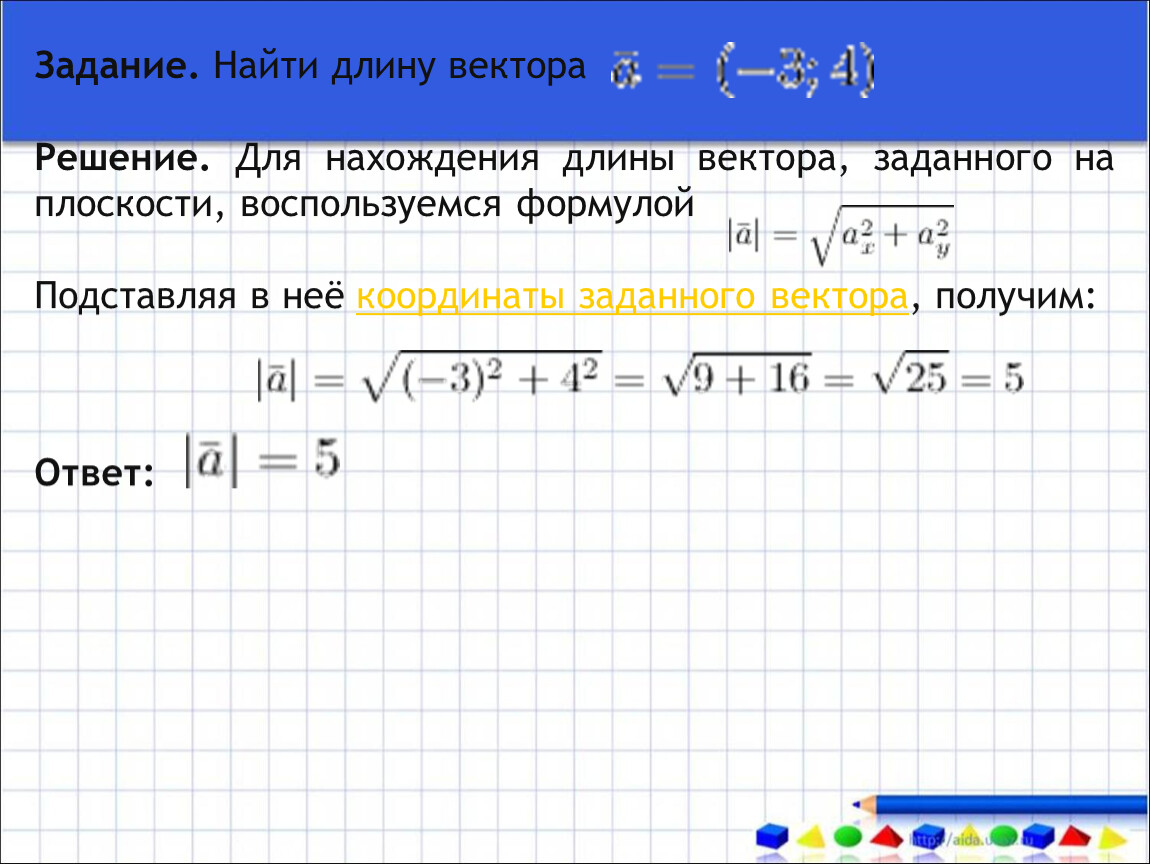 е. старательно
е. старательно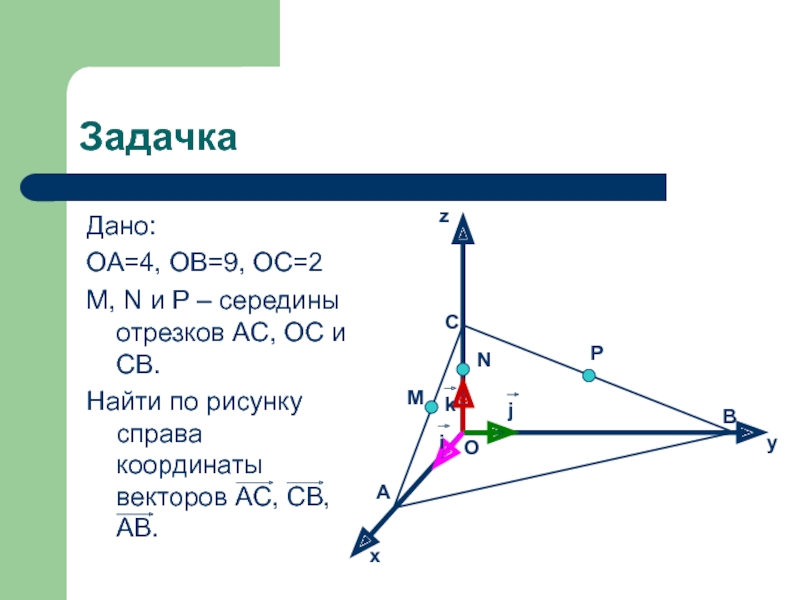 Найдите координаты вектора MN, если M (4;-5) , N(7; -9).
Найдите координаты вектора MN, если M (4;-5) , N(7; -9). Найдите координаты вектора MN, если M (4;-5) , N(7; -9).
Найдите координаты вектора MN, если M (4;-5) , N(7; -9). Найдите координаты вектора MN, если M (4;-5) , N(7; -9).
Найдите координаты вектора MN, если M (4;-5) , N(7; -9). Е. Разделены диаметром окружности.
Е. Разделены диаметром окружности.


 схему).
схему).