Средняя скорость. Ускорение | 7 класс Онлайн
Конспект по физике для 7 класса «Средняя скорость. Ускорение». ВЫ УЗНАЕТЕ: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. ВСПОМНИТЕ: В каком случае тело движется неравномерно? Что такое путь? Что такое скорость? Каковы единицы скорости? Как определить скорость тела при равномерном движении?
Средняя скорость. Ускорение
В окружающем нас мире мы крайне редко сталкиваемся с равномерным движением. Обычно скорость тела изменяется с течением времени, и за одинаковые промежутки времени тетю проходит неодинаковые пути. Такое движение является неравномерным. Однако никого не удивляет, когда мы говорим, что ехали на автомобиле со скоростью 60 км/ч, хотя при этом подразумевается, что мы и тормозили, и останавливались перед светофорами, и вновь ускорялись. О какой же скорости тогда идёт речь?
СРЕДНЯЯ СКОРОСТЬ
Для характеристики неравномерного движения вводят понятие средней скорости. Средняя скорость тела при неравномерном движении находится так же, как и скорость при равномерном движении, т. е. весь пройденный телом путь необходимо разделить на полное время движения тела, включая остановки.
Средняя скорость тела при неравномерном движении находится так же, как и скорость при равномерном движении, т. е. весь пройденный телом путь необходимо разделить на полное время движения тела, включая остановки.
путь
———— = средняя скорость
время
Полученное значение показывает среднюю скорость движения тела на всём пути, и оно может не совпадать со значением скорости в различные моменты времени движения.
Предположим, что автомобиль проехал путь s, состоящий из участков s1, s2, и s3, причём прохождение каждого из них заняло соответственно время t1, t2и t3. Для определения средней скорости движения автомобиля надо весь пройденный путь разделить на общее время движения:
ʋср = (s1 + s2 + s3) / (t1 + t2 + t3)
Зная среднюю скорость движения тела и время движения, можно найти пройденный за это время путь по формуле s = t ʋср.
Если нам известны средняя скорость движения и пройденный путь, мы можем определить время движения по формуле t = s ʋср.
ГРАФИКИ ЗАВИСИМОСТИ ПУТИ И СКОРОСТИ ОТ ВРЕМЕНИ
В отличие от графиков прямолинейного равномерного движения при неравномерном движении графики зависимости скорости и пути от времени могут выглядеть совершенно по-разному в зависимости от конкретной задачи.
Рассмотрим пример. Пусть велосипедист при движении из одного города в другой сначала проехал 8 км за 20 мин. Затем, отдохнув 10 мин, проехал ещё 6 км за 30 мин, а оставшиеся 2,5 км прошёл пешком за 30 мин. Как будут выглядеть соответствующие графики, если в пределах каждого временного интервала велосипедист двигался с постоянными скоростями?
РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ
Предположим, в начале определённого отрезка времени мы движемся в автомобиле со скоростью ʋ0. Автомобиль начинает увеличивать скорость, и через время t его скорость становится равной ʋ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.
Автомобиль начинает увеличивать скорость, и через время t его скорость становится равной ʋ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.
Прямолинейным равнопеременным движением называется движение, при котором траекторией тела является прямая линия и за любые равные промежутки времени скорость тела изменяется (увеличивается или уменьшается) на одно и то же значение.
УСКОРЕНИЕ
В физике существует величина, характеризующая изменение скорости тела при равнопеременном движении. Она называется ускорением и обозначается латинской буквой а. Для того чтобы вычислить ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло, т. е. от значения его конечной скорости нужно отнять значение начальной скорости и полученный результат разделить на рассматриваемое время движения.
В Международной системе единиц (СИ) за единицу ускорения принимают ускорение такого равнопеременного движения, при котором скорость движущегося тела за время 1 с изменяется на 1 м/с.
Эту единицу называют 1 метр на секунду в квадрате и обозначают 1 м/с2.
Ускорение может принимать как положительное, так и отрицательное значение. Действительно, если скорость тела в начале движения (ʋ0) меньше скорости тела в конце движения (ʋ), то при нахождении ускорения положительное число (ʋ — ʋ0) мы делим на положительное число (t) и получаем положительное значение ускорения. Если же тело замедляется, то значение начальной скорости оказывается больше значения скорости в конце движения, разность ʋ — ʋ0 становится отрицательной и значение ускорения тоже оказывается меньше нуля.
Вы смотрели Конспект по физике для 7 класса «Средняя скорость. Ускорение»: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).
Ускорение»: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела. Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).
Средняя скорость-Скоростьв физике
Средняя скорость
Средняя скорость – не
самое сложное понятие в кинематике. Однако для многих учащихся простота этого
понятия оказывается обманчивой.
Известно, что средняя скорость – это величина, равная отношению
пути, пройденного телом, ко времени, за которое пройден этот путь: Краткость
и простота определения скрывают от некоторых учеников важные для решения задач
вопросы и ответы на них.
1. Какое время следует учитывать при расчете средней
скорости, если тело в пути делало остановки?
В определении указано: “…ко времени, за которое пройден
этот путь”, то есть ко всему промежутку времени с момента, когда тело
тронулось в этот путь (представьте, что Вы включили секундомер), до момента,
когда тело преодолело этот путь (только в этот момент Вы останавливаете
секундомер!).
2. Как правильно
рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило
его в пункте В, но по дороге из А в В поворачивало назад (может быть ни
один раз!), а затем вновь продолжало движение к пункту В?
В определении указано “…равная отношению пути, пройденного
телом…”, значит, при расчете средней скорости определяющим является не
расстояние между точками (пунктами) начала и окончания движения, а реальный
путь, которое прошло тело.
Пример 1. Найти среднюю скорость человека на пути от дома до
станции, расстояние между которыми l =800 м, если, пройдя четверть пути,
он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через мин
продолжил путь на станцию. Скорость движения человека постоянна и равна v
=4 км/ч.
Скорость движения человека постоянна и равна v
=4 км/ч.
Решение. Началом движения человека, конечно, следует считать момент времени, когда он первый раз вышел из дома. Четверть пути составляет расстояние l1/4 =l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l1/4 =400 м. После этого он вышел из дома второй раз и дошел до станции. Путь, пройденный человеком с начала движения, составит:
S = 2l1/4 + l =400 + 800 =1200 м =1,2 км.
Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна (
1,2 км : 4
км/ч =0,3 ч =18 мин.
Тогда все время, затраченное человеком, составляет:
t =+ T = 2 + 18 =20 мин =1/3 ч.
Найдем среднюю скорость:
1,2 км : ч =3,6 км/ч.
Ответ: vср =3,6 км/ч.
Среднюю скорость движения человек оценивает довольно часто, но судит о ней, глядя на часы. Торопящийся человек соотносит расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это, после чего делает вывод (хотя числовое значение средней скорости вряд ли при этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще поднажать, иначе не успею”.
Вернемся к рассмотренному примеру. Будем считать, что скорость v0 =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t0 =12 мин =0,2 ч:
= 0,8 км : 0,2 ч =4 км/ч.
По существу, это – средняя скорость,
поскольку доподлинно неизвестно, с какой скоростью человек идет в каждый момент
времени. Двигаясь с такой скоростью и затрачивая время t0,
человек ежедневно успевает на станцию вовремя. Если приходится возвращаться
домой (увеличивать путь, который надо преодолеть и на это требуется
дополнительное время) или останавливаться (увеличивая время, необходимое на
преодоление пути), выбранная скорость движения v0 не
подходит: можно опоздать на станцию. Значит, надо увеличивать скорость
движения. Но как это сделать без напрасных затрат сил?
Двигаясь с такой скоростью и затрачивая время t0,
человек ежедневно успевает на станцию вовремя. Если приходится возвращаться
домой (увеличивать путь, который надо преодолеть и на это требуется
дополнительное время) или останавливаться (увеличивая время, необходимое на
преодоление пути), выбранная скорость движения v0 не
подходит: можно опоздать на станцию. Значит, надо увеличивать скорость
движения. Но как это сделать без напрасных затрат сил?
Пример 2. Человек обычно доходит из дома до станции за время t0
=12 мин, проходя расстояние l =800 м. Однажды, пройдя четверть пути, он
вспоминает, что не выключил электроприборы, и возвращается домой, выключает
электроприборы, затрачивая время= 2 мин, и
снова идет на станцию. С какой наименьшей скоростью надо двигаться человеку,
после того как он повернул домой, чтобы успеть на станцию в обычное время (и не
опоздать на электричку).
Решение.
1. Обычно человек двигается со скоростью
м/мин =4 км/ч.
2. Пройдя с такой скоростью четверть пути, он затратил время : 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время Т2 =t0 – T1 =12 – 3 =9 мин.
3. За время Т2 человек должен
преодолеть путь до дома, а затем снова до станции:
м =1 км и, кроме того, часть времени (= 2 мин)
потратить дома. Поэтому путь S человеку придется преодолевать за время
ч,
то есть со скоростью, не меньшей, чем
1 км : ч =км/ч =км/ч » 8,6 км/ч.
Проверьте, что добежав до дома со скоростью км/ч, а
затем шагая со скоростью v2 =2v0 =8 км/ч,
человек придет на станцию вовремя.
Ответ: человеку необходимо двигаться со скоростью, не меньшей, чем км/ч.
Обратите внимание, что средняя скорость за время (t =12 минут) от начала
движения до его окончания составляет
м/мин =100 м/мин =6 км/ч.
Найденное значение vср в полтора раза выше, чем v0, и показывает, с какой начальной скоростью следует выходить человеку из дома, если он забывчив.
На рис.1 показан график зависимости скорости человека от времени для примера 2 в случае, если человек бежит домой со скоростью v1 =3v0 ==12 км/ч, а затем идет до станции очень быстрым шагом со скоростью v2 =2v0 =8 км/ч. Штрихпунктирной линией указан график движения со скоростью v0, а тонкой линией – со скоростью vср =6 км/ч.
Подсчитаем среднее арифметическое для значений скорости v0, v1, v2:
км/ч.
Это значение не равно значению средней
скорости vср. Убедитесь в этом и не совершайте в дальнейшем
распространенную ошибку: не пытайтесь искать среднюю скорость как среднее
арифметическое значение (оно не имеет физического смысла!).
Пример 3. Автомобиль проезжает первую треть пути равномерно со
скоростью v1 =108 км/ч, а остальные две трети пути – со
скоростью v2 =72 км/ч. Найти среднюю скорость автомобиля.
Решение. Неверно считать, что средняя скорость совпадает со средним
арифметическим значением v1 и v2, которое
составляет
км/ч.
1. Найдем время t1 движения
со скоростью v1, полагая, что весь путь равен L [км].
Из условия ясно, что
2. Время t2 движения на оставшемся участке пути составляет
3. Итак, время на продолжение пути L составляет
4. По определению средней скорости
км/ч.
Ответ: средняя скорость vср =81 км/ч.
Значение средней скорости совпадает со средним арифметическим значением скорости
 Таким образом, тело двигается со скоростью v1 в течение
времени t1=T, со скоростью v2 в
течение времени t2=T, со скоростью v3
в течение времени t3=T и т.д. Если на протяжении пути
скорость изменялась n раз, то пройденный путь
Таким образом, тело двигается со скоростью v1 в течение
времени t1=T, со скоростью v2 в
течение времени t2=T, со скоростью v3
в течение времени t3=T и т.д. Если на протяжении пути
скорость изменялась n раз, то пройденный путь S =v1t1 + v2t2 + v3t3 + … +vntn =T(v1 + v
2 + v3 + … +vn).Время t, за которое пройден путь, составляет
t =t1 + t2 + t3 + … + tn =T*n.
По определению:
.
Не запрещено для этого частного случая
двигаться со скоростью v0=0, т. е. делать остановки. Но время
остановки должно составлять t0 =T.
е. делать остановки. Но время
остановки должно составлять t0 =T.
Пример 4. Вертолет пролетает без остановок равномерно и прямолинейно над пунктами А, В, С (в указанном порядке) и возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Расстояние между А и В составляет LAB =150 км, между В и С LBC =200 км, между
Решение. 1. Находим скорость движения вертолета на каждом участке:
км/ч;
км/ч;
км/ч.
2. Поскольку t =0,5 ч одинаково для всех участков движения, то
км/ч.
3. Если расстояние LСА =200 км и tCA=1ч, то не меняется vCA=200 км/ч. Но в этом случае нельзя подсчитывать (для простоты) среднюю скорость как среднее арифметическое, так как tCА ? tAB ==tBC.
км/ч.
Ответ: 1) vcp1 =300 км/ч; 2) vcp2 =275 км/ч.
Контрольные задания на эту тему
Мгновенная и средняя скорость | Физика
1. Мгновенная скорость
В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.
На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.
Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.
Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).
Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).
Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.
Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.
Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.
Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.
В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!
Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.
? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.
Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).
Как найти мгновенную скорость по графику зависимости координаты от времени
На рисунке 4. 4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.
4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.
Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.
Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).
Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.
На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).
Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.
2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?
Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).
4.6).
Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.
? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.
2. Средняя скорость
Во многих задачах используют среднюю скорость, связанную с пройденным путем:
vср = l/t. (1)
Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)
(Иногда во избежание недоразумений ее называют средней путевой скоростью.)
Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.
? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?
Средняя скорость на двух участках движения
Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:
vср = (l1 + l2)/(t1 + t2), (2)
где l1 и t1 – путь и время для первого участка, а l2 и t2 – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.
А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.
? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.
В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.
? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.
Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?
? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.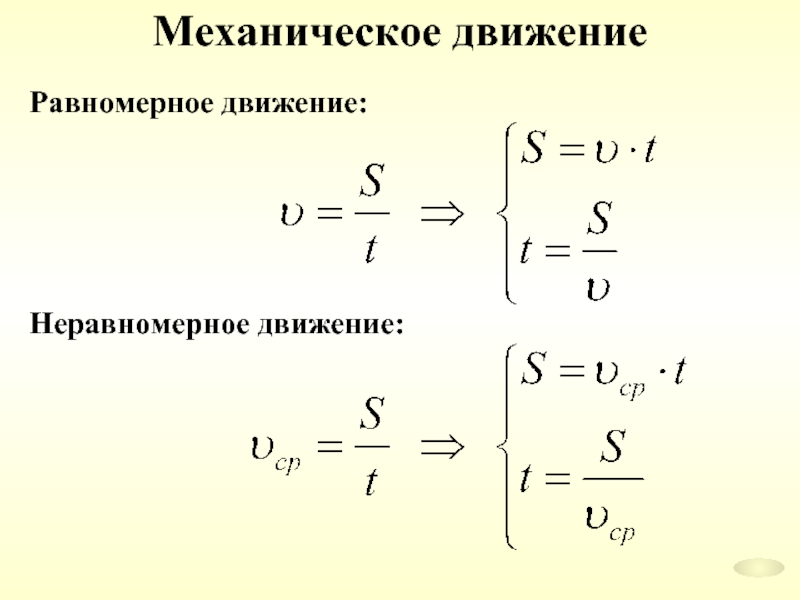
Обобщим рассмотренные выше ситуации.
Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.
Пусть первую половину всего времени движения тело двигалось со скоростью v1, а вторую половину – со скоростью v2. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?
Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.
Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l1 и l2.
? 8. Выразите через v1, v2 и t:
a) l1 и l2; б) l; в) среднюю скорость.
Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.
Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.
Пусть теперь первую половину всего пути тело двигалось со скоростью v1, а вторую половину – со скоростью v2. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t1 и t2.
? 9. Выразите через v1, v2 и l:
а) t1 и t2; б) t; в) среднюю скорость.
Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.
? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.
? 11. На первом участке пути тело двигалось со скоростью v1, а на втором – со скоростью v2. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v1 и v2?
Дополнительные вопросы и задания
12. Одну треть всего времени движения поезд ехал со скоростью v1, а оставшееся время – со скоростью v2.
а) Выразите пройденный поездом путь через v1, v2 и все время движения t.
б) Выразите среднюю скорость поезда через v1 и v2.
в) Найдите числовое значение средней скорости при v1 = 60 км/ч, v2 = 90 км/ч.
13. Автомобиль ехал три четверти всего пути со скоростью v1, а оставшийся участок пути – со скоростью v2.
а) Выразите все время движения автомобиля через v1, v2 и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v1 и v2.
в) Найдите числовое значение средней скорости при v1 = 80 км/ч, v2 = 100 км/ч.
14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?
15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.
16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t2.
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.
| 0101. Физические величины, единицы измерения и размерности Предмет физики: расстояния от очень маленького до очень большого отличаются в 1040…1050 раз. Основные единицы измерения системы SI (кг, м и с) называются размерностями. Через эти три размерности можно выразить большнство единиц измерения в механике. Пример: Преобразование единиц измерения (световой год — в метры и скорость из m/s — в km/h). Загрузить расчет. | ||
| 0102. Физические измерения и погрешности Физический эксперимент не имеет смысла, если неизвестны погрешности измерений. В качестве примера измерений автор осуществляет градуировку аналогового оптического датчика расстояния. Расстояние до отражающей поврхности измеряется рулеткой, а показания датчика — цифровым вольтметром. Второй пример — запись координаты робота бортовым УЗ-датчиком расстояния. Обсуждается замедление робота в середине траектории: влияние погрешности измерения или наезд на препятствие? Практикум 1: Градуировка датчика расстояния. Данные: расстояние, m — показания датчика, mV. Практикум 2: Движение робота x(t) Данные: время ms — координата, сm. Загрузить данные и расчеты (zip) | ||
| 0103. Анализ размерности Метод анализа размерности состоит в проверке совпадения размерности правой и левой частей предполагаемой формулы и позволяет получить ее с точностью до множителя В качестве примера приводится вывод зависимости времени падения объекта (под действием гравитации) от высоты, с которой он падает. Для отношения времен (для двух разных высот падения) получается точная формула. | ||
| 0104. Анализ размерности. Демонстрация: измерение времени свободного падения Автор экспериментально проверяет формулу зависимости времени падения от высоты, полученную из соображений анализа размерности. Он бросает шарик вниз и фиксирует падение на видеокамеру планшета. Анализируя кадры (картинка здесь), можно оценить высоту и время падения шарика. Расчеты отношений пар времен падения демонстрируют работу полученной из анализа размерности формулы (с учетом погрешности) и позволяют вычислить неизвестный коэффициент, входящий в формулу. Практикум:Измерение времени свободного падения в зависимости от пройденного расстояния. Данные: номер кадра (частота кадров 30 s-1) — относительная координата (х 8.5 cm) Загрузить данные и расчеты (zip) | ||
| 0105. Оценка погрешности измерений Какую роль играет точность в физике? Как можно повысить точность измерений? Автор измеряет расстояние тремя независимыми способами: рулеткой, ультразвуковым и оптическим датчиками, вычисляет среднее значение и анализирует ошибку среднего После этого он возвращается к задаче градуировки оптического датчика расстояния и использует метод наименьших квадратов для того чтобы получить связь между показаниями датчика и искомым расстоянием s. Оказывается, что в определенном диапазоне расстояний можно установить линейную связь 1/s=Ax+b. Без вывода приводятся оценки погрешности коэффициентов A и b. Практикум:Метод наименьших квадратов. Данные: расстояние, m — показания датчика, mV. Загрузить данные и расчеты (zip) | ||
| 0201. Скорость Демонстрация: робот начинает движение и, двигаясь по прямой вперед-назад, совершает несколько разворотов и возвращается на исходную позицию. В ходе движения текущая координата робота фиксируется бортовым сенсором расстояния. В ролике приведена компьютерная модель движения (при помощи Microsoft Robotics Developer Studio), а реальная демонстрация приведена здесь. Автор отмечает наугад несколько точек (время t и координату x), характеризующих траекторию движения (для дальнейшего обсуждения). Начальная и конечная точки совпадают: x1=x5. Средняя скорость — это расстояние, которое прошел робот за некоторое время t, отнесенное к этому времени. Автор обсуждает значение средней скорости на нескольких интервалах, делая акцент на его знаке (знак зависит от выбора направления оси х). Мгновенная скорость — это предел отношения расстояния к промежутку времени (при стремлении этого промежутка к нулю), т.е. производная v=dx/dt. Демонстрация: Движение робота (на видеоролике помечены точки x1…x5). Приложение: Диаграмма управления роботом (программа Microsoft Robotics Developer Studio). | ||
| 0202. Графики x(t), v(t) По данным датчика расстояния, записанным в ходе предыдущей демонстрации, можно построить график зависимости координаты робота x от времени t. Автор откладывает на графике точки (t1,x1)…(t5,x5) и оценивает по нему среднюю скорость на разных промежутках траектории (не отвлекаясь на анализ погрешностей, который отложен до следующей лекции). На одних участках она положительна, а на других — отрицательна. Средняя скорость всего движения равна нулю, т.к. x1=x5. Обсуждается различие между терминами «скорость» (velocity) и «модуль скорости» (speed). Мгновенная скорость в каждый момент времени задается наклоном кривой x(t). Там, где график идет вверх — скорость положительна, где вниз — отрицательна, а в точках максимума и минимума она равна нулю. Соответственно, по графику x(t) можно оценить зависимость v(t). Практикум 1: Градуировка датчика расстояния. Данные в двух файлах: 1. время, с; 2. расстояние, сm. Загрузить данные и расчеты (zip) | ||
| 0203. Измерение скорости Демонстрация: робот начинает движение и, быстро набрав скорость, двигается с постоянной скоростью по прямой. В определенный момент времени он разворачивается и начинает двигаться в обратном направлении, останавливаясь на прежнем месте. Измерения координаты осуществляются бортовым датчиком расстояния с периодичностью 1 раз в секунду. Автор рассчитывает среднюю скорость робота (отдельно для движения вперед и назад) и оценивает мгновенную скорость (в зависимости от времени). В заключение производится оценка средней скорости по наклону графика x(t) методом наименьших квадратов. Практикум: Измерение скорости робота. Данные: координата, сm (в одном файле, период между измерениями — 1s). Загрузить данные и расчеты (zip) | ||
| 0204. Ускорение Ускорение — это скорость изменения скорости. Среднее ускорение равно отношению изменения скорости к промежутку времени. Мгновенное ускорение равно производной скорости по времени (и второй производной координаты по времени). Ускорение может быть, как положительным, так и отрицательным или нулевым. Знак ускорения зависит от выбора направления координатной оси. Автор оценивает ускорение по графику x(t) и указывает на то, что ускорение характеризует быстроту изменения его наклона. | ||
| 0205. Пример уравнения движения В качестве примера исследуется одномерное движение объекта с заданным уравнением движения x(t)=8-6t+t2. Результат расуждений обобщается на произвольный случай равноускоренного движения по прямой. Практикум: Уравнение движения x(t)=8-6t+t2. Загрузить расчет (zip) | ||
| 0206. Измерение ускорения Демонстрация: робот движется равноукоренно (мощность вращения колес робота, согласно программе, нарастает линейно со временем). Измерения координаты осуществляются бортовым датчиком расстояния с периодичностью 1 раз в секунду. Автор по формулам, полученным на пошлом занятии, определяет среднее ускорение робота, а также качественно оценивает его мгновенное ускорение на всем промежутке движения. Практикум: Измерение времени свободного падения в зависимости от пройденного расстояния. Данные: время и координата (в двух разных файлах) Загрузить данные и расчеты (zip) | ||
| 0207. Демонстрация: измерение ускорения свободного падения Автор экспериментально измеряет значение ускорения свободного падения. Он бросает шарик вниз и фиксирует падение на видеокамеру планшета. Анализируя кадры (картинка здесь: каждая метка — это номер кадра и «координата»), можно оценить высоту и время падения шарика. Само падение длится 2/3 секунды, и по зависимости времени падения от пройденного растояния, рассчитывается значение ускорения шарика. Практикум: 1. График уравнения движения в поле тяжести. 2. Измерение времени свободного падения в зависимости от пройденного расстояния. Данные: номер кадра (частота кадров 30 s-1) — относительная координата «в дощечках» (х 8.5 cm) Загрузить данные и расчеты (zip) |
Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Определение 1Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеСредняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
Пример 1Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Пример 2Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
Что такое средняя путевая скорость
☰
В физике существует два понятия средней скорости. Одно — средняя путевая скорость. Второе — средняя скорость по перемещению. В чем же их сходство и различие?
Вообще понятие средней скорости вводится, когда движение тела является неравномерным, т. е. за равные промежутки времени тело двигается с разной скоростью. Например, за первую секунду тело двигалось со скоростью 10 км/ч, а за вторую — со скоростью 6 км/ч. Тогда средняя скорость тела за 2 секунды по-идее должна быть равна 8 км/ч, т. к. (10 + 6) / 2 = 8.
Однако, как известно, скорость можно вычислять по формуле 1) v = s/t или 2) v = Δx/t.
В первом случае s — это прошедший телом путь, или расстояние. Данная величина не может быть отрицательной, она не является вектором. И в таком случае vср будет скалярной величиной. Например, тело в течение одного часа двигалось из точки A в точку B по прямой линии 10 км, затем развернулось назад и за следующий час проехало еще 14 км, оказавшись в точке C на той же прямой линии. В данном случае средняя путевая скорость будет равна 12 км/ч, так как (14 км + 10 км) / 2 ч = 12 км/ч. Общее расстояние, покрытое движущимся телом, будет равно 24 км. Можно сказать, что в случае средней путевой скорости направление движения тела нас не интересует вообще. Нас интересуют лишь покрытые телом расстояния.
Во втором случае Δx (Δx = x2 — x1) — это разница между конечной и начальной координатами тела. Эта величина может быть как положительной, так и отрицательной (если конечная координата x2 меньше начальной x1). Таким образом, Δx является векторной величиной, а следовательно и скорость по перемещению будет векторной величиной. В примере, рассмотренном выше, Δx будет равно -4 км (0 + 10 — 14). Тогда vср = -4 км / 2 ч = -2 км/ч. Из этого примера видно, насколько сильно может отличаться средняя путевая скорость от средней скорости по перемещению.
Однако часто при прямолинейном движении модули обеих средних скоростей совпадают. Если бы тело из примера двигалось только до точки B, то средние скорости как путевая, так и по перемещению были бы равны 10 км/ч.
Итак, что такое средняя путевая скорость? Это скалярная физическая величина, равная отношению пройденного телом пути к длительности промежутка времени, за который тело прошло этот путь.
Средняя скорость по перемещению — это векторная физическая величина, равная отношению перемещения, совершенного телом, к длительности промежутка времени, за которое перемещение было совершено.
План-конспект урока «Неравномерное движение. Средняя скорость»
План-конспект урока по теме «Неравномерное движение.
Средняя скорость»
Дата: ______________
Цели:
- Образовательная: формирование знаний и представлений о неравномерном (переменном) движении, а также о средней скорости;
- Развивающая: развитие и формирование практических умений пользоваться физическими понятиями и величинами для описания равномерного прямолинейного движения; развивать познавательный интерес;
- Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений, воспитывать внимательность, наблюдательность.
Тип урока: урок усвоения новых знаний
Оборудование и источники информации:
Исаченкова, Л. А. Физика : учеб. для 7 кл. учреждений общ. сред. образования с рус. яз. обучения / 2017, рабочая тетрадь (Исаченкова), часть 1.
Содержание урока
- Организационный момент (проверка присутствующих в классе, проверка выполнения домашнего задания, озвучивание темы и основных целей урока)
- Актуализация опорных знаний
- Что выражает график пути?
- Для какого движения график пути представляет собой прямую?
- Как по графику скорости определить пройденный путь?
- Изучение нового материала
Равномерное движение – большая редкость. Обычно движущиеся тела меняют свою скорость. Проанализируем движение автобуса. Он уменьшает скорость перед остановкой. Затем в течение какого-то промежутка времени стоит на остановке, т. е.
его скорость равна нулю, после чего скорость увеличивается. Значит, скорость автобуса в процессе движения изменяется. Такое движение называется неравномерным.
|
Определение. Неравномерное (переменное) движение – движение, при котором тело проходит за равные промежутки времени разные пути (движение, при котором скорость изменяется). |
Практически все движения, наблюдаемые в природе и технике, — неравномерные. С изменяющейся скоростью движутся, например, люди, птицы, дельфины, поезда,
падают предметы. Но как же тогда характеризовать это движение?
Неравномерное движение характеризуется средней скоростью. Как определить среднюю
скорость?
Рассмотрим пример: Туристы прошли 12 километров за 3 часа и сделали привал на 1 час. Оставшиеся 9,6 километра туристы прошли за 2 часа. Надо найти их скорость на отдельных участках дороги и среднюю скорость на всём пути.
Весь путь туристов состоит из 3 частей: первая часть пути длилась 3 часа, вторая часть пути (отдых) длилась 1 час и последняя часть пути (переход) длилась 2 часа. Попробуем найти скорость туристов на каждом отрезке пути.
Мы нашли мгновенные скорости (υ1, υ2, υ3) туристов на отдельных участках.
|
Мгновенная скорость – скорость тела в данный момент времени. |
Но, чтобы узнать скорость на всём пути, надо использовать понятие средней скорости.
Среднюю скорость находят путем деления всего пути на всё затраченное время, за который этот путь пройден. Обозначим среднюю скорость 〈v〉 (в скобках-ромбиках) и измеряется в м/с (метры в секунду). Запишем формулу:
Средняя скорость показывает, какой скоростью обладало бы тело, если бы двигалось равномерно и преодолело бы такой же путь за это же время.
Найдём среднюю скорость в нашем примере:
Обратите внимание: Средняя скорость на всём пути не равна среднему арифметическому скоростей на отдельных участках пути:
(то есть нельзя складывать разные скорости тела на разных участках и делить на их количество, чтобы найти среднюю скорость).
|
|
График неравномерного движения серьёзно отличается от графика равномерного: он строится из отдельных отрезков, на которых тело имело постоянную скорость. |
Рассмотрим пример решения задачи со стр. 66
- Физкультминутка
- Закрепление знаний
А сейчас поработаем с карточками по теме «Неравномерное (переменное) движение. Средняя скорость» (приложение 1)
Карточка по теме «Неравномерное (переменное) движение. Средняя скорость»
Выполните задания и решите задачи
Заполните таблицу, ответьте устно на контрольные вопросы, решите задачи.
- Заполните таблицу.
|
Неравномерное движение (определение) |
Средняя скорость |
|
|
определение |
формула |
|
|
|
|
|
- Чем отличается неравномерное движение тела от равномерного?
- Как найти среднюю скорость неравномерного движения?
- Какое физическое значение имеют слова «всего» и «весь» в определении средней скорости
Задача 1. Яблоко падало с высоты h = 2,2 м в течение времени t = 0,67 с. Найдите среднее значение скорости падения яблока.
Задача 2. По данным графика (см. рисунок) опишите движение мотоциклиста.
Ответ: сначала мотоциклист за 3 секунды разогнался до скорости 6 м/с, затем 6 секунд ехал с постоянной скоростью равной 6 м/с, а после начал тормозить и через 3,5 секунды остановился.
- Итоги урока
Итак, подведем итоги:
- Характеристикой неравномерного движения является средняя скорость.
- Для вычисления средней скорости нужно путь разделить на весь промежуток
времени, затраченный на прохождение этого пути.
Организация домашнего задания
§18,ответить на контрольные вопросы.
Решить задачи (Рабочая тетрадь ст.81 задачи 1,2):
- Определите среднюю скорость своего движения от дома до школы. Оцените полученный результат.
- Знаете ли вы, что ручная черепаха, сбежавшая от своих хозяев в Англии, была найдена через 2 года на расстоянии 385 км от дома. Рассчитайте среднюю скорость движения черепахи и выразите её в м/с (примите путь равным расстоянию).
Рефлексия
Продолжите фразы:
- Сегодня на уроке я узнал…
- Было интересно…
- Знания, которые я получил на уроке, пригодятся.
Как найти среднюю скорость (формула и примеры)
Определение средней скорости
Средняя скорость объединяет две идеи в двух словах: средняя, что означает среднее значение, полученное из множества отдельных точек данных, и скорость, которая представляет собой изменение положения.
Вы можете рассчитать среднюю скорость для любого типа движения, если можете рассчитать время движения и измерить расстояние.
Содержание
- Определение средней скорости
- Формула средней скорости
- Как рассчитать среднюю скорость
- Проблемы со средней скоростью
Формула средней скорости
Средняя скорость — это общее расстояние, пройденное для рассматриваемого объекта, деленное на общее время, затраченное на преодоление расстояния, то есть общий период времени.Формула средней скорости:
Средняя скорость (с) = общее пройденное расстояние
Средняя скорость отличается от мгновенной скорости.
Мгновенная скорость
Средняя скорость учитывает все событие, такое как ускорение автомобиля с места остановки, ускорение, некоторое движение, затем замедление на желтый свет и, наконец, остановка.
Автомобиль движется с разной скоростью. В любой момент автомобиль не движется со скоростью 55 миль в час (миль в час).Это может быть 0 миль в час, затем 7 миль в час в другой момент, затем 53 миль в час, затем 61 миль в час и, наконец, 3 мили в час, прежде чем вернуться к 0 миль в час.
Чтобы упростить измерения и добиться прогресса в решении физико-математической задачи, вы берете среднюю скорость всех дискретных событий, говоря, что автомобиль проехал 5,5 миль за 6 минут:
с = 5,5 миль 6 мин. = 55 миль / ч
Все остальные измерения в определенные моменты путешествия — это мгновенные скорости . В большинстве случаев вы делаете , а не , вам нужно знать формулу для мгновенной скорости, v , находя предел, когда изменение во времени («мгновение») приближается к 0:
.v = lim △ t → 0 △ x △ t
Мгновенные скорости колеблются во время события.Найти среднюю скорость намного проще и, как правило, гораздо полезнее, чем вычислить мгновенную скорость.
Скалярные и векторные величины
Скорость — это скалярная величина . У него нет направления. У него есть только размер, то есть величина или масштаб. Скалярные величины могут изменяться от 0 (нет скорости) до бесконечно высокой.
Векторная величина имеет размер и направление, как в случае с движением самолета в небе. Скорость — это векторная величина.
Скорость, будучи скалярной величиной, никогда не может быть меньше 0. Средняя и мгновенная скорости всегда являются скалярными величинами, что означает, что вы всегда можете измерить их числом. Расстояние и время также являются скалярными величинами и также могут быть измерены числами.
Как рассчитать среднюю скорость
Чтобы вычислить среднюю скорость объекта, вы должны знать общее расстояние, которое проходит объект, и общее время, затраченное на его полное путешествие.
Треугольник расстояние / скорость / время удобен для вычисления этой и двух других скалярных величин (расстояния и времени):
Три части треугольника математически расположены в правильных положениях:
- Чтобы получить среднюю скорость, с, разделите общее расстояние на затраченное время: Dt
- Чтобы получить истекшее время t, разделите общее расстояние на скорость: Ds
- Чтобы получить расстояние D, умножьте скорость на количество времени: s × t
Допустим, вы хотите найти среднюю скорость тихоокеанской афалины.Вам говорят, что он может преодолеть расстояние 89,7 километра за 3 часа.
Вставьте эти два заданных числа в треугольник в их двух углах, чтобы получить:
с = 89,7 км3 часов = 29,9 километров в час (км / ч)
Если вам известны две из трех переменных: расстояние, время и скорость, то вы можете использовать алгебру, чтобы найти то, что вам не хватает.
Если вам нужно общее время, у вас должны быть расстояние и скорость. Вы вставляете эти две скалярные величины в их части треугольника, чтобы получить:
т = 89.7 км 29,9 км / ч = 3 часа
Если вам нужно общее расстояние, у вас должны быть скорость и время:
D = 29,9 км / ч × 3 часа = 89,7 км
Средняя скорость особенно полезна, потому что она учитывает реальность события, а не предполагает, что что-то или кто-то движется с постоянной скоростью.
Морская свинья могла начать медленно, ускориться, остановиться для игры и продолжить. Этот трехпалый ленивец, возможно, остановился на мгновение, чтобы отдышаться, прежде чем поспешить дальше.Возможно, вам придется делать множество остановок во время прогулки с собакой, но во всех трех случаях вы можете легко вычислить среднюю скорость, разделив общее пройденное расстояние на общее затраченное время.
A Предостережение
Средняя скорость часто определяется из единиц расстояния или времени, которые необходимо преобразовать в другие единицы для окончательного ответа. Будьте осторожны при этом. Обычные преобразования заключаются в умножении единиц в секунду на 60 или 3600, чтобы получить единицы в минуту и единицы в час. Просто убедитесь, что ваш ответ дан в правильную единицу времени.
Если изменяется только одна единица измерения, вам нужно будет выполнить только одну математическую операцию (например, умножить секунды, чтобы получить минуты или часы). Если две единицы изменяются (футы в секунду на мили в час), вам необходимо как умножить, так и разделить (или умножить на десятичное значение).
Проблемы со средней скоростью
Проверьте свои знания на примере задач со словами:
- Тарпон (разновидность рыбы) может преодолеть 105 миль за 3 часа. Какая у него средняя скорость?
- Голубой тунец может проплыть 286 миль за обычный школьный день из 6 человек.5 часов. Какова его средняя скорость, когда вы проводите день в классе?
- Мировой рекорд по максимальной скорости бега назад (при жонглировании!) Принадлежит Джо Солтеру, который преодолел 5280 футов за 457 секунд. Какова была его средняя скорость в милях за часов ? (умножьте на 3600 и затем разделите на 5280; или умножьте на 0,681818)
- Гепард может преодолеть 0,6 мили за 36 секунд. Какова средняя скорость гепарда в милях за секунд ? Как насчет скорости в милях за часов ? (умножить на 3600)
- Касатка может двигаться со средней крейсерской скоростью 8 миль в час.Большая белая акула может преодолеть расстояние до 35 миль за семь часов. Какая скорость у большой белой акулы и какое животное движется быстрее?
- Самый быстрый человек в воде преодолел 22,9 метра за 10 секунд. Кальмар Гумбольта может преодолеть 399,6 метра за 60 секунд. Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольта, чтобы знать, кто кого может обогнать.
Мы знаем, что вы сначала выполните работу, прежде чем проверять эти ответы, верно?
- Рассчитайте среднюю скорость тарпона следующим образом: s = 105 миль3 часа, что означает, что рыба может двигаться со средней скоростью 35 миль в час.
- Формула синего тунца будет выглядеть так: s = 286 миль 6,5 часов, поэтому средняя скорость рыбы составляет 44 мили в час.
- Джо Солтер преодолел 5280 футов за 457 секунд, поэтому s = 5280 футов 457 секунд дает 11,5536 футов в секунду. Мы умножаем это на 3600 (количество секунд в часе), а затем делим это на 5280 (футов в миле), чтобы получить среднюю скорость 7,87745 миль в час.
- Формула средней скорости гепарда будет s = 0,6 мили 36 секунд, что дает вам 0.01666 (повторяющееся десятичное число, поэтому мы приблизим 0,01666) как мили за секунд , которые вы можете умножить на 3600, чтобы получить среднюю скорость 60 миль в час.
- Косатка может двигаться со средней крейсерской скоростью 8 миль в час, в то время как средняя скорость большой белой акулы s = 35 миль, 7 часов = 5 миль в час. Касатка плавает быстрее.
- Самый быстрый человек в воде проплыл 22,9 метра за 10 секунд, поэтому средняя скорость s = 22,9 м · 10 секунд = 2,29 метра в секунду, или м / с. Кальмар Гумбольта может путешествовать 399.6 метров за 60 секунд, поэтому s = 399,6 м 60 секунд = 6,67 м / с, что значительно быстрее, чем у самого быстрого человека-пловца. Будем надеяться, что вас никогда не преследует кальмар Гумбольта!
Следующий урок:
Диагональная формула
2.2 Скорость и скорость — физика
Задачи обучения раздела
К концу этого раздела вы сможете делать следующее:
- Расчет средней скорости объекта
- Связать смещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, Руководство лаборатории по физике для старших классов рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Раздел Основные термины
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителя
Поддержка учителя
В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.
[BL] [OL] Перед тем, как студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто используются как синонимы в повседневной жизни, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это нечто большее, чем расстояние и перемещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, — это его скорость. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, потому что у нее есть величина, но не направление. Поскольку скорость — это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Единицей времени в СИ является секунда (с), а единицей измерения скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v avg , представляет собой пройденное расстояние, разделенное на время, в течение которого происходит движение.
vavg = distancetimevavg = distancetimeВы, конечно, можете изменить уравнение для решения либо расстояния, либо времени
время = distancevavg.time = distancevavg. distance = vavg × timedistance = vavg × timeПредположим, например, что автомобиль проезжает 150 километров за 3 секунды.2 часа. Его средняя скорость за поездку —
. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени — это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.
Поддержка учителей
Поддержка учителей
[OL] [AL] Предупредите учащихся, что средняя скорость не всегда равна средней начальной и конечной скорости объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км — со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.
[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на повседневном языке часто называют просто скоростью.Подчеркните важность использования правильной терминологии в науке, чтобы избежать путаницы и правильно передавать идеи.
Рисунок 2.8 За 30 минут до магазина и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода туда и обратно равно нулю, потому что не было чистого изменения положения.
Рабочий пример
Расчет средней скорости
Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?
Стратегия
Мы знаем расстояние, которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / сОбсуждение
Средняя скорость — это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды — это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
8.Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?
- 40 м / с
- -40 м / с
- 0,03 м / с
- 8,5 м / с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?
- 146 с
- 0.01 с
- 2,50 мин.
- 287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость — это смещение, деленное на время, в течение которого смещение происходит.
vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления во временном интервале больше влияет на скорость и скорость.
Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или отступил, прежде чем он добрался до задней части самолета. Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направлявшегося к задней части самолета, показаны более мелкие отрезки его полета.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.
Watch Physics
Расчет средней скорости или скорости
В этом видео рассматриваются векторы и скаляры и описывается, как рассчитать среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.
Проверка захвата
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору требуется только величина, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору требуется только величина, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
Поддержка учителей
Поддержка учителей
Это видео хорошо подчеркивает разницу между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Перед тем, как ученики посмотрят видео, укажите, что преподаватель использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является обычным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются обычные сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.
Рабочий пример
Расчет средней скорости
Студент перемещается на 304 м к северу за 180 с. Какая была средняя скорость ученика?
Стратегия
Мы знаем, что смещение составляет 304 м к северу, а время — 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.
Решение
vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны включить в ответ направление и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с — только двух, поэтому частное должно состоять только из двух значащих цифр.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.
Поддержка учителей
Поддержка учителей
Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные вычисления. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание на то, что это приведет к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда носить с собой одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение для смещения, когда известны средняя скорость и время
Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток2,2
Обсуждение
Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.
Советы для успеха
Размерный анализ — хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица компенсирует, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны смещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?
Стратегия
Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.
Решение
vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с2,3
Обсуждение
Здесь мы снова должны были использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
10.Дальнобойщик проезжает по прямой трассе 0,25 ч со смещением 16 км к югу.Какова средняя скорость дальнобойщика?
- 4 км / ч север
- 4 км / ч юг
- 64 км / ч север
- 64 км / ч юг
Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?
- 42 м запад
- 6 м запад
- 6 м на восток
- 42 м на восток
Virtual Physics
The Walking Man
В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графическом движении позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость — отрицательным. Затем посмотрите, сможете ли вы сделать обратное.
Проверка захвата
Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Человек движется от 0 слева от 0
- Человек движется от 0 справа от 0
Поддержка учителей
Поддержка учителей
Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Введение . Вкладку Charts можно использовать после того, как студенты узнают о графическом движении позже в этой главе.
Проверьте свое понимание
12.Два бегуна движутся по одному и тому же прямому пути. Они начинаются в одно и то же время и заканчиваются в одно и то же время, но на полпути у них разные мгновенные скорости. Могут ли они иметь одинаковую среднюю скорость для поездки?
- Да, потому что средняя скорость зависит от чистого или полного смещения.
- Да, потому что средняя скорость зависит от общего пройденного расстояния.
- Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
- Нет, потому что мгновенные скорости бегунов должны оставаться такими же на полпути, но могут быть разными в другом месте.
Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?
- Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
- Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. Оба варианта одинаковы, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.
Может ли средняя скорость быть отрицательной?
- Да, в случаях, когда чистое смещение отрицательное.
- Да, если тело постоянно меняет направление во время движения.
- Нет, средняя скорость описывает только величину, а не направление движения.
- Нет, средняя скорость описывает только величину в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание », чтобы оценить достижение учащимися учебных целей по разделам. Если учащиеся не справляются с какой-либо конкретной целью, Check Your Understanding поможет определить, кто из них и направит их к соответствующему содержанию.Тестовые задания в TUTOR позволят вам переоценить.
кинематика — средняя скорость
кинематика — средняя скорость[Глава 2 цели]
BHS -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница
Средняя скорость
Средняя скорость объекта показывает (среднюю) скорость при который покрывает расстояние. Если средняя скорость автомобиля составляет 65 миль за час, это означает, что положение автомобиля изменится (в среднем) на 65 миль каждый час.
Средняя скорость скорость . В кинематике ставка — это всегда количество, деленное на время, затраченное на получение этого количество (прошедшее время ). Поскольку средний скорость — скорость изменения положения, средняя скорость = расстояние путешествовал / затраченное время.
Пример:
Автомобиль проезжает между двумя городами, разделенными на 60 миль, за 2 часа. Что такое
его средняя скорость?
Ответ:
средняя скорость = расстояние / время Следовательно, средняя скорость машина 60 миль / 2 часа = 30 миль / час.
Пример:
Если человек может ходить со средней скоростью 2 метра в секунду, как
куда они пойдут за 4 минуты?
Ответ:
В 1 минуте 60 секунд, поэтому 4 (60 секунд) =
240 секунд за 4 минуты. Кроме того, если средняя скорость = расстояние / время,
тогда расстояние = (средняя скорость) (время). Следовательно, расстояние
человек перемещается (2 м / с) (240 с) = 480 метров.
Единицы измерения скорости
Так как средняя скорость всегда рассчитывается как расстояние (длина), разделенное на время, единицы средней скорости всегда единица расстояния, деленная на единицу времени. Общие единицы скорости метры в секунду (сокращенно м / с), сантиметры в секунду (см / с), километров в час (км / час), миль / час (миль / час — старайтесь избегать обычных сокращение mph) и многие другие.
Пример:
Что из следующего может быть измерением скорости?
- 2.5 метров
- 2,5 секунды / метр
- 2,5 м / сек
- 2,5 м / сек / сек
Ответ:
Измерение скорости может быть всего 2,5 метра в секунду. Скорость всегда имеет единицы измерения расстояния (длины), деленные на единицу времени.
Какое расстояние?
Фермер Джонс едет 6 миль по прямой дороге.Она разворачивается и проезжает 4 мили назад. Какой у нее был средний скорость для этой поездки, если на это ушло 1 час? |
Ваш ответ на эту проблему зависит от вашей интерпретации «пройденный путь». Можно сказать:
- Общее расстояние , пройденное фермером Джонсом составляет 10 миль. Следовательно, ее средняя скорость составляет 10 миль / час.
- Чистое расстояние , пройденное фермером Джонсом , составляет 2 мили.Следовательно, ее средняя скорость составляет 2 мили / час.
Есть веские причины использовать любую интерпретацию — в основном дело предпочтений. Мы будем интерпретировать «пройденное расстояние» как Чистое расстояние ( также называется смещением ). Средняя скорость Фермер Джонс составляла 2 мили / час.
ПРИМЕЧАНИЕ: Могут использоваться разные тексты. другие условности! Фактически, в нашем тексте AP Physics используется общая расстояние для расчета скорости, но чистое расстояние для расчета скорость.Будьте осторожны!
Опасности усреднения
Вот интересная задача:
Сьюзи запланировала поездку в город, расположенный в 60 милях. Она желает иметь во время поездки среднюю скорость 60 миль / час. Должное к пробке, однако, она развивает среднюю скорость 30 миль / час для первых 30 миль. Как быстро ей нужно идти оставшиеся 30 миль, так что ее средняя скорость будет 60 миль / час за всю поездку?
Скорее всего, вы подумали: «О, 90 миль / час — так как среднее значение 30 и 90 — это 60! Мальчик, это просто! »
Однако, к сожалению, ответ , а не 90 миль / час.Вот почему: вы знаете, что средняя скорость = расстояние / время (v = d / t). Чтобы иметь среднюю скорость 60 миль / час на расстояние 60 миль, вы должны завершить поездку за 1 час:
Но у Сюзи уже есть час (на то, чтобы идти 30, нужно час). миль со средней скоростью 30 миль / час) — а она всего половина способ! Для нее это невозможно, завершить поездку со средней скоростью 60 миль / час! Ей придется уйти бесконечно быстро!
Обратите внимание, что на покрытие последних 30 миль со скоростью 90 миль / час.Общее время ее поездки составит 1,33 часов, а ее средняя скорость будет:
Попробуйте этот расчет для при любой скорости для второй половины поездка — средняя скорость за всю поездку не может быть 60 миль / час! Мораль истории: Не среднее средние!
Измерение скорости движения
Это было бы хорошее время для измерения Скоростная активность, в которой вы:
- определить некоторые средние скорости путем измерения расстояний и раз, и
- определить неизвестное расстояние путем измерения времени, чтобы преодолеть расстояние при известной скорости
[Глава 2 цели] BHS -> МистерСтэнбро -> Физика -> Механика -> Кинематика -> эта страница
последнее обновление 22 ноября 2005 г., автор: JL Stanbrough
Расчет средней скорости: формулы и практические задачи — видео и стенограмма урока
Расчет средней скорости
Если объект движется с постоянной скоростью, то формула для скорости объекта определяется как:
Общее расстояние — это расстояние, пройденное объектом с постоянной скоростью. Истекшее время — это время, за которое объект преодолел общее расстояние. В большинстве случаев объект будет перемещаться на определенном расстоянии с разной скоростью. Например, автомобиль, путешествующий из одного города в другой, редко будет двигаться с постоянной скоростью. Более вероятно, что скорость автомобиля будет колебаться во время поездки. Автомобиль может какое-то время двигаться со скоростью 65 миль в час, а затем замедляться до 25 миль в час. Возможно, что в определенное время автомобиль даже стоит на полной остановке (например, на красный свет).Чтобы вычислить среднюю скорость автомобиля, нас не волнуют колебания его скорости. Нас интересует только общее расстояние, пройденное автомобилем, и время, затраченное на преодоление этого расстояния.
Формула средней скорости:
Важно отметить, что эта формула идентична формуле постоянной скорости. Средняя скорость измеряется в единицах расстояния за время. Общие единицы измерения включают мили в час (миль / ч), километры в час (км / ч), метры в секунду (м / с) или футы в секунду (фут / с).
Что касается вашего новенького красного спортивного автомобиля, ваш друг был совершенно прав в своих расчетах средней скорости. Он использовал расстояние, пройденное автомобилем (45 миль), разделенное на затраченное время (1,25 часа). Строительство на трассе и череда красных светофоров на местных дорогах сильно тормозили. Большое истекшее время привело к низкой средней скорости.
Примеры
Давайте посмотрим на некоторые другие примеры средней скорости:
1. Предположим, грузовой поезд преодолевает расстояние 120 миль за 3 часа.Какая средняя скорость поезда?
Ответ:
Его средняя скорость
2. Предположим, грузовик движется по сегментам, описанным в следующей таблице:
| Сегмент | Расстояние (мили) | Время (часы) |
|---|---|---|
| 1 | 30 | 1 |
| 2 | 45 | 2 |
| 3 | 50 | 1 |
| 4 | 65 | 2 |
Какова средняя скорость грузовика?
Ответ:
На основе предоставленной информации его средняя скорость по четырем сегментам может быть рассчитана как
3.Автомобиль едет со скоростью 50 миль в час из Чикаго, штат Иллинойс, в Миннеаполис, штат Миннесота, и 65 миль в час в обратном направлении. Какова средняя скорость автомобиля за весь путь туда и обратно?
Ответ:
В этом примере нам даны две скорости. Предположим, что расстояние, пройденное во время поездки из Чикаго в Миннеаполис, составляет D , тогда расстояние, пройденное в обратном пути, также составляет D . Общее расстояние за всю поездку — 2 * D . Схема ниже иллюстрирует ситуацию.
Используя формулу для средней скорости, можно отдельно рассчитать время, прошедшее от Чикаго до Миннеаполиса ( t1 ) и обратно ( t2 ). Расчеты показаны ниже.
Используя формулу средней скорости, общее расстояние и затраченное время, можно рассчитать среднюю скорость для всей поездки как:
Обратите внимание, что средняя скорость не (50 + 65) / 2 = 57.5 миль в час! Помните, что средняя скорость определяется как общее пройденное расстояние, разделенное на затраченное время. Два элемента, которые нам нужны для расчета средней скорости:
1) Общее пройденное расстояние
2) Истекшее время, чтобы преодолеть это расстояние
Расстояние туда и обратно можно представить как 2 * D (если мы разрешим односторонний расстояние составляет D ), а затраченное время в оба конца равно ( D / с1 ) + ( D / с2 ) (поскольку прошедшее время в одну сторону равно расстоянию в одну сторону, разделенному на скорость пути).
4. Бегун завершает забег в соответствии с графиком дистанция-время, показанным ниже. Какая средняя скорость бегуна в первые 10 секунд? Какая средняя скорость бегуна за всю гонку?
Ответ:
График расстояние-время показывает расстояние, пройденное бегуном за истекшее время. Используя график, мы видим, что бегун пробежал 0 м в начале забега. Через 10 секунд он пробежал 75 метров.
Средняя скорость бегуна в первые 10 секунд рассчитывается как:
Через 30 секунд он завершает забег и пробегает общую дистанцию 200 метров.
Средняя скорость бегуна за весь забег рассчитывается как:
Итоги урока
Давайте рассмотрим. Средняя скорость объекта — это общее расстояние, пройденное объектом, деленное на время, затраченное на преодоление этого расстояния.Чтобы вычислить среднюю скорость объекта, нас не интересуют колебания его скорости. Ключевые элементы, которые нам нужны:
1) Общее пройденное расстояние
2) Время, затраченное на преодоление этого расстояния
Запоминание
| Средняя скорость | |
|---|---|
| Общее расстояние, пройденное объектом, деленное на затраченное время, чтобы преодолеть это расстояние | |
| Скалярная величина, определяемая только величиной | |
| Колебания скорости не имеют значения |
Результаты обучения
Когда вы закончите, вы сможете:
- Указать разницу между средней скоростью и средней скоростью
- Напишите уравнение для расчета средней скорости
- Рассчитать среднюю скорость объекта
Зависимость скорости от скорости
Так же, как расстояние и смещение имеют совершенно разные значения (несмотря на их сходство), то же самое делают и скорость и скорость.Скорость — это скалярная величина, которая указывает, «насколько быстро движется объект». Скорость можно представить как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткое время. Сравните это с медленно движущимся объектом с низкой скоростью; он преодолевает относительно небольшое расстояние за то же время. Объект, который вообще не движется, имеет нулевую скорость.
Скорость как векторная величинаСкорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение.«Представьте, что человек быстро движется — один шаг вперед и один шаг назад — всегда возвращается в исходное исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Потому что человек всегда возвращается в исходное положение , движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость, с которой изменяется положение, это движение приводит к нулевой скорости. Если движущийся человек хочет максимизировать свою скорость, то этот человек должен приложить все усилия чтобы максимально увеличить их смещение от исходного положения.Каждый шаг должен продвигать этого человека дальше от того места, где он начал. Наверняка человек никогда не должен менять направление и начинать возвращаться в исходное положение.
Скорость — это векторная величина. Таким образом, скорость с учетом направления . Оценивая скорость объекта, нужно следить за его направлением. Недостаточно сказать, что объект имеет скорость 55 миль / час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта.Например, вы должны описать скорость объекта как 55 миль / ч, к востоку, . Это одно из существенных различий между скоростью и скоростью. Скорость — это скалярная величина, и не отслеживает направление ; скорость является векторной величиной и учитывает направление .
Определение направления вектора скорости
Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта.Неважно, ускоряется объект или замедляется. Если объект движется вправо, его скорость описывается как правая. Если объект движется вниз, его скорость описывается как нисходящая. Таким образом, самолет, движущийся на запад со скоростью 300 миль / час, имеет скорость 300 миль / час на западе. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент — это просто значение скорости с направлением.
Расчет средней скорости и средней скорости
Когда объект движется, его скорость часто меняется.Например, во время обычной поездки в школу происходит много изменений скорости. Вместо того, чтобы измеритель скорости поддерживать стабильные показания, стрелка постоянно перемещается вверх и вниз, отражая остановку и запуск, а также ускорение и замедление. В один момент автомобиль может двигаться со скоростью 50 миль / час, а в другой момент он может быть остановлен (т. Е. 0 миль / час). Тем не менее, во время поездки в школу человек может в среднем 32 мили / час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра.Если бы показания спидометра можно было собирать с интервалами в 1 секунду (или интервалы 0,1 секунды или …), а затем усреднять вместе, можно было бы определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть ярлык. Читать дальше. Средняя скорость движения часто вычисляется по следующей формуле:Напротив, средняя скорость часто вычисляется по этой формуле
Давайте начнем реализацию нашего понимания этих формул со следующей задачи:
Вопрос: Во время отпуска Лиза Карр преодолела расстояние в 440 миль.Поездка заняла 8 часов. Какая у нее была средняя скорость?
Чтобы вычислить ее среднюю скорость, мы просто разделим пройденное расстояние на время поездки.
Это было просто! Лиза Карр в среднем развивала скорость 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль / час. Она, несомненно, была остановлена в какой-то момент времени (возможно, на перерыв в туалете или на обед), и, вероятно, в другие моменты времени она, вероятно, ехала со скоростью 65 миль в час.Тем не менее, она развивала в среднем 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Средняя скорость в сравнении с мгновенной скоростью
Поскольку движущийся объект часто меняет свою скорость во время движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.
- Мгновенная скорость — скорость в любой момент времени.
- Средняя скорость — среднее значение всех мгновенных скоростей; можно найти просто по соотношению расстояние / время.
Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой момент времени, а о средней скорости как о среднем значении всех показаний спидометра во время поездки. Поскольку задача усреднения показаний спидометра была бы довольно сложной (и, возможно, даже опасной), средняя скорость обычно рассчитывается как отношение расстояния / времени.
Движущиеся объекты не всегда перемещаются с неустойчивой и изменяющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый равный промежуток времени. Например, бегун может бежать с постоянной скоростью 6 м / с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, которое проходит каждую секунду, будет таким же. Бегун преодолевал расстояние в 6 метров каждую секунду.Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение менялось бы на 6 метров каждую секунду. Это будет разительно контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разное расстояние каждую секунду. В приведенных ниже таблицах данных показаны объекты с постоянной и изменяющейся скоростью.
А теперь давайте снова рассмотрим движение того учителя физики. Учитель физики идет 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.Все движение длилось 24 секунды. Определите среднюю скорость и среднюю скорость.
Учитель физики прошел дистанцию 12 метров за 24 секунды; таким образом, ее средняя скорость составляла 0,50 м / с. Однако, поскольку ее смещение составляет 0 метров, ее средняя скорость составляет 0 м / с. Помните, что смещение относится к изменению положения, а скорость основывается на этом изменении положения. В этом случае движения учителя изменяется положение на 0 метров и, следовательно, средняя скорость составляет 0 м / с.
Вот еще один пример, подобный тому, что мы видели ранее при обсуждении расстояния и смещения. На диаграмме ниже показано положение лыжника в разное время. В каждый из указанных моментов лыжник разворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта A в пункт B, из пункта C в пункт D.
Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут.По завершении нажмите кнопку, чтобы просмотреть ответ.
В качестве последнего примера рассмотрим футбольного тренера, который ходит взад и вперед по боковой линии. На диаграмме ниже показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в противоположном направлении. Другими словами, тренер переходит из позиции A в позицию B, затем из позиции C в позицию D.
Какова средняя и средняя скорость тренера? По завершении нажмите кнопку, чтобы просмотреть ответ.
В заключение, скорость и скорость — это кинематические величины, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это отношение расстояния (скалярной величины) к времени. Скорость без учета направления . С другой стороны, скорость — это векторная величина; это с учетом направления . Скорость — это скорость изменения позиции. Средняя скорость — это отношение смещения или изменения положения (векторная величина) за время.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Name That Motion Interactive. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять концепции скорости, скорости и ускорения.Посетите Назовите это движение.
Скорость и скорость | Безграничная физика
Средняя скорость: графическая интерпретация
Средняя скорость определяется как изменение положения (или смещения) за время движения.
Цели обучения
Контрастность скорости и скорости в физике
Основные выводы
Ключевые моменты
- Среднюю скорость можно рассчитать, разделив общее смещение на общее время движения.
- Средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой.
- Средняя скорость отличается от средней скорости тем, что учитывает направление движения и общее изменение положения.
Ключевые термины
- скорость : векторная величина, которая обозначает скорость изменения положения относительно времени или скорость с направленным компонентом.
В повседневном использовании термины «скорость» и «скорость» используются как синонимы.Однако в физике это разные величины. Скорость — это скалярная величина, имеющая только величину. С другой стороны, скорость — это векторная величина, поэтому она имеет как величину, так и направление. Это различие становится более очевидным, когда мы вычисляем среднюю скорость и скорость.
Средняя скорость рассчитывается как расстояние, пройденное за общее время поездки. Напротив, средняя скорость определяется как изменение положения (или смещения) за общее время движения.
Средняя скорость : Кинематическая формула для расчета средней скорости представляет собой изменение положения за время движения.
Единица измерения скорости в системе СИ — метры в секунду или м / с, но обычно используются многие другие единицы (например, км / ч, миль / ч и см / с). Предположим, например, что пассажиру самолета потребовалось пять секунд, чтобы переместиться на -4 м (отрицательный знак указывает, что смещение происходит в сторону задней части самолета). Его средняя скорость будет:
v = Δ x / t = -4 м / 5 с = -0.8 м / с
Знак минус указывает, что средняя скорость также направлена к задней части самолета.
Однако средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой. Например, мы не можем сказать по средней скорости, останавливается ли пассажир самолета на мгновение или отступает, прежде чем он доберется до задней части самолета. Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени.
Чтобы проиллюстрировать разницу между средней скоростью и средней скоростью, рассмотрим следующий дополнительный пример. Представьте, что вы идете по маленькому прямоугольнику. Вы идете три метра на север, четыре метра на восток, три метра на юг и еще четыре метра на запад. Вся прогулка займет у вас 30 секунд. Если вы рассчитываете среднюю скорость, вы должны рассчитать все расстояние (3 + 4 + 3 + 4 = 14 метров) за общее время, 30 секунд. Отсюда вы получите среднюю скорость 14/30 = 0.47 м / с. Однако при вычислении средней скорости вы смотрите на смещение во времени. Поскольку вы вошли в полный прямоугольник и оказались там, где начали, ваше смещение составляет 0 метров. Следовательно, ваша средняя скорость или смещение во времени составит 0 м / с.
Средняя скорость в сравнении со средней скоростью : Если вы начали идти с одного угла и обошли весь прямоугольник за 30 секунд, ваша средняя скорость будет 0,47 м / с, но ваша средняя скорость будет 0 м / с.
Постоянная скорость: графическая интерпретация
Мгновенная скорость — это скорость объекта в одной точке во времени и пространстве, вычисленная по наклону касательной.
Цели обучения
Отличить мгновенную скорость от других способов определения скорости
Основные выводы
Ключевые моменты
- Когда скорость постоянно меняется, мы можем оценить нашу скорость, глядя на мгновенную скорость.
- Мгновенная скорость вычисляется путем определения наклона касательной к кривой в интересующей точке.
- Мгновенная скорость аналогична определению того, сколько метров объект пролетит за одну секунду в определенный момент.
Ключевые термины
- мгновенно : (То же, что и по скорости) — возникает, возникает или действует без какой-либо задержки; происходит в незаметно короткий промежуток времени.
Обычно движение не с постоянной скоростью или скоростью.Например, во время движения в машине мы постоянно ускоряемся и замедляемся. Следовательно, графическое представление нашего движения с точки зрения расстояния и времени будет более изменчивым или «извилистым», чем прямая линия, указывающая на движение с постоянной скоростью, как показано ниже. (Мы ограничиваем наше обсуждение одномерным движением. Это должно быть несложно для обобщения на трехмерные случаи.)
Движение с изменяющейся скоростью : движение часто наблюдается с изменяющейся скоростью.Это привело бы к извилистой линии при отображении расстояния с течением времени.
Чтобы вычислить скорость объекта по графику, представляющему постоянную скорость, все, что нужно, — это найти наклон линии; это будет указывать на изменение расстояния с течением времени. Однако изменить скорость не так просто.
Поскольку наша скорость постоянно меняется, мы можем оценивать скорость по-разному. Один из способов — посмотреть на нашу мгновенную скорость, представленную одной точкой на нашей кривой линии движения, на которой показан график зависимости расстояния отвремя. Чтобы определить нашу скорость в любой момент, мы должны определить наклон в этой точке. Для этого мы находим линию, которая представляет нашу скорость в этот момент, показанную графически. Эта линия будет касательной к кривой в этой точке. Если мы продолжим эту линию, мы сможем легко вычислить смещение расстояния во времени и определить нашу скорость в данной точке. Скорость объекта в любой данный момент — это наклон касательной, проходящей через соответствующую точку на его оси x vs.t график.
Определение мгновенной скорости : Скорость в любой данный момент определяется как наклон касательной линии, проходящей через соответствующую точку на графике.
Мгновенная скорость, ускорение, рывок, наклоны, графики в зависимости от времени : Так начинается кинематика.
В расчетах определение наклона кривой f (x) при x = x 0 эквивалентно нахождению первой производной:
[латекс] \ frac {\ text {df} (\ text {x})} {\ text {dx}} | _ {\ text {x} = \ text {x} _0} [/ latex].
Одна из интерпретаций этого определения состоит в том, что скорость показывает, сколько метров объект пролетел бы за одну секунду, если бы он продолжал двигаться с той же скоростью в течение как минимум одной секунды.
Время, скорость и скорость | Физика
Цели обучения
К концу этого раздела вы сможете:
- Объясните взаимосвязь между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, смещением и временем.
- Вычислить скорость и скорость с учетом начального положения, начального времени, конечного положения и конечного времени.
- Постройте график зависимости скорости от времени с учетом графика положения от времени.
- Расскажите о графике зависимости скорости от времени.
Движение — это нечто большее, чем расстояние и перемещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.
Как обсуждалось в разделе «Физические величины и единицы», наиболее фундаментальные физические величины определяются тем, как они измеряются. Так обстоит дело со временем. Каждое измерение времени включает в себя измерение изменения некоторой физической величины. Это может быть число на цифровых часах, сердцебиение или положение Солнца на небе. В физике время определяется просто: время, — это изменение, или интервал, в течение которого происходит изменение. Невозможно знать, что время прошло, если что-то не изменится.
Время или изменение калибруется путем сравнения со стандартом. Единицей измерения времени в системе СИ является секунда, сокращенно с. Мы можем, например, наблюдать, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно, подключая маятник к часовому механизму, который регистрирует время на циферблате. Это позволяет нам не только измерить количество времени, но и определить последовательность событий.
Как время связано с движением? Обычно нас интересует время, затраченное на конкретное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета.Чтобы найти истекшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00 утра. и закончится в 11:50 утра, чтобы прошедшее время составило 50 минут. Истекшее время Δ t — разница между временем окончания и временем начала,
Δ т = т f — т 0 ,
, где Δ t — изменение во времени или прошедшее время, t f — время в конце движения, а t 0 — время начала движения.(Как обычно, символ дельты, Δ, означает изменение количества, которое следует за ним.)
Жизнь проще, если время начала t 0 принять равным нулю, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если t 0 = 0, то Δ t = t f ≡ t .
В этом тексте для простоты
- движение начинается в момент времени, равный нулю ( t 0 = 0)
- символ t используется для истекшего времени, если не указано иное (Δ t = t f ≡ t )
Ваше понятие скорости, вероятно, совпадает с ее научным определением.Вы знаете, что если у вас есть большое смещение за небольшой промежуток времени, у вас есть большая скорость, и эта скорость выражается в единицах расстояния, разделенных на время, например, в милях в час или в километрах в час.
Средняя скоростьСредняя скорость — это смещение (изменение положения), деленное на время перемещения ,
[латекс] \ bar {v} = \ frac {\ Delta x} {\ Delta t} = \ frac {{x} _ {f} — {x} _ {0}} {{t} _ {f} — {t} _ {0}} [/ latex],
, где [латекс] \ bar {v} [/ latex] — это среднее значение , (обозначено полосой над v ) скорость, Δ x — изменение положения (или смещения), а x f и x 0 — конечная и начальная позиции в моменты времени t f и t 0 соответственно.Если время пуска t 0 принять равным нулю, то средняя скорость будет просто
[латекс] \ bar {v} = \ frac {\ Delta x} {t} [/ latex].
Обратите внимание, что это определение указывает, что скорость является вектором, потому что смещение является вектором . У него есть и величина, и направление. Единица измерения скорости в системе СИ — это метры в секунду или м / с, но широко используются многие другие единицы, такие как км / ч, миль / ч (также записываемые как мили в час) и см / с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на −4 м (отрицательный знак указывает, что смещение происходит в сторону задней части самолета).Его средняя скорость будет
.[латекс] \ bar {v} = \ frac {\ Delta x} {t} = \ frac {-4 \ text {m}} {5 \ text {s}} = — \ text {0,8 м / с. } [/ латекс]
Знак минус указывает, что средняя скорость также направлена к задней части самолета.
Однако средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой. Например, по средней скорости мы не можем сказать, останавливается ли пассажир самолета на мгновение или отступает назад, прежде чем он уйдет в заднюю часть самолета.Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени.
Чем меньше временные интервалы, учитываемые в движении, тем более подробная информация. Когда мы доводим этот процесс до его логического завершения, у нас остается бесконечно малый интервал. В течение такого интервала средняя скорость становится мгновенной скоростью или скоростью в конкретный момент . Например, автомобильный спидометр показывает величину (но не направление) мгновенной скорости автомобиля.(Полиция выдает билеты на основе мгновенной скорости, но при расчете времени, которое потребуется, чтобы добраться из одного места в другое во время поездки, вам необходимо использовать среднюю скорость.) Мгновенная скорость v — это средняя скорость при заданной скорости. конкретный момент времени (или бесконечно малый интервал времени).
Математически, нахождение мгновенной скорости v в точный момент времени t может включать определение предела, операцию вычисления, выходящую за рамки этого текста.Однако во многих случаях мы можем найти точные значения мгновенной скорости без расчетов.
В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. В физике, однако, они не имеют одинакового значения и представляют собой разные концепции. Одно из основных различий заключается в том, что скорость не имеет направления. Таким образом, скорость — это скаляр . Так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.
Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в один момент времени имел мгновенную скорость -3,0 м / с (минус означает направление к задней части самолета). При этом его мгновенная скорость составляла 3,0 м / с. Или предположим, что однажды во время похода по магазинам ваша мгновенная скорость составляет 40 км / ч на север. Ваша мгновенная скорость в этот момент будет 40 км / ч — такая же величина, но без указания направления.Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, разделенное на затраченное время.
Мы отметили, что пройденное расстояние может быть больше перемещения. Таким образом, средняя скорость может быть больше средней скорости, которая представляет собой смещение, деленное на время. Например, если вы едете в магазин и возвращаетесь домой через полчаса, а одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.(Смещение — это изменение положения и, таким образом, равно нулю для поездки туда и обратно.) Таким образом, средняя скорость равна , а не просто величине средней скорости.
Другой способ визуализировать движение объекта — использовать график. График положения или скорости как функции времени может быть очень полезным. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рисунке 4.