Концентричные объекты — Википедия

Материал из Википедии — свободной энциклопедии

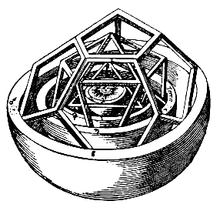Мишень для стрел, содержащая равномерно распределённые концентрические окружности, которые окружают «Яблочко». Космологическая модель Кеплера образована концентричными сферами и правильными многогранниками

Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности,^[1]правильные многоугольники^[2], правильные многогранники^[3] и сферы^[4] могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры^[5] (имея общую коаксиальную ось).

В двумерном пространстве две концентрические окружности обязательно имеют различные радиусы

[6]. Однако окружности в трёхмерном пространстве могут быть концентрическими, иметь тот же самый радиус, и, тем не менее, быть различными. Например, два различных меридиана^[en] земного глобуса концентричны между собой и самим земным глобусом (если рассматривать Землю как сферу). Более обще, любые два больших круга на сфере концетричны один относительно другого и самой сфере^[7].

По теореме Эйлера в геометрии о расстоянии между центром описанной окружности и центром вписанной окружности треугольника две концентрические окружности (с нулевым расстоянием между центрами) являются описанной и вписанной окружностями для треугольника тогда и только тогда, когда радиус одной вдвое больше радиуса другой, и в этом случае треугольник будет правильным.^[8].

Описанная и вписанная окружности правильного n-угольника и сам правильный n-угольник концентричны. Для отношения радиусов описанной окружности к радиусу вписанной окружности для различных

n — см. Бицентрический многоугольник^[en].

Область плоскости между двумя концентрическими окружностями является кольцом и, аналогично, область пространства между двумя концентрическими сферами является сферической оболочкой^[4].

Для заданной точки c на плоскости множество всех окружностей, имеющих точку c в качестве центра, образуют пучок окружностей. Любые две окружности в пучке концентричны и имеют различные радиусы. Любая точка на плоскости, за исключением общего центра, принадлежит ровно одной окружности пучка. Любые две непересекающиеся окружности и любые гиперболические пучки окружностей могут быть преобразованы в множество концентрических окружностей путём преобразования Мёбиуса^[9][10].

Рябь, образованная падением маленьких объектов в спокойную воду, образует систему концентрических окружностей^[11]

. Равномерно распределённые окружности на мишени, используемые при стрельбе из лука^[12] или подобных спортивных дисциплинах, дают другой известный пример концентрических окружностей.

Коаксиальный кабель — это тип электрического кабеля, в котором комбинация нейтрального слоя и земля окружают полностью центральный проводник(и) в виде концентрических цилиндрических слоёв^[13].

Книга «Тайна мироздания» Иоганна Кеплера представляет космологическую систему в виде концентрических правильных многогранников и сфер^[14].

Концентрические окружности также обнаруживаются в диоптрических прицелах (вид механических прицелов), обычно используемых на винтовках. Они обычно представляют собой большой диск с отверстием малого диаметра рядом с глазом стрелка и сферическую мушку (окружность, находящуюся внутри другой окружности, называемой туннелем). Когда элементы прицела правильно выровнены, точка попадания будет в середине фронтального кольца.

1. ↑ Alexander, Koeberlein, 2009, с. 279.
2. ↑ Hardy, 1908, с. 107.
3. ↑ Gillard, 1987, с. 137, 139.
4. ↑ ^{1 2} Apostol, 2013, с. 140.
5. ↑ Spurk, Aksel, 2008, с. 174.
6. ↑ Cole, Harbin, 2009, с. 6 (§2).
7. ↑ Morse, 1812, с. 19.
8. ↑ Svrtan, Veljan, 2012, с. 198.
9. ↑ Hahn, 1994, с. 142.
10. ↑ Brannan, Esplen, Gray, 2011, с. 320–321.
11. ↑ Fleming, 1902, с. 20.
12. ↑ Haywood, Lewis, 2006, с. xxiii.
13. ↑ Weik, 1997, с. 124.
14. ↑ Meyer, 2006, с. 436.

• Walter A. Meyer. Geometry and Its Applications. — 2nd. — Academic Press, 2006. — С. 436. — ISBN 9780080478036.
• George M. Cole, Andrew L. Harbin. Surveyor Reference Manual. — www.ppi2pass.com, 2009. — ISBN 9781591261742.
• Jedidiah Morse. The American universal geography;: or, A view of the present state of all the kingdoms, states, and colonies in the known world, Volume 1. — Thomas & Andrews, 1812. — С. 19.
• Dragutin Svrtan, Darko Veljan. Non-Euclidean versions of some classical triangle inequalities. — Forum Geometricorum, 2012. — Т. 12. — С. 197–209.
• Daniel C. Alexander, Geralyn M. Koeberlein. Elementary Geometry for College Students. — Cengage Learning, 2009. — С. 279. — ISBN 9781111788599.
• Godfrey Harold Hardy. A Course of Pure Mathematics. — The University Press, 1908. — С. 107.
• Robert D. Gillard. Comprehensive Coordination Chemistry: Theory & background. — Pergamon Press, 1987. — С. 137, 139. — ISBN 9780080262321.
• Joseph Spurk, Nuri Aksel. Fluid Mechanics. — Springer, 2008. — С. 174. — ISBN 9783540735366.
• Tom Apostol. New Horizons in Geometry. — Mathematical Association of America, 2013. — Т. 47. — С. 140. — (Dolciani Mathematical Expositions). — ISBN 9780883853542.
• Liang-shin Hahn. Complex Numbers and Geometry. — Cambridge University Press, 1994. — С. 142. — (MAA Spectrum). — ISBN 9780883855102.
• David A. Brannan, Matthew F. Esplen, Jeremy J. Gray. Geometry. — Cambridge University Press, 2011. — С. 320–321. — ISBN 9781139503709.
• Sir John Ambrose Fleming. Waves and Ripples in Water, Air, and Æther: Being a Course of Christmas Lectures Delivered at the Royal Institution of Great Britain. — Society for Promoting Christian Knowledge, 1902. — С. 20.
• Kathleen Haywood, Catherine Lewis. Archery: Steps to Success. — Human Kinetics, 2006. — С. xxiii. — ISBN 9780736055420.
• Martin Weik. Fiber Optics Standard Dictionary. — Springer, 1997. — С. 124. — ISBN 9780412122415.

Окружность на сфере — Википедия

Материал из Википедии — свободной энциклопедии

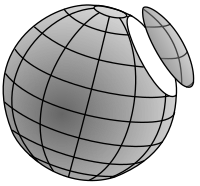Малая окружность

Окружность на сфере получается при пересечении сферы с плоскостью. Если плоскость проходит через центр сферы (то есть является диаметральной плоскостью), то получившаяся окружность будет иметь максимальный возможный радиус. Такая окружность называется большой окружностью (иногда большим кругом). Если пересекающая плоскость не проходит через центр, то получившаяся окружность называется малой окружностью. В сферической геометрии окружности на сфере являются аналогом окружностей в плоской геометрии, при этом большие окружности являются аналогом прямых^[1].

Многие свойства окружностей и прямых в плоской геометрии имеют аналоги для малых и больших окружностей в сферической геометрии. Например, через любые три точки на сфере, не лежащие на одной большой окружности, можно провести единственную малую окружность^[2].

Малая окружность делит сферу на две области, называемые сферическими сегментами. Меньший сегмент называется сферическим кругом^[1].

Сферический центр и сферический радиус[править | править код]

Окружность на сфере можно также определить как геометрическое место точек сферы, равноудалённых от данной точки сферы. Этим же свойством обладает и диаметрально противоположная точка. Для малых окружностей та из этих двух точек, для которой сферическое расстояние от неё до точек данной окружности меньше, называется сферическим центром этой окружности. А само расстояние сферическим радиусом. Для больших окружностей эти две точки называются полюсами больших окружностей. Их так же можно считать центрами большой окружности^[3]. Сферический радиус большого круга равен квадранту, и обратно, круг на сфере со сферическим радиусом, равным квадранту, есть большой круг^[4].

Например, геометрическая дальность видимого горизонта без учета земной рефракции, представляет собой сферический радиус, измеряется она обычно в километрах, хотя расстояния на сфере в сферической тригонометрии обычно измеряются в градусах (или радианах).

Радикальный центр — Википедия

Материал из Википедии — свободной энциклопедии

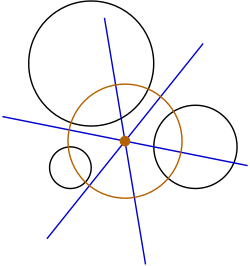Радикальный центр (оранжевая точка) является центром единственной окружности (также оранжевой), пересекающей три заданные окружности под прямыми углами.

В геометрии радикальный центр трёх окружностей — точка пересечения трёх радикальных осей пар окружностей. Если радикальный центр лежит вне всех трёх окружностей, то он является центром единственной окружности (радикальной окружности), которая пересекает три данных окружности ортогонально. Построение этой ортогональной окружности соответствует задаче Монжа. Это специальный случай теоремы о трёх конических сечениях.

Три радикальных оси пересекаются в одной точке, радикальном центре, по следующей причине: радикальная ось пары окружностей определяется как множество точек, имеющих одинаковую степень

h относительно обеих окружностей. Например, для любой точки P на радикальной оси окружностей 1 и 2, степени относительно каждой из окружностей равны h₁ = h₂. Таким же образом для любой точки на радикальной оси окружностей 2 и 3 степени должны быть равны h₂ = h₃. Таким образом, в точке пересечения двух этих прямых эти три степени должны совпадать: h₁ = h₂ = h₃. Из этого следует, что h₁ = h₃, и эта точка должна лежать на радикальной оси окружностей 1 и 3. Таким образом, все три радикальные оси проходят через одну точку — радикальный центр.

Радикальный центр имеет несколько приложений в геометрии. Он играет важную роль при решении задачи Аполлония, опубликованной Джозефом Диасом Жергонном в 1814 году. В диаграмме степени

[en] системы окружностей все вершины диаграммы лежат в радикальных центрах троек окружностей. Центр Шпикера треугольника является радикальным центром его вневписанных окружностей^[1]. Также существуют другие радикальные центры, такие как радикальный центр окружностей Люка.

• Две окружности, пересекающиеся под прямым углом, называются ортогональными. Окружности можно считать ортогональными, если они образуют прямой угол друг с другом.
• Две пересекающиеся в точках A{\displaystyle A} и B{\displaystyle B} окружности с центрами O{\displaystyle O} и O′{\displaystyle O’} называются ортогональными, если являются прямыми углы OAO′{\displaystyle OAO’} и OBO{\displaystyle OBO}. Именно это условие гарантирует прямой угол между окружностями. В этом случае перпендикулярны радиусы (нормали) двух окружностей, проведенные в точку их пересечения. Следовательно, перпендикулярны и касательные двух окружностей, проведенные в точку их пересечения. Касательная окружности перпендикулярна радиусу (нормали), проведенному в точку касания. Обычно угол между кривыми — это угол между их касательными, проведенными в точке их пересечения.
• Возможно другое дополнительное условие. Пусть две пересекающиеся в точках A и B окружности имеют середины пресекающихся дуг в точках C и D, то есть дуга AС равна дуге СB, дуга AD равна дуге DB. Тогда эти окружности называются ортогональными, если являются прямыми углы СAD и СBD.

• C. Stanley Ogilvy. Excursions in Geometry. — Dover, 1990. — С. 23. — ISBN 0-486-26530-7.
• Г. С. М. Коксетер, С. Л. Грейтцер. Новые встречи с геометрией. — Москва: «Наука», Главная редакция физико-математической литературы., 1978. — С. 43—48. — (Библиотека математического кружка).
• Johnson R. A. Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle. — reprint of 1929 edition by Houghton Miflin. — New York: Dover Publications, 1960. — С. 32–34. — ISBN 978-0-486-46237-0.
• Wells D. The Penguin Dictionary of Curious and Interesting Geometry. — New York: Penguin Books, 1991. — С. 35. — ISBN 0-14-011813-6.
• Dörrie H. §31 Monge’s Problem // 100 Great Problems of Elementary Mathematics: Their History and Solutions. — New York: Dover, 1965. — С. 151—154.
• Lachlan R. An elementary treatise on modern pure geometry. — London: Macmillan, 1893. — С. 185.
• Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10.

Окружность, круг, секущая и сектор

Окружность и круг — геометрические фигуры, взаимосвязанные между собой. Окружность есть граничная ломаная линия (кривая) круга,

Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.

Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.

Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.

Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов, лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D).

Правило. Диаметр окружности равен двум ее радиусам.

d = 2r
D = 2R

Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.

Длина окружности обозначается латинской большой буквой «цэ» (C). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:

C = ¶d
C = 2¶r

• Примеры
• Дано: d = 100 см.
• Длина окружности: C = 3,14 * 100 см = 314 см
• Дано: d = 25 мм.
• Длина окружности: С = 2 * 3,14 * 25 = 157 мм

Секущая окружности и дуга окружности

Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.

Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.

Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.

Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой, уменьшается по мере удаления секущей от центра окружности.

Определение. Кругом называется часть плоскости, лежащая внутри окружности.

Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.

Так как круг — это часть плоскости, то одним из его параметров является площадь.

Правило. Площадь круга (S) равна произведению квадрата радиуса ( r ² ) на число ¶.

• Примеры
• Дано: r = 100 см
• Площадь круга:
• S = 3,14 * 100 см * 100 см = 31 400 см ² ≈ 3м ²
• Дано: d = 50 мм
• Площадь круга:
• S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм ² ≈ 20 см ²

Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами. Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности.

Определение. Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.

Площадь сектора составляет только часть площади круга, и ее величина пропорциональна длине дуги m или зависит от величины центрального угла a, образованного двумя радиусами с вершиной в центре круга.

Формула для вычисления площади сектора:

где S — площадь сектора; m — длина дуги; r — радиус круга; а — угловая величина дуги (и градусах).

Хорда (геометрия) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Хорда. 1 — секущая, 2 — хорда AB (отмечена красным цветом), 3 — сегмент (отмечен зелёным цветом), 4 — дуга

Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).

Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. Плоская фигура, заключённая между кривой и её хордой называется сегментом, а часть кривой, находящаяся между двумя крайними точками хорды называется дугой. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды. Хорда, проходящая через центр окружности, является её диаметром. Диаметр — самая длинная хорда в окружности.

Хорда и расстояние до центра окружности[править | править код]

• Если расстояния от центра окружности до хорд равны, то эти хорды равны.
• Если хорды равны, то расстояния от центра окружности до этих хорд равны.
• Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше.
• Если расстояние от центра окружности до хорды меньше, то эта хорда больше. Если расстояние от центра окружности до хорды больше, то эта хорда меньше.
• Наибольшая возможная хорда является диаметром.
• Наименьшая возможная хорда является точкой.
• Если хорда проходит через центр окружности, то эта хорда является диаметром.
• Если расстояние от центра окружности до хорды равно радиусу, то эта хорда является точкой.
• Серединный перпендикуляр к хорде проходит через центр окружности.

Хорда и диаметр[править | править код]

• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде.
• Если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам.
• Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
• Если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу.
• Если диаметр перпендикулярен хорде, то этот диаметр делит дуги, стягиваемые этой хордой, пополам.
• Если диаметр делит дугу пополам, то этот диаметр перпендикулярен хорде, стягивающей эту дугу.

Хорда и радиус[править | править код]

• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде.
• Если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам.
• Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
• Если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
• Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам.
• Если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Хорда и вписанный угол[править | править код]

• Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны.
• Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
• Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла.
• Если вписанный угол опирается на диаметр, то этот угол является прямым.

Хорда и центральный угол[править | править код]

• Если хорды стягивают равные центральные углы, то эти хорды равны.
• Если хорды равны, то эти хорды стягивают равные центральные углы.
• Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
• Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.

Хорда и дуга[править | править код]

• Если хорды стягивают равные дуги, то эти хорды равны.
• Если хорды равны, то эти хорды стягивают равные дуги.
• Из дуг, меньших полуокружности, большая дуга стягивается большей хордой, меньшая дуга стягивается меньшей хордой.
• Из дуг, меньших полуокружности, большая хорда стягивает большую дугу, меньшая хорда стягивает меньшую дугу.
• Из дуг, больших полуокружности, меньшая дуга стягивается большей хордой, большая дуга стягивается меньшей хордой.
• Из дуг, больших полуокружности, большая хорда стягивает меньшую дугу, меньшая хорда стягивает большую дугу.
• Хорда, стягивающая полуокружность, является диаметром.
• Если хорды параллельны, то дуги, заключённые между этими хордами (не путать с дугами, стягиваемыми хордами), равны.

Другие свойства[править | править код]

Рис. 1. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}

• При пересечении двух хорд AB и CD в точке E получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рис. 1): AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.
• Если хорда делится пополам какой-либо точкой, то её длина самая маленькая по сравнению с длинами проведённых через эту точку хорд.

Теорема Декарта (геометрия) — Википедия

В геометрии теорема Декарта утверждает, что для любых четырёх взаимно касающихся окружностей радиусы окружностей удовлетворяют некоторому квадратному уравнению. Решив это уравнение, можно построить четвёртую окружность, касающуюся остальных трёх заданных окружностей. Теорема названа в честь Рене Декарта, который сформулировал её в 1643 году.

Геометрические задачи на касающиеся окружности обсуждались в течение тысячелетий. В древней Греции в III веке до нашей эры Аполлоний Пергский посвятил целую книгу этой теме. К сожалению, книга, носившая название О касаниях, не сохранилась, погибнув при пожаре Александрийской библиотеки.

Рене Декарт обсуждал задачу кратко в 1643 году в письме принцессе Елизавете Богемской. Он пришёл совершенно к тому же решению, что приведено ниже в уравнении (1), и тем самым вписал своё имя в теорему.

Фредерик Содди повторно открыл уравнение в 1936 году. Касающиеся окружности в этой задаче иногда упоминаются как Окружности Содди, возможно потому, что Содди выбрал публикацию своей версии теоремы в виде поэмы, озаглавленной The Kiss Precise (Аккуратный поцелуй), который напечатан в журнале Nature (20 июня 1936). Содди обобщил теорему на сферы. Торольд Госсет обобщил теорему на произвольные размерности.

Более древняя история[править | править код]

Взгляд Игоря Шарыгина^[1]: В течение большей части периода Эдо (1603—1867) Япония находилась почти в полной изоляции от западного мира и развивалась своими путями, без влияния западных цивилизаций. Однако это не помешало развитию японской науки, в частности математики. Особенно процветала геометрия. Японцы полагали, что искусство геометрии угодно Богу. Ею увлекались представители всех сословий, от крестьян до самураев. Свои открытия, теоремы они изображали яркими цветными красками на досках — сангаку — и вывешивали при храмах — большей частью синтоистских, реже буддистских — и усыпальницах. Эти доски являлись одновременно и приношением почитаемому божеству, и «публикацией» автора о сделанном им красивом открытии. Словесные пояснения почти отсутствовали. Автор как бы говорил: «Смотри и, если сможешь, докажи!»… Прекрасные задачи и теоремы, собранные в книге «Японская храмовая геометрия» — это своеобразное «исчисление окружностей», «гимн окружности». Среди них находим не только формулу Содди, но и её обобщение на трёхмерный случай. Первое упоминание о соотношении между радиусами окружностей появилось на доске (сангаку) в 1796 году в Токийской префектуре, полное доказательство было опубликовано в 1830-м. Интересно, что пример, показывающий связь между радиусами пяти соприкасающихся сфер, был описан на доске, найденной там же, а позднее утерянной, уже в 1785 году. В середине XIX столетия в Японии было опубликовано полное доказательство «обобщённой формулы для пяти соприкасающихся шаров»…

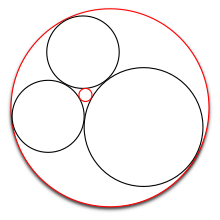Касающиеся окружности. Если даны три взаимно касающиеся окружности (чёрные), какой радиус может иметь четвёртая касающаяся окружность? В общем случае имеется два возможных ответа (красные).

Теорему Декарта проще всего сформулировать в терминах кривизны окружностей. Кривизна окружности определяется как k = ±1/r, где r — её радиус. Чем больше окружность, тем меньше величина её кривизны, и наоборот.

Знак плюс в k = ±1/r ставится, если окружность имеет внешнее касание к другой окружности, как три чёрных окружности на рисунке. Для касающихся окружностей внутренне, как большая красная окружность на рисунке, которая описывает остальные окружности, ставится знак минус.

Если считать, что прямая линия — это вырожденная окружность с нулевой кривизной (а следовательно, с бесконечным радиусом), теорема Декарта применима также и к прямой и двум окружностям, касающимся друг друга попарно. В этом случае теорема даёт радиус третьей окружности, касающейся двух других и прямой.

Если четыре окружности касаются друг друга в шести различных точках и окружности имеют кривизны k_i (для i = 1, …, 4), теорема Декарта утверждает^[2]:

(k1+k2+k3+k4)2=2(k12+k22+k32+k42).{\displaystyle (k_{1}+k_{2}+k_{3}+k_{4})^{2}=2\,(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2}).} (1)

Если пытаться отыскать радиус четвёртой окружности, касающейся трёх касающихся друг друга окружностей, уравнение лучше записать в виде:

k4=k1+k2+k3±2k1k2+k2k3+k3k1.{\displaystyle k_{4}=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.} (2)

Знак ± отражает факт, что в общем случае имеется два решения. Если исключить вырожденный случай прямой линии, одно решение положительно, другое же может быть как положительным, так и отрицательным. Если решение отрицательно, оно представляет окружность, описывающую первых три (как показано на рисунке).

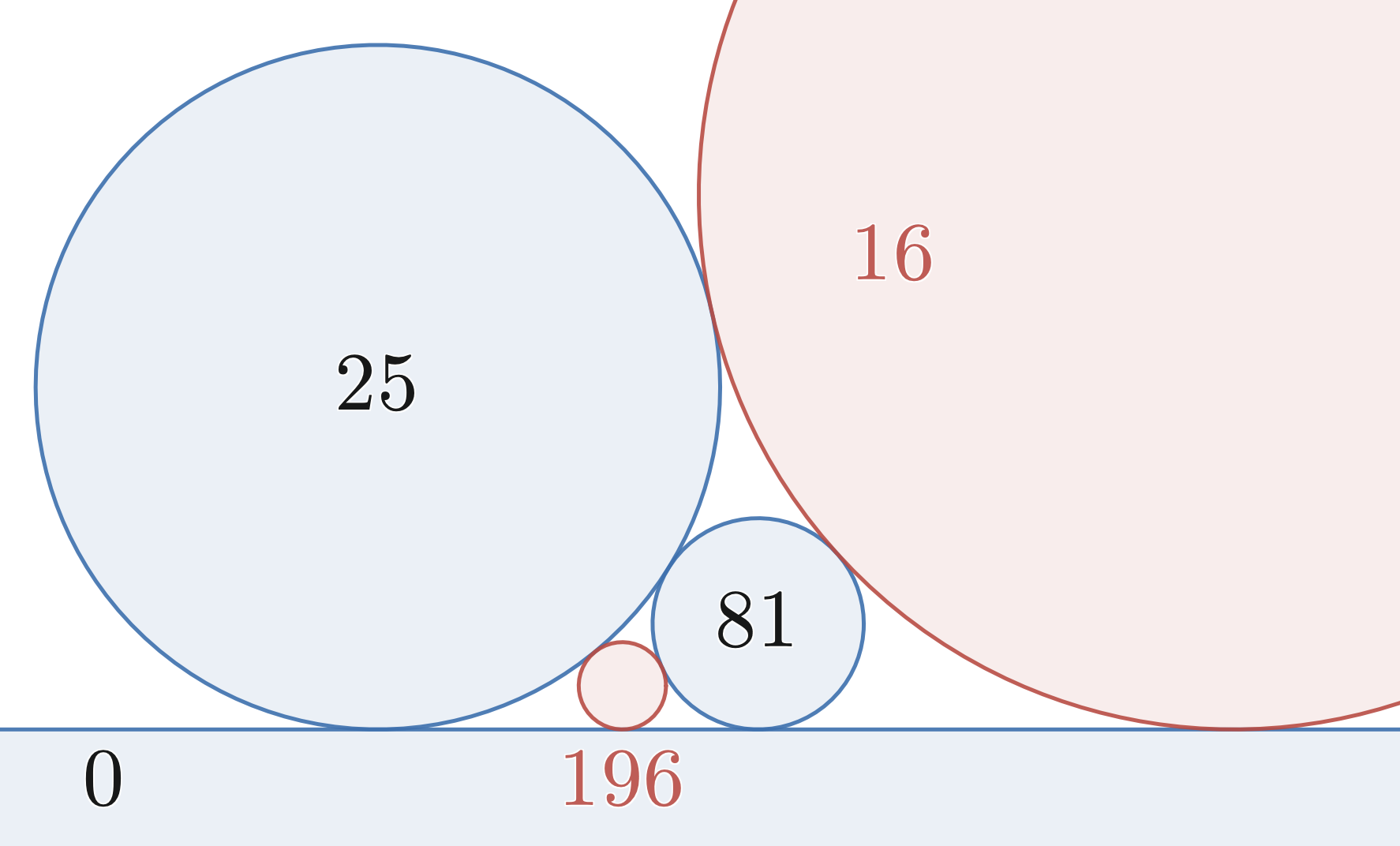
Одна из окружностей заменена прямой (с нулевой кривизной). Теорема Декарта остаётся верной.

Здесь все три окружности касаются друг друга в одной точке и теорема Декарта неприменима.

Если одну из окружностей заменить на прямую линию, то одно из чисел k_i, скажем, k₃, будет нулевым и выпадает из уравнения (1). Уравнение (2) становится много проще:

k4=k1+k2±2k1k2.{\displaystyle k_{4}=k_{1}+k_{2}\pm 2{\sqrt {k_{1}k_{2}}}.} (3)

Если две окружности заменить прямыми, касание между двумя окружностями заменяется параллельностью двух прямых. Две другие оставшиеся окружности должны быть равны. В этом случае, с k₂ = k₃ = 0, уравнение (2) становится тривиальным

k4=k1.{\displaystyle \displaystyle k_{4}=k_{1}.}

Невозможно заменить три окружности прямыми, поскольку одна окружность и три прямые не могут касаться друг друга попарно. Теорема Декарта неприменима также к случаю, когда все четыре окружности касаются друг друга в одной точке.

Ещё один специальный случай — когда k_i являются квадратами,

(v2+x2+y2+z2)2=2(v4+x4+y4+z4){\displaystyle (v^{2}+x^{2}+y^{2}+z^{2})^{2}=2\,(v^{4}+x^{4}+y^{4}+z^{4})}

Эйлер показал, что эквивалентно тройке пифагоровых троек,

(2vx)2+(2yz)2=(v2+x2−y2−z2)2{\displaystyle (2vx)^{2}+(2yz)^{2}=\,(v^{2}+x^{2}-y^{2}-z^{2})^{2}}

(2vy)2+(2xz)2=(v2−x2+y2−z2)2{\displaystyle (2vy)^{2}+(2xz)^{2}=\,(v^{2}-x^{2}+y^{2}-z^{2})^{2}}

(2vz)2+(2xy)2=(v2−x2−y2+z2)2{\displaystyle (2vz)^{2}+(2xy)^{2}=\,(v^{2}-x^{2}-y^{2}+z^{2})^{2}}

и может быть задано параметрическое представление. Если выбрать отрицательный знак кривизны,

(−v2+x2+y2+z2)2=2(v4+x4+y4+z4){\displaystyle (-v^{2}+x^{2}+y^{2}+z^{2})^{2}=2\,(v^{4}+x^{4}+y^{4}+z^{4})}

уравнение можно представить в виде хорошо известного параметрического решения^[3],

[v,x,y,z]=[2(ab−cd)(ab+cd),(a2+b2+c2+d2)(a2−b2+c2−d2),2(ac−bd)(a2+c2),2(ac−bd)(b2+d2)]{\displaystyle [v,x,y,z]=\,[2(ab-cd)(ab+cd),(a^{2}+b^{2}+c^{2}+d^{2})(a^{2}-b^{2}+c^{2}-d^{2}),2(ac-bd)(a^{2}+c^{2}),2(ac-bd)(b^{2}+d^{2})]},

где

a4+b4=c4+d4{\displaystyle a^{4}+b^{4}=\,c^{4}+d^{4}}.

Для определения окружности полностью нужно знать не только её радиус (или кривизну), но нужно ещё знать и её центр. Соответствующее уравнение лучше всего написать, когда координаты (x, y) представлены в виде комплексного числа z = x + iy. Уравнение тогда выглядит подобно уравнению в теореме Декарта и поэтому называется комплексной теоремой Декарта.

Если даны четыре окружности с кривизнами k_i и центрами z_i (i = 1…4), вдобавок к равенству (1) выполняется следующее равенство:

(k1z1+k2z2+k3z3+k4z4)2=2(k12z12+k22z22+k32z32+k42z42).{\displaystyle (k_{1}z_{1}+k_{2}z_{2}+k_{3}z_{3}+k_{4}z_{4})^{2}=2\,(k_{1}^{2}z_{1}^{2}+k_{2}^{2}z_{2}^{2}+k_{3}^{2}z_{3}^{2}+k_{4}^{2}z_{4}^{2}).} (4)

После того, как k₄ будет найдено при помощи равенства (2), можно начать вычисление z₄ путём изменения уравнения (4) к виду, похожему на (2):

z4=z1k1+z2k2+z3k3±2k1k2z1z2+k2k3z2z3+k1k3z1z3k4.{\displaystyle z_{4}={\frac {z_{1}k_{1}+z_{2}k_{2}+z_{3}k_{3}\pm 2{\sqrt {k_{1}k_{2}z_{1}z_{2}+k_{2}k_{3}z_{2}z_{3}+k_{1}k_{3}z_{1}z_{3}}}}{k_{4}}}.}

Снова, в общем случае, имеется два решения для z₄, соответствующие двум решениям для k₄.

Обобщение для n-мерного пространства иногда упоминается как теорема Содди-Госсе, хотя это сделано уже в 1886 Лахланом (R. Lachlan). В n-мерном евклидовом пространстве максимальное число взаимно касающихся (n — 1)-мерных сфер равно n + 2. Например, в 3-мерном пространстве могут взаимно касаться пять сфер. Кривизны гиперсфер удовлетворяют уравнению

(∑i=1n+2ki)2=n∑i=1n+2ki2{\displaystyle \left(\sum _{i=1}^{n+2}k_{i}\right)^{2}=n\,\sum _{i=1}^{n+2}k_{i}^{2}}

и случай k_i = 0 соответствует гиперплоскости, точно как в двумерном случае.

Хотя нет 3-мерных аналогов комплексным числам, связь между местоположениями центров можно представить в виде матричных уравнений^[4].