Знак подобия в геометрии
Определение и знак подобия в геометрии
ОПРЕДЕЛЕНИЕ Два треугольника и называются подобными, если у них равные углы и пропорциональные стороны.Обозначают подобие треугольников знаком «».
Пример. (читают: треугольник подобен треугольнику ).
Коэффициент подобия треугольников и знак подобия
Иногда над знаком подобия ставят коэффициент подобия треугольников, т.е. .
Знак «» представляет собой типографский знак «тильда», который изображается в виде волнистой черты. Этот знак может быть как надстрочным, так и междустрочным.
В математике «тильда» используется для обозначения различных видов отношений эквивалентности, в частности, отношения подобия.
Знак «тильда» (или «двойная тильда» ), который стоит перед числом может означать «примерно», «приблизительно равно».
В алгебре высказываний знак «» обозначает логическую операцию «эквиваленция».
Если знак «тильда» сочетать со знаком равенства: «», то он будет обозначать отношение конгруэнтности.
Также знак «тильда» активно используется в информатике и вычислительной технике. Например, в редакторе Tex этот знак означает «неразрывный пробел».
ru.solverbook.com
Знак подобия в геометрии ℹ️ определение, правило обозначения подобия треугольников, значение коэффициента подобия в доказательстве теоремы
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
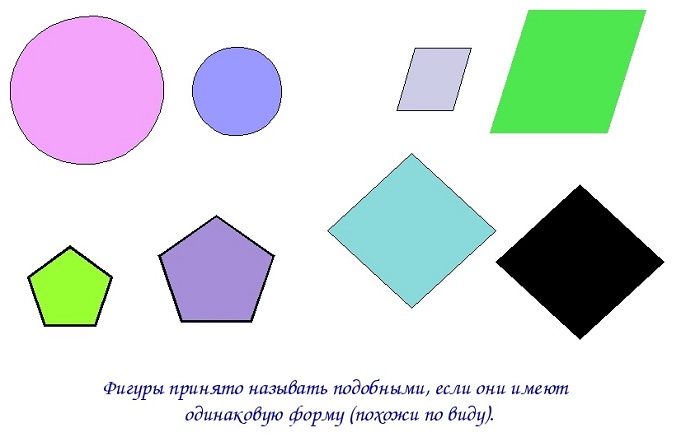
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
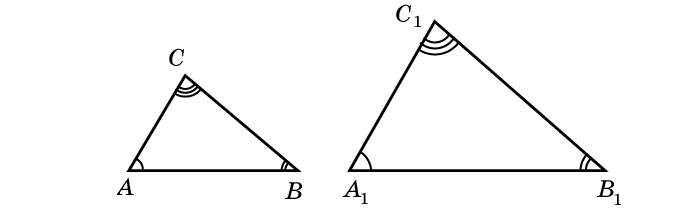
∆ABC ~ ∆A1B1C1 — треугольники ABC и A1B1C1 подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
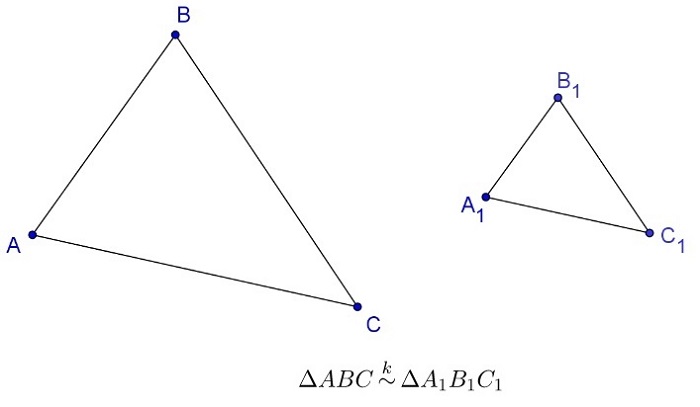
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком ~ обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
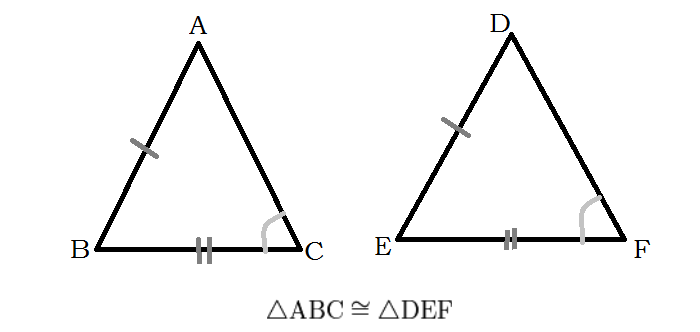
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
Утверждения:
-
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
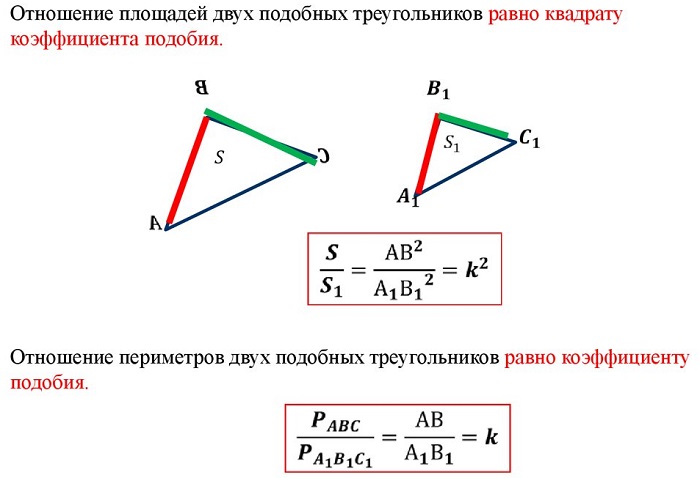
-
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
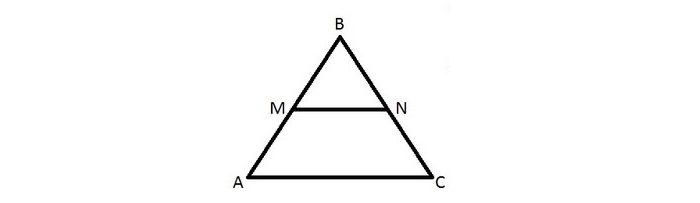
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
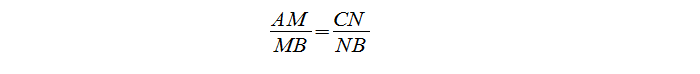
Отсюда делаем вывод, что ∆MBN ~ ∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»

_____________________________________________________________________
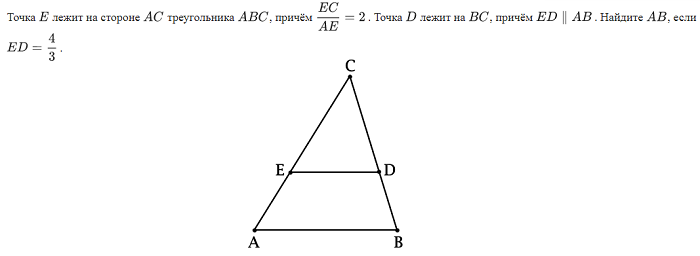

Подобие общих фигур. Видеоурок. Геометрия 8 Класс
Как мы уже знаем, фигурой в геометрии называется множество точек на плоскости. Прямая, отрезок, луч, треугольник, окружность, квадрат и так далее – всё это примеры геометрических фигур.
В повседневной жизни нас с вами окружают множество различных предметов. Часть из них имеют одинаковые размеры и одинаковую форму. Например, две одинаковые ручки или две одинаковых монеты и т.д. В геометрии фигуры, имеющие одинаковые размеры и форму, называются равными фигурами.
Из этого определения следует, например, что если прямоугольник и квадрат имеют равные площади, то это не значит, что они являются равными фигурами, так как это разные по форме фигуры. Другой пример: любые две окружности имеют одну и ту же форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры. Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами.
Следует отметить, что не все фигуры можно сравнивать. Нельзя определить равенство прямых, т. к. любая прямая бесконечна и, следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца.
Если же мы имеем дело с произвольными фигурами, то иногда даже сложно определить, имеют ли они одинаковую форму. Таким образом, нужно иметь надежный метод сравнения фигур. Он заключается в следующем: две геометрические фигуры называются равными, если их можно совместить наложением.
Но как быть в том случае, когда, скажем, длина стороны треугольника равна  км? В данном случае можно воспользоваться признаками равенства треугольников, которые мы рассматривали на предыдущих уроках. Смысл этих признаков в следующем: равенство трех элементов треугольников гарантирует равенство самих треугольников, а значит, и равенство остальных элементов, которые совместятся при наложении (биссектрис, высот, медиан).
км? В данном случае можно воспользоваться признаками равенства треугольников, которые мы рассматривали на предыдущих уроках. Смысл этих признаков в следующем: равенство трех элементов треугольников гарантирует равенство самих треугольников, а значит, и равенство остальных элементов, которые совместятся при наложении (биссектрис, высот, медиан).
А что если форму оставить без изменений, а все размеры пропорционально изменить (увеличить или уменьшить в одинаковое количество раз)?
Рассмотрим данную ситуацию на примере треугольника.
Пример 1
Пусть дан правильный треугольник 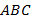 со стороной
со стороной 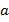 (см. рис. 1).
(см. рис. 1).
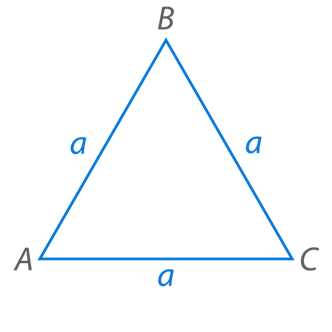
Рис. 1. Правильный треугольник 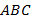
Уменьшив стороны треугольника 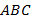 в
в 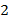 раза, получим правильный треугольник
раза, получим правильный треугольник 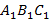 со стороной
со стороной 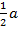 (см. рис. 2). То есть форма треугольника осталась прежней, а все размеры изменились (уменьшились) в
(см. рис. 2). То есть форма треугольника осталась прежней, а все размеры изменились (уменьшились) в 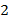
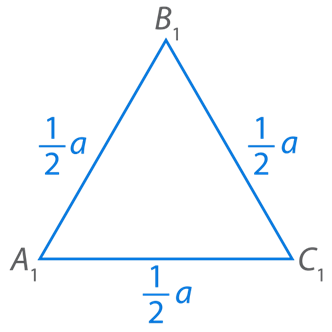
Рис. 2. Правильный треугольник 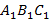 с уменьшенными сторонами
с уменьшенными сторонами
Доказательство:
Такой треугольник мы уже встречали на предыдущих уроках. Это треугольник, вершины которого лежат на серединах сторон исходного треугольника (см. рис. 3).
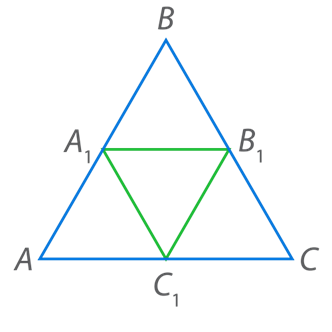
Рис. 3. Иллюстрация к доказательству
То есть из исходного правильного треугольника мы получили другой правильный треугольник, длина стороны которого уменьшилась в 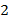 раза.
раза.
Такие треугольники в геометрии называются подобными.
Обозначение: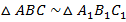 .
.
Коэффициент подобия – это число, равное отношению сходственных сторон в подобных фигурах. В нашем случае коэффициент подобия равен  .
.
Обозначение: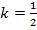 .
.
Пример 2
Дом на большом расстоянии имеет форму прямоугольника. Если постепенно приближаться к нему можно заметить, что его форма не меняется, но его размеры увеличиваются. Из этого можно сделать вывод, что его размеры изменяются в одинаковое число раз. Это ещё один пример подобных фигур.
Пример 3
Подобие фигур также используется при нанесении местности на карту. Возьмем, например, Крым и его изображение на карте с масштабом  . Понятно, что форма Крыма на карте аналогична реальной форме, но размеры изменены в
. Понятно, что форма Крыма на карте аналогична реальной форме, но размеры изменены в 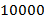 раз.
раз.
Таковы примеры подобных фигур – фигур, которые имеют одинаковую форму, но разные размеры. Причем размеры изменяются в одно и то же число раз.
Можно сформулировать признаки подобия треугольников. Эти признаки позволяют по некоторой информации об исходных треугольниках получить более подробную (дополнительную) информацию о них.
Пример 4
Пусть есть 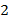 подобных треугольника
подобных треугольника 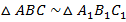 с коэффициентом подобия
с коэффициентом подобия  . Тогда можно утверждать, что соотношение длин соответствующих сторон треугольников пропорционально
. Тогда можно утверждать, что соотношение длин соответствующих сторон треугольников пропорционально  . То есть:
. То есть:  . Как и в случае признаков равенства, гарантируется пропорциональность соответствующих элементов треугольников (медиан, биссектрис, высот и т.д.).
. Как и в случае признаков равенства, гарантируется пропорциональность соответствующих элементов треугольников (медиан, биссектрис, высот и т.д.).
Рассмотрим еще один подобный пример.
Пример 5
Предположим, что коэффициент подобия треугольников 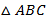 и
и  равен
равен 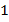 . Тогда для них можно записать следующее соотношение:
. Тогда для них можно записать следующее соотношение: 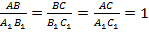 . Из этого следует, что
. Из этого следует, что  . Как мы уже знаем, по третьему признаку эти треугольники будут равными (Второй и третий признаки равенства треугольников). Отсюда можно сделать вывод, что равенство фигур является частным случаем подобия фигур с коэффициентом
. Как мы уже знаем, по третьему признаку эти треугольники будут равными (Второй и третий признаки равенства треугольников). Отсюда можно сделать вывод, что равенство фигур является частным случаем подобия фигур с коэффициентом 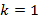 .
.
Признаки подобия фигур, в частности признаки подобия треугольников, являются полезными приемами в математике, они применяются для упрощения и решения множества задач. Однако для изучения этих признаков необходимо перевести некоторые понятия на строгий математический язык.
Пропорциональные отрезки
Понятия «отношение» и «пропорциональность» играют важную роль в изучении признаков подобия фигур.
Для начала рассмотрим понятие отношения отрезков на примере отрезков 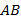 и
и  (см. рис. 4).
(см. рис. 4).
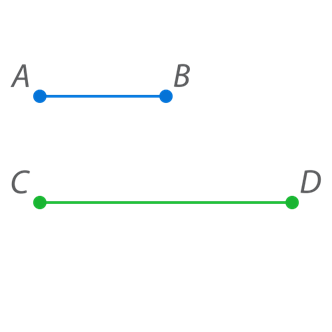
Рис. 4. Отрезки 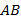 и
и 
Определение
Отношение длин отрезков 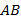 и
и  называется отношением отрезков
называется отношением отрезков 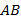 и
и  .
.
Рассмотрим задачу на данное определение.
Задача 1
Дано
Два отрезка 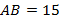 и
и 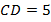
Найти
Отношение отрезков 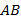 и
и 
Решение
Поскольку отношение отрезков – это отношение длин соответствующих отрезков, то имеем:

Ответ: .
.
Отметим, что отношение отрезков – это безразмерная величина.
Теперь предположим, что отношение пары отрезков 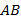 и
и  равно отношению пары других отрезков
равно отношению пары других отрезков 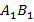 и
и 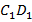 . Это записывается следующим образом:
. Это записывается следующим образом:

В таком случае говорят о пропорциональности отрезков. А именно: отрезки 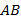 и
и  пропорциональны отрезкам
пропорциональны отрезкам 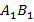 и
и 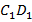 соответственно.
соответственно.
По свойству пропорции  и
и 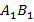 можно поменять местами:
можно поменять местами:  . От этого смысл выражения не поменяется.
. От этого смысл выражения не поменяется.
Пропорциональные отрезки встречаются в формулировке обобщенной теоремы Фалеса (Задачи на параллелограмм).
Теорема Фалеса
Стороны угла рассекаются параллельными прямыми на пропорциональные части (см. рис.5). То есть:
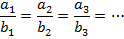
Аналогичное соотношение можно записать и для суммы длин отрезков:
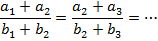
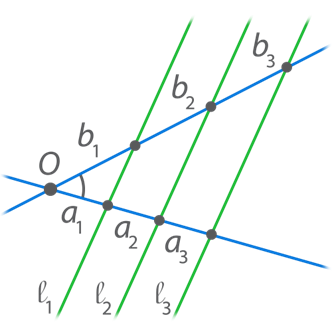
Рис. 5. Иллюстрация к теореме Фалеса
Рассмотрим два треугольника 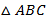 и
и  , у которых соответствующие углы равны (см. рис. 6):
, у которых соответствующие углы равны (см. рис. 6):
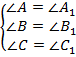
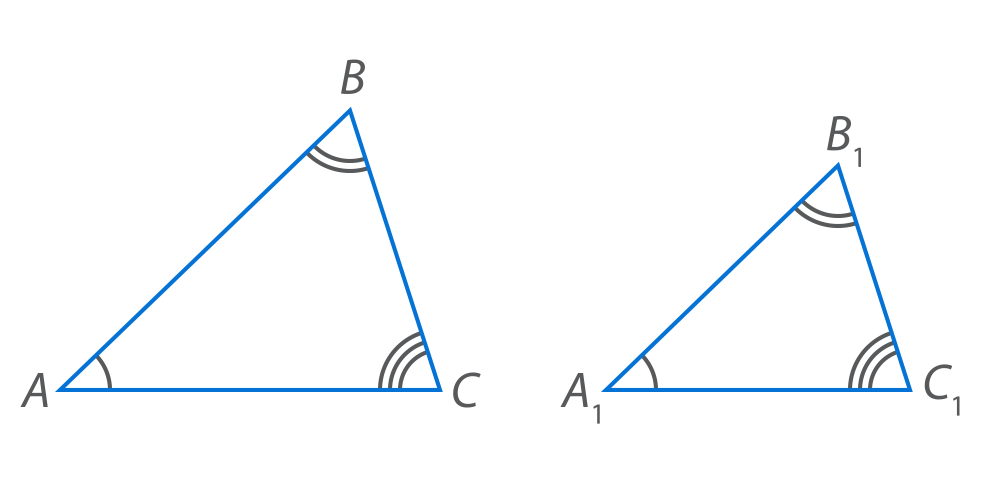
Рис. 6. Треугольники с равными углами
Стороны, которые лежат против равных углов треугольников, называются сходственными.
Перечислим сходственные стороны: 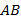 и
и 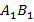 (лежат против равных углов
(лежат против равных углов 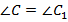 ),
),  и
и 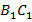 (лежат против равных углов
(лежат против равных углов 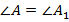 ),
),  и
и 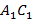 (лежат против равных углов
(лежат против равных углов 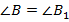 ).
).
Определение
Два треугольника 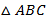 и
и  называются подобными, если соответствующие углы равны, а сходственные стороны – пропорциональны:
называются подобными, если соответствующие углы равны, а сходственные стороны – пропорциональны:

Причем 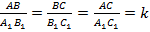 , где
, где 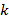 – это коэффициент подобия треугольников.
– это коэффициент подобия треугольников.
Оказывается, можно ограничиться лишь некоторыми из этих равенств чтобы гарантировать факт подобия. В этом заключается суть признаков подобия треугольников, которые подробно будут рассмотрены на следующих уроках.
Можно заметить, что пропорциональные отрезки играют важную роль в определении подобных треугольников. Рассмотрим задачу на пропорциональность отрезков.
Задача на пропорциональность отрезков
Теорема
Биссектриса угла треугольника рассекает противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Докажем эту теорему.
Дано
Произвольный треугольник 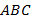 ,
, 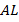 – биссектриса угла
– биссектриса угла  .
.
Доказать
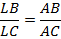
Доказательство
Запишем выражения для площадей образовавшихся треугольников 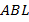 и
и  . Для этого опустим высоту из вершины
. Для этого опустим высоту из вершины  .Выполним рисунок к задаче (см. рис. 1).
.Выполним рисунок к задаче (см. рис. 1).
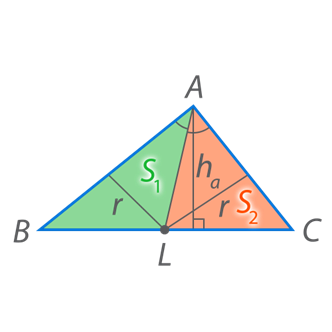
Рис. Иллюстрация к доказательству теоремы
Поскольку площадь треугольника равна половине произведения основания на высоту получаем: 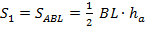 ,
, 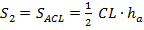 . Теперь найдем отношение этих площадей:
. Теперь найдем отношение этих площадей:
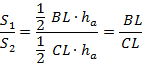
С другой стороны, биссектриса – это геометрическое место точек, равноудаленных от сторон угла. Этим свойством обладают все точки, принадлежащие биссектрисе, в том числе точка 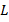 . Поэтому расстояние от точки
. Поэтому расстояние от точки 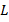 до сторон одинаковое, обозначим его
до сторон одинаковое, обозначим его 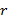 . Тогда высоты треугольников
. Тогда высоты треугольников 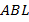 и
и  , опущенные к соответствующим основаниям
, опущенные к соответствующим основаниям 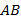 и
и  , равны
, равны 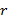 . Можно переписать отношение площадей этих треугольников:
. Можно переписать отношение площадей этих треугольников:

Левые части этих двух равенств равна, значит и правые часть также равны:
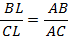
Теорема доказана.
На данном уроке мы рассмотрели подобие фигур, вспомнили признаки равенства треугольников, дали определение подобным треугольникам. Вспомнили о пропорциональности отрезков, теорему Фалеса и их роль в решении данных задач.
Список рекомендованной литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Пол
interneturok.ru
Подобие Википедия
У этого термина существуют и другие значения, см. Подобие (значения). Подобные фигуры на рисунке имеют одинаковые цвета
Подобные фигуры на рисунке имеют одинаковые цветаПодо́бие — преобразование евклидова пространства, при котором для любых двух точек A{\displaystyle A}, B{\displaystyle B} и их образов A′{\displaystyle A’}, B′{\displaystyle B’} имеет место соотношение |A′B′|=k⋅|AB|{\displaystyle |A’B’|=k\cdot |AB|}, при некотором фиксированном k≠0{\displaystyle k\neq 0}, называемым коэффициентом подобия.
Понятие подобия определяется аналогично для метрических, для римановых пространств (см. раздел Обобщения).
Содержание
- 1 История
- 2 Примеры
- 3 Связанные определения
- 4 Метод подобия
- 5 Свойства
- 6 Обобщения
- 7 См. также
- 8 Примечания
- 9 Ссылки
История[ | ]
Подобные фигуры рассматривались в Древней Греции в V—IV веках до нашей эры; они появляются в трудах Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и в VI книге «Начал» Евклида.
Примеры[ | ]
- Каждая гомотетия является подобием.
- Каждое движение (в том числе и тождественное) также можно рассматривать как преобразование подобия с коэффициентом k=1{\displaystyle k=1}.
Связанные определения[ | ]
- Фигура F{\displaystyle F} называется подобной фигуре
ru-wiki.ru
Подобие — это… Что такое Подобие?
Подобие — преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где — положительное число, называемое коэффициентом подобия.
Примеры
- Каждая гомотетия является подобием.
- Каждое движение (в том числе и тождественное) также можно рассматривать как преобразование подобия с коэффициентом .
 Подобные фигуры на рисунке имеют одинаковые цвета.
Подобные фигуры на рисунке имеют одинаковые цвета.Связанные определения
- Фигура называется подобной фигуре , если существует преобразование подобия, при котором .
Свойства
- Подобие есть взаимно однозначное отображение евклидова пространства на себя.
- Подобие сохраняет порядок точек на прямой, то есть если точка лежит между точками , и , , — соответствующие их образы при некотором подобии, то также лежит между точками и .
- Точки, не лежащие на прямой, при любом подобии переходят в точки, не лежащие на одной прямой.
- Подобие преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.
- При подобии угол сохраняет величину.
- Подобие с коэффициентом , преобразующее каждую прямую в параллельную ей прямую, является гомотетией с коэффициентом или .
- Каждое подобие можно рассматривать как композицию движения и некоторой гомотетии с положительным коэффициентом.
- Подобие называется собственным (несобственным), если движение является собственным (несобственным). Собственное подобие сохраняет ориентацию фигур, а несобственное — изменяет ориентацию на противоположную.
- Два треугольника являются подобными, если
- Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).
Обобщения
Аналогично определяется подобие (с сохранением указанных выше свойств) в 3-мерном евклидовом пространстве, а также в n-мерном евклидовом и псевдоевклидовом пространствах.
В метрических пространствах так же, как в -мерных римановых, псевдоримановых и финслеровых пространствах подобие определяется как преобразование, переводящее метрику пространства в себя с точностью до постоянного множителя.
Совокупность всех подобий n-мерного евклидова, псевдоевклидова, риманова, псевдориманова или финслерова пространства составляет -членную группу преобразований Ли, называемой группой подобных (гомотетических) преобразований соответствующего пространства. В каждом из пространств указанных типов -членная группа подобных преобразований Ли содержит -членную нормальную подгруппу движений.
См. также
Ссылки
dic.academic.ru
Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞
Нажмите, чтобы скопировать и вставить символ
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
- знаки операций – сложение, вычитание, деление, умножение, сумма, тождество;
- символы интегралов – двойные, тройные, интеграл по объему, поверхности, с правым и левым обходом;
- знаки сравнения – больше, меньше, равно;
- геометрические символы – отображение угла, пропорции, диаметра;
- геометрические фигуры;
- знак извлечения из корня, степень;
- иные символы – бесконечность, множество, квантор существования.
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциуму Юникода не чужды проблемы учёных, поэтому в таблицу было включено множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах математические символы, разнообразные математические символы-A, разнообразные математические символы-B, дополнительные математические операторы. Буквы для формул можно взять в наборе греческие буквы и блоке математические буквенно-цифровые символы.
Числа для степеней составляются из маленьких цифр. Там же собраны дроби.
unicode-table.com
знак подобия — это… Что такое знак подобия?
ЗНАК — материальный объект (артефакт), выступающий в коммуникативном или трансляционном процессе аналогом другого объекта (предмета, свойства, явления, понятия, действия), замещающий его. 3. является осн. средством культуры, с его помощью… … Энциклопедия культурологии
ЗНАК — традиционно материальный, чувственно воспринимаемый предмет (событие, действие или явление), выступающий в познании в качестве указания, обозначения или представителя другого предмета, события, действия, субъективного образования. Предназначен… … История Философии: Энциклопедия
ЗНАК — материальный, чувственно воспринимаемый предмет (событие, действие или явление), выступающий в познании в качестве указания, обозначения или представителя другого предмета, события, действия, субъективного образования. Предназначен для… … Новейший философский словарь
Знак равенства — … Википедия
ЗНАК — традиционно материальный, чувственно воспринимаемый предмет (событие, действие или явление), выступающий в познании в качестве указания, обозначения или представителя другого предмета, события, действия, субъективного образования. Предназначен… … История Философии: Энциклопедия
ЗНАК — предмет, служащий замещению и представлению другого предмета (свойства или отношения) и используемый для хранения, переработки и передачи сообщения. 3. это интерсубъективный посредник, структур медиатор в обществе. В индоевропейских языках,… … Современный философский словарь
Иконический знак — Иконический знак: знак, отражающий образ технического объекта в картинно воспринимаемом упрощенно графическом виде с определенной степенью подобия (соответствия) этому техническому объекту (в бестекстурном или текстурном исполнении)… Источник:… … Официальная терминология
иконический знак — 3.8 иконический знак: Знак, отражающий образ технического объекта в картинно воспринимаемом упрощенно графическом виде с определенной степенью подобия (соответствия) этому техническому объекту (в бестекстурном или текстурном исполнении). Источник … Словарь-справочник терминов нормативно-технической документации
тильда — (Tilde) I (Tilde) Один из верхних акцентов [надстрочный или подстрочный знак]. Диакритический знак в виде волнистой черты. Применяется над гласными во вьетнамском, португальском, эстонском и др. языках и над согласными в испанском, кечуа,… … Шрифтовая терминология
tilde — Тильда (Tilde) I (Tilde) Один из верхних акцентов [надстрочный или подстрочный знак]. Диакритический знак в виде волнистой черты. Применяется над гласными во вьетнамском, португальском, эстонском и др. языках и над согласными в испанском,… … Шрифтовая терминология
СИМВОЛ — (от греч. знак, примета) 1) в искусственных формализованных языках понятие, тождественное знаку; 2) в эстетике и философии искусства универсальная категория, отражающая специфику образного освоения жизни искусством содержат,… … Энциклопедия культурологии
universal_ru_en.academic.ru